SUMMARY
In many situations in survival analysis, it may happen that a fraction of individuals will never experience the event of interest: they are considered to be cured. The promotion time cure model takes this into account. We consider the case where one or more explanatory variables in the model are subject to measurement error, which should be taken into account to avoid biased estimators. A general approach is the simulation-extrapolation algorithm, a method based on simulations which allows one to estimate the effect of measurement error on the bias of the estimators and to reduce this bias. We extend this approach to the promotion time cure model. We explain how the algorithm works, and we show that the proposed estimator is approximately consistent and asymptotically normally distributed, and that it performs well in finite samples. Finally, we analyse a database in cardiology: among the explanatory variables of interest is the ejection fraction, which is known to be measured with error.
Keywords: Bias correction, Cure fraction, Measurement error, Promotion time cure model, Semiparametric method.
1. INTRODUCTION
When analysing time-to-event data, it often happens that a certain proportion of subjects will never experience the event of interest. For example, in medical studies where one is interested in the time until recurrence of a certain disease, it is known that, for some diseases, some patients will never suffer a relapse. In studies in econometrics on duration of unemployment, some unemployed people will never find a new job, and in sociological studies on the age at which a person marries, some people will stay unmarried for their whole life. Other examples can be found in finance, marketing, demography, and education, where each time there is a certain proportion of subjects whose time to event is infinite; they are said to be cured. Since classical survival models implicitly assume that all individuals will eventually experience the event of interest, they cannot be used in such contexts, as they would lead to incorrect results such as overestimation of the survival of the non-cured subjects. This is why specific models, called cure models, have been developed.
In order to model the impact of a set of covariates on the time-to-event variable, two main streams of cure models, as well as proposals that overarch both, can be found in the literature. The first is the so-called mixture cure model, which supposes that the conditional survival function is 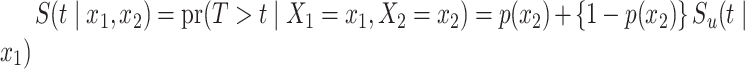 , where
, where 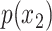 is the probability of being cured for a given vector of covariates
is the probability of being cured for a given vector of covariates 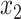 , and
, and 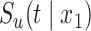 is the conditional survival function of the non-cured subjects, where
is the conditional survival function of the non-cured subjects, where 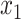 is another set of covariates, possibly with common components. This model has been studied by, among others, Boag (1949), Berkson & Gage (1952), Farewell (1982), Kuk & Chen (1992), Taylor (1995), Peng & Dear (2000), Sy & Taylor (2000), Peng (2003) and Lu (2008). A second class of models is based on an adaptation of the Cox (1972) model to allow for a cure fraction. It is called the class of promotion time cure models and supposes that
is another set of covariates, possibly with common components. This model has been studied by, among others, Boag (1949), Berkson & Gage (1952), Farewell (1982), Kuk & Chen (1992), Taylor (1995), Peng & Dear (2000), Sy & Taylor (2000), Peng (2003) and Lu (2008). A second class of models is based on an adaptation of the Cox (1972) model to allow for a cure fraction. It is called the class of promotion time cure models and supposes that
| (1) |
where 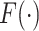 is a proper baseline cumulative distribution function and
is a proper baseline cumulative distribution function and 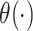 captures the effect of the covariates on the conditional survival function. Unlike the mixture cure model, this formulation has a proportional hazards structure. One often chooses
captures the effect of the covariates on the conditional survival function. Unlike the mixture cure model, this formulation has a proportional hazards structure. One often chooses 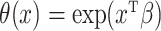 , where the first component of the
, where the first component of the 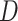 -dimensional covariate
-dimensional covariate 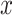 is supposed to be 1, in order to include an intercept in the model. The Cox model without cure fraction does not include an intercept, since it supposes that
is supposed to be 1, in order to include an intercept in the model. The Cox model without cure fraction does not include an intercept, since it supposes that 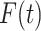 tends to infinity when
tends to infinity when 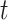 tends to infinity, and an intercept would therefore not be identifiable. References on the promotion time cure model include Yakovlev & Tsodikov (1996), Tsodikov (1998a,b, 2001), Chen et al. (1999), Ibrahim et al. (2001), Tsodikov et al. (2003), Zeng et al. (2006) and Carvalho Lopes & Bolfarine (2012).
tends to infinity, and an intercept would therefore not be identifiable. References on the promotion time cure model include Yakovlev & Tsodikov (1996), Tsodikov (1998a,b, 2001), Chen et al. (1999), Ibrahim et al. (2001), Tsodikov et al. (2003), Zeng et al. (2006) and Carvalho Lopes & Bolfarine (2012).
In this paper we consider the promotion time cure model (1) in which we leave 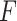 unspecified. We suppose that the survival time
unspecified. We suppose that the survival time 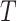 is subject to random right censoring, i.e., instead of observing
is subject to random right censoring, i.e., instead of observing 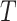 we observe
we observe 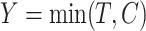 and
and 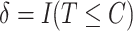 , where the censoring time
, where the censoring time 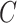 is independent of
is independent of 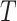 given
given 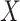 . An immediate consequence is that for the censored observations, we do not observe whether they are cured or not cured, the latter observations being called susceptible.
. An immediate consequence is that for the censored observations, we do not observe whether they are cured or not cured, the latter observations being called susceptible.
In addition to being exposed to censoring, the data can also be subject to another type of incompleteness. As is often the case in practice, some continuous covariates are subject to measurement error. For instance, in medical studies the error can be caused by imprecise medical instruments, and in econometric studies variables like welfare or income often cannot be measured precisely. Although measurement error is rarely taken into account, ignoring it can lead to incorrect conclusions (Carroll et al., 2006). In order to deal with this measurement error, some assumptions about its form are necessary. We consider a classical additive measurement error model for the continuous covariates, so that we have, for the whole vector of covariates,
| (2) |
where 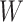 is the vector of observed covariates and
is the vector of observed covariates and 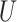 is the vector of measurement errors. We further assume that
is the vector of measurement errors. We further assume that 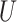 is independent of
is independent of 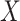 and follows a continuous distribution with mean zero and known covariance matrix
and follows a continuous distribution with mean zero and known covariance matrix 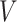 , where the elements of
, where the elements of 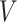 corresponding to covariates with no measurement error, including the noncontinuous covariates and possibly some continuous ones, are set to 0. It is also assumed that
corresponding to covariates with no measurement error, including the noncontinuous covariates and possibly some continuous ones, are set to 0. It is also assumed that 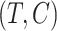 and
and 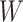 are independent given
are independent given 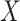 . When
. When 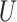 is assumed to be normally distributed, (2) is the measurement error model studied, for example, by Cook & Stefanski (1994) and Ma & Yin (2008).
is assumed to be normally distributed, (2) is the measurement error model studied, for example, by Cook & Stefanski (1994) and Ma & Yin (2008).
Methods designed to deal with measurement error in the covariates can be classified into structural modelling and functional modelling approaches (Carroll et al., 2006). In structural modelling, the distribution of the unobservable covariates 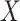 must be modelled, usually parametrically, while in functional modelling, no assumptions are made regarding the distribution of
must be modelled, usually parametrically, while in functional modelling, no assumptions are made regarding the distribution of 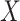 . When the distributional assumptions are met, the approaches of the first type yield higher efficiency. However, an obvious advantage of methods of the second type is their robustness with respect to possible misspecification of the distribution of
. When the distributional assumptions are met, the approaches of the first type yield higher efficiency. However, an obvious advantage of methods of the second type is their robustness with respect to possible misspecification of the distribution of 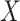 .
.
In this paper we use the so-called simulation-extrapolation, or simex, approach to correct for the measurement error. The basic idea of simex has two steps. In the first we consider increasing levels of measurement error, and simulate a large number of datasets for each level. At each level we estimate the vector 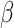 of regression coefficients ignoring the measurement error. In the second step we extrapolate the estimators corresponding to the different levels of error to the situation where the covariates are observed without error. This algorithm, proposed by Cook & Stefanski (1994), has a number of advantages; see §6. The method has been considered in many different contexts. In survival analysis, it has been used in the Cox model (Carroll et al., 2006), the Cox model with nonlinear effect of mismeasured covariates in a 2006 Johns Hopkins University working paper by Crainiceanu et al., the multivariate Cox model (Greene & Cai, 2004) and the frailty model (Li & Lin, 2003), but, as far as we know, not in cure models. It has also been applied to nonparametric regression (Carroll et al., 1999) and to general semiparametric problems (Apanasovich et al., 2009) where if
of regression coefficients ignoring the measurement error. In the second step we extrapolate the estimators corresponding to the different levels of error to the situation where the covariates are observed without error. This algorithm, proposed by Cook & Stefanski (1994), has a number of advantages; see §6. The method has been considered in many different contexts. In survival analysis, it has been used in the Cox model (Carroll et al., 2006), the Cox model with nonlinear effect of mismeasured covariates in a 2006 Johns Hopkins University working paper by Crainiceanu et al., the multivariate Cox model (Greene & Cai, 2004) and the frailty model (Li & Lin, 2003), but, as far as we know, not in cure models. It has also been applied to nonparametric regression (Carroll et al., 1999) and to general semiparametric problems (Apanasovich et al., 2009) where if 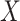 is mismeasured and
is mismeasured and 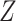 is measured exactly, then the loglikelihood is of the form
is measured exactly, then the loglikelihood is of the form 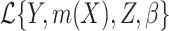 or
or 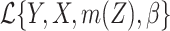 , with an unknown function
, with an unknown function 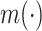 .
.
To the best of our knowledge, the problem considered in this paper has previously been addressed only by Ma & Yin (2008), who also studied a promotion time cure model with right-censored responses and mismeasured covariates. But instead of using the simex approach, they introduced a corrected score approach to deal with the measurement error in the covariates. Their approach yields consistent and asymptotically normal estimators when the measurement error variance is known and the error is normally distributed. However, their method only works for the specification 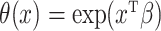 , while the simex algorithm can be used for any parametric version of
, while the simex algorithm can be used for any parametric version of 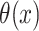 . Moreover, they do not study non-Gaussian measurement error in detail.
. Moreover, they do not study non-Gaussian measurement error in detail.
2. METHODOLOGY
Suppose that we have 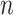 independent and identically distributed right-censored observations
independent and identically distributed right-censored observations 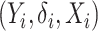 . We denote by
. We denote by 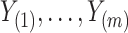 the
the 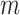 distinct ordered event times, so that
distinct ordered event times, so that 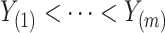 . We use model (1), where we consider
. We use model (1), where we consider 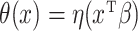 for some given function
for some given function 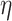 . Two examples are
. Two examples are 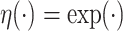 and
and 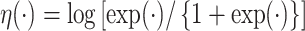 . We present the simex algorithm for the case where the error
. We present the simex algorithm for the case where the error 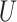 is normally distributed. However, as mentioned in §1, this is not essential, as the algorithm below remains valid without any modification, as long as the extrapolation function is correctly specified.
is normally distributed. However, as mentioned in §1, this is not essential, as the algorithm below remains valid without any modification, as long as the extrapolation function is correctly specified.
The general idea of the simex algorithm consists in adding successively increasing amounts of artificial noise to the covariates subject to measurement error, estimating the model without taking the measurement error into account, and extrapolating back to the case of no measurement error. Two types of parameters have to be chosen: the levels of added noise 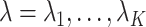 and the number
and the number 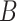 of simulations for each value of
of simulations for each value of 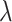 . Some common values are
. Some common values are 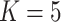 and
and 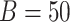 (Cook & Stefanski, 1994; Carroll et al., 1996).
(Cook & Stefanski, 1994; Carroll et al., 1996).
The simex algorithm for the promotion time cure model is as follows.
For 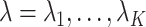 ,
, 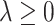 , and for
, and for 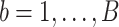 , we generate independent and identically distributed
, we generate independent and identically distributed 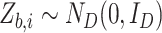 independently of the observed data and construct
independently of the observed data and construct 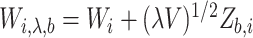 for each individual
for each individual  , where
, where  is the known covariance matrix of the error term, as defined in §1. The covariance matrix of the contaminated
is the known covariance matrix of the error term, as defined in §1. The covariance matrix of the contaminated  is
is
which converges to the zero matrix as 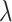 converges to
converges to 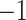 . We replace
. We replace 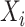 by
by 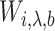 in the promotion time cure model, giving
in the promotion time cure model, giving
When the 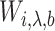 are known, this model is the standard promotion time cure model. We obtain the estimates
are known, this model is the standard promotion time cure model. We obtain the estimates 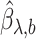 of
of 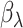 , by using a naive estimation method that does not take the measurement error into account.
, by using a naive estimation method that does not take the measurement error into account.
For 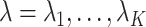 ,
, 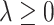 , we obtain
, we obtain 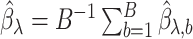 .
.
We then choose an extrapolant, e.g., linear, quadratic or fractional, for each parameter, i.e., for each element 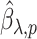 of the vector
of the vector 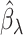 , as a function of the
, as a function of the 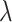 s:
s: 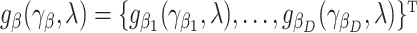 depending on a vector of parameters
depending on a vector of parameters 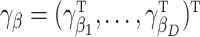 . In the case of the quadratic extrapolant, one obtains
. In the case of the quadratic extrapolant, one obtains
where 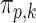 are the error terms in the extrapolant model, assumed to be independent and to have mean zero. We fit these parametric models for each
are the error terms in the extrapolant model, assumed to be independent and to have mean zero. We fit these parametric models for each 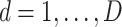 in order to obtain
in order to obtain 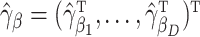 . In practice, this function is often an approximation of the true extrapolation function, which will then yield an estimator that converges in probability to some constant approximately equal to the true parameter (Cook & Stefanski, 1994). There are some cases in semiparametric models where the exact extrapolant is known: Cox regression, with
. In practice, this function is often an approximation of the true extrapolation function, which will then yield an estimator that converges in probability to some constant approximately equal to the true parameter (Cook & Stefanski, 1994). There are some cases in semiparametric models where the exact extrapolant is known: Cox regression, with 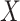 and
and 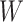 normally distributed and homoscedastic (Prentice, 1982), and the partially linear model
normally distributed and homoscedastic (Prentice, 1982), and the partially linear model 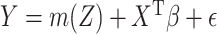 ,
, 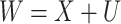 , with
, with  independent (Liang et al., 1999).
independent (Liang et al., 1999).
Finally, we obtain the simex estimated values
We use the results of Zeng et al. (2006) and Ma & Yin (2008) to estimate the model parameters 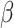 and
and 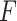 when there is no measurement error in the covariates. They show that the loglikelihood of the promotion time cure model without measurement error is
when there is no measurement error in the covariates. They show that the loglikelihood of the promotion time cure model without measurement error is
| (3) |
where 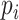 is the jump size of
is the jump size of 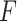 at
at 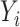 . We use
. We use 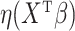 instead of the particular case
instead of the particular case 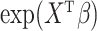 considered by the authors. As Zeng et al. (2006) explain, it can be shown that the nonparametric maximum likelihood estimator for
considered by the authors. As Zeng et al. (2006) explain, it can be shown that the nonparametric maximum likelihood estimator for 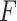 is a function with point masses at the distinct observed failure times
is a function with point masses at the distinct observed failure times 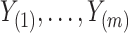 only. If
only. If 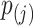 denotes the jump size of
denotes the jump size of 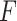 at
at 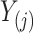 , then
, then 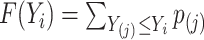 . Moreover, the authors also explain that, in order for this semiparametric model to be identifiable in
. Moreover, the authors also explain that, in order for this semiparametric model to be identifiable in 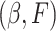 , we need a threshold
, we need a threshold 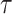 , called the cure threshold, such that all censored individuals with a censoring time greater than this threshold are treated as if they were known to be cured, i.e.,
, called the cure threshold, such that all censored individuals with a censoring time greater than this threshold are treated as if they were known to be cured, i.e., 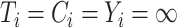 . In practice, the estimated baseline cumulative distribution function is forced to be
. In practice, the estimated baseline cumulative distribution function is forced to be 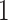 beyond the largest observed failure time,
beyond the largest observed failure time, 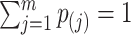 . This implies that no event can occur after this time: the cure threshold is then determined to be
. This implies that no event can occur after this time: the cure threshold is then determined to be 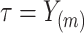 .
.
The parameters can then be estimated by solving the score equations related to the likelihood in which the baseline cumulative distribution function is replaced by a step function.
If interest also lies in estimating the baseline cumulative distribution function 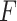 , exactly the same simex procedure can be applied to the
, exactly the same simex procedure can be applied to the 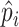 , yielding the
, yielding the 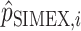 . In order to ensure that their sum is equal to
. In order to ensure that their sum is equal to 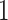 , each of them is divided by their sum:
, each of them is divided by their sum: 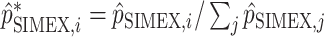 . Finally, we obtain
. Finally, we obtain 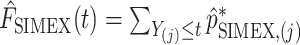 .
.
3. ASYMPTOTIC PROPERTIES
We present some theorems regarding consistency and asymptotic normality of the simex estimators of the regression parameters 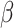 and the baseline cumulative distribution function
and the baseline cumulative distribution function 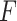 . Theorem 1 states their consistency; its proof can be found in the Supplementary Material. Theorem 2 establishes their asymptotic normality and is proved in the Appendix. Both results rely on the assumption that the true extrapolation function is known, which is rarely the case in practice. As explained by Cook & Stefanski (1994) and mentioned in §2, since the extrapolation function used in the algorithm is often an approximation to the true one, we will obtain an estimator which converges in probability to some constant that is approximately equal to the true parameter. This is sometimes called approximate consistency. In this case, in all the results that follow,
. Theorem 1 states their consistency; its proof can be found in the Supplementary Material. Theorem 2 establishes their asymptotic normality and is proved in the Appendix. Both results rely on the assumption that the true extrapolation function is known, which is rarely the case in practice. As explained by Cook & Stefanski (1994) and mentioned in §2, since the extrapolation function used in the algorithm is often an approximation to the true one, we will obtain an estimator which converges in probability to some constant that is approximately equal to the true parameter. This is sometimes called approximate consistency. In this case, in all the results that follow, 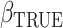 and
and 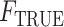 are replaced in the results by
are replaced in the results by 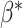 and
and 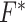 , the limiting values with this extrapolant. In the parametric case, when
, the limiting values with this extrapolant. In the parametric case, when 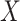 is scalar, with
is scalar, with 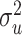 being the measurement error variance, the bias of a polynomial extrapolant of order
being the measurement error variance, the bias of a polynomial extrapolant of order 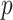 is
is 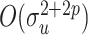 , see Cook & Stefanski (1994, p. 1317), although they only consider
, see Cook & Stefanski (1994, p. 1317), although they only consider 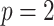 .
.
Here, we assume that the 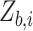 that are generated in the simulation step follow a truncated Gaussian distribution with large truncation limits, which will always be the case in practice. We also assume that the expectation of the loglikelihood has a unique maximizer, whether or not there is measurement error in the covariates.
that are generated in the simulation step follow a truncated Gaussian distribution with large truncation limits, which will always be the case in practice. We also assume that the expectation of the loglikelihood has a unique maximizer, whether or not there is measurement error in the covariates.
Theorem 1.
Under the regularity conditions (C1)–(C4) of Zeng et al. (2006), by replacing
that appears there by
(
) for each
, if the measurement error variance and the true extrapolant function are known, then, with probability 1,
Theorem 2.
Under the regularity conditions (C1)–(C4) of Zeng et al. (2006), by replacing
that appears there by
(
) for each
, if the measurement error variance and the true extrapolant function are known, then
converges in distribution to
, where
is given by (A1) in the Appendix. Moreover,
converges weakly to a zero-mean Gaussian process
whose covariance function is given by (A2) in the Appendix.
The regularity conditions (C1)–(C4) of Zeng et al. (2006) are the usual constraints pertaining to the independence of the right-censoring variable, the boundedness of the covariate, the compactness of the set of possible values for 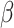 , the differentiability of the baseline cumulative distribution function and the monotonicity and differentiability of the link function
, the differentiability of the baseline cumulative distribution function and the monotonicity and differentiability of the link function 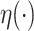 .
.
The variance of the simex estimator can be estimated using the method introduced by Stefanski & Cook (1995) and summarized, for example, in Carroll et al. (2006). The variance estimator can be computed as 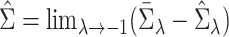 , where
, where  is the extrapolation function corresponding to
is the extrapolation function corresponding to 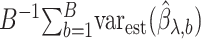 , where
, where 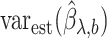 is the estimated covariance matrix of
is the estimated covariance matrix of 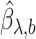 when using the variance estimator corresponding to the naive estimation method, and
when using the variance estimator corresponding to the naive estimation method, and 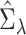 is the extrapolation function corresponding to
is the extrapolation function corresponding to 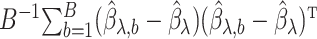 , i.e., the empirical covariance matrix of
, i.e., the empirical covariance matrix of 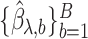 .
.
4. SIMULATION STUDIES
4.1. Settings
The objective of our first three simulation studies is to investigate the properties of the proposed estimator in finite samples and to compare it with the naive method based on (3), which does not take measurement error into account, and the corrected score method of Ma & Yin (2008).
In the next three subsections, we focus on our proposed estimator. In §4.5 and in the Supplementary Material, we present the results of simulation studies for examining the effect of the choice of the extrapolation function and of the grid of values of 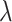 on the simex estimator. Subsections 4.6 and 4.7 contain results pertaining to the robustness of the simex estimator with respect to misspecification of the error distribution and variance.
on the simex estimator. Subsections 4.6 and 4.7 contain results pertaining to the robustness of the simex estimator with respect to misspecification of the error distribution and variance.
An extensive simulation study investigating the robustness of both the simex algorithm and the corrected score approach of Ma & Yin (2008) with respect to the assumptions of normal distribution and known variance of the error can be found in a 2016 article by A. Bertrand et al., available at http://hdl.handle.net/2078.1/171508.
In the following, for the simex algorithm, we used 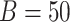 and
and 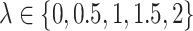 except in the simulations regarding the choice of this grid, and a quadratic extrapolant except in §4.5. The variables
except in the simulations regarding the choice of this grid, and a quadratic extrapolant except in §4.5. The variables 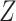 appearing in the simulation step of the algorithm are always taken to be Gaussian. For each setting, 500 simulated datasets were analysed.
appearing in the simulation step of the algorithm are always taken to be Gaussian. For each setting, 500 simulated datasets were analysed.
4.2. One mismeasured covariate
The first set of simulation studies that we conduct is the first in Ma & Yin (2008). They assume that the follow-up is infinite, and that the censoring distribution and the failure distribution have infinite support, so that each individual is known to be either cured, dead or censored, when 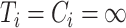 ,
, 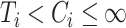 or
or 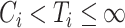 , respectively. The censored individuals for whom
, respectively. The censored individuals for whom 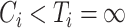 are actually cured. In such a case, a cure threshold is not needed for estimation. Each subject has a probability of
are actually cured. In such a case, a cure threshold is not needed for estimation. Each subject has a probability of 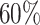 of having an infinite censoring time. Because of the infinite follow-up, this does not correspond to a realistic case, but is useful for assessing the proposed method in an ideal situation.
of having an infinite censoring time. Because of the infinite follow-up, this does not correspond to a realistic case, but is useful for assessing the proposed method in an ideal situation.
The model under study is
for 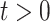 and we generate the data from this model with
and we generate the data from this model with 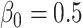 ,
, 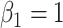 ,
, 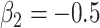 ,
, 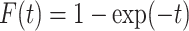 and
and 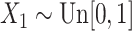 ,
, 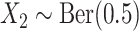 ;
; 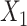 is subject to measurement error so that
is subject to measurement error so that 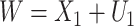 is observed, where
is observed, where 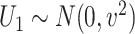 , with
, with 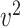 the only nonzero element of
the only nonzero element of 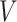 . Moreover, the censoring time
. Moreover, the censoring time 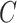 is independent of
is independent of 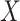 and of
and of 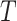 given
given 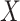 , and the finite censoring times follow an exponential distribution with mean
, and the finite censoring times follow an exponential distribution with mean 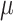 .
.
Eight different settings are obtained by considering two possible values for sample size, 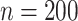 or
or 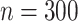 , variance of the measurement error,
, variance of the measurement error, 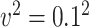 or
or 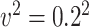 , and mean of the finite censoring times,
, and mean of the finite censoring times, 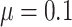 or
or 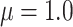 . The average cure rate, i.e., the rate of observations for which
. The average cure rate, i.e., the rate of observations for which 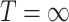 , is
, is 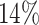 , the average proportion of subjects with
, the average proportion of subjects with 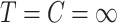 , considered cured for the estimation, is
, considered cured for the estimation, is 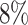 ; and the average censoring rate is
; and the average censoring rate is 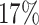 when
when 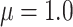 and
and 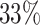 when
when 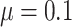 .
.
The results for the four settings with 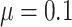 are summarized in Table 1, while those corresponding to
are summarized in Table 1, while those corresponding to 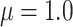 can be found in the Supplementary Material.
can be found in the Supplementary Material.
Table 1.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the settings with one mismeasured covariate, when 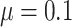
| Ma & Yin method | Naive method | Simex method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
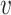
|
Estimate |
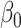
|

|
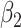
|
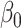
|
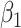
|
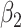
|
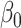
|
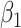
|
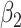
|
| 200 | 0.1 | Bias | -1.0 | 3.2 | -0.2 | 4.3 | -9.2 | 0.2 | -0.4 | 1.5 | -0.1 |
| Emp. var. | 5.3 | 13.2 | 4.1 | 4.7 | 9.9 | 4.0 | 5.2 | 12.8 | 4.1 | ||
| Est. var. | 5.3 | 13.0 | 3.6 | 4.6 | 9.8 | 3.6 | 5.2 | 12.4 | 3.6 | ||
| 95% cv | 94.6 | 94.8 | 93.6 | 93.6 | 93.4 | 93.8 | 94.2 | 94.2 | 93.8 | ||
| MSE | 5.3 | 13.3 | 4.1 | 4.8 | 10.8 | 4.0 | 5.2 | 12.8 | 4.1 | ||
| 200 | 0.2 | Bias | -3.0 | 8.5 | -0.5 | 14.2 | -31.5 | .7 | 3.6 | -7.6 | 0.1 |
| Emp. var. | 6.9 | 22.6 | 4.4 | 4.1 | 7.5 | 4.0 | 5.4 | 14.3 | 4.2 | ||
| Est. var. | 7.4 | 22.7 | 3.9 | 4.0 | 7.4 | 3.6 | 5.2 | 12.7 | 3.7 | ||
| 95% cv | 96.0 | 96.8 | 93.2 | 88.4 | 78.8 | 93.4 | 93.8 | 92.4 | 93.0 | ||
| MSE | 7.0 | 23.4 | 4.4 | 6.1 | 17.5 | 4.0 | 5.5 | 14.8 | 4.2 | ||
| 300 | 0.1 | Bias | -1.1 | 3.7 | -1.4 | 4.2 | -8.4 | -1.1 | -0.5 | 2.3 | -1.4 |
| Emp. var. | 3.9 | 9.4 | 2.6 | 3.4 | 7.1 | 2.5 | 3.8 | 9.0 | 2.6 | ||
| Est. var. | 3.5 | 8.7 | 2.4 | 3.1 | 6.5 | 2.4 | 3.4 | 8.3 | 2.4 | ||
| 95% cv | 95.6 | 94.4 | 96.6 | 93.4 | 93.2 | 96.6 | 95.4 | 94.2 | 96.6 | ||
| MSE | 3.9 | 9.5 | 2.6 | 3.6 | 7.8 | 2.5 | 3.8 | 9.1 | 2.6 | ||
| 300 | 0.2 | Bias | -2.1 | 6.8 | -1.8 | 14.2 | -31.0 | -0.6 | 3.6 | -6.9 | -1.3 |
| Emp. var. | 4.9 | 14.5 | 2.7 | 3.0 | 5.1 | 2.5 | 3.9 | 9.7 | 2.6 | ||
| Est. var. | 4.6 | 13.9 | 2.6 | 2.7 | 4.9 | 2.4 | 3.4 | 8.4 | 2.5 | ||
| 95% cv | 96.6 | 95.8 | 95.8 | 85.2 | 71.6 | 95.4 | 93.8 | 93.4 | 95.8 | ||
| MSE | 5.0 | 14.9 | 2.7 | 5.0 | 14.7 | 2.5 | 4.1 | 10.2 | 2.6 | ||
Emp. var., empirical variance; Est. var., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
The empirical and estimated variances are always quite close to each other, while both the corrected score and the simex approaches yield coverage probabilities close to the nominal 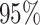 . Compared to the naive estimation method, both correction methods decrease the bias in the intercept and the parameter corresponding to the mismeasured covariate, but at the cost of a larger variance. Although the simex algorithm and the method of Ma & Yin (2008) cannot really be distinguished on the basis of the bias, the former leads to a smaller variance for
. Compared to the naive estimation method, both correction methods decrease the bias in the intercept and the parameter corresponding to the mismeasured covariate, but at the cost of a larger variance. Although the simex algorithm and the method of Ma & Yin (2008) cannot really be distinguished on the basis of the bias, the former leads to a smaller variance for 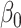 and
and 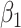 when
when 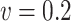 , and to similar variances when
, and to similar variances when 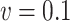 . This results in a mean squared error which is, when
. This results in a mean squared error which is, when 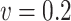 , the smallest for simex, compared to the naive and corrected score methods. When the measurement error variance is smaller, the naive method yields a smaller mean squared error than both correction methods. This is to be expected since bias correction methods have a larger variance than the naive method.
, the smallest for simex, compared to the naive and corrected score methods. When the measurement error variance is smaller, the naive method yields a smaller mean squared error than both correction methods. This is to be expected since bias correction methods have a larger variance than the naive method.
4.3. Two mismeasured covariates
We now introduce, in the previous setting, an additional covariate with measurement error. In this case, 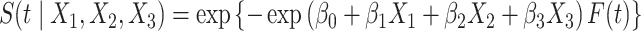 ,
, 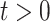 . We generate the data with
. We generate the data with 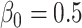 ,
, 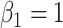 ,
, 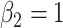 ,
, 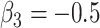 ,
, 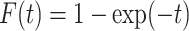 and
and 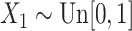 ,
, 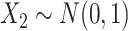 ,
, 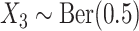 ;
; 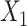 and
and 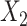 are subject to measurement error so that
are subject to measurement error so that 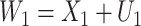 and
and 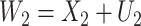 are observed, where
are observed, where 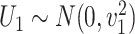 ,
, 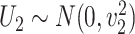 and
and 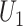 and
and 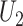 are uncorrelated.
are uncorrelated.
The average censoring rate is 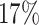 when
when 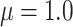 and
and 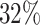 when
when 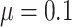 . The average proportion of subjects considered cured for the estimation is
. The average proportion of subjects considered cured for the estimation is 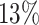 , while the average cure rate is
, while the average cure rate is 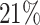 .
.
The results for the four settings with 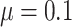 are summarized in Table 2, while those corresponding to
are summarized in Table 2, while those corresponding to 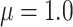 can be found in the Supplementary Material.
can be found in the Supplementary Material.
Table 2.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the settings with two mismeasured covariates, when 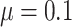
| Ma & Yin method | Naive method | Simex method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate |
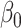
|
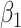
|
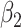
|
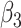
|
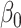
|
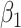
|
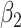
|
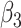
|
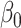
|
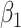
|
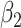
|
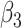
|
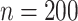 ,
, 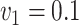 , , 
| ||||||||||||
| Bias | 0.1 | 2.0 | 1.6 | -1.2 | 4.9 | -10.7 | -0.7 | -0.6 | 0.7 | 0.1 | 1.2 | -1.1 |
| Emp. var. | 7.0 | 15.4 | 1.7 | 4.0 | 6.1 | 11.5 | 1.6 | 3.9 | 6.8 | 14.8 | 1.7 | 4.0 |
| Est. var. | 6.1 | 13.8 | 1.5 | 3.9 | 5.2 | 10.2 | 1.4 | 3.8 | 5.9 | 13.1 | 1.5 | 3.9 |
| 95% cv | 93.2 | 93.8 | 95.0 | 94.8 | 92.2 | 93.4 | 93.0 | 95.0 | 93.0 | 94.6 | 95.0 | 95.0 |
| MSE | 7.0 | 15.4 | 1.7 | 4.0 | 6.4 | 12.6 | 1.6 | 3.9 | 6.8 | 14.8 | 1.7 | 4.0 |
 ,
,  , , 
| ||||||||||||
| Bias | -1.9 | 8.1 | 3.0 | -1.8 | 13.3 | -33.4 | -5.6 | 0.3 | 4.7 | -9.4 | 0.7 | -0.9 |
| Emp. var. | 9.8 | 27.9 | 2.2 | 4.6 | 5.6 | 8.8 | 1.5 | 3.9 | 7.6 | 17.3 | 1.9 | 4.3 |
| Est. var. | 8.6 | 25.2 | 1.9 | 4.3 | 4.6 | 7.7 | 1.3 | 3.8 | 6.0 | 13.6 | 1.6 | 4.1 |
| 95% cv | 94.2 | 96.2 | 95.8 | 94.2 | 88.8 | 75.8 | 90.2 | 94.0 | 91.8 | 92.4 | 94.8 | 94.2 |
| MSE | 9.8 | 28.6 | 2.3 | 4.6 | 7.4 | 20.0 | 1.8 | 3.9 | 7.9 | 18.2 | 1.9 | 4.3 |
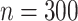 ,
, 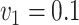 , , 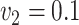
| ||||||||||||
| Bias | 2.0 | 0.8 | 1.2 | -1.3 | 6.6 | -11.5 | -1.0 | -0.8 | 2.4 | -0.7 | 0.9 | -1.2 |
| Emp. var. | 4.1 | 9.9 | 0.9 | 2.4 | 3.6 | 7.5 | 0.9 | 2.3 | 4.0 | 9.6 | 0.9 | 2.4 |
| Est. var. | 3.9 | 9.0 | 1.0 | 2.6 | 3.4 | 6.8 | 0.9 | 2.5 | 3.8 | 8.6 | 1.0 | 2.6 |
| 95% cv | 94.4 | 94.2 | 96.4 | 95.2 | 92.4 | 93.6 | 95.8 | 95.6 | 93.8 | 94.2 | 96.4 | 95.2 |
| MSE | 4.1 | 9.9 | 1.0 | 2.4 | 4.0 | 8.9 | 0.9 | 2.3 | 4.1 | 9.6 | 0.9 | 2.4 |
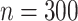 ,
, 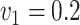 , , 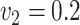
| ||||||||||||
| Bias | 0.8 | 4.7 | 2.2 | -1.6 | 14.9 | -34.0 | -5.9 | 0.2 | 6.6 | -10.1 | 0.5 | -1.0 |
| Emp. var. | 5.3 | 16.3 | 1.2 | 2.6 | 3.2 | 5.9 | 0.8 | 2.4 | 4.4 | 11.2 | 1.1 | 2.5 |
| Est. var. | 5.2 | 14.9 | 1.2 | 2.8 | 3.0 | 5.1 | 0.9 | 2.5 | 3.9 | 8.9 | 1.1 | 2.7 |
| 95% cv | 95.0 | 95.6 | 96.2 | 95.4 | 86.8 | 66.2 | 90.6 | 94.8 | 90.6 | 91.2 | 95.8 | 95.0 |
| MSE | 5.3 | 16.6 | 1.3 | 2.7 | 5.4 | 17.4 | 1.2 | 2.4 | 4.8 | 12.2 | 1.1 | 2.5 |
Emp. var., empirical variance; Est. var., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
The three methods perform similarly as far as 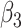 is concerned. None clearly has lowest bias overall. For larger values of the measurement error variances, the method of Ma & Yin (2008) is the best for
is concerned. None clearly has lowest bias overall. For larger values of the measurement error variances, the method of Ma & Yin (2008) is the best for 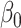 and
and 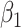 , while simex is preferred for
, while simex is preferred for 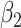 . However, when also taking the variance of the estimators into account, the mean squared error indicates that the naive method is preferable for small values of
. However, when also taking the variance of the estimators into account, the mean squared error indicates that the naive method is preferable for small values of 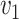 and
and  , while simex outperforms the corrected score approach and the naive method for larger values of
, while simex outperforms the corrected score approach and the naive method for larger values of 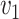 and
and 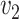 .
.
4.4. A more realistic case
In practice, neither the failure times nor the censoring times can be infinite. Consequently, none of the cured subjects are observed to be cured. The cure threshold, i.e., the largest observed event time, as mentioned in §2, is thus needed for the estimation of the model parameters. Moreover, depending on the context, the censoring and cure rates can be much larger than the values considered in the two previous settings. We therefore consider the model
where 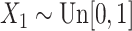 ,
, 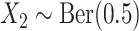 ;
; 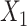 is subject to measurement error so that
is subject to measurement error so that 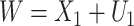 is observed, where
is observed, where 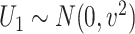 .
.
For the baseline cumulative distribution function 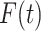 , we use an exponential distribution with mean
, we use an exponential distribution with mean 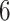 which is truncated at
which is truncated at 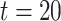 . Consequently, the maximum event time is
. Consequently, the maximum event time is 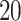 . The censoring times are independent of the covariates and are generated from an exponential distribution with mean
. The censoring times are independent of the covariates and are generated from an exponential distribution with mean 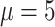 , which is truncated at
, which is truncated at 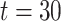 .
.
Four different settings are obtained by considering two possible values for sample size, 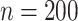 or
or 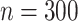 , and variance of the measurement error,
, and variance of the measurement error, 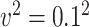 or
or 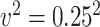 . The average censoring rate is
. The average censoring rate is 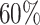 and the average proportion of cured subjects is
and the average proportion of cured subjects is 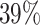 , while the average observed cure rate is
, while the average observed cure rate is 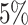 . The results are summarized in Table 3.
. The results are summarized in Table 3.
Table 3.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the realistic settings with one mismeasured covariate
| Ma & Yin method | Naive method | Simex method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
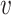
|
Estimate |
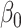
|
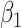
|
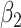
|
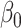
|
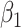
|
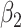
|
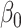
|
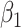
|
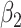
|
| 200 | 0.1 | Bias | -2.1 | 1.3 | -2.2 | 3.8 | -10.6 | -2.1 | -1.4 | -0.3 | -2.2 |
| Emp. | 12.6 | 21.2 | 6.7 | 11.2 | 16.2 | 6.7 | 12.4 | 20.6 | 6.7 | ||
| Est. | 11.4 | 22.1 | 6.3 | 9.8 | 16.7 | 6.2 | 10.7 | 19.1 | 6.3 | ||
| 95% cv | 94.4 | 97.2 | 94.8 | 94.2 | 95.4 | 95.0 | 93.4 | 96.2 | 94.8 | ||
| MSE | 12.6 | 21.2 | 6.8 | 11.4 | 17.3 | 6.7 | 12.4 | 20.6 | 6.8 | ||
| 200 | 0.25 | Bias | -5.6 | 9.3 | -2.6 | 19.9 | -42.9 | -1.9 | 7.4 | -18.6 | -2.0 |
| Emp. | 18.5 | 45.0 | 7.1 | 9.4 | 10.0 | 6.7 | 12.1 | 20.7 | 6.8 | ||
| Est. | 21.8 | 57.8 | 6.9 | 7.9 | 10.5 | 6.2 | 9.7 | 14.6 | 6.3 | ||
| 95% cv | 97.2 | 97.4 | 96.0 | 88.6 | 74.2 | 95.4 | 92.7 | 88.6 | 95.1 | ||
| MSE | 18.8 | 45.9 | 7.2 | 13.3 | 28.4 | 6.7 | 12.6 | 24.2 | 6.8 | ||
| 300 | 0.1 | Bias | -3.1 | 2.5 | -1.3 | 2.5 | -9.4 | -1.2 | -2.5 | 1.3 | -1.3 |
| Emp. | 10.0 | 16.7 | 4.3 | 9.2 | 12.8 | 4.3 | 9.8 | 16.4 | 4.3 | ||
| Est. | 7.9 | 14.4 | 4.1 | 7.2 | 11.0 | 4.1 | 7.6 | 12.5 | 4.1 | ||
| 95% cv | 93.2 | 94.8 | 95.6 | 93.0 | 92.4 | 95.8 | 92.8 | 93.8 | 95.6 | ||
| MSE | 10.1 | 16.8 | 4.4 | 9.3 | 13.6 | 4.3 | 9.9 | 16.4 | 4.4 | ||
| 300 | 0.25 | Bias | -6.8 | 10.5 | -1.9 | 18.7 | -41.2 | -1.1 | 6.0 | -15.8 | -1.4 |
| Emp. | 15.3 | 37.1 | 4.7 | 7.4 | 8.2 | 4.3 | 9.9 | 17.4 | 4.4 | ||
| Est. | 14.4 | 37.5 | 4.6 | 5.6 | 6.9 | 4.1 | 6.9 | 9.7 | 4.2 | ||
| 95% cv | 96.0 | 96.8 | 95.6 | 85.0 | 63.2 | 95.8 | 89.7 | 83.9 | 95.6 | ||
| MSE | 15.8 | 38.2 | 4.7 | 10.9 | 25.2 | 4.3 | 10.3 | 19.9 | 4.4 | ||
Emp., empirical variance; Est., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
As might be expected, differences between the methods appear only for  and, in some cases, for
and, in some cases, for 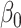 . In terms of the bias, both correction methods are preferable to the naive one. When
. In terms of the bias, both correction methods are preferable to the naive one. When 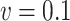 , simex is the best for
, simex is the best for 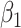 , while the method of Ma & Yin (2008) is the best for this parameter when
, while the method of Ma & Yin (2008) is the best for this parameter when 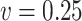 . When
. When 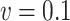 the mean squared error of the naive estimator is the smallest. When
the mean squared error of the naive estimator is the smallest. When 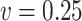 , the mean squared error of the simex estimator is the smallest, while the method of Ma & Yin (2008) yields the largest mean squared error.
, the mean squared error of the simex estimator is the smallest, while the method of Ma & Yin (2008) yields the largest mean squared error.
4.5. Impact of the choice of the extrapolation function
In order to compare the performance of simex with different choices of extrapolant, we consider the setting in the previous subsection, and we estimate the model parameters using, in addition to the quadratic extrapolant, a linear and a cubic extrapolant. Table 4 reports the results.
Table 4.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the realistic settings, for simex with three different extrapolation functions
| Simex (linear) | Simex (quadratic) | Simex (cubic) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
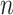
|
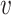
|
Estimate |
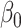
|
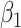
|
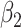
|
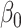
|
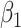
|
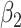
|
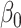
|
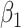
|
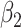
|
| 200 | 0.1 | Bias | 0.0 | -3.0 | -2.2 | -1.4 | -0.3 | -2.2 | -1.4 | 0.0 | -2.2 |
| Emp. var. | 12.0 | 19.2 | 6.7 | 12.4 | 20.6 | 6.7 | 12.5 | 21.2 | 6.7 | ||
| Est. Var. | 10.2 | 17.9 | 6.3 | 10.7 | 19.1 | 6.3 | 11.0 | 19.4 | 6.3 | ||
| 95% cv | 93.6 | 95.6 | 94.8 | 93.4 | 96.2 | 94.8 | 93.2 | 95.0 | 94.4 | ||
| MSE | 12.0 | 19.3 | 6.8 | 12.4 | 20.6 | 6.8 | 12.5 | 21.2 | 6.8 | ||
| 200 | 0.25 | Bias | 14.5 | -32.5 | -1.9 | 7.4 | -18.6 | -2.0 | 3.6 | -10.6 | -1.9 |
| Emp. var. | 10.4 | 14.1 | 6.7 | 12.1 | 20.7 | 6.8 | 13.8 | 26.5 | 6.8 | ||
| Est. Var. | 8.8 | 11.2 | 6.2 | 9.7 | 14.6 | 6.3 | 16.0 | 18.2 | 6.3 | ||
| 95% cv | 90.9 | 80.8 | 95.4 | 92.7 | 88.6 | 95.1 | 93.1 | 89.9 | 95.7 | ||
| MSE | 12.5 | 24.7 | 6.7 | 12.6 | 24.2 | 6.8 | 14.0 | 27.6 | 6.9 | ||
| 300 | 0.1 | Bias | -1.1 | -1.6 | -1.3 | -2.5 | 1.3 | -1.3 | -2.5 | 1.9 | -1.2 |
| Emp. var. | 9.5 | 15.2 | 4.3 | 9.8 | 16.4 | 4.3 | 10.8 | 17.1 | 4.3 | ||
| Est. Var. | 8.0 | 11.8 | 4.1 | 7.6 | 12.5 | 4.1 | 7.8 | 12.8 | 4.1 | ||
| 95% cv | 92.8 | 93.8 | 95.6 | 92.8 | 93.8 | 95.6 | 92.8 | 93.6 | 95.4 | ||
| MSE | 9.5 | 15.2 | 4.3 | 9.9 | 16.4 | 4.4 | 10.8 | 17.1 | 4.4 | ||
| 300 | 0.25 | Bias | 13.1 | -30.0 | -1.2 | 6.0 | -15.8 | -1.4 | 1.9 | -6.8 | -1.6 |
| Emp. var. | 8.4 | 11.7 | 4.4 | 9.9 | 17.4 | 4.4 | 11.4 | 22.4 | 4.5 | ||
| Est. Var. | 8.1 | 7.4 | 4.1 | 6.9 | 9.7 | 4.2 | 8.1 | 12.1 | 4.2 | ||
| 95% cv | 87.2 | 72.9 | 95.6 | 89.7 | 83.9 | 95.6 | 91.8 | 85.2 | 95.2 | ||
| MSE | 10.1 | 20.7 | 4.4 | 10.3 | 19.9 | 4.4 | 11.4 | 22.9 | 4.5 | ||
Emp. var., empirical variance; Est. var., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
In these simulations, varying the extrapolation function used in the simex algorithm has no effect on the estimation of 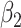 . This is not the case for the other two parameters. When the measurement error variance is rather low, the smallest bias for
. This is not the case for the other two parameters. When the measurement error variance is rather low, the smallest bias for 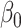 is obtained by the linear extrapolant, while there is no clear conclusion regarding
is obtained by the linear extrapolant, while there is no clear conclusion regarding 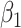 . However, for the largest variance, the higher the extrapolation order, the smaller the bias. In terms of mean squared error, the lowest order of extrapolation yields the best results for
. However, for the largest variance, the higher the extrapolation order, the smaller the bias. In terms of mean squared error, the lowest order of extrapolation yields the best results for 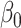 , but the differences among extrapolants are quite limited. For
, but the differences among extrapolants are quite limited. For 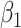 , the mean squared error increases with the order of the extrapolation when the measurement error variance is low, while the quadratic extrapolant outperforms the other ones when the variance is larger.
, the mean squared error increases with the order of the extrapolation when the measurement error variance is low, while the quadratic extrapolant outperforms the other ones when the variance is larger.
These findings are consistent with the general behaviour of the simex estimator: the lower the order of the extrapolant, the more conservative the correction (Cook & Stefanski, 1994). Consequently, the extrapolation function has to be chosen in the context of the bias-variance trade-off; the quadratic extrapolant has seemed to be a good compromise in many cases (Cook & Stefanski, 1994; Carroll et al., 2006) and is widely used (He et al., 2007; Li & Lin, 2003).
4.6. Robustness with respect to misspecification of the error distribution
In this subsection, the effect of a misspecification of the measurement error distribution is investigated through another simulation study, again using the settings of §4.4 with 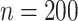 and the quadratic extrapolant. The measurement error is now generated using two distributions which are very different from the Gaussian: a uniform and a chi-squared distribution, with standard deviation
and the quadratic extrapolant. The measurement error is now generated using two distributions which are very different from the Gaussian: a uniform and a chi-squared distribution, with standard deviation 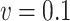 and
and  , assumed to be known. When
, assumed to be known. When 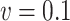 , we see in Table 5 that, for this setting, the misspecification has no impact on the mean squared error; the impact on the bias is very limited except, to some extent, for
, we see in Table 5 that, for this setting, the misspecification has no impact on the mean squared error; the impact on the bias is very limited except, to some extent, for 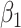 with the chi-squared distribution. For the largest value of the measurement error standard deviation,
with the chi-squared distribution. For the largest value of the measurement error standard deviation, 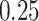 , the estimation of
, the estimation of 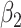 is not influenced by the true distribution. The mean squared errors of
is not influenced by the true distribution. The mean squared errors of 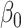 and
and 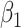 increase slightly. With the uniform distribution, the biases of these two parameters stay nearly constant, while with a chi-squared error, they increase quite markedly.
increase slightly. With the uniform distribution, the biases of these two parameters stay nearly constant, while with a chi-squared error, they increase quite markedly.
Table 5.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the simulations investigating the robustness of simex with respect to a misspecification of the error distribution
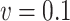
|
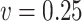
|
||||||
|---|---|---|---|---|---|---|---|
| True distribution | Estimate |

|
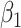
|
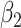
|
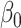
|
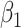
|
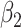
|
| Gaussian | Bias | -0.014 | -0.3 | -2.2 | 7.2 | -18.2 | -2.0 |
| Emp. var. | 12.4 | 20.6 | 6.7 | 12.1 | 21.0 | 6.8 | |
| Est. var. | 10.8 | 19.1 | 6.3 | 9.7 | 14.8 | 6.3 | |
| 95% cv | 93.4 | 95.8 | 94.8 | 92.7 | 88.8 | 95.1 | |
| MSE | 12.4 | 20.6 | 6.8 | 12.7 | 24.3 | 6.8 | |
| Chi-squared | Bias | -0.4 | -2.0 | -2.1 | 11.6 | -25.1 | -2.0 |
| Emp. var. | 12.8 | 21.0 | 6.8 | 12.4 | 19.9 | 7.0 | |
| Est. var. | 10.8 | 18.6 | 6.3 | 9.2 | 12.8 | 6.3 | |
| 95% cv | 93.2 | 93.8 | 94.0 | 90.2 | 83.3 | 94.4 | |
| MSE | 12.8 | 21.0 | 6.9 | 13.8 | 26.2 | 7.0 | |
| Uniform | Bias | -1.0 | -0.7 | -2.0 | 7.1 | -17.7 | -1.9 |
| Emp. var. | 12.6 | 20.2 | 6.9 | 13.5 | 21.9 | 7.1 | |
| Est. var. | 10.7 | 19.1 | 6.3 | 82.6 | 15.2 | 6.3 | |
| 95% cv | 93.1 | 95.0 | 94.4 | 91.3 | 86.1 | 94.2 | |
| MSE | 12.7 | 20.2 | 7.0 | 14.0 | 25.0 | 7.1 | |
Emp. var., empirical variance; Est. var., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
4.7. Robustness with respect to misspecification of the error variance
We now investigate the behaviour of our estimator when the measurement error variance is misspecified. More precisely, we consider the same setting as in §4.4 with 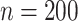 , where the error is simulated with standard deviations
, where the error is simulated with standard deviations 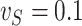 and
and 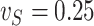 . However, in the estimation process, the variance is misspecified as
. However, in the estimation process, the variance is misspecified as 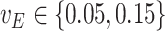 for
for 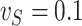 and as
and as 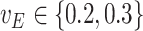 for
for 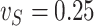 . The extrapolation function is quadratic.
. The extrapolation function is quadratic.
The results, reported in Table 6, show that, in these simulations, a misspecification of the measurement error variance has no impact on the estimation of 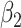 . Both
. Both 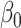 and
and 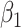 are influenced, in terms of both the bias and the mean squared error. The latter increases with the value of the variance assumed in the estimation procedure, although this increase is less marked when switching from the underspecified variance to the true one, compared to when switching from the true variance to the overspecified one. When the true value of the measurement error variance is low, the lowest bias is obtained when the correct variance is assumed; when the true variance is higher, the bias decreases when the specified variance increases.
are influenced, in terms of both the bias and the mean squared error. The latter increases with the value of the variance assumed in the estimation procedure, although this increase is less marked when switching from the underspecified variance to the true one, compared to when switching from the true variance to the overspecified one. When the true value of the measurement error variance is low, the lowest bias is obtained when the correct variance is assumed; when the true variance is higher, the bias decreases when the specified variance increases.
Table 6.
Empirical bias, empirical and estimated variances, coverages and mean squared errors for the simulations investigating the robustness of simex with respect to a misspecification of the error variance
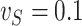
|
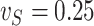
|
|||||||
|---|---|---|---|---|---|---|---|---|
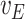
|
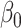
|
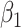
|
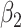
|
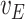
|
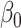
|
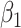
|
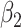
|
|
| 0.05 | Bias | 2.5 | -8.1 | -2.1 | 0.20 | 11.6 | -26.2 | -2.1 |
| Emp. var. | 11.5 | 17.1 | 6.7 | 11.4 | 17.2 | 6.7 | ||
| Est. Var. | 11.2 | 17.3 | 6.2 | 9.2 | 13.8 | 6.3 | ||
| 95% cv | 94.4 | 95.8 | 94.8 | 92.3 | 86.3 | 95.4 | ||
| MSE | 11.5 | 17.8 | 6.7 | 12.8 | 24.0 | 6.8 | ||
| 0.1 | Bias | -01.4 | -0.3 | -2.2 | 0.25 | 7.2 | -18.2 | -2.0 |
| Emp. var. | 12.4 | 20.6 | 6.7 | 12.1 | 21.0 | 6.8 | ||
| Est. Var. | 10.8 | 19.1 | 6.3 | 9.7 | 14.8 | 6.3 | ||
| 95% cv | 93.4 | 95.8 | 94.8 | 92.7 | 88.8 | 95.1 | ||
| MSE | 12.4 | 20.6 | 6.8 | 12.7 | 24.3 | 6.8 | ||
| 0.15 | Bias | -8.0 | 13.0 | -2.2 | 0.30 | 2.9 | -9.3 | -2.1 |
| Emp. var. | 14.1 | 26.6 | 6.8 | 13.3 | 26.5 | 7.0 | ||
| Est. Var. | 11.7 | 21.8 | 6.3 | 10.1 | 15.9 | 6.3 | ||
| 95% cv | 93.2 | 92.4 | 94.6 | 92.9 | 88.8 | 94.8 | ||
| MSE | 14.8 | 28.3 | 6.8 | 13.4 | 27.4 | 7.0 | ||
Emp. var., empirical variance; Est. var., estimated variance; 95% cv, coverage probabilities of 95% confidence intervals computed based on the asymptotic normal distribution; MSE, mean squared error. All numbers were multiplied by 100.
5. AORTIC INSUFFICIENCY DATABASE
We illustrate our methodology on data from patients suffering from aortic insufficiency, a cardiovascular disease. Between 1995 to 2013, 393 patients underwent echocardiography for severe aortic insufficiency at the Brussels Saint-Luc University Hospital, Belgium. These data were collected by one of the authors, C. de Meester, and include information from the diagnosis of the pathology, between 1981 and 2013. %The main event of interest in this study is death from AI. Although aortic insufficiency can be lethal, it is known that a proportion of patients will never die from it. Since the patients considered in this study have no or limited other known morbidity, those who survive for a sufficiently long period after the diagnosis can be considered as long-term survivors. % from their heart disease. The main objective of this study is to investigate the link between the ejection fraction measured at baseline and the survival of the patients. The ejection fraction is the ratio of the difference between the end-diastolic and end-systolic volumes over the end-diastolic volume and therefore measures the fraction of blood which leaves the heart each time it contracts. It is typically high for healthy individuals and is one of the main indicators appearing in the guidelines used to decide whether a patient should be operated on (Bonow et al., 1998; Vahanian et al., 2007). However, the ejection fraction is measured with error (Otterstad et al., 1997), and this should be taken into account when evaluating its impact on survival.
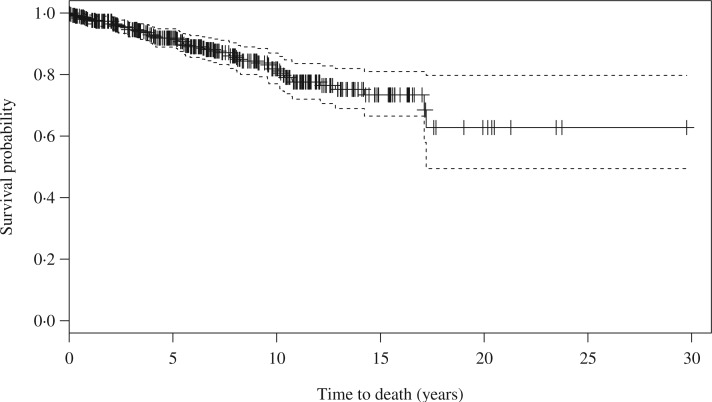
After a median follow-up of 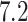 years, only 58 patients had died, and the Kaplan–Meier estimate of the survival curve for these patients shows a clear plateau after about 17 years, as can be seen in Fig. 1. As explained in §2, the cure threshold is the largest observed event time: all patients surviving up to
years, only 58 patients had died, and the Kaplan–Meier estimate of the survival curve for these patients shows a clear plateau after about 17 years, as can be seen in Fig. 1. As explained in §2, the cure threshold is the largest observed event time: all patients surviving up to 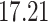 years are considered as not being at risk of dying of their aortic insufficiency. To take into account the presence of cured patients and the measurement error in the covariate of interest, we apply the promotion time cure model estimated with the simex algorithm with the quadratic extrapolant. We compare our results with those obtained by the method of Ma & Yin (2008), as well as with those from a naive promotion time cure model ignoring measurement error. In our data the ejection fraction takes values between 0
years are considered as not being at risk of dying of their aortic insufficiency. To take into account the presence of cured patients and the measurement error in the covariate of interest, we apply the promotion time cure model estimated with the simex algorithm with the quadratic extrapolant. We compare our results with those obtained by the method of Ma & Yin (2008), as well as with those from a naive promotion time cure model ignoring measurement error. In our data the ejection fraction takes values between 0 19 and 0
19 and 0 84, median 0
84, median 0 56, and based on previous work (Otterstad et al., 1997) we consider a standard deviation of the measurement error
56, and based on previous work (Otterstad et al., 1997) we consider a standard deviation of the measurement error 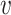 of 0
of 0 05 and 0
05 and 0 10. Our model is adjusted for other patient characteristics, measured without error, namely: gender, with
10. Our model is adjusted for other patient characteristics, measured without error, namely: gender, with 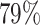 male; age at diagnosis, with median 52 and range 17–88, standardized for the analysis; and surgery strategy chosen by the cardiologist for this patient, with
male; age at diagnosis, with median 52 and range 17–88, standardized for the analysis; and surgery strategy chosen by the cardiologist for this patient, with 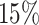 of the patients having no surgery,
of the patients having no surgery, 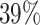 surgery within the first three months and
surgery within the first three months and 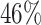 surgery after the first three months. See Table 7.
surgery after the first three months. See Table 7.
Fig. 1.
Kaplan–Meier estimate (solid) and 95% pointwise confidence limits (dashed) of the survival curve for the patients from the aortic insufficiency database.
Table 7.
Regression coefficient estimates, estimated standard deviations and confidence intervals based on the asymptotic normal distribution for the aortic insufficiency data
| Estimate | EF | Gender | Age | Surgery | Surgery |
|---|---|---|---|---|---|
| (standardized) |
 months
months |
 months
months |
|||
| Naive | -1.22 | 0.63 | 1.23 | 0.14 | -0.73 |
| (Estimated SD) | (1.38) | (0.28) | (0.20) | (0.37) | (0.40) |
| 95% C.I. (lower bound) | -3.92 | 0.08 | 0.85 | -0.60 | -1.51 |
| 95% C.I. (upper bound) | 1.48 | 1.19 | 1.62 | 0.87 | 0.05 |
Ma & Yin method (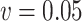 ) ) |
-1.50 | 0.63 | 1.23 | 0.12 | -0.73 |
| (Estimated SD) | (1.69) | (0.29) | (0.20) | (0.38) | (0.40) |
| 95% C.I. (lower bound) | -4.80 | 0.07 | 0.85 | -0.62 | -1.51 |
| 95% C.I. (upper bound) | 1.81 | 1.19 | 1.61 | 0.86 | 0.04 |
Ma & Yin method (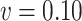 ) ) |
-3.94 | 0.63 | 1.17 | -0.03 | -0.77 |
| (Estimated SD) | (4.21) | (0.31) | (0.21) | (0.43) | (0.40) |
| 95% C.I. (lower bound) | -12.19 | 0.02 | 0.76 | -0.89 | -1.55 |
| 95% C.I. (upper bound) | 4.31 | 1.24 | 1.58 | 0.82 | 0.01 |
Simex (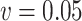 ) ) |
-1.45 | 0.63 | 1.23 | 0.12 | -0.73 |
| (Estimated SD) | (1.48) | (0.29) | (0.20) | (0.38) | (0.40) |
| 95% C.I. (lower bound) | -4.35 | 0.07 | 0.85 | -0.62 | -1.50 |
| 95% C.I. (upper bound) | 1.45 | 1.19 | 1.61 | 0.86 | 0.05 |
Simex (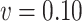 ) ) |
-2.09 | 0.62 | 1.22 | 0.10 | -0.73 |
| (Estimated SD) | (1.71) | (0.29) | (0.20) | (0.38) | (0.39) |
| 95% C.I. (lower bound) | -5.44 | 0.06 | 0.84 | -0.64 | -1.50 |
| 95% C.I. (upper bound) | 1.26 | 1.19 | 1.61 | 0.85 | 0.04 |
SD, standard deviation; C.I., confidence interval; EF, ejection fraction.
We also estimated the model with the logarithm of the ejection fraction instead of this variable in its natural scale, which allows one to take into account the potential case in which the measurement error would be multiplicative rather than additive. The qualitative conclusions are identical: both correction methods yield a larger negative estimated effect of the ejection fraction, compared to the naive method. The estimated coefficients of the covariates without measurement error hardly change.
The parameter most affected by taking the measurement error into account is the coefficient of the ejection fraction. Both methods correct in the same direction. However, the simex approach with a quadratic extrapolant yields a more conservative correction, as reported by Carroll et al. (2006). This smaller correction is associated with a smaller estimated standard deviation, which is consistent with what was observed in the simulation study, and hence a narrower confidence interval. Correcting for the measurement error increases the size of the estimated effect of the ejection fraction. In the promotion time cure model, a negative coefficient implies an increase in the cure probability and in survival at all times, when the value of the covariate increases. The results hence indicate that, all other things being equal, the higher the ejection fraction, the higher the cure probability and the better the survival for the susceptible subjects. This is consistent with expectations and with existing guidelines, which advise performing surgery when the ejection fraction is below a given threshold (Bonow et al., 1998; Vahanian et al., 2007). As far as the surgery strategy is concerned, our results indicate better survival for patients having undergone surgery more than three months after the discovery of the disease, and the worst for those with surgery within the first three months, although the effect is reduced when measurement error is taken into account. These results should, however, be interpreted carefully. First, the patients having undergone surgery more than three months after the discovery of the disease have, by definition, lived at least three months after the discovery of their disease. Second, and probably more importantly, the two groups are not comparable at baseline, as the decision of whether to operate immediately was taken according to existing guidelines, based on the prognosis of the patients. Therefore, the worse survival for patients having surgery within the first three months can be explained by the fact that 80% of these patients met at least one of the guideline criteria for surgery, including the presence of symptoms in 62% of them. The survival of severe aortic insufficiency patients with symptoms is worse than for those without (Dujardin et al., 1999), as also observed in post-operative survival (Klodas et al., 1997).
We also considered introducing an interaction between the ejection fraction level and the surgery strategy. However, an interaction term between a mismeasured covariate and a correctly measured one is actually a mismeasured covariate whose variance depends on the latter covariate. The simex algorithm can easily be tuned to accommodate such a case and yield parameter estimates; however, our asymptotic results do not then hold. Nevertheless, the bootstrap could be used to perform inference on the estimated parameters. It is unclear how to modify the method of Ma & Yin (2008) to allow a dependence between an error term and a covariate. In Table 8, we report the results for this model. When the measurement error is not taken into account, one of the interaction terms is significant, and its introduction modifies the significance of other parameters. The estimated parameters obtained with simex are also reported: as before, the correction leads to estimated effects of higher size for the mismeasured covariates, but also for the covariates included in the interaction terms. We observe a negative estimated effect of the ejection fraction on the survival for patients with surgery after more than three months, as well as for those without surgery: this means, as in the previous model, that a higher value of the ejection fraction is associated with better survival. This effect is less impressive for patients without surgery. According to the naive estimates, there is no significant effect of the ejection fraction in the patients having undergone surgery within the first three months, probably because these patients are operated on due to the presence of symptoms, as explained in the previous paragraph, independently of their ejection fraction.
Table 8.
Regression coefficient estimates, estimated standard deviations and confidence intervals based on the asymptotic normal distribution when interaction terms are included in the model for the aortic insufficiency data
| Estimate | EF | Gender | Age | Surgery | Surgery | EF  Surgery Surgery |
EF  Surgery Surgery |
|---|---|---|---|---|---|---|---|
| (stand.) |
 months
months |
 months
months |
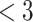 months
months |
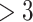 months
months |
|||
| Naive | -6.73 | 0.71 | 1.27 | -4.33 | -2.36 | 8.56 | 3.17 |
| (Estimated SD) | (2.16) | (0.27) | (0.19) | (1.43) | (1.38) | (2.74) | (2.72) |
| 95% C.I. (lower bound) | -11.04 | 0.17 | 0.88 | -7.19 | -5.11 | 3.08 | -2.28 |
| 95% C.I. (upper bound) | -2.41 | 1.26 | 1.65 | -1.48 | 0.40 | 14.05 | 8.62 |
Simex (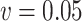 ) ) |
-7.59 | 0.72 | 1.27 | -5.10 | -2.63 | 9.96 | 3.68 |
Simex (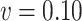 ) ) |
-10.56 | 0.77 | 1.27 | -7.01 | -3.10 | 13.62 | 4.65 |
SD, standard deviation; C.I., confidence interval; EF, ejection fraction.
6. DISCUSSION
The simex algorithm has several advantages that make it very appealing, especially in applied problems. First, since it allows one to graphically represent the effect of the measurement error and of the correction on the bias, it helps justify the need for a correction. Secondly, its intuitive nature makes it appealing in applied problems, particularly to users not familiar with the issue of measurement error. Finally, the scope of the correction can be tuned, making a conservative correction possible. Compared to the alternative approach introduced by Ma & Yin (2008), simex can be applied to a broader class of models, since 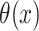 can take any parametric form, including non-penalized fixed-knot B-splines. Also, when using the simex approach, the additive error can have any distribution, whereas Ma & Yin (2008) only study the normal case in detail. Moreover, the practical implementation of the simex method is easier, since it only requires software to estimate the parameters of the model without measurement error.
can take any parametric form, including non-penalized fixed-knot B-splines. Also, when using the simex approach, the additive error can have any distribution, whereas Ma & Yin (2008) only study the normal case in detail. Moreover, the practical implementation of the simex method is easier, since it only requires software to estimate the parameters of the model without measurement error.
Supplementary Material
Acknowledgments
ACKNOWLEDGEMENT
The authors thank J.-L. Vanoverschelde for providing the data, and Y. Ma for sharing her programs. A. Bertrand, C. Legrand and I. Van Keilegom were supported by the Interuniversity Attraction Poles Programme of the Belgian government and by Action de Recherche Concertée of the Communauté française de Belgique. I. Van Keilegom was also supported by the European Research Council. R. J. Carroll was supported by the U.S. National Cancer Institute. R. J. Carroll is also Distinguished Professor, School of Mathematical and Physical Sciences, University of Technology Sydney, Broadway NSW 2007, Australia.
SUPPLEMENTARY MATERIAL
Supplementary material available at Biometrika online includes the proof of Theorem 1 and further simulation results.
Appendix
Proof of Theorem 2
For showing the asymptotics under this model, we follow the approach proposed by Zeng et al. (2006), using 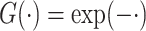 . In the case of no measurement error, the loglikelihood function is
. In the case of no measurement error, the loglikelihood function is
where  is the density function corresponding to
is the density function corresponding to  . Then, the true
. Then, the true 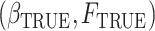 maximizes the expected loglikelihood
maximizes the expected loglikelihood 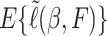 over the class
over the class 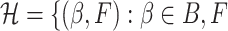 a cumulative distribution function
a cumulative distribution function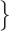 , for some compact set
, for some compact set 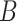 .
.
With measurement error, we define
where 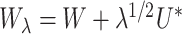 with
with 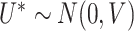 , and we suppose that
, and we suppose that 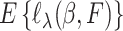 has a unique maximizer
has a unique maximizer  . Therefore, we can follow exactly the same reasoning as in Zeng et al. (2006), replacing
. Therefore, we can follow exactly the same reasoning as in Zeng et al. (2006), replacing  by
by  in all their calculations.
in all their calculations.
For a fixed  and a fixed
and a fixed 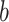 , it follows from equation (A.7) in Zeng et al. (2006) that
, it follows from equation (A.7) in Zeng et al. (2006) that
uniformly over all 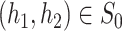 . Here,
. Here, 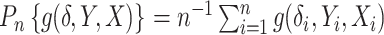 is the empirical measure of
is the empirical measure of 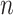 independent and identically distributed observations,
independent and identically distributed observations, 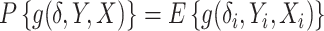 is the expectation,
is the expectation, 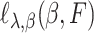 is the derivative of
is the derivative of 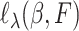 with respect to
with respect to 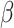 ,
, 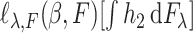 is the derivative of
is the derivative of 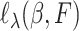 along the path
along the path 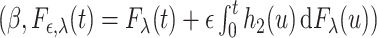 ,
, 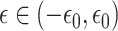 for a small constant
for a small constant 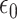 , and
, and 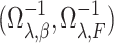 is the inverse of the linear operator
is the inverse of the linear operator 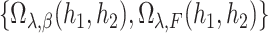 defined in Appendix A.2 in Zeng et al. (2006). Finally,
defined in Appendix A.2 in Zeng et al. (2006). Finally,
with the total variation of 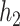 defined as the supremum over all finite partitions
defined as the supremum over all finite partitions 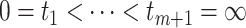 ,
,
Of course, 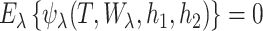 for all
for all 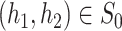 .
.
Next, for fixed 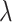 , the class
, the class 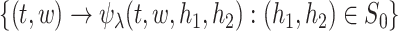 is Donsker (Zeng et al., 2006), and hence the class
is Donsker (Zeng et al., 2006), and hence the class
is also Donsker, since sums of Donsker classes are Donsker; see van der Vaart & Wellner (1996), Lemma 2.10.6. It now follows that the process
converges weakly to a zero-mean Gaussian process GP indexed by 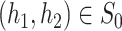 ; see Zeng et al. (2006) after equation (A.7).
; see Zeng et al. (2006) after equation (A.7).
The covariance between GP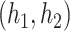 and GP
and GP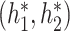 is
is
However, since for any 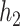 in the class
in the class
we have 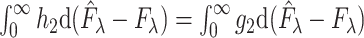 , where
, where 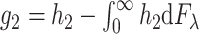 , we can also consider this process as a process indexed by
, we can also consider this process as a process indexed by 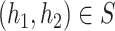 .
.
Finally, we take a finite grid 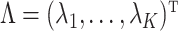 . The foregoing reasoning based on a single value of
. The foregoing reasoning based on a single value of 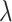 can be redone in exactly the same way for the vector
can be redone in exactly the same way for the vector 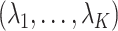 . At the end we have that
. At the end we have that
converges to a 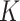 -dimensional Gaussian process of mean zero. The covariance function between the
-dimensional Gaussian process of mean zero. The covariance function between the 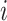 th and
th and 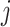 th components (
th components (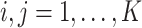 ) is
) is
We consider two particular cases. First, consider the class
where 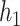 is a vector containing
is a vector containing 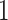 at the
at the 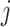 th position (
th position (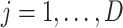 ) and
) and 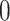 elsewhere. Then, we get weak convergence of the vector
elsewhere. Then, we get weak convergence of the vector 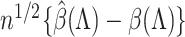 to a multivariate normal random variable of dimension
to a multivariate normal random variable of dimension 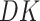 ,
, 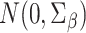 , where
, where 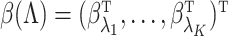 . The second class that we consider is
. The second class that we consider is
Then, we get weak convergence of 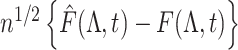 to a Gaussian process
to a Gaussian process 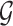 indexed by
indexed by 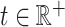 , where
, where 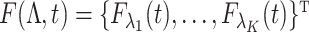 .
.
We will now prove the asymptotic normality of  . Suppose that
. Suppose that 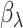 can be specified using a parametric model
can be specified using a parametric model 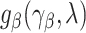 depending on a vector of parameters
depending on a vector of parameters 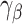 . Assuming that
. Assuming that 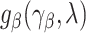 is the true extrapolation function, we have that
is the true extrapolation function, we have that 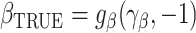 and
and 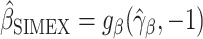 , where
, where 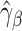 solves, by the least-squares estimation method,
solves, by the least-squares estimation method,
and 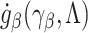 is the
is the 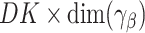 matrix of partial derivatives of the elements of
matrix of partial derivatives of the elements of 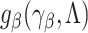 with respect to the elements of
with respect to the elements of 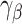 . We then have that
. We then have that
converges to 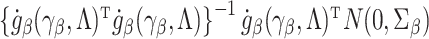 . Because
. Because 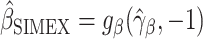 and
and 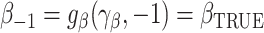 , using the delta method we have that
, using the delta method we have that
with variance
| (A.1) |
Finally, we show that 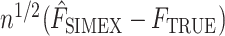 converges weakly to a Gaussian process. For a fixed
converges weakly to a Gaussian process. For a fixed 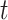 , suppose that
, suppose that 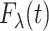 is determined by a parametric model
is determined by a parametric model 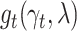 depending on a parameter vector
depending on a parameter vector 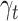 . Under the assumption that this is the true extrapolation function, we have that
. Under the assumption that this is the true extrapolation function, we have that  and
and 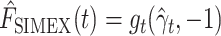 , where
, where 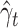 is a solution of
is a solution of
and 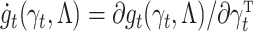 . It now follows that
. It now follows that
for all 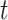 , and hence the process
, and hence the process 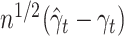 indexed by
indexed by 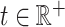 converges to the Gaussian process
converges to the Gaussian process
Since by definition 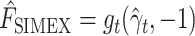 and
and 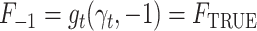 , using the delta method we obtain that as
, using the delta method we obtain that as 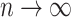 ,
,
| (A.2) |
References
- Apanasovich T. V., Carroll R. J. & Maity A.. (2009). Simex and standard error estimation in semiparametric measurement error models. Electron. J. Statist. 3, 318–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkson J. & Gage R. P.. (1952). Survival curve for cancer patients following treatment. J. Am. Statist. Assoc. 47, 501–15. [Google Scholar]
- Boag J. W. (1949). Maximum likelihood estimates of the proportion of patients cured by cancer therapy. J. R. Statist. Soc. B 11, 15–44. [Google Scholar]
- Bonow R. O., Carabello B., de Leon A. C., Edmunds L. H., Fedderly B. J., Freed M. D., Gaasch W. H., Mc Kay C. R., Nishimura R. A., O’Gara P. T.. et al. (1998). Guidelines for the management of patients with valvular heart disease: Executive summary. A report of the American College of Cardiology/American Heart Association task force on practice guidelines (Committee on Management of Patients with Valvular Heart Disease). Circulation 98, 1949–84. [DOI] [PubMed] [Google Scholar]
- Carroll R. J., Kuchenhoff H., Lombard F. & Stefanski L. A.. (1996). Asymptotics for the simex estimator in nonlinear measurement error models. J. Am. Statist. Assoc. 91, 242–50. [Google Scholar]
- Carroll R. J., Maca J. D. & Ruppert D.. (1999). Nonparametric regression in the presence of measurement error. Biometrika 86, 541–54. [Google Scholar]
- Carroll R. J., Ruppert D., Stefanski L. A. & Crainiceanu C. M.. (2006). Measurement Error in Nonlinear Models: A Modern Perspective. Boca Raton: Chapman and Hall/CRC, 2nd ed. [Google Scholar]
- Carvalho Lopes C. M. & Bolfarine H.. (2012). Random effects in promotion time cure rate models. Comp. Statist. Data Anal. 56, 75–87. [Google Scholar]
- Chen M.-H.Ibrahim J. G. & Sinha D.. (1999). A new Bayesian model for survival data with a surviving fraction. J. Am. Statist. Assoc. 94, 909–19. [Google Scholar]
- Cook J. R. & Stefanski L. A.. (1994). Simulation-extrapolation in parametric measurement error models. J. Am. Statist. Assoc. 89, 1314–28. [Google Scholar]
- Cox D. R. (1972). Regression models and life-tables. J. R. Statist. Soc. B 34, 187–220. [Google Scholar]
- Dujardin K. S., Enriquez-Sarano M., Schaff H. V., Bailey K. R., Seward J. B. & Tajik A. J.. (1999). Mortality and morbidity of aortic regurgitation in clinical practice: A long-term follow-up study. Circulation 99, 1851–7. [DOI] [PubMed] [Google Scholar]
- Farewell V. T. (1982). The use of mixture models for the analysis of survival data with long-term survivors. Biometrics 38, 1041–6. [PubMed] [Google Scholar]
- Greene W. F. & Cai J.. (2004). Measurement error in covariates in the marginal hazards model for multivariate failure time data. Biometrics 60, 987–96. [DOI] [PubMed] [Google Scholar]
- He W., Yi G. Y. & Xiong J.. (2007). Accelerated failure time models with covariates subject to measurement error. Statist. Med. 26, 4817–32. [DOI] [PubMed] [Google Scholar]
- Ibrahim J. G., Chen M.-H. & Sinha D.. (2001). Bayesian semiparametric models for survival data with a cure fraction. Biometrics 57, 383–8. [DOI] [PubMed] [Google Scholar]
- Klodas E., Enriquez-Sarano M., Tajik A. J., Mullany C. J., Bailey K. R. & Seward J. B.. (1997). Optimizing timing of surgical correction in patients with severe aortic regurgitation: Role of symptoms. J. Am. College Cardiol. 30, 746–52. [DOI] [PubMed] [Google Scholar]
- Kuk A. Y. C. & Chen C.-H.. (1992). A mixture model combining logistic regression with proportional hazards regression. Biometrika 79, 531–41. [Google Scholar]
- Li Y. & Lin X.. (2003). Functional inference in frailty measurement error models for clustered survival data using the simex approach. J. Am. Statist. Assoc. 98, 191–203. [Google Scholar]
- Liang H., Härdle W. & Carroll R. J.. (1999). Estimation in a semiparametric partially linear errors-in-variables model. Ann. Statist. 27, 1519–35. [Google Scholar]
- Lu W. (2008). Maximum likelihood estimation in the proportional hazards cure model. Ann. Inst. Statist. Math. 60, 545–74. [Google Scholar]
- Ma Y. & Yin G.. (2008). Cure rate model with mismeasured covariates under transformation. J. Am. Statist. Assoc. 103, 743–56. [Google Scholar]
- Otterstad J. E., Froeland G., St John Sutton M. & Holme I.. (1997). Accuracy and reproducibility of biplane two-dimensional echocardiographic measurements of left ventricular dimensions and function. Eur. Heart J. 18, 507–13. [DOI] [PubMed] [Google Scholar]
- Peng Y. (2003). Fitting semiparametric cure models. Comp. Statist. Data Anal. 41, 481–90. [Google Scholar]
- Peng Y. & Dear K. B. G.. (2000). A nonparametric mixture model for cure rate estimation. Biometrics 56, 237–43. [DOI] [PubMed] [Google Scholar]
- Prentice R. L. (1982). Covariate measurement errors and parameter estimation in a failure time regression model. Biometrika 69, 331–42. [Google Scholar]
- Stefanski L. A. & Cook J. R.. (1995). Simulation-extrapolation: The measurement error jackknife. J. Am. Statist. Assoc. 90, 1247–56. [Google Scholar]
- Sy J. P. & Taylor J. M. G.. (2000). Estimation in a Cox promotional hazards cure model. Biometrics 56, 227–36. [DOI] [PubMed] [Google Scholar]
- Taylor J. M. G. (1995). Semi-parametric estimation in failure time mixture models. Biometrics 51, 899–907. [PubMed] [Google Scholar]
- Tsodikov A. (1998a). Asymptotic efficiency of a proportional hazards model with cure. Statist. Prob. Lett. 39, 237–44. [Google Scholar]
- Tsodikov A. (1998b). A proportional hazards model taking account of long-term survivors. Biometrics 54, 1508–16. [PubMed] [Google Scholar]
- Tsodikov A. (2001). Estimation of survival based on proportional hazards when cure is a possibility. Math. Comp. Model. 33, 1227–36. [Google Scholar]
- Tsodikov A., Ibrahim J. G. & Yakovlev A. Y.. (2003). Estimating cure rates from survival data: An alternative to two-component mixture models. J. Am. Statist. Assoc. 98, 1063–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vahanian A., Baumgartner H., Bax J., Butchart E., Dion R., Filippatos G., Flachskampf F., Hall R., Iung B., Kasprzak J.. et al. (2007). Guidelines on the management of valvular heart disease: The task force on the management of valvular heart disease of the European Society of Cardiology. Eur. Heart J. 28, 230–68. [DOI] [PubMed] [Google Scholar]
- van der Vaart A. W. & Wellner J. A.. (1996). Weak Convergence and Empirical Processes. New York: Springer. [Google Scholar]
- Yakovlev A. Y. & Tsodikov A. D.. (1996). Stochastic Models of Tumor Latency and Their Biostatistical Applications. Singapore: World Scientific. [Google Scholar]
- Zeng D., Yin G. & Ibrahim J. G.. (2006). Semiparametric transformation models for survival data with a cure fraction. J. Am. Statist. Assoc. 101, 670–84. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.