A tug-of-war mechanism for pattern formation in a genetic network

Abstract

Synthesizing spatial patterns with genetic networks is an ongoing challenge in synthetic biology. A successful demonstration of pattern formation would imply a better understanding of systems in the natural world and advance applications in synthetic biology. In developmental systems, transient patterning may suffice in order to imprint instructions for long-term development. In this paper we show that transient but persistent patterns can emerge from a realizable synthetic gene network based on a toggle switch. We show that a bistable system incorporating diffusible molecules can generate patterns that resemble Turing patterns but are distinctly different in the underlying mechanism: diffusion of mutually inhibiting molecules creates a prolonged “tug-of-war” between patches of cells at opposing bistable states. The patterns are transient but longer wavelength patterns persist for extended periods of time. Analysis of a representative small scale model implies the eigenvalues of the persistent modes are just above the threshold of stability. The results are verified through simulation of biologically relevant models.

Graphical Abstract

Introduction

Patterning in living organisms has been a topic of interest across many fields of study and is readily observed in body coloration (1, 2), embryonic development in Drosophila (3) and organization of neural networks (4). However, reproducing these patterns in synthetic biology remains a challenge. Zaikin and Zhabotinsky (5) were the first to obtain spontaneous two-dimensional dynamic patterns in a chemical reaction system. This was also the first experimental observation of patterns with biological implications and a physical explanation of this was provided in (6). Shortly after, more concrete relations between patterns and biological systems were developed through models (7, 8). Since then, there have been a multitude of models that have been shown to give rise to similar patterns (9, 10). Many of the models relevant to biological systems stem from Turing’s famous 1952 publication (11) and the activator-inhibitor system built on Turing’s theory by Gierer and Meinhardt (7). The activator-inhibitor system has been synthesized experimentally in chemical reaction systems (12–14); however, proving the plausibility of Turing patterns emerging from a genetic regulatory network has been a challenge still in pursuit today. The main limitation is the narrow parameter range that satisfies the patterning criteria and the lack of biological parts available to fine-tune a genetic circuit that meets these criteria.

Several results in the literature depart from the activator-inhibitor architecture and propose alternatives based on more readily realizable genetic networks. Mechanisms involving one diffusive signaling molecule have been proposed through mathematical models (15, 16). Experimental designs have departed from the Turing mechanism altogether and have created patterns through growth rate dynamics coupled with a single diffusive molecule (17, 18), spatial manipulation of inducers (19, 20) and spatial arrangement of multicellular systems with quorum signaling molecules (21, 22).

In this paper, we show that patterns can also emerge from a bistable system where diffusible molecules create a “tug-of-war” between opposing states. This could have significant implications towards pattern formation by genetic regulatory networks in synthetic biology. Obtaining the necessary parts and parameter range for pattern formation is more feasible since there are a multitude of genetic network motifs that can result in bistable behavior (23) as observed in many biological systems, such as the Drosophila embryonic patterning network (24, 25), two-component signaling networks (26), and the galactose regulatory network (27, 28).

We show that we can obtain specific patterns through spatially-cued initial conditions and that spontaneous patterns can also emerge from homogeneous initial conditions. Previous work tells us that non-homogeneous steady state solutions in a convex domain are unstable (29–35); however, we show that long wavelength stationary spatial profiles can persist on long enough time scales to be relevant in biological contexts. Such behavior has been observed in chemical reaction networks (36) and phase transition in fluids (37) but has not been explored in genetic networks. The primary purpose of this paper is to demonstrate the relevance of this phenomenon in spatial patterning by genetic networks, in particular, a network of synthetic toggle switches coupled with diffusive molecules.

The tug-of-war mechanism is different from the spatio-temporal instability revealed by Turing. In Turing patterns, the zeroth spatial mode around a homogeneous steady state is stable and higher modes are destabilized by diffusion; this is categorized as type-I instability (38). By contrast, the zeroth spatial mode corresponding to the saddle point of the bistable system is already unstable, giving rise to what is termed type-III instability in (38). Each type of instability can be further categorized into stationary and oscillatory depending on whether the eigenvalues at the onset of instability are real or complex. In the case of type-III instability, linear analysis predicts the possibility for stationary patterning on a large length scale; however, most of the analysis to date on type-III systems is focused on oscillatory instabilities (38).

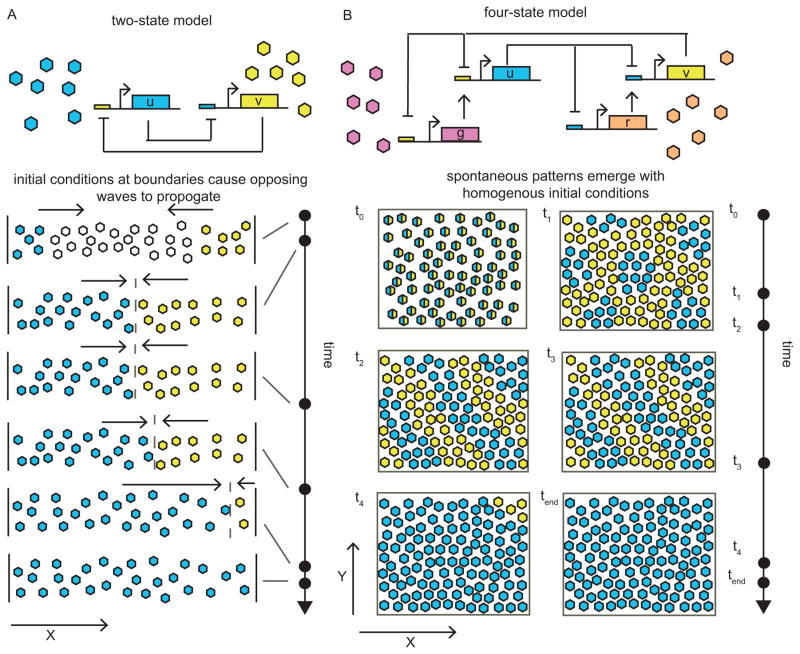
We focus on toggle switch dynamics, as mutual gene repression is an archetype readily found in genetic networks (Fig. 1). We first conduct an in depth study of boundary formation in a one-dimensional space (Fig. 1A) as a precursor to pattern formation in a higher order model in two-dimensional space (Fig. 1B). We use a representative model to gain insight into the key dynamics at play. We next proceed to two dimensions and demonstrate patterning through simulation of a bistable system architecture proposed in (39). We investigate pattern formation in the presence of leaky gene-expression (or nonzero gene expression under full repression) and cross-talk, which occurs when transcription factors bind to non-corresponding promoter sites. We find that a small amount of leakiness and cross-talk permits higher frequency modes to persist longer but too much obliterates patterning altogether. Finally, we consider an asymmetric circuit reflected by unequal diffusion coefficients and production rates. We show that a perfectly symmetric system is not required to sustain patterning.

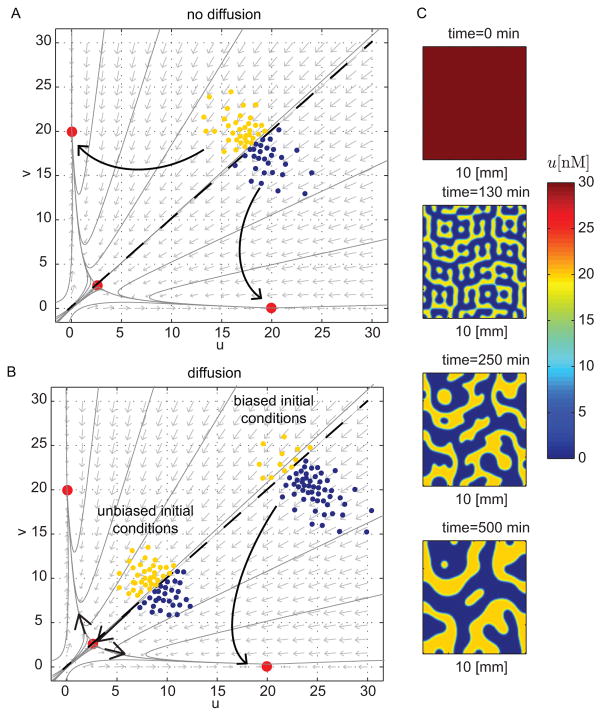
Figure 1. Prolonged transient patterns emerging from unbiased initial conditions in a bistable system.

(A) Schematic of transient boundaries observed in a two-state model in one-dimensional space. The boundary quickly forms and the tug-of-war persists for some time before one state wins over. (B) Schematic of transient patterning in a four-state model in two-dimensional space resulting from a tug-of-war initiated at time t₀. Patterns emerge after some time but high frequency modes quickly dissipate. Low frequency modes persist longer before one state wins over the space.

Results and discussion

A toggle switch with diffusion can generate prolonged spatially-cued patterns in a one-dimensional space

We first consider the case of a bistable system with diffusion in a one-dimensional space to understand the factors at play in patterning. Analysis in one dimension further gives insight into methods of boundary formation in the development of organisms. For example the gap gene network involved in Drosophila embryonic patterning can be described as two weakly coupled toggle switches (40) and it has been proposed that bistability allows for sharp boundary formation (24).

We consider a two-state model of two mutual genetic repressors with diffusion, adapted from Gardner et al. (41) to include diffusion

$$\begin{gathered} \frac{\partial u(t,x)}{\partial t}=D\frac{{\partial }^{2}u(t,x)}{\partial x^2}+f(v(t,x))-\gamma u(t,x) \\ \frac{\partial v(t,x)}{\partial t}=D\frac{{\partial }^{2}v(t,x)}{\partial x^2}+f(u(t,x))-\gamma v(t,x) \end{gathered}$$ (1)

with Neumann boundary conditions

$$\frac{\partial u(t,0)}{\partial x}=\frac{\partial u(t,L)}{\partial x}=\frac{\partial v(t,0)}{\partial x}=\frac{\partial v(t,L)}{\partial x}=0$$ (2)

and repression expressed by the following nonlinear function

$$f(z)=\alpha \frac{1}{1+z^2}.$$ (3)

We choose the initial gradients such that they represent induction from potential transient morphogens (Fig. 2A). For example, early regulation of mRNA in the gap gene network is based on maternal gradients and cross-regulatory interactions are delayed during early accumulation of proteins (42). Hence, we consider initial conditions that equally bias each side towards an opposing state described by the following equations

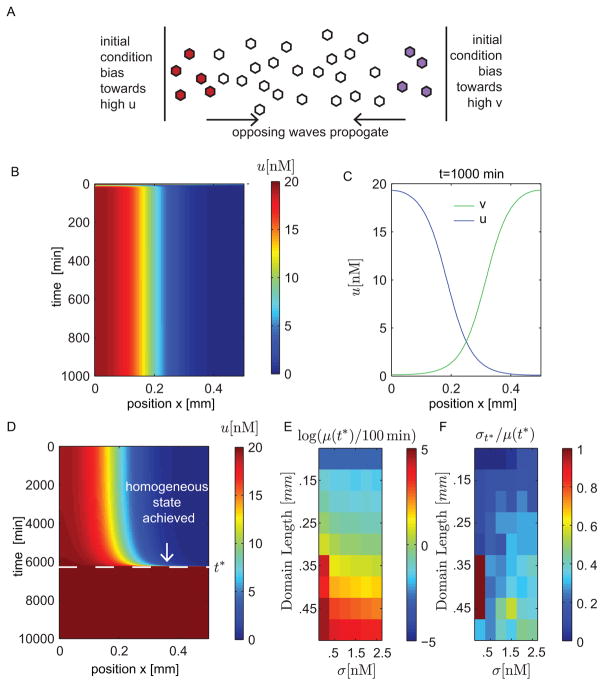
Figure 2. A toggle switch with diffusion can generate prolonged boundary formations.

(A)–(D): Simulations of system (1,4) with parameters D = .001mm²/min, γ = .5 min⁻¹, α = 10nM/min, A₀ = 100nM, μ = 5mm⁻¹, and σ = .5 nM. (A) Illustration of initial conditions. (B) Simulation with L = .5mm. (C) Spatial profiles of u and v at time t = 1000 min for L = .5mm. (D) Simulations showing boundary formations are transient by extending the simulation time. (E)–(F): We study the effects of the domain length L and the standard deviation σ in the random initial conditions (4) on the time t = t^* required to reach a homogeneous state. We run 50 simulations for each condition and calculate the average t^*, μ(t^*), and standard deviation σ^t* . (E) Plot of average time μ(t^*) until spatial homogeneity is achieved. We normalize by 100 min and apply a logarithmic transformation. (F) Plot of corresponding coefficient of variation σ^t*/μ(t^*).

$$\begin{gathered} u(0,x)=u^{\ast }+A_0{e}^{\mu (-x)}+\text{randn}(\sigma ,x)[\text{nM}] \\ v(0,x)=v^{\ast }+A_0{e}^{\mu (x-L)}+\text{randn}(\sigma ,x)[\text{nM}], \end{gathered}$$ (4)

where u^* = v^* is the saddle point of the bistable system. Note that we add a noise term to represent spatial variability in gene expression. The term randn(σ, x) represents a pseudorandom number selected from a normal distribution with standard deviation σ and zero mean at point x in space.

Figure 2B shows a simulation of system (1,4) with σ = .5 nM. The number of molecules u are plotted as a function of time and space. Figure 2C shows the spatial profiles of u and v at time t = 1000 min. In this case we see that there is a clear and persistent divide between the side dominated by u and the side dominated by v. It may appear from Fig. 2B that we have reached a stable steady state profile. However, if we continue to simulate the system for a longer time, we find that the divide breaks eventually and one state wins over the entire space, as seen in Fig. 2D. The tension between the two opposing states on either end creates the tug-of-war that results in this prolonged spatial profile. In the following sections we show mathematically that non-homogeneous steady state profiles like the one observed in Fig. 2B–C indeed exist, but are unstable due to an eigenvalue barely above the threshold of stability. The proximity of this eigenvalue to zero results in the prolonged transient near this steady state.

In Fig. 2E–F, we examine the effects of the domain length and stochastic initial conditions on the transients of the boundaries. Given that the initial conditions are stochastic, we run 50 simulations at each chosen domain length and find the time required, t^*, to reach a homogeneous state. Numerically, we define the system to have a homogeneous state when the difference between minimum and maximum expression levels across the domain is less that .01nM. This gives a measure of the persistence of spatial inhomogeneity. For each condition we calculate the average time, μ(t^*), and the corresponding coefficient of variation σ^t*/μ(t^*). As the domain length increases, we find that the co-existence of the two states persists longer, however, there is an increase in variability of the transients as measured by σ^t*/μ(t^*). The shorter transients at smaller domain lengths have the least variability.

A representative bistable model highlights conditions for non-homogeneous steady state solutions

To gain further insight we analyze a simpler model that exhibits the same mechanisms for pattern formation. Derivation of a stability condition for the saddle point gives the range of spatial modes that can exist and a lower bound on the domain length required to sustain a non-homogeneous solution. Steady state analysis verifies that such solutions exist.

We replace the repressive Hill function by a symmetric nonlinear function that is simpler to work with but is, similarly, bounded and monotonically decreasing. To ease analysis without loss of generality we set γ = 1. We choose to model the mutual repression by the nonlinear function

$$f(z)=-\alpha {tan}^{-1}(z),$$ (5)

where α > 1 for bistability. We find that the stability condition for each of the spatial modes at the saddle point is given by

$$\gamma >\alpha -D{\left(\frac{k\pi }{L}\right)}^2.$$ (6)

See Text S3 for the derivation. Note that the zeroth mode is unstable but as k increases we move closer towards the threshold for stability, which confirms a type-III instability (38). We should expect observed patterns to be dominated by the unstable spatial modes. It follows from equation (6) that, for

$$L<\pi \sqrt{\frac{D}{\alpha -\gamma }}$$ (7)

all modes aside from the zeroth mode are stable and thus, we do not expect a non-homogeneous solution.

We now consider steady state solutions by setting the time derivatives to zero. This allows us to then rewrite the two-state PDE (1) as a four-state ODE system with respect to the spatial variable x:

$$\begin{gathered} \frac{d}{dx}\left[\begin{array}{c}u(x)\\ v(x)\end{array}\right]=\left[\begin{array}{c}{u}^{\prime }(x)\\ v^{\prime }(x)\end{array}\right] \\ \frac{d}{dx}\left[\begin{array}{c}{u}^{\prime }(x)\\ v^{\prime }(x)\end{array}\right]=-D^{-1}\left[\begin{array}{c}f(u(x))\\ f(v(x))\end{array}\right]+D^{-1}\left[\begin{array}{c}u(x)\\ v(x)\end{array}\right]. \end{gathered}$$ (8)

Given the odd symmetry of f(·), setting v = –u allows us to reduce (8) to a two-dimensional Hamiltonian system (Text S1). Trajectories of the Hamiltonian system (Fig. 3A) from x = 0 to x = L correspond to steady state solutions of the PDE with spatial domain [0, L], and the boundary conditions are satisfied if the trajectory starts and ends on the horizontal axis:

$$u^{\prime }(0)=u^{\prime }(L)=0.$$ (9)

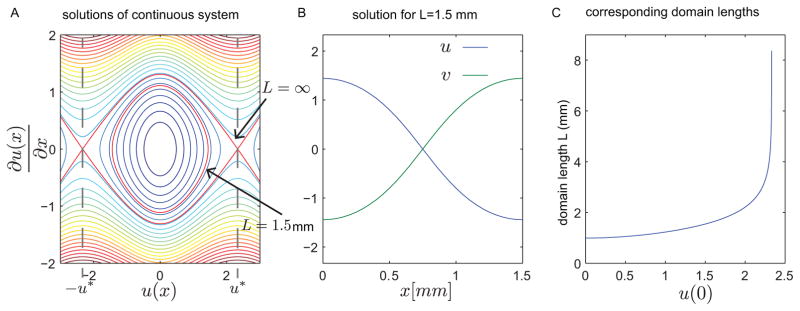
Figure 3. A representative bistable system with diffusion shows the existence of non-homogenous solutions.

(A) Steady state solutions of the PDE (1) with f(z) = –α tan⁻¹(z), D = .1mm, and α = 2nM/min. Each solution corresponds to zero flux boundary conditions (i.e. u′(0) = u′(L) = 0) and varying state boundary conditions u(0) = –u(L). The equilibrium points of the bistable system are indicated by Ŧu^*. (B) Spatial profile corresponding to a half circle trip of the solution indicated in panel A with domain length L = 1.5mm. (C) Calculated domain length for each of the steady state solutions. The domain length approaches infinity as the boundary condition u(0) approaches Ŧu^*.

Similar methods have been applied to finding traveling wave solutions in domains of infinite length (43). In Fig. 3A the concentric circles represent solutions with different state boundary conditions. The corresponding domain length is the half circle trip time given by

$$\stackrel{\sim }{L}={\int }_{u(0)}^{u(L)}\frac{du}{du/dx}.$$ (10)

We note that the length is normalized by the diffusion coefficient through the change of variable $\stackrel{\sim }{x}=x\sqrt{D}$. Therefore, increasing the length is equivalent to decreasing the diffusion coefficient. Figure 3B shows the steady state solution corresponding to L = 1.5mm. Figure 3C shows the calculated domain length corresponding to each solution. The domain length approaches infinity as u(0) approaches the stable equilibrium points Ŧu^* of the bistable system. As the boundary condition u(0) approaches zero, the corresponding domain length approaches a finite positive value that is consistent with the threshold in (7). Non-homogeneous solutions do not exist for domain lengths below this value.

Eigenvalue analysis explains the prolonged transient behavior of non-homogeneous steady state solutions

Since we are concerned with the transients of the solutions, we first discretize the PDE (1) in space to find steady state solutions analogous to the ones found above for the PDE. Next, we calculate the eigenvalues of the linearization about the computed steady state profiles. We let n = ⌊L/Δx⌋ and select Δx = .01mm for a close approximation. The diffusion term is replaced by a coupling term across neighbors (i.e. d(u^l−1+u^l+1−2u^l), where l ∈ [1, n−1] is a spatial index), and the zero flux boundary condition with d(u² – u¹) and d(uⁿ⁻¹ – uⁿ) on the ends of the domain. The parameter mapping is given by d ≡ D/(Δx)² (Text S2). Figure 4A shows the solution profile synonymous to a half circle trip in Fig. 3A. We plot the maximum eigenvalue for the linearization around this profile for various domain lengths in Fig. 4B. Although there is always a single positive eigenvalue implying instability, this unstable eigenvalue approaches zero as the normalized domain length increases. This explains the slow transients with longer domain lengths seen in Fig. 2E.

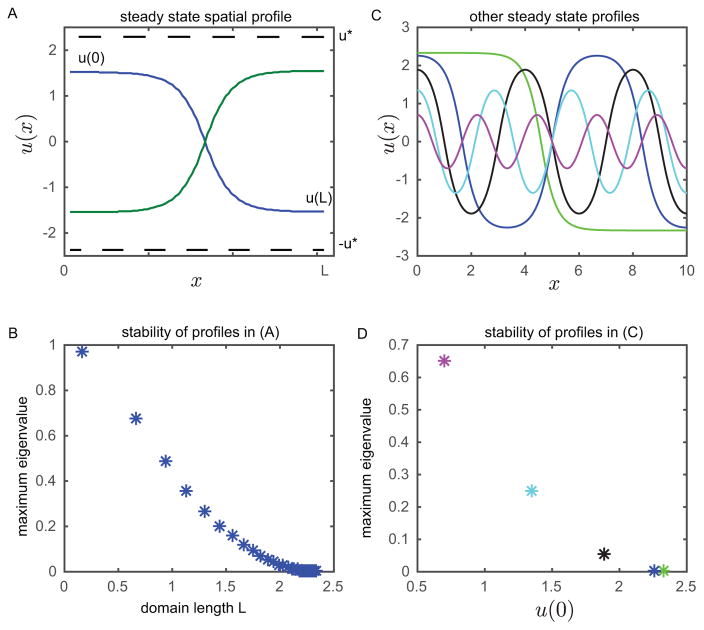
Figure 4. Stability analysis of the representative model (1,5) discretized in space shows patterns are transient.

(A) Steady state spatial profile for the discretized system with D = .1mm²/min, Δx = .01mm, and α = 2nM/min. (B) Maximum eigenvalues of the linearized system about the steady state spatial profile in (A) for varying domain lengths. (C) Higher frequency steady state profiles. (D) Maximum eigenvalue for the higher frequency steady state profiles. Colors are matched to solutions in (C). We see that the instability associated with high frequency profiles is more severe. The three smallest eigenvalues have time constants 18 min, 594 min, and 3.56 × 10⁹ min.

Next, we investigate whether higher frequency patterns can exist. In Fig. 4C, we choose a domain length L = 10mm, and plot all the solutions corresponding to the boundary conditions u(0) = –u(L). Indeed, the system does admit higher frequency steady states, which are synonymous with a full circle or even multiple circular trips in Fig. 3A. We plot the maximum eigenvalue of the linearized system for each profile in Fig. 4D. We see that although the system admits multiple periodic steady states, the instability associated with higher frequency steady states is more severe. In this specific example three of the patterns yield small eigenvalues with time constants 18 min, 594 min, and 3.56 × 10⁹ min. Therefore, we expect to see prolonged patterns composed of low spatial frequency steady states.

An unbiased “tug-of-war” leads to spontaneous patterns in two-dimensional space

We have shown that non-homogeneous steady state solutions exist in one-dimensional space. We now explore the implications of the tug-of-war mechanism in two-dimensional space and we show that spontaneous patterns can emerge from unbiased initial conditions. Consider again the two-state model of the toggle switch

$$\begin{gathered} \frac{\partial u(t,x,y)}{\partial t}=D_u\frac{{\partial }^{2}u(t,x,y)}{\partial x^2}+D_u\frac{{\partial }^{2}u(t,x,y)}{\partial y^2}+\frac{{\alpha }_u}{1+v{(t,x,y)}^2}-{\gamma }_{u}u(t,x,y) \\ \frac{\partial v(t,x,y)}{\partial t}=D_v\frac{{\partial }^{2}v(t,x,y)}{\partial x^2}+D_v\frac{{\partial }^{2}v(t,x,y)}{\partial y^2}+\frac{{\alpha }_v}{1+u{(t,x,y)}^2}-{\gamma }_{v}v(t,x,y), \end{gathered}$$ (11)

with diffusive molecules and Neumann boundary conditions. Figures 5A–B show a phase portrait for a symmetric toggle switch (i.e., α_u = α_v and γ_u = γ_v). There is one unstable saddle point and two stable equilibria. The scattered points represent varying initial conditions in space. Without diffusion, none of the individual trajectories assumed by each of the initial conditions can cross the separatrix (see Fig. 5A). With diffusion, a set of initial conditions biased towards one steady state will cause all points to converge to that steady state (see Fig. 5B). However, a non-homogeneous profile can be prolonged through random initial conditions with high variability (Text S4). In the case of unbiased initial conditions, the equally attracting forces due to diffusion keep the trajectories centered on the separatrix for an extended period of time (see Fig. 5B). This phenomenon allows patterns to emerge without any spatial cues. The tug-of-war keeps the zeroth mode from growing while the rest of unstable modes grow. Figure 5C shows simulations of system (11).

Figure 5. A toggle switch with diffusion can produce patterns in two-dimensional space.

(A) Phase portrait of a bistable system illustrating evolution of the dynamics of systems uncoupled by diffusion. (B) Phase portrait of a bistable system illustrating evolution of the dynamics coupled by diffusion. Opposing forces from unbiased initial conditions prolong the tug-of-war. (C) Simulations of system (11) with initial conditions u(0, x, y) = v(0, x, y) = 100nM. The parameter values are D_u,v = .001mm²/min, α_u,v = 10nM/min, and γ_u,v = .5 min⁻¹. We allow only numerical noise to break homogeneity.

A toggle switch with quorum sensing molecules produces patterns in two-dimensional space

We now explore patterning in realizable network based on the toggle switch. Nikolaev and Sontag in (39) propose a symmetric toggle switch design with quorum-sensing molecules and apply monotone systems theory to find conditions for guaranteed homogeneity in the system’s steady state response. In this work we investigate the potential for pattern formation from this design by adding a spatial dimension to the lumped model of (39).

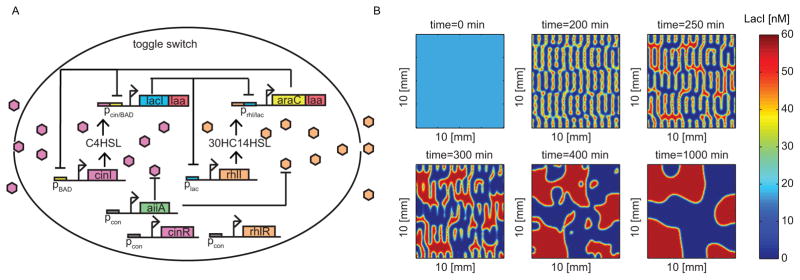
We describe an example of such a system that can be built with current tools in synthetic biology in Fig. 6A. We propose a design utilizing biological components and cellular signaling systems used in (44). Starting with the toggle switch conceptual design in (41) we can modify the promoter into a hybrid promoter (45), where the repressors still mutually repress each other but are additionally up-regulated by their respective signaling molecules. To couple the dynamics across cells we consider the use of the homoserine lactone molecules used in (44). In this case lacI is up-regulated by C4-HSL (a signaling molecule produced by synthase enzyme CinI), which is in turn down-regulated by AraC. Similarly, araC is up-regulated by 3-OHC14-HSL (a signaling molecule produced by synthase enzyme RhlI), which is in turn down-regulated by LacI. Activation of response of promoters to signaling molecules is mediated by expression of cinR and rhlR, which encode transcription factors that respond to the signaling molecules to regulate their respective promoters. These are constitutively expressed inside the cell along with the expression of enzyme AiiA which degrades the signaling molecules (46). Proteins LacI and AraC are degraded enzymatically by the ClpXP protease via ssrA tags (47).

Figure 6. Simulations of a toggle switch design with quorum sensing molecules produces patterns.

(A) Example construction of the toggle switch design with quorum sensing. The toggle switch is composed of two genes lacI and araC encoding repressors, which are up-regulated by their respective signaling molecules (C4-HSL and 3-OHC14-HSL) and down-regulated by each other. Additionally, each repressor down-regulates each other’s activators. In order to implement degradation, the repressors are tagged for enzymatic degradation and constitutive expression of aiiA produces an enzymes that degrades the signaling molecules. (B) Simulation of system (12) with initial conditions u(0, x, y) = v(0, x, y) = 100nM and no leakiness or cross talk. The parameter values are D_C4 = D_C14 = .001mm²/min, a_lacI = a_araC = 10nM/min, a₂ = 20nM/min, and γ = .5 min⁻¹.

We model the system as follows

$$\begin{gathered} \frac{\partial u(t,x,y)}{\partial t}=\frac{a_{\mathit{lacI}}}{1+v{(t,x,y)}^2}+\frac{a_2(g(t,x,y)+\delta r(t,x,y))}{1+g(t,x,y)+\delta r(t,x,y)}-{\gamma }_{p}u(t,x,y) \\ \frac{\partial v(t,x,y)}{\partial t}=\frac{a_{\mathit{araC}}}{1+u{(t,x,y)}^2}+\frac{a_2(r(t,x,y)+\delta g(t,x,y))}{1+r(t,x,y)+\delta g(t,x,y)}-{\gamma }_{p}v(t,x,y) \\ \frac{\partial g(t,x,y)}{\partial t}=D_{C14}\frac{{\partial }^{2}g(t,x,y)}{\partial x^2}+D_{C14}\frac{{\partial }^{2}g(t,x,y)}{\partial y^2}+\frac{a_{\mathit{lacI}}}{1+v{(t,x,y)}^2}+l-{\gamma }_{s}g(t,x,y) \\ \frac{\partial r(t,x,y)}{\partial t}=D_{C4}\frac{{\partial }^{2}r(t,x,y)}{\partial x^2}+D_{C4}\frac{{\partial }^{2}r(t,x,y)}{\partial y^2}+\frac{a_{\mathit{araC}}}{1+u{(t,x,y)}^2}+l-{\gamma }_{s}r(t,x,y). \end{gathered}$$ (12)

The states u and v correspond to concentrations of LacI and AraC. The states g and r are the signaling molecules C4-HSL and 3-OHC14-HSL that couple single cell dynamics or intracellular protein concentrations of u and v. These molecules are not directly regulated by the repressors but to simplify the model we assume that the production rate is proportional to that of CinI and RhlI, the enzymes involved in their production. That is, we assume saturating concentrations of the substrates involved and that synthesis of the signaling molecules, produced through a series of biochemical reactions, happen on a faster time-scale than gene regulation. The degradation constants γ_p and γ_s correspond to degradation rates mediated by enzymes ClpXP and AiiA, respectively. Furthermore, we add a factor δ to account for potential cross-talk and another factor l to account for basal expression of the signaling molecules. The basal expression is what is referred to as leaky gene expression. This accounts for the non-zero probability of transcription initiation occurring even when a repressive transcription factor is bound to the promoter site. Cross-talk is the undesirable behavior of signaling molecules up-regulating gene expression for a non-target protein.

To simulate the system we consider domains on the scale of mm with zero flux boundary conditions. We again must consider initial conditions that are experimentally realistic. One method of controlling initial conditions is through the use of inducers. In our proposed design, we can use inducers IPTG and arabinose to deactivate P_lac and P_BAD promoter activity. The inducer molecules bind to the repressors, resulting in a protein conformational change that reduces the binding affinity of the repressor to its respective promoter site (48). Introducing both inducers simultaneously should remove cross regulation and allow both proteins to accumulate at similar rates. We find that it is important to establish an initial condition that results in competition for a tug-of-war to be initiated. Once the inducers are removed, each state begins to fight for majority in its immediate vicinity. This tug-of-war results in the emergence of patterns.

For our initial studies we choose the unbiased initial conditions

$$\begin{gathered} u(0,x,y)=100[\text{nM}] \\ v(0,x,y)=100[\text{nM}]. \end{gathered}$$ (13)

Both states are chosen to be uniform in space and at equal concentrations above the saddle point. Figure 6B shows simulations of system (12) at different time-points. We see that a high frequency pattern initially emerges but as time passes neighboring cells reach consensus and only a low frequency pattern is prolonged. We have seen in the one-dimensional case that the low frequency patterns have the potential to linger depending on diffusion coefficients and length of the domain. It is worth noting from Fig. 6B that even the high frequency pattern persisted for hours.

Leakiness and crosstalk can improve patterning

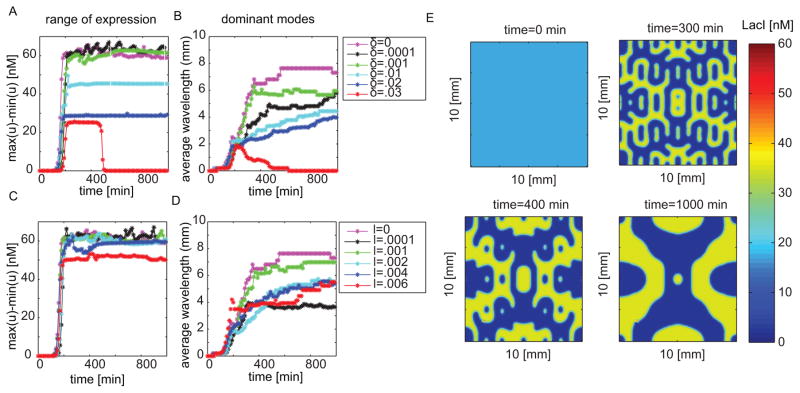
We next investigate the effects of leaky gene expression and cross-talk in patterning. For this, we keep the deterministic initial conditions (13) to maintain a fair comparison. We run multiple simulations for various values of δ and l in system (12). We look at the range of protein expression and dominant modes present in the pattern as a function of time (Fig. 7). Figure 7A shows that the range of expression between the differentiated states gets smaller as cross talk increases. Eventually, patterning is no longer sustained. Figure 7B plots the average of the dominant modes found through application of a discrete cosine transform to the image at each time point. As cross talk increases, we find that higher frequency modes persist. This leads to more regular patterns with higher modes.

Figure 7. Leakiness and cross talk can help improve transient patterns observed.

All simulations where done with same parameters as Fig. 6 with initial conditions u(0, x, y) = v(0, x, y) = 100nM for fair comparison. (A) Range of expression as a function of time for various cross talk values. (B) Average of the dominant modes as a function of time for various cross talk values. (C) Range of expression as a function of time for various leakiness values. (D) Average of the dominant modes as a function of time for various leakiness values. (E) simulation with δ = .01 and l = .0001nM/min.

Next, we investigate leakiness. Figure 7C–D shows that patterns appear to be highly sensitive to the presence of leakiness. While leakiness is small enough to permit patterning, it does not significantly influence the range of expression in the differentiated states. However, like cross talk, too much leakiness breaks the pattern and this happens at extremely low thresholds. The result on dominant modes is less easily understood. A seemingly negligible amount of leakiness drastically increases the frequency of pattern observed; however, a further increase in leakiness reduces the frequency of the pattern again. As we continue to increase leakiness, we find that the dominant modes converge.

With the results obtained from investigating the effects of cross talk and leakiness, we should expect to see improved patterning with the parameters δ = .01 and l = .0001nM/min. Figure 7E shows resulting simulations with δ = .01 and l = .0001nM/min. Indeed, we find that more complex patterns emerge.

Patterning is maintained with unequal diffusion coefficients

It is known that the transport rate of C4 is slightly faster than that of C14 due to its larger size (49) and so we verify the emergence of spontaneous patterns despite unequal diffusion coefficients. We also consider the following unbiased random initial conditions

$$\begin{gathered} u(0,x,y)=u^{\ast }+1000+\text{randn}(\sigma ,x,y)[\text{nM}] \\ v(0,x,y)=v^{\ast }+1000+\text{randn}(\sigma ,x,y)[\text{nM}], \end{gathered}$$ (14)

where u^* = v^* is the saddle point of the bistable system. The term randn(σ, x, y) represents a pseudo-random number selected from a normal distribution with standard deviation σ = .01nM and zero mean at point (x, y) in space. Such initial conditions can be achieved through an initial presence of inducers. Figure 8 shows simulations of this more realistic scenario. The difference in diffusion coefficients causes the patterns to dissipate more quickly. It is expected that LacI dominates, given that its respective signaling molecule C4 has a larger diffusion coefficient. However, the patterns can be clearly seen to persist for some non-negligible amount of time. The wavelength of the patterns that emerge is dependent on the size of the domain. Recall from Fig. 4 that increasing the domain length moves the higher frequency modes closer to the stability boundary.

Figure 8. Transient patterns emerge despite different diffusion constants and stocahstic initial conditions.

Simulation of system (12) with D_C14 = .001 mm²/min, D_C4 = .0015 mm²/min, l = 0nM/min, δ = .01, and σ = .01nM.

Pre-patterned spatial profiles persist despite unequal production rates

Finally, we look at the case where the system is pre-patterned through initial conditions. This simulates the effects of transient morphogens on long term patterns. Until now we have assumed that with our ability to modify promoter and ribosomal binding sites, we can tune expression rates to be equal (50, 51). To test the robustness of the patterns we consider unequal promoter strengths in addition to unequal diffusion coefficients. The pre-patterning is done through the following initial conditions

$$\begin{gathered} u(0,x,y)=u^{\ast }+10+\text{randn}(\sigma ,x,y)+100\ast sin(2\pi x/\lambda )\ast sin(2\pi y/\lambda )+100[\text{nM}] \\ v(0,x,y)=v^{\ast }+10+\text{randn}(\sigma ,x,y)-100\ast sin(2\pi x/\lambda )\ast sin(2\pi y/\lambda )+100[\text{nM}]. \end{gathered}$$ (15)

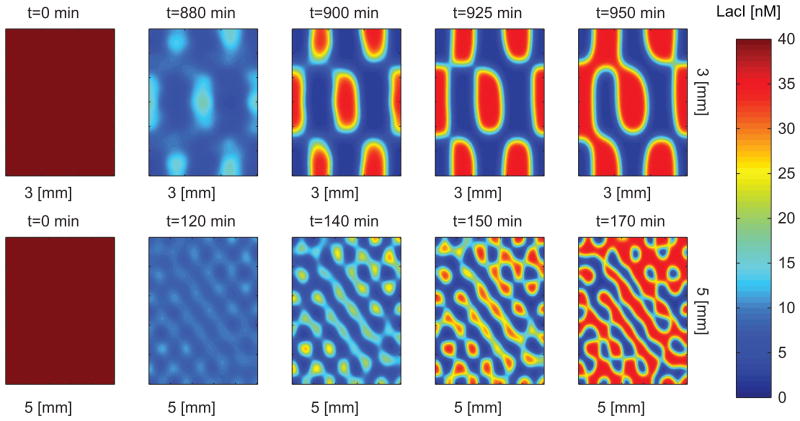
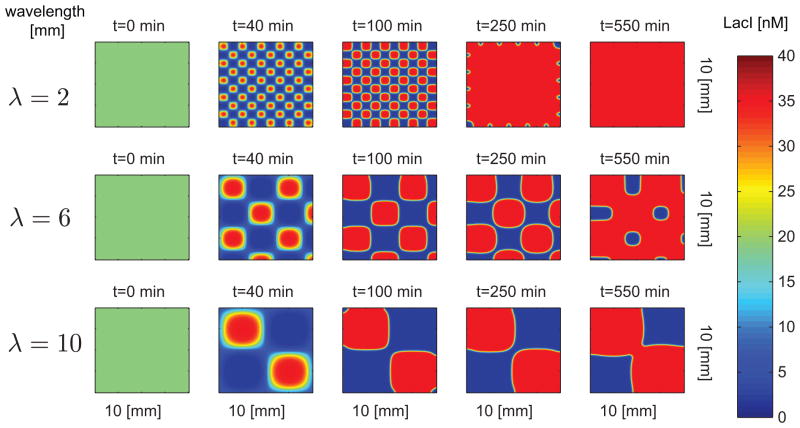
Figure 9 shows simulations for the pre-patterned system for various wavelengths. We initially see a refinement in the patterning occur over time and then the protein with the higher promoter strength begins to take over. The patterns persists for an extended amount of time despite asymmetry in the circuit. As predicted, the large wavelength pattern persists longer.

Figure 9. Longer wavelengths in patterning persist longer.

Simulation of system (12) with D_C14 = .001 mm²/min, D_C4 = .0015 mm²/min, l = 0nM/min, δ = .01, σ = .01 nM, a_araC = 10.5nM/min. Additionally, the strength of the maximal production rate of the LacI promoter

Discussion

We demonstrated that spontaneous patterns can emerge in a two-component bistable system coupled by quorum sensing molecules in E. coli. Additionally, the existence of these solutions and their slow transients give way to persistence of pre-patterned spatial profiles relevant in developmental biology.

The model describing this bistable system is simple but sheds light on more complex networks found in nature. Although the non-homogeneous spatial patterns are unstable, investigation of the transients through analysis of a representative model showed that low frequency patterns have the potential to persist beyond any of the simulation times examined in this paper. Analysis of a discrete approximation gave insight into the instability of non-homogeneous steady state profiles. We showed that low frequency profiles can be marginally close to being stable, which explains the prolonged transient patterns. This phenomena has been investigated in the field of phase transitions (37), where there are similar underlying dynamics, but has not been previously investigated for a toggle switch. Simulations of the toggle switch with quorum sensing molecules showed high frequency patterns did not persist as long but remained for hours just as predicted.

Furthermore, we are able to show that leaky gene expression and promiscuous promoter binding may be advantages to generating patterns within some threshold, after which, they aid to obliterate pattern formation. The role of leaky gene expression and promiscuous promoter binding in network response is an interesting topic to investigate further given its presence in gene regulation. In related work, Ishihara et al. demonstrated generation of spatial stripes from cross talk in a chain of feed-forward network motifs (52). Other results have demonstrated the positive role of noise in dynamics such as noise induced stability (53 – 56) and noise induced patterning (57–59). However, there remains a lot of unexplored work on the role of small coupling through cross talk or basal gene expression in stability and patterning.

In summary, although much focus has been on permanent patterning, transient patterns from bistability may be sufficient in biological applications. For example, spatial regulation of eve stripes in Drosophila embryogenesis is dominated by weakly coupled toggle switches (?), where Bothma et al. (60) show that eve stripe 2 expression persists for only 15 min. This is sufficient to correctly achieve the next stage in development. Another example of the effectiveness of bistability in patterning with transient inducers is given in (61). The authors propose and investigate a detailed model of patterning of the dorsal surface of the Drosophila embryo based on experiments (62) and show that boundary refinement can be achieved with unrefined transient inducers. In this mechanism, mutual inhibition is not the source of bistability; however, much like our first example, resulting patterns are shown to depend on the history of morphogen exposure rather than to a concentration. Moreover, we showed that spatially-cued patterns are much more tolerant to asymmetric conditions. We only need to initially create contrasting biases towards one state or another to generate prolonged patterning with sharp boundaries.

Methods

Simulations

Simulations for the 1D cases were done in Matlab using the PDE solver pdepe. The 2D simulations were done in Comsol using the time-dependent solver. The mesh settings were set to “Physics-controlled mesh” with an extra fine element size. The Backward differentiation formula (BDF) was chosen as the numerical ODE solver for the built in finite element method. The maximum and minimum orders of the BDF solver were set to 5 and 1, respectively. The initial step size was set to .0001 and the setting for steps taken by the solver was set to “Strict.” Data were saved for time points in increments of 10 min. The data were exported in csv files for image analysis in Matlab.

Calculation of average dominant modes

Using Matlab we apply the discrete cosine transform in two-dimensional space using the command dct2. Before applying the transform, we subtract the mean value of the matrix since we are interested in finding the dominant non-homogeneous modes. After applying the cosine transform we normalize each element in the output matrix by the “total energy” of the system in order to compare across different simulations. We define B = dct2(A) ∈ ℝ^N×M and normalize the coefficients by

$$\overline{B}=B\frac{N\times M}{{\sum }_{i=1}^N{\sum }_{j=1}^M{\mid B_{i,j}\mid }^2}.$$ (16)

We then set a threshold to find the dominant modes. Any coefficient with magnitude greater than one is considered sufficiently large. The corresponding maximum wavelength of the mode is calculated from

$${\lambda }_{ij}=\frac{2L}{max([i,j])}$$ (17)

where L is the length of the domain. We then plot the average of all the calculated wavelengths present in the image.

Supplementary Material

supplement

S1 File. Steady state solutions of the representative model. Derivation of steady state solutions with corresponding domain lengths.

S2 File. Stability analysis of the discretized representative model. Derivation of linearized state matrix used for stability analysis of steady state solutions.

S3 File. Linear stability analysis of PDE. Derivation of stability conditions for the saddle point.

S4 File. Extended analysis of asymmetric circuits. An extended study showing that random initial conditions can recover non-homogeneous profiles in asymmetric systems.