Abstract
Neuronal subthreshold voltage-dependent currents determine membrane properties such as the input resistance (Rin) and the membrane time constant (τm) in the subthreshold range. In contrast with classical cable theory predictions, the persistent sodium current (INaP), a non-inactivating mode of the voltage-dependent sodium current, paradoxically increases Rin and τm when activated. Furthermore, this current amplifies and prolongs synaptic currents in the subthreshold range. Here, using a computational neuronal model, we showed that the creation of a region of negative slope conductance by INaP activation is responsible for these effects and the ability of the negative slope conductance to amplify and prolong Rin and τm relies on the fast activation of INaP. Using dynamic clamp in hippocampal CA1 pyramidal neurons in brain slices, we showed that the effects of INaP on Rin and τm can be recovered by applying an artificial INaP after blocking endogenous INaP with tetrodotoxin. Furthermore, we showed that injection of a pure negative conductance is enough to reproduce the effects of INaP on Rin and τm and is also able to prolong artificial excitatory post synaptic currents. Since both the negative slope conductance and the almost instantaneous activation are critical for producing these effects, the INaP is an ideal current for boosting the amplitude and duration of excitatory post synaptic currents near the action potential threshold.
Introduction
The membrane input resistance (Rin) and membrane time constant (τm) are traditionally viewed as a result of the passive non-voltage dependent leak or background channels, based on classical passive cable theory (1, 2, 3, 4). However, the electrical behavior of neurons is never purely passive, because most neurons express voltage-dependent currents activated at subthreshold membrane potentials, making Rin and τm voltage dependent (5, 6, 7, 8). Thus, classical passive cable theory is insufficient to explain the subthreshold membrane properties of the neuron.
The persistent sodium current (INaP) is a subthreshold non-inactivating voltage-dependent current that is expressed in several neuronal types (9, 10, 11, 12, 13, 14, 15, 16, 17). INaP rapidly activates and deactivates (τ < 250 μs) but has a pronounced slow inactivation, remaining active for hundreds of ms (10, 18). INaP is generated by the same NaV subunits that produce transient Na+ current, and it depends on the interaction of the NaV α-subunit with β-subunits (19, 20). INaP affects substantially neuronal excitability by boosting depolarizations near the threshold and producing spontaneous firing (13, 16, 17), and mutations in NaV subunits that increase the expression of INaP are related to epilepsy (reviewed in (21)).
Like the voltage dependence of classical transient voltage-dependent sodium current, INaP has a non-monotonic I/V relationship originating from the interaction between its channel-activation voltage dependence and the Na+-current reversal potential, although with an activation curve shifted toward the hyperpolarizing direction (22, 23). Thus, the INaP I/V relationship displays a negative slope conductance (dI/dV) during the activation phase of the curve (8, 22, 23, 24). Despite increased conductance, INaP increases Rin and τm in its negative slope conductance region (5, 8, 25, 26, 27, 28, 29, 30, 31); however, a causal relationship of the negative conductance with these effects was not determined.
For more than three decades, it has been known that the amplitude and duration of excitatory post synaptic potentials (EPSPs) are voltage dependent, and that depolarizing the membrane potential to values close to the action-potential threshold amplifies EPSP amplitude and prolongs its decay phase (15, 32, 33). In cortical and hippocampal pyramidal cells, these effects are mediated mainly by INaP (34, 35, 36, 37). One of the consequences of the EPSP prolongation by INaP is the so-called near-perfect synaptic integration that has been observed in different brain regions (38, 39) which can produce neurophysiological effects (40). The mechanism for the amplification of the EPSP amplitude was postulated to be a consequence of the fast activation of INaP (8, 36). However, again, there is no direct demonstration that the negative conductance created by INaP is responsible for these effects. Additionally, no satisfactory explanation has been provided for the prolongation of the EPSP at depolarized potentials. From an intuitive point of view, the slow inactivation of INaP could explain the longer duration of EPSPs near threshold. However, another non-inactivating inward current active at subthreshold potentials, the non-inactivating h current (Ih), has the opposite effect and shortens the duration of the EPSP and membrane time constant (8, 41). Since both INaP and Ih are depolarizing and non-inactivating currents, neither aspect is likely to be responsible for their opposite effects on EPSP-time-course prolongation.
Although the effect of a negative conductance on Rin can be explained theoretically, its effect on the τm, and consequently on the duration of the EPSPs, is not well understood. In this work, we aimed to establish the biophysical mechanisms underlying prolongation of EPSP decay in CA1 pyramidal cells. For this, we derived, to our knowledge, a novel analytical expression for the steady-state slope conductance of non-inactivating voltage-dependent currents to elucidate the mechanism by which INaP activation increases Rin and τm. Computational simulations and electrophysiological recordings applying artificial INaP to hippocampal pyramidal cells using dynamic clamp were used to establish the mechanism responsible for the increase of Rin and τm by the negative slope conductance of INaP. Finally, we investigated the effect of a purely negative linear conductance on Rin, τm, and the time course of EPSPs. Our hypothesis was that the ability of INaP to increase Rin, τm, and the duration of EPSPs is related only to its instantaneous negative slope conductance. Our experimental and theoretical results confirmed that it is specifically the negative slope conductance of INaP that is responsible for increasing Rin and τm in the subthreshold membrane potentials.
Methods
Hippocampal slices and electrophysiology
The experimental procedures were approved by the Ethics Committee on Animal Experimentation at our institution. Male Wistar rats (P18–P22) were anesthetized with isoflurane, after which they were decapitated and their brains were removed. Coronal slices (300 μm thick) containing the dorsal hippocampus were obtained with a vibratome in an ice-cold solution containing (in mM) 87 NaCl, 2.5 KCl, 1.25 NaH2PO4, 25 NaHCO3, 0.2 CaCl2, 7 MgCl2, 25 dextrose, and 75 sucrose (pH 7.4) when oxygenated with 95% O2/5% CO2. The slices were incubated in an artificial cerebrospinal solution (aCSF) for 45 min at 35°C and thereafter at room temperature (25°C). The aCSF contained (in mM) 120 NaCl, 2.5 KCl, 1.25 NaH2PO4, 25 NaHCO3, 2 CaCl2, 1 MgCl2, and 20 dextrose (pH 7.4) when gassed with 95% O2/5% CO2 (osmolality ∼310 mOsmol/kg H2O). CA1 pyramidal cells were visualized with a microscope (BX51W, Olympus, Center Valley, PA) equipped with DIC-IR optics using a 40× water immersion objective. Recordings were obtained with borosilicate microelectrodes (BF150-86-10, Sutter Instruments, Novato, CA) presenting a resistance between 4 and 6 MΩ when filled with the internal solution (in mM) 138 K-gluconate, 8 KCl, 10 Na2-phosphocreatine, 10 HEPES, 0.5 EGTA, 4 Mg-ATP, and 0.3 Na-GTP (pH 7.4) adjusted with KOH, and 295 mOsmol/kg H2O.
Pyramidal cells were identified based on the location on the CA1 pyramidal layer, firing behavior, and the triangular shape of the soma. Whole-cell patch-clamp recordings were performed using an EPC-10 patch-clamp amplifier (Heka, Holliston, MA). The slices were continuously perfused (1 mL/min) with aCSF. Temperature was maintained at 33–36°C using an in-line heater (Scientifica, East Sussex, United Kingdom). Series resistance was monitored throughout the experiment and neurons with access resistance >20 MΩ were discarded. Series resistance was compensated at 80%. All the recordings were done in the presence of the GABAA antagonist picrotoxin (20 μM). Voltage-clamp experiments used a holding potential of −80 mV. To measure INaP, voltage ramps were applied from −90 to −30 mV for 4 s. This slow depolarization inactivated the transient sodium currents, leaving INaP (8). INaP was obtained by subtracting the currents produced by the ramps before and after tetrodotoxin (TTX) (100 nM).
V-I curves in current clamp were obtained by injecting 1 s current pulses with 20 pA steps from −400 to 0 pA and depolarizing current pulses with 10 or 20 pA steps from 0 to +400 pA.
To determine the effect of the INaP on the amplitude and duration of the EPSP, artificial EPSCs (aEPSC) were injected through the recording pipette while the membrane potential was changed. aEPSCs were built using two consecutive current ramps (2 ms rising and 5 ms decay). The maximum current amplitude (200 pA) was set to obtain an aEPSP of ∼5 mV at −90 mV.
Data were acquired using PATCHMASTER (Heka) at a 40 kHz rate and filtered with a low-pass filter (Bessel, 3 kHz). Drugs were prepared in aliquots 1000× concentrated in water and diluted into the perfusion solution on the day of the experiment. Picrotoxin was obtained from Sigma-Aldrich (St. Louis, MO) and TTX was obtained from Alomone Labs (Jerusalem, Israel).
Dynamic-clamp
Our dynamic clamp was implemented in a Hewlett-Packard (Palo Alto, CA) notebook running Linux with RTAI (RealTime Application Interface for Linux). Comedi library packages allowed the control of a DAQ board (6062E; National Instruments, Austin, TX) plugged to the EPC 10 amplifier (42). Codes were written in C and the equations were solved using the first-order exponential Euler method with 50 μs steps (2). An artificial INaP was injected in neurons bathed in aCSF with TTX. Artificial INaP was calculated and injected in real time using the equations
| (1) |
| (2) |
| (3) |
where the maximum conductance is = 5 nS, the reversal potential is ENa = +50 mV, and the activation time constant is τNaP = 2 ms. A slow τNaP of 100 ms was used in some experiments. The values of V1/2 = −50 and k = −6 mV were in agreement with experimental data from (8). Membrane potential was sampled and the calculated current was updated at 20 kHz. Membrane potential was recorded and corrected on-line for the liquid junction potential (10 mV) before the equations were solved.
Artificial linear currents were simulated using dynamic clamp. We tested two linear currents, one with a positive conductance and the other with a negative conductance (5, 43), following the equation , where is the conductance in nS and Erev is the reversal potential in mV. We simulated positive conductance with = 0.5 nS and Erev = 50 mV and negative conductance with = −4 nS and Erev = −80 mV. These conductance values were chosen from the NaP I/V relationship slope conductance and chord conductance, respectively, for the membrane potential range between −75 and −70 mV (see Fig. 3, B and C). In the experiments using negative conductance, we restricted the dynamic clamp-current injection to the range between −80 and −60 mV to prevent instabilities.
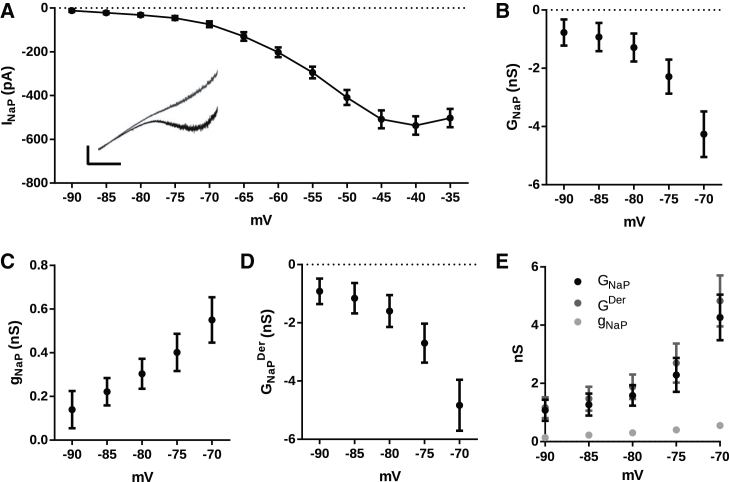
Figure 3.
(A) Average I/V curve for the persistent sodium current (INaP) (n = 10) obtained by the subtraction of currents elicited by slow ramp command in control aCSF (black) and during perfusion with TTX (100 nM) (gray). (Inset) Representative current traces. Scale bar, vertical, 200 pA; horizontal, 1 s. (B) INaP slope conductance (GNaP) determined from the I/V curves in (A) (n = 9). (C) INaP chord conductance (gNaP) (n = 10). (D) INaP derivative conductance (GNaPDer) obtained by subtracting GNaP from gNaP (n = 9). (E) Summary of the absolute values of GNaP, gNaP, and GNaPDer from (B)–(D).
Data analysis
Measured liquid junction potential was of 10 mV and was subtracted off-line. Input (membrane) resistance was measured in current-clamp mode by analyzing voltage-current (V-I) relationships before and after application of TTX. The steady-state potential was measured during the last 100 ms of the pulse. The input resistance around a given membrane potential was determined from the slope of the linear regression of three consecutive steady-state responses, centered on the chosen potential. Membrane time constant at different potentials was measured by first injecting current to achieve the desired test potential and then injecting an additional small current (+20 pA) and fitting a single exponential to the first 100 ms of the voltage change, starting after the voltage drop caused by the series resistance.
We observed that the aEPSP presented a decay with two phases, one fast and one slow, with the fast phase likely produced by the voltage drop by the series resistance, which was not sensitive to changes in membrane resistance by TTX or artificial conductance. For this reason, we were unable to fit the aEPSP decay using a single-exponential function, and to evaluate the effects on aEPSP time course, we measured the aEPSP peak amplitude and time integral (area under the curve) and calculated the ratio of area to peak amplitude. The parameters in the simulation were analyzed similarly, except for membrane resistance, which was measured as ΔV/ΔI, where ΔV was the change in voltage produced by the injection of a small depolarizing current (10 pA).
Data were analyzed using programs written in Igor Pro (Wavemetrics, Portland, OR) and MATLAB (The MathWorks, Natick, MA). Data are presented as the mean ± SE. Differences in means were statistically compared using one-way repeated-measures analysis of variance (ANOVA), two-way repeated-measures ANOVA, and linear regression in GraphPad Prism (Graphpad Software, La Jolla, CA). Statistical significance was set below p = 0.05.
Neuron model
We considered a single-compartment model neuron with only linear (IL) and persistent sodium current (INaP). The membrane voltage is described by the equation , where C is the membrane capacitance and I(t) the injected current. In the steady state (i.e., dV/dt = 0), this equation implies . Using the Hodgkin-Huxley formalism to represent ionic currents in the steady state regime, one obtains
| (4) |
where and EL are the conductance and the reversal potential, respectively, of the linear current.
Input conductance/resistance
The infinitesimal or differential definition of the input conductance in the steady state, Gin, is , where Vss is the steady-state membrane potential. The input conductance of a single-compartment model neuron with only IL and INaP is obtained by differentiating Eq. 4 with respect to V:
| (5) |
where is the slope conductance of INaP. Thus, the input conductance corresponds to the sum of the slope conductances of the steady-state ionic currents (the slope conductance of a linear or passive current is equal to its chord conductance). Finally, the inverse of the input conductance is the slope resistance, or input resistance: .
Computational simulations
The single compartment was a cylinder with length and basis diameter 70 μm. The maximal conductance and reversal potential of the INaP current were = 6 nS and ENa = 50 mV, respectively. The maximal conductance and reversal potential of the IL current were = 10 nS and EL = −90 mV, respectively. Simulations were run in NEURON with a time step of 0.01 ms and analyzed in MATLAB.
Results
The slope conductance is the sum of the chord and derivative conductances
Differentiating the current equation for INaP (Eq. 1), we obtain its slope conductance, GNaP,
| (6) |
Equation 6 is composed of the sum of two terms: the first is the so-called chord conductance, and the second is the change in current that occurs due to the voltage dependence of the gating variable, the so-called derivative conductance (3). The chord conductance, which we will denote as gNaP, is always positive, whereas the derivative conductance, which we will denote as can be positive or negative (3). Then, with these definitions, we rewrite Eq. 6 as
| (7) |
The negative slope conductance of INaP predicts an increase in τm by increasing Rin
First, we show how an Ohmic leak current plus INaP determines Rin and τm. INaP has a fast activation kinetics when compared with τm, i.e., τNaP ≪ τm. Since INaP activation had very fast kinetics (18), its steady-state slope conductance (GNaP) equals its instantaneous slope conductance. Thus, it is possible to rewrite Eq. 1 as a linear current with a slope conductance equal to GNaP (see Fig. 1 A):
where the reversal potential E′Na is now voltage dependent, i.e., E′Na = E′Na(V). However, if a small current ΔI is injected, sufficiently small to assume that GNaP(V) = GNaP(Vini) and E′Na(V) = E′Na(Vini), i.e., neither GNaP nor E′Na changes and both are independent of the membrane potential and time, this equation can be written as
Thus, INaP behaves as a linear Ohmic current for a very small injected current, ΔI, and now its chord conductance is equivalent to GNaP. In this case, the sum of the passive conductances equals the input conductance of the membrane, as in Eq. 5:
so the contribution of INaP to the membrane time constant, τm, is by its slope conductance, GNaP. This means that the INaP negative slope conductance increases τm by decreasing GT, whereas the linear current decreases τm by increasing GT.
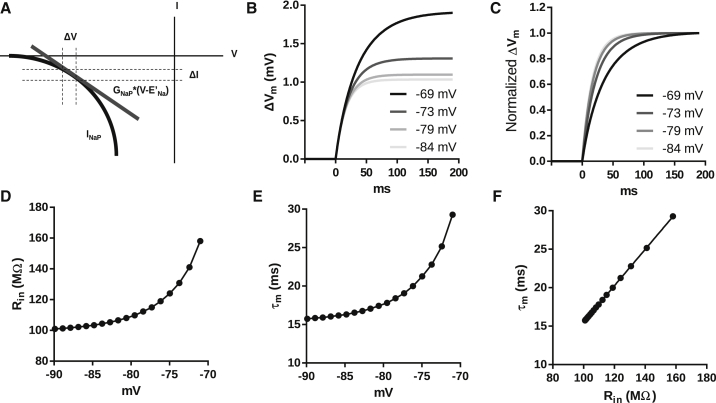
Figure 1.
Computational simulations of voltage dependence of Rin and τm. (A) Approximation of the instantaneous I/V curve of INaP (black) using a linear negative conductance (gray) within the region limited by the dotted lines. (B) Voltage dependence of membrane potential changes in response to a current of 10 pA. (C) Voltage dependence of the rise time of the responses in (B) The amplitudes are normalized to the maximal response. (D) Voltage dependence of Rin. (E) Voltage dependence of τm. (F) Pearson correlation coefficient of τm and Rin. R2 = 1.
We performed computational simulations of a single-compartment neuron containing a linear current and INaP as in Eq. 1 and Fig. 1. The response to small constant current injection depends on the initial membrane potential, becoming larger and slower at depolarized membrane potentials (Fig. 1, B and C). Thus, in the presence of INaP, Rin and τm are voltage dependent and increase with depolarization (Fig. 1, D and E). Even though Rin and τm are voltage dependent, when measured over a range of voltages, they remain correlated, just as for a purely passive membrane where τm = CmRin. Our model showed that this relationship also applies for a membrane containing INaP.
Fast INaP is necessary for the amplification of the EPSP in a neuron model
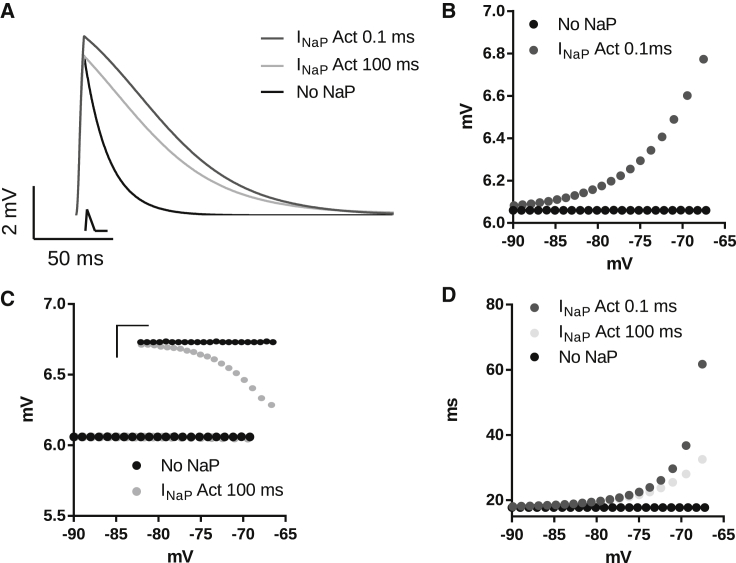
We next explored how the activation kinetics of INaP relates to its effects on EPSP amplitude and time course. For this, we conducted computational simulations of responses to synaptic stimulation using models with either fast (τNaP = 0.1 ms) or slow (τNaP = 100 ms) activation/deactivation kinetics. Fig. 2 A shows examples of EPSPs produced by triangular currents in the absence and presence of INaP. For both fast and slow INaP, the decay time of the EPSP was prolonged compared to a model with no INaP; however, the amplification was bigger with a fast INaP. In the presence of INaP with a fast activation constant, the EPSP amplitude increases with membrane potential depolarization (Fig. 2 B). In contrast, in the presence of INaP with slow activation (100 ms), the EPSP amplitude decreases only slightly with depolarization of the membrane potential (Fig. 2 C). INaP, with its actual fast activation and deactivation values (18) (τNaP = 0.1 ms), increases normalized EPSP area in a voltage-dependent manner (Fig. 2 D). This effect was less pronounced with the INaP with a slower activation/deactivation (τNaP = 100 ms; Fig. 2 D). These simulations showed that INaP both amplifies and broadens EPSPs, and that fast activation is required for best amplification and prolongation of the EPSPs.
Figure 2.
(A) Representative EPSPs obtained from computational simulations for INaP with fast activation (τNaP = 0.1 ms) and slow activation (τNaP = 100 ms), where V = −67 mV. The aEPSC is drawn below the trace. (B) EPSP amplitude for a model containing only linear current (No NaP) or linear plus INaP with fast activation (τNaP = 0.1 ms) for different membrane potentials. (C) The same as in (B), except that the model used INaP with slow activation (τNaP = 100 ms). (Inset) Zoom of the plot. Scale bar, vertical, 0.005 mV; horizontal, 5 mV. (D) EPSP area normalized by the amplitude for only linear current (No NaP) and linear plus INaP with fast or slow activation/deactivation time constant (τNaP = 0.1 or 100 ms, respectively).
GNaP is composed mainly by its derivative conductance
For the slope conductance to be negative, the derivative conductance must be also negative and bigger than the chord conductance, which is positive. Thus, it is clear that in the region of negative slope conductance of INaP, the derivative conductance (GNaPDer) is bigger than the chord conductance (gnap) (see Eq. 7), but the magnitude of the contributions of each component to the slope conductance of INaP (GNaP) and how predominant the GNaPDer might be are unknown in real neurons. Thus, we analyzed experimentally the contributions of both factors contributing to INaP in CA1 hippocampal pyramidal neurons.
We next attempted to determine the relative contribution of chord conductance (gnap) and derivative conductance (GNaPDer) to the total conductance of INaP. Hippocampal CA1 pyramidal cells express INaP, and this current produces a region of negative slope conductance (8, 10, 18). Application of a slow ramp (15 mV/s) produced an inward current that started to develop at ∼−85 mV and peaked around −40 mV (Fig. 3 A). This current was abolished by TTX (100 nM; Fig. 3 A) and the TTX-sensitive current had a peak of −537 ± 42 pA at the potential of −40 mV. Assuming a calculated sodium reversal potential ENa = 70 mV, we calculated an NaP chord conductance (gNaP) of 4.9 ± 0.4 nS at −40 mV. INaP had a half-activation potential of −55.6 ± 0.9 mV and a slope factor of 6.2 ± 0.4 mV (n = 10; Fig. 3 A), in line with previous reports (8, 18).
We then measured the slope conductance GNaP using the first derivative of the current (dI/dV) and, accordingly, found that it is negative and voltage dependent, increasing with depolarization (p = 0.0008; one-way repeated-measures ANOVA; Fig. 3 B). On the other hand, the chord conductance, gNaP, is equally voltage dependent but is positive and 10-fold smaller than GNaP (p = 0.0045; one-way repeated-measures ANOVA; Fig. 3 C). When we calculated the derivative conductance, GNaPDer, using Eq. 7, we found that it is very similar to GNaP, with similar magnitude and negative voltage dependence (p = 0.0003; one-way repeated-measures ANOVA) (Fig. 3 D). Fig. 3 E summarizes the absolute values of GNaP, gNaP, and GNaPDer at different potentials, showing that the major contribution of GNaP comes from the GNaPDer.
The negative slope conductance of INaP is sufficient to increase Rin
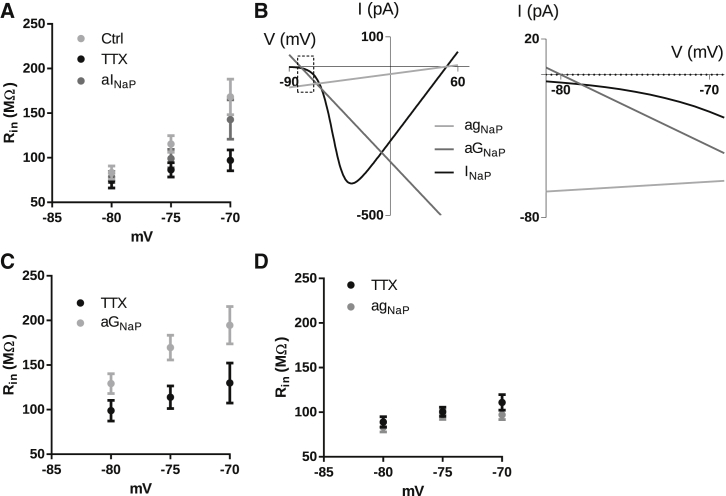
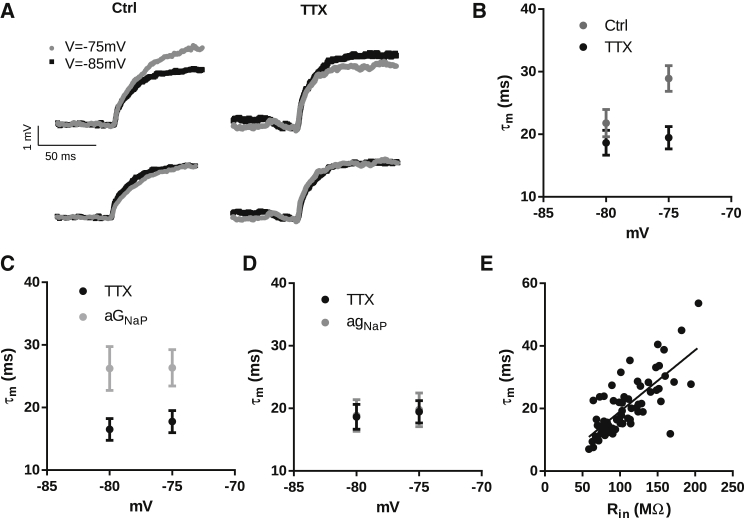
We then proceeded to investigate the role of the negative slope conductance of INaP on the membrane input resistance of hippocampal CA1 neurons. For this, we measured the membrane input resistance of CA1 neurons by injecting small depolarizing currents at different membrane potentials. In accordance to our theoretical prediction and to previous reports (8, 27), Rin is voltage dependent, and TTX (100 nM) significantly decreases the voltage dependence of Rin, indicating a role for INaP in the voltage dependence of Rin (Fig. 4 A; p < 0.0001; two-way repeated-measures ANOVA, n = 6). Since the mean resting membrane potential was −78.3 ± 1.1 mV, these results show that the effect of INaP on Rin is stronger for potentials above the resting membrane potential. To demonstrate that TTX decreases Rin by inhibiting the negative slope conductance produced by INaP, we conducted experiments with TTX and applied to the neuron an artificial INaP (aINaP) using a dynamic clamp. Fig. 4 A shows that aINaP largely restores the voltage dependency of Rin after TTX (two-way repeated-measures ANOVA, n = 6) by increasing Rin at more positive potentials (−75 mV; Tukey’s multiple comparison test).
Figure 4.
(A) Voltage dependence of Rin before (Ctrl) and after the application of TTX and during the application of aINaP in the presence of TTX (n = 6). (B) I/V curves of agNaP, aGNaP, and aINaP (left) and expanded plot focusing on the membrane potential region in which aGNaP was applied (−80 mV < Vm < −70 mV) (right). Notice that all three currents are depolarizing. (C) Voltage dependence of Rin in the presence of TTX, before (TTX) and after application of aGNaP (n = 9). (D) Voltage dependence of Rin in the presence of TTX, before (TTX) and after application of agNaP (n = 8).
To confirm that the ability for INaP to increase Rin is related to its negative slope conductance, we used the dynamic clamp to introduce either negative or positive conductances. In these experiments, the current with positive conductance is meant to reproduce gNaP (agNaP) whereas the current with negative conductance represents GNaP (aGNaP) (Fig. 4 B). We observed that aGNaP was able to restore the high values of Rin associated with the presence of INaP (TTX versus aGNaP; two-way repeated-measures ANOVA, n = 9; Fig. 4 C). On the other hand, agNaP did not change Rin (Fig. 4 D). It is worth noting that when we compared the current values in the range between −80 and −70 mV for aGNaP, agNaP, and aINaP used in these experiments (Fig. 4 B, right), the resultant current of agNaP was bigger than the resultant current of aGNaP and aINaP, showing that the effect observed on Rin reflects more the rate of change of the currents (i.e., the slope conductances) than their absolute value (i.e., instantaneous currents).
The membrane time constant is voltage dependent and is determined by the voltage dependence of Rin
Having determined that the negative slope conductance of INaP is responsible for increasing membrane input resistance, we next explored which component of INaP is responsible for the prolongation of the membrane time constant. In accordance with our theoretical prediction and with previous observations (8), we observed that τm is voltage dependent and increases with depolarization, an effect abolished by TTX application (Fig. 5, A and B; two-way repeated-measures ANOVA, n = 11). Similar to what was observed with Rin, TTX application decreases τm significantly in more depolarized potentials (−75 mV, p < 0.05 using Sidak’s multiple-comparison test). We then tested whether applying an aGNaP would increase τm in the presence of TTX. Fig. 5 C shows that aGNaP increases τm to values similar to τm measured without TTX at −75 mV (two-way repeated-measures ANOVA, n = 10; Fig. 5 C). In contrast, agNaP did not change τm (Fig. 5 D; two-way repeated-measures ANOVA, n = 11). Similarly, as already discussed above with Rin, aGNaP, and not agNaP, was effective in influencing τm, showing that τm reflects the rate of the change of the currents (i.e., the slope conductance) and not their absolute value (i.e., instantaneous currents).
Figure 5.
(A) Top: Voltage responses of the same neuron to injected current before (control) and after TTX application. Bottom: Same traces as in the top plot, but normalized. The current injected was 20 pA. (B) Voltage dependence of τm before (control) and after TTX (n = 11). (C) Voltage dependence of τm in the presence of TTX, before (TTX) and after application of aGNaP (n = 10). (D) Voltage dependence of τm in the presence of TTX, before (TTX) and after application of agNaP (n = 11). (E) Diagram of dispersion between Rin versus τm for the control group for all the membrane potentials. The straight line is the linear regression fit.
As discussed above, the relationship τm = CRin holds for a passive membrane. Our modeling indicates that the same relationship holds in the presence of INaP, which imparts voltage dependence to Rin and τm. To validate our modeling in a real cell, we calculated the Pearson correlation coefficient between the values of Rin and τm for all membrane potentials for the control group and observed a positive correlation between them (p < 0.0001, R2 = 0.556, n = 12 neurons). Moreover, the slope of the correlation coefficient curve determined by linear regression was 196 pF, which is in good agreement with measurements of the capacitance of CA1 pyramidal neurons (44).
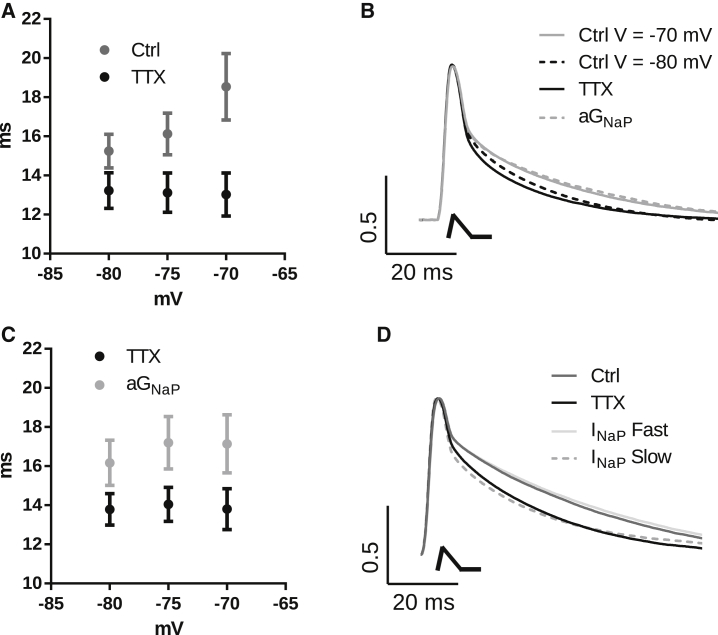
The negative slope conductance amplifies EPSPs
To assess the effect of the INaP and its chord and slope-conductance components to fast membrane potential changes similar to those observed in synaptic potentials, we applied artificial EPSCs (aEPSCs; see Methods) to produce artificial EPSPs (aEPSPs). We tested whether INaP could increase the amplitude and decay time of an artificial EPSP (aEPSP) by measuring the amplitude and area of aEPSPs at different membrane potentials before and after TTX application. The aEPSP amplitude is not very sensitive to depolarization, increasing by only 5% in the range from −85 to −70 mV, but application of TTX abolished this voltage dependency (data not shown), showing that this small effect probably is produced by INaP. However, we found that the duration of the aEPSPs (measured as the area normalized by the amplitude of the aEPSP) was more sensitive to membrane potential increasing with depolarization by 20% (Fig. 6, A and B). Application of TTX abolished this voltage dependency, confirming the role of INaP in amplifying the aEPSPs (two-way repeated-measures ANOVA, n = 8; Fig. 6, A and B). Thus, we decided to compare the area of aEPSPs rather than their amplitude.
Figure 6.
(A) aEPSP area normalized by peak amplitude for control recordings (Ctrl) and in the presence of TTX. (B) Average of the normalized aEPSP of all tested cells for control at −70 and −80 mV, after TTX (V = −70 mV), and in TTX with aGNaP (V = −70 mV). aEPSC is drawn below the traces. (C) aEPSP normalized area in the presence of TTX, before (TTX) and after application of aGNaP. (D) Averaged traces of normalized aEPSP of all tested cells for control, TTX, and TTX with aINaP with a fast or slow activation/deactivation time constant (τNaP = 2 or 100 ms, respectively) (all recorded at V = −70 mV). The aEPSC is drawn below the traces. The fast initial decay phase of the aEPSPs is mainly caused by the series resistance voltage drop.
We then tested whether the prolongation of the aEPSP by INaP was caused by its negative slope conductance, GNaP. To do this, we applied artificial GNaP in the presence of TTX to know whether it can prolong aEPSPs. As can be seen in Fig. 6, B and C, the injection of aGNaP increases the EPSP area normalized by the amplitude by 15% in a voltage-independent manner (two-way repeated-measures ANOVA, n = 9). The normalized aEPSP area in TTX and after aGNaP was similar to that observed in control conditions around the potentials of −70/−75 mV, the potentials around which INaP starts to activate. These results strongly suggest that EPSP amplification by INaP is mainly due to its negative slope conductance.
Our model showed that an INaP with a fast activation/deactivation kinetics is more effective in amplifying the EPSPs. To test this theoretical observation, we compared the effect of two artificial INaPs, one with a fast (2 ms) and the other with a slow (100 ms) activation/deactivation constant, on the aEPSP duration (n = 4). We found that only the INaP with a fast activation/deactivation constant was effective in amplifying the aEPSPs (Fig. 6 D). We conclude that in a real neuron, the fast activation/deactivation kinetics of INaP is crucial for its effect on amplifying the EPSPs.
Discussion
In this work we derived, to our knowledge, a new analytical expression for the slope conductance of the persistent sodium current to understand the mechanisms by which INaP activation increases membrane input resistance and prolongs the membrane time constant. Using computational and experimental approaches, we established the biophysical mechanism by which a negative slope conductance increases Rin and τm. Our results show that INaP increases the amplitude and prolongs the decay time of subthreshold EPSPs through its negative slope conductance. Additionally, we showed that INaP is well suited for this because of its very fast activation kinetics, which produces an almost instantaneous current change and a near-linear portion of its I/V with negative slope during its activation phase.
We observed that endogenous INaP increases Rin and τm in a voltage-dependent manner, as previously reported (5, 8, 25, 26, 27, 28, 29, 30, 31). These previous reports suggested that this paradoxical increase in Rin produced by activation of the NaP current was due to a negative slope conductance region generated by INaP. On the other hand, they were not conclusive about the effect on τm. Our dynamic-clamp experiments showed that injection of a purely negative linear conductance (aGNaP) increased both Rin and τm, validating the hypothesis that the ability for INaP to increase Rin and τm is related to its negative slope conductance. Thus, the electrical behavior of INaP is sufficient to explain the observed increases of Rin and τm, and these effects do not require other conductance activated by Na+ or other subthreshold conductances (45).
Our computational simulations determined that because INaP has fast activation/deactivation kinetics when compared with the cell membrane time constant, INaP reaches the steady state so fast that it is able to control τm via its steady-state slope conductance, GNaP. Our simulations also showed that τm is directly proportional to Rin, independently of the membrane potential, in accordance with the relation τm = CRin and in agreement with the classical cable theory, despite INaP being a voltage-dependent current.
Previous reports established that the slope conductance of noninactivating voltage-dependent currents can be decomposed as the sum of a passive term (i.e., the chord conductance) and a derivative term that depends on the voltage dependence of channel activation (3, 46, 47). Here, we measured both components separately, which allowed us to determine the magnitude of the contributions of each component to the slope conductance of INaP. We found that the derivative conductance of INaP, is always negative and that its magnitude is 10-fold larger than the chord conductance, gNaP, resulting in a negative overall GNaP.
These results resolve an apparent paradox whereby block of persistent Na+ current with TTX was observed to decrease Rin and shorten τm (5, 8). We show that blocking a channel can, perhaps counter-intuitively, decrease Rin when that channel presents a region of negative conductance, as is the case for INaP. The derivative component of the slope conductance does not represent a physical conductance (i.e., membrane ionic permeability) but rather an addition component of dI/dV caused by channel activation. However, for a channel with very fast gating, it acts the same as a physical conductor, except that it can take on negative values when dI/dV is negative, as is the case for INaP. In this circumstance, the slope conductance is more appropriate than the chord conductance to explain its effects on input resistance. The INaP provides a perfect example of an instantaneous current that influences the Rin and τm by its slope conductance and not by its chord conductance. This theoretical distinction has been recognized previously (3, 28, 48). Here, we present, to our knowledge, the first experimental demonstration that negative conductance reproduces the increase of the Rin and τm observed by the activation of endogenous INaP.
Here, we propose that, for INaP, it is the slope conductance, and not the chord conductance, that is the most relevant property affecting Rin and τm. In this case, the slope conductances (positive and negative) from each channel (linear and voltage-dependent) are in parallel, and sum algebraically, and it is this sum that determines Rin and τm (49). It is important to note that this case is only valid for voltage-dependent currents with fast kinetics. Thus, in the near-threshold region of CA1 pyramidal cells, where Ih contributes less than the leak current, negative GNaP opposes the positive slope conductance of the leak current (8), which leads to a decrease of the total positive slope conductance and an increase of the Rin of the neuron.
These concepts can be extended to understand the effect of other ionic currents, besides INaP, that also present negative-slope-conductance regions, such as some voltage-dependent Ca2+ channels, NMDA receptors, and inward rectifier potassium currents. For instance, the anomalous Rin increase observed during activation of NMDA receptors can be explained as a consequence of a negative-slope-conductance region (3, 50, 51, 52, 53). In addition, prolongation of the EPSP decay time attributed to Ca2+-channel opening has been reported (39).
The observed effects of negative conductance on Rin and τm have important consequences for neurotransmission. Activation of the INaP increases the amplitude and duration of EPSPs (34, 35, 36, 54), and we show that this effect can be completely reproduced by introducing a negative conductance via dynamic clamp. These results support the hypothesis that INaP amplification of EPSP is mainly due to its negative slope conductance. Our results contribute to the understanding of the mechanisms behind the amplification of EPSPs, since increasing the EPSP amplitude and prolonging its decay time can be interpreted as a direct consequence of the increase of Rin and τm by the negative slope conductance of INaP.
Further evidence supporting our hypothesis that the negative slope conductance of INaP prolongs the EPSP decay is given by the recently proposed quasi-active cable theory approximation that shows that INaP increases the EPSP amplitude and prolongs its decay time (48). Moreover, it was shown (55) that applying a positive conductance via dynamic clamp, but not a current, shortens the prolongation of the EPSP decay enhanced by INaP. Furthermore, it was shown (38) that in an extreme situation, the INaP negative slope conductance can cancel the positive slope conductance due to the other subthreshold currents, creating a voltage range with near-zero slope conductance, establishing an extremely long membrane time constant and, consequently, very-slow-decay EPSPs that will strongly enhance temporal summation of EPSPs.
Computational simulations predict that INaP with fast activation kinetics will increase the EPSP amplitude, whereas slow activation leads to a small decrease of the EPSP amplitude. These results can be explained by the fact that when the activation is fast, GNaP dominates and amplifies the EPSP, whereas when the activation is slow, gNaP dominates, which tends to diminish the EPSP (48). Strikingly, computational simulations also predict that INaP fast activation/deactivation kinetics (τNaP = 0.1 ms) is more effective in prolonging the EPSP decay than INaP with a slow kinetics (τNaP = 100 ms). This is in agreement with experimental data showing that INaP kinetics in CA1 pyramidal cells is extremely fast (18). Interestingly, our dynamic-clamp experiments showed that an artificial INaP with a slow kinectics (τNaP = 100 ms) was not effective in amplifying the aEPSPs in the real neuron. We believe that this difference is because our model does not incorporate other near-threshold positive conductances, such as IM and IKA, which can damp the effect of the slow INaP in the real neuron. These results support our claim that it is the negative slope conductance of INaP, and not slow channel kinetics, that causes the prolongation of the EPSP decay time.
In general, activation of inward currents may amplify the EPSPs, whereas outward currents counter these effects (35). However, it is difficult to predict the effect of a given current on the EPSPs based solely on the current being inward or outward. For instance, the activation of the h-current, which is an inward current, decreases the amplitude of EPSPs and reduces their decay time (41), as some outward potassium currents also do (56, 57). On the other hand, INaP which is also an inward current, amplifies the inhibitory postsynaptic potentials (IPSPs) (58, 59), but no known outward current amplifies IPSPs. Also, a leak current could be inward or outward according to its reversal potential, although leak currents always decrease EPSP and IPSP amplitudes and reduce their decay time. Our results provide a theoretical framework to understand these experimental data. We emphasized that an appropriate analysis requires the dissociation of two main concepts: 1) the direction of the current flux through the channel, i.e., inward or outward, and 2) the slope conductance of the current. A current with negative slope conductance and fast kinetics increases the input resistance and amplifies both EPSPs and IPSPs regardless of the direction of current flow. The opposite is true for current with a positive slope conductance. This claim is supported by previous theoretical investigations (e.g., (48)).
Author Contributions
C.C.C., A.C.R., and R.M.L. designed the research. C.C.C. performed the experiments and the simulations. C.C.C., A.C.R., and R.M.L. analyzed the data and wrote the article.
Acknowledgments
We thank Dr. Christopher Kushmerick and Dr. Wamberto Varanda for reviewing the manuscript and for critical discussions.
This work was supported by grants from the São Paulo Research Foundation (FAPESP) (2016/01607-4 to R.M.L. and 2013/07699-0 to A.C.R.) and the Brazilian National Council for Scientific and Technological Development (CNPq) (470745/2012-6 to R.M.L. and 306251/2014-0 to A.C.R.). C.C.C. is the recipient of a PhD scholarship from the Brazil Ministry of Education’s Institute of Internation Education (CAPES).
Editor: Eric Sobie.
Contributor Information
Antonio C. Roque, Email: antonior@ffclrp.usp.br.
Ricardo M. Leão, Email: leaor@fmrp.usp.br.
References
- 1.Enyedi P., Czirják G. Molecular background of leak K+ currents: two-pore domain potassium channels. Physiol. Rev. 2010;90:559–605. doi: 10.1152/physrev.00029.2009. [DOI] [PubMed] [Google Scholar]
- 2.Dagostin A.A., Lovell P.V., Leão R.M. Control of phasic firing by a background leak current in avian forebrain auditory neurons. Front. Cell. Neurosci. 2015;9:471. doi: 10.3389/fncel.2015.00471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Koch C. Oxford University Press; New York: 1998. Biophysics of Computation: Information Processing in Single Neurons. [Google Scholar]
- 4.Zhou M., Xu G., Chen H. TWIK-1 and TREK-1 are potassium channels contributing significantly to astrocyte passive conductance in rat hippocampal slices. J. Neurosci. 2009;29:8551–8564. doi: 10.1523/JNEUROSCI.5784-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fernandez F.R., Malerba P., White J.A. Non-linear membrane properties in entorhinal cortical stellate cells reduce modulation of input-output responses by voltage fluctuations. PLoS Comput. Biol. 2015;11:e1004188. doi: 10.1371/journal.pcbi.1004188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nisenbaum E.S., Wilson C.J. Potassium currents responsible for inward and outward rectification in rat neostriatal spiny projection neurons. J. Neurosci. 1995;15:4449–4463. doi: 10.1523/JNEUROSCI.15-06-04449.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Surges R., Freiman T.M., Feuerstein T.J. Input resistance is voltage dependent due to activation of Ih channels in rat CA1 pyramidal cells. J. Neurosci. Res. 2004;76:475–480. doi: 10.1002/jnr.20075. [DOI] [PubMed] [Google Scholar]
- 8.Yamada-Hanff J., Bean B.P. Activation of Ih and TTX-sensitive sodium current at subthreshold voltages during CA1 pyramidal neuron firing. J. Neurophysiol. 2015;114:2376–2389. doi: 10.1152/jn.00489.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Crill W.E. Persistent sodium current in mammalian central neurons. Annu. Rev. Physiol. 1996;58:349–362. doi: 10.1146/annurev.ph.58.030196.002025. [DOI] [PubMed] [Google Scholar]
- 10.French C.R., Sah P., Gage P.W. A voltage-dependent persistent sodium current in mammalian hippocampal neurons. J. Gen. Physiol. 1990;95:1139–1157. doi: 10.1085/jgp.95.6.1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Del Negro C.A., Koshiya N., Smith J.C. Persistent sodium current, membrane properties and bursting behavior of pre-Bötzinger complex inspiratory neurons in vitro. J. Neurophysiol. 2002;88:2242–2250. doi: 10.1152/jn.00081.2002. [DOI] [PubMed] [Google Scholar]
- 12.Leão R.M., Kushmerick C., von Gersdorff H. Presynaptic Na+ channels: locus, development, and recovery from inactivation at a high-fidelity synapse. J. Neurosci. 2005;25:3724–3738. doi: 10.1523/JNEUROSCI.3983-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Leao R.M., Li S., Tzounopoulos T. Diverse levels of an inwardly rectifying potassium conductance generate heterogeneous neuronal behavior in a population of dorsal cochlear nucleus pyramidal neurons. J. Neurophysiol. 2012;107:3008–3019. doi: 10.1152/jn.00660.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Magistretti J., Ragsdale D.S., Alonso A. High conductance sustained single-channel activity responsible for the low-threshold persistent Na+ current in entorhinal cortex neurons. J. Neurosci. 1999;19:7334–7341. doi: 10.1523/JNEUROSCI.19-17-07334.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stafstrom C.E., Schwindt P.C., Crill W.E. Properties of persistent sodium conductance and calcium conductance of layer V neurons from cat sensorimotor cortex in vitro. J. Neurophysiol. 1985;53:153–170. doi: 10.1152/jn.1985.53.1.153. [DOI] [PubMed] [Google Scholar]
- 16.Raman I.M., Gustafson A.E., Padgett D. Ionic currents and spontaneous firing in neurons isolated from the cerebellar nuclei. J. Neurosci. 2000;20:9004–9016. doi: 10.1523/JNEUROSCI.20-24-09004.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pennartz C.M.A., Bierlaagh M.A., Geurtsen A.M.S. Cellular mechanisms underlying spontaneous firing in rat suprachiasmatic nucleus: involvement of a slowly inactivating component of sodium current. J. Neurophysiol. 1997;78:1811–1825. doi: 10.1152/jn.1997.78.4.1811. [DOI] [PubMed] [Google Scholar]
- 18.Carter B.C., Giessel A.J., Bean B.P. Transient sodium current at subthreshold voltages: activation by EPSP waveforms. Neuron. 2012;75:1081–1093. doi: 10.1016/j.neuron.2012.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aman T.K., Grieco-Calub T.M., Raman I.M. Regulation of persistent Na current by interactions between beta subunits of voltage-gated Na channels. J. Neurosci. 2009;29:2027–2042. doi: 10.1523/JNEUROSCI.4531-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qu Y., Curtis R., Scheuer T. Differential modulation of sodium channel gating and persistent sodium currents by the β1, β2, and β3 subunits. Mol. Cell. Neurosci. 2001;18:570–580. doi: 10.1006/mcne.2001.1039. [DOI] [PubMed] [Google Scholar]
- 21.Stafstrom C.E. Persistent sodium current and its role in epilepsy. Epilepsy Curr. 2007;7:15–22. doi: 10.1111/j.1535-7511.2007.00156.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Izhikevich E.M. MIT Press; Cambridge, MA: 2007. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. [Google Scholar]
- 23.Ghigliazza R.M., Holmes P. Minimal models of bursting neurons: how multiple currents, conductances, and timescales affect bifurcation diagrams. SIAM. J. App. Dyn. Syst. 2004;3:636–670. [Google Scholar]
- 24.Stafstrom C.E., Schwindt P.C., Crill W.E. Negative slope conductance due to a persistent subthreshold sodium current in cat neocortical neurons in vitro. Brain Res. 1982;236:221–226. doi: 10.1016/0006-8993(82)90050-6. [DOI] [PubMed] [Google Scholar]
- 25.Wilson C.J. The mechanism of intrinsic amplification of hyperpolarizations and spontaneous bursting in striatal cholinergic interneurons. Neuron. 2005;45:575–585. doi: 10.1016/j.neuron.2004.12.053. [DOI] [PubMed] [Google Scholar]
- 26.Yamada-Hanff J., Bean B.P. Persistent sodium current drives conditional pacemaking in CA1 pyramidal neurons under muscarinic stimulation. J. Neurosci. 2013;33:15011–15021. doi: 10.1523/JNEUROSCI.0577-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Economo M.N., Martínez J.J., White J.A. Membrane potential-dependent integration of synaptic inputs in entorhinal stellate neurons. Hippocampus. 2014;24:1493–1505. doi: 10.1002/hipo.22329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jacobson G.A., Diba K., Yarom Y. Subthreshold voltage noise of rat neocortical pyramidal neurones. J. Physiol. 2005;564:145–160. doi: 10.1113/jphysiol.2004.080903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yaron-Jakoubovitch A., Jacobson G.A., Yarom Y. A paradoxical isopotentiality: a spatially uniform noise spectrum in neocortical pyramidal cells. Front. Cell. Neurosci. 2008;2:3. doi: 10.3389/neuro.03.003.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Buchanan J.T., Moore L.E., Grillner S. Synaptic potentials and transfer functions of lamprey spinal neurons. Biol. Cybern. 1992;67:123–131. doi: 10.1007/BF00201019. [DOI] [PubMed] [Google Scholar]
- 31.Waters J., Helmchen F. Background synaptic activity is sparse in neocortex. J. Neurosci. 2006;26:8267–8277. doi: 10.1523/JNEUROSCI.2152-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Deisz R.A., Fortin G., Zieglgänsberger W. Voltage dependence of excitatory postsynaptic potentials of rat neocortical neurons. J. Neurophysiol. 1991;65:371–382. doi: 10.1152/jn.1991.65.2.371. [DOI] [PubMed] [Google Scholar]
- 33.Thomson A.M., Girdlestone D., West D.C. Voltage-dependent currents prolong single-axon postsynaptic potentials in layer III pyramidal neurons in rat neocortical slices. J. Neurophysiol. 1988;60:1896–1907. doi: 10.1152/jn.1988.60.6.1896. [DOI] [PubMed] [Google Scholar]
- 34.Stuart G., Sakmann B. Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron. 1995;15:1065–1076. doi: 10.1016/0896-6273(95)90095-0. [DOI] [PubMed] [Google Scholar]
- 35.Fricker D., Miles R. EPSP amplification and the precision of spike timing in hippocampal neurons. Neuron. 2000;28:559–569. doi: 10.1016/s0896-6273(00)00133-1. [DOI] [PubMed] [Google Scholar]
- 36.Vervaeke K., Hu H., Storm J.F. Contrasting effects of the persistent Na+ current on neuronal excitability and spike timing. Neuron. 2006;49:257–270. doi: 10.1016/j.neuron.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 37.Andreasen M., Lambert J.D. Somatic amplification of distally generated subthreshold EPSPs in rat hippocampal pyramidal neurones. J. Physiol. 1999;519:85–100. doi: 10.1111/j.1469-7793.1999.0085o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Farries M.A., Kita H., Wilson C.J. Dynamic spike threshold and zero membrane slope conductance shape the response of subthalamic neurons to cortical input. J. Neurosci. 2010;30:13180–13191. doi: 10.1523/JNEUROSCI.1909-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Prescott S.A., De Koninck Y. Integration time in a subset of spinal lamina I neurons is lengthened by sodium and calcium currents acting synergistically to prolong subthreshold depolarization. J. Neurosci. 2005;25:4743–4754. doi: 10.1523/JNEUROSCI.0356-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Branco T., Tozer A., Sternson S.M. Near-perfect synaptic integration by Nav1.7 in hypothalamic neurons regulates body weight. Cell. 2016;165:1749–1761. doi: 10.1016/j.cell.2016.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Magee J.C. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J. Neurosci. 1998;18:7613–7624. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ceballos C.C., Li S., Leão R.M. Ih equalizes membrane input resistance in a heterogeneous population of fusiform neurons in the dorsal cochlear nucleus. Front. Cell. Neurosci. 2016;10:249. doi: 10.3389/fncel.2016.00249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bose A., Golowasch J., Nadim F. The role of linear and voltage-dependent ionic currents in the generation of slow wave oscillations. J. Comput. Neurosci. 2014;37:229–242. doi: 10.1007/s10827-014-0498-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tamagnini F., Novelia J., Randall A.D. Altered intrinsic excitability of hippocampal CA1 pyramidal neurons in aged PDAPP mice. Front. Cell. Neurosci. 2015;9:372. doi: 10.3389/fncel.2015.00372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hage T.A., Salkoff L. Sodium-activated potassium channels are functionally coupled to persistent sodium currents. J. Neurosci. 2012;32:2714–2721. doi: 10.1523/JNEUROSCI.5088-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wessel R., Kristan W.B., Jr., Kleinfeld D. Supralinear summation of synaptic inputs by an invertebrate neuron: dendritic gain is mediated by an “inward rectifier” K+ current. J. Neurosci. 1999;19:5875–5888. doi: 10.1523/JNEUROSCI.19-14-05875.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ferreira H.G., Marshall M.W. Cambridge University Press; Cambridge, United Kingdom: 1985. The Biophysical Basis of Excitability. [Google Scholar]
- 48.Remme M.W., Rinzel J. Role of active dendritic conductances in subthreshold input integration. J. Comput. Neurosci. 2011;31:13–30. doi: 10.1007/s10827-010-0295-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Moore L.E., Buchanan J.R., Murphey C.R. Anomalous increase in membrane impedance of neurons during NMDA activation. In: Eeckman F.H., editor. Computation in Neurons and Neural Systems. Kluwer Academic; 1994. pp. 21–26. [Google Scholar]
- 50.Crunelli V., Mayer M.L. Mg2+ dependence of membrane resistance increases evoked by NMDA in hippocampal neurones. Brain Res. 1984;311:392–396. doi: 10.1016/0006-8993(84)90107-0. [DOI] [PubMed] [Google Scholar]
- 51.Moore L.E., Buchanan J.T., Murphey C.R. Localization and interaction of N-methyl-D-aspartate and non-N-methyl-D-aspartate receptors of lamprey spinal neurons. Biophys. J. 1995;68:96–103. doi: 10.1016/S0006-3495(95)80163-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sutor B., Jordan W., Zieglgänsberger W. Evidence for a magnesium-insensitive membrane resistance increase during NMDA-induced depolarizations in rat neocortical neurons in vitro. Neurosci. Lett. 1987;75:317–322. doi: 10.1016/0304-3940(87)90542-8. [DOI] [PubMed] [Google Scholar]
- 53.MacDonald J.F., Porietis A.V., Wojtowicz J.M. L-Aspartic acid induces a region of negative slope conductance in the current-voltage relationship of cultured spinal cord neurons. Brain Res. 1982;237:248–253. doi: 10.1016/0006-8993(82)90575-3. [DOI] [PubMed] [Google Scholar]
- 54.Schwindt P.C., Crill W.E. Amplification of synaptic current by persistent sodium conductance in apical dendrite of neocortical neurons. J. Neurophysiol. 1995;74:2220–2224. doi: 10.1152/jn.1995.74.5.2220. [DOI] [PubMed] [Google Scholar]
- 55.Zsiros V., Hestrin S. Background synaptic conductance and precision of EPSP-spike coupling at pyramidal cells. J. Neurophysiol. 2005;93:3248–3256. doi: 10.1152/jn.01027.2004. [DOI] [PubMed] [Google Scholar]
- 56.Hoffman D.A., Magee J.C., Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- 57.Mathews P.J., Jercog P.E., Golding N.L. Control of submillisecond synaptic timing in binaural coincidence detectors by Kv1 channels. Nat. Neurosci. 2010;13:601–609. doi: 10.1038/nn.2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stuart G. Voltage-activated sodium channels amplify inhibition in neocortical pyramidal neurons. Nat. Neurosci. 1999;2:144–150. doi: 10.1038/5698. [DOI] [PubMed] [Google Scholar]
- 59.Hardie J.B., Pearce R.A. Active and passive membrane properties and intrinsic kinetics shape synaptic inhibition in hippocampal CA1 pyramidal neurons. J. Neurosci. 2006;26:8559–8569. doi: 10.1523/JNEUROSCI.0547-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]