Abstract
The heterologous overexpression of integral membrane proteins in Escherichia coli often yields insufficient quantities of purifiable protein for applications of interest. The current study leverages a recently demonstrated link between co-translational membrane integration efficiency and protein expression levels to predict protein sequence modifications that improve expression. Membrane integration efficiencies, obtained using a coarse-grained simulation approach, robustly predicted effects on expression of the integral membrane protein TatC for a set of 140 sequence modifications, including loop-swap chimeras and single-residue mutations distributed throughout the protein sequence. Mutations that improve simulated integration efficiency were 4-fold enriched with respect to improved experimentally observed expression levels. Furthermore, the effects of double mutations on both simulated integration efficiency and experimentally observed expression levels were cumulative and largely independent, suggesting that multiple mutations can be introduced to yield higher levels of purifiable protein. This work provides a foundation for a general method for the rational overexpression of integral membrane proteins based on computationally simulated membrane integration efficiencies.
Keywords: flow cytometry, membrane protein, molecular dynamics, protein expression, protein translocation, Sec translocon, TatC, topogenesis
Introduction
Integral membrane proteins (IMPs)4 play crucial roles in the transport of molecules, energy, and information across the membrane and are an important focus of structural and biophysical studies. However, the production of sufficient levels of IMPs is a limiting factor in their characterization (1). Even among homologous IMP sequences, expression levels can vary widely (1–6), and the mechanistic basis for this variability is often unclear. Extensive efforts have been committed to identify IMP sequences, expression conditions, and host modifications that yield IMP expression at sufficient levels for further study (7–10). Despite these efforts, general guidelines for successful overexpression for IMPs are lacking.
Biogenesis of IMPs in Escherichia coli involves multiple steps that are potential bottlenecks for overexpression, including correct targeting to the inner membrane (11, 12), membrane integration (2, 13–17), and folding (18–21). For a given sequence, understanding how each of these steps affects observed expression levels may lead to improved strategies for IMP overexpression.
Previous work indicates that the Sec-facilitated membrane integration step of biogenesis is a limiting factor in the overexpression of the TatC IMP (2). Sequence changes in the C-tail that alter the efficiency of membrane integration efficiency, determined either from coarse-grained (CG) simulations or experimentally, were shown to correlate with experimentally observed IMP expression levels. Further work is necessary to explore the generality of this link and its potential for enabling the rational enhancement of IMP expression.
The current study demonstrates the predictive capacity of simulated integration efficiency for experimental expression by examining a wide range of sequence modifications to TatC homologs across the protein sequence. The studied sequence modifications include point mutations, loop-swap chimeras, and double-loop-swap chimeras, and it is shown that the simulated integration efficiency, as predicted by CG simulations, broadly correlates with IMP expression. An ampicillin resistance assay is employed to directly validate the simulated integration efficiencies and to confirm the mechanistic interpretation. We further demonstrate cumulative and largely independent effect of multiple mutations on both the simulated integration efficiency and the experimentally observed expression levels. Finally, we provide a methodology that can be used to generally identify sequence regions in other IMPs that may exhibit correlations like those elucidated here for TatC, yielding a broadly applicable tool for the computational prediction of sequence modifications that improve IMP overexpression.
Results
TatC expression levels are changed by loop swaps
TatC is an IMP with six transmembrane domains and a cytoplasmic N and C terminus (Fig. 1A) that is a component of the bacterial twin-arginine translocation pathway (22). A representative pool of 111 loop-swap chimeras was generated by replacing a single loop in one of 10 wild-type TatC homologs (Aquifex aeolicus, Bordetella parapertussis, Campylobacter jejuni,Deinococcus radiodurans, E. coli, Hydrogenivirga species 128-5-R1, Mycobacterium tuberculosis, Staphylococcus aureus, Vibrio cholera, and Wolinella succinogenes) with the corresponding loop from one of the other nine homologs (Fig. 1A). Loop domains were identified by sequence alignment and membrane topology predictions (23) (sequences listed in supplemental Table 1). Both mutant and wild-type expression levels were determined using a C-terminal GFP tag (24) (see “Experimental procedures”), and the relative effect of each mutation on expression was quantified in terms of the ratio,
| (Eq. 1) |
Values greater than unity (>1.0) indicate improvement in expression due to the sequence modification.
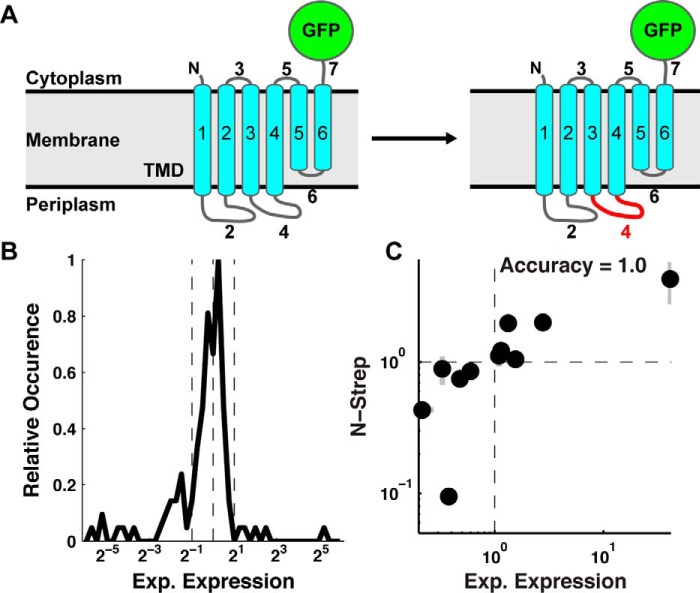
Figure 1.
TatC loop-swap chimeras demonstrate a range of expression outcomes. A, a schematic of a wild-type (left) and loop-swap chimera (right) sequence for the TatC IMP with a C-terminal GFP tag. Corresponding loop domains are swapped between TatC homologs to create loop-swap chimeras, as illustrated for loop 4. B, distribution of experimental expression values (mutant/wild-type) for the pool of 111 single-loop-swap TatC chimeras. Vertical dashed lines indicate 2-fold change in experimental expression about the mean of the distribution. C, correlation between experimental expression levels quantified using a C-terminal GFP tag (Exp. Expression) versus using an N-terminal Strep tag (N-strep). Error bars, S.E.
The set of loop swaps exhibit a wide range of values for this experimental expression ratio, as shown in Fig. 1B. The effect of single-loop swaps ranges from 0.02- to 40-fold changes, with 43% of the studied loop swaps yielding improved expression. Control studies were performed to confirm that the C-terminal GFP tag does not substantially alter the experimentally measured expression levels. A set of 11 single-loop-swap chimeras and their corresponding wild-type sequences were cloned into an alternative construct containing an N-terminal Strep tag (WSHPQFEK) with no C-terminal tag (see “Experimental procedures”). The experimental expression ratio in Equation 1 was measured for each N-terminal Strep tag construct and compared against quantification via C-terminal GFP fluorescence. Fig. 1C shows this comparison, revealing agreement for all studied cases between measured expression levels using either tag. This result, additionally supported by extensive studies in which IMP-GFP fluorescence is shown to be a robust quantifier of expression (24, 25), indicates that the experimental expression outcomes are robust with respect to the means of quantifying the expression levels.
Simulated integration efficiency is predictive of TatC expression
Correlation between simulated integration efficiency and experimentally observed expression levels was previously identified in TatC based on a limited set of mutations (2); here, we systematically test the predictive capacity of simulated integration efficiency for expression in a diverse set of 111 loop-swap chimeras. CG simulations were performed for each chimera and wild-type sequence (see “Experimental procedures”), and the effect of each mutation on simulated integration efficiency was quantified in terms of the ratio,
| (Eq. 2) |
where PCin corresponds to the fraction of simulated trajectories for which the C-tail domain is correctly localized with respect to the cell membrane; below, we investigate the use of sequence features other than the C-tail for quantifying integration efficiency. Receiver operator characteristic (ROC) curves (Fig. 2A) (26) provide a statistical measure of the predictive capacity of simulated integration efficiency, with values in excess of 0.5 for the area under the ROC curve (AUC) indicating predictive capacity.
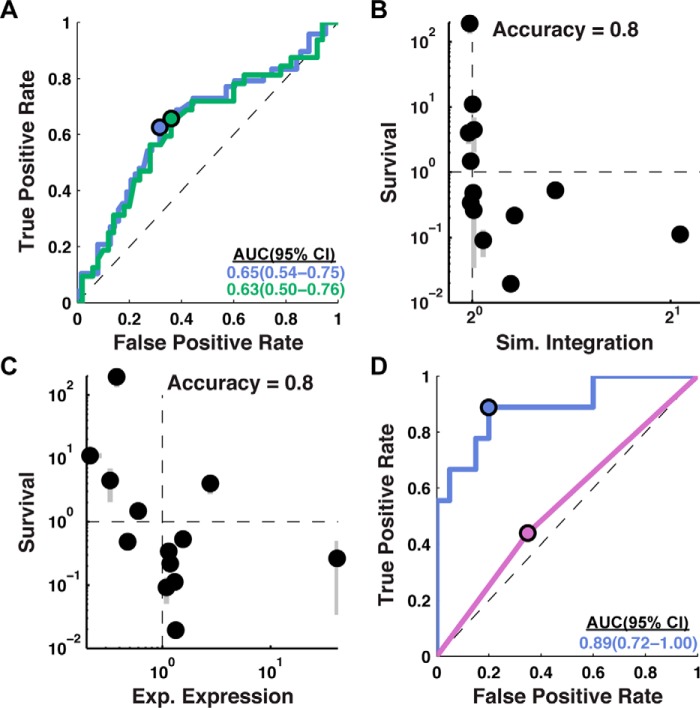
Figure 2.
C-tail localization is predictive of experimental expression. A, the predictive capacity of simulated integration efficiency for experimental expression is assessed using an ROC curve for all single-loop-swap chimeras (blue; 111 sequence modifications) and all single-loop-swap chimeras excluding those in which the C-tail was swapped (green; 82 sequence modifications). Significant predictive capacity is observed for both sets, as indicated by the AUC values (bottom right, in colors matching the corresponding ROC curves). B, comparison of simulated integration efficiency and ampicillin resistance for TatC loop-swap chimeras. A negative correlation between survival and simulated integration efficiency indicates that the C-tail topology predicted by the CG simulations occurs in vivo. One sequence had a survival level below the plotted range. The reported measure of accuracy corresponds to the fraction of sequences for which the simulation predicts changes in topology that are consistent with the direction of changes in the experimental expression. C, comparison of experimental expression with relative ampicillin resistance for TatC loop-swap chimeras. A negative correlation between survival and experimental expression indicates that the C-tail mislocalizes in poorly expressing chimeras, consistent with the mechanism predicted by the CG simulations. One sequence had a survival level below the plotted range. D, the predictive capacity of simulated integration efficiency for experimental expression assessed using a ROC curve for TatC point mutants (29 sequence modifications). Simulated integration efficiency from the CG model (blue) has greater predictive capacity for experimental expression than the positive inside rule (purple). Error bars, S.E.
ROC curves in Fig. 2A are shown for data sets corresponding to all 111 loop-swap chimeras (blue) and to the subset of 82 loop-swap chimeras that exclude C-tail swaps (green). This plot demonstrates the predictive capacity of simulated integration efficiency for experimental expression, with AUC values exceeding 0.5 beyond 95% statistical confidence. The similarity of the two curves indicates that the predictive capacity of the simulated integration efficiency is relatively insensitive to whether the loop swap involves the C-tail domain.
Also, indicated in Fig. 2A (blue and green dots) are the points along the ROC curve that correspond to the cut-off value (defining positive prediction) for the simulated integration efficiency ratio in Equation 2 that offers the greatest predictive capacity for experimentally observed expression; for both data sets, this optimal value is found to be 1.0, indicating that increases or decreases in the simulated integration efficiency straightforwardly predict the corresponding changes in experimental expression levels.
Experimental confirmation of simulated integration efficiency values
To experimentally confirm that the in vivo integration efficiency is correctly described by the CG simulations, we apply a previously developed ampicillin resistance assay (2) (see “Experimental procedures”). Upon fusing a C-terminal β-lactamase tag to the TatC sequence, ampicillin resistance is imparted when the C-tail is mislocalized (i.e. oriented into the periplasm) during expression. Therefore, an increase in ampicillin resistance is a direct in vivo test of any decrease in correct C-tail localization predicted from the CG simulations.
The survival metric reported in Fig. 2B is the ratio of colonies observed following ampicillin treatment between a loop-swap chimera and the corresponding wild-type TatC sequence. For a subset of 14 loop-swap chimeras, Fig. 2B compares the relative survival to simulated integration efficiency; this subset was selected randomly from the full set of single-loop swap chimeras and includes five C-tail-swap chimeras (sequences listed in supplemental Table 1). For 11 of these 14 cases, the corresponding data points in Fig. 2B fall into the diagonal quadrants of the plot, indicating good agreement between the experimental and simulated measures of integration efficiency (accuracy = 0.8 ± 0.2, 95% confidence interval).
Fig. 2C plots the correlation between ampicillin resistance and experimental expression for the same set of loop-swap chimeras. As expected (given the positive correlation between simulated integration efficiency and experimental expression in Fig. 2A and the negative correlation between the simulated integration efficiency and the survival assay in Fig. 2B), Fig. 2C indicates strong negative correlation between ampicillin resistance and experimental expression, with 11 of the 14 data points falling in the diagonal quadrants (accuracy = 0.8 ± 0.2, 95% confidence interval). Taken together, Fig. 2, B and C, demonstrates that simulated integration is a reliable predictor of the C-tail orientation, which is in turn a reliable predictor of experimental expression.
The effect of point mutations on integration efficiency is predictive for expression
Rather than loop-swap mutations, we now consider the effect of single-point mutations on both experimental expression and simulated integration efficiency. Point mutants introduce minimal changes to the wild-type sequence and are often used for protein sequence design (27–29). The blue curve in Fig. 2D shows the ROC curve for a set of 29 point mutants; each exhibits a single mutation at a position in the wild-type sequence that is not universally conserved across homologs, with the mutation either increasing or decreasing the charge at that position (sequences listed in supplemental Table 1). The blue curve in Fig. 2D indicates that the simulated integration efficiencies from the CG method have predictive capacity (AUC = 0.89) that is even higher than was found in Fig. 2A for loop-swap mutations (AUC = 0.65).
For comparison, the purple curve in Fig. 2D explores the predictive capacity of a simpler measure of integration efficiency based only on the positive inside rule, which observes that positively charged residues are more likely to be localized to the cytosolic side of the cell membrane (30) and that modification of the positively charged residues can change IMP topology (19–21, 31). As employed here, the positive inside rule simply predicts that a mutation will have increased integration efficiency (and thus a positive effect on expression) if it increases the net charge of the cytosolic loops minus the net charge of the periplasmic loops, and vice versa. It is clear from the Fig. 2D that in contrast to the prediction of the CG model (blue), the positive inside rule has little predictive capacity for expression when employed in this way. These results emphasize that the molecular processes and interactions that govern IMP integration are more complex, and they are more completely described using the CG simulations than by simple analysis of charged residues.
The effects of sequence mutations on simulated integration efficiency and experimental expression are largely independent
To determine whether multiple sequence modifications have a combinatory effect on expression and simulated integration efficiency, a set of 12 double-loop-swap chimeras was generated (sequences listed in supplemental Table 1) and tested against the corresponding effect of the constituent single-loop-swap mutations. Fig. 3 shows that for both simulated integration efficiency (A) and experimental expression (B), comparison of the -fold change (Equations 1 and 2) observed for the double-loop-swap chimera is strongly correlated with the product of -fold changes for the corresponding single-loop-swap chimeras (Pearson's correlation coefficient, r = 0.9). Linear fits of the data are plotted as solid lines. The slope of the linear fits for both simulated integration efficiency (Fig. 3A, slope = 0.8) and experimental expression (Fig. 3B, slope = 0.7) deviate only slightly from unity, indicating that the effect of each mutation is largely independent. The results in Fig. 3 suggest that the introduction of multiple mutations is a viable strategy for enhancing expression and that simulated integration efficiency largely captures the effect of these multiple mutations.
Figure 3.
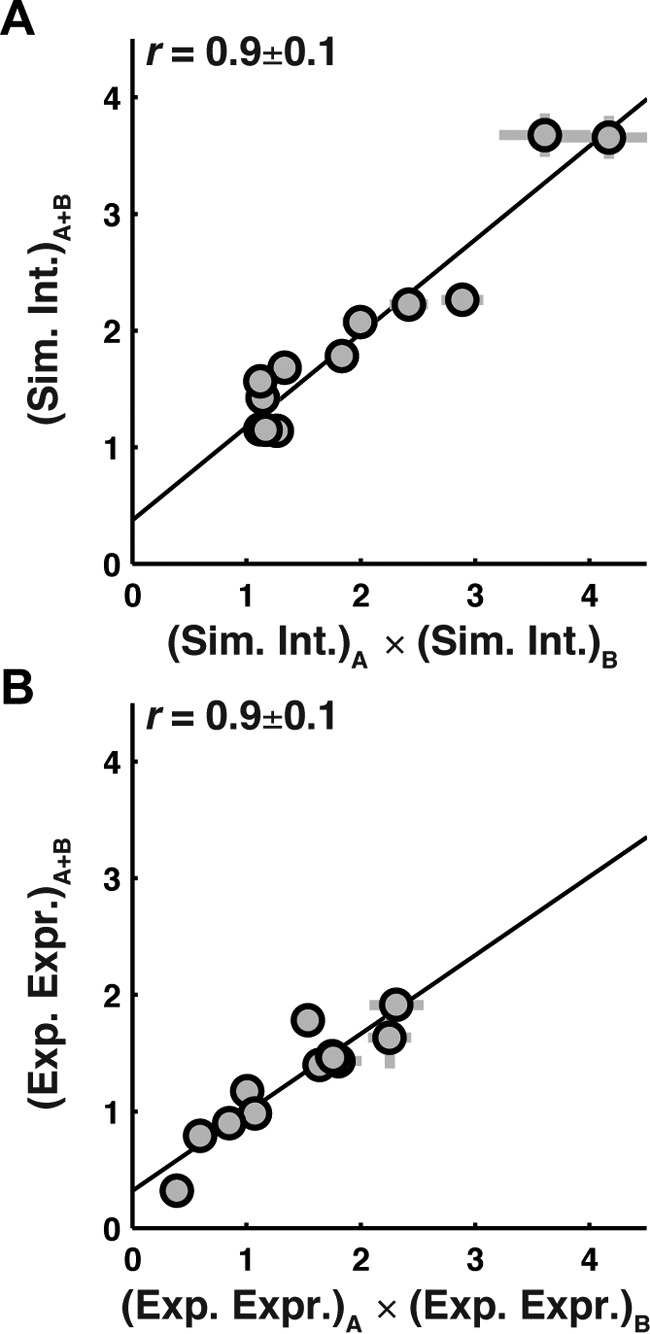
Effect of multiple sequence modifications on simulated integration efficiency and experimental expression is cumulative and nearly independent. A, the simulated integration efficiency of double-loop-swap chimeras (vertical axis) versus the product of the simulated integration efficiencies of the constituent single-loop-swap chimeras (horizontal axis). The guideline with a slope of 0.8 indicates that the effect of loop-swap mutations on simulated integration efficiency is cumulative and largely independent. B, the experimental expression of double-loop-swap chimeras (vertical axis) versus the product of the experimental expression values of the constituent single-loop-swap chimeras (horizontal axis). The guideline with a slope of 0.7 indicates that the effect of loop-swap mutations on experimental expression is also cumulative and largely independent. Error bars, S.E.
TatC topology features, other than C-tail localization, are not predictive for expression
Using the fraction of CG trajectories for which the TatC C-tail reaches correct localization with respect to the membrane as the measure of successful IMP integration, the results in Fig. 2, along with previous work (2), support the conclusion that simulated integration efficiency reliably predicts experimental expression in TatC. However, other features of the TatC topology (such as the localization of other soluble loops) could have been employed to quantify IMP integration from the CG simulations. We now investigate the predictive capacity of the CG simulations for experimental expression, using alterative measures of IMP integration.
The alternative measures of IMP integration that are considered include 1) p(i), the fraction of CG trajectories for which soluble loop i reaches correct localization with the respect to the membrane, 2) p(All), the fraction of CG trajectories for which all soluble loops reach correct localization, and 3) p(N), the fraction of CG trajectories for which correct localization is achieved for the soluble loop that includes the mutation. In this notation, the previously discussed measure of IMP integration based on the C-tail is given by p(7).
Using each of these measures of IMP integration, we obtained ROC curves that compare the simulated integration efficiency with observed experimental expression, and the corresponding AUC values are presented in Fig. 4A. In all cases, the ROC curves were determined using the data set with all 140 TatC loop-swap and point mutations discussed above. The AUC for the C-tail measure (p(7)) is 0.73, indicating the strong predictive capacity of this measure. However, it is clear that all other measures of integration efficiency fail to offer predictive capacity (yielding AUC values that are within 95% confidence of 0.5). Even when the measure of integration efficiency is based on the localization of the loop in which the mutation occurs (i.e. p(N)), the predictive capacity is significantly worse than using the C-tail (i.e. p(7)).
Figure 4.
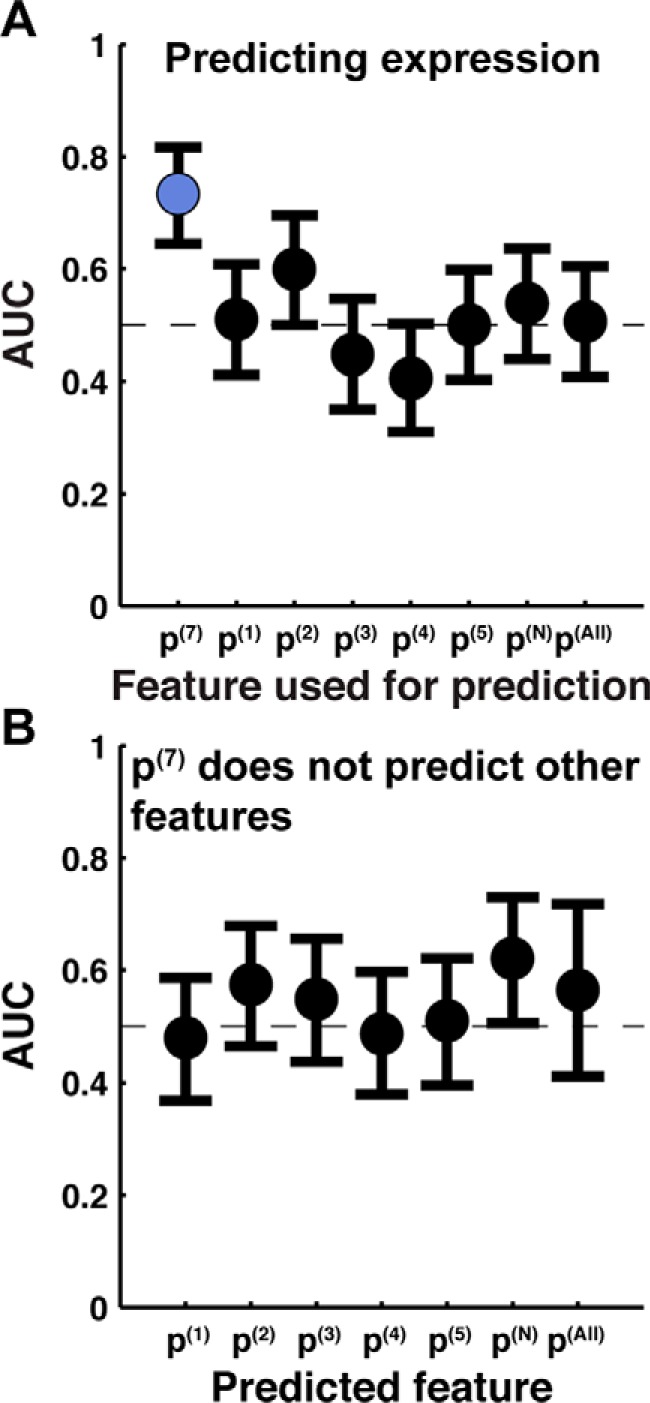
Simulated integration efficiency using the C-tail (p(7)) measure of integration is predictive of experimental expression of TatC, whereas other measures are not. A, AUC obtained by using various measures of integration efficiency (p(1), p(2), p(3), p(4), p(5), p(7), p(N), and p(All); defined under “Results”) to predict experimental expression. p(7) (i.e. C-tail localization) is the only measure with statistically significant predictive capacity. B, AUC obtained by using C-tail localization (p(7)) to predict other measures of integration efficiency. Error bars, 95% confidence intervals.
The results in Fig. 4A raise the question of the underlying mechanism for the predictive capacity of the C-tail localization for TatC. One hypothesis is that the C-tail acts as “aggregator” of all preceding errors in the IMP integration, providing a cumulative report on the TatC topology. A second hypothesis is that the C-tail is akin to a “canary in the coal mine,” particularly sensitive to mutations, regardless of where in the sequence the mutation occurs. Finally, a third hypothesis is that the unique features of the C-tail could make it more amenable to accurate description by the CG method than the other TatC loops.
We directly tested the aggregator hypothesis by investigating the degree to which the C-tail measure of integration efficiency is predictive of the alternative measures. Fig. 4B presents the resulting AUC values, obtained from ROC curves for p(7) versus the alternative measures, using the full data set of 140 TatC loop-swap and point mutations. It is clear from the figure that there is no significant correlation between p(7) and the other measures, a finding that is inconsistent with the aggregator hypothesis. Fig. 4 (both A and B) emphasizes that the C-tail is a unique reporter of TatC integration efficiency, at least among the diverse set of measures considered here.
The second hypothesis reasons that the C-tail of TatC is particularly sensitive to sequence modification and is thus a useful reporter of integration efficiency, regardless of where in the sequence the mutation occurs. Although this hypothesis is difficult to test directly, it is consistent with the results from the ampicillin resistance assay, which found that C-tail localization was substantially impacted by mutations in other parts of the TatC sequence, even for mutations in other loops. Possibly contributing to the conformational sensitivity of the C-tail is that the preceding TM domains (TM5 and TM6) are relatively short and do not fully span the cell membrane in the A. aeolicus TatC (AaTatC) structure (32, 33).
With regard to the third hypothesis, we note that the CG model does not explicitly describe sequence-specific interactions and packing effects among the TM domains; the model is thus expected to be most reliable for describing the topology of TM domains with weak tertiary interactions, such as the C-tail of TatC (32, 33). This explanation leaves open the possibility that improvements to the CG model in terms of its description of tertiary IMP interactions could lead to more robust measures of simulated integration efficiency (34).
The analysis in this section is central to the question of how generally the CG simulations will be able to predict membrane protein expression for IMPs other than TatC. It is very possible that for other IMPs, the C-tail localization will not be the most useful measure of IMP integration for predicting expression levels (35). Below, we thus describe a simple strategy for identifying a useful measure of IMP integration on the basis of limited experimental expression data.
Predictors for expression can be identified from limited training data
Utilization of simulated integration efficiency to predict IMP expression in IMPs other than TatC requires a useful measure of IMP integration to compute from the CG simulations. The results in Figs. 2 and 3 use C-tail localization for this purpose, but as is illustrated in Fig. 4, other reasonable measures of simulated integration efficiency are not predictive for expression. For the study of an arbitrary IMP, we are thus faced with determining, as efficiently as possible, a measure of simulated integration efficiency to compute from the CG method.
Here, we present a simple strategy for identifying a useful measure of IMP integration, based on comparison of the CG simulations with limited experimental expression data. For the case of TatC, Fig. 5 presents the results of an analysis in which the predictive capacity of various candidate measures of IMP integration is evaluated using a limited number of comparisons between experimental expression measurements and CG simulations. We consider randomly selected subsets of the full data set of 140 TatC loop-swap and point mutations, and for each subset, we employ the various measures of integration efficiency to evaluate the AUC that reflects the predictive capacity of simulated integration efficiency in comparison with experimental expression data. As a function of the subset size, the figure plots the fraction (M(i)) of random subsets for which each measure of integration efficiency (indexed by i) yields the highest AUC value. These results show that with expression data for only a small training set, the most predictive measure of IMP integration can be identified. In the case of TatC, <20 sequences are needed to determine p(7) as most predictive.
Figure 5.
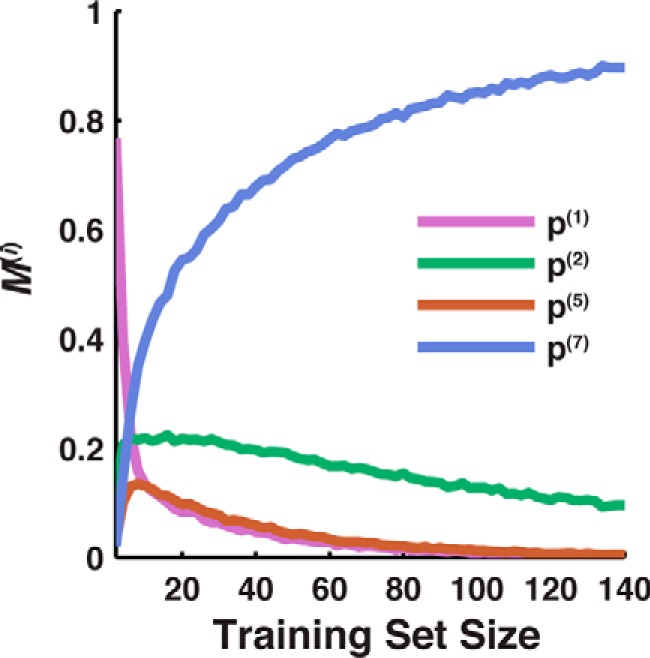
Determination of useful measures of integration efficiency based on limited data. Shown is the probability that each measure of integration is the most predictive for expression (M(i), described under “Results”), based on training data sets of increasing size. The p(7) measure (based on C-tail localization) is identified as the most predictive based on data sets with <20 sequences. For clarity, only features with values of M(i) > 0.1 are shown in the plot; not shown but included in the analysis are p(3), p(4), p(N), and p(All).
The strategy in Fig. 5 illustrates that for cases in which limited IMP expression data are available, a useful measure of IMP integration from the CG simulations can be identified without other prior knowledge, thus yielding a general strategy for enhancing IMP expression in systems other than TatC. However, there will be cases in which even limited IMP expression data are not available. For these cases, a reasonable strategy is to use a measure of IMP integration that involves a sequence domain that is expected to be prone to mislocalization with respect to the cell membrane. Analyses of sequence conservation (36) and residue co-evolution (37–39) provide reasonable strategies for identifying such sequence domains. For the case of TatC, this approach would again be consistent with the use of the C-tail for measuring of integration efficiency, because this sequence domain is not conserved across homologs and was not resolved in the reported TatC crystal structures (32, 33).
Discussion
We address the problem of heterologous IMP expression in E. coli by utilizing the link between simulated integration efficiency and experimental expression outcomes (2) to predict sequence modifications that improve expression for the TatC. Simulated integration efficiency is determined using CG molecular dynamics of the co-translational integration of the IMP via the Sec translocon (17) and is compared against experimental expression measurements for a set of 140 TatC sequence modifications. For both loop-swap modification (Fig. 2A) and point mutations (Fig. 2D), the simulated integration efficiency is shown to provide clear predictive capacity of experimental expression, and the effect of multiple sequence modifications (Fig. 3) is shown to be cumulative and likewise captured by the simulated integration efficiency. For the combined set of 140 sequence modifications, the diagnostic odds ratio (40) obtained from comparison of simulated integration efficiency with experimental expression yields a value of 3.9 (1.9–9.1, 95% confidence interval), indicating that sequence modifications that improve simulated integration efficiency are 4-fold enriched in terms of improved experimental expression.
Although successful strategies for improving IMP overexpression have been demonstrated previously (7–9), these approaches leave unclear the mechanism by which expression is improved, requiring a case-by-case implementation that can be costly in terms of both time and material resources. The strategy employed in the current work aims to optimize IMP expression on the basis of a particular step in IMP biogenesis: successful integration into the membrane and adoption of the correct multispanning topology. Additional work is needed to demonstrate the degree to which improving membrane integration efficiency will lead to improved expression levels in other IMPs, but the central role of membrane integration in IMP biogenesis suggests that the approach may prove successful for other IMPs.
Finally, we note that the current work is unique in that CG simulations form the basis for the prediction of enhanced IMP expression. Although molecular simulations have been successfully employed in the context of other biomolecular design problems, such as the de novo protein structure design (41–43) or enzyme design (44–46), the current work suggests that rational enhancement of IMP expression is a new application domain in which molecular simulations may prove useful.
Experimental procedures
Cloning
All TatC coding sequences were either created using primer extension or synthesized by Twist Bioscience (San Francisco, CA). Loop-swap chimeras involved modification of loops 1–5 and 7, avoiding the short loop 6. The pool of 111 loop-swap chimera sequences was selected from all 540 possible combinations. Each wild-type homolog was used between 6 and 15 times as a parent and between 7 and 19 times as a source for the mutant loop, and each loop was mutated between 8 and 29 times. Point mutants were chosen to affect a change in charge through mutation of neutral residues to charged residues or through mutation of charged residues to the opposite charge. All sequences used are provided in supplemental Table 1. Each loop-swap chimera coding sequence was cloned into the pET28(a+)-GFP-ccdB vector (2, 47) using the Gibson cloning protocol (48), resulting in each IMP possessing a C-terminal GFP tag. For constructs containing the β-lactamase tag, the GFP sequence was replaced with a β-lactamase sequence using Gibson cloning. For constructs containing the N-terminal Strep tag, the GFP and poly-His sequence were removed during PCR, and the Strep tag was added using primer extension; the final vectors were constructed using Gibson cloning.
Heterologous expression in E. coli
Heterologous expression of IMPs in E. coli was performed as described previously (2). In short, IMPs were expressed in BL21 Gold (DE3) (Agilent Technologies, Santa Clara, CA) cells at 16 °C for ∼16 h before either flow cytometry, Western blot, or ampicillin resistance analysis.
Flow cytometry
Flow cytometry was performed as described previously (2). In short, cultures of cells expressing TatC IMPs with a C-terminal GFP tag were resuspended in PBS and subjected to flow cytometry. Whole-cell fluorescence from the B1/FITC channel was measured using a MACSQuant10 Analyzer (Miltenyi Biotec, Bergisch Galbach, Germany). Mean fluorescence values were calculated using FlowJo (Ashland, OR).
Western blotting
All samples of cells expressing IMPs with an N-terminal Strep tag were subjected to the following protocol for Western blot analysis. Samples were normalized to an A600 of 3.0 in PBS and subjected to three freeze-thaw cycles using liquid nitrogen and applied to 10% SDS-PAGE followed by Western blotting. Relative protein levels were determined by incubation of the Western blot membrane with an anti-Strep tag primary rabbit antibody (NWSHPQFEK antibody, GenScript, Piscataway, NJ) followed by incubation with an IRDye® 800CW donkey anti-rabbit secondary antibody (LI-COR, Lincoln, NE) and visualization using a LI-COR IR Western blot scanner (LI-COR, Lincoln, NE). Relative band intensities were quantified using ImageJ (49).
Description of the CG simulations
We applied a previously developed CG approach (2, 17, 50) to simulate the minute-time scale dynamics of co-translational membrane integration via the Sec translocon. The CG model was applied and implemented as described in detail (2), with key features of the CG model summarized here.
The CG simulations explicitly describe the configurational dynamics of the IMP, conformational gating of the Sec translocon lateral gate, and ribosomal translation (at 24 residues/s). The IMP is represented as a freely jointed chain of CG beads, where each CG bead represents three amino acids and has a diameter of 8 Å, equal to the Kuhn length of a polypeptide chain (51, 52). To avoid a frameshift in the mapping of amino acids to CG beads upon a loop-swap sequence modification, dummy atoms were introduced, as described previously (2). Bonding interactions between neighboring CG beads are described using the finite extension nonlinear elastic potential (53), short-range non-bonding interactions are modeled using a Lennard–Jones potential, and electrostatic interactions are modeled using the Debye-Hückel potential. Factors that prevent backsliding of large translocated hydrophilic loops are included, as described (17), for consistency with previous work but have only a modest effect in TatC. Solvent interactions are described using a position-dependent potential based on the water–membrane transfer free energy for each CG bead (2).
The configuration of the IMP is time-evolved using overdamped Langevin dynamics, with the CG beads confined to a two-dimensional subspace that runs along the axis of the translocon channel and between the two helices of the LG. Conformational gating of the LG corresponds to the LG helices moving out of the place of confinement for the IMP, allowing the IMP to pass into the membrane bilayer. The rate of stochastic LG opening and closing is dependent on the sequence of the CG beads that occupy the translocon channel (17, 54). Ribosomal translation is directly simulated via growth of the IMP at the ribosomal exit channel; throughout translation, the C terminus of the IMP is held fixed, and new beads are sequentially added at a rate of 24 residues/second. Upon completion of translation, the C terminus is released from the ribosome.
Trajectories use a step size of 100 ns for time integration and are terminated 31 s after the end of translation. For each protein sequence, at least 400 independent trajectories are calculated.
Determination of measures of integration from CG simulations
The simulated integration efficiency for a protein sequence was calculated from the CG model as described previously (2). The topology of a protein was analyzed over the last 6 s of the CG simulation trajectories, starting 25 s after the end of protein translation by the ribosome. For each loop, i, the location of the loop during this time-window is described by a variable λi, where λi = 1 if the loop is in the cytosol, λi = −1 if the loop is in the periplasm, and λi = 0 otherwise. For each trajectory, we assessed whether a given measure of integration is visited during the analysis time window. The various measures of integration efficiency used in this work are described throughout.
Ampicillin resistance assay
The ampicillin resistance assay was performed as described previously (2). In short, cells that had expressed IMPs with a C-terminal β-lactamase tag overnight at 16 °C were resuspended to an A600 of 0.1 and grown to an A600 of 0.5, after which ampicillin was added; cells were then incubated for an additional 1.5 h, followed by plating on kanamycin LB agar plates. The relative number of observed colonies between loop-swap chimera and wild-type was used to determine the change in C-tail translocation, with a ratio > 1 indicating an increase in translocation of the C-tail to the periplasm due to the sequence modification.
Statistical significance calculations
Reported experimental measurements, including values for experimental expression, survival, and protein levels quantified using Western blotting, correspond to averages over at least three independent trials, with error bars representing S.E. unless otherwise noted. Simulated integration efficiencies represent the average outcome of at least 400 independent CG simulation trajectories, with error bars indicating S.E. Confidence intervals on AUC values were determined by bootstrapping. Specifically, 1,000,000 samples of simulated integration and expression pairs, with size equal to the set of sequence modification, were drawn with replacement from the set of sequence modifications; the AUC was calculated for each sample, and the relevant percentile of the resulting AUC value distribution determined the confidence intervals.
A similar procedure was used to generate the randomly selected subsets of the full data set of 140 TatC loop-swap and point mutations used in Fig. 5. For each subset size, 1,000,000 independent samples of that size were chosen with replacement from the full data set of 140 TatC loop-swap and point mutations.
Author contributions
M. J. M. N., S. S. M., W. M. C., and T. F. M. conceived and designed the study, analyzed the data, and wrote the manuscript. S. S. M. executed and analyzed the experiments for experimental expression, survival, in-gel fluorescence, and Western blotting. M. J. M. N. executed and analyzed the CG simulations. T. F. M. and W. M. C. provided computational resources and reagents.
Acknowledgments
Computational resources were provided by the National Energy Research Scientific Computing Center (NERSC), a United States Department of Energy Office of Science User Facility (DE-AC02-05CH11231), and the Extreme Science and Engineering Discovery Environment (XSEDE) (55), which is supported by National Science Foundation Grant ACI-1053575.
This work was supported by NIGMS, National Institutes of Health, Grant 1R01GM125063 (to T. F. M. and W. M. C.). Work in the Clemons laboratory was supported by National Institutes of Health Pioneer Award 5DP1GM105385 (to W. M. C.), funds from Caltech's Center for Environmental Microbial Interactions, and NRSA, National Institutes of Health, Training Grant 5T32GM07616 (to S. S. M.). Work in the Miller group is supported in part by Office of Naval Research Grant N00014-10-1-0884. The authors declare that they have no conflicts of interest with the contents of this article. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
This article was selected as one of our Editors' Picks.
This article contains supplemental Table 1.
- IMP
- integral membrane protein
- CG
- coarse-grained
- ROC
- Receiver operator characteristic
- AUC
- area under the curve.
References
- 1. Lewinson O., Lee A. T., and Rees D. C. (2008) The funnel approach to the precrystallization production of membrane proteins. J. Mol. Biol. 377, 62–73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Marshall S. S., Niesen M. J. M., Müller A., Tiemann K., Saladi S. M., Galimidi R. P., Zhang B., Clemons W. M. Jr., and Miller T. F. 3rd (2016) A link between integral membrane protein expression and simulated integration efficiency. Cell Rep. 16, 2169–2177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gordon E., Horsefield R., Swarts H. G., de Pont J. J., Neutze R., and Snijder A. (2008) Effective high-throughput overproduction of membrane proteins in Escherichia coli. Protein Expr. Purif. 62, 1–8 [DOI] [PubMed] [Google Scholar]
- 4. Korepanova A., Gao F. P., Hua Y., Qin H., Nakamoto R. K., and Cross T. A. (2005) Cloning and expression of multiple integral membrane proteins from Mycobacterium tuberculosis in Escherichia coli. Protein Sci. 14, 148–158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Lundstrom K. (2006) Structural genomics for membrane proteins. Cell Mol. Life Sci. 63, 2597–2607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ma P., Varela F., Magoch M., Silva A. R., Rosário A. L., Brito J., Oliveira T. F., Nogly P., Pessanha M., Stelter M., Kletzin A., Henderson P. J., and Archer M. (2013) An efficient strategy for small-scale screening and production of archaeal membrane transport proteins in Escherichia coli. PLoS One 8, e76913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Schlegel S., Klepsch M., Gialama D., Wickström D., Slotboom D. J., and de Gier J. W. (2010) Revolutionizing membrane protein overexpression in bacteria. Microb. Biotechnol. 3, 403–411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Wagner S., Bader M. L., Drew D., and de Gier J. W. (2006) Rationalizing membrane protein overexpression. Trends Biotechnol. 24, 364–371 [DOI] [PubMed] [Google Scholar]
- 9. Scott D. J., Kummer L., Tremmel D., and Plückthun A. (2013) Stabilizing membrane proteins through protein engineering. Curr. Opin. Chem. Biol. 17, 427–435 [DOI] [PubMed] [Google Scholar]
- 10. Romero P. A., and Arnold F. H. (2009) Exploring protein fitness landscapes by directed evolution. Nat. Rev. Mol. Cell Biol. 10, 866–876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Saraogi I., and Shan S. O. (2014) Co-translational protein targeting to the bacterial membrane. Biochim. Biophys. Acta 1843, 1433–1441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Akopian D., Shen K., Zhang X., and Shan S. O. (2013) Signal recognition particle: an essential protein-targeting machine. Annu. Rev. Biochem. 82, 693–721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Rapoport T. A. (2007) Protein translocation across the eukaryotic endoplasmic reticulum and bacterial plasma membranes. Nature 450, 663–669 [DOI] [PubMed] [Google Scholar]
- 14. Driessen A. J. M., and Nouwen N. (2008) Protein translocation across the bacterial cytoplasmic membrane. Annu. Rev. Biochem. 77, 643–667 [DOI] [PubMed] [Google Scholar]
- 15. Shao S., and Hegde R. S. (2011) Membrane protein insertion at the endoplasmic reticulum. Annu. Rev. Cell Dev. Biol. 27, 25–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Cymer F., von Heijne G., and White S. H. (2015) Mechanisms of integral membrane protein insertion and folding. J. Mol. Biol. 427, 999–1022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Zhang B., and Miller T. F. 3rd. (2012) Long-timescale dynamics and regulation of Sec-facilitated protein translocation. Cell Rep. 2, 927–937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Lu Y., Turnbull I. R., Bragin A., Carveth K., Verkman A. S., and Skach W. R. (2000) Reorientation of aquaporin-1 topology during maturation in the endoplasmic reticulum. Mol. Biol. Cell 11, 2973–2985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Woodall N. B., Yin Y., and Bowie J. U. (2015) Dual-topology insertion of a dual-topology membrane protein. Nat. Commun. 6, 8099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Van Lehn R. C., Zhang B., and Miller T. F. 3rd (2015) Regulation of multispanning membrane protein topology via post-translational annealing. Elife 10.7554/eLife.08697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Fluman N., Tobiasson V., and von Heijne G. (2017) Stable membrane orientations of small dual-topology membrane proteins. Proc. Natl. Acad. Sci. U.S.A. 114, 7987–7992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bogsch E. G., Sargent F., Stanley N. R., Berks B. C., Robinson C., and Palmer T. (1998) An essential component of a novel bacterial protein export system with homologues in plastids and mitochondria. J. Biol. Chem. 273, 18003–18006 [DOI] [PubMed] [Google Scholar]
- 23. Tsirigos K. D., Peters C., Shu N., Käll L., and Elofsson A. (2015) The TOPCONS web server for consensus prediction of membrane protein topology and signal peptides. Nucleic Acids Res. 43, W401–W407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Drew D., Slotboom D. J., Friso G., Reda T., Genevaux P., Rapp M., Meindl-Beinker N. M., Lambert W., Lerch M., Daley D. O., Van Wijk K. J., Hirst J., Kunji E., and De Gier J. W. (2005) A scalable, GFP-based pipeline for membrane protein overexpression screening and purification. Protein Sci. 14, 2011–2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Fluman N., Navon S., Bibi E., and Pilpel Y. (2014) mRNA-programmed translation pauses in the targeting of E. coli membrane proteins. Elife 10.7554/eLife.03440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Swets J. A., Dawes R. M., and Monahan J. (2000) Better decisions through science. Sci. Am. 283, 82–87 [DOI] [PubMed] [Google Scholar]
- 27. Magnani F., Shibata Y., Serrano-Vega M. J., and Tate C. G. (2008) Co-evolving stability and conformational homogeneity of the human adenosine A2a receptor. Proc. Natl. Acad. Sci. U.S.A. 105, 10744–10749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Serrano-Vega M. J., Magnani F., Shibata Y., and Tate C. G. (2008) Conformational thermostabilization of the β1-adrenergic receptor in a detergent-resistant form. Proc. Natl. Acad. Sci. U.S.A. 105, 877–882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Schlinkmann K. M., Honegger A., Türeci E., Robison K. E., Lipovšek D., and Plückthun A. (2012) Critical features for biosynthesis, stability, and functionality of a G protein-coupled receptor uncovered by all-versus-all mutations. Proc. Natl. Acad. Sci. U.S.A. 109, 9810–9815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Heijne G. (1986) The distribution of positively charged residues in bacterial inner membrane proteins correlates with the trans-membrane topology. EMBO J. 5, 3021–3027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Seppälä S., Slusky J. S., Lloris-Garcerá P., Rapp M., and von Heijne G. (2010) Control of membrane protein topology by a single C-terminal residue. Science 328, 1698–1700 [DOI] [PubMed] [Google Scholar]
- 32. Ramasamy S., Abrol R., Suloway C. J., and Clemons W. M. Jr. (2013) The glove-like structure of the conserved membrane protein TatC provides insight into signal sequence recognition in twin-arginine translocation. Structure 21, 777–788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Rollauer S. E., Tarry M. J., Graham J. E., Jääskeläinen M., Jäger F., Johnson S., Krehenbrink M., Liu S. M., Lukey M. J., Marcoux J., McDowell M. A., Rodriguez F., Roversi P., Stansfeld P. J., Robinson C. V., et al. (2012) Structure of the TatC core of the twin-arginine protein transport system. Nature 492, 210–214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Niesen M. J., Wang C. Y., Van Lehn R. C., and Miller T. F. 3rd (2017) Structurally detailed coarse-grained model for Sec-facilitated co-translational protein translocation and membrane integration. PLoS Comput. Biol. 13, e1005427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Saladi S. M., Müller A., Javed N., and Clemons W. M. (2017) Decoding sequence-level information to predict membrane protein expression. bioRxiv 10.1101/098673 [DOI] [Google Scholar]
- 36. Altschul S. F., Gish W., Miller W., Myers E. W., and Lipman D. J. (1990) Basic local alignment search tool. J. Mol. Biol. 215, 403–410 [DOI] [PubMed] [Google Scholar]
- 37. Marks D. S., Hopf T. A., and Sander C. (2012) Protein structure prediction from sequence variation. Nat. Biotechnol. 30, 1072–1080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Kamisetty H., Ovchinnikov S., and Baker D. (2013) Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. U.S.A. 110, 15674–15679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Tress M. L., and Valencia A. (2010) Predicted residue-residue contacts can help the scoring of 3D models. Proteins 78, 1980–1991 [DOI] [PubMed] [Google Scholar]
- 40. Glas A. S., Lijmer J. G., Prins M. H., Bonsel G. J., and Bossuyt P. M. (2003) The diagnostic odds ratio: a single indicator of test performance. J. Clin. Epidemiol. 56, 1129–1135 [DOI] [PubMed] [Google Scholar]
- 41. DeGrado W. F., Summa C. M., Pavone V., Nastri F., and Lombardi A. (1999) De novo design and structural characterization of proteins and metalloproteins. Annu. Rev. Biochem. 68, 779–819 [DOI] [PubMed] [Google Scholar]
- 42. Huang P. S., Boyken S. E., and Baker D. (2016) The coming of age of de novo protein design. Nature 537, 320–327 [DOI] [PubMed] [Google Scholar]
- 43. Dahiyat B. I., and Mayo S. L. (1997) De novo protein design: fully automated sequence selection. Science 278, 82–87 [DOI] [PubMed] [Google Scholar]
- 44. Jiang L., Althoff E. A., Clemente F. R., Doyle L., Röthlisberger D., Zanghellini A., Gallaher J. L., Betker J. L., Tanaka F., Barbas C. F. 3rd, Hilvert D., Houk K. N., Stoddard B. L., and Baker D. (2008) De novo computational design of retro-aldol enzymes. Science 319, 1387–1391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Tantillo D. J., Chen J., and Houk K. N. (1998) Theozymes and compuzymes: theoretical models for biological catalysis. Curr. Opin. Chem. Biol. 2, 743–750 [DOI] [PubMed] [Google Scholar]
- 46. Bolon D. N., and Mayo S. L. (2001) Enzyme-like proteins by computational design. Proc. Natl. Acad. Sci. U.S.A. 98, 14274–14279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Drew D. E., von Heijne G., Nordlund P., and de Gier J. W. (2001) Green fluorescent protein as an indicator to monitor membrane protein overexpression in Escherichia coli. FEBS Lett. 507, 220–224 [DOI] [PubMed] [Google Scholar]
- 48. Gibson D. G., Young L., Chuang R. Y., Venter J. C., Hutchison C. A. 3rd, Smith H. O. (2009) Enzymatic assembly of DNA molecules up to several hundred kilobases. Nat. Methods 6, 343–345 [DOI] [PubMed] [Google Scholar]
- 49. Schneider C. A., Rasband W. S., and Eliceiri K. W. (2012) NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Zhang B., and Miller T. F. 3rd. (2012) Direct simulation of early-stage Sec-facilitated protein translocation. J. Am. Chem. Soc. 134, 13700–13707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Hanke F., Serr A., Kreuzer H. J., and Netz R. R. (2010) Stretching single polypeptides: the effect of rotational constraints in the backbone. Europhys. Lett. 92, 5 [Google Scholar]
- 52. Staple D. B., Payne S. H., Reddin A. L. C., and Kreuzer H. J. (2008) Model for stretching and unfolding the giant multidomain muscle protein using single-molecule force spectroscopy. Phys. Rev. Lett. 101, 248301. [DOI] [PubMed] [Google Scholar]
- 53. Kremer K., and Grest G. S. (1990) Dynamics of entangled linear polymer melts: a molecular-dynamics simulation. J. Chem. Phys. 92, 5057–5086 [Google Scholar]
- 54. Zhang B., and Miller T. F. 3rd. (2010) Hydrophobically stabilized open state for the lateral gate of the Sec translocon. Proc. Natl. Acad. Sci. U.S.A. 107, 5399–5404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Towns J., Cockerill T., Dahan M., Foster I., Gaither K., Grimshaw A., Hazlewood V., Lathrop S., Lifka D., Peterson G. D., Roskies R., Scott J. R., and Wilkins-Diehr N. (2014) XSEDE: accelerating scientific discovery. Comput. Sci. Eng. 16, 62–74 [Google Scholar]