Abstract
Drug development targeting the central nervous system (CNS) is challenging due to poor predictability of drug concentrations in various CNS compartments. We developed a generic physiologically based pharmacokinetic (PBPK) model for prediction of drug concentrations in physiologically relevant CNS compartments. System‐specific and drug‐specific model parameters were derived from literature and in silico predictions. The model was validated using detailed concentration‐time profiles from 10 drugs in rat plasma, brain extracellular fluid, 2 cerebrospinal fluid sites, and total brain tissue. These drugs, all small molecules, were selected to cover a wide range of physicochemical properties. The concentration‐time profiles for these drugs were adequately predicted across the CNS compartments (symmetric mean absolute percentage error for the model prediction was <91%). In conclusion, the developed PBPK model can be used to predict temporal concentration profiles of drugs in multiple relevant CNS compartments, which we consider valuable information for efficient CNS drug development.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Lack of knowledge of the target‐site concentrations in the CNS is a major hurdle in the development of new CNS drugs.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ A generic PBPK model in the rat CNS was proposed.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE
☑ The developed PBPK model was able to predict time‐dependent concentration profiles of many drugs with distinctively different physicochemical properties in multiple physiologically relevant compartments in the CNS.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ The developed model structure can be used to predict concentration‐time profiles in rats and offers a scientific basis for the development of CNS drugs, in principle, without the need of using animals.
The development of drugs targeting diseases of the central nervous system (CNS) represents one of the most significant challenges in the research of new medicines.1 Characterization of exposure‐response relationships at the drug target site may be of critical importance to reduce attrition. However, unlike for many other drugs, prediction of target‐site concentrations for CNS drugs is complex, among other factors, due to the presence of the blood‐brain barrier (BBB) and the blood‐cerebrospinal fluid barrier (BCSFB). Moreover, direct measurement of human brain concentrations is highly restricted for ethical reasons. Therefore, new approaches that can robustly predict human brain concentrations of novel drug candidates based on in vitro and in silico studies are of great importance.
Several pharmacokinetic (PK) models to predict CNS exposure have been published with different levels of complexity.2 The majority of these models depend on animal data. Furthermore, these models have typically not been validated against human CNS drug concentrations.2 We previously published a general multicompartmental CNS PK model structure, which was developed using PK data obtained from rats.
Quantitative structure‐property relationship (QSPR) models can be used to predict drug BBB permeability and Kp,uu,brainECF (unbound brain extracellular fluid‐to‐plasma concentration ratio)3, 4, 5 without performing novel experiments, but these QSPR models have not taken into account the time course of CNS distribution. Therefore, there exists an unmet need for approaches to predict drug target‐site concentration‐time profiles without the need of in vivo animal experiments.
Physiologically based pharmacokinetic (PBPK) modeling represents a promising approach for the prediction of CNS drug concentrations. Previously, such models have been widely used to predict tissue concentrations.6 The PBPK models typically distinguish between drug‐specific and system‐specific parameters, therefore, enabling predictions across drugs and species. However, PBPK models for the CNS have been of limited utility due to a lack of relevant physiological details for mechanism of transport across the BBB and BCSFB, and for drug distribution within the CNS.2
Capturing the physiological compartments, flows, and transport processes in a CNS PBPK model is critically important to predict PK profiles in the CNS. The CNS comprises of multiple key physiological compartments,2 including brain extracellular fluid (brainECF), brain intracellular fluid (brainICF), and multiple cerebrospinal fluid (CSF) compartments. The brainECF and brainICF compartments are considered highly relevant target sites for CNS drugs, whereas CSF compartments are often used to measure CNS‐associated drug concentrations, if brainECF and brainICF information cannot be obtained. Furthermore, cerebral blood flow (CBF) and physiological flows within the CNS, such as the brainECF flow and CSF flows, influence drug distribution across CNS compartments. Next to binding to protein and lipids, pH‐dependent distribution in subcellular compartments, such as trapping of basic compounds in lysosomes, needs to be considered. With regard to the transfer processes across the BBB and BCSFB, passive diffusion via the paracellular and transcellular pathways and active transport by influx and/or efflux transporters need to be addressed.
At both BBB and BCSFB barriers, the cells are interconnected by tight junctions, which limit drug exchange via the paracellular pathway.7 Paracellular and transcellular diffusion depend on the aqueous diffusivity coefficient and membrane permeability of the compound, which can be related to the physicochemical properties. The combination of these transport routes may differ between individual drugs, which complicate the prediction of plasma‐brain transport.
System‐specific information on physiological parameters can be used in scaling between species. Many of these system‐specific parameters can or have been obtained from in vitro and in vivo experiments. Drug‐specific parameters can be derived by in vitro and QSPR approaches, and can be used for the scaling between drugs. A comprehensive CNS PBPK model can integrate system‐specific and drug‐specific parameters to potentially enable the prediction of the brain distribution of drugs without the need to conduct in vivo animal studies.
The purpose of the current work is to develop a comprehensive PBPK model to predict drug concentration‐time profiles in the multiple physiologically relevant compartments in the CNS, based on system‐specific and drug‐specific parameters without the need to generate in vivo data. We specifically consider the prediction of PK profiles in the CNS during pathological conditions, which may have distinct effects on paracellular diffusion, transcellular diffusion, and active transport. Therefore, we include a range of such transport mechanisms in our CNS PBPK model. This model is evaluated using previously published detailed multilevel brain and CSF concentration‐time data for 10 drugs with highly diverse physicochemical properties.
MATERIALS AND METHODS
We first empirically modeled plasma PK using available plasma PK data, which was used as the basis for the CNS PBPK model. This CNS model was based entirely on parameters derived from literature and in silico predictions. Model development was performed using NONMEM version 7.3.
Empirical plasma PK model
Plasma PK models were systematically developed using in vivo data with a mixed‐effects modeling approach. One, two, and three‐compartment models were evaluated. Interindividual variability and interstudy variability were incorporated on each PK parameter using exponential models. Proportional and combined additive‐proportional residual error models were considered. Model selection was guided by the likelihood ratio test (P < 0.05), precision of the parameter estimates, and standard goodness of fit plots.8
CNS PBPK model development
A generic PBPK model structure was developed based on the previously published generic multicompartmental CNS distribution model (Figure 1),9 which consists of plasma, brainECF, brainICF, CSF in the lateral ventricle (CSFLV), CSF in the third and fourth ventricle (CSFTFV), CSF in the cisterna magna (CSFCM), and CSF in the subarachnoid space (CSFSAS) compartments. We added new components: (1) an acidic subcellular compartment representing lysosomes to account for pH‐dependent drug distribution; (2) a brain microvascular compartment (brainMV) to account for CBF vs. permeability rate‐limited kinetics; and (3) separation of passive diffusion at the BBB and BCSFB into its transcellular and paracellular components.
Figure 1.
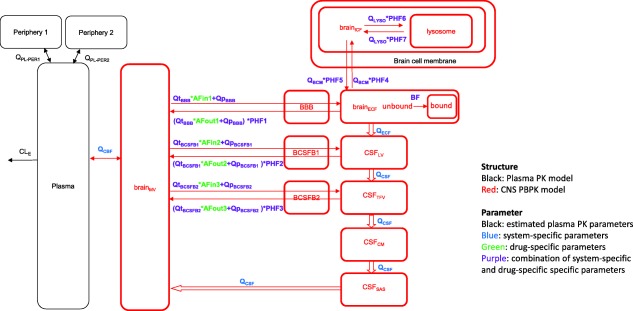
The developed model structure. The model consists of a plasma pharmacokinetic (PK) model and a central nervous system (CNS) physiologically based pharmacokinetic (PBPK) model with estimated plasma PK parameters, and system‐specific and drug‐specific parameters (colors) for CNS. Peripheral compartments 1 and 2 were used in cases where the plasma PK model required them to describe the plasma data adequately. AFin1–3, asymmetry factor into the CNS compartments 1–3; AFout1–3, asymmetry factor out from the CNS compartments 1–3; BBB, blood‐brain barrier; BCSFB, blood‐cerebrospinal fluid barrier; BF, binding factor; brainECF, brain extracellular fluid; brainICF, brain intracellular fluid; brainMV, brain microvascular; CSFCM, cerebrospinal fluid in the cisterna magna; CSFLV, cerebrospinal fluid in the lateral ventricle; CSFSAS, cerebrospinal fluid in the subarachnoid space; CSFTFV, cerebrospinal fluid in the third and fourth ventricle; PHF1–7, pH‐dependent factor 1–7; QBCM, passive diffusion clearance at the brain cell membrane; QCBF, cerebral blood flow; QCSF, cerebrospinal fluid flow; QECF, brainECF flow; QLYSO, passive diffusion clearance at the lysosomal membrane; QpBBB, paracellular diffusion clearance at the BBB; QpBCSFB1, paracellular diffusion clearance at the BCSFB1; QpBCSFB2, paracellular diffusion clearance at the BCSFB2; QtBBB, transcellular diffusion clearance at the BBB; QtBCSFB1, transcellular diffusion clearance at the BCSFB1; QtBCSFB2, transcellular diffusion clearance at the BCSFB2.
System‐specific parameters
Physiological values of the distribution volumes of all the CNS compartments, flows, surface area (SA) of the BBB (SABBB), SA of the BCSFB (SABCSFB), SA of the total brain cell membrane (BCM; SABCM), and the width of BBB (WidthBBB) were collected from literature. The SABCFSB was divided into SABCSFB1, which is a surface area around CSFLV, and SABCSFB2, which is a surface area around CSFTFV. The lysosomal volume was calculated based on the volume ratio of lysosomes to brain intracellular fluid of brain parenchyma cells (1:80),10 and the SA of the lysosome (SALYSO) is calculated by obtaining the lysosome number per cell using the lysosomal volume and the diameter of each lysosome.11 Transcellular and paracellular diffusion were separately incorporated into the models, therefore, the ratio of SABBB and SABCSFB for transcellular diffusion and paracellular diffusion were required for the calculation. Based on electron microscopic cross‐section pictures of brain capillary, the length of a single brain microvascular endothelial cell was estimated to be around 17 µm and the length of the intercellular space was estimated to be around 0.03 µm.12 The presence of tight junctions in the intercellular space of the BBB and BCSFB significantly reduces paracellular transport.7 Therefore, correcting for the effective pore size for paracellular diffusion is important. The transendothelial electrical resistance (TEER) is reported to be around 1,800 Ω cm2 at the rat BBB,13 whereas the TEER is around 20–30 Ω cm2 at the rat BCSFB.14 According to a study on the relationship between TEER and the pore size,15 the pore size at the BBB and BCSFB can be assumed to be around 0.0011 µm and 0.0028 µm, respectively. Thus, it was expected that 99.8% of total SABBB and 99.8% of total SABCSFB is used for the transcellular diffusion (SABBBt and SABCSFBt, respectively), whereas 0.006% of total SABBB and 0.016% of total SABCSFB are used for paracellular diffusion (SABBBp and SABCSFBp, respectively). Note that, due to the presence of tight junction proteins, not all intercellular space can be used for paracellular diffusion.
Drug‐specific parameters
Aqueous diffusivity coefficient
The aqueous diffusivity coefficient was calculated using the molecular weight of each compound with the following equation16:
| (1) |
where Daq is the aqueous diffusivity coefficient (in cm2/s) and MW is the molecular weight (in g/mol).
Permeability
Transmembrane permeability was calculated using the log P of each compound with the following equation17:
| (2) |
where is the transmembrane permeability (in cm/s), log P is the n‐octanol lipophilicity value.
Active transport
The impact of the net effect of active transporters on the drug exchange at the BBB and BCSFB was incorporated into the model using asymmetry factors (AFin1–3 and AFout1–3). The AFs were calculated from Kp,uu,brainECF, Kp,uu,CSFLV (unbound CSFLV‐to‐plasma concentration ratio) and Kp,uu,CSFCM (unbound CSFCM‐to‐plasma concentration ratio), such that they produced the same Kp,uu values within the PBPK model at the steady‐state. Therefore, the AFs were dependent on both the Kp,uu values and the structure and parameters of the PBPK model. If the Kp,uu values were larger than 1 (i.e., net active influx), then AFin1, AFin2, and AFin3 were derived from Kp,uu,brainECF, Kp,uu,CSFLV, and Kp,uu,CSFCM, respectively, whereas AFout1–3 were fixed to 1. If the Kp,uu values were smaller than 1 (i.e., net active efflux), then AFout1, AFout2, and AFout3 were derived from Kp,uu,brainECF, Kp,uu,CSFLV, and Kp,uu,CSFCM, respectively, whereas AFin1–3 were fixed to 1. In the analysis, Kp,uu,brainECF, Kp,uu,CSFLV, and Kp,uu,CSFCM were derived from previous in vivo animal experiments.9 The steady‐state differential equations in the PBPK model were solved using the Maxima Computer Algebra System (http://maxima.sourceforge.net) to obtain algebraic solutions for calculating AFs from the Kp,uu values. The detailed algebraic solutions for each AF are provided in Supplementary Material S1.
Combined system‐specific and drug‐specific parameters
Passive diffusion across the brain barriers
Passive diffusion clearance at the BBB and BCSFB (QBBB and QBCSFB, respectively) was obtained from a combination of paracellular and transcellular diffusion, Qp and Qt, respectively (Eq. (3)).
| (3) |
where QBBB/BCSFB represents the passive diffusion clearance at the BBB/BCSFB, QpBBB/BCSFB represents the paracellular diffusion clearance at the BBB/BCSFB, and QtBBB/BCSFB represents the transcellular diffusion clearance at the BBB/BCSFB.
The paracellular diffusion clearance was calculated with the aqueous diffusivity coefficient (Daq), WidthBBB/BCSFB, and SABBBp or SABCSFBp using Eq. (4).
| (4) |
The transcellular diffusion clearance was calculated with the transmembrane permeability and SABBBt or SABCSFBt using Eq. (5).
| (5) |
where the factor 1/2 is the correction factor for passage over two membranes instead of one membrane in the transcellular passage.
Active transport across the brain barriers
To take into account the net effect of the active transporters at the BBB and BCSFB, AFs were added on QtBBB/BCSFB (Eqs. (6) and (7)).
| (6) |
| (7) |
where QBBB/BCSFB_in represents the drug transport clearance from brainMV to brainECF/CSFs, and QBBB/BCSFB_out_withoutPHF represents the drug transport clearance from brainECF/CSFs to brainMV without taking into account the pH‐dependent kinetics (to be taken into account separately; see below).
Cellular and subcellular distribution
Passive diffusion at the BCM (QBCM) and at the lysosomal membrane (QLYSO) was described with the transmembrane permeability together with SABCM or SALYSO, respectively (Eqs. (8) and (9)).
| (8) |
| (9) |
where QBCM represents the passive diffusion clearance at the BCM, and QLYSO represents the passive diffusion clearance at the lysosomal membrane.
pH‐dependent partitioning
We considered the differences in pH in plasma (pH 7.4) and in relevant CNS compartments, namely brainECF (pHECF 7.3), CSF (pHCSF 7.3), brainICF (pHICF 7.0), and lysosomes (pHlyso 5.0).18 The impact of pH differences on the passive diffusion clearance from brainECF to brainMV (PHF1), from CSFLV to brainMV (PHF2), from CSFTFV to brainMV (PHF3), from brainECF to brainICF (PHF4), from brainICF to brainECF (PHF5), from brainICF to lysosomes (PHF6), and from lysosomes to brainICF (PHF7) were described by pH‐dependent factors, which were defined as the ratio of the unionized fraction of each compound at the pH in a particular compartment and the unionized fraction in plasma. The PHFs were calculated from the pKa of each compound and the pH of a particular compartment. The equations are developed using the classical Henderson‐Hasselbalch equation,19, 20 and are based on the assumption that there is no active transport.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where PHFbase1‐7 are PHF1‐7 for basic compounds, PHFacid1‐7 are PHF1‐7 for acidic compounds, and 7.4 is the pH in the plasma compartment.
The impact of pH differences on the drug distribution among brainECF, CSF, brainICF, and lysosomes was added on QBCM and QLYSO using PHFs with the following Eqs. (18), (19), (20), (21), (22), (23), (24) based on the assumption that the transport clearance is proportional to the unionized fraction of each compound.
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where QBBB_out represents the drug transport clearance from brainECF to brainMV, QBCSFB1_out represents the drug transport clearance from CSFLV to brainMV, QBCSFB2_out represents the drug transport clearance from CSFTFV to brainMV, QBCM_in represents the drug transport clearance from brainECF to brainICF, and QBCM_out represents the drug transport clearance from brainICF to brainECF. The QLYSO_in represents the drug transport clearance from brainICF to lysosomes, and QBCM_out represents the drug transport clearance from lysosomes to brainICF.
Drug binding
Drug binding to brain tissue components was taken into account in the model using a binding factor (BF) under the assumption that drug binding to the tissue happens instantly. The BF was calculated from Kp (total brain‐to‐plasma concentration ratio) by solving the BF that results in the same Kp value in the model, using the Maxima program, as described above (Supplementary Material S1). The Kp for each compound was calculated using the compounds' log P, the composition of brain tissue and plasma, free fraction in plasma (fu,p) and free fraction in brain (fu,b) with the following equation21:
| (25) |
where Vnlb, Vphb, Vwb, Vnlp, Vphp, and Vwp represent the rat volume fractions of brain neutral lipids (0.0392), brain phospholipids (0.0533), brain water (0.788), plasma neutral lipids (0.00147), plasma phospholipids (0.00083), and plasma water (0.96), respectively.22
In vivo data collection for model evaluation
In vivo data obtained from multiple brain locations were used to evaluate the developed model.9, 23, 24, 25, 26, 27, 28, 29 An overview of experimental design and data for 10 compounds with substantially different physicochemical characteristics is provided in Table 1.9, 23, 24, 25, 26, 27, 28, 29 All data were previously published, except the remoxipride total brain tissue data. General animal surgery procedures, experimental protocol, and bioanalytical methods for remoxipride total brain tissue data are described in Supplementary Material S2, and experimental protocol details for each drug are summarized in Supplementary Table S1.
Table 1.
Summary of rat multilevel brain and CSFs data for model evaluation
| Acetaminophen | Atenolol | Methotrexate | Morphine | Morphine | Paliperidone | Phenytoin | Quinidine | Raclopride | Remoxipride | Remoxipride | Risperidone | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Study design | ||||||||||||
| No. of animals | 16 | 5 | 23 | 65 | 18 | 21 | 14 | 41 | 19 | 29 | 65 | 16 |
| Dosage, mg/kg (infusion time, min) | 15 (10) | 10 (1) | 40, 80 (10) | 4, 10, 40 (10) | 10, 40 (10) | 0.5 (20) | 20, 30, 40 (10) | 10, 20 (10) | 0.56 (10) | 4, 8, 16 (30) | 0.7, 5.2, 14 (10) | 2 (20) |
| Data | ||||||||||||
| Plasma | X | X | X | X | X | X | X | X | X | X | X | X |
| BrainECF | X | X | X | X | X | X | X | X | X | X | X | X |
| CSFLV | X | X | X | X | ||||||||
| CSFCM | X | X | X | X | X | X | ||||||
| Total brain tissue | X | X | X (new data) | X (new data) | ||||||||
| References | 24 | 25 | 23 | 26 | 27 | 9 | 9 | 28 | 30 (except total brain tissue data) | 9 (except total brain tissue data) | 9 | |
BrainECF, brain extracellular fluid compartment; CSFLV, cerebrospinal fluid compartment in the lateral ventricle; CSFCM, cerebrospinal fluid compartment in the cisterna magna.
Evaluation of the PBPK model
The PBPK model performance was evaluated by the comparison of model predictions with the concentration‐time profiles in brainECF, CSFLV, CSFCM, and total brain tissue of 10 compounds. We performed 200 simulations for each compound, including random effect estimates for the plasma PK model. Based on these, we calculated the prediction error (PE) and symmetric mean absolute percentage error (SMAPE), see Eqs. (26) and (27).
| (26) |
| (27) |
where YOBS,ij is the jth observation of the ith subject, YPRED,ij is the jth mean prediction of the ith subject, and N is the number of observations.
RESULTS
Plasma PK model
The estimated parameters for the descriptive plasma PK models were obtained with good precision and summarized in Table 2. The models describe plasma concentration‐time profiles very well for all compounds except risperidone (Supplementary Figure S1). For remoxipride, a small underprediction was observed at later time points.
Table 2.
Parameter estimates for plasma pharmacokinetics of the 10 compounds
| Parameter estimates (RSE, %) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acetaminophen | Atenolol | Methotrexate | Morphine | Paliperidone | Phenytoin | Quinidine | Raclopride | Remoxipride | Risperidone | ||
| CLPL | mL/min | 15.8 (9.10) | 7.13 (20.6) | 8.04 (15.9) | 22.6 (7.70) | 196 (13.0) | 36.0 (8.90) | 162 (4.10) | 46.4 (4.30) | 42.2 (4.90) | 886 (33.2) |
| QPL_PER1 | mL/min | 33.8 (33.7) | NA | 28.5 (30.7) | 30.8 (10.0) | 61.5 (86.2) | 265 (12.7) | 829 (6.80) | 13.4 (27.5) | 33.8 (20.7) | NA |
| QPL_PER2 | mL/min | NA | NA | 3.33 (34.8) | 7.21 (10.2) | NA | NA | NA | 69.2 (7.50) | 14.0 (10.1) | NA |
| VPL | mL | 49.5 (59.0) | 256 (27.0) | 28.0 (55.0) | 152 (11.1) | 26,400 (12.6) | 943 (21.5) | 670 (13.3) | 48.9 (16.3) | 83.7 (18.3) | 43,100 (28.1) |
| VPER1 | mL | 363 (33.1) | NA | 111 (14.6) | 530 (9.10) | 3,580 (35.8) | 2,050 (7.50) | 11,300 (3.20) | 684 (19.2) | 253 (10.9) | NA |
| VPER2 | mL | NA | NA | 83.5 (34.9) | 1,200 (10.8) | NA | NA | NA | 493 (18.3) | 757 (4.00) | NA |
| Fraction | 0.693 (19.6) | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| Interindividual variabilitya | |||||||||||
| ɷ_CLPL | % | NA | NA | 37.4 (46.8) | 17.8 (39.5) | 42.0 (62.5) | 73.8 (12.5) | 23.9 (15.3) | 14.4 (29.8) | 31.0 (12.0) | 72.5 (38.7) |
| ɷ_QPL_PER1 | % | NA | NA | NA | 28.8 (29.4) | NA | NA | 24.3 (28.2) | NA | 25.1 (12.1) | NA |
| ɷ_QPL_PER2 | % | NA | NA | 42.5 (42.0) | 86.7 (19.3) | NA | NA | NA | NA | 76.7 (13.5) | NA |
| ɷ_VPL | % | NA | NA | 40.4 (75.5) | 80.6 (17.2) | 47.5 (81.4) | 75.0 (27.2) | NA | NA | 64.1 (32.9) | 53.7 (78.8) |
| ɷ_VPER1 | % | 51.8 (86.0) | NA | NA | 46.0 (15.3) | NA | NA | 12.8 (26.6) | NA | NA | NA |
| ɷ_VPER2 | % | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Interoccasional variabilityb | |||||||||||
| ɷ_study1 | % | NA | NA | NA | 42.7 (16.2) | NA | NA | NA | NA | NA | NA |
| ɷ_study2 | % | NA | NA | NA | 29.7 (30.5) | NA | NA | NA | NA | NA | NA |
| Residual errorc | |||||||||||
| σ_plasma proportional | % | 23.7 (35.0) | 48.6 (56.1) | 15.1 (17.2) | 24.6 (8.80) | 22.7 (15.6) | 13.0 (10.6) | 24.5 (7.70) | 14.1 (8.60) | 31.0 (11.2) | 47.2 (49.1) |
| σ_plasma additive | ng/mL | NA | NA | 5,400 (42.6) | NA | NA | NA | NA | NA | NA | 0.0244 (27.6) |
CLPL, clearance from the central compartment; Fraction, percentage of the drug which is reabsorbed by enterohepatic circulation; NA, not applicable; QPL_PER1, intercompartmental clearance between the central compartment and the peripheral compartment 1; QPL_PER2, intercompartmental clearance between the central compartment and the peripheral compartment 2; RSE, relative standard error; VPL, distribution volume of the central compartment; VPER1, distribution volume of the peripheral compartment 1; VPER2, distribution volume of the peripheral compartment 2.
a,bθih = θ×e^(ηi+ ηh), where θih represents the parameters of the ith subject and hth study, θ represents the population mean value of the parameter, ηi is the random effect of the ith subject under the assumption of a normal distribution with a mean value of 0 and variance of ω1 2, and ηh is the random effect of the hth study under the assumption of a normal distribution with a mean value of 0 and variance of ω2 2. cCij = YIPRED,ij×(1+ɛij) or Cij = YIPRED,ij×(1+ɛ1,ij)+ɛ2,ij, where Cij represents the jth observed concentration of the ith subject, YIPRED,ij represents the jth individual prediction of the ith subject, and ɛij is the random effect of the jth observed concentration of the ith subject under the assumption of a normal distribution with a mean value of 0 and variance of σ2.
CNS PBPK model
The NONMEM model codes for the 10 compounds are provided in Supplementary Material S3–S13. The values of the system‐specific and drug‐specific parameters are summarized in Tables 4, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 and 3, respectively. The combined system‐specific and drug‐specific parameters are summarized in Table 5. Overall, the developed generic PBPK model could adequately predict the rat data in brainECF, CSFLV, CSFCM, and total brain tissue. Figure 2 shows the PE for each compound and each CNS compartment. The PE for risperidone brainECF and CSFCM showed modest underprediction. For the other drugs, the PEs were distributed within two standard deviations and no specific trends were observed across time, compounds, and CNS locations. The SMAPEs for the model prediction in brainECF, CSFLV, CSFCM, and total brain tissue were 72%, 71%, 69%, and 91%, respectively, indicating that the model could predict concentration‐time profiles in these compartments with less than twofold prediction error. The concentration‐time plots of individual predictions vs. observations across drugs and dose levels are provided (Supplementary Figure S1).
Table 4.
System‐specific parameters of the PBPK model
| Description | Parameter | Value | Reference | |
|---|---|---|---|---|
| Volumes | Brain | Vtot | 1880 µl | 30 |
| BrainECF | VbrainECF | 290 µl | 31 | |
| BrainICF | VbrainICF | 1440 µl | 32 | |
| Total lysosome | VLYSO | 18 µl | Calculateda | |
| CSFLV | VCSFLV | 50 µl | 33, 34 | |
| CSFTFV | VCSFTFV | 50 µl | 33, 34 | |
| CSFCM | VCSFCM | 17 µl | 35, 36 | |
| CSFSAS | VCSFSAS | 180 µl | 33, 37 | |
| BrainMV | VMV | 60 µl | 38 | |
| Flows | Cerebral blood flow | QCBF | 1.2 mL/min | 44 |
| BrainECF flow | QECF | 0.0002 mL/min | 39 | |
| CSF flow | QCSF | 0.0022 mL/min | 31 | |
| Surface areas | BBB | SABBB | 263 cm2 b | 40 |
| BCSFB | SABCSFB | 25 cm2 c, d | 41 | |
| Total BCM | SABCM | 3000 cm2 | 42 | |
| Total lysosomal membrane | SALYSO | 1440 cm2 | Calculatede | |
| Width | BBB | WidthBBB | 0.3–0.5 µm (0.5 was used in the model) | 43 |
BBB, blood‐brain barrier; BCM, brain cell membrane; BCSFB, blood‐cerebrospinal barrier; CBF, cerebral blood flow; CM, cisterna magna; CSF, cerebrospinal fluid; ECF, extracellular fluid; ICF, intracellular fluid; LV, lateral ventricle; LYSO, lysosome; MV, microvascular; SA, surface area; SAS, subarachnoid space; TFV, third and fourth ventricle; TOT; total; V, volume.
Based on the volume ratio of lysosomes to brainICF (1:80).10
A total of 99.8% of SABBB are used for transcellular diffusion, and 0.006% of SABBB are used for paracellular diffusion.
A total of 99.8% of SABCSFB are used for transcellular diffusion and 0.016% of SABCSFB are used for paracellular diffusion.
SABCSFB1 and SABCSFB2 are assumed to be 12.5 cm2 and 12.5 cm2, respectively.
Based on the lysosome number per cell which was calculated using the total lysosomal volume and diameter of each lysosome (0.5–1.0 µm).11
Table 3.
Drug‐specific parameters of the PBPK model
| Acetaminophen | Atenolol | Methotrexate | Morphine | Paliperidone | Phenytoin | Quinidine | Raclopride | Remoxipride | Risperidone | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Drug specific parameters | ||||||||||||
| Transmembrane permeability | cm/min | 1.1*10^‐4 | 5.7*10^‐5 | 6.1*10^‐7 | 2.5*10^‐4 | 0.0018 | 0.0077 | 0.058 | 6.6*10^‐4 | 0.0035 | 0.0082 | |
| Aqueous diffusivity coefficient (paracellular diffusion) | cm2/min | 4.6*10^‐4 | 3.5*10^‐4 | 2.8*10^‐4 | 3.4*10^‐4 | 2.8*10^‐4 | 3.6*10^‐4 | 3.2*10^‐4 | 3.1*10^‐4 | 3.0*10^‐4 | 2.9*10^‐4 | |
| AF | AFin1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.2 | 1.0 | 1.0 | 1.0 | |
| AFin2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.4 | 1.0 | 1.0 | 1.0 | ||
| AFin3 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.4 | 1.0 | 1.0 | 1.0 | ||
| AFout1 | 12 | 40 | 4.6*10^4 | 11a, 20b | 3.0 | 4.2 | 1.0 | 1.4 | 1.7 | 1.3 | ||
| AFout2 | 29 | 82 | 4.7*10^5 | 20a, 38b | 3.7 | 7.6 | 1.0 | 1.1 | 1.7 | 1.3 | ||
| AFout3 | 32 | 110 | 1.0*10^6 | 26a, 49b | 4.7 | 7.7 | 1.0 | 1.9 | 2.1 | 1.5 | ||
| Partitioning coefficient between compartments | ||||||||||||
| Kp,uu,brainECF | 0.51 | 0.37 | 0.018 | 0.38a, 0.23b | 0.50 | 0.26 | 1.5 | 1.1 | 0.80 | 0.97 | ||
| Kp,uu,CSFLV | 0.51 | 0.37 | 0.0066 | 0.38a, 0.23b | 0.50 | 0.26 | 1.5 | 1.1 | 0.80 | 0.97 | ||
| Kp,uu,CSFCM | 0.51 | 0.37 | 0.0024 | 0.38a, 0.23b | 0.50 | 0.26 | 1.5 | 1.1 | 0.80 | 0.97 | ||
| Kp | 1.0 | 0.94 | NA | 1.3 | 1.3 | 2.3 | 13 | 11 | 5.5 | 2.1 | ||
| Free fraction | ||||||||||||
| fu,p | 0.81 | 0.91 | 0.45 | 0.83 | 0.080 | 0.090 | 0.14 | 0.070 | 0.74 | 0.070 | ||
| fu,b | 0.80 | 0.90 | NA | 0.76 | 0.065d | 0.080 | 0.090 | 0.13 | 0.57c | 0.065 | ||
| Physicochemical properties | ||||||||||||
| Molecular weight | 151 | 266 | 454 | 285 | 426 | 252 | 324 | 347 | 371 | 410 | ||
| log P | 0.5 | 0.2 | −1.9 | 0.9 | 1.8 | 2.5 | 3.4 | 1.3 | 2.1 | 2.5 | ||
| pKa (acid) | 9.5 | 14.1 | 3.4 | 10.3 | 13.7 | 9.5 | 13.9 | 5.9 | 13.1 | |||
| pKa (base) | −4.4 | 9.7 | 2.8 | 9.1 | 8.8 | −9.0 | 9.1 | 9.0 | 8.4 | 8.8 | ||
| Charge class | Neutral | Base | Acid | Base | Base | Neutral | Base | Zwitterion | Base | Base | ||
AF, asymmetry factor; Kp,uu,brainECF, unbound brain extracellular fluid‐to‐plasma concentration ratio; Kp,uu,CSFLV, unbound CSFLV‐to‐plasma concentration ratio; Kp,uu,CSFCM, unbound CSFCM‐to‐plasma concentration ratio; Kp, total brain‐to‐plasma concentration ratio; fu,p, free fraction in plasma; fu,b, free fraction in brain.
AFin1–3 and AFout1–3 were calculated from Kp,uu,brainECF, Kp,uu,CSFLV, and Kp,uu,CSFCM, respectively.
4 mg/kg.
10, 40 mg/kg.
Calculated from Vu,brain, and Kp,uu,cell.
Assumed to be the same as risperidone.
Table 5.
Combined parameters of system‐specific and drug‐specific parameters in the PBPK model
| Acetaminophen | Atenolol | Methotrexate | Morphine | Paliperidone | Phenytoin | Quinidine | Raclopride | Remoxipride | Risperidone | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Unit | ||||||||||
| QBBB_in | mL/min | 0.16 | 0.12 | 0.087 | 0.14 | 0.33 | 1.1 | 9.1 | 0.18 | 0.55 | 1.2 |
| QBBB_out | mL/min | 0.31 | 0.33 | 4.8 | 0.38a, 0.62b | 0.65 | 4.4 | 5.1 | 0.18 | 0.69 | 1.2 |
| QtBBB | mL/min | 0.014 | 0.0075 | 8.0*10^‐5 | 0.033 | 0.24 | 1.0 | 7.6 | 0.086 | 0.46 | 1.1 |
| QpBBB | mL/min | 0.14 | 0.11 | 0.087 | 0.11 | 0.090 | 0.11 | 0.10 | 0.099 | 0.096 | 0.091 |
| PHF1 | 1.0 | 0.80 | 1.3 | 0.80 | 0.80 | 1.0 | 0.80 | 0.80 | 0.81 | 0.80 | |
| QBCSFB1_in | mL/min | 0.019 | 0.014 | 0.011 | 0.015 | 0.023 | 0.063 | 0.52 | 0.020 | 0.034 | 0.063 |
| QBCSFB1_out | mL/min | 0.038 | 0.034 | 2.2 | 0.036a, 0.059b | 0.042 | 0.38 | 0.21 | 0.013 | 0.040 | 0.063 |
| QtBCSFB1 | mL/min | 6.8*10^‐4 | 3.6*10^‐4 | 3.8*10^‐6 | 0.0016 | 0.011 | 0.048 | 0.36 | 0.0041 | 0.022 | 0.051 |
| QpBCSFB1 | mL/min | 0.018 | 0.014 | 0.011 | 0.014 | 0.011 | 0.014 | 0.013 | 0.012 | 0.012 | 0.012 |
| PHF2 | 1.0 | 0.80 | 1.3 | 0.80 | 0.80 | 1.0 | 0.80 | 0.80 | 0.81 | 0.80 | |
| QBCSFB2_in | mL/min | 0.019 | 0.014 | 0.011 | 0.015 | 0.023 | 0.063 | 0.52 | 0.017 | 0.034 | 0.063 |
| QBCSFB2_out | mL/min | 0.040 | 0.042 | 4.9 | 0.044a, 0.073b | 0.052 | 0.38 | 0.21 | 0.016 | 0.047 | 0.073 |
| QtBCSFB2 | mL/min | 6.8*10^‐4 | 3.6*10^‐4 | 3.8*10^‐6 | 0.0016 | 0.011 | 0.048 | 0.36 | 0.0041 | 0.022 | 0.051 |
| QpBCSFB2 | mL/min | 0.018 | 0.014 | 0.011 | 0.014 | 0.011 | 0.014 | 0.013 | 0.012 | 0.012 | 0.012 |
| PHF3 | 1.0 | 0.80 | 1.3 | 0.80 | 0.80 | 1.0 | 0.80 | 0.80 | 0.81 | 0.80 | |
| QBCM_in | mL/min | 0.33 | 0.14 | 0.0023 | 0.61 | 4.4 | 23 | 140 | 1.6 | 8.4 | 20 |
| QBCM_out | mL/min | 0.33 | 0.068 | 0.0046 | 0.31 | 2.2 | 23 | 70 | 0.80 | 4.4 | 10 |
| PHF4 | 1.0 | 0.80 | 1.3 | 0.80 | 0.80 | 1.0 | 0.80 | 0.80 | 0.81 | 0.80 | |
| PHF5 | 1.0 | 0.40 | 2.5 | 0.40 | 0.41 | 1.0 | 0.40 | 0.40 | 0.42 | 0.41 | |
| QLYSO_in | mL/min | 0.16 | 0.033 | 0.0022 | 0.15 | 1.1 | 11 | 33 | 0.38 | 2.1 | 4.8 |
| QLYSO_out | mL/min | 0.16 | 0.00033 | 0.21 | 0.0015 | 0.011 | 11 | 0.34 | 0.0039 | 0.022 | 0.049 |
| PHF6 | 1.0 | 0.40 | 2.5 | 0.40 | 0.41 | 1.0 | 0.40 | 0.40 | 0.42 | 0.41 | |
| PHF7 | 1.0 | 0.0040 | 250 | 0.0041 | 0.0041 | 1.0 | 0.0041 | 0.0041 | 0.0044 | 0.0041 | |
| BF | 1.1 | 0.92 | NA | 1.8a, 3.9b | 0.91 | 8.2 | 7.2 | 8.5 | 5.3 | 0.49 | |
BBB, blood‐brain barrier; BCM, brain cell membrane; BCSFB, blood‐cerebrospinal fluid barrier; BF, binding factor; LYSO, lysosome; PHF, pH‐dependent factor; QBBB, passive diffusion clearance at the BBB; QtBBB, transcellular diffusion clearance at the BBB; QpBBB, paracellular diffusion clearance at the BBB; QBCSFB1, passive diffusion clearance at the BCSFB1; QtBCSFB1, transcellular diffusion clearance at the BCSFB1; QpBCSFB1, paracellular diffusion clearance at the BCSFB1; QBCSFB2, passive diffusion clearance at the BCSFB2; QtBCSFB2, transcellular diffusion clearance at the BCSFB2; QpBCSFB2, paracellular diffusion clearance at the BCSFB2; QBCM, passive diffusion clearance at the brain cell membrane; QLYSO, passive diffusion clearance at the lysosomal membrane.
QBBB_in = QpBBB + QtBBB*AFin1, QBBB_out = (QpBBB + QtBBB*AFout1)*PHF1, QpBBB = (aqueous diffusivity coefficient/widthBBB)*SABBBp, QtBBB = 1/2*transmembrane permeability*SABBBt
QBCSFB1_in = QpBCSFB1 + QtBCSFB1*AFin2, QBCSFB1_out = (QpBCSFB1+ QtBCSFB1*AFout2)*PHF2, QpBCSFB1 = (aqueous diffusivity coefficient/widthBCSFB1)*SABCSFB1p, QtBCSFB1 = 1/2* Transmembrane permeability *SABCSFB1t.
QBCSFB2_in = QpBCSFB2 + QtBCSFB2*AFin3, QBCSFB2_out = (QpBCSFB2 + QtBCSFB2*AFout3)*PHF3, QpBCSFB2 = (aqueous diffusivity coefficient/widthBCSFB2)*SABCSFB2p, QtBCSFB2 = 1/2* transmembrane permeability *SABCSFB2t.
QBCM_in = Transmembrane permeability *SABCM*PHF4, QBCM_out = transmembrane permeability *SABCM*PHF5.
QLYSO_in = transmembrane permeability *SALYSO*PHF6, QLYSO_in = transmembrane permeability *SALYSO*PHF7.
PHF1, PHF2, PHF3, PHF4, PHF5, PHF6, and PHF7 were calculated from pKa of each compound and pH of each compartment, respectively.
BF was calculated from Kp of each compound.
4 mg/kg.
10, 40 mg/kg.
Figure 2.
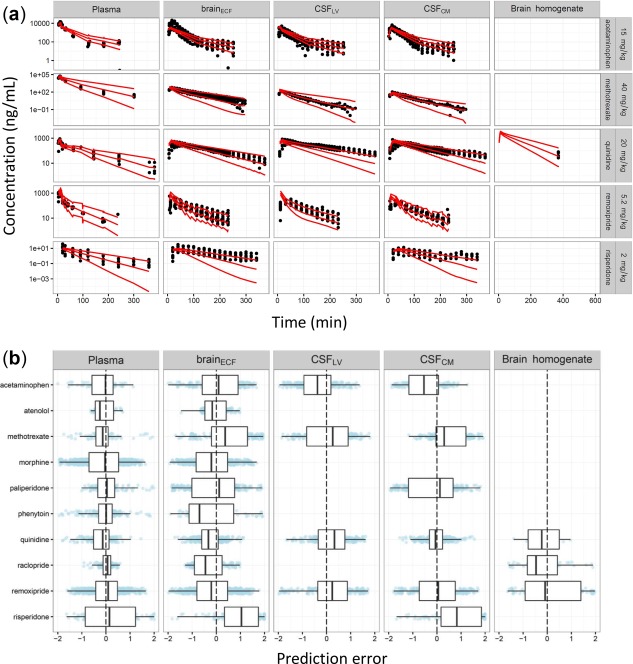
Prediction accuracy of the physiologically based pharmacokinetic (PBPK) model. The plots were stratified by the central nervous system (CNS) compartments (panels). (a) Selected individual observed drug concentrations (dots) and 95% prediction interval (red lines). (b) Box‐whisker plots for the prediction errors (PEs) across all 10 drugs evaluated. Blue dots are PEs for each observation.
Impact of cerebral blood flow
Cerebral blood flow (QCBF) is 1.2 mL/min.44 Therefore, for strong lipophilic compounds, for instance, quinidine, the drug transport clearance from plasma to the brainECF (BBB permeability) is limited by QCBF because QBBB_in and QBBB_out of quinidine were 9.1 and 5.1 mL/min, respectively (Tables 4 and 5).
Impact of distinct paracellular and transcellular pathways on total diffusion at the BBB, and BCSFB (QBBB, QBCSFB1, and QBCSFB2)
The QBBB, QBCSFB1, and QBCSFB2 were determined by the combination of paracellular and transcellular diffusion in the model. Even though the SABBBp is very small compared to the SABBBt (0.006: 99.8), paracellular diffusion had an impact on the values of QBBB, QBCSFB1, and QBCSFB2 especially for hydrophilic compounds. For instance, the values of transcellular diffusion (QtBBB) and paracellular diffusion (QpBBB) for methotrexate, which is the most hydrophilic compound in this study, were 0.000080 and 0.087 mL/min, respectively (Table 5). Thus, the QBBB of methotrexate was determined mainly by paracellular diffusion. For quinidine, which is the most lipophilic compound in the study, the QBBB was mainly determined by CBF limited transcellular diffusion (QtBBB and QpBBB were 7.6 and 0.10 mL/min, respectively).
Rate limiting drug transport clearance for intra‐extracellular exchange (QBCM_in and QBCM_out)
The QBCM_in and QBCM_out were higher than QBBB_in and QBBB_out for acetaminophen, paliperidone, phenytoin, quinidine, raclopride, remoxipride, and risperidone. The QBCM_in and QBCM_out are lower than QBBB_in and QBBB_out for methotrexate (Table 5). This suggests that the transport clearance from brainMV, via brainECF, to brainICF is limited by QBBB_in and QBBB_out for acetaminophen, paliperidone, phenytoin, quinidine, raclopride, remoxipride, and risperidone, whereas it is limited by QBCM_in and QBCM_out for methotrexate.
Surface area of BCSFB to determine the paracellular and transcellular diffusion clearance around CSFLV and CSFTFV
In our model, we assumed that the SA of the BCSFB around CSFLV (SABCSFB1) and CSFTFV (SABCSFB2) are equal in size (50% of the total SABCSFB for each). The SA is one of the key factors that determine the paracellular and transcellular diffusion clearance across the BCSFB1 and BCSFB2. However, the early‐time predictions for CSFLV for acetaminophen, quinidine, and remoxipride indicate an overprediction of the paracellular and transcellular diffusion clearance (Figure 2 and Supplementary Figure S1), suggesting that the SA of BCSFB1 is <50% of the total SABCSFB.
Impact of active transporters to determine the extent of drug exposure in the CNS compartments
Active transporters govern the extent of drug exposure in the brain and CSFs. For most of the compounds, the impact of active transporters among Kp,uu,brainECF, Kp,uu,CSFLV, and Kp,uu,CSFCM was assumed to be identical, except for methotrexate. Different Kp,uu,CSFLV (0.0066) and Kp,uu,CSFCM (0.0024) were observed for methotrexate, which were taken into account in the PBPK model by asymmetry factors AFout2 and AFout3. The extent of drug entry into the brain and CSF was predicted well for all compounds, except for morphine at the 4 mg/kg dose (Supplementary Figure S1).
DISCUSSION
The developed CNS PBPK model resulted in adequate predictions of concentration‐time courses for 10 diverse drugs in the brainECF, CSFLV, CSFCM, and total brain tissue with less than twofold prediction error. In comparison, QSPR studies that predict Kp,uu,brainECF of drugs have similar prediction error magnitudes, even though only one parameter was predicted.4, 5 Therefore, the twofold prediction error is considered to be a good result.
A small underprediction was observed in brainECF and CSFCM for risperidone, and in brainECF for morphine at the 4 mg/kg dose. The underprediction of risperidone brainECF and CSFCM concentrations (Figure 2) likely results from difficulties in the plasma PK modeling of risperidone, which leads to propagation of an error in the PBPK model. Risperidone plasma PK data appeared to follow a two‐compartment PK model but data were insufficient to describe this two‐compartment kinetics. The small underprediction for morphine brainECF profiles at a dosage of 4 mg/kg might be related to a large interstudy variability for morphine, because the predictions for morphine at the other dosage groups could adequately capture the observations (Supplementary Figure S1 and Table S1).
This is the first time that the transcellular and paracellular diffusion clearance at the BBB/BCSFB were addressed separately, by using the information of the intercellular space and the effective pore size. As the contribution of these pathways may depend on the condition of the barriers (i.e., in certain disease conditions the tight junctions may become less tight), therefore, assessment of these system‐specific parameters is important. From the electron microscopic cross‐section picture of brain capillary,12 the intercellular space was measured to be 0.03 µm, which is comparable to the 0.02 µm width reported.45 Based on the relationship of the pore size and TEER, which were obtained from in vitro studies,15 we assumed the effective pore size of the BBB and BCSFB to be 0.0011 µm and 0.0028 µm, respectively. The effective pore size derived for the rat BBB (0.0011 µm) is within the range reported in literature (0.0007–0.0018 µm).46, 47 Therefore, it is reasonable to assume that our estimations for these system‐specific parameter values are appropriate. In this study, no compound with sole paracellular transport (such as mannitol) has been used, as no such data were available in literature.
For the PBPK model, the drug‐specific parameters were obtained from in silico predictions using the compounds' physicochemical properties, except for AF values. The AF values were calculated using Kp,uu values, as obtained from the previously published in vivo animal experiments.9 It should be noted that Kp,uu values can also be obtained from several published QSPR models using the compound's physicochemical properties.3, 4, 5
Unlike previously developed PBPK models for the CNS,2 our PBPK model contains a number of key relevant physiological processes and compartments.
We discriminated between paracellular and transcellular diffusion processes. The relative impact of the paracellular diffusion on QBBB or QBCSFB for each compound varied from around 100% (methotrexate) to 1.3% (quinidine). For hydrophilic compounds, QBBB and QBCSFB were impacted most by paracellular diffusion, whereas transcellular diffusion largely determined the QBBB and QBCSFB of lipophilic compounds. The separation of the two processes is expected to be meaningful for the prediction of the CNS drug concentrations in disease conditions, because pathophysiological conditions may differently affect paracellular and transcellular diffusion.
We also demonstrated the relevance of considering CBF‐limited kinetics on the drug transfer at the BBB. For the lipophilic compounds, QBBB_in and QBBB_out are higher than QCBF, indicating that the drug transfer clearance on the BBB is largely determined by QCBF.
The importance of the separation between brainECF and brainICF compartments was shown. The QBCM_in and QBCM_out were either higher or lower than QBBB_in and QBBB_out, depending on the molecular weight, the log P, and the pKa of the compound, which led to differences in drug distribution into brainICF from brainMV.
We identified differences in methotrexate drug concentration in CSFLV and CSFCM.23 Therefore, it is expected that the expression level (function) of some of the active transporters may be different between the BCSFB around CSFLV and CSFTFV. Methotrexate is known to be a substrate of various transporters, such as RFC1, MRP, BCRP, OATP, and OAT transporters,23 even though there is no detailed information about their exact location. Therefore, we incorporated this in our model by including QBCSFB1 and QBCSFB2 to describe transport for methotrexate.
All of the parameters for our CNS PBPK model can be derived from either literature or in silico predictions. Therefore, the model can be used to assess newly developed CNS drugs without in vivo data and contributes to the “refinement, reduction, and replacement” of animals in drug research. Although the reported values of the system‐specific parameters for humans are sparse and variable,2 theoretically, the model can be scaled to humans by replacing the system‐specific parameters to predict target‐site concentrations in the human brain, representing an important tool for translational development of new CNS drugs.
Conflict of Interest
The authors have no conflicts of interest that are directly relevant to the contents of this research article.
Author Contributions
E.C.M.L., Y.Y., P.A.V., D.R., J.H.P., A.V., W.K., M.W.B., M.D., and J.G.C.H. wrote the manuscript; E.C.M.L. designed the research; E.C.M.L., Y.Y., P.A.V., and J.G.C.H. performed the research; D‐J.B., R.H., and Y.C.W. analyzed the data.
Supporting information
Supplementary S1 Algebraic solutions for calculating AFs and BF using Maxima Computer Algebra System
Supplementary S2 General animal surgery and experimental setting
Supplementary S3 Model code for acetaminophen
Supplementary S4 Model code for atenolol
Supplementary S5 Model code for methotrexate
Supplementary S6 Model code for morphine (4 mg/kg)
Supplementary S7 Model code for morphine (10 and 40 mg/kg)
Supplementary S8 Model code for paliperidone
Supplementary S9 Model code for phenytoin
Supplementary S10 Model code for quinidine
Supplementary S11 Model code for raclopride
Supplementary S12 Model code for remoxipride
TABLE SI. Summary of the in vivo experimental set‐up for rat data
Supplementary Figure S1 Prediction of the PBPK model.
Supplementary Material
Acknowledgments
This research article was prepared within the framework of project number D2–501 of the former Dutch Top Institute Pharma, currently Lygature (Leiden, The Netherlands; www.lygature.org). J.G.C.H. received funding from the European Union Marie Curie programme (Project ID 661588).
This article was published online on 13 October 2017. An error was subsequently identified in the author line. This notice is included in the online version to indicate this version has been corrected 27 October 2017.
References
- 1. Kola, I. & Landis, J. Can the pharmaceutical industry reduce attrition rates? Nat. Rev. Drug Discov. 3, 711–715 (2004). [DOI] [PubMed] [Google Scholar]
- 2. Yamamoto, Y. , Danhof, M. & de Lange, E.C.M. Microdialysis: the key to physiologically based model prediction of human CNS target site concentrations. AAPS J. 19, 891–909 (2017). [DOI] [PubMed] [Google Scholar]
- 3. Fridén, M. et al Structure‐brain exposure relationships in rat and human using a novel data set of unbound drug concentrations in brain interstitial and cerebrospinal fluids. J. Med. Chem. 52, 6233–6243 (2009). [DOI] [PubMed] [Google Scholar]
- 4. Loryan, I. et al Molecular properties determining unbound intracellular and extracellular brain exposure of CNS drug candidates. Mol. Pharm. 12, 520–532 (2015). [DOI] [PubMed] [Google Scholar]
- 5. Chen, H. , Winiwarter, S. , Fridén, M. , Antonsson, M. & Engkvist, O. In silico prediction of unbound brain‐to‐plasma concentration ratio using machine learning algorithms. J. Mol. Graph. Model. 29, 985–995 (2011). [DOI] [PubMed] [Google Scholar]
- 6. Jones, H. & Rowland‐Yeo, K. Basic concepts in physiologically based pharmacokinetic modeling in drug discovery and development. CPT Pharmacometrics Syst. Pharmacol. 2, e63 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Engelhardt, B. & Sorokin, L. The blood‐brain and the blood‐cerebrospinal fluid barriers: function and dysfunction. Semin. Immunopathol. 31, 497–511 (2009). [DOI] [PubMed] [Google Scholar]
- 8. Nguyen, T.H. et al Model evaluation of continuous data pharmacometric models: metrics and graphics. CPT Pharmacometrics Syst. Pharmacol. 6, 87–109 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Yamamoto, Y. et al A generic multi‐compartmental CNS distribution model structure for 9 drugs allows prediction of human brain target site concentrations. Pharm. Res. 34, 333–351 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Nicholson, C. & Syková, E. Extracellular space structure revealed by diffusion analysis. Trends Neurosci. 21, 207–215 (1998). [DOI] [PubMed] [Google Scholar]
- 11. Hardin, J. , Bertoni, G.P. & Kleinsmith, L.J. Becker's World of the Cell, Books a la Carte Edition (8th Edition) (Pearson Education, San Francisco, CA, 2011).
- 12. Weiss, N. , Miller, F. , Cazaubon, S. & Couraud, P.O. The blood‐brain barrier in brain homeostasis and neurological diseases. Biochim. Biophys. Acta 1788, 842–857 (2009). [DOI] [PubMed] [Google Scholar]
- 13. Crone, C. & Olesen, S.P. Electrical resistance of brain microvascular endothelium. Brain Res. 241, 49–55 (1982). [DOI] [PubMed] [Google Scholar]
- 14. Olesen, S.P. & Crone, C. Electrical resistance of muscle capillary endothelium. Biophys. J. 42, 31–41 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Adson, A. et al Quantitative approaches to delineate paracellular diffusion in cultured epithelial cell monolayers. J. Pharm. Sci. 83, 1529–1536 (1994). [DOI] [PubMed] [Google Scholar]
- 16. Avdeef, A. , Nielsen, P.E. & Tsinman, O. PAMPA – a drug absorption in vitro model 11. Matching the in vivo unstirred water layer thickness by individual‐well stirring in microtitre plates. Eur. J. Pharm. Sci. 22, 365–374 (2004). [DOI] [PubMed] [Google Scholar]
- 17. Grumetto, L. , Russo, G. & Barbato, F. Immobilized artificial membrane HPLC derived parameters vs PAMPA‐BBB data in estimating in situ measured blood‐brain barrier permeation of drugs. Mol. Pharm. 13, 2808–2816 (2016). [DOI] [PubMed] [Google Scholar]
- 18. Fridén, M. et al Measurement of unbound drug exposure in brain: modeling of pH partitioning explains diverging results between the brain slice and brain homogenate methods. Drug Metab. Dispos. 39, 353–362 (2011). [DOI] [PubMed] [Google Scholar]
- 19. Henderson, L.J. Concerning the relationship between the strength of acids and their capacity to preserve neutrality. Am. J. Physiol. 21, 173–179 (1908). [Google Scholar]
- 20. Henderson, L.J. The theory of neutrality regulation in the animal organism. Am. J. Physiol. 21, 427–448 (1908). [Google Scholar]
- 21. Berezhkovskiy, L.M. Volume of distribution at steady state for a linear pharmacokinetic system with peripheral elimination. J. Pharm. Sci. 93, 1628–1640 (2004). [DOI] [PubMed] [Google Scholar]
- 22. Poulin, P. & Theil, F.P. Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J. Pharm. Sci. 91, 1358–1370 (2002). [DOI] [PubMed] [Google Scholar]
- 23. Westerhout, J. , van den Berg, D.J. , Hartman, R. , Danhof, M. & de Lange, E.C. Prediction of methotrexate CNS distribution in different species – Influence of disease conditions. Eur. J. Pharm. Sci. 57, 11–24 (2014). [DOI] [PubMed] [Google Scholar]
- 24. Westerhout, J. , Ploeger, B. , Smeets, J. , Danhof, M. & de Lange, E.C. Physiologically based pharmacokinetic modeling to investigate regional brain distribution kinetics in rats. AAPS J. 14, 543–553 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. de Lange, E.C. , Danhof, M. , de Boer, A.G. & Breimer, D.D. Critical factors of intracerebral microdialysis as a technique to determine the pharmacokinetics of drugs in rat brain. Brain Res. 666, 1–8 (1994). [DOI] [PubMed] [Google Scholar]
- 26. Groenendaal, D. , Freijer, J. , de Mik, D. , Bouw, M.R. , Danhof, M. & de Lange, E.C. Population pharmacokinetic modelling of non‐linear brain distribution of morphine: influence of active saturable influx and P‐glycoprotein mediated efflux. Br . J. Pharmacol. 151, 701–712 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Bouw, M.R. , Gårdmark, M. & Hammarlund‐Udenaes, M. Pharmacokinetic‐pharmacodynamic modelling of morphine transport across the blood‐brain barrier as a cause of the antinociceptive effect delay in rats–a microdialysis study. Pharm. Res. 17, 1220–1227 (2000). [DOI] [PubMed] [Google Scholar]
- 28. Westerhout, J. , Smeets, J. , Danhof, M. & de Lange, E.C. The impact of P‐gp functionality on non‐steady state relationships between CSF and brain extracellular fluid. J. Pharmacokinet. Pharmacodyn. 40, 327–342 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Stevens, J. , Ploeger, B.A. , van der Graaf, P.H. , Danhof, M. & de Lange, E.C. Systemic and direct nose‐to‐brain transport pharmacokinetic model for remoxipride after intravenous and intranasal administration. Drug Metab. Dispos. 39, 2275–2282 (2011). [DOI] [PubMed] [Google Scholar]
- 30. Kawakami, J. , Yamamoto, K. , Sawada, Y. & Iga, T. Prediction of brain delivery of ofloxacin, a new quinolone, in the human from animal data. J. Pharmacokinet. Biopharm. 22, 207–227 (1994). [DOI] [PubMed] [Google Scholar]
- 31. Cserr, H.F. , Cooper, D.N. , Suri, P.K. & Patlak, C.S. Efflux of radiolabeled polyethylene glycols and albumin from rat brain. Am. J. Physiol. 240, F319–F328 (1981). [DOI] [PubMed] [Google Scholar]
- 32. Thorne, R.G. , Hrabetová, S. & Nicholson, C. Diffusion of epidermal growth factor in rat brain extracellular space measured by integrative optical imaging. J. Neurophysiol. 92, 3471–3481 (2004). [DOI] [PubMed] [Google Scholar]
- 33. Condon, P. et al Use of magnetic resonance imaging to measure intracranial cerebrospinal fluid volume. Lancet. 1, 1355–1357 (1986). [DOI] [PubMed] [Google Scholar]
- 34. Kohn, M.I. et al Analysis of brain and cerebrospinal fluid volumes with MR imaging. Part I. Methods, reliability, and validation. Radiology 178, 115–122 (1991). [DOI] [PubMed] [Google Scholar]
- 35. Robertson, E.G. Developmental defects of the cisterna magna and dura mater. J. Neurol. Neurosurg. Psychiatry 12, 39–51 (1949). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Adam, R. & Greenberg, J.O. The mega cisterna magna. J. Neurosurg. 48, 190–192 (1978). [DOI] [PubMed] [Google Scholar]
- 37. Bass, N.H. & Lundborg, P. Postnatal development of bulk flow in the cerebrospinal fluid system of the albino rat: clearance of carboxyl‐(14 C)inulin after intrathecal infusion. Brain Res. 52, 323–332 (1973). [DOI] [PubMed] [Google Scholar]
- 38. Liu, X. et al Use of a physiologically based pharmacokinetic model to study the time to reach brain equilibrium: an experimental analysis of the role of blood‐brain barrier permeability, plasma protein binding, and brain tissue binding. J. Pharmacol. Exp. Ther. 313, 1254–1262 (2005). [DOI] [PubMed] [Google Scholar]
- 39. Neuwelt, E. et al Strategies to advance translational research into brain barriers. Lancet Neurol. 7, 84–96 (2008). [DOI] [PubMed] [Google Scholar]
- 40. Patabendige, A. , Skinner, R.A. & Abbott, N.J. Establishment of a simplified in vitro porcine blood‐brain barrier model with high transendothelial electrical resistance. Brain Res. 1521, 1–15 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Strazielle, N. & Ghersi‐Egea, J.F. Choroid plexus in the central nervous system: biology and physiopathology. J. Neuropathol. Exp. Neurol. 59, 561–574 (2000). [DOI] [PubMed] [Google Scholar]
- 42. Trapa, P.E. , Belova, E. , Liras, J.L. , Scott, D.O. & Steyn, S.J. Insights from an integrated physiologically based pharmacokinetic model for brain penetration. J. Pharm. Sci. 105, 965–971 (2016). [DOI] [PubMed] [Google Scholar]
- 43. Cornford, E.M. & Hyman, S. Localization of brain endothelial luminal and abluminal transporters with immunogold electron microscopy. NeuroRx 2, 27–43 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Sasaki, Y. & Wagner, H.N. Jr. Measurement of the distribution of cardiac output in unanesthetized rats. J. Appl. Physiol. 30, 879–884 (1971). [DOI] [PubMed] [Google Scholar]
- 45. Farquhar, M.G. & Palade, G.E. Junctional complexes in various epithelia. J. Cell. Biol. 17, 375–412 (1963). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Crone, C. Lack of selectivity to small ions in paracellular pathways in cerebral and muscle capillaries of the frog. J. Physiol. 353, 317–337 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Zhang, T.T. , Li, W. , Meng, G. , Wang, P. & Liao, W. Strategies for transporting nanoparticles across the blood‐brain barrier. Biomater. Sci. 4, 219–229 (2016). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary S1 Algebraic solutions for calculating AFs and BF using Maxima Computer Algebra System
Supplementary S2 General animal surgery and experimental setting
Supplementary S3 Model code for acetaminophen
Supplementary S4 Model code for atenolol
Supplementary S5 Model code for methotrexate
Supplementary S6 Model code for morphine (4 mg/kg)
Supplementary S7 Model code for morphine (10 and 40 mg/kg)
Supplementary S8 Model code for paliperidone
Supplementary S9 Model code for phenytoin
Supplementary S10 Model code for quinidine
Supplementary S11 Model code for raclopride
Supplementary S12 Model code for remoxipride
TABLE SI. Summary of the in vivo experimental set‐up for rat data
Supplementary Figure S1 Prediction of the PBPK model.
Supplementary Material


