In curved environments, geometric constraints can result in cellular competition for space. Quantitative information about cell geometry was extracted to explore how columnar-like cells fit within the curved anterior of the Drosophila embryo. Cell deformations and cell rearrangements enable packing in this highly curved region.
Abstract
Organ and tissue formation are complex three-dimensional processes involving cell division, growth, migration, and rearrangement, all of which occur within physically constrained regions. However, analyzing such processes in three dimensions in vivo is challenging. Here, we focus on the process of cellularization in the anterior pole of the early Drosophila embryo to explore how cells compete for space under geometric constraints. Using microfluidics combined with fluorescence microscopy, we extract quantitative information on the three-dimensional epithelial cell morphology. We observed a cellular membrane rearrangement in which cells exchange neighbors along the apical-basal axis. Such apical-to-basal neighbor exchanges were observed more frequently in the anterior pole than in the embryo trunk. Furthermore, cells within the anterior pole skewed toward the trunk along their long axis relative to the embryo surface, with maximum skew on the ventral side. We constructed a vertex model for cells in a curved environment. We could reproduce the observed cellular skew in both wild-type embryos and embryos with distorted morphology. Further, such modeling showed that cell rearrangements were more likely in ellipsoidal, compared with cylindrical, geometry. Overall, we demonstrate that geometric constraints can influence three-dimensional cell morphology and packing within epithelial tissues.
INTRODUCTION
Epithelial tissues are sheets of closely adhered cells that play an important role in many processes, including organ growth in development (Guillot and Lecuit, 2013). Cells within the epithelial tissue interact, both chemically and mechanically, with their neighbors and with the extracellular matrix. Passive (e.g., viscoelastic resistance) and active (e.g., cytoskeletal tension) processes shape the cells and the overall tissue morphology (Lecuit and Lenne, 2007). How the cells arrange themselves within the tissue is referred to as cell packing. The packing density is defined as the average number of neighbors for a cell. The optimal cell shape on a flat surface is typically hexagonal (i.e., packing density of six), as this minimizes surface tension (Thompson, 1917; Hayashi and Carthew, 2004). However, biological systems are often more complex, with, for example, cell proliferation, polarization, and competition altering the geometric order (Lewis, 1926; Zallen and Zallen, 2004; Classen et al., 2005; Gibson et al., 2006; Ma et al., 2008). Differences in cell packing can alter the diffusivity of morphogens through tissues (Muller et al., 2013), thereby altering the positioning and precision of gene expression boundaries (Bollenbach et al., 2008).
Epithelial tissues are often found within highly curved environments, where the radius of curvature is comparable to a few cells lengths. Processes potentially affected by such curved environments include cell renewal in the intestinal crypts (Hannezo et al., 2011; Shyer et al., 2013), cell formation in the anterior pole during early Drosophila embryogenesis (Blankenship and Wieschaus, 2001), and gut folding and shaping (Taniguchi et al., 2011; Savin et al., 2012). Geometric constraints could also be relevant in ectodermal organ formation, such as tooth growth and hair follicle formation (Panousopoulou and Green, 2016; Pearl et al., 2017). A consequence of the Euler-Poincare equation—which relates the number of vertices, edges, and faces of polygons embedded in three-dimensional space—is that patterning the surface of a sphere (e.g., a soccer ball) with hexagons requires the inclusion of exactly 12 pentagons. In this case, the packing density is reduced below six. Such differences can potentially play an important role in the function of the system; for example, cells are extruded at the ends of highly curved villi within the intestinal crypt. Currently, our knowledge of how cells pack in three dimensions within curved environments is limited.
The three-dimensional nature of epithelial cells themselves must also be considered. Such cells have apical-basal polarity (Gibson and Perrimon, 2003), which plays essential roles in processes such as adhesive junction formation (Knust and Bossinger, 2002; Wang et al., 2012) and cellularization (Lecuit and Wieschaus, 2000). There has been significant work on processes occurring on or near the apical surface, for example, directed cell rearrangement (Blankenship et al., 2006; Rauzi et al., 2008, 2010; Collinet et al., 2015), apical constriction (Leptin and Grunewald, 1990; Martin et al., 2009), and cell competition in the Drosophila larval wing (Aigouy et al., 2010) and pupal abdominal epidermis (Umetsu et al., 2014). In particular, a group of four cells can alter their neighbors by remodeling junctions such that the junction between two neighboring cells shrinks until there is no clear cell interface, and a new junction forms between the other two (now) adjacent cells. This process is known as a T1 transition (Bertet et al., 2004; Blankenship et al., 2006) (Figure 1A). Though more difficult to image, three-dimensional epithelial tissue behavior has been explored during the formation of the Drosophila egg respiratory appendages (Osterfield et al., 2013, 2015) and in epithelial folding in the mouse oviduct (Koyama et al., 2016). Recent work has also shown during germ-band extension in Drosophila that the basal surface of intercalating cells typically precedes apical rearrangements (Sun et al., 2017). Hence, the three-dimensional cell architecture needs to be considered when analyzing epithelial tissues.
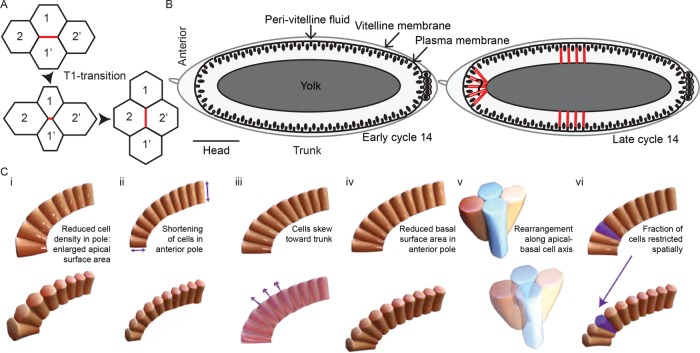
FIGURE 1:
Cell arrangements in the Drosophila embryo. (A) Schematic representation of four cells undergoing a T1 transition. Initially, the cells 1 and 1′ are neighbors. The cell interface denoted in red then shortens (intermediate panel) and then forms a new cell interface between cells 2 and 2′. (B) Schematic representation of cellularization in the Drosophila embryo. In early cellularization (left), cell walls invaginate perpendicular to the embryo surface. Nuclei are denoted by black ovals. In late cycle 14 (right), the cell basal surface extends (denoted by red lines) below the nuclei. In the polar regions, the embryo curvature potentially results in cell shape changes away from columnar cells. (C) Possible scenarios for cell shape and packing in the anterior pole: (i) lower cell density in the anterior; (ii) reduced basal surface extension of cells in the anterior, reducing the geometric effects of the curvature; (iii) cells skew toward the trunk, which is under less geometric constraint; (iv) the basal surface of the anterior-most cells reduce in cross-section, with the cells becoming more pyramid-like; (v) cells undergo rearrangements from apical-to-basal to fit into the restricted space as the basal surface extends (in the lower image, the red and yellow cells are neighbors at the basal surface); (vi) a subset of cells fail to extend fully (purple cell), thereby providing more space for neighboring cells.
To explore the effects of geometry on epithelial tissues, we focused on the process of cellularization in the Drosophila embryo. The embryo is approximately ellipsoidal in shape with length ∼500 μm and diameter 200 μm (Figure 1B). During cellularization (nuclear cycle 14), the plasma membrane at the surface of the embryo forms furrows and invaginates between the nuclei to form the cells, Figure 1B (Mazumdar and Mazumdar, 2002). This process lasts 1 h and can be divided into two phases: a slow phase lasting around 35–40 min, during which there is gradual membrane invagination, and then a fast phase of around 20 min, characterized by a marked increase of furrow ingression after the invagination has extended beyond the nucleus (Lecuit and Wieschaus, 2000). At the end of cellularization, cells reach a depth of around 35 μm in the trunk. An actomyosin contractile ring, which is initially assembled at the apical surface and descends as the furrow ingresses, basally constricts to close the cells (Warn et al., 1980; Young et al., 1991). During the period of cellularization there are no cell divisions, nor significant cell movements, and so cell packing in three dimensions can be explored with relatively constant cell number and position. In the embryo trunk (>100 μm from the poles) the cells are columnar, with smaller basal surface compared with the apical surface (Leptin and Grunewald, 1990). In this way, the basal furrow can invaginate without significant neighbor rearrangement or competition.
Here we ask whether geometry can alter cell shape and arrangements in the polar regions since cells are more geometrically confined (Figure 1B). We find that epithelial cells in the anterior and trunk display distinct properties. Whereas trunk cells extend perpendicular to the surface, a subset of cells in the anterior skew toward the embryo trunk. This skew sets in soon after the cells extend beyond the nucleus basal surface. In mutant embryos that are significantly rounder, the skew decreases, which is consistent with a model of skew induced by asymmetric geometric constraints. Further, we find that cells in the anterior rearrange neighbors along the apical-basal axis of the cell significantly more frequently than in the trunk. In mutant embryos with increased apical-basal distance in anterior cells, we see a substantial increase in a subset of cells with reduced basal surface area. We complement these experiments with theoretical analysis that demonstrates how geometric constraints are sufficient to explain our above observations. Overall, epithelial cells embedded within a highly curved environment display distinct topological behavior to those within relatively flat environments, and our work highlights that studies of such tissues in vivo need to investigate the full three-dimensional cellular environment.
RESULTS
Mechanisms for cell packing in curved environments
We highlight six possible scenarios by which cell packing can occur (Figure 1C). (i) The cell density at the poles may be reduced, resulting in more space for each individual cell. This would create large apical to basal variations in the cross-sectional area of the cell. (ii) Cells in the anterior pole could have reduced basal extension, which would result in reduced curvature effects. (iii) Polar cells may extend their basal surface toward the trunk region, thereby becoming skewed along the apical-basal axis toward the embryo center. (iv) Cells in the polar regions could reduce their basal surface area compared with the trunk region to squeeze into the reduced available volume as cellularization occurs. (v) Cells may rearrange with their neighbors along their apical-basal axis, to compensate for the spatial constraints, resulting in neighbor exchange along the apical and basal cell axis. (vi) A subset of cells could have restricted basal surfaces, thereby making space for neighboring cells.
This list, while not exhaustive, provides a general overview of possible mechanisms by which cells pack within geometrically constrained environments. Packing is achieved through either reduced cell number, altered apical and/or basal surface properties in the poles compared with the trunk, and/or the skewing or repositioning of polar cells to compensate for embryo curvature. Scenarios (i) and (ii) in Figure 1C have been reported previously (Blankenship and Wieschaus, 2001) and are dependent on anterior Bicoid (Bcd) morphogen signaling. However, what role such variation in cell morphology and density plays in cell packing in the anterior region is unclear. In particular, it is unknown whether conditions (i) and (ii) are sufficient to compensate for the competition in trying to arrange columnar-like cells into the ellipsoidal-like embryo.
Quantifying three-dimensional cell volumes in the anterior pole of the developing Drosophila embryo
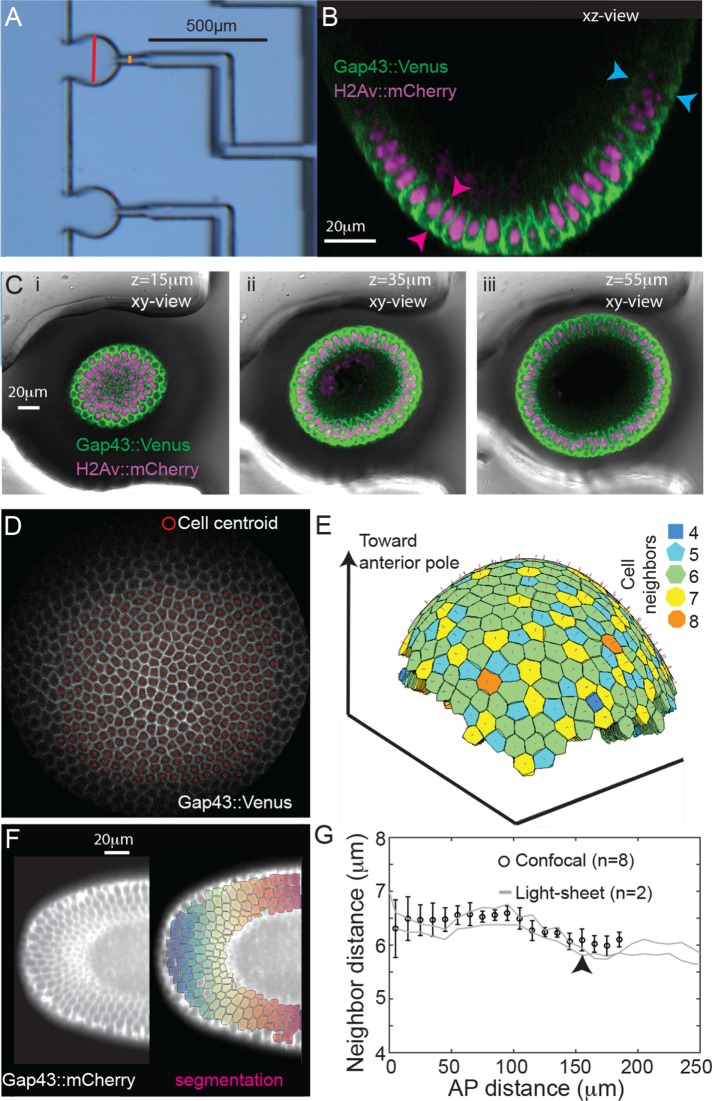
We imaged Drosophila embryos in cycle 14 with confocal microscopy and utilizing a microfluidic device for reliable mounting (Chung et al., 2010) (Figure 2, A–C, and Supplemental Movie S1). These data were supplemented by light-sheet microscopy (Rauzi et al., 2015). Cell segmentation of confocal data was performed using stereographic projections of the embryo poles (Krzic et al., 2012; Heemskerk and Streichan, 2015) (Figure 2, D and E, Supplemental Figure S1, and Supplemental Movie S2) and for light-sheet data a three-dimensional iterative watershed algorithm was used (Figure 2F, Supplemental Figure S2). Segmentation details are provided in Materials and Methods and the Supplemental Material. To confirm the quality of our quantification, we checked the cell nearest-neighbor distance (from geometric cell center); there was a small but reproducible decrease in cell separation around 150 μm from the pole, corresponding to the position of the future cephalic furrow (black arrow, Figure 2G) (Blankenship and Wieschaus, 2001). Furthermore, using cross-sectional views of the embryo, we confirmed that the cell invagination depth was 10 ± 6% shorter in the anterior (n = 12 embryos, p = 0.03, Figure 2B) (Blankenship and Wieschaus, 2001). Using this three-dimensional data of cell morphology during cellularization, we next explored whether cells deform or rearrange differently in the anterior region compared with the embryo trunk.
FIGURE 2:
Quantitative image analysis of cell morphology in the Drosophila embryo anterior. (A) Microfluidic device for mounting embryos vertically. Red bar denotes the cross-section of the well. (B) Transverse view of an embryo expressing H2Av::mCherry (magenta) and Gap43::mVenus (green) positioned in the microfluidic device. (C) Three cross-sectional views from the embryo shown in B (i–iii) with the microfluidic device shown. (D) Projected cells following the stereographic projection with identification of cell centers, see Materials and Methods. (E) Reconstructed cell surfaces after segmentation of projected data. Color coding represents neighbor number of each cell. (F) Left: Light-sheet image of a Drosophila embryo expressing Gap43::mCherry. Right: Segmentation from adaptive watersheds superimposed with color coding representing distance from anterior pole. (G) Nearest-neighbor distance for each segmented cell in confocal (black circles, n = 8 embryos) and light-sheet images (gray lines correspond to two different embryos) at the end of slow phase. Black arrow denotes approximate location of future cephalic furrow. Error bars = SD.
Cells rearrange neighbors along their apical-basal axis
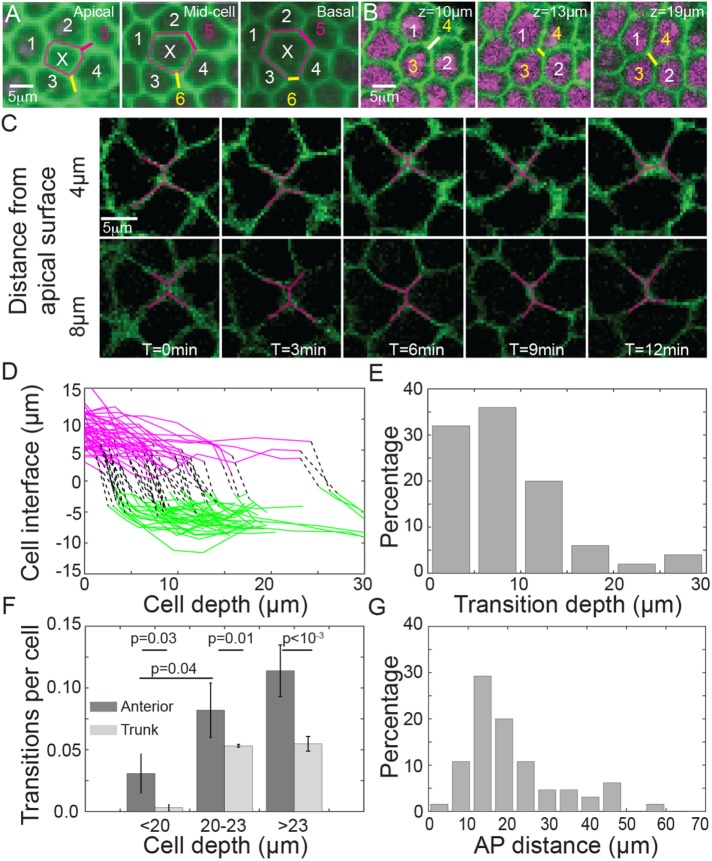
Strikingly, we observed T1-like spatial transitions (which we henceforth refer to as pseudo-T1 transitions) along the apical-basal axis of cells toward the anterior pole at a fixed time point (Figure 3, A–C). Representative cells undergoing a pseudo-T1 transition along the apical-basal axis are shown in Supplemental Movie S3. T1 transitions, which occur in time (Figure 3C) were distinguished from pseudo-T1 transitions, which occur in space at a fixed time point (Figure 3, A and B). Of course, the pseudo-T1 transitions we observed in fixed embryos were the result of dynamic neighbor rearrangements. By tracking the length of the cell interface before and after these pseudo-T1 transitions (Figure 3D), we see that the transitions are not restricted to one particular region of the cell. However, most transitions are observed within 15 μm of the apical cell surface (Figure 3E).
FIGURE 3:
Pseudo-T1 cellular rearrangements along the apical-basal cell axis in the embryo anterior. (A) Example cell, denoted by X, which increases from four to six neighbors between apical and basal surfaces. Pseudo-T1 transitions denoted by magenta and yellow lines. Embryo expressing H2b::mCherry (magenta) and Gap43::mVenus (green). (B) Further example of cells undergoing a pseudo-T1 transition, where z denotes linear distance from anterior pole. (C) Time-lapse images of cells undergoing a pseudo-T1 transition at 4 μm from the apical surface but not at 8 μm from the apical surface. (D) Cell interface length during pseudo-T1 transitions. Magenta denotes interface length before transition, and green corresponds to interface length (with new cells) after the pseudo-T1 transition. Black lines represent the position of the transition. n = 10 embryos at end of slow phase, with 60 individual cell rearrangements. (E) Distribution of the position of the identified pseudo-T1 transitions shown in D along the apical–basal axis (0 μm represents the cell apical surface). (F) The frequency of pseudo-T1 transitions per cell observed in the anterior (dark gray) and trunk (light gray) regions depends on the cell depth. Error bars = SEM. (G) The percentage of observed pseudo-T1 transitions compared with the linear distance from the anterior pole; data collected as in D.
We compared the number of identified pseudo-T1 transitions with cell depth (Figure 3F). Few pseudo-T1 transitions were observed during early cellularization. The number of pseudo-T1 transitions in the anterior region increased sharply after cells had reach depths of 20 μm. We found pseudo-T1 transitions occurring in the trunk at the same time but at significantly lower frequency (Figure 3F), and such transitions typically involved small changes in the cell interfaces (Supplemental Figure S3). Such pseudo-T1 transitions in the trunk could well be due to fluctuations in the cell-cell contact surface. In the anterior pole, the frequency of pseudo-T1 transitions and the significant change in the cell junction length after rearrangements (Figure 3, A and B) suggests that these neighbor rearrangements are not a consequence of cell surface contact fluctuations.
We did not notice any particular pattern in the orientation of the pseudo-T1 transitions. This is in contrast to T1 transitions that occur during germ-band elongation (Bertet et al., 2004; Blankenship et al., 2006). Most transitions were observed between 10 and 30 μm from the anterior pole (Figure 3G). This region, which we henceforth refer to as the proximal tip region, corresponds to where curvature places the largest asymmetric stress on the cells (see modeling below). Overall, we see that cells in the anterior undergo significant neighbor rearrangements in both space and time that are distinct from the cell behavior in the trunk region.
Neighbor rearrangements in the anterior pole do not correspond to changes in actin and myosin localization
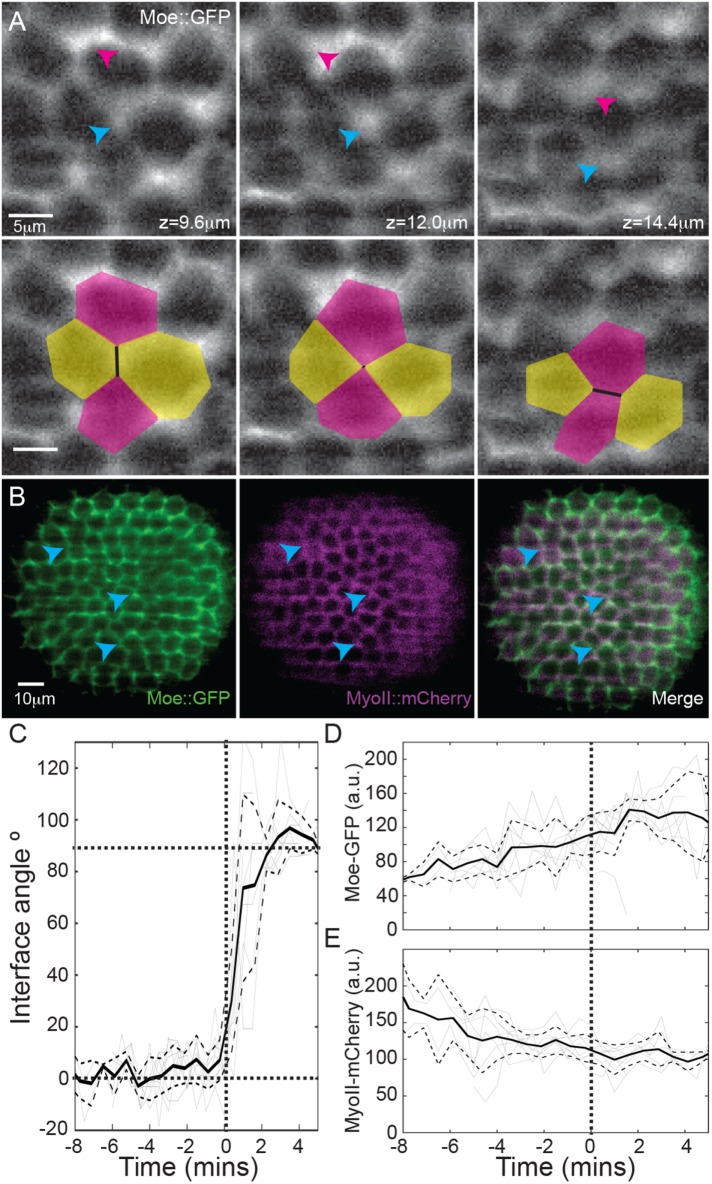
Actomyosin contractility plays a critical role in driving cell rearrangements during germ-band extension. To test whether such a process drives the spatial rearrangements we observed, we quantified the localization of actin and myosin in the anterior pole during cellularization by imaging embryos expressing Moesin (Moe)::GFP and Spaghetti Squash (Sqh)::mCherry using light-sheet microscopy (Figure 4, A and B, and Supplemental Figure S4A). The Moe::GFP and Sqh::mCherry signals were quantified during the T1 transitions (Figure 4, C–E). Although the neighbor rearrangement occurred rapidly (Figure 4C; on a time scale similar to active T1 transitions [ Bertet et al., 2004]), the variation in Moe::GFP and Sqh::mCherry signals was minimal during the rearrangements (Figure 4, D and E). The Sqh::mCherry signal decreased smoothly with time, attributable to the myosin ring descending from the apical to basal surface (Supplemental Figure S4, B and C). Although some pseudo-T1 transitions had high levels of Moe::GFP, we suspect that the increase was due to the small distance between two junctions; indeed, high Moe::GFP signal was also observed at locations that lacked rearrangements (Figure 4A, magenta arrows). We also confirmed that DE-cadherin showed no localization effects at pseudo-T1 transitions (Supplemental Figure S4, D–F). We observe that neighbor rearrangements in the cellularizing Drosophila embryo do not correlate with neither changes in actin nor myosin intensity.
FIGURE 4:
Cell rearrangements do not correlate with actin or myosin localization. (A) Embryos expressing Moe::GFP (gray) and MyoII::mCherry (see also Supplemental Figure S4A). Top row: blue arrow denotes location of pseudo-T1 transition, with the magenta arrow showing the region of high Moe::GFP intensity that does not undergo cell rearrangements. Bottom row: as above, but with cell outlines during pseudo-T1 transition. (B) Merge of Moe::GFP (green) and MyoII::mCherry (magenta) signals. Blue arrows highlight regions with pseudo-T1 transitions. (C) Angle change during pseudo-T1 transitions in the anterior (n = 4 embryos, 8 pseudo-T1 transitions), where 0° represents initial interface alignment. Solid black line denotes the mean angle, with ±1SD denoted by dashed lines. Gray lines represent tracks of the angle in individual pseudo-T1 transitions. Bold dotted lines are guides to the eye. T = 0 min denotes the beginning of the pseudo-T1 transition at a given apical–basal position within each cell. (D) Moe::GFP and (E) MyoII::mCherry intensity on cell interfaces undergoing pseudo-T1 transitions, with nomenclature same as in C.
Cell density and neighbor number do not significantly vary in the anterior pole
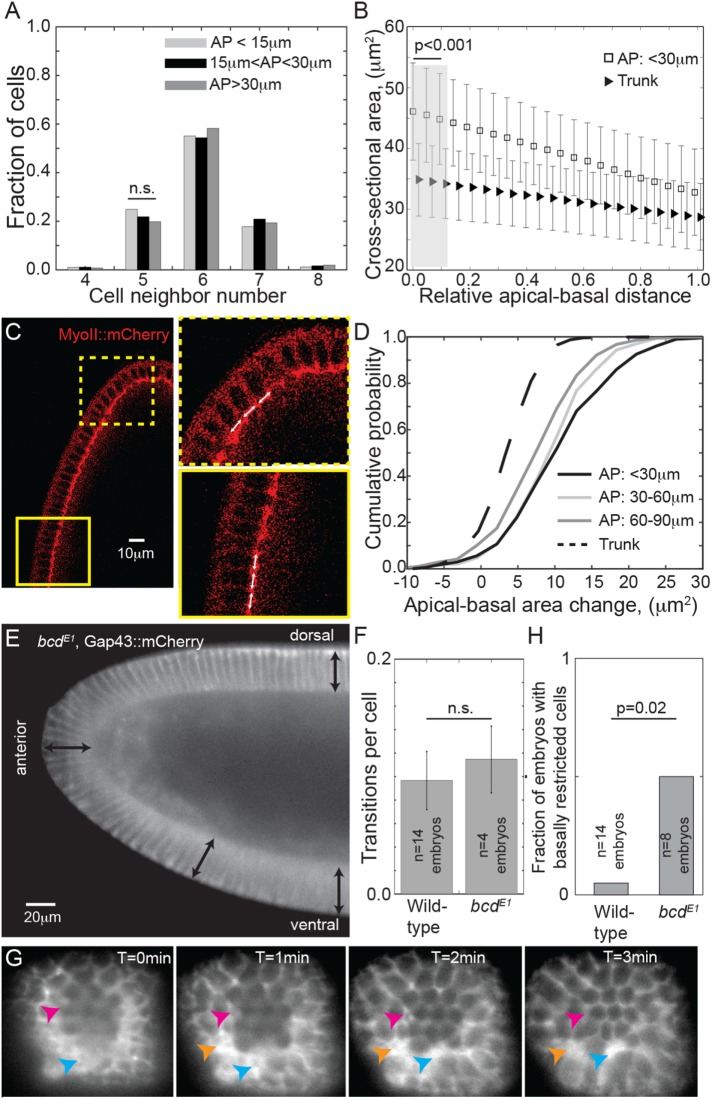
Using our cell segmentation data, we calculated the packing density (average neighbor number) in the anterior. Despite the higher curvature and lower cell density in the polar region, we did not observe a significant decrease in the packing density in the head compared with trunk (Figure 5A). Furthermore, there was no variation between the average neighbor number distributions at the apical and basal surfaces (Supplemental Figure S5A). This precludes models of cell packing in the polar regions where a significant subset of cells has significantly reduced basal surface (e.g., scenario (vi) in Figure 1C).
FIGURE 5:
Cell packing and shape in the anterior pole. (A) Cell neighbor number distribution for cells at different distances from the anterior pole. n = 10 embryos, >1000 cells. No significant change in packing density is observed. (B) The cross-sectional surface area of the cells from apical to basal surfaces in the trunk (triangles) and within 30 μm of the anterior pole (squares). n = 10 embryos, >1000 cells. Error bars = SD. The apical surface area is significantly larger in the anterior pole compared with the trunk (gray region). (C) Embryo expressing Sqh::mCherry in the anterior pole during cellularization. Yellow boxes denote zoomed regions. The white arrows are the same length. (D) Cumulative probability distribution for the change in area from apical to basal surface for cells at different positions relative to the anterior pole. n = 10 embryos, >1000 cells. The area change in the anterior is significantly different from the trunk (p < 10–3, using a Kolmogorov-Smirnov test). (E) Lateral view of bcdE1 embryo expressing Gap43::mCherry, imaged on a light-sheet microscope. Black arrows are equal length. (F) The frequency of pseudo-T1 transitions is similar in wild-type and bcdE1 embryos in the anterior. Error bars = SEM. (G) Anterior–posterior axis view of bcdE1 embryo expressing Gap43::mCherry, imaged on a light-sheet microscope. Arrows denote cells with significantly reduced basal surface compared with their neighbors. (H) Comparison of fraction of wild-type and bcdE1 embryos with cells that have significantly reduced basal surface in the anterior region. p-value calculated using two-proportion z-test.
Cell morphology varies between the anterior and trunk regions of the embryo
We next tested whether there was significant variation in the apical and basal cell surfaces between the anterior and trunk regions of the embryo. Most anterior cells have a larger apical surface area compared with the trunk (Figure 5B). This is unsurprising, as the cell density is not increased in the pole and due to the highly curved anterior pole the effective available surface area is larger. The difference in the basal surface area between head and trunk regions was considerably smaller (Figure 5, B and C). Though the basal surface area toward the anterior was larger than in the trunk (Blankenship and Wieschaus, 2001), the difference was small, which discounts mechanism (iv) in Figure 1C as a significant contributor to cell packing in the anterior of wild-type embryos. This result is consistent with the known cell properties during this phase of development: the basal surface is formed from a tight actomyosin meshwork while the apical surface does not have fully formed cell junctions and is generally under low stress (Young et al., 1991; Knust and Bossinger, 2002; Mazumdar and Mazumdar, 2002). In embryos with enlarged perivitelline space between the epithelium and the vitelline membrane, we noted blebbing-like behavior at the apical surface of cells, indicative of low membrane tension (Supplemental Figure S5B) (Tinevez et al., 2009). We confirmed this by laser ablating junctions on the apical surface of the cells during cellularization (Hara et al., 2016). We saw no significant relaxation of the surrounding cells (n = 5 embryos), which suggested the tension at the apical surface was low (Supplemental Figure S5C and Supplemental Movie S4).
There was a significant increase in area change between apical and basal surfaces in the head compared with trunk regions, p < 10−3 (Figure 5D). As expected, this difference was largest near the pole and gradually reduced toward the trunk. Although the cells in the anterior have distinct changes in apical surface, the cells typically remained columnar throughout the embryo (Supplemental Figure S5, D–F).
Perturbing cell shape alters geometric effects on cellular arrangements
To explore the role of cell shape, we quantified the prevalence of pseudo T1-transitions in bcdE1 mutants (Frohnhöfer and Nüsslein-Volhard, 1986) (Figure 5E) where the cell invagination depth increases in the anterior (Blankenship and Wieschaus, 2001). The frequency of pseudo-T1 transitions in the anterior of bcdE1 embryos is similar to that of wild-type embryos (Figure 5F). However, in four of eight embryos imaged, we observed a subset of cells that had significantly reduced basal surface compared with their neighbors (Figure 5G and Supplemental Figure S5, G and H), similarly to scenario (vi) in Figure 1C. These embryos were excluded from the calculation of the pseudo-T1 transition number shown in Figure 5F. This contrasts with the observation of one such cell in the anterior of 14 wild-type embryos (Figure 5H).
Cellular skew precedes neighbor rearrangements
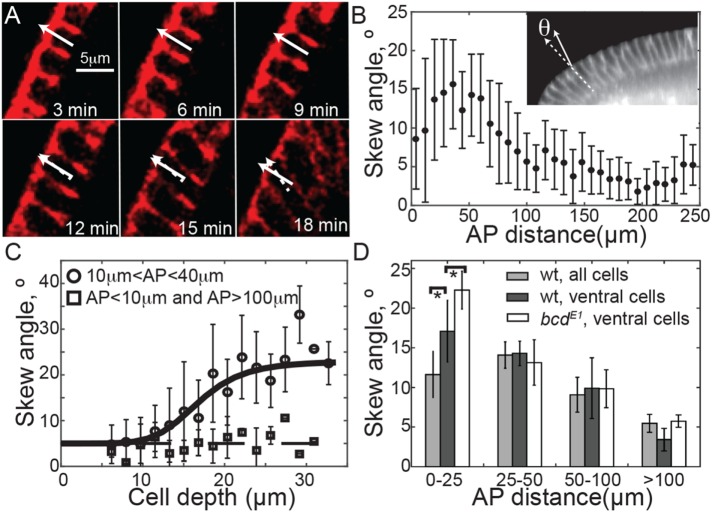
We next investigated the influence of cell angle on cell packing. Initially, the cell membrane invaginated perpendicular to the embryo surface. However, we observed that a subset of anterior cells—typically within the proximal tip region—skewed toward the embryo trunk after their basal surfaces had extended around 15 μm corresponding to scenario (iii) in Figure 1C (Figure 6, A and B, and Supplemental Figure S6, A and B). The onset of skew within the proximal tip region is quite sudden (Figure 6C). In contrast, we noted that cells at the tip or trunk had little skew (squares in Figure 6C).
FIGURE 6:
Cells in the anterior skew during cellularization toward the embryo trunk. (A) Time-lapse images of cells expressing Gap43::Venus, imaged on a confocal microscope undergoing skew during cellularization. Solid white arrow denotes normal to apical surface of marked cell and dashed arrow represents its orientation. (B) Quantification of the cellular skew angle as a function of distance from the anterior pole using Gap43::mCherry-expressing embryos imaged on a light-sheet microscope. Measured skew angles were always taken as positive (i.e., independent of orientation), n = 3 embryos, 447 cells. Inset shows example of cellular skew measurement. Error bars = SD. (C) The average skew angle as a function of cell depth using confocal movies of Gap43::Venus. n = 3 embryos, 34 cells tracked in region 10 μm < AP < 40 μm, 11 cells tracked in pole and trunk (squares), error bars = SD. (D) Comparison of skew angle in wild-type (wt) (n = 3) and bcdE1 (n = 5) embryos expressing Gap43::mCherry. p values calculated using two-tailed test of means, *p < 0.05. Error bars = SEM.
If cell skewing occurred as a consequence of geometric constraints, then we predict differences in cell skew will also be evident among dorsal, ventral, and lateral sides of the embryo, since the dorsal side is flatter. Using the light-sheet in toto images of embryos expressing Gap43::mCherry, we measured the degree of skew at different dorsal-ventral positions. Indeed, the skew was highest on the (more curved) ventral side, and lowest on the (flatter) dorsal side of the embryo, p < 10−3 (Figure 6D). It appears that a subset of cells located near the anterior deform to arrange the cells within the geometric constraints of the space. To test the role of cell size on the skew, we quantified the degree of skew in bcdE1 embryos. Away from the tip, skew in bcdE1 embryos is similar to that in wild-type embryos (Figure 6D). However, at the ventral side of the embryo where the skew is largest, the cells within the proximal tip region are more skewed than in wild-type embryos (p = 0.025).
To probe whether cell skewing occurs as a result of tissue specific properties, we measured the degree of skew in snail-twist and bcd-nanos-torso-like (bnt) embryos (Supplemental Figure S6C). Snail-twist mutants are entirely ectoderm with no mesoderm—there are no tissue boundaries in the dorsal-ventral axis. However, we still observed neighbor rearrangements and cell skew, though the skew is reduced compared with wild-type embryos (Supplemental Figure S6D). This may be due to defects in the tissue integrity and in cell formation. bnt mutants—which lack anterior–posterior polarity—showed similar phenotype to bcdE1 embryos (Supplemental Figure S6, E and F). These results suggest that our observations of cell skew and spatial rearrangements are not cell-type specific.
Perturbing embryo geometry effects cell packing
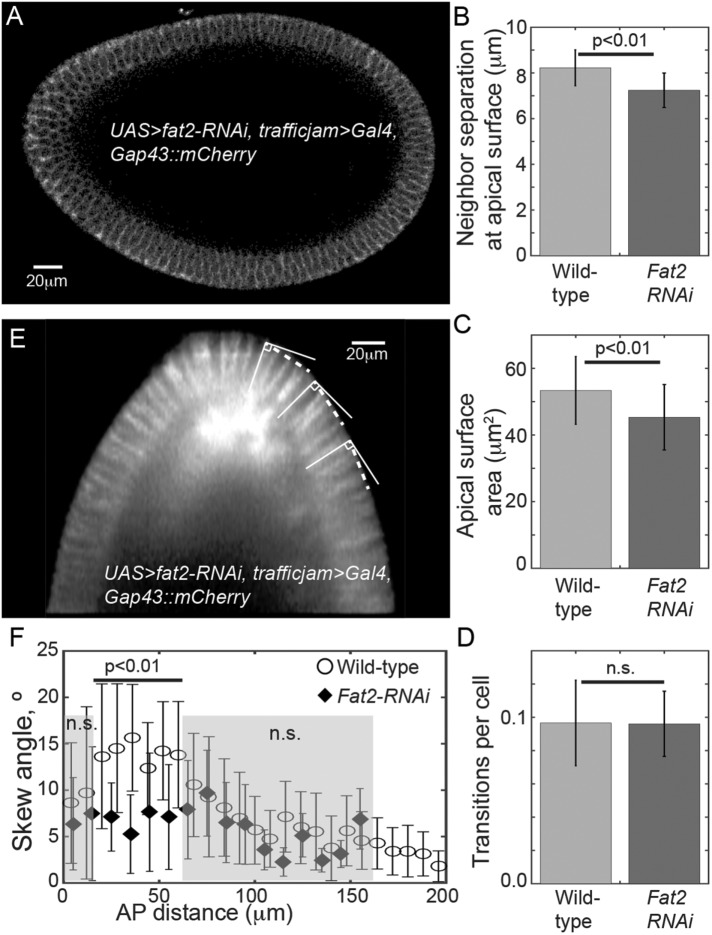
Can perturbing the shape of the embryo significantly alter cell packing? To test this, we used embryos expressing Gap43::mCherry with UAS>fat2-RNAi driven by trafficjam>Gal4 (referred to as fat2-RNAi embryos), which resulted in significantly smaller and rounder embryos, with a 20–40% reduction in embryo length (Horne-Badovinac et al., 2012) (Figure 7A and Supplemental Figure S7, A and B). Despite this shape change, fat2-RNAi embryos still hatched as apparently healthy larvae. Cell depth was comparable to wild type with anterior cells being 11 ± 5% shorter than trunk cells at the beginning of fast phase, and all embryos analyzed gastrulated (Supplemental Movie S5). We quantified the nearest-neighbor separation and cell surface area at the apical surface in the anterior region. The fat2-RNAi embryos showed a small but significant reduction both in cell area and nearest-neighbor difference at the apical surface (Figure 7, B and C) consistent with a greater density of cells. Pseudo-T1 transitions were observed at similar frequency to wild-type embryos (Figure 7D). Cell skew was reduced in the anterior proximal region (Figure 7, E and F) while the cell skew toward the trunk was similar to wild type. Therefore, we see that altering embryo geometry alters cell shape in the anterior. We discuss these observations further below.
FIGURE 7:
Distorting embryo geometry can alter cell arrangement. (A) Embryo expressing Gap43::mCherry with UAS>fat2-RNAi, trafficjam>Gal4. Embryo oriented anterior to left and dorsal at top. Note that the dorsal side is more curved than in wild-type embryos. (B) fat2-RNAi embryos show reduced neighbor separation and (C) reduced apical surface area (n = 6 for fat2-RNAi embryos and n = 5 for wild-type embryos, with >250 cells in total for each genotype). Error bars are SD. (D) There is not a significant change in the frequency of pseudo-T1 transitions (n = 6 for fat2-RNAi embryos), error bars SEM. (E) Skew in fat2-RNAi embryos is reduced. The dashed line shows the direction parallel to the surface at each point. The same angle is used for all three cells highlighted. (F) Skew against distance from anterior pole for wild-type and fat2-RNAi embryos. Skew is reduced in fat2-RNAi embryos compared with wild type within the proximal tip (p < 0.01). Error bars are SD.
Geometric constraints are sufficient to explain observed neighbor rearrangements and cell shape changes
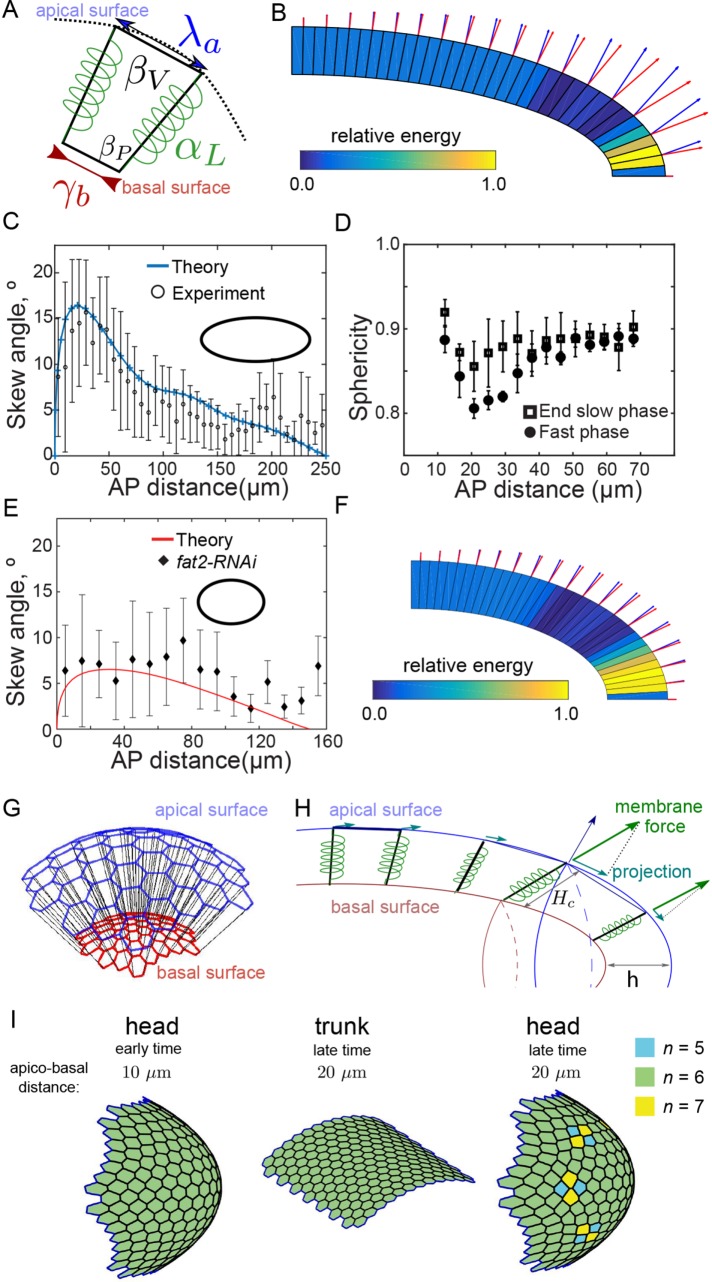
We developed a two-dimensional vertex model to examine more rigorously the effect of the confining geometry on cell morphology. In this model, cells are represented as four-sided polygons (two vertices per basal and apical sides, Figure 8A) along which forces such as cortex tension and volume regulation are applied (Fletcher et al., 2013). We derive the expression of cellular forces from the following expression of an effective cell energy:
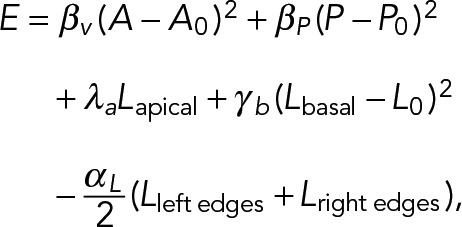 (1) (1)
|
where the first two terms regulate the area and the membrane length of the cell by penalizing values of the area A and perimeter P that differ from their target values A0 and P0, respectively (Figure 8A). The third term represents the tension exerted on the apical side; we set λa < 0 (extensive tension) as a model of the reaction of the compressed nucleus, which lies close to the apical surface. The fourth term corresponds to a regulation of the basal tension to a preferred basal surface L0—following the experimental observation that the basal area is conserved. The last term corresponds to a cell–cell lateral energy, which we expect to lower the energy (αL > 0) due to cadherin–cadherin adhesions (Hannezo et al., 2014) (Figure 8A).
FIGURE 8:
Vertex model incorporating geometric constraints is consistent with both observed cellular skew and cellular rearrangements. (A) Parameters of the vertex model: αL, γb, λa control tension along the lateral, basal, and apical edges, respectively; βV and βP represent regulations of cell volume and membrane area. Vertices on the apical side are constrained to move along an ellipse (dashed line) that models the interaction with the fixed vitelline membrane (see also Supplemental Figure S8). (B) Output from vertex model simulation. The skew is defined as the angle between the normal to the apical surface (blue arrow) and the cellular edge (red arrow, the size of arrows is proportional to the value of the tilt angle). Cells are colored according to their energy level (in units of the maximal energy level). (C) Cellular skew, as measured in experiments (black circles, error bars = SD) and simulations (blue). Ellipse represents geometry simulated, where the long axis is 2.5 times longer than the short axis. (D) The nucleus sphericity (1 = perfect sphere, 0 = line) as a function of distance from the anterior pole at the end of slow phase (squares, n = 4 embryos, >600 nuclei) and during fast phase (circles, n = 4 embryos, >600 nuclei). Error bars = SD. (E) Comparison of model prediction for skew in fat2-RNAi embryos with experimentally measured skew. Parameters same as for C except the geometry simulated, where the long axis is 1.5 times longer than the short axis. (F) As in B but with reduced embryo length, as in fat2-RNAi embryos. (G) Schematic of vertex model used to explore role of geometry on cell arrangements in three dimensions. (H) Resulting force on tricellular junctions due to cell growth and confinement. The apical (blue) and basal (red) surfaces are connected by lateral cell walls, modeled as springs (black junctions connecting apical and basal vertices). (I) Cell packing on the apical surface. Color coding represents neighbor number of each cell. At initiation (left), all cells are hexagonal. At later times, after 10 μm of effective cell invagination, T1 transitions are only observed on ellipsoidal surfaces (right) and not cylindrical surfaces (center).
The vertex dynamics result from a step-by-step energy minimization of Eq. 1 (see the Supplemental Material), and a simulation result is presented in Figure 8B. The parameters are chosen to obtain a quantitative fit of the cellular skew (Figure 8C) while conserving volume (i.e., conserved area in two dimensions) and basal surface (i.e., conserved basal length) (Supplemental Figure S8). We also noticed that the effective cell energy E is maximal within the proximal tip region (Figure 8B). This reveals a zone of high tension and is in agreement with our observations that the nuclei (as revealed by expression H2b::mCherry) of cells undergoing skew became significantly more oblate than those at the tip or trunk (Figure 8D). We reran the simulations using the same parameters except for reduced embryo length (40% reduction in the anterior–posterior [AP] axis) to compare with the fat2-RNAi embryos. Under this condition, the skew was reduced within the proximal tip region (Figure 8E), and the effective cell energy maximum was more spread due to the embryos being more round (Figure 8F).
The increased tension within the proximal tip region hints at a possible explanation for the increased frequency of T1 transitions in the anterior compared with the trunk region (Etournay et al., 2015). To test this further, we developed a minimal three-dimensional vertex model where we considered two sheets of hexagonally packed vertices describing the basal and apical network of tricellular junctions (Figure 8G). We performed simulations in regions corresponding to a limited portion of the Drosophila embryo; an ellipsoid cap for the anterior or a portion of a cylinder for the trunk; see the Supplemental Material for implementation details of the vertex model. Within this simplified model, furrow invagination effectively results in an increasing force between vertices at the apical surface (Figure 8H). After initiation, the position of the basal vertices was fixed, and we considered only the movement of apical vertices. This is a considerable simplification of the underlying system, but it provides a minimal model that allows us to explore the specific role of geometry on vertex rearrangements.
Within this model, as the separation between the two surfaces increased (effectively simulating cell basal surface invagination), we observed T1 transitions in ellipsoidal geometries but not in cylindrical geometries (Figure 8I, Supplemental Movies S6 and S7, and Supplemental Figure S8). In the ellipsoidal geometries, the transitions were not observed at the tip—where curvature is highest—but in a region 5–10 cell diameters from the tip. This region also corresponds to the position of the largest skew within the simulations. These simulations suggest why the frequency of pseudo-T1 transitions does not increase in fat2-RNAi embryos as shown in Figure 7D. Although there is greater competition for space (which by our hypothesis should increase pseudo-T1 transition frequency), the anisotropic effects are reduced as the embryos are more spherical (which reduces the number of pseudo-T1 transitions). Therefore, our model can qualitatively explain the cell behavior under different boundary conditions.
DISCUSSION
In Figure 1C we outlined six plausible scenarios for cell packing in the anterior of the Drosophila embryo. While scenarios (i) and (ii) have been reported previously (Blankenship and Wieschaus, 2001) (and confirmed here), we also find that cellular skew (scenario (iii)) and spatial cell rearrangements (scenario (v)) also could facilitate packing of columnar-like cells into the highly curved anterior of the Drosophila embryo. Evidence for scenario (vi) is found only in mutant embryos with extended cells (Figure 5G), while we see no significant change in basal surface area in the anterior, suggesting scenario (iv) likely plays no major role in cell packing in this system. Interestingly, the pseudo-T1 transitions do not occur at the basal surface as the cell grows but instead appear to occur later, when stress is higher. This suggests that the lateral surfaces of the cell are relatively flexible, allowing deformation in accommodating rearrangements. Such rearrangements appear to be a response to the anisotropic stress due to embryo curvature and not due to active processes. In the bcdE1 and fat2-RNAi embryos—in which we predicted an increase in stress in the anterior region due to larger cells and geometric constraints, respectively—we did not see a significant increase in the frequency of pseudo-T1 transitions. For the former case, we instead observed in half the embryos that a subset of cells had reduced basal surface area. This suggests that the cell competition is in tight balance in the anterior and that perturbations—such as by increasing cell length—can alter the balance of this competition. The fat2-RNAi embryos are more spherical, which reduces the anisotropic stress in the anterior, hence limiting the frequency of neighbor rearrangements. The tissue integrity itself—such as from the actomyosin-rich basal surface and formation of cell–cell adhesions later in cellularization—may also limit the extent of neighbor rearrangements. The decreased cell density and furrow invagination depth in the anterior, which has been previously reported, may also be important in cell packing.
Our results demonstrate that considering the full three-dimensional geometry of the cell is important in understanding cellular interactions within constrained geometries. These findings could be applicable to other curved systems, such as cell shape in the intestinal epithelia where significant cell skew has been reported (Bellis et al., 2012) and in developing ectodermal organs such as teeth (Pearl et al., 2017). Whether these cells also undergo neighbor exchange along their apical–basal axis is not known. Topological defects—which we have shown can be induced by geometric constraints—can play an important role in cell extrusion (Saw et al., 2017). In highly dynamic systems, such as in the Drosophila pupal notum (Bosveld et al., 2016), there could also be potential apical-to-basal variations if the effective cell migration rate varies between the apical and basal surfaces.
One of the original aims of this work was to explore whether geometric constraints can alter the packing ratio in an in vivo tissue. However, it is not surprising that we were unable to observe a significant change in the cell packing ratio. Assuming the tip is hemispherical, only six pentagons are required to closely pack the cells. However, there are around 200 cells in the anterior region of the embryo, and therefore any change in packing density is likely obscured by other factors, including segmentation errors (see the Supplemental Material for further discussion). Such results are consistent with observations in the curved compound Drosophila eye, which packs hexagonally with very high precision (Wolff and Ready, 1993; Kim et al., 2016).
Cell skew in the anterior sets in soon after the basal membrane has extended beneath the nucleus. The nucleus—which is positioned toward the apical surface—likely impedes skew in membranes before they extend beyond the basal surface of the nucleus. Pseudo-T1 transitions are not typically observed until cells have extended their basal membranes a further 5 μm after the initiation of cellular skew. Therefore, it is unlikely that these neighbor rearrangements are solely a consequence of the skew. A possible factor is the increasing effective curvature as the basal membrane extends, which leads to greater force applied to the cells, and after the basal membrane has extended to around 20 μm, this force then appears to be sufficient to drive cell rearrangement along the cell apical–basal axis. Our modeling approach further demonstrated that such behavior can be explained as a response of the cell to the local curvature, without active mechanical processes. A further issue here is whether the spatial cell rearrangements are reversible. We did not see reversibility in the pseudo-T1 transitions experimentally. However, in our simulations we saw relaxation of the spatial rearrangements at long times. A possible explanation for this discrepancy is that the large-scale morphological changes that occur soon after cellularization, such as gastrulation, happen before the tissue has time to relax.
In addition to experimental observation, there has been extensive theoretical work aimed at understanding cell packing and arrangement in epithelial tissues. Some of these efforts include using analogies to soap bubbles (Hayashi and Carthew, 2004) and probabilistic Markov models (Gibson et al., 2006) and incorporate mechanical feedback (Farhadifar et al., 2007; Aegerter-Wilmsen et al., 2010) and tension (Sanchez-Gutierrez et al., 2016). Interestingly, recent theoretical work has suggested that in hexagonal tissues, cells must actively do work to rearrange their shape, but at lower packing densities a phase transition from solid-to-fluid-like behavior allows cell rearrangements to occur with low energy cost (Bi et al., 2015). A three-dimensional framework for understanding free-standing epithelial tissues has also been provided (Hannezo et al., 2014). Here we consider the relaxation of a tissue within an imposed geometry, due to the rigid outer vitelline membrane. In particular, this system seems well suited to the testing of three-dimensional vertex models (Honda et al., 2004; Du et al., 2014; Fletcher et al., 2014; Murisic et al., 2015; Okuda et al., 2015; Misra et al., 2016). Note that these models typically do not allow neighbor rearrangements along the apical–basal axis of each cell.
Overall, epithelial cell shape and neighbor interactions are altered by the geometry in which the tissue is embedded. We find that epithelial cells are able to exchange cell neighbors along the apical–basal axis of the cell and distort (skew) to compensate for geometric confinement. Future work can explore whether these ideas are pertinent within other curved tissues, a good target being the developing gut, and whether such geometric constraints are important in the biological function of the tissue.
MATERIALS AND METHODS
Fly stocks
The fly strains used in this study: nanos>GAP43::mVenus was used to label membrane (Martin et al., 2010), and H2Av::mCherry (Krzic et al., 2012) was used to label histone. bnt and sna twi mutants are described in Rauzi et al. (2015), and moesin::GFP and sqh::mCherry (Young et al., 1991) were used to label actin (Moesin) and myosin (sqh) (Martin et al., 2009) and bcdE1 mutant allele from Frohnhöfer and Nüsslein-Volhard (1986). UAS>fat2-RNAi and trafficjam>Gal4 lines were used to generate smaller embryos (Horne-Badovinac et al., 2012).
Imaging the anterior pole of Drosophila embryos
Embryos expressing GAP43::mVenus and H2Av::mCherry were collected in a time window within 3 h after egg depostion. These embryos were dechorionated with household bleach and fixed in 4% paraformaldehyde for 20 min at room temperature. For confocal imaging, a microfluidic device was used to mount these embryos along their AP axis (up to 100 per mounting) (Chung et al., 2010). Imaging was carried on a Nikon A1R confocal microscope with 60× water immersion lens (Figure 2, A–C, Supplemental Movie S1). The Z interval was 1 µm. Embryos were staged by the membrane ingression length. Any embryo that touched the coverslip was discarded as the anterior pole was flattened, resulting in distorted cell morphology (Supplemental Figure S1A). We supplement these high-quality fixed data with live imaging using confocal and light-sheet microscopy. Light-sheet data for snail-twist and bnt mutants was collected as described in Rauzi et al. (2015). Movies of embryos expressing moe::GFP and sqh::mCherry were collected at 30-s intervals on a custom-built multi-view light-sheet microscope with a Z interval of 2–2.5 μm (Krzic et al., 2012). Movies of bcdE1 and fat2-RNAi embryos expressing Gap43::mCherry were collected on the same microscope under similar imaging conditions. Laser ablation experiments performed as described in Hara et al. (2016) and embryos were ablated toward the end of the slow phase, near the embryo trunk. Ablating cells in the anterior is more challenging than in the trunk due to mounting problems and due to difficulty in ensuring that ablation is performed perpendicular to the apical surface.
Image analysis
Stereographic projection.
We used a stereographic projection of the cells into two dimensions to make segmentation easier and more intuitive (Krzic et al., 2012; Schmid et al., 2013; Heemskerk and Streichan, 2015) (Figure 2, D and E, and Supplemental Figure S1, B–E). The embryo surface was fitted to a function of the form aebz for each polar angle (Supplemental Figure S1B). We used angle steps of 0.3° for each fitting. The normal to this curve was calculated, and then we moved the surface in by a fixed distance δr = 0.57 μm to project the inner surfaces (Supplemental Figure S1C). Cells were segmented using interactive watershed algorithm in custom-written Matlab code, and an interactive pipeline was developed to enable manual correction (Supplemental Figure S1D). The segmented projected data was then transformed back into three dimensions to check quality (Supplemental Figure S1E). This approach also allowed straightforward neighbor counting.
Adaptive watersheds.
We used adaptive watershed algorithms to segment the cell boundaries in three dimensions using the light-sheet data, see the Supplemental Material for details. Using this approach, we extracted the full three-dimensional cell shape. Typically, from each image of the anterior pole, we could segment and analyze around 150 cells in the anterior region. We compared these data with images collected of the trunk region under the same conditions.
Skew measurements
The skew of cells was measured both directly and computationally. Light-sheet and confocal data were used for the quantifications. Data shown in the main figures are from direct measurements performed using the angle tool in ImageJ. To avoid bias, all angles of each phenotype (wild-type, bcdE1, fat2-RNAi, bnt, and snail-twist) were measured before analysis was performed. The direct measurements were checked against computational analysis (Supplemental Figure S5B).
Mathematical model
Mathematical details of the modeling are outlined in the Supplemental Material.
Statistical analysis
p values were calculated using two-tailed t-test comparison of means, unless stated otherwise in the text of figure legends.
Supplementary Material
ACKNOWLEDGMENTS
We thank S. Shvartsman for help and training with the microfluidic device and Jacques Prost for invigorating discussions about modeling the system. We are very grateful to EMBL-Heidelberg, and in particular Matteo Rauzi, Lars Hufnagel, and Maria Leptin, for providing early data for this project and interesting discussion and feedback. We thank Sham Tlili and Nishchhal Verma for invaluable contributions to the vertex model. We thank the two referees for their thoughtful and constructive criticism. Flies were received from the Bloomington stock center, and the Fat2 lines and trafficjam>Gal4 are from Sally Horne-Badovinac. We thank Y. Toyama for assistance with the laser ablations. We thank the Saunders lab, particularly Christopher Amourda, for assistance and advice. We are grateful to the MBI Science Communications Unit for illustrations and editing. We acknowledge funding and institutional support from a National Research Foundation (NRF) Fellowship awarded to T.E.S. (Grant No. 2012NRF-NRFF001-094), the Mechanobiology Institute (J.-F.R.), and the Institute of Molecular and Cellular Biology (K.H.O., W.Y., and T.E.S.).
Abbreviations used:
- Bcd
Bicoid
- Moe
Moesin
- Sqh
Spaghetti Squash.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E17-01-0060) on October 4, 2017.
REFERENCES
- Aegerter-Wilmsen T, Smith AC, Christen AJ, Aegerter CM, Hafen E, Basler K. Exploring the effects of mechanical feedback on epithelial topology. Development. 2010;137:499–506. doi: 10.1242/dev.041731. [DOI] [PubMed] [Google Scholar]
- Aigouy B, Farhadifar R, Staple DB, Sagner A, Röper J-C, Jülicher F, Eaton S. Cell flow reorients the axis of planar polarity in the wing epithelium of Drosophila. Cell. 2010;142:773–786. doi: 10.1016/j.cell.2010.07.042. [DOI] [PubMed] [Google Scholar]
- Bellis J, Duluc I, Romagnolo B, Perret C, Faux MC, Dujardin D, Formstone C, Lightowler S, Ramsay RG, Freund JN, De Mey JR. The tumor suppressor Apc controls planar cell polarities central to gut homeostasis. J Cell Biol. 2012;198:331–341. doi: 10.1083/jcb.201204086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertet C, Sulak L, Lecuit T. Myosin-dependent junction remodelling controls planar cell intercalation and axis elongation. Nature. 2004;429:667–671. doi: 10.1038/nature02590. [DOI] [PubMed] [Google Scholar]
- Bi D, Lopez JH, Schwarz JM, Manning ML. A density-independent rigidity transition in biological tissues. Nat Phys. 2015;11:1074–1079. [Google Scholar]
- Blankenship JT, Backovic ST, Sanny JSP, Weitz O, Zallen JA. Multicellular rosette formation links planar cell polarity to tissue morphogenesis. Dev Cell. 2006;11:459–470. doi: 10.1016/j.devcel.2006.09.007. [DOI] [PubMed] [Google Scholar]
- Blankenship JT, Wieschaus E. Two new roles for the Drosophila AP patterning system in early morphogenesis. Development. 2001;128:5129–5138. doi: 10.1242/dev.128.24.5129. [DOI] [PubMed] [Google Scholar]
- Bollenbach T, Pantazis P, Kicheva A, Bokel C, Gonzalez-Gaitan M, Julicher F. Precision of the Dpp gradient. Development. 2008;135:1137–1146. doi: 10.1242/dev.012062. [DOI] [PubMed] [Google Scholar]
- Bosveld F, Markova O, Guirao B, Martin C, Wang Z, Pierre A, Balakireva M, Gaugue I, Ainslie A, Christophorou N, et al. Epithelial tricellular junctions act as interphase cell shape sensors to orient mitosis. Nature. 2016;530:495–498. doi: 10.1038/nature16970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung K, Kim Y, Kanodia JS, Gong E, Shvartsman SY, Lu H. A microfluidic array for large-scale ordering and orientation of embryos. Nat Methods. 2010;8:171–176. doi: 10.1038/nmeth.1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Classen A-K, Anderson KI, Marois E, Eaton S. Hexagonal packing of drosophila wing epithelial cells by the planar cell polarity pathway. Dev Cell. 2005;9:805–817. doi: 10.1016/j.devcel.2005.10.016. [DOI] [PubMed] [Google Scholar]
- Collinet C, Rauzi M, Lenne P-F, Lecuit T. Local and tissue-scale forces drive oriented junction growth during tissue extension. Nat Cell Biol. 2015;17:1247–1258. doi: 10.1038/ncb3226. [DOI] [PubMed] [Google Scholar]
- Du X, Osterfield M, Shvartsman SY. Computational analysis of three-dimensional epithelial morphogenesis using vertex models. Phys Biol. 2014;11:1–15. doi: 10.1088/1478-3975/11/6/066007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etournay R, Popovic´ M, Merkel M, Nandi A, Blasse C. Interplay of cell dynamics and epithelial tension during morphogenesis of the Drosophila pupal wing. eLife. 2015;4:07090. doi: 10.7554/eLife.07090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- Fletcher AG, Osborne JM, Maini PK, Gavaghan DJ. Implementing vertex dynamics models of cell populations in biology within a consistent computational framework. Prog Biophys Mol Biol. 2013;113:299–326. doi: 10.1016/j.pbiomolbio.2013.09.003. [DOI] [PubMed] [Google Scholar]
- Fletcher AG, Osterfield M, Baker RE, Shvartsman SY. Vertex models of epithelial morphogenesis. Biophy J. 2014;106:2291–2304. doi: 10.1016/j.bpj.2013.11.4498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frohnhöfer HG, Nüsslein-Volhard C. Organization of anterior pattern in the Drosophila embryo by the maternal gene bicoid. Nature. 1986;324:120–125. [Google Scholar]
- Gibson MC, Patel AB, Nagpal R, Perrimon N. The emergence of geometric order in proliferating metazoan epithelia. Nature. 2006;442:1038–1041. doi: 10.1038/nature05014. [DOI] [PubMed] [Google Scholar]
- Gibson MC, Perrimon N. Apicobasal polarization: epithelial form and function. Curr Opin Cell Biol. 2003;15:747–752. doi: 10.1016/j.ceb.2003.10.008. [DOI] [PubMed] [Google Scholar]
- Guillot C, Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science. 2013;340:1185–1189. doi: 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
- Hannezo E, Prost J, Joanny J-F. Instabilities of monolayered epithelia: shape and structure of villi and crypts. Phys Rev Lett. 2011;107:078104–5. doi: 10.1103/PhysRevLett.107.078104. [DOI] [PubMed] [Google Scholar]
- Hannezo E, Prost J, Joanny J-F. Theory of epithelial sheet morphology in three dimensions. Proc Natl Acad Sci USA. 2014;111:27–32. doi: 10.1073/pnas.1312076111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hara Y, Shagirov M, Toyama Y. Cell boundary elongation by non-autonomous contractility in cell oscillation. Curr Biol. 2016:1–10. doi: 10.1016/j.cub.2016.07.003. [DOI] [PubMed] [Google Scholar]
- Hayashi T, Carthew RW. Surface mechanics mediate pattern formation in the developing retina. Nature. 2004;431:647–652. doi: 10.1038/nature02952. [DOI] [PubMed] [Google Scholar]
- Heemskerk I, Streichan SJ. Tissue cartography: compressing bio-image data by dimensional reduction. Nat Methods. 2015;12:1139–1142. doi: 10.1038/nmeth.3648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda H, Tanemura M, Nagai T. A three-dimensional vertex dynamics cell model of space-filling polyhedra simulating cell behavior in a cell aggregate. J Theor Biol. 2004;226:439–453. doi: 10.1016/j.jtbi.2003.10.001. [DOI] [PubMed] [Google Scholar]
- Horne-Badovinac S, Hill J, Gerlach G, Menegas W, Bilder D. A screen for round egg mutants in Drosophila identifies tricornered, furry, and misshapen as regulators of egg chamber elongation. G3. 2012;2:371–378. doi: 10.1534/g3.111.001677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Cassidy JJ, Yang B, Carthew RW, Hilgenfeldt S. Hexagonal patterning of the insect compound eye: Facet area variation, defects, and disorder. Biophys J. 2016;111:2735–2746. doi: 10.1016/j.bpj.2016.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knust E, Bossinger O. Composition and formation of intercellular junctions in epithelial cells. Science. 2002;298:1955–1959. doi: 10.1126/science.1072161. [DOI] [PubMed] [Google Scholar]
- Koyama H, Shi D, Suzuki M, Ueno N, Uemura T, Fujimori T. Mechanical regulation of three-dimensional epithelial fold pattern formation in the mouse oviduct. Biophys J. 2016;111:650–665. doi: 10.1016/j.bpj.2016.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krzic U, Gunther S, Saunders TE, Streichan SJ, Hufnagel L. Multiview light-sheet microscope for rapid in toto imaging. Nat Methods. 2012;9:730–733. doi: 10.1038/nmeth.2064. [DOI] [PubMed] [Google Scholar]
- Lecuit T, Lenne P-F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat Rev Mol Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- Lecuit T, Wieschaus E. Polarized insertion of new membrane from a cytoplasmic reservoir during cleavage of the Drosophila embryo. J Cell Biol. 2000;150:849–860. doi: 10.1083/jcb.150.4.849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leptin M, Grunewald B. Cell shape changes during gastrulation in Drosophila. Development. 1990;110:73–84. doi: 10.1242/dev.110.1.73. [DOI] [PubMed] [Google Scholar]
- Lewis FT. The effect of cell division on the shape and size of hexagonal cells. Anat Rec. 1926;33:331–355. [Google Scholar]
- Ma D, Amonlirdviman K, Raffard RL, Abate A, Tomlin CJ, Axelrod JD. Cell packing influences planar cell polarity signaling. Proc Natl Acad Sci USA. 2008;105:18800–18805. doi: 10.1073/pnas.0808868105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AC, Gelbart M, Fernandez-Gonzalez R, Kaschube M, Wieschaus EF. Integration of contractile forces during tissue invagination. J Cell Biol. 2010;188:735–749. doi: 10.1083/jcb.200910099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AC, Kaschube M, Wieschaus EF. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457:495–501. doi: 10.1038/nature07522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazumdar A, Mazumdar M. How one becomes many: blastoderm cellularization in Drosophila melanogaster. Bioessays. 2002;24:1012–1022. doi: 10.1002/bies.10184. [DOI] [PubMed] [Google Scholar]
- Misra M, Audoly B, Kevrekidis IG, Shvartsman SY. Shape transformations of epithelial shells. Biophys J. 2016;110:1670–1678. doi: 10.1016/j.bpj.2016.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller P, Rogers KW, Yu SR, Brand M, Schier AF. Morphogen transport. Development. 2013;140:1621–1638. doi: 10.1242/dev.083519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murisic N, Hakim V, Kevrekidis IG, Shvartsman SY, Audoly B. From discrete to continuum models of three-dimensional deformations in epithelial sheets. Biophys J. 2015;109:154–163. doi: 10.1016/j.bpj.2015.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuda S, Inoue Y, Watanabe T, Adachi T. Coupling intercellular molecular signalling with multicellular deformation for simulating three-dimensional tissue morphogenesis. Interface Focus. 2015;5:20140095–20140111. doi: 10.1098/rsfs.2014.0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osterfield M, Du X, Schüpbach T, Wieschaus E, Shvartsman SY. Three-dimensional epithelial morphogenesis in the developing drosophila egg. Dev Cell. 2013;24:400–410. doi: 10.1016/j.devcel.2013.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osterfield M, Schupbach T, Wieschaus E, Shvartsman SY. Diversity of epithelial morphogenesis during eggshell formation in drosophilids. Development. 2015;142:1971–1977. doi: 10.1242/dev.119404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panousopoulou E, Green JBA. Invagination of ectodermal placodes is driven by cell intercalation-mediated contraction of the suprabasal tissue canopy. PLoS Biol. 2016;14:e1002405. doi: 10.1371/journal.pbio.1002405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl EJ, Li J, Green JBA. Cellular systems for epithelial invagination. Philos Trans R Soc Lond B Biol Sci. 2017;372:20150526. doi: 10.1098/rstb.2015.0526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauzi M, Krzic U, Saunders TE, Krajnc M, Ziherl P, Hufnagel L, Leptin M. Embryo-scale tissue mechanics during Drosophila gastrulation movements. Nat Commun. 2015;6:8677. doi: 10.1038/ncomms9677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauzi M, Lenne P-F, Lecuit T. Planar polarized actomyosin contractile flows control epithelial junction remodelling. Nature. 2010;468:1110–1114. doi: 10.1038/nature09566. [DOI] [PubMed] [Google Scholar]
- Rauzi M, Verant P, Lecuit T, Lenne P-F. Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
- Sanchez-Gutierrez D, Tozluoglu M, Barry JD, Pascual A, Mao Y, Escudero LM. Fundamental physical cellular constraints drive self-organization of tissues. EMBO J. 2016;35:77–88. doi: 10.15252/embj.201592374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savin T, Kurpios NA, Shyer AE, Florescu P, Liang H, Mahadevan L, Tabin CJ. On the growth and form of the gut. Nature. 2012;476:57–62. doi: 10.1038/nature10277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saw TB, Doostmohammadi A, Nier V, Kocgozlu L, Thampi S, Toyama Y, Marcq P, Lim CT, Yeomans JM, Ladoux B. Topological defects in epithelia govern cell death and extrusion. Nature. 2017;544:212–216. doi: 10.1038/nature21718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid B, Shah G, Scherf N, Weber M, Thierbach K, Campos CPER, Roeder I, Aanstad P, Huisken J. High-speed panoramic light-sheet microscopy reveals global endodermal cell dynamics. Nat Commun. 2013;4:1–10. doi: 10.1038/ncomms3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shyer AE, Tallinen T, Nerurkar NL, Wei Z, Gil ES, Kaplan DL, Tabin CJ, Mahadevan L. Villification: how the gut gets its villi. Science. 2013;342:212–218. doi: 10.1126/science.1238842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Z, Amourda C, Shagirov M, Hara Y, Saunders TE, Toyama Y. Basolateral protrusion and apical contraction cooperatively drive Drosophila germ-band extension. Nat Cell Biol. 2017;19:375–383. doi: 10.1038/ncb3497. [DOI] [PubMed] [Google Scholar]
- Taniguchi K, Maeda R, Ando T, Okumura T, Nakazawa N, Hatori R, Nakamura M, Hozumi S, Fujiwara H, Matsuno K. Chirality in planar cell shape contributes to left-right asymmetric epithelial morphogenesis. Science. 2011;333:339–341. doi: 10.1126/science.1200940. [DOI] [PubMed] [Google Scholar]
- Thompson DW. On Growth and Form. Cambridge, UK: Cambridge University Press; 1917. [Google Scholar]
- Tinevez J-Y, Schulze U, Salbreux G, Roensch J, Joanny J-F, Paluch E. Role of cortical tension in bleb growth. Proc Natl Acad Sci USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umetsu D, Aigouy B, Aliee M, Sui L, Eaton S, Jülicher F, Dahmann C. Local increases in mechanical tension shape compartment boundaries by biasing cell intercalations. Curr Biol. 2014;24:1798–1805. doi: 10.1016/j.cub.2014.06.052. [DOI] [PubMed] [Google Scholar]
- Wang Y-C, Khan Z, Kaschube M, Wieschaus EF. Differential positioning of adherens junctions is associated with initiation of epithelial folding. Nature. 2012;484:390–393. doi: 10.1038/nature10938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warn RM, Bullard B, Magrath R. Changes in the distribution of cortical myosin during the cellularization of the Drosophila embryo. J Embryol Exp Morphol. 1980;57:167–176. [PubMed] [Google Scholar]
- Wolff T, Ready DF. Pattern formation in the Drosophila retina. In: The Development of Drosophila Melanogaster. Cold Spring Harbor Laboratory Press; 1993. [Google Scholar]
- Young PE, Pesacreta TC, Kiehart DP. Dynamic changes in the distribution of cytoplasmic myosin during Drosophila embryogenesis. Development. 1991;111:1–14. doi: 10.1242/dev.111.1.1. [DOI] [PubMed] [Google Scholar]
- Zallen JA, Zallen R. Cell-pattern disordering during convergent extension in Drosophila. J Phys Condens Matter. 2004;16:S5073–S5080. doi: 10.1088/0953-8984/16/44/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.