Bayesian penalized spline model-based inference for finite population proportion in unequal probability sampling

Abstract

We propose a Bayesian Penalized Spline Predictive (BPSP) estimator for a finite population proportion in an unequal probability sampling setting. This new method allows the probabilities of inclusion to be directly incorporated into the estimation of a population proportion, using a probit regression of the binary outcome on the penalized spline of the inclusion probabilities. The posterior predictive distribution of the population proportion is obtained using Gibbs sampling. The advantages of the BPSP estimator over the Hájek (HK), Generalized Regression (GR), and parametric model-based prediction estimators are demonstrated by simulation studies and a real example in tax auditing. Simulation studies show that the BPSP estimator is more efficient, and its 95% credible interval provides better confidence coverage with shorter average width than the HK and GR estimators, especially when the population proportion is close to zero or one or when the sample is small. Compared to linear model-based predictive estimators, the BPSP estimators are robust to model misspecification and influential observations in the sample.

1. Introduction

Unequal probability sampling designs are commonly employed in data collection by science and government. Perhaps the simplest unequal probability design is stratified sampling, which samples units from different strata with different inclusion probabilities. Another important form of unequal probability sampling is probability-proportional-to-size (pps) sampling, in which the inclusion probability is proportional to the value of a size variable measured for all population units.

An unequal probability sampling design such as pps sampling is often used for efficient estimation of population means of continuous variables, for which the variance increases with size of unit. However, inferences about discrete variables are often also of interest in a multipurpose survey (e.g., Lehtonen and Veijanen 1998, Lehtonen, Särndal and Veijanen 2005). In this paper, we focus on methods of inference for finite population proportions from unequal probability sampling designs, based on an auxiliary variable measured for all the units in the population. We use pps sampling as a specific design to illustrate and assess our methods.

The inclusion probabilities play important and somewhat different roles in design-based and model-based inference from unequal probability survey samples (Smith 1976, 1994; Kish 1995; Little 2004). In design-based inference, survey variables are fixed, and inference is based on the distribution of the sample inclusion indicators; the standard design-based approaches to estimation such as the Horvitz-Thompson (HT) estimator (1952) and its extensions weight sampled units by the inverse of their inclusion probabilities. These estimators are design consistent (Isaki and Fuller 1982) and provide reliable inferences in large samples without the need for modeling assumptions. However, these estimators are potentially very inefficient, as illustrated in Basu's (1971) famous elephant example. Also, variance estimation is cumbersome because it requires second-order inclusion probabilities. Corresponding confidence intervals are based on asymptotic theory, and may deviate from nominal levels for moderate or small sample sizes.

Model-based inference predicts values of survey variables in the non-sampled units by including the inclusion probabilities as covariates in the prediction model (Little 2004). Model-based prediction estimators are consistent and efficient under the assumed model, but are subject to bias when the underlying model is misspecified. This limitation motivates the development of flexible statistical models that are more robust to model misspecification. For continuous survey data, Zheng and Little (2003) estimated the finite population total using a nonparametric regression on a penalized spline (p-spline) of the inclusion probabilities. We propose here Bayesian P-Spline Predictive (BPSP) estimators that are suitable for a binary, as opposed to continuous, outcome. We adopt a Bayesian approach to inference for this model, since Bayesian methods often yield better inference for small sample problems, and are conveniently implemented for our proposed model via the Gibbs' sampler. In this approach, auxiliary variables other than the inclusion probability can also be included in the model, but the inclusion probability is singled out since modeling of this variable is prone to model misspecification.

We compare the performance of BPSP estimators with Hájek (HK, Horvitz-Thompson-type) estimators and with Generalized Regression (GR) estimators for a binary outcome proposed by Lehtonen and Veijanen (1998). The GR approach is a popular model-assisted modification of the design-based estimators that combines predictions from a model with design-weighted model residuals (Montanari 1998), to yield estimates that are approximately design unbiased.

Zheng and Little (2003; 2005) compared HT, p-spline prediction, and GR estimates of the total of a continuous survey variable by simulation. They found that p-spline model-based estimators had better root mean squared error than the other methods, and with jackknife standard errors providing superior confidence coverage to HT or GR inferences. We conduct similar comparisons for inference about a population proportion for a binary outcome, and show similar advantages for our BPSP estimator over the HK and GR alternatives.

2. Design-based estimator

Suppose that we have a finite population consisting of N identifiable units. Let Y be the binary survey variable of interest and $p=N^{-1}{\sum }_{i=1}^N{Y}_i$ be the proportion of the population for which Y = 1. Let π_i denote the probability of inclusion for unit i, which is assumed to be known for all units in the finite population before a sample is drawn. An unequal probability random sample s with elements y₁, …y_n is then drawn from the finite population according to the inclusion probabilities π₁, …π_N. The design-based HK estimator in the discussion of Basu (1971) is defined as

$${\widehat{p}}_{\text{HK}}=\frac{\sum _{i\in s}{y}_i/{\mathrm{\pi }}_i}{\sum _{i\in s}1/{\mathrm{\pi }}_i}.$$ (1)

The variance for p̂_HK can be estimated via linearization of the Yates-Grundy estimator (1953) of totals,

$$\begin{array}{c}{\widehat{V}}_{\text{YG}}({\widehat{p}}_{\text{HK}})={(\sum _{k\in s}1/{\mathrm{\pi }}_k)}^{-2}\\ \sum _{i=1}^{n-1}\sum _{j=i+1}^n\left(\frac{{\mathrm{\pi }}_i{\mathrm{\pi }}_j-{\mathrm{\pi }}_{ij}}{{\mathrm{\pi }}_{ij}}\right){(\frac{y_i-{\widehat{p}}_{\text{HK}}}{{\mathrm{\pi }}_i}-\frac{y_j-{\widehat{p}}_{\text{HK}}}{{\mathrm{\pi }}_j})}^2\end{array}.$$ (2)

The Yates-Grundy variance estimator requires pairwise inclusion probabilities. When the pairwise inclusion probabilities are not available, as in our simulations, the approximate formula proposed by Hartley and Rao (1962),

$$\begin{array}{c}{\mathrm{\pi }}_{ij}\approx \frac{n-1}{n}{\mathrm{\pi }}_i{\mathrm{\pi }}_j\\ +\frac{n-1}{n^2}({\mathrm{\pi }}_i^2{\mathrm{\pi }}_j+{\mathrm{\pi }}_i{\mathrm{\pi }}_j^2)-\frac{n-1}{n^3}{\mathrm{\pi }}_i{\mathrm{\pi }}_j\sum _{k=1}^N{\mathrm{\pi }}_k^2,\end{array}$$

has frequently been used. An approximate 1 – α level confidence interval for the population proportion p̂_HK is then obtained based on the normal approximation.

3. Bayesian P-Spline Predictive (BPSP) estimator

Royall (1970) argued for the use of models for finite-population descriptive inferences by predicting the unobserved values based on models, since model-based inferences should be more efficient than design-based inferences. To model the relationship between the binary outcome Y and the continuous inclusion probability π we need to fit a binary regression of Y on π. Parametric binary regressions, such as the linear or quadratic logistic or probit model, may not be adequate in fitting the data. One solution for this problem of inflexibility is to fit a binary regression on a spline of π by adding some knots. However, too many knots may result in the roughness of model fit. One way to overcome this problem is to retain all of the knots but to constrain their influence, by fitting a binary p-spline regression model.

Common methods for modeling a binary outcome are logistic and probit regressions, and they generally give similar results. We choose to adopt probit models in our study for computational convenience. The probit regression model for binary outcomes has an underlying truncated normal regression structure on latent continuous data. If the latent continuous data are known, the parameters in binary p-spline regression models can be estimated using standard approaches for normal p-spline regression models. In a Bayesian context, the posterior distribution of parameters in the probit p-spline model can be computed using Gibbs sampling (Albert and Chib 1993; Ruppert, Wand and Carroll 2003, chapter 16). In contrast, the logistic p-spline regression model requires a more complicated computation procedure such as the Metropolis-Hastings algorithm. The computational advantage makes the probit link function more desirable than the logit link function in Bayesian binary p-spline regression models.

There are various types of p-splines. When applying p-splines, we need to make choices on the degree and knot locations, and the basis functions used to present the model. We choose to use the truncated polynomial p-splines because they are simple and intuitive. More numerically stable estimators can be obtained using B-splines via orthogonalizing the truncated power bases (Eilers and Marx 1996). The probit truncated polynomial p-spline regression model has a generalized linear mixed model representation,

$$\begin{array}{c}{\mathrm{\Phi }}^{-1}(E(y_i|\mathrm{\beta },b,{\mathrm{\pi }}_i))={\mathrm{\beta }}_0+\sum _{k=1}^p{\mathrm{\beta }}_k{\mathrm{\pi }}_i^k+\sum _{l=1}^m{b}_l{({\mathrm{\pi }}_i-k_l)}_{+}^p\\ b_l~N(0,{\mathrm{\tau }}^2)\\ l=1,\dots ,m;& i=1,\dots ,n,\end{array}$$ (3)

where Φ⁻¹ (·) denote the inverse CDF of a standard normal distribution, and the constants k₁ < … < k_m are m selected fixed knots. A function such as ${({\mathrm{\pi }}_i-k)}_{+}^p$ is called a truncated polynomial spline basis function with power p, where ${(u)}_{+}^p$ is equal to {u × I(u ≥ 0)}^p for any real number u. Since the truncated polynomial spline basis function has p – 1 continuous derivatives, higher values of p lead to smoother spline functions. By specifying a normal distribution for b, the influence of the m knots is constrained in Model (3), which is equivalent to smooth the splines via the penalized likelihood.

The parameters in Model (3) can be estimated using generalized linear mixed model methods. An alternative Bayesian approach that simplifies computation is to assume weak prior and hyperprior distributions and use Gibbs sampling to obtain draws from the posterior distributions of the parameters as follow: the probit regression model for binary responses has an underlying normal regression structure on latent continuous data; if the latent data are known, the posterior distribution of the parameters can be computed using standard results for normal regression models; and given the posterior distribution of the parameters, the latent continuous data can be simulated from a suitable truncated normal distribution. (Ruppert et al. 2003, page 290) The detailed algorithm of Gibbs sampling is in the Appendix. In addition, the Bayesian inference for p-spline regression can also been implemented using WinBUGS, the standard Bayesian analysis software (Crainiceanu, Ruppert and Wand 2005).

The posterior distribution of the population proportion is simulated by generating a large number D of draws and using the predictive estimator form ${\widehat{p}}_{\text{PR}}^{(d)}=N^{-1}({\sum }_{i\in s}{y}_i+{\sum }_{j\notin s}{\widehat{y}}_j^{(d)})$, where ${\widehat{y}}_j^{(d)}$ is a draw from the posterior predictive distribution of the j^th non-sampled unit of the binary outcome. The average of these draws simulates the Bayesian P-Spline Predictive (BPSP) estimator of the finite population proportion, and is denoted as p̂_BPSP, where

$${\widehat{p}}_{\text{BPSP}}=D^{-1}\sum _{d=1}^D{\widehat{p}}_{\text{PR}}^{(d)}.$$ (4)

The Bayesian analog of a 100 × (1 – α)% confidence interval for the population proportion is a 100 × (1 – α)% credible interval, which can be formed in a number of different ways. We split the tail area α equally between the upper and lower endpoints in the simulations.

Firth and Bennett (1998) showed that any parametric logistic regression model containing an intercept term and the inverse of inclusion probabilities as a covariate, fitted by ordinary, unweighted maximum likelihood, was “internally bias calibrated” (IBC) for population proportions, and thus yields design consistency. This property is also true for logistic truncated polynomial p-spline regression models on the inverse of inclusion probabilities, fitted via penalized likelihood. With the probit link function used instead of the logit link function and fitted via Markov chain Monte Carlo algorithm instead of maximum penalized likelihood, the BPSP estimator may no longer have the IBC property. However, the similarity between the probit model and the logistic model implies that the predictive estimator based on a probit p-spline regression model is approximately design-consistent. We believe that obtaining efficient estimates with close to nominal confidence coverage in finite samples is more important than exact design consistency.

4. Generalized Regression (GR) estimator

For the estimation of class frequencies of a discrete response variable, Lehtonen and Veijanen (1998) proposed a GR estimator t̂_GR of the total, which combines the predicted values ŷ_i = P̂r(Y_i = 1| π_i) based on a suitable model and the HT estimator for the residuals r_i = y_i – ŷ_i of the sampled units,

$${\widehat{t}}_{\text{GR}}=\sum _{i=1}^N{\widehat{y}}_i+\sum _{i\in s}{r}_i/{\mathrm{\pi }}_i.$$ (5)

The GR estimator in Equation (5) is then used in constructing an estimator for population proportions by dividing by the known population size N (Duchesne 2003),

$${\widehat{p}}_{\text{G\_R}\_1}=\frac{1}{N}(\sum _{i=1}^N{\widehat{y}}_i+\sum _{i\in s}{r}_i/{\mathrm{\pi }}_i).$$ (6)

We also consider here another version of the GR estimator for the estimation of finite population proportions, in which the denominator of the bias calibration term for the residuals r_i is the estimated population size Σ_i∈s1/π_i,

$${\widehat{p}}_{\text{G\_R}\_2}=\frac{1}{N}\sum _{i=1}^N{\widehat{y}}_i+(\sum _{i\in s}{r}_i/{\mathrm{\pi }}_i){(\sum _{i\in s}1/{\mathrm{\pi }}_i)}^{-1}.$$ (7)

For the variance estimate of (6), we use the variance estimator of the estimated total of a discrete response variable, given by Lehtonen and Veijanen (1998), divided by N². For the variance estimate of (7), we apply the Taylor linearization technique (Särndal, Swensson and Wretman 1992, page 182). These two variance estimators are shown in equations (8) and (9), respectively.

$$\widehat{V}({\widehat{p}}_{\text{GR}\_1})=\frac{1}{N^2}\sum _{k\in s}\sum _{l\in s}\frac{{\mathrm{\pi }}_{kl}-{\mathrm{\pi }}_k{\mathrm{\pi }}_l}{{\mathrm{\pi }}_{kl}}\frac{r_k}{{\mathrm{\pi }}_k}\frac{r_l}{{\mathrm{\pi }}_l},$$ (8)

$$\widehat{V}({\widehat{p}}_{\text{GR}\_2})={(\sum _{i\in s}1/{\mathrm{\pi }}_i)}^{-2}\sum _{k\in s}\sum _{l\in s}\frac{{\mathrm{\pi }}_{kl}-{\mathrm{\pi }}_k{\mathrm{\pi }}_l}{{\mathrm{\pi }}_{kl}}\frac{e_k}{{\mathrm{\pi }}_k}\frac{e_l}{{\mathrm{\pi }}_l},$$ (9)

where e_k = r_k – (Σ_i∈sr_i/π_i)(Σ_i∈s1/π_i)⁻¹. These variance estimators also require pairwise inclusion probabilities, which can be approximated by the method of Hartley and Rao (1962).

However, the Hartley and Rao approximation may lead to bias in the variance estimator. Thus, we also consider the jackknife method for variance estimation (Shao and Wu 1989). The sample is stratified into n/G strata each of size G with similar values of inclusion probabilities, and the G subgroups are then constructed by selecting one element at a time from each stratum without replacement (Zheng and Little 2005). Let p̂_(g) same GR estimators in (6) and (7) calculated from the reduced sample without the elements in the g^th subgroup, and let p̄ average of the G estimators based on the G reduced samples. The jackknife variance estimator of p̂_GR is

$${\widehat{V}}_{\text{jackknife}}({\widehat{p}}_{\text{GR}})=\frac{G-1}{G}\sum _{g=1}^G{({\widehat{p}}_{(g)}-\overline{p})}^2.$$ (10)

A design-weighted logistic regression model on other covariates was used as the assisting model to predict ŷ_i in the GR estimators for binary outcomes (Lehtonen and Veijanen 1998; Lehtonen et al. 2005). Since our interest here is in comparisons of GR estimators with the BPSP estimator, we apply the estimators (6) and (7) with linear probit regression models and probit p-spline models, as described in detail in Section 5. For the GR estimator using a linear probit model as the assisting model, we use the inclusion probability as a covariate as well as a weight in our simulations.

5. Simulation study

5.1 Design of the simulation study

Simulation studies are conducted to study the performance of the BPSP estimator compared with the HK estimator, the GR estimators, and the linear model-based predictive estimators for a variety of populations in pps sampling. We present the simulation results for the following six estimators:

1. HK, the Hájek estimator defined by equation (1).

2. LR, predictive estimator of the form ${\widehat{p}}_{\text{LR}}=N^{-1}({\sum }_{i\in s}{y}_i+{\sum }_{j\notin s}{\widehat{y}}_j^{\text{LR}}$ with prediction ${\widehat{y}}_j^{\text{LR}}$ obtained with the maximum likelihood predictions from the linear logistic regression model containing a constant term and the reciprocal inclusion probability as the covariate. LR has the IBC property, and hence is design-consistent. LR is exactly the same as its GR estimator in equation (6).

3. PR, predictive estimator of the form ${\widehat{p}}_{\text{PR}}=N^{-1}({\sum }_{i\in s}{y}_i+{\sum }_{j\notin s}{\widehat{y}}_j^{\text{PR}}$ with prediction ${\widehat{y}}_j^{\text{PR}}$ from the Bayesian linear probit model containing an intercept term and the inclusion probability as the covariate.

4. PR_GR, the GR estimator in equation (7), where ŷ_i is the prediction for unit i with unknown parameters replaced by weighted maximum likelihood estimates from the probit model with a constant term and the inclusion probability as the covariate.

5. BPSP, the BPSP estimator defined by equation (4) with p = 1 and inverse-gamma prior distribution for τ² and using 15 knots.

6. BPSP_GR, the GR estimator in equation (7), where ŷ_i is the posterior mean of Pr (Y_i = 1|π from the BPSP model.

We only report the simulation results based on the linear splines for the BPSP estimator, since simulations not shown here suggest that linear splines perform as well as quadratic splines or cubic splines in all the simulation scenarios. We choose two fixed numbers of knots (15 or 30), and place knots at evenly spaced sample percentiles. The choices of knots work well and a number of 15 knots is good enough to catch the curvatures in our simulations. In addition, the GR estimators in (6) perform similarly to the estimators in (7); some differences between these estimators emerge in the real application in Section 6, leading us to prefer (7) over (6).

We simulated two artificial populations of size 2,000, using two different distributions, with sampling rates of 5% and 10%, where the size variable takes the consecutive integer values 71, 72, …, 2,070. The inclusion probabilities in the population were then calculated as proportional to the size variable, with the maximum value about 30 times the minimum values.

Continuous data Z were first generated from normal distributions with mean structure f (π) and constant error variance 0.04. Two different mean structures f (π) were simulated: a linearly increasing function (LINUP) f (π_i)= k₁π_i and an exponential function (EXP) f (π_i) = exp(−4.64 + k₂π_i). To make the range of Z similar across different mean structures, k₁ takes values of 3 and 6, and k₂ takes values of 26 and 52, when the sampling rate is 10% and 5%, respectively. Figure 1 plots the two populations. We then generated the binary outcome variable Y₁, where Y₁ is equal to one if Z is less than or equal to its superpopulation 10^th percentile, otherwise Y₁ is equal to zero. Similarly, we generated the binary outcomes Y₂ and Y₃ by using the superpopulation 50^th and 90^th percentiles of Z as cut-off values. The target of inference here is the population proportion with Y equal to one.

Figure 1.

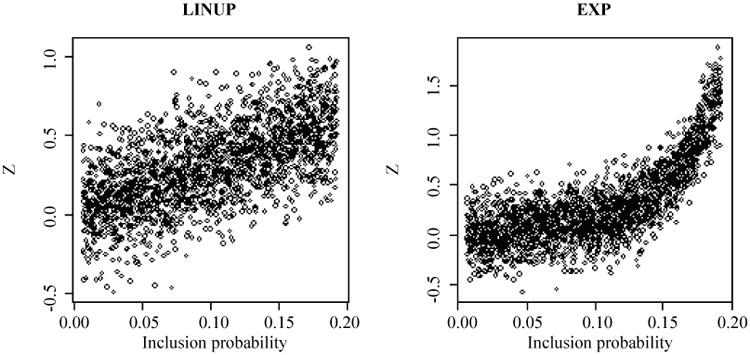
Two simulated artificial populations (N = 2,000)

In each simulation replicate, a finite population was generated before a sample was drawn, and the true finite population proportion with Y equal to one was calculated and denoted as p. A pps sample was then drawn systematically from a randomly ordered list of the finite population. For each population and sample size combination, 1,000 replicates were obtained and the six estimators were compared in terms of empirical bias, root mean squared error (RMSE), and the non-coverage rate of the 95% confidence /credible interval. Simulation results are presented in Tables 1 through 3. Let p̂_i be an estimate of p_i based on the i^th pps sample, the empirical bias and RMSE are defined as follow,

Table 1. Empirical bias × 1,000 of six estimators (Minimum absolute bias within a row is in italic print).

Population	n	True prop.	HK	LR	PR	PR_GR	BPSP	BPSP_GR
LINUP	100	0.10	-0.01	13.0	10.3	1.6	8.0	1.2
		0.50	-4.0	-2.9	-4.3	-3.0	-5.2	-3.3
		0.90	-0.4	0.3	-2.5	0.3	-2.9	0.08
	200	0.10	2.5	7.9	5.8	1.5	5.1	1.4
		0.50	3.3	-0.1	-1.3	-0.06	-1.7	-0.2
		0.90	1.6	0.4	-1.0	0.3	-1.2	0.3
EXP	100	0.10	1.2	18.1	25.8	4.7	17.0	3.9
		0.50	-4.0	-3.5	12.5	-1.6	-1.4	-3.4
		0.90	-1.3	-0.2	-1.0	-0.1	-1.0	-0.2
	200	0.10	3.1	11.0	22.1	3.5	13.4	2.7
		0.50	3.8	-0.6	14.0	0.4	0.01	-0.7
		0.90	2.3	0.1	-0.7	0.1	-0.7	0.02

Table 3. Noncoverage rate of 95% CI × 100 of six estimators (noncoverage rate within a row closest to 5 is in italic print).

Population	n	True prop.	HK	LR	PR	PR_GR		BPSP	BPSP_GR
						V1	V2		V1	V2
LINUP	100	0.10	16.2	18.0	8.4	20.9	16.1	9.0	18.4	14.2
		0.50	7.5	9.4	5.0	7.2	7.6	4.4	7.3	7.1
		0.90	7.4	11.4	5.7	8.0	9.4	5.4	8.4	7.1
	200	0.10	10.8	12.6	6.4	13.9	10.9	6.2	12.6	9.4
		0.50	5.5	8.3	5.5	6.2	5.9	5.1	6.0	5.5
		0.90	6.0	8.4	4.4	6.1	4.4	4.7	6.3	5.5
EXP	100	0.10	15.0	18.1	10.5	19.4	14.8	9.2	18.4	14.4
		0.50	7.4	13.5	12.2	9.0	11.4	8.9	10.2	8.4
		0.90	6.1	10.5	7.9	9.9	7.6	7.0	9.8	7.2
	200	0.10	10.8	13.3	9.9	12.5	11.7	7.5	12.4	9.4
		0.50	6.0	11.5	14.3	7.2	8.5	6.2	7.5	6.9
		0.90	5.5	8.8	5.5	6.8	4.6	5.5	6.6	3.7

^*V1: variance estimator using linearization; V2: jackknife variance estimator.

$$\text{Bias}=\frac{1}{1,000}\sum _{i=1}^{1,000}({\widehat{p}}_i-p_i),$$

$$\text{RMSE}=\sqrt{\frac{1}{1,000}\sum _{i=1}^{1,000}{({\widehat{p}}_i-p_i)}^2}.$$

5.2 Simulation results

Figure 2 shows the posterior means of Pr (Y_i = 1| π_i) and 95% credible intervals based on the Bayesian probit linear p-spline model for a random pps sample from the EXP case. The upper left plot is the scatter plot of the continuous variable Z in a pps sample, with three horizontal parallel lines superimposed, representing the superpopulation 10^th, 50^th, and 90^th percentiles, respectively. In the upper right plot, the binary variable Y, defined as 1 if Z is less than or equal to the superpopulation 10^th percentile, are plotted with black circles, and the superpopulation Pr (Y_i = 1|π_i) are plotted with a solid black curve. The solid grey curve and two dashed grey curves are the posterior means of Pr (Y_i = 1|π_i) and 95% credible intervals based on the Bayesian probit linear p-spline regression model. The other two plots are similar to the upper right plot, but with superpopulation 50^th and 90^th percentiles as cut-off values in defining Y. These plots show that the true probabilities of Y = 1 fall within the 95% credible intervals, and are close to the posterior means of Pr (Y_i = 1|π_i). We conclude that the Bayesian probit p-spline regression model fits well for the binary outcomes in the nonlinear case.

Figure 2.

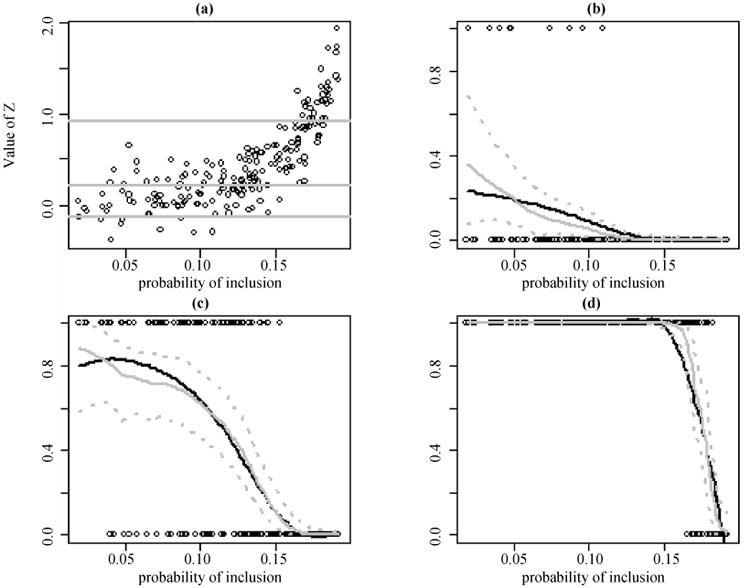
A random pps sample from the EXP case (n = 200, N = 2,000): (a) scatter plot of Z; the three grey lines are the superpopulation 10^th, 50^th, and 90^th percentiles, respectively. (b) black circles are observed units of binary survey variable Y in the sample, defined as Y = I (Z ≤ 10^th percentile); the grey solid and dashed curves are posterior means of Pr (Y_i = 1|π_i) and 95% credible intervals, respectively, simulated based on a probit p-spline model on π; and the black curve is the superpopulation Pr(Y_i = 1|π_i). (c) similar to (b), but with Y = I (Z ≤ 50^th percentile). (d) similar to (b), but with Y = I (Z ≤ 90^th percentile)

Table 1 shows the empirical bias (×10³) for the six estimators in the two populations generated via LINUP and EXP. Overall the design-based estimators (a, d, and f) are less biased than the model-based estimators (b, c, and e). In the LINUP case, the linear probit regression model is correctly specified, so that the empirical bias of the PR estimators are similar to the empirical bias of the BPSP estimator; while in the EXP case, a nonlinear probit regression is needed to fit the data, and thus the PR estimator is more biased than the BPSP estimator when the true population proportions are 0.1 and 0.5. However, the LR estimator has similar to the BPSP estimator empirical bias because of the IBC property. Compared to the model-based PR and BPSP estimators, the PR_GR and BPSP_GR estimator reduce the bias by adding the bias calibration term. Moreover, no matter which assisting models were used, both GR estimators achieve similar empirical bias.

Table 2 shows the empirical root mean squared error (×10³) for the six estimators. The BPSP estimator has much smaller empirical root mean squared error than the HK estimator, except when p is 0.1 in the EXP case. Overall the PR estimator performs similarly to the BPSP estimator. To protect again model misspecification, the GR estimators lose some efficiency compared to their corresponding model-based predictive estimators. The PR_GR estimator has similar to the BPSP_GR estimator RMSE, but both of the two GR estimators have smaller RMSE compared to the HK estimator by using assisting models.

Table 2. Empirical RMSE × 1,000 of six estimators (Minimum RMSE within a row is in italic print).

Population	n	True prop.	HK	LR	PR	PR_GR	BPSP	BPSP_GR
LINUP	100	0.10	55.1	57.1	46.3	51.3	47.2	51.7
		0.50	65.2	50.8	47.1	49.7	47.7	50.0
		0.90	26.3	22.6	23.3	22.7	23.5	22.9
	200	0.10	39.3	40.9	31.8	36.1	32.0	36.2
		0.50	45.7	35.9	32.8	34.3	32.8	34.6
		0.90	17.8	15.4	15.5	15.4	15.5	15.3
EXP	100	0.10	51.2	60.1	54.4	51.6	51.8	52.4
		0.50	66.1	56.0	43.0	53.2	47.0	51.7
		0.90	24.2	12.4	12.3	12.4	12.3	12.3
	200	0.10	35.9	42.4	39.6	35.6	36.0	36.2
		0.50	45.1	38.9	31.3	36.1	32.1	35.1
		0.90	15.8	8.0	8.1	8.0	8.0	8.0

Table 3 shows the noncoverage probability (×10²) of 95% confidence/credible intervals, the probability that the true finite population proportion is outside the 95% CI of the estimators. To calculate the variances of estimators, we use the Yates-Grundy variance estimator as defined in equation (2) for the HK estimator; use jackknife resampling method defined by equation (10) for the LR estimator; and use both the linearization (V1) method defined by equation (9) and the jackknife resampling (V2) method for the PR_GR and BPSP_GR estimators. Overall, the confidence coverage of credible interval for the BPSP estimator is closer to the nominal level than the other five estimators, especially when the population proportion p is close to zero or one or when few observations are selected into sample in the tails. Specifically, the BPSP estimator achieves significant improvement in coverage when p is close to zero in both the LINUP and EXP cases, since little data are included in the sample from the lower tail of the two populations. Note that the improved coverage of the BPSP estimator is achieved with intervals that are narrower on average than those of the HK, LR, PR_GR, and BPSP_GR estimators. Similar to the empirical bias and RMSE, the BPSP_GR does not improve the coverage in comparison to the PR_GR estimator by using a flexible assisting model.

The choice of prior and hyperprior distributions in mixed models can have a big effect on inferences. We used a prior distribution N (0,10⁶) for the fixed effects parameters, β_i. In our simulations, we report results based on a proper inverse-gamma prior distribution for τ², namely τ² ∝ IG (0.1,0.1). To assess sensitivity to the choice of prior distributions, we also computed results using τ² ∝ IG(0.01,0.01) and τ² ∝ IG(0.001,0.001), as well as an improper uniform prior distribution on τ (Gelman 2006). These different priors had little impact on posterior inference of the proportion of interest.

6. Example of tax auditing

We now compare the BPSP estimator with alternative methods on a real population involving income tax auditing data (Compumine 2007). The data set consists of 3,119 Swedish income tax returns for persons who during the year sold mutual funds managed in a foreign country. The outcome of interest Y is whether the income tax return is incorrect (coded as 1 for incorrect, and 0 for correct), and it is measured for all observations in this data set. We treated the 3,119 income tax returns as a finite population here, so that the true population proportion of incorrect income tax returns is 0.517. Since the amount of the realized positive profit is an important feature for determining the amount the tax payer has hidden from taxation for his return of income from the sale of a foreign fund, it was chosen as the size variable used in drawing pps sampling. When the primary measure of interest is the total amount the tax payer has hidden from taxation, it is reasonable to assign a value of 1 Swedish Krona to negative profits, the minimum amount of the positive profits, where negative values are not allowed in the size variable.

One thousand repeated systematic pps samples of size 300 and 600 were drawn without replacement from randomly ordered population lists. The returns with largest profits were included with certainty into the samples of size 300 and 600: there were 78 and 241 such returns respectively. Figure 3 shows that the probability of inclusion has a right-skewed distribution for the population even after excluding the observations with inclusion probability of 1.

Figure 3.

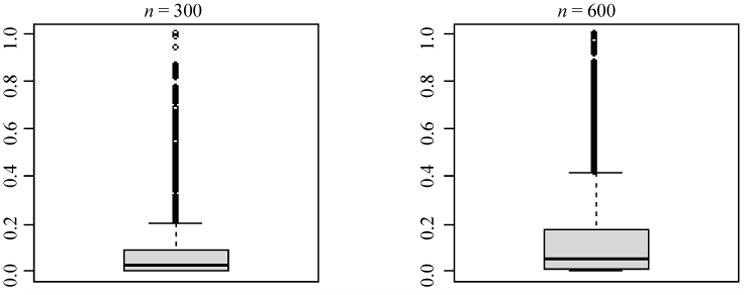
Box plots of the probabilities of inclusion for two sample sizes in the tax auditing example

We applied the same six estimators as in the simulation study with 30 knots on the pps samples, and compared their performances in terms of empirical bias, RMSE, and average width and noncoverage rate of the 95% confidence/credible interval. For the BPSP estimator, a fixed number of 30 knots are placed at evenly spaced sample percentiles of the inclusion probabilities. For the GR estimators, neither the linearization nor the jackknife variance estimator has predominantly better performance than the other, we present the inference based on the linearization variance estimator for simple calculation. We report the GR estimators based on both equations (6) and (7). The results are displayed in Table 4.

Table 4. Comparison of various estimators for empirical bias, root mean squared error, and average width and noncoverage rate of 95% CI, in the tax return example.

Methods	bias*100		RMSE*100		average width*100		noncoverage*100
	300	600	300	600	300	600	300	600
HK	-2.4	-1.8	12.4	10.2	36	29	14.1	10.2
LR	6.7	5.5	11.9	9.2	27	21	43.5	45.6
PR	-11.6	-10.1	12.4	10.6	18	14	69.8	83.4
PR GR1	-1.2	-0.4	11.5	8.7	31	25	22.4	16.8
PR_GR2	-1.2	-0.3	11.5	8.8	33	26	16.1	11.4
BPSP	-6.8	-2.7	9.3	5.2	27	19	14.2	5.0
BPSP GR1	-3.0	-0.5	102.6	56.9	77	57	14.4	9.2
BPSP_GR2	-0.7	0.2	12.0	10.1	34	26	15.9	12.8

^*GR_1: GR estimators using equation (6);

GR_2: GR estimators using equation (7).

Table 4 shows that the BPSP estimator has slightly increased bias but smaller RMSE, shorter average width and closer to the nominal level credible interval than the design-based estimators (a), (d), and (f). Results not shown here indicate that the BPSP estimator with a uniform prior distribution has slightly better performance than that with inverse-gamma prior distribution with respect to empirical bias, RMSE, and coverage rate, because there are more fluctuations in the data and the uniform prior allows the fitted function to have more flexibility. The BPSP_GR estimator is less biased, but achieves less efficiency and worse coverage rate than the BPSP estimator. The predictive estimator using the probit linear regression model as prediction model performs poorly here since the model is misspecified, but its GR estimator does reduce bias and RMSE and improve coverage rate. The BPSP_GR estimator based on equation (6) performs very poorly in terms of RMSE compared to the estimator in equation (7), because a situation similar to that in Basu's (1971) circus elephant example occurs, where one or more observations having very low inclusion probabilities are selected into the sample and hence receive large weights. However, the PR_GR estimator in equation (6) performs as well as that in equation (7) with predictions obtained from the weighted maximum likelihood estimates, where inclusion probability is used as a covariate as well as the sample weights. Overall, the GR estimator in equation (7) is more desirable than that in equation (6). As the sample size increases from 300 to 600, the noncoverage probability of the 95% credible interval of the BPSP estimator approaches the nominal level of 5% quickly from 14% to 5%, but the coverages are consistently below the nominal level for the other estimators.

Compared to the linear model-based predictive estimators, the BPSP estimator is robust not only to model misspecification, but also to the influential observations in the sample. To demonstrate the robustness to the influential observations, we compare the changes in the model fitting using probit p-spline models, linear probit model, and quadratic probit model based on the pps sample only in Figure 4, and based on the pps sample as well as the observations with inclusion probabilities of 1 in Figure 5. In each figure, the population is stratified by the 100 quantiles of the probabilities of inclusion, and the true probabilities of Y = 1 are calculated and plotted with a black dot for each stratum. The grey curves are the posterior means of Pr (Y_i = 1|π_i) from 10 random pps samples using 3,000-iterate Gibbs sampler and linear spline in the left plot, using linear probit regression in the middle plot, and using quadratic probit regression in the right plot. Figure 4 shows that the probity p-spline regression model is more flexible in catching the pattern among the observations than the parametric models. From Figure 4 to Figure 5, the posterior means of Pr (Y_i = |π_i) do not change except for those with very large inclusion probabilities using the p-spline model. However, the posterior means curves change dramatically using the quadratic probit regression. These comparisons indicate that probit p-spline regression model is less likely affected by influential observations, and hence is a good choice of prediction model in the model-based inference.

Figure 4.

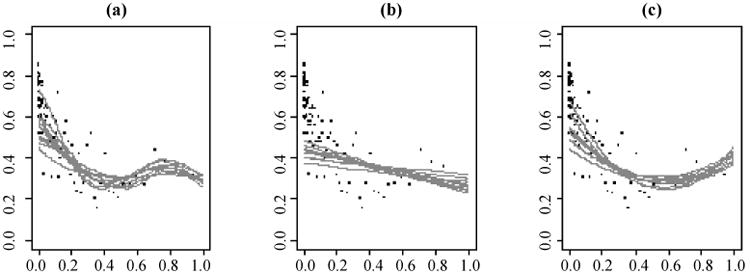
Predictions based on pps samples only in the tax auditing example, X-axis: inclusion probabilities π, Y-axis: P(Y = 1|π); black dots are the true P(Y = 1|π) within each percentile of π; grey curves are ten realizations of the posterior means of P(Y = 1|π). The prediction models are (a) probit linear p-spline regression, (b) linear probit regression, (c) quadratic probit regression

Figure 5.

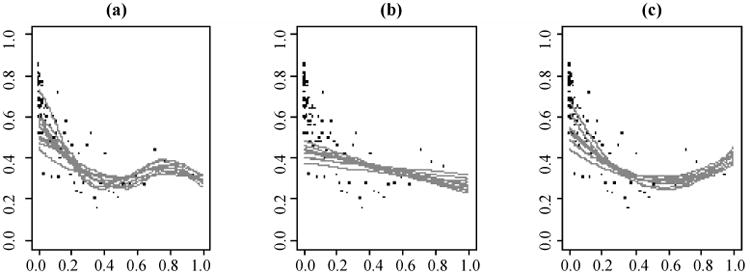
Predictions based on the combined data of pps samples and the observations sampled with certainty in the tax auditing example, X-axis: inclusion probabilities π, Y-axis: P(Y = 1|π); black dots are the true P(Y = 1|π) within each percentile of π; grey curves are ten realizations of the posterior mean of P(Y = 1|π). The prediction models are (a) probit linear p-spline regression, (b) linear probit regression, (c) quadratic probit regression

7. Discussion

Bayesian inferences based on the p-spline model outperform the HK estimator, the GR estimators, and linear model-based prediction estimators in our simulations. The BPSP estimators are more efficient than the HK and GR estimators, and despite slightly higher empirical bias, their 95% credible intervals provide better confidence coverage and shorter average interval width, especially when the population proportion is closer to zero or one and few data are selected into the sample in the tails. This suggests the importance of current research in estimating finite population prevalence of rare events.

The BPSP estimator is a natural extension of the regular linear regression model-based estimators of finite population proportions. Compared to linear model-based predicttive estimators, the BPSP estimator achieves robustness to model misspecification and influential observations in the sample by using a flexible p-spline model, without much loss of efficiency for the sample sizes considered. Therefore, the BPSP estimator is easy to understand while requires complex computation. However, with the availability of WinBUGS, the Bayesian statistical software, the BPSP estimator can be easily implemented by survey practitioners.

The BPSP estimators are not sensitive to two choices of prior distributions of τ² considered here, though it appears from the tax auditing example that the uniform prior yields slightly smaller bias and RMSE, shorter 95% credible intervals, and better coverage when a nonlinear prediction model is needed. The tax auditing example also shows that in the GR estimator, an estimated population size using the sum of inverse inclusion probabilities is more desirable than the true population size when one or more observations with very low inclusion probability are included in the sample, since the GR estimator with denominator N has high variance and low efficiency in this case.

The design-based estimators and their 95% confidence intervals can provide valid inferences for population proportions when the sample is large. However, these asymptotic properties do not appear to hold when the sample size is moderate or small. The BPSP approach can provide more valid inferences for small samples, especially when the true population proportion to be estimated is close to 0 or 1, although confidence coverage appears to be less than nominal when the sample size gets small, and lack of parsimony of the model is an issue. When estimating proportions away from tails, the BPSP estimator leads to slightly smaller RMSE and closer to the nominal level confidence coverage than the HK and GR estimators, but the improvement is not so significant as in the tails. In this scenario, to avoid the complex computation of the BPSP estimator, the PR_GR estimator based on equation (7) is an alternative to the survey practitioners.

The choice of variance estimator is problematic for some unequal probability designs for the design-based estimators, but the Bayesian p-spline prediction approach provides a simulation approximation of the full posterior distribution of the population proportion. Extra work is not needed to estimate the variance or 95% credible interval for the BPSP estimator, as it can be obtained simultaneously with the point estimators. In Zheng and Little (2005), three variance estimators of the p-spline model-based estimator for finite population total in a pps sample were compared, including the model-based empirical Bayes variance estimator, the jackknife variance estimate, and the balanced repeated replication (BRR) variance estimate. The simulation studies showed that the jackknife method worked well, whereas the BRR method tended to yield conservative standard errors and the model-based empirical Bayes estimator was vulnerable to misspecification of the variance structure. In the present work, the 1 – α level credible interval for the BPSP estimator of population proportion is constructed by splitting α equally between the upper and lower endpoints of the posterior distribution of p. This pure Bayesian approach based on draws from the posterior distributions seems to work well in our setting and avoids the heavy computation associated with the jackknife and BRR method.

The BPSP estimator we propose here can be extended to include additional auxiliary covariates by adding linear terms for these variables. For domain estimation, an interaction term between the spline of inclusion probabilities and the domain indicator should also be modeled. Both the additive effects of auxiliary variables and the interaction between the domain indicator and inclusion probabilities can be represented in a mixed model (Ruppert et al. 2003, page 231) and estimated using Gibbs sampling or WinBUGS (Crainiceanu et al. 2005). The BPSP estimator for finite population proportions can also be extended to a more general case of a polychotomous response. The Gibbs sampling approach for the binary case can be generalized to the case of ordered categories, and can be applied to the unordered categories with a latent multinomial distribution (Albert and Chib 1993). Another extension for the BPSP estimator is in the small area estimation, by combing small area random effects with the smooth spline on the inclusion probabilities (Opsomer, Claeskens, Ranalli, Kauermann and Breidt 2008). This extension will be the focus of future research.

Finally, one reviewer questioned whether the proposed approach can be applied in a multipurpose survey with many outcomes, since the modeling procedure does not provide a single set of weights and needs to be repeated for all variables of interest. It is true that our methods are more computationally intensive than existing approaches, but the BPSP method can be easily implemented with a Gibbs sampling algorithm or using WinBUGS, so computing is not a major obstacle. We point out that the simulations in the paper involved repeating the iterative Gibbs analysis 6,000 times, so an equivalent level of computation on a single survey of comparable size would allow the implementation of the BPSP method for 6,000 outcomes! These were done on a garden-variety laptop PC. While we do not advocate automatic use of any analytical method, design or model-based, our point is that computational complexity is no longer a major obstacle to applying these methods. We suggest that the statistical properties of a method are more important than computing time, given modern day computing resources.

Algorithm of Gibbs sampling

Model (3) can also be written in the matrix form, Φ⁻¹(E(y_i | β,b,X,Z)) = (Xβ+ Zb)_i, i = 1,…,n β = (β₀, β₁, …, β_p)^T, b = (b₁, …, b_m) ∼ N_m(0,τ²I_m)

$$X=\left(\begin{array}{llll}1\hfill & {\mathrm{\pi }}_1\hfill & \dots \hfill & {\mathrm{\pi }}_1^p\hfill \\ \cdot \hfill & \cdot \hfill & \dots \hfill & \cdot \hfill \\ \cdot \hfill & \cdot \hfill & \dots \hfill & \cdot \hfill \\ \cdot \hfill & \cdot \hfill & \dots \hfill & \cdot \hfill \\ 1\hfill & {\mathrm{\pi }}_n\hfill & \dots \hfill & {\mathrm{\pi }}_n^p\hfill \end{array}\right),Z=\left(\begin{array}{lll}{({\mathrm{\pi }}_1-k_1)}_{+}^p\hfill & \dots \hfill & {({\mathrm{\pi }}_1-k_m)}_{+}^p\hfill \\ \cdot \hfill & \dots \hfill & \cdot \hfill \\ \cdot \hfill & \dots \hfill & \cdot \hfill \\ \cdot \hfill & \dots \hfill & \cdot \hfill \\ {({\mathrm{\pi }}_n-k_1)}_{+}^p\hfill & \dots \hfill & {({\mathrm{\pi }}_n-k_m)}_{+}^p\hfill \end{array}\right).$$

The algorithm of Gibbs sampling for estimating the parameters in Model (3) is as follows:

1. The probit regression model for the binary outcome y = [y₁, …, y_n]^T corresponds to a normal regression model for a latent continuous data $y^{\ast }={[y_1^{\ast },\dots ,y_n^{\ast }]}^T$, which has a truncated multivariate normal distribution with mean (Xβ + Zb) and identity covariance matrix (Albert and Chib 1993), and y_i is the indicator that $y_i^{\ast }>0$. With some initial values of (β, b), values of the latent continuous data $y_i^{\ast }$ can be simulated.

2. Specifying a proper flat normal prior distribution N (0,10⁶) on β and an inverse gamma distribution IG (0.1,0.1) on τ², the posterior distribution of (β, b, τ²) given the simulated latent continuous data y* is

   $$(\mathrm{\beta },b)|{\mathrm{\tau }}^2,y^{\ast }~{\text{MVN}}_{m+p+1}({(C^{T}C+D/{\mathrm{\tau }}^2)}^{-1}{C}^T{y}^{\ast },{(C^{T}C+D/{\mathrm{\tau }}^2)}^{-1}){\mathrm{\tau }}^2|\mathrm{\beta },b~\text{IG}(0.1+m/2,0.1+{\Vert b\Vert }^2/2)$$ (11)

   where C = [X, Z] and D is a diagonal matrix with p + 1 values of 10^-6 followed by m ones on the diagonal. Gelman (2006) recommended a uniform prior distribution on τ, which results in the posterior distribution for τ² as

   $${\mathrm{\tau }}^2|\mathrm{\beta },b~\text{IG}((m-1)/2,{\Vert b\Vert }^2/2)$$ (12)

3. At iteration t, draws of (β^(t), b^(t),τ^2(t)) from the posterior distribution in equation (11) or (12) are used to generate new latent data ŷ*^(t) conditional on observed binary variable y for the sample, and to obtain the posterior predicted values ŷ^(t) for non-sample units. We then can obtain draws from the posterior distribution of the finite population proportion at iteration t as ${\widehat{p}}_{\text{PR}}^{(t)}=N^{-1}(\sum _{i\in s}{y}_i+\sum _{j\notin s}{\widehat{y}}_j^{(t)})$