Applying a New Bilateral Mammographic Density Segmentation Method to Improve Accuracy of Breast Cancer Risk Prediction

Abstract

Purpose

How to optimally detect bilateral mammographic asymmetry and improve risk prediction accuracy remains a difficult and unsolved issue. Our aim was to find an effective mammographic density segmentation method to improve accuracy of breast cancer risk prediction.

Methods

A dataset including 168 negative mammography screening cases was used. We applied a mutual threshold to bilateral mammograms of left and right breasts to segment the dense breast regions. The mutual threshold was determined by the median grayscale value of all pixels in both left and right breast regions. For each case, we then computed three types of image features representing asymmetry, mean and the maximum of the image features, respectively. A two-stage classification scheme was developed to fuse three types of features. The risk prediction performance was tested using a leave-one-case-out cross-validation method.

Results

By using the new density segmentation method, the computed area under the receiver operating characteristic curve was 0.830±0.033 and overall prediction accuracy was 81.0%, significantly higher than those of 0.633±0.043 and 57.1% achieved by using the previous density segmentation method (p < 0.01, t-test).

Conclusions

A new mammographic density segmentation method based on a bilateral mutual threshold can be used to more effectively detect bilateral mammographic density asymmetry and help significantly improve accuracy of near-term breast cancer risk prediction.

I. INTRODUCTION

Due to the potential harmful effects of cumulative radiation exposure [1], unnecessary biopsies [2], high cost and limited healthcare resources [3], the current population-based mammography screening paradigm remains quite controversial [4]. In order to solve this clinical dilemma, developing an optimal breast cancer screening paradigm to detect early cancers has attracted extensive research interest recently [5].

The success of establishing an optimal personalized breast cancer screening paradigm depends on developing a reliable risk prediction model. Although many epidemiology study-based breast cancer risk models, such as Gail, Claus, and Tyrer-Cuzick model [6] have been developed, they typically aim to assess the risk of a woman developing breast cancer in a long term or lifetime. Thus, it is required to develop new models that have higher discriminatory power in predicting the risk of individual women developing breast cancer in the near-term [7]. Based on the computed quantitative image features, several research groups have developed and tested a number of new risk stratification models to predict breast cancer risk [8–12]. These image features could be divided into two major categories: unilateral features (depicting the information of every single breast mammogram), and concurrent features (describing the asymmetry of bilateral mammograms of left and right breasts) [13]. Using unilateral features, including mammographic texture and density features, has shown the value in breast cancer risk assessment [14]. A recent study also demonstrated a moderately high positive association between the risk prediction scores generated by the mammographic density related image feature analysis and the actual risk of women having an image-detectable breast cancer in the next subsequent examinations [10]. Despite that mammographic density has the highest discriminatory power besides women’s age in the existing epidemiology-based risk models [6], its discriminatory power at the individual level remains low and controversial [15,16].

In our studies, we hypothesized that bilateral mammographic density asymmetry may be an important indicator of breast cancer development [4]. To test this hypothesis, we have preliminarily investigated computerized methods to detect bilateral mammographic density asymmetry features and the potential of using asymmetry scores to predict near-term breast cancer risk [13, 17, 18]. However, how to optimally detect bilateral mammographic asymmetry and improve risk prediction accuracy remains a difficult and unsolved issue.

In this study, we investigated a new bilateral mammographic asymmetry detecting approach and tested whether it can help significantly improving the performance of near-term breast cancer risk prediction. Specifically, we proposed to use a single “mutual” threshold to bilateral mammograms of left and right breasts to segment dense breast regions and compute relevant image features, and developed a unique two-stage classification scheme to fuse the image features for breast cancer risk prediction.

II. Materials

We retrospectively assembled an image dataset, which includes two sequential mammographic screening examinations acquired from 168 women. Each examination includes two full-field digital mammography (FFDM) images representing the craniocaudal (CC) view of the left and right breasts. All images were acquired using Hologic Selenia FFDM systems (Hologic Inc., Bedford, MA, USA).

For each case (woman), the first (“prior”) examination and the next (“current”) examination were acquired within a time lag of 12–36 months. All the “prior” examinations were interpreted by radiologists as “negative”. Among the “current” examinations, 83 were positive cases with cancer verified and 85 were negative (cancer-free) cases. The average ages and standard deviations were 57.5±11.8 and 52.5±10.9 years old for the positive and negative groups of women, respectively. In this study, only “prior” screening images were used for computing features and building prediction models, which were divided into two different classes based on their status in the “current” examinations.

In this study, we only focused on predicting whether women will develop breast cancers in the next sequential screening after the first negative screening. It was not validated whether the “negative” cases remained in the “cancer-free” status in the third sequential examinations.

III. Methods

The new risk model was developed using four steps including (1) segmenting breast regions, (2) creating local pixel value fluctuation maps, (3) computing image features, and (4) optimizing classification scheme.

A. Breast Region Segmentation

For each case, a pair of bilateral CC view images were analyzed. We applied an automatic segmentation scheme on each image to extract the whole breast region as described in [19, 20]. In brief, a gray level histogram of the image was plotted and an iterative searching method was used to detect the smoothest curvature between the breast tissue and background or air region. The pixels in the background were discarded and the skin region was removed by a morphological erosion operation (Fig.1). In addition, we also segmented the dense breast region from each image. In the previous studies, the dense breast region of each image (left or right mammographic image) was defined as the region that encompasses the pixel values above the median value of the whole breast region[7,21–22]. In these studies, dense regions of left and right mammographic images were segmented using their respective medians as thresholds. It was found that some individual features computed for the dense breast areas showed good correlation with the radiologists’ ratings [21] and some texture features computed on the dense breast regions are most effective for breast cancer risk prediction [7]. In this study, we also used median value for thresholding to take its advantage, but in a different way. It is possible that the thresholding method used in previous studies may reduce the capability of detecting bilateral density asymmetry. In this study, we used a single “mutual” threshold, instead of two different thresholds, to segment dense regions from left and right mammographic images (Fig.1). The “mutual” threshold was defined as median grayscale value of all pixels in the whole breast regions of both left and right mammographic images. This was done to investigate a new approach aiming to more accurately detect bilateral mammographic density or tissue asymmetry and test whether it can help further improve the performance of applying quantitative image feature analysis methods to predict near-term breast cancer risk.

Fig. 1.

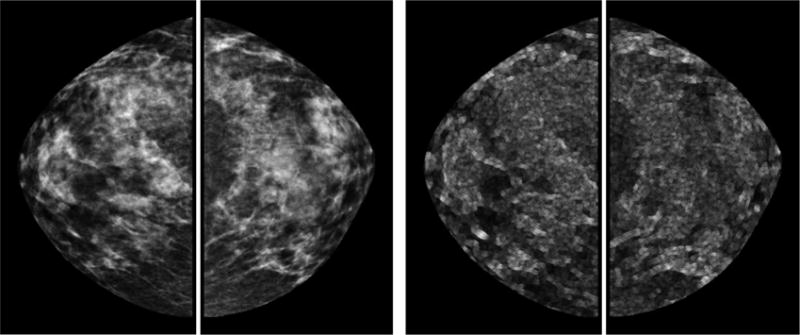
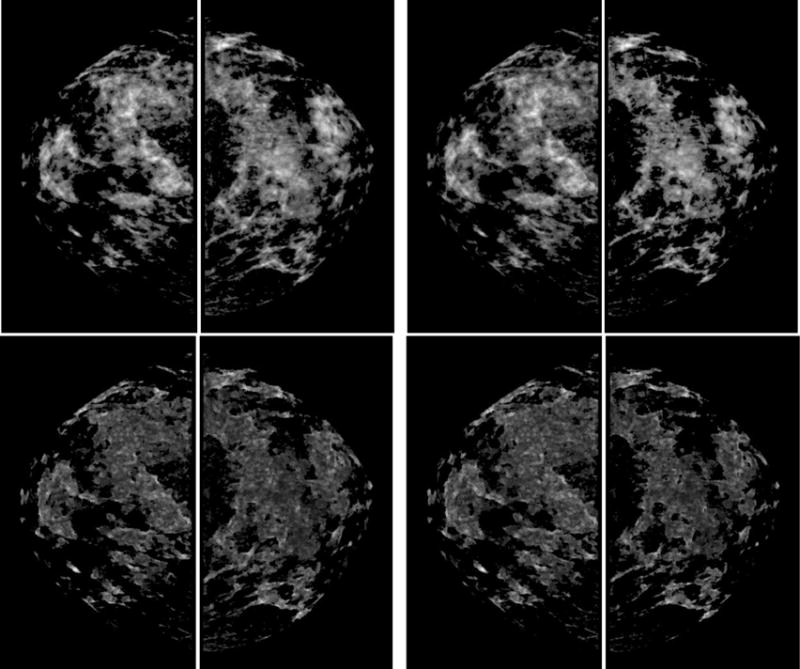
Example of a positive case acquired from the “prior” screening examination. It shows the segmented whole breast regions of original images (top left) and local pixel value fluctuation maps (top right), dense breast regions of original images segmented with the new segmentation method (middle left) and previous segmentation method (middle right), dense breast regions of local pixel value fluctuation maps segmented with the new segmentation method (bottom left) and previous segmentation method (bottom right).

B. Local Pixel Value Fluctuation Map Generation

In order to compute image features of higher predictive power, we generated local pixel value fluctuation (LPVF) maps for each image by applying a 5×5 square convolution kernel to scan the image with the segmented whole breast region and dense breast region, respectively (Fig.1). The absolute pixel value differences between the center pixel and each of the other pixels inside the kernel were computed. The maximum difference value computed inside the kernel was used to replace the original pixel value in the map (center pixel). As a result, unlike the original mammogram, the generated LPVF map can better show the image features related to the pixel value fluctuation and/or the local density variation, which may provide useful and complementary information to the image features acquired or computed from the original mammogram. Similar image conversion method was also used in [4, 18].

C. Image Feature Computation

Various studies have analyzed the correlation of mammographic image features with breast cancer risk [23–26]. In this study, we computed some features that have been proposed in the literature, as well as redefined some existing features and explored some new features that have never been examined for breast cancer risk prediction.

For each case, after reducing the gray level range of the original mammographic images from 4,096 to 256 gray levels, we computed the same 220 features from (1) whole breast regions and (2) dense breast regions in the original bilateral CC view images, which are named as WBR-ORG and DBR-ORG images, respectively, (3) whole breast regions and (4) dense breast regions in the bilateral LPVF maps, which are named as WBR-LPVF and DBR-LPVF maps, respectively. In the following, these features will be name as NF_i (i = 1,2,…,220×4). For comparison, we also computed the same 220×4 features from the original mammographic images and the LPVF maps in which the dense breast regions were segmented by applying two different thresholds separately to two bilateral mammograms (previous segmentation method). These features will be name as PF_i (i = 1,2,…,220×4).

Each group of 220 features were divided into three distinct types namely: (1) 76 asymmetry features, which were represented by the absolute subtraction of two matched bilateral feature values computed from the left and right images; (2) 72 mean features, which were computed by taking average value of two matched bilateral feature values; and (3) 72 maximum features, which were represented by the greater one of two matched bilateral feature values.

1) Asymmetry Features

The asymmetry features can be divided into five subgroups. The first subgroup include 13 image statistics based features (NF_i and PF_i, i = 1,2,…,13) [17], which are average local value fluctuation of gray level histogram, mean of gray level histogram values, standard deviation of gray level histogram values, statistics based features computed from the pixel value distributions of the ROI (region of interest) including mean value, variance, standard deviation, skewness, kurtosis, energy, and entropy, statistics based features computed from the local pixel value fluctuation map of the ROI including mean value, standard deviation, and skewness.

The second subgroup includes 4 fractal dimension related breast tissue composition features (NF_i and PF_i, i = 14,15,16,17) [21], which are estimated with variation method, mathematical morphology, two slopes of fitting lines using textural edgeness and Gaussian subtraction.

The third subgroup has 39 texture related image features (NF_i and PF_i, i = 18,19,…,56) [27], which include 8 Gray-level co-occurrence matrix based features, 13 Gray-level run-length matrix based features, 13 Gray-level size zone matrix based features, and 5 Neighborhood gray-tone difference matrix based features.

The fourth subgroup includes 16 features (NF_i and PF_i, i = 57,58,…,72) modified from those used in [17] to compute a variety of percentage of mammographic density (PMD) for mimicking Breast Imaging Reporting and Data System (BIRADS) used in clinical practice. These features are defined and computed as following: NF₅₇ (or PF₅₇) = N_HA/N_U, NF₅₈ (or PF₅₈) = N_HA/N_U, NF₅₉ (or PF₅₉) = N_HA/N_B and NF₆₀ (or PF₆₀) = N_HA/N_B. Where, N_U is the total number of pixels in the ROI of left or right breast; N_B is the total number of pixels in the ROIs of both left and right breasts. For NF₅₇ and NF₅₉, N_HA is the number of pixels in the ROI of left or right breast with gray value larger than the average value of all pixels in the ROIs of both left and right breasts. For PF₅₇ and PF₅₉ N_HA is the number of pixels in the ROI of left or right breast with gray value larger than the average value of all pixels in the ROI. For NF₅₈ and NF₆₀, N_HM is the number of pixels in the ROI of left or right breast with gray value larger than the median value of all pixels in the ROIs of both left and right breasts. For PF₅₈ and PF₆₀, N_HM is the number of pixels in the ROI of left or right breast with gray value larger than the median value of all pixels in the ROI. These 4 features are redefined from a feature used in Ref 25.

Next, to mimic BIRADS, we computed 3 features (NF_i (or PF_i) = I_K/I_S,i = 61,62,63). Specifically, I_S is the average gray value of all breast tissue pixels in one image and I_K are the average gray values of the pixels whose gray values are under the threshold of K = 25%, 50%, 75% of the maximum breast tissue pixel value in the image, respectively. In addition, we also computed other 3 features (NF_i(or PF_i) = N_K/N_S,i = 64,65,66), where N_S is the total number of breast tissue pixels in a single image and N_K are numbers of pixels whose gray values are under the threshold of K = 25%, 50%, 75% of the maximum pixel value in the image, respectively. Similarly, we also computed another set of 6 features combining all pixels in two bilateral images (NF_i(or PF_i) = I_K/I_B,i = 67,68,69) and (NF_i(or PF_i) = N_K/N_B,i = 70,71,72), where I_B is the average pixel value of total breast tissue pixels (N_B) of both left and right mammograms.

The last subgroup includes 4 newly explored features (NF_i or PF_i, i = 73,74,75,76) which are defined and computed as following:

$$N{F}_{73}(\text{and}P{F}_{73})=\mathit{abs}(P{V}_{max}^L-P{V}_{max}^R),$$

$N{F}_{74}(\text{and}P{F}_{74})=\mathit{abs}(P{V}_{max}^L-P{V}_{max}^R)/G{V}_h$, where $P{V}_{max}^L$ and $P{V}_{max}^R$ are the maximum breast tissue pixel values in the left and right images, respectively; GV_h is the number of gray levels in the ROI of left or right breast, in which the maximum pixel value is higher. Specifically, if $P{V}_{max}^L>P{V}_{max}^R$, GV_h refers to the number of gray levels in the ROI of the left breast; otherwise GV_h refers to the number of gray levels in the ROI of the right breast.

$$N{F}_{75}\left(\text{and}P{F}_{75}\right)=N_g$$

$$N{F}_{76}\left(\text{and}P{F}_{76}\right)=N_g/N_h$$

Where, N_g is the number of pixels in the ROI of higher maximum pixel value with gray values higher than the maximum pixel value of another ROI; N_h is the total number of pixels in the ROI of higher maximum pixel value. Specifically, if $P{V}_{max}^L>P{V}_{max}^R$, N_g refers to the number of pixels in the ROI of the left breast with gray values higher than $P{V}_{max}^R$ and N_h refers to the number of pixels in the ROI of the left breast; otherwise N_g refers to the number of pixels in the ROI of the right breast with gray values higher than $P{V}_{max}^L$ and N_h refers to the number of pixels in the ROI of the right breast.

From each pair of matched ROIs, the first 72 asymmetry features were independently computed for the left and right breasts. Each asymmetry feature was computed by the absolute difference of two feature values computed from the two matched ROIs. The last 4 asymmetry features were computed directly from each pair of matched ROIs.

2) Mean Features

This type includes 72 features (NF₇₇ to NF₁₄₈ (or PF₇₇ to PF₁₄₈)), which were similar to the first 72 features in type 1 (NF₁ to NF₇₂ (or PF₁ to PF₇₂)). From each of two matched ROIs of left and right breasts, each of the 72 features was independently computed. Then, the average of two values of the same feature was used to represent the mean feature.

3) Maximum Features

This type includes another set of 72 features (NF₁₄₉ to NF₂₂₀ (or PF₁₄₉ to PF₂₂₀)), which were similar to the features in type 1 (NF₁ to NF₇₂ (or PF₁ to PF₇₂)). From each of two matched ROIs of left and right breasts, each of the 72 features was also independently computed. Then, the greater one of the two values of the same feature was chosen to represent the maximum feature.

D. Risk Prediction and Performance Assessment

The mean and standard deviation of values of different features may vary widely. In order to compare different features, a normalization process was applied for each feature to normalize the values to the range of 0 to 1. Similar normalization process was applied in [17, 18]. We used two analysis approaches to assess discriminatory power of these features to predict near-term breast cancer risk. In the first approach, we split the feature data 168 times and aggregated the validation performance of all splits. In each split, data of 167 cases were used for “optimal” feature selection (redundant and uninformative features may downgrade the classification accuracy) and data of the left out 1 case was used to test discriminatory power of the “optimal” features. In the feature selection step, the cross-validation method was carried out by using a publicly available WEKA data mining and machine learning software package [28]. In the validation step, the “optimal” features of the test case were fused with 3 simple methods (taking the average, maximum, and minimum value) [29] to generate 3 new classification scores, which were used for validating the prediction performance. The feature selection and performance validation protocol is characterized by a ‘double-cross-validation-loop’: an inner selection loop and an outer validation loop [30,31]. Prediction performance of the new classification scores of all 168 cases was assessed with an area under a receiver operating characteristic curve (AUC). The AUCs were computed applying a publically available ROC curve fitting program (ROCKIT, http://www-radiology.uchicago.edu/krl/).

In the second analysis approach, we trained a “two-stage” classification scheme using WEKA. As shown in Fig. 2. In the first stage, 3 ANNs (Artificial Neural Networks) were independently trained using the 76×4 = 304 asymmetry features, 72×4 = 288 mean features, and 72×4 = 288 maximum features, respectively. In the second stage, the 3 sets of scores produced by the 3 ANNs was further fused by another ANN to derive the final risk prediction scores. For comparison, we also trained another “one-stage” ANN, which was built using the mixed pool of all three types of features.

Fig. 2.

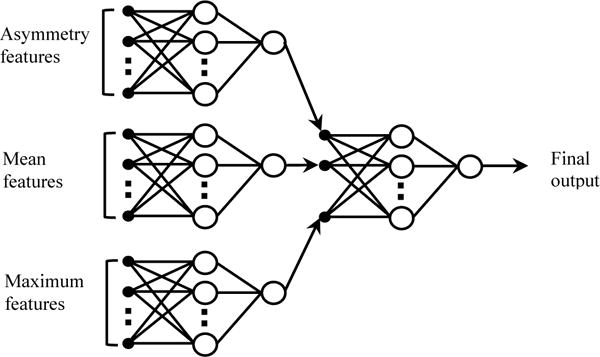
A two-stage “scoring fusion” RBFN-based ANN classification scheme, whereby the final classification score is derived by optimally fusing the prediction scores produced by 3 ANNs trained using bilateral asymmetrical features, mean features, and the maximum features, respectively. In the ANNs, the circles and black dots represent artificial neurons analogous to human neural units, the connecting lines represent links between adjacent artificial neurons analogous to neural axons.

In using WEKA, we chose the classifier of “AttributeSelectedClassifier” to integrate the normalized Gaussian Radial Basis Function Network (RBFN) as a base classifier, the wrapper subset evaluator (WSE) as a feature evaluator, and the “BestFirst” (searches the space of feature subsets by greedy hillclimbing augmented with a backtracking facility) as a feature search method. RBFN has drawn much attention due to its good generalization ability and simple network structure [32]. Past research has shown that any nonlinear function over a compact set with arbitrary accuracy can be approximated by RBFN [33]. In this study, the ANNs were trained using a leave-one-case-out (LOCO) based cross-validation method [34]. In each of LOCO training/testing iterations, 1 case was selected as an independent testing case and the remaining 167 cases were used as a training dataset. Feature selection was performed on the training dataset (redundant and uninformative features may downgrade the classification accuracy) and the selected features were then used to train a RBFN based classifier. The trained classifier was applied to the testing case to generate a risk prediction score ranging from 0 to 1. According to this validation method, in each training and testing iteration cycle, different image features may be selected from the initial feature pool and used to build a corresponding classifier.

We used AUC and prediction accuracy to compare performance of the asymmetry feature based classifier, mean feature based classifier, the maximum feature based classifier, the one-stage classification scheme, and the two-stage classification scheme. We compared the prediction accuracy on “positive”, “negative”, and all cases by applying a threshold of 0.5 on the classification scores to divide the 168 testing cases into two predicted groups.

IV. RESULTS

Table 1 compares two sets of AUCs yielded by 8 schemes. Using the previous segmentation method, AUCs ranged from 0.603±0.043 to 0.641±0.042. Using the new segmentation method, AUCs ranged from 0.603±0.043 to 0.830±0.033, which yields a significantly higher maximum AUC value (p < 0.01, t-test). Fig. 3 shows 2 sets of ROC curves generated using the classification scores yielded by 5 ANN-based classification schemes. Fig. 4 compares two ROC curves generated using the classification scores yielded by the two-stage classification scheme. By using the new segmentation methods, AUC was significantly increased from 0.633±0.043 to 0.830±0.033 (p < 0.01, t-test).

TABLE 1.

Comparison of AUC values and corresponding standard deviations of 8 different prediction schemes by using 2 dense breast region segmentation methods.

Feature fusion method	New dense breast region segmentation method	Previous dense breast region segmentation method
Scheme 1 (Taking maximum value of the selected features)	0.603±0.043	0.603±0.043
Scheme 2 (Taking minimum value of the selected features)	0.690±0.040	0.606±0.043
Scheme 3 (Taking mean value of the selected features)	0.640±0.043	0.621±0.043
Scheme 4 (one-stage classification scheme)	0.813±0.034	0.641±0.042
Scheme 5 (asymmetry feature based classifier)	0.807±0.035	0.623±0.043
Scheme 6 (mean feature based classifier)	0.657±0.043	0.603±0.043
Scheme 7 (maximum feature based classifier)	0.704±0.040	0.616±0.043
Scheme 8 (two-stage classification scheme)	0.830±0.033	0.633±0.043

Fig. 3.

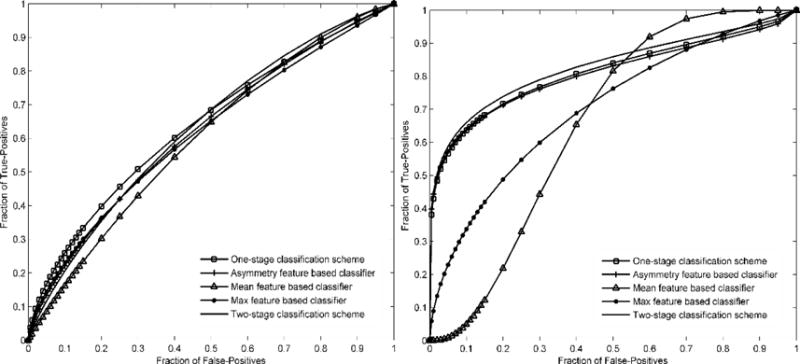
Comparison of receiver operating characteristic (ROC) curves generated by 5 breast cancer risk prediction schemes. Left and right correspond to the previous and new dense breast region segmentation methods, respectively

Fig. 4.

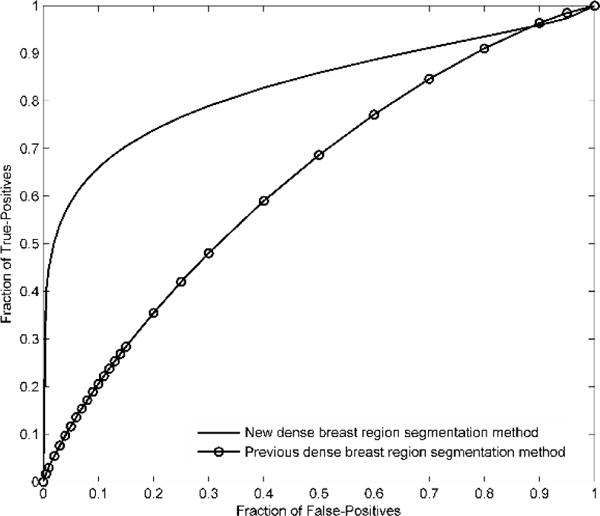
Comparison of receiver operating characteristic (ROC) curves generated by the proposed two-stage classification scheme. Two curves correspond to the previous and new dense breast region segmentation methods, respectively

Table 2 summarizes the prediction accuracy values yielded by 5 classification schemes. The right column shows 5 groups of prediction accuracy values yielded by using the previous dense breast tissue segmentation method, which are comparable with relatively low overall prediction accuracy (i.e., ≤ 60%). When using the new dense breast tissue segmentation method, the overall prediction accuracy was significantly increased (p < 0.01, t-test). For example, using the “two-stage” ANN-based classifier, it reached 81%. Table 2 also shows that the prediction accuracy for the positive cases is substantially higher than that for the negative cases (95.2% versus 67.1%).

TABLE 2.

Comparison of the overall prediction accuracy, prediction accuracy for the case groups with and without breast cancer of 5 different prediction schemes by using 2 dense breast region segmentation methods.

Feature fusion method	Overall prediction accuracy, prediction accuracy for cases with cancer, and prediction accuracy for cases without cancer (%)
	New dense breast region segmentation method	Previous dense breast region segmentation method
Scheme 4 (one-stage classification scheme)	59.5	55.9
	42.2	38.6
	76.5	72.9
Scheme 5 (asymmetry feature based classifier)	54.2	60.7
	36.1	42.2
	71.8	78.8
Scheme 6 (mean feature based classifier)	50.0	54.2
	62.7	38.6
	37.6	69.4
Scheme 7 (maximum feature based classifier)	69.0	57.1
	60.2	38.6
	77.6	75.3
Scheme 8 (two-stage classification scheme)	81.0	57.1
	95.2	60.2
	67.1	54.1

V. DISCUSION

The contribution of this study is that we successfully demonstrated that a “mutual” threshold approach could play a surprisingly important role to significantly improve performance of near-term breast cancer risk prediction.

It was demonstrated that bilateral mammographic density asymmetry was a significantly stronger breast cancer risk factor than woman’s age, and mammographic density rated or assessed based on single images by either radiologists (BIRADS) or computerized schemes [18]. Thus, this study aims to investigate a new bilateral mammographic asymmetry detecting approach with and an assumption that it can help improving near-term breast cancer prediction. The assumption is based on several underlying scientific evidences and validated experimental observations: (1) mammographic tissue asymmetry is an important radiographic image phenotype related to the biological processes [35], (2) radiologists routinely examine the bilateral mammographic tissue asymmetry pattern and change over time when making clinical decisions [36].

We observed in the literature that image features computed from the dense mammographic regions had higher discriminatory power than those computed from the whole mammographic regions. However, how to optimally segment dense mammographic regions is important, which determines the subsequently computed image features. In this study, we developed a new mammographic image segmentation approach, in which the dense breast regions of bilateral mammograms were segmented using a “mutual” threshold instead of two individual thresholds. The threshold was determined according to the pixel grayscale value distribution of the CC view images of both left and right breasts.

From our study, we can make the following observations. First, by using the new “mutual” threshold segmentation method, bilateral mammographic density asymmetry related image features can be more sensitively detected and the discriminatory power of these features can be increased.

Second, previous study reported that using the maximum features to train an ANN yielded higher performance than the ANN trained using the bilateral asymmetrical features. However, we observed in this study, by using our new segmentation approach, the ANN trained using asymmetry features yielded much higher performance than the ANNs trained using the maximum features (Table 1). Therefore, defining an optimal dense mammographic region segmentation method is important for developing an optimal near-term breast cancer risk model.

Third, we observed that asymmetry, mean, and the maximum features of two bilateral images might contain complementary information. As a result, comparing to training one large integrated ANN using all three types of features, developing a two-stage ANN based classifier that fuses the prediction outcomes of 3 ANNs, which were separately trained with 3 types of features, yielded much higher prediction performance (AUC=0.830±0.033 vs AUC=0.813±0.034). The AUC is much higher than that of 0.633±0.043 achieved by using the previous density segmentation method and those of 0.761±0.025 and 0.725±0.018 reported in [18] and [21] achieved by using image features related to bilateral mammographic asymmetry for breast cancer prediction.

Last, we also observed that by using the proposed two-stage classification scheme, the prediction accuracy for the “positive” cases was substantially higher than that for the “negative” cases (95.2% versus 67.1%). This observation indicates high sensitivity and lower specificity, which is a potentially weakness of applying this risk prediction model in the real screening environment. Thus, improving specificity is important to improve efficacy of mammography screening. This is our goal in the future.

Despite the promising results and new observations, this study is with a number of limitations. First, the size of the dataset used is small and the ratio between positive and negative cases also does not represent the actual cancer prevalence ratio. Hence, the clinical utility of our new risk model needs to be eventually tested in future large prospective studies. Second, studies have shown that age is an important breast cancer risk factor [18] and association between mammographic density and breast cancer may be weaker in women with larger breasts [37]. In this study, we didn`t incorporate age and breast size as features in our new risk model or check their influence on the prediction accuracy. We will take them into account in the future study work. Third, only RBFN based ANN was trained and tested. Other machine learning methods can be developed for this purpose too.

In summary, we tested and demonstrated a new quantitative image segmentation and feature analysis approach to more accurately detect bilateral mammographic density asymmetry, as well as to improve performance in predicting near-term breast cancer risk. The initial testing results are promising. However, the robustness of this new approach and risk prediction model needs to be further evaluated before it can be clinically acceptable to help establish a new optimal and personalized breast cancer screening paradigm.