Phosphomimetic S3D cofilin binds but only weakly severs actin filaments

Abstract

Many biological processes, including cell division, growth, and motility, rely on rapid remodeling of the actin cytoskeleton and on actin filament severing by the regulatory protein cofilin. Phosphorylation of vertebrate cofilin at Ser-3 regulates both actin binding and severing. Substitution of serine with aspartate at position 3 (S3D) is widely used to mimic cofilin phosphorylation in cells and in vitro. The S3D substitution weakens cofilin binding to filaments, and it is presumed that subsequent reduction in cofilin occupancy inhibits filament severing, but this hypothesis has remained untested. Here, using time-resolved phosphorescence anisotropy, electron cryomicroscopy, and all-atom molecular dynamics simulations, we show that S3D cofilin indeed binds filaments with lower affinity, but also with a higher cooperativity than wild-type cofilin, and severs actin weakly across a broad range of occupancies. We found that three factors contribute to the severing deficiency of S3D cofilin. First, the high cooperativity of S3D cofilin generates fewer boundaries between bare and decorated actin segments where severing occurs preferentially. Second, S3D cofilin only weakly alters filament bending and twisting dynamics and therefore does not introduce the mechanical discontinuities required for efficient filament severing at boundaries. Third, Ser-3 modification (i.e. substitution with Asp or phosphorylation) “undocks” and repositions the cofilin N terminus away from the filament axis, which compromises S3D cofilin's ability to weaken longitudinal filament subunit interactions. Collectively, our results demonstrate that, in addition to inhibiting actin binding, Ser-3 modification favors formation of a cofilin-binding mode that is unable to sufficiently alter filament mechanical properties and promote severing.

Introduction

Numerous fundamental biological processes, including cell division, growth, and motility, rely on rapid remodeling of the actin cytoskeleton and filament severing by the regulatory protein cofilin (1–3). Human cofilin binds vertebrate actin filaments cooperatively and promotes severing preferentially at or near the boundaries of bare and cofilin-decorated segments (4–7). Severing activity peaks when filaments are half-saturated with cofilin, where the density of boundaries between bare and cofilin-decorated segments is maximal (5–7).

Cofilin increases filament twist and subunit tilt (8–10) and renders filaments more compliant in bending and twisting (7, 11, 12). Mechanical and structural discontinuities within the filament lattice probably promote preferential severing at boundaries between bare and cofilin-decorated segments (5, 7, 13–15). Mechanical loads and filament strain are predicted to enhance cofilin severing activity (16, 17).

Phosphorylation of cofilin at Ser-3 by LIM kinase regulates cofilin severing activity (18–20). Phosphomimetic S3D cofilin (aspartate substitution at position 3) is used routinely to study cofilin regulation in vitro and in vivo (18–23). S3D substitution or phosphorylation weakens cofilin binding to actin filaments (21, 22, 24), and phosphocofilin or phosphomimetics localize differently to actin structures (e.g. growth cones, actin rods, and the cell leading edge (19, 23)).

Central to developing predictive models of cofilin regulation in cells is knowledge of how Ser-3 modification impacts the ability of cofilin to bind and sever actin filaments. It is generally asserted that Ser-3 modification weakens cofilin binding and that subsequent reduction in occupancy inhibits filament severing (21, 24). Such a mechanism predicts that filament severing can be achieved with higher S3D cofilin concentrations and fractional occupancies.

Here, we directly test this prediction for cofilin regulation. In agreement with previous studies (21), we find that S3D cofilin binds actin filaments more weakly than WT cofilin. However, S3D cofilin severs filaments weakly over a broad range of occupancies, indicating that compromised binding alone does not render S3D cofilin severing-deficient. Time-resolved phosphorescence anisotropy, electron cryomicroscopy, and all-atom molecular dynamics simulations favor a mechanism in which cofilin Ser-3 phosphorylation or substitution displaces the cofilin N terminus away from actin. N terminus undocking compromises the ability of bound cofilin to disrupt actin–cofilactin interfaces (e.g. boundaries) and filament mechanical properties. S3D cofilin also binds filaments with higher cooperativity than wild-type cofilin, thus lowering the bare–decorated boundary density and further lowering the overall filament-severing probability.

Results

S3D cofilin binds actin filaments more weakly than WT cofilin but with higher cooperativity

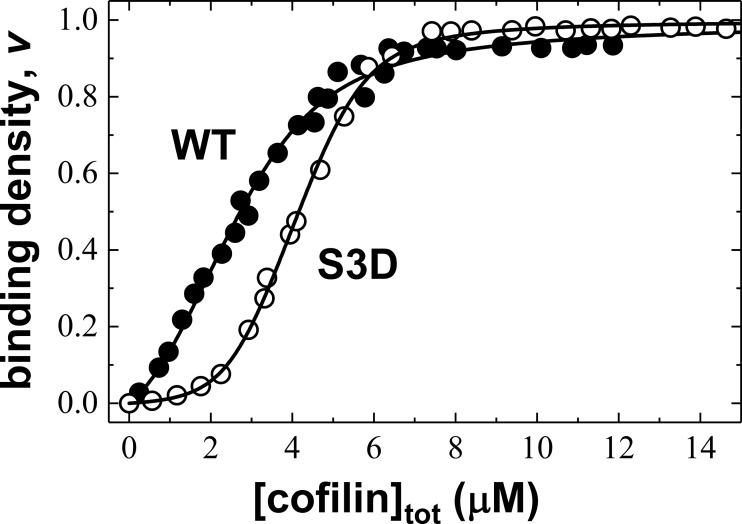
WT and S3D cofilin both quench the fluorescence intensity of pyrene-labeled actin filaments by ∼90%. Higher S3D cofilin concentrations are needed to half-saturate filaments compared with WT cofilin (Fig. 1), consistent with previous reports of S3D binding with weaker affinity than WT cofilin (21). Fitting the data to a cooperative lattice-binding model (Equations 2 and 4 and Table 1) indicates that S3D cofilin binds actin filaments with a ∼15-fold lower intrinsic binding affinity than WT cofilin (K_d = 10 ± 2 and 154 ± 20 μm for WT and S3D, respectively) but with ∼10-fold higher cooperativity (ω = 5 ± 1 and 47 ± 6 for WT and S3D, respectively).

Figure 1.

S3D cofilin binds actin filaments with lower affinity but higher cooperativity than WT cofilin. Shown are equilibrium binding titrations of WT (black circles) or S3D (white circles) cofilin and pyrene-labeled actin filaments. The solid lines through the data represent the best fits to Equations 2 and 4.

Table 1.

Cofilin binding and severing parameters

Uncertainties are S.D. from fitting. 0 uncertainty indicates that parameters were constrained during fitting.

Cofilin	Binding parametersa		Severing parametersb
	Kd	ω	k′dc	k′sc	k′iso
	μm		s−1	s−1	s−1
WT	9.7 ± 2.0	5.3 ± 1.1	0.35 ± 0.51	17.3 ± 3.5	4.6 ± 6.7
S3D	154.1 ± 20.3	47.3 ± 6.2	0.48 ± 0.15	4.2 ± 1.2	0

^a From fits to Equations 2 and 4 (Fig. 1) with the value of ω unconstrained.

^b From fits to Equation 1 (Fig. 4A) with the value of ω constrained to 5 and 47 for WT and S3D cofilin, respectively.

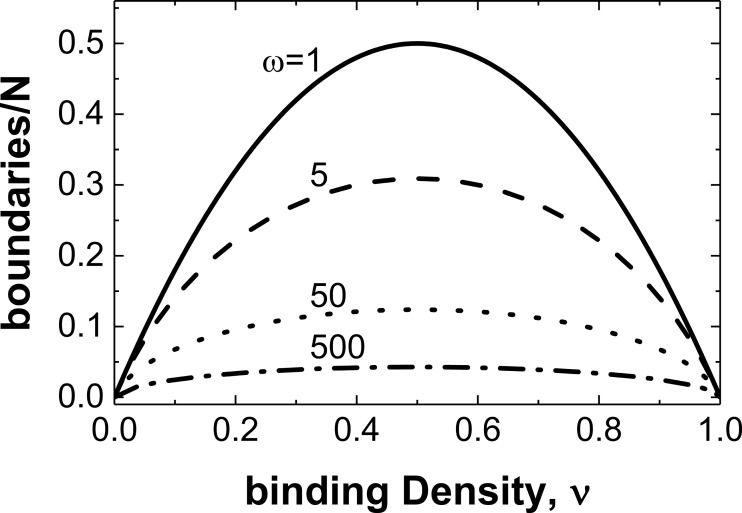
The cluster size of bound cofilin along filaments depends on binding density and cooperativity (4, 25, 26). The higher positive cooperativity of S3D cofilin means it will form larger clusters along filaments than WT cofilin over most binding densities and thus generate fewer boundaries between bare and decorated segments. It also predicts a 3-fold reduction in average boundary density at half-occupancy, compared with WT cofilin (Fig. 2). We note that ligands that bind with no cooperativity and decorate lattices randomly have the highest probability of introducing boundaries (Fig. 2).

Figure 2.

A higher S3D binding cooperativity reduces the number of boundaries between bare and cofilin-decorated segments. The boundary density calculated using Equation 5 is plotted against binding density for ligands that bind non-cooperatively (ω = 1, solid line) and cooperatively with ω = 5 (dashed line), 50 (dotted line), or 500 (dashed-dotted line). Note that the boundary density is symmetric and peaks at 50% occupancy (ν = 0.5).

WT and S3D cofilin binding to actin filaments is linked to cation release

WT cofilin binding to actin filaments is salt-dependent and coupled to the release of filament-associated cations (14, 27–29). Cation release contributes to the overall cofilin binding energetics (27), changes in filament mechanical properties (30), and cofilin severing efficiency (14). Cooperative interactions, in contrast, are independent of solution salt concentration and not coupled to cation release (27, 29).

S3D cofilin binding to actin filaments is also salt-dependent and coupled to cation release (Fig. 3 and Table 2). S3D cofilin binding dissociates ∼1 Mg²⁺ or ∼2 K⁺ from actin, similar to WT cofilin (27). Salts minimally affect cooperativity of S3D cofilin binding. These results indicate that the release of filament-associated cations associated with cofilin occupancy is local in nature and similar for S3D and WT cofilin. We note that the melting temperature of cofilin depends weakly on solution salt concentration (supplemental Fig. S1 and Table 3), consistent with the interpretation that cofilin–cation interactions in solution are weak and that released cations originate from the actin filament surface.

Figure 3.

S3D binding affinity but not cooperativity is linked to cation release. A, binding titrations of S3D (from left to right) in 10 (squares), 25 (circles), 50 (upright triangles), 75 (diamonds), or 100 mm KCl (rightward triangles). B, binding titrations of S3D (from left to right) in 0.5 (squares), 2 (circles), or 5 mm MgCl₂ (triangles). The smooth lines though data in A and B are fits to Equations 2 and 4. C and D, the KCl and MgCl₂ concentration dependence of the intrinsic S3D cofilin binding affinity (K_d) (C) and binding cooperativity (ω) (D) obtained from the fits to Equations 2 and 4 in A and B. KCl and MgCl₂ dependence of K_d in C yields slopes of −1.9 ± 0.6 and −1.4 ± 0.2, respectively, corresponding to dissociation of ∼2.3 K⁺ or ∼0.9 Mg²⁺ with S3D binding (see Ref. 27 for details on calculations). These values compare with the number of ions released with WT cofilin binding (Table 2) (27). In D, S3D cofilin binding cooperativity depends weakly on the solution salt concentration, similarly to WT cofilin (27).

Table 2.

Number (n) of monovalent (K⁺) and divalent (Mg²⁺) cations released with cofilin binding to actin filaments determined from the salt concentration dependence of the intrinsic binding constant (K_a) and cooperativity parameter (ω)

Uncertainties are from linear fits (Fig. 3).

Cofilin	n (Ka)	n (ω)
S3D	2.3 ± 0.7 K+	∼0
	0.9 ± 0.1 Mg2+	∼0
WT	1.7 ± 0.2 K+	∼0
	0.7 ± 0.1 Mg2+	∼0

Table 3.

Melting properties of WT and S3D cofilin at various KCl concentrations

Parameters are from the best fits of the data shown in supplemental Fig. S1 to Equation 7. All S.D. values from the best fits are smaller than half of the last decimal position digit, so they are not presented.

Cofilin	KCl	Tm	ΔH0′u	ΔCpo′u	θn	θu
	mm	oC	kJ mol−1	kJ mol−1 T−1	degree cm2 mol−1	degree cm2 mol−1
WT	25	60.6	212.5	1.3	−64.8	−4.1
	50	61.1	95.6	0.6	−67.1	0.1
	100	62.1	102.3	0.6	−61.8	0.1
S3D	25	62.6	348.2	2.1	−61.6	−11.3
	50	59.5	146.5	0.9	−61.7	−2.9
	100	62.4	122.1	0.7	−61.7	0.1

S3D cofilin weakly severs actin filaments over a broad range of binding densities

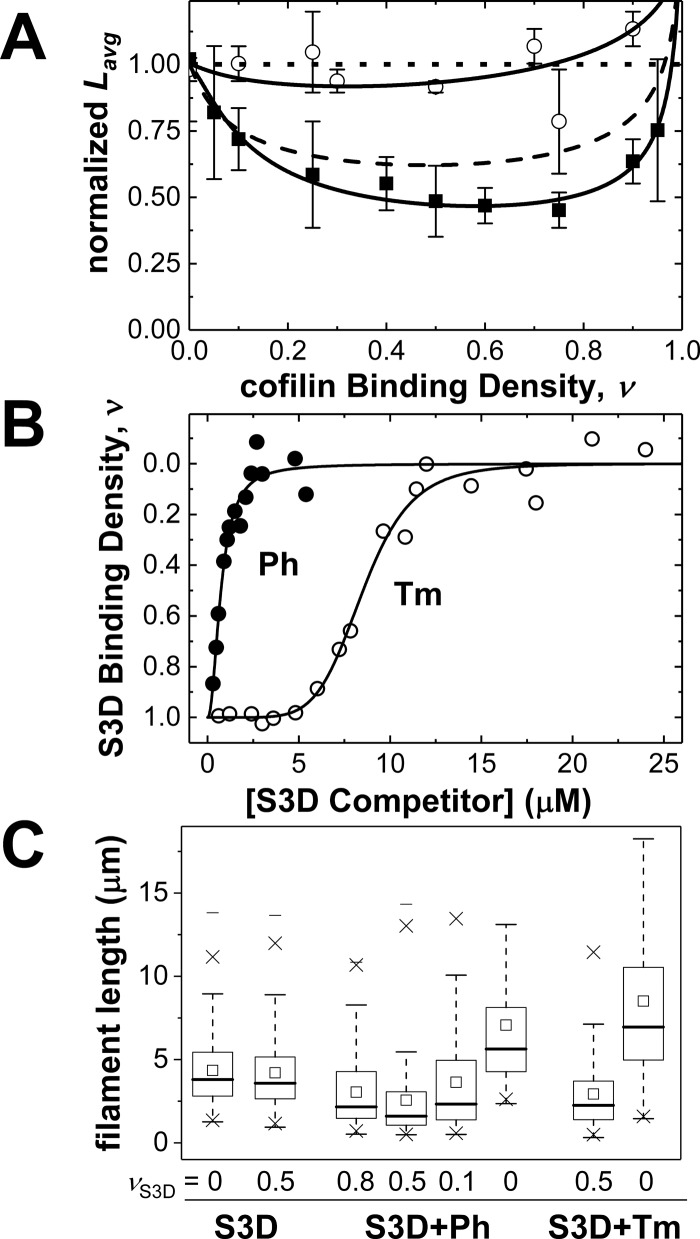
The actin filament-severing activity of cofilin was measured over a range of binding densities by comparing the average actin filament length in the presence and absence of cofilin(Fig. 4A and Table 4). Little change in average actin filament length was detected at any of the S3D cofilin binding densities investigated (range ν = 0–0.9; Fig. 4A). Even near half-occupancy (ν = 0.5), where WT cofilin-mediated severing activity is highest, very little severing by S3D cofilin is observed (Fig. 4A). Similar behavior was observed with non-muscle βγ actin filaments (L/L_avg = 0.91 ± 0.07 and 0.93 ± 0.05 at ν = 0.5 and 0.9, respectively), indicating a lack of actin isoform dependence.

Figure 4.

S3D cofilin severs weakly and inclusion of competitors enhances severing activity. A, normalized equilibrium average lengths (L_avg) of Alexa-labeled actin filaments at various WT (black squares) or S3D (white circles) binding densities, n ≥ 200 per condition. Solid black lines though WT and S3D cofilin binding data represent fits of the data to a discrete, site-specific severing model (Equation 1) (14) with fixed cooperativity values of ω = 5 and 47, respectively. The top horizontal dotted line with the value L_avg = 1 denotes average length of bare actin filaments. The dashed black line shows a simulation of average filament lengths (Equation 1) with WT cofilin apparent severing rate constants but with S3D cooperativity (ω = 47), demonstrating that the increased cooperativity alone cannot account for S3D severing deficiency. Error bars, S.E. B, binding competition of phalloidin (black circles) or non-muscle tropomyosin Tpm3.1 (white circles) with S3D for pyrene-labeled actin filaments. Smooth lines though data are fits to the Hill equation and are strictly for visualization purposes. C, equilibrium mean lengths (open squares in boxes) of Alexa-labeled actin filaments that are either bare, half-decorated with S3D cofilin, or partially decorated with S3D cofilin and a competitor (Tm or Ph). Equilibrium distribution of filament lengths (n ≥ 200) is indicated by a 25 or 75% marker (horizontal line) connected by vertical dashed lines. The marker × indicates percentile 1 or 90, whereas the floating marker (heavy horizontal line) represents the maximum or minimum of filament length.

Table 4.

Filament mechanical flexibility properties

Uncertainties are S.D. from fitting.

	Filament bending persistence length Lpa	Intersubunit torsional rigidity Csubb	Intersubunit torsional constant αc
	μm	newtons m2 radians−1	newtons m2 radians−1
Bare	8.3 ± 0.4	1.09 ± 0.07 × 10−27	3.95 ± 0.26 × 10−19
WT	2.6 ± 0.3	0.21 ± 0.05 × 10−27	0.75 ± 0.02 × 10−19
S3D	6.3 ± 1.2	1.26 ± 0.17 × 10−27	4.60 ± 0.63 × 10−19

^a From cosine correlation analysis of filaments (Eq. 6).

^b Calculated from C_sub = αh, assuming a subunit height (h) of 2.75 nm (12).

^c From model-dependent analysis of phosphorescence anisotropy decay in Fig. 5 (12).

The weak severing activity of S3D relative to WT cofilin could potentially arise from the reduction in boundary density due to higher cooperativity (3-fold reduction at half-occupancy; Fig. 2). If we assume that S3D cofilin has the same severing rate constants as WT cofilin at equivalent occupancies (i.e. weak severing results entirely from the reduction in bare–decorated boundary density), lowering the boundary density 3-fold (S3D versus WT cofilin) has only a small effect on the average filament length (24% reduction in average filament length at half-occupancy; Fig. 4A, dashed line). Accordingly, the severing rate constants of S3D cofilin must differ from those of WT cofilin.

S3D cofilin severs at boundaries more slowly than WT cofilin

The equilibrium average filament length, L_avg, is determined by the balance of filament severing and reannealing. The average filament length data of WT and S3D cofilin were analyzed with a “site-severing model” (14) that explicitly accounts for the four different classes of severing sites along filaments: within (a) bare and (b) cofilin-decorated segments as well as at (c) boundaries of bare and cofilin-decorated segments and (d) isolated (e.g. non-contiguous) bound cofilin sites. According to this model, the average filament length depends on the cofilin binding density (ν) and cooperativity (ω) according to the following expression (14),

$$L_{\text{avg}}=\frac{L_{\text{avg},\text{spon}}}{\sqrt{k{\prime }_{\text{dc}}\nu {\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^2+k{\prime }_{\text{sc}}\frac{\left(R-1\right)(1-2\left(1-\omega \right)\nu -R)}{2\nu {\left(\omega -1\right)}^2}+k{\prime }_{\text{iso}}\frac{{\left(R-1\right)}^2}{4\nu {\left(\omega -1\right)}^2}+1-\nu }}$$ (Eq. 1)

where R = $\sqrt{{\left(1-2\nu \right)}^2+4\omega \nu \left(1-\nu \right)}$, L_avg,spon is average filament length of bare actin, and k′_dc, k′_sc, and k′_iso are the rate constants (relative to the intrinsic severing rate constant of bare actin) for severing at cofilins bound in a doubly contiguous (i.e. within a bound cofilin cluster $\begin{array}{c}\text{dc}\\ \downarrow \\ \dots •••\dots \end{array}$), singly contiguous (at edge of bound cofilin cluster $\begin{array}{c}\text{sc}\\ \downarrow \\ \dots ○••\dots \end{array}$ or $\begin{array}{c}\text{sc}\\ \downarrow \\ \dots ••○\dots \end{array}$), or isolated (non-contiguous $\begin{array}{c}\text{iso}\\ \downarrow \\ \dots ○•○\dots \end{array}$) binding mode, respectively. The best fits of the WT and S3D cofilin data to Equation 1 (smooth lines through data in Fig. 4A) indicate that severing at boundaries between bare and S3D cofilin-decorated segments occurs >4-fold more slowly than at bare–WT cofilin boundaries (Table 1, k_sc). Therefore, the observed severing deficiency of S3D cofilin originates from a slower severing rate constant at boundaries as well as a reduction in overall boundary density.

We note that the isolated WT cofilin severing rate constant is estimated to be ∼5-fold more rapid than the spontaneous fragmentation of bare actin and that isolated S3D cofilin is predicted to have little or no severing activity (Table 1, k_iso). However, because the population of isolated bound cofilin molecules comprises <7% of potential severing sites at all WT and S3D cofilin binding densities, the net contribution to severing from isolated cofilin is negligible. Accordingly, the best fit of the WT cofilin data to Equation 1 constraining k_iso = 0 is essentially identical to fits allowing k_iso to float unconstrained.

In addition to this “site-severing model,” we evaluated an “interface-severing model” (see “Appendix” for derivation; supplemental Fig. S2) that explicitly accounts for the three different classes of protein interfaces: adjoining (a) two unoccupied, bare actin filament sites (i.e. actin–actin interface), (b) two bound cofilin sites (i.e. cofilactin–cofilactin interface), and (c) a bare actin–cofilactin site (i.e. boundary). The only difference between these two microscopically distinct models is how the number of severing sites associated with an isolated, non-contiguously bound cofilin is counted. The site-severing model considers isolated cofilactin to be a single severing site, whereas the interface-severing model treats an isolated, bound cofilin as two potential severing interfaces: one to the left and another to the right. Fitting of the experimental data to both models predicts that severing occurs most readily at boundaries (supplemental Table S1). The site-severing model, however, accounts for the experimental data better than the interface model, particularly at low and high cofilin occupancies (supplemental Fig. S2), presumably because it does not overcount potential contributions from isolated cofilins.

Severing occurs more readily at boundaries between bare and cofilin-decorated segments than within bare or decorated segments (5–7, 14–17, 31, 32). Thus, the severing activity of cofilin is proportional to and dominated by the boundary density. Recent imaging studies suggest that clusters of bound cofilin must reach a critical size to sever filaments and that small clusters of bound cofilin (n < 13 (33), n < 23 (34), or n < 100 (32)) do not sever filaments. If this were the case, the cofilin binding density dependence of the severing-competent boundary density would be markedly asymmetric and not reach a maximum at ∼50% occupancy (supplemental Fig. S3). Accordingly, the overall filament-severing activity would peak at cofilin binding densities considerably greater than 0.5 if the critical cluster size for severing is >2, in contrast to what is observed here (Fig. 4) and reported previously by several groups (5–7, 30, 31, 35, 36). Rather, there will be little or no observed severing or change in filament length at low cofilin occupancies (supplemental Fig. S3). Therefore, the data presented here favor a mechanism in which the minimal cofilin cluster size required for severing is small (n ≤ 3 bound cofilins), as previously suggested (4, 5, 7, 35, 36).

Cofilin competitors promote filament severing by S3D cofilin

We hypothesized that the addition of competitors that randomly displace S3D cofilin could promote S3D cofilin-mediated actin filament severing by introducing more boundaries (31). To test this hypothesis, two cofilin competitors, phalloidin and tropomyosin Tpm3.1, were titrated into pyrene-labeled actin filaments saturated with S3D cofilin.

Bound S3D cofilin quenches pyrene actin filament fluorescence (Fig. 1), and displacement of bound S3D cofilin by phalloidin or Tpm3.1 recovers the fluorescence (Fig. 4B). Less phalloidin than Tpm3.1 is needed to displace bound S3D cofilin, indicating that it binds with higher affinity (37, 38). The sigmoidal shape of the Tpm3.1 competition data indicates that Tpm3.1 binds actin with strong positive cooperativity.

Competitive displacement of bound S3D cofilin to partial occupancy with either phalloidin or Tpm3.1 was sufficient to enhance the filament-severing activity of S3D cofilin (Fig. 4C). The highest severing activity (i.e. shortest filaments) was observed at an S3D binding density of 0.5 (calculated from the pyrene fluorescence). Neither phalloidin nor Tpm3.1 alone had any actin filament-severing activity over a range of occupancies. Rather, the addition of either competitor alone resulted in longer actin filaments (Fig. 4C), consistent with stabilization (39, 40). Therefore, the simplest interpretation of these data is that competitive displacement of S3D cofilin enhances filament severing by increasing the number of boundaries. This may explain, at least partially, why Tpm3.1 is inefficient at protecting filaments from cofilin (41), although both compete for actin binding.

S3D cofilin weakly affects filament bending and twisting dynamics

WT cofilin increases the actin filament bending flexibility much more than S3D cofilin (Table 4). The bending persistence length L_p of WT cofilin–decorated filaments measured here is 2.6 ± 0.3 μm (Table 4), consistent with previous determinations (7, 11, 14, 17, 42). The bending L_p of S3D cofilin-decorated (ν > 0.9) filaments (6.3 ± 1.2 μm) is comparable with that of bare actin filaments (8.3 ± 0.4 μm; Table 4).

WT cofilin also increases the actin filament intersubunit torsional flexibility (12, 17) much more than S3D cofilin (Table 4). The filament intersubunit torsional constants (α) estimated from the phosphorescence anisotropy decays (Fig. 5) using model-dependent analysis (12) indicate that bare and S3D cofilin–decorated actin filaments have similar intersubunit torsional constants, within uncertainty (Table 4), that are much stiffer than that of WT cofilin–decorated actin filaments.

Figure 5.

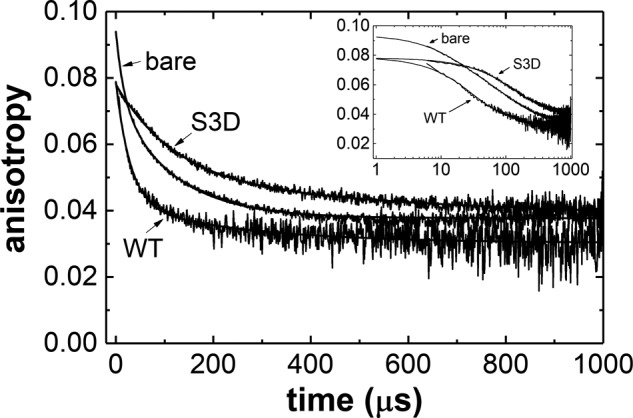
S3D decoration weakly affects actin filament torsional dynamics. Shown are phosphorescence anisotropy decays for ErIA-labeled actin, WT-decorated (ν ∼0.9), and S3D-decorated (ν ∼0.9) fitted to a double exponential (smooth lines through data). Fit residuals are 1–2% of signal, and the fitting parameters are listed in Table 5. The inset shows data in log scale to reveal differences at early time scales. A model-dependent analysis (12) of the anisotropy decays was also performed to calculate the filament intersubunit torsional constant α and torsional rigidity C (Table 4).

Time courses of filament (bare, WT cofilin–decorated, and S3D cofilin–decorated) phosphorescence anisotropy decays are well-fitted to a sum of two exponentials (Fig. 5). The initial anisotropy (r₀) values of both WT- and S3D-decorated actin filaments are comparable and significantly lower than that of bare actin (Fig. 5 and Table 5), indicating more rapid submicrosecond rotational motions of the actin C terminus with (WT or S3D) cofilin binding, consistent with previous observations made with WT cofilin (12). A final anisotropy value (r_∞) greater than zero represents a chromophore with rotational motion constrained during the lifetime of phosphorescence decay (43, 44). The final anisotropy values of bare and S3D-decorated filaments are notably larger than those of WT cofilin–decorated filaments (Fig. 5), suggesting that the actin C terminus (where the chromophore is conjugated) is more dynamic with bound WT cofilin than when bare and decorated with S3D cofilin.

Table 5.

Phosphorescence anisotropy decay parameters

All uncertainties are S.D. from the sum of exponential fits. If an uncertainty value is absent, it is beyond the last decimal position and therefore omitted.

Anisotropy decay model-independent analysis: sum of exponentialsa	Bare	WT	S3D
r0	0.094 ± 0.002 (100%)	0.079 ± 0.003 (84%)	0.078 ± 0.005 (83%)
r∞	0.038 (40%)	0.030 (32%)	0.036 ± 0.004 (38%)

^a Total phosphorescence anisotropy decays after a 5-μs dead time were fitted to a double exponential in the form r(t) = r₁ e^−t/φ1 + r₂ e^−t/φ2 + r_∞ to obtain the initial r₀ = r₁ + r₂ + r_∞ and final r_ω anisotropy values at time infinity. The percentage in parenthesis is relative to the initial total anisotropy value of bare actin filaments.

S3D cofilactin has a structure similar to that of WT cofilactin

At large scale, the structure of S3D cofilactin filaments determined by electron cryomicroscopy to 8.1 Å resolution (supplemental Fig. S4) is essentially identical to that of WT cofilactin filaments (Fig. 6; 8.5 Å resolution, supplemental Fig. S4) and previously reported WT cofilin 2–decorated actin filaments (10). The filament twist and subunit tilt are indistinguishable between the structures, and S3D cofilin is bound in the same position as WT cofilin, where it disrupts a discrete, filament-specific cation-binding site (Fig. 3 and Table 2) (14, 28, 30).

Figure 6.

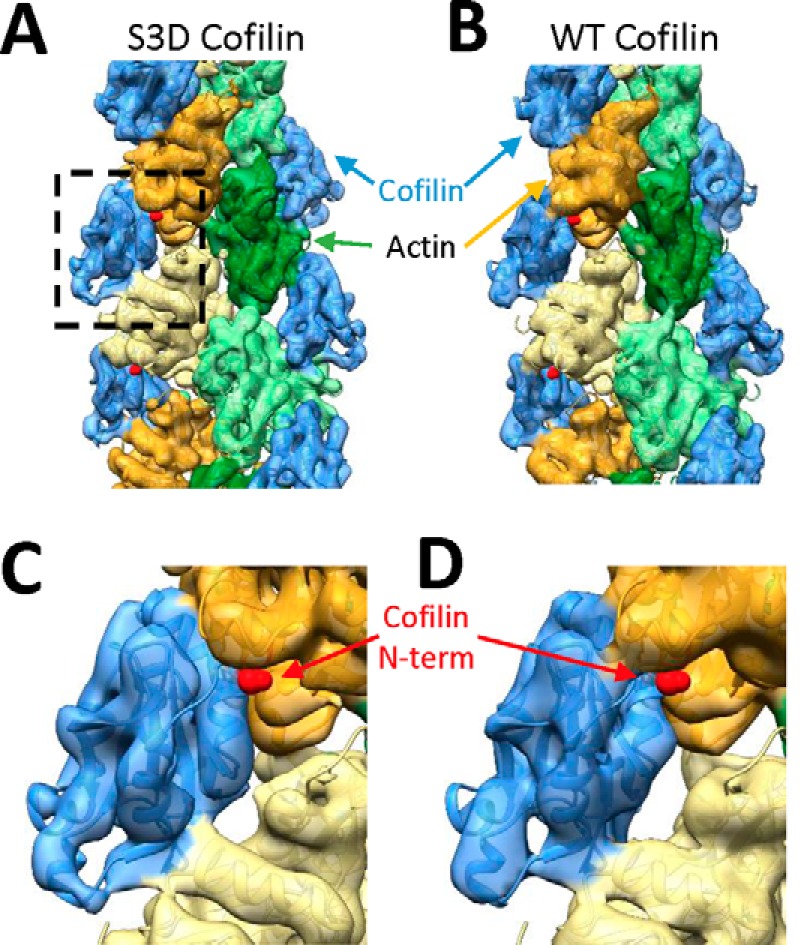
Wild-type cofilin– and S3D cofilin–decorated actin filaments adopt similar structures. A and B, electron cryomicroscopy structure of S3D cofilin–decorated (A) or WT cofilin–decorated (B) actin filaments overlaid with an atomic WT cofilin–decorated actin filament model (Protein Data Bank code 3J0S) (10). Cofilin is colored blue, and actin subunits are colored green or yellow. C and D, close-up view of a single cofilin subunit (WT, S3D) with the N terminus of cofilin indicated with a red arrow.

Structural similarity between S3D- and WT-decorated actin filaments suggests that large-scale changes in intersubunit surface area and filament twist between bare and cofilin-decorated actin do not drive changes in filament mechanical properties or severing. Rather, local structural changes are more likely to drive alterations in filament mechanics and severing by WT cofilin.

Ser-3 modification repositions the cofilin N terminus away from actin

All-atom molecular dynamics simulations reveal that the S3D substitution or Ser-3 phosphorylation compromises the interaction of the cofilin N terminus with actin. Specifically, modifying cofilin Ser-3 introduces a steric clash in the cofilactin structure and displaces the five N-terminal cofilin residues from a small cleft in the actin filament lattice. These residues are repositioned an average of 2–3 Å from their binding position on the adjacent actin observed in the WT cofilactin structure (Fig. 7 and supplemental Movies S1 and S2). This shift in cofilin N-terminal interactions is not observed with WT cofilin. In addition to this increase in average distance, the variance of this coordinate increases substantially upon modification of Ser-3 (Fig. 7), reflecting a weaker association. Little to no change occurs in other regions of cofilin or in the actin filament, consistent with the lack of large-scale changes between S3D and WT-decorated filaments obtained by cryo-EM (Fig. 6). The resolution of the cryo-EM structure does not distinguish changes at this level comprising the first three amino acids of cofilin (these residues are disordered in cofilactin cryo-EM structures).

Figure 7.

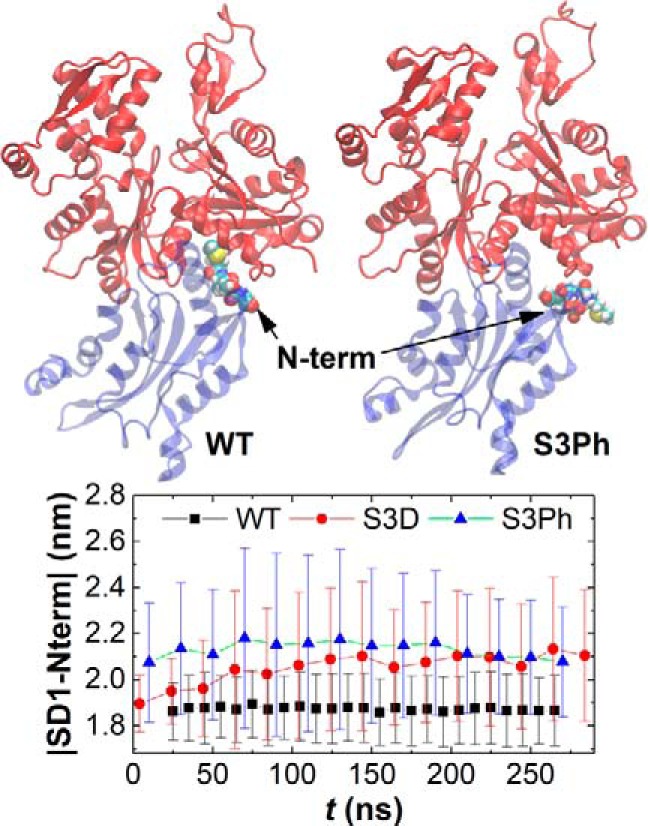
Serine 3 modification repositions the cofilin N terminus away from the filament. Top, isolated single cofilactin interface from MD simulation of a cofilactin filament (11 actin filament subunits with 11 bound cofilin molecules). Actin is colored red, whereas cofilin is colored blue with N-terminal residues 1–4 shown as space-filling models. Bottom, time course of the distance in average position of the four cofilin N-terminal residues from the center of actin subdomain 1, as observed in MD simulations. The WT cofilin N terminus remains docked to the adjacent actin subunit, but either mutation of Ser-3 (S3D) or phosphorylation (S3Ph) compromises this docking, as indicated by the increased distance between the cofilin N terminus and actin subdomain 1. See also supplemental Movies 1 and 2.

The greater variance in observed position of the mutant and phosphocofilin (Fig. 7) N-terminal residues suggests that Ser-3 modification is associated with a more dynamic N terminus. The variance lies within the starting (e.g. “docked”) N terminus position, suggesting that it reflects a dynamic process. Moreover, undocking of cofilin's N terminus from the filament surface could be dynamically coupled to a small rotation of bound cofilin and reorientation of the cofilin F-loop (Fig. 7 and Ref. 45). This may contribute to the observed differences in binding affinity, cooperativity, and severing activity. However, rotation of F-loop in the MD simulations appears to be quite small (Fig. 7 and supplemental Movies S1 and S2).

Discussion

Effects of cofilin Ser-3 modification on actin filament-binding interactions

S3D cofilin binds actin filaments ∼15-fold more weakly than WT cofilin (Table 1). Residues Ser-3, Gly-4, and Val-6 of the WT cofilin-2 N terminus form part of the cofilin–actin filament interface (46, 47). The S3D substitution or Ser-3 phosphorylation introduces a steric clash that dissociates and repositions the cofilin N terminus away from actin (Fig. 7), thereby reducing the total number of actin–cofilin interface contacts and weakening the intrinsic cofilin binding affinity (Table 1). When bound, however, S3D cofilin alters the filament twist and subunit tilt similar to WT cofilin (Fig. 6), indicating that these conformational changes are tightly coupled to cofilin occupancy (but not changes in filament mechanics or severing, discussed below).

S3D cofilin binds filaments with ∼10-fold higher cooperativity than WT cofilin (Table 1). The higher cooperativity of S3D cofilin reflects a larger and more favorable (i.e. more negative) cooperative free energy (ΔG⁰′_coop = −RT lnω), which yields larger clusters of bound cofilin along filaments and thus fewer boundaries between bare and decorated segments than WT cofilin (Fig. 2). Because bound cofilin molecules do not directly interact (8–10), cooperative cofilin binding interactions (i.e. the value of ω) must be mediated through cofilin-induced conformational changes in the actin filament (4). This relationship implies that the actin conformational change coupled to cooperative cofilin binding must differ between S3D and WT cofilins. Given that the structures of S3D cofilin– and WT cofilin–decorated filaments are indistinguishable at our resolution (Fig. 6), the differences in actin conformation accounting for the higher cooperativity are probably small and/or located in the bare–decorated boundary region. We cannot eliminate the existence of long-range allosteric effects contributing to cooperative cofilin binding (29) and the possibility that larger S3D cofilin clusters propagate allosterically further than WT cofilin clusters.

Role of the cofilin N terminus in modulating actin filament mechanical properties

S3D cofilin binding weakly affects actin filament mechanical properties (Table 4), in contrast to WT cofilin, which renders filaments more compliant in bending and twisting. Both WT and S3D cofilins change the (average) filament twist and subunit tilt in a similar manner, within our resolution (Fig. 6). Thus, twist and tilt changes do not account for the enhanced filament bending and twisting compliance (or severing, discussed below) associated with WT cofilin occupancy.

The most significant structural difference between S3D and WT cofilactin filaments is the repositioning of the cofilin N terminus away from actin with Ser-3 substitution or phosphorylation (Fig. 7). Insertion of the WT cofilin N terminus into the actin SD1-SD3 cleft probably compromises filament intersubunit contacts and interface stiffness, causing filaments to bend and twist more easily (17). Accordingly, unbinding of the cofilin N terminus with Ser-3 modification presumably accounts for the reduced ability of S3D cofilin to affect filament mechanical properties.

It has been suggested that the linked dissociation of a filament-specific cation by WT cofilin drives changes in filament mechanics and subsequent severing (14). However, the analysis presented here demonstrates that S3D cofilin binding dissociates filament-associated cations similar to WT cofilin but minimally alters filament mechanics and severs them weakly (Tables 1, 2, and 4). Therefore, ion release per se is not the sole source for alterations in filament mechanical properties (or severing, discussed below). Cofilin must also intercalate its N terminus to compromise filament intersubunit interactions and enhance overall filament bending and intersubunit twisting.

Effects of Ser-3 modification reveal factors contributing to cofilin-severing efficiency

S3D cofilin severs filaments more weakly than WT cofilin over a broad range of binding densities (Fig. 4 and Table 1). This behavior is accounted for by three factors identified in this study: (a) the higher cooperativity of S3D cofilin binding, (b) the weak effect of S3D cofilin on filament mechanical properties, and (c) repositioning of the S3D cofilin N terminus away from the longitudinal actin subunit interface. Because S3D cofilin changes the filament twist and subunit tilt in a manner similar to WT cofilin (Fig. 6), we can conclude that neither the changes in filament compliance nor severing result from changes in filament twist or subunit tilt.

S3D cofilin binds filaments with 10-fold higher cooperativity than WT cofilin (Fig. 1 and Table 1) and will therefore generate larger clusters of bound cofilin and 3-fold fewer boundaries between bare and cofilin-decorated segments (Fig. 2), at which severing occurs preferentially (5–7). Thus, cooperative binding compromises net cofilin severing activity. Inclusion of the competing ligands phalloidin and tropomyosin introduces additional boundaries and partially recovers the severing activity of S3D cofilin (Fig. 4).

Previous works demonstrate that a mechanical discontinuity (i.e. steep mechanical gradient) is necessary for severing at and near boundaries between bare and cofilin-decorated actin segments (11, 14, 16, 17). S3D cofilin weakly affects filament bending and twisting mechanical properties (Fig. 5 and Table 4), so S3D cofilin occupancy introduces a minimal mechanical discontinuity, and severing efficiency is compromised, relative to WT cofilin.

Boundaries between bare and cofilin-decorated segments rupture at smaller deformations than those needed for severing within a bare or cofilactin filament segment (7, 16, 17). In other words, boundaries fragment more easily than uniform (actin or cofilactin) segments, analogous to the adhesive joint failure of non-protein materials (5, 13). The fragmentation rate constant at boundaries is ∼4-fold more rapid with WT cofilin than with S3D cofilin (Table 1). We favor an interpretation where insertion of the cofilin N terminus between actin filament subunits weakens longitudinal intersubunit contacts at boundaries, which lowers the interaction free energy and renders boundaries more vulnerable to fragmentation. Because severing is the essential function of cofilin in cells (14), the critical role played by the cofilin N terminus in severing explains why its deletion yields a lethal phenotype in yeast (48).

The conformation of the WT cofilin N terminus is probably variable, such that inserted (“docked”) and free (“undocked”) modes exist in a reversible equilibrium while cofilin remains bound to actin. These docked and undocked binding modes may correspond to the two cofilactin-binding modes identified in kinetic analysis (49), time-resolved spectroscopy (12), and visualization of single filament fragmentation events (7). If this is the case, then the microscopic severing rate constants reported here (Table 1) and previously (14) represent composite rate constants that depend on the lifetime of the “docked” conformation. In other words, a kinetic competition between severing and N terminus undocking controls the overall severing activity. Consequently, factors that shift the distribution of docked and undocked modes and/or alter the lifetime of the docked conformation can greatly influence severing. Such a mechanism may partially explain how some Aip1 isoforms enhance the observed severing activity of cofilin (50–53). Similarly, filament shape deformations driven by thermal or applied external forces may influence cofilin N terminus docking and subsequent severing (7, 13, 15–17).

Based on the results of this study, we conclude that the severing activity of cofilin is largely attributable to the insertion of its N terminus into actin filaments, which weakens longitudinal intersubunit contacts at boundaries and changes the dynamic bending and twisting mechanical properties of actin filaments in cofilin-decorated regions. Whereas the changes in filament mechanics appear to be necessary for severing, they are not sufficient.

Materials and methods

Protein expression, purification, and labeling

All buffer chemical reagents were of the highest purity commercially available and purchased from American Bioanalytical or Sigma-Aldrich. Actin was purified from rabbit back and leg muscle; labeled with pyrenyl-iodoacetamide (efficiency >0.9), erythrosine ErIA, Alexa-488, or Alexa-594-succimidyl ester (efficiency ∼0.3) (Molecular Probes); and gel-filtered over an S-300 gel column (0.2 mm ATP, 0.1 mm CaCl₂, 0.5 mm DTT, 1 mm NaN₃, 2 mm Tris-HCl, pH 8.0, 4 °C) (12, 14, 30). Actin monomers were converted to Mg²⁺-actin on ice by the addition of 0.2 mm EGTA and 20–80 μm MgCl₂ and then polymerized with 0.1 volume of 10× polymerizing buffer (500 mm KCl, 20 mm MgCl₂, 100 mm imidazole, pH 6.8 (KMI buffer)) supplemented with freshly dissolved DTT (1 mm final) (4). Non-muscle actin (∼85% β-actin, 15% γ-actin from human platelets) was purchased from Cytoskeleton. Recombinant human non-muscle cofilin 1, WT, and the phosphomimetic S3D were expressed and purified from E. coli as described for WT cofilin (4), and final concentrations were determined spectroscopically (54). Recombinant human tropomyosin Tpm3.1 (55) was purified as described (56). A 1 mm phalloidin stock (Thermo Scientific) was prepared in methanol. Experiments were carried out in KMI buffer at pH 6.8 for internal consistency and comparison with our previous studies (4, 27) and because some cofilin isoforms sever but do not depolymerize filaments under these conditions (57).

Equilibrium binding assays

WT and S3D cofilin binding to pyrene-labeled actin filaments was assayed by fluorescence (λ_ex = 366 nm, λ_em = 407 nm, 25 °C) using a SpectraMax Gemini XPS plate reading fluorimeter (Molecular Devices) or a PTI fluorimeter (4, 27, 31). Cofilin binding densities were calculated from the fit of the observed [cofilin]-dependent fluorescence intensities (4, 27, 31). The observed pyrene-actin filament fluorescence intensity (F) scales linearly with cofilin occupancy, expressed as the binding density (ν), such that the following is true,

$$F=F_0+\left(F_{\infty }-F_0\right)\nu$$ (Eq. 2)

where F₀ and F_∞ are the bare and cofilin-decorated pyrene-actin filament fluorescence values. The cofilin binding density (ν) satisfies the following implicit equation for non-cooperative binding (i.e. ω = 1) and cooperative binding with nearest neighbor interactions (i.e. ω ≠ 1), respectively (26),

$$\frac{\nu }{C_{\text{tot}}-\nu A_{\text{tot}}}=\frac{\left(1-n\nu \right)}{K_d}{\left(\frac{1-n\nu }{1-n\nu +\nu }\right)}^{n-1}$$ (Eq. 3)

for ω = 1 or

$$\frac{\nu }{C_{\text{tot}}-\nu A_{\text{tot}}}=\frac{\left(1-n\nu \right)}{K_d}{\left(\frac{\left(2\omega -1\right)\left(1-n\nu \right)+\nu -R}{2\left(\omega -1\right)\left(1-n\nu \right)}\right)}^{n-1}\times {\left(\frac{1-\left(n+1\right)\nu +R}{2\left(1-n\nu \right)}\right)}^2$$ (Eq. 4)

where $\sqrt{{\left(1-n\nu -\nu \right)}^2+4\omega \nu \left(1-n\nu \right)}$; K_d is the equilibrium constant for binding to an isolated site (i.e. intrinsic affinity for binding with no neighbors); ω is a dimensionless cooperativity parameter; n is the binding stoichiometry (n = 1 cofilin per actin filament subunit); and C_tot and A_tot are total cofilin and actin concentrations, respectively. The measured C_tot-dependent fluorescence data were fitted to Equation 2 and either Equation 3 or Equation 4 following a numerical procedure with parameters K_d and ω unconstrained. During fitting iterations, ν is calculated using Equation 3 if the testing parameter ω = 1 and using Equation 4 if ω ≠ 1. WT and S3D cofilin equilibrium binding with unlabeled, pyrene-labeled (supplemental Fig. S5), or Alexa-labeled actin filaments (7) showed no detectable depolymerization, assayed by centrifugation.

Boundary density calculation

The (average) fraction of total cofilin binding sites that comprise a boundary between a bare and decorated segment (s̄_b, expressed as boundaries/total binding sites) is calculated as described in detail (see “Appendix,” and the supplemental material in Ref. 14). Briefly, singly contiguous bound cofilin (s̄_sc) is treated as a single boundary (see Refs. 11, 14, and 26) for definitions) and isolated bound cofilin (s̄_iso) as two boundaries, as defined by the following relation (7, 14, 26),

$${\overline{s}}_{\text{b}}={\overline{s}}_{\text{sc}}+2{\overline{s}}_{\text{iso}}=2\left(1-\nu \right)\left(f{b}_1\right)\left(b_n{b}_1\right)+2\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right)=2\left(1-\nu \right)\left(f{b}_1\right)\left(\left(b_n{b}_1\right)+\left(b_{n}f\right)\right)=2\left(1-\nu \right)\left(f{b}_1\right)=\{\begin{array}{l}2\nu \left(1-\nu \right)\hfill \\ \omega -1,\text{non-cooperative}\hfill \\ \frac{\sqrt{{\left(1-2\nu \right)}^2+4\omega \nu \left(1-\nu \right)}-1}{\omega -1}\hfill \\ \omega \ne 1,\text{cooperative}\hfill \end{array}$$ (Eq. 5)

where the terms f and b refer to free and bound cofilin, respectively (see “Appendix” for specific definitions of each term). These expressions have been used previously (7), but the final printed forms contain a typographical error.

Fluorescence microscopy, bending mechanics, and severing assays

Microscope coverslips and slides were cleaned with absolute ethanol and rinsed with doubly deionized water. Actin filaments (2–3 μm labeled with either Alexa 488 or Alexa 594), equilibrated with WT or S3D cofilin for at least 1 h, were diluted 100-fold in KMI buffer supplemented with 10 mm DTT, 1 mm ATP, and cofilin to ensure that cofilin binding density did not change upon dilution (7). Filaments were immobilized on poly-l-lysine–treated coverslips and imaged at room temperature (∼22 °C) using a Till iMic digital microscope equipped with a ×100 objective (Olympus) and Andor iXon897 EMCCD camera (7, 30, 31). ImageJ software (National Institutes of Health) was used to process and skeletonize digital images. A custom Matlab script, Persistence, was used to reconstruct single actin filaments and calculate the contour and bending persistence lengths (42). Average filament contour lengths (L_avg) were determined from the population mean, and bending persistence length (L_p) values were fit from angular correlation analyses of >20 images with n = 200–500 filaments, according to the equation,

$$\langle \cos \left(\theta \left(s\right)-\theta \left(0\right)\right)\rangle =e^{-\frac{S}{2L_p}}$$ (Eq. 6)

where s is the filament segment length and θ is the tangent angle along the filament (11, 42).

Phosphorescence intensity and anisotropy decay measurement and analysis

WT or S3D cofilin was equilibrated with ErIA-labeled actin filaments for at least 1 h. ErIA-labeled actin in KMI buffer was excited at 540 nm with a vertically polarized 10-ns pulse from a XeCl-pumped dye laser (Compex 120, Lambda Physik) at a repetition rate of 100 Hz. Emission was selected by a 670-nm filter (Corion), detected by a photomultiplier (R928, Hamamatsu), and digitized (CompuScope 14100, GaGe) with a resolution of 1 μs/channel (analog filter time constant 3 μs) (12). Intensity and anisotropy decay time courses were fitted to a sum of exponentials, omitting data within the 5-μs dead time (12).

The (cofil)actin filament intersubunit torsional constants α were calculated using the theory of Schurr (58, 59). Filaments are modeled as a series of cylinders approximating actin subunit dimensions and anisotropy decays fit to a sum of exponentials containing population-weighted contributions from filaments of different lengths (12, 60, 61).

Circular dichroism

Circular dichroism spectra of WT and S3D cofilins (25 μm, 0.5 mg/ml) were collected on an Applied Photophysics Chirascan spectrometer. Molar ellipticity was monitored at 223 nm (α-helical conformation) (62) while heating from 10 to 80 °C at a rate of 1 °C min⁻¹. Five readings were acquired at each temperature and averaged. The measured temperature-dependent molar ellipticity data were fitted to the following equation to determine WT and S3D thermal melting properties (63),

$${\theta }_{\text{obs}}\left(T\right)=\frac{{\theta }_n-{\theta }_{\text{u}}{e}^{-\frac{\Delta H_u^{0\prime }}{RT}}\left(1-\frac{T}{T_m}\right)+\frac{\Delta C_{pu}^{0\prime }}{RT}\left(T\hspace{0.17em}\ln \left(\frac{T}{T_m}\right)+T_m-T\right)}{1+e^{-\frac{\Delta H_u^{0\prime }}{RT}}\left(1-\frac{T}{T_m}\right)+\frac{\Delta C_{pu}^{0\prime }}{RT}\left(T\hspace{0.17em}\ln \left(\frac{T}{T_m}\right)+T_m-T\right)}$$ (Eq. 7)

where θ_obs is the observed molar ellipticity value; θ_n and θ_u are the molar ellipticities of native (folded) and unfolded species, respectively; ΔH⁰′_u and ΔC_p⁰′_u are the standard enthalpy and heat capacity changes (at constant pressure) associated with the unfolding reaction; R is the gas constant (8.31 J K⁻¹ mol⁻¹); T is the scanning temperature in Kelvin; and T_m is the transition (melting) temperature of unfolding.

Electron cryomicroscopy and structure refinement

Unlabeled actin was polymerized in 5 mm MgCl₂, 1 mm ATP, 10 mm DTT, and 10 mm imidazole (pH 6.8). Following a 2-h incubation at room temperature, filaments (5–10 μm) were equilibrated with S3D cofilin at saturating concentrations (∼10-fold higher than actin). Samples on carbon grids (Quantifoil R1.2/1.3, no glow discharge) were plunge-frozen into liquid ethane using a FEI Vitrobot Mark III system or a manual plunge system.

Images were collected on a FEI-F20 electron microscope (×27,000 magnification, 1.867 Å/pixel) equipped with a Gatan K2 Summit direct electron-counting camera with a 3 frame/s collection rate and net dose of ∼35–60 electrons/Ų. Multiple frames from a given sample area were aligned and dose-corrected using MotionCor2 (64) with defocuses and astigmatism parameters for micrographs estimated by Gctf (65).

Structure refinement was performed with helical processing in RELION (66, 67). The atomic model for cofilactin filaments reported by Galkin et al. (10) was used as an initial reference volume after low-pass filtering to 60 Å. Movie processing was incorporated into the refinement (“particle polishing”) for WT cofilactin only. To estimate the resolution of the final reconstructions, a solvent mask was applied to independently refined half-data set maps (“gold standard” Fourier shell correlation); a high-resolution noise substitution step was utilized to minimize bias due to masking. The resolution of the reconstructions was estimated to be 8.5 Å (WT cofilactin) and 8.1 Å (S3D cofilactin). Before subsequent analysis, these reconstructions were filtered to 8.6 and 8.5 Å resolution, respectively, after applying a B-factor of −300. Atomic coordinates were fit into density maps using UCSF Chimera (68).

Molecular dynamics simulations

A periodic starting structure for cofilactin containing 11 actin subunits and 11 bound cofilins (69) was generated based on the electron microscopy–derived filament model (10), with the structure generated after 100 ns of simulation used as the starting point in this study. The 11 cofilin serine 3 residues were either mutated to aspartic acids or phosphorylated using VMD (70) where indicated. Waters far from the filament were replaced with potassium ions to neutralize the system and keep the concentration of KCl at the initial value of 0.18 m. The system was re-equilibrated per the original protocol using the CHARMM22+CMAP force field (71). This procedure consists of minimizing the structure using NAMD (72) while successively releasing constraints on the water, protein backbone, protein side chains, and finally the bound nucleotides and magnesium ions, followed by a gradual heating at constant volume followed by equilibration at constant temperature and pressure over 2 ns (see Ref. 73 for full details) followed by unconstrained equilibration for 10 ns. Simulations were then started from these two equilibrated structures using Gromacs version 5.1.2 (74) using a 2-fs time step, particle mesh–Ewald electrostatics (75) with a 1.2-nm cut-off, the Bussi–Parrinello thermostat with a time constant of 0.1 ps, and a Parrinello–Rahman barostat with a 2-ps time constant (76). Data in the figures for wild-type cofilin correspond to the time window of 125–400 ns in Ref. 69, whereas data for the mutant and phosphorylated cases correspond to times after the equilibration described above.

Author contributions

W. A. E., W. C., H. K., and E. M. D. L. C. conceived the project. W. A. E., W. C., H. K., A. H., E. P., A. C. S., K. N., J. G., and T. T. B. performed experiments. G. M. H. performed MD simulations. W. C. and E. M. D. L. C. developed the theory and mathematical modeling. W. A. E., W. C., and E. M. D. L. C. wrote the article, with revisions and assistance from coauthors. D. D. T., G. A. V., and C. V. S. were involved with analyzing and interpreting data and provided expertise in limitations of our methods and results. All authors analyzed data and edited the manuscript.

Appendix

Interface model for cofilin severing actin filaments

The simplest mechanism for the reversible severing and annealing of N number of actin filaments is given by the following reaction scheme (7, 14),

$$N\underset{k_{\text{anneal}}}{\overset{k_{\text{sever}}}{\rightleftarrows }}N+\text{d}N$$ (Eq. A1)

where k_sever and k_anneal are the average, fundamental, filament-severing and -annealing rate constants, respectively, and dN is the change in total filament number. The term k_sever represents a microscopic rate constant, such that the overall observed severing rate constant is equal to k_sever times the number of potential severing sites.

The differential equation corresponding to scheme A1 is given by the following,

$$\frac{\text{d}N}{\text{d}t}=n{k}_{\text{sever}}-k_{\text{anneal}}{N}^2$$ (Eq. A2)

where n is the total number of actin filament subunits. At equilibrium, dN/dt = 0, and Equation A2 can be solved in terms of the average filament number,

$$N=\sqrt{\frac{n{k}_{\text{sever}}}{k_{\text{anneal}}}}$$ (Eq. A3)

and the average filament length (average number of actin subunits per filament) (7, 14).

$$L_{\text{avg}}=\frac{n}{N}=n\sqrt{\frac{k_{\text{anneal}}}{n{k}_{\text{sever}}}}=\sqrt{\frac{n{k}_{\text{anneal}}}{k_{\text{sever}}}}$$ (Eq. A4)

The interface severing model assumes that severing occurs only at three distinct filament subunit interfaces: between two bound cofilin molecules (cofilactin–cofilactin interface), between a bound cofilin and a bare actin subunit (cofilactin–actin interface), or between two bare actin subunits (actin–actin interface). According to this model, the average observed severing rate constant k_sever reflects the weighted average of the three interface severing rate constants,

$$k_{\text{sever}}=k_{\text{c}-\text{c}}{\overline{s}}_{\text{c}-\text{c}}+k_{\text{c}-\text{a}}{\overline{s}}_{\text{c}-\text{a}}+k_{\text{a}-\text{a}}{\overline{s}}_{\text{a}-\text{a}}=k_{\text{a}-\text{a}}\left(\frac{k_{\text{c}-\text{c}}}{k_{\text{a}-\text{a}}}{\overline{s}}_{\text{c}-\text{c}}+\frac{k_{\text{c}-\text{a}}}{k_{\text{a}-\text{a}}}{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}\right)=k_{\text{a}-\text{a}}\left(k{\prime }_{\text{c}-\text{c}}{\overline{s}}_{\text{c}-\text{c}}+k{\prime }_{\text{c}-\text{a}}{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}\right)$$ (Eq. A5)

where k and s̄ are the severing rate constant and mole fraction of cofilactin–cofilactin (c-c), cofilactin–actin (c-a), or actin–actin (a-a) interfaces (indicated by subscripts), respectively, whereas k′_c-c and k′_c-a represent the corresponding severing rate constants relative to that at an actin–actin interface. Applying Equation A5 allows Equation A4 to be rewritten as follows,

$$L_{\text{avg}}=\sqrt{\frac{n{k}_{\text{anneal}}}{k_{\text{c}-\text{c}}{\overline{s}}_{\text{c}-\text{c}}+k_{\text{c}-\text{a}}{\overline{s}}_{\text{c}-\text{a}}+k_{\text{a}-\text{a}}{\overline{s}}_{\text{a}-\text{a}}}}=\frac{\sqrt{\frac{n{k}_{\text{anneal}}}{k_{\text{a}-\text{a}}}}}{\sqrt{\frac{k_{\text{c}-\text{c}}}{k_{\text{a}-\text{a}}}{\overline{s}}_{\text{c}-\text{c}}+\frac{k_{\text{c}-\text{a}}}{k_{\text{a}-\text{a}}}{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}}}=\frac{L_{\text{avg},\text{intrinsic}}}{\sqrt{k{\prime }_{\text{c}-\text{c}}{\overline{s}}_{\text{c}-\text{c}}+k{\prime }_{\text{c}-\text{a}}{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}}}$$ (Eq. A6)

where

$$L_{\text{avg},\text{intrinsic}}=\sqrt{\frac{n{k}_{\text{anneal}}}{k_{\text{a}-\text{a}}}}$$ (Eq. A7)

represents the average filament length of bare actin (i.e. in the absence of regulatory proteins) defined by the intrinsic bare actin filament severing and annealing reactions.

In the following derivation of the expressions for severing at the three distinct cofilactin filament interfaces, we adhere to the same probability expressions used in the derivation of expressions defining severing at distinct filament sites (i.e. the actin-severing site model (14)). The terms (ff), (fb₁), (b_nb₁), (b_nf) and P_g are taken directly from Ref. 26. P_c is derived in Ref. 14 and based on the work in Ref. 26. All of these terms are defined as probabilities: the probability of finding a free site with either a free site (ff) or bound regulatory protein (fb₁) at right, a bound regulatory protein with either a bound regulatory protein (b_nb₁) or a free site (b_nf) at right, a contiguous gap of g vacant sites (P_g), or a bound regulatory protein cluster of length c along a filament (P_c). The mole fractions of cofilactin–cofilactin (s̄_c-c), cofilactin–actin (s̄_c-a), and actin–actin (s̄_a-a) interfaces are defined by these conditional probabilities and the cofilin binding density (ν) formulized using the techniques analogous to those of McGhee and von Hippel (26). For a length c cofilin cluster, there are c − 1 c-c interfaces and 2 c-a interfaces. In a cofilin cluster, the average number of c-c interfaces is ${\displaystyle {\sum }_{c=2}^{\infty }\left(c-1\right)P_c}$, whereas the average number of c-a interfaces is $2{\displaystyle {\sum }_{c=1}^{\infty }{P}_c}$. For binding density ν, the cofilin free binding site density is 1 − ν, and it is also approximately equal to the cofilin cluster density (i.e. number of cofilin clusters, counting all cofilin clusters of size c ≥ 0) divided by the total number of binding sites). Accordingly, s̄_c-c = cluster density times the average number of c-c interfaces in a single cluster = $\left(1-\nu \right){\displaystyle {\sum }_{c=2}^{\infty }\left(c-1\right)P_c}$, and s̄_c-a = cluster density times the average number of c-a interfaces in a single cluster = $\left(1-\nu \right)\times 2{\displaystyle {\sum }_{c=1}^{\infty }{P}_c}$. Similarly, for a free site gap of length g, there are g − 1 a-a interfaces and 2 c-a interfaces. In a free site gap, the average number of a-a interfaces is ${\displaystyle {\sum }_{g=2}^{\infty }\left(g-1\right)P_g}$, whereas the average number of c-a interfaces is $2{\displaystyle {\sum }_{c=1}^{\infty }{P}_g}$. For binding density ν, the free site gap density is approximately ν (i.e. number of gaps, counting all gaps of size g ≥ 0 divided by the total number of binding sites). Consequently, s̄_a-a = gap density times the average number of a-a interfaces in a single gap = $\nu {\displaystyle {\sum }_{g=2}^{\infty }\left(g-1\right)P_g}$, and s̄_c-a = gap density times the average number of c-a interfaces in a single gap = $\nu \times 2{\displaystyle {\sum }_{g=1}^{\infty }{P}_g}$. The expressions of mole fraction of interfaces are derived as follows.

$${\overline{s}}_{\text{c}-\text{c}}=\left(1-\nu \right){\displaystyle \sum _{c=2}^{\infty }\left(c-1\right)P_c=\left(1-\nu \right)}{\displaystyle \sum _{c=2}^{\infty }\left(c-1\right)\left(f{b}_1\right){\left(b_n{b}_1\right)}^{c-1}\left(b_{n}f\right)=\left(1-\nu \right)}\left(f{b}_1\right)\left(b_n{b}_1\right)\left(b_{n}f\right)\left(1+2\left(b_n{b}_1\right)+3{\left(b_n{b}_1\right)}^2+\dots +k{\left(b_n{b}_1\right)}^{k-1}+\dots \right)=\left(1-\nu \right)\frac{\left(f{b}_1\right)\left(b_{n}f\right)\left(b_n{b}_1\right)}{{\left(1-\left(b_n{b}_1\right)\right)}^2}=\left(1-\nu \right)\frac{\left(f{b}_1\right)\left(b_n{b}_1\right)}{\left(b_{n}f\right)}$$ (Eq. A8)

$${\overline{s}}_{\text{c}-\text{a}}=2\left(1-\nu \right){\displaystyle \sum _{c=1}^{\infty }{P}_c=2\left(1-\nu \right)\left(f{b}_1\right)=2\nu }{\displaystyle \sum _{g=1}^{\infty }{P}_g=2\nu \left(b_{n}f\right)}$$ (Eq. A9)

$${\overline{s}}_{\text{a}-\text{a}}=\nu {\displaystyle \sum _{g=2}^{\infty }\left(g-1\right)P_g=}\hspace{0.17em}\nu {\displaystyle \sum _{g=2}^{\infty }\left(g-1\right)\left(b_{n}f\right){\left(ff\right)}^{g-1}\left(f{b}_1\right)=\nu \left(b_{n}f\right)\times \left(ff\right)\left(f{b}_1\right)\left(1+2\left(ff\right)+3{\left(ff\right)}^2+\dots \right)=\nu \frac{\left(b_{n}f\right)\left(ff\right)\left(f{b}_1\right)}{{\left(1-\left(ff\right)\right)}^2}}=\nu \frac{\left(b_{n}f\right)\left(ff\right)\left(f{b}_1\right)}{{\left(f{b}_1\right)}^2}=\nu \frac{\left(b_{n}f\right)\left(ff\right)}{\left(f{b}_1\right)}$$ (Eq. A10)

The conditional probability terms (ff), (fb₁), (b_nb₁), and (b_nf) differ for regulatory protein ligands that bind cooperatively and non-cooperatively (26). For non-cooperative binding,

$${\overline{s}}_{\text{c}-\text{c}}=\left(1-\nu \right)\frac{\left(f{b}_1\right)\left(b_n{b}_1\right)}{\left(b_{n}f\right)}=\left(1-\nu \right)\frac{\nu \nu }{1-\nu }={\nu }^2$$ (Eq. A11)

$${\overline{s}}_{\text{c}-\text{a}}=2\left(1-\nu \right)\left(f{b}_1\right)=2\nu \left(b_{n}f\right)=2\nu \left(1-\nu \right)$$ (Eq. A12)

$${\overline{s}}_{a-a}=\nu \frac{\left(b_{n}f\right)\left(ff\right)}{\left(f{b}_1\right)}=\nu \frac{\left(1-\nu \right)\hspace{0.17em}\left(1-\nu \right)}{\nu }={\left(1-\nu \right)}^2$$ (Eq. A13)

and

$$L_{\text{avg}}=\frac{L_{\text{avg},\text{intrinsic}}}{\sqrt{k{\prime }_{\text{c}-\text{c}}{\nu }^2+2k{\prime }_{\text{c}-\text{a}}\nu \left(1-\nu \right)+{\left(1-\nu \right)}^2}}$$ (Eq. A14)

For cooperative binding,

$${\overline{s}}_{\text{c}-\text{c}}=\left(1-\nu \right)\frac{\left(f{b}_1\right)\left(b_n{b}_1\right)}{\left(b_{n}f\right)}=\left(1-\nu \right)\frac{\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}\frac{1-2\nu \left(1-\omega \right)-R}{2\nu \left(\omega -1\right)}}{\frac{R-1}{2\nu \left(\omega -1\right)}}=\frac{1-2\nu \left(1-\omega \right)-R}{2\left(\omega -1\right)}$$ (Eq. A15)

$${\overline{s}}_{\text{c}-\text{a}}=2\left(1-\nu \right)\left(f{b}_1\right)=2\nu \left(b_{n}f\right)=2\left(1-\nu \right)\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}=\frac{R-1}{\omega -1}$$ (Eq. A16)

$${\overline{s}}_{a-a}=\nu \frac{\left(b_{n}f\right)\left(ff\right)}{\left(f{b}_1\right)}=\nu \frac{\frac{R-1}{2\nu \left(\omega -1\right)}\frac{\left(2\omega -1\right)\left(1-\nu \right)+\nu -R}{2\left(\omega -1\right)\left(1-\nu \right)}}{\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}}=\frac{\left(2\omega -1\right)\left(1-\nu \right)+\nu -R}{2\left(\omega -1\right)}$$ (Eq. A17)

and

$$L_{\text{avg}}=\frac{L_{\text{avg},\text{intrinsic}}}{\sqrt{k{\prime }_{\text{c}-\text{c}}\frac{1-2\nu \left(1-\omega \right)-R}{2\left(\omega -1\right)}+k{\prime }_{\text{c}-\text{a}}\frac{R-1}{\omega -1}+\frac{\left(2\omega -1\right)\left(1-\nu \right)+\nu -R}{2\left(\omega -1\right)}}}$$ (Eq. A18)

Summation of the fractional interfaces for non-cooperative binding,

$${\overline{s}}_{\text{c}-\text{c}}+{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}={\nu }^2+2\nu \left(1-\nu \right)+{\left(1-\nu \right)}^2={\left(\nu +1-\nu \right)}^2=1$$ (Eq. A19)

or for cooperative binding

$${\overline{s}}_{\text{c}-\text{c}}+{\overline{s}}_{\text{c}-\text{a}}+{\overline{s}}_{\text{a}-\text{a}}=\frac{1-2\nu \left(1-\omega \right)-R}{2\left(\omega -1\right)}+\frac{R-1}{\omega -1}+\frac{\left(2\omega -1\right)\left(1-\nu \right)+\nu -R}{2\left(\omega -1\right)}=\frac{1-2\nu \left(1-\omega \right)-R+2R-2+\left(2\omega -1\right)\left(1-\nu \right)+\nu -R}{2\left(\omega -1\right)}=\frac{1-2\nu +2\nu \omega -2+2\omega -1-2\omega \nu +\nu +\nu }{2\left(\omega -1\right)}=\frac{-2+2\omega }{2\left(\omega -1\right)}=1$$ (Eq. A20)

equals unity, indicating that there is no counting problem in the derived expressions.

Critical cluster size for severing >3 predicts an asymmetric cofilin binding density dependence of severing activity

It has been reported that bound cofilin clusters have to be equal to or larger than 13 (33), 23 (34), or 100 (32) molecules long to sever filaments. In other words, severing requires a critical cluster size (c̄_crit) of bound cofilin. To evaluate how c̄_crit size influences the experimentally observed cofilin binding density dependence of severing, we calculate the density of severing-competent boundaries (i.e. flanking clusters ≥c̄_crit; defined as s̄_b (c ≥ c̄_crit ≥ 1) using the conditional probabilities defined above and in Refs. 14 and 26.

For simplicity and without losing generality, we define a single bound isolated cofilin as two boundaries (note that this species is neglected when c̄_crit > 1). Therefore, similar to Equation A9, to calculate the fraction of total actin filament sites that comprise severing-competent boundaries (s̄_b (c ≥ c̄_crit ≥ 1)) for all of the severing-competent clusters,

$$\begin{array}{c}{\overline{s}}_{\text{b}}\left(c\ge {\overline{c}}_{\text{crit}}\ge 1\right)=2\left(1-\nu \right){\displaystyle {\sum }_{c={\overline{c}}_{\text{crit}}}^{\infty }{P}_c}\\ =2\left(1-\nu \right){\displaystyle \sum _{c={\overline{c}}_{\text{crit}}}^{\infty }\left(f{b}_1\right){\left(b_n{b}_1\right)}^{c-1}\left(b_{n}f\right)}\\ =2\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right)\left({\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}+{\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}}+\dots \right)\\ =2\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}\left(1+\left(b_n{b}_1\right)+{\left(b_n{b}_1\right)}^2+\dots \right)\\ =\frac{2\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}}{1-\left(b_n{b}_1\right)}\\ =\frac{2\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}}{\left(b_{n}f\right)}\\ =2\left(1-\nu \right)\left(f{b}_1\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}\\ =2\left(1-\nu \right)\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}{\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\\ =\frac{R-1}{\left(\omega -1\right)}{\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\end{array}$$ (Eq. A21)

For completeness, using the same technique when formulizing Equations A8–A10, we provide expressions for the fractions of total bound cofilin, s̄ (c ≥ c̄_crit ≥ 1) = s̄_b(c ≥ c̄_crit ≥ 1) + s̄_dc(c ≥ c̄_crit ≥ 1) and cofilin bound doubly contiguously, s̄_dc(c ≥ c̄_crit ≥ 1), for a given critical cluster size. Note that doubly contiguous cofilin exists only for clusters ≥3.

$${\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=1\right)={\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=2\right)={\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=3\right)$$ (Eq. A22)

Therefore,

$$\begin{array}{c}{\overline{s}}_{dc}\left(c\ge {\overline{c}}_{\text{crit}}\ge 3\right)=\left(1-\nu \right){\displaystyle \sum _{c={\overline{c}}_{\text{crit}}}^{\infty }\left(c-2\right)P_c}\\ =\left(1-\nu \right){\displaystyle \sum _{c={\overline{c}}_{\text{crit}}}^{\infty }\left(c-2\right)\left(f{b}_1\right){\left(b_n{b}_1\right)}^{c-1}\left(b_{n}f\right)}\\ =\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right)\left(\left({\overline{c}}_{\text{crit}}-2\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}+\left({\overline{c}}_{\text{crit}}-1\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}}+{\overline{c}}_{\text{crit}}{\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}+1}+\dots \right)\\ =\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\left({\overline{c}}_{\text{crit}}-2\right)+\left({\overline{c}}_{\text{crit}}-1\right)\left(b_n{b}_1\right)+{\overline{c}}_{\text{crit}}{\left(b_n{b}_1\right)}^2+\dots \right)\\ =\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}\times \left(\frac{{\overline{c}}_{\text{crit}}-3}{1-\left(b_n{b}_1\right)}+\frac{1}{{\left(1-\left(b_n{b}_1\right)\right)}^2}\right)\\ =\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right){\left(b_n{b}_1\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\frac{{\overline{c}}_{\text{crit}}-3}{\left(b_{n}f\right)}+\frac{1}{{\left(b_{n}f\right)}^2}\right)\\ =\left(1-\nu \right)\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}{\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\times \left({\overline{c}}_{\text{crit}}-3+\frac{1}{\frac{R-1}{2\nu \left(\omega -1\right)}}\right)\\ ={\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\frac{\left({\overline{c}}_{\text{crit}}-3\right)\left(R-1\right)}{2\left(\omega -1\right)}+\nu \right)\end{array}$$ (Eq. A23)

where the following relation is applied.

$$\left({\overline{c}}_{\text{crit}}-2\right)+\left({\overline{c}}_{\text{crit}}-1\right)\left(b_n{b}_1\right)+{\overline{c}}_{\text{crit}}{\left(b_n{b}_1\right)}^2+\dots =\frac{{\overline{c}}_{\text{crit}}-3}{1-\left(b_n{b}_1\right)}+\frac{1}{{\left(1-\left(b_n{b}_1\right)\right)}^2}$$ (Eq. A24)

Accordingly, the fraction of bound cofilin in severing-competent clusters is given by the sum of the single- and double-contiguously bound species.

$$\overline{s}\left(c\ge {\overline{c}}_{\text{crit}}=1\right)={\overline{s}}_{\text{sc}}\left(c\ge {\overline{c}}_{\text{crit}}=1\right)+{\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=1\right)=\overline{s}\left(c\ge {\overline{c}}_{\text{crit}}=1\right)+{\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=3\right)=\left(1-\nu \right)P_{c=1}+{\overline{s}}_{\text{b}}\left(c\ge {\overline{c}}_{\text{crit}}=2\right)+{\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=3\right)=\left(1-\nu \right)\left(f{b}_1\right)\left(b_{n}f\right)+{\overline{s}}_{\text{b}}\left(c\ge {\overline{c}}_{\text{crit}}=2\right)+{\overline{s}}_{\text{dc}}\left(c\ge {\overline{c}}_{\text{crit}}=3\right)=\left(1-\nu \right)\frac{R-1}{2\left(\omega -1\right)\left(1-\nu \right)}\frac{R-1}{2\nu \left(\omega -1\right)}+\frac{R-1}{\left(\omega -1\right)}\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)+\nu {\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^2=\nu$$ (Eq. A25)

$$\overline{s}\left(\ge {\overline{c}}_{\text{crit}}=2\right)={\overline{s}}_{\text{sc}}\left(\ge {\overline{c}}_{\text{crit}}=2\right)+{\overline{s}}_{\text{dc}}\left(\ge {\overline{c}}_{\text{crit}}=2\right)={\overline{s}}_{\text{sc}}\left(\ge {\overline{c}}_{\text{crit}}=2\right)+{\overline{s}}_{\text{dc}}\left(\ge {\overline{c}}_{\text{crit}}=3\right)=\frac{R-1}{\left(\omega -1\right)}\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)+\nu {\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^2=\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)\left(\frac{R-1-2\left(1-\omega \right)\nu }{2\left(1-\omega \right)}\right)=-\frac{{\left(R-1\right)}^2-4{\left(1-\omega \right)}^2{\nu }^2}{4\nu {\left(1-\omega \right)}^2}$$ (Eq. A26)

$$\overline{s}\left(\ge {\overline{c}}_{\text{crit}}\ge 3\right)={\overline{s}}_{\text{sc}}\left(\ge {\overline{c}}_{\text{crit}}\ge 3\right)+{\overline{s}}_{\text{dc}}\left(\ge {\overline{c}}_{\text{crit}}\ge 3\right)=\frac{R-1}{\omega -1}{\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}+{\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\frac{\left({\overline{c}}_{\text{crit}}-3\right)\left(R-1\right)}{2\left(\omega -1\right)}+\nu \right)={\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\frac{R-1}{\omega -1}+\frac{\left({\overline{c}}_{\text{crit}}-3\right)\left(R-1\right)}{2\left(\omega -1\right)}+\nu \right)={\left(\frac{1-2\left(1-\omega \right)\nu -R}{2\nu \left(\omega -1\right)}\right)}^{{\overline{c}}_{\text{crit}}-1}\left(\frac{\left({\overline{c}}_{\text{crit}}-3\right)\left(R-1\right)}{2\left(\omega -1\right)}+\nu \right)$$ (Eq. A27)