All-atom Continuous Constant pH Molecular Dynamics With Particle Mesh Ewald and Titratable Water

Abstract

Development of a pH stat to properly control solution pH in biomolecular simulations has been a long-standing goal in the community. Towards this goal recent years have witnessed the emergence of the so-called constant pH molecular dynamics methods. However, the accuracy and generality of these methods have been hampered by the use of implicit-solvent models or truncation-based electrostatic schemes. Here we report the implementation of the particle mesh Ewald (PME) scheme into the all-atom continuous constant pH molecular dynamics (CpHMD) method, enabling CpHMD to be performed with a standard MD engine at a fractional added computational cost. We demonstrate the performance using pH replica-exchange CpHMD simulations with titratable water for a stringent test set of proteins, HP36, BBL, HEWL and SNase. With the sampling time of 10 ns per replica, most pK_a’s are converged, yielding the average absolute and root-mean-square deviations of 0.61 and 0.77, respectively, from experiment. Linear regression of the calculated vs experimental pK_a shifts gives a correlation coefficient of 0.79, a slope of 1 and an intercept near 0. Analysis reveals inadequate sampling of structure relaxation accompanying a protonation-state switch as a major source of the remaining errors, which are reduced as simulation prolongs. These data suggest PME-based CpHMD can be used as a general tool for pH-controlled simulations of macromolecular systems in various environments, enabling atomic insights into pH-dependent phenomena involving not only soluble proteins but also transmembrane proteins, nucleic acids, surfactants and polysaccharides.

Graphical abstract

Introduction

Extending thermodynamic ensembles to include constant solution pH has been a longstanding goal in the advancement of molecular dynamics (MD) methodologies. Towards this goal two constant pH frameworks have been developed over the past decade to offer control of solution pH while propagating atomic positions. The first framework, referred to as discrete constant pH MD, combines MD with Monte-Carlo sampling of discrete protonation states,^1–4 while the second one, referred to as continuous constant pH MD (CpHMD), makes use of the λ-dynamics⁵ based extended Hamiltonian to propagate a set of continuous titration coordinates.^6,7 Until recently, all constant pH methods relied on dielectric continuum models such as Poisson-Boltzmann theory¹ or generalized-Born implicit-solvent models for sampling protonation states, while either continuum models^2,6,7 or explicit-solvent description was used for conformational dynamics.^1,3,8 The latter is also referred to as the hybrid-solvent constant pH MD. These methods enabled pK_a predictions of proteins^9,10 as well as lipids and surfactants,^11,12 and mechanistic studies of pH-coupled conformational dynamics (see a recent review¹³ for references). However, the underlying approximations in the implicit-solvent models hinders the systematic improvement of accuracy and generalization to systems that necessitate fully explicit-solvent description, for example, highly charged molecules such as nucleic acids and those involving heterogeneous dielectric environments such as transmembrane proteins.

To overcome the limitations imposed by continuum models, the CpHMD framework has been recently extended to fully explicit-solvent (all-atom) simulations by three groups.^14–16 In the work of Donnini et al, which was implemented in the GROMACS program,¹⁷ the particle mesh Ewald (PME) scheme^18,19 was used to model long-range electrostatics in conformational dynamics; however, it was not mentioned as to whether PME forces were applied to λ dynamics.¹⁴ The development was tested on several model compounds with a single titratable site.¹⁴ Making use of the force shifting scheme for electrostatics in both conformational and λ dynamics, CpHMD based on multi-site λ dynamics,¹⁵ which was implemented in CHARMM,²⁰ has been developed and validated using pK_a calculations of a ribozyme,²¹ proteins²² and a transmembrane helix.²³ The development of Shen and coworkers,¹⁶ which was also implemented in CHARMM,²⁰ utilized the generalized reaction field (GRF) scheme by Tironi et al.²⁴ for both conformational and λ dynamics, and it was validated based on pK_a calculations of proteins,²⁵ surfactants embedded in micelle and bilayer environments,²⁶ and sol-gel transition of polysaccharides.²⁷ Another major difference between the latter and former two groups’ work is with respect to the system net charge. While the latter utilized co-titrating ions¹⁶ and later titratable water²⁵ to ensure charge neutrality, the other two developments neglected the effect of fluctuating net charge in the system.

The objective of this work is to develop the PME-based all-atom CpHMD and validate the implementation using pK_a calculation of a set of proteins including a challenging one, staphylococcal nuclease (SNase), which has not been demonstrated using force shifting¹⁵ or GRF-based CpHMD.²⁵ Our motivation is several fold. First, GRF schemes invoke a spherical representation,^24,28 which is not suitable for anisotropic systems such as those involving membranes which are a major application target of constant pH MD. In fact, the use of GRF in membrane protein simulations (with CHARMM27 lipid force field²⁹) resulted in significant shrinkage of the bilayer in terms of area per lipid (unpublished data), although lipid bilayers are known to be very sensitive to simulation setting and CHARMM27 was developed using PME.²⁹ Second, our previous analysis showed force shifting or GRF-based CpHMD favors neutral species in titration due to the underestimation of favorable charging free energies and solvation free energies of charged solutes.³⁰ This may be a major cause for the systematic overestimation of pK_a shifts of buried residues,²⁵ although we acknowledge that the deviations may be reduced by performing the finite-size correction for charging free energies as shown by Reif et al.^31,32 in the context of simulations with the Baker-Watts reaction field.²⁸ Lastly, although it remains somewhat debatable as to whether PME outperforms GRF for charged proteins,^33,34 PME is arguably the most widely used electrostatic method in MD simulations, and the highly parallel as well as GPU versions have been implemented in all major molecular dynamics packages such as AMBER,³⁵ CHARMM²⁰ and GROMACS.¹⁷ With judicious use, i.e., avoiding small box size which may give rise to periodicity related artifacts³⁶ and including counter ions to neutralize the simulation box, PME has enabled accurate simulations of not only soluble proteins,³⁴ but also nucleic acids,³⁷ lipid bilayers³⁸ and transmembrane proteins.³⁹

In this work we report the implementation of PME-based all-atom CpHMD in CHARMM.²⁰ Test simulations employing titratable water, which we previously introduced to ensure the simulation system is charge neutral during titration,²⁵ demonstrate significantly higher accuracy and faster convergence compared to the GRF-based all-atom CpHMD. The average absolute and maximum absolute errors of the calculated pK_a’s for a stringent test set of proteins, HP36, BBL, HEWL and SNase, are 0.61 and 2.0 units with a sampling time of 10 ns per pH replica, as compared to the respective errors of 1.1 and 3.6 using the same amount of sampling by the GRF-based variant. Thus, PME-based all-atom CpHMD with titratable water is expected to become a general tool for conducting pH-controlled molecular dynamics simulations.

Methods and implementation

Continuous constant pH molecular dynamics

CpHMD employs an extended Hamiltonian to simultaneously propagate spatial (real) and titration (virtual) coordinates,^6,7

$$\mathcal{H}(\{{\mathbf{r}}_{\mathbf{i}}\},\{{\mathit{\theta }}_{\mathbf{t}}\})=\sum _{\mathbf{i}}^{{\mathbf{N}}_{\text{atom}}}\frac{\mathbf{1}}{\mathbf{2}}{\mathbf{m}}_{\mathbf{i}}{\stackrel{.}{\mathbf{r}}}_{\mathbf{i}}^{\mathbf{2}}+{\mathbf{U}}^{\text{bond}}(\{{\mathbf{r}}_{\mathbf{i}}\})+{\mathbf{U}}^{\text{nbond}}(\{{\mathbf{r}}_{\mathbf{i}}\},\{{\mathit{\theta }}_{\mathbf{t}}\})+\sum _{\mathbf{t}}^{{\mathbf{N}}_{\text{titr}}}\frac{\mathbf{1}}{\mathbf{2}}{\mathbf{m}}_{\mathbf{t}}{\stackrel{.}{\theta }}_{\mathbf{t}}^{\mathbf{2}}+{\mathbf{U}}^{\ast }({\mathit{\theta }}_{\mathbf{t}}),$$ (1)

where i and t refer to the atomic and titration-site index, respectively, r_i represents the spatial coordinate, and θ_t is related to the titration coordinate λ_t by λ_t = sin²(θ_t). Thus, λ_t is continuous and bound between 0 and 1, corresponding to the protonated and deprotonated states, respectively. In practice, 0 and 1 are replaced with two cutoffs, λ^P and λ^U, for defining the protonated and deprotonated states, respectively. Previous CpHMD studies^{7–9,16,25,40,41} as well as current work show the calculated pK_a’s are insensitive to the exact cutoffs, e.g., 0.1/0.9 or 0.2/0.8. This topic will be further discussed in Computational Details.

In Eq. 1, the first and the fourth terms give the kinetic energies of the real (atoms) and virtual (λ) particles, respectively. The second term gives the titration-independent bonded energy. Note, although the change in bonded terms due to a switch in protonation state is small or negligible in current force fields, this is an approximation that will be eliminated in future work. The last term represents the biasing potential which is a sum of three terms,

$$U^{\ast }({\mathit{\theta }}_t)=-U^{\text{barr}}({\mathit{\theta }}_t)-U^{mod}({\mathit{\theta }}_t)+U^{\text{pH}}({\mathit{\theta }}_t).$$ (2)

U^barr a harmonic potential centered at 0.5 (midpoint of the λ value range) to suppress the population of unphysical intermediate states,

$$U^{\text{barr}}=4{\beta }_t{({\lambda }_t-1/2)}^2$$ (3)

where β_t is a parameter that specifies the barrier height and therefore controls the fraction of mixed states, i.e., λ^P ≤ λ ≤ λ^U. One β value (typically about 2.0 kcal/mol) is assigned for each model compound, e.g., Asp/Glu/His. This topic will be further discussed in Computational Details. U^mod is the potential of mean force (PMF) function for deprotonation of the model compound, e.g., blocked amino acid in solution; and U^pH represent the free energy imposed on the deprotonation equilibrium to account for the deviation of the solution pH from the model pK_a value,

$$U^{\text{pH}}({\lambda }_t)=ln(10)k_{b}T(p{K}_a^{mod}-\text{pH}){\lambda }_t.$$ (4)

By invoking the linear response approximation, i.e., the charging free energy of an ion in polar solvent is quadratic in the charge perturbation and the charging potential is linear in the perturbation,^42,43 the model PMF can be expressed as a quadratic function of λ,

$$U^{mod}({\lambda }_t)=A_t{({\lambda }_t-B_t)}^2,$$ (5)

where A_t and B_t are fitting parameters. It follows that the average force, 〈∂U/∂λ〉, is linear in λ. In practice, thermodynamic integration is applied to obtain the average forces at various λ values, which are fit to a linear function to obtain A_t and B_t. Note that linear response is formally exact when continuum solvation models are used for λ-dynamics, e.g., in implicit-^6,7 and hybrid-solvent CpHMD.⁸ In fully explicit-solvent (all-atom) CpHMD, nonlinearity of solvent response is expected; however, surprisingly, in the GRF-based all-atom CpHMD simulations with co-ions¹⁶ or titratable water,²⁵ the degree of nonlinearity was found to be very small and negligible. Thus, the quadratic function will continue to be used in PME-CpHMD to fit the PMFs of model compounds and titratable water (hydronium/hydroxide). Finally, we turn to the third term in Eq. 1, which represents the non-bond energy that depends on both spatial and titration coordinates, realizing the coupling between conformational dynamics and proton titration. Specifically, the van der Waals interactions involving titratable hydrogens and the partial charges on the titratable residues are linearly interpolated between the two end states.⁷ The latter results in a change in the electrostatic energy, which is the focus of the current development.

Particle-mesh Ewald electrostatics

Following the notation of Essmann et al.,¹⁹ the electrostatic energy of N point charges {q_i} within a unit cell satisfying the condition ${\sum }_i^N{q}_i=0$ can be written as a lattice sum,

$$U^{\text{elec}}=\frac{1}{2}\underset{\mathbf{n}}{{\sum }^{\prime }}\sum _i\sum _j\frac{q_i{q}_j}{\mid {\mathbf{r}}_{\mathbf{i}}-{\mathbf{r}}_{\mathbf{j}}+\mathbf{n}\mid }$$ (6)

In the above equation the outer sum is over the vector n = n₁a₁ + n₂a₂ + n₃a₃, where vectors a₁, a₂ and a₃ are the edges of the unit cell; integers n₁, n₂ and n₃ indicate the location of the image. The prime indicates the summation excludes the term with i = j and n = 0 (self-interactions).

In the particle-mesh Ewald (PME) method, the Coulomb lattice sum is decomposed into three terms,^18,19

$$U^{\text{elec}}=U^{\text{dir}}+U^{\text{rec}}+U^{\text{corr}}.$$ (7)

The direct sum U^dir represents the short-range electrostatic energy calculated in real space,

$$U^{\text{dir}}=\frac{1}{2}\sum _{\mathbf{n}}^{\ast }\sum _{i,j=1}^N\frac{q_i{q}_j\text{erfc}(\beta \mid {\mathbf{r}}_{\mathbf{j}}-{\mathbf{r}}_{\mathbf{i}}+\mathbf{n}\mid )}{\mid {\mathbf{r}}_{\mathbf{j}}-{\mathbf{r}}_{\mathbf{i}}+\mathbf{n}\mid },$$ (8)

where the asterisk denotes that self-interactions and those in the excluded list (for example, up to the second nearest neighbors) are omitted; erfc is the complementary error function; and β is an arbitrary constant which determines the relative convergence rate of U^dir and U^rec.

The reciprocal sum U^rec represents the long-range electrostatics calculated in Fourier space as^18,19

$$U^{\text{rec}}=\frac{1}{2\pi V}\sum _{\mathbf{m}\ne 0}\frac{\mathit{exp}(-{\pi }^2{\mathbf{m}}^2/{\beta }^2)}{{\mathbf{m}}^2}S(\mathbf{m})S(-\mathbf{m}).$$ (9)

Here m is the reciprocal lattice vector $\mathbf{m}=m_1{\mathbf{a}}_1^{\ast }+m_2{\mathbf{a}}_2^{\ast }+m_3{\mathbf{a}}_3^{\ast }$, where m₁, m₂ and m₃ are integers not all zero. ${\mathbf{a}}_{\alpha }^{\ast }$ is the conjugate reciprocal vector of a_α, which satisfies ${\mathbf{a}}_{\alpha }^{\ast }·{\mathbf{a}}_{\beta }={\delta }_{\alpha \beta }$, where α, β = 1, 2, 3. V = a₁ · a₂ × a₃ refers to the volume of the unit cell, and S(m) is the structure factor,

$$S(\mathbf{m})=\sum _{j=1}^N{q}_j\text{exp}(2\pi i\mathbf{m}·{\mathbf{r}}_j).$$ (10)

The reciprocal term can be approximated as^18,19

$$U^{\text{rec}}=\frac{1}{2}\sum _{m_1=0}^{K_1-1}\sum _{m_2=0}^{K_2-1}\sum _{m_3=0}^{K_3-1}Q(m_1,m_2,m_3)·({\mathrm{\Theta }}_{\text{rec}}★Q)(m_1,m_2,m_3).$$ (11)

Here K_α, with α = 1, 2, 3, is the size of reciprocal lattice. Q is a three-dimensional array filled with charges on the reciprocal lattice grids. Θ_rec is the coefficient array independent of atomic charges. Convolution Θ_rec ★ Q was achieved by one inverse and one forward three-dimensional discrete fast Fourier transformations (3D-FFT).¹⁹

The correction term U^corr is given as^18,19,44

$$U^{\text{corr}}=-\frac{1}{2}\sum _{(i,j)\in M}\frac{q_i{q}_j\text{erf}(\beta \mid {\mathbf{r}}_{\mathbf{i}}-{\mathbf{r}}_{\mathbf{j}}\mid )}{\mid {\mathbf{r}}_{\mathbf{i}}-{\mathbf{r}}_{\mathbf{j}}\mid }-\frac{\beta }{\sqrt{\pi }}\sum _{i=1}^N{q}_i^2-\frac{\pi }{2{\beta }^{2}V}{(\sum _i{q}_i)}^2.$$ (12)

Here the first term denotes the bonded pairs subtracted from U^rec, the second term represents the self energy, and the third term accounts for the interaction with a uniform background charge (plasma) included to neutralize the net charge of the system (if present). Note, in U^corr the dipole moment of the unit cell is neglected, i.e., conductive tinfoil boundary condition. Also, the last two terms are not evaluated in the atomic force calculations as they are independent of coordinates. Note that to obtain energies in the unit of kcal/mol, the electrostatic constant, κ = 1/4πε₀ = 332.0 kcal · Å · mol⁻¹e⁻², is multiplied to Eqs. 6, 8, 11 and 12.

Given the PME energies, electrostatic force on λ particles can be obtained by differentiating the direct, reciprocal and correction terms with respect to λ (subscript t is omitted for clarity),

$$\frac{\partial U^{\text{elec}}}{\partial \lambda }=\frac{\partial U^{\text{dir}}}{\partial \lambda }+\frac{\partial U^{\text{rec}}}{\partial \lambda }+\frac{\partial U^{\text{corr}}}{\partial \lambda },$$ (13)

and realizing that λ is linearly related to the atomic partial charges of the titratable group,

$$q_i=\lambda q_i^{\mathrm{U}}+(1-\lambda )q_i^{\mathrm{P}};\frac{\partial q_i}{\partial \lambda }=q_i^{\mathrm{U}}-q_i^{\mathrm{P}}.$$ (14)

In the above equations, q_i represents the partial charge on atom i, and the superscript U and P denote the unprotonated and protonated states, respectively. While the λ derivatives of U^dir and U^corr are straightforward, the derivative of U^rec can be written as

$$\frac{\partial U^{\text{rec}}}{\partial \lambda }=\sum _{m_1=0}^{K_1-1}\sum _{m_2=0}^{K_2-1}\sum _{m_3=0}^{K_3-1}\frac{\partial Q(m_1,m_2,m_3)}{\partial \lambda }·({\mathrm{\Theta }}_{\text{rec}}★Q)(m_1,m_2,m_3).$$ (15)

Note, the factor 1/2 in Eq. 11 does not appear here because of the contribution from the convolution term where Q is linear in λ.

Correction of finite-size effects on pK_a calculation

It is well known that charging free energies calculated with lattice-sum methods under periodic boundary conditions are dependent on the periodic box size.^45–47 The finite-size error has several physical origins, including the periodicity induced net charge interaction and undersolvation, discrete solvent effects, as well as residual integratd potential effects.⁴⁷ Rocklin et al. recently showed that, for a system neutralized with counter-ions, the finite-size error in the charging free energy of a ligand (with +1 or −1 charge) is dominated by the discrete solvent effects due to an offset potential that compensates for the potential generated by discrete solvent.⁴⁷ The corresponding offset energy in charging a titratable group is given as⁴⁷

$$\mathrm{\Delta }{G}^{\text{offset}}=\frac{2\pi }{3}\kappa {\gamma }^{\text{solv}}Q{\rho }^{\text{solv}},$$ (16)

where κ is the electrostatic constant, ρ^solv is the solvent number density, ρ^solv = N^sol/V, where N^solv and V are the number of solvent molecules and volume of the periodic box, respectively. Q is the charge of the titratable site, i.e., −1 for Asp/Glu or +1 for His/Lys, and γ^solv is the quadrupole moment trace of the solvent model relative to a van der Waals interaction site. For a solvent model with a single van der Waals interaction site, e.g., TIP3P,⁴⁸ it is ${\gamma }^{\text{solv}}={\sum }_{\mathrm{i}}^n{q}_i{r}_i^2$, where n is the number of atoms, q_i is the atomic partial charge, and r_i is the distance to the van der Waals interaction site (oxygen). For TIP3P model γ^solv is calculated as 0.764 e· Ų.

From Eq. 16 we can obtain the difference in the offset potential between the protein and model compound simulations,

$$\mathrm{\Delta }\mathrm{\Delta }{G}^{\text{offset}}=\frac{2\pi }{3}\kappa {\gamma }^{\text{solv}}Q\left(\frac{N_{\text{prot}}^{\text{solv}}}{V_{\text{prot}}}-\frac{N_{mod}^{\text{solv}}}{V_{mod}}\right),$$ (17)

where the subscripts prot and mod refer to the protein and model, respectively. In the model compound simulations, since the solute is very small compared to the simulation box, the solvent number density approaches that of the pure solvent ρ^pure, which is 0.0333679 ų for water at ambient temperature and pressure. Combining Eq. 16 and 4, we obtain the corresponding pK_a correction,

$$\mathrm{\Delta }p{K}_a^{\text{corr}}=\pm \frac{\mathrm{\Delta }\mathrm{\Delta }{G}^{\text{offset}}}{ln(10)RT}.$$ (18)

where the negative sign is for acid groups and positive sign is for basic groups. Note, charging a basic group refers to the opposite of the deprotonation reaction. Thus, ΔpK_a^corr is negative for both acidic and basic groups.

Results and Discussion

Model parameterization and titration

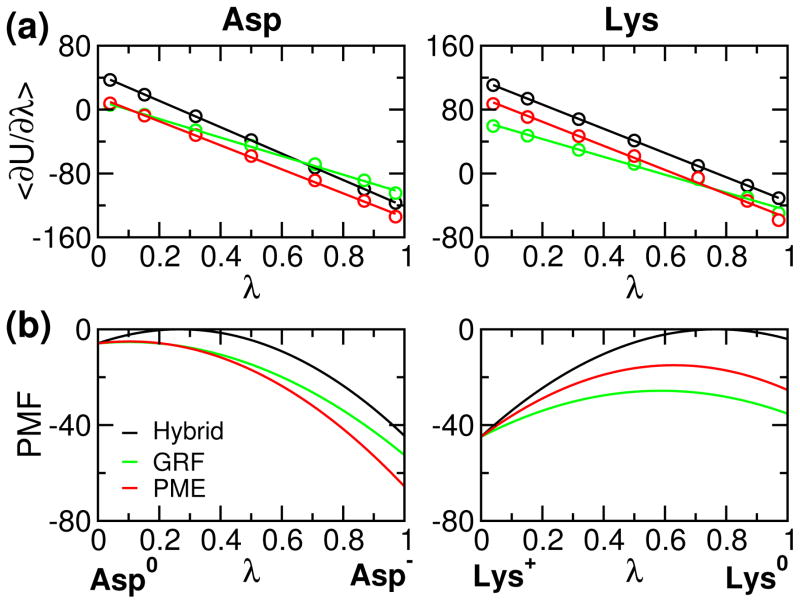
To validate the implementation, we first examine the PMF for model compound titration. It is expected that the GRF- and PME-based results are similar, while they are quite different from the hybrid-solvent simulation since the latter uses the GB model to calculate electrostatic forces along titration coordinates. Fig. 1 shows the average force obtained from thermodynamic integration and corresponding PMF for model Asp and Lys. It can be seen that linear fitting of the average force is perfect for hybrid-solvent simulations, while there is a small but negligible deviation for GRF- and PME-based simulations due to the use of explicit solvent (see earlier discussion). Thus, quadratic function is an accurate approximation of the PMF function for model compound titration. Comparing the GRF- and PME-based forces, we see that the deviation between the two becomes larger as λ approaches 1 for Asp (Asp⁻) and 0 for Lys (Lys⁺). This is because PME provides more stabilization for the charged state as compared to GRF, as shown in our previous study.³⁰ Consequently, the free energy of deprotonation, i.e., charging for Asp and discharging for Lys, is larger in the PME-based simulation, consistent with our previous finding.³⁰ It is worthwhile noting that the charging free energy for Asp and Lys (PMF difference between λ 0 and 1) is very similar in the hybrid-solvent but not in the GRF- and PME-simulations. This is because the all-atom simulations are able to capture the phenomenon of charge asymmetry, attributable to the stronger interactions of anions with water,^42,49 which is neglected in the GBSW implicit-solvent model.

Figure 1.

Average force and corresponding potential of mean force (PMF) for deprotonation of model compounds Asp and Lys. (a) Average force 〈∂U/∂λ〉 calculated at different values of λ. The average force was obtained from the second half of the 1-ns thermodynamic Integration (SI). Lines are the best fits to a linear function 2A(λ − B) (see Eq. 5). (b) Corresponding PMF function of λ (integration of the average force). In (a) and (b), data from the hybrid-solvent,⁸ GRF-²⁵ and PME-based CpHMD simulations are shown in black, green and red, respectively. The unit of force or PMF is kcal/mol.

Next we examine the titration simulations of model compounds using PME-based CpHMD in comparison to the hybrid-solvent and GRF-based CpHMD (Table 1). It is encouraging that, with 5 ns sampling per replica, the PME-based CpHMD is able to achieve a precision similar to experiment (0.04–0.08 for the model alanine pentapeptide Ac-AA-X-AA-NH₂ where X denotes the titratable residue).⁵⁰ This precision is on par with the hybrid-solvent CpHMD, which is known to deliver very fast convergence due to the use of the GB model for calculation of solvation forces along titration coordinates.^8,9 Remarkably, the performance of the PME-based simulations is much better than that of the GRF-based simulations. With half of the sampling time per replica, random errors are reduced by more than half, which may be attributed to the energy fluctuation in the cutoff-based electrostatic methods. We note that, due to small fitting errors and perhaps nonlinearity in solvent response (see earlier discussion), there is often a small deviation between the calculated model pK_a and reference value. In this work using the original fitting parameters, the deviations for Lys/Asp/Glu/His were 0, 0.1, 0.2 and 0.3, respectively. The deviations were then minimized using the iteration of titration simulation, pK_a calculation and parameter adjustment (details see Table S5).

Table 1.

Calculated pK_a’s for model Asp, Glu and His

Model	Ref	Hybrid	GRF	PME
Asp	4.0	3.8±0.02	3.5±0.17	4.0±0.09
Glu	4.4	4.1±0.01	4.1±0.13	4.5±0.09
His	6.5	6.9±0.01	6.8±0.10	6.5±0.02
His-Nδ	6.6	–	–	6.7±0.03
His-Nε	7.0	–	–	6.9±0.03
Lys	10.4	10.4±0.02	10.4±0.12	10.4±0.04

Average pK_a’s and standard deviations based on five independent sets of pH-replica CpHMD simulations. Reference pK_a’s refer to the experimentally measured pK_a’s of blocked single amino acids.⁵¹ The microscopic pK_a’s of His-N^δ and His-N^ε are taken from Ref.⁵² All these values are identical to the previous CpHMD work.^6–8,25 The hybrid-solvent simulation used 5 replicas, each of which was sampled for 10 ns with λ-update every 10 MD steps. The GRF-based simulation used 10 pH replicas, each of which was sampled for 10 ns.²⁵ The PME-based simulation used 5 pH replicas, each of which was sampled for 5 ns. The PMF functions with parameters slightly adjusted to minimize the deviations from the reference pK_a’s were used (see Table S5).

Convergence of protein titration simulations

We test the performance of PME-CpHMD using titration simulations of four proteins, HP36, BBL, HEWL and SNase. These proteins were chosen, since they have been used to benchmark the previous versions of CpHMD methods,^8,25,40 and more importantly, they contain residues with large pK_a shifts and coupled titration and as such serve as a stringent test for the accuracy of pK_a calculations. ⁵³ The pK_a’s of SNase are particularly challenging for the traditional PB-based electrostatic calculations and empirical pK_a prediction methods,^53–56 as there are many buried residues clustered together and titrating in a similar pH range (strong coupling).

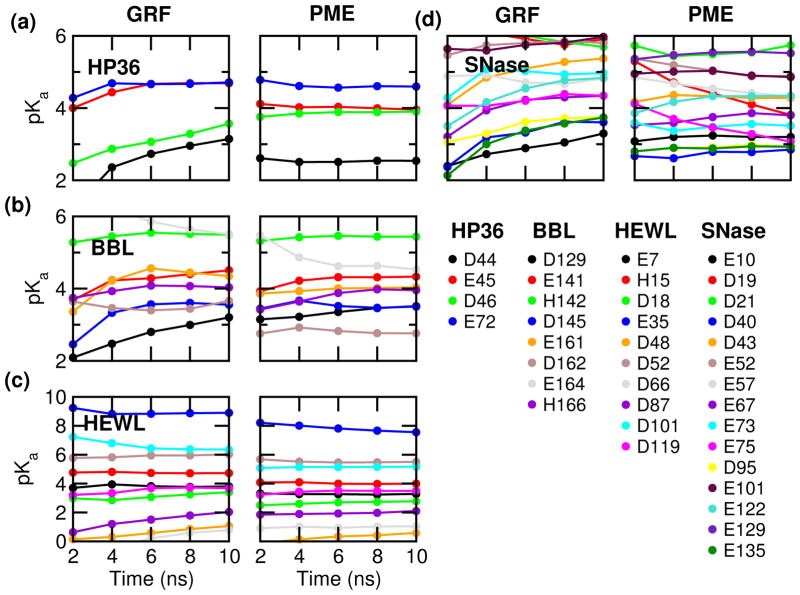
We first examine the pK_a convergence by monitoring the pK_a’s cumulatively calculated as a function of simulation time (Fig. 2) and comparing the pK_a values calculated with the first and second half of the 10-ns simulation. Compared to the GRF-based simulations, the convergence is much faster for all four proteins. Half of the 37 pK_a’s converge within 5 ns (per replica), defined as the difference between the first and second half of the simulation below 0.1 units. In contrast, only 7 pK_a’s become stable after 5 ns in the GRF-based simulations. At 10 ns, most pK_a’s are converged in the PME-based simulations but not in the GRF-based simulations.

Figure 2.

Convergence of the calculated pK_a’s for HP36 (a), BBL (b), HEWL (c) and SNase (d). pK_a calculation was performed every 2 ns per replica based on the cumulative values of the unprotonated fractions at all pH. The left and right panels present the GRF-²⁵ and PME-based CpHMD simulations.

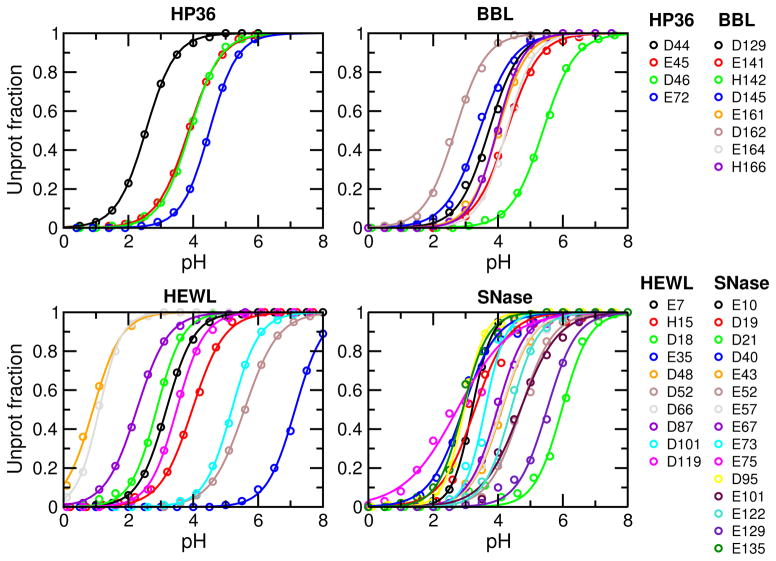
To evaluate convergence, we also inspect the titration plots, i.e., fitting of the unprotonated fractions at different pH to the generalized Henderson-Hasselbalch (HH) equation, as unconverged pK_a’s typically manifest themselves in the “non-HH” behavior of the unprotonated fractions. As shown in Fig. 3, the fitting quality is excellent for all residues, with the chi-square value ranging from 0.00017 to 0.038 and correlation coefficient greater than 0.9955, even for Asp19 and Asp21 of SNase, which appear to have slightly larger fitting errors than other residues based on visual examination (see later discussion). These data are consistent with the overall good convergence. Finally, convergence of protonation state sampling can perhaps be best judged by examining the unprotonated fractions (S) cumulatively calculated as a function of simulation time. This is because S values are the direct representation of protonation state sampling and as such they are more sensitive than pK_a values. Consistent with the calculated pK_a’s vs. time (Figure 2), most S values converge after 10 ns, except for Glu35/Asp48 of HEWL, and Asp19/Asp21/Glu75 of SNase, which are among those with large pK_a errors (Supporting Information, Fig. S1–S4). However, encouragingly, the changes of S are all but one in the direction of decreasing the pK_a deviations from experiment (see later for more discussion).

Figure 3.

Titration plots of HP36, BBL, HEWL and SNase. Unprotonation fractions at different pH were calculated based on the 10-ns CpHMD simulations. Solid curves represent best fits to the generalized HH equation. For all curves, chi-square of fitting is in the range 0.00017–0.038 and correlation coefficient is in the range 0.9955–0.999965.

Overall accuracy of protein titration simulations

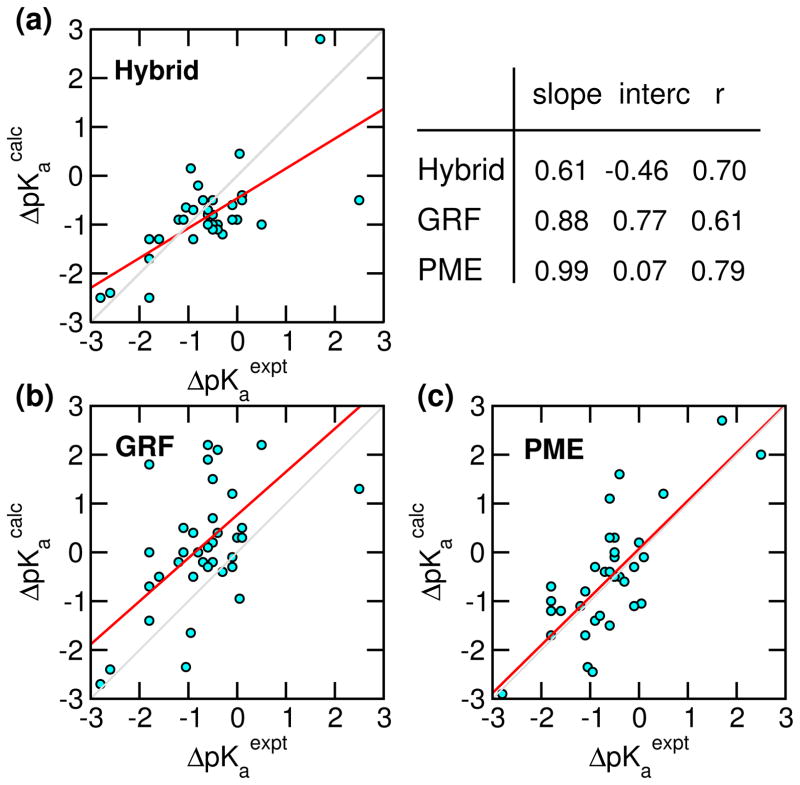
Next we examine the accuracy of the calculated pK_a’s in comparison to the GRF-based as well as the hybrid-solvent CpHMD data (Table 2 and Fig. 4). The latter are used because hybrid-solvent CpHMD gives the most accurate pK_a prediction thus far within the CpHMD framework.^8,57 The overall average absolute and rms deviations from the PME-based simulations are respectively 0.61 and 0.77, significantly lower than the GRF-based simulations (1.1 and 1.4), and similar to the hybrid-solvent data (0.59 and 0.76). Linear regression of the calculated pK_a shifts (relative to model values) vs. experimental data gives a correlation coefficient of 0.79 for the PME-based simulations, significantly higher than the GRF-based (0.61) and hybrid-solvent data (0.70). Remarkably, the regression slope is about 1 and intercept is nearly 0 for the PME-based data, suggesting the absence of significant systematic errors. In contrast, the GRF-based data gives a sizable intercept of 0.77, indicative of a systematic overestimation of pK_a shifts, which may be attributed, in part to the overstabilization of neutral states by GRF as shown in our previous work,³⁰ and in part to the lack of a finite-size correction as shown by Reif et al. in simulations based on the Baker-Watts reaction field.^31,32 The hybrid-solvent data shows a slope well below one (0.61), indicative of a systematic underestimation of pK_a shifts, which is due to the underestimation of desolvation penalty by the GBSW model (”too wet”).^8,9,57 The above-mentioned trend can also be seen from the histogram of pK_a deviations, pK_a^calc - pK_a^expt (Fig. S6). Accordingly, the histogram of hybrid-solvent simulations shows a larger population in the negative region, while the histogram of GRF simulations shows a larger population in the positive region. In contrast, the histogram of PME simulations is more or less symmetric around 0.

Table 2.

Calculated and experimental pK_a’s of four proteins HP36, BBL, HEWL and SNase

Residue	Expt	Hybrid	GRF	PME	Resdue	Expt	Hybrid	GRF	PME
HP36					SNase
Asp44	3.1	2.7 (0.1)	3.5 (0.5)	2.6 (0.0)	Glu10	2.8	3.1(0.1)	3.9 (0.5)	3.2 (0.0)
Glu45	4.0	3.4 (0.3)	4.8 (0.1)	3.9 (0.0)	Asp19*	2.2	2.3 (0.1)	5.8 (0.1)	3.3 (0.6)
Asp46	3.5	3.0 (0.1)	4.2 (0.6)	3.9 (0.0)	Asp21	6.5	3.5 (0.3)	5.3 (0.5)	6.0 (0.3)
Glu72	4.4	3.5 (0.2)	4.7 (0.0)	4.6 (0.0)	Asp40*	3.9	3.1 (0.2)	3.9 (0.3)	2.9 (0.0)
max		0.90	0.80	0.50	Glu43	4.3	3.8 (0.1)	5.6 (0.3)	4.1 (0.1)
avg		0.60	0.55	0.30	Glu52*	3.9	3.9 (0.0)	5.9 (0.0)	4.7 (0.2)
BBL					Glu57	3.5	3.7 (0.2)	4.8 (0.0)	4.1 (0.3)
Asp129	3.9	3.1 (0.0)	3.7 (0.5)	3.7 (0.2)	Glu67	3.8	3.7 (0.1)	4.5 (0.2)	4.0 (0.2)
Glu141	4.5	4.0 (0.0)	4.7 (0.2)	4.3 (0.0)	Glu73	3.3	3.5 (0.1)	4.9 (0.0)	3.6 (0.1)
His142*	6.5	6.9 (0.1)	5.5 (0.0)	5.4 (0.0)	Glu75*	3.3	3.5 (0.3)	4.4 (0.2)	2.7 (0.4)
Asp145	3.7	2.8 (0.2)	3.6 (0.0)	3.4 (0.1)	Asp77	<2.2	<0	<−1	<−1
Glu161	3.7	3.9 (0.3)	4.2 (0.2)	4.0 (0.0)	Asp83	<2.2	2.5 (0.1)	−0.2	0.0
Asp162	3.2	3.8 (0.3)	4.0 (0.3)	2.7 (0.1)	Asp95	2.2	2.7 (0.6)	4.0 (0.3)	3.0 (0.0)
Glu164	4.5	3.9 (0.1)	4.9 (0.6)	4.3 (0.2)	Glu101*	3.8	3.6 (0.1)	6.3 (0.3)	4.7 (0.2)
His166*	5.4	5.8 (0.1)	4.1 (0.0)	4.1 (0.2)	Glu122	3.9	3.6 (0.0)	5.1 (0.4)	4.4 (0.0)
max		0.90	1.3	1.3	Glu129*	3.8	3.7 (0.1)	6.6 (0.2)	5.5 (0.0)
avg		0.55	0.56	0.51	Glu135*	3.8	3.4 (0.2)	4.1 (0.5)	2.9 (0.0)
HEWL					max		3.0	3.6	1.7
Glu7	2.6	2.7 (0.0)	3.7 (0.1)	3.2 (0.0)	avg		0.46	1.5	0.70
His15*	5.5	6.6 (0.1)	4.8 (0.0)	4.0 (0.0)
Asp18	2.8	3.1 (0.1)	3.8 (0.4)	2.9 (0.1)
Glu35*	6.1	7.2 (0.2)	9.0 (0.1)	7.1 (0.4)
Asp48	1.4	1.6 (0.5)	1.6 (0.6)	0.9 (0.3)
Asp52*	3.6	2.9 (0.1)	6.1 (0.1)	5.6 (0.1)
Asp66	1.2	1.5 (0.6)	1.3 (0.7)	1.1 (0.0)
Asp87	2.2	1.5 (0.4)	2.6 (0.7)	2.3 (0.2)
Asp101	4.5	3.0 (0.1)	6.2 (0.2)	5.2 (0.0)	All
Asp119	3.5	2.9 (0.0)	3.8 (0.2)	3.5 (0.0)	max		3.0	3.6	2.0
max		1.5	2.9	2.0	avg		0.59	1.1	0.61
avg		0.66	1.1	0.66	rmsd		0.76	1.4	0.77

Experimental pK_a values were determined by NMR titration for HP36,⁶¹ BBL,^62,63 HEWL⁶⁴ and SNase.⁶⁵ pK_a’s were determined by following ¹³C chemical shifts except for those of the two histidine in BBL, which were determined by following the sidechain proton chemical shifts.⁶² The accuracy of pK_a’s derived from ¹³C and sidechain protons is believed to be about 0.5 and 0.1–0.2 pH units.⁶⁴ The hybrid-solvent data was taken from Ref.,⁸ where pK_a’s were calculated based on the last 0.75 ns of the 1-ns (per replica) simulations. The pK_a’s of Asp and Glu residues of BBL were not reported in Ref.⁸ The GRF data was taken from Ref.²⁵ except for the simulation of SNase which was performed in this work using the same protocol as in Ref.²⁵ The pK_a’s of GRF- and PME-CpHMD were calculated from the second half of the 10-ns (per replica) simulations. An estimate of statistical uncertainty was calculated as half of the difference between the first and second half of the simulations. Residues denoted with an asterisk have absolute pK_a errors above 0.6 pH units and are discussed in the main text.

Figure 4.

Correlation between the experimental and calculated pK_a shifts relative to model compound values for hybrid-solvent, GRF-, and PME-based CpHMD simulations. The diagonal gray line is added to guide the eye. The red line represents linear regression with the slope, intercept (interc) and correlation coefficient (r) indicated. The corresponding pK_a’s are given in Table 2.

Sources for the deviations between calculated and experimental pK_a’s

To understand the cause for the deviations between experimental and calculated pK_a’s by PME-CpHMD, we identified 11 residues that show absolute errors above 0.6 units (Table 2, highlighted with asterisks): His142 (−1.1) and His166 (−1.3) of BBL; His15 (−1.5), Glu35 (1.0) and Asp52 (2.0) of HEWL; Asp19 (1.1), Asp40 (−1.0), Glu52 (0.8), Glu101 (0.9), Glu129 (1.7) and Glu135 (−0.8) of SNase. Among these residues, except for Asp40 and Glu135 of SNase, the calculated pK_a’s for the acidic groups are too high, while those for histidines are too low, indicating that the neutral state was consistently overly favored in the simulation. We examine the structural environment and dynamical interactions involving these residues.

First, acidic residues that form persistent salt bridges show underestimated pK_a’s to favor the charged state. For example, Asp40 and Glu135 of SNase form salt-bridge interactions with Arg35 and Arg105, respectively, leading to the underestimation of the pK_a’s by 0.9 and 0.8 units, respectively. This type of error is also seen in the hybrid-solvent data (Table 2, underestimation of 0.8 and 0.4 units, respectively) as well as the previous GB-based CpHMD simulations,⁸ which can be reduced given more extensive sampling of the solvent-separated configurations.^8,40 In fact, the significant improvement (by 0.6 units) of the pK_a of Asp48 from HEWL in the second 5 ns of the simulation is due to the weakened salt bridge with Arg61 (Fig. S7).

Second, (partially) buried residues that form persistent hydrogen bonds have the pK_a’s overly shifted to favor the neutral state. For example, His15 of HEWL forms persistent hydrogen bond with the hydroxyl group of Thr89, showing an overly downward-shifted pK_a by 1.5 units. Glu129 of SNase is in persistent hydrogen bonding with the backbone amide group of Val111, showing a calculated pK_a too high by 1.7 units. We suggest the overstabilization of the neutral state in these cases is due to the inadequate structural relaxation of the buried site, which results in an overestimation of the desolvation penalty. The same trend can be seen in the GRF-based data, although the overshifts there are exacerbated. Such overshifts are not seen in the hybrid-solvent simulations, which may be in part attributed to the fortuitous cancellation of errors between the underestimation of desolvation by the GBSW model and the overestimation of desolvation resulting from inadequate structural relaxation based on our previous studies of buried residues.^9,57

The third group of residues with moderately large pK_a errors (1–1.5 units) are those whose solvent accessibility is blocked by hydrophobic groups in direct contact. In order for CpHMD to reproduce experimental pK_a’s of buried residues, our previous work showed that the ionization-induced increase in solvent exposure needs to be accurately captured in the simulation, which sometimes requires local unfolding.⁵⁷ The latter aspect has been also demonstrated by the work of Warshel group⁵⁸ and Garcia-Moreno group.⁵⁹ In the PME-based simulations, we found that H142, H166 of BBL and Glu101 of SNase are in persistent contact with Leu167, Leu144 and Leu124, respectively, preventing them from becoming fully exposed to solvent upon charging. As a result, the charged state is insufficiently stabilized, leading to the pK_a underestimation by 1.1, 1.3 units for H142, H166 and overestimation by 0.9 units for Glu101. Note, the overestimated pK_a shifts due to under-solvation of charged state can also be seen in the GRF-based results, although the deviation for Glu101 is much worse (pK_a is 2.5 units too high). The pK_a overshifts are not seen in the hybrid-solvent simulations due to the error cancellation mentioned previously.

The last group of residues, Glu35 and Asp52 of HEWL and Asp19 and Asp21 of SNase, showing large pK_a deviations from experiment are the so-called coupled residues, which are often found as catalytic dyad in enzyme active sites. with one elevated and one depressed pK_a relative to the model value. In addition to desolvation and electrostatic repulsion, these residues may also be involved in hydrogen bonding and electrostatic interactions, making the pK_a’s challenging to predict, as individual energetics needs to be modeled accurately. Our calculated pK_a’s for Glu35 and Asp52 of HEWL are 7.1 and 5.6, respectively, in correct order but respectively 1.0 and 2.0 units higher than experiment (6.1 and 3.6). The calculated pK_a shift of Asp52 has a wrong direction and carries the largest absolute error among all the calculated pK_a’s. We suggest the error can be attributed to the aforementioned inadequate structure relaxation in the presence of persistent hydrogen bonding with the sidechain amide group of Asn59 in addition to the insufficient sampling of the coupled titration. The significant improvement (by 0.7 units) of the calculated pK_a for Glu35 in the second 5 ns of the simulation is due to a deprotonation-induced increase in the solvent exposure (Fig. S7).

The highly coupled pK_a’s for Asp19 and Asp21 of SNase are notoriously difficult to predict due to hydrogen bonding between Asp19 and the backbone amide group of Asp21. In fact, in the blind pK_a prediction exercise of 2009,⁵⁴ neither the empirical PROPKA,⁵⁶ Poisson-Boltzmann calculations⁵⁵ or GBSW-based CpHMD⁹ were able to reproduce the experimental pK_a order. Remarkably, our calculated pK_a’s for Asp19 and Asp21 of SNase are 3.3 and 6.0, in correct order, although respectively 1.1 units too high and −0.5 units too low compared to experiment (2.2 and 6.5). The overestimation of the pK_a of Asp19, which is the lower of the two catalytic pK_a’s, is consistent with that of Asp52 in HEWL (calculation error of 2 units), and can be linked to the stable hydrogen bonding network with the sidechain hydroxyl, backbone amide of Thr22 and the backbone amide of Asp21. In addition to the correct order, the splitting of the two pK_a’s (4.3) is well reproduced by the PME-based CpHMD (2.7), as compared to the GRF- (−0.5) and hybrid-solvent (1.2) simulations.

Effect of prolonged sampling

The above analysis suggests that inadequate sampling of structural relaxation accompanying the switch in protonation state is a major contributor to the deviations between experimental and calculated pK_a’s with 10-ns sampling time. To investigate the sampling issue, which is particularly relevant for SNase where out of 17 Asp/Glu residues, 12 titrate in the pH range 3–4 (Fig. 3), we prolonged the simulations to 16 ns per replica. Time series of the unprotonated fractions and pK_a’s of Asp19/Asp21/Glu75 that are not converged at 10 ns are converged after 12 ns (Fig. S4 and S5). To understand if the extra 6-ns sampling offers improvement in accuracy, we compare the pK_a’s calculated based on 10–16 ns to those based on 5–10 sampling for the aforementioned residues with absolute deviations greater than 0.6, Asp19 (1.1), Asp40 (−1.0), Glu52 (0.8), Glu101 (0.9), Glu129 (1.7) and Glu135 (−0.8). For Asp19, Asp21, Asp40 and Glu135, the deviations are decreased by 0.1, 0.3, 0.4 and 0.2, respectively; for Glu52 and Glu129 the deviations are increased by 0.2, 0.1; and for Glu101 the deviation is unchanged. Overall, the maximum, average and rmsd of the calculated pK_a’s based on 10–16 ns are nearly the same as those based on 5–10 ns. These data suggest that while improvement is visible (for example, coupled residues Asp19 and Asp21), significant longer simulations may be needed in order to achieve overall improvement.

Concluding remarks

We developed the PME-based all-atom CpHMD and demonstrated the accuracy and convergence in protein titration simulations. Using 10 ns sampling per replica, the average absolute and rms errors of the calculated pK_a’s are significantly lower than those from the GRF-CpHMD, and similar to the hybrid-solvent CpHMD (average absolute and RMS deviations are smaller by 0.01). The correlation with experimental pK_a shifts are significantly improved over both GRF- and hybrid-solvent based simulations. Remarkably, the PME-based simulations give a linear regression slope of 1 and intercept near 0, suggesting that systematic errors are largely absent.

Analysis showed that large deviations are from buried residues and those in stable hydrogen bond or salt bridge, which presents kinetic barrier to the configurations favored by the alternative protonation state. These data suggest that the pK_a deviations observed in this work can be reduced given more extensive sampling of the ionization-induced change in solvent exposure as well as the breakage of hydrogen bond or salt bridge. Additional 6 ns sampling for SNase showed that, while some pK_a’s are brought closer to experimental values, an overall improvement may require significantly longer simulations. Nevertheless, the agreement between the predicted and experimental pK_a’s for the highly coupled catalytic dyad Asp19/Asp21 in SNase (in correct order and deviations of 1.1/−0.5 with 10 ns or 1.0/−0.2 with 16 ns simulations) is remarkable and suggests that the method may be deployed for the investigation of pH-coupled conformational dynamics of enzymes.

We note a major limitation of the current implementation is speed. Compared to the conventional PME MD, PME-CpHMD adds about 30% CPU time (based on the timing statistics of the four test proteins), similar to the hybrid-solvent and GRF-based CpHMD. However, we should note that current implementation is not optimized and is based on an MD engine CHARMM c36b2 which does not utilize the more recent parallelization methods. In principle, PME-based CpHMD adds only a fractional computational cost, because the number of titration coordinates is about two orders of magnitude smaller than the number of solute atoms. Another area of improvement is in the use of titratable water,^16,25 which allows solute-solvent proton exchange and serves to maintain the total system charge neutral, an important part in PME-based simulations.⁴⁵ However, for the latter purpose, alternatives such as the recently developed proton buffer method⁶⁰ may be computationally more efficient. Thus, with the emergence of GPUs and new algorithms of parallel processing, we expect the integration of PME-based CpHMD in standard MD packages to enable pH-controlled MD simulations on the order of hundreds of nano seconds on routine basis. As such we also anticipate a systematic improvement of accuracy in the calculated pK_a’s. Finally, we shall emphasize that the PME-CpHMD can be applied to any system that current force fields can represent, thus opening a door to new insights into pH-dependent phenomena involving not only soluble proteins but also transmembrane proteins, nucleic acids, surfactants and polysaccharides.

Computational Details

Preparation of simulation systems

Model compounds are single amino acids (Asp, Glu, His and Lys) acetylated at N-terminus (ACE) and N-methylamidated at C-terminus (CT₃), hydronium (H₃O⁺) and hydroxide (OH⁻). The four test proteins are: the 36-residue subdomain of villin headpiece, HP36(PDB: 1VII), 45-residue binding domain of 2-oxoglutarate dehydrogenase multienzyme complex, BBL (PDB: 1W4H), 129-residue hen egg white lysozyme, HEWL (PDB: 2LZT), and 135-residue hyperstable variant (Δ+PH) of staphylococcal nuclease (PDB: 3BDC). N-terminus of all proteins was left in the free and charged form, while the C-terminus was blocked with CT3. The terminal groups were not made titratable, as they do not interact with the protein and often times no experimental pK_a’s are available to compare with. However, this is an issue that will be addressed in our future work, perhaps by utilizing the model data obtained and collected by Pace group^50,66 For protein structures, the crystal waters and hydrogens (if any) were stripped and the HBUILD function in CHARMM was used to add hydrogen atoms. Model compounds were constructed using CHARMM.²⁰ The structure was solvated in a box (cubic for model compounds and truncated octahedron for proteins) filled with the CHARMM modified TIP3P water²⁰ with a distance of at least 10 Å between the solute and edges of the box. The unit-cell lattice parameters are: 30 (model compounds), 54 (HP36), 59 (BBL), 69 (HEWL) and 70 Å (SNase). To test the finite-size effects and corrections, additional box sizes were considered for the two smaller proteins HP36 (43 Å) and BBL (49 Å).

To maintain a constant net charge for the system, N_titr randomly chosen TIP3P water was replaced with titratable water that can convert to hydroxide or hydronium.²⁵ For simplicity, we refer to the former titratable water as hydroxide and the latter as hydronium. For model compounds, 1 hydroxide or hydronium was added for the titration of model Asp/Glu or model His/Lys. For proteins, 4 hydroxide were added for HP36, 2 hydronium/6 hydroxide for BBL, 1 hydronium/9 hydroxide for HEWL, and 2 hydronium/17 hydroxide for SNase. To neutralize the simulation box, Na⁺ or Cl⁻ counterions were then added. For proteins, additional salt ions were added to reach the experimental ionic strength: 150 mM for HP36,⁶⁷ 200 mM for BBL,^62,63 50 mM for HEWL,⁶⁴ and 100mM for SNASE.⁶⁵ Thus, the model compound simulations contained 1 Na⁺ for Asp/Glu and 1 Cl⁻ for His/Lys, while the protein simulations contained 10 Na⁺/13 Cl⁻ for HP36, 16 Na⁺/20 Cl⁻ for BBL, 2 Na⁺/12 Cl⁻ for HEWL, and 15 Na⁺/24 Cl⁻ for SNASE.

Simulation protocol

The method described in this work was implemented in an inhouse modified version of CHARMM (release c36b2).²⁰ Particle mesh Ewald (PME) method was added to the PHMD module to account for the electrostatic force on the fictitious λ-particles. The CHARMM22/CMAP additive force field was used to represent the proteins and the CHARMM modified TIP3P water model was used to represent nontitratable solvent. The force field parameters for titratable water are taken from our previous work.²⁵

All simulations were performed using the pH replica-exchange (pH-REX) protocol,⁸ where each replica underwent constant NPTpH molecular dynamics (MD) at 300 K, 1 atm pressure and specified pH. The temperature, pressure and pH were controlled by Hoover thermostat,⁶⁸ Langevin piston pressure coupling algorithm,⁶⁹ and CpHMD,^6,7 respectively. Periodic boundary condition was applied to all simulations. The SHAKE algorithm was applied to all bonds involving hydrogen atoms to allow a 2-fs integration time step. In the PME calculation, the real-space cutoff was 12 Å and grid spacing was 1 Å. The van der Waals energies and forces were smoothly turned off over the range of 10–12 Å via a switching function. The titration (λ) coordinates were propagated using the Langevin algorithm with a collision frequency of 5 ps⁻¹ (default setting in PHMD). The mass of the λ particles was set to 10 atomic mass units (default setting in PHMD). The parameter β used in U^barr was set to 2.0 kcal/mol for all titratable residues (see Table S5).

For derivation of model PMF functions, thermodynamic integration was performed using 1-ns CPT MD at θ values of 0.2, 0.4, 0.6, 0.7854, 1.0, 1.2, and 1.4. The second half of the trajectory was used to determine the average force 〈∂U/∂θ〉. Five independent pH-REX simulations were conducted for each model compound. Each pH-REX simulation utilized five pH replicas occupying the pH conditions of pK_a^ref−2, pK_a^ref−1, pK_a^ref, pK_a^ref+1, pK_a^ref+2, where pK_a^ref refers to the reference model pK_a value. Each pH replica was simulated for 5 ns.

Prior to simulations energy minimization was performed using steepest descent (SD) and adoptive basis Newton-Ralphson (ABNR) methods. Three rounds of minimization each consisting of 50 steps SD followed by 50 steps ABNR were performed. Finally, 100 steps of SD followed by 100 steps of ABNR minimization were performed. Protein simulations began with a heating stage followed by equilibration at pH 7 before invoking pH-REX simulations. In the heating stage, the desired temperature of 300K was achieved in 120 ps with the heavy atoms harmonically restrained by a force constant of 5.0 kcal/mol·Å. In the equilibration stage, two 20-ps simulations were performed with the force constants of 1.0 and 0.1 kcal/mol·Å, respectively, followed by a 20-ps unrestrained MD.

In the pH-REX simulation, identical starting structure was used in all pH replicas and unless otherwise noted each replica was simulated for 10 ns. The pH spacing was 0.5 pH unit and the pH range extended at least 1 unit above and below the highest and lowest experimental pK_a values. Specifically, the pH range was 1 to 6.5 for HP36, 0.5 to 8.0 for BBL, −1.0 to 9.5 for HEWL and SNase. An exchange between adjacent pH replicas was attempted every 100 MD steps or 0.2 ps in model compound titration and 500 steps or 1 ps in protein simulations. The average replica-exchange ratio was above 40%. In the simulations of HP36, BBL and HEWL, most replicas walked through the entire pH range, while in the simulation of SNase, only half of the replicas did so (Fig. S8–S11).

pK_a calculation

Based on the λ values, which were collected after each exchange step, the unprotonated fractions (S) were calculated using the same two cutoffs (0.9/0.1) as in the previous versions of CpHMD,^{6–8,16,25,40}

$$S=\frac{N^{\mathrm{U}}}{N^{\mathrm{P}}+N^{\mathrm{U}}}$$ (19)

Here N^U and N^P represent the number of deprotonated (λ > 0.9) and protonated (λ < 0.1) states, respectively. The pK_a was then calculated by fitting S at simulated pH conditions to the generalized Henderson-Hasselbalch or Hill equation,

$$S=\frac{1}{1+{10}^{n(\mathrm{p}{K}_a-\text{pH})}},$$ (20)

where n is the Hill coefficient.

We compared the pK_a’s calculated using two sets of λ cutoffs: 0.1/0.9 and 0.2/0.8 (see Table S6). Most pK_a’s are the same; the largest difference is 0.1; the overall comparison with experiment is also very similar. The RMSD, regression slope and intercept from the calculations using the 0.1/0.9 cutoffs are 0.77, 0.98 and 0.06, while the corresponding values with the 0.2/0.8 cutoffs are 0.76, 1.01 and 0.11. This behavior is consistent with the previous versions of CpHMD.^{6–8,16,25,40} With the two sets of cutoffs, the fraction of mixed states is in the range of 0.1–0.45 and 0.05–0.3, respectively. Very low fractions of mixed states are typically found at low and high pH conditions, whereas higher fractions are found around the titration pH. We note that, given a set of cutoffs such as 0.1/0.9, the parameter β that controls the barrier height can be adjusted to achieve a desired fraction of mixed states, taking into account higher barrier height leads to slower λ transition. Optimization of the β parameter will be a topic in our future work.

Finite-size correction of protein pK_a’s

We applied Eqs. 17 and 18 to calculate the pK_a corrections to account for the box size dependence. It follows that the corrections are: −0.5 for Asp/Glu of HP36; −0.5 for Asp and −0.4 for Glu/His of BBL; −0.9 for Asp/Glu and −0.8 for His of HEWL; and −0.9 for Asp/Glu/His of SNase. These corrections are very similar to those pre-calculated using the lattice-parameter-based volume of the protein system (Table S1 and S2). Thus, the pK_a corrections will be incorporated into the reference pK_a’s and implemented in the CpHMD code in the future. More details are given in SI. Finally, to test the finite-size effects and validate the pK_a corrections, we performed additional simulations for two small proteins, HP36 and BBL, using a smaller box. The differences in the pK_a’s are very similar to those estimated using the finite-size corrections (Table S3).