Dopamine reward prediction error signal codes the temporal evaluation of a perceptual decision report

Significance

How do animals learn to take correct actions based on uncertain observations? Although dopamine neurons can guide learning in conditioning experiments, their role in decision-making tasks is poorly understood. How can they code reward prediction errors and simultaneously exhibit decision-making processes and beliefs about the state of the environment? Using modeling work and analysis of data recorded from monkeys detecting weak stimuli delivered at uncertain times, we propose some answers to these questions. Specifically, we explain how the certainty about the presence of a stimulus is communicated to midbrain dopamine neurons through transient cortical events and why that certainty becomes visible in their response to a relevant task event.

Abstract

Learning to associate unambiguous sensory cues with rewarded choices is known to be mediated by dopamine (DA) neurons. However, little is known about how these neurons behave when choices rely on uncertain reward-predicting stimuli. To study this issue we reanalyzed DA recordings from monkeys engaged in the detection of weak tactile stimuli delivered at random times and formulated a reinforcement learning model based on belief states. Specifically, we investigated how the firing activity of DA neurons should behave if they were coding the error in the prediction of the total future reward when animals made decisions relying on uncertain sensory and temporal information. Our results show that the same signal that codes for reward prediction errors also codes the animal’s certainty about the presence of the stimulus and the temporal expectation of sensory cues.

When an inexperienced animal hears a soft rustle in the nearby foliage, it does not associate this cue with the escaping prey that it observes immediately after. How does the animal get to learn that the correct action to take is to approach it and try to get it? In perceptual decision-making experiments, animals learn how to make decisions based on their perception of weak sensory stimuli, receiving a reward for their correct choices, which they are taught to communicate by means of a specific motor action (1–7). The learning of these tasks is presumably mediated by the activity of midbrain dopamine (DA) neurons (8). Although DA recordings made while animals are engaged in making such difficult decisions are scarce, experiments on Pavlovian and instrumental conditioning have shown that under a novel stimulus–reward association, DA neurons respond to the unexpected reward with an activity burst. Remarkably, after training this phasic response is shifted to the conditioned stimulus where it works as a signal predicting the future reward (8–12). From a computational standpoint, reinforcement learning (RL) methods (13) have been successfully applied to explain this and many other observations (ref. 14 and for reviews see refs. 15–17). According to the reward prediction error (RPE) hypothesis (18, 19), the DA phasic activity signals an error in the prediction of the expected total reward (20–22) and it is used to learn associations between rewards and task events.

In classical and instrumental conditioning the reward acts as a reinforcement, strengthening the association with the stimulus, provided the animal follows the task instructions. In some experiments the reward was delivered only after the animal made a choice between alternative options (20, 23, 24). However, in those studies the task events were unambiguous: The animals’ reports were mostly correct and there was a well-defined temporal relationship between the perceived stimulus and reward delivery. However, this is very different from the real-world situation described above in which the reward is announced by a muted sound produced in a noisy environment at an unexpected time. Consequently, little is known about the DA signal in such uncertain conditions and up to now few experiments have attempted to fill this gap. The existing studies seem to indicate that the DA signal has a much richer structure than in simple choice paradigms. For example, in ref. 25 it was found that the response to visual dynamic random dot stimuli is more complex than the response to the stimuli commonly used in previous studies. The DA activity seemed to follow a more elaborate temporal profile, first responding abruptly to the onset of the stimulus (presumably due to its detection) and then producing a more extended response (supposedly due to the decision-making process) (25, 26). In another recent study (27) the authors recorded DA neurons while a monkey was engaged in the detection of weak vibrotactile stimuli. In this task, when the animal was instructed to communicate its choice by pushing one of two push buttons, DA neurons coded the uncertainty associated with a perceptual judgment about the presence or absence of the stimulus.

Here, we combined data analysis and computational modeling to investigate the DA signal recorded from midbrain neurons as monkeys detected weak vibrotactile stimuli applied at random times (Fig. 1A and SI Materials and Methods). In this task (6, 28), a start cue indicated the beginning of a trial and was followed by an interval of variable duration after which, with probability 0.5, the vibrotactile stimulus was applied. After a fixed interval, a go cue instructed the monkey to communicate its decision about the presence or absence of the stimulus by pushing one of two buttons. The animal was rewarded in all correct trials. The difficulty of the task stems from the use of very weak stimulus amplitudes and from the uncertainty about the time of possible stimulation. It has been proved that because of these uncertainties, the firing activity of frontal lobe cortex neurons codes internal processes associated with the elaboration of the decision reports in this task (29–31).

Fig. 1.

Detection task and temporal profile of the DA neurons’ activity. (A) Trials began with a start cue instruction, i.e., when the stimulator probe indented the skin of one fingertip of the restrained hand. The monkey reacted by placing its free hand on an immovable key (key down event). In stimulus-present trials, after a variable prestimulus period (1.5–3.5 s), a vibratory 0.5-s stimulus was presented. Then, after a fixed delay period (3 s), the go cue (stimulator probe tip lifted off the skin) was delivered and the monkey communicated its decision by pressing one of the two buttons (push button event). The reward was delivered immediately after the push button event in correct choice trials. Stimulus-absent trials had the same temporal structure with the only difference that the vibrotactile stimulus was not presented. (B) Mean population firing rate of midbrain DA neurons (black line, ±SEM colored bands) plotted as a function of time for the four trial types. Activity is aligned to the start cue (Left), go cue (Center), and reward delivery (Right). The dashed line indicates the baseline activity (5.1 spikes per second). Before the go cue the activity exhibited a pronounced decay with respect to the baseline in all trial types. (C) Responses of DA neurons at the stimulus onset (SO) in yes-decision trials sorted by stimulus amplitude. Data showed a positive linear increase of the response with the amplitude of the stimulus (R² = 0.98, P < 0.001) (see SI Materials and Methods for more details on data analysis).

A key result in the midbrain DA system was that the neurons’ response to the go cue is weaker in trials with stimulus-present choices (hit and false alarm trials) than in trials with stimulus-absent choices (correct rejection and miss trials) (27). This was attributed to the higher certainty of the animal in “yes” responses. The result is important because it indicates that the DA phasic response reflects internal processes; however, several issues have been left unanswered. For instance, the nature of those processes was attributed to decision certainty on the basis of a comparison of the probabilities of reward in stimulus-present vs. stimulus-absent choices, which was higher in the former case. However, in the task the animal made a choice and received a reward only after the delivery of the go cue. It is then not clear whether the DA phasic response to that signal was related to the choice itself or to some other process that occurred during the formation of the decision. Besides, whatever the nature of the process, it should be explained why it became visible in the DA activity under the application of the go cue. Finally, the response to this event was different in each of the four trial types and the reason for this gradation in the DA activity was not explained.

In addition to the uncertain presence or absence of the stimulus the detection task also has temporal uncertainty. The effect of the trial-to-trial variability in the trial duration on the DA activity was not considered in the previous work (27). However, it is known to have important consequences over prefrontal neurons (29, 31) and it is reasonable to believe that it will also affect the midbrain DA system. In fact, effects of temporal variability on DA neurons have been reported several times in tasks without stimulus uncertainty (32–34) or with it (25). To investigate these issues further we have taken a different approach, proposing a model based on the RL framework and using it to interpret the activity of DA neurons. Because of the uncertainty on the stimulus amplitude and on trial duration, the model estimates the total reward and RPEs using belief states (35–37).

Results

Temporal Profile of the DA Response.

Behavior can be described in terms of the four possible trial types of the vibrotactile detection task. Stimulus-present trials can be correct (hits) or wrong (misses) responses, while stimulus-absent trials produce correct rejection (CR) or false alarm (FA) responses. Reward is delivered only in trials with correct responses. The electrophysiological results presented in this work were obtained from midbrain DA neurons responding to reward delivery with a positive phasic activation in correct (rewarded) trials and with a pause in error (unrewarded) trials (23, 33). These are 23 of the 69 neurons analyzed in ref. 27 (see Fig. S1 and SI Materials and Methods for the selection criteria). We started the analysis of the selected DA neurons by computing their average firing rate during the vibrotactile detection task (Fig. 1B). Its temporal profile is similar to that of the firing rate of the larger population of midbrain DA neurons analyzed before (27). However, there seems to be an important difference between the two datasets: In Fig. 1B, the DA activity immediately before the go cue exhibits a pronounced decay in all trial types. Instead, the firing rate of the discarded neurons does not show this modulation (Fig. S2).

Transient DA Activity During the Possible Stimulation Period.

If the DA response to the go cue codes some type of certainty, we wondered how the activity of the DA midbrain neurons might have acquired this property. We reasoned that a detection process and the certainty about detected events could have been elaborated in cortical circuits and then transmitted to midbrain neurons, producing transient changes in their activity. We then investigated the existence of transient activation of the DA neurons during the possible stimulation window (Fig. 1A; the interval between 1.5 s and 3.5 s after the key down event).

It has been suggested that the initial response of DA neurons to external stimuli reflects their physical salience (26). In fact, Fig. 1B shows that in hit trials the vibrotactile stimulus generates a clear transient response with a linear dependence of the neurons’ firing rate at the stimulus onset as a function of the stimulus amplitude (Fig. 1C). This effect had been observed for the larger dataset (27), but here we show that it is also present for neurons compatible with the RL framework.

Fig. 1B indicates that the vibrotactile stimulus generates a phasic response in the DA neurons only in hit trials (0.5-s stimulus window) (27). However, there are reasons to believe that the apparent unresponsiveness of DA neurons in FA and miss trials requires a more detailed analysis. For example, in FA trials the animal indicated the presence of a stimulus and this perception could somehow be reflected in the activity of DA neurons. Also, since the majority of miss trials occur for low-amplitude stimuli, the existence of a transient response to high-amplitude stimuli might be hidden in the mean over all miss trials (neurons in cortical areas are activated by the stimulus even in miss trials) (6). Hence, one should not discard that in high-amplitude miss trials the information about the presence of a stimulus is transmitted to midbrain neurons.

We then investigated whether there are transient DA responses in high-amplitude miss trials and FA trials. In miss trials the onset of the stimulus seems not to produce any evident modulation of the firing rate (Fig. 1B); it could then be argued that in these trials the stimulus was not detected by cortical frontal neurons. Indeed, most miss trials occur when the stimulus amplitude is weak and the firing rate of DA neurons is not modulated by its application (green trace in Fig. 2A, Left). However, when high-amplitude miss trials are analyzed, we see that the firing rate of the cells did increase at stimulus onset (blue trace in Fig. 2A, Left).

Fig. 2.

Signatures of detection in FA trials and high-amplitude miss trials. (A, Left) In high-amplitude miss trials DA neurons responded transiently to the vibrotactile stimulus. (A, Right) The activity of neurons after the SO, standardized with respect to a prestimulus window (SI Materials and Methods), showed a significant phasic activation (P < 0.05, two-sample t test) in high-amplitude miss trials compared with low-amplitude ones. (B, Left) The mean activity in FA trials (SI Materials and Methods) exhibited a significant positive modulation with respect to that in CR trials during the PSW (P < 0.05, two-sample one-tailed t test) but not outside it (P = 0.80, two-sample one-tailed t test). (B, Right) On the contrary, the activity in low-amplitude miss trials was indistinguishable from that in CR ones both outside (P = 0.28) and within (P = 0.11) the PSW.

In FA trials, although the subject reported the presence of a stimulus, the firing rate in Fig. 1B does not show any apparent modulation. Thus, it is not clear how a stimulus-present choice was elaborated during the trial. A recent work about frontal lobe cortex neurons recorded while monkeys performed the same detection task (31) sheds light on this issue. In FA trials, those cortical neurons underwent transient activity increases resembling the response to a weak true stimulus. These transient FA events occurred at random times within the possible stimulation window, that is, inside the 2-s interval starting 1.5 s immediately after the key down event (Fig. 1A). We have then assumed that these events are transmitted to DA neurons in a way similar to that of true stimuli. If this assumption were correct, then the mean firing rate of DA neurons in FA trials, computed during the possible stimulation period, should be slightly higher than the mean firing rate in CR trials evaluated during the same period. To test this hypothesis, we aligned all FA trials to the key down event and compared their mean firing rate in the possible stimulation window with the mean firing rate of CR trials computed in the same temporal window. The results indicate that the mean firing rate in FA trials is significantly higher than in CR trials (Fig. 2B, Left). This seems to be an exclusive property of this particular temporal interval: The mean firing rates in FA and CR trials computed outside the possible stimulation window are rather similar (Fig. 2B, Left). As a further test that the elevation of the firing rate during the possible stimulation period is specific to FA trials, we did a similar analysis with low-amplitude miss trials aligned to the key down event (Fig. 1A). In contrast to what happened with FA trials, the mean firing rate in low-amplitude miss trials was not significantly different from that of CR trials either within the possible stimulation window or outside the possible stimulation window (Fig. 2A, Right).

The transient events discussed above are presumably related to detection processes taking place before their reception by midbrain DA neurons and much before the animal reports its choice. We interpret them as contributing to the certainty about the detection of transient activity fluctuations in circuits presynaptic to the midbrain DA system, distinguishing it from certainty about the choice, a term which should be used after the animal indicates its decision (38). A precise definition of certainty about the presence of the stimulus is given later, in the context of our RL model (Certainty About Stimulus Presence); however, we now give a qualitative argument explaining why the transient events contribute to this certainty. Regardless of whether the transient activation was produced by a true stimulus (as in hit and high-amplitude miss trials) or by some internal process (as in FA trials), the transient event works as a subjective confirmation that a stimulus was detected and hence it increases the certainty about its presence. The degree to which the transient event contributes to the certainty would depend on its strength. For instance, transient events generated in FA trials have a similar effect on DA neurons to those produced by true low-amplitude stimuli (Fig. S4) and they could convey a similar level of certainty about their detection.

According to the conjecture explained above the activity of DA neurons could covary with the animal’s choice during the presentation of the stimulus. This is because the firing rates of cortical premotor neurons exhibit this covariation (6, 28, 30). The area under the receiver operating characteristic curve (AUROC) confirms that during most of the possible stimulation window (PSW) the firing-rate distributions in hit and miss trials differ significantly (P < 0.01; Fig. S5).

Salience of the Go Cue.

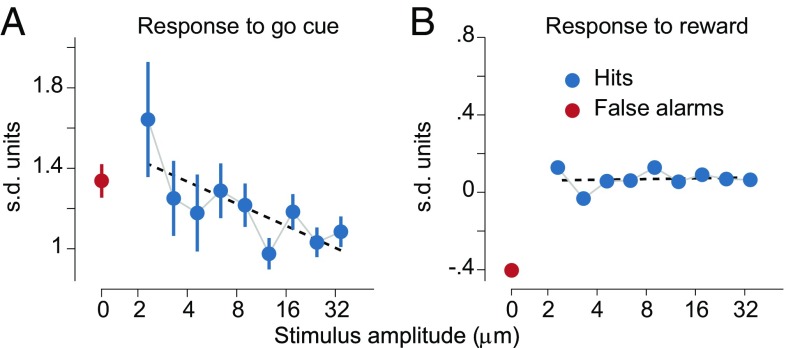
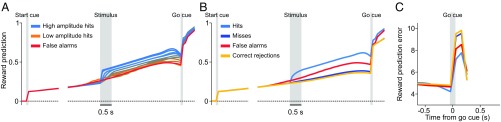
To obtain further insight about how the response to the go cue acquired a dependence on the certainty about the presence of a vibrotactile stimulus, we investigated the effect of the stimulus amplitude on this task event. First, we note the DA response to the go cue decreases linearly as a function of the stimulus amplitude (Fig. 3A); this is similar to the results found previously for the larger dataset (27). For the moment we do not make any interpretation about this result, preferring to discuss it in the context of the model presented below. Instead, we now wonder whether the response to the reward delivery also exhibits a dependence on the stimulus amplitude. The analysis shows that the dependence disappears (Fig. 3B).

Fig. 3.

Responses to the go cue and to the reward delivery. (A) In stimulus-present decisions the DA response at the go signal linearly decreased with the amplitude of the stimulus. (B) The dependence on the amplitude completely disappeared in DA activity at the reward delivery (R² = 0.58, P = 0.02 for the linear regression at the go cue; R² = 0.02, P = 0.72 for the linear regression at the reward delivery). For details about the standardized responses to the go cue and to the reward delivery see SI Materials and Methods.

Our interpretation of this observation is that the go cue acts as a physically salient signal that erases from the DA activation (at least partially) the dependence on the properties of previous task events. In fact, the responsiveness of DA neurons to the physical salience of stimuli has been discussed frequently (e.g., ref. 26). A specific implementation of this concept is performed in our computational model (The Reinforcement Learning Model: Formulation).

Effects of Temporal Uncertainty.

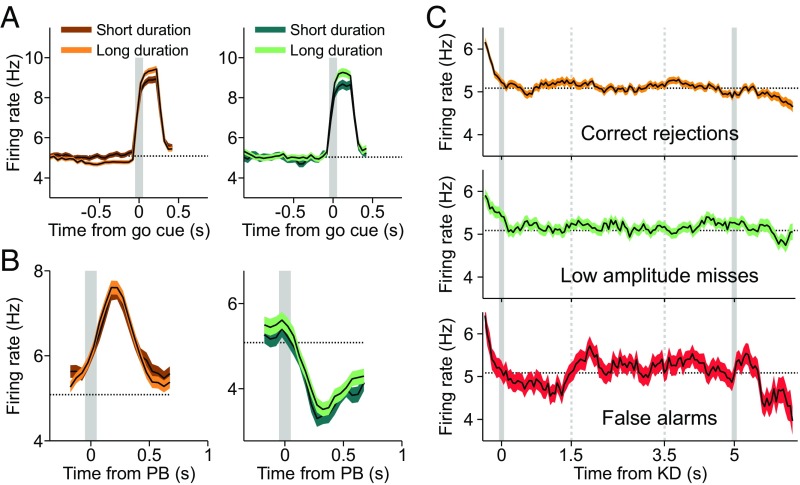
The effects of the trial-to-trial variability in the duration of the interval immediately before the go cue are visible in the phasic DA responses to that event. The data analysis shows that, in both CR (Fig. 4A, Left) and low-amplitude miss trials (Fig. 4A, Right), longer trial duration leads to stronger DA phasic activation. This is opposite to what was found in some other studies (25, 32) but agrees with ref. 33. We come back to this issue later, when we explain this result with our RL model. In contrast, the response to the delivery of reward is the same for long-duration and short-duration trials, both in CR and low-amplitude miss trials (Fig. 4B).

Fig. 4.

Temporal expectation. (A) Trial duration modulated the phasic DA response to the go cue but did not affect its response after the reward delivery. (A) When CR trials were sorted according to the duration of the key down event–go cue interval (Left), the DA response to the go signal was stronger for long-duration trials. (A, Right) The same effect is observed for miss trials of low amplitude. The gray lines indicate the go cue. (B) The response of neurons to the reward delivery was independent of the trial duration. (B, Left) CR trials. (B, Right) Miss trials of low amplitude. The gray lines indicate the push button (PB) event. (C) In the four trial types before the go cue the DA firing rate showed a slow negative modulation (Fig. 1B). (C, Top) The mean population activity of DA neurons in CR trials aligned to the key down (KD) event. The activity started to decrease around the first time when the go cue could appear (gray vertical line on the right). This negative deviation from the baseline increases as the time elapses and the go instruction becomes more and more expected. (C, Middle) The same effect is observed in low-amplitude miss trials. Given the lack of response to the stimulus presentation in this fraction of miss trials, the DA activity anticipated the go cue presentation similarly to what was observed in CR trials. (C, Bottom) FA trials exhibited a similar temporal behavior.

The variability of the duration of the trials also produces a modulation of the DA activity during the period previous to the go cue (Fig. 1B; downward trend before the go cue). To analyze this effect, we aligned CR trials at the key down event. The resulting firing rate has a negative modulation starting at the earliest time that a trial can end (Fig. 4C, Top). We then asked whether low-amplitude miss trials, when aligned to the key down event, showed a temporal profile similar to that of CR trials. Indeed, in low-amplitude miss trials, the DA phasic response to the stimulus was not present (Fig. 2A), and the mean firing rates inside and outside the possible stimulation window are not significantly different (Fig. 2B, Right). Clearly, their alignments to the key down event are also comparable; starting about 2 s immediately before the go cue, the RPEs exhibit a tonic negative modulation, the same as the one quantified in CR trials (Fig. 4C, Middle). A similar effect is seen for FA trials (Fig. 4C, Bottom).

The Reinforcement Learning Model: Formulation.

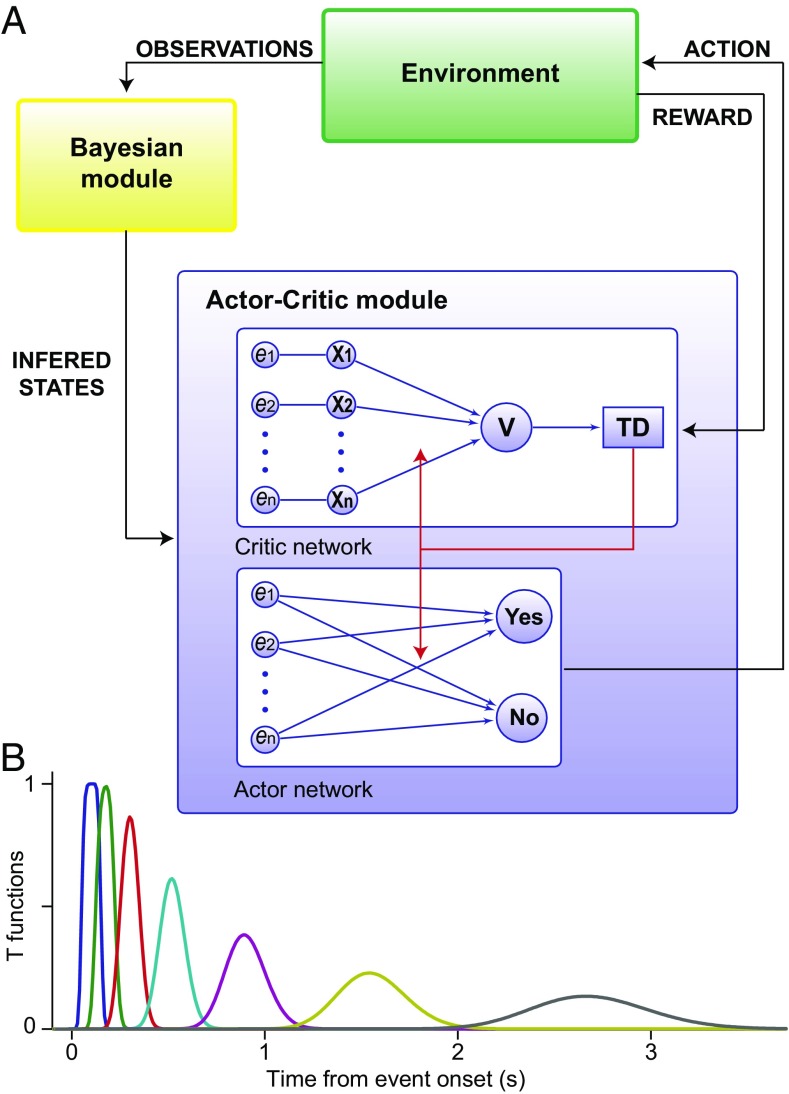
It has been suggested that when the brain does not have full access to the correct value of the physical attributes of the stimuli, the cerebral cortex uses noisy observations to infer them (39, 40) and that the midbrain DA neurons and striatal neuronal circuits evaluate the state of the environment to select the appropriate actions based on the results of that inference (35–37). In this scheme, the outcome of the inference process is a posterior probability about the state of the environment, which is interpreted as a measure of the belief about that state (41). In line with these ideas, we have assumed that a Bayesian module (representing cortical circuits) accumulates sensory evidence to compute a time-dependent posterior probability about the presence of the vibrotactile stimulus [hereafter referred to simply as the belief and denoted as b_sp(t)]. The belief is then sent to a RL module, representing midbrain DA neurons and striatal neuronal circuits (Fig. 5A). This is a valuation and action selection module that makes predictions about the future reward, computes the error of this prediction (the RPE), and chooses whether to press one button indicating a stimulus-present choice or press another button indicating the stimulus-absence choice.

Fig. 5.

Model architecture and temporal representation of task events. (A) The model relied on two structures: a Bayesian module and a RL module. The Bayesian module used the noisy observations received from the environment to compute a time-dependent posterior probability (the belief) about the presence of external events and sent it to a RL module. The RL module consisted of an actor–critic architecture (13). It used the information inferred by the Bayesian module to evaluate and to select actions (see SI Materials and Methods for more details on the model). (B) Each task event was represented across time via a set of functions reproducing the event at different latencies from its onset. Importantly, the resolution of the representation degraded with the passage of time (43).

A crucial question is, When and how does the outcome of the accumulation process (the belief state) affect the reward prediction and action selection operations? In the analysis of the experimental data we found that DA neurons are activated transiently in hit trials and in high-amplitude miss trials by the vibrotactile stimulus and also in FA trials during the PSW by a stimulus-independent process. A simple and plausible assumption is that the events responsible for those activations are related to a belief evaluated by cortical circuits that exceeded a threshold value [the maximum a posteriori (MAP) criterion sets the threshold at 0.5]. Specifically, in the model we assume that when the belief computed by the Bayesian module grows beyond that threshold, it is sent to the relevant downstream structures. When this happens, a representation of the stimulus is turned on in the RL module and it is used to establish associations between the reward and the stimulus. To accomplish this function, the RL module operates following RL rules based on belief states with two other important additions, inspired from the previous data analysis. First, on the basis of the physical salience of the go cue observed in the data (Fig. 3), we introduce in the RL module a reset mechanism that allows events predicting a high reward to disrupt the internal representations of earlier events (42). This mechanism does not introduce any parameter in the model (SI Materials and Methods). Second, given the effects of the variable duration of the trials found with the data analysis (Figs. 1B and 4), each task event is represented with a temporal resolution that degrades with the passage of time (43) (Fig. 5B). To update the value of states and actions, the RL module computes the error made in the prediction of the reward as δ(t) = r(t) + TD(t), where r(t) is the reward received at time t in a trial and TD(t) is the temporal difference between the total rewards predicted at times t + 1 and t (13) (see SI Materials and Methods for further details on the model). According to the RPE hypothesis, δ(t) should be compared with the population average of the mean firing rate of the DA neurons.

In the following we use the model to show that these mechanisms, belief states, transmission of detected events, salience, and a temporal representation with limited resolution, suffice to explain the DA response to the go signal. We start by verifying that the salience of the go signal actually produces a RPE after the reward delivery independent of the stimulus amplitude. Then we analyze the events transmitted from the Bayesian to the RL module in hit trials, high-amplitude miss trials, and FA trials. After that, we present the model explanation of how belief states produce a RPE at the go cue that depends on the trial type, reproducing the graded response of the DA neurons to this task event, exhibited in Fig. 1B. The explanation of this observation is one of the main objectives of the proposed model. Finally, we close the analysis of the model with a study of how temporal expectation modulates the RPE and propose an explanation of the differences in various experimental observations about the dependence on trial duration of phasic responses.

Salience of the Go Cue in the RL Model.

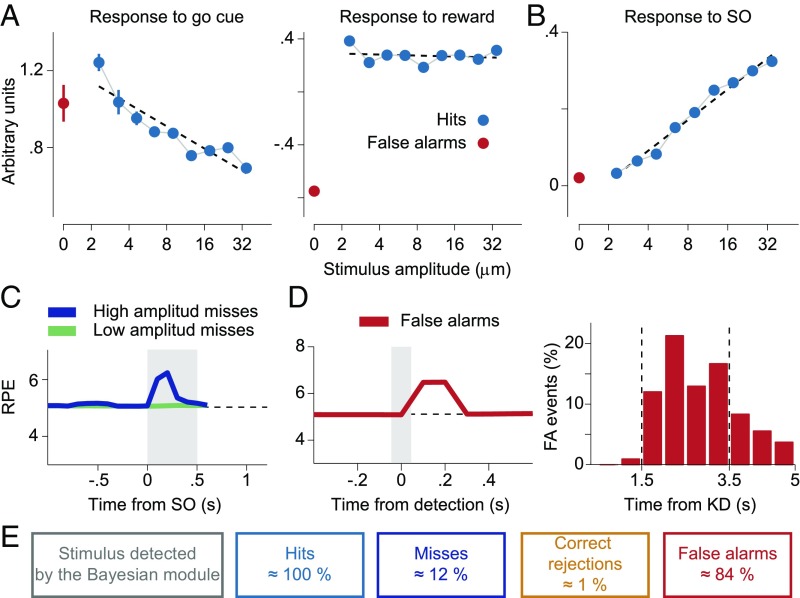
Data show that although the DA phasic activation at the go cue depends on the stimulus amplitude, this dependence disappears in the response to the reward (Fig. 3), supposedly as a consequence of the physical salience of the cue signal. This property led us to formulate a RL model in which the task events are endowed with a reset mechanism. We now analyze in the model the effect of this mechanism on the dependence on the stimulus amplitude of the RPE at the go cue. In agreement with the data (Fig. 3), numerical simulations of the model exhibit a decreasing linear dependence of the RPE at the go cue with the stimulus amplitude (Fig. 6A, Left) whereas after the delivery of the reward the analysis does not show a significant slope (Fig. 6A, Right).

Fig. 6.

Basic properties of the RPE. (A) The RPE at the go cue depended on the stimulus amplitude but this dependence was lost at the reward delivery. (A, Left) In stimulus-present decisions the RPE at the go cue linearly decreased (R² = 0.84, P < 0.001) with the amplitude of the stimulus. (A, Right) The dependence on the amplitude completely disappeared in the RPE at the reward delivery (R² = 0.03, P = 0.64) as a consequence of the reset property of the go signal. This should be compared with the DA activity in Fig. 3. (B) Responses at the SO in yes-decision trials as predicted by the model sorted by stimulus amplitude. The model showed a positive linear increase of the response with the amplitude of the stimulus (R² = 0.98, P < 0.001). See SI Materials and Methods for more details on the model analysis). (C) The model predicted a response to the stimulus as a consequence of a Bayesian detection in miss trials when the amplitude is high. A similar response was apparent in the data Fig. 2B. (D, Left) The RPE in FA trials after an erroneous detection showed a phasic response. (D, Right) In the model these erroneous detection events were produced mainly within the PSW. KD denotes the key down event. (E) Percentage of trials where a transient event was detected by the Bayesian module, for each of the four task contingencies. Note how the occurrence of a detected event in the Bayesian module did not by itself generate perception (miss trials). The values of the model parameters are given in Table S1.

Transmitted Events During the Period of Possible Stimulation.

We start by verifying that the belief transmitted from the Bayesian to the RL module produces transient changes in the RPE in correspondence to those observed in the DA activity. In hit trials, after the application of the vibrotactile stimulus, the RPE increases linearly with the stimulus amplitude (Fig. 6B), as the DA response does (Fig. 1C).

An immediate prediction of the model is that miss trials can arise in two possible ways. The most frequent ones happen when the stimulus is too weak to be detected by the Bayesian module. Less often, for stronger amplitudes, even if the stimulus is detected (Fig. 6C), the variability of the action selection process may generate a stimulus-absent choice, an effect that in our simulation occurred in about 12% of all miss trials. In fact, data show that in high-amplitude miss trials the animal reported stimulus absence, although the firing rate of the cells did increase at stimulus onset (blue trace in the Fig. 2A, Left). Similar mismatches between the cortical detection and action selection outcomes are also present in CR and FA trials (Fig. 6E).

In the RL model, the times when the belief exceeds its threshold value are known. FA trials aligned to those times evidence a transient increase of the RPE signal δ(t) at the time of the FA events (Fig. 6D, Left). Furthermore, those detection times are distributed mainly during the possible stimulation window (Fig. 6D, Right). Interestingly, the distribution is similar to the one found from the activity of prefrontal neurons (31). Note that in FA trials perception arises from detected transient events in the cortical module followed by a yes response.

Certainty About Stimulus Presence.

We now turn to the main issue we want to address with the model: how a RL module receiving uncertain information through a Bayesian inference process can explain the graded phasic response to the go cue. The computations carried out by the DA neurons during the delay period are crucial to understanding and interpreting their responses to the go cue. The immediate effect of a large stimulus belief on the RL module is to initiate the evaluation of how much reward it predicts until the end of the trial, that is, the estimated value of the stimulus. Fig. 7A shows the reward predicted by the stimulus in trials with stimulus-present choices. The predicted reward increases in a graded manner with the stimulus amplitude. The gradation is maintained during all of the delay period, until the presentation of the go cue. Note that the transient events in FA trials predict a reward similar to that estimated by low-amplitude stimuli (red line in Fig. 7A). The predicted reward increases with time during the delay period, as a consequence of the smaller temporal discount.

Fig. 7.

Predicted reward during the delay period and responses to the go cue and to the reward delivery. (A) In trials with stimulus-present choices during the delay period the predicted reward increased with the stimulus amplitude in a graded manner. In FA trials (red line) its temporal profile was similar to that observed when a low-amplitude stimulus is perceived. (B) The predicted reward during the delay period was higher in trials where the Bayesian module detected a stimulus. It was higher in miss than in CR trials due to the detection of the stimulus when the amplitude was high. At the go cue, because of the reset mechanism, the reward predictions in the four trial types collapsed in approximately the same value and immediately after they separated into two values corresponding to the possible decisions. (C) The RPEs at the go cue were lower in stimulus-present decisions (hit and FA trials) than in stimulus-absent choices (miss and CR trials). According to the model this gradation was determined by the modulation of the reward prediction described in A and B and by the reset mechanism.

The total predicted rewards in trials with stimulus-absent choices lie below those estimated in trials with stimulus-present choices (Fig. 7B). This is because in the first case the key down event is the only task event contributing to the prediction, and instead in the second case the detection of an event increases the belief about the presence of the stimulus so that it can reach its threshold and generate an extra contribution. Another relevant observation is that the predicted reward is slightly higher in miss than in CR trials. As we noted before, miss trials behave the same as CR trials, but only when low-amplitude stimuli are presented; for high-amplitude stimuli, a detected event increases the belief which then is transmitted from the cortical to the RL module, producing a somewhat higher estimated value.

When the go cue is applied, its high physical salience partly erases the information about the stimulus amplitude and the corresponding reward predictions collapse in approximately the same value (Fig. 7A). Since the error of each of these predictions at the time of the go cue, δ(t), is the difference between the reward predicted by this event and the prediction at the time preceding it, the response to the go cue should be higher in FA than in hit trials, a result which is verified by the data (compare the RPE in Fig. 7C with the response of DA neurons to the go cue in Fig. 1B). A similar argument explains why the response to the go cue in CR trials is slightly higher than in miss trials (Figs. 1B and 7C); here the small difference comes from the higher value of miss trials during the delay period (Fig. 7B). Finally, since during the delay period the predicted reward in trials with stimulus-absent choices is smaller than in trials with stimulus-present choices, the responses to the go cue are larger in the former case than in the latter. The resulting model prediction for the response to the go cue in the four trial types is summarized in Fig. 7C.

The above arguments explaining the response to the go cue can be phrased in terms of how the subject’s certainty about a detected event evolves throughout the delay period. This certainty can be defined as the probability of a correct detection. Since the Bayesian module decides about the presence of a stimulus using the MAP criterion, the probability of a correct cortical detection is either the posterior probability about the stimulus-present state [i.e., the belief b_sp(t)], if this posterior is above 0.5, or the posterior about the stimulus-absent state [i.e., 1 − b_sp(t)], if it is below 0.5. When the Bayesian module transmits the belief to the RL module, we can then say that all of the subsequent computations done in this module are based on the certainty that the received information is correct. In particular, the different responses to the go cue in hit and FA trials are due to the difference in certainty of these two trial types. Also, the difference between the responses in miss and CR trials comes from the higher level of certainty in a fraction of miss trials. The smaller response to the go cue in stimulus-present choices than in stimulus-absent choices can be attributed to the larger certainty of the animal when it reports the stimulus presence.

The go cue predicts the total future reward averaged over yes and no responses. After its delivery, because of the reset mechanism, the RPE ceases to depend on the trial type and starts coding the possible choices. This is seen in the response to the reward both in the model and in the data (Fig. S2). The smaller RPE in hit trials than in CR ones is explained by a larger fraction of rewarded trials of the former type.

Temporal Expectation.

In the detection task used here, the time sequence of some events is not fixed and their presentation cannot be predicted. Studies in cortical areas indicate that this produces an expectation of the forthcoming events that is governed by the subjective hazard of occurrence of the expected event (44). This temporal expectation might affect DA neurons by modulating their firing rate during the intervals between task events (25, 32, 33). In our detection task this is particularly evident during the interval preceding the go cue, where the firing rate in the four contingencies decreases with respect to its baseline value (Fig. 1B). Note, however, that the duration of this interval depends on the trial type. While in stimulus-present trials the delay period has a fixed duration (3 s), in stimulus-absent trials the interval between the key down event and the go cue varies from trial to trial, taking values between 5 s and 7 s (Fig. 1A). However, the fact that the decay is also observed in hit trials with a fixed stimulus onset–go cue interval suggests that there must be other factors responsible for the decrease of the firing rate. According to the model, the possible causes are the following: In some hit trials, particularly those with weak stimulus amplitude, the event detected by the Bayesian module was not the stimulus itself but a noisy fluctuation, similar to what happens in FA trials. In these trials, the effective duration of the delay period depends on the time when the fluctuation occurs, which lies within a 2-s temporal window (31). However, these are only a small fraction of the total number of hit trials and this effect is expected to give a small contribution. Even rarer are those weak-amplitude trials in which the stimulus was not detected, but variability in the selection of the action led to the correct response. Finally, an imprecise estimate of the duration of the delay period could also lead to an effective variability of this interval. This effect occurs in all trials and it could be the most important explanation of the decaying tonic activity in hit trials. The coarse resolution of the temporal representation of the task events that we introduced in the model (Fig. 5B and SI Materials and Methods) allows us to test this conclusion. To analyze its action on the RPE, we aligned the simulated hit trials at the onset of the stimulus and confirmed that the limited temporal resolution does generate a negative modulation of the tonic activity that starts about 0.5 s immediately before the go cue (cyan line in Fig. 8A).

Fig. 8.

The RPE is modulated by temporal expectation only before the go cue delivery. (A) In the four trial types before the go cue the RPE showed a slow negative modulation similar to that observed in the data (Fig. 1B). The decreasing tonic activity was particularly evident in hit trials where it was generated by the finite resolution of the temporal representation used in the model. (B, Top) The RPE in FA trials aligned with the KD event. Note the slight positive modulation inside the possible stimulation window. (B, Middle) The RPE aligned with the KD for CR trials. In both the data and the model the activity started to decrease around the first time when the go cue could appear (gray vertical line on the right). This negative deviation from the baseline seemed to code a form of negative RPE that became more pronounced as the time elapsed and the expectation of the go instruction increased. (B, Bottom) Same as in B, Top but for low-amplitude miss trials. Given the lack of response to the stimulus presentation in this fraction of miss trials both the RPE and the DA activity anticipated the go cue presentation similarly to what was observed in CR trials. (C, Left) When CR trials were sorted according to the duration of the key down event–go cue interval, the RPE at the go cue was stronger for long-duration trials. (C, Right) The same effect is seen for miss trials of low amplitude. The gray lines in A and B indicate the go cue. (D, Left and Right) The response of neurons to the reward delivery was independent of the trial duration in CR trials (Left) and in miss trials of low amplitude (Right). The gray lines in C and D indicate the PB event.

The model also predicts a decreasing activity in all of the other types of trials (Fig. 8B). In CR trials both the coarse resolution of the temporal representation and the variability in the duration of the interval between the key down event and the go cue could contribute to this effect. Since this variability spans a 2-s interval, the decay is expected to start about 2 s immediately before the go cue. To check this in the model, we aligned simulated CR trials at the key down event and averaged them by keeping each trial only until the time when the go cue was presented. The resulting quantity exhibits the expected decay (Fig. 8B, Middle). Since the precision of this timing is affected by the limited resolution of the temporal representation, this signal starts decreasing slightly sooner. The effect is weak, but it is apparent in the traces in Fig. 8B.

According to the model, most FA trials (84%, Fig. 6E) arise from transient events that occur at random times during the possible stimulation window (Fig. 6D, Right). Since FA events behave as low-amplitude true stimuli, they generate an expectation of the go cue roughly 3.5 s immediately after their time occurrence. Therefore, they produce a slow negative modulation in the RPE beginning ∼5 s after the key down event (because the first possible production time of FA events is around 1.5 s after the key down event), as shown in Fig. 8B, Top. Also, note the slight elevation of the RPE during the window of possible stimulation, as a consequence of the random production times of the FA events (as described in Fig. 6D). Similar effects are seen in the data (Fig. 4C, Bottom).

To complete the study of temporal expectation in the detection task, we now come back to the analysis of the dependence on the duration of the trial of the phasic response to the go cue. As we have already seen, the largest DA firing activity occurs for long durations (Fig. 4A). The same behavior is seen in the model simulations in both CR (Fig. 8C, Left) and low-amplitude miss trials (Fig. 8C, Right). It could be argued that long trials should produce a response smaller than short ones because the longer the interval, the higher the hazard for the occurrence of the go cue and the better its prediction by the RL module (32). However, the response to the go cue is also affected by the finite resolution of the temporal representation. Longer intervals are represented more coarsely than short intervals and the occurrence of the go cue becomes more difficult to predict in these trials. Hence, for some value of the temporal resolution, the response to the go cue becomes larger for long intervals than for short intervals. Again in agreement with the data, where the DA phasic activation at reward delivery does not depend on trial duration (Fig. 4B), the RPE after that event is the same for long-duration trials and short-duration trials. This result is shown in Fig. 8D, Left and Right, for CR trials and low-amplitude miss trials, respectively.

Summarizing, during the variable interval in the task, the RPE is modulated by the hazard function for the occurrence of the go signal. The limited resolution in the estimation of time intervals produces a similar modulation in hit trials. The hazard function, together with the imprecise temporal estimation, determines the phasic response to the go cue.

Discussion

When the state of the environment is uncertain, noisy observations have to be combined with an internal estimate of the state, referred to as the belief state. This is the basic scheme followed in early proposals about how to extend the RL framework to model the DA activity in decision-making tasks (35–37). In this approach, the belief state is used to predict rewards, to compute the error in the prediction, and to select the action that indicates the final choice. On the experimental side, in ref. 27 the authors studied a detection task in which in each trial the animal made a choice about the presence or absence of a vibrotactile stimulus. Their main finding was that the response of midbrain DA neurons to a go signal reflected an internal process that they termed decision certainty, that is, the certainty the animal had on its choice. Here, to investigate this and related issues further in the midbrain DA activity, we adopted a different approach that allowed us to identify the type of certainty coded by the go signal and to elucidate the reasons why this certainty becomes visible at that task event. To achieve this, we defined a RL model based on the belief about the presence of the stimulus and three other features, suggested by our empirical observations: the transmission of transient activity events from a Bayesian module to a RL module, the salience of the task events, and a temporal representation of those events with limited resolution. Although other authors have included belief states (36), reset mechanisms (42), and temporal representations with finite resolution (45) separately in RL models, the need to consider them together in tasks with uncertain reward-predicting stimuli has not been noted before.

Transient increases in the firing rates of DA neurons appear in hit trials, in high-amplitude miss trials at the onset of the stimulus, and plausibly in FA trials during a possible stimulation window. In the model, the strength of these transient events conveys the belief (and certainty) about the presence of the vibrotactile stimulus. This certainty remains hidden during the period preceding the go cue but it becomes evident in the response to this signal, generating a gradation of the RPE according to the trial type. This visibility is due to two robust properties of the model: (i) Transmitted transient events of higher strength predict a higher reward (Fig. 7A), and (ii) because of the salience of the go signal, the predicted reward after the delivery of the go cue is roughly independent of the occurrence of a transient event and of its strength (Fig. 7 A and B). As a consequence, the RPE is smallest for transient events of large strength and is largest in the absence of those events. This means that the RPE is large in CR trials, is slightly smaller in miss trials, and takes its smallest values in FA trials followed by hit trials (Fig. 7C), in agreement with the graded DA phasic response to the go signal observed in the data (Fig. 1B).

Our results help to clarify up to which point the DA response to the vibrotactile stimulus correlates with its perception. The uncertainties about the presence or absence of the vibrotactile stimulus and the time when it is applied cause a trial-type–dependent activity in DA neurons during the possible stimulation window. Part of this variability comes from a detection process occurring in a Bayesian module. Detection of a true stimulus produces a transient response in a RL module and leads to hit trials. Nondetected stimuli lead to miss trials. A perhaps less expected phenomenon is that in high-amplitude miss trials, the stimulus is detected, but the variability of the action selection process produces a stimulus-absent choice. In these trials, the model predicts that the cortical detection of the stimulus activates the DA neurons, although the animal’s report indicates that it did not perceive it. More interesting is the case of FA trials. The average of the firing rate of DA neurons over these trials exhibits a positive modulation throughout the interval of possible stimulation. A modulation is not apparent in CR trials, although in both trial types the stimulus was not presented. The explanation comes from a recent study on cortical premotor neurons (31) that found that FA trials arose from transient activity events similar to those evoked by low-amplitude stimuli. Consistent with this finding, our study found that the positive modulation observed in the DA activity might arise from transient cortical inputs produced at random times within the period when the stimulus is expected. In conclusion, perception is normally accompanied by a transient increase of the DA activity during the PSW, except in high-amplitude miss trials. In this case, although the stimulus induced a response of the DA neurons, the animal indicated that it did not perceive it.

Interestingly, the DA activity during the period preceding the go cue codes temporal expectation. The mean firing rate starts to deviate from its baseline value around the first time when the go cue can appear. As time elapses, the deviation increases in magnitude, resembling a form of negative RPE strictly related to temporal expectation of the forthcoming cue. In addition to this negative slow modulation, we found that also the DA phasic activation at the go cue depends on the duration of the temporal interval preceding it, resulting in a stronger response for long intervals. While some previous results appear not to be in contradiction with this pattern of phasic activation (46), other studies (25, 32, 47) reported an opposite trend (stronger response for short intervals). Here we propose an explanation for this discrepancy: The size of the response to the go cue is determined by the hazard of occurrence of this event and by the finite resolution in the estimation of the elapsed time, which is worse for long (as in our work) than for short intervals (as, e.g., in ref. 32). This explanation is consistent with an argument made in a somewhat different investigation: In a contextual instrumental task in which the hazard of occurrence of a rewarded cue increased with the number of trials elapsed since its previous appearance, in ref. 48 it was found that during the early stage of learning, the response to this cue did not decrease with that number. It was argued to be due to the large counting errors produced during that stage. As in our detection task, the different responses after long or short intervals are due to the limited resolution in the estimation of time.

In our model, task events initiate an internal representation with coarse temporal resolution. Recent works have provided direct evidence for a representation of time in the striatum that is distributed over a set of neurons (49, 50) and that DA neurons may directly modulate timing (47). The specific set of functions adopted in our work (43, 51) is a possible realization of these findings. Although there are alternative temporal representations (45) and approaches (52), our choice was dictated for the sake of simplicity and because there exist detailed studies of this internal representation that make its use attractive (53).

The main results of the model rely on robust features that depend little on the precise parameter values. Partly for this reason and also because of the difficulty of the computation, we did not attempt to fit the model to the DA electrophysiological data. Instead, we preferred to identify the mechanisms that can explain how the DA activity is modulated by the stimulus and temporal uncertainties present in the task. In addition, some parameters have been set according to physiological constraints; this is the case of the input noise, where in the model it appears as Poisson spike trains with firing rates set to values similar to those observed in prefrontal neurons. Hence, the events transmitted to the RL module were not controlled by tuning the input noise. Other features of the model did not require new parameters; for instance, the reset induced by the salience of the task events is based on the direct comparison between the reward predicted by the current event and that predicted by the events preceding it, without including any specific threshold parameter. The parameters associated with the limited resolution of the temporal representation of the task events were set in such a way that the decay of the RPE at the end of the interval preceding the go signal was similar to the decay observed in the data. The same values of those parameters yield a dependence of the phasic response to the go signal on the duration of the trial larger for the longest trial durations. The discount factor, also relevant to describe this phenomenon, was fixed at γ = 0.98, which is a standard value for this parameter.

Assessing the generality of our conclusions would require consideration of other experimental paradigms to guide the search for relevant features to be included in more complete RL models. An intriguing case is the discrimination between two sequential stimuli, when some physical property of one of them has to be kept in working memory before the presentation of the second one. An example of this is the somatosensory discrimination task thoroughly studied in several cortical areas (3, 7). In the purely temporal domain, the study of tasks that compare two temporal patterns of pulse stimuli (54) would help to define the most convenient temporal representations. A systematic study of these and other paradigms often used to investigate decision-making processes would contribute to understanding how DA influences the learning of associations between stimulus and reward under uncertain conditions.

The results obtained in the model and experimental data show that the RPE signal codes also (i) the animal’s certainty about the presence of the stimulus; (ii) the temporal expectation of reward predicting sensory cues; and (iii) to some extent, also the perception of uncertain stimulus. As it is proposed by the model, these processes take place in a Bayesian (plausibly cortical) module, which are then sent to a RL module (plausibly the midbrain DA system and the striatum). The results of the model and the experimental data show that the activity of the DA neurons is not a mere reflection of the cortical signals but rather that they are transformed into a new signal with a quite different function. However, some expressions of the original inputs are still visible in the firing rate of the DA neurons. These are, for example, the transient events that are related to decision-making processes, the certainty about the presence of these events originates a hierarchy of responses to cues predicting reward, and the acquired knowledge about the stochastic temporal structure of the trials produces a declining DA activity during the intervals between task events. Whether these processes depend only on the inputs to the DA neurons and the RL computations performed over them or whether there is further elaboration in the midbrain DA system is an open question.

Materials and Methods

Methods for analyses and the model are provided in SI Materials and Methods. Animals were handled in accordance with standards of the National Institutes of Health and Society for Neuroscience. All protocols were approved by the Institutional Animal Care and Use Committee of the Instituto de Fisiología Celular.