Genome-wide prediction of minor-groove electrostatic potential enables biophysical modeling of protein–DNA binding

Abstract

Protein–DNA binding is a fundamental component of gene regulatory processes, but it is still not completely understood how proteins recognize their target sites in the genome. Besides hydrogen bonding in the major groove (base readout), proteins recognize minor-groove geometry using positively charged amino acids (shape readout). The underlying mechanism of DNA shape readout involves the correlation between minor-groove width and electrostatic potential (EP). To probe this biophysical effect directly, rather than using minor-groove width as an indirect measure for shape readout, we developed a methodology, DNAphi, for predicting EP in the minor groove and confirmed the direct role of EP in protein–DNA binding using massive sequencing data. The DNAphi method uses a sliding-window approach to mine results from non-linear Poisson–Boltzmann (NLPB) calculations on DNA structures derived from all-atom Monte Carlo simulations. We validated this approach, which only requires nucleotide sequence as input, based on direct comparison with NLPB calculations for available crystal structures. Using statistical machine-learning approaches, we showed that adding EP as a biophysical feature can improve the predictive power of quantitative binding specificity models across 27 transcription factor families. High-throughput prediction of EP offers a novel way to integrate biophysical and genomic studies of protein–DNA binding.

INTRODUCTION

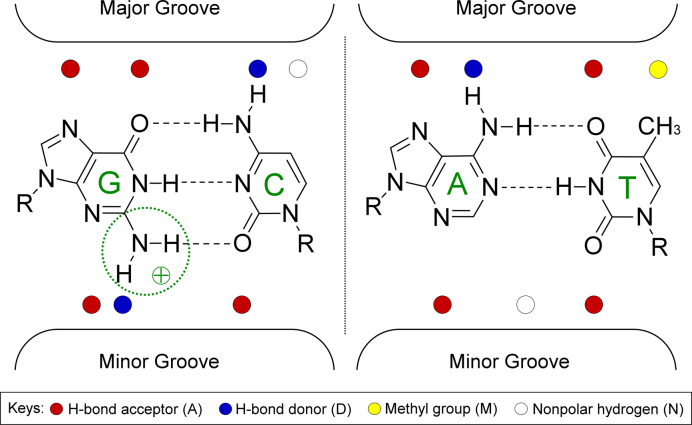
The recognition by proteins of DNA binding sites among the many putative targets in the genome is a key determinant of biological regulatory processes. Transcription factors (TFs) and other DNA binding proteins employ two different DNA readout mechanisms to recognize their genomic target sites (1,2). Base readout refers to hydrogen bonds and hydrophobic contacts between amino acid side chains and functional groups of the bases (3). These contacts are highly sequence-specific only when formed in the major groove; contacts in the minor groove cannot distinguish A/T and T/A base pairs (bp), or G/C and C/G bp, because of degeneracy in the pattern of functional groups (4) (Figure 1).

Figure 1.

Functional groups of C/G and A/T bp exposed on major and minor grooves. Proteins recognize binding sites mainly through contacts with unique functional groups in the major groove (base readout), whereas the pattern is degenerate in the minor groove. For example, in the major groove, a G/C bp can be distinguished by its unique functional-group pattern ‘AADN’ (A: hydrogen bond acceptor; D: hydrogen bond donor; N: nonpolar hydrogen) as it differs from a C/G bp pattern (‘NDAA’), an A/T bp pattern (‘ADAM’) and a T/A bp pattern (‘MADA’) with ‘M’ representing the thymine methyl group. In the minor groove, the G/C bp shares the same functional-group pattern ‘ADA’ with a C/G bp. Likewise, the functional-group pattern is identical for A/T and T/A bp (‘ANA’). The positively charged guanine amino group in the minor groove (circled) can affect EP in the minor groove by partially neutralizing the negative EP.

Shape readout refers to the recognition of structural features of a DNA binding site (4–7). These structural features include sequence-dependent conformational properties and flexibility within a core binding site and its flanking regions (8). Using molecular modeling approaches, intrinsic DNA structure can be predicted as a function of sequence. Molecular dynamics (9) or Monte Carlo (MC) simulations (10) thereby fill the gap due to the incomplete sequence coverage of experimentally solved structures (11). Data mining of molecular simulation trajectories enabled development of methods for the high-throughput (HT) prediction of DNA shape features, such as minor-groove width (MGW) (12,13), and their use in quantitative models of TF–DNA binding (14,15).

We previously showed that variations of electrostatic potential (EP) upon changes in minor-groove topography represent a biophysical source of protein–DNA binding specificity (16). Variations in the three-dimensional (3D) structure of DNA alter its dielectric boundary with surrounding solvent. These structural changes deform electric field lines, resulting in enhanced negativity of the EP in regions of narrow minor groove (16). This phenomenon, called electrostatic focusing (17), was originally discovered for proteins (18) and, more recently, was applied to protein–DNA interactions and used to explain biophysically why arginine (16), lysine (19) and histidine (20) residues often recognize DNA sequences with a narrow minor groove. However, because EP could only be calculated for individual structures (16), it was not accessible on a genome-wide basis and could be used only indirectly in modeling TF binding specificity due to its correlation with MGW (14,15). While a correlation between EP and MGW holds for narrow minor-groove regions, MGW is not a proxy for EP in general. To capture the actual biophysical contribution of minor-groove EP to TF binding, knowledge of EP on a genome-wide basis is required for analysis of HT binding data.

Experimentally determined structures of protein–DNA complexes represent atomic-resolution data on interactions between TFs and their DNA binding sites (21), thus providing crucial insights into binding mechanisms (22). However, co-crystal structures are available for relatively few TFs and are typically limited to complexes where a protein or its DNA binding domain binds to a single DNA sequence. Rarely, structural biology provides insights into the binding of a TF to multiple DNA sequences (22–27). To fill this gap and probe the binding of a given TF to many DNA sequences, technologies for measuring protein–DNA binding specificity in a HT manner have advanced tremendously in the last decade (1,28–31). Assays, such as protein-binding microarray (PBM) (32), genomic-context PBM (gcPBM) (8), high-throughput SELEX (HT-SELEX) (33–35) and SELEX-seq (36), have enabled measurements of binding affinities of one protein or protein complex against thousands or even millions of different DNA sequences. Such HT approaches to DNA binding specificity provide an alternative path to infer protein–DNA binding mechanisms without requiring time-consuming structural biology experiments or molecular simulations (1,36,37).

The minor-groove EP of DNA can be obtained by solving the non-linear Poisson–Boltzmann (NLPB) equation, as provided by the DelPhi program (17). Previous work showed that DelPhi represents an accurate description of electrostatic interactions involving DNA in atomic-resolution structures (16,22,38–40). However, NLPB calculations are computationally costly and cannot be used on massive or genome-scale DNA sequences. To infer minor-groove EP in a HT manner, we previously developed a HT method, DNAshape (12), which enables prediction of MGW for massive experimental and computational data. Prediction results can be used to measure minor-groove EP somewhat indirectly, although correspondence between EP and MGW is only well established for narrow minor-groove regions (22).

A/T and C/G bp carry different partial charge distributions in the minor groove (due primarily to the guanine amino group). These partial charges, in addition to charges on the phosphates, will affect minor-groove EP (Figure 1). Therefore, we asked whether we could account for minor-groove EP directly, rather than using MGW, to capture the effects of partial charges of bases and to reveal novel base-specific electrostatic interactions. To address this question, we developed an approach for the HT prediction of EP in the minor groove, called DNAphi (Figure 2). We designed this approach based on the mining of numerical solutions to the NLPB equation provided by the DelPhi program (17). DNAphi is a HT method that enables efficient calculation of minor-groove EP for an unlimited number and length of DNA sequences, without the requirement of NLPB calculations on an atomic-level 3D structure.

Figure 2.

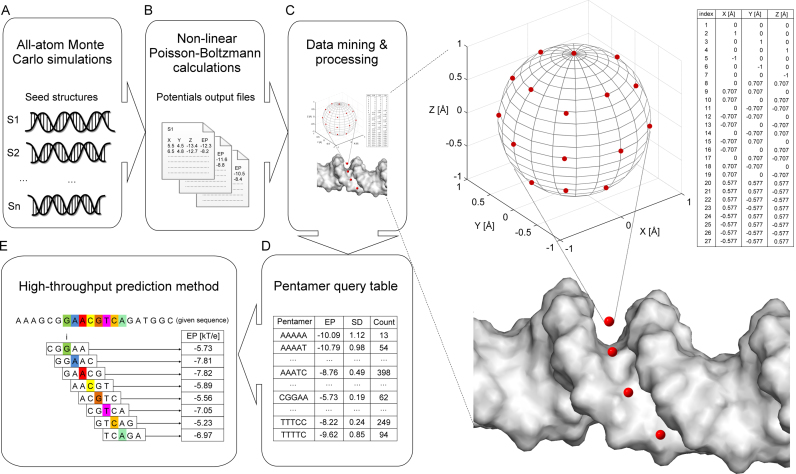
Overview of DNAphi method. (A) All-atom MC simulations were used to generate seed structures from 2297 DNA fragments. (B) We solved the NLPB equation to calculate EPs on these seed structures and (C) defined a sphere at the center of the minor groove in the plane of each bp. We derived the EP values at the center and at 26 points on the surface of each sphere. The average EP value at these points was assigned to be the EP of the respective pentamer. (D) EP values for all occurrences of the same pentamer were averaged to form a query table of (E) HT predictions of EP as a function of nucleotide sequence.

Using machine-learning (ML) techniques, we can exploit EP as a biophysical feature to model quantitatively protein–DNA binding on massive sequencing data. This approach provides a novel way to investigate how biophysical characteristics of the genome affect the strength of protein binding, thereby leading to a better understanding of protein–DNA binding mechanisms. Traditionally, such predictive ML models were built based on nucleotide sequence (41–46). We previously extended the sequence models by integrating DNA shape features derived from DNAshape (12) to build models that integrate structural information (14,15,37). In these studies, we used MGW as a ‘proxy’ for EP, based on the observation that MGW correlates closely with EP when the minor groove is narrow (16,22). Here, we revisited this assumption and demonstrated that the direct use of EP in quantitative models of protein–DNA binding specificities can yield similarly or more accurate models and potentially reveal new biophysical recognition mechanisms (Supplementary Figure S1). We tested our new biophysical models on 239 TFs from 27 different protein families.

MATERIALS AND METHODS

Poisson–Boltzmann calculation of EP

We carried out NLPB calculations for an exhaustive sampling of pentameric conformations of nucleotides. All-atom MC simulations were used for the structural sampling of 2297 different DNA fragments ranging from 12 to 27 bp in length. Each simulation was started from a canonical B-DNA conformation and extended over 2 million MC cycles. We considered the first 500 000 MC cycles to be the equilibration period. We recorded snapshots every 10th MC cycle along the MC trajectory and generated an average conformation for each DNA fragment (Figure 2A). This dataset represents an extension of the one used for the DNAshape method (12) to expand sequence coverage.

We used the DelPhi program (17) to carry out NLPB calculations (see Supplementary Materials and Methods for details) on all MC-derived average conformations of DNA fragments (Figure 2B) at a physiological ionic strength of I = 0.145 M. Partial charges of DNA were derived from the AMBER force field (47). The dielectric boundary between solute (internal dielectric ε = 2) and surrounding solvent (ε = 80) was determined by using a probe radius of 1.4 Å (48). Space filling of the solute molecule was increased in five focusing steps, with a cubic grid size of 165, by following a previously described protocol (16). We verified the stability of NLPB calculations by comparison with a cubic grid size of 501 using three focusing steps and otherwise identical DelPhi parameters. In addition, we identified contributions of different chemical groups of a nucleotide (i.e. phosphate, base and sugar moiety) based on additive linear Poisson–Boltzmann (LPB) calculations. For each component, we solved the LPB equation for 2297 structures by considering only the partial charges for atoms corresponding to that chemical group.

High-throughput prediction of EP

To define EP as a function of nucleotide sequence, for a given nucleotide index i, we obtained EP at the midpoint between O4’ atoms of nucleotides i+1 on the Watson strand and i–1 on the Crick strand from the DelPhi-calculated potential map (16). This midpoint is approximately located within the plane of bp i. To capture fluctuations of EP due to different distances of this midpoint to the dielectric boundary of the DNA segments with various deformations, we derived EP values at 26 points that were equally distributed on a sphere with 1 Å radius surrounding midpoint i (49) (Figure 2C). Excluding extreme EP values (due to clashes with the molecular surface of the solute DNA in certain conformations) and averaging EP values at the remaining points, we assigned an average value to each sphere. This approach prevents the inclusion of outlier values in the EP calculation. Sphere i lies at the approximate center of the minor groove in the plane of bp i. In this way, EP can be defined as a function of sequence, with one value per bp.

By mapping EP values of 2297 DNA fragments, we calculated the average value at the central bp of each unique pentamer and generated a query table of average values for each occurrence of the 512 possible pentamers in our dataset (see Supplementary Materials and Methods for details). Each pentamer occurred in our dataset about 45 times (Figure 2D). This pentamer lookup table was integrated in a sliding-window approach to predict minor-groove EP for any sequence, regardless of length, or for millions of sequences (Figure 2E). Likewise, we used the pentamer sliding-window method to generate pentamer query tables for the HT prediction of deconvolved EP values based on each chemical group of a nucleotide (phosphate, base and sugar).

The DNAphi web server facilitates EP prediction on a HT scale in genome-wide studies and is available at http://rohslab.usc.edu/DNAphi/. DNAphi was also implemented in the statistical programming language R and integrated in the Bioconductor package DNAshapeR (50), available at http://www.bioconductor.org/packages/devel/bioc/html/DNAshapeR.html.

EP-augmented protein–DNA binding models

We used DNAshapeR (50) to encode DNA sequence, EP and shape feature vectors for ML analysis. For the sequence feature vector, the nucleotide at each position in a given sequence of length L was encoded as four binary numbers (adenine = 1000, cytosine = 0100, guanine = 0010 and thymine = 0001), resulting in a binary vector of length 4L (14). EP and shape features included the bp parameters EP, MGW and propeller twist (ProT), and the bp-step parameters Roll and helix twist (HelT). For a sequence of length L, the length of the nucleotide feature vector was L–4, and the length of the bp-step feature vector was L–3 (see Supplementary Materials and Methods for details).

We used HT-SELEX data for 215 mammalian TFs from 27 protein families (33), which were re-sequenced with an average 10-fold increase in sequencing depth (15). Sequencing data were obtained from the European Nucleotide Archive (ENA; study identifier PRJEB14744) and pre-processed following our recently published protocol (15). We also included SELEX-seq data for eight Drosophila Hox proteins, including Hox mutants, in the presence of their cofactor Extradenticle (Exd) (37). The 21 Exd-Hox datasets can be downloaded from the Gene Expression Omnibus (GEO; accession number GSE65073). Sequences with multiple occurrences of the core motif were removed from this analysis. In addition, we used gcPBM data for three human basic helix-loop-helix (bHLH) proteins (14). These data contained 36-bp genomic sequences centered at a putative TF binding site and can be downloaded from the GEO (accession number GSE59845).

We trained multiple linear regression (MLR) models on each dataset to predict the relative binding affinity for every sequence bound by a given TF. To measure the predictive power of regression models in an unbiased and robust manner, we adopted a 10-fold cross-validation approach (51). Each dataset was randomly partitioned into ten equally sized subsets. One subset was retained as validation data for testing the model, while the other nine subsets were used for training. Thus, models were always tested on data that had been excluded in the training process. The cross-validation process on each dataset was repeated ten times. Each time, we calculated the coefficient of determination (R²) between predicted and observed values of response variables for all DNA sequences in the validation dataset. R² values from the ten tests were averaged to produce a single estimate to be reported. Because the relative binding affinities were derived in separate experiments, the MLR models were trained and assessed for each TF binding dataset individually. Prediction and validation processes were performed using the Caret package (http://caret.r-forge.r-project.org). Source code for the prediction method is available at https://github.com/TsuPeiChiu/DNAphi_analysis.

To evaluate the predictive power of EP for TF–DNA recognition, we compared multiple models built from different combinations of features, including DNA sequence and EP (sequence+EP models), sequence and MGW (sequence+MGW models), sequence and shape (sequence+shape models), models that combine sequence with EP and the three shape features ProT, Roll and HelT (sequence+3shapes+EP models), and models that combine sequence with EP and all four shape features including MGW (sequence+shape+EP models).

RESULTS AND DISCUSSION

Validation of EP prediction

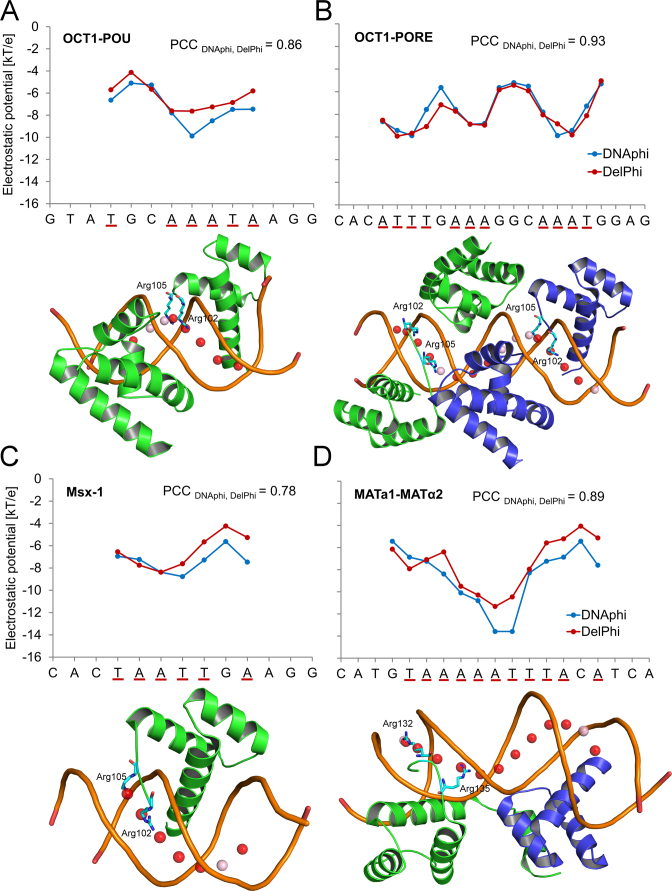
To examine whether the advantage of a fast EP calculation without the requirement of a 3D structure, as provided by DNAphi, compromises the accuracy of the EP prediction, we validated DNAphi through direct comparison with NLPB calculations using DelPhi (17) on crystal structures where protein atoms were removed. We first targeted the minor-groove EP of DNA binding sites from various crystal structures (22,52–62), for which we previously established the importance of minor-groove shape readout (12,16). The DNAphi predictions agreed well with actual NLPB calculations for DNA binding sites in crystal structures of protein–DNA complexes, as indicated by Pearson correlation coefficients (PCCs) ranging from 0.43 to 0.93 (Figure 3 and Supplementary Figures S2 and S3). Stability of the DelPhi calculations was shown for the TF binding sites illustrated in Figure 3 by using different grid spacing (Supplementary Figure S4). Differences in predictions between DNAphi and DelPhi might result from different types of input. DelPhi takes DNA structure as input, which can possibly get deformed by protein binding following the initial protein–DNA recognition process (63). In contrast, DNAphi only uses DNA sequence as input and estimates EP based on population-based statistics rather than individual calculations, which can yield more robust results. Arginine residues tended to be located near positions with lower minor-groove EP as predicted by DNAphi (Figure 3 and Supplementary Figures S2 and S3). These observations confirmed our previous finding that the binding of arginine residues to narrow minor grooves is a commonly used mode for protein–DNA recognition (16).

Figure 3.

Validation of HT EP predictions using TF–DNA binding sites. Minor-groove EP values of binding sites of (A) OCT1-POU (PDB ID 1OCT) (52), (B) OCT1-PORE (PDB ID 1HF0) (56), (C) Msx-1 (PDB ID 1IG7) (54) and (D) MATa1-MATα2 (PDB ID 1AKH) (55), whose binding interface includes an arginine inserted into the minor groove, were predicted using DNAphi (blue) and DelPhi (red), respectively. Pearson correlation coefficients (PCCs) demonstrate the statistical similarity between EP profiles derived from these two approaches. We highlighted the more negative minor-groove EP values (≤ –6.505 kT/e, which is the average value in the EP query table) predicted by DNAphi by underlining the respective x-axis labels (red). Corresponding spheres defined by DNAphi are represented by spheres in each structure, with red indicating below-average EP values ≤ –6.505 kT/e and pink indicating EP values > –6.505 kT/e. Protein residues of minor-groove contact defined by DNAproDB (21) are shown in each structure.

In addition to direct validation through comparisons with NLPB calculations on experimentally solved structures, we examined the predictive efficiency of the pentameric sliding-window approach. We applied leave-one-out cross-validation using a pentameric sliding window to mine training data derived from NLPB calculations. In each round of cross-validation, we removed one of the 2297 assigned all-atom average conformations derived from MC simulations. We recompiled the pentamer query table of our HT approach with the remaining training data and predicted the EP of the removed structure. These steps were repeated for each of the 2297 structures. Predictions were concatenated and compared to the direct NLPB calculations. The results showed a strong correlation (PCC = 0.84), demonstrating that our pentameric sliding-window approach captures EP derived from direct PB calculations with high accuracy.

Correlation between EP and MGW

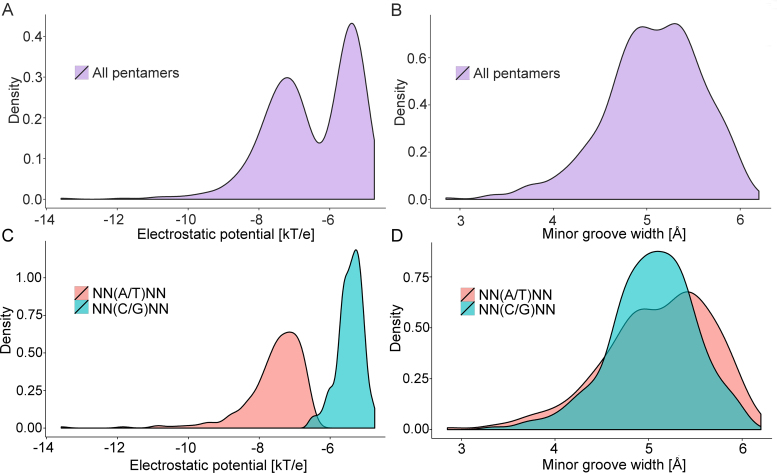
MGW closely correlates with EP due to the shape-dependent focusing of electric field lines (16,22,64). However, there is degeneracy in the sequence-to-MGW mapping, such that functional groups in the minor groove can affect EP despite similar MGW. For example, the presence of the partial positive charge of the guanine amino group can partially neutralize a negative EP in the minor groove (Figure 1). This effect was observed in distribution plots of EP and MGW for the 512 pentamers in the query table. EP appeared to follow a bimodal distribution with two clear peaks (Figure 4A), whereas the MGW distribution was essentially unimodal (Figure 4B). The two distinct EP distributions could be distinguished by classifying pentamers into categories based on their central bp (A/T or C/G) (Figure 4C).

Figure 4.

Comparison of EP and MGW distributions of 512 unique pentamers categorized by central bp. (A) EP distribution shows two separated peaks, reflecting bimodal behavior. (B) Pronounced separate peaks are not observed in the MGW distribution. (C) EP distribution forms two subgroups, defined by the identity of the central bp, which (D) is not the case for the MGW distribution.

We further identified contributions from different chemical components of a nucleotide using additive LPB calculations (Supplementary Figure S5A). Although EP contributions from the bases separated pentamers with central A/T versus C/G bp most distinctly (Supplementary Figure S5B), EP contributions from phosphate groups (Supplementary Figure S5C) and sugar moieties (Supplementary Figure S5D) also exhibited shifted peaks of overlapping distributions. These results demonstrate that functional groups of the bp can strongly affect minor-groove EP, an effect that cannot be fully captured by MGW (Figure 4D).

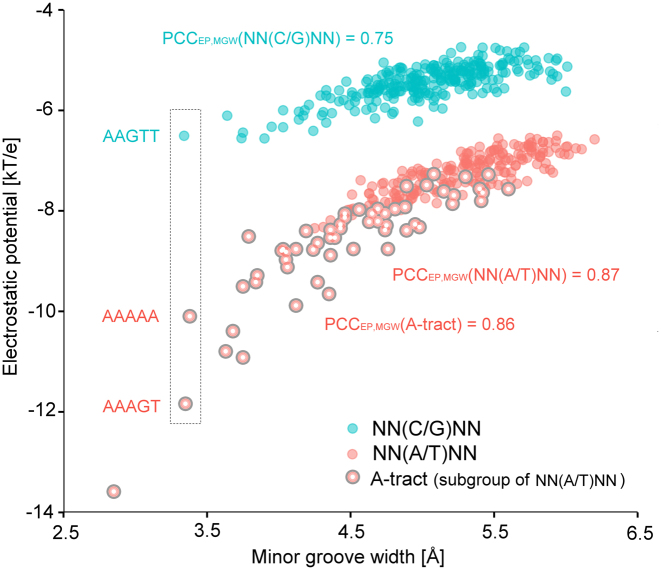
Distinct subgroups with a central A/T bp (NN(A/T)NN pentamer) or central C/G bp (NN(C/G)NN pentamer) were distinguished when EP was directly plotted against MGW (Figure 5). EP showed a higher correlation with MGW in the subgroup of pentamers with a central A/T bp (PCC = 0.87) than in the subgroup with a central C/G bp (PCC = 0.75). In particular, the A-tract subgroup (pentamers containing ApA, ApT or TpT steps formed by at least three bp) showed a narrower MGW and enhanced negative EP, resulting in a slightly higher correlation with EP (PCC = 0.86) than the subgroup excluding A-tract pentamers (PCC = 0.85). These results confirm our previous finding of a high correlation between EP and MGW in AT-rich sequences (16,22). In some cases, EP is more sensitive than MGW to chemical signatures (e.g. pentamers AAGTT, AAAAA and AAAGT in dashed box of Figure 5), suggesting that EP may provide a more sensitive approach to the prediction of protein–DNA binding affinities.

Figure 5.

Scatter plot for EP and MGW values of all 512 unique pentamers. Two separate groups reflect different correlations between EP and MGW. The subgroup with a central A/T bp (red) demonstrates a stronger correlation between EP and MGW than the subgroup with a central C/G bp (cyan). The A/T subgroup representing A-tracts (large red) exhibits more negative EP and narrower MGW compared to other groups. EP variation over an order of magnitude can be seen in narrower MGW (dashed box).

Correlation of EP and Fis protein binding affinity

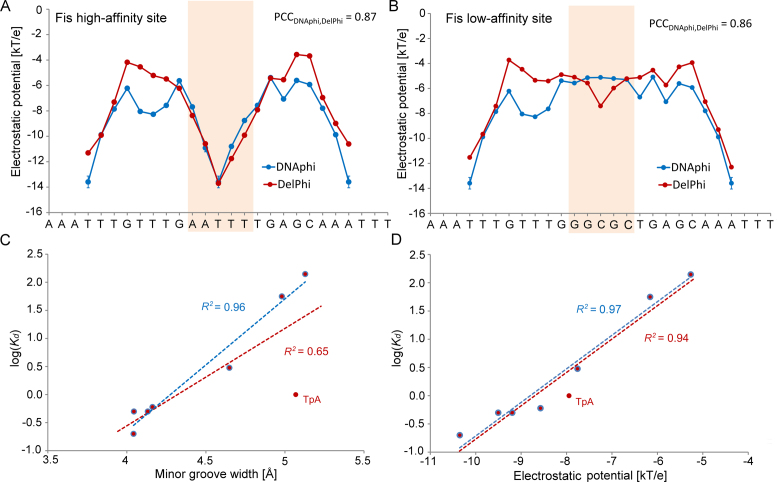
Next, we targeted eight DNA binding sites, which exhibit Escherichia coli Fis protein-binding affinities differing over three orders of magnitude depending on the DNA sequence in the central region (23,25) (see Supplementary Materials and Methods for details on datasets). Fis binds non-specifically to the bacterial genome (65). Using DNAphi (with DNA sequence as input) and DelPhi (with DNA structure with proteins removed as input), we predicted the minor-groove EP values of six DNA binding sites for which crystal structures of Fis-DNA complexes were available (Supplementary Table S1). Our HT predictions demonstrated good agreement with direct NLPB calculations (Figure 6A and B). The Fis protein binds various DNA sequences with an affinity that depends on the MGW in the central region of its binding site (23). The average MGW over the five central nucleotides predicted by DNAshapeR (50) was highly correlated with the logarithm of binding affinity K_d when we excluded a particular sequence with a central TpA dinucleotide, representing a flexible ‘hinge’ step (Figure 6C) (12). We calculated the average EP over the same five central nucleotides and obtained a stronger correlation, even when we included the sequence with the central TpA step (Figure 6D).

Figure 6.

High-throughput EP predictions for Fis-binding sites. EP as a function of sequence was predicted for (A) high-affinity (K_d = 0.2 nM) and (B) low-affinity (K_d = 140 nM) binding sites using DNAphi (blue) and DelPhi (red). Pearson correlation coefficients (PCCs) demonstrate the statistical similarity between EP profiles derived by the two approaches. HT predictions of (C) MGW and (D) EP over five central bp of eight Fis binding sites correlate with the logarithm of binding affinity. Coefficients of determination (R²) between the logarithm of K_d and (C) MGW and (D) EP, respectively, were calculated for all eight Fis binding sites (red) compared to seven Fis binding sites without the central TpA ‘hinge’ step (blue).

We expanded this analysis to additional groups of sequence variants in the Fis protein binding site (25) (Supplementary Figure S6A) and observed similar improvements in the correlation between EP and the logarithm of binding affinity. The correlation was either already high (Supplementary Figure S6B) or improved by using EP rather than MGW due to the removal of outliers (Supplementary Figure S6C and D). Exception were the sequence variants that differed solely by A/T versus G/C bp, which caused EP to change through the addition or removal of the guanine amino group (Supplementary Figure S6E and F). In flanking regions of Fis binding sites, EP values correlated better than MGW with the logarithm of binding affinity (Supplementary Figure S6G and H).

To decipher the contribution of individual nucleotide components, we further deconvolved contributions into chemical groups (base, sugar moiety and phosphate groups) by solving the LPB equation for the subset of Fis binding sites analyzed in Figure 6. The contribution from partial base charges showed a higher correlation with the logarithm of binding affinity than the contribution from phosphate groups, demonstrating the importance of the effects of bases (Supplementary Figure S7).

EP-based modeling of DNA binding affinity for 27 protein families

In a HT approach to the modeling of TF binding specificity, we added EP as an explicit biophysical feature in our ML approach for quantitative prediction of DNA binding specificities of TFs (14). We targeted the most extensive mammalian TF binding data available to date derived from re-sequenced HT-SELEX experiments (15), in addition to SELEX-seq data for Drosophila Exd-Hox complexes (37) and gcPBM experiments for human bHLH TFs (8). In total, these data included 239 TFs from 27 different protein families (see Supplementary Materials and Methods for details on datasets). Directly integrating EP as a biophysical feature in the analysis of HT sequencing data enabled the testing of its contribution to quantitative binding models. We used L2-regularized MLR to train predictive models based on different combinations of EP, sequence and shape features, to predict binding affinity for all DNA sequences in a dataset that can determine TF–DNA binding specificity. For this purpose, we concatenated feature vectors, as previously introduced (14), which were comprised of binary features representing sequence combined with DNA shape and EP features (feature encoding is described in Supplementary Materials and Methods). DNA shape and EP values were normalized between 0 and 1, as previously described (50). We evaluated different models based on the coefficient of determination (R²) between measured and predicted binding affinities using 10-fold cross-validation.

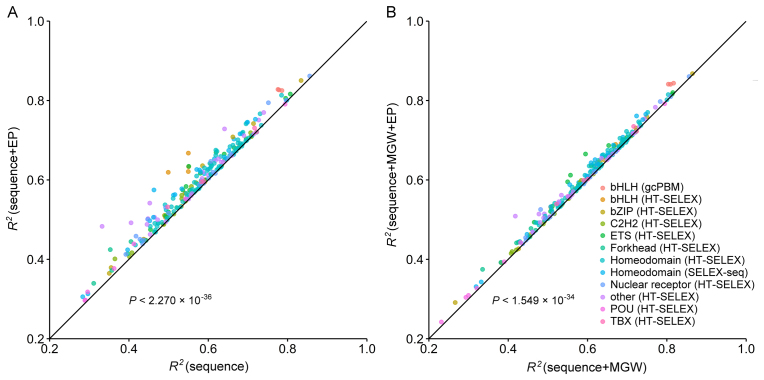
Sequence+EP models outperformed sequence-only models for 233 of the 239 tested TFs (P < 2.270 × 10⁻³⁶, Figure 7A) (statistical testing is described in Supplementary Materials and Methods). This observation indicates that EP plays an important role in TF binding specificity, consistent with our previous conclusion that DNA shape readout is important for TF binding specificity (18). To test whether EP has additional predictive power beyond MGW, we added EP to our sequence+MGW models. The resulting sequence+MGW+EP models outperformed sequence+MGW models (P < 1.549 × 10⁻³⁴, Figure 7B). Our interpretation of this observation is that EP and MGW encode largely overlapping but not identical information. EP describes base-specific charged groups in the minor groove in addition to shape-dependent electrostatic focusing. MGW also includes geometric information on the possibility of contacts with the sugar and phosphate groups.

Figure 7.

Performance comparison of binding specificity predictions for 239 TFs derived from HT-SELEX, SELEX-seq and gcPBM HT binding assays. Each data point demonstrates performances of two models (denoted by x- and y-axis labels). The model labeled on the y-axis outperforms the model labeled on the x-axis if the data point is located above the diagonal line. (A) The sequence+EP models outperform the sequence-only models and contribute to the increased prediction accuracy of DNA binding specificities based on L2-regularized MLR and 10-fold cross validation. (B) The sequence+MGW+EP models likewise outperform the sequence+MGW models. The P values were calculated by using the t-test hypothesis testing method with performance increase in terms of R² as the alternative hypothesis.

Similarly, when we added EP to our sequence+shape models, which contain information on all four shape features, the resulting sequence+shape+EP models outperformed sequence+shape models (P < 4.569 × 10⁻⁴¹, Supplementary Figure S8A). Although the relatively small improvement was due to overlapping information, this result nevertheless implies that directly using EP contributes predictive power to models that are based on DNA sequence and shape. When we replaced MGW by EP, the sequence+3shapes+EP model slightly outperformed the sequence+shape models (P < 6.748 × 10⁻⁴, Supplementary Figure S8B). In contrast, the sequence+EP models did not outperform sequence+MGW models (Supplementary Figure S8C), and EP models did not outperform MGW models (Supplementary Figure S8D). The latter result is not surprising because DNA shape or EP alone does not contain information on hydrogen bonding opportunities, which are necessary for TF–DNA readout (4).

Although the performance gain was quite small when DNA shape was already included in the model, it was highly significant (P < 1.549 × 10⁻³⁴ for sequence+MGW+EP versus sequence+MGW models; P < 4.569 × 10⁻⁴¹ for sequence+shape+EP versus sequence+shape models; P < 6.748 × 10⁻⁴ for sequence+3shapes+EP versus sequence+shape). Nevertheless, our results demonstrate the added information content of biophysical features compared to purely geometric DNA shape information. The performance gain for EP-augmented models based on high-quality gcPBM datasets for human bHLH TFs was higher than for models based on other datasets (Supplementary Figure S9). This improvement was probably influenced by the consideration of genomic flanks comprising 15 bp 5′ and 3′ of the core binding sites (enhancer or E-box), which likely increases information content derived from the flanking regions. To investigate whether EP in the flanking region contributes to the binding specificity of different TF families, we targeted binding sites of human bHLH TF dimers Mad1/Max (‘Mad’), Max/Max (‘Max’) and c-Myc/Max (‘Myc’) derived from gcPBM experiments (66). Whereas the E-box (CANNTG) as the core-binding motif is shared among all three TF complexes (Supplementary Figure S10A), differential DNA binding specificities can be detected through the analysis of EP preferences between TFs (Supplementary Figure S10B). These differences can be due to EP variations in the flanking sequences. As protein loops can contact these flanking regions (8), this result suggests a mechanism of how the flanks biophysically contribute to the selection of binding sites in the genome.

Base versus phosphate EP contributions in quantitative models

To decipher the additional information that EP might contain relative to MGW, we deconvolved the EP originating from bases versus phosphate groups by using the LPB equation (due to its additivity) (16). Using the deconvolved contributions to EP in ML methods to predict TF–DNA binding specificities, we found that EPs originating from bases (Supplementary Figure S11A and B) or phosphate groups (Supplementary Figure S11C and D) contributed similarly to the performance of sequence+EP compared to sequence models and, likewise, to the performance of sequence+MGW+EP compared to sequence+MGW models. This difference in performance increased when the added EP information was largely from the contributions of phosphate groups in bHLH TFs in the gcPBM data. On the other hand, there was essentially no improvement for EP contributions from the bases. This observation indicates that contacts with phosphate groups in the flanking regions of core binding sites contribute to binding specificity. Contacts of basic side chains in linker regions of bHLH proteins with phosphates in the regions flanking their core binding sites have been reported in co-crystal structures for Max (67) and USF (68).

Our EP dissection combined with quantitative modeling revealed this readout mechanism without the need of an experimentally solved structure. Thus, our results suggest that EP contributes to TF–DNA binding specificity, and that a direct analysis of EP might reveal the biophysical origin of DNA shape readout mechanisms.

EP contributions to Hox-DNA binding specificity

The performance gain of SELEX-seq datasets for Exd-Hox protein complexes was higher than the gain of all HT-SELEX datasets (Supplementary Figure S9). The improvement difference between the SELEX-seq datasets for Exd-Hox heterodimers and HT-SELEX datasets for monomeric homeodomains was likely due to the fact that the minor-groove readout for SELEX-seq data depends in part on the linker region between the Hox protein and its Exd cofactor (37). In contrast, the HT-SELEX data were derived from the binding of homeodomains in monomeric form (15) and, therefore, were not influenced by latent specificity (36).

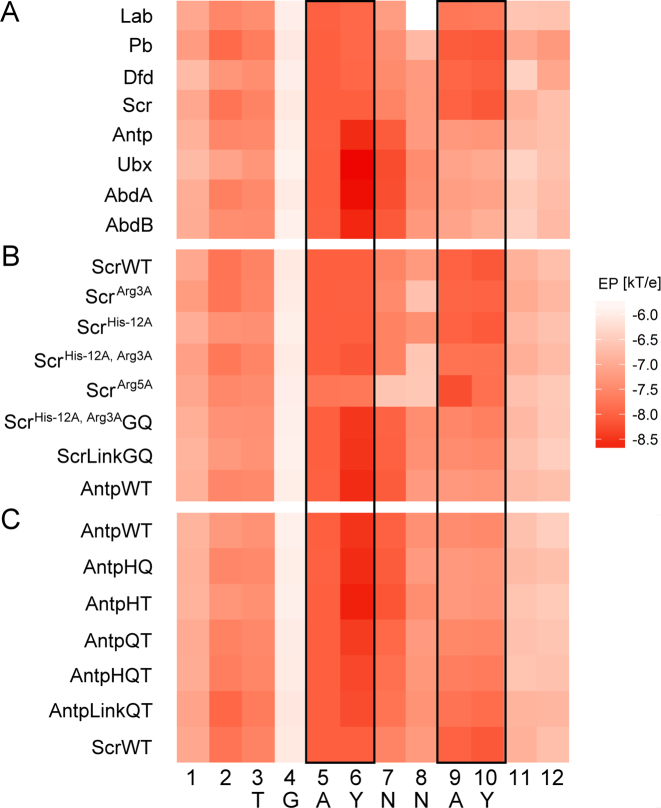
To examine the contributions of EP to Hox-DNA binding specificity in detail, we used DNAphi to predict minor-groove EP for sequences derived from SELEX-seq experiments for Drosophila Exd-Hox heterodimers. We averaged EP predictions at each nucleotide position of the sequences selected by each Hox protein. This family of TFs uses positively charged amino acids to recognize the enhanced negative EP in the minor groove of the Exd-Hox consensus site GAYNNAY (with Y = C or T) (36). For example, Arg5 within the Hox linker region selects for more negative EP at A₅Y₆ positions, whereas Arg3/His–12 preferentially binds to sequences with more negative EP at A₉Y₁₀ positions (Figure 8).

Figure 8.

Heat map of average EP at each position of 16-mers selected by each Exd-Hox heterodimer. Dark and light red colors represent regions of more negative and less negative EP, respectively. Black boxes indicate A₅Y₆ positions of 16-mers containing the TGAYNNAY core where, in the case of Scr, Arg5 contacts the minor groove, and A₉Y₁₀ positions where Arg3 and His–12 bind to the minor groove. (A) EP profiles for selected sequences vary between anterior and posterior Hox proteins. (B) EP profiles for sequences selected by Scr mutants suggest a loss in the ability to recognize the EP profile when minor groove-contacting residues are mutated. (C) EP profiles for sequences selected by Antp mutants, where Scr-linker residues are inserted into the Antp protein, show the restored ability to recognize a second minimum of enhanced negative EP.

Although most sequences were predicted to have more negative EP in the minor groove at A₅Y₆ positions, the largest variation among binding sites of different Hox proteins occurred at A₉Y₁₀ positions. This characteristic EP pattern cannot be explained by nucleotide composition alone and correlates with our previous observations on DNA shape (22). For example, EP varied gradually at A₉Y₁₀ positions from more negative EP for sites of anterior Hox proteins to less negative EP for sequences selected by posterior Hox proteins. As a result, anterior Hox proteins (Lab, Pb, Dfd and Scr) selected sequences with two regions of more negative EP, whereas posterior Hox proteins (Antp, Ubx, AbdA and AbdB) selected sequences with only one region of more negative EP at A₅Y₆ positions (Figure 8A). Scr mutants (in which Arg3, His–12 or Arg5 was mutated to alanine) demonstrated the effect of losing a positive charge on the ability to recognize regions of enhanced negative EP (Figure 8B). Antp mutants (in which minor groove-contacting residues from Scr were engineered into the Scr linker) regained the ability to read two regions of more negative EP (Figure 8C).

CONCLUSIONS

Multiple determinants, including DNA sequence and shape, contribute to TF–DNA binding specificity (1). Albeit related to shape, EP adds an additional layer—a biophysical determinant—to the complexity of protein–DNA binding. Before the development of our new approach, HT analysis of EP was not possible for large datasets due to the limitations of unavailable structures and constrained computing power. Although EP can be inferred indirectly by HT DNA shape prediction (12) or experiment-based methods (64), quantitative EP prediction on a genomic scale required a new approach.

In this study we introduced DNAphi, a HT approach to derive EP features from massive sequencing data. This method is based on the data mining of results from Poisson–Boltzmann calculations on DNA structures obtained from MC simulations. Validation of DNAphi by using available data revealed improved prediction accuracy based on a biophysical feature of protein–DNA binding. Statistical models of TF–DNA binding specificity consistently benefited from EP-augmented models.

Approaches to calculate EP at surfaces of biological molecules and complexes have been widely and successfully applied in many studies of molecular recognition (18,39,49,69–73). DNAphi, however, is the first methodology to enable rapid calculation of EP in the minor groove of double-stranded DNA as a function of nucleotide sequence. The HT approach makes electrostatic information accessible for whole-genome analysis. By combining knowledge from biophysics and genomics, this work suggests a new path toward understanding protein–DNA binding and function, with the possibility of extensions to investigate higher-level effects from, for example, chromatin and cooperativity. In addition, because EP can be defined at diverse molecular surfaces, we envision that EP analysis will be more generally applicable than MGW of double-helical DNA to, for instance, protein-RNA binding specificity studies.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R35GM118336 to R.S.M.; U54CA209997 in part to B.H.; R01GM106056 and U01GM103804 to R.R.; R01HG003008 in part to R.R.]; Alfred P. Sloan Foundation (Alfred P. Sloan Research Fellowship to R.R.); USC Graduate School (Research Enhancement Fellowship and Manning Endowed Fellowship to T.P.C.); Andrew J. Viterbi Fellowship (to S.R.). Funding for open access charge: National Institutes of Health [R01GM106056 to R.R.].

Conflict of interest statement. None declared.