Role of Conformational Dynamics in the Evolution of Retro-Aldolase Activity

Abstract

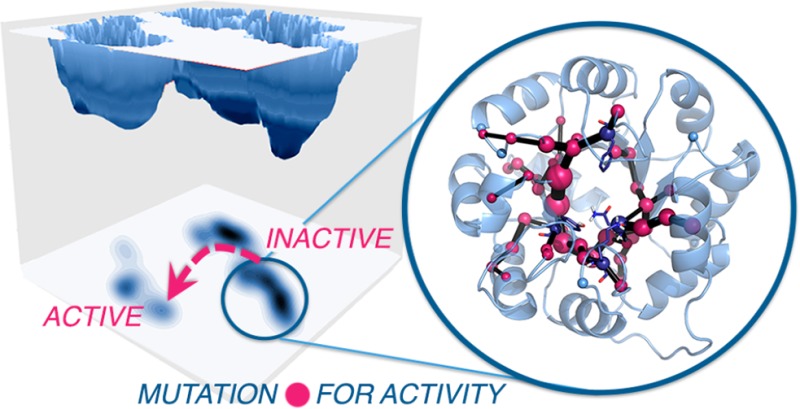
Enzymes exist as ensembles of conformations that are important for function. Tuning these populations of conformational states through mutation enables evolution toward additional activities. Here we computationally evaluate the population shifts induced by distal and active site mutations in a family of computationally designed and experimentally optimized retro-aldolases. The conformational landscape of these enzymes was significantly altered during evolution, as pre-existing catalytically active conformational substates became major states in the most evolved variants. We further demonstrate that key residues responsible for these substate conversions can be predicted computationally. Significantly, the identified residues coincide with those positions mutated in the laboratory evolution experiments. This study establishes that distal mutations that affect enzyme catalytic activity can be predicted computationally and thus provides the enzyme (re)design field with a rational strategy to determine promising sites for enhancing activity through mutation.

Introduction

The most proficient catalysts known on Earth are enzymes, which accelerate diverse chemical reactions by many orders of magnitude. Their extraordinary catalytic power is mainly attributed to highly preorganized active sites, which properly position the catalytic machinery for efficient transition state (TS) stabilization.¹⁻⁵ The existence of a link between active site dynamics and the chemical step has been recently investigated and debated;^1,6−9 however, this is totally independent of the fact that enzymes are inherently dynamic entities that sample a vast ensemble of conformational states important for their function.^10,11 The ability of enzymes to fluctuate between different well-defined thermally accessible conformations is important for substrate binding, regulation, inhibition, and product release.

Enzymes exist as an ensemble of conformational substates, whose populations can be shifted by substrate binding and also by introducing mutations during evolution toward novel function. The concept of population shifts or redistributions of protein conformational states underlies efforts to rationalize substrate binding mechanisms and allosteric regulation.^10,12 The alteration of enzyme function by introducing mutations to its sequence¹³ can be compared with the phenomenon of allosteric regulation, as mutations may directly affect the populations of individual conformational substates of the enzyme,¹⁴⁻¹⁶ which in turn influences catalytic activity. Notably, such mutations are often distant from the active site.¹⁷⁻¹⁹ Several studies have examined the conformational dynamics of some specialized enzymes^16,20 and the role of population shifts induced by mutations in enzyme evolution.^21,22 The ability of some enzymes to catalyze promiscuous reactions has been associated with their conformational plasticity and changes in the conformational landscape.²³ In a recent study, Campbell and co-workers demonstrated for a model system that a change in function can be achieved through population of pre-existing conformational substates.¹⁴ Static X-ray structures of several intermediate variants for evolving a phosphotriesterase into an arylesterase were analyzed.

Many computational strategies are available to study protein dynamics. Molecular dynamics (MD) simulations, a widely accepted tool for evaluating the enzyme conformational dynamics in atomistic detail,^24,25 is particularly useful in this regard. Long-time-scale MD, for example, has been used to explore the role of allosteric regulation and distal active site mutations on the conformational dynamics of an acyltransferase (LovD) enzyme.^18,26 MD, in contrast to X-ray crystallography, was able to elucidate the reasons for catalytic activity differences observed in LovD variants. Nuclear magnetic resonance (NMR) experiments have also provided key information about conformational ensembles of enzymes and changes in amino acid networks in the different substates.^27,28 All of these studies based on different techniques support the idea that enzymes can have low populations of many different conformational states, which can be gradually tuned to become major states to allow novel function.

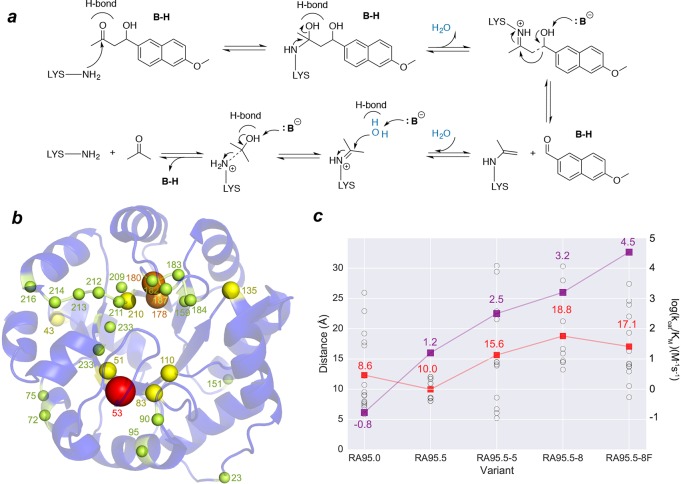
Retro-aldolases (RA) that cleave the methodol substrate (see Figure 1a) are, from a mechanistic perspective, the most complex computationally designed enzymes to date.^13,29,30 They follow a multistep pathway involving enzyme-bound Schiff base intermediates that convert substrate into product. Analysis of initial computational designs generated with Rosetta³¹ revealed that the most active enzymes only offer a 10⁵-fold k_cat/k_uncat improvement due to the lack of precision and specificity in their interactions with the substrate.^32,33 Further laboratory-directed evolution (DE) engineering of the computationally designed RA95 boosted its specific activity by more than 4400-fold.³⁴ The kinetic characterization of the variants indicated that the increase in catalytic efficiency was mainly due to an improvement in k_cat, which was principally achieved via mutations located all around the enzyme structure (see Figure 1b,c). These distal active site mutations caused pronounced molecular changes. Surprisingly, the computationally designed catalytic lysine was unexpectedly abandoned in favor of a new lysine residue in the opposite site of the binding pocket created during the DE evolution.³⁴ The variant RA95.5-8 presents a higher activity than RA95.0, RA95.5, and RA95.5-5 (Figure 1b). It is also a promiscuous variant catalyzing asymmetric Michael additions of carbanions to unsaturated ketones,³⁵ Knoevenagel condensations of electron-rich aldehydes and activated methylene donors,³⁶ and the synthesis of γ-nitroketones.³⁷ Very recently, Hilvert and co-workers using a new ultrahigh-throughput droplet-based microfluidic screening platform evolved RA95.5-8 into the highly active artificial aldolase RA95.5-8F, whose activity rivals the efficiency of natural class I aldolases.¹⁹ This new variant features a catalytic tetrad that emerged along the DE pathway, highlighting that sophisticated active sites can be created even in laboratory-evolved enzymes.

Figure 1.

Reaction mechanism catalyzed by designed and evolved RA95 variants. (a) Scheme showing amine catalysis of the retro-aldol reaction mechanism. (b) Representation of the mutation sites introduced by Directed Evolution (DE). Sphere sizes are weighted according to the number of times the position was mutated along the evolutionary pathway (spheres are also colored from yellow to red depending on the mutation frequency of the position). (c) Representation of the catalytic efficiencies of the RA95 variants (in purple, right axis in log(k_cat/K_M)), together with the distances (in Å) between the C_α of the different mutations (shown in black spheres) and the catalytic lysine (nitrogen atom of side chain). The mean mutation distance is marked with a red square. The catalytic efficiencies of the enzymes (k_cat/K_M in M^–1 s^–1) are represented in purple. For RA95.0, only the 11 mutations introduced with Rosetta are shown.

In this study, we demonstrate that the mutation points introduced for achieving the highly active artificial aldolase RA95.5-8F could have been predicted a priori from long-time-scale MD simulations coupled to residue-by-residue correlation measures. Our study starts with the evaluation of the active site conformational dynamics of the different retro-aldolase variants obtained during laboratory-based evolution, followed by a detailed analysis of the population shift induced by mutations. Finally, we demonstrate that MD simulations coupled to residue-by-residue correlation can identify the residues involved in the population shift toward the catalytically active states. Interestingly, the residues identified with MD and the positions mutated along the evolutionary process for achieving a highly proficient retro-aldolase coincide. This study thus provides a rational strategy to determine promising sites for enhancing novel activity by mutation.

Results

Evolution of Active Site Conformational Dynamics

Our analysis starts with the exploration of the RA95 active site conformational dynamics to evaluate the molecular changes induced by the distal active site mutations (the mean distance between the catalytic lysine and the introduced mutations from RA95.5 to RA95.5-8F is ca. 15 Å; see Figure 1c).^19,34 We analyze both the apo and Schiff base intermediate states (see Figure 1a). In Figure 2, an overlay of the different structures visited along the long-time-scale MD simulations is provided together with key catalytic distances. The available X-ray structures of the RA95 variants with a diketone inhibitor bound are also shown.

Figure 2.

Representation of the enzyme active site conformational dynamics: (a) RA95.0; (b) RA95.5; (c) RA95.5-5; (d) RA95.5-8; (e) RA95.5-8F with Tyr180 acting as the base; (f) RA95.5-8F with Tyr51 deprotonated; (g) plot of the distance between the base and the β-alcohol that will be deprotonated along the three 1 μs MD trajectories. Catalytic residues are represented by blue sticks (for visualization purposes Asn110 has not been included). X-ray structures with the diketone inhibitor bound are displayed for: RA95.0 (PDB 4A29, in purple), RA95.5 (PDB 4A2S, in two types of green, lime green for the inhibitor bound to position 83 and light green for position 210), RA95.5-5 (PDB 4A2R, orange), RA95.5-8F (PDB 5AN7, in yellow).

The computational design RA95.0, created from a (βα)₈ barrel scaffold (16 mutations on PDB, 1LBL; see Table S1 in the Supporting Information), contains Glu53 that was assumed to activate a water molecule to promote the C–C bond cleavage at the Schiff base intermediate. Our simulations indicate that ca. 11 water molecules are present around the catalytic Lys210 in the apo state (Figure S3 in the Supporting Information). We observe a rather long distance between Glu53 and the catalytic Lys210 (ca. 7.1 ± 2.8 Å at the Schiff base intermediate; see Figure 2 and Figure S1 in the Supporting Information), suggesting a minor role of Glu53 in positioning a preorganized water molecule ready for catalysis. Indeed, our observations are in line with the reported low activity of the computational RA95.0 variant and the fact that full activity is retained after mutating Glu53 to alanine.

The initial RA95.0 computational design was further evolved through DE to RA95.5, where six mutations were introduced (Table S1 in the Supporting Information).³⁴ Interestingly, a second lysine appeared at position 83, which in the case of the most evolved RA variants was found to be more effective than Lys210 as a catalytic group under normal turnover conditions.³⁴ Glu53 was replaced by serine (E53S), and a new tyrosine residue at position 51 was installed (V51Y) for promoting the β-alcohol deprotonation (see Figure 1c). In our MD simulations of the Schiff base intermediate, we observe two clear conformations of the L6 loop (residues 180–190), which induce two different orientations of the intermediate (see Figure 2b and Figure S7 in the Supporting Information). The positions of these conformations coincide with the two possible binding modes of the inhibitor (one bound to position 83 and another to position 210) observed in the RA95.5 crystallographic structure. This high flexibility of the Schiff base intermediate leads to a poorly preorganized active site, with a catalytic distance of ca. 5.0 ± 1.4 Å between the base and the β-alcohol (the distance is ca. 4.9 ± 1.2 Å in the apo state; see Figure S1 in the Supporting Information). The mean hydrogen bond angle is ca. 74 ± 52° (Figure S4 in the Supporting Information); therefore, an ideal hydrogen bond conformation is hardly sampled during the MD runs. The active site of the enzyme is solvent exposed with ca. 10 water molecules around Lys83 (see Figure S3 in the Supporting Information), indicating that water could also play a crucial role in assisting the reaction.

RA95.5-5, generated by additional rounds of mutagenesis and plate screening, has six additional mutations, three of them at the enzyme active site (E53T, S110N, and G178S), and the rest on the protein surface (R23H, R43S, and T95M, see Table S1 in the Supporting Information). The X-ray of this variant in the presence of a diketone inhibitor confirmed that it is exclusively bound at Lys83 (see Figure 2c, X-ray in orange). Our MD simulations revealed that the Schiff base intermediate is still not well positioned for catalysis, as the distance between the base and the β-alcohol is ca. 5.4 ± 1.1 Å and the angle is ca. 73 ± 30° (Figure S4 in the Supporting Information). A further evolved variant, RA95.5-8, contains five additional mutations: three near the active site (S178 V, K135N, and G212D), and two distal (S43R, F72Y, see Table S1). This new variant is ca. 60-fold more active than RA95.5, which is mainly due to an increase in k_cat rather than K_M. The MD simulations performed indicate that the distance between Lys83 and Tyr51 is ca. 4.6 ± 0.8 Å in the apo state (Figure S1 in the Supporting Information) but ca. 5.5 ± 1.6 Å for the Schiff base intermediate. The hydrogen bond angles for deprotonating the β-alcohol are quite broad, but the average angle (ca. 98 ± 36°) is larger than in the other variants, consistent with the higher catalytic efficiency observed for this enzyme (see Figure S4). As observed in Figure 2d, the Schiff base intermediate is still quite flexible and can occupy two different pockets. It can be oriented in a conformation similar to that observed for RA95.5-5, as well as in the catalytically productive binding pose observed for the highly evolved RA95.5-8F (see below). The latter state is, however, hardly visited along the MD simulation of this variant.

We finally evaluated the highly evolved RA95.5-8F variant, which provides a >10⁹ rate enhancement. This enzyme exhibits a k_cat value of 10.8 s^–1 and a k_cat/K_M value of 34000 M^–1 s^–1, values comparable to those of natural class I aldolases.¹⁹ RA95.5-8F contains 13 additional mutations scattered throughout the whole protein (see Figure 1b,c). This enzyme possesses a catalytic tetrad composed by the RA95.5-8 triad Lys83, Tyr51, and Asn110, with an additional Tyr180 (due to the F180Y mutation). Of particular note, the original catalytic Lys210 is mutated to leucine. Our MD simulations, like the X-ray structure, show that the catalytic tetrad is perfectly arranged to bind the substrate and adapt to geometric and electrostatic changes occurring during the mechanistically complex reaction pathway. In the apo state, the distance between Tyr51 and Lys83 is ca. 4.6 ± 0.9 Å but ca. 7.2 ± 1.4 Å between Tyr180 and Lys83 (see Figure S1 in the Supporting Information). For the Schiff base intermediate, we investigated the possibility of either Tyr51 or Tyr180 acting as the base for deprotonating the β-alcohol (compare Figure 2e,f). Our results indicate that Tyr180 is substantially better positioned for deprotonating the alcohol, as it stays at ca. 3.1 ± 0.8 Å (ca. 5.9 ± 1.2 Å for Tyr51) with an angle close to the ideal 180° (ca. 143 ± 38°, see Figure S4 in the Supporting Information). This stable and catalytically competent conformation of the Schiff base intermediate is mainly due to the formation of a hydrogen bond between the oxygen atom of the β-alcohol and Tyr51. In fact, when the Y180F mutation is introduced in RA95.5-8F, slightly longer distances are observed (ca. 3.6 ± 1.3 Å between Tyr51 and the alcohol). However, a more drastic effect is observed in the Y51F variant (ca. 4.6 ± 2.1 Å for Tyr180-O_Schiff). In Y51F, the key hydrogen bond with Tyr51 for maintaining the catalytically competent conformation of the Schiff base intermediate is lost (see Figure S15 in the Supporting Information). This is in line with the 4- and 90-fold decreases in k_cat observed experimentally for Y180F and Y51F, respectively.¹⁹ The importance of both Tyr51 and Tyr180 for catalysis was also found experimentally, as replacing both residues resulted in a 17000-fold decrease in k_cat.¹⁹ The overlay of some representative MD snapshots with the X-ray structure reveal a highly preorganized active site, with the Schiff base intermediate properly positioned for catalysis most of the simulation time because of the enhanced hydrogen bond network due to the presence of Tyr180. These results are in line with the recent finding by the Hilvert laboratory that the rate-limiting step of the process in the most evolved RA95.5-8 and RA95.5-8F variants is not the C–C bond scission (as in RA95.0), but rather the product release step.³⁸

The Schiff base conformation adopted in RA95.5-8F matches that observed in the X-ray structure, but interestingly, the binding pose is well matched with that of the computational design RA95.0 (check purple and yellow structures in Figure 2e). The decrease in the pK_a of the catalytic lysine observed experimentally^19,34 is in line with the decrease in the water solvation shell of Lys83 (from 11 to 6), which favors its deprotonated form, and thus facilitates Schiff base formation (see Figure S3 and Table S2 in the Supporting Information).

Evolution of Conformational Dynamics for Enhancing Retro-Aldolase Activity

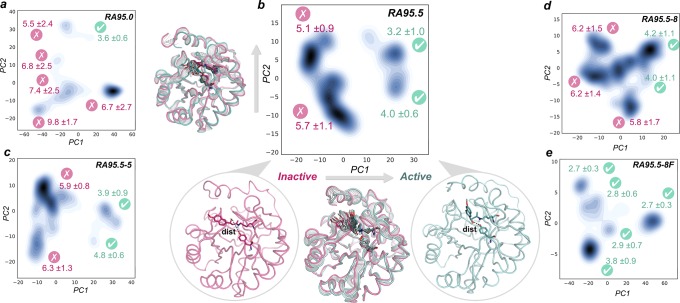
The evaluation of the enzyme active site conformational dynamics has revealed that distal mutations progressively stabilized the catalytically competent arrangement for catalysis. This is especially true for the highly evolved RA95.5-8F enzyme, which features a catalytic tetrad that stays in the catalytically competent arrangement for the entire simulation. The analysis of the structural differences observed along the MD simulations using Principal Component Analysis (PCA) indicates that a population shift occurred along the evolutionary pathway (see Figure 3 and Figure S9 and movies in the Supporting Information). The first principal component (PC1) is able to distinguish inactive states (those presenting a long distance between the base and the β-alcohol, in red in Figure 3b) from the catalytically competent states (active, marked in green in Figure 3b). The main difference between both states arises from the different binding modes of the Schiff base intermediate in the enzyme active site and conformational changes in the flexible loops L1 (residues 52–66), L2 (82–89), L6 (180–190), and L7 (211–215) (see movies in the Supporting Information).

Figure 3.

Representation of the MD trajectories projected into the two most important principal components (PC1, PC2) based on C_α contacts for (a) RA95.0, (b) RA95.5, (c) RA95.5-5, (d) RA95.5-8, and (e) RA95.5-8F Schiff base intermediates. For each substate, the mean distance between the heteroatom of the base and the oxygen of the Schiff base β-alcohol is represented together with the standard deviation (in Å). Those states exploring distances in the 2.0–4.0 Å range are shown in green: i.e., they are catalytically competent, and other states are shown in red. PC1 (x axis) differentiates inactive states (low PC1 values, pink structure in (b)) that present long catalytic distances from those properly oriented for the catalysis (high PC1 values, green structure in (b)). An overlay of the interpolated structures along PC1 and PC2 is also displayed for RA95.5.

The least proficient enzymes (RA95.0) explore conformational substates that barely sample catalytically proficient distances (marked in pink in Figure 3). This is observed for all variants from RA95.0 to RA95.5-8. DE mutations progressively stabilize catalytically competent substates (see conformational states marked in green in Figure 3). The major conformational states in RA95.5-8F have the catalytic Tyr180 properly positioned to deprotonate the alcohol of the Schiff base intermediate. What is more important is that all conformational states are catalytically productive. Our microsecond time scale MD simulations have thus been able to capture significant differences in the conformational substates sampled by the evolved DE variants. Nevertheless, we are aware that much longer or multiple short MD simulations will be needed to capture both kinetics and thermodynamic aspects of this system.³⁹

RA95.0 is substantially more flexible than the rest of the variants (see Figure S7 in the Supporting Information), and a gradual reduction in the conformational flexibility of loops L1 (residues 52–66) and L6 (residues 180–190) is observed, RA95.5-8F being substantially less flexible than the other variants. DE mutations decreased enzyme flexibility and thus increased its thermostability, as observed experimentally.¹⁹

Identification of Residue Pathways for Novel Function

Our microsecond time scale MD simulations have provided a rationalization of the differences in the catalytic efficiencies of the designed and evolved DE variants. They have also demonstrated that the conformational landscape along the evolutionary pathway is significantly altered, with the catalytically active conformational substates progressively populated to an increasing extent. This study, together with work on other enzymes,^18,25,26,40 demonstrates the power of MD for rationalizing DE evolutionary pathways. However, the main question is whether MD can be used as a predictive tool to determine, a priori, which changes might enable novel function. By analogy to DE, the latter changes could be located either close to the enzyme reaction center or at distal positions. Although some studies have used MD to propose mutations in the past,^13,39,41 the predictions were always restricted to the active site.

As shown in the previous sections, RA enzymes sample different conformational states that are not equally populated and these populations shift upon introduction of mutations. The population shift concept has been used previously to rationalize substrate binding mechanisms and allosteric regulation.^10,42 From a computational perspective, allosteric processes have been evaluated via MD to generate molecular ensembles coupled with community network analysis, which identifies clusters of highly connected residues based on residue-by-residue correlation and proximity.^42,43 Given the high similarity of both processes, we hypothesized that correlation-based measures might be useful in the enzyme design field as well.

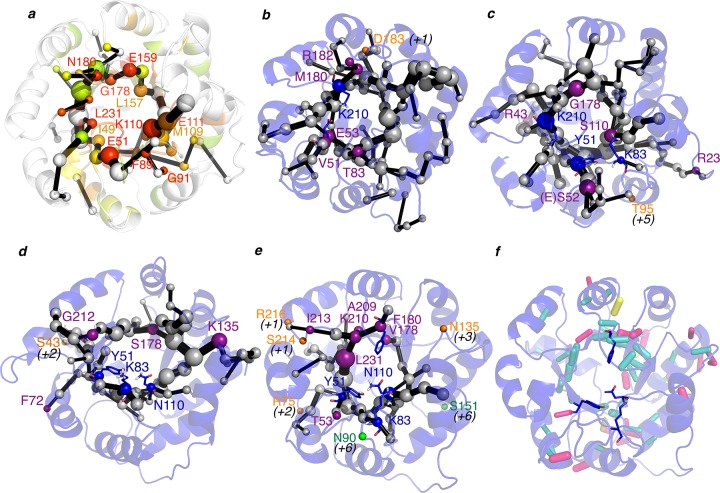
We developed a new tool, DynaComm.py, that explores residue-by-residue correlated movements and inter-residue distances as in previous allosteric studies^42,44 (see Computational Details for more details). This generates a complex graph based on proximity and correlation. We further evaluated the latter graph by making use of the Dijkstra algorithm as implemented in the igraph module⁴⁵ to identify the shortest path lengths. This generates a map that we call the shortest path map (SPM), which identifies pairs of residues that have a higher contribution to the communication pathway. We applied this tool to the accumulated 3 μs MD simulations performed for the studied enzyme variants and compared the SPMs obtained with the DE mutation sites (see Figures 1b, 4, and 5 and Figure S8 and S12–S14 in the Supporting Information). When the structures in Figure 4b–e were compared, it was found that the residues identified by SPM and the positions mutated experimentally during DE are strikingly similar. What is more important is that the SPM can be constructed along the DE process to track which positions could be mutated for pursuing novel RA activity (see Figures 4, and 5). In RA95.0, five out of six DE mutations are included in the SPM (marked in purple in Figure 4); the missing site is located at an adjacent position (D183 in orange; see Figure 4b). The same happens in RA95.5, where the exact mutation sites or adjacent positions are predicted by SPM (only T95 is displaced five positions from SPM). The same holds for RA95.5-5 (four out of five predicted, one out of five in an adjacent position, see S43 in Figure 4d). The most evolved RA95.5-8F variant, which contains a highly preorganized catalytic tetrad, was generated from the previous RA95.5-8 enzyme. Interestingly, the SPM of RA95.5-8 highlights that the catalytic Lys83, Try51, and Asn110 are all contained in the SPM, and more importantly Phe180, which was subsequently mutated to Tyr180 to complete the catalytic tetrad, is also included in the path. This evidences the correlated movement of these positions. In RA95.5-8, seven mutations are predicted, four are in adjacent positions, and only two are displaced six positions from SPM (see S151 and N90 in Figure 4e).

Figure 4.

Representation of the shortest path map (SPM) along the evolutionary pathway: (a) 1LBL; (b) RA95.0; (c) RA95.5; (d) RA95.5-5; (e) RA95.5-8. The size of the sphere is indicative of the importance of the position, and black edges represent the communication path: i.e., how the different residues are connected. Those points mutated via DE are marked in purple (if they are included in the SPM), in orange if they are located in adjacent positions of the SPM (in parentheses is shown how far in the sequence from the closest residue included in SPM), and in green if the mutation is located at more than five positions away in sequence from the SPM. In 1LBL (a), the positions have been colored according to their evolutionary conservation using Evolutionary Trace Server (most conserved in red; less conserved in gray).⁴⁶ (f) Analysis of the H-bond network in RA95.5-8. Those hydrogen bonds that have been maintained at least half of the simulation time are represented by sticks: in blue those hydrogen bonds that occur between backbone atoms, in pink those contacts between backbone and side-chain positions, and finally in yellow hydrogen bonds between side chains. The weight of the hydrogen bond (HB) stick indicates how frequently the HB is observed.

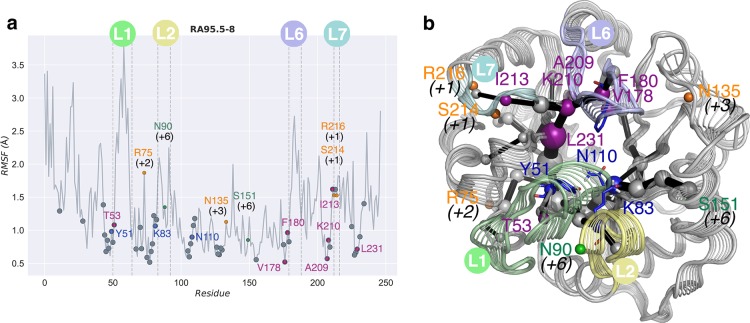
Figure 5.

(a) Root mean square fluctuation (RMSF, in Å) for RA95.5-8 variant along the microsecond time scale MD simulations. Amino acids identified with the Shortest Path Map (SPM) for each enzyme are indicated using gray dots. Directed evolution (DE) mutations are marked with dots in purple (if they are included in the SPM), orange (if displaced by a few positions from SPM), and green (if located more than five positions from the path). The locations of the most mobile loops L1 (residues 52–66), L2 (residues 82–89), L6 (residues 180–190), and L7 (residues 211–215) are marked. The catalytic residues, also included in the SPM, are marked with blue dots. (b) Shortest path map computed for RA95.5-8 projected over the interpolated structures along PC1. Loops L1, L2, L6, and L7 are colored in light green, yellow, blue, and cyan, respectively.

The analysis of the most conserved hydrogen bonds (HB) along the MD trajectories indicates that some of the residues included in the SPM also participate in the protein HB network (see Figure 4 and Figure S12 in the Supporting Information). We also find that there is not a direct correlation between the residues included in the path and the most flexible parts of the protein (see Figure 5 and Figure S8 in the Supporting Information). However, most of the residues included in SPM are located adjacent to flexible regions of the enzyme (see Figure 5 and Figure S12). Interestingly, a detailed analysis of the evolutionary conservation of the positions included in the SPM on the original scaffold 1LBL (see Figure 4a) reveals that many of them are quite conserved.⁴⁶ SPM thus successfully identifies the residues involved in the conversion between the sampled conformational states, which seem to be the target points for DE for enhancing the novel function.

Discussion

Enzymes display a variety of conformational substates that can be converted into major catalytically competitive states by introducing both active sites and distal mutations. The existence of such accessible conformational substates implies that catalytic promiscuity is an inherent characteristic of some enzymes, which might be exploited to enable the emergence of novel functions as has been done in some examples.^{14,15,35,36,47} Long-time-scale molecular dynamics (MD) simulations can assess these enzyme conformational landscapes and thus identify conformational substates, whose populations can be shifted to enhance new catalytic activities. The main question that remains to be answered is how one can identify which mutations are required to favor the desired population shift. Directed evolution (DE) has shown us that these amino acid changes occur not only at the enzyme active site but also at distal positions. So far, the computational prediction of these mutation points has been extremely challenging, especially for distal residues that are usually key for activity.^17,18

Our study provides evidence that MD, coupled to correlation-based tools similar to those used to investigate processes such as allosteric regulation and molecular recognition, can be successfully applied in the enzyme (re)design field. We have developed the shortest path map (SPM), which analyzes the different conformational substates sampled along the MD trajectory and identifies which residues are important for the substate interconversion. Therefore, if catalytically competent states are sampled in the MD simulation, the new tool facilitates identification of residues that contribute to the inactive-to-active interconversion. SPM thus identifies not only active sites but also distal residues that could lead to a population shift toward the catalytically competent conformation for novel activity. This is totally unprecedented and thus opens the door to new computational paradigms that are not restricted to active site alterations. We are currently developing additional strategies based on the analysis of possible hydrogen bond and noncovalent interactions of the identified SPM position and surrounding residues to propose specific amino acid changes for novel function.

Interestingly, application of the SPM tool to the original scaffold 1LBL that was used to generate the RA95.0 computational design already identifies the key mutation sites that were ultimately modified via DE (see Figure 4a and Figure S14 in the Supporting Information). This indicates that the residues identified with SPM presenting a higher contribution (i.e., larger spheres in the graph) could be used for the design of smart libraries for experimental evolution. Thus, this study suggests that the highly active RA95.5-8F retro-aldolase variant could have been generated much more efficiently had the SPM tool been applied at the start of the process.

The success of SPM in this particular enzyme could be related to the fact that the original scaffold (1LBL) is an indole-3-glycerol phosphate synthase.⁴⁸ This enzyme has 30% sequence identity to imidazole-glycerol phosphate synthase (IGPS), which is a known allosterically regulated enzyme.^44,49 Nussinov and co-workers argued that allostery is an intrinsic property of all dynamic (nonfibrous) proteins, which suggests that the SPM tool might be applied to other cases as well.¹² The recent study of Hilvert and co-workers on these RA enzymes has indicated that, especially in the most evolved variants, product release is rate-limiting.⁵⁰ Although we have restricted our study to the retro-aldolase evolution case, our laboratory is investigating the applicability of this tool to other unrelated systems that are also limited by product release. Another important observation is that both 1LBL and IGPS are (βα)₈ barrel enzymes, which is the most common enzyme fold in the Protein Data Bank.⁵¹ In addition, many of the residues included in SPM are quite conserved, especially those located at the end of the β-sheets. This is of importance, as the catalytic groups in (βα)₈ barrel enzymes are usually located at the ends of these different β-strands.⁵²

Conclusions

This work demonstrates that more active enzymes could be designed computationally if the conformational dynamics of the enzyme were exploited. Most of the currently available computational strategies are highly focused on optimizing the chemistry and overlook other equally essential steps such as substrate binding, product release, and associated conformational changes often required for catalysis. Future computational enzyme design strategies will need to extensively evaluate the enzyme conformational dynamics if more proficient enzyme variants are to be pursued.

Computational Details

Molecular Dynamics Simulations

MD simulations in explicit water were performed using the AMBER 16 package.⁵³ The Amber 99SB force field (ff99SB) was used, and parameters for the Schiff base intermediates were generated using the general AMBER force field (gaff),⁵⁴ with partial charges set to fit the electrostatic potential generated at the HF/6-31G(d) level by the restrained electrostatic potential (RESP) model.⁵⁵ Amino acid protonation states were predicted using the H++ server (http://biophysics.cs.vt.edu/H++). Water molecules were treated using the SHAKE algorithm, and long-range electrostatic effects were considered using the particle mesh Ewald method.⁵⁶ The Langevin equilibration scheme was used to control and equalize the temperature with a 2 fs time step at a constant pressure of 1 atm and temperature of 300 K, and an 8 Å cutoff was applied to Lennard–Jones and electrostatic interactions. Production trajectories were run for 1000 ns and were analyzed using the cpptraj module included in the AMBER 16 package. PCA analysis was done with the pyEMMA software.⁵⁷

Shortest Path Map Analysis

The first step of the shortest path map (SPM) calculation relies on the construction of a graph based on the computed mean distances and correlation values, in a fashion similar to that in previous studies (see the Supporting Information for further details).^42,44 The graph is then further simplified by making use of the Dijkstra algorithm as implemented in the igraph module⁴⁵ to identify the shortest path lengths. The algorithm goes through all nodes of the graph and identifies which is the shortest length path to go from the first until the last protein residue. The method therefore identifies which edges of the graph are shorter, i.e. more correlated, and that are more central for the communication pathway. Only those edges having a higher contribution are represented, and they are weighted according to their contribution (see the Supporting Information for more details).

All of these algorithms have been implemented in the new developed DynaComm.py python code, and all structure figures were illustrated using PyMOL (http://www.pymol.org). A web-based server of DynaComm.py will be available on our group webpage (http://silviaosuna.wordpress.com/tools).

Glossary

Abbreviations

TS

transition state

MD

molecular dynamics

NMR

nuclear magnetic resonance

RA

retro-aldolases

DE

directed evolution

SPM

shortest path map

PCA

principal component analysis

RMSF

root-mean-square fluctuation

HB

hydrogen bonds

Supporting Information Available

Supporting Information containing are provided. The Supporting Information is available free of charge on the ACS Publications Web site. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscatal.7b02954.

• Full description of computational methods, and additional figures and tables as described in the text (PDF)

• Movies of PCA analysis (ZIP)

Author Contributions

^§ A.R.-R. and M.G.-B. contributed equally to this work.

Author Contributions

S.O. developed the tools and planned research, M.G.-B. and S.O. designed the project, A.R.-R. and M.G.-B. performed MD simulations, and all authors analyzed data and wrote the paper.

The authors declare no competing financial interest.