Abstract
It remains unclear whether resting state functional magnetic resonance imaging (rfMRI) networks are associated with underlying synchrony in energy demand, as measured by dynamic 2-deoxy-2-[18F]fluoroglucose (FDG) positron emission tomography (PET). We measured absolute glucose metabolism, temporal metabolic connectivity (t-MC) and rfMRI patterns in 53 healthy participants at rest. Twenty-two rfMRI networks emerged from group independent component analysis (gICA). In contrast, only two anti-correlated t-MC emerged from FDG-PET time series using gICA or seed-voxel correlations; one included frontal, parietal and temporal cortices, the other included the cerebellum and medial temporal regions. Whereas cerebellum, thalamus, globus pallidus and calcarine cortex arose as the strongest t-MC hubs, the precuneus and visual cortex arose as the strongest rfMRI hubs. The strength of the t-MC linearly increased with the metabolic rate of glucose suggesting that t-MC measures are strongly associated with the energy demand of the brain tissue, and could reflect regional differences in glucose metabolism, counterbalanced metabolic network demand, and/or differential time-varying delivery of FDG. The mismatch between metabolic and functional connectivity patterns computed as a function of time could reflect differences in the temporal characteristics of glucose metabolism as measured with PET-FDG and brain activation as measured with rfMRI.
Keywords: 2-Deoxyglucose, blood-oxygenation level dependent contrast, energy metabolism, magnetic resonance imaging, pharmacokinetics
Introduction
‘Resting-state’ functional magnetic resonance imaging (rfMRI), a simple non-invasive technique to study brain functional connectivity at rest,1 has attracted the attention of the neuroimaging community in recent years.2–4 However, rfMRI is far from being considered the ‘gold standard’ technique to study brain connectivity because the blood-oxygenation level dependent- (BOLD) signals only indirectly reflect neuronal activity and are prone to the ‘draining/pial vein problem’ that limits the spatial localization of the neural activation.5 On the other hand, the measures of metabolic rate of glucose (MRGlu) as assessed with positron emission tomography (PET) and 2-deoxy-2-[18F]fluoroglucose (FDG) provide an indication of the rate of glucose utilization by neuronal tissue that directly reflects neuronal and glial activity.6
Metabolic connectivity (MC)7–11 has emerged as an alternative approach to map brain connectivity. MC has shown promise as a biomarker for certain neuropsychiatric diseases, their progression and treatment response.7,12,13 However, because PET measures of MRGlu are stationary and restricted by their poor temporal resolution (average measure over 20–30-min period), the correlational analyses between different brain regions needed to map MC have been carried across subjects.14–19 Recently, Passow et al.20 studied for the first time the slow temporal fluctuations in glucose uptake measured with a dynamic PET acquisition and reported within-subject (across time) temporal MC (i.e. t-MC) between cortical regions using similar methodology to that used in rfMRI studies.
rfMRI and t-MC may complement each other, which may lead to a better understanding of disorders that target energy-demanding hubs in the human brain and to biomarkers of clinical utility.21–26 However, the findings by Passow et al.20 could reflect regional differences in the very slow pharmacokinetics associated with FDG uptake in the brain (> 10 min) rather than the relatively faster fluctuations in glucose phosphorylation associated with the energy cost of information processing as captured by rfMRI. Furthermore, since t-MC requires global signal normalization, a procedure that could introduce anti-correlations among regions,27,28 we expected t-MC patterns to be predominantly driven by regional-differences in the pharmacokinetics of FDG rather than by functional interactions between remote brain regions. We studied temporal functional connectivity (t-FC) and t-MC at rest in 53 healthy participants to test these hypotheses. Seed-voxel correlations and group independent component analysis (gICA) were used to assess the t-MC and spatial correlation was used to assess the associations between t-MC, MRGlu and t-FC.
Materials and methods
Participants
Non-smoking subjects older than 18 years of age were recruited and screened to exclude ferromagnetic implants, psychoactive medications and major medical problems, past or present history of drug abuse, and neurological or psychiatric disorders (including eating disorders such as binge eating) as assessed by an abbreviated Structured Clinical Interview for the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV). Women were studied in the mid follicular phase and were neither pregnant nor breastfeeding. The 53 healthy right-handed subjects provided informed consent to participate in the study and were naturally split into two groups due to changes in the MRI acquisition methods (blinding was not possible). Participants which were scanned between March and December 2015 were assigned to the “Discovery” group (N = 28; 37 ± 13 years old, mean ± sd., 11 females) and those that were scanned between January and July 2016 were assigned to the “Validation” group (N = 25; 46 ± 15 years old, 13 females).
The study was approved by the Ethics Committee of the National Institutes of Health (Combined Neurosciences White Panel) and was in accordance with the Declaration of Helsinki. All subjects gave informed written consent before participating in the study.
PET imaging
Both subject groups (discovery and validation) underwent the same PET imaging protocol. Specifically, they were asked to fast (except water) for at least 4 h prior to the PET imaging session, which was performed using a high-resolution research tomography (HRRT) scanner (Siemens AG; Germany). Venous catheters were placed in the antecubital vein for radiotracer injection, and in the dorsal hand vein (arterialization was achieved by warming the hand to 44–50℃) to measure the concentration of radioactivity in plasma (every minute from 1 to 10 min and then at 15, 20, 30, 40, 50, 60 and 75 min after FDG injection). After the patient was positioned in the scanner, a transmission scan was obtained with a 137 Cesium rotating pin source to correct emission images for attenuation. Commercially manufactured FDG (8 mCi) was injected intravenously over a period of approximately 1 min. Then a PET emission scan of the brain with ∼1.23 mm isotropic resolution was obtained using 3D list mode starting immediately after FDG injection for up to 75 min. Fasting glucose levels were measured prior to FDG injection, 30 min after injection, and at the end of the PET scan. During the PET imaging procedures, the subjects rested quietly under dim illumination and minimal acoustic noise. To ensure that subjects did not fall asleep they were monitored throughout the procedure and were asked to keep their eyes open. During the PET scan, a cap with small light reflectors was placed on the subject’s head to monitor head position with a Polaris Vicra head tracking system (Northern Digital Inc., ON, Canada). Information about head movement was used in the PET image reconstruction process to minimize motion-related image blurring. The raw data were reconstructed into 45 timeframes of 100 s duration.
Standardized uptake values (SUVs) for FDG were calculated after normalization of focal FDG uptake for body weight and injected dose. MRGlu was computed at each voxel using Patlak analysis.29 For Freesurfer’s anatomical ROIs, MRGlu was computed using Sokoloff’s model6 with a 2-tissue compartment model neglecting FDG-6-PO dephosphorylation (i.e. k4 = 0). Specifically, we assumed a blood volume fraction,30 ν = 4%, and that the activity at each voxel, A(t)
| (1) |
reflects the concentrations of FDG in arterial plasma, Cp(t), and in the reversible, C1(t), and irreversible, C2(t), compartments which are given by the system of differential equations
| (2) |
The Livermore solver for ordinary differential equations31 was used to solve equation (1) and compute C1(t) and C2(t). The Levenberg–Marquardt algorithm for non-linear least squares fitting32 was used to fit equation (1) to the experimental data (Cp and A) with three adjustable parameters (k1, k2, and k3). The interactive data language (IDL, ITT Visual Information Solutions, Boulder, CO) was used for the 2-tissue compartment modeling described above. The lumped constant (LC = 0.52) and the plasma glucose concentration (PG (mmol/l)) were used to validate the MRGlu from Patlak analysis
| (3) |
The MRGlu map and the dynamic FDG scans were aligned to the subject’s structural MRI image and then normalized to the MNI template with 2 mm isotropic resolution using FLIRT, the Linear Image Registration Tool of the FSL Software Library (version 5.0; http://www.fmrib.ox.ac.uk/fsl).33,34 Relative FDG time series were computed in IDL to account for the time-varying activity due to inflow and uptake of FDG.20 Specifically, for each time frame, the average activity 〈A(t)〉 was computed across voxels with an intensity > 75% of the whole-brain mean, and this value was used as a rescaling factor 104/〈A(t)〉. In addition, relative FDG time series using the cerebellum as a reference region were computed to address potential confounds arising from the selection of the reference region.
MRI acquisition
All subjects underwent MRI on a 3.0 T Magnetom Prisma scanner (Siemens Medical Solutions USA, Inc., Malvern, PA). For the Discovery group, a 20-channel head coil and a single-shot gradient echo-planar imaging (EPI) sequence (repetition time/echo time, TR/TE = 1500/30 ms; flip angle, FA = 70°; matrix = 64, 36 axial slices; 4 mm thickness; interleaved acquisition; no gap between slices; 3 mm in-plane resolution) covering the whole brain were used to acquire rfMRI time series with 600 time points, while the participants relaxed with their eyes open during the 15-min rfMRI scan. A fixation cross was presented on a black background under dimmed room lighting using MRI-compatible goggles (Resonance Technology Inc., Northridge, CA). T1-weighted 3D magnetization-prepared gradient-echo image35 (MP-RAGE)(TR/TE = 2200/4.25 ms; FA = 9°, 1 mm isotropic resolution) and T2-weighted spin-echo multi-slice (TR/TE = 8000/72 ms; 1.1 mm in-plane resolution; 94 slices, 1.7 mm slice thickness; matrix = 192) pulse sequences were used to acquire high-resolution anatomical brain images. For the Validation group, a 32-channel head coil and a multiplexed EPI sequence36 with multiband factor = 8, anterior-posterior phase encoding, TR/TE = 720/37 ms, FA = 52°, matrix = 104, 72 slices were used to acquire rfMRI time series with 2 mm isotropic voxels and 1238 time points, while the participant relaxed with their eyes open. A fixation cross was presented on a black background under dimmed room lighting using a liquid-crystal display screen (BOLDscreen 32, Cambridge Research Systems; UK). The 3D MP-RAGE (TR/TE = 2400/2.24 ms, FA = 8 deg) and variable flip angle turbo spin-echo37 (Siemens SPACE; TR/TE = 3200/564 ms) pulse sequences were used to acquire high-resolution anatomical brain images with 0.8 mm isotropic voxels, field-of-view (FOV) = 240 × 256 mm, matrix = 300 × 320, and 208 sagittal slices.
We used the minimal preprocessing pipelines38 of the Human Connectome Project (HCP) for the spatial normalization of the structural and functional scans. Specifically, FreeSurfer version 5.3.0 (http://surfer.nmr.mgh.harvard.edu) was used to automatically segment the anatomical MRI scans into cortical and subcortical gray matter ROIs39 and for spatial normalization to the stereotactic space of the Montreal Neurological Institute (MNI).
rfMRI preprocessing
For rfMRI time series, the HCP functional pipeline was used for gradient distortion correction, rigid body realignment, field map processing, and spatial normalization to the stereotactic MNI space. Global scaling was used to compute relative rfMRI time series in analogy that used to compute the relative FDG time series. Specifically, for each time frame, the average MRI signal 〈S(t)〉 was computed across brain voxels and this value was used as a rescaling factor 104/〈S(t)〉; 0.1 Hz low-pass filtering was used to assess the low-frequency fluctuations in the rfMRI data.
Framewise displacements (FDs) were computed from head translations and rotations using a 50 mm radius to convert angle rotations to displacements. Scrubbing, implemented in IDL, was used to remove time points excessively contaminated with motion. Specifically, time points were excluded if the root mean square change in the BOLD signal (DVARS) from volume to volume met the following criteria: DVARS > 0.5% and FD > 0.5.40
Group ICA
Probabilistic independent component analysis41 was carried with FSL’s multivariate exploratory linear decomposition into independent components (MELODIC). Specifically, the relative FDG and rfMRI time series underwent temporal concatenation, masking of non-brain voxels, voxel-wise de-meaning, normalization of the voxel-wise variance, whitening and projection into a 40-dimensional subspace.
Seed-voxel correlations
The coordinates of the ventral precuneus (11 mm, −66 mm, 25 mm), which correspond to the location of the strongest rfMRI hub in the brain,42 and the cerebellar vermis, which emerged as one of the strongest t-MC hubs in the brain (1 mm, −60 mm, −15 mm), were used for seed-voxel correlations (cubic seed regions; 125 voxels; 1 ml). Specifically, the Pearson correlation was used to compute the strengths of the t-FC and the t-MC between time-varying signals at the seed location and those in other brain voxels. The Fisher’s z-transformation was used to normalize the step-distributed correlation coefficients.
Across-subjects MC and local MC hubs
The MRGlu maps corresponding to each subject were concatenated to form a 4D subject series; then seed-voxel correlation and group ICA patterns were computed across subjects as described above. In addition, local metabolic connectivity density (lMCD) was computed at every voxel as the number of elements in the local connectivity cluster using a “growing” algorithm, in analogy to the local functional connectivity density.42 Pearson correlation was used to assess the strength of the connectivity, Rij, between voxels i and j in the brain, and a correlation threshold Rij > 0.6 was selected to ensure significant correlations between signal fluctuations across subjects at PFWE < 0.05, corrected for multiple comparisons with family-wise error (FWE) correction. A voxel (xj) was added to the list of voxels metabolically connected with x0 only if it was adjacent to a voxel that was linked to x0 by a continuous path of connected voxels and R0j > 0.6. This calculation was repeated for all brain voxels that were adjacent to those that belonged to the list of voxel metabolically connected to x0 in an iterative manner until no new voxels could be added to the list.
Statistical methods
We used one-sample and paired t-tests in the statistical parametric mapping (SPM8; Wellcome Trust Centre for Neuroimaging, London, UK) to assess the statistical significance of the t-MC, t-FC and lMCD patterns. Conservative voxelwise inference based on a familywise error (FWE) rate was implemented to control for false positives.43 Specifically, voxels were considered statistically significant if they had PFWE < 0.05, corrected for multiple comparisons with the random field theory. Assuming 5% Type I error rate and 20% Type II error rate, a sample size of 26 subjects would allow us to detect effect sizes of 0.57 or better. A less stringent cluster-level correction for multiple comparisons based on a cluster-defining threshold (CDT) P = 0.001 (two-sided) and a minimum cluster size of 100 voxels was used to rule out potential weaker effects.
Results
rfMRI networks
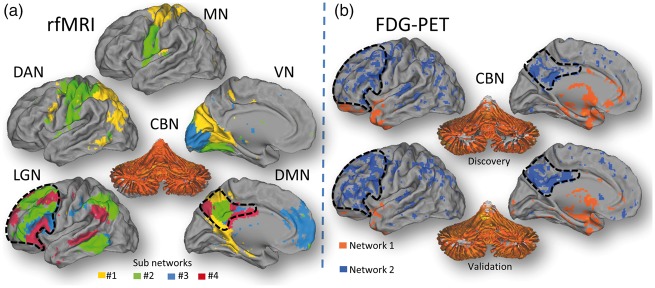
Group ICA on the rfMRI data identified 22 different subnetwork components that integrate major networks such as the cerebellar (CBN), visual (VN), motor (MN), language (LGN), dorsal attention (DAN) and default-mode (DMN) networks (Figure 1(a) and Supplementary material), which is consistent with the emergence of multiple “temporal functional modes,” that subdivide the traditional resting state networks.44 This rich array of networks was not reproduced in the FDG discovery dataset. Specifically, group ICA on the relative FDG discovery datasets identified only two meaningful networks that were anti-correlated.
Figure 1.
Network synchrony. (a) Thirteen of the 22 networks identified by gICA in the Discovery rfMRI datasets were recognized as sub components of six major networks: cerebellum (CBN) language (LNG), motor (MN), visual (VN), dorsal attention (DAN) and default-mode (DMN). Different colors indicate different independent components within each of the major network. gICA reproduced successfully these synchronous networks in the Validation rfMRI datasets. (b) gICA on the FDG-PET Discovery datasets (N = 28) identified two anti-correlated networks, a pattern that was reproduced in the Validation datasets (N = 25).
Network #1 included the cerebellum, pons, anterior thalamus and regions of the medial temporal cortex (hippocampus, parahippocampus, amygdala/temporal; Figure 1(b); orange); the synchrony of the relative glucose metabolism was maximal for cerebellar vermis (z-score = 5.82). Network #2 included cortical regions that encompassed dorsolateral prefrontal and parietal regions (including precuneus, angular gyrus and supramarginal gyrus), and the superior and middle temporal cortices (Figure 1(b); blue). The anti-correlated metabolic networks were reproduced by gICA in the validation dataset (Figure 1(b), bottom panel). Group ICA on the relative FDG datasets that used the cerebellum as a reference region did not identify meaningful networks.
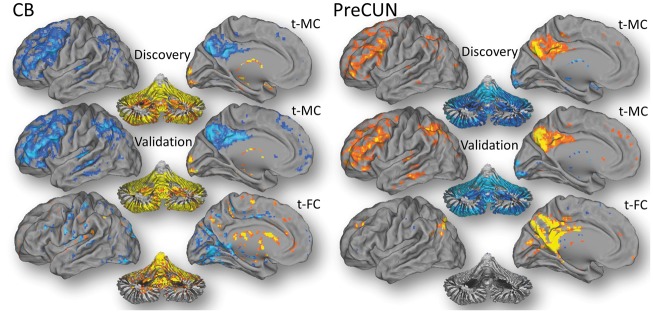
The analysis of t-MC with the cerebellar vermis seed, the t-MC hub that emerged from group ICA, also demonstrated the synchrony of a large fraction of the cerebellar gray matter, that was anti-correlated with cortical gray matter regions including the LGN and posterior DMN (Figure 2). The precuneus seed revealed the opposite t-MC pattern to that of the cerebellar vermis seed (Figure 2). These t-MC patterns were strikingly similar for the discovery and validation cohorts.
Figure 2.
Seed-voxel correlations. Metabolic (t-MC) and functional (t-FC) connectivities for the cerebellar vermis (CB) and precuneus (PreCUN) seed regions in the Discovery cohort (N = 28). t-MC and t-FC patterns were reproduced in the Validation cohort (N = 25).
Brain glucose metabolism
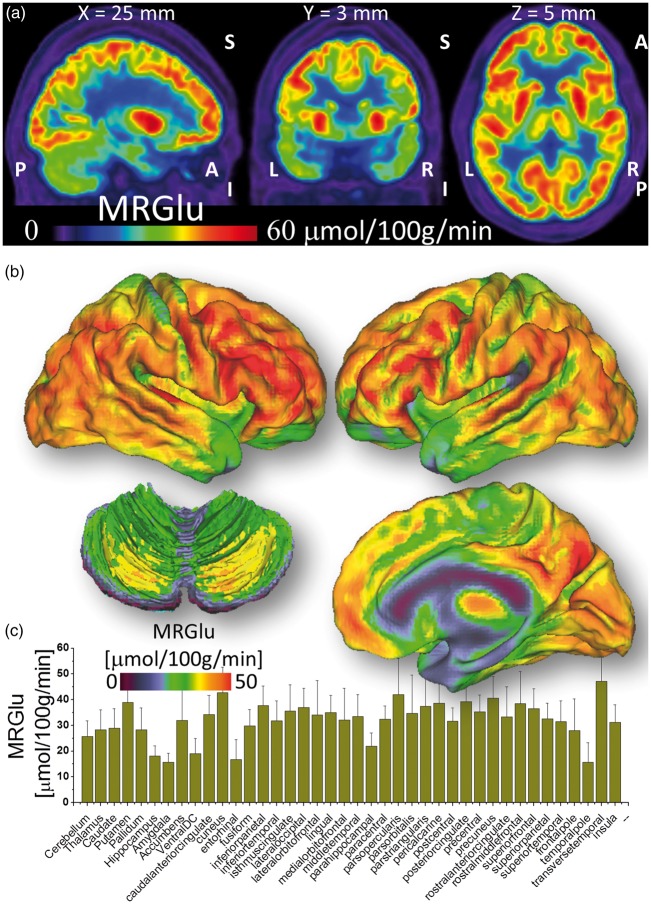
Amygdala, hippocampus, enthorinal cortex, parahippocampus, ventral diencephalon (ventralDC, i.e. midbrain), and temporal pole were the brain regions with the lowest MRGlu (Figure 3). Cerebellum, thalamus, caudate, nucleus accumbens (ventral striatum) and globus pallidum demonstrated intermediate MRGlu levels. Putamen and the other cortical regions showed the highest MRGlu.
Figure 3.
Absolute glucose metabolism. (a) Spatial distribution of the metabolic rate of glucose (MRGlu) overlaid on three orthogonal views of the brain for a randomly selected subject. (b) Average MRGlu across subjects superimposed on dorsal (top) and medial (right bottom) surface views of the cerebrum and a dorsal view of the cerebellum (left bottom). (c) FreeSurfer-based ROI analysis reflecting the average MRGlu within 40 bilateral cortical and subcortical anatomical regions and across 28 healthy subjects (Discovery sample). Patlak analysis was used to quantify MRGlu.
t-MC versus MRGlu
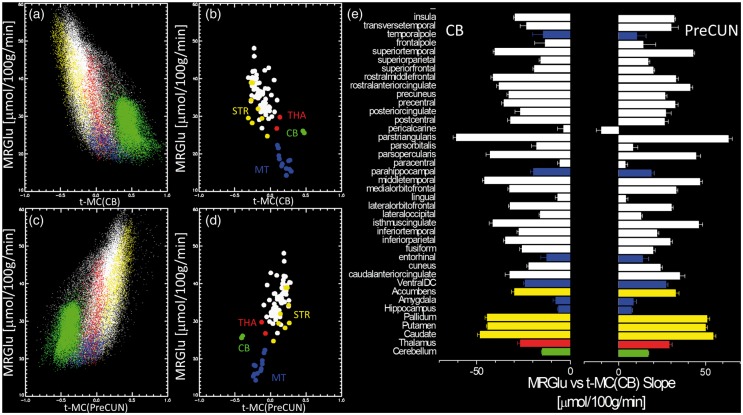
A negative linear association between absolute metabolism and network synchrony emerged from the spatial correlation (across voxels) between cerebellar t-MC and the average MRGlu (Figure 4(a) and (b)). Specifically, the higher the MRGlu in the cortex and the striatum, the higher the negative t-MC of these regions with the cerebellar vermis seed. The reverse pattern emerged for the linear association between MRGlu and the t-MC for the precuneus seed (Figure 4(c)). Note 2D plots in Figure 4(a) and (c) differentiate voxels in the CB (green) from those in the cortex, thalamus and basal ganglia. These findings were validated across the 84 gray matter ROIs (Figure 4(b) and (d)). The slope of the linear regression between MRGlu and t-MC varied significantly across regions and was statistically significant (P < 0.01) in all anatomical regions-of-interest (ROIs) except for the t-MC of the cerebellar vermis and the pericalcarine cortex (Figure 4(e)).
Figure 4.
Absolute metabolism and network synchrony. Linear regression across voxels (a and c) and across ROI measures (b and d) between the average MRGlu and the average MC for the cerebellum (CB, top left) and precuneus (PreCUN, bottom left). Colors in (a) and (c) distinguish voxels in different ROIs (b and d). The green dots highlight voxels in the cerebellum. (e) Linear regression slope for 40 bilateral cortical and subcortical anatomical regions. Error bars are standard errors. Discovery sample (N = 28).
Tracer delivery and t-MC
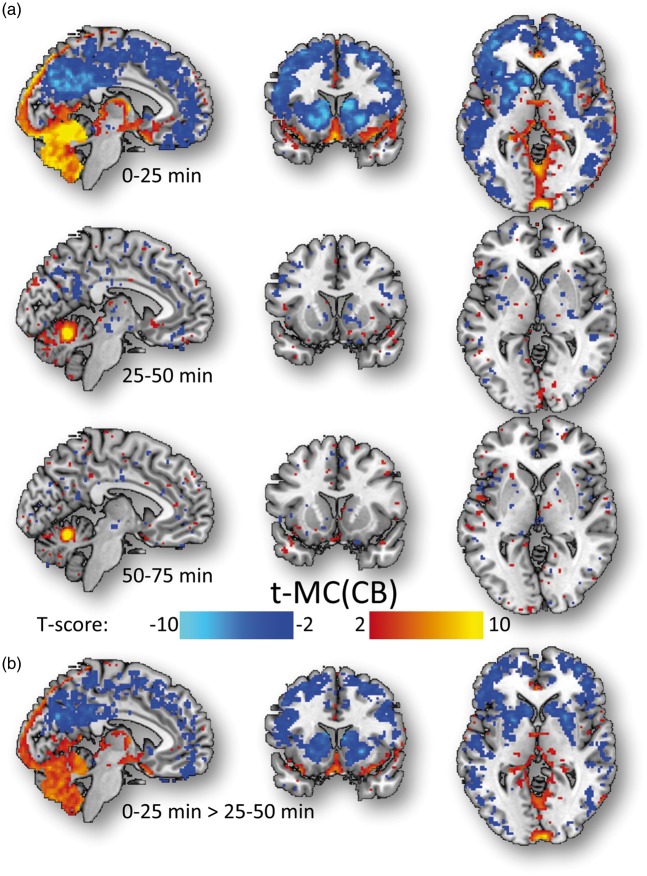
The pharmacokinetics of FDG was strikingly different for the cerebellum compared to the rest of the brain. Specifically, the average parameters of the 2-tissue compartment model k1 and k3 were lower, and those of k2 were higher for the cerebellum (k1 = 0.062 ± 0.004 min−1; k2 = 0.159 ± 0.016 min−1; k3 = 0.027 ± 0.001 min−1) than for the cortex, thalamus and basal ganglia (k1 = 0.082 ± 0.005 min−1; k2 = 0.133 ± 0.005 min−1; k3 = 0.049 ± 0.009 min−1; P < 0.005). Similarly, the average ratio k1/k2 was lower for the cerebellum (k1/k2 = 0.39 ± 0.04) than for the cerebrum (k1/k2 = 0.63 ± 0.04; P < 0.001), suggesting lower tracer delivery for the cerebellum than for the cerebrum. In order to assess potential effects of tracer delivery on t-MC, we segmented the 75-min long FDG time series into three periods (0–25 min; 25–50 min; 50–75 min). The positive and negative t-MC patterns of the cerebellar vermis seed were stronger when we computed t-MC from the 0 to 25-min datasets than when we computed t-MC from 25 to 50 or 50 to 75-min datasets (Figure 5).
Figure 5.
Tracer delivery and t-MC. Statistical significance for the t-MC of the cerebellum computed for three different periods of 25 min (0–25 min; 25–50 min, and 50–75 min; (a), and statistical differences in cerebellar t-MC between the first two periods (b) superimposed on three orthogonal views of the human brain. The anti-correlated t-MC patterns emerged during the first 25 min after tracer injection, likely from pronounced tissue-differences in tracer delivery. Discovery cohort (N = 28).
MC across subjects
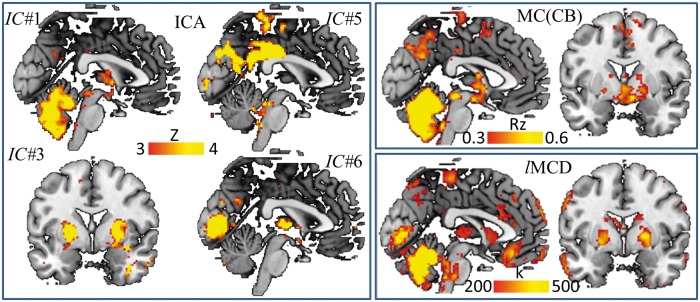
In addition to the within-subject temporal correlation analyses described above, we also studied the MC across subjects using ICA, seed-voxel correlations and lMCD, which is a novel voxelwise metric that quantifies the hubness of the MC (Figure 6). Four bilateral metabolic networks emerged from ICA (P < 0.001, cluster volume 200 voxels). The cerebellar network (IC#1) comprised the cerebellar cortex, thalamus and caudate. The putamen network (IC#3) included the lentiform nucleus (putamen and globus pallidus) and the orbitofrontal cortex. The precuneus/posterior cingulum network (IC#5) comprised posterior DMN regions (including the angular gyrus). The calcarine network (IC#6) included the primary visual cortex and the thalamus. Figure 6 additionally shows MC patterns emerging from the cerebellar vermis seed that encompassed the cerebellar gray matter and anterior thalamus (P < 0.001, cluster volume 200 voxels), and lMCD patterns highlighting strong metabolic hubs in the cerebellum (lMCD > 500), thalamus, globus pallidus and in the calcarine cortex (500 > lMCD > 200).
Figure 6.
MC across subjects. The MRGlu maps from all 53 subjects were concatenated and used to extract the connectivity patterns across subjects. ICA (left panel) revealed four networks comprising: cerebellum (IC#1), putamen/pallidum (IC#3), precuneus/posterior cingulum (IC#5) and calcarine cortex (IC#6). IC#1 is consistent with the seed-voxel correlation pattern for the cerebellum (MC; right upper panel) and IC#1, IC#3 and IC#6, combined, are consistent with the distribution of local hubs of metabolic connectivity (lMCD; right bottom panel).
Discussion
This study is the first to quantify the linear association between t-MC and MRGlu in the brain. In contrast to previous t-MC studies that did not quantify the parameters for the absolute glucose metabolic rate,20 the present study quantifies MRGlu, and the rates of phosphorylation (k3) and glucose transport (k1 and k2). Whereas a constellation of 22 independent networks emerged from rfMRI time series, consistent with the subdivision of the traditional resting state networks,44 only two anti-correlated networks emerged from time-varying relative metabolic activity. The cerebellum, pons, medial temporal lobe (hippocampus, parahippocampus, amygdala/temporal pole) and anterior thalamus showed synchronous fluctuations in glucose uptake that were in phase opposition to those in the cerebral cortex and basal ganglia. The t-MC pattern emerging from these fluctuations was positive and stronger in cortical regions with higher MRGlu, whereas it was negative in the cerebellum. The anti-correlated networks revealed by the temporal analysis of the dynamic FDG-PET data from the Discovery cohort was reproduced in the validation cohort.
The brain is the most metabolically active organ in the body and derives most of its energy requirements through oxidative metabolism of glucose.45,46 The ratio between oxygen consumption and glucose utilization at rest (∼5.5) suggests a close “coupling” between the blood-oxygenation-level-dependent (BOLD) contrast used in rfMRI studies and MRGlu in the brain. The synchrony in the delivery of oxygen/glucose as a function of time among brain regions gives rise to t-FC/t-MC. However, glucose delivery and oxygen delivery have different time scales. Whereas the slow rates of the pharmacokinetics of FDG (k1, k2, and k3) limit the temporal resolution of t-MC to Δt > 1 min, the faster response of the neurovascular coupling that reflects the BOLD signal limits the temporal resolution of t-FC to Δt > 1 s. Thus, the very different patterns emerging from t-FC and t-MC suggest that t-MC networks were driven by regional differences in FDG pharmacokinetics rather than by functional interactions between remote brain regions.
The anti-correlated t-MC patterns could reflect differences in tissue composition between the cerebellum and the cerebral cortex. Whereas the cerebellum contains ∼80% of brain neurons and ∼20% of other brain cells, in the cerebral cortex the ratio of neurons to glia is much lower being estimated to be between 20% and 50% of other brain cells.47,48 Different from the neocortex, which contains six layers and is the most recent part of the cerebral cortex to develop in evolutionary terms,49 the medial temporal lobe, the more ancient part of the cerebral cortex,50 and the cerebellar cortex have only three neuronal layers.51 In the cerebellum, the granular and molecular layers have characteristic architectures that match vascular densities and energy consumption.52
Here we document lower MRGlu levels in cerebellum and medial temporal regions (amygdala, hippocampus, parahippocampal gyrus, temporal pole and the entorhinal cortex) than other cortical and subcortical regions. Interestingly, previous studies reported marked regional differences in the rate of aerobic glycolysis in the human brain that was lower in the cerebellum and medial temporal cortex than in most cortical regions,53 which for the most part did not differ significantly from one another.54 Thus, the anti-correlation patterns between cortex and cerebellum could emerge from anatomical differences between the cerebellum and the cerebral cortex on the relative rate of glucose that is metabolized via aerobic glycolysis versus that metabolized via oxidative phosphorylation. However, we cannot rule out the possibility that the anti-correlated activity between cortical regions and cerebellum could also reflect counter regulation of activity between these two networks.55 Indeed, the negative association between t-MC in cerebellum and MRGlu in cortical regions could reflect a compensatory interplay between these two networks such that higher cerebellar t-MC might enhance the efficiency of cortical regions with a concomitant decrease in MRGlu.
It is nonetheless noteworthy that the two anti-correlated networks correspond well with the territories of perfusion of the anterior artery (internal carotids) versus those of the posterior (basilar) artery. Thus, the anti-correlated activity could also reflect differential regulation of the posterior and the anterior vascular territories,56,57 including differences in glucose transporter density between the cerebellum and the cortex.58 The predominance of t-MC during the first 25 min after tracer injection (Figure 5) and the differences in glucose transport rates (k1 and k2) further support a role of tissue differences in tracer delivery in the strength of the t-MC. Thus, the emergence of t-MC from dynamic FDG data could reflect synchronous glucose utilization or, more likely, similar tissue properties in these regions (glucose transport, phosphorylation, clearance or the ratio of aerobic glycolysis to oxidative phosphorylation).
Different from previous studies that reported significant spatial overlap between seed-voxel correlations patterns emerging from rfMRI and relative FDG time series,20 we observed overlapping patterns in the vicinity of the seeds only. We found, however, a linear relationship between MRGlu and t-MC, which is consistent with the metabolic cost of brain connectivity.20,23,24 Specifically, previously we showed an association between higher MRGlu and higher degree of connectivity, which is consistent with the energy-efficiency of the cerebellum.23 The relatively lower levels of MRGlu in the cerebellum likely reflect metabolism of glucose via oxidative phosphorylation, which is more efficient than aerobic glycolysis. This energy-efficiency might render the cerebellum less sensitive to metabolic disorders such as Alzheimer’s disease,59,60 which contrast with the high metabolic demand of cortical hubs such as the precuneus, which make them prone to neurodegenerative disorders.23,61 On the other hand, the ability of the cerebellum to rely on alternative substrates (i.e. acetate) for energy utilization, as occurs during alcohol intoxication,62 may render the cerebellum more sensitive to the adverse effects of alcoholism.
In contrast to the uniformity of the time-varying metabolic networks (two networks in phase opposition were found in this study), four major metabolic networks were identified by spatial ICA across-subjects (Figure 6), consistent with previous studies.14–19 These networks were also consistent with some of the networks detected in larger MC studies of clinical relevance.18,19 In particular, the cerebellar metabolic network had previously been reported to discriminate amyotrophic lateral sclerosis patients from controls with 96% accuracy or better.18 The cerebellar network also showed hypo MC in dementia with Lewy bodies63 and hyper MC in psychogenic non-epileptic seizures.64 Dysfunctions in the MC of anterior default mode network (including the orbitofrontal cortex) were associated with early onset Alzheimer’s disease.65 Whereas the slow rates of FDG’s PK (k1, k2, and k3) limit the temporal resolution of t-MC to 1 min, the faster response of the neurovascular coupling that reflects the BOLD signal limits the temporal resolution of t-FC to 1 s. Additionally, the temporal resolution of the PET measures is also restricted by the number of counts that are required to obtain a good signal-to-noise ratio, which limited our ability to use shorter time windows in the dynamic images. Thus, t-MC and t-FC take advantage of different temporal dynamics and measure functional connectivity at different time scales in the brain. The different structures of the functional brain networks emerging from the different time scales of dynamic PET-FDG and BOLD-fMRI likely reflect differences in the delivery of oxygen and glucose across brain regions as well as differences in the temporal resolution of PET and fMRI. The exact mechanisms driving t-FC and t-MC are unclear because they depend on parameters that exhibit temporal covariance (BOLD contrast reflects oxygen extraction fraction, blood flow and blood volume, whereas glucose metabolism reflects glucose phosphorylation and transport rates). Our results identify distinct patterns for t-MC than for t-FC. In contrast, MC patterns obtained across subjects were consistent with those previously reported to have overlap with the t-FC patterns, which are likely to reflect distinct glucose metabolic costs reflective of their coordinated neuronal activities.
Supplementary Material
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was accomplished with support from the National Institute on Alcohol Abuse and Alcoholism (Y1AA-3009).
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors’ contributions
DT, NDV designed the study. DT, ESK, GJW, NDV, CEW, EL, GM, SK, ŞBD, EAC performed research. DT, ESK, SK, analyzed data. DT, NDV wrote paper.
Supplementary material
Supplementary material for this paper can be found at the journal website: http://journals.sagepub.com/home/jcb
References
- 1.Biswal B, Yetkin F, Haughton V, et al. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med 1995; 34: 537–541. [DOI] [PubMed] [Google Scholar]
- 2.Biswal B, Mennes M, Zuo X, et al. Toward discovery science of human brain function. Proc Natl Acad Sci USA 2010; 107: 4734–4739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Di Martino A, Yan C, Li Q, et al. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Mol Psychiatry 2014; 19: 659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Glasser M, Smith S, Marcus D, et al. The Human Connectome Project’s neuroimaging approach. Nat Neurosci 2016; 19: 1175–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ugurbil K. What is feasible with imaging human brain function and connectivity using functional magnetic resonance imaging. Philos Trans R Soc Lond B Biol Sci 2016; 371: pii: 20150361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Phelps M, Huang S, Hoffman E, et al. Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann Neurol 1979; 6: 371–388. [DOI] [PubMed] [Google Scholar]
- 7.Volkow N, Wolf A, Brodie J, et al. Brain interactions in chronic schizophrenics under resting and activation conditions. Schizophr Res 1988; 1: 47–53. [DOI] [PubMed] [Google Scholar]
- 8.Lee D, Kang H, Kim H, et al. Metabolic connectivity by interregional correlation analysis using statistical parametric mapping (SPM) and FDG brain PET: methodological development and patterns of metabolic connectivity in adults. Eur J Nucl Med Mol Imaging 2008; 35: 1681–1691. [DOI] [PubMed] [Google Scholar]
- 9.Feigin A, Kaplitt M, Tang C, et al. Modulation of metabolic brain networks after subthalamic gene therapy for Parkinson’s disease. Proc Natl Acad Sci USA 2007; 104: 19559–19564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huang C, Mattis P, Tang C, et al. Metabolic brain networks associated with cognitive function in Parkinson’s disease. Neuroimage 2007; 34: 714–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Horwitz B, Duara R, Rapoport S. Intercorrelations of glucose metabolic rates between brain regions: application to healthy males in a state of reduced sensory input. J Cereb Blood Flow Metab 1984; 4: 484–499. [DOI] [PubMed] [Google Scholar]
- 12.Eckert T, Tang C, Eidelberg D. Assessment of the progression of Parkinson’s disease: a metabolic network approach. Lancet Neurol 2007; 6: 926–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Holtbernd F, Ma Y, Peng S, et al. Dopaminergic correlates of metabolic network activity in Parkinson’s disease. Hum Brain Mapp 2015; 36: 3575–3585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Choi H, Kim Y, Kang H, et al. Abnormal metabolic connectivity in the pilocarpine-induced epilepsy rat model: a multiscale network analysis based on persistent homology. Neuroimage 2014; 99: 226–236. [DOI] [PubMed] [Google Scholar]
- 15.Choi H, Choi Y, Kim K, et al. Maturation of metabolic connectivity of the adolescent rat brain. eLife 2015; 4: e11571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Carbonell F, Charil A, Zijdenbos A, et al. Hierarchical multivariate covariance analysis of metabolic connectivity. J Cereb Blood Flow Metab 2014; 34: 1936–1943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zou N, Chetelat G, Baydogan M, et al. Metabolic connectivity as index of verbal working memory. J Cereb Blood Flow Metab 2015; 35: 1122–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pagani M, Öberg J, De Carli F, et al. Metabolic spatial connectivity in amyotrophic lateral sclerosis as revealed by independent component analysis. Hum Brain Mapp 2016; 37: 942–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Di X, Biswal B. Metabolic brain covariant networks as revealed by FDG-PET with reference to resting-state fMRI networks. Brain Connect 2012; 2: 275–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Passow S, Specht K, Adamsen T, et al. Default-mode network functional connectivity is closely related to metabolic activity. Hum Brain Mapp 2015; 36: 2027–2038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li Z, Zhu Y, Childress A, et al. Relations between BOLD fMRI-derived resting brain activity and cerebral blood flow. Plos One 2012; 7: e44556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liang X, Zou Q, He Y, et al. Coupling of functional connectivity and regional cerebral blood flow reveals a physiological basis for network hubs of the human brain. Proc Natl Acad Sci USA 2013; 110: 1929–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tomasi D, Wang G, Volkow N. Energetic cost of brain functional connectivity. Proc Natl Acad Sci USA 2013; 110: 13642–13647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Riedl V, Bienkowska K, Strobel C, et al. Local activity determines functional connectivity in the resting human brain: a simultaneous FDG-PET/fMRI study. J Neurosci 2014; 34: 6260–6266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Aiello M, Salvatore E, Cachia A, et al. Relationship between simultaneously acquired resting-state regional cerebral glucose metabolism and functional MRI: a PET/MR hybrid scanner study. Neuroimage 2015; 113: 111–121. [DOI] [PubMed] [Google Scholar]
- 26.Nishida M, Juhász C, Sood S, et al. Cortical glucose metabolism positively correlates with gamma-oscillations in nonlesional focal epilepsy. Neuroimage 2008; 42: 1275–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aguirre G, Zarahn E, D’esposito M. The variability of human, BOLD hemodynamic responses. Neuroimage 1998; 8: 360–369. [DOI] [PubMed] [Google Scholar]
- 28.Gavrilescu M, Shaw ME, Stuart GW, et al. Simulation of the effects of global normalization procedures in Functional MRI. Neuroimage 2002; 17: 532–542. [PubMed] [Google Scholar]
- 29.Patlak C, Blasberg R. Derivation of equations for the steady-state reaction velocity of a substance based on the use of a second substance. J Cereb Blood Flow Metab 1981; 5: 584–590. [DOI] [PubMed] [Google Scholar]
- 30.Leenders K, Perani D, Lammertsma A, et al. Cerebral blood flow, blood volume and oxygen utilization. Normal values and effect of age. Brain 1990; 113: 27–47. [DOI] [PubMed] [Google Scholar]
- 31.Hindmarsh A. LSODE and LSODI, two new initial value ordinary differnetial equation solvers. ACM SIGNUM Newslett 1980; 15: 10–11. [Google Scholar]
- 32.Press W, Teukolsky S, Vetterling W, et al. Numerical recipes in C. The art of scientific computing, New York: Cambridge University Press, 1992. [Google Scholar]
- 33.Jenkinson M, Bannister P, Brady M, et al. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002; 17: 825–841. [DOI] [PubMed] [Google Scholar]
- 34.Smith S, Jenkinson M, Woolrich M, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004(23 Suppl 1): S208–S219. [DOI] [PubMed] [Google Scholar]
- 35.Mugler, Brookeman J. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE). Magn Reson Med 1990; 15: 152–157. [DOI] [PubMed] [Google Scholar]
- 36.Moeller S, Yacoub E, Olman C, et al. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med 2010; 63: 1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mugler, Bao S, Mulkern R, et al. Optimized single-slab three-dimensional spin-echo MR imaging of the brain. Radiology 2000; 216: 891–899. [DOI] [PubMed] [Google Scholar]
- 38.Glasser M, Sotiropoulos S, Wilson J, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 2013; 80: 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fischl B, Salat D, Busa E, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron 2002; 33: 341–355. [DOI] [PubMed] [Google Scholar]
- 40.Power J, Barnes K, Snyder A, et al. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 2012; 59: 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Beckmann C, Smith S. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans Med Imaging 2004; 23: 137–152. [DOI] [PubMed] [Google Scholar]
- 42.Tomasi D, Volkow N. Functional Connectivity Density Mapping. Proc Natl Acad Sci USA 2010; 107: 9885–9890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Eklund A, Nichols T, Knutsson H. Cluster failure: why fMRI inferences for spatial extent have inflated false-positive rates. Proc Natl Acad Sci USA 2016; 113: 7900–7905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Smith S, Miller K, Moeller S, et al. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci USA 2012; 109: 3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shulman R, Hyder F, Rothman D. Lactate efflux and the neuroenergetic basis of brain function. NMR Biomed 2001; 14: 389–396. [DOI] [PubMed] [Google Scholar]
- 46.Gruetter R. Glycogen: the forgotten cerebral energy store. J Neurosci Res 2003; 74: 179–183. [DOI] [PubMed] [Google Scholar]
- 47.Azevedo F, Carvalho L, Grinberg L, et al. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J Comp Neurol 2009; 513: 532–541. [DOI] [PubMed] [Google Scholar]
- 48.García-Cabezas M, John Y, Barbas H, et al. Distinction of neurons, glia and endothelial cells in the cerebral cortex: an algorithm based on cytological features. Front Neuroanat 2016; 10: 107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rakic P. Evolution of the neocortex: a perspective from developmental biology. Nat Rev Neurosci 2009; 10: 724–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Allen T, Fortin N. The evolution of episodic memory. Proc Natl Acad Sci USA 2013. June(110 Suppl 2): 10379–10386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Abrahám H, Tornóczky T, Kosztolányi G, et al. Cell formation in the cortical layers of the developing human cerebellum. Int J Dev Neurosci 2001; 19: 53–62. [DOI] [PubMed] [Google Scholar]
- 52.Howarth C, Peppiatt-Wildman C, Attwell D. The energy use associated with neural computation in the cerebellum. J Cereb Blood Flow Metab 2010; 30: 403–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Vaishnavi S, Vlassenko A, Rundle M, et al. Regional aerobic glycolysis in the human brain. Proc Natl Acad Sci USA 2010; 107: 17757–17762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hyder F, Herman P, Bailey C, et al. Uniform distributions of glucose oxidation and oxygen extraction in gray matter of normal human brain: no evidence of regional differences of aerobic glycolysis. J Cereb Blood Flow Metab 2016; 36: 903–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kros L, Eelkman Rooda O, Spanke J, et al. Cerebellar output controls generalized spike-and-wave discharge occurrence. Ann Neurol 2015; 77: 1027–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gierthmühlen J, Allardt A, Sawade M, et al. Role of sympathetic nervous system in activity-induced cerebral perfusion. J Neurol 2010; 257: 1798–1805. [DOI] [PubMed] [Google Scholar]
- 57.Mikhail Kellawan J, Harrell J, Roldan-Alzate A, et al. Regional hypoxic cerebral vasodilation facilitated by diameter changes primarily in anterior versus posterior circulation. J Cereb Blood Flow Metab Epub ahead of print 12 July 2016. DOI: 10.1177/0271678X16659497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cornford E, Hyman S, Cornford M, et al. A single glucose transporter configuration in normal primate brain endothelium: comparison with resected human brain. J Neuropathol Exp Neurol 1998; 57: 699–713. [DOI] [PubMed] [Google Scholar]
- 59.Xu J, Begley P, Church S, et al. Graded perturbations of metabolism in multiple regions of human brain in Alzheimer’s disease: snapshot of a pervasive metabolic disorder. Biochim Biophys Acta 2016; 1862: 1084–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kushner M, Tobin M, Alavi A, et al. Cerebellar glucose consumption in normal and pathologic states using fluorine-FDG and PET. J Nucl Med 1986; 28: 1667–1670. [PubMed] [Google Scholar]
- 61.Crossley N, Mechelli A, Scott J, et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain 2014; 137: 2382–2395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Volkow N, Kim S, Wang G, et al. Acute alcohol intoxication decreases glucose metabolism but increases acetate uptake in the human brain. Neuroimage 2013; 64: 277–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Caminiti S, Tettamanti M, Sala A, et al. Metabolic connectomics targeting brain pathology in dementia with Lewy bodies. J Cereb Blood Flow Metab 2017; 37: 1311–1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Arthuis M, Micoulaud-Franchi J, Bartolomei F, et al. Resting cortical PET metabolic changes in psychogenic non-epileptic seizures (PNES). J Neurol Neurosurg Psychiatry 2015; 86: 1106–1112. [DOI] [PubMed] [Google Scholar]
- 65.Ballarini T, Iaccarino L, Magnani G, et al. Neuropsychiatric subsyndromes and brain metabolic network dysfunctions in early onset Alzheimer’s disease. Hum Brain Mapp 2016; 37: 4234–4247. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.