Abstract
Ordinal outcomes collected at multiple follow-up visits are common in clinical trials. Sometimes, one visit is chosen for the primary analysis and the scale is dichotomized amounting to loss of information. Multistate Markov models describe how a process moves between states over time. Here, simulation studies are performed to investigate the type I error and power characteristics of multistate Markov models for panel data with limited non-adjacent state transitions. The results suggest that the multistate Markov models preserve the type I error and adequate power is achieved with modest sample sizes for panel data with limited non-adjacent state transitions.
Keywords: Multistate models, panel data, type I error, power, stroke
1. Introduction
Most randomized trials in acute stroke neuroprotection treatment have failed to show efficacy for new interventions (Bath et al., 2012). Mergenthaler and Meisel (2012) provide several explanations to describe the lack of positive trials in stroke including heterogeneity in stroke pathophysiology and incomplete preclinical testing (Mergenthaler & Meisel, 2012). Two of the explanations cited by the Optimising Analysis of Stroke Trials Collaboration are inadequate study designs and inappropriate statistical methods, specifically the analysis of the primary outcome (Bath et al., 2007).
The modified Rankin Scale (mRS) score at 90 days post-randomization is a commonly used primary outcome measure in Phase III clinical trials of acute stroke therapy (Saver, 2011). The mRS is a seven-point ordinal scale that measures degree of disability of stroke patients (Table I). Analyzing the mRS as an ordinal scale has only recently gained acceptance (Bath et al., 2007; Bath et al., 2012; DeSantis et al., 2014). Many trials have chosen to dichotomize the mRS into success, scores of 0 or 1 (or 0 to 2), or failure, scores greater than 1 (or 2), for the primary analysis (Savitz et al., 2007). Though models used for dichotomous outcomes are easier to implement and some prefer the clinically meaningful interpretations, dichotomization can result in a loss of statistical power (Bath et al., 2007). It is intuitive that some patients with severe stroke may never have the potential to achieve a success as defined by the dichotomy. Thus, the prognostic heterogeneity of subjects does not allow for potential equal contribution to the estimation of the treatment effect for all subjects (Price et al., 2013).
Table I.
Modified Rankin Scale.
| Score | Description |
|---|---|
| 0 | No symptoms at all |
| 1 | No significant disability despite symptoms; able to carry out all usual duties and activities |
| 2 | Slight disability; unable to carry out all previous activities but able to look after own affairs without assistance |
| 3 | Moderate disability requiring some help, but able to walk without assistance |
| 4 | Moderately severe disability; unable to walk without assistance and unable to attend to own bodily needs without assistance |
| 5 | Severe disability; bedridden, incontinent, and requiring constant nursing care and attention |
| 6 | Dead |
Recently, an emphasis has been placed on exploring alternate analytic methods for the mRS outcome data from acute stroke trials. Results indicate that the mRS should be analyzed in such a way that maintains the original structure of the scale as much as possible (Bath et al., 2007; Bath et al., 2012). Linear regression and analysis of variance have been suggested to analyze the mRS scale as a continuous variable. Although results from these models are generally intuitive, the application to the mRS leads to summary statistics that will not have a clear interpretation. Non-integer values from an ordinal scale do not have a clear meaning when they are treated as continuous.
Another popular alternative method for mRS outcome data is sliding dichotomy analysis. The sliding dichotomy method allows for the definition of success to vary based on patient-specific baseline prognostic variables while maintaining a dichotomized outcome (Garofolo et al., 2013). Commonly, re-analysis of acute stroke trial data using the sliding dichotomy defines pre-specified cut-points for prognostic group inclusion based on the National Institutes of Health Stroke Scale (NIHSS) score (Garofolo, 2012). The mRS is unavailable immediately after randomization so models of acute stroke trial data often adjust for baseline severity using the NIHSS, a score that ranges from 0 (no neurological deficit) to 42. Often, three prognostic groups are defined using the baseline NIHSS for the sliding dichotomy as ‘mild’, ‘moderate’, and ‘severe’ and the definition for ‘success’ differs for each group. One example is to define favorable outcome as mRS = 0 for mild strokes, mRS = 0–1 for moderate strokes and mRS = 0–2 for severe strokes. Since baseline severity is a strong predictor of outcome in stroke patients, this baseline severity adjusted approach has been considered for use over the traditional dichotomy.
While the sliding dichotomy has the potential to be a powerful tool in some settings, it has limitations. Some simulation studies have shown that the utilization of the sliding dichotomy provides higher sensitivity to detect true treatment effects (Young et al., 2005). For example, when the probability of favorable outcome is high (greater than 0.5), the sliding dichotomy provides higher power (Price et al., 2013). This is not a general result; however, as other studies have shown that the traditional dichotomy is more powerful than the sliding dichotomy in many situations (Price, 2009). When the probability of favorable outcome is lower, the traditional dichotomy is more powerful (Price et al., 2013). In addition, determining the number of prognostic groups to use is not an obvious decision and can be difficult to justify. Moreover, determining how to choose the cut points for the different groups can be a difficult task. Although the use of three groups (mild, moderate and severe) is common in the literature, methods used to determine severity cut points vary and need to be verified (Garofolo et al., 2013). Poor selection of the number of prognostic groups and cut points could result in a loss of power. Furthermore, while the sliding dichotomy allows for a baseline severity adjusted outcome, it still ignores any non-‘success’ transition from one mRS score to another even though each mRS category (except 5 to 6) represents a clinically meaningful difference in health state (Lees et al., 2012). The recovery and outcome of subjects following a stroke realistically lies on a continuum. Ordinal analysis of the mRS scores can provide a more complete understanding of this process than analysis of the dichotomized scale (CPMP, 2001).
Recently, methods using the full ordinal scale have been demonstrated (Bath et al., 2012; DeSantis et al., 2014; Nunn et al., 2016). The proportional odds model is a cumulative logistic regression model that has been proposed for analysis of mRS outcome data, Use of this model requires the assumption of proportional odds- the odds ratio comparing treatment to control in subjects with mRS = 0 versus 1–6 is the same as the odds ratio for mRS = 0–1 versus 2–6, and so on. In data where the proportional odds assumption does not hold, shift analysis, an assumption-free ordinal test, can be used (Savitz et al., 2007). Shift analysis can be performed using the van Elteren test, an extension of the two-sample Wilcoxon rank-sum test. Though shift analysis does not require assumptions, it does not produce a summary statistic which is often desired by clinicians. Alternatively, in cases where the proportional odds assumption is unreasonable, the partial proportional odds model or adjacent categories logit model can be used. The partial proportional odds model includes an additional term to allow for the odds ratios to increase proportional to the outcome scale (DeSantis et al., 2014). The adjacent categories logit model calculates odds ratios for each adjacent category of response in relation to covariates. Both of these models are more flexible than the proportional odds model but lack a single summary statistic.
An additional drawback of focusing the primary outcome on the 90-day time point is the lack of use of available longitudinal data. Many acute stroke trials collect the mRS at discharge and/or at 30 days from randomization and also at periodic intervals through 12 months, if long-term follow-up is planned. The longitudinal data are not often used in the primary analysis. Repeated measures analysis, which incorporates outcome data from all follow-up visits, may provide a more comprehensive clinical understanding of the treatment effect on outcome after a stroke (Feng et al., 2011).
In this article, a novel approach using multistate Markov modeling is proposed for the mRS scores. Multistate Markov modeling incorporates the longitudinal ordinal data and provides clinically relevant summary statistics to describe treatment effect. The mRS has more disease ‘states’ (here, the seven levels of the ordinal response) than many previously considered clinical applications of multistate Markov models. An example of the typical data structure of the observed mRS could be illustrated in Table II. In this example, mRS outcome data from a mock acute stroke trial of 1,000 subjects was created for three follow-up visits. The ‘transition’ from one state to another that occurred from one visit to the next is described in Table II. For example, 79 of the 145 subjects that had mRS = 1 at time 1 also had mRS = 1 at time 2. Only 17 of the 145 subjects with mRS = 1 at time 1 transitioned to mRS = 2 at time 2. This is an example of an ‘adjacent-state’ transition. Throughout the table, a majority of the observations are instances where the subjects remained in the same state, or had the same mRS score from one time to the next. Most of the subjects that transitioned to a different state display adjacent-state transitions, with a limited number of non-adjacent state transitions.
Table II.
mRS transition example.
| mRS at time 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | Total | ||
| mRS at time 1 | 0 | 84 | 20 | 5 | 1 | 0 | 0 | 0 | 110 |
| 1 | 45 | 79 | 17 | 2 | 1 | 0 | 1 | 145 | |
| 2 | 12 | 50 | 56 | 15 | 8 | 6 | 1 | 148 | |
| 3 | 2 | 25 | 46 | 63 | 17 | 3 | 0 | 156 | |
| 4 | 1 | 2 | 23 | 77 | 89 | 23 | 5 | 220 | |
| 5 | 0 | 0 | 2 | 7 | 41 | 48 | 22 | 120 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 101 | 101 | |
| Total | 144 | 176 | 149 | 165 | 156 | 80 | 130 | 1000 | |
| mRS at time 3 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | Total | ||
| mRS at time 2 | 0 | 108 | 26 | 5 | 3 | 1 | 1 | 0 | 144 |
| 1 | 38 | 123 | 12 | 2 | 0 | 1 | 0 | 176 | |
| 2 | 9 | 31 | 86 | 18 | 2 | 1 | 2 | 149 | |
| 3 | 3 | 5 | 32 | 116 | 8 | 1 | 0 | 165 | |
| 4 | 0 | 1 | 4 | 34 | 102 | 13 | 2 | 156 | |
| 5 | 0 | 0 | 0 | 2 | 18 | 45 | 15 | 80 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 130 | 130 | |
| Total | 158 | 186 | 139 | 175 | 131 | 62 | 149 | 1000 | |
A literature review conducted of an online database yielded a total of 40 articles using the following keywords: multistate, Markov, panel, clinical, application, continuous-time, and the following excluded words: piecewise, non homogeneous, nonhomogeneous, inhomogeneous, semi Markov, hidden, random effects. An article was excluded if (a) the content was actually theoretical and there was no application, (b) it was a review with no new content, (c) multistate models were referenced, flagging it for review but the models were not actually fit, or (d) the models were actually discrete-time. Of the remaining 26 articles, 25 fit models to data with five or fewer states and two fit models to data with six states (Aalen, 2012; Alessandrino et al., 2013; Allen & Farewell, 2009; Batina et al., 2016; Cao et al., 2013; Chauvel et al., 2007; Chui, 2002; Combescure et al., 2003; Elbasha et al., 2009; Gangnon et al., 2012; Garcia et al., 2016; Haeussler et al., 2016; Hanly et al., 2016; Jackson et al., 2012; Jambarsang et al., 2015; Joutard et al., 2012; Liu et al., 2003; Ndumbi et al., 2013; Nunez et al., 2016; Raiche et al., 2012, 2014; Rodriguez-Girondo & de Una-Alvarez, 2012; Saint-Pierre et al., 2006; Tung et al., 2006; Zhang et al., 2014). One publication used a six-state model to analyze a dataset with much more data than is typically collected in acute stroke trials- approximately 5,000 patients (Gangnon et al., 2014).
The multistate Markov model is introduced in Section 2. The main focus of the paper is to approximate the power and type I error probabilities for multistate Markov models of data structures similar to the longitudinal mRS outcomes observed in acute stroke trials. In Section 2, continuous-time multistate Markov models are defined and the simulation scenarios for estimation of the operating characteristics of these models are described. In Section 3, the type I error probabilities and power are approximated for varying design elements and power of the multistate models is compared with that of repeated measures logistic regression. In Section 4, the findings are summarized and discussed.
2. Methods
Multistate Markov modeling is an alternative approach to analyze repeated measures data with an ordinal outcome. The multistate Markov model describes how a process moves between states over time, which is desirable in the description of disease processes that naturally move through increasing stages of severity (Jackson, 2011). Subjects can improve and worsen over the course of follow-up and these movements back and forth between disease states are all incorporated in the estimation of the model. Multistate Markov models can provide a better clinical understanding of the disease process since the information from the entire course of the disease is used to estimate the parameters of the model. These models have been used in numerous clinical applications including: multiple sclerosis (Gani et al., 2007; Mandel et al., 2013), periodontal disease (Mdala et al., 2014), alcoholism (Shirley et al., 2010), and psychiatry (Gharoodi et al., 2009). This approach has not been used before for mRS data and therefore, in this article a simulation study is performed to examine the operating characteristics of the proposed approach.
2.1 Multistate Markov models
The use of multistate Markov modeling requires that the Markov property holds for the observed data. Consider a stochastic process with a finite state-space S = {1,2,3,…I}, where I represents the number of states in the model. Let X(s) be the state occupied at time s. The series of observations has the Markov property if the conditional distribution of X(s + t), given FX(s) ={X(v):v ≤ s}, where FX(s) denotes all of the information pertaining to the history of X up to time s (Chiang, 1980), satisfies
| (1) |
In other words, a Markov process is one such that the conditional probability distribution of the state of a process at a given time is dependent only on the immediately preceding observation and not on the earlier ones.
Markov models may be defined for discrete time as well as continuous. Although the course of disease is a continuous process, clinical trials often only collect data at intermittent follow-up visits. In the context of stroke, the exact time of progression or recovery, or change of state, of disease is not observed. Data of this type, representative of a continuous process that is only observed at discrete time points, is known as panel data (Titman, 2007). Both discrete and continuous time multistate Markov models can be used to describe panel data. If the sampling times are equally spaced, a continuous model that has been adapted for panel data is preferred over a discrete model (Kalbfleisch & Lawless, 1985). In many acute stroke trials, the mRS is collected at follow-up visits that are not evenly spaced. In such instances, continuous time models are appropriate. A continuous model for panel data can only be used in cases where the sampling times are considered to be non-informative (Jackson, 2011). An example of non-informative sampling is a fixed observation scheme, where the interval of follow-up is specified in advance. However if observations are not fixed or random and are self-selected by the subject (informative), this modeling technique is not appropriate without properly adjusting for the additional information (Jackson, 2011). For instance, these models cannot be used in a scenario where observations occur when a subject visits a doctor because they are in poor-condition. A model that incorporates the information from the sampling times must be used for this type of self-selected follow-up outcome data. In acute stroke trials, the follow-up visits are usually specified in advance and are non-informative so continuous modeling is appropriate.
A common assumption when fitting continuous-time Markov models is the time-homogeneity assumption. This is the assumption that the transition probabilities remain constant over time. When time-homogeneity is assumed, the probability that the next move of the process is from state i to state j can be written,
| (2) |
Thus, the probabilities only depend on the length of the time interval, t. The pij(t) are elements of the transition probability matrix, P(t). The (i, j)th entry of P(t) is the probability of being in state j given the starting state is i after a time interval of t.
The movement of a subject between states is described by λij, the transition intensities:
| (3) |
The intensities represent the instantaneous rate of moving from state i to state j ≠ i. The intensities form the generator matrix, Λ, whose rows sum to zero and the diagonal entries are . P(t) can be solved by taking a matrix exponential of Λ scaled by the time interval,
| (4) |
where Λk is the kth power of the generator matrix Λ.
Suppose now that we observe X over t1 < t2 <…< tM. Let i1, i2,…, iM be the observed states over these time points. Then, the associated likelihood function is
| (5) |
Using (4) and (5), the likelihood is therefore
| (6) |
where is the initial probability that the process is at i1.
The effects of covariates can also be investigated by modeling the intensity as a function of the variables of interest, z(t). The transition intensity matrix elements λij are replaced by
| (7) |
where represent the baseline intensities (without covariates) and βij are the effect of covariates on the transition from state i to state j (Jackson, 2011). To determine the significance of a covariate, a likelihood ratio test is used to compare nested models. In Section 3, the model including treatment is compared to a model without treatment. Thus, the resulting intensities are
| (8) |
where represent the intensities without the covariate and z(t) is the treatment assignment (0 for control and 1 for treatment) for subject n. Thus, the null and alternative hypotheses for the test of the effect of treatment are
The null hypothesis will be rejected using the asymptotic distribution of −2ln(L0/L1) where L0 is the maximum value of the likelihood of the reduced model and L1 is the maximum value of the likelihood of the full model. For large n, this asymptotic distribution is a χ2 with k degrees of freedom, where k is the difference in the number of parameters in the two models.
The difficult part in this process is obtaining the maximum likelihood estimates. Often methods such as Newton-Raphson can cause issues because the computation of the second derivative can be costly in terms of time. Additionally, if the Hessian matrix is non-negative definite away from the optimum, slow or non-convergence may occur. To avoid this, other approaches have been proposed. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) method is used to maximize the likelihood with analytic gradients and can be used with or without analytic first derivatives (Jackson, 2011; Kalbfleisch & Lawless, 1985). The BFGS algorithm approximates Newton’s iterative method for finding the roots of differentiable functions (Dai, 1997). In this algorithm, the Hessian matrix of second derivatives is not evaluated directly. Instead, it approximates the Hessian using gradients. If too many transitions are considered with not enough data in a multistate model, the maximum likelihood estimate could lie on boundary of the parameter space (when one or more transition intensities equal 0). If this occurs, the maximum likelihood estimate may be inconsistent since asymptotic theory requires the assumption that the true parameter value lies away from the boundary.
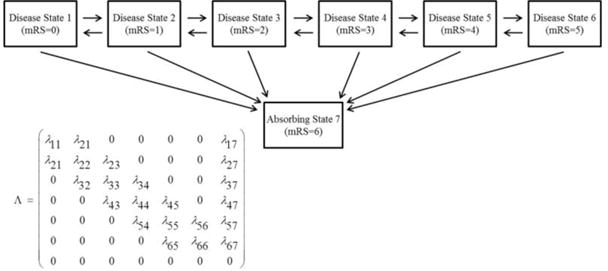
It is important to consider which transitions can realistically occur in continuous time. When the states represent levels of disease severity it is assumed that in order for a subject to travel from one state to a non-adjacent state, the subject also had to travel through the intermediate states. Thus, in this application of these models, a reduced transition intensity matrix where nonadjacent state transition intensities are fixed to equal zero should be assumed. The exception is with mRS = 6, we assume that death can occur from any state and transitions cannot occur out of it because it is an absorbing state. The allowable transitions are displayed in Figure 1.
Figure 1.
2.2 Simulation scenarios
In this section, the procedures for examining the operating characteristics of multistate Markov models under a variety of conditions are described. First, whether or not the multistate Markov model preserves the type I error probability is examined through simulations. Next, given the type I error probability, the desired power is examined for two clinically relevant scenarios, each with two sets of follow-up trajectories for each of the models. The power of the multistate Markov model is compared with that of repeated logistic regression. The motivating example of this simulation study is the limited non- adjacent state transitions observed in mRS data. The simulation scenarios are generated such that the assigned transition probabilities mimic real acute stroke trial as closely as possible. Data from three different phase III acute stroke trials were considered when assigning transition probabilities.
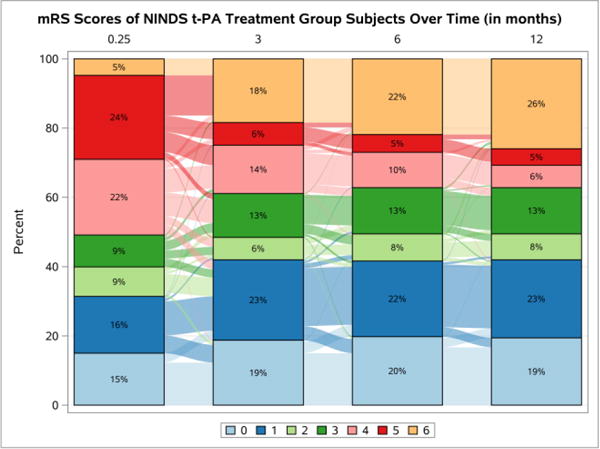
The first trial used is the National Institute of Neurologic Disorders and Stroke (NINDS) tissue-Plasminogen Activator (t-PA) study (“NINDS rt-PA Stroke Study Group,” 1995). The NINDS t-PA trial compared t-PA versus placebo in subjects with acute ischemic stroke. The primary analysis showed a significant global test score for four (Barthel Index, mRS, Glasgow Outcome Scale, and NIHSS) outcomes as well as for the mRS alone (Tilley et al., 1996). To further illustrate the structure of acute stroke trial data, the mRS scores for the control and treatment groups are displayed in Sankey plots in Figures 2 and 3 (Rosanbalm, 2015), respectively. The Sankey plots allow for a visualization of changes within each treatment group over time. The longitudinal bar chart shows the percentage of subjects with each mRS score at each follow-up visit. In addition, the wavy lines between each bar, the links, describe the change in the number of subjects in each state, over time. A thick line indicates that a large number of subjects transition between two states. Note that as illustrated in Table II with the mock data, the percentage of transitions that occur between non-adjacent states is small.
Figure 2.
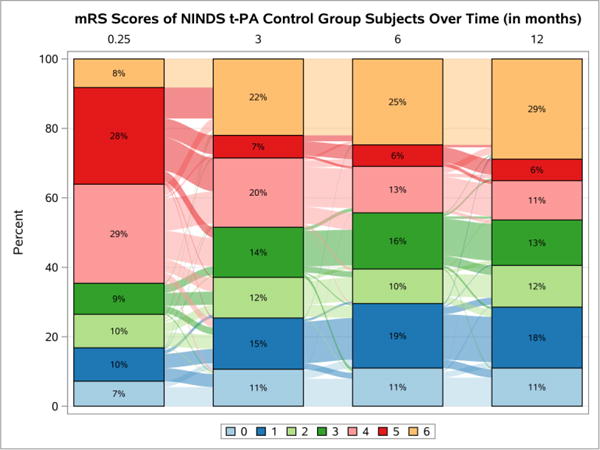
Figure 3.
The other two trials considered for data generation were the albumin in acute stroke (ALIAS) II trial and the Interventional Management of Stroke (IMS) III trial (Broderick et al., 2013; Ginsberg et al., 2013). ALIAS II was designed to compare 25% human serum albumin and saline in patients with acute ischemic stroke. IMS III was designed to compare intravenous t-PA plus an intra-arterial device therapy and/or additional intra-arterial t-PA versus t-PA alone. Both ALIAS II and IMS III were stopped early for futility.
For each of the previously mentioned trials, the observed transition counts for each follow-up visit are combined in one table to calculate aggregate observed transition probabilities. To illustrate, data in Table II would be combined in an aggregate table with 192 (84 + 108) instances where a subject stayed in state 0 out of the total 254 (110 + 144) instances where a subject started in state 0. Thus, for example, the observed aggregate transition probability of remaining in state 0 is 0.76 (192/254), in the mock trial. These observed transition probability matrices are calculated for each study to illustrate the structure for mRS outcome data from acute stroke trials. As previously mentioned, the notable characteristic of the mRS outcome data from these trials is the limited number of non-adjacent state transitions.
To evaluate power, data are generated under the alternative hypothesis that a treatment effect exists. In each multistate Markov model, multiple parameters describe a single covariate effect. Therefore, there are many ways in which a significant treatment effect could exist. In order to simplify, we consider two different clinically relevant scenarios. The first scenario considers a case where only one of the assigned transition probabilities differs between the control and treatment groups. For this set of simulations, the transition probabilities are assigned such that they are all the same for both groups except for the transition from mRS = 3 to mRS = 2 (as well as the transition from mRS = 2 to 1, mRS = 2 to 0, and mRS = 1 to 0, as the intermediate transitions may not be observed). The second scenario for sample size estimation is one where the treatment effect exists in all transitions. The positive transitions are assigned higher probabilities in the treatment group, making them more likely. The negative transitions are assigned a larger probability in the control group.
It is likely that other ordinal scales collected over time have a longitudinal structure similar to the mRS, where non-adjacent state transitions are sparse. In order to consider scales with differing numbers of states, we used the data generated to mimic the mRS described above and collapsed the estimated transition probability matrices to create six-, five-, and four-state models. The method in which the states are aggregated is described in Table III.
Table III.
Modified Rankin Scale inclusion categories
| Symbol | Model | mRS Scores |
|---|---|---|
| 7-state | mRS 0, mRS 1, mRS 2, mRS 3, mRS 4, mRS 5, mRS 6 | |
| 6-state | mRS 0, mRS 1, mRS 2, mRS 3, mRS 4–5, mRS 6 | |
| 5-state* | mRS 0–1, mRS 2, mRS 3, mRS 4–5, mRS 6 | |
| 5-state | mRS 0, mRS 1, mRS 2–3, mRS 4–5, mRS 6 | |
| 4-state | mRS 0–1, mRS 2–3, mRS 4–5, mRS 6 |
In practice, collapsing states is a decision that should be made with caution. For example, if there is clinical evidence that two health states are not distinct, it may be acceptable to combine them. If two health states are aggregated that are vastly different there could be a loss of power. In order to illustrate this point, for the 5-state (and subsequently the 4-state) model, mRS = 2 and mRS = 3 are aggregated. In the scenario where only the transition from mRS = 3 to mRS = 2 differs, there is an expected loss in power for these aggregated models. Thus, in the case where only one transition differs, an additional scenario was considered where mRS = 2 and mRS = 3 are not combined, referred to as the 5-state* model.
The probabilities used to assign outcome trajectories are listed in Appendices A–C. Using these probabilities, the data generation includes the following steps:
Generate a sample of treatment assignments from a random uniform(0, 1) distribution where the probability that the mth subject is assigned to treatment is 0.5.
Generate random uniform variables for all t.
Assign a state for t = 0 using the probabilities described in the appendices.
For each t > 0 use the probabilities to assign a state conditional on the state occupied at t − 1.
To determine the type I error, data are generated under the null hypothesis of no treatment effect. The simulation scenarios for estimation of type I error include differing number of states and increasing sample size per group, starting at 200.
The simulation studies for power are repeated for each set of simulation parameters (Table IV) allowing the number of subjects in each treatment group to vary, as well as the number of follow-up visits (three or six visits). Each set of simulations is carried out using 1,000 runs. For each set of parameters the sample size is set to observe approximately 80% power. The type I error for the multistate Markov model is set to the observed value from the previously described simulations. The resulting power is compared to that of the repeated logistic regression model.
Table IV.
Simulation scenarios for power.
| Number of subjects per group | |||
|---|---|---|---|
| States | Visits | One differing transition | All differing transitions |
| 7 | 3 | 200, 300, 400, 500, 600, 800, 1000 | 300, 400, 500, 600, 800, 1000 |
| 6 | 100, 150, 200, 250, 300, 400, 500 | 100, 150, 200, 250, 300, 400, 500 | |
| 6 | 3 | 200, 300, 400, 500, 600, 800, 1000 | 300, 400, 500, 600, 800, 1000 |
| 6 | 100, 150, 200, 250, 300, 400, 500 | 100, 150, 200, 250, 300, 400, 500 | |
| 5* | 3 | 200, 300, 400, 500, 600, 800, 1000 | |
| 6 | 100, 150, 200, 250, 300, 400, 500 | ||
| 5 | 3 | 200, 300, 400, 500, 600, 800, 1000 | 200, 300, 400, 500, 600, 800, 1000 |
| 6 | 100, 150, 200, 250, 300, 400, 500 | 100, 150, 200, 250, 300, 400, 500 | |
| 4 | 3 | 200, 300, 400, 500, 600, 800, 1000 | 200, 300, 400, 500, 600, 800, 1000 |
| 6 | 100, 150, 200, 250, 300, 400, 500 | 100, 150, 200, 250, 300, 400, 500 | |
The data used were simulated using SAS 9.4 statistical software. SAS 9.4 was also used to run the Generalized Estimating Equation models for repeated measures logistic regression with PROC GENMOD. The Markov models were fitted in R statistical software version 3.3.0 using the ‘msm’ package for multistate Markov models (Jackson, 2011).
3. Results
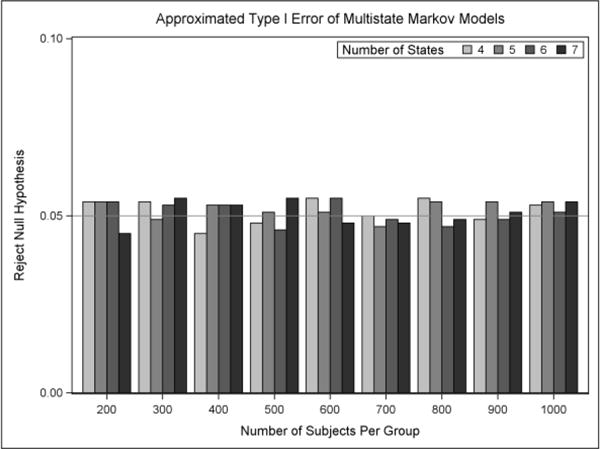
In this section, the behavior of the type I error and power is evaluated. The simulation results of the type I error are displayed in Figure 4. For the application considered, with data structured similar to the three acute stroke trials described in Section 2, the type I error probability is preserved for all of the multistate Markov models. In order to examine whether the chi-square approximation of the likelihood ratio test is appropriate for comparing the nested models, p-values under the appropriate chi-square distribution were obtained and are shown in Appendix D. The p-values appear to be approximately uniform and the test-statistic sampling distribution approximates the chi-square distributions quite adequately.
Figure 4.
For considering power we need to set alternative hypotheses. There are many potential alternative hypotheses so we consider two scenarios that are clinically relevant. In the first scenario, transition probabilities are assigned such that the only difference between treatment groups is in the transition from mRS = 3 to mRS = 2. The results with three and six follow-up visits are displayed in Figures 5a and 5b, respectively. The transition probabilities assigned for these simulations are presented in Appendix B. The results indicate that for a seven-state model with three follow-up visits, approximately 500 subjects are needed in each group to obtain 80% power. There is a marginal increase in power when states mRS = 4 and mRS = 5 are combined in the six-state model. When mRS = 2 and mRS = 3 are combined for the original five-state model we see an extreme decrease in power. This is expected because the model was misspecified. The only difference between treatment groups was in the transition from mRS = 3 to mRS = 2 so when these two states are combined, there are virtually no differences to detect. The same phenomenon is observed in the four-state model because the difference is still lost from aggregating mRS = 2 and mRS = 3. If we consider the fact that the difference lies between those two states and instead collapse mRS = 0 and mRS = 1 in the alternative five-state model (5*) then we see another marginal increase in power. The observed increases in power are expected because there are no differences in the two groups in the aggregated states and there are fewer parameters to estimate in the model.
Figure 5.
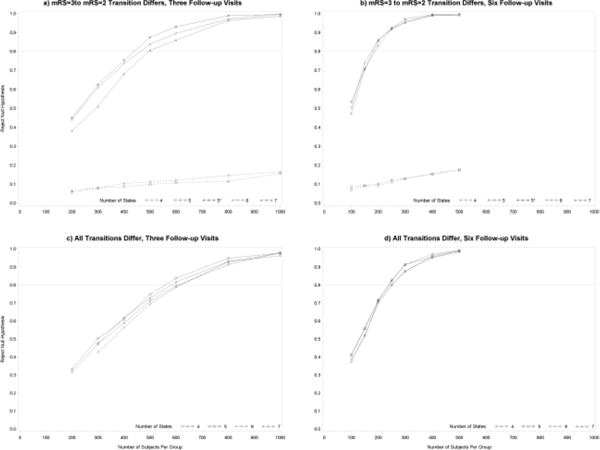
Figure 5b displays the approximated power in the scenario where only the transition from mRS = 3 to mRS = 2 differs, now with six follow-up visits instead of three. The results for the models with six follow-up visits are similar to those in the models with three follow-up visits, except that the power is significantly increased. The power for the seven-, six- and five-state* model are all very similar. Each of these models requires approximately 150 subjects in each group to obtain 80% power. When mRS = 2 and mRS = 3 are combined in the five-state model (and subsequently in the four-state model), there is an extreme loss of power, as previously observed.
The results of the power simulations in the second scenario, where the treatment effect exists for all transitions, are displayed in Figures 5c and 5d. The assumed transition probabilities are described in Appendix C. The approximate power for the three follow-up visit case is displayed in Figure 5c. In the six- and seven- state model, the iteration to obtain the estimates do not converge for sample sizes as small as 200. There are negligible differences in power between each of the models. Since there are differences in all transitions, there will be some loss of power by aggregating states. However, there is a gain in power with fewer parameters in a reduced model. These two facts lead to very minimal change in power. For any given model with three follow-up visits in this scenario, approximately 600 subjects are needed per group to attain 80% power.
Figure 5d displays the approximated power where all assumed transition probabilities differ between groups and the number of follow-up visits is increased from three to six. As observed in the first scenario, the results from the models with six follow-up visits are similar to those from the models with three follow-up visits, with a significant increase in power. The increase in power is expected since there are twice as many observation per subject contributing to the estimation of the model parameters. In this case, approximately 250 subjects are needed per group to reach 80% power.
The approximated power from the models displayed in Figure 5 is compared with that from repeated logistic regression in Tables V and VI. Table V lists the power for the models with three follow-up visits and Table VI lists the power for the models with six follow-up visits. Repeated logistic regression was performed using the dichotomized mRS scores, where scores of 0 or 1 were defined as successes and scores greater than 1 were defined as failures.
Table V.
Comparison of power for models with three follow-up visits.
| Multistate Markov models | |||||||
|---|---|---|---|---|---|---|---|
| Scenario | N per group | Repeated logistic | 7-state | 6-state | 5-state* | 5-state | 4-state |
| 3 to 2 only | 200 | 14.0 | 38.3 | 44.1 | 45.2 | 5.9 | 6.7 |
| 300 | 16.4 | 51.2 | 61.0 | 62.6 | 8.1 | 8.1 | |
| 400 | 23.2 | 68.3 | 73.8 | 75.5 | 8.8 | 10.5 | |
| 500 | 28.3 | 80.7 | 83.9 | 87.6 | 10.0 | 11.3 | |
| 600 | 30.3 | 86.1 | 89.7 | 93.1 | 10.9 | 12.2 | |
| 800 | 41.7 | 96.5 | 97.3 | 99.0 | 11.6 | 14.7 | |
| 1000 | 46.8 | 98.7 | 99.7 | 99.7 | 15.8 | 16.6 | |
| All shifts | 200 | 61.5 | – | – | – | 33.3 | 31.7 |
| 300 | 79.3 | 48.0 | 42.8 | – | 50.5 | 47.4 | |
| 400 | 89.9 | 62.1 | 56.5 | – | 61.1 | 59.0 | |
| 500 | 95.3 | 72.9 | 69.6 | – | 75.0 | 71.3 | |
| 600 | 96.9 | 81.8 | 78.9 | – | 83.9 | 79.7 | |
| 800 | 99.6 | 93.1 | 93.0 | – | 94.9 | 91.5 | |
| 1000 | 99.8 | 97.8 | 96.3 | – | 97.9 | 97.9 | |
Table VI.
Comparison of power for models with six follow-up visits.
| Multistate Markov models | |||||||
|---|---|---|---|---|---|---|---|
| Scenario | N per group | Repeated logistic | 7-state | 6-state | 5-state* | 5-state | 4-state |
| 3 to 2 only | 100 | 12.8 | 47.5 | 50.4 | 53.5 | 7.3 | 8.8 |
| 150 | 17.9 | 70.6 | 74.2 | 71.1 | 9.2 | 9.5 | |
| 200 | 20.8 | 83.3 | 86.2 | 85.7 | 9.3 | 10.3 | |
| 250 | 25.1 | 92.0 | 92.0 | 92.6 | 11.3 | 12.5 | |
| 300 | 30.6 | 95.3 | 95.9 | 97.2 | 13.0 | 13.0 | |
| 400 | 35.6 | 99.3 | 99.0 | 99.6 | 15.5 | 15.6 | |
| 500 | 46.9 | 99.4 | 99.4 | 99.9 | 17.3 | 18.0 | |
| All shifts | 100 | 63.0 | 41.2 | 38.8 | – | 41.3 | 37.3 |
| 150 | 83.3 | 55.8 | 52.3 | – | 56.2 | 51.8 | |
| 200 | 91.7 | 71.8 | 70.0 | – | 71.6 | 71.1 | |
| 250 | 96.0 | 82.6 | 79.8 | – | 82.9 | 80.6 | |
| 300 | 98.0 | 91.3 | 87.7 | – | 91.5 | 87.8 | |
| 400 | 99.8 | 97.3 | 96.3 | – | 95.5 | 95.2 | |
| 500 | 100.0 | 99.3 | 99.0 | – | 99.2 | 98.3 | |
When only one assigned transition probability differs between groups, in correctly specified models, the multistate Markov model requires significantly fewer subjects than the repeated logistic regression model to be adequately powered. When the multistate model is misspecified, the repeated logistic regression is more powerful. When all assumed transition probabilities differ between groups, the repeated logistic regression requires fewer subjects per group to reach 80% power. When there are three follow-up visits, the repeated logistic regression model only requires about 300 subjects per group to be adequately powered, compared to 600 in the multistate model. In the six follow-up visit case, approximately 150 subjects are needed per group compared to 250 in the multistate Markov model.
Summary and discussion
The mRS, one of the most commonly used outcome measures in acute stroke trials, is ordinal but is often dichotomized for analysis. The loss of information from dichotomizing the ordinal variable was examined in this article. In addition, despite the availability of multiple mRS scores over time in many trials, a single measurement is often chosen for primary analysis. The additional information available from the longitudinal data could add further efficiency to the analysis. Multistate Markov modeling is presented here as an alternative analytic approach for ordinal outcomes collected longitudinally. The multistate Markov model describes how a process moves between states over time, which is desirable because it lends itself to clinically relevant interpretations.
In this paper, we have considered time-homogenous continuous Markov multistate models for mRS outcome data observed in phase III acute stroke trials. Simulations demonstrated that the desired type I error probability is preserved for the likelihood ratio test comparing a multistate Markov model including treatment to one without. Power was examined for two different clinically relevant scenarios. The two scenarios represented two diverse instances where a treatment effect exists. In the first scenario all of the assigned transition probabilities were the same for the two treatment groups except the transition from mRS = 3 to mRS = 2. The assigned treatment probabilities in the second scenario differed between the groups for all transitions, representing a positive treatment effect for all shifts.
The key findings of the simulation studies could be summarized as follows:
- When the only difference between the treatment groups in assigned transition probabilities is from mRS = 3 to mRS = 2,
-
○misspecification of the five-state (and four-state) multistate model drastically decreases power as this masks the only difference between groups, the transition from mRS = 3 to mRS = 2
-
○the multistate model yielding the highest power is the 5-state* model where mRS = 4 and mRS = 5 are combined, as well as mRS = 0 and mRS = 1
-
○power is not drastically different for the seven- six- or five-state* Markov model
-
○the multistate model, when correctly specified, is more powerful than repeated logistic regression
-
○
- When all assigned transition probabilities differ between groups,
-
○power is essentially equal for all four multistate Markov models considered
-
○the repeated logistic regression models are more powerful than the multistate Markov models
-
○
For both scenarios, and all combinations of states considered, increasing the number of follow-up visits from three to six drastically increased power.
We considered a case where two distinct states were combined to examine the effects of misspecification. It is important to note that for a process that is truly Markov on I states, a reduced-state model will not satisfy the Markov property (Regnier & Shechter, 2013). The sojourn time will be non-exponential for the merged states and bias can be expected through the misspecification. This highlights the importance of correctly specifying models when using the multistate Markov approach. A modified version of Akaike’s criterion could aid in model selection (Thom et al., 2015).
We conclude that multistate Markov modeling can be a more efficient approach to analysis of mRS data from acute stroke trials. There are situations where dichotomization might not lose efficiency and may be more powerful than the multistate Markov model. Depending on the observed data structure, either technique could be more powerful. In every model, however, increasing the number of follow-up visits from three to six dramatically improved the power to detect a treatment difference.
A limitation of this study is the computational intensity required to run the simulations. For the scenarios with a larger number of states, the time required to complete the simulations was lengthy. Because of the time these simulations take, each was only repeated 1,000 times. Larger simulation studies, say with 10,000 runs rather than 1,000, would improve the precision on the estimates of the operating characteristics. A second limitation of this study is the lack of effect size measurement. In order to quantify an effect size, we would need to be able to define what outcome would be of interest. For example, some previous studies have considered a 10% difference in proportion of good outcome, where good outcome is defined by a dichotomized mRS scale. Quantification of the effect is not straightforward when using Markov multistate modeling. This is a practical question to consider in the future.
A future direction of this work could be to compare the results of multistate Markov modeling to repeated cumulative logistic regression. At the time of submission the authors could not find any publications where longitudinal proportional odds models or adjacent categories logit models were applied to mRS data. Interesting issues arise about how to handle the proportional odds assumption and how to compare models when the assumption fails. This may be a useful extension of the analysis of longitudinal mRS data.
Appendix A: assumed transition probabilities for type I error simulations
In this appendix, we present Tables A.1–A.4, which show the probabilities used to determine the trajectories for the subjects in the type I error simulation study.
Table A.1.
Assumed transition probabilities for the seven-state model.
| Probabilities for time = 1 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0.1000 | 0.1200 | 0.1300 | 0.1500 | 0.2300 | 0.1400 | 0.1300 | |
| Conditional Transition Probabilities for time > 1 | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 0.8000 | 0.1700 | 0.0200 | 0.0050 | 0.0030 | 0.0010 | 0.0010 |
| 1 | 0.2000 | 0.6800 | 0.0800 | 0.0200 | 0.0100 | 0.0050 | 0.0050 |
| 2 | 0.0500 | 0.2800 | 0.5400 | 0.1100 | 0.0100 | 0.0010 | 0.0090 |
| 3 | 0.0200 | 0.0800 | 0.2200 | 0.6000 | 0.0600 | 0.0050 | 0.0150 |
| 4 | 0.0050 | 0.0150 | 0.0600 | 0.2300 | 0.6000 | 0.0700 | 0.0200 |
| 5 | 0.0005 | 0.0070 | 0.0075 | 0.0450 | 0.2800 | 0.4800 | 0.1800 |
Table A.2.
Assumed transition probabilities for the six-state model
| Probabilities for time = 1 | ||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0.100 | 0.120 | 0.130 | 0.150 | 0.370 | 0.130 | |
| Conditional Transition Probabilities for time > 1 | ||||||
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0 | 0.800 | 0.170 | 0.020 | 0.005 | 0.004 | 0.001 |
| 1 | 0.200 | 0.680 | 0.080 | 0.020 | 0.015 | 0.005 |
| 2 | 0.050 | 0.280 | 0.540 | 0.110 | 0.011 | 0.009 |
| 3 | 0.020 | 0.080 | 0.220 | 0.600 | 0.065 | 0.015 |
| 4/5 | 0.003 | 0.011 | 0.034 | 0.138 | 0.714 | 0.100 |
Table A.3.
Assumed transition probabilities for the five-state model
| Probabilities for time = 1 | |||||
|---|---|---|---|---|---|
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0.100 | 0.120 | 0.280 | 0.370 | 0.130 | |
| Conditional Transition Probabilities for time > 1 | |||||
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0 | 0.800 | 0.170 | 0.025 | 0.004 | 0.001 |
| 1 | 0.200 | 0.680 | 0.100 | 0.015 | 0.005 |
| 2/3 | 0.035 | 0.180 | 0.735 | 0.038 | 0.012 |
| 4/5 | 0.003 | 0.011 | 0.172 | 0.714 | 0.100 |
Table A.4.
Assumed transition probabilities for the four-state model.
| Probabilities for time = 1 | ||||
|---|---|---|---|---|
| 0/1 | 2/3 | 4/5 | 6 | |
| 0.220 | 0.280 | 0.370 | 0.130 | |
| Conditional Transition Probabilities for time > 1 | ||||
| 0/1 | 2/3 | 4/5 | 6 | |
| 0/1 | 0.924 | 0.063 | 0.010 | 0.003 |
| 2/3 | 0.215 | 0.735 | 0.038 | 0.012 |
| 4/5 | 0.014 | 0.172 | 0.714 | 0.100 |
Appendix B: assumed transition probabilities for the scenario with only one differing assumed transition
In this appendix, we present Tables B.1–B.5, which show the probabilities used to determine the trajectories for the subjects in the simulation study to approximate power when the treatment effect exists for only one transition (from mRS = 3 to mRS = 2).
Table B.1.
Assumed transition probabilities for the seven-state model.
| Probabilities for time = 1 (control) | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0.110 (0.090) |
0.130 (0.110) |
0.150 (0.110) |
0.110 (0.190) |
0.230 (0.230) |
0.140 (0.140) |
0.130 (0.130) |
|
| Conditional transition probabilities for time > 1 (control) | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 0.800 (0.800) |
0.170 (0.170) |
0.020 (0.020) |
0.005 (0.005) |
0.003 (0.003) |
0.001 (0.001) |
0.001 (0.001) |
| 1 | 0.200 (0.200) |
0.680 (0.680) |
0.080 (0.080) |
0.020 (0.020) |
0.010 (0.010) |
0.005 (0.005) |
0.005 (0.005) |
| 2 | 0.050 (0.050) |
0.280 (0.280) |
0.540 (0.540) |
0.110 (0.110) |
0.010 (0.010) |
0.001 (0.001) |
0.009 (0.009) |
| 3 | 0.030 (0.010) |
0.110 (0.050) |
0.300 (0.140) |
0.480 (0.720) |
0.060 (0.060) |
0.005 (0.005) |
0.015 (0.015) |
| 4 | 0.005 (0.005) |
0.015 (0.015) |
0.060 (0.060) |
0.230 (0.230) |
0.600 (0.600) |
0.070 (0.070) |
0.020 (0.020) |
| 5 | .0005 (.0005) |
0.007 (0.007) |
.0075 (.0075) |
0.045 (0.045) |
0.280 (0.280) |
0.480 (0.480) |
0.180 (0.180) |
Table B.2.
Assumed transition probabilities for the six-state model.
| Probabilities for time = 1 (control) | ||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0.110 (0.090) | 0.130 (0.110) | 0.150 (0.110) | 0.110 (0.190) | 0.370 (0.370) | 0.130 (0.130) | |
| Conditional transition probabilities for time > 1 (control) | ||||||
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0 | 0.800 (0.800) | 0.170 (0.170) | 0.020 (0.020) | 0.005 (0.005) | 0.004 (0.004) | 0.001 (0.001) |
| 1 | 0.200 (0.200) | 0.680 (0.680) | 0.080 (0.080) | 0.020 (0.020) | 0.015 (0.015) | 0.005 (0.005) |
| 2 | 0.050 (0.050) | 0.280 (0.280) | 0.540 (0.540) | 0.110 (0.110) | 0.011 (0.011) | 0.009 (0.009) |
| 3 | 0.030 (0.010) | 0.110 (0.050) | 0.300 (0.140) | 0.480 (0.720) | 0.065 (0.065) | 0.015 (0.015) |
| 4/5 | 0.003 (0.003) | 0.011 (0.011) | 0.034 (0.034) | 0.138 (0.138) | 0.714 (0.714) | 0.100 (0.100) |
Table B.3.
Assumed transition probabilities for the five-state* model
| Probabilities for time = 1 (control) | |||||
|---|---|---|---|---|---|
| 0/1 | 2 | 3 | 4/5 | 6 | |
| 0.240 (200) | 0.150 (0.110) | 0.110 (.190) | 0.370 (.370) | 0.130 (0.130) | |
| Conditional transition probabilities for time > 1 (control) | |||||
| 0/1 | 2 | 3 | 4/5 | 6 | |
| 0/1 | 0.925 (0.925) | 0.050 (0.050) | 0.012 (0.012) | 0.010 (0.010) | 0.003 (0.003) |
| 2 | 0.330 (0.330) | 0.540 (0.540) | 0.110 (0.110) | 0.011 (0.011) | 0.009 (0.009) |
| 3 | 0.140 (0.060) | 0.300 (0.140) | 0.480 (0.720) | 0.065 (0.065) | 0.015 (0.015) |
| 4/5 | 0.014 (0.014) | 0.034 (0.034) | 0.138 (0.138) | 0.714 (0.714) | 0.100 (0.100) |
Table B.4.
Assumed transition probabilities for the five-state model.
| Probabilities for time = 1 (control) | |||||
|---|---|---|---|---|---|
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0.110 (0.090) | 0.130 (0.110) | 0.260 (.300) | 0.370 (.370) | 0.130 (0.130) | |
| Conditional transition probabilities for time > 1 (control) | |||||
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0 | 0.800 (0.800) | 0.170 (0.170) | 0.025 (0.025) | 0.004 (0.004) | 0.001 (0.001) |
| 1 | 0.200 (0.200) | 0.680 (0.680) | 0.100 (0.100) | 0.015 (0.015) | 0.005 (0.005) |
| 2/3 | 0.040 (0.030) | 0.195 (0.165) | 0.715 (0.755) | 0.038 (0.038) | 0.012 (0.012) |
| 4/5 | 0.003 (0.003) | 0.011 (0.011) | 0.172 (0.172) | 0.714 (0.714) | 0.100 (0.100) |
Table B.5.
Assumed transition probabilities for the four-state model
| Probabilities for time = 1 (control) | ||||
|---|---|---|---|---|
| 0/1 | 2/3 | 4/5 | 6 | |
| 0.120 (0.100) | 0.150 (0.120) | 0.230 (0.280) | 0.500 (0.500) | |
| Conditional transition probabilities for time > 1 (control) | ||||
| 0/1 | 2/3 | 4/5 | 6 | |
| 0/1 | 0.924 (0.924) | 0.063 (0.063) | 0.010 (0.010) | 0.003 (0.003) |
| 2/3 | 0.235 (0.195) | 0.715 (0.755) | 0.038 (0.038) | 0.012 (0.012) |
| 4/5 | 0.014 (0.014) | 0.172 (0.172) | 0.714 (0.714) | 0.100 (0.100) |
Appendix C: assumed transition probabilities for scenario with global treatment effect
In this appendix, we present Tables C.1–C.4, which show the probabilities used to determine the trajectories for the subjects in the simulation study to approximate power when the treatment effect exists for all transitions.
Table C.1.
Assumed transition probabilities for the seven-state model.
| Probabilities for time = 1 (control) | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0.150 (0.100) |
0.150 (0.100) |
0.140 (0.100) |
0.100 (0.150) |
0.200 (0.250) |
0.200 (0.230) |
0.060 (0.070) |
|
| Conditional transition probabilities for time > 1 (control) | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 0.800 (0.720) |
0.186 (0.230) |
0.010 (0.042) |
0.001 (0.002) |
0.001 (0.002) |
0.001 (0.002) |
0.001 (0.002) |
| 1 | 0.200 (0.160) |
0.693 (0.676) |
0.080 (0.120) |
0.001 (0.002) |
0.005 (0.010) |
0.001 (0.002) |
0.020 (0.030) |
| 2 | 0.050 (0.030) |
0.280 (0.220) |
0.509 (0.528) |
0.100 (0.140) |
0.020 (0.030) |
0.001 (0.002) |
0.040 (0.050) |
| 3 | 0.020 (0.010) |
0.130 (0.080) |
0.230 (0.200) |
0.560 (0.620) |
0.040 (0.050) |
0.010 (0.020) |
0.010 (0.020) |
| 4 | 0.010 (0.005) |
0.030 (0.020) |
0.060 (0.050) |
0.250 (0.200) |
0.510 (0.565) |
0.070 (0.080) |
0.070 (0.080) |
| 5 | 0.002 (0.001) |
0.010 (0.005) |
0.010 (0.005) |
0.070 (0.050) |
0.250 (0.200) |
0.408 (0.439) |
0.250 (0.300) |
Table C.2.
Assumed transition probabilities for the six-state model.
| Probabilities for time = 1 (control) | ||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0.150 (0.100) | 0.150 (0.100) | 0.140 (0.100) | 0.100 (0.150) | 0.400 (0.480) | 0.060 (0.070) | |
| Conditional transition probabilities for time > 1 (control) | ||||||
| 0 | 1 | 2 | 3 | 4/5 | 6 | |
| 0 | 0.800 (0.720) | 0.186 (0.230) | 0.010 (0.042) | 0.001 (0.002) | 0.002 (0.004) | 0.001 (0.002) |
| 1 | 0.200 (0.160) | 0.693 (0.676) | 0.080 (0.120) | 0.001 (0.002) | 0.006 (0.012) | 0.020 (0.030) |
| 2 | 0.050 (0.030) | 0.280 (0.220) | 0.509 (0.528) | 0.100 (0.140) | 0.021 (0.032) | 0.040 (0.050) |
| 3 | 0.020 (0.010) | 0.130 (0.080) | 0.230 (0.200) | 0.560 (0.620) | 0.050 (0.070) | 0.010 (0.020) |
| 4/5 | 0.006 (0.003) | 0.020 (0.013) | 0.035 (0.028) | 0.160 (0.125) | 0.619 (0.641) | 0.160 (0.190) |
Table C.3.
Assumed transition probabilities for the five-state model.
| Probabilities for time = 1 (control) | |||||
|---|---|---|---|---|---|
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0.150 (0.100) | 0.150 (0.100) | 0.240 (0.250) | 0.400 (0.480) | 0.060 (0.070) | |
| Conditional transition probabilities for time > 1 (control) | |||||
| 0 | 1 | 2/3 | 4/5 | 6 | |
| 0 | 0.800 (0.720) | 0.186 (0.230) | 0.011 (0.044) | 0.002 (0.004) | 0.001 (0.002) |
| 1 | 0.200 (0.160) | 0.693 (0.676) | 0.081 (0.122) | 0.006 (0.012) | 0.020 (0.030) |
| 2/3 | 0.035 (0.020) | 0.205 (0.150) | 0.700 (0.745) | 0.035 (0.050) | 0.025 (0.035) |
| 4/5 | 0.006 (0.003) | 0.020 (0.013) | 0.195 (0.153) | 0.619 (0.641) | 0.160 (0.190) |
Table C.4.
Assumed transition probabilities for the four-state model
| Probabilities for time = 1 (control) | ||||
|---|---|---|---|---|
| 0/1 | 2/3 | 4/5 | 6 | |
| 0.300 (0.200) | 0.240 (0.250) | 0.400 (0.480) | 0.060 (0.070) | |
| Conditional transition probabilities for time > 1 (control) | ||||
| 0/1 | 2/3 | 4/5 | 6 | |
| 0/1 | 0.939 (0.893) | 0.046 (0.083) | 0.004 (0.008) | 0.011 (0.016) |
| 2/3 | 0.240 (0.170) | 0.700 (0.745) | 0.035 (0.050) | 0.025 (0.035) |
| 4/5 | 0.026 (0.016) | 0.195 (0.153) | 0.619 (0.641) | 0.160 (0.190) |
Appendix D: plots of p-values and test-statistics from type I error simulation study
In this appendix, we present Figures D.1 and D.2, which display the distribution of the p-values and test-statistics from the likelihood ratio tests from the type I error simulation study.
Figure D.1.
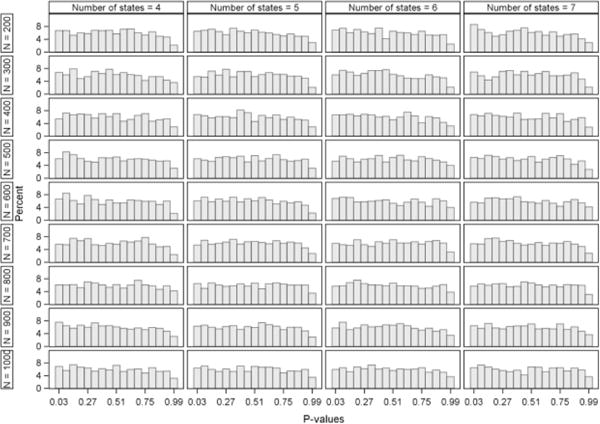
Distribution of p-values from the likelihood ratio tests calculated in the type I error simulation study.
Figure D.2.
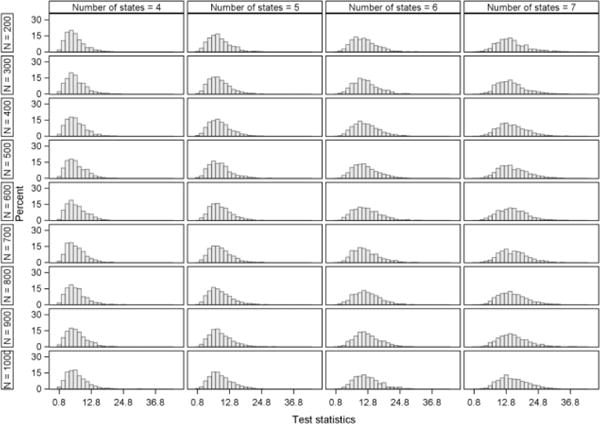
Distribution of test-statistics from the likelihood ratio tests calculated in the type I error simulation study.
References
- Aalen OO. Armitage lecture 2010: Understanding treatment effects: the value of integrating longitudinal data and survival analysis. Stat Med. 2012;31(18):1903–1917. doi: 10.1002/sim.5324. [DOI] [PubMed] [Google Scholar]
- Alessandrino EP, Della Porta MG, Malcovati L, Jackson CH, Pascutto C, Bacigalupo A, van Lint MT, Falda M, Bernardi M, Onida F, Guidi S, Iori AP, Cerretti R, Marenco P, Pioltelli P, Angelucci E, Oneto R, Ripamonti F, Rambaldi A, Bosi A, Cazzola M, Gruppo Italiano Trapianto di Midollo, O Optimal timing of allogeneic hematopoietic stem cell transplantation in patients with myelodysplastic syndrome. American Journal of Hematology. 2013;88(7):581–588. doi: 10.1002/ajh.23458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen EJ, Farewell VT. Pragmatic Analysis of Longitudinal Data on Disease Activity in Systemic Lupus Erythematosus. Communications in Statistics- Theory and Methods. 2009;38(18):3369–3388. [Google Scholar]
- Bath PMW, Gray LJ, Collier T, Pocock S, Carpenter J. Can We Improve the Statistical Analysis of Stroke Trials? Statistical Reanalysis of Functional Outcomes in Stroke Trials. Stroke. 2007;38(6):1911–1915. doi: 10.1161/STROKEAHA.106.474080. [DOI] [PubMed] [Google Scholar]
- Bath PMW, Lees KR, Schellinger PD, Altman H, Bland M, Hogg C, Howard G, Saver JL. Statistical Analysis of the Primary Outcomes in Acute Stroke Trials. Stroke. 2012;43(4):1171–1178. doi: 10.1161/STROKEAHA.111.641456. [DOI] [PubMed] [Google Scholar]
- Batina NG, Crnich CJ, Anderson DF, Dopfer D. Models to predict prevalence and transition dynamics of methicillin-resistant Staphylococcus aureus in community nursing homes. American Journal of Infection Control. 2016;5(1):507–514. doi: 10.1016/j.ajic.2015.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broderick JP, Palesch YY, Demchuk AM, Yeatts SD, Khatri P, Hill M, Jauch EC. Endovascular Therapy after Intravenous t-PA versus t-PA Alone for Stroke. N Engl J Med. 2013;368(10):893–903. doi: 10.1056/NEJMoa1214300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Q, Postmus D, Hillege HL, Buskens E. Probability Elicitation to Inform Early Health Economic Evaluations of New Medical Technologies: A Case Study in Heart Failure Disease Management. Value in Health. 2013;16(4):529–536. doi: 10.1016/j.jval.2013.02.008. [DOI] [PubMed] [Google Scholar]
- Chauvel O, Lacombe K, Bonnard P, Lascoux-Combe C, Molina JM, Miailhes P, Girard PM, Carrat F. Risk factors for acute liver enzyme abnormalities in HIV-hepatitis B virus-coinfected patients on antiretroviral therapy. Antiviral Therapy. 2007;12:1115–1126. [PubMed] [Google Scholar]
- Chiang CL. An Introduction to Stochastic Processes and Their Applications. New York: Robert E. Krieger Publishing Co.; 1980. [Google Scholar]
- Chui M. Nonparametric Simultaneous Modelling of Operative Mortality and Long-Term Survival after Coronary Artery Bypass Surgery. 2002 doi: 10.1002/sim.822. Retrieved from http://summit.sfu.ca/item/7574. [DOI] [PubMed]
- Combescure C, Chanez P, Daures JP, Proudhon H, Godard P, group, A Assessment of variations in control of asthma over time. Eur Respir J. 2003;22:298–304. doi: 10.1183/09031936.03.00081102. [DOI] [PubMed] [Google Scholar]
- CPMP. Points to Consider on Clinical Investigation of Medicinal Products for the Treatment of Acute Stroke. 2001 Retrieved from London: http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003342.pdf.
- Dai YH. A Perfect Example for the BFGS Method. 1997 Retrieved from Beijing. [Google Scholar]
- DeSantis SM, Lazaridis C, Palesch Y, Ramakrishnan V. Regression analysis of ordinal stroke clincial trial outcomes: An application to the NINDS t-PA trial. International Journal of Stroke. 2014;9:226–231. doi: 10.1111/ijs.12052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elbasha EE, Szucs T, Chaudhary MA, Kumar RN, Roediger A, Cook JR, Opravil M. Cost-effectiveness of Raltegravir in Antiretroviral Treatment-Experienced HIV-1–Infected Patients in Switzerland. HIV Clinical Trials. 2009;10(4):233–253. doi: 10.1310/hct1004-233. [DOI] [PubMed] [Google Scholar]
- Feng W, Vasquez G, Suri M, Lakshminaryan K, Qureshi A. Repeated-Measures Analysis of the National Institute of Neurological Disorders and Stroke rt-PA Stroke Trial. Journal of Stroke and Cerebrovascular Diseases. 2011:241–246. doi: 10.1016/j.jstrokecerebrovasdis.2010.01.003. [DOI] [PubMed] [Google Scholar]
- Gangnon RE, Lee KE, Klein BEK, Iyengar SK, Sivakumaran TA, Klein R. Misclassification can explain most apparent regression of age-related macular degeneration: results from multistate models with misclassification. Invest Opthalmol Vis Sci. 2014;55:1780–1786. doi: 10.1167/iovs.13-12375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gangnon RE, Lee KE, Klein BK, Iyengar SK, Sivakumaran TA, Klein R. Effect of the y402h variant in the complement factor h gene on the incidence and progression of age-related macular degeneration: Results from multistate models applied to the beaver dam eye study. Archives of Ophthalmology. 2012;130(9):1169–1176. doi: 10.1001/archophthalmol.2012.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gani R, Nixon RM, Hughes S, Jackson CH. Estimating the rates of disability progression in people with active relapsing-remitting multiple sclerosis. Journal of Medical Economics. 2007;10:79–89. [Google Scholar]
- Garcia ME, Lee A, Neuhaus J, Gonzalez H, To TM, Haan MN. Diabetes Mellitus as a Risk Factor for Development of Depressive Symptoms in a Population-Based Cohort of Older Mexican Americans. Journal of the American Geriatrics Society. 2016;64(3):619–624. doi: 10.1111/jgs.14019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garofolo KM. The Analysis of Acute Stroke Clinical Trials with Responder Analysis Outcomes. Medical University of South Carolina 2012 [Google Scholar]
- Garofolo KM, Yeatts SD, Ramakrishnan V, Jauch EC, Johnston KC, Durkalski VL. The effect of covariate adjustment for baseline severity in acute stroke clinical trials with responder analysis outcomes. Trials. 2013;14(98) doi: 10.1186/1745-6215-14-98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gharoodi ZR, Ganjali M, Berridge D. A Transition Model for Ordinal Response Data with Random Dropout: An Application to the Fluvoxamine Data. J Biopharm Stat. 2009;19:658–671. doi: 10.1080/10543400902964100. [DOI] [PubMed] [Google Scholar]
- Ginsberg MD, Palesch YY, Hill MD, Martin RH, Investigators High-dose albumin treatment for acute ischaemic stroke (ALIAS) part 2: a randomised double-blind, phase 3, placebo-controlled trial. The Lancet Neurology. 2013;12(11):1049–1058. doi: 10.1016/S1474-4422(13)70223-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haeussler K, van den Hout A, Baio G. A dynamic Bayesian Markov model for health economic evaluations of interventions against infectious diseases. 2016 doi: 10.1186/s12874-018-0541-7. Retrieved from Cornell University Library: http://arxiv.org/abs/1512.06881. [DOI] [PMC free article] [PubMed]
- Hanly JG, Su L, Urowitz MB, Romero-Diaz J, Gordon C, Bae SC, Bernatsky S, Clarke AE, Wallace DJ, Merrill JT, Isenberg DA, Rahman A, Ginzler EM, Petri M, Bruce IN, Dooley MA, Fortin P, Gladman DD, Sanchez-Guerrero J, Steinsson K, Ramsey-Goldman R, Khamashta MA, Aranow C, Alarcón GS, Fessler BJ, Manzi S, Nived O, Sturfelt GK, Zoma AA, van Vollenhoven RF, Ramos-Casals M, Ruiz-Irastorza G, Sam Lim S, Kalunian KC, Inanc M, Kamen DL, Peschken CA, Jacobsen S, Askanase A, Theriault C, Farewell V. A Longitudinal Analysis of Outcomes of Lupus Nephritis in an International Inception Cohort Using a Multistate Model Approach. Arthritis & Rheumatology. 2016 doi: 10.1002/art.39674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson CH. Multi-state models for panel data: the msm package for R. Journal of Statistical Software. 2011;38(8):1–29. [Google Scholar]
- Jackson DJ, Evans MD, Gangnon RE, Tisler CJ, Pappas TE, Lee WM, Gern JE, Lemanske RF. Evidence for a Causal Relationship between Allergic Sensitization and Rhinovirus Wheezing in Early Life. American Journal of Respiratory and Critical Care Medicine. 2012;185(3):281–285. doi: 10.1164/rccm.201104-0660OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jambarsang S, Baghban AA, Nazari SSH, Zayeri F, Nikfarjam A, Moradi A. Effect of baseline CD4 count on efficacy of highly-active antiretroviral therapy for HIV patients. International Journal of Biology, Pharmacy and Allied Sciences. 2015;e4(11):700–713. [Google Scholar]
- Joutard X, Paraponaris A, Teyssier LS, Ventelou B. Continuous-Time Markov Model for Transitions Between Employment and Non-Employment: The Impact of a Cancer Diagnosis. Annals of Economics and Statistics. 2012;(107/108):239–265. [Google Scholar]
- Kalbfleisch JD, Lawless JF. The Analysis of Panel Data Under a Markov Assumption. J Am Stat Assoc. 1985:863–871. [Google Scholar]
- Lees KR, Bath PMW, Schellinger PD, Kerr DM, Fulton R, Hacke W, Matchar D, Sehra R, Toni D. Contemporary Outcome Measures in Acute Stroke Research: Choice of Primary Outcome Measure. Stroke. 2012:1163–1170. doi: 10.1161/STROKEAHA.111.641423. [DOI] [PubMed] [Google Scholar]
- Liu WJ, Lee LT, Yen MF, Tungt TH, Williams R, Duffy SW, Chen THH. Assessing progression and efficacy of treatment for diabetic retinopathy following the proliferative pathway to blindness: implication for diabetic retionpathy screeing in Taiwan. Diabetic Medicine. 2003;20:727–733. doi: 10.1046/j.1464-5491.2003.01019.x. [DOI] [PubMed] [Google Scholar]
- Mandel M, Mercier F, Exkert B, Chin P, Betensky RA. Estimating Time to Disease Progression Comparing Transition Models and Survival Models- an Analysis of Multiple Sclerosis Data. Biometrics. 2013;69(1):225–234. doi: 10.1111/biom.12002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mdala I, Olsen I, Haffajee AD, Socransky SS, Thoresen M, de Blasio BF. Comparing clinical attachment level and pocket depth for predicting periodontal disease progression in healthy sites of patients with chronic periodontis using multi-state Markov models. J Clin Periodontol. 2014;41:837–845. doi: 10.1111/jcpe.12278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mergenthaler P, Meisel A. Do Stroke Models Model Stroke? Disease Models and Mechanisms. 2012;5(6):718–725. doi: 10.1242/dmm.010033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ndumbi P, Gillis J, Raboud JM, Cooper C, Hogg RS, Montaner JSG, Burchell AN, Loutfy MR, Machouf N, Klein MB, Tsoukas CM, collaboration, C Clinical implications of altered T-cell homeostasis in treated HIV patients enrolled in a large observational cohort. AIDS. 2013;27(18):2863–2872. doi: 10.1097/01.aids.0000432471.84497.bc. [DOI] [PubMed] [Google Scholar]
- Nunez J, Nunez E, Bayes-Genis A, Fonarow GC, Minana G, Bodi V, Pascual-Figal D, Santas E, Garcia-Blas S, Chorro FJ, Rizopoulos D, Sanchis J. Long-term serial kinetics of N-terminal pro B-type natriuretic peptide and carbohydrate antigen 125 for mortality risk prediction following acute heart failure. European Heart Journal: Acute Cardiovascular Care. 2016 doi: 10.1177/2048872616649757. [DOI] [PubMed] [Google Scholar]
- Nunn A, Bath PMW, Gray LJ. Analysis of the Modified Rankin Scale in Randomised Controlled Trials of Acute Ischaemic Stroke: A Systematic Review. Stroke Research and Treatment. 2016 doi: 10.1155/2016/9482876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price M. Issues in Causal Inference and Applications to Public Health 2009 [Google Scholar]
- Price M, Hertzberg V, Wright DW. Does the sliding dichotomy result in higher powered clinical trials for stroke and traumatic brain injury research? Clinical Trials. 2013;10(6):924–934. doi: 10.1177/1740774512458601. [DOI] [PubMed] [Google Scholar]
- Raiche M, Hebert R, Dubois MF, Gueye NDR, Dubuc N. Yearly transitions of disability profiles in older people living at home. Archieves of Gerontology and Geriatrics. 2012;55(2):399–405. doi: 10.1016/j.archger.2011.12.007. [DOI] [PubMed] [Google Scholar]
- Raiche M, Hebert R, Dubois MF, Gueye NDR, Dubuc N. Covariates of Disability-Profile Transitions in Older People Living at Home. Journal of Biosciences and Medicines. 2014;2:25–36. [Google Scholar]
- Regnier ED, Shechter SM. State-space size considerations for disease-progresssion models. Stat Med. 2013;32:3862–3880. doi: 10.1002/sim.5808. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Girondo M, de Una-Alvarez J. A nonparametric test for Markovianity in the illness-death model. Stat Med. 2012;30:4416–4427. doi: 10.1002/sim.5619. [DOI] [PubMed] [Google Scholar]
- Rosanbalm S. Getting Sankey with Bar Charts. 2015 Retrieved from Chapel Hill. [Google Scholar]
- Saint-Pierre P, Bourdain A, Chanez P, Daures JP, Godard P. Are overweight asthmatics more difficult to control? Allergy. 2006;61:79–84. doi: 10.1111/j.1398-9995.2005.00953.x. [DOI] [PubMed] [Google Scholar]
- Saver JL. Optimal End Points for Acute Stroke Therapy Trials: Best Ways to Measure Treatment Effects of Drugs and Devices. Stroke. 2011:2356–2362. doi: 10.1161/STROKEAHA.111.619122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savitz SI, Lew R, Bluhmki E, Hacke W, Fisher M. Shift Analysis Versus Dichotomization of the Modified Rankin Scale Outcome Scores in the NINDS and ECASS-II Trials. Stroke. 2007;38(12):3205–3212. doi: 10.1161/STROKEAHA.107.489351. [DOI] [PubMed] [Google Scholar]
- Shirley KE, Small DS, Lynch KG, Maisto SA, Oslin DW. Hidden Markov Models for Alcoholism Treatment Trial Data. The Annals of Applied Statistics. 2010;4(1):366–395. [Google Scholar]
- Thom HH, Jackson CH, Commenges D, Sharples LD. State Selection in Markov Models for Panel Data with Application to Psoriatic Arthritis. Stat Med. 2015;34(16):2456–2475. doi: 10.1002/sim.6460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilley B, Marler J, Geller N, Lu M, Legler J, Brott T, Lyden P, Grotta J. Use of a Global Test for Multiple Outcomes in Stroke Trials With Application to the National Institute of Neurological Disorders and Stroke t-PA Stroke Trial. Stroke. 1996;(27):2136–2142. doi: 10.1161/01.str.27.11.2136. [DOI] [PubMed] [Google Scholar]
- Tissue Plasminogen Activator for Acute Ischemic Stroke. N Engl J Med. 1995;333:1581–1587. doi: 10.1056/NEJM199512143332401. [DOI] [PubMed] [Google Scholar]
- Titman AC. Model diagnostics in multi-state models of biological systems. 2007 doi: 10.1177/0962280209105541. Retrieved from Cambridge: http://www.maths.lancs.ac.uk/~titman/thesis.pdf. [DOI] [PubMed]
- Tung TH, Chen SJ, Shih HC, Chou P, Li AF, Shyong MP, Lee FL, Luiu JH. Assessing the Natural Course of Diabetic Retinopathy: A Population-Based Study in Kinmen, Taiwan. Opthalmic Epidemiology. 2006;13(5):327–333. doi: 10.1080/09286580600826637. [DOI] [PubMed] [Google Scholar]
- Young FB, Lees KR, Weir CJ. Improving Trial Power Through use of Prognosis-Adjusted End Points. Stroke. 2005 doi: 10.1161/01.STR.0000154856.42135.85. [DOI] [PubMed] [Google Scholar]
- Zhang SK, Kang LN, Chang IJ, Zhao FH, Hu SY, Chen W, Shi JF, Zhang X, Pan QJ, Li SM, Qiao YL. The Natural History of Cervical Cancer in Chinese Women: Results from an 11-Year Follow-Up Study in China Using a Multistate Model. Cancer Epidemiol Biomarkers Prev. 2014;23 doi: 10.1158/1055-9965.EPI-13-0846. [DOI] [PubMed] [Google Scholar]


