The Impact of Bottlenecks on Microbial Survival, Adaptation and Phenotypic Switching in Host-Pathogen Interactions

Abstract

Microbial pathogens and viruses can often maintain sufficient population diversity to evade a wide range of host immune responses. However, when populations experience bottlenecks, as occurs frequently during initiation of new infections, pathogens require specialized mechanisms to regenerate diversity. We address the evolution of such mechanisms, known as stochastic phenotype switches, which are prevalent in pathogenic bacteria. We analyze a model of pathogen diversification in a changing host environment that accounts for selective bottlenecks, wherein different phenotypes have distinct transmission probabilities between hosts. We show that under stringent bottlenecks, such that only one phenotype can initiate new infections, there exists a threshold stochastic switching rate below which all pathogen lineages go extinct, and above which survival is a near certainty. We determine how quickly stochastic switching rates can evolve by computing a fitness landscape for the evolutionary dynamics of switching rates, and analyzing its dependence on both the stringency of bottlenecks and the duration of within-host growth periods. We show that increasing the stringency of bottlenecks or decreasing the period of growth results in faster adaptation of switching rates. Our model provides strong theoretical evidence that bottlenecks play a critical role in accelerating the evolutionary dynamics of pathogens.

INTRODUCTION

In the biology of infections, microbial populations are often subject to reductions in numbers as they are transmitted from one host to another or translocate across anatomical barriers within a host. These reductions in population size are often described metaphorically as bottlenecks (reviewed in (Amos and Harwood, 1998)). Microbial bottlenecks reduce the variation in the gene pool of a population and the reduced genetic diversity takes time to be restored and may not be representative of the original population. The impact of bottlenecks on population fitness is potentially complex. We consider two broad classes of bottlenecks – non-selective bottlenecks, in which all cells are equally likely to survive, and selective bottlenecks in which some cells are more likely to survive than others. In a non-selective bottleneck, the fitness of the population may be reduced if the future progeny, subjected to genetic drift, is founded by less fit genotypes. On the other hand, there can be an increase in population fitness under selective bottlenecks because certain genotypes will be more likely to survive, and less fit genotypes will be eliminated. In either of these scenarios, which are not mutually exclusive over the history of any given pathogen, there are potentially profound consequences for understanding the evolutionary trends of the commensal and pathogenic behaviour of microbes and of their hosts. Naturally occurring and experimental infections provide direct information on the population dynamics of spread between and within hosts and the impact of bottlenecks. Some of the most important examples are afforded by observations on viruses.

Clinical observations of HIV-1 infection in humans shows that the virus undergoes a severe population bottleneck during sexual transmission and yet must rapidly generate diversity to adapt to the earliest immune responses of the new host. The transmission bottleneck has been inferred to consist typically of a single virion and involves both stochastic and selective events in the donor, during transmission and within the recipient host (da Silva, 2012). These dynamics have major implications for HIV prevention, for example the use of treatment in pre-exposure prophylaxis.

In experimental poliovirus infection of mice, the probability of occurrence of central nervous system infection depends critically on population size and genomic diversity. Here, bottlenecks are an inevitable consequence of within host selection of the rare variants that facilitate disease progression (Pfeiffer, 2010). More generally, RNA viruses are endowed with relatively high mutation rates and these can be modulated through greater or lesser fidelity of RNA polymerases (Campagnola et al., 2014). Fidelity of RNA polymerase in replication and the effective population size determine whether sufficient variants are generated within the population for infection to occur. For example, studies on human influenza infection show that transmission may in some circumstances involve profound bottlenecks whereas in others spread between hosts does not involve a significant reduction in genetic diversity (Poon et al., 2016; Varble et al., 2014).

In the case of bacterial infections, population bottlenecks resulting from antibiotic treatment are implicated in the origin and spread of major pathogens. Clonal expansion and spread of a tetracycline-resistant lineage is now responsible for the majority of the current cases of Group B streptococci neonatal sepsis world-wide (Da Cunha et al., 2015). Whole genome sequencing of Staphylococcus aureus carriage isolates from patients who later develop septicaemia also provide circumstantial evidence of tight bottlenecks whereby clonal expansion of rare variants predominate in the blood, an example of drift and/or selection (Golubchik et al., 2013).

A recent review has summarised much of the data on experimental infections with bacteria and the importance of within-host bottlenecks (Abel et al., 2015). There are many convincing animal models of bacteraemia and sepsis using indirect (mucosal) and direct (intravenous) challenge routes in which the entire population of organisms in the blood and distant systemic sites of infection (e.g. cerebrospinal fluid) results from a single cell bottleneck (Gerlini et al., 2014; Meynell, 1957; Moxon and Murphy, 1978; Pluschke et al., 1983). There are many fewer experimental studies of bacterial transmission, but extreme bottlenecks occur in mouse models of bacterial infection (Kono et al., 2016; Wickham et al., 2007).

The purging of genetic diversity of microbes through population bottlenecks has major implications in the outcomes of transmission between hosts or translocation across different anatomical barriers within hosts during infections (Bergstrom et al., 1999; Elena et al., 2001). Since adaptation depends, in part, on the supply of variants in a population, it follows that bottlenecks would be expected to exert selective pressures on microbial mechanisms for generating diversity. In instances where bacterial populations undergo extreme bottlenecks, even to the point where an infection is founded by a single organism, the challenge of adaptation through natural variation is especially stringent. The evolutionary pressure to continually regenerate diverse populations from single individuals may favor microbes with specific mechanisms of hyper-mutation or alternative phenotypic diversification strategies.

Phase variation is a microbial diversification strategy in which cell surface molecules that are involved in host-pathogen interactions are stochastically and combinatorially varied across the pathogen population (van der Woude and Bäumler, 2004). This cell surface variability is controlled by the expression of different subsets of genes, known as contingency loci, in different cells, such that each locus can be turned on or off stochastically (Moxon et al., 1994, 2006). Stochastic expression of contingency loci is effected by simple-sequence repeats in the coding regions or promoters of these genes, which generate a high frequency of insertion and deletion (indel) mutations each time a cell divides. In coding regions, indels that lead to frameshifts turn contingency loci on or off reversibly and stochastically, while indels in promoter regions can modulate gene expression by altering the binding affinity of regulators. This repeat-based mechanism for phenotypic diversification provides localised hyper-mutation that increases adaptive potential at specific genes, without increasing the genome-wide deleterious mutational load as often occurs in mutator strains (Cox, 1976; Denamur and Matic, 2006; Wielgoss et al., 2013). Phase variation can also be mediated by epigenetic mechanisms (Manso et al., 2014; van der Woude and Henderson, 2008) and more broadly, the key features of reversible, spontaneous, stochastic switching can be achieved by a wide range of molecular mechanisms (Davidson and Surette, 2008; Rando and Verstrepen, 2007; Srikhanta et al., 2010).

The evolution of stochastic phenotypic switching has been analyzed theoretically in a number of different contexts. Under temporally variable environments for large populations without bottlenecks, it was shown that switching mechanisms whose rates match the environment’s own transition rates tend to maximize the population’s long-term growth rate (Gaal et al., 2010; Kussell and Leibler, 2005; Lachmann and Jablonka, 1996; Patra and Klumpp, 2015). Other studies have generalized on these results, e.g. by considering density-dependent growth (Filiba et al., 2012), finite population sizes (King and Masel, 2007), spatial dynamics (Palmer and Feldman, 2011), demographic fluctuations (Xue and Leibler, 2017), and other effects (Lancaster and Masel, 2009; Palmer et al., 2013). In laboratory experiments, bottlenecks have been shown to provide a critical benefit in evolving stochastic switches de novo (Beaumont et al., 2009), and a related modeling study provided further support for this finding (Libby and Rainey, 2011). While a number of studies have analyzed the capacity for microbes to adapt in the presence of bottlenecks (Campos and Wahl, 2009; Patwa and Wahl, 2010; Wahl and Gerrish, 2001), including in the context of host-host transmission (Bergstrom et al., 1999; Elena et al., 2001; Handel and Bennett, 2008), the potential impact of bottlenecks on the evolution of stochastic switching mechanisms and phenotypic diversification strategies has received little attention.

We here consider the effect of bottlenecks on phenotypic switching frequency, its evolution and impact on pathogen survival through analysis of a simple mathematical model. We analyze the fitness landscape for stochastic switching for selective and non-selective bottlenecks, and show that the stringency of selection during bottlenecks strongly affects the shape of the landscape and thus the speed with which switching rates evolve. We demonstrate the existence of an extinction-survival switching rate, below which pathogen lineages are guaranteed to go extinct. We suggest that this threshold rate may play a basic role in maintaining stochastic switching strategies generically in pathogens that experience bottlenecks. Above the threshold, we characterize the evolutionary dynamics by which switching rates adapt toward their optimum, and we predict that short growth durations and stringent bottlenecks accelerate the evolution of stochastic switching. We discuss the implications of these results for future studies on the evolution and population genetics of pathogens.

RESULTS

We study the evolutionary advantage of stochastic phenotype switching in pathogen populations using the simple mathematical model described below (“Model and Definitions”). We determine the probability of extinction in this model, as a function of the stochastic switching rate and the transmission probability from one host to the next. We then analyze the fitness landscape for the evolution of stochastic switching rates, and determine the impact of selective bottlenecks on the rate of adaptation.

A. Model and Definitions

We will consider a pathogen population that grows within each host for a given duration before being able to infect a new host. We call the pathogen population within each host a local population, and the pathogen population over all infected hosts the global population. A pathogen lineage will refer to all descendants arising from a single pathogen cell over time and across all future hosts.

Within a given host, the pathogen exhibits two distinct phenotypes, a growing phenotype A, and a non-growing phenotype B. Cells with phenotype A proliferate and occasionally switch to phenotype B, while cells with phenotype B cannot proliferate. Upon transfer to a new host, the phenotype labels are reversed – the previously non-growing cells now proliferate, while the previously growing cells do not.

The mathematical model is parameterized as follows. The total number of hosts initially infected is denoted by N_host. Within each host, growing cells replicate at a fixed rate f per unit time. Each time a cell divides, the daughter cell has probability s to switch to the non-growing phenotype, while the mother cell retains its growing phenotype. The pathogen population grows for a fixed time period τ within the host. At the end of the period, the population experiences a transmission bottleneck such that each cell has a fixed probability of being transferred to a new host and initiating a new infection. Phenotype A and B cells have distinct probabilities of transmission, which we denote r_a and r_b, with 0 ≤ r_a ≤ r_b ≤ 1 i.e. non-growing cells can have a higher probability of initiating new infections. Sampling from the local population with these probabilities yields the numbers of transmitted cells of each phenotype that initialize new infections in the next round.

The model provides a coarse-grained representation of the complexity of real microbial infection, in which certain parameter combinations are analogous to quantities that are well-known in the biology of infectious disease. The value τf represents the number of generations of the pathogen within the host before clearance. Equivalently, the exponential of this value is the total number of cell divisions that the pathogen undergoes. The parameters that control whether or not the bottleneck is selective are r_a and r_b, which specify the probability that any given cell of type A or B, respectively, will successfully initiate a new infection. If r_a < r_b, then the bottleneck is selective, and if r_a = r_b, it is non-selective. The stringency of the bottleneck is measured by how different the two values are. The smaller the ratio r_a/r_b, the more stringent the bottleneck. If r_a = 0 and r_b > 0, then the bottleneck is extremely stringent, and only the type B cells can make it through. Our goal here is to present and analyze the simplest model that captures key features of the evolutionary dynamics. Predictive modeling for clinical infectious disease would require additional details to be explicitly represented.

B. Extinction probability in a simple model of host-pathogen dynamics

We begin by examining the case of strong selective bottlenecks in which a phenotypic switch from A to B is required in order to initiate a new infection. In this case, currently growing cells cannot infect new hosts, or r_a = 0, while 0 < r_b ≤ 1. If no cells are transmitted, the population goes extinct. However, if one or more cells are successfully transmitted, then the process restarts and continues in each of the new hosts. We consider an infection initiated from a single cell of the growing phenotype A. Using a standard generating function approach (Appendix A), the extinction probability of the local population after a single round of growth and transmission is calculated as

$$P_{\mathit{extinct}}=\frac{1-s+s{r}_b}{1-s+s{r}_b{e}^{\tau f(1-s+s{r}_b)}},$$ (1)

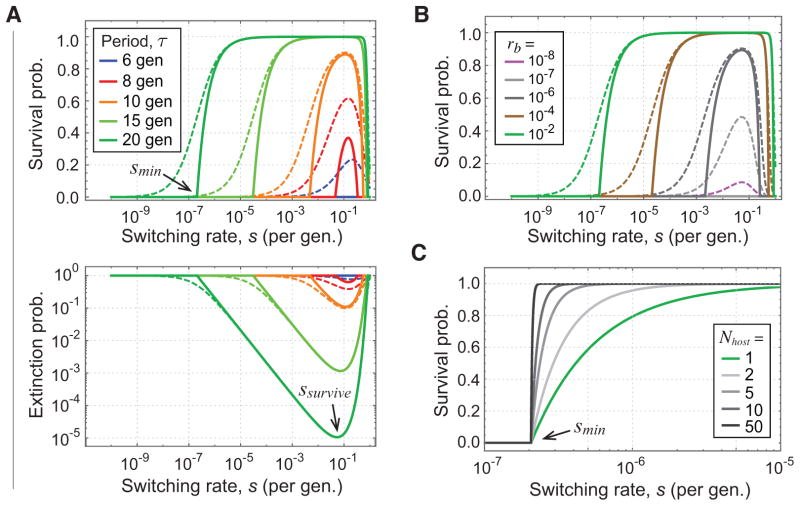
and the survival probability as P_survive = 1− P_extinct. In Fig. 1A, the dashed lines show the dependence of P_survive on the switching rate. As τ increases, we see that the fitness landscape takes on a mesa-like shape (e.g. green dashed curves in Fig. 1A, top panel), rising from zero at low switching rates to values close to one as switching rates increase, and then appearing nearly flat over several orders of magnitude before decaying back toward zero. Along the mesa top, as shown on a logarithmic scale in the lower panel of Fig. 1A, the extinction probability continues to decay over orders of magnitude before reaching a minimum at a value that we denote as s_survive.

FIG. 1.

Dependence of survival probability on stochastic switching and infection rates. (A) Upper panel shows the survival probability of the local pathogen population as a function of switching rate s for different growth period durations τ in units of generations (gen.), i.e. f = 1; lower panel shows the extinction probability on a logarithmic scale. Dashed curves are the survival (P_survive) or extinction (P_extinct) probability of a local population after a single growth period; solid curves indicate long-term survival (P̂_survive) or extinction (P̂_extinct) probability of a pathogen lineage. The minimum value of the switching rate that allows long-term survival, s_min, and the switching rate that maximizes survival, s_survive, are indicated. Plots show results for infection probability r_a = 0 and r_b = 0.01 using Eq. 1 to calculate P_extinct and Eq. 30 to obtain P̂_extinct. (B) Dependence of survival probability of a local population on transmission probability r_b, for r_a = 0 and τ = 20 gen. (C) Survival probability of the global pathogen population approaches a step function with increasing N_host, the number of initially infected hosts. The extinction-survival threshold s_min is shown. Curves plot 1−(P̂_extinct)^N_host for the values of N_host indicated using r_a = 0, r_b = 0.01, and τ = 20 gen.

Decreasing the transmission probability r_b causes the survival curves to shift to the right (Fig. 1B), requiring higher switching rates to obtain the same survival rates. Comparing Fig. 1A and Fig. 1B, we see that survival curves are very sensitive to small changes in the period τ, while requiring order-of-magnitude changes in r_b to cause the same overall shift. For example, consider the dashed green curves in Figs. 1A and 1B, which have identical parameters with τ = 20 and r_b = 0.01. A slight change of period to τ = 15 yields the light green curve in Fig. 1A, whereas a hundredfold reduction in transmission to r_b = 10⁻⁴ yields the nearly identical brown curve in Fig. 1B. These dependencies are clear from the functional form of Eq. 1. We confirmed by simulations the calculation of P_extinct, with simulation results agreeing closely with the theoretical prediction (Fig. S1).

We next calculate the long-term survival probability, P̂_survive, over many rounds of host-to-host transmission for r_a = 0, starting from a single cell of phenotype A. At the end of each growth period, each cell that successfully initiates an infection is propagated in a new host starting from a single growing cell. If n cells are successfully transmitted at the end of a round, we restart n new infections from a single growing cell in n new hosts, and we propagate this branching process indefinitely for all pathogen lineages. Eventually, either all lineages will go extinct, or the number of successful lineages will grow indefinitely and the pathogen population will survive over the long term, provided there is always an abundance of new hosts to infect. The probabilities P̂_survive and P̂_extinct ≡ 1−P̂_survive are shown in solid curves in Fig. 1A (see Appendix B for details of the calculation). In contrast to the single round P_survive, which is positive for all values of s, the long-term P̂_survive is identically zero for s ≤ s_min, where s_min is a threshold value, and it only begins rising for switching rates larger than the threshold.

The value of s_min itself can be calculated using a basic result from the theory of branching processes: a general branching process has extinction probability one if and only if each individual generates on average no more than one offspring (Karlin and Taylor, 1975, p. 397). Starting from a single cell of phenotype A, the local population grows to size ~ e^τf and the proportion of cells with phenotype B will be ≈ s e^τf. Since each B cell has probability r_b to infect the next host, the average number of cells transmitted will be ≈ r_b s e^τf. Extinction is therefore guaranteed if and only if r_b s e^τf ≤ 1, from which we obtain

$$s_{\mathit{min}}\approx (1/r_b)e^{-\tau f},$$ (2)

(see Appendix B for derivations). For s ≫ s_min, we see that P_extinct and P̂_extinct are nearly identical (Fig. 1A). This is a consequence of the fact that for high values of s any lineage that does not go extinct in the first round produces on average many transmitted cells. The probability of extinction in subsequent rounds is thus tiny compared to extinction in the first round, hence the dominant contribution to the long-term P̂_extinct is the single round P_extinct.

The evolutionary implication of the threshold s_min is that for any value of s ≤ s_min, the global pathogen population is guaranteed to go extinct regardless of the number of hosts N_host initially infected, since the lineage of each local pathogen population will go extinct with probability P̂_extinct = 1. Conversely, for values of s > s_min, P̂_extinct < 1, and the probability of extinction of the global pathogen population is (P̂_extinct)^N_host, or exponentially small in the number of infected hosts. Thus, the probability of global pathogen survival approaches a step function as N_host increases (Fig. 1C): it is identically zero for s ≤ s_min, and extremely close to one for s > s_min. In light of this, we will refer to s_min as the extinction-survival threshold. This result could explain the maintenance of high stochastic switching rates in pathogens, as lineages that evolve to values of s ≤ s_min are pruned out by extinction and thus occur only transiently in nature, while lineages with s > s_min survive indefinitely.

C. Fitness landscape for evolution of stochastic switching rates

To analyze the evolution of stochastic switching rates, we consider the evolutionary pressures experienced by two pathogen lineages with distinct switching rates s and s′. Our analysis above shows that extinction will eliminate any lineages with switching rate lower than s_min, so we can assume that s, s′ > s_min. Since the rates are above the extinction-survival threshold, both lineages are expected to survive indefinitely when propagated in isolation of each other, i.e. in separate sets of hosts. However, if the lineages infect a common set of hosts, one lineage will outcompete the other if it is capable of infecting more hosts per round, or equivalently of transmitting more cells at the end of each growth period. We would like to be able to predict which lineages will eventually outcompete others, and to determine conditions that favor adaptation of stochastic switching rates.

We quantify the competitive advantage of a pathogen lineage by computing its growth rate. In the case of strong selective bottlenecking, as before we have r_a = 0, and the lineage growth rate Λ is given by the logarithm of the average number of phenotype B cells transmitted, n^*, per period, or

$$\mathrm{\Lambda }=(1/\tau )log{n}^{\ast }.$$ (3)

We calculate n^* by taking the expectation over the stochastic process of growth and switching (see Appendix B) or equivalently by solving the deterministic equations for the population vector x(t) = (x_A, x_B), which gives the expected cell numbers of types A and B, respectively,

$$x_A^{\prime }(t)=f(1-s)x_A(t)$$ (4)

$$x_B^{\prime }(t)=fs{x}_A(t).$$ (5)

Using the initial condition x(0) = (1, 0), we have

$$x_B(t)=\frac{s}{1-s}\left[e^{tf(1-s)}-1\right],$$ (6)

from which we obtain n^* = r_b · x_B(τ). The growth rate is given by

$$\mathrm{\Lambda }={\tau }^{-1}log\left[e^{\tau f(1-s)}-1\right]+{\tau }^{-1}log\left[r_{b}s/(1-s)\right],$$ (7)

and for τf ≫ 1 we find

$$\mathrm{\Lambda }\approx f(1-s)+{\tau }^{-1}log[r_{b}s/(1-s)].$$ (8)

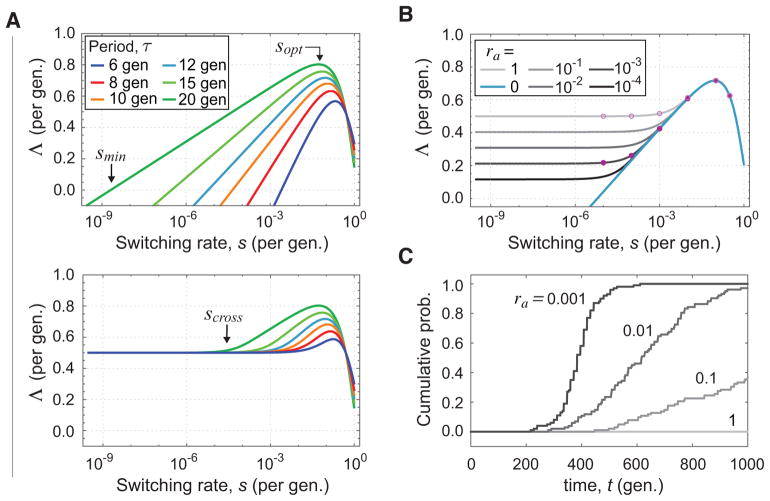
We plot Λ using Eq. 7 for different growth periods τ over s on a logarithmic scale (Fig. 2A, upper panel). At extremely low values of s, Λ is negative, indicating that the lineage will go extinct, since the expected number of transmitted cells is less than one. The extinction-survival threshold s_min is determined by Λ = 0, and it is seen from Eq. 8 that for s ≪ 1 we obtain s_min = (1/r_b)e^−τf as before. For switching rates s_min < s ≪ 1, the function increases linearly with log(s), and its slope is 1/τ indicating that the shorter the growth phase within each host, the more evolutionarily advantageous it is for the pathogen to increase its switching rate. This is apparent from the increasing slopes of the curves in the upper panel of Fig. 2A from left to right. In other words, a more rapidly changing host environment selects more strongly for increased switching rates. At high values of s ≫ s_min, the function reaches a maximum at a value that we call the optimal switching rate, s_opt. We calculate s_opt by setting ∂Λ/∂s = 0 in Eq. 8, which yields

FIG. 2.

Fitness landscape for evolution of stochastic switching rates, for different stringency of selective bottlenecks. (A) Fitness landscape with a strong selective bottleneck (r_a = 0, upper panel) or a non-selective bottleneck (r_a = 1, lower panel). Each panel shows the long-term growth rate Λ as a function of switching rate s for different durations of proliferation τ, for transmission probability r_b = 1. We use f = 1 so that rates are expressed per generation. (B) Dependence of the fitness landscape for increasingly stringent bottleneck selection via decreasing r_a. Full (open) pink circles indicate the expected long-term growth rate using τ = 12 generations for strains with different switching rates with (without) bottleneck selection, showing that stronger selective bottlenecking leads to a steeper landscape and predicting faster evolution. (C) Evolutionary dynamics of stochastic switching rates for τ = 12 gen. Curves show the cumulative probability of fixation of the optimal switching strain (s = 0.1) over the set of simulations for the given value of r_a, each of which were initialized with a single cell of the lowest switching strain (s = 10⁻⁵). Mutations that alter switching rates occur with rate μ = 10⁻⁵ (reversibly), and change the switching rate by an order of magnitude. Six different switching rates can occur, at the values indicated by circles in panel B. The average population size in simulations is 10⁷ − 10⁸ cells. Fixation is defined as reaching a frequency greater than 0.9 in the population. Each curve is computed using at least 100 simulations. Each simulation was run for 1000 generations. For the values of r_a shown, extinction occurred in < 2% of simulation runs, and those runs were not used for analysis. The network of genotypes and phenotypes, average traces of simulated dynamics, and further simulation details are given in Fig. S2 and Appendix D.

$$s_{\mathit{opt}}=\frac{1}{\tau f},$$ (9)

i.e. the optimal switching rate is proportional to the environmental rate of change, 1/τ, a well-known result from previous theoretical studies (Kussell and Leibler, 2005; Lachmann and Jablonka, 1996; Patra and Klumpp, 2015). We note that s_opt and s_survive are approximately equal when the transmission probability per cell is small (r_b ≪ 1) (Appendix C), which is the case in most biologically relevant scenarios, indicating that maximization of long-term growth rate simultaneously maximizes survival probability.

We now generalize the analysis to vary the stringency of the bottleneck, such that both phenotypes A and B have non-zero probability of transmission, with 0 < r_a ≤ r_b ≤ 1. To compute Λ, we must consider the population dynamics over multiple rounds of growth in different hosts. We denote by x⁽ⁱ⁾(t) the population vector in the i-th round for 0 ≤ t ≤ τ. For each round with initial condition x⁽ⁱ⁾(0), the population vector satisfies Eqs. 4 and 5, or

$$\frac{d}{dt}{\mathbf{x}}^{(i)}(t)=G{\mathbf{x}}^{(i)}(t),\text{where}G\equiv \left(\begin{array}{cc}f-fs& 0\\ fs& 0\end{array}\right).$$ (10)

We account for selective bottlenecking and the swapping of phenotype labels at each host-to-host transfer by setting

$${\mathbf{x}}^{(i+1)}(0)=R{\mathbf{x}}^{(i)}(\tau ),\text{where}R=\left(\begin{array}{cc}0& r_b\\ r_a& 0\end{array}\right).$$ (11)

Solving Eqs. 10 and 11, we obtain

$${\mathbf{x}}^{(i+1)}(0)=R{e}^{G\tau }{\mathbf{x}}^{(i)}(0).$$ (12)

The above recursion shows that over the long term, the population vector grows according to the repeated application of the matrix Re^G_τ : the population vector approaches the direction of the leading eigenvector of this matrix, and the long-term growth rate is given by

$$\mathrm{\Lambda }=\frac{1}{\tau }log{\lambda }_1(R{e}^{G\tau }),$$ (13)

where λ₁(·) denotes the maximal eigenvalue. The explicit expression for Λ is given in Appendix C, Eq. 32. Using this, one can easily check that for the case r_a = 0, we recover the value of Λ computed in Eq. 7.

In Fig. 2A, lower panel, we plot Λ for the case of no selective bottleneck, in which r_a = r_b = 1. At low switching rates, the landscape is essentially flat, and a noticeable gradient appears only as s begins to approach s_opt. In contrast, the fitness landscape under strong selective bottlenecks (Fig. 2A, upper panel) exhibits a gradient over the entire range of s from very low values all the way to s_opt. To determine how selective bottlenecking changes the landscape, we progressively reduce the value of r_a, and plot Λ for fixed τ in Fig. 2B. First, we find that for sufficiently high switching rates, all of the curves overlap, and appear to be independent of r_a. Second, at low switching rates for r_a > 0 the curves are flat and the growth rate shifts downward linearly for each order-of-magnitude reduction in r_a.

To explain these behaviors, we calculate Λ in the limits of low and high switching rates (see Appendix C). For high switching rates, where s ≫ (1/r_b)e^−τf, we find that Λ is independent of r_a, and we obtain the identical form as previously computed in Eq. 8, showing that all curves in Fig. 2B indeed collapse on the r_a = 0 curve. In this case the degree of selective bottlenecking r_a is irrelevant, since the transmitted B cells have sufficient time in each subsequent host to completely outgrow any residual A cells that are transferred. In the opposite limit for sufficiently small s, most cells do not switch phenotype during any given growth period. We can therefore consider the growth rate of a non-switching single cell as it is transferred from host to host. An initially type A cell grows with rate f for time τ, to a population of size e^fτ, and is then bottlenecked by a factor r_a in the next host where it persists without growing as a type B cell for another period τ before being bottlenecked by a factor of r_b and resuming growth as type A in the next host. Over a total time 2τ, the population expanded from one cell to r_br_ae^fτ cells, which corresponds to a growth rate of

$$\mathrm{\Lambda }=\frac{1}{2\tau }log\left(r_b{r}_a{e}^{f\tau }\right)=\frac{f}{2}+\frac{log\left(r_a{r}_b\right)}{2\tau },$$ (14)

consistent with the dependence of Λ on r_a seen in Fig. 2B (see Appendix C).

We can estimate the switching rate at the cross-over region between flat and steep portions of the landscape, denoted s_cross (see Fig. 2A, lower panel), by setting equal the two limiting forms of Λ from Eqs. 8 and 14, and solving for s. This yields

$$s_{\mathit{cross}}\approx r_a{e}^{-\tau f/2},$$ (15)

indicating that reduction of r_a proportionally reduces the value of s_cross, thereby increasing the size of the region over which the landscape exhibits a gradient. As r_a is reduced, s_cross approaches the value of s_min, and using Eq. 2 we find that for r_a < (1/r_b)e^−τf/2, we have s_cross < s_min yielding an evolutionary landscape of switching rates that exhibits a gradient all the way from s_min to s_opt. We see therefore that sufficiently strong selective bottlenecking changes substantially the adaptive landscape, enhancing the capacity for rapid stochastic switching to evolve.

D. Simulated evolution of stochastic switching rates

To test these evolutionary predictions, we carried out extensive stochastic simulations of the evolutionary process at various degrees of selective bottlenecking. We considered a set of genotypes each with a different switching rate s, spanning several orders of magnitude of switching rates from s = 10⁻⁵ to s = 0.3. The values of switching rates of the genotypes are shown as pink circles in Fig. 2B. Mutations occurring with rate μ = 10⁻⁵ per cell division alter the genotype, increasing or decreasing the switching rate according to a linear arrangement of the genotypes shown in Fig. S2A. Our analysis predicts that the corresponding values of Λ for each genotype will depend strongly on r_a, such that more stringent bottlenecking selection via lower r_a will lead to a steeper gradient of the evolutionary landscape (Fig. 2B). For example, from Fig. 2B we predict that evolution of switching rates using r_a = 0.001 (closed circles) will proceed much faster toward s_opt than evolution using r_a = 1 (open circles).

We propagated in simulation a pathogen lineage starting from a single cell with the genotype corresponding to the lowest switching rate s = 10⁻⁵, with growth in each host lasting τ = 12 generations (see Appendix D for simulation details). In this case, the genotype s = 0.1 has the highest value of Λ among the available genotypes. Simulations were run over a range of values r_a, and we tracked the speed of the evolutionary dynamics by recording the time at which the genotype s = 0.1 first achieved a frequency of 90% in the population, which we will refer to as the adaptation time. In Fig. 2C, we show the cumulative distribution of adaptation times over 100 independent simulations for each value of r_a (for a more detailed view of the evolutionary trajectories, see Fig. S2B,C). For a non-selective bottleneck (r_a = 1), none of the simulations exhibit adaptation within 1000 generations, while for increasingly stringent bottlenecking, using r_a = 0.1, 0.01, and 0.001, adaptation is achieved in a greater number of runs. Once the genotype s = 0.1 is fixed in the population, genotypes with both higher (0.3) and lower (0.01) switching rates are maintained at much lower frequencies at mutation-selection balance (Fig. S2B). A median adaptation time of about 400 generations is found for r_a = 0.001, with all simulations evolving to the best genotype by 1000 generations. These results confirm the predicted impact of selective bottlenecks on evolutionary rates.

For comparison, we computed the evolutionary dynamics in the infinite population size limit (Fig. S2D). In this case, since population size is not limiting, all genotypes appear in the population instantaneously, with each subsequent genotype appearing at a frequency μ = 10⁻⁵ times that of its predecessor. Rapid evolution of the optimal genotype ensues within ≈ 200 generations. In reality, such rapid evolution would only be possible in a sufficiently large population of size N > 10²⁸, which is comparable to the total number of bacterial cells on Earth, and much larger than the estimated effective population sizes of bacteria. It is therefore remarkable that bottlenecking selection with r_a = 0.001 (Fig. S2B) achieves a comparable evolutionary rate (≈ 400 generations) in a population of size N ~ 10⁸.

DISCUSSION

Stochastic switches have been studied in a wide range of pathogenic organisms, and are thought to evolve as a survival mechanism under fluctuating and unpredictable environments. In many instances, such switches were discovered in connection with host-pathogen interactions, including variation in surface antigens (Moxon et al., 2006; van der Woude and Bäumler, 2004). Understanding the evolutionary pressures that drive the emergence of stochastic switches, and modulate their rates, has been a subject of both theoretical and experimental studies. A body of theoretical work has examined the adaptive utility of stochastic switches as a function of several key parameters including the environmental fluctuation rates, the uncertainty of external conditions, phenotype-specific growth rates, and the cost of alternative strategies such as sensing (Donaldson-Matasci et al., 2010; Filiba et al., 2012; Gaal et al., 2010; Kussell et al., 2005; Kussell and Leibler, 2005; Lachmann and Jablonka, 1996; Lancaster and Masel, 2009; Palmer and Feldman, 2011; Patra and Klumpp, 2015; Rivoire and Leibler, 2011; Thattai and van Oudenaarden, 2004; Wolf et al., 2005). When switching rates are able to adapt thereby increasing long-term population growth rates, the optimal switching rates in a slowly fluctuating environment are inversely proportional to the environmental durations (Gaal et al., 2010; Kussell and Leibler, 2005; Lachmann and Jablonka, 1996; Patra and Klumpp, 2015). The role of finite population size and the conditions in which optimal switching rates can evolve were characterized in (Fudenberg and Imhof, 2012; King and Masel, 2007). When populations are too small, e.g. if phenotypic switches occur less often in a population than environments change, it becomes difficult for optimal switching rates to evolve, and strains would be expected to exhibit suboptimal switching. More recently, the relation between fluctuating population sizes and stochastic switching was studied in the context of dispersal and extinction dynamics (Xue and Leibler, 2017).

We considered a simple model in which pathogens can switch reversibly and stochastically between two phenotypic states, a growing and a non-growing state. When transferred to a new host, the phenotypes swap their behavior – the previously growing phenotype becomes the presently non-growing phenotype, and vice versa. In this model, which was previously analyzed in (Kussell et al., 2005; Lachmann and Jablonka, 1996; Thattai and van Oudenaarden, 2004), it is beneficial for cells to switch phenotype stochastically with a non-zero rate, otherwise the lineage of any given cell would only be able to proliferate in every other host, and thus achieve only half of its maximal possible long-term growth rate. Stochastic switching is also detrimental, since phenotypic switches that occur before transfer to the new host yield non-growing cells, compromising the growth potential of the population within the current host. It is therefore best for cells to switch at an optimal rate, s_opt, which optimizes the trade off between maintaining non-growing cells in the present host and their growth potential in the next host, maximizing the population’s long-term growth rate. Yet, whether and how quickly switching rates can evolve is determined by the fitness landscape for stochastic switching, given by the long-term growth rate as a function of switching rate. Our goal here has been to determine how switching rates evolve when pathogens experience frequent selective bottlenecks, a scenario that is typical in many host-pathogen interactions. By computing the shape of the fitness landscape for stochastic switching, we found that selective bottlenecks increase its slope and accelerate the evolution of switching rates.

We showed that in the absence of selective bottlenecks, switching rates can adapt rapidly only in the vicinity of the optimal switching rate, s_opt, while for much smaller switching rates the fitness landscape is essentially flat (Fig. 2A, lower panel). We demonstrated that selective bottlenecks substantially alter the fitness landscape for stochastic switching rates, causing a slope that extends all the way from switching rates in the vicinity of s_min to s_opt (Fig. 2B). We verified by stochastic simulations that this effect is pronounced, and leads to a dramatic acceleration of adaptation speed when bottlenecks are sufficiently stringent (Fig. 2C and Fig. S2). We showed that the crossover between flat and sloped portions of the landscape occurs at a value s_cross ≈ r_ae^−τf/2, and therefore increasing the stringency of selective bottlenecks via reduction of r_a leads to proportional reduction of s_cross, facilitating evolution over a wider range of switching rates. For very stringent bottlenecks, s_cross is less than s_min, and the population can in principle adapt rapidly across all viable switching rates. However, for switching rates above but close to s_min, the risk of eventual extinction of any single lineage increases (Fig. 1A, solid curves). We showed that this effect may be negligible if N_host, the number of initially infected hosts, is sufficiently large (Fig. 1C). In that case, s_min is effectively an extinction-survival threshold, above which the global pathogen population survives with near certainty, and below which extinction is guaranteed for any value of N_host.

It is important to note that if bottlenecks are non-selective, i.e. r_a = r_b, then the theoretical analysis shows that the bottleneck does not accelerate evolution of switching rates, regardless of bottleneck size. Stochastic switching is still beneficial in this case since it enables growth in subsequent hosts, but it provides no advantage in initiating infections. A non-selective bottleneck affects the population size, which sets the magnitude of demographic fluctuations, but it does not impact the mean composition of the transmitted population and thus has no effect on the fitness landscape. The impact of non-selective bottlenecks on bacterial phase variation was recently studied in (Aidley et al., 2017), where the effect of bottleneck size on patterns of diversity was analyzed. It was shown that populations that are passaged through single cell bottlenecks exhibited patterns of diversity that varied significantly from their ancestral populations, in contrast to the case of wide bottlenecks where the ancestral composition was largely maintained. Thus, while non-selective bottlenecks do not influence the fitness landscape of stochastic switching, they can impact the host-to-host variability of pathogen populations.

The existence of an extinction-survival threshold switching rate, which is a general feature of the stochasticity associated with bottlenecks, provides a simple and general evolutionary mechanism for maintenance of stochastic switches in natural populations. Indeed, the values and distributions of switching rates that evolve in a population are clearly dependent on multiple effects, e.g. in our model these include growth durations τ, transmission probabilities r_a and r_b, mutation rate μ, and the local and global population sizes; while in nature many more effects exist, such as variability in τ, in population sizes, in hosts and their immune systems, etc. The extinction-survival threshold dictates only that switching rates remain above some minimal value, regardless of all other effects that determine precisely how adaptation will proceed. In this sense, stochastic switches with sufficiently high rates are expected to be maintained in pathogens that experience strong selective bottlenecks. In our simple model, a strong selective bottleneck is defined by the condition that in the absence of switching, less than one cell on average would survive host transmission, or r_br_ae^τf < 1 (see Eq. 14). In a more general model, where growth rates f, growth durations τ, and transmission probability r are random variables that depend on the host environment, the condition becomes $\overline{\tau f}+\overline{logr}<0$, where the average is taken over the distribution of hosts. When this condition is satisfied, an extinction-survival threshold exists, and stochastic switches are predicted to be maintained in the pathogen population.

Extensive laboratory studies of stochastic switches have characterized their molecular mechanisms (reviewed in (Ackermann, 2015; Moxon et al., 2006; van derWoude and Bäumler, 2004)), while a smaller number of studies have assessed their adaptive advantages in fluctuating environments (Acar et al., 2008; Van den Bergh et al., 2016; Lin and Kussell, 2016; Lin et al., 2015; New et al., 2014), yet rigorous measurements of an evolutionary fitness landscape as a function of switching rates have not previously been made. A remarkable laboratory evolution experiment, however, successfully evolved a stochastic switching strain de novo (Beaumont et al., 2009), and highlighted the importance of selective bottlenecks, which were termed an “exclusion rule” in further modeling work (Libby and Rainey, 2011). In the absence of such bottlenecks, it was apparently not possible to evolve a stochastic switching strain. This finding is consistent with our prediction that strong selective bottlenecks are needed to evolve switching rates from initially very low values, which may be comparable for example to mutation rates (i.e. on the order of 10⁻¹⁰ −10⁻⁹ per generation in bacteria), to much higher values (Fig. 2B,C). In the absence of bottlenecks, the fitness landscape is extremely flat for very low switching rates, which means that a series of small evolutionary steps leading from low to high switching rates is not a viable evolutionary path. Evolution to high switching rates could only occur if a high switching rate were obtained by a single mutational step, which appears to be an unlikely scenario at least in laboratory evolution.

Recently, a number of studies have begun to probe the evolutionary dynamics of stochastic switching in natural populations of pathogens (Alamro et al., 2014; Bidmos and Bayliss, 2014). Ideally, one would like to reconstruct from their dynamics the fitness landscape that evolutionarily tunes switching rates in these organisms. Our work provides a first theoretical step in this direction, by determining how fitness landscapes depend on population dynamic parameters in simple models. It may be possible to infer evolutionary fitness landscapes for stochastic switching pathogens by precisely characterizing switching rate variation. For example, in contingency loci that are well-known in many pathogenic bacteria including Haemophilus influenzae, Neisseria meningitidis, and Campylobacter jejuni, simple sequence repeats cause high-frequency reversible switching of gene expression across different genetic pathways. The length of repeats is strongly correlated with switching rates both in the lab (Richardson et al., 2002) and in natural populations (Lin and Kussell, 2012). Hence, by measuring repeat lengths at multiple loci (Lango-Scholey et al., 2016) across strains and over time, with sufficient statistical power it may become possible to draw key inferences about the natural evolutionary dynamics of stochastic switches.

In summary, our results identify a major shift in the evolutionary pressures acting on stochastic switches that occurs due to selective bottlenecks. We propose that such bottlenecks are instrumental in the evolution of stochastic switches in pathogenic organisms, since they enable the key evolutionary steps that select for an increase of switching rates from very small values that are comparable to mutation rates to rates that are orders of magnitude larger. These findings provide a new foundation for analysis of the evolutionary mechanisms that underlie rapid generation of genetic and non-genetic diversity in pathogens.

APPENDICES

Appendix A. Population dynamics and extinction in a branching process model

We compute the probability P_t(m, n) of observing m cells of type A and n cells of type B at time t. The probability satisfies the following master equation,

$$\frac{d}{dt}{P}_t(m,n)=-fm{P}_t(m,n)+f(1-s)(m-1)P_t(m-1,n)+fsm{P}_t(m,n-1).$$ (16)

The generating function,

$${\stackrel{\sim }{P}}_t(w,z)\equiv \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{w}^m{z}^n{P}_t(m,n),$$ (17)

satisfies the partial differential equation

$$\frac{\partial \stackrel{\sim }{P}}{\partial t}=\left[-fw+f{w}^2(1-s)+f\mathit{swz}\right]\frac{\partial \stackrel{\sim }{P}}{\partial w},$$ (18)

which is found by multiplying Eq. 16 by w^mzⁿ and summing over all values of m and n. This equation is solved by the method of characteristics, yielding a general solution of the form

$${\stackrel{\sim }{P}}_t(w,z)=F(logw-log[1-w+sw-sz]+tf[sz-1]),$$ (19)

where F is an arbitrary function to be determined. If the process is initialized from a single cell of type A at time zero, we have P₀(1, 0) = 1 and P₀(m, n) = 0 for m ≠ 1. This implies P̃₀(w, z) = w, and using Eq. 19 we have

$$F(logw-log[1-w+sw-sz])=w.$$ (20)

Setting u = logw − log(1 − w + sw − sz), and solving for w in terms of u yields w = (1 − sz)/(1 − s + e^−u), which we substitute in Eq. 20 to obtain

$$F(u)=\frac{1-sz}{1-s+e^{-u}}.$$ (21)

Using the above form in Eq. 19, the generating function is found to be

$${\stackrel{\sim }{P}}_t(w,z)=\frac{w(1-sz)}{w(1-s)+(1-w+sw-sz)e^{tf(1-sz)}}$$ (22)

The extinction probability after a single growth period τ is given by

$$P_{\mathit{extinct}}={\stackrel{\sim }{P}}_{\tau }(1-r_a,1-r_b)=\frac{(1-r_a)(1-s+s{r}_b)}{(1-r_a)(1-s)+[s{r}_b+(1-s)r_a]e^{\tau f(1-s+s{r}_b)}}.$$ (23)

Substituting r_a = 0 above we obtain the expression in Eq. 1.

Appendix B. Long-term extinction probability

To compute the long-term extinction probability P̂_extinct under strong selective bottlenecks we proceed as follows. Starting from a single A cell at time zero, the random number of B cells, n, is distributed according to the marginal distribution

$$P_t^B(n)\equiv \sum _{m=0}^{\infty }{P}_t(m,n)$$ (24)

with generating function

$${\stackrel{\sim }{P}}_t^B(z)={\stackrel{\sim }{P}}_t(1,z)=\frac{(1-sz)}{(1-s)+s(1-z)e^{tf(1-sz)}}.$$ (25)

Conditional on n, the number of B cells present at the end of the period, the number of transmitted cells l is a Poisson-distributed random variable with rate nr_b. We let Q(l) be the probability that l cells are transmitted after a single period τ, with generating function

$$\stackrel{\sim }{Q}(z)\equiv \sum _{l=0}^{\infty }{z}^{l}Q(l),$$ (26)

and we have

$$\stackrel{\sim }{Q}(z\mid n)=e^{n{r}_b(z-1)},$$ (27)

which is the generating function for a Poisson random variable. Taking expectation over

$$\stackrel{\sim }{Q}(z)=\sum _{n=0}^{\infty }{e}^{n{r}_b(z-1)}{P}_{\tau }^B(n)={\stackrel{\sim }{P}}_{\tau }^B[e^{r_b(z-1)}]=\frac{1-s{e}^{r_b(z-1)}}{1-s+s[1-e^{r_b(z-1)}]e^{\tau f[1-s{e}^{r_b(z-1)}]}}.$$ (28)

After transmission to the new host, the phenotype labels are reversed, and the cells begin growing as phenotype A. The generating function at the end of M rounds, Q̃^(M)(z), therefore satisfies the recursion

$${\stackrel{\sim }{Q}}^M(z)=\stackrel{\sim }{Q}[{\stackrel{\sim }{Q}}^{(M-1)}(z)]$$ (29)

If we let P̂_extinct be the eventual probability of extinction, we have P̂_extinct = lim_M→∞ Q̃^(M)(0). Taking this limit on both sides of Eq. 29, we obtain

$${\widehat{P}}_{\mathit{extinct}}=\stackrel{\sim }{Q}({\widehat{P}}_{\mathit{extinct}}),$$ (30)

i.e. P̂_extinct is a fixed point for the mapping Q̃(z). It is well-known from the theory of branching processes that (i) P̂_extinct is the smallest positive root of Eq. 30, (ii) there is at most one positive root less than one, and (iii) P̂_extinct = 1 if and only if the average number of offspring per cell per round is less than or equal to one (Karlin and Taylor, 1975, p. 397). We numerically solve Eq. 30 using the expression in Eq. 28 to obtain the solid curves in Fig. 1. To determine the value of s_min, we compute the average number of B cells transmitted after a single round,

$$n^{\ast }={\stackrel{\sim }{Q}}^{\prime }(1)=\frac{r_{b}s}{1-s}\left[e^{\tau f(1-s)}-1\right],$$ (31)

and determine s_min using the condition n^* = 1, which can be solved numerically. For s ≪ 1 and τ ≫ 1/f, we find that n^* > 1 when s ≥ (1/r_b)e^−τf , from which it follows that s_min ≈ (1/r_b)e^−τf .

Appendix C. Optimization of long-term growth rate vs. long-term survival

The general expression for Λ computed using Eq. 13 is

$$\mathrm{\Lambda }=\frac{1}{\tau }log\frac{s{r}_b\left(e^{\tau f[1-s]}-1\right)+\sqrt{2e^{\tau f(1-s)}{r}_b(2r_a{[1-s]}^2-r_b{s}^2+r_b{s}^{2}cosh[\tau f(1-s)])}}{2(1-s)}$$ (32)

In the limit in which sr_be^τf ≫ 1, i.e. on average many B cells are transferred at each round, the leading order term within the square root is (sr_b)²e^2τf(1−s), using which we find

$$\mathrm{\Lambda }\approx \frac{1}{\tau }log\frac{s{r}_b{e}^{\tau f(1-s)}}{1-s}=f(1-s)+{\tau }^{-1}log[r_{b}s/(1-s)].$$ (33)

In this limit, the value of Λ is independent of r_a, hence all of the curves in Fig. 2B overlap for large s. In this case, as in Eq. 9, we find that s_opt = 1/(τf), and is therefore independent of both r_a and r_b. In the opposite limit, for s ≪ 1 and r_a > 0, we have

$$\mathrm{\Lambda }\approx \frac{1}{\tau }log\left(r_a{r}_b{e}^{\tau f/2}\right)=f/2+log(r_a{r}_b)/(2\tau ).$$ (34)

Due to this dependence, we see that for the case r_a = r_b = 1 shown in Fig. 2A, lower panel, all curves overlap for small s and are independent of τ ; and in Fig. 2B for small s, we see that Λ indeed varies as log r_a for decreasing values of r_a.

The value of s that maximizes the survival probability, s_survive, can be found in the limit s ≪ 1 and τf ≫ 1, by using Eq. 1 to obtain

$$ln{P}_{\mathit{extinct}}\approx -ln(s{r}_b)-\tau f[1-s+s{r}_b].$$ (35)

Minimizing the above with respect to s yields

$$1/s+\tau f(r_b-1)=0,$$ (36)

from which

$$s_{\mathit{survive}}\approx \frac{1}{\tau f(1-r_b)}.$$ (37)

In this limit, we find that s_survive = s_opt/(1 − r_b) (see Eq. 9), and thus for r_b ≪ 1, the rates s_survive and s_opt are nearly equal. More generally, this results from the fact that for r_b ≪ 1,

$$P_{\mathit{extinct}}={\stackrel{\sim }{P}}_{\tau }(1,1-r_b)\approx 1-r_b\overline{n}+\mathcal{O}(r_b^2),$$ (38)

where n̄ is the expected number of B cells at time τ, hence minimizing extinction is equivalent to maximizing the average number of transmitted cells n^* = r_b n̄. In most cases, this is the biologically relevant limit since transmission rates per cell are small.

Appendix D. Stochastic simulation of evolutionary dynamics

To simulate a local population of cells with switching between phenotype A and B cells, we perform stochastic simulations in which each cell division event is tracked. The simulation tracks the number of cells m and n with phenotypes A and B, respectively. At each simulation step, the random time to the next cell division event is determined by drawing from an exponential distribution with mean (fm)⁻¹. We increment the time variable t by this amount, and determine randomly whether the newborn cell has switched to phenotype B, which occurs with probability s; if it has, we increment n, otherwise we increment m. The simulation step process is repeated until one of the following events occurs: A transmission event occurs when t = τ, the current growth period ends, and a new growth period is initialized at t = 0 with Poisson-distributed numbers of A and B cells, with means nr_B and mr_A, respectively, which accounts for the swapping of phenotype labels; a resampling event occurs when the total population size m+n reaches the maximal local population size N_max, and the population is resampled down to an average size N_min by Poisson sampling, with means mN_min/N_max and nN_min/N_max for A and B cells, respectively. We used N_max = 10⁸ and N_min = 10⁷ in simulations. The resampling step, which is equivalent to serial dilution, maintains the population in a continuously proliferating state while preventing it from growing without bound in simulations, which would be computationally intractable. Simulation steps resume after either of these two events occur. If extinction occurs during a transmission event, the simulation ends.

This basic simulation method was used in two different ways in the text. To determine the extinction probabilities in Fig. S1 at different values of τ and s, in each simulation we initialized the population using a single cell of type A, and ran a single growth period τ and transmission step, recording whether or not extinction occurred. We averaged this value over 1000 independent simulations to determine the extinction probability at a given value of s and τ. To simulate the evolutionary dynamics shown in Fig. S2 and Fig. 2C, we used the genotype network shown in Fig. S2A, keeping track of the numbers m_i and n_i of A and B cells, respectively, of each genotype i = 1. . . 6. The mutation rate is a constant μ = 10⁻⁵ (horizontal arrows), while the phenotype switching rate s_i (vertical arrows) depends on the genotype as shown. All aspects of the simulation for each genotype were as above, with the addition of mutation occurring with probability μ each time a cell divided. When an A cell of genotype i divides, we determine which of the following mutually exclusive events has occurred in the daughter cell: (a) a mutation occurs to genotype i + 1 (for i < 6), and we then increment m_i+1; (b) a mutation occurs to genotype i − 1 (for i > 1), and we then increment m_i−1; (c) a phenotype switch occurs, and we increment n_i; or (d) none of the above occur, and we increment m_i. The probabilities of events (a) – (c) are μ, μ, and s_i, respectively.