Active turbulence in a gas of self-assembled spinners

Significance

Turbulent fluid motion is widespread in nature and is observed across diverse length and time scales, ranging from high-Reynolds number hydrodynamics to active fluids, such as bacterial suspensions and cytoskeletal extracts. It is recognized as one of the unsolved challenges in theoretical physics. Here, we explore out-of-equilibrium magnetic colloidal particles at liquid interfaces that exhibit complex collective behavior, resulting in emergence of an active spinner phase. Self-assembled spinners (active spinning without self-propulsion) induce vigorous vortical flows, demonstrating the properties of a 2D hydrodynamic turbulence. Our findings provide insight into the behavior of active spinner liquids and ways to control the collective dynamics and transport in active colloidal materials.

Abstract

Colloidal particles subject to an external periodic forcing exhibit complex collective behavior and self-assembled patterns. A dispersion of magnetic microparticles confined at the air–liquid interface and energized by a uniform uniaxial alternating magnetic field exhibits dynamic arrays of self-assembled spinners rotating in either direction. Here, we report on experimental and simulation studies of active turbulence and transport in a gas of self-assembled spinners. We show that the spinners, emerging as a result of spontaneous symmetry breaking of clock/counterclockwise rotation of self-assembled particle chains, generate vigorous vortical flows at the interface. An ensemble of spinners exhibits chaotic dynamics due to self-generated advection flows. The same-chirality spinners (clockwise or counterclockwise) show a tendency to aggregate and form dynamic clusters. Emergent self-induced interface currents promote active diffusion that could be tuned by the parameters of the external excitation field. Furthermore, the erratic motion of spinners at the interface generates chaotic fluid flow reminiscent of 2D turbulence. Our work provides insight into fundamental aspects of collective transport in active spinner materials and yields rules for particle manipulation at the microscale.

Turbulent fluid motion can be found across multiple length and time scales. It has fascinated scientists for centuries and still poses a major challenge for theoretical physics (1, 2). The well-known high-Reynolds number hydrodynamic turbulence in three dimensions is triggered by energy injection at the macroscale and cascading of energy to smaller scales. As an extension, the notion of active turbulence was recently introduced in the context of active fluids exemplified by suspensions of swimming bacteria, mixtures of microtubules and molecular motors, and other nonequilibrium systems (3–10). In contrast to hydrodynamic turbulence, the complex spatiotemporal behavior is caused by energy injection at the microscopic scale and subsequent cascading of energy toward larger scales. Active turbulence formally occurs at exceedingly small Reynolds numbers, rendering the fluid inertia negligible. Not surprisingly, statistical properties of active turbulence appear to be different from its classical counterpart. Active turbulence does not exhibit a wide inertial range (4, 11), and a nonuniversal power-law behavior at large scales was recently reported (12).

A related problem is diffusion and transport in active systems (13–17). Active bacterial baths (13, 15), chemically propelled catalysts (18), field-driven colloids (19–21), or even macroscopic entities such as fish, insects, or birds (22, 23) are examples of active systems where the units driving the motion generate local forces that overwhelm the thermal agitation (if any is observable in the first place). Such systems exhibit not only a wealth of directed collective behavior but also regimes where the collective motion is on average nondirectional, which gives rise to active (self-driven) diffusion.

A predictive description of active fluids is challenging due to the complexity of the individual building blocks (e.g., bacteria, molecular motors, etc.). In this respect, a simple physical model system, where interactions between particles are well-characterized, is highly desirable. Suspensions of colloidal particles energized by external fields provide a unique opportunity to model active systems in a well-controlled environment. This was first demonstrated at the macroscopic level in a system of magnetized disks suspended at a liquid–air interface and powered by a rotating magnetic field. Same-wise rotation of particles resulting in stable ordered phases similar to crystals (24, 25) has been observed. Similarly, computer simulations of spinning discs (26, 27) and dumbbells (28) in two dimensions yield various ordered and disordered states. Studies of ferromagnetic colloids confined at the interfaces and energized by an alternating magnetic field demonstrated a wealth of self-organized phenomena, from the formation of dynamic clusters and self-propelled entities (magnetic snakes, asters) (29–31) to rollers (32, 33) and self-assembled spinners (34). Interfacial spinners generated by a uniaxial alternating magnetic field emerge as a result of spontaneous symmetry breaking of clock/counterclockwise (CW/CCW) rotations. The self-assembled spinners inject the energy by a torque transfer via generation of local vortex flows. The energy injection rate and the corresponding injection scale can be tuned by the frequency and amplitude of the applied magnetic field.

Here, we report on an experimental and computational study of active turbulence and transport in a system of self-assembled ferromagnetic spinners. We find that the spinners and added inert particles exhibit active diffusion (diffusive motion is promoted by the activity of the system), while the diffusion arising from thermal noise is negligible in our system. We show that the active diffusion coefficient increases nearly linear with the spinner density and is approximately independent of the frequency of the driving magnetic field. We reveal a nonmonotonic dependence of the active diffusion coefficient on the inert particle size, where Stokes–Einstein relation holds for large inert particles (larger than a spinner) and diffusion is suppressed for small particles. We uncover dynamic segregation and clustering of spinners with the same sense of rotation.

Erratic motion of spinners in the container results in a turbulent-like 2D velocity field. This field exhibits the inverse energy-scaling $k^{-5/3}$ with wave number $k$, consistent with high-Reynolds number ($Re$) 2D turbulence (1), while $Re\approx \mathrm{\hspace{0.17em}30}$ for the flow-generating spinners in our system. The results are reminiscent of observations of fluid velocities in forced turbulence in 2D conducting fluid layers, surfactant films, and 2D bubbly flows (35–38). Furthermore, our experimental observations are in good qualitative agreement with the direct numerical simulations of discs suspended in a 2D fluid performed in the framework of a particle-based mesoscale hydrodynamic approach (multiparticle collision dynamics, MPC). Overall, our findings expand our understanding of synthetic tunable active systems with activity originating from rotations rather than self-propulsion and provide predictive tools for active-particle manipulation at the microscale.

Results

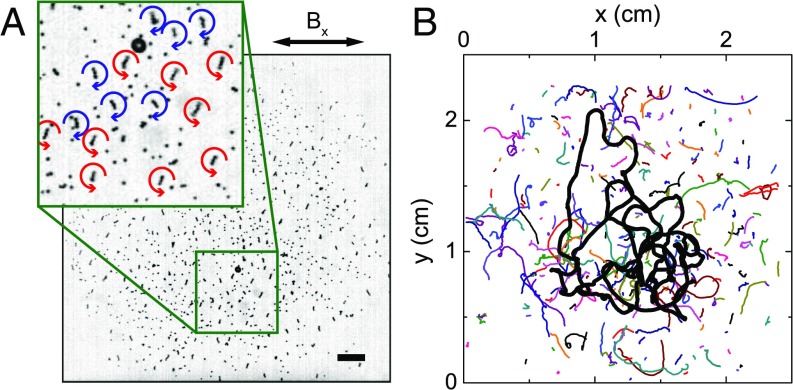
Out-of-equilibrium magnetic suspensions driven by a uniaxial in-plane magnetic field exhibit a peculiar spinner phase in a certain range of driving-field parameters (34). The spinner phase is populated by three subsystems of particles: active spinners, individual ferromagnetic colloids, and nonmagnetic (inert) particles. (Fig. 1A and Movie S1). Magnetic spinners are self-assembled multiparticle chains of approximately equal length controlled by the frequency of the excitation field (34, 39) and come in two kinds—rotating CW or CCW. The length is determined by a balance between magnetic and viscous torques exerted on a chain at the liquid interface and does not depend on a particle number density. The system is dynamic by nature, and magnetic particles frequently change their dynamic states (individual particles join spinners or spinners disintegrate into individual particles). Our simulations (see Materials and Methods) faithfully reproduced the observed phenomenology of the spinner phase (see Movie S2). While the spinners are not self-propelling entities (activity comes from rotation only), they get advected by the flows generated by the neighboring spinners. The motion of the spinners induces a large-scale vortical flow field (40). The spinners are the dominant active component in our system that induces a diffusive motion of the inert particles. Fig. 1B illustrates short-lived active-spinner trajectories (thin colored lines) and a long-lived inert particle trajectory (thick black line).

Fig. 1.

(A) An experimental snapshot of self-assembled magnetic spinners with an inert spherical particle. A uniaxial in-plane alternating magnetic field $B_x$ creates a swarm of spinners at the water–air interface. A nonmagnetic particle is used to investigate diffusion. (Scale bar, $2\text{mm}$.) Inset shows a large inert particle and multiple CW (blue) and CCW (red) spinners. (B) Typical inert particle (thick black line) and spinner trajectories (colored). The magnetic field amplitude was $B_0=2.7\text{mT}$ and the frequency of the field $f_B=60\text{Hz}$. The active particle number density $S_A=3.5\pm 0.5{\text{mm}}^{-2}$, and the inert particle diameter $\sigma =500\pm 20\mu \text{m}$.

Dynamic Clustering of Spinners.

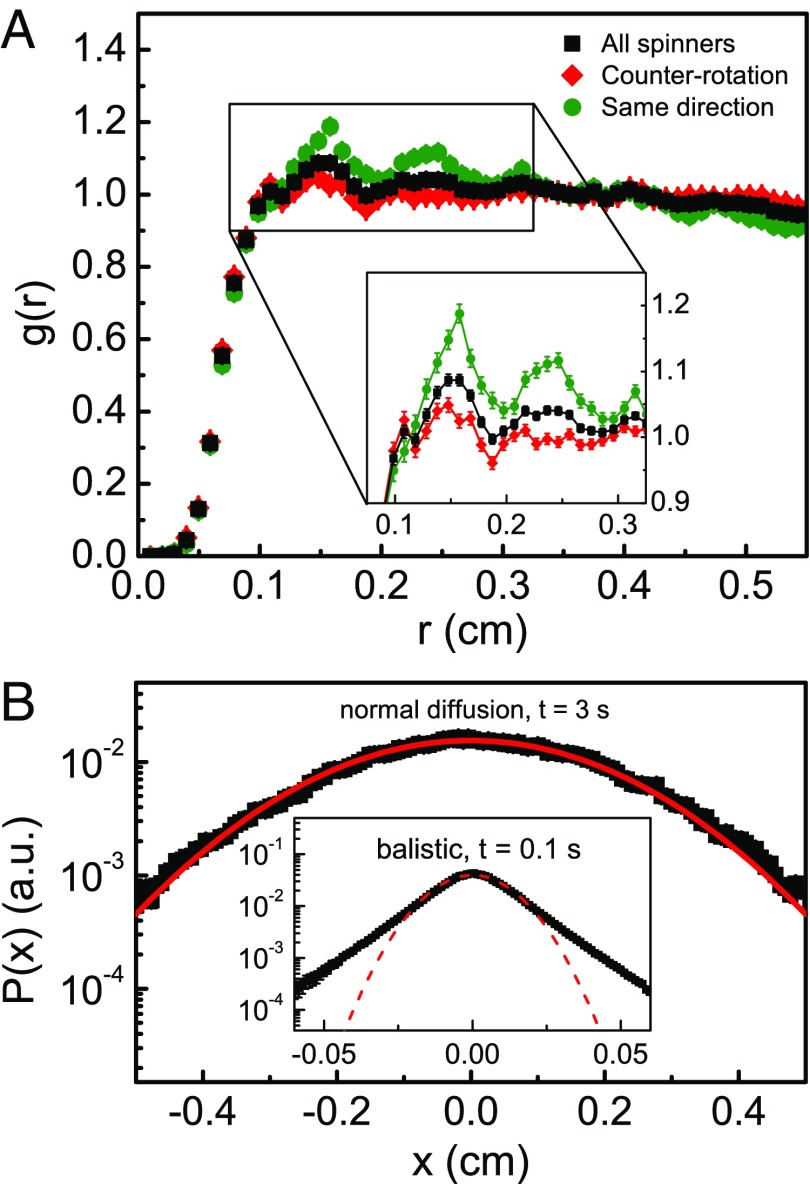
Analysis of the spinner subsystem revealed the presence of a short-range dynamic order (Fig. 2A, black squares) in the spatial spinner arrangement. A closer inspection of the radial distribution function $g(r)$ indicates more pronounced peaks for spinners with the same sense of rotation (Fig. 2A, green circles) compared with neighboring spinners rotating in the opposite direction (Fig. 2A, red diamonds). This apparent clustering is similar to that observed in simulations of higher density microrotors (41, 42), where a macroscopic phase separation was numerically observed. However, our system is significantly more complex because the spinner number is not fixed and fluctuates around a well-defined average prescribed by the parameters of the driving field (34) (see also SI Appendix), as they are perpetually created and annihilated with a lifetime of the order of a second (40).

Fig. 2.

Spinner clustering and diffusion. (A) Normalized radial pair-distribution function $g(r)$ for all spinners (black squares). A clustering can be observed by comparing $g(r)$ for spinners rotating in the same direction (green circles) and counterrotating ones (red diamonds). Inset is a blow-up of the first two peaks. (B) The spinners’ displacement probability distribution function indicates the diffusive ($t=3\text{s}$) and the ballistic regime ($t=0.1\text{s}$). Red lines are least square fits to $\exp (-x^2/4Dt)$. The experimental parameters:$B_0=2.7\text{mT}$, $f_B=60\text{Hz}$, and $S_A=3.5\pm 0.5/{\text{mm}}^{-2}$.

Active Transport and Diffusion.

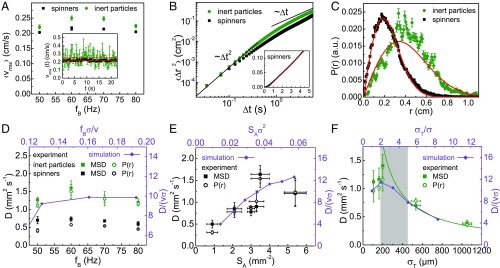
The spinners erratically move over the water–air interface being advected by the self-generated flows (see Movie S3). We identify two regimes of the spinner dynamics: for short times, ballistic, and for long times, diffusive motion (Fig. 2B). The ballistic motion is characterized by a mean velocity, which we chose as root-mean-square (rms) velocity of the ensemble average over the spinners or inert particles, respectively—that is, $v_{rms}(t)=\sqrt{⟨v^2(t)⟩}$. As displayed in Fig. 3A, $v_{rms}(t)$ fluctuates around an average value as a function of time, where the displacements are larger for inert particles (Fig. 3A, Inset). Correspondingly, the time average value $⟨v_{rms}⟩$ of inert particles is ∼10% larger than that of spinners. In the frequency range of the spinner phase, $⟨v_{rms}⟩$ depends only weakly on the frequency of the applied external field.

Fig. 3.

Active transport and diffusion. (A) The dependence of the time-averaged velocity $⟨v_{rms}⟩$ on the frequency $f_B$ for spinners (squares) and inert particles (circles). (Inset) A typical time evolution of the rms velocity $v_{rms}$ at $f_B=60\text{Hz}$; the red line is a linear fit. (B) MSDs for spinners (squares) and inert particles (circles). The black lines illustrate ballistic ($\propto \mathrm{\Delta }{t}^2$) and active diffusion, with the same scaling as normal diffusion ($\propto \mathrm{\Delta }t$). (Inset) The spinner MSD on linear scales. The red line is a least squares fit to Eq. 1 for the active diffusive part of the curve. (C) Radial probability density function $P(r)$ in the active diffusive regime for spinners (squares, $t=3\text{s}$) and inert particles (circles, $t=4\text{s}$). Red lines are least squares fits to Eq. 2. (A–C) $f_B=60\text{Hz}$, $S_A=3.5\pm 0.5{\text{mm}}^{-2}$, and ${\sigma }_T=500\pm 20\mu \text{m}$. (D) Frequency dependence of the active diffusion coefficient for spinners (solid symbols) and inert particles (open symbols) as obtained from the MSD (squares) and $P(r)$ (circles); $S_A=3.5\pm 0.5{\text{mm}}^{-2}$ and ${\sigma }_T=500\pm 20\mu \text{m}$. Results of simulations (violet) are shown for comparison. (E) Active diffusion coefficient as a function of the active particle number density $S_A$ for inert particles as obtained from experiments [MSD, squares, $P(r)$; circles, $f_B=60\text{Hz}$ and ${\sigma }_T=500\pm 20\mu \text{m}$] and simulations (violet). (F) The active diffusion coefficient is a nonmonotonic function of the inert particle size for experiments (green; $f_B=60\text{Hz}$ and $S_A=3.0\pm 0.2{\text{mm}}^{-2}$) and simulations (violet). The green line indicates the dependence $\propto \mathrm{\hspace{0.17em}1}/{\sigma }_T$. The gray area corresponds to the range of spinner sizes. (A–F) $B_0=2.7\text{mT}$.

A characteristic velocity scale can be estimated from the Stokes flow around a spherical (disk-like) particle of diameter $L_s$ (spinner length), which is given by $v(\overline{r})=\pi f_B{L}_s{(L_s/2\overline{r})}^{\delta -\mathrm{\hspace{0.17em}1}}$ in $\delta$ dimensions. Here, the typical distance $\overline{r}$ of inert particles and spinners is determined by the spinner concentration—that is, $\overline{r}\sim \mathrm{\hspace{0.17em}1}/\sqrt{S_A}$, where $S_A$ is the colloid number density. For the experimental parameters (see SI Appendix), this implies $v\approx 0.13{\text{cm s}}^{-1}$, in reasonable agreement with Fig. 3A. Note that the flow field decays less rapidly in strict two dimensions opposite to the quasi-2D experimental situation with 3D hydrodynamics, which implies larger characteristic velocities in simulations.

To characterize activity-induced transport in the system, we determined the diffusion coefficient $D$ for spinners and inert particles via the mean square displacement (MSD)

$$⟨\mathrm{\Delta }{r}^2⟩=\mathrm{\hspace{0.17em}4}D\mathrm{\Delta }t,$$ [1]

from both experimental and simulation results, as well as the probability distribution function

$$P(r,t)\propto r\exp \left(-\frac{r^2}{4Dt}\right)$$ [2]

from experiments, where $r$ is the displacement at time $t$. Fig. 3B illustrates the initial ballistic motion followed by a crossover to free diffusion. No anomalous diffusion was observed. The time scale for the cross-over between ballistic and diffusive regime is set by the spinner mean free time (time between a collision with another spinner or a free particle). As discussed before, the $⟨v_{rms}⟩$ is larger for inert particles than spinners. Consequently, the diffusion coefficient for inert particles is larger than that for spinners (Fig. 3D). We attribute this to hindered spinner motion due to their strong magnetic and hydrodynamic interactions with their neighbors. Simulations yield a similar behavior (see SI Appendix, Fig. S6). However, the lifetime of the spinners in simulations just exceeds the crossover time between ballistic and diffusive motion such that no pronounced diffusive regime is obtained and no spinner diffusion coefficient can be extracted. In contrast, a clear diffusive regime is obtained for inert particles.

Diffusion coefficients for the spinners and inert particles are displayed in Fig. 3D as a function of the frequency $f_B$. $D$ values were extracted independently from the MSD and the displacement distribution functions $P(r)$ (Eq. 2) (see also Fig. 3C). The latter figure shows that long-time displacements are well described by a Gaussian stochastic process. There is a good agreement between the values extracted by the two methods and also qualitative agreement with simulation results. We attribute the frequency independence of the diffusion coefficient to a competition between a faster rotation leading to faster fluid motion and the decreasing spinner length with increasing frequency $f_B$ of the field (experiments and simulation show a similar trend; see SI Appendix, Fig. S4).

To investigate the dependence of diffusion on activity in the system, we analyzed the inert particle diffusion coefficient at different active particle number densities $S_A$. Obtained results are shown in Fig. 3E. The inert particle diffusion coefficient exhibits a monotonic increase with the number density until the system becomes too dense to sustain the spinner phase (immobile agglomerates of magnetic particles are formed for high number densities) (34). The observed nearly linear dependence qualitatively resembles previously observed enhanced tracer diffusion in suspensions of swimming microorganisms (13, 15, 43, 44). However, we have to keep in mind that Reynolds numbers in suspensions of swimming microorganisms are typically much smaller than unity, whereas here $Re\approx \mathrm{\hspace{0.17em}30}$. Furthermore, there are significant differences in the origin of the emerging flow fields: Swimmers usually exhibit a characteristic dipolar flow field, while spinners create a rotational flow field.

To gain additional insights on activity-induced transport in active spinner material, we explored the inert particle size dependence of the diffusion. For inert particles larger than spinners (particle diameter ${\sigma }_T>$spinner length), the inert particle diffusion coefficient follows the Stokes–Einstein relation $D\propto \mathrm{\hspace{0.17em}1}/{\sigma }_T$ (Fig. 3F). Hence, the stirred fluid appears as a random, white-noise environment. Remarkably, for smaller particles, the trend is inverted, and the diffusion coefficient decreases with size. The nonmonotonic dependence indicates a change in the statistical properties of the ambient fluid. A diffusion coefficient independent of particle size has been obtained, for example, for particles embedded in an active fluid with temporal exponentially correlated noise (45). In contrast, for larger particles, the fluid acts as a thermal bath. Similarly, a nonmonotonic size dependence of particle diffusion was recently observed in bacterial suspensions (44). The monotonic dependence breaks down once a particle size becomes comparable with a characteristic fluid flows scale. In the case of our system, this scale approximately corresponds to the size of a spinner, while in a bacterial suspension (44), it is determined by a typical size of self-organized bacterial flows. Moreover, our results imply that there is an optimal passive particle size for fastest mixing for a given active system, indicated by the maximum diffusion coefficient. These findings clearly demonstrate that active transport can be tuned. Simulations are in good qualitative agreement with the observed experimental trends (Fig. 3 D–F). The results of simulations are presented as dimensionless quantities, with $\sigma$ and $\sigma /v$ as relevant length and time scales. It is important to note, however, that the flow fields in three (experiment) and two dimensions (simulations) imply different velocities scales (as discussed above); therefore, a quantitative match is not expected. Despite that, both experiments and simulations yield the same dependencies of diffusion coefficients on the frequency, active particle density, and inert particle size (Fig. 3 D–F).

Energy Spectra.

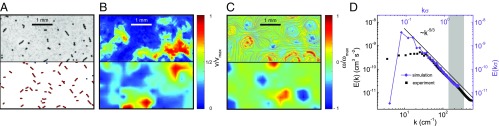
The magnitude of the hydrodynamic velocity field, induced by the rotating spinners (Fig. 4A), illustrates that the flows are concentrated around the spinners (Fig. 4B). To further investigate the self-induced interface flows in the spinner phase, we calculate the energy spectrum of turbulent fluctuations in our system. A typical energy spectrum $E(k)$ of the flows as extracted from experiments is shown in Fig. 4D. It resembles that of an inverse energy cascade in 2D turbulence (1). The broad energy-injection scale (gray area in Fig. 4D) arises from a spinner-size heterogeneity. Although the size constraints of our experimental and simulation systems limit the values of the accessible wave numbers $k$, a characteristic power-law behavior can be clearly observed over more than an order of magnitude in length scale. The power-law decay $k^{-5/3}$ of the energy spectrum showed no dependence on spinner density within the boundaries of the spinner phase (see also SI Appendix, Fig. S7) and corresponds to that typically found in a high-Reynolds number turbulence.

Fig. 4.

2D turbulence. (A–C) Selected snapshots of experimental (Top) and simulation (Bottom) states. The normalized velocity magnitude $v/v_{max}$ and normalized vorticity $\omega /{\omega }_{max}$ fields are visually similar for the experiment (Top) and the simulation (Bottom). $\omega /{\omega }_{max}$ enables a distinction between CW (blue) and CCW (red) rotating spinners. Streamlines are superimposed to give a sense of flow. (D) Energy spectrum $E(k)$ of the surface flows as obtained from experiments (black) and simulations (violet). 2D turbulent flow reverse energy cascade toward small wave numbers $k$ (large scales) with $k^{-5/3}$ scaling. The energy injection region is broad due to a heterogeneity of spinner sizes (gray area). The experimental parameters: $B_0=2.7\text{mT}$, $f_B=60\text{Hz}$, and $S_A=3.91\pm 0.05{\text{mm}}^{-2}$. Simulation parameters: $f_B\sigma /v=\mathrm{\hspace{0.17em}0.16}$, $\mu =\mathrm{\hspace{0.17em}480}\sqrt{k_{B}T{a}^3/{\mu }_0}$, and $B_0=\mathrm{\hspace{0.17em}0.8}\sqrt{k_{B}T{\mu }_0/a^3}$ (see SI Appendix for details).

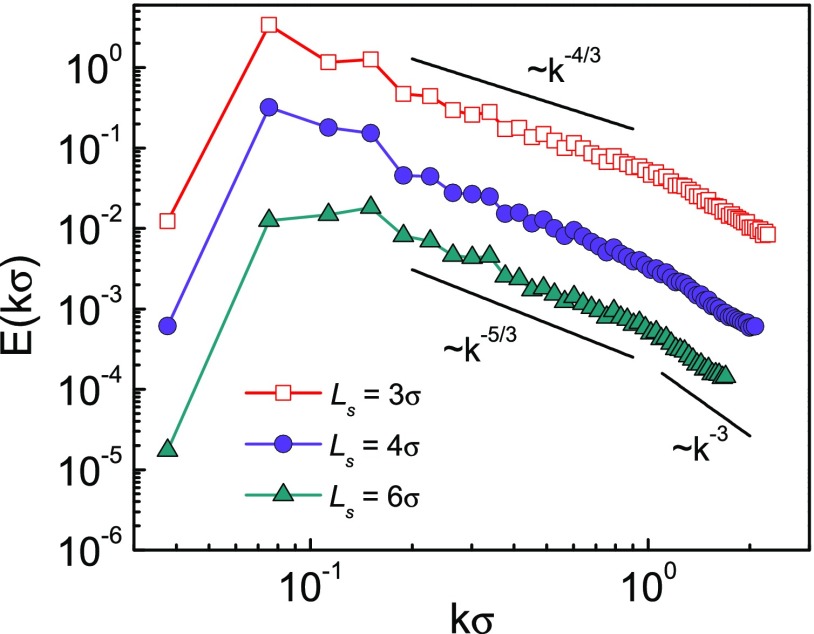
The self-organized spinner systems encompass various sources of randomness, such as spinner size and life time. Moreover, the study of particle packing fraction effects is difficult, since spinners are stable in a very narrow packing fraction range only. We shed light on the relevance of these aspects on the energy spectrum by performing simulations of spinners with a monodisperse length distribution at various concentrations. We find that the energy spectra and corresponding exponents for the monodisperse systems with average spinner lengths $L_s=\mathrm{\hspace{0.17em}3}\sigma$ and $4\sigma$, shown in Fig. 5, are similar to the exponent observed in the experiment and simulations (Fig. 4D) for the polydisperse system, with average spinner length $⟨L_s⟩\approx \mathrm{\hspace{0.17em}3.5}\sigma$. Hence, polydispersity is of minor importance for active turbulence in our system. Moreover, simulations of a polydisperse system with fixed length of spinners and length distribution of the self-organized system yield very similar energy spectra. Further increase in the spinner length in simulations ($L_s/\sigma =\mathrm{\hspace{0.17em}4}-\mathrm{\hspace{0.17em}6}$) leads to the slight increase of the magnitude of the energy exponent. Simulations reveal that very short spinners ($L_s/\sigma <3$) behave like white-noise sources, and a minimal spinner length is necessary to generate turbulence at the considered Reynolds number. In addition, at high concentrations, the exponent starts to deviate from the hydrodynamic turbulence value, $-\mathrm{\hspace{0.17em}5}/3$ (see SI Appendix, Fig. S7), since other interactions (e.g., steric or magnetic) become more relevant and the system undergoes a transition to another dynamic phase comprising nonrotating aggregates. Finally, Fig. 5 also exhibits a crossover to a power law with exponent $-3$ at length scales smaller than the energy-injection scale, the value characteristic for enstrophy flux of hydrodynamic turbulence, both in 2D and 3D (1).

Fig. 5.

Energy spectrum for monodisperse spinners from simulations. Shown are spectra for spinners of lengths $L_s/\sigma =\mathrm{\hspace{0.17em}3}$, $4$, and $6$ at the spinner packing fraction ${\varphi }_s=\mathrm{\hspace{0.17em}0.113}$. In all cases, the Reynolds number is $Re\approx \mathrm{\hspace{0.17em}38}$. The top and bottom curves are shifted vertically by a constant factor with respect to the middle curve, for better distinction.

Mesoscale Turbulence—Relation to Other Systems.

Similar turbulent behavior was observed for low-to-moderate Reynolds numbers in forced turbulence in 2D conducting fluid layers (1), surfactant films (38), and bubbly flows (35, 36). There the turbulence was forced either by a fixed grid or by a fixed array of magnets (ordered or randomly positioned) beneath the films with a typical $Re$ number in the range of ${10}^2-{\mathrm{\hspace{0.17em}10}}^4$. The existence and robustness of the inverse energy cascade and (−5/3) scaling were well established (1). Turbulent features have been also observed in viscoelastic polymer solutions (elastic turbulence) at $Re$ numbers as low as ${10}^{-3}$ (46). The turbulence there is driven by a slow nonlinear response of the polymer solution to external shear due to long relaxation times of the polymers, and the corresponding exponent is believed to be close to $(-1)$ (46). In bacterial turbulence observed in dense bacterial suspensions (4, 5), an apparent turbulent motion is associated with the onset of collective behavior, and the reported experimental exponents seem to be close to $(-8/3)$. However, this scaling was observed only in a very narrow range of the wave numbers and for conditions not applicable to our system. This scaling behavior was attributed to an apparent visco-elastic response of highly concentrated bacterial suspension. In a follow-up study (47), active turbulence in a model of rigid self-propelled colloidal rods was explored by simulations, and power-law spectra with a classical exponent $-5/3$ consistent with hydrodynamic 2D turbulence in the inertial regime were observed. Our system is relatively dilute ($1\%-\mathrm{\hspace{0.17em}5}\%$ area fraction), and no collective motion has been observed. A feature of our experimental system is that it actively injects vorticity at the microscale without self-propulsion. The injection process is spatially and temporally random due to perpetual self-assembly, advection, and collisions of spinners. It suggests that 2D turbulence might be fully developed over a much wider range of Reynolds numbers than in three dimensions, provided that the driving is spatially and temporarily random.

Conclusions.

We have studied in detail the transport properties of active spinner suspensions comprised of self-assembled spinners with both CW and CCW types of rotational symmetry, confined at a liquid–air interface. The spinner suspension induces vigorous vortical flows at the interface that exhibit properties of well-developed 2D hydrodynamic turbulence despite the orders of magnitude lower Reynolds number ($Re\approx \mathrm{\hspace{0.17em}30}$). The energy spectrum of generated flows shows the characteristic $k^{-5/3}$ decay. Our system presents a realization of nonequilibrium systems displaying active turbulence behavior. The uniqueness of this particular system comes from the fact that activity originates from rotations only and is not associated with self-propulsion. Our simulation studies matched experimental observations. Moreover, embedded inert particles exhibit an unusual diffusion behavior, a finding that illustrates that the active transport can be tuned by external parameters. Hence, active-particle suspension constitutes a class of materials with tunable properties.

Materials and Methods

Experimental Setup.

Ferromagnetic Ni microparticles (Alfa Aesar) with an average diameter of $\sigma \approx 90\mu \text{m}$ ($75-106\mu \text{m}$ uniform size distribution) were dispersed at the water–air interface in a cylindrical beaker (diameter $5.5\text{cm}$, water depth $7\text{cm}$). The microparticles (magnetic moment is about 0.01 $\mu \mathrm{A}\cdot {\mathrm{m}}^2$ per particle) were supported by the surface tension and remained confined at the interface throughout the experiment. The driving in-plane magnetic field [$B_x=B_0\sin (2\pi f_{B}t)$, $B_0=2.7\text{mT}$] was created by a pair of precision electromagnetic coils. The initial condition of each experiment was a fully dispersed assembly of microparticles achieved by applying a static magnetic field ($B_z=16.25\text{mT}$) perpendicular to the water–air interface. Measurements were performed after the spinner phase was equilibrated for $30\text{s}$.

The number density of the system $S_A$ is defined as the total number of all magnetic microparticles divided by the total area of the liquid interface they occupy. Corresponding packing fractions in our experiments were in the range of $0.007-\mathrm{\hspace{0.17em}0.05}$.

The Reynolds number is defined with respect to spinners and rotational flows they generate. A typical rotational velocity of the end point of a spinner is $\omega L_s/2$. The rotation rate is defined by the magnetic field frequency $f_B$. The average spinner size $L_s$ at $f_B=\mathrm{\hspace{0.17em}60}Hz$ is about 4 particle diameters ($\sim 400\mu \text{m}$). The Reynolds number is calculated as $Re=\pi f_B{L}_s^2/\eta \approx \mathrm{\hspace{0.17em}30}$; here $\eta$ is kinematic viscosity of water (bulk value).

Inert (nonmagnetic) particles for diffusion coefficient measurements were as follows: glass (Ceroglass Technologies Inc.: GSR-10 and GSR-5; Novum Glass LLC: U-150 and U-90) and polystyrene (Phosphorex Inc.: 2112G). The particle tracking and particle image velocimetry (PIV) were carried out with ImageJ, MatPIV package for Matlab, and custom codes. Hydrodynamic flows were visualized by spherical gold powder ($3.0–5.5\mu \text{m}$, Alfa Aesar) and rheoscopic liquid (Novostar). The energy spectrum was calculated from a radially averaged 2D Fourier transform of the velocity field.

Simulation Setup.

A 2D system is considered, with circular colloids embedded in an explicit solvent. A colloid is comprised of $18$ point particles of mass $M$, uniformly distributed over the circumference of a circle of diameter $\sigma$, with an additional point particle at the center. The shape is maintained by strong harmonic bonds, both between the nearest neighbors and each particle with the center. Each colloid carries a magnetic dipole (see SI Appendix, Fig. S3). The dynamics of the colloids is treated by standard molecular dynamics simulations. The embedding fluid is modeled by the MPC approach (48, 49), a particle-based mesoscale simulation technique that correctly captures hydrodynamic properties (50). Here, we use an angular-momentum conserving variant of the algorithm (51, 52) (for details, see SI Appendix). As in experiments, an oscillating external magnetic field leads to self-assembled spinners of average length $L_s\approx \mathrm{\hspace{0.17em}3.51}\sigma$ at the frequency $f_B\sigma /v=\mathrm{\hspace{0.17em}0.16}$. Thereby, we use the field strength $B_0=\mathrm{\hspace{0.17em}0.8}\sqrt{k_{B}T{\mu }_0/a^3}$ and the magnetic moment of a colloid $\mu =\mathrm{\hspace{0.17em}480}\sqrt{k_{B}T{a}^3/{\mu }_0}$, where $a$ is the length unit (the size of MPC collision cell) and ${\mu }_0$ is the magnetic constant. The detailed algorithm and the MPC parameters are described in SI Appendix. The simulation results are presented in units of the colloid diameter $\sigma$ and the characteristic velocity $v$. The latter follows from the ballistic short-time MSD of passive particles. The spinner packing fraction ${\varphi }_s$ in Fig. 5 is defined as a packing fraction considering each spinner as a disc of diameter $L_s$. The value ${\varphi }_s=\mathrm{\hspace{0.17em}0.113}$ corresponds to a colloid packing fraction of 0.028, in the range of the experimental values.