Quantitative computational models of molecular self-assembly in systems biology

Abstract

Molecular self-assembly is the dominant form of chemical reaction in living systems, yet efforts at systems biology modeling are only beginning to appreciate the need for and challenges to accurate quantitative modeling of self-assembly. Self-assembly reactions are essential to nearly every important process in cell and molecular biology and handling them is thus a necessary step in building comprehensive models of complex cellular systems. They present exceptional challenges, however, to standard methods for simulating complex systems. While the general systems biology world is just beginning to deal with these challenges, there is an extensive literature dealing with them for more specialized self-assembly modeling. This review will examine the challenges of self-assembly modeling, nascent efforts to deal with these challenges in the systems modeling community, and some of the solutions offered in prior work on self-assembly specifically. The review concludes with some consideration of the likely role of self-assembly in the future of complex biological system models more generally.

1. Introduction

Self-assembly reactions account for the overwhelming majority of the reaction events occurring in the cell. Most eukaryotic proteins function normally in complexes and self-assembly of these complexes is a key step in nearly all major cellular functions [8]. Examples of processes critically dependent on self-assembly include genome replication [147, 195, 172, 19]; gene transcription and transcript degradation [19, 111, 127]; protein synthesis and degredation [112, 53]; cell movement and shape control [200, 45, 34, 81]; cell-to-cell communication including gap-junction assembly and regulation [188]; formation of membrane complexes such as pore-forming toxins [12]; and mechanotransduction [198, 202, 9]. Through these processes, the assembly and disassembly of molecular complexes and machines plays a crucial role in essentially all regulatory processes in cell biology. Given the centrality of self-assembly to cell biology, one cannot hope to develop truly comprehensive quantitative models of systems biology without tackling self-assembly. Yet self-assembly has until recently been largely absent from major efforts at developing general systems biology modeling tools (e.g., [146, 82, 60, 65, 182, 181, 108, 160, 185]) or handled only with one-off special cases for particular systems of importance (e.g.,[59, 199, 96]). Even the most ambitious efforts at large-scale biochemical modeling largely focus on traditional enzymatic chemistry or transcriptional dynamics and only implicitly model the self-assembly reactions involved in those processes (e.g., recent comprehensive models of whole-cell or whole-organism transcriptional and metabolomic modeling [189, 18]). This situation is beginning to change as some major systems biology tools (e.g., [69, 68, 55]) and modeling efforts [96] have begun to incorporate methods suitable to complex self-assembly, but major challenges remain.

These challenges of self-assembly modeling largely arise from the extremely large space of possible pathways accessible to the intermediate species of a self-assembly reaction network. The number of possible reaction trajectories by which a set of free monomers can assemble into a complex grows in general exponentially in the complex size, leading to an enormous combinatorial explosion in pathway space for even moderate-sized assemblies and astronomical numbers for large complexes, such as virus capsids or cytoskeletal networks. This is problematic for experimental study of assembly systems, as it is rarely possible to discriminate experimentally among these pathways except at a coarse level, particularly for highly symmetric or repetitive structures. It likewise creates problems for the most popular modeling methods. Mass action differential equation (DE) models are generally unsuitable for non-trivial assemblies because they require either extensive simplifications [70, 56, 125] or enormous numbers of equations and variables to account for the many possible intermediates [90]. Brownian dynamics (BD) models, even highly coarse-grained [167, 17, 51, 10], are likewise challenged by the large numbers of reactants and long timescales typical of self-assembly systems, requiring themselves great simplifications of reaction processes that generally make them unsuitable for accurate quantitative modeling [58]. Methods based on Gillespie’s stochastic simulation algorithm (SSA) can provide an effective balance between DE and BD, but face their own challenges because the underlying reaction networks are too large to model explicitly [26, 59, 64]. For similar reasons, self-assembly networks are extremely challenging for experimental characterization [27, 29, 93, 100, 141, 222, 223] and model inference as well [104, 210]. For example, the high computational cost and large numbers of intermediate species make it computationally infeasible to learn models via prevailing Bayesian parameter inference schemes [67], which require large numbers of simulation trajectories.

Over the recent decades, however, a specialized literature on self assembly modeling has grown for handling a number of challenging systems of independent importance. Cytoskeletal assembly (i.e., actin and microtubule assembly) has been the subject of extensive modeling work, leading to many seminal results in the basic biophysics of molecular assembly processes. Viral capsid assembly [70] has a long history as one of the primary model systems for macromolecular self assembly, both from an experimental and a computational perspective. Another key model system is amyloid aggregation, the basis for many major public health threats, including Alzheimers disease, Huntington’s disease, Parkinsons disease, prion disease, and type II diabetes. Fig. 1 shows a few examples of important model systems for self-assembly and models through which they have been studied. The practical importance of these and other systems has led them to attract their own modeling communities to find solutions to the special challenges of molecular self-assembly to computational modeling. In these fields, one can find studies both anticipating the challenges beginning to face broader systems biology efforts and often offering at least partial solutions to these challenges.

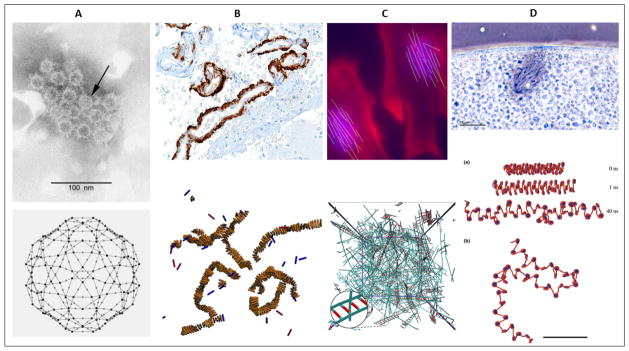
Figure 1.

Example model systems for self-assembly simulation. (A) Viral capsid assembly. Top: Hepatitis virus [77], Bottom: Coarse-grained SSA simulation of HPV assembly [211]. (B) Amyloid aggregation. Top: High magnification micrograph of cerebral amyloid angiopathy with senile plaques in the cerebral cortex (amyloid beta, as seen in Alzheimer disease) [23], Bottom: Coarse-grained Monte Carlo simulation of amyloid aggregation with two state monomer model [11]. (C) Cytoskeletal assembly and disassembly. Top: Highly oriented actin fibers in shear stress cultivated rat cells [2], Bottom: BD simulation of actin cytoskeleton composed mainly of actin and actin crosslinking proteins [98]. (D) Genome organization. Top: Chromatin fibers during mitosis, Xenopus egg [22], Bottom: BD simulations of nucleosome structure and dynamics [151]. For more on nucleosome assembly, see [19].

The remainder of this review will consider in more detail both the special diffculty of self-assembly modeling and the literature addressing it. It will first discuss some of the important roles of self-assembly in cellular biochemistry as well as the role of systems modeling methods in understanding these systems. It will then discuss some of the successful approaches to self-assembly modeling that have emerged through this literature, as well as continuing challenges. It will conclude with consideration of how quantitative self-assembly modeling may shape future efforts in modeling biological systems more generally.

2. Why does self-assembly (SA) matter?

2.1. The role of self-assembly in general cell biology

Self-assembly is everywhere in biology, beginning with the most fundamental processes of molecular biology, all of which depend on the self-assembly of specialized complexes, structures, or molecular machines. Examples of self-assembled molecular machines fundamental to molecular biology include DNA polymerases (replication), RNA polymerases (transcription), the spliceasome (splicing), the ribosome (translation), and the proteasome (protein degradation). Each of these processes is critical in different ways to the regulation of complex biological systems and thus has been the focus of specialized modeling efforts. For example, the transcription complex is one of the most well studied systems in molecular biology, with experimental work on the interaction of classic 1D and 3D diffusion of transcription factors [74] inspiring kinetic models of the recruitment process [95]. More specialized examples of self-assembly continue to be elucidated, with prominent recent examples including the RISC complex involved in miRNA [168, 116, 137, 88] and the Cas9-gRNA complex [33] implementing the CRISPR/Cas system [138, 186].

Within eukaryotic biology specifically, a more specialized set of self-assembly systems have evolved critical roles. The cytoskeleton is an unusually large, dynamic, and complicated molecular assembly, making it a crucial target of modeling efforts. The cytoskeleton itself is essential to intracellular transport [150, 152], cell movement and shape control [7, 149], mechanotransduction [201], and cell division [79], among many other functions. Furthermore, the dynamic process of assembly and disassembly is central to each of these functions. Actin and microtubule assembly and disassembly have been key model systems for self-assembly from the early days of molecular biology [91, 134, 61, 49, 170, 124, 204, 20, 62] and have inspired numerous computational models (e.g., [159, 130, 52, 179, 57, 161]). Transport processes in the eukaryotic cell frequently depend on other kinds of specialized self-assemblies, in addition to the cytoskeleton. For example, much eukaryotic transport involves the assembly of specialized machinery for construction and scission of cargo-carrying vesicles, such as the clathrin and COPI/COP-II coat systems [136, 50], which have inspired their own modeling literature (e.g., [37, 117, 87]).

Beyond its role in general cell and molecular biology, self-assembly is crucial to a number of disease-specific processes. Amyloid diseases are perhaps the prime example of a disease specifically of self-assembly, where aberrant assembly is the mechanism of illness. Numerous such diseases are known, including many major public health threats. Perhaps best known are Alzheimer’s disease (characterized by aggregates of the Aβ peptide and the Tau protein[122, 94]), Huntington’s disease (characterized by aggregates of the Huntingtin protein [113]), Parkinson’s disease [169], amytrophic lateral sclerosis [197], type II diabetes, and a variety of known prion diseases such as Creutzfeldt-Jakob [133, 28]. Alzheimer’s and dementia, for example, are strongly associated with aging and affected roughly 36 million people in 2010 [208, 209]. It is becoming increasingly clear that the ability to form the amyloid state is a widespread, generic property of proteins [102] making the process of amyloidogenesis an important topic of theoretical study. From a physical perspective, the main question is what forces stabilize the aggregates into the oligomer (small soluble disordered clusters) and fibrillar (long, many-chain highly structured -sheet-containing aggregates) states associated with neurotoxicity [165]. For a broader discussion of these forces, see [109, 110, 139]. From a computational perspective, the focus is both on identifying the structure of oligomeric intermediates and fibers but also elucidating the kinds of assembly pathways available. This is an especially challenging computational problem due to the intrinsic disorder in the system.

Viral illnesses form another broad class of self-assembly-driven illness, in which assembly of large complexes (i.e., the viruses themselves) are the mechanism of the disease process. Virus assembly is of obvious medical importance, given the millions who die each year from viral illnesses, e.g., 1.5 million from AIDS alone [38]. A fundamental understanding of this crucial aspect of the viral life cycle and infectivity may offer avenues for therapeutics or vaccines [223]. Additionally, there many factors making viruses appealing to the modeling community, including the deep experimental literature on their assembly and a high degree of symmetry in the final structure that allows for large complexes to be produced from small numbers of distinct subunit types. Viral assembly modeling has thus become a subfield in itself. Virus assembly has been a crucial platform for many basic advances in self-assembly modeling, including the use of DE [220], BD [167, 144, 71, 128], and SSA [218, 78, 97] methods. It has likewise been a platform for developing a variety of specialized versions of these modeling methods, such as rule-based approaches to simulating extremely large reaction networks [89] and derivative-free optimization approaches to model inference [104, 210]. Viral capsids have been a focus of intense theoretical study into the basic biophysics of self-assembly [70, 71, 42, 187, 24] as well as for identifying potential new avenues for assembly-mediated treatment [105, 31, 106, 187, 203, 215, 101, 43, 86, 171, 143].

3. Self-assembly modeling and simulation

3.1. The challenge of quantitative modeling of self-assembly reaction networks

At the root of much of the diffculty of modeling self-assembly is the extraordinarily large number of intermediates and pathways potentially accessible to a self-assembly system. Large number of reactants present problems in different ways to most conventional modeling and model inference methods (see Section 3.2 below). They likewise present a challenge to experimental characterization of such systems, as there is no practical way to monitor huge numbers of distinct molecular species. While details vary by geometry, in general the number of possible intermediates (partially built structures) one might encounter on the way to a complete assembly will blow up exponentially in the assembly size. This problem has probably been most intensively studied in the virus assembly literature, as it is particularly pronounced for large, highly symmetric structures, of which viral capsids are a prime example. Even a coarse-grained model of an icosahedral virus capsid, consisting of just twelve subunits, has 750 possible intermediate structures [120]. For real viral structures, which typically have several hundred proteins, the numbers of potential intermediates will be astronomical. Similar problems will arise to a lesser degree with large, asymmetric assemblies (e.g., the ribosome [103, 126]) as well as with larger but less symmetric assemblies such as the cytoskeleton. While the number of species possible for a linear filament is small, once one allows for branching [216], numbers of possible branched filaments or networks can blow up exponentially in the structure size as well. Note that this is not a unique challenge of self-assembly, as similar issues arise in other combinatorially explosive systems, such as signaling networks [16, 80].

A related concern for modeling, particularly with respect to self-assembly in cell biology, is the issue of small copy numbers [63, 194] resulting in an inherently discrete and stochastic reaction system. The issue occurs for many cellular systems involving reactants that occur in just a few copies per cell, but is especially an issue for self-assembly because the large number of intermediates guarantees that most are present in zero or one copies at any given time [135]. The issue is exacerbated by the fact that self-assembly reactions are frequently nucleation-limited, meaning that they are characterized by slow and relatively rare nucleation events followed by comparatively rapid polymerization. Nucleation-limited growth is well established for several of the major model systems in self-assembly, such as virus capsids [141, 217], amyloids [107], and actin and tubulin fibers [14]. A large body of theory suggests the nucleation-limited growth is crucial to their robust operation [156, 142, 141, 44, 191, 140]. In nucleation-limited systems, nearly every species is unpopulated at most times. Small copy numbers are problematic computationally in part because they mean that discretization errors inherent to efficient continuum models became substantial. In part, they are problematic because they mean that self-assembly must be treated as a stochastic system, forcing the use of less efficient simulation methods than the continuum approximations usable when all species are well populated [63, 194, 41] (see Section 3.4).

A second major challenge of self-assembly reactions is their long timescales (see Figure 2), and in particular the large gap between timescales of the full assembly reaction and the individual polymerization steps of assembly. Full assembly reactions of large complexes in vitro may have timescales measured in minutes to days (although assembly in vivo may be substantially faster [115, 36, 175]) while individual reaction steps are typically many orders of magnitude faster [180, 222]. In part, this is a side effect of nucleation-limited growth mentioned above: nucleation reactions are necessarily much slower than the subsequent elongation reactions [167, 221]. Furthermore, the nucleation reactions themselves may in fact require extensive trial-and-error involving much faster formation and breakdown of transient partial intermediates [221, 217, 184]. Large timescales, and a large dynamic range of timescales, are challenges for essentially all standard modeling methods, whether that manifests in a need for large numbers of timesteps in a continuum method or large numbers of discrete events for a stochastic simulation.

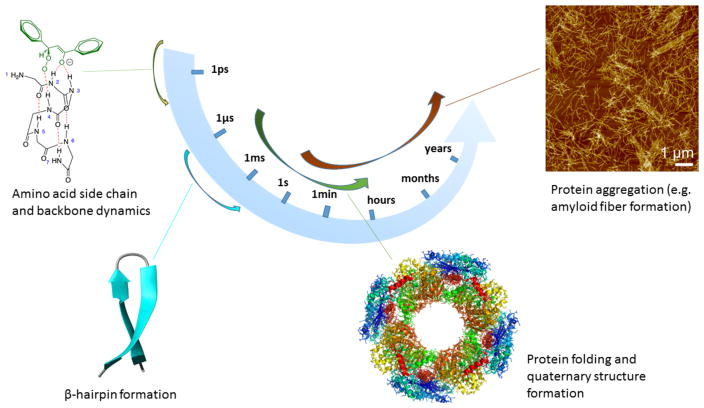
Figure 2.

Timescales for protein dynamics and aggregation. The figure illustrates some of the basic biological processes that go into self-assembly and their relevant timescales, illustrated by the specific example of amyloid aggregation. Figure based on material from [6, 21, 207, 206]

A third class of challenge arises from the fact that self-assembly reactions are unusually sensitive to the many ways in which the physical biology of the cell differs from that of in vitro models. For example, physical confinement — by the cell membrane, subcellular compartments, or other large structures such as the cytoskeleton or genome — is commonly neglected in modeling reaction systems yet cannot be ignored when dealing with reactions that result in products comparable in size to the spaces in which they form. A related issue is that self-assembly processes are also well known to be unusually sensitive to macromolecular crowding [148, 119, 75], a key distinguishing feature of the cellular environment. Numerous theoretical and experimental studies have suggested both the need for and the challenge to correcting simulation methods to account for the effects of crowding on assembly processes (e.g., [129, 166]). Examples include the effects on several aspects of DNA replication such as helicase activity and the sensitivity of DNA polymerase to salt [1], on protein-protein binding affinity and specificity [99], on the kinetics and morphology of amyloid self-assembly [115], on the stochasticity of gene expression machinery [76], and on viral capsid assembly [175, 36].

3.2. Modeling methodologies

Despite the difficulties they present to modelers, a variety of modeling methods have proven valuable for self-assembly. Table 1 describes a few of the primary methods that have emerged for self-assembly modeling. While most are drawn from older techniques for more general reaction chemistry modeling, in the self-assembly context they often present novel challenges or require specialized adaptations. This section covers three of the most successful methodologies that have been developed for self-assembly, some of the particular challenges they have faced in the self-assembly context, and how they have been adapted to meet those challenges.

Table 1.

Common modeling methodologies for self-assembly. The table lists principal techniques for self-assembly modeling, some systems biology software packages implementing them, and some notable applications in self-assembly modeling.

Reaction Representation	Description	Software Packages	Applications
Law of Mass Action (Deterministic)	Expresses any well-mixed chemical system as a collection of coupled non-linear first order differential equations which typically must be numerically integrated. PDEs must be used when space is explicitly included	BioNetGen [15], COPASI [82], VCell [146], DBSolve [66]	Virus Assembly: [125, 173, 27, 70], Metabolomic Networks[90]
SSA/Gillespie Approaches	Provides a way to simulate kinetically correct trajectories consistent with the Chemical Master Equation	Moleculizer [114], BioNetGen [15], VCell [146], DESSA [218]	Virus assembly: [184, 97]
Spatial Stochastic	Usually combine Gillespie or Stochastic Langevin with diffusion or subunit geometry	MCell [182], StochSim [108], VCell [146], Smoldyn [4], SRSim [69]	Geometric Constraints with Diffusion: [68], Amyloid-Beta: [192]
Rule-Based	Primarly network-free rule-based methods which may incorporate stochasticity and spatial modeling	RuleMonkey [32], BioNetGen, ML-Space [13], VCell [164], SRSim [69]	Multivalent ligand-receptor interactions: [213], Prion Aggregation [154], Virus Assembly: [167, 218]
Brownian Dynamics	An explicitly spatial model where Brownian motion is computed with the Langevin equation	Smoldyn [4], MCell [182]	Multiscale Reaction-Diffusion [58], Virus Assembly: [167, 71, 128, 46, 47, 17], Crowding/Amyloids: [205], Clathrin Cage Formation: [87]

3.2.1. Mass action differential equation (DE) models

Much modeling of reaction systems classically has arisen, at least initially, from DE models based on the chemical Law of Mass Action. Such models represent any generic chemical reaction network

$$\begin{gathered} a_{11}{X}_1+a_{12}{X}_2+\dots +a_{1n}{X}_{n{k}_{1-}}{\to }^{k_{1+}}{b}_{11}{X}_1+b_{12}{X}_2+\dots +b_{1n}{X}_n \\ \cdots \\ {a}_{m1}{X}_1+a_{m2}{X}_2+\dots +a_{mn}{X}_{n{k}_{m-}}{\to }^{k_{m+}}{b}_{m1}{X}_1+b_{m2}{X}_2+\dots +b_{mn}{X}_n \end{gathered}$$

in terms of a system of differential equations of the form

$$\frac{d{X}_i}{dt}=(k_{i+}{b}_{1i}-k_{i-}{a}_{1i})X_1^{a_{11}}{X}_2^{a_{12}}\cdots X_n^{a_{1n}}+\dots +(k_{i+}{b}_{mi}-k_{i-}{a}_{mi})X_1^{a_{m1}}{X}_2^{a_{m2}}\cdots X_n^{a_{mn}}$$

Accumulating these contributions across a full set of reactions and reactant species defines a system of differential equations modeling the time evolution of all reactants in the system. Such DE models were the basis of many of the earliest cell simulation systems, such as E-cell [193], ProMoT/Diva [65], Virtual Cell [162], GEPASI [118] and others. Later extensions of these models allowed for consideration of spatial heterogeneity via partial differential equation (PDE) reaction-diffusion models:

$$\frac{\partial X_i}{\partial t}=d_i{\nabla }^2{X}_i+(k_{i+}{b}_{1i}-k_{i-}{a}_{1i})X_1^{a_{11}}{X}_2^{a_{12}}\cdots X_n^{a_{1n}}+\dots +(k_{i+}{b}_{mi}-k_{i-}{a}_{mi})X_1^{a_{m1}}{X}_2^{a_{m2}}\cdots X_n^{a_{mn}}$$

for reactant-specific diffusion coefficients d_i.

DE models provided a basis for some of the first approaches to modeling many self-assembly systems. Classic results on molecular assembly of polymers derived from such models include [132, 131] and they were integral to seminal models of microtubule polymerization [39]. They likewise were used for early attempts at more complex systems, such as the first dynamic models of viral self-assembly [223, 221], where they provided early insights into the parameter space of self-assembly [221]. They continue to prove valuable in that context for such problems as interpreting complex experimental data [70, 173, 27]

The most substantial challenge to DE models on self-assembly systems is computational tractability, as such models need to keep explicit track of all species that might be present in a given simulation. While that number grows only linearly in assembly size for linear polymers, it blows up exponentially in size for more complex structures such as viruses. In practice, the solution to that problem has typically been to simplify: either manually via simplified versions of structures or conflation of subsets of structures [220, 221] or through automated methods for pruning low-usage pathways [48]. While there is good empirical evidence that such strategies can yield quantitatively accurate models [223, 48], degrees of accuracy can be sensitive to structure and pathways used [120]. DE models further provide no good solution for the problem of modeling discretization of small copy number reactions.

3.3. Brownian dynamics (BD) models

The challenges self-assembly modeling presents to DEs led to an alternative approach based on Brownian dynamics (BD) particle models. In a BD approach, we explicitly model a finite set of assembly subunits in three dimensional space. These subunits diffuse through space under a model of Brownian motion, implemented by a variant of damped Langevin dynamics [51]. Models of binding dynamics can be implemented either by discrete reactions occuring upon particle collisions or via short-range binding forces, leading to gradual agglomeration of particles over the course of a simulation. BD models have the considerable advantage over DE models that one need not devote computational resources to any species not present at a specific instant in time. Run time thus depends on the number of particles modeled, not the number of species they might in principle form.

Such models have perhaps been most pronounced in their use with viral capsid systems, perhaps because their exceptionally large space of intermediates makes them especially challenging for DE models. Through viral capsid work, they have been the basis of numerous important insights into the basic biophysics of self-assembly. BD models were introduced to capsid studies nearly two decades ago [167], have seen a series of important methodological advances since [144, 71, 128] and continue to be the basis of new approaches and applications (e.g., [10, 51, 17]). They have also seen important roles in modeling various other challenging assembly systems, such as clathrin [87]. Insights arising from BD models include understanding the importance of nucleation limited growth to ensuring robust assembly and preventing kinetic trapping [73], the sensitivity to numerous parameter variations [46], and the potential sources of misassembly [46, 71]. In more recent years, these models have been extended to issues diffcult to model with other methods, such as understanding the role of the genome in RNA virus assembly [47].

The advantages of BD methods, however, come with some significant tradeoffs. First, the large size and long timescale of assembly reactions generally requires substantial structural simplifications. Second, such models typically can accommodate only modest numbers of particles, ranging up to a few thousand per simulation for state-of-the-art methods [17, 72, 155]. For relatively large structures, that may be too few to capture more than a small fraction of possible assembly trajectories. Third, they generally cannot produce quantitatively correct assembly rates, because of the large gap between diffusion rates and assembly rates. Effectively, systems need to be shifted into domains of extremely rapid assembly, through unrealistically high binding rates or concentrations, in order to yield computationally tractable simulations of the complete assembly process. Some more advanced versions of this approach can somewhat mitigate these issues, for example the use of Green’s function reaction dynamics (GFRD) to reduce the computational time needed to compute trajectories of particles between collision events [196].

3.4. Stochastic simulation algorithm (SSA) methods

Just as BD models were introduced to self-assembly modeling to address the weaknesses of DE models, so have models based on the stochastic simulation algorithm (SSA) [63] (also known as “Gillespie models” after their inventor) been adopted to address the weaknesses of BD models. In an SSA model, we represent a system at an instant in time by discrete counts of molecular species (monomers or partial assemblies). Simulation progress proceeds via reaction events, which for a self-assembly system will largely consist of single binding or dissociation reactions. Classically, one assumes a uniform, well-mixed system, in which reaction times can be approximated with exponential waiting time distributions [63]. The SSA approach can also accommodate spatial heterogeneity through modeling as an array of well-mixed, discretized spatial compartments, a variant known as spatial SSA, e.g. [183, 5].

SSA models offer considerable advantages but also involve important tradeoffs with the previously considered methods. They can be implemented to have run times independent of the number of potential species, unlike DE models, and can thus handle arbitrarily large reaction networks [64]. However, their run time does depend on the number of discrete particles present, limiting them to finite numbers of protein copies, as do BD models. They are, however, typically much more efficient than comparable BD models since they do not need to model diffusion explicitly [64] and are practical over a much broader range of parameter domains [184]. In addition, they provide an explicit quantitative model yielding kinetically correct samples from a set of reactions and associated rate constants. However, because they do not explicitly model space, they do not easily handle steric constraints that are important to such processes as aberrant assembly [167], interaction of proteins with a flexible genome [47, 214], or any form of continuous flexibility in proteins or complexes [153, 81].

SSA methods have needed some special adaptations to deal with the challenges of self-assembly. Probably the most important advance is the use of rule-based modeling (e.g. [177]), a strategy independently developed for the self-assembly field under the name local rule modeling [167] and later introduced to SSA models under that name [218]. Rule-based models allow one to avoid explicitly constructing the reaction network, an infeasible task for all but trivial self-assembly systems, and rather represent only the current state of the system and its immediate neighbors [54, 218]. This reduces run time from dependence on the size of the network to dependence only on the number of species and reactions present at any instant in time. While steric constraints are a challenge for rule-base models, that challenge has been overcome for some systems, e.g., in modeling multivalent ligand-receptor interactions [123]. Further improvements to queuing methods for discrete event implementations of SSA [89, 40] made it possible to accelerate run time by eliminating quadratic time/memory dependencies in the standard algorithms. Additionally, a set of more specialized theory has been developed to deal with the problem of extreme divergence between timescales of monomeric reactions versus the complete assembly process. Generic methods for accelerating SSA can be helpful, e.g., [145, 25], as well as more specialized variants specifically for self-assembly [121]. Other improvements include hybrid methods combining SSA with ideas from agent-based modeling [3].

While SSA methods have not yet seen as wide use as BD in the self-assembly field, they have proven to have important applications for which neither DE nor BD methods are suitable. Because of their ability to handle complex geometries and long time scales, SSA models have proven valuable for exploring parameter dependence of assembly systems by making it practical to sample large numbers of trajectories over long time scales [211] and to sample trajectories from particularly complex geometries or pathway sets [97]. They have also become a valuable platform for fitting models to experimental data, where their ability to fit an explicit timescale, to function over wide parameter ranges, and to model complex geometries are all crucial features [211, 210, 175, 176].

4. Self-assembly in broader systems biology modeling

In recent years, efforts at systems biology modeling have begun increasingly to recognize the importance of self-assembly to comprehensive modeling of complex biochemical systems. For example, a number of general systems biology simulation tools have begun to incorporate handling of self-assembly in various ways. An early example was Moleculizer [114], which incorporated basic models of assembly reactions via a rule-based SSA model with special purpose corrections accounting for altered diffusion rates of growing species. Similar kinds of models have become important more generally in modeling tools, such as RuleBender [212], which have made it possible to integrate similar rule-based SSA models into other tools for systems biology modeling. The Virtual Cell [163] has recently added handling of self-assembly reactions, using a special-purpose extension based on a form of coarse-grained BD models of self-assembly [4, 35], as well as explicit handling of rule-based modeling [164]. The most recent version of the E-Cell [193] simulation environment (ECell4) has also been updated to include capabilities for modeling self-assembly such as a network-free rule model [54] and a spatial SSA method [183]. While none of these systems yet incorporates all of the specializations found in such methods in self-assembly specific contexts, they represent important steps towards generic tools for modeling complex reaction networks that include but are not specific to self-assembly.

This need for handling the kind of combinatorial explosive reaction network that characterizes self-assembly is also beginning to be reflected in systems biology language design. For example, the Systems Biology Markup Language (SBML) [85, 84], which has become the de facto standard for specifying models in systems biology, has been updated in more recent versions to accommodate the kind of network-free rule-based models needed for self-assembly work [83]. While it has long been possible to generate SBML from a rule specification through external tools, such as BioNetGen [55], native support of the modeling language is necessary to achieve the benefits of network-free modeling needed to make complicated self-assembly modeling tractable. Handling of steric constraints that become imporant in formation of more complicated assemblies remains a hard problem for the field, however, and is so far handled only in more specialized self-assembly simulation languages [218].

Recent years have also seen claims of the first true whole-cell simulations [96, 157], an effort that necessarily involves modeling numerous processes that depend on self-assembly. In practice, such efforts have not relied on a general-purpose simulation engine suitable to both self-assembly and more conventional reaction chemistry, favoring instead general purpose methods ill-suited to self-assembly coupled to special-purpose handling of particular kinds of self-assembly. The landmark work of Karr et al. [96] establishing a comprehensive simulation of M. genitalium biochemistry, relied on a series of special-purpose modules, several of which involved ad hoc methods for specific examples of self-assembly, such as macromolecular complexation and ribosome assembly. Nonetheless, even this kind of special-purpose handling remains the exception in similar efforts at comprehensive modeling of whole-cell reaction networks (e.g., [189, 18]).

5. Conclusions

Self-assembly is a greatly important but long neglected issue in the quantitative modeling of biological systems. While it is conventionally seen as a specialized form of chemistry, it is in fact the dominant form of reaction in living systems. It poses distinctive challenges for modeling methods, though, that prevailing methods in systems biology cannot handle. Self-assembly modeling has, however, been studied intensively in many more specialized contexts, leading to an appreciation of these challenges and a variety of ways they can be addressed. As more general systems biology efforts are beginning to embrace the necessity of accommodating self-assembly, this specialized literature can provide guidance and at least partial answers to some of the biggest obstacles these efforts will encounter. This review was intended to provide a brief overview of the particular challenges of self-assembly modeling, how they have been approached to date, and how these methods have been used in the past and are beginning to be incorporated into comprehensive models of systems biology. The hope behind this review is that better awareness of obstacles and solutions already identified by self-assembly modelers can assist the broader systems modeling community in anticipating and navigating the same issues.

An appreciation for the past literature allows us to predict some of the future paths comprehensive systems modeling efforts are likely to follow. For the most part, where general efforts systems biology modeling has considered self-assembly, it has been as special cases with special-purpose methods for specific systems (e.g., [17, 47, 211, 174, 158, 92, 99, 178, 155, 10, 219, 210]). Given the many examples of self-assembly in cell biology, it is safe to say this is not a sustainable solution; rather general systems biology efforts will need to start to think of self-assembly as the normal case that must be accommodated and integrated into simulation design via both model specifications and simulation algorithms. Modeling methods that will work for both self-assembly and for other kinds of chemistry exist [13, 199, 3, 146, 15, 114, 185, 32], but will need to become the standard for modeling tools and languages. More foresighted efforts in a variety of systems modeling contexts can help point the way (e.g., [114, 193, 4, 96, 35, 164]), although most remain behind the state-of-the-art in modeling of self-assembly specifically.

At the same time, there are many challenges for which good solutions do not yet exist. For example model inference [30] remains an extremely difficult problem for self-assembly systems [223, 104, 211, 210], where the Bayesian methods usually favored by the field [67] are unusable in practice, and it is likely advances in both biotechnology and inference algorithms will be needed to address it. The field is beginning to tackle this challenge, e.g., with BioNetFit [190], which uses a genetic algorithm to provide curve fitting capabilities compatible with ODE (BioNetGen) and Network Free (NFSim) model specifications and has proven successful in fitting to steady-state and time-series oligomerization data. There are also, as yet, no universally good methods for modeling hard self-assembly systems. Each of the major approaches covered here — SSA [64], BD [167], and DE [220] — has tradeoffs that make them unsuitable for some questions. It remains to be seen whether more general solutions might arise from advances in one or more of these methods, clever hybrid approaches, or some wholly new ideas. It is also worth noting that self-assembly systems are challenging to characterize experimentally, for similar reasons to their challenge to modelers. The solutions to that issue, as well, are likely to lie in pooled efforts by experimentalists and computational researchers to advance experimental biotechnology and model-fitting algorithms in complementary ways. Indeed, self-assembly may be a particularly valuable test case for addressing the hard problems in building detailed and predictive quantitative models of complex biological systems, where the field can begin to think of modelers and experimentalists not as two communities but as two inseparable pieces of the future practice of biological discovery.