Polyenergetic known-component CT reconstruction with unknown material compositions and unknown x-ray spectra

Abstract

Metal artifacts can cause substantial image quality issues in computed tomography. This is particularly true in interventional imaging where surgical tools or metal implants are in the field-of-view. Moreover, the region-of-interest is often near such devices which is exactly where image quality degradations are largest. Previous work on known-component reconstruction (KCR) has shown the incorporation of a physical model (e.g. shape, material composition, etc.) of the metal component into the reconstruction algorithm can significantly reduce artifacts even near the edge of a metal component. However, for such approaches to be effective, they must have an accurate model of the component that include energy-dependent properties of both the metal device and the CT scanner, placing a burden on system characterization and component material knowledge. In this work, we propose a modified KCR approach that adopts a mixed forward model with a polyenergetic model for the component and a monoenergetic model for the background anatomy. This new approach called Poly-KCR jointly estimates a spectral transfer function associated with known components in addition to the background attenuation values. Thus, this approach eliminates both the need to know component material composition a prior as well as the requirement for an energy-dependent characterization of the CT scanner. We demonstrate the efficacy of this novel approach and illustrate its improved performance over traditional and model-based iterative reconstruction methods in both simulation studies and in physical data including an implanted cadaver sample.

1. Introduction

Many imaging scenarios involve known devices in the field-of-view. Examples in orthopedics include pedicle screw and rods for spine surgery, knee and hip implants for joint replacement, and plates and screw for fixation in trauma cases. In image-guided procedures, surgical tools are often within an intraoperative imaging field. When these components are metallic and one utilizes a 3D cone-beam imaging system, one can find substantial artifacts that appear as bright or dark streaks, “blooming” of the metal components, and other nonuniform shadings in the reconstructed volume. The causes of metal artifacts include beam hardening, partial volume effects, photon starvation, and scattered radiation behind metal implants in the data acquisition.

Such artifacts tend to be particularly troublesome in interventional imaging since image quality degradations are most pronounced in regions immediately surrounding the metal components which tends to be the region which is of greatest interest. For example, in spine fixation surgery, pedicle screws are inserted into vertebrae. These screws need to be placed within the pedicle and body of the vertebra avoiding any breaches that might the damage the spinal cord, damage tissues anterior to the vertebra, or lead to instability in the fixation hardware. The identification and localization of such problems is greatly complicated by metal artifacts that can obscure the surrounding anatomy.

There has been a great deal of work on methods for metal artifact reduction. Such methods can generally be categorized into two groups: 1) Techniques that identify and attempt to correct data that correspond to measurements through metal; and 2) Methods that attempt to model the reduced data fidelity associated with metal devices within the reconstruction algorithm. Correction methods generally attempt to replace projection data containing metal with synthesized projections based on surrounding projection samples via interpolation (Kalender et al 1987, Watzke and Kalender 2004, Li et al 2010, Meyer et al 2009). Such approaches can use sophisticated techniques including wavelet decompositions (Zhao et al 2000), Laplacian diffusion (Zhang et al 2007), or inpainting techniques (Arias et al 2009, Xinhui Duan et al 2008, Meyer et al 2012). Other approaches attempt to use prior imaging studies to replace the missing data (Bal and Spies 2006, Paudel et al 2013, Heußer et al 2014, Koehler et al 2012, Lell et al 2012). Some techniques apply additional corrections in a second pass (Prell et al 2009, 2010) or in a iterative fashion with refined interpolations based on the initial reconstruction. All of these approaches generally necessitate an algorithm to identify which projections contain metal and replacement of those projections with synthesized projections which can be subject to error and miss details that were obscured by the metal. Thus, while these methods typically mitigate the most severe artifacts, regions immediately adjacent to metal components often have residual image quality issues and/or missing features.

Model-based reconstruction methods have also shown utility in the reduction of metal artifacts. A relatively simple statistical reconstruction that weighs measurements based on their variance will show some advantage since projections with metal tend to be substantially down-weighted (Buzug and Oehler 2007, Ge Wang et al 1996). Other iterative approaches combine model-based reconstruction and data interpolation (Lemmens et al 2009). One can also treat the projections with metal as missing data effectively weighting those data to zero and rely on regularization to “fill in” what is missing (De Man et al 1999). These techniques are effectively performing a kind of interpolation in the image domain based on their regularization that can also result in missing features. More sophisticated approaches avoid interpolation and use all of the projection data by including not only a noise model but also model that accommodates spectral effects and beam hardening. That is, a polyenergetic beam and energy-dependence in patient attenuation is integrated into the reconstruction algorithm, which can be very successful in reducing metal artifacts (De Man et al 2001, Idris A and Fessler 2003, Elbakri and Fessler 2002). Unfortunately, these approaches tend to be complex, necessitating specific spectral models and system characterization as well as an algorithm with increased computational requirements. Related work (Verburg and Seco 2012) uses material specific beam-hardening corrections and monoenergetic iterative reconstruction, but still requires knowledge of material compositions.

One of the principal difficulties with all metal correction methods is that there is fundamental lack of information in regions near metal. One possible way to improve performance within a model-based approach is to inject more information into the reconstruction problem by integrating knowledge of the shape and composition of metal components directly into the reconstruction algorithm. In interventional imaging, in particular, the exact implants, surgical tools, or other devices are often known prior to imaging and shape models (e.g., CAD models) and material compositions may be available as auxiliary information. Both the constrained optimization methods of Snyder et al. (Snyder et al 2001) and the Known Component Reconstruction (KCR) technique (Stayman et al 2012a) leverage such additional information. These approaches solve a joint estimation problem consisting of a registration of the known metal components to placing the metal device model in the correct position within the anatomy as well as a “standard” reconstruction of the surrounding attenuation material. Such model-based methods with known component knowledge have demonstrated an ability to dramatically reduce metal artifacts. However, residual artifacts remain when a simple monoenergetic model is used.

Extensions of known component methods have attempted to further reduce artifacts by integrating a polyenergetic forward model (Zbijewski et al 2012, Williamson et al 2002). Other extensions have included generalized registration methods to integrate component knowledge for devices whose shape is not known exactly (Stayman et al 2012b) and a generalization where metal components are modeled at much higher spatial resolution than the surrounding anatomy to minimize nonlinear partial volume errors (Stayman et al 2013). While such extensions can yield improved results (particularly in close proximity to a metal device), this advantage comes with additional complexity – both in terms computational burden and the increased information required by the reconstruction algorithm. Polyenergetic system models typically require both a parameterization of the energy-dependence for the materials present in a scan as well as a calibrated model of the x-ray spectrum and detector energy sensitivity. In practice, there are additional complexities since x-ray tube voltage often varies for different studies.

In this work, we leverage the same kind of decomposition as used in (Stayman et al 2013) which decouples physical effects in the patient anatomy with those effects due to the metal components. This permits a mixed-fidelity system model where metal components can be modeled with high-fidelity using a simple parameterized energy dependence (i.e., a spectral transfer function), while the surrounding patient anatomy can be modeled with a “standard-fidelity” monoenergetic model. We integrate this model within a polyenergetic KCR technique and, additionally, eliminate the need for specific material component composition knowledge as well as the need for x-ray beam spectral characterization through joint estimation of the spectral parameters as part of the reconstruction.

In the following sections we introduce the mixed-fidelity system model, the spectral transfer function, which characterizes energy dependence, and derive a reconstruction algorithm that jointly estimates the spectral parameters associated with metal components and reconstructs the patient anatomy from a single tomographic scan. Simulations were conducted to investigate the convergence and the performance of calibration-free polyenergetic KCR framework. Performance of the proposed methodology was also evaluated in physical phantom and cadaver torso test bench data. Comparisons to traditional filtered-backprojection (FBP), FBP with metal artifact reduction, penalized weighted least-squares (Bouman and Sauer 1993), monoenergetic KCR (Stayman et al 2012a), and pre-calibrated polyenergetic KCR were performed.

2. Methods

2.1. Mixed Object and Forward Models for Polyenergetic X-ray CT

Consider the following monoenergetic measurement model for a transmission tomography system

$$\overline{y}=\mathbf{D}\{g\}exp(-\mathbf{A}\mu ),$$ (1)

where ȳ denotes the mean measurement vector, the operator D{·} forms a diagonal matrix from its vector argument, g represents a vector of system-dependent gain terms including photon fluence, A is a discretized linear projection operator, and μ is a vector of object attenuation values. While (1) represents a traditional forward model, we choose to integrate additional specific knowledge of components through a modification of the object model. Specifically, along the lines of previous work (Stayman et al 2012a), we parameterize the object as the combination of an unknown anatomical background μ_* and an arbitrary number of components, each of which is composed of a homogeneous material and is represented by the vector ${\mu }_I^{\{n\}}$. This modified object model is

$$\mu ={\mu }_{\ast }(\mathrm{\Lambda })+{\mathrm{\sum }}_{\{n=1\}}^{N}T\left({\lambda }^{\{n\}}\right){\mu }_I^{\{n\}},$$ (2)

where n known components, ${\mu }_I^{\{n\}}$, are registered in the field of view through the transformation T. The registration for each component is parameterized by the vector λⁿ and Λ denotes the collection of registration parameters for all components. Due to the additive form in (2) the background anatomy, μ_*, must be appropriately chosen to not contribute in regions where the components lie. In previous work (Stayman et al 2012a) this was enforced via a masking operation

$${\mu }_{\ast }(\mathrm{\Lambda })=\left({\mathrm{\Pi }}_{\{n=1\}}^N\mathbf{D}\left\{T\left({\lambda }^{\{n\}}\right)s^{\{n\}}\right\}\right)\stackrel{\sim }{\mu },$$ (3)

where s^{n} is the mask for the n^th component that is zero for voxels inside the component and one outside, and μ̃ denotes an unmasked parameterization of the background anatomy. The masks must be registered in accordance with the component transforms making the background parameterization dependent on Λ. For mathematical simplicity in the following algorithm derivation, we express the object in terms of μ_*(Λ), which contains the voxel values where there are no components (as opposed to the full object parameterization μ̃ which has attenuation values that are essentially nuisance parameters since they are always masked out). However, the masking operation remains important to avoid “double-counting” background and component attenuation within the same voxel. This operation is shown explicitly in the final pseudocode.

The object model in (2) permits the following factorization of the forward model in (1):

$$\begin{gathered} \overline{y}=\mathbf{D}\{g\}exp\left(-\mathbf{A}{\mu }_{\ast }(\mathrm{\Lambda })\right)exp\left({\mathrm{\sum }}_{\{n=1\}}^N-\mathbf{A}T\left({\lambda }^{\{n\}}\right){\mu }_I^{\{n\}}\right) \\ =\mathbf{D}\{g\}exp\left(-\mathbf{A}{\mu }_{\ast }(\mathrm{\Lambda })\right){\mathrm{\Pi }}_{\{n=1\}}^{N}exp\left(-\mathbf{A}T\left({\lambda }^{\{n\}}\right){\mu }_I^{\{n\}}\right), \end{gathered}$$ (4)

Note that the common monoenergetic Beer’s law model for projections appears separately for the background anatomy and for each of the components. This yields the opportunity to refine the physical model for x-ray propagation through the components only which is arguably where higher-fidelity modeling is needed most (e.g. due to artifacts associated with metal components). Moreover, since individual components often have compact support in both image and projection domains, high-fidelity component models can be applied efficiently in terms of storage and computation using small image volumes and small projection areas (as opposed to approaches that attempt a high-fidelity model for the entire image volume).

Equation (4) permits a mixed fidelity model where the model for the background anatomy is monoenergetic and the model for the components includes polyenergetic beam and attenuation effects. This is potentially a very useful model for metal devices since spectral effects are most pronounced for the measurements involving metal components. We write the modified model as

$$\overline{y}=\mathbf{D}\{g\}exp\left(-\mathbf{A}{\mu }_{\ast }(\mathrm{\Lambda })\right){\mathrm{\Pi }}_{\{n=1\}}^N{f}^{\{n\}}(\mathbf{A}T\left({\lambda }^{\{n\}}\right)b_I^{\{n\}}),$$ (5)

where $b_I^{\{n\}}$ denotes the binary component mask representing the shape of each homogeneous component. The exponential in (4) has been replaced with fⁿ(·) which we refer to as the spectral transfer function (STF) relating path length through the n^th registered component to the transmissivity. This spectral transfer function can accommodate both beam quality and energy-dependent detector effects, and may change component-to-component due to differing compositions. Inspired by beam-hardening correction strategies (Hsieh et al 2000), in this work, we propose a STF that uses a polynomial expansion inside an exponential which is written as

$$f^{\{n\}}\left(p^{\{n\}};{\kappa }^{\{n\}}\right)=exp\left({\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n\}}{\left(p^{\{n\}}({\lambda }^{\{n\}})\right)}^k\right),$$ (6)

where f^{n} is a function of path length through the component, p^{n}, and is further parameterized by the vector κ^{n}. Thus, for incorporation in the modified forward model in (5) we have

$$p^{\{n\}}({\lambda }^{\{n\}})=\mathbf{A}T\left({\lambda }^{\{n\}}\right)b_I^{\{n\}}.$$ (7)

The κ^{n} vector parameterizes the shape of the STF for each component. For a monoenergetic X-ray imaging system, ${\kappa }_k^{\{n\}}$ is the negative attenuation value for the component for k = 1, and zero for all other k. For polyenergetic systems, the κ values allow approximation of energy-dependent effects on the survival probability of X-ray photons passing through the known components.

2.2. Polyenergetic Known Component Reconstruction Objective Functions

With the modified forward model in (5) and the definition of the STF in (6), we derive a reconstruction objective function. Applying a log transformation on (5) and presuming a Gaussian model, we write the following penalized weighted least squares (PWLS) estimator:

$$\begin{gathered} \{{\widehat{\mu }}_{\ast },\widehat{\kappa },\widehat{\mathrm{\Lambda }}\}=\text{argmin}\mathrm{\Phi }({\mu }_{\ast },\kappa ,\mathrm{\Lambda };y)=\text{argmin}L({\mu }_{\ast },\kappa ,\mathrm{\Lambda };y)-\beta R({\mu }_{\ast }) \\ L({\mu }_{\ast },\kappa ,\mathrm{\Lambda };y)={\Vert \mathbf{A}{\mu }_{\ast }(\mathrm{\Lambda })-{\mathrm{\sum }}_{\{n=1\}}^N{\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n\}}{\left(p^{\{n\}}\left({\lambda }^{\{n\}}\right)\right)}^k-log(\mathbf{D}\{g\}\ast {\overline{y}}^{-1})\Vert }_W^2 \\ R({\mu }_{\ast })={\mathrm{\sum }}_j{\sigma }_j^2{\mathrm{\sum }}_{\{k\in N_j\}}\psi \left({\mu }_{\ast j}(\mathrm{\Lambda })-{\mu }_{\ast k}(\mathrm{\Lambda })\right), \end{gathered}$$ (8)

where L denotes the negative log-likelihood for the transformed measurements, the weighted 2-norm includes a weight vector equal to the inverse of the variance of the transformed measurements (Sauer and Bouman 1993), and a general regularization term, R, is incorporated that penalizes pairwise differences in voxel values and is controlled by the regularization parameter β.

The estimator in (8) is general and forms the basis for a new polyenergetic KCR. Rather than performing simultaneous estimation of μ̂_*, κ̂, and Λ̂, we adopt a staged estimation strategy of component registration followed by reconstruction. This permits us to take advantage of previously developed registration tools perform the 3D-2D component registration, fix Λ, and then solve (8) for μ̂_* and κ̂. The staged estimation strategy is discussed in detail in the following section.

Before introducing the staged estimation strategy, we would like to introduce a competing approach for dealing with unknown material composition and beam quality based on a simplification of (8). Specifically, one might opt to (pre)estimate κ̂ values using a specialized prescan of components in air. This approach may be a clinically practical solution to characterize unknown energy dependencies since implants and surgical devices could be scanned prior to an image-guided procedure that involves scanning of the implanted patient. By scanning in air, there is no longer any anatomical background, μ̂_*, and (8) becomes

$$\{\widehat{\kappa },\widehat{\mathrm{\Lambda }}\}=\text{argmin}{\Vert {\mathrm{\sum }}_{\{n=1\}}^N{\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n\}}{\left(p^{\{n\}}\left({\lambda }^{\{n\}}\right)\right)}^k-logD(b)\ast {\overline{y}}^{-1}\Vert }_W^2$$ (9)

permitting a precalibration wherein the spectral coefficients for each component can be estimated. (We note that registration parameters must also be estimated as nuisance parameters that are not relevant to subsequent acquisitions.) Following this precalibration step, reconstructions of subsequent acquisitions (with background patient anatomy) may be performed using (8) with fixed κ̂ values – simplifying the reconstruction process. Both the precalibration approach as well as the (staged) calibration-free approach are implemented and evaluated in following sections.

2.3. Preregistration of Known Components using Gradient Correlation

A staged registration-then-reconstruction estimation framework permits the use previously developed, fast and robust registration methods, and simplifies the subsequent reconstruction step. Focusing on rigid registration, each component pose is parameterized as follows: The coordinate frame of each component is defined at the center of the component volume and its position and orientation with respect the world coordinate frame is represented as a 6-element vector of translation and rotations λ^{n} = (x^{n} y^{n} z^{n} η^{n} θ^{n} ϕ^{n}) using the ZYX Euler angle.

We choose a 3D-2D registration method that computes the gradient correlation (GC) between the acquired image data and simulated projections of known components with no anatomical background. This approach is described in detail in (Uneri et al 2015). The method was evaluated in (Uneri et al 2015) and found to be robust for the pedicle screw registration problem providing target registration errors of 0.2 mm and 0.2 degrees in cadaver studies using only three projection views. In this application where many projection views are available, we expect equal or better performance. The general approach is briefly described below.

The gradient correlation between two images, y₀ and y₁, is defined as

$$\begin{gathered} GC(y_0,y_1)=\frac{1}{2}\{\mathit{NCC}\left(\frac{d}{du}{y}_0,\frac{d}{du}{y}_1\right)+\mathit{NCC}\left(\frac{d}{dv}{y}_0,\frac{d}{dv}{y}_1\right)\}, \\ \mathit{NCC}(y_0,y_1)=\frac{{\mathrm{\sum }}_{\{u,v\}}(y_0(u,v)-\text{mean}\{y_0\})(y_1(u,v)-\text{mean}\{y_1\})}{\sqrt{{\mathrm{\sum }}_{\{u,v\}}{(y_0(u,v)-\text{mean}\{y_0\})}^2}\sqrt{{\mathrm{\sum }}_{\{u,v\}}{(y_1(u,v)-\text{mean}\{y_1\})}^2}}, \end{gathered}$$ (10)

where u and v denote image coordinates and NCC denotes normalized cross correlation. This metric forms the basis of the registration objective function which is denoted:

$${\widehat{\lambda }}^{(n)}=\text{argmax}{\mathrm{\sum }}_{\alpha }GC\left(y_{\alpha },{\overline{y}}_{\alpha }\left({\lambda }^{\{n\}};{\mu }_I^{\{n\}}\right)\right).$$ (11)

where y_α denotes the α^th projection image, and ȳ_α is the simulated α^th projection image of the n^th component with no anatomical background. We estimate a solution to (11) using the CMA-ES approach (Hansen and Kern 2004). This algorithm was implemented in MATLAB with function calls to an externally compiled CUDA/C++ library for fast computation of projections and objective function values on a GPU.

2.4. High fidelity forward projector

After the 3D-2D registrations for each component are applied, one has an estimate of the collection of registration vectors, Λ. Thus, the path length of the n^th positioned component p^{n} (λ^{n}) in (7) may be precomputed prior to reconstruction. It is possible to further improve accuracy of the mixed fidelity forward model by adopting finer discretization when computing p^{n} (λ^{n}). Since the components are compact and relatively small (as compared with the whole object volume), and since a high-resolution p^{n} (λ^{n}) need only be calculated once, there is little computational cost.

In principle, to compute path length, geometric transformations are applied to each known component (represented by the 3D binary component mask) and then the transformed component is forward projected according to the fixed system geometry. Unfortunately, this procedure can result in additional blur due to the inherent interpolation in the transformation operation. This small amount of error can lead to potential data mismatches in the forward model and objective function and result in residual artifacts in the final reconstructed results. Thus, instead of transformation and interpolation on each component, we propose a transformation of the projection geometry itself to avoid the interpolation. The original (system) projection geometry is specified by a series of projection matrices (PM) that parameterize the source position with respect to the world coordinate system. We modify these projection matrices with translations and rotations of the associated with the estimated component pose. This results in the following modified projection matrix relating a 3D point and its projection in the 2D detector plane:

$$\left[\begin{array}{c}u\\ v\end{array}\right]~P{M}_{3\times 4}\left[\begin{array}{cc}\left[R_{3\times 3}({\eta }^n,{\theta }^{(n)},{\varphi }^n)\right]& \begin{array}{c}{x}^n\\ y^n\\ z^n\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right],$$ (13)

where (x, y, z)^T are component volume coordinates, (u, v)^T is the projected location in the detector coordinate frame, R_3x3 is the rotation matrix for the component with respect to the detector frame parameterized by ((ηⁿ, θⁿ, ϕⁿ), PM_3x4 is the original projection matrix and the ~ symbol denotes that the left and right sides are equal to within scalar multiplication. A trapezoidal separable footprints forward and back projector (Long et al 2010) were employed for all investigations.

While the blur with transformations of the shape model is undesirable, there is physical blur associated with an extended focal spot and the detection process. We apply a Gaussian blur function with width parameter, δ on the path length calculation inside the exponential to approximate the system blur effects for the component forward model. We note that blur effects on the background anatomy are not modeled; however, this is arguably less important for the reduction of noise and artifact issues associated with high-density components. Hence, we replace the path length model of (7) with

$$p^{\{n\}}({\lambda }^{\{n\}})=\mathit{Gaussian}({\mathbf{A}}^H\left({\lambda }^{\{n\}}\right)b_{I,H}^{\{n\}},\delta ),$$ (14)

where we denote the high-fidelity (without transformation interpolation) forward projector by A^H. The width parameter, δ, is tuned to minimize edge artifacts near the component in reconstructions.

2.5. Optimization Approach and implementation

Pseudocode for our reconstruction approach is illustrated in Table 1. This table shows the iterative reconstruction process post-estimation of component registration. The algorithm begins with initialization of parameters and precomputation of a number of important variables including 1) The transformed component masks, ω; 2) the component path lengths, p^{n}, using the previously described high-fidelity approach and Gaussian blur operation; and 3) the total ray length minus the length through all components, L_*, that is used for normalization. The main body of the algorithm computes the modeled line integrals through the components, l, and the background, l_*, as well as alternating updates to 1) the background anatomy using a separable quadratic surrogates (SQS) approach (Erdoğan and Fessler 1999a, 1999b) and to 2) the spectral transfer function coefficients using iterative coordinate descent. Details of both updates can be found in the appendix.

Table 1.

Pseudocode for iterative solution of the poly-KCR objective

Λ = {λn} registration vector all components
μ(0)= Initial reconstruction (e.g. FBP)
κ(0) = Initial guess for STF coefficients
$\omega (\mathrm{\Lambda })=\left({\mathrm{\Pi }}_{\{n=1\}}^N\mathbf{D}\{T\left({\lambda }^{\{n\}}\right)s^{\{n\}}\}\right)$	% Generate transformed masks
${\mu }_{\ast }^{(0)}(\mathrm{\Lambda })=\omega (\mathrm{\Lambda }){\mu }^{(0)}$,	% Apply mask to background estimate
for all components n ∈ [1 N]
$p^{\{n\}}=\mathit{Gaussian}({\mathbf{A}}^H\left({\lambda }^{\{n\}}\right)b_{I,H}^{\{n\}},\delta )$	% Component path length with blur
end
% Calculate path length for background volume
L* = A1→	% 1→ denotes the all 1s vector
for all components n ∈ [1 N]
L* = L* − p{n}
end
for t = 1 to max_iterations	% [t−1] denotes (t−1)th iteration value
$l=-{\mathrm{\sum }}_{\{n=1\}}^N{\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n\}[t-1]}{\left(p^{\{n\}}\right)}^k$	% Spectral correction to path length
$l_{\ast }=\mathbf{A}{\mu }_{\ast }^{[t-1]}(\mathrm{\Lambda })$	% Forward projection of background
% Background volume update (Appendix 6.2)
for all voxels, j
$${\mu }_{\ast ,j}^{[t]}={\mu }_{\ast ,j}^{[t-1]}+\frac{{\mathrm{\sum }}_i^M{w}_i{a}_{\ast ,ij}\left(log\frac{g_i}{y_i}-(l_{\ast }+l)\right)-R^{\prime }}{{\mathrm{\sum }}_i^M{w}_i{L}_{\ast ,i}{a}_{\ast ,ij}+R^{″}}$$
end
% Spectral coefficient update (Appendix 6.1)
for all components q ∈ [1 N]
for all coefficients l ∈ [1 K]
$${\kappa }_l^{\{q\}[t]}={\kappa }_l^{\{q\}[t-1]}+\frac{{\mathrm{\sum }}_i^M{w}_i{\left(p_i^{\{q\}}\right)}^l\left(l_{\ast ,i}-{\mathrm{\sum }}_{\{n=1\}}^N{\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n\}[t-1]}{\left(p_i^{\{n\}}\right)}^k-log(\frac{g_i}{y_i})\right)}{{\mathrm{\sum }}_i^M{w}_i{\left(p_i^{\{q\}}\right)}^{2l}}$$
end
end
end

2.6. Experimental methods

To investigate the performance of the proposed approach, we conducted a number of studies using both a simulated CBCT system and real test bench system. In this initial investigation of the polyenergetic approach, we concentrate on the single metal component scenario. Various reconstruction methods were used for comparison. Details of these experiments follow.

(a) Reconstruction approaches used in the comparison studies

This paper has introduced two new approaches for evaluation. First, a polyenergetic known component reconstruction method that jointly estimates the STF based on the objective in (8) and the algorithm in Table 1. This method uses a staged pre-estimation of component registration coefficients and we will refer to this approach as Poly-KCR. A second approach based on pre-calibration of the STF using (9) and in-air component scans is referred to as PreCal-KCR.

For comparison, we considered the original monoenergetic formulation of KCR (Mono KCR) from (Stayman et al 2012a). This KCR formulation presumes complete knowledge of both the morphology of the component as well as its composition and spectral characterization of the imaging system – meaning known components have a single energy-independent attenuation value (μ₀) and a monoenergetic forward model is appropriate. For physical data experiments where Mono-KCR was applied and the spectral characterization of the system is presumed to be known, we selected μ₀ = −κ₁ from the Poly-KCR STF coefficient estimates. For the δ parameter in equation (14) which permits accommodation of additional system blur (e.g. due to focal spot and/or detector blur) we empirically chose a value of 0.85 pixels full-width, half-maximum for the Gaussian blur for all of the physical data experiments.

We also applied a traditional filtered-backprojection (FBP) approach and a standard model-based reconstruction approach. Specifically, we adopt FBP with a Hamming filter with α = 0.5 and a cutoff frequency of 0.8. Additionally, we implemented a metal artifact reduction approach for use with FBP (FBP-MAR). We followed the approach described in (Hsieh 2009) where projection values behind metal objects are replaced by a synthesized projection based on the neighboring projection samples that do not contain metal implants. Metal containing projections were segmented using simple thresholding. New projection values were synthesized using the MATLAB (MathWorks, Natick, MA) command roifill which performs smooth 2D interpolation by solving Laplace’s equation using pixel values at the boundary of the inpainted region. Subsequent reconstruction was performed with the same FBP method as discussed above. A standard (linearized) monoenergetic penalized-weighted least squares (PWLS) (Sauer and Bouman 1993) was also applied.

For all model-based approaches, including PWLS and KCR methods, we chose a Huber penalty (Huber 1981) with a linear-quadratic transition at 10⁻³ mm⁻¹ that penalizes first-order neighborhood voxel differences in the volume. A location-dependent weighting (Xu et al 2015) of the penalty function was applied to encourage more uniform resolution, and the regularization parameter β =5e − 2 was chosen to qualitatively achieve a comparable resolution to FBP. The initial guess for the background anatomy for KCR was the FBP volume truncated at an upper value of 0.03 mm⁻¹ (in a coarse attempt to remove the pedicle screw from the anatomy). Both PWLS and KCR used 50 SQS iterations with 10 ordered-subsets. Additional acceleration was achieved by applying momentum-based image updates, first developed in (Nesterov 1983) and applied to CT reconstruction in (Kim et al 2015).

(b) Simulation experiments

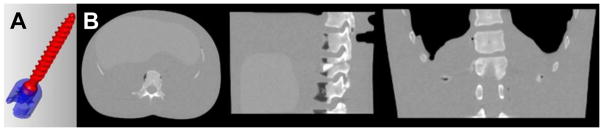
A number of simulation studies were conducted to investigate the performance and convergence properties of the Poly-KCR approach under idealized conditions (e.g., a simplified forward model with known STF). For these studies, we employed the component and anatomical models illustrated in Figure 1. Specifically, we used a CAD model of pedicle screw used in vertebral fusion interventions and combined this model with a digital anthropomorphic phantom based on a high-quality conventional CT scan of a custom phantom. The physical phantom was composed of soft tissue equivalent plastics, a human skeleton, and empty/air recesses to emulate the lung region. The digital version of this phantom was modified to include simulated fractures in vertebra. While the pedicle screw model has two elements a pivoting head and a threaded screw base we presumed a fixed monolithic component for these studies.

Figure 1.

Illustration of A) the CAD model of a pedicle screw used in simulation experiments and B) a digital thorax and abdominal phantom used for the anatomical background.

For simulation experiments, a pedicle screw was transformed (rotated and translated) and voxelized into binary volume with the same voxel size as the anthropomorphic background (1 mm). The screws were placed into vertebra region to simulate a spine fixation intervention (See Figure 4A). Simulated data were generated by combining a monoenergetic forward model for the anatomical background and the polyenergetic forward model with the STF as in equation (5). No additive scatter was modeled in this simulation data. The pedicle screw used a STF emulating a titanium material composition with spectral coefficients of κ = [−0.3, 0.02198, −0.000971, 2.144e-05, −1.797e-07]. The STF corresponding to these coefficients is plotted in Figure 4C.

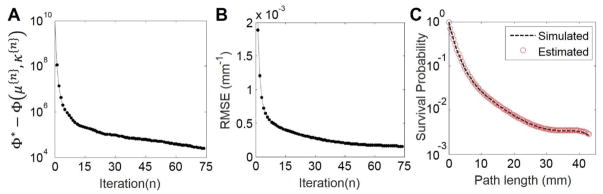
Figure 4.

Illustration of Poly-KCR convergence properties and STF estimate quality. A) Objective function value differences from the solution Φ* as a function of iteration. B) RMSE as a function of iteration. C) The STF associated with the pedicle screw in the simulation. Note the close agreement between the true simulated and estimated STFs.

The system geometry was chosen to emulate a flat-panel detector C-arm system with a source-to-detector distance of 1200 mm and source-to-axis distance of 700 mm. Projections used 1920 × 160, 0.388 × 0.388 mm square pixels and were simulated over 360° using 360 angles. Poisson noise was added and incident exposure levels were set at a uniform level of g =10⁶ photons per detector element.

Using this data we compare reconstructed volumes from poly-KCR and standard FBP reconstruction. To investigate the limits of imaging performance, we presumed that the position and pose of the known components was known exactly and used the true registration parameters for each component. We investigated the convergence properties of poly-KCR in terms of objective function value, Φ in equation (5), as well as root mean square error (RMSE) between the anatomical background reconstruction (no components) and the known truth. STF estimate was also compared with the true value. For this study, we presumed that the true monoenergetic attenuation value (−κ₁) was known and initialized Poly-KCR with κ = [−0.3, 0.0, 0.0, 0.0, 0.0] (e.g. a monoenergetic STF with μ = 0.3 mm⁻¹).

Recognizing that the monoenergetic attenuation will not be known exactly, we conducted a robustness study where initial conditions were varied – sweeping κ₁ (from −0.2 to −0.4) with other entries of κ; equal to zero (i.e., a monoenergetic initialization from μ = 0.2 mm⁻¹ to μ = 0.4 mm⁻¹). Errors in the reconstructed volumes and STF estimates were investigated over this range.

(c) CBCT Test-bench experiments

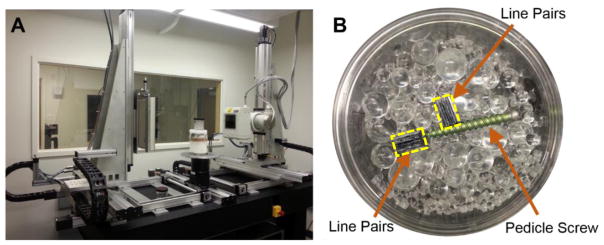
Physical data experiments were also conducted on a CBCT test-bench to evaluate the poly-KCR approach in a realistic setting with unknown beam spectrum and unknown material compositions (e.g. unknown STF). The CBCT test-bench is illustrated in Figure 2A and consisted of an X-ray source (DU694 insert in a DA10 housing; Dunlee, Aurora, IL), a flat-panel detector (PaxScan 4030CB flat-panel detector with 2048 × 1536 pixels at 0.388 mm pixel pitch after 2×2 binning; Varian Medical System, Palo Alto, CA), and a motion control system (Parker Hannifin, OH). Two different physical experiments were conducted: 1) investigations on a simple image quality phantom with a pedicle screw placed within the interior, and 2) a study using a cadaveric torso sample with a pedicle screw placed within a thoracic vertebra. Both experiments used the same shape model of titanium pedicle screw. To reduce partial volume effects, a CAD model for the pedicle screw was voxelized into a compact volume with a small voxel size of 0.05 mm and served as an input for all mixed-fidelity model KCR processing. Projections of the CAD model were performed on a projection grid with the same sampling as the measured data.

Figure 2.

Illustration of A) the CBCT test-bench and B) the image quality phantom with water-and-spheres background, titanium pedicle screw, and two medium-contrast, 9 lp/cm, line pair blocks outlined in yellow.

The simple image quality phantom (Figure 2B) was approximately 85 mm in diameter and composed of water and a mixture of acrylic spheres ranging from 3.2 to 9.5 mm in diameter. Two medium-contrast line pair blocks (9 lp/cm constructed from alternating polycarbonate and acetal sheets) were placed adjacent to the pedicle screw to investigate image quality in the vicinity of the screw. (e.g., detection of a fracture near the implant).

For the phantom studies, a 1184 mm source-to-detector distance and 595 mm source-to-axis distance were used. Projection data was acquired at 1° intervals over 360° and the acquisition technique used 90 kVp and 63 mAs total. Reconstructions were performed on a 1000×1000×200 volume with 0.1 mm (cubic) voxels and included FBP, FBP-MAR, PWLS, Mono-KCR, PreCal-KCR, and Poly-KCR approaches. All KCR approaches used the previously described staged registration. No scatter correction was applied.

A second physical test-bench experiment was also performed with a cadaver torso. This study emulated a clinical scenario in which a screw has been inserted into the spine by a surgeon for the purposes of spine fusion. For our study, we intentionally misplaced the pedicle at the wrong angle and so that there is a lateral breach through the cortical bone of the vertebra. The test-bench configuration was different than the image quality phantom studies, in part, to accommodate the larger sample and used a PaxScan 4343CB flat-panel detector with 1536 × 1536 pixels at 0.278 mm pixel pitch after 2 × 2 binning. The system geometry used a 1500 mm source-to-detector distance and a 1200 mm source-to-axis distance. The volumes were reconstructed using 1160 × 1160 × 120, cubic 0.25 mm voxels. The scan was acquired with 360 projections over 360° and a technique of 100 kVp and 450 mAs total. This protocol represents a clinically relevant acquisition protocol. The exposure range falls within those specified in (Douglas-Akinwande et al 2006) of 250–500 mAs for implant imaging in the thoracic and lumbar spine (though we note that the relatively long 1200 mm source-to-axis distance translates to a lower equivalent dose than one would find for an equivalent exposure in a modern CT scanner). The selected tube potential falls in the middle of the diagnostic range for many intraoperative cone-beam CT systems including mobile C-arms. From bare-beam measurements of the variance and presuming a Poisson noise model, we estimate that the above protocol yields 3 × 10⁴ photons per detector element. The minimum attenuation coefficient for the titanium pedicle screw in the cadaver for the 100 kVp technique is at 100 keV, which is 0.1226 mm⁻¹. For the 45 mm screw, this places an upper bound on the survival probability of photons through the long axis of the implant at 0.4%. Presuming an additional 20 cm of water in the x-ray beam (cadaver soft tissues) with an attenuation of 0.01707 mm⁻¹ (at 100 keV) yields a survival probability of 3.29%. Thus, combining probabilities, one would expect a maximum of about 4 primary (non-scattered) photons to travel the entire path through the long axis of the implant to the detector – representing significant photon starvation.

Reconstructions using FBP, FBP-MAR, PWLS, and Poly-KCR were conducted using the same methodology as discussed previously. Again, no scatter correction was applied for any of the reconstruction methods.

3. Results

3.1. Simulation results

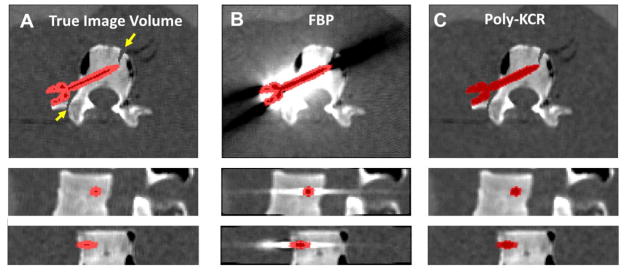
Reconstruction results from the simulation investigation are illustrated in Figure 3. Figure 3A shows the ground truth image volume around the vertebra. Note simulated fractures in the transverse process and anterior portion of the vertebral body. The pedicle screw is shown using a red image overlay. The FBP reconstruction (Figure 3B) exhibits strong metal artifacts associated with unmodeled energy-dependent effects and noise. These artifacts obscure anatomy near the boundary of the implant and background anatomy making it difficult to visualize the simulated fractures. Moreover, the exact position of the screw is unclear (without the addition of the color overlay with true screw positions). In contrast, Poly-KCR is able to leverage shape information provided by the component model of the screw, and integrates that component knowledge into the reconstruction to provide better images. Specifically, we see a substantial reduction in metal artifacts and better noise control through the statistical model. The resulting improvements in image quality are sufficient to visualize features near the pedicle screw.

Figure 3.

Reconstructions of digital phantom data that includes one pedicle screw with a priori unknown material properties. A) The ground truth image volume with the screw shown as a red color overlay. Simulated fractures are indicated by the yellow arrows. B) FBP reconstruction of the digital phantom shows prominent metal artifacts arising from energy-dependent effects and photon starvation. These artifacts obscure anatomy near the screw including the simulated fractures. C) The Poly-KCR approach effectively uses the shape of the known component to greatly improve image quality. Artifacts and noise are largely mitigated permitting good visualization near the boundary of the screw implant and the background anatomy.

We present convergence plots for the Poly-KCR approach in Figure 4. Specifically, Figure 4A shows the value of the objective function at the solution, Φ* (estimated using 150 iterations of our momentum-accelerated SQS approach), minus the current value of the objective at the end of each iteration. Note that each iteration consists of both image updates and STF coefficient updates. We see that the objective function increases monotonically over the first 75 iterations. Because we have a truth image in the simulated data, we may also compute RMSE (computed only for the background anatomy) as a function of iteration. We see that the error reaches a plateau relatively quickly at around 50 iterations suggesting relatively fast convergence.

Estimated versus true STF values are illustrated in Figure 4C. We note that a monoenergetic system without spectral dependencies would form a line on this plot of path length versus the logarithm of the survival probability. In contrast, the simulated STF profile is nonlinear and decreases less for increasing path lengths. This is represents classical beam-hardening, where low-energy x-rays are preferentially attenuated and for longer path lengths x-rays have higher average energy leading to an effective lower degree of attenuation. There is very good agreement between the STF curves used in the simulation and those estimated by the Poly-KCR approach with the simulated and estimated curves being virtually indistinguishable.

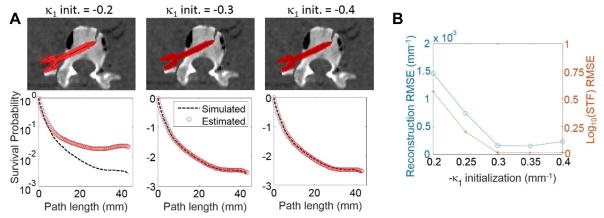
Figure 5 details the Poly-KCR robustness investigation over varying monoenergetic initializations from 0.2 mm⁻¹ to 0.4 mm⁻¹ representing a very broad range of ~10,000 HU. The STF estimates are less accurate for initializations at the lower end of the range (particularly at the longest path lengths) suggesting increased sensitivity to initialization and/or the need for more iterations. However, despite these errors, reconstructions across the entire range are remarkably similar with only very mild under-attenuation near the head of the pedicle screw for the lowest initialization value. This suggests lower sensitivity to getting an accurate STF for longest path lengths – likely due to the inherent statistical down-weighting of these measurements.

Figure 5.

Illustration of Poly-KCR robustness to different monoenergetic initializations from 0.02 to 0.04 mm⁻¹. A) Sample reconstructions and STF estimations for 0.2, 0.3 (truth), and 0.4 mm⁻¹ cases are shown. B) RMSE for both the reconstruction and log10(STF) are plotted as a function of the initialization.

3.2. Physical image quality phantom studies

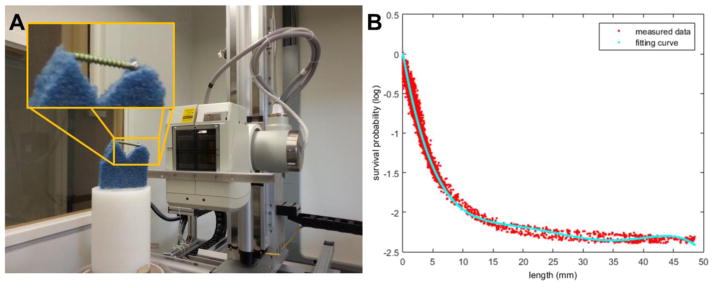
The results of “in-air” precalibration are shown in Figure 6B. Using staged component registration and equation (9), we estimate a STF using the component-only scan. Using a fifth-order polynomial for the STF, K = 5 in equation (5), we obtain the fitted STF curve. The corresponding STF coefficients were estimated to be κ = [−0.432, 0.0347, −1.40e-3, 2.74e-5, −2.07e-7]. We see relatively good agreement between the STF model and a sparse sampling of the entire projection data set. A slight “hysteresis-like” can be seen in the data fit particularly at the longer path lengths through the pedicle screw. We believe that this is the result of small residual registration errors (either due to the registration itself or uncertainties in the system geometry) that contribute to a small positive or negative bias in matching the survival probability to the path length. We believe these errors to be minor and the STF model from Figure 6B is used in subsequent reconstruction of the image quality phantom data using PreCal-KCR.

Figure 6.

Illustration of the STF precalibration process. A) Component-only scanning using a very low attenuation foam platform. B) Comparison of a subsampling of measured data survival probabilities (red) and the estimated STF (cyan) for a range of path lengths through the registered known component (pedicle screw).

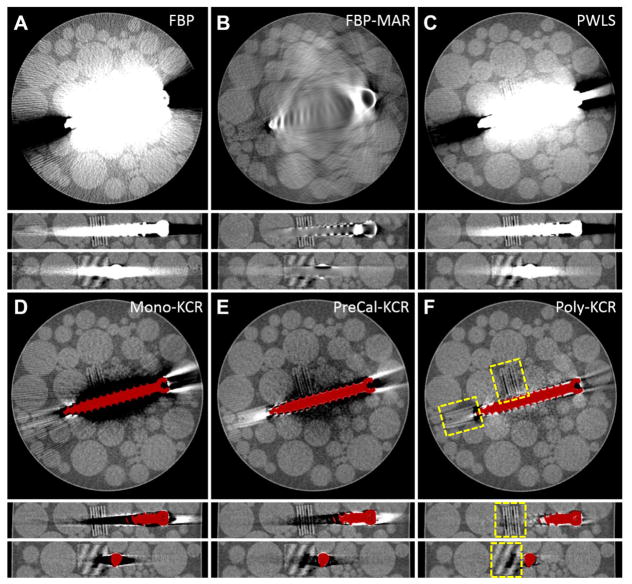
Figure 7 illustrates reconstructions of the image quality phantom using six different reconstruction approaches. The FBP reconstruction in Figure 7A shows similar metal artifacts as were found in the simulation study resulting from noise and beam hardening effects. The artifact reduction of FBP-MAR (Figure 7B) substantially reduces the so-called “blooming” artifact associated with the high attenuation values of the metal screw. Unfortunately, because this approach replaces regional (“with-metal”) data with relatively smooth synthetic projection values, there is significant loss of internal features including both medium contrast line pair blocks. Thus, this type of metal artifact reduction does not help with visualization near the screw boundary. The statistical method, PWLS (Figure 7C), offers some advantages in terms of better noise control at the periphery and slightly less blooming than FBP. However, visualization near the implant remains difficult and both sets of line pair block are obscured.

Figure 7.

Reconstructions of the image quality phantom with a titanium pedicle screw using A) FBP; B) FBP-MAR; C) PWLS; D) Mono-KCR; E) PreCal-KCR; and F) Poly-KCR. A common grayscale is adopted for all images of 0.018 mm⁻¹ to 0.028 mm⁻¹ and line pair blocks are outline in yellow. FBP exhibits significant metal artifacts due to beam hardening and noise. Metal artifact reduction based on replacing measurements through metal with synthetic projection values greatly reduces “blooming” effects but also eliminates features near the screw boundary. PWLS reduces artifacts somewhat through better noise control but substantial artifacts due to energy-dependence remain. Mono-KCR provides some improvements over PWLS but spectrally induced artifacts remain. PreCal-KCR offers more improvements, greatly reducing artifacts; however, there are additional spectral differences (e.g. beam hardening due to the background object) that limit complete mitigation of artifacts. Poly-KCR offers the greatest image quality improvement – providing the best visualization of the boundary between the pedicle screw and the background. Relatively small artifacts persist associated with the longest path lengths through the metal component.

The three KCR methods are shown in Figure 7D–F. Mono-KCR has the statistical advantages of noise reduction, like PWLS, with additional artifact reduction. Notably, the bright blooming has been replaced by a systematic under-attenuation surrounding the screw. This offers a little improvement for visualization around the screw, but significant artifacts remain. PreCal-KCR shows greater image quality improvement and much better visualization near the boundary between the pedicle screw and background, yet some shading artifacts remain (particularly in the center of the phantom). We conjecture that this is due to additional spectral differences between the precalibration component-only scan and the additional energy-dependence induced by the background object. One might perform a more sophisticated pre-calibration scan in a water phantom to provide a better spectral characterization including beam hardening and scatter due to soft tissues. However, such a calibration places an additional burden on the clinical workflow beyond the “simple” air-scan of the components. Not only would a water phantom be required, but accurate characterization would rely on a phantom matched in size and density to the patient.

In contrast, Poly-KCR demonstrates the best improvement of the investigated approaches with good visualization of most of the background object without the need for pre-calibration. The joint estimation of background and spectral coefficients appears to accommodate the additional spectral differences induced by the background (where PreCal-KCR cannot model those differences). We note excellent visualization of the line pair block in the view that is nearly orthogonal to the screw axis. Line pairs are clear and an air bubble defect between adjacent layers of the block is evident. These same features are less visible or completely obscured in other methods. Relatively mild residual artifacts remain – primarily associated with the longest path length through the screw, where one would expect small model biases to be most detrimental. Such artifacts could arise from a number of potential sources including a less accurate STF estimates due to view-dependent scatter, slight misregistration errors, and photon starvation; lack of scatter correction in the reconstruction; and nonlinear partial volume effects. The authors have previously explored additional modifications to KCR methods using a mixed forward model where the component and its projections are modeled using much smaller voxels and sub-pixel integration at the detector to help reduce nonlinear partial volume effects. (Stayman et al 2013) Such model enhancements for Poly-KCR are the subject of future work as are modified statistical weightings that account for the additional uncertainties in long path lengths through metal.

3.3. Cadaver data study

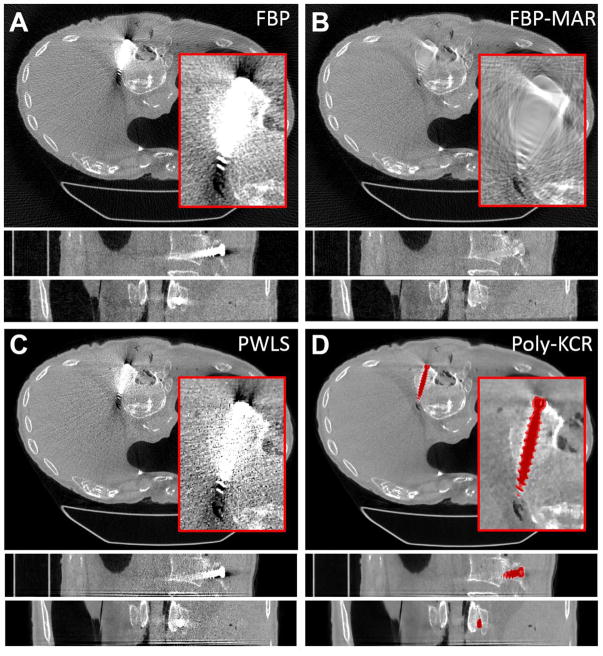
Reconstructions of the cadaveric torso are shown in Figure 8. The results shown in the cadaver experiment parallel the findings in the image quality phantom experiment. FBP exhibited significant metal artifacts associated with the pedicle screw. Noise and streaking in the image obscure the anatomy immediately surrounding the screw making it hard to assess screw placement. While FBP-MAR can mitigate the “blooming” effect surrounding the screw, interpolation associated with the metal artifact reduction also eliminates many anatomical features in the vicinity of the implant. PWLS performs somewhat better than FBP, but significant blooming and streak artifacts remain. In contrast, the Poly-KCR approach effectively removes blooming artifacts and nearly all of the streaks. The improved image quality in the Poly-KCR image is sufficient to visualize the screw placement and identify a lateral breach in the vertebral body. Moreover, there is good visualization of anatomy near the boundary of the bone and screw. These findings suggest a significant improvement in diagnostic performance if Poly-KCR is applied.

Figure 8.

Reconstructions from the cadaver torso investigations. For each method a zoomed region-of-interest is shown in the axial slice. The grayscale is linear for all images from 0.018 mm⁻¹ to 0.028 mm⁻¹. A) FBP reconstruction exhibited substantial metal artifacts around the pedicle screw. Streaks and increased noise prevent good visualization of the pedicle screw placement within the vertebral body. B) FBP-MAR shows a significant reduction in “blooming” artifacts; however, data interpolation has obscured many features in the vicinity of the pedicle screw. C) PWLS reconstruction shows a slight improvement over FBP but significant artifacts remain. D) The Poly-KCR approach yielded substantial reductions in artifacts largely eliminating blooming and streaking effects. Relatively small residual artifacts can be seen at the head of the screw. However, image quality in the vicinity of the implant is good showing bone details, an air bubble near the tip of the implant, and the lateral breach in the body of the vertebra is easily seen suggesting a potentially significant improvement in diagnostic quality.

4. Discussion

In this paper, a calibration-free poly-energetic KCR framework is derived based on our previous work. In the framework, we apply a staged preregistration of component models leveraging a widely used registration strategy that is both computationally efficient and accurate. Previous work coupled registration and reconstruction leading to a more complex implementation – whereas decoupling the two estimation phases permits easier implementation and the opportunity to explore other registration approaches. Using preregistered component models (e.g. CAD models of the shape of the component), we reformed the reconstruction problem to be a joint estimation of the anatomical background and one or more spectral transfer functions, or STFs, which characterizes the energy-dependence in the imaging system (including both x-ray beam quality and the material composition of the known component implants). This estimation conducted based on a single patient scan and greatly reduces the inconvenience associated with other version of KCR that require either 1) explicit knowledge of the energy-dependence through polyenergetic system models and complete knowledge of the material composition of component or 2) precalibration steps where components are characterized with specialized component-only scans – which must be performed for each component and acquisition technique (e.g. kVp) of interest. Moreover, we have found that the joint STF and background estimation approach of Poly-KCR can outperform methods based on precalibration approaches. We believe this is because of the ability of the Poly-KCR approach to accommodate additional physical effects (e.g. beam-hardening due to the background anatomy) that are disregarded in the precalibration approaches.

Among all the methods investigated, which included traditional FBP and model-based iterative reconstruction approaches as well as an approach with explicit metal artifact correction, we found Poly-KCR to have the best imaging performance. Not only are large scale metal artifacts like the bright “blooming” artifacts around the implant and major streaks eliminated with our proposed approach, but we also see greatly improved visualization near the boundary of the anatomy and the known component. This suggests great potential for clinical application due to the better localization of the implant and ability to assess anatomy near the implant boundary.

It is important to note that the advantages of Poly-KCR are shown in a realistic clinical scenario that exhibits significant photon starvation. While it is generally true that fewer photons means lower data fidelity, many metal artifact reduction methods indiscriminately interpolate over all projections containing metal discarding potentially valuable information as seen in the loss of bone details in Figure 8B. Moreover, while model-based reconstruction weighs measurements by statistical fidelity, the ability to extract useful information degrades with an incomplete forward model that does not account for the significant beam hardening due to metal. In contrast, the Poly-KCR approach both models the spectral effects (without having to know material composition and beam quality a priori) and is able to extract useful information from the projections. However, even Poly-KCR is limited in the extreme when data is truly missing. This is evident in the phantom experiment where the line pairs placed at the tip of the screw lose some frequency content along the major axis of the pedicle screw. Specifically, some centrally located line pairs along the axis of the screw cannot be seen (Figure 7F) due to extreme photon starvation/missing data and regularization takes over to smooth out this region. However, Poly-KCR is able to recover image features in all but these most extreme situations.

Two main pieces of information are used by the Poly-KCR approach: 1) the shape of the component model; and 2) knowledge that the component is homogeneous in material composition. The latter requirement can be relaxed by breaking an inhomogeneous component into a number of homogeneous sub-components, though this may complicate the registration task. In other work (Stayman et al 2012b), we have attempted to relax the first knowledge requirement by allowing the shape of components to be inexactly known (e.g. using a deformable model). Ongoing work has sought to extend the KCR methodology where shape models are not known a priori through an initial segmentation of reconstructed data to build a shape model (Zhang et al 2017). Additional generalizations of component knowledge to accommodate surgical tools, implants, and other components for which prior knowledge of structure is not well-established could permit more widespread application of these approaches. These modifications would allow more general application of the methodology to other imaging scenarios like onboard imaging for radiotherapy (e.g., prostate imaging in the presence of unknown hip prostheses). Such general application of the methodology introduces additional performance analysis beyond simple artifact correction including local Hounsfield accuracy near metal implants. Moreover, modifications of the Poly-KCR approach to include scatter correction methods will likely help to further reduced artifacts associated with the investigations will also necessitate a careful investigation of the relationship between component characterization, accurate scatter correction, and Hounsfield accuracy in the reconstruction which have not been conducted in this initial investigation.

Future work will also include investigations exercising multiple component derivation provided in this initial work. Such studies will include more challenging clinical scenarios with large spine complexes with many components as well as larger metal implants (e.g., hip and knee prostheses). While these future investigations are important, the preliminary results presented here suggest the great potential for the Poly-KCR approach and demonstrate that specific knowledge of the X-ray beam spectrum and material composition of components is not required for effective handling of the energy-dependence and photon-starvation to obtain high-quality CT reconstructions.

6. Appendix

6.1. Derivation of STF update

We employ iterative coordinate descent approach to estimate STF coefficients. Given the objective function as shown in equation (8), the derivative of L(κ) with respect to ${\kappa }_j^q$, the j^th element of the coefficient vector associated with the q^th component, can be written:

$$\frac{\partial L(\kappa )}{\partial {\kappa }_j^q}=\sum _{i=1}^M{w}_i\left(l_{\ast ,i}-\sum _{n=1}^N\sum _{k=1}^K{\kappa }_k^{\{n\}}{\left(p_i^{\{n\}}\right)}^k-log\left(\frac{g_i}{y_i}\right)\right){\left(-p_i^{\{q\}}\right)}^j$$

To find ${\kappa }_j^{\{q,t\}}$, the solution at the t^th iteration, we substitute κ^{q} = κ^{{q,t − 1}}, the coefficient vector updated at (t−1)^th iteration. Then ${\kappa }_j^{\{q,\mathrm{t}\}}$ was derived by the following substitution

$${\mathrm{\sum }}_{i=1}^m{w}_i\left(l_{\ast ,i}-{\mathrm{\sum }}_{n=1}^N{\mathrm{\sum }}_{k=1}^K{\kappa }_k^{\{n,t-1\}}{\left(p_i^{\{n\}}\right)}^k-log\left(\frac{g_i}{y_i}\right)+\left({\kappa }_j^{\{q,t-1\}}-{\kappa }_j^{\{q,t\}}\right){\left(p_i^{\{q\}}\right)}^j\right)\left(-{\left(p_i^{\{q\}}\right)}^j\right)=0.$$

Solving for ${\kappa }_j^{\{q,\mathrm{t}\}}$, we obtain the following update function:

$${\kappa }_j^{\{q,t\}}={\kappa }_j^{\{q,t-1\}}+\frac{{\mathrm{\sum }}_i^M{w}_i{\left(p_i^{\{q\}}\right)}^j\left(l_i^{\ast }-{\mathrm{\sum }}_{\{n=1\}}^N{\mathrm{\sum }}_{\{k=1\}}^K{\kappa }_k^{\{n,t-1\}}{\left(p_i^{\{n\}}\right)}^k-log(\frac{g_i}{y_i})\right)}{{\mathrm{\sum }}_i^M{w}_i{\left(p_i^{\{q\}}\right)}^{2j}}.$$

To update all coefficients for all components, this update is applied for all q and j.

6.2. Derivation of volume update

Poly-KCR volume updates use a separable quadratic surrogate approach.(Erdoğan and Fessler 1999b) Following previous work, the linear projection of the anatomical background, Aμ_*(Λ), from equation (8) can be written as

$$\sum _j^N{a}_{\ast ,ij}{\mu }_{\ast ,j}=\sum _j^N{\eta }_{\ast ,ij}(\frac{a_{\ast ,ij}}{{\eta }_{\ast ,ij}}\left({\mu }_{\ast ,j}-{\mu }_{\ast ,j}^{\{t-1\}}\right)+\sum _j^N{a}_{\ast ,ij}{\mu }_{\ast ,j}^{\{t-1\}}),$$

where

$$\begin{gathered} {\eta }_{\ast ,ij}=\frac{a_{\ast ,ij}}{L_{\ast ,i}}, \\ {L}_{\ast ,i}={\mathrm{\sum }}_j^N{a}_{\ast ,ij}. \end{gathered}$$

The L_*,i term represents the total path length in the anatomical background at the i^th detector and a_*,ij denotes the path length intersected between the i^th detector and j^th voxel in anatomical background region (e.g., excluding integration over the known component regions).

Given the pre-calculated Λ and a fixed κ, we may find a separable quadratic surrogate for L in equation (8) using the convexity trick of De Pierro (De Pierro 1993) using the following mathematical steps:

$$\begin{gathered} L({\mu }_{\ast };y)=\sum _i^M\frac{w_i}{2}{\left(\sum _j^N{\eta }_{\ast ,ij}\left(\frac{a_{\ast ,ij}}{{\eta }_{\ast ,ij}}\left({\mu }_{\ast ,j}-{\mu }_{\ast ,j}^{\{t-1\}}\right)+\sum _j^N{a}_{ij}{\mu }_{\ast ,j}^{\{t-1\}}\right)+l-log\frac{g_i}{y_i}\right)}^2 \\ \le \sum _i^M\frac{w_i}{2}\sum _j^N{\eta }_{\ast ,ij}{\left(\left(\frac{a_{\ast ,ij}}{{\eta }_{\ast ,ij}}\left({\mu }_{\ast ,j}-{\mu }_{\ast ,j}^{\{t-1\}}\right)+\sum _j^N{a}_{ij}{\mu }_j^{\ast ,\{t-1\}}\right)+l-log\frac{g_i}{y_i}\right)}^2 \\ =Q({\mu }_{\ast };{\mu }_{\ast ,}^{\{t-1\}},y) \end{gathered}$$

The iterative update for the regularized objective function Φ in Eq. (8) is found by applying Newton’s method to the above surrogate function to obtain:

$$\begin{gathered} {\mu }_{\ast ,j}^{\{t\}}={\mu }_{\ast ,j}^{\{t-1\}}+\frac{Q^{\prime }{\left({\mu }_{\ast };{\mu }_{\ast ,}^{\{t-1\}},y\right)}_{{\mu }_{\ast }^{\{t-1\}}}-R^{\prime }}{Q^{″}{\left({\mu }_{\ast };{\mu }_{\ast ,}^{\{t-1\}},y\right)}_{{\mu }_{\ast }^{\{t-1\}}}+R^{″}} \\ ={\mu }_{\ast ,j}^{\{t-1\}}+\frac{{\mathrm{\sum }}_i^M{w}_i{a}_{\ast ,ij}(log\frac{g_i}{y_i}-(l_{\ast }+l))-R^{\prime }}{{\mathrm{\sum }}_i^M{w}_i{L}_{\ast ,i}{a}_{\ast ,ij}+R^{″}}. \end{gathered}$$

Where R′ and R″ denote the gradient and Hessian of the regularization term, respectively, with respect to the background anatomy.