Abstract
DNA hybridization is an essential molecular reaction in biology with many applications. The nearest-neighbor (NN) model for nucleic acids predicts DNA thermodynamics using energy values for the different base pair motifs. These values have been derived from melting experiments in monovalent and divalent salt and applied to predict melting temperatures of oligos within a few degrees. However, an improved determination of the NN energy values and their salt dependencies in magnesium is still needed for current biotechnological applications seeking high selectivity in the hybridization of synthetic DNAs. We developed a methodology based on single molecule unzipping experiments to derive accurate NN energy values and initiation factors for DNA. A new set of values in magnesium is derived, which reproduces unzipping data and improves melting temperature predictions for all available oligo lengths, in a range of temperature and salt conditions where correlation effects between the magnesium bound ions are weak. The NN salt correction parameters are shown to correlate to the GC content of the NN motifs. Our study shows the power of single-molecule force spectroscopy assays to unravel novel features of nucleic acids such as sequence-dependent salt corrections.
INTRODUCTION
DNA melting is the process by which two complementary DNA strands forming a duplex dissociate into single strands. DNA melting makes it possible the readout of DNA bases and genetic inheritance across generations that are essential steps for genomic maintenance (1,2). It is also widely used in PCR-based amplification techniques where optimization of the heating/cooling protocols leads to increased reaction efficiencies. Methods to predict the free energy difference between the duplex and melted states of arbitrary nucleic acid sequences have been developed and refined over the last decades (3–5) and are relevant to achieve high selectivity in the hybridization of synthetic DNAs (6). Applications are the design of programmable structures based on DNA bonds (7) such as DNA origami (8–11), DNA-guided crystallization of colloids (12–14) and DNA-mediated nanoparticle superlattices (15–17), high resolution melting analysis of DNA for genotyping (18) or epigenetics (19–21), formation of oligomeric DNA structures (22,23), antigen targeting and siRNA design (10) to cite a few. Moreover, these prediction methods are used for the interpretation of single-molecule experiments (24) and for the parameterization of coarse-grained numerical models of nucleic acids (25).
The nearest-neighbor (NN) model for nucleic acids (26,27) predicts the free energy of formation of a duplex from its dissociated strands by summing all energy contributions of adjacent Nearest-Neighbor Base Pair (NNBP) stacks along the sequence. Recently, we introduced a novel methodology to derive the NNBP energies in DNA in the presence of monovalent salt ions using single-molecule unzipping experiments (28). By pulling apart the two strands of a long (several kilobases) DNA hairpin using optical tweezers we could measure the reversible (unzipping = rezipping) force versus distance curve (FDC) between the native hairpin and the fully dissociated single-stranded state. The FDC shows a sawtooth pattern that is sequence specific and might be used to identify a specific DNA sequence in a database (29). Statistical data analysis allowed us to extract the NNBP energies with 0.1 kcal/mol precision over two orders of magnitude of monovalent salt concentration. These values are currently used by the uMelt server to predict melting temperatures. (https://www.dna.utah.edu/umelt/umelt.html) (30).
Force techniques present several advantages compared to bulk methods (e.g. calorimetry, UV absorbance, fluorescence). First, the two-state assumption applied to melting curves (31) is not needed anymore. Second, unzipping measurements on a single long DNA polymer give all NNBP energies, whereas bulk methods require measurements over many sequences. Third, unzipping experiments can be carried out quasi-statically, something difficult to achieve in melting experiments on long polymers (32). Fourth, single molecule methods improve free energy prediction by excluding collective inter-strand effects potentially present in bulk measurements (33). Fifth, heat capacity changes in the melting transition, which are often assumed to vanish (34), are directly measurable with force methods in temperature-controlled optical tweezers (35). Finally, deviations from the NN model might be indicative of sequence dependent next-nearest-neighbor effects. The main disadvantage of unzipping methods is that they require determining the ideal elastic response of ssDNA. In this paper we extend the domain of applicability of the methodology to the much less studied case of divalent salt (MgCl2). Divalent ions such as Mg2+ are known to have a significant effect on DNA and RNA hybridization as compared to monovalent ions such as Na+ (20,36,37). In particular, a given concentration of divalent ions (e.g. [Mg2+] = 1 mM) has an effect on hybridization comparable to a hundredfold concentration of monovalent ions (i.e. [Na+] = 100 mM, SI Appendix A). Consequently magnesium is conveniently used in many applications (e.g. in DNA origami formation) in order to improve and accelerate DNA folding (38). The effect of divalent ions has been traditionally estimated using empirical laws in the form of logarithmic salt corrections to the NNBP energies that are valid in specific salt concentration ranges. Moreover, the competitive effect between monovalent and divalent ions has been shown to lead to strong non-linear (e.g. squared logarithmic in salt concentration) energy corrections that are poorly known. In this paper, we explore the effect of divalent ions in polymeric DNA unzipping experiments to find the dependence of the free energy of the NN motifs on divalent salt over a wide range of concentrations.
Our approach follows the conceptual scheme introduced in (28) where cation activity was found to be NNBP dependent, leading to heterogeneous salt corrections for the energies of the different motifs. In other words, while all NNBP energy corrections are taken to depend logarithmically on salt concentration they do so with different pre-factors corresponding to motif-dependent cation activities. Heterogeneous salt corrections may be taken as evidence of motif-dependent charge screening entropic effects due to the geometry of the phosphates in the single stranded DNA (39). The new scheme incorporates three important features of the NN model that were not considered in (28). First, we account for the circular symmetry of the NN model further reducing the overall number of NNBP energy values from ten to eight (40,41). Second, we specifically include end effects into the NN model via initiation factors known to improve melting temperature prediction for short oligos (42). As we demonstrate below, they also lead to improved FDC prediction from unzipping data. Third, we give a prescription to treat non-equilibrium hysteresis effects along the FDC to reconstruct the reversible (unzipping = rezipping) FDC from the measured data. Overall, the new methodology notably reduces melting temperature prediction errors in divalent salt buffers over oligo sequences of different lengths. By applying the methodology introduced in (28) to the magnesium case we have developed an improved scheme capable of deriving not only NNBP energies but also initiation factors in the magnesium and sodium cases. We have also provided evidence of strong heterogeneous salt corrections of the different NNBP energies in magnesium, a feature that has yet remained inaccessible to bulk studies of melting temperature data. In particular, we have found that the energy salt corrections of the different NN motifs are correlated with their GC content. Such correlation has been quantitated for the different NNBP and found to agree with the melting temperature prediction formulae reported in the literature therefore validating the newly discovered heterogeneous salt corrections.
MATERIALS AND METHODS
Molecular synthesis
The procedure for DNA synthesis is simple and involves a few steps as previously described (28). A 6770 bp fragment from λ phage DNA digested with BamHI is simultaneously annealed with four different oligonucleotides, forming the hairpin tetraloop (5′-ACTA-3′), and two short handles of 29bp each. A micro-dialysis step is performed to exchange buffer and remove potential contaminants, followed by DNA ligation. DNA synthesis and impurity errors, if present, are not different than those expected in bulk studies. Finally our 6.7 kb sequence contains an even amount of all different NN motifs, to exclude misrepresentation of any of them (SI Appendix B). All results shown in the paper correspond to unzipping experiments of the above-mentioned single DNA sequence of 6.8 kb at various salt conditions. In [28] we already demonstrated how different hairpin sequences led to the same NNBP energies. This is expected as NNBP energies and initiation factors are local parameters solely dependent on individual base pairs and the nearest neighbors.
Measurement protocol
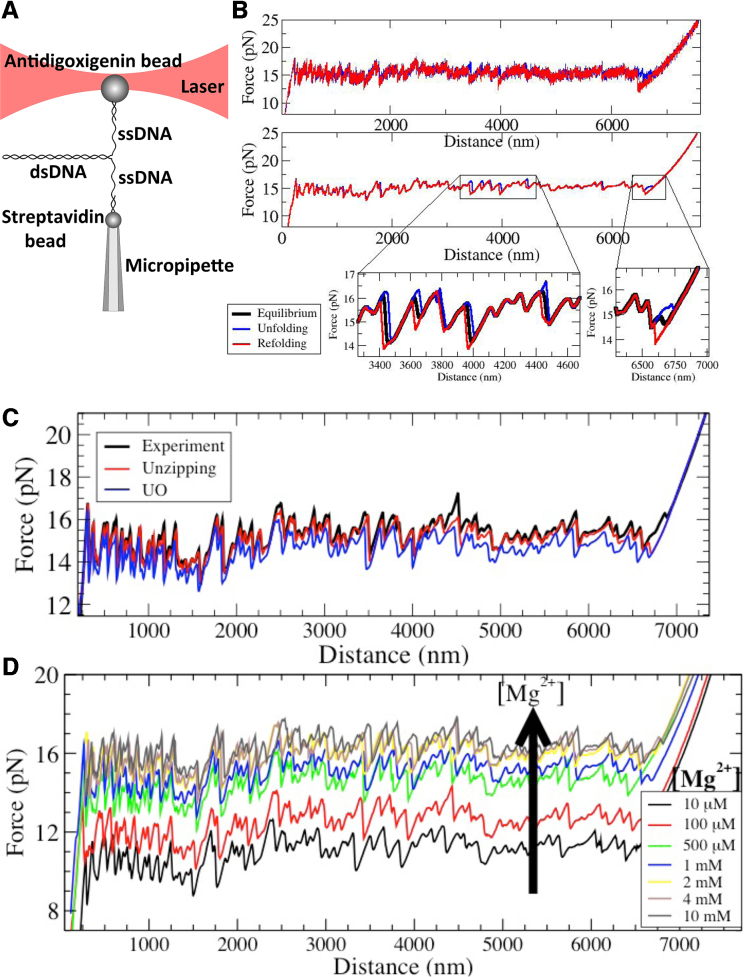
The 6.8 kb DNA hairpin is tethered between an optically trapped bead and a bead held at the tip of a pipette (Figure 1A). By moving the optical trap at a very low speed (20 nm/s) the DNA molecule is progressively unzipped while the FDC is measured (Figure 1B, top, blue curve). Once the molecule is fully unzipped the pulling direction is reversed (Figure 1B, top, red curve) and the refolding FDC measured to complete a full stretching-releasing cycle. In order to extract the thermodynamic FDC, thermal force fluctuations are averaged with a boxcar filter of 1 Hz. Although most parts of the unfolding and refolding FDCs are identical (Figure 1B, middle), there are some regions along the sequence that systematically exhibit hysteresis (Figure 1B, zoomed regions) indicating that the dissociation/formation process of the duplex in such regions cannot equilibrate at that pulling speed. The equilibrium FDC in such irreversible regions is then extracted from the potential of mean force estimated from the unzipping and rezipping curves (see SI Appendix C and the black curve in zoomed regions in Figure 1B ). The final equilibrium unzipping curve is shown in Figure 1C where the experimental FDC for a given DNA molecule (black curve) was compared with the prediction of the thermodynamic unzipping curve using the unified oligonucleotide (hereafter referred to as UO) NNBP energies (blue) and the one obtained using our derived energies as described below (red curve). These results show the high sensitivity of unzipping assays that reveal systematic differences between both energy sets.
Figure 1.
Experimental setup and unzipping FDCs. (A) Experimental setup. (B) Filtering of data and hysteresis effects. Unzipping/rezipping (red/blue) FDCs are obtained filtering the 1 kHz raw data down to 1 Hz. Some regions still show hysteresis at the lowest attainable pulling speed. In the lower panels we show the reconstructed equilibrium FDC as explained in the text. (C) Unzipping FDC (black) compared to the theoretical FDCs obtained using optimized NNBP energies (red) and the UO values (blue). (D) FDCs at different [Mg2+] concentrations as shown in the legend.
RESULTS
Experimental measurement of NNBP energies
We have performed unzipping experiments over a range of divalent salt concentrations spanning three orders of magnitude (Figure 1D). We use 10 mM Tris buffer at pH 7.5 and 0.01% of NaN3 and vary the amount of Mg2+ ions by changing the concentration of MgCl2. Figure 1D shows that the mean unzipping force of the DNA molecule increases with the concentration of Mg2+, demonstrating that divalent cations stabilize the duplex as expected.
The FDC is a fingerprint of the DNA sequence, which depends on the free energy of formation of the different NN motifs along the sequence: the higher the stabilizing free energy of the motifs, the larger the average unzipping force. A theoretical equilibrium FDC can be predicted by combining the NN model with elastic models for ssDNA (43). The NNBP energies can be adjusted by fitting the theoretical FDC to the experimental one using stochastic optimization algorithms (28). In Figure 1B, the comparison of experimental data (black) with an optimized theoretical curve (red) is shown together with a FDC predicted using the UO energy values (blue), as found in (36,44). Fitting the NNBP energies to the experimental curves leads to an improved FDC prediction.
Salt corrections
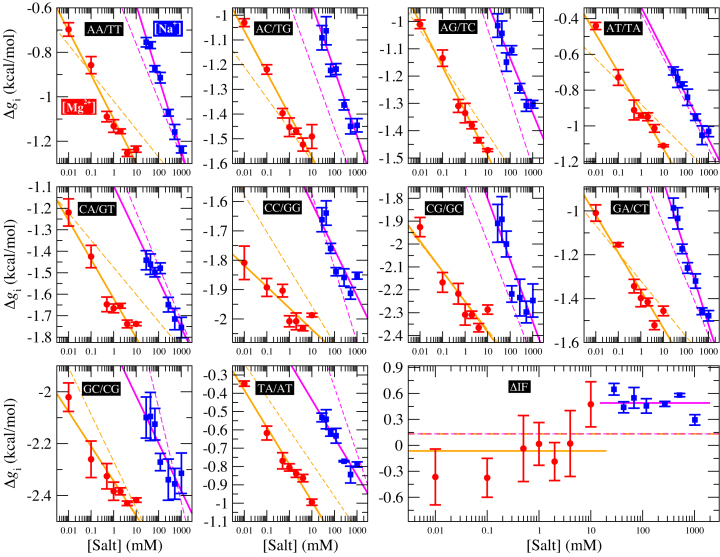
Figure 2 shows the optimal NNBP energies at different salt concentrations. There we show the results for MgCl2 together with previously published results for the monovalent case (NaCl) (28) analyzed with the current method. Strong differences between unzipping and UO values are apparent for the divalent case. In both cases the free energy of each motif exhibits a simple linear logarithmic dependency with salt concentration:
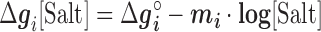 |
(1) |
where 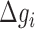 is the energy of motif
is the energy of motif 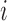 at a given salt concentration
at a given salt concentration 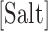 in molar units,
in molar units, 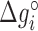 is the energy of motif
is the energy of motif 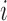 at the reference condition
at the reference condition 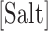 = 1 M,
= 1 M, 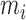 is a specific correction factor and
is a specific correction factor and 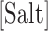 might be either [Na+] or [Mg2+] in our experiments. The linear logarithmic dependency describes well salt corrections in free energy and melting temperature in our regime ([Mg2+]<10mM) where ion fluctuations and correlation effects are weak. Additional corrections might be needed at higher salt concentrations.
might be either [Na+] or [Mg2+] in our experiments. The linear logarithmic dependency describes well salt corrections in free energy and melting temperature in our regime ([Mg2+]<10mM) where ion fluctuations and correlation effects are weak. Additional corrections might be needed at higher salt concentrations.
Figure 2.
Heterogeneous salt corrections to NNBP energies and the IF. Each panel shows the energy of an NN motif at 298K. The lower right panel shows the initiation factor energy difference 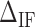 . Blue points show the experimental results of unzipping at different Na+ concentrations, while red points show the same results for different Mg2+ concentrations. Straight lines show the fits to Equation (1) and dotted lines show the UO prediction. Magenta (orange) lines are fits to Na+ (Mg2+) data. The values of the results show the mean and the standard error.
. Blue points show the experimental results of unzipping at different Na+ concentrations, while red points show the same results for different Mg2+ concentrations. Straight lines show the fits to Equation (1) and dotted lines show the UO prediction. Magenta (orange) lines are fits to Na+ (Mg2+) data. The values of the results show the mean and the standard error.
Figure 2 shows the energies of the 10 NNBP, of which only eight are independent. The other two (GC/CG and TA/AT) can be derived from the eight independent motifs using the circular symmetry of the NN model (SI Appendix D). Details about the fitting procedure are described in the SI Appendix E. Our results demonstrate the presence of heterogeneous salt corrections (i.e. different 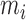 values for the different NN motifs). This confirms previous results in the NaCl case where we found heterogeneous corrections for the four purine-purine stacks (28). Heterogeneity effects are now more apparent for the Mg2+ case but apparently unrelated to any specific kind of stacks. Table 1 summarizes the values of the fits to Equation (1) for each motif. Although the salt dependency of some motifs is similar between our results and the homogeneous UO prediction (e.g. CG/GC motif for Mg2+ or AT/TA motif for Na+), the results from our unzipping experiments are definitely incompatible with a homogeneous salt correction. Although salt correction parameters m appear unrelated to the type of stacks, there is a clear correlation with the amount of GC bps in the NN motif. We have looked at such correlation by plotting the NN dependent salt correction parameter m as a function of the GC content of the NN motif which can be 0 (e.g. AA/TT), 0.5 (e.g. AC/TG), 1 (e.g. CC/GG). As we show in SI Appendix F such correlation is clear for the magnesium case in agreement with (45), but weaker (although still present) in the sodium case (37). This result agrees with most published results on salt corrections to free energies and melting temperature data of duplex sequences (e.g. (45,49)) which exhibit a clear dependence on the fraction of GC content. This fact suggests that salt corrections in magnesium are due to correlations and fluctuations between the divalent cations tightly bound to GC base pairs. Besides, the UO set assumes that the salt correction for the monovalent ions is exactly twice the correction for the divalent ones
values for the different NN motifs). This confirms previous results in the NaCl case where we found heterogeneous corrections for the four purine-purine stacks (28). Heterogeneity effects are now more apparent for the Mg2+ case but apparently unrelated to any specific kind of stacks. Table 1 summarizes the values of the fits to Equation (1) for each motif. Although the salt dependency of some motifs is similar between our results and the homogeneous UO prediction (e.g. CG/GC motif for Mg2+ or AT/TA motif for Na+), the results from our unzipping experiments are definitely incompatible with a homogeneous salt correction. Although salt correction parameters m appear unrelated to the type of stacks, there is a clear correlation with the amount of GC bps in the NN motif. We have looked at such correlation by plotting the NN dependent salt correction parameter m as a function of the GC content of the NN motif which can be 0 (e.g. AA/TT), 0.5 (e.g. AC/TG), 1 (e.g. CC/GG). As we show in SI Appendix F such correlation is clear for the magnesium case in agreement with (45), but weaker (although still present) in the sodium case (37). This result agrees with most published results on salt corrections to free energies and melting temperature data of duplex sequences (e.g. (45,49)) which exhibit a clear dependence on the fraction of GC content. This fact suggests that salt corrections in magnesium are due to correlations and fluctuations between the divalent cations tightly bound to GC base pairs. Besides, the UO set assumes that the salt correction for the monovalent ions is exactly twice the correction for the divalent ones 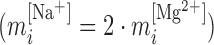 . Our unzipping experiments clearly disprove this relationship demonstrating that the stabilizing effects of divalent and monovalent ions are qualitatively different (45). Remarkably enough, both Na+ and Mg2+ salt corrections can be unified into a unique approximated expression by defining the equivalent monovalent salt concentration,
. Our unzipping experiments clearly disprove this relationship demonstrating that the stabilizing effects of divalent and monovalent ions are qualitatively different (45). Remarkably enough, both Na+ and Mg2+ salt corrections can be unified into a unique approximated expression by defining the equivalent monovalent salt concentration, 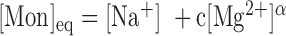 , where
, where 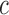 is a constant and
is a constant and 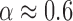 which shows that one divalent cation is equivalent to 1.6 (rather than 2, if α were equal to 0.5) monovalent ions a result possibly indicative of competition between Na+ and Mg2+ ions (SI Appendix G). In fact, throughout all our conditions R = [Mg]1/2/[Mon] is larger than 0.22, a regime where magnesium competes with or dominates sodium (45). Hereafter, we assume that Equation (1) together with the parameters of Table 1 provide satisfactory values for the NNBP energies in a wide range of salt concentrations.
which shows that one divalent cation is equivalent to 1.6 (rather than 2, if α were equal to 0.5) monovalent ions a result possibly indicative of competition between Na+ and Mg2+ ions (SI Appendix G). In fact, throughout all our conditions R = [Mg]1/2/[Mon] is larger than 0.22, a regime where magnesium competes with or dominates sodium (45). Hereafter, we assume that Equation (1) together with the parameters of Table 1 provide satisfactory values for the NNBP energies in a wide range of salt concentrations.
Table 1. NNBP energies, 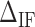 and heterogeneous salt corrections obtained from unzipping experiments in Na+ and Mg2+ compared with UO values. All numbers are at T = 298 K in kcal/mol units.
and heterogeneous salt corrections obtained from unzipping experiments in Na+ and Mg2+ compared with UO values. All numbers are at T = 298 K in kcal/mol units.
| Na+ | Mg2+ | |||||||
|---|---|---|---|---|---|---|---|---|
| Unzipping | UO | Unzipping | UO | |||||
| NNBP |
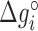
|
mi |
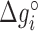
|
mi |
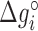
|
mi |
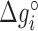
|
mi |
| AA/TT | −1.24 (0.02) | 0.142 (0.007) | −1.27 | 0.114 | −1.69 (0.06) | 0.086 (0.008) | −1.40 | 0.055 |
| AC/TG | −1.49 (0.03) | 0.115 (0.014) | −1.71 | 0.114 | −1.91 (0.07) | 0.073 (0.009) | −1.84 | 0.055 |
| AG/TC | −1.33 (0.03) | 0.087 (0.012) | −1.53 | 0.114 | −1.81 (0.03) | 0.070 (0.004) | −1.66 | 0.055 |
| AT/TA | −1.07 (0.02) | 0.107 (0.010) | −1.12 | 0.114 | −1.55 (0.06) | 0.092 (0.008) | −1.26 | 0.055 |
| CA/GT | −1.76 (0.03) | 0.096 (0.011) | −1.72 | 0.114 | −2.17 (0.07) | 0.078 (0.009) | −1.85 | 0.055 |
| CC/GG | −1.92 (0.04) | 0.069 (0.018) | −2.08 | 0.114 | −2.18 (0.05) | 0.032 (0.007) | −2.21 | 0.055 |
| CG/GC | −2.34 (0.06) | 0.117 (0.026) | −2.50 | 0.114 | −2.65 (0.08) | 0.057 (0.011) | −2.63 | 0.055 |
| GA/CT | −1.52 (0.03) | 0.142 (0.013) | −1.57 | 0.114 | −1.88 (0.07) | 0.075 (0.009) | −1.70 | 0.055 |
| GC/CG | −2.38 (0.03) | 0.080 (0.014) | −2.53 | 0.114 | −2.74 (0.05) | 0.06 (0.006) | −2.66 | 0.055 |
| TA/AT | −0.84 (0.02) | 0.089 (0.005) | −0.84 | 0.114 | −1.38 (0.03) | 0.087 (0.003) | −0.97 | 0.055 |

|
0.49 (0.04) | 0 | −0.113 | 0 | −0.06 (0.10) | 0 | −0.113 | 0 |
Experimental measurement of the initiation factor
The core of the NN model focuses on the Watson–Crick base pairs and their thermodynamic properties, the stacking interaction between adjacent base pairs being a main contribution to the stability of the duplex. However, the base pairs located at the two extremities of the duplex only have one neighbor introducing corrective end effects to the total energy. In order to account for end effects the NN model introduces an extra contribution called Initiation Factor (IF) to the total energy of formation of the duplex. For each extremity the UO dataset assumes that the IF equals a constant term plus an energy penalty if base pairs are adenine or thymine (36). The self-consistent relations (Eqs. (S13) and (S14) in SI Appendix D) derived from circular symmetry are applicable to the 10 NN ‘polymeric’ energies. These two relations then reduce the total number of NNBP energies from 10 to 8. Parameters for end effects can then be treated separately and there are four of them (50,51). Here we assume that, out of the four end parameters, there are only two independent. This is in line with existing thermodynamic studies (52) which show how the assumption EA/TE = ET/AE and EC/GE = EG/CE (E stands for ‘end’) is a reliable and acceptable approximation given the smallness of the initiation factors and the current measurement accuracy. The IFs are not only smaller than the typical NNBP values, their contribution to the total energy becomes less important as the length of the duplex increases. However, for short oligos (10–15 bp) this contribution might significantly affect the prediction of thermodynamic properties of the duplex and the melting temperature. IFs can be inferred from melting experiments by collecting melting temperature data over several sequences and determining the values that best fit data. Instead of repeating experiments over different sequences, unzipping experiments in a long polymeric DNA hairpin allow us to probe different free ends from the high number of intermediates that are sequentially visited as the molecule unzips: an intermediate state corresponding to a partially unzipped molecule exposing either a CG or an AT bp at the opening fork extremity. Therefore in unzipping experiments we can only measure the relative IF differences between intermediates exposing different ends. Here we follow the UO model and consider the simplest case of two values (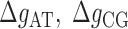 ) for the IF contribution depending on whether the end is AT or CG.
) for the IF contribution depending on whether the end is AT or CG.
We define 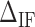 as the difference between IF contributions of exposing an AT or CG at the hairpin end:
as the difference between IF contributions of exposing an AT or CG at the hairpin end:
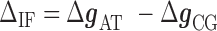 |
(2) |
where 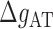 ,
, 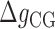 are the IF contributions when the bps at the extremity are AT and CG respectively. The contribution of the IF to the energy difference between consecutive intermediates should be most important around interphases separating abundant regions of CG and AT bps along the sequence. As shown in Figure 3A, an AT-rich region preceding a GC-rich region should be characterized by a minimum along the FDC located at the interphase between both regions (Figure 3A, upper right boxes) whereas in the reverse situation (a GC-rich preceding an AT-rich region) a maximum is expected (Figure 3A, lower right boxes). As such interphases between AT-rich and GC-rich regions coincide with maxima and minima along the FDC the contribution of
are the IF contributions when the bps at the extremity are AT and CG respectively. The contribution of the IF to the energy difference between consecutive intermediates should be most important around interphases separating abundant regions of CG and AT bps along the sequence. As shown in Figure 3A, an AT-rich region preceding a GC-rich region should be characterized by a minimum along the FDC located at the interphase between both regions (Figure 3A, upper right boxes) whereas in the reverse situation (a GC-rich preceding an AT-rich region) a maximum is expected (Figure 3A, lower right boxes). As such interphases between AT-rich and GC-rich regions coincide with maxima and minima along the FDC the contribution of 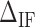 is most evident at these extreme points. The effect is illustrated in Figure 3B. The more negative (red) or positive (blue) the value of
is most evident at these extreme points. The effect is illustrated in Figure 3B. The more negative (red) or positive (blue) the value of 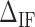 , the more peaked the extreme (minimum or maximum, respectively) is. Therefore fitting the FDC over the multiple cusps and valleys along the FDC leads to an accurate determination of
, the more peaked the extreme (minimum or maximum, respectively) is. Therefore fitting the FDC over the multiple cusps and valleys along the FDC leads to an accurate determination of 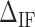 . We adjusted the value of
. We adjusted the value of 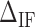 for all the experimental FDCs finding a net corrective improving effect. This is performed by keeping the energies of all NN motifs fixed and plotting the mean squared error between the experimental and the theoretical FDCs,
for all the experimental FDCs finding a net corrective improving effect. This is performed by keeping the energies of all NN motifs fixed and plotting the mean squared error between the experimental and the theoretical FDCs, 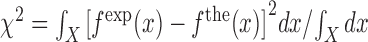 as a function of
as a function of 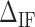 (Figure 3C). This curve exhibits a minimum for all molecules and salt conditions showing that there is an optimal value for
(Figure 3C). This curve exhibits a minimum for all molecules and salt conditions showing that there is an optimal value for 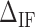 .
.
Figure 3.
Initiation factor. (A) Initiation factor contributions are mostly observed at interphases separating AT from GC (GC from AT) rich regions corresponding to valleys (peaks) along the FDC. 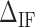 corresponds to the free energy difference of exposing an GC rather than an AT to the solvent at the unzipping fork. (B) Effect of
corresponds to the free energy difference of exposing an GC rather than an AT to the solvent at the unzipping fork. (B) Effect of 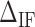 on the FDC. A higher (lower)
on the FDC. A higher (lower) 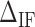 makes the force rips sharper (smoother). (C)
makes the force rips sharper (smoother). (C) 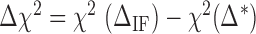 versus
versus 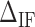 for three molecules at different Mg2+ concentrations,
for three molecules at different Mg2+ concentrations, 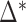 being the optimal fitting value. (D)
being the optimal fitting value. (D) 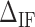 at different Mg2+ and Na+ salt concentrations. All values at 298 K.
at different Mg2+ and Na+ salt concentrations. All values at 298 K.
Figure 3D shows the average values of 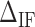 at different salt concentrations of MgCl2 and NaCl. There is no clear evidence of salt dependency for
at different salt concentrations of MgCl2 and NaCl. There is no clear evidence of salt dependency for 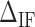 neither in Na+ nor Mg2+ and a constant value has been taken for each case. Last row of Table 1 summarizes the results.
neither in Na+ nor Mg2+ and a constant value has been taken for each case. Last row of Table 1 summarizes the results.
Derivation of enthalpies and entropies from melting data in Mg2+
From the unzipping experiments at 25°C we get the NNBP energies and the initiation factor difference  at various salt concentrations. In order to derive the IF contributions
at various salt concentrations. In order to derive the IF contributions 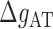 ,
, 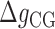 (Equation 2) together with enthalpies and entropies of all motifs we need to use additional data from other sources. Here we use the exhaustive data on the melting temperature of DNA oligos published in (45), corresponding to different DNA sequences and lengths in a wide range of Mg2+ concentrations. We have fit the enthalpies and entropies of the NN motifs in order to optimize the melting temperature predictions with the NN model (SI Appendix H). The fit minimizes the mean square error of a data set of melting temperatures according to:
(Equation 2) together with enthalpies and entropies of all motifs we need to use additional data from other sources. Here we use the exhaustive data on the melting temperature of DNA oligos published in (45), corresponding to different DNA sequences and lengths in a wide range of Mg2+ concentrations. We have fit the enthalpies and entropies of the NN motifs in order to optimize the melting temperature predictions with the NN model (SI Appendix H). The fit minimizes the mean square error of a data set of melting temperatures according to:
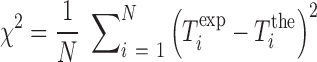 |
(3) |
where 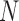 is the total number of oligos and
is the total number of oligos and 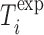 ,
, 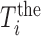 are the experimentally measured and theoretically predicted melting temperature for the
are the experimentally measured and theoretically predicted melting temperature for the 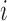 th oligo. The theoretically predicted value of the melting temperature Tm of a non-palindromic DNA duplex is obtained in the two-state model from the total enthalpy (
th oligo. The theoretically predicted value of the melting temperature Tm of a non-palindromic DNA duplex is obtained in the two-state model from the total enthalpy (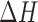 ) and entropy (
) and entropy (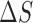 ) of the duplex and the total oligo concentration (
) of the duplex and the total oligo concentration (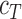 ) during the melting experiment, by using the equation:
) during the melting experiment, by using the equation: 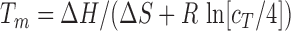 , where
, where 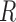 is the gas constant. The total enthalpy and entropy is just the sum of enthalpies and entropies of the adjacent NN motifs plus the corresponding IF contributions, according to the NN model (36). Unzipping experiments give the salt dependencies of the free energies of the NN motifs. However, we have no direct measurement of the salt dependency of enthalpies and entropies. Here we assume that the Mg2+ salt dependency of the enthalpies and entropies of the NN motifs are described by the same equations that are used in the case of Na+. Therefore the enthalpies of the NNBP take a constant value for all [Mg2+] whereas the NN entropies depend logarithmically linear on [Mg2+], as in Equation (1). Thus, the whole thermodynamic picture of the NN model in Mg2+ is summarized by the following set of relation :
is the gas constant. The total enthalpy and entropy is just the sum of enthalpies and entropies of the adjacent NN motifs plus the corresponding IF contributions, according to the NN model (36). Unzipping experiments give the salt dependencies of the free energies of the NN motifs. However, we have no direct measurement of the salt dependency of enthalpies and entropies. Here we assume that the Mg2+ salt dependency of the enthalpies and entropies of the NN motifs are described by the same equations that are used in the case of Na+. Therefore the enthalpies of the NNBP take a constant value for all [Mg2+] whereas the NN entropies depend logarithmically linear on [Mg2+], as in Equation (1). Thus, the whole thermodynamic picture of the NN model in Mg2+ is summarized by the following set of relation :
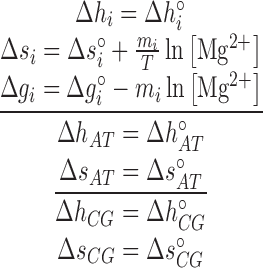 |
(4) |
where 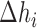 ,
, 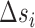 and
and 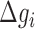 are the enthalpies, entropies and free energies of the eight independent NN motifs (
are the enthalpies, entropies and free energies of the eight independent NN motifs ( = AA/TT, AC/TG, …);
= AA/TT, AC/TG, …); 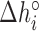 ,
, 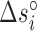 and
and 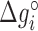 are their values at standard conditions ([Mg2+] = 1 M, T = 25°C), and
are their values at standard conditions ([Mg2+] = 1 M, T = 25°C), and 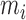 are the Mg2+ salt corrections pre-factors.
are the Mg2+ salt corrections pre-factors. 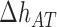 (
(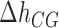 ), and
), and 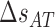 (
(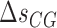 ) are the enthalpy and the entropy of the AT (CG) initiation factor; they are taken equal to their values
) are the enthalpy and the entropy of the AT (CG) initiation factor; they are taken equal to their values 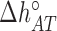 (
(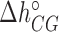 ), and
), and 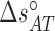 (
(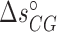 ) at standard conditions. Equation (4) provides the simplest set of relations that agrees with our unzipping data (Figures 2 and 3) an conforms to general assumptions in the field (42). Some of the parameters in Equation (4) are directly given by the unzipping experiments (e.g.
) at standard conditions. Equation (4) provides the simplest set of relations that agrees with our unzipping data (Figures 2 and 3) an conforms to general assumptions in the field (42). Some of the parameters in Equation (4) are directly given by the unzipping experiments (e.g. 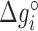 ) while others are subject to constraints (e.g.
) while others are subject to constraints (e.g. 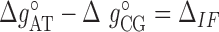 ). We have also explored other schemes that introduce more parameters to account for salt dependent enthalpies or initiation factors. However, these schemes tend to overfit data so we keep the simplest model described by Equation (4). Melting temperature fits contain 11 fitting parameters: ten enthalpies (eight NNBP and the two IF enthalpies,
). We have also explored other schemes that introduce more parameters to account for salt dependent enthalpies or initiation factors. However, these schemes tend to overfit data so we keep the simplest model described by Equation (4). Melting temperature fits contain 11 fitting parameters: ten enthalpies (eight NNBP and the two IF enthalpies, 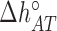 and
and 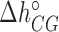 ) and one IF energy (
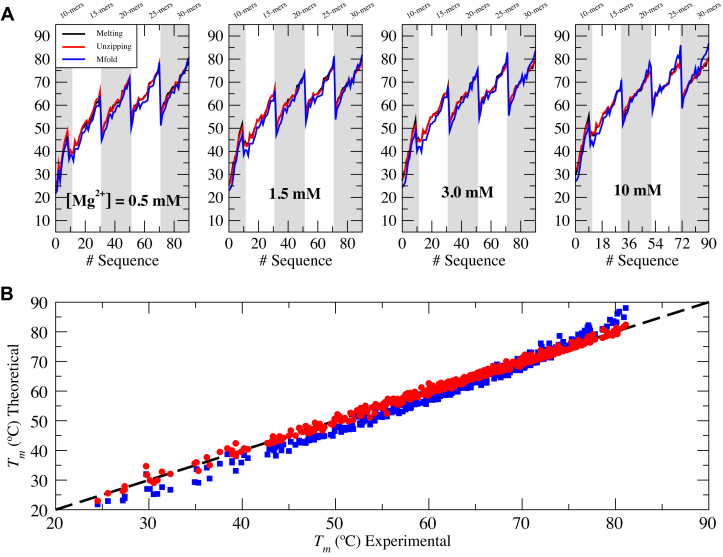
) and one IF energy (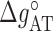 ). Melting data include 92 different oligos of length 10–30 bp at four different salt concentrations ([Mg2+] = 0.5, 1.5, 3, 10 mM) spanning two orders of magnitude, corresponding to measurements reported in (45) falling in the salt concentration range explored in our experiments. Table 2 shows the values of the parameters obtained after fitting the data.
). Melting data include 92 different oligos of length 10–30 bp at four different salt concentrations ([Mg2+] = 0.5, 1.5, 3, 10 mM) spanning two orders of magnitude, corresponding to measurements reported in (45) falling in the salt concentration range explored in our experiments. Table 2 shows the values of the parameters obtained after fitting the data.
Table 2. NNBP energies, enthalpies, entropies and salt correction factors at T = 298 K. Enthalpies and entropies are obtained fitting melting temperatures of oligos in Mg2+ buffer combined with NN parameters obtained from unzipping experiment.
| NNBP |
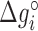 (kcal/mol) (kcal/mol) |
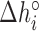 (kcal/mol) (kcal/mol) |
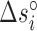 (cal/mol/K) (cal/mol/K) |
mi (kcal/mol) |
|---|---|---|---|---|
| AA/TT | −1.69 | −8.46 | −22.7 | 0.086 |
| AC/TG | −1.91 | −8.67 | −22.7 | 0.074 |
| AG/TC | −1.81 | −7.65 | −19.6 | 0.070 |
| AT/TA | −1.55 | −8.62 | −23.7 | 0.093 |
| CA/GT | −2.17 | −9.99 | −26.2 | 0.079 |
| CC/TT | −2.18 | −9.90 | −25.9 | 0.032 |
| CG/GC | −2.65 | −11.03 | −28.1 | 0.058 |
| GA/CT | −1.88 | −8.59 | −22.5 | 0.075 |
| GC/CG | −2.74 | −11.22 | −28.4 | 0.058 |
| TA/AT | −1.38 | −7.49 | −20.4 | 0.088 |
| IFat | 0.91 | 2.77 | 6.2 | |
| IFcg | 0.97 | 2.65 | 5.6 |
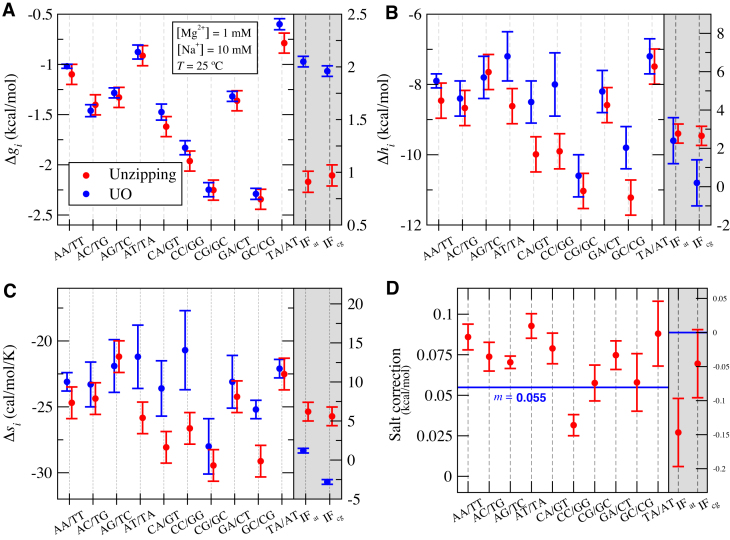
Figure 4 shows a comparison between values obtained from our fit and the UO prediction at one experimental condition ([Mg2+] = 1 mM,[Na+] = 10 mM). Our NNBP energies appear compatible with the UO results (Figure 4A), however we observe significant differences in the enthalpy and entropy of some motifs such as AT/TA, CA/GT and CC/GG (Figure 4B and C). Our fits predict the melting temperature of all oligos with a mean square error (Equation 3) of χ2 = 3.37(°C)2 while UO predicts melting temperatures for the same oligos with χ2 = 9.1(°C)2, demonstrating the power of the approach. Figure 5 shows how both sets of values perform at different salt concentrations with the UO prediction exhibiting larger error for the highest and lowest melting temperatures (Figure 5B). This might be due to the fact that UO uses homogeneous salt corrections and our experiments were performed on a larger range of low salt concentrations (down to 10 μM of Mg2+) whereas bulk melting temperature data measurements are mostly done in the mM range corresponding to typical reaction conditions of PCR and DNA sequencing. We have challenged our newly derived energy values with a bootstrap re-sampling of all available data plus an independent validation dataset of 58 melting temperatures extracted from (45). We have performed 5744 bootstrap re-samplings of the data and our NN model has been fit to each subset of data. We have collected the fitting parameters (enthalpy, entropy and initiation factors) for all re-samplings and we have computed the mean and the standard deviation of all of them. The mean and standard deviation of the temperature errors for all the re-samplings is 3.2 ± 0.2 °C. The results are shown in SI Appendix I and contribute to show the reliability of our energy numbers. Finally, we have performed the same analysis on the Na+ data published in (28) and (37) with the same thermodynamic dependencies as described in Equation (4) (replacing [Mg2+] by [Na+]). The results are shown in SI Appendix J and demonstrate how the introduction of end effects further improves melting temperature prediction for the shortest oligos.
Figure 4.
Thermodynamic parameters of NNBP in [Mg2+]. Panels show free energies, enthalpies, entropies and salt correction factors for the NN motifs and initiation factors. UO values (blue) are compared with those obtained from unzipping experiments (red) at one of the experimental conditions of our experiments (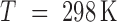 , [Mg2+] = 1 mM, [Na+] = 10 mM). Note that these are not standard conditions. The rightmost grey-shaded panels show the values for the IF (scale on the right vertical axis).
, [Mg2+] = 1 mM, [Na+] = 10 mM). Note that these are not standard conditions. The rightmost grey-shaded panels show the values for the IF (scale on the right vertical axis).
Figure 5.
Melting temperature predictions. Unzipping versus UO. (A) Comparison at different salt conditions. (Experimental data taken from [45] in black, predictions from UO and unzipping experiments in blue and red respectively.) (B) Global comparison of prediction.
DISCUSSION
In this paper we have extended and improved the methodology to derive the NNBP energies in DNA from single molecule experiments. The introduction of the circular symmetry in the NN model allows us to reduce the number of NNBP energies from ten to eight. The circular symmetry was already noticed in (28) where a stability analysis of the minimum reached by stochastic optimization in the ten NNBP energy space highlighted a two-dimensional manifold of optimal solutions. Such 2-fold degeneracy agreed with the two self-consistent NNBP energy relations employed here (SI Appendix D). By avoiding such degeneracy stochastic optimization becomes faster and more reliable in the eight parameters space. Moreover we have demonstrated that end effects in duplex melting can be directly measured by mechanically unzipping long DNA hairpins. The difference between the AT and the CG initiation factor (IF) contributions is most important around the maxima and minima along the FDC. The incorporation of circular symmetry and IFs in the analysis has led to better adjusted salt-correction values and a more accurate prediction of melting temperatures of oligo sequences.
Our results report Mg2+ base-pair-specific salt-correction values that are strongly heterogeneous or sequence-dependent. This fact was already observed in (28) in Na+ but to a lesser extent and it has now been further confirmed in the Mg2+ case. In (46), it has been shown that stacking (rather than base pairing) fully determines the salt dependency of DNA stability parameters in monovalent conditions. This is in agreement with (28), where monovalent salt corrections were found to depend upon the type of stack (purine/purine or purine/pyrimidine). In contrast, in magnesium a clear correlation is observed between salt dependent corrections and NNBP GC-content showing that base pairing rather than base stacking determines salt dependency. This sequence correlation has been quantitated and agrees with melting temperature prediction data as reported in Ref.(28) (SI Appendix F). This agreement validates the newly discovered heterogeneous nature of NNBP salt corrections.
Combining the results of this work with those of (28), we now have all the parameters for a global and consistent NN model in a wide range of temperature and salt condition where fluctuations and correlation effects between the magnesium bound ions are weak. As far as we can see the unzipping energy numbers that we present appear to be fully compatible (given some assumptions on the temperature and salt dependences of the enthalpy and entropies) with the widely employed UO dataset. This result is far from trivial as the UO dataset is obtained from thermal denaturation experiments at high temperatures whereas unzipping data are obtained from force methods at room temperature. Indeed, the task of matching energy numbers measured over so widely separated temperature regimes is not straightforward. Moreover the end state is completely different in both cases (unfolded random coil in the first case, stretched polymer in the other). These results demonstrate the compatibility of the thermodynamic datasets derived in thermal denaturation experiments in bulk and unzipping force assays, thereby providing a new and independent validation of the NN model so central in nucleic acid thermodynamics.
Summing up, despite the complicated nature of the logarithmic salt corrections to NNBP free energies, our heterogeneous NNBP base-pair salt correction provides a mathematically simple fitting scheme to both melting temperature and unzipping data over nearly two orders of magnitude of magnesium concentration. The good performance of the linear-logarithmic correction also suggests that below 10 mM of Mg2+ correlation and fluctuation effects between the bound magnesium ions are weak albeit showing a strong correlation with GC content. The observed sequence dependent effects due to the heterogeneous nature of salt corrections are sufficient to explain all unzipping and melting data in that regime. In this regard, our rationale to reproduce all available experimental data in the <10 mM range is based on assuming heterogeneous salt corrections for the different NNBP, a fact that has been overlooked in previous studies but which is directly supported by our experimental data. For example, both the highly predictive tightly bound ion (TBI) model (53,54) and Poisson–Boltzmann theory are mean-field approaches that treat DNA as a uniformly charged polyelectrolyte where it is difficult to include specific nucleotide effects. In this regard, the experimental demonstration of heterogeneous NNBP dependent salt corrections is a relevant result useful to develop new approaches on nucleic acid electrostatics that go beyond currently existing mean-field theories.
Future studies should consider ion correlation effects by carrying out unzipping experiments at magnesium concentrations higher than 10 mM. The energy numbers determined in that case might allow us to find new salt dependences for the NNBP energies beyond the linear logarithmic correction. This would be relevant to better understand fluctuation and correlation ion effects in nucleic acids and, at the same time, correctly predicting melting temperatures without the need to introduce empirical formulas that assume homogeneous salt corrections and include squared logarithmic corrections that are difficult to interpret (36,45).
Finally, our study does not address competition effects between Na+ and Mg2+ ions and further experiments are needed to determine them. The preliminary results we have reported here allow us to interpolate the salt dependency of the NNBP energies between the Na+ and Mg2+ cases indicating that the stabilizing effects of 1.6 Na+ are roughly equivalent to a single Mg2+. Other studies should also consider the direct measurement of NNBP enthalpies and entropies by doing unzipping experiments at different temperatures (35), heat capacity effects on the melting of DNA (47,48), the contribution of base stacking and hydrogen bonding to the NNBP energies (46,54) and, finally, the evaluation of Next-Nearest Neighbor corrections from the unzipping curves, as the next step to improve the NN model.
Supplementary Material
ACKNOWLEDGEMENTS
Author contributions: J.M.H., M.R-C. and F.R. designed research; J.M.H., C.V.B. and M.R-C. performed research; J.M.H. and M. R-C. analyzed data; and J.M.H., M.R.-C. and F.R wrote the paper.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
FP7 EU program [308850 INFERNOS, 267862 MAGREPS]; Spanish Research Council [FIS2013-47796-P, FIS2016-80458-P]; Catalan Government [Icrea Academia prize 2013]. Funding for open access charge: Spanish Research Council.
Conflict of interest statement. None declared.
REFERENCES
- 1. Calladine C., Drew H., Luisi B., Travers A.. Understanding DNA: The Molecule and How it Works. 1992; 3rd ednAmsterdam: Elsevier Academic Press. [Google Scholar]
- 2. Frank-Kamenetskii M.D. Biophysics of the DNA molecule. Phys. Rep. 1997; 288:13–60. [Google Scholar]
- 3. Breslauer K.J., Frank R., Blocker H., Marky L.A.. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. U.S.A. 1986; 83:3746–3750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Owczarzy R., Vallone P.M., Gallo F.J., Paner T.M., Lane M.J., Benight A.S.. Predicting sequence-dependent melting stability of short duplex DNA oligomers. Biopolymers. 1997; 44:217–239. [DOI] [PubMed] [Google Scholar]
- 5. Markham N.R., Zuker M.. DINAMelt web server for nucleic acid melting prediction. Nucleic Acids Res. 2005; 33:W577–W581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Shoemaker D.D., Schadt E.E., Armour C.D., He Y.D., Garrett-Engele P., McDonagh P.D., Loerch P.M., Leonardson A., Lum P.Y., Cavet G. et al. Experimental annotation of the human genome using microarray technology. Nature. 2001; 409:922–927. [DOI] [PubMed] [Google Scholar]
- 7. Jones M.R., Seeman N.C., Mirkin C.A.. Programmable materials and the nature of the DNA bond. Science. 2015; 347:1260901. [DOI] [PubMed] [Google Scholar]
- 8. Rothemund P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature. 2006; 440:297–302. [DOI] [PubMed] [Google Scholar]
- 9. Douglas S.M., Dietz H., Liedl T.H., Graf F., Shih W.M.. Self-assembly of DNA into nanoscale three-dimensional shapes. Nature. 2009; 459:414–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Dorsett Y., Tuschl T.. siRNAs: applications in functional genomics and potential as therapeutics. Nat. Rev. Drug. Discov. 2004; 3:318–329. [DOI] [PubMed] [Google Scholar]
- 11. Dunne K.E., Dannenberg F., Ouldridge T.E., Kwiatkowska M., Turberfield A.J., Bath J.. Guiding the folding pathway of DNA origami. Nature. 2015; 525:82–86. [DOI] [PubMed] [Google Scholar]
- 12. Nykypanchuk D., Maye M.M., van der Lelie D., Gang O.. DNA-guided crystallization of colloidal nanoparticles. Nature. 2008; 451:549–552. [DOI] [PubMed] [Google Scholar]
- 13. Angioletti-Uberti S., Mognetti B.M., Frenkel D.. Re-entrant melting as a design principle for DNA-coated colloids. Nat. Mater. 2012; 11:518–522. [DOI] [PubMed] [Google Scholar]
- 14. Rogers B.W., Manoharan V.N.. Programming colloidal phase transitions with DNA strand displacement. Science. 2015; 347:639–642. [DOI] [PubMed] [Google Scholar]
- 15. Alivisatos A.P., Johnsson K.P., Peng X., Wilson T.E., Loweth C.J., Bruchez M.P., Schultz P.G.. Organization of ‘nanocrystal molecules’ using DNA. Nature. 1996; 382:609–611. [DOI] [PubMed] [Google Scholar]
- 16. Park S.Y., Lytton-Jean A.K., Lee B., Weigand S., Schatz G.C., Mirkin C.A.. DNA-programmable nanoparticle crystallization. Nature. 2008; 451:553–556. [DOI] [PubMed] [Google Scholar]
- 17. Zhang Y., Pal S., Srinivasan B., Vo T., Kumar S., Gang O. Selective transformations between nanoparticle superlattices via the reprogramming of DNA-mediated interactions. Nat. Mater. 2015; 14:840–847. [DOI] [PubMed] [Google Scholar]
- 18. Wittwer C.T. High-resolution DNA melting analysis: advancements and limitations. Hum. Mutat. 2009; 30:857–859. [DOI] [PubMed] [Google Scholar]
- 19. Wojdacz T.K., Dobrovic A.. Methylation-sensitive high resolution melting (MS-HRM): a new approach for sensitive and high-throughput assessment of methylation. Nucleic Acids Res. 2007; 35:e41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bizarro C.V., Alemany A., Ritort F.. Non-specific binding of Na+ and Mg2+ to RNA determined by force spectroscopy methods. Nucleic Acids Res. 2012; 40:6922–6935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Wojdacz T.K., Dobrovic A., Hansen L.L.. Methylation-sensitive high-resolution melting. Nat. Prot. 2008; 3:1903–1908. [DOI] [PubMed] [Google Scholar]
- 22. Plum G.E., Park Y.W., Singleton S.F., Dervan P.B., Breslauer K.J.. Thermodynamic characterization of the stability and the melting behavior of a DNA triplex: a spectroscopic and calorimetric study. Proc. Natl. Acad. Sci. U.S.A. 1990; 87:9436–9440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Lilley D.M. Structures of helical junctions in nucleic acids. Q. Rev. Biophys. 2000; 33:109–159. [DOI] [PubMed] [Google Scholar]
- 24. Gross P., Laurens N., Oddershede L.B., Bockelmann U., Peterman E.J., Wuite G.J.. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011; 7:731–736. [Google Scholar]
- 25. Šulc P., Romano F., Ouldridge T.E., Rovigatti L., Doye J.P., Louis A.A.. Sequence-dependent thermodynamics of a coarse-grained DNA model. J. Chem. Phys. 2012; 137:135101. [DOI] [PubMed] [Google Scholar]
- 26. Devoe H., Tinoco I.J.. The stability of helical polynucleotides: base contributions. J. Mol. Biol. 1962; 4:500–517. [DOI] [PubMed] [Google Scholar]
- 27. Crothers D.M., Zimm B.H.. Theory of the melting transition of synthetic polynucleotides: evaluation of the stacking free energy. J.Mol. Biol. 1964; 9:1–9. [DOI] [PubMed] [Google Scholar]
- 28. Huguet J.M., Bizarro C.V., Forns N., Smith S.B., Bustamante C., Ritort F.. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. U.S.A. 2010; 107:15431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Barbieri C., Cocco S., Jorg T., Monasson R.. Reconstruction and identification of DNA sequence landscapes from unzipping experiments at equilibrium. Biophys. J. 2014; 106:430–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Dwight Z., Palais R., Wittwer C.T.. uMELT: prediction of high-resolution melting curves and dynamic melting profiles of PCR products in a rich web application. Bioinformatics. 2011; 27:1019–1020. [DOI] [PubMed] [Google Scholar]
- 31. Marky L.A., Breslauer K.J.. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers. 1987; 26:1601–1620. [DOI] [PubMed] [Google Scholar]
- 32. Vologodskii A.V., Amirikyan B.R., Lyubchenko Y.L., Frank-Kamenetskii M.D.. Allowance for heterogeneous stacking in the DNA helix-coil transition theory. J. Biomol. Struct. Dyn. 1984; 2:131–148. [DOI] [PubMed] [Google Scholar]
- 33. Holbrook J.A., Capp M.W., Saecker R.M., Record M.T.J.. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms coupled processes of formation and association of single stranded helices. Biochemistry. 1999; 38:8409–8422. [DOI] [PubMed] [Google Scholar]
- 34. Schroeder S.J., Turner D.H.. Optical Melting Measurements of Nucleic Acid Thermodynamics. Methods Enzymol. 2009; 468:371–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. De Lorenzo S., Ribezzi-Crivellari M., Arias-Gonzalez J.R., Smith S.B., Ritort F.. A Temperature-Jump Optical Trap for Single-Molecule Manipulation. Biophys. J. 2015; 108:2854–2864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. U.S.A. 1998; 95:1460–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Owczarzy R., Moreira B., You Y., Manthey J.A., Huang L., Behlke M.A., Walder J.. Effects of sodium ions on DNA duplexoligomers: improved predictions of melting temperatures. Biochemistry. 2004; 43:3537–3554. [DOI] [PubMed] [Google Scholar]
- 38. Martin T.G., Dietz H.. Magnesium-free self-assembly of multi-layer DNA objects. Nat. Commun. 2012; 3:1103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Nakano S.I., Fujimoto M., Hara H., Sugimoto N.. Nucleic acid duplex stability: influence of base composition on cation effects. Nucleic Acids Res. 1999; 27:2957–2965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Gray D.M., Tinoco I. Jr. A new approach to the study of sequence-dependent properties of polynucleotides. Biopolymers. 1970; 9:223–244. [Google Scholar]
- 41. Licinio P., Guerra J.C.O.. Irreducible representation for nucleotide sequence physical properties and self-consistency of nearest-neighbor dimer sets. Biophys. J. 2007; 92:2000–2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. SantaLucia J. Jr, Hicks D.. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004; 33:415–440. [DOI] [PubMed] [Google Scholar]
- 43. Bosco A., Camunas-Soler J., Ritort F.. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 2014; 42:2064–2074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Peyret N. Prediction of Nucleic Acid Hybridization: Parameters and Algorithms. 2000; Detroit: Wayne State University, Ph.D. Thesis, Section 5.4.2, 128. [Google Scholar]
- 45. Owczarzy R., You Y., Moreira B., Manthey J.A., Huang L., Behlke M.A., Walder J.. Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations. Biochemistry. 2008; 47:5336–5353. [DOI] [PubMed] [Google Scholar]
- 46. Yakovchuk P., Protozanova E., Frank-Kamenetskii M.D.. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006; 34:564–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Rouzina I., Bloomfield V.. Heat capacity effects on the melting of DNA. 1. General aspects. Biophys. J. 1999; 77:3242–3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Rouzina I., Bloomfield V.A.. Heat capacity effects on the melting of DNA. 2. Analysis of nearest-neighbor base pair effects. Biophys. J. 1999; 77:3252–3255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Tan Z.J., Chen S.J.. Nucleic acid helix stability: effects of salt concentration, cation valence and size, and chain length. Biophys. J. 2006; 90:1175–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Gray D.M. Derivation of nearest-neighbor properties from data on nucleic acid oligomers. I. Simple sets of independent sequences and the influence of absent nearest neighbors. Biopolymers. 1997; 42:783–793. [DOI] [PubMed] [Google Scholar]
- 51. Guerra J.C.O., Licinio P.. Terminal contributions for duplex oligonucleotide thermodynamic properties in the context of nearest neighbor models. Biopolymers. 2010; 95:194–201. [DOI] [PubMed] [Google Scholar]
- 52. Sugimoto N., Nakano S.-I., Yoneyama M., Honda K.-I.. Improved thermodynamic parameters and helix initiation factor to predict stability of DNA duplexes. Nucleic Acids Res. 1996; 24:4501–4505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Tan Z.J., Chen S.J.. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J. Chem. Phys. 2005; 122:044903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Kilchherr F., Wachauf C., Pelz B., Rief M., Zacharias M., Dietz H.. Single-molecule dissection of stacking forces in DNA. Science. 2016; 353:aaf5508. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.