Blood pressure and the risk of Chronic Kidney Disease progression using multistate marginal structural models in the CRIC Study

Abstract

In patients with chronic kidney disease (CKD), clinical interest often centers on determining treatments and exposures that are causally related to renal progression. Analyses of longitudinal clinical data in this population are often complicated by clinical competing events, such as end-stage renal disease (ESRD) and death, and time-dependent confounding, where patient factors that are predictive of later exposures and outcomes are affected by past exposures. We developed multistate marginal structural models (MS-MSM) to assess the effect of time-varying systolic blood pressure on disease progression in subjects with CKD. The multistate nature of the model allows us to jointly model disease progression characterized by changes in the estimated glomerular filtration rate (eGFR), the onset of ESRD, and death, and thereby avoid unnatural assumptions of death and ESRD as non-informative censoring events for subsequent changes in eGFR. We model the causal effect of systolic blood pressure on the probability of transitioning into one of six disease states given the current state. We use inverse probability weights with stabilization to account for potential time-varying confounders, including past eGFR, total protein, serum creatinine, and hemoglobin. We apply the model to data from the Chronic Renal Insufficiency Cohort (CRIC) Study, a multisite observational study of patients with CKD.

1. Introduction

In studies of chronic kidney disease (CKD), endpoints of various types are often of interest. Time-to-event endpoints such as time to end-stage renal disease (ESRD) are considered as well as longitudinal outcomes such as change in the estimated glomerular filtration rate (eGFR). Studies with a primary interest in longitudinal outcomes are typically challenged by the occurrence of death or ESRD, which censor follow-up during the observation period. When these clinical events, which preclude subsequent measurement of the longitudinal outcome, are interpreted as censoring events, inferences concerning longitudinal changes may be biased due to informative censoring. More fundamentally, estimands dependent on measurements of the longitudinal outcome subsequent to these events can be difficult to interpret, as described in the truncation by death literature [1, 2]. Alternatively, inferences restricted to the time-to-clinical-event outcomes provide limited information concerning effects of treatments or exposures for patients with more modest declines in kidney function. Recent reviews have emphasized likelihood-based shared random effects approaches for joint modeling of longitudinal processes and time-to-event in CKD studies[3, 4]. These methods are challenged by difficulty in implementation, and are subject to the same limitations as standard regression models in that when estimating joint exposure effects across time, neither adjustment nor non-adjustment of time-dependent confounders, which we next describe, result in an unbiased estimate of the causal joint exposure effect.

In the analysis of ESRD, often the primary outcome of interest in CKD studies, changes in longitudinal outcomes, such as eGFR, prior to the absorbing event, e.g., ESRD, may serve as confounding factors for the effects of exposures. When exposures are time-varying, interim longitudinal outcomes can cause time-dependent confounding, where time-dependent confounders are variables that are affected by prior exposures and predictive of later exposures and outcomes. In CKD, several variables could potentially serve as time-dependent confounders given the complex, and often bi-directional, interplay between blood pressure and kidney function, other clinical factors, and treatment decisions. Further, death is a competing risk for ESRD.

To estimate the effect of time-varying exposures on CKD progression defined by both time-to-event and longitudinal outcomes such as ESRD and changes in eGFR, respectively, with proper adjustment of time-dependent confounding, we propose multistate marginal structural models (MS-MSMs). Marginal Structural Models (MSMs) are a class of causal models[5] that may be used to consistently estimate effects of time-varying exposures in the presence of time-dependent confounding. MS-MSMs are particularly suited to this setting for several reasons. First, hypertension is both a risk factor and effect of CKD. As a result, several factors that are associated with CKD are likely to function as time-dependent confounders for the effect of changes in blood pressure on CKD outcomes. As an example, hypertension may lead to decreased eGFR, which in turn can elevate subsequent blood pressure levels and also the risk of ESRD or death. Unbiased estimation of the causal effect of time-varying blood pressure on CKD progression therefore requires statistical methods that can accommodate time-dependent confounders. Standard methods of longitudinal and survival analysis such as Cox proportional hazards regression with time-dependent covariates and mixed models or semi-parametric regression methods such as generalized estimating equations (GEE) cannot handle time-dependent confounding appropriately [5]. Alternatively, MSMs with inverse probability weighting [6], may be used to consistently estimate causal effects of time-varying exposures on longitudinal and time-to-event outcomes.

Our main objective is to introduce MS-MSMs with estimation by inverse probability weighting to estimate the effect of time-dependent exposures on joint longitudinal and time-to-event outcomes by a Markov multinomial model approach. In formulating MS-MSMs, we define states that are jointly characterized by longitudinal and time-to-event endpoints and model the effect of exposures on transitions among these states. [7] recently used inverse probability weighting to estimate the causal effect of alternative employee benefit programs on transitions among employment states. This analysis considered a time-independent exposure variable and Cox and Aalen models for estimating transition intensities. Our approach is generalized to time-dependent exposures, and we estimate transition intensities using a generalized linear model approach. Our model is structurally similar to the MSM for cause-specific hazards in the analysis of time-to-event data of multiple outcome types developed by [8], but differs substantially in the interpretation since our model accommodates both the absorbing states encountered in the survival literature and the non-absorbing states observed in repeated-measures settings. We can use our model to estimate the probability of patients cycling among multiple states defined by longitudinal outcomes during the progression and regression of a chronic condition while simultaneously estimating the probability of a patient experiencing an absorbing event. As a result, our model is better suited for the analysis of CKD since clinical interest lies in characterizing a patient’s trajectory over time [9] in addition to evaluating time to clinical, terminal events. We apply our methodology to a study of the effect of systolic blood pressure (SBP) on CKD progression within the Chronic Renal Insufficiency Cohort (CRIC) Study, a multisite, prospective cohort study of nearly 4,000 subjects with mild to moderate CKD at study entry.

In Section 2, we define notation and formalize identification assumptions for the causal effects of time-varying exposures on multistate outcomes, where MSMs model the causal effect of time-varying exposures on the probability of transitions among states. We then utilize transition probabilities to determine the marginal probability of being in a potential state at the end of observation under a specified joint exposure. In Section 3 we conduct a simulation study to illustrate the properties of inverse probability weighted estimators for multistate outcomes, comparing weights with and without truncation, and in Section 4 we use our MS-MSMs to determine the effect of SBP on CKD progression among mild to severe CKD as defined the level of eGFR and clinical endpoint states including ESRD and death.

2. Methods

2.1. Notation

We first define our notation and then describe our causal model and identifying assumptions. Our notation follows that introduced by [5] for time-varying exposures and scalar outcomes. First considering the observed data, let Y_i,j+1 denote an outcome taking levels 1,2,…,K, indicating the i^th subject’s state at time j + 1 for j=0,1, 2, …, J. Similarly, let A_i,j denote subject i^’s exposure level at time j. Covariates measured at time j are represented by L_i,j and may include baseline as well as time-varying covariates. Finally, C_i,j indicates whether a subject is censored by the beginning of the j^th observation time with C_i,j = 1 denoting that a subject is censored and C_i,j = 0 representing that a subject is still under observation. Within each time interval we assume that variables are observed in the temporal order (L_i,j,A_i,j,C_i,j+1,Y_i,j+1). Overbars are used to denote variable history, such that ${\overline{Y}}_{i,j+1}=\left(Y_{i,1},Y_{i,2},\dots ,Y_{i,j+1}\right)$. Causal effects of exposures are defined using potential outcomes notation [10], where $Y_{i,j+1}^{\overline{a}}$ is the outcome that would have been observed for subject i at time j+1 had he or she received the joint exposure ā = (a₀,a₁,…,a_j). At the population level, interest often lies in comparing mean potential outcomes under different joint exposures ā, where a nonzero average causal effect is indicated by $E[Y_{i,j}^{\overline{a}}]\ne E[Y_{i,j}^{{\overline{a}}^{\prime }}]$ for joint exposures ā ≠ ā′. Our multistate approach targets comparisons of $P(Y_{i,J+1}^{\overline{a}}=k)$, the marginal probability of a potential outcome state at the end of observation under alternative joint exposures ā ≠ ā′.

2.2. Model

Multistate models facilitate estimation of the marginal probabilities of outcome states by first modeling the probability of transitioning to an outcome state at a given time j + 1 conditional on previous outcome states. We take this same approach using potential outcomes to estimate causal effects on multistate outcomes. First we factor the joint likelihood of the full history of potential outcome states $f\left({\overline{Y}}_{i,J+1}^{\overline{a}}\right)=\left(Y_{i,1}^{\overline{a}},Y_{i,2}^{\overline{a}},\dots ,Y_{i,J+1}^{\overline{a}}\right)$ from time 1 to J + 1 as a product of conditional distributions $f\left({\overline{Y}}_{i,J+1}^{\overline{a}}\right)={\displaystyle \prod _{j=0}^{J}f}\left(Y_{i,J+1}^{\overline{a}}/Y_{i,J}^{\overline{a}}\right)$. Under a first order Markov assumption we further simplify the product of conditional distributions as ${\displaystyle \prod _{j=0}^{J}f}\left(Y_{i,J+1}^{\overline{a}}|{\overline{Y}}_{i,J}^{\overline{a}}\right)={\displaystyle \prod _{j=0}^{J}f}\left(Y_{i,J+1}^{\overline{a}}|Y_{i,J}^{\overline{a}}\right)$, indicating that the probability of a given outcome state at time j+1 depends solely on the most recent potential outcome state rather than all states from time 1 to time j. The first order Markov assumption is chosen for convenience but may be relaxed if data provide evidence in favor of a higher order Markov assumption. The implications of higher order assumptions for modeling state transitions are discussed in Section 5. For the multistate potential outcomes considered, multinomial models may be used to characterize the probability of outcome state k at time j + 1 conditional on the state at time j. Our multistate marginal structural model is

$$\log \left(\frac{P\left(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}^{\overline{a}}=k^{\prime }\right)}{P\left(Y_{i,j+1}^{\overline{a}}=k^{\prime }|Y_{i,j}^{\overline{a}}=k^{\prime }\right)}\right)=h_1\left({\overline{a}}_{i,j};{\beta }^{k^{\prime },k}\right)+h_2\left(j;{\alpha }^{k^{\prime },k}\right)$$ (1)

for known functions h₁(·) and h₂(·) up to the unknown parameters β^k′^,k and α^k′^,k. The probability of transitioning from state k′ to k from time j to j + 1 under joint exposure ā_i,j is modeled by the log odds of $Y_{i,j+1}^{\overline{a}}=k$ versus the reference outcome state $Y_{i,j+1}^{\overline{a}}=k^{\prime }$. The parameter β^k′^,k measures the causal effect of exposure ā on the probability of transition to one potential outcome state given the previous potential outcome state, and function h₂(j;α^k′^,k) defines the probability of transition for the reference exposure group (ā = (0,…,0)), accounting for underlying temporal trends in the relative likelihood of transitioning to state k versus reference state k′. The assumption of additivity of h₁(ā_i,j;β^k′^,k) and h₂ (j;α^k′^,k) implies that the effect, of exposure a_i,j on transition probabilities does not change over time. As an example, one might consider the model $h_1\left({\overline{a}}_{i,j};{\beta }^{k,k^{\prime }}\right)={\beta }^{k^{\prime },k}{a}_{i,j}$ for a binary treatment A_i,j, where β^k′^,k would then denote the log odds ratio of transitioning to state k versus state k′ from state k′ under binary treatment a_i,j = 1 at time j compared to under control a_i,j = 0 at time j. Another model might consider $h_1\left({\overline{a}}_{i,j};{\beta }^{k,k^{\prime }}\right)={\beta }^{k^{\prime },k}{\displaystyle \sum _{t=0}^j{a}_{i,t}}$ in which the log odds ratio of transitioning to state k versus k′ from state k′ depends on the cumulative exposure history, where for binary exposures ${\displaystyle \sum }_{t=0}^j{a}_{i,t}$ is the number of times a subject was exposed through time j. The reference function $h_2\left(j;{\alpha }^{k^{\prime },k}\right)$ may include polynomial terms or splines to flexibly capture temporal changes in the probability of transitions among states.

The predicted outcomes of model (1) define the elements of the K×K transition matrix

$${\lambda }_j^{\overline{a}}=\left[\begin{array}{cccc}{\lambda }_j^{\overline{a},1,1}& {\lambda }_j^{\overline{a},1,2}& \dots & {\lambda }_j^{\overline{a},1,K}\\ {\lambda }_j^{\overline{a},2,1}& {\lambda }_j^{\overline{a},2,2}& \cdots & {\lambda }_j^{\overline{a},2,K}\\ ⋮& \ddots & \ddots & ⋮\\ {\lambda }_j^{\overline{a},K,1}& {\lambda }_j^{\overline{a},K,2}& \dots & {\lambda }_j^{\overline{a},K,K}\end{array}\right],$$ (2)

where ${\lambda }_j^{\overline{a},k^{\prime },k}=P\left(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}^{\overline{a}}=k^{\prime }\right)$ for transitions among possible states under joint exposure ā.

Robins (1998) states that the causal parameter β^k′^,k is identified under the following assumptions[6]:

1. Sequential Ignorability/Exchangeability. $Y_{i,j+1}^{\overline{a}}\perp A_{i,j}|{\overline{Y}}_{i,j}$, ${\overline{A}}_{i,j-1}$, ${\overline{\mathrm{L}}}_{i,j}$

   Given the previous state and exposure and covariate history, potential outcomes under treatment ā at time j + 1 are independent of the observed exposure A_i,j.

2. Consistency. For ${Ā}_{i,j}={\overline{a}}_{i,j}$, $Y_{i,j}=Y_{i,j}^{\overline{a}}$ For a subject who is actually observed to have joint exposure ā_i,j, the observed outcome Y_i,j equals the potential outcome under that exposure history.

3. Positivity. For every ${\overline{L}}_{i,j}$ such that $f_{{\overline{L}}_{i,j}}\left(\overline{l}\right)>0$, $f_{A_{i,j}|{\overline{L}}_{i,j}}(a_{i,j}|\overline{l})>0$ for all possible treatment levels a_i,j. This states that for any observed covariate history, where past outcomes Y_i,j are included in, ${\overline{L}}_{i,j}$, there is a nonzero probability of any possible exposure level at time j.

2.3. Estimation of Transition Probabilities $P(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}^{\overline{a}}=k^{\prime })$

Robins (2000) describes that the causal parameter of MSMs β^k,k′ may be estimated semiparametrically by weighted estimating equations, where the observed data are weighted using subject-specific, time-specific inverse probability of treatment weights (IPW) [5]. IPW accounts for time-varying confounding by creating a pseudo-population in which covariates at each time of exposure are not associated with the subsequent exposure, but the transition probabilities $P\left(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}^{\overline{a}}=k^{\prime }\right)$ remain the same as in the source population. The observed data association model is

$$\log \left(\frac{P\left(Y_{i,j+1}=k|Y_{i,j}=k^{\prime },{\overline{A}}_{i,j}\right)}{P\left(Y_{i,j+1}=k^{\prime }|Y_{i,j}=k^{\prime },{\overline{A}}_{i,j}\right)}\right)=h_1\left({\overline{a}}_{i,j};{\theta }^{k^{\prime },k}\right)+h_2\left(j;{\eta }^{k^{\prime },k}\right),$$ (3)

and weighted estimating equations are

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{k-1}{\widehat{\omega }}_{i,j}}}\left(Y_{i,j+1,k}-\frac{\text{exp}\left\{h_1({\overline{a}}_{i,j;}{\theta }^{k^{\prime },k})+h_2(j;{\eta }^{k^{\prime },k})\right\}}{1+{\displaystyle \sum _{k\ast \ne K}\text{exp}}\left\{h_1\left({\overline{a}}_{i,j};{\theta }^{k^{\prime },k\ast }\right)+h_2\left(j;{\eta }^{k^{\prime },k\ast }\right)\right\}}\right)}=0,$$ (4)

where Y_i,j+1,k = I(Y_i,j+1 = k), and estimated stabilized weights ${\widehat{\omega }}_{i,j}=\frac{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(A_{i,t}=a|{\overline{A}}_{i,t-1}\right)}{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(A_{i,t}=a|{\overline{A}}_{i,t-1},{\overline{L}}_{i,t}\right)}$ account for time-dependent confounding. Stabilized weights are estimated by fitting two models. The first one models the likelihood of the observed exposure A_i,j given past exposure Ā_i,j−1 and time-dependent covariates ${\overline{L}}_{i,j}$. It informs the denominator of the stabilized weight and is required to be correct to consistently estimate the causal parameter. The second model for the numerator, which is not required to be correctly specified for consistent estimation, is based on a model for exposure A_i,j given past exposure Ā_i,j−1. In the pseudo-population the exposure-outcome relationship is no longer confounded by time-dependent exposure so that the associational parameter θ^k,k′ is equivalent to the causal parameter β^k,k′[5].

For binary exposures, the IPW may be estimated by pooled logistic regression. The probabilities of categorical exposures of greater than two levels may be estimated by pooled multinomial logistic regression. We take this approach in modeling SBP as an exposure, defining clinically relevant levels for normal, moderately elevated, and elevated SBP as used by prior investigators. For continuous exposures, inverse density weighting is possible by specifying a density function for the exposure distribution and estimating components of that density by a standard modeling approach. An alternative approach for continuous exposures is to use a pooled multinomial model considering quantiles of the continuous exposure [11]. For each subject, predicted probabilities of observed exposure level at each time are calculated, and the product is taken within subject over time to estimate ${\widehat{\omega }}_{i,j}$. In categorizing continuous exposures, investigators should be conscious of a tradeoff between the positivity and consistency assumptions. For continuous exposures, it is less likely that every level of the exposure occurs for each level of observed treatment and confounders at each time, thus raising concerns of potential positivity violations. In reducing treatment levels through categorization, it is more plausible that each treatment level is possible at each level of observed treatment and confounders, but violations of the consistency assumption are possible as different continuous exposure levels that result in the same categorical exposure variable could potentially have different implications for potential outcomes, which in turn would violate consistency as a lack of multiple versions of treatment[12], and is particularly relevant for exposures that are biological characteristics[13]. We therefore caution investigators with these considerations when categorizing continuous exposures.

When subjects leave the study prior to the end of the observation period θ^k′^,k are subject to selection bias when exposures and time-dependent factors are predictive of study withdrawal [5]. In this case, estimation equations are,

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{k-1}I\left(C_{i,j+1}=0\right)\omega \ast i,j}}\left(Y_{i,j+1,k}-\frac{\text{exp}\left\{h_1({\overline{a}}_{i,j;}{\theta }^{k^{\prime },k})+h_2(j;{\eta }^{k^{\prime },k})\right\}}{1+{\displaystyle \sum _{k\ast \ne K}\text{exp}}\left(h_1\left({\overline{a}}_{i,j};{\theta }^{k^{\prime },k\ast }\right)+h_2\left(j;{\eta }^{k^{\prime },k\ast }\right)\right)}\right)}=0,$$ (5)

and weights $\widehat{\omega }{\ast }_{i,j}=\frac{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(A_{i,t}=a|{\overline{A}}_{i,t-1},C_{i,t}=0\right)}{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(A_{i,t}=a|{\overline{A}}_{i,t-1},C_{i,t}=0,{\overline{L}}_{i,t}\right)}\times \frac{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(C_{i,t}=0|{\overline{A}}_{i,t-1},C_{i,t-1}=0\right)}{{\mathrm{\Pi }}_{t=0}^j\widehat{P}\left(C_{i,t}=0|{\overline{A}}_{i,t-1},C_{i,t-1}=0,{\overline{L}}_{i,t-1}\right)}$ are the product of the stabilized inverse probability of the observed joint exposure and stabilized inverse probability of being uncensored. Standard errors and confidence intervals of parameter estimates ${\widehat{\beta }}^{k^{\prime },k}$ may be calculated using the robust variance estimator as for Generalized Estimating Equations [14], which is available in standard statistical software packages and provides asymptotically conservative standard error estimates provided that the weights are consistently estimated [15], or by a resampling technique such as the nonparametric bootstrap [16].

2.4. Estimating Marginal Probabilities $P(Y_{i,J+1}^{\overline{a}}=k)$

The predicted probabilities from the multinomial model yield $P\left(Y_{i,J+1}^{ā}=k|Y_{i,j}^{\overline{a}}=k^{\prime }\right)$, the probability of a potential outcome state at time j + 1 under a specified joint exposure at time j given the outcome state at time j. Although the significance of the causal effect of exposures on multistate outcomes may be tested by the null hypothesis that β^k′^,k = 0 and the direction of effect inferred by the suggested odds ratio, the interpretation and magnitude of the effect are more readily understood by comparing the marginal probability of the final outcome state $P\left(Y_{i,J+1}^{\overline{a}}=k\right)$ under various joint exposures. We show in the supplementary material that the marginal probabilities ${\mathrm{\Lambda }}_{J+1,k}^{\overline{a}}=P\left(Y_{i,J+1}^{\overline{a}}=k\right)$ of the final outcome state are determined by

$${\mathrm{\Lambda }}_{J+1}^{\overline{a}}={\gamma }_0^{\mathrm{T}}{\displaystyle \prod _{j=0}^J{\lambda }_{j+1}^{\overline{a}}},$$ (6)

where ${\mathrm{\Lambda }}_{J+1}^{\overline{a}}$ is the vector of length K with the k^th element of ${\mathrm{\Lambda }}_{J+1}^{\overline{a}}=P\left(Y_{i,J+1}^{\overline{a}}=k\right)$, ${\gamma }_0={\left({\gamma }_0^1,{\gamma }_0^2,\dots ,{\gamma }_0^K\right)}^{\mathrm{T}}={\left(P\left(Y_{i,0}=1\right),P\left(Y_{i,0}=2\right),\dots ,P\left(Y_{i,0}=K\right)\right)}^{\mathrm{T}}$, characterizing the marginal distribution of Y_i,₀, and ${\lambda }_j^{\overline{a}}$ as defined in (2). We consider joint exposures of the type ā = (a*,a*,…,a*) for a∗ a specified level of a categorical exposure, although generalization to other joint exposures is straightforward. For our CKD analysis, marginal probabilities are thus interpreted as the probability of a potential outcome state under the case in which a subject maintains the same SBP category for the duration of follow up. Confidence intervals for $P\left(Y_{i,J+1}^{\overline{a}}\right)$ may be obtained by the nonparametric bootstrap.

3. Simulation Study

We conducted a simulation study to evaluate the properties of our MS-MSM estimator, including evaluating the impact of truncating stabilized weights. [17] demonstrated how to simulate time-to-event outcomes based on a conditional likelihood that induces time-varying confounding and is consistent with a marginal structural model that marginalizes over all covariates and contains a noncollapsible link function. We adapt this approach to simulate transition states that are consistent with our MS-MSM.

Our simulation study considered transitions among four possible states, with state 4 absorbing, determined by the homogenous transition matrix ${\lambda }_j^{\overline{a}=0}={\lambda }^{\overline{a}=0}=\left[\begin{array}{cccc}0.6& 0.3& 0& 0.1\\ 0& 0.6& 0.25& 0.15\\ 0& 0& 0.8& 0.2\\ 0& 0& 0& 1\end{array}\right]$ for the reference exposure of ā = (0,0,…,0), and the reference transition matrix and MS-MSM for non-reference joint exposures, where the MS-MSM is given by

$$\log \left\{\frac{P\left(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}^{\overline{a}}=k^{\prime }\right)}{P\left(Y_{i,j+1}^{\overline{a}}=k^{\prime }|Y_{i,j}^{\overline{a}}=k^{\prime },\right)}\right\}={\alpha }^{k^{\prime },k}+{\beta }^{k^{\prime },k}{\displaystyle \sum _{t=0}^j{a}_{i,t}},$$

with β^k′,k = −0.5 and ${\alpha }^{k^{\prime },k}=\mathit{log}\left(\frac{{\lambda }^{\overline{a}=0,k^{\prime },k}}{{\lambda }^{\overline{a}=0,k^{\prime },k^{\prime }}}\right)$. The true values of the marginal probabilities ${\mathrm{\Lambda }}_{J+1}^{\overline{a}}$ assuming all subjects started in state 1 were (0.006,0.030,0.152,0.812) for ā = (0,0,…,0) and (0.40, 0.307, 0.083,0.210) for ā = (1,1,…,1) as determined by the product of the true transition intensity matrices for j+1=1 to 10.

Following [17], the data generating algorithm induced time-varying confounding through uniform random variables U_i, that were common causes of an intermediate covariate L_i,j and outcomes Y_i,j+1. For each subject, we first generated a vector ${\mathbf{U}}_{i,0}=\left(U_{i,0}^{1,1},U_{i,0}^{1,2},U_{i,0}^{2,1},U_{i,0}^{2,2},U_{i,0}^3\right)$ of independent uniform (0,1) random variables which we used to define thresholds for transition probabilities as we next describe. Y_i,₀ was set to 1 for all subjects, indicating that all subjects started in state 1.

At baseline (j = 0) censoring for each subject was set to C_i,₀ = 0, indicating that all subjects were present. The baseline covariate L_i,₀ was generated as Φ⁻¹(Ū_i,₀) + ε_i,₀, where Φ⁻¹ is the inverse cumulative distribution function for the standard normal distribution and ε_i,₀ ~ N(0,0.2) and Ū_i,₀ is the mean of all elements of the vector U_i,₀. Treatment A_i,₀ was Bernoulli(p_i,₀), with logit(p_i,₀) = −0.8 − 0.8L_i,₀. Y_i,₁ followed a multinomial model with

$$\log \left\{\frac{P\left(Y_{i,1}=k|Y_{i,0}=1,A_{i,0}\right)}{P\left(Y_{i,1}=1|Y_{i,0}=1,A_{i,0}\right)}\right\}={\alpha }^{1,k}+{\beta }^{1,k}{A}_{i,0},$$

with β^1,k = −0.5 and ${\alpha }^{1,k}=\mathit{log}\left(\frac{{\lambda }^{\overline{a}=0,1,k}}{{\lambda }^{\overline{a}=0,1,1}}\right).$

To generate Y_i,₁ consistent with λ^ā=0 and the MS-MSM, $U_{i,0}^{1,1}$ was compared to λ^ā,1,1 (λ^ā,1,1=0.6 for a_i,₀ = 0 and 0.71 for a_i,₀= 1). For $1-{\lambda }^{ā,1,1}<U_{i,0}^{1,1}$, Y_i,₁ was set to Y_i,₁ = 1, indicating that the subject remained in state 1 for j=1. For $1-{\lambda }^{\overline{a},1,1}\ge U_{i,0}^{1,1}$, $\frac{P\left(Y_{i,1}=2|Y_{i,0}=1,Y_{i,1}\ne 1,A_{i,0}=a_{i,0}\right)}{P\left(Y_{i,1}\ne 1|Y_{i,0}=1,A_{i,0}=a_{i,0}\right)}$, the conditional probability of state 2 given that the subject did not remain in state 1, was then compared to $U_{i,0}^{1,2}$ such that for $U_{i,0}^{1,2}<1-\frac{P\left(Y_{i,1}=2|Y_{i,0}=1,Y_{i,1}\ne 1,A_{i,0}=a_{i,0}\right)}{P\left(Y_{i,1}\ne 1|Y_{i,0}=1,A_{i,0}=a_{i,0}\right)}$, Y_i,₁ = 2 and Y_i,₁ = 4 otherwise, noting that P (Y_i,₁ = 3|Y_i,₀ = 1,A_i,₀) = 0 according to λ^ā=0.

For subsequent time points j = 1,…,9, C_i,j+1 was generated according to the model $\log \left\{\frac{P\left(C_{i,j+1}=1|C_{i,j}=0,{\overline{A}}_{i,j},{\overline{L}}_{i,j}\right)}{1-P\left(C_{i,j+1}=1|C_{i,j}=0,{\overline{A}}_{i,j},{\overline{L}}_{i,j}\right)}\right\}=-5.0-0.2A_{i,j}+0.6L_{i,j}$. Then for C_i;j+1 = 0 and Y_i;j ≠ 4, the time-varying confounder L_i,j+1 was generated as 0.7L_i,j − 0.5A_i,j−1 + Φ⁻¹(Ū_i,₀), and treatment A_i,j+1 was Bernoulli(p_i,j+1), with logit(p_i,j+1) = −0.8 − 0.8L_i,j+1 − 0.4L_i,j + 0.3A_i,j.−Y_i,j+1 was generated according to Y_i,j as follows based on the reference matrix ${\lambda }_j^{\overline{a}=0}$ and the multinomial model

$$\log \left(\frac{P\left(Y_{i,j+1}=k|Y_{i,j}=k^{\prime },{\overline{A}}_i\right)}{P\left(Y_{i,j+1}=1|Y_{i,j}=1,{\overline{A}}_{i,j}\right)}\right)={\alpha }^{k^{\prime },k}+{\beta }^{k^{\prime },k}{\displaystyle \sum _{t=0}^j{A}_{i,t}},$$

with β^k′^,k = −0.5 and ${\alpha }^{k^{\prime },k}=\mathit{log}\left(\frac{{\lambda }^{\overline{a}=0,k^{\prime },k}}{{\lambda }^{\overline{a}=0,k^{\prime },k^{\prime }}}\right)$.

• For Y_i,j=1, Y_i,j+1 was generated as described for the transition from Y_i,₀ to Y_i,₁ based on λ^ā for ā

• For Y_i,j =2, $U_{i,0_{2,1}}$ was compared to λ^ā,2,2. For $1-{\lambda }^{\overline{a},2,2}<U_{i,0}^{2,1},Y_{i,j+1}=2$, indicating that the subject remained in state 2. For $1-{\lambda }^{\overline{a},2,2}\ge U_{i,0}^{2,1}$, $\frac{P\left(Y_{i,j+1}=3|Y_{i,j}=2,Y_{i,j+1}\ne 2,{\overline{A}}_{i,j}\right)}{P\left(Y_{i,j+1}\ne 2|Y_{i,j}=2,{\overline{A}}_{i,j}\right)}$ was then compared to $U_{i,0}^{2,2}$, such that for $U_{i,0}^{2,2}<1-\frac{P\left(Y_{i,j+1}=3|Y_{i,j}=2,Y_{i,j+1}\ne 2,{\overline{A}}_{i,j}\right)}{P\left(Y_{i,j+1}\ne 2|Y_{i,j}=2,{\overline{A}}_{i,j}\right)}$, Y_i,j+1=3 and Y_i,j+1=4 otherwise

• For Y_i,j =3, U_i,₀₃ was compared to λ^ā,3,3 such that for $1-{\lambda }^{\overline{a},3,3}<U_{i,0}^3$, Y_i,j+1 = 3, indicating that the subject remained in state 3. For $1-{\lambda }^{\overline{a},3,3}\le U_{i,0}^3$, Y_i,j+1 = 4.

Each replicated dataset had 1000 patients, and the maximum number of time intervals was set to J = 10 for subjects who remained uncensored. Results are based on 1000 replicated datasets.

In applying MS-MSMs to the simulated data, time-varying treatment and censoring weights were determined according to the correct models in the denominator, and numerator terms for stabilizing weights included the most recent treatment level A_i,j for modeling C_i,j+1 and A_i,j+1. Results were generated for unweighted estimates, estimates based on stabilized weights without truncation, and estimates based on weights that were truncated at 98^th percentile. Model fitting was stratified by current state, resulting in 5 estimates of the causal log odds ratio parameter for the effect of exposure on transitioning from: 1) State 1 to 2 (β^1,2), 2) State 1 to 4 (β^1,4), 3) State 2 to 3 (β^2,3), 4) State 2 to 4 (β^2,4), and 5) State 3 to 4 (β^3,4). For each stratified regression, staying in the current state was the reference transition, hence no model parameters were estimated for that transition.

Simulation results are shown in Tables 1 and 2. Bias of unweighted coefficient estimates ranged from 4.6–35.3%, whereas bias was small for IPW estimates with and without truncation (bias 0.2–7.2%). The IPW estimates, however, were less efficient than unweighted estimates, with Monte Carlo standard errors of estimators based on weights without truncation double to triple the Monte Carlo standard errors of unweighted estimates. The efficiency of weighted estimation was improved by truncation but still had larger standard errors than the unweighted estimates. The robust variance estimator seemed to underestimate the asymptotic variance when weights without truncation were used. For the marginal probability vector ${\mathrm{\Lambda }}_{J+1}^{\overline{a}}$, unweighted estimation resulted in underestimation of the probability of being in the most severe outcome state 4 at the end of follow up for ā = (0,0,…,0) (0.714 estimated versus 0.812 true) compared to weighted estimation (0.814 without truncation, 0.793 with truncation) and overestimation of the probability of being in outcome states 2 or 3. The opposite occurred for (ā = (1,1,…,1)), with underestimation of the probability of ending in milder states 1 and 2 without weighting (0.365 estimated versus 0.40 true and 0.286 estimated versus 0.307 true for states 1 and 2, respectively) and overestimation of the probability of ending in more severe states. Bias in the estimation of marginal probabilities was small for the estimated MS-MSM. Compared to weighted estimation without truncation, the marginal probability estimates resulting from weight truncation at the 98^th percentile show greater bias but less variability despite similar bias between the coefficient estimates.

Table 1. Simulation Study Results: MS-MSM Coefficients.

Estimation of Multistate Marginal Structural Model (MS-MSM) parameters using 1) Standard, unweighted regression, 2) Inverse Probability Weighting without weight truncation, and 3) Inverse Probability Weighting with weight truncation at the 98^th percentile. Parameters $\widehat{\beta }{k}^{\prime ,\prime }$ indicate the effect of treatment in the logit in the causal multinomial transition state model for transition from state k′ to state k. Estimation was stratified by k′, and for each model, k′ was the reference for the multinomial transition model. Mean Estimate – sample mean of estimated causal parameters where the true value is ψ = −0.5. Bias – the difference of the true parameter and the mean estimate. —%Bias— – Absolute value of the bias divided by true parameter × 100%.

Estimator	Parameter	Mean Estimate	Bias	%Bias	MCSE	Mean ASE
Unweighted	β1,2	−0.47	0.02	4.57	0.037	0.038
	β1,4	−0.37	0.14	27.0	0.055	0.054
	β2,3	−0.46	0.04	7.27	0.044	0.043
	β2,4	−0.32	0.18	35.3	0.049	0.048
	β3,4	−0.37	0.13	25.2	0.07	0.07
Weighted	β1,2	−0.51	−0.01	1.32	0.095	0.075
	β1,4	−0.52	−0.02	4.02	0.122	0.100
	β2,3	−0.51	−0.01	2.71	0.122	0.090
	β2,4	−0.52	−0.02	3.65	0.130	0.107
	β3,4	−0.54	−0.04	7.22	0.193	0.134
Weights Truncated at 98th Percentile	β1,2	−0.50	0.00	0.20	0.055	0.055
	β1,4	−0.49	0.01	1.92	0.088	0.086
	β2,3	−0.49	0.01	1.25	0.066	0.064
	β2,4	−0.47	0.03	6.53	0.079	0.800
	β3,4	−0.48	0.02	3.64	0.111	0.102

MCSE – Monte Carlo Standard Error calculated as the standard deviation of $\widehat{\beta }$ estimates across 1000 simulated datasets. Mean ASE – Mean Asymptotic Standard Error, calculated as the sample average of asymptotic standard error estimates across 1000 replicates.

Table 2. Simulation Study Results: Marginal Probability.

$P\left(Y_{J+1}^{\overline{a}}=k\right)$. Estimation of the marginal probability of state at the end of follow up 1) Standard, unweighted regression, 2) Inverse Probability Weighting without weight truncation, and 3) Inverse Probability Weighting with weight truncation at the 98^th percentile. The true values of P (Y^ā = k) were (0.0006, 0.030, 0.152, 0.812), and (0.40, 0.307, 0.082, 0.21) for states 1–4 for always control and always treated joint exposores, respectively. Mean Estimate – sample mean of estimated marginal probability over 1000 replicates. % Bias – the difference of the true parameter and the mean estimate divided by true parameter × 100%.

	ā=(0,0,…0) (Control)				ā=(1,1,…1) (Treated)
Estimator	Parameter	Mean Estimate	% Bias	MCSE	Parameter	Mean Estimate	% Bias	MCSE
Unweighted	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.007	21.0	0.0014	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.365	−9.06	0.026
	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.044	44.3	0.0058	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.286	−6.79	0.0222
	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.235	54.4	0.0234	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.087	5.19	0.0113
	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.714	−12.0	0.0244	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.262	25.3	0.0212
Weighted	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.006	0.80	0.0017	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.398	−0.67	0.0667
	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.030	0.10	0.0086	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.305	−0.57	0.0674
	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.150	−1.49	0.0435	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.083	0.78	0.0386
	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.814	0.27	0.0456	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.213	1.82	0.0451
Weights Truncated at 98th Percentile	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.006	3.04	0.0014	$P\left(Y_{J+1}^{\overline{a}}=1\right)$	0.395	−1.43	0.0369
	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.032	6.97	0.0057	$P\left(Y_{J+1}^{\overline{a}}=2\right)$	0.302	−1.77	0.0326
	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.168	10.5	0.0281	$P\left(Y_{J+1}^{\overline{a}}=3\right)$	0.084	1.87	0.0162
	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.793	−2.25	0.0293	$P\left(Y_{J+1}^{\overline{a}}=4\right)$	0.219	4.59	0.0259

MCSE – Monte Carlo Standard Error calculated as the standard deviation of estimates across 1000 simulated datasets.

4. Analysis of the Chronic Renal Insufficiency Cohort Study

Our study of SBP and CKD progression includes 3,708 participants from the CRIC Study previously described by Anderson et al.(2015), who examined the effect of SBP on time to ESRD (defined as receipt of maintenance dialysis or a kidney transplant) or halving of eGFR[11]. Patients were assessed annually for 0 to 7 years with variable follow up per patient. Over half of patients (2133 (57.5%)) had 5 or more visits; 442 (11.9%) only contributed 1 visit, 317 (8.5%) contributed 8 visits, and median follow up was 5.7 years. Systolic blood pressure was defined categorically at each year of follow up based on the mean of 3 seated measurements as < 120 mmHg (A_i,j = 1), [120,130) mmHg (A_i,j = 2), [130,140) mmHg(A_i,j = 3), and ≥ 140 mmHg(A_i,j = 4). We defined the CKD outcome state according to levels of eGFR at each year, ESRD, or death, such that Y_i,j+1 = 1 for eGFR ≥ 60, Y_i,j+1 = 2 for eGFR [45,60), Y_i,j+1 = 3 for eGFR of [30,45), Y_i,j+1 = 4 for eGFR of (0,30), Y_i,j+1 = 5 for ESRD, and Y_i,j+1 = 6 for death. For patients observed to develop the clinical events of ESRD or death the event was assigned to the first annual visit after the occurrence of the event. At baseline 658 (17.7%) were in state 1 indicating mild CKD, 1041 (28.0%) were in state 2, 1261(34.0%) were in state 3, and 748(20.2%) were in state 4, the most severe level of CKD. A total of 1481 (39.9%) patients had SBP<120 mmHg, 713 (19.2%) were in the interval [120,130), 559 (15.1%) fell within [130,140), and 955 (25.7%) had SBP ≥ 140mmHg. For the purpose of our analysis, both ESRD and death were absorbing states such that death indicated death prior to the occurrence of ESRD. Baseline demographic and clinical variables were sex, race, education level, self-reported hypertension, and baseline values of all time-dependent covariates, where time-dependent covariates were age, presence of cardiovascular disease, diabetes, BMI, use of angiotensin converting enzyme or angiotensin receptor blockers (ACEs/ARBs), number of antihypertensive medications, proteinuria, and past eGFR. Each of the time-dependent covariates potentially confounds the association between blood pressure at any given time and CKD state changes. Additionally, it is plausible that earlier blood pressure values could affect subsequent level of kidney function (i.e., eGFR) or damage (i.e., level of proteinuria), use of anti-hypertensive medications, and occurrence of cardiovascular disease, justifying the exploration of these variables as potential time-dependent confounders.

Loss to follow up was the only censoring event.

The causal model relating state transitions to the previous SBP history is shown in (7)

$$\log \left(\frac{P\left(Y_{i,j+1}^{\overline{a}}=k|Y_{i,j}=k^{\prime },{\overline{A}}_{i,j}\right)}{P\left(Y_{i,j+1}^{\overline{a}}=k^{\prime }|Y_{i,j}=k^{\prime },{\overline{A}}_{i,j}\right)}\right)={\beta }_0^{k^{\prime },k}+{\beta }_2^{k^{\prime },k}\frac{1}{j+1}{\displaystyle \sum _{l=0}^{j}I}\left(a_{i,l}=2\right)+{\beta }_3^{k^{\prime },k}\frac{1}{j+1}{\displaystyle \sum _{l=0}^{j}I\left(a_{i,l}=3\right)+}{\beta }_4^{k^{\prime },k}\frac{1}{j+1}{\displaystyle \sum _{l=0}^{j}I\left(a_{i,j}=4\right)}+{\alpha }^{k^{\prime },k}f\left(j\right),$$ (7)

where f (j) is a spline function for time. In this model, the odds ratio of transition from state k′ at time j to state k versus k′ is modeled as a function of blood pressure level through time j and time. Coefficients ${\beta }_a^k$ may be interpreted as the log odds ratios of transitioning into state k versus k′ for always having an SBP level in category a versus always having an SBP level < 120 mm Hg. Our model did not constrain the direction of transitions at all, therefore allowing subjects to transition into improved states. Transitions that were observed fewer than 5 times were assigned zero probability to ensure stability of modeling. These were transitions from eGFR ≥ 60 to eGFR < 30 or ESRD, eGFR [45,60) to ESRD, and eGFR < 30 to eGFR ≥60. Our model included a spline term f (j) to flexibly allow for non-homogeneity in the Markov process. The transition diagram corresponding to our analysis is shown in Figure 1.

Figure 1. Transition Diagram for Chronic Kidney Disease Progression.

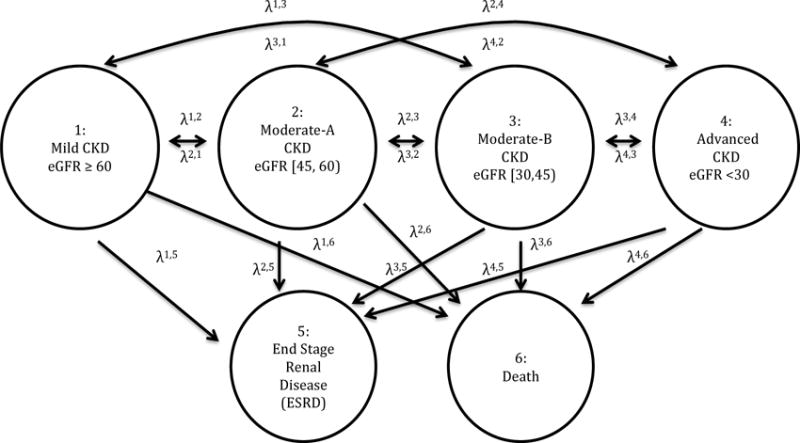
Parameters λ^k′,k denotes the probability of transition from state k′ to state k. The model allowed for transition to more or less severe states defined by eGFR. Death and ESRD were absorbing states.

Stabilized MSM treatment and censoring weights were determined by pooled multinomial and logistic regression, respectively. The final weights were truncated at the 1st and 99th percentile(0.08 and 8.47, respectively). The complete distribution of weights before and after truncation is shown in the supplementary material. Figures 2–5 show the log odds ratios for the effect of blood pressure on transitions among states as estimated by the MS-MSM and standard, unweighted analysis. MS-MSM estimates generally suggest decreased likelihood of improving and increased likelihood of progressing with increasing blood pressure. Figure 4 particularly shows a strong, monotone effect of blood pressure on transitions to ESRD, with the ≥140 mm Hg level leading to a significantly greater likelihood of transitioning to ESRD than the reference <120 mm Hg blood pressure level. Coefficient estimates from unweighted, standard regression were farther from the null than respective MS-MSM estimates. The estimated marginal probabilities for being in a given state at the end of 7 years if always in a given SBP category are shown in Figure 6 and Table 3 with respective 95% bootstrap confidence intervals based on 1000 bootstrap replicates. Marginal probabilities based on unweighted estimation are shown in Table 4 for comparison. Several significant differences were observed between the joint exposure of always having low (< 120 mm Hg) versus high(≥ 140 mm Hg) SBP, with favorable effects estimated for low blood pressure. Monotonic relationships were observed for blood pressure effects on mild CKD and ESRD. For increasing levels of SBP, subjects were less likely to be in a mild CKD state at the end of the observation period and more likely to have experienced ESRD. Under consistently low SBP, 22.9% (95% CI 19.4–26.4) of participants would have mild CKD at the end of follow up, whereas under high SBP, only 4.2%(3.1–5.3) of patients would be expected to have mild CKD. The probability of developing ESRD, however, was significantly higher under high SBP (43.4%, 95% CI 38.4%–48.4%) than low SBP (13.4%, 95% CI 11.0%–15.8%). No significant differences were detected for the probability of death as an effect of blood pressure. Similar to the odds ratio estimates, marginal probability estimates based on unweighted estimation overstated the effect of blood pressure (Table 4), suggesting that 9.3% (7.6–11.0) of subjects with consistently low SBP experience ESRD by the end of follow up as compared to 53.9%(50.2–57.6) with consistently high SBP. At any given time interval, it is possible that participants with controlled blood pressure (< 120 mm Hg) were otherwise healthier, as indicated potentially by a better eGFR history, greater use of blood pressure-controlling medications, lack of cardiovascular disease, and other measured patient factors, and thus more likely to have a favorable prognosis than patients with high blood pressure, which could result in incorrectly attributing favorable outcomes to blood pressure such that the standard analysis overstates the beneficial effect of blood pressure. Our time-dependent weights account for such differences throughout the observation period by including these intermediate indicators of overall health in the weights such that estimated effects reflect only blood pressure differences and not these other factors. In general, however, the impact of time-dependent confounding on effect estimates is difficult to disentangle with the large number of time-varying confounders considered that are complexly related to blood pressure and disease progression.

Figure 2. Log Odds Ratios of Blood Pressure Effects for Transitions from State 1.

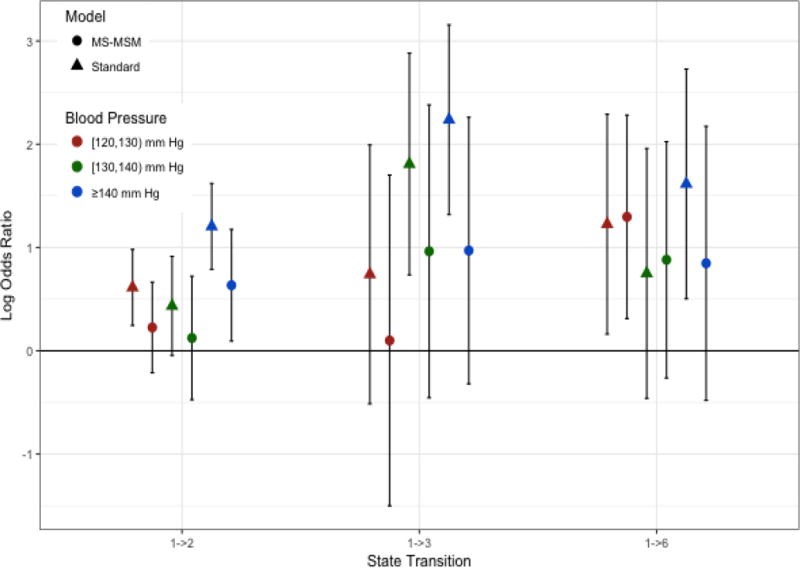
Log odds ratios shown are for the odds of transitioning into the indicated state versus staying in state 1 for always being in the indicated blood pressure category versus always being in the reference state of < 120 mm Hg

Figure 5.

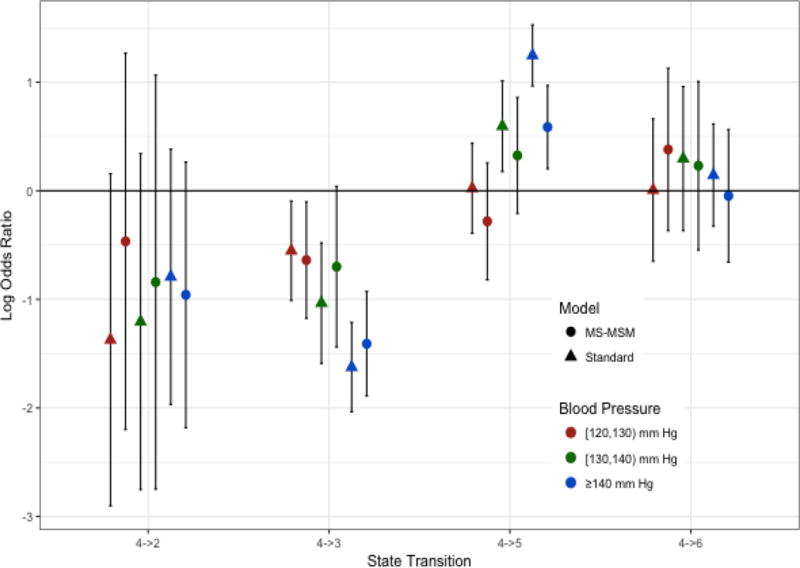
Log Odds Ratios of Blood Pressure Effects for Transitions from State 4. Log odds ratios shown are for the odds of transitioning into the indicated state versus staying in state 4 for always being in the indicated blood pressure category versus always being in the reference state of < 120 mm Hg

Figure 4.

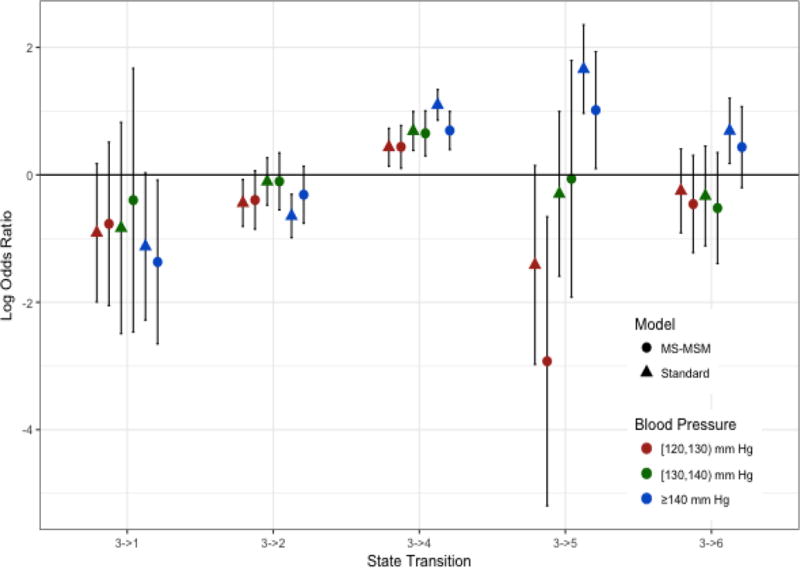
Log Odds Ratios of Blood Pressure Effects for Transitions from State 3. Log odds ratios shown are for the odds of transitioning into the indicated state versus staying in state 3 for always being in the indicated blood pressure category versus always being in the reference state of < 120 mm Hg

Figure 6.

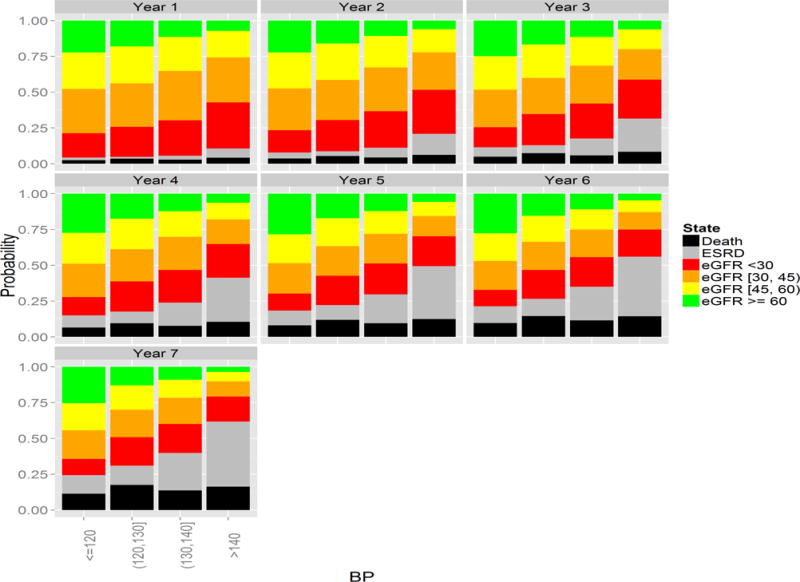
Yearly Marginal Distribution of States by Systolic Blood Pressure Trajectory.

Table 3. Marginal Probability of State at the End of Observation Period.

Weighted Estimates. Marginal probabilities are shown as the percentage of subjects in the population who would be in a given state at the end of the observation period under the joint exposure of always being in the indicated SBP category. 95% Confidence intervals were obtained by the bootstrap percentile method with 1000 replicates.

SBP		eGFR Level			Absorbing
	≥ 60	[45,60)	[30,45)	< 30	ESRD	Death
< 120	22.9 (19.4,26.4)	18.9 (16.0, 21.8)	20.5 (17.6, 23.4)	11.5 (9.3, 13.7)	13.4 (11.0, 15.8)	12.7 (9.7, 15.7)
[120,130)	14.3 (9.9, 18.7)	16.0 (11.9, 20.1)	18.5 (14.0, 23.0)	19.9 (15.1, 24.7)	14.0 (9.5, 18.5)	17.3 (11.7, 22.9)
[130,140)	10.3 (6.5, 14.1)	12.2 (8.4, 16.0)	17.2 (12.6, 21.8)	19.4 13.7, 25.1)	27.8 (20.0, 35.6)	13.1 (6.8, 19.4)
≥ 140	4.2 (3.1, 5.3)	7.3 (5.8, 8.8)	11.1 (9.3, 12.9)	17.5 (14.6, 20.4)	43.4 (38.4, 48.4)	16.6 (12.2, 21.1)

Table 4. Marginal Probability of State at the End of Observation Period.

Unweighted Estimates. Marginal probabilities are shown as the percentage of subjects in the population who would be in a given state at the end of the observation period under the joint exposure of always being in the indicated SBP category. 95% Confidence intervals were obtained by the bootstrap percentile method with 1000 replicates.

SBP		eGFR Level			Absorbing
	≥ 60	[45,60)	[30,45)	< 30	ESRD	Death
< 120	27.4 (24.8, 30.0)	19.9 (17.7, 22.1)	20.6 (18.4, 22.8)	10.9 (9.2, 12.6)	9.3 (7.6, 11.0)	11.9 (9.7, 14.1)
[120,130)	14.2 (10.9, 17.5)	18.1 (14.9, 21.3)	20.2 (16.9, 23.5)	19.7 (16.3, 23.1)	13.3 (10.1, 16.5)	14.5 (10.6, 18.4)
[130,140)	8.0 (5.2, 10.8)	12.4 (9.5, 15.3)	18.3 (15.0, 21.6)	20.7 (16.5, 24.9)	26.4 (20.7, 32.1)	14.2 (9.6, 18.8)
≥ 140	2.1 (1.2, 3.0)	4.7 (3.6, 5.8)	8.1 (6.8, 9.4)	15.1 (13.0, 17.2)	53.9 (50.2, 57.6)	16.1 (13.0, 19.2)

5. Discussion

We have formulated MSMs to estimate the causal effect of time-varying exposures subject to time-dependent confounding on multistate outcomes. Our model allows the consideration of both longitudinal and time-to-event outcomes that are simultaneously accommodated in a multistate outcome framework. This allows the examination of the effect of exposures on progressing to both moderate and advanced disease states and avoids the treatment of clinical outcomes as informative censoring events for examining longitudinal outcome while also accounting for changes in longitudinal outcomes on assessing progression to clinical endpoints. As with similar marginal model longitudinal approaches applied to panel data, our method easily accommodates unbalanced data characterized by a different number of observations per participant provided that causes for such differential follow up are measured or it is unrelated to unobserved outcome states.

In specifying our model, we make a first order Markov assumption that the transition probabilities depend only on the most recent state and not previous states. We also illustrate how to construct the transition matrices under this assumption and to estimate the marginal state probabilities under a joint exposure through a simple matrix product. When this assumption is violated, the estimates of the MS-MSMs may still be interpreted causally as odds ratios for the likelihood of transitioning from one outcome state to another given the current state and marginalizing over all previous states. However, the estimated marginal probability of each state under a joint exposure at the end of the observation period may not be consistent under our simplified marginalization approach. The dependence of the transition probabilities on additional past outcome states may be tested empirically by adding additional previous outcomes to the MS-MSMs. Evaluation of the first order Markov assumption in the CRIC dataset did reveal that additional prior states were in some cases predictive of transition probabilities. For example, considering all possible transitions from current state 2, i.e., eGFR of [45 – 60), patients who were in state 2 in the previous year were less likely to transition to state 1, i.e., eGFR≥ 60 in the following year than patients who were in state 1 in the previous year. Further considering transitions from current state 2, those who were in eGFR state 3, i.e., eGFR of [15,30), in the previous year were more likely to die than those who were in state 1 the previous year. This encourages the exploration of alternative model specifications and more generalized marginalization techniques. To improve the plausibility of a first order Markov assumption, one can redefine the state representation by including additional prior state information using a summary measure of previous states. For example, one can summarize a patient’s trajectory over the past several time periods using a slope term, which can then be used to define states. Clinical knowledge can inform reasonable state definitions that are more likely to satisfy the first order assumption. If a reasonable dimension reduction of state history is not available, the model may be fit under higher-order Markov assumptions. The calculation of marginal probabilities, however, is complicated by marginalizing over multiple previous states such that transition matrices are larger in dimension. For example, when there are K outcome states and transitions depend on both the current and previous state, consecutive yearly transitions may be represented by a matrix of dimension K² × K², where a state is now defined jointly by consecutive states. Due to the overlap in definition of consecutive joint states, many elements of joint state transition matrices will be zero, which provides some simplification of subsequent matrix products. An alternative approach may consider stratified models for each outcome time j + 1 where each model contains the full prior outcome history. This approach would be less efficient as it does not allow borrowing of information across time, but would result in consistent estimation of transition conditional probabilities that could then be entered into a generalized marginalization formula to obtain marginal probabilities at the end of follow up. Stratified models for each outcome time j + 1 might be used to develop additional model checking or sensitivity analysis methods to evaluate the impact of violations of the first-order Markov assumption on estimated marginal probabilities. Our method also relies upon a correctly specified multinomial MSM for the transition probabilities and consistent estimation of the denominators of the censoring and treatment weights. When any of these assumptions are violated the parameter estimates and resulting marginal probabilities are subject to bias for the true average causal odds ratio for exposure. We also assume an additive model for the effects of treatment and time on the transition intensity matrix. This assumption may be relaxed to include interactions of exposures with exogenous time-varying factors such as time, but not endogenous time-varying covariates potentially affected by exposures such as individual patient characteristics[6, 18].

In addition to the first order Markovian assumption, it is important not to lose sight of the dependence of causal inferences under our MS-MSM model to the assumptions of exchangeability, positivity, and consistency. We note, in particular, that the magnitudes of the effect of BP on progression of CKD given in this report appear to be larger than would be expected from the estimated effects of low BP targets on CKD progression reported in previous randomized trials [19, 20, 21]. Thus unmeasured confounding violating the exchangeability assumption cannot be ruled out. In addition, the application of frameworks for causal inference based on counterfactuals has been criticized for applications where the treatment is a biological parameter due to concerns regarding the validity of the consistency assumption [22]. In our example, the concern may be raised that the difference in the values of eGFR that would be observed at two different levels of blood pressure may differ depending on the mechanism by which blood pressure is modified between the two levels being compared; the ”effect” of a given change in blood pressure might differ depending on whether the blood pressure level is modified by changes in diet, physical activity, or by different classes of antihypertensive medication. Thus the marginal structural model described in this paper depends on the assumption that the causal effects of a given change in blood pressure on eGFR are independent of the mechanism used to modify blood pressure. The concept that a given modification of blood pressure level produces similar effects on outcomes irrespective of the mechanism by which blood pressure is modified has been advanced in the cardiovascular disease literature.

In our application we treated ESRD as a terminal event. This follows from the original scientific question of causes of CKD progression, for which ESRD is the final stage. Transitions from ESRD to death may be modeled in MS-MSM; however, patients who develop ESRD are expected to differ substantially from patients at milder CKD states in the behavior of their blood pressure. Modeling of the causal effect of SBP on the transition to death would require a separate pooled logistic regression model for exposure status, which, depending on the level of incidence of ESRD in the cohort, may be fit on a relatively small subset of the cohort. In specifying MSMs for multistate outcomes, it is necessary to consider whether a single pooled logistic model is reasonable across all states, or if interactions of treatment and previous state should be considered, and whether enough variability in states is observed to estimate such interactions.

Our analysis is consistent with previous time-to-event MSM Cox analysis which showed increased risk of ESRD for patients with higher blood pressure [11]. Novel to our analysis are the trends noted in transitions among moderate CKD states denoted by changes in eGFR. We anticipate that these methods can be used in further studies of CKD and other chronic conditions for which both longitudinal and clinical endpoints are important.

Figure 3.

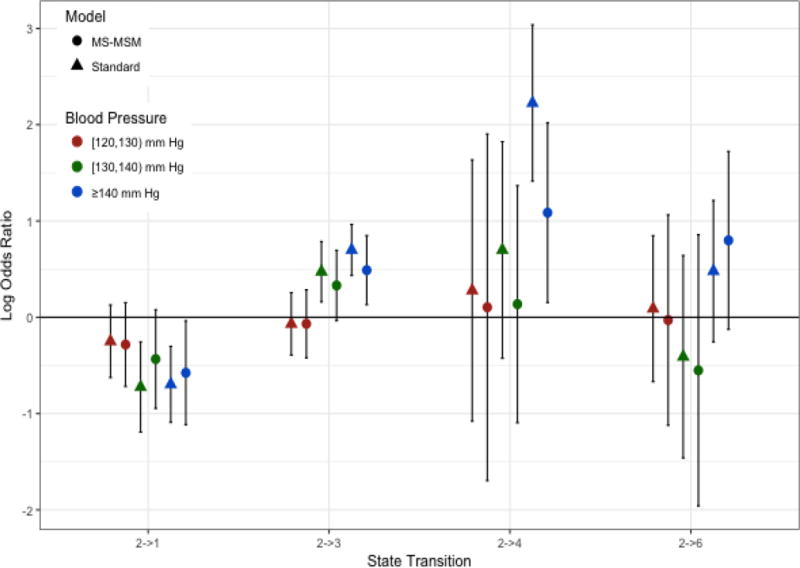
Log Odds Ratios of Blood Pressure Effects for Transitions from State 2. Log odds ratios shown are for the odds of transitioning into the indicated state versus staying in state 2 for always being in the indicated blood pressure category versus always being in the reference state of < 120 mm Hg