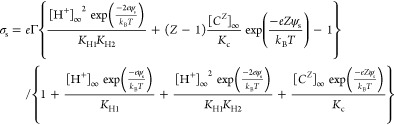Abstract
High-resolution atomic force microscopy is used to map the surface charge on the basal planes of kaolinite nanoparticles in an ambient solution of variable pH and NaCl or CaCl2 concentration. Using DLVO theory with charge regulation, we determine from the measured force–distance curves the surface charge distribution on both the silica-like and the gibbsite-like basal plane of the kaolinite particles. We observe that both basal planes do carry charge that varies with pH and salt concentration. The silica facet was found to be negatively charged at pH 4 and above, whereas the gibbsite facet is positively charged at pH below 7 and negatively charged at pH above 7. Investigations in CaCl2 at pH 6 show that the surface charge on the gibbsite facet increases for concentration up to 10 mM CaCl2 and starts to decrease upon further increasing the salt concentration to 50 mM. The increase of surface charge at low concentration is explained by Ca2+ ion adsorption, while Cl– adsorption at higher CaCl2 concentrations partially neutralizes the surface charge. Atomic resolution imaging and density functional theory calculations corroborate these observations. They show that hydrated Ca2+ ions can spontaneously adsorb on the gibbsite facet of the kaolinite particle and form ordered surface structures, while at higher concentrations Cl– ions will co-adsorb, thereby changing the observed ordered surface structure.
Introduction
Clays are naturally occurring aluminosilicate minerals that are not only of interest to the geologist. Millions of tons of these particles are utilized annually in a large variety of applications in material processing, agriculture, environmental remediation, and construction engineering.1,2 Particularly, kaolinite (Al2Si2O5(OH)4) particles are often used because of their unique physical and chemical properties.2 For some applications their physical properties, such as shape, size, color, softness, and nonabrasiveness of the particle, are essential;for other applications their chemical properties are exploited, such as low cation exchange capacity, low shrink–swell capability, and relative insolubility.3 In enhanced oil recovery (EOR) the presence of clay minerals, i.e., kaolinite, turns out to be a key requirement for successful low-salinity EOR.4−9 In these applications, the surface charge characteristics of kaolinite particles play an important role. However, in spite of a few decades of research, the adsorption–desorption mechanism of ions on kaolinite, and clay minerals in general, and so the resulting charge densities, are still not understood.10−12 The literature on kaolinite shows a large variation in the measured surface charge and isoelectric point (IEP).13,14 For instance, the pHIEP (the pH value at which the net surface charge is equal to zero) for kaolinite particles determined by titration varies from pH 415 to pH 7.5.16 Analyses with the electrophoresis, electroacoustic, and other electrokinetic techniques reveal a smaller value (pH < 3) for the isoelectric point of kaolinite,17−20 with one exception of pH 3.8 obtained by Hu and Liu.21 A review on the isoelectric point for kaolinite particles is given in refs (22 and 23). To find the cause of these differences, two aspects should be addressed. First, the complexity of the system, with its high degree of structural heterogeneity and facet-specific properties, makes a consistent interpretation of the experimental results rather difficult. Second, most experimental techniques do not allow for facet-specific investigations at a molecular scale.
Kaolinite particles have a flat plate-like structure with two basal planes, on one side a Si–O tetrahedral sheet (silica facet) and on the other side a Al–O octahedral sheet (gibbsite facet). The region near the rim of the particle is called an edge (with an irregular surface). For edge and basal planes two different charging mechanisms are proposed. Based on measurements carried out with conventional macroscopic techniques (i.e., ζ potential measurement, potentiometric titration, and so on), the basal surfaces of kaolinite are supposed to exhibit a permanent, negative charge density. This charge should arise from the isomorphic substitution of the central ions in the crystal lattice (Al3+ by Si4+ on the silica facet and Mg2+ substituting Al3+ on the gibbsite facet). Therefore, the resulting surface charge is not expected to depend on the proton concentration near the surface. The charge density near the edges is supposed to result from the deprotonation of the local hydroxyl groups, and therefore it will depend on the pH of the surrounding solution.24−29 The attribution of surface charge on kaolinite to an isomorphous substitution is called the constant basal surface charge (CBSC) model.30,31 This idea was originally presented by van Olphen32 and supported by many other researchers in this field.28−30,33,34 On the other side, results of Gupta et al.35 and Liu et al.36 contradict results with the CBSC model.35−38 Using colloidal probe AFM technique, they were able to determine the charge density on the gibbsite and silica facet of the particle, separately. They found that both the gibbsite and the silica basal planes exhibit pH-dependent charging behavior. This suggests proton uptake or release from the functional surface groups.
Despite this first step in the characterization of a specific surface of distinct particles, experimental evidence with higher lateral resolution, as well as more insight in the impact of surface defects on surface charge, is required to obtain a truly microscopic understanding of the complex structure of such interfaces.
Not only protonation/deprotonation and the influence of pH but also ion adsorption/desorption on kaolinite have been addressed in various publications.39−43 Kaolinite and several of its modifications have drawn attention as suitable absorbers for heavy toxic metal cations (viz., As3+, Cd2+, Cr3+, Co2+, Cu2+, Fe3+, Pb2+, Mn2+, Ni2+, and Zn2+) from polluted water.30 The binding mechanism of cations to the kaolinite surface has not yet been studied in great detail, but it is believed that the OH groups on the basal planes show hardly any chemical reactivity, while the OH groups near the edges are expected to bind cations and/or organic molecules. However, in most cases this interpretation fails to explain the experimental observations, especially when divalent cations are involved. For instance, in order to explain the nonmonotonic behavior of the ζ potential of kaolinite as a function of pH, Yukselen and Kaya44 and Hunter and James45 assumed that, additionally to edges, divalent ions adsorb also to the basal planes of a kaolinite particle. However, these assumptions were never validated since conventional macroscopic techniques (i.e., ζ potential, potentiometric titrations, and so on) cannot offer a microscopic mechanistic insight, i.e., not infer a molecular picture of the adsorption mechanisms, and are not able to distinguish between specific adsorption of cations on the edges or on the basal planes.
Using recent advances in atomic force microscopy, we want to examine in this study the diffuse-layer charge distribution on both the silica-like and the gibbsite-like basal planes of a kaolinite particle. More precisely, this research will focus on the following: (1) determination of the pH dependence of the surface charge on the gibbsite facet and the silica facet; (2) determination of the CaCl2 concentration dependence of the surface charge on the gibbsite facet of the kaolinite particle. The net effective diffuse-layer surface charge densities on a single facet, determined with a lateral resolution of 50 nm, are obtained by analyzing the recorded force–distance curves, using DLVO theory with charge regulation at the substrates. Atomic scale images at much higher resolution give a direct view on the lateral and normal ordering of ions on the substrate. In order to get a better understanding, on the molecular level, of the charging mechanism due to ion adsorption to the kaolinite facets, we also perform density functional theory (DFT) calculations and compare our high-resolution images and AFM spectroscopy data with the DFT results.
Results and Discussion
Macroscopic Characterization of a Nanoparticle
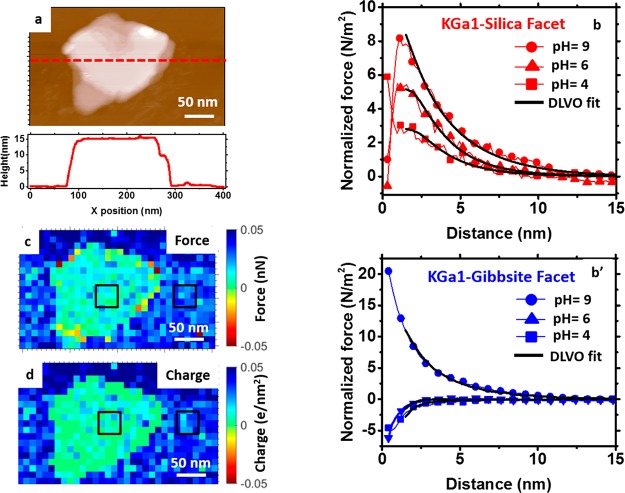
Atomic force microscopy topography images are used to reveal the surface features and characteristics of individual particles. The particles display a plate-like pseudohexagonal morphology with rather sharp corners and flat areas on the basal planes as expected for well-crystallized kaolinite particles (KGa-1 kaolinite)46 (Figure 1a and Supporting Information Figure S1). The majority of the particles has a relatively high aspect ratio. The height varies between 10 and 50 nm while the lateral dimension ranges from several tens to a few hundred nanometers. The majority of the basal planes (gibbsite and silica) appears smooth across 20–200 nm regions (Figure 1a), but many particles also display regions with defects and cascade-like growth structures forming steps with a height of around 2 nm.
Figure 1.
(a) Topography image and height profile of kaolinite particle adsorbed on sapphire imaged in 10 mM NaCl solution at pH 4. (c) Force map showing tip sample interaction forces on the kaolinite particle in 10 mM NaCl solution at pH 4. Note: The map is shown at 1 nm distance from the surface. (d) Surface charge map calculated by analyzing the tip sample interaction forces with DLVO theory. Force vs distance curves along with theoretical calculated forces (black lines) on (b) silica and (b′) gibbsite facet in 10 mM NaCl solution at pH 4, 6, and 9. Note: Representative force curves corresponding to each condition are taken from the area marked on the force maps at kaolinite particle. Tip parameters: for silica facet, Q = 2.16, f0= 16.97 kHz, kc= 0.367 N/m, and R= 13 ± 2 nm; for gibbsite facet, Q = 2.37, f0= 17.06 kHz, kc= 0.448 N/m, and R= 18 ± 2 nm.
Interaction Forces at Kaolinite Faces
As described in our earlier publications,47−49 AM-AFM force spectroscopy was used to map the spatial distribution of the surface charge on the silica facet and the gibbsite facet of kaolinite particles as a function of the pH of the electrolyte solution. Force–distance (FD) curve maps are measured with a lateral resolution of 10 nm. From these FD maps the local surface charge is determined as described above. Figure 1c shows a representative tip–sample interaction force map on a kaolinite–sapphire system in a 10 mM NaCl, pH 4 solution. A complete overview of force maps over all electrolytes for silica and gibbsite basal plane can be found in the Supporting Information. The data are presented as a 2D projection on the substrate of the force measured 1 nm above the particle/substrate, being extracted from 3D FD maps. The colors red and blue represent repulsive and attractive interaction forces, respectively. Because the SiO2 surface of the AFM tip is negatively charged for pH > 3, we conclude from these force maps that the gibbsite facet of the kaolinite particle and the sapphire substrate are positively charged at pH 4 and 6 and negatively charged at pH 9. The silica facet of the kaolinite particle and the mica substrate are negatively charged at all conditions (pH 4, 6, and 9). Our measurements reveal a significant heterogeneity in the force distribution on both basal planes (Figures 1 and SI1). Substantial lateral variations are found not only near topographic defects but also on the topographically flat parts of the surface (terraces). This heterogeneity in the force distribution over the two facets reflects the heterogeneity in surface charge due to a varying surface chemistry. While the exact conversion of the observed force into local surface charge close to the edge or near terrace steps on the particles is difficult, our raw data clearly show that the tip–sample force decreases upon approaching these regions, suggesting (in the case of the gibbsite facet) a less positive, if not negative, local charge density here. However, our further discussion focuses on the forces and charge on the terraces of the basal planes.
Surface Charge at Kaolinite Facets: Effect of pH
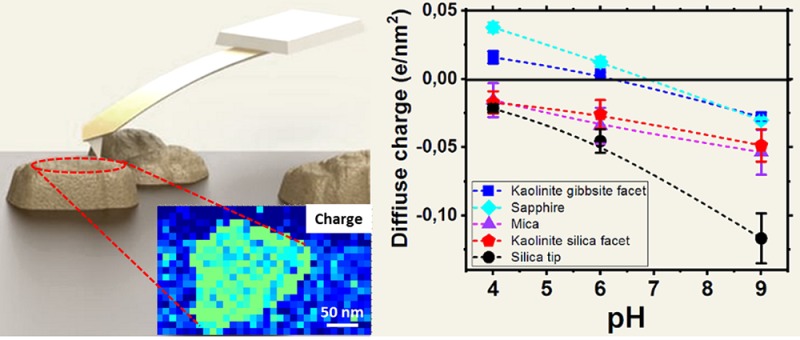
The normalized average force–distance curves across a flat region (marked with black boxes on the force maps) in the center of the particle in 10 mM NaCl electrolyte solution at different pH values are shown in Figure 1b,b′. Figure 1b shows that raising the pH leads to an increase in the magnitude of the long-range repulsive force between the SiO2 tip and the silica facet of kaolinite. An increase of the repulsive interaction with increasing pH implies that at least one of the two involved surfaces (tip or silica facet) becomes more negatively charged. On the gibbsite facet, the attractive interaction force only weakens with increasing pH from 4 to 6 and becomes repulsive at pH 9, indicating a negatively charged gibbsite facet. The force curves on the gibbsite facet of kaolinite and the sapphire substrate are comparable, and of similar magnitude. The solid lines give the best fitting model calculations. From these fits the diffuse surface charge (and surface potential) is extracted (see Experimental Section for details). It should be pointed out that in our approach the diffuse-layer charge, σd, is measured. This charge density is equal in magnitude to the charge density resulting from protonation and deprotonation of the substrate, σ0, and from ion adsorption, σi, so σd = −(σ0 + σi). This procedure is applied to all force–distance curves. The resulting charge maps, with spatial resolution of 10 nm, show the dependence on pH for both kaolinite facets on an individual particle (Figures 1d and SI1). The silica facet of kaolinite, mica substrate, and the silica-tip surface are negatively charged under all probed pH conditions (Figure 2). The surface charge on the silica facet changes very little, from −0.016 to −0.023 e/nm2, when the pH varies from 4 to 6. The charge increases more strongly (−0.023 to −0.044 e/nm2) when the pH of the solution is increased from 6 to 9 (Figure 2). The surface charge of the silicon tip varies from −0.025 to −0.125 e/nm2 when the pH increases from 4 to 9. The gibbsite facets of the kaolinite particle are positively charged for pH 4 and 6 (+0.018 and +0.004 e/nm2, respectively) but become negative (−0.028 e/nm2) at pH 9. Sapphire shows similar behavior, although for pH 4 and 6 the charge values are higher than on the gibbsite facet (Figure 2). Interestingly, the gibbsite facet behaves more or less identical to the sapphire surface in terms of the surface charge dependence as a function of pH, despite the difference in crystal structure. These results are corroborated by the work of Veeramasuneni and Lange50 and Tulpar et al.,51 who show that the protonation behavior of a hydroxylated sapphire-c plane is more or less identical to the behavior of the basal plane of gibbsite. Infrared (IR) spectral studies,52 X-ray diffraction measurements,53 and simulations54−57 also reveal that behavior of a sapphire surface in contact with water resembles that of gibbsite. In our case, clean hydroxylated sapphire surfaces are obtained through plasma treatment at room temperature. With plasma treatment, not only the organic contamination is removed from the surface but also the number of reactive sites such as edges and vacancies is increased significantly, as well as the fraction of singly coordinated surface hydroxyl groups. Moreover, plasma treatment increases the IEP of a sapphire surface from 4 to 8. For a review on the differences in point of zero charge (PZC) between crystalline and particulate alumina and how the PZC depends on surface treatment, the reader is referred to Franks et al.58,59
Figure 2.
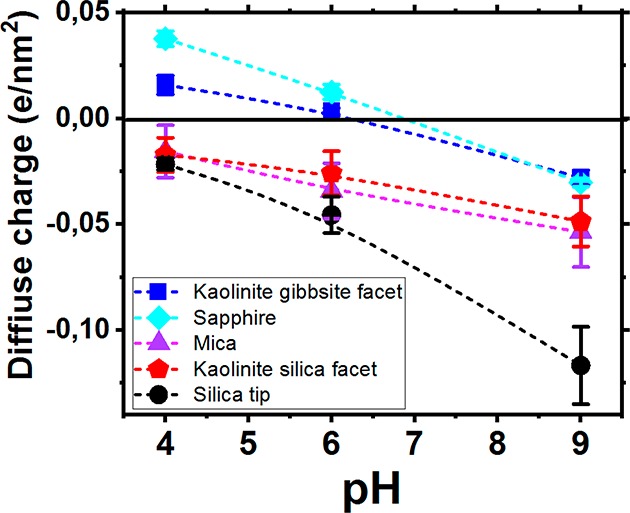
Surface charge of mica, silica tip, sapphire, and two facets of kaolinite particle as a function of pH for NaCl = 10 mM. Note: These surface charge values are calculated by averaging over the areas marked on the force maps shown in Figure 1 and Figures S1 and S2. Surface potential data are shown in Figure S5.
Our results show clearly that the pH strongly affects the surface charge on the basal planes of the kaolinite particle. The gibbsite octahedral facet of kaolinite shows an isoelectric point at pH 6.5, whereas the silica tetrahedral facet of kaolinite is negatively charged for all pH conditions, which implies an isoelectric point below pH 4. These findings contradict the earlier interpretation of titration data that attributed the pH responsive sites only to the edges.25 But they support the more recent view that proton active sites are present also on both basal planes of kaolinite. Because protonation/deprotonation occurs on both the silica and gibbsite facets, the pH dependence of the surface charge is comparable with the pH dependence on Al2O3 and amorphous SiO2, as Figure 2 shows.
Surface Charge at the Gibbsite Facet of Kaolinite: Effect of CaCl2
An intriguing charging behavior is observed on the gibbsite facet of the kaolinite particles in the presence of CaCl2. As can be observed in Figure 3, initially, σ increases with increasing salinity, reaching a maximum at 10 mM, and then decreases as the concentration further increases to 50 mM. This strong nonmonotonic charging behavior with a pronounced maximum near 10 mM was observed on the sapphire substrate as well. Synthetic nanoparticles of gibbsite show a similar charging behavior.49 This can be explained by the competition between specific adsorption of divalent cations and anions as observed in AFM images which are taken with atomic resolution.
Figure 3.
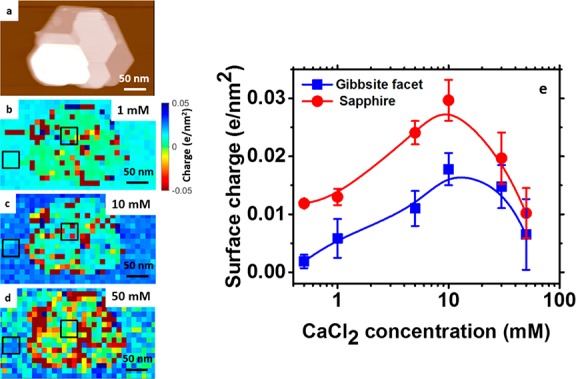
(a) Topography image of kaolinite particle adsorbed on sapphire imaged under 10 mM CaCl2, pH 6 solution. (b–d) Surface charge maps for kaolinite particle adsorbed on sapphire under different (1, 10, and 50 mM) CaCl2 concentrations. (e) Surface charge in e/nm2 (1 e/nm2 = 160 mC/m2) as a function of salt concentration for gibbsite face (blue line) and sapphire substrate (red line). Note: The surface charges corresponding to each condition are averaged over the areas marked by the black squares in panels b–d. Tip parameters: Q = 2.94, f0= 22,67 kHz, kc = 0.71 N/m, and R= 10 ± 2 nm. Surface potential data are shown in Figure S5.
Atomic Resolution Imaging of Gibbsite Facet of Kaolinite
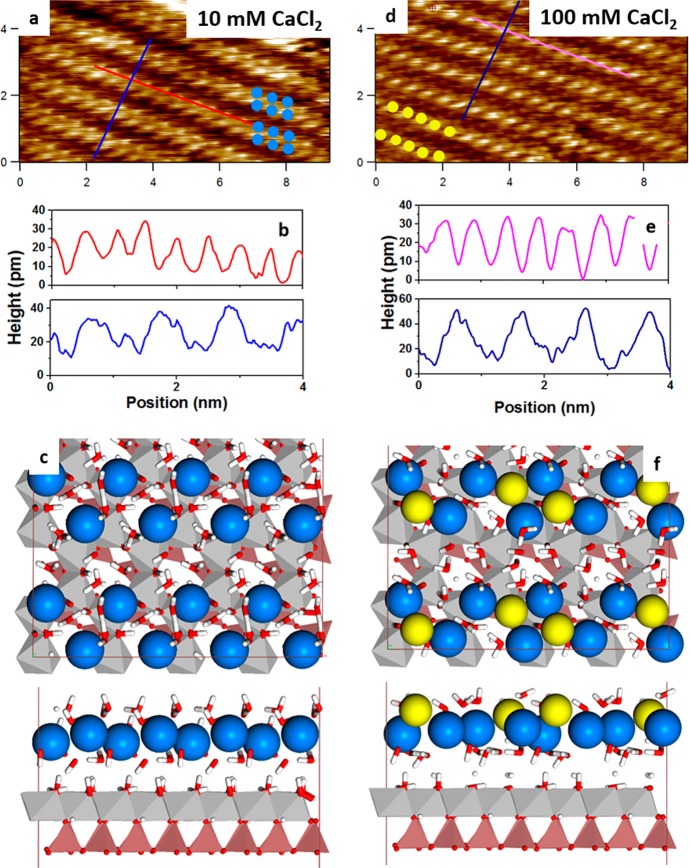
To reveal the periodic ordered structures that are formed by Ca2+ and Cl– ions at the gibbsite facet of the kaolinite particles, we image the gibbsite facet at atomic resolution in CaCl2 solutions. Recently, we reported for the gibbsite facet a pseudohexagonal pattern (surface unit cell, a = 0.49 nm and b = 0.93 nm) when imaging the kaolinite particle in deionized water or in solutions of monovalent salts at various concentrations.60 The appearance of the gibbsite facet changes drastically when imaged in 10 mM CaCl2 (Figure 4a). Instead of the hexagonal pattern, the surface displays an array of parallel double rows of protrusions aligned along the b direction of the lattice (Figure 4a). Within each double row, the protrusions are arranged in a zigzag fashion. Averaging over several periods of the surface, we find periodicities of a = 0.96 nm and b = 0.49 nm perpendicular and parallel to the double rows, respectively, in good agreement with the crystallographic lattice of the kaolinite gibbsite basal plane (see Figure 4b for a typical topographic cross-section). It makes sense to suppose that these protrusions represent adsorbed ions from the solution. At first glance, one might think that the bumps in the double row structure represent Cl– anions, since the positive charge of the surface should lead to a repulsion of the Ca2+ cations. However, this would be incompatible with the simultaneous increase of the positive surface charge. Also, a surface charge value of 0.02 e/nm2 (3.2 mC/m2) would correspond to only one positive charge in about 40 unit cells. Therefore, almost every unit cell on the basal plane is electrically neutral. Strongly hydrated Ca2+ ions can easily approach the neutral parts of the surface “in between” adjacent repulsive charges thereby avoiding the electrostatic repulsion. Hence, we suppose that these protrusions are Ca2+ ions: two per unit cell. The charge of these Ca2+ ions is for a large part compensated by the presence of OH– ions in the substrate; see the DFT discussion below. Several AFM49,61 and X-ray studies62,63 as well as DFT and MD calculations64−67 show that the existence of a particular hydration landscape can promote adsorption of ions in a specific manner. Similar double row zigzag structures formed by hydrated Ca2+ ions were also observed on the basal plane of synthetic gibbsite nanoparticules.49
Figure 4.
Atomic resolution topographic images of the gibbsite facet of kaolinite imaged in (a) 10 mM CaCl2 solution showing double row structure and (d) 100 mM CaCl2 showing single row structure. Height profiles (b and e; directions indicated by corresponding colored lines in panels a and b, respectively) displaying periodicities of a = 0.96 nm, b = 0.49 nm and a = 1.07, b = 0.48, respectively. Equilibrium structure of adsorbed (c) Ca2+ (blue) and (f) Cl– (yellow) on the gibbsite facet of kaolinite in aqueous solution predicted by DFT calculations. Top (upper) and side (lower) views of the optimized geometry for outer shell adsorption of Ca2+ and Cl– for high salt concentation. Adsorption plane of Cl– is 0.1–0.15 nm above Ca2+.
As we increase the CaCl2 concentration to 100 mM, we observe a change in the appearance of the surface. The original double row structure transforms into two inequivalent parallel rows of brighter and fainter protrusions, (Figure 4d). The periodicities both along and perpendicular to the rows agree closely with the dimensions of the surface unit cell, a = 1.07 nm and b = 0.48 nm (Figure 4e). This transition from a double row structure to single rows of bumps coincides with the decrease in surface charge observed at 50 mM in Figure 3. Synthetic nanoparticles of gibbsite show a similar behavior.49 Such a decrease in surface charge could be caused by desorption of the initially adsorbed Ca2+ cations or by co-adsorption of Cl– anions. Adsorption of Cl– ions is most likely, because increase of the Ca2+ concentration should promote adsorption and not desorption. The anion adsorption can be facilitated by an increase of the initially relatively low positive surface charge due to the adsorbed cations. Recent numerical simulations of smectite in contact with CaCl2 and NaCl suggest that Cl– ions do form ion pair complexes with adsorbed Ca2+ ions at sufficiently high concentrations.68 Also optical reflectivity measurements and MC simulations indicate an enhancement of the Cl– density on silica near the earlier adsorbed divalent ions.69 A question that arises from these observations is, do Ca2+ ions adsorb in outer-sphere configuration as for synthetic gibbsite nanoparticles basal planes or form an inner-sphere configuration with the surface? For instance, Bargar et al.62,63,70,71 using grazing-incidence X-ray absorption fine structure (GI-XAFS) spectroscopy clearly show that small structural and chemical composition differences of α-Al2O3 and α-Fe2O3 surfaces have a great impact on adsorption configuration (inner-sphere vs outher-sphere) and reactivity of Pb(II) and Co(II) ions to hematite and sapphire surfaces.
Density Functional Theory Calculations
To explain our experimental findings from an atomistic point of view, we performed DFT calculations to examine the adsorption of Ca2+, OH–, and Cl– onto the gibbsite facet of kaolinite. We used the COSMO-RS implicit solvent model with periodic boundary conditions to calculate the equilibrium structure of the adsorbed ions on the gibbsite facet of kaolinite. We scrutinize our models not only on their stability but also on the ability to reproduce and confirm our experimental findings. Figure 4c shows the optimized geometry in the case of cation adsorption. Because of limitations in using periodic calculations and the fact that the observed surface charge was low, we used a neutral structure. This means that every adsorbed Ca2+ is accompanied by two monovalent anions from the solution. The cations form indeed a zigzag row structure, which reproduces the features observed with atomic resolution AFM (Figure 4a). The DFT/COSMO-RS formation energies for the divalent ion structures were −127 (kJ/mol)/Ca(OH)2. These formation energies predict that the zigzag structure should begin to form already at ∼0.01 mM and pH 6 based on the equilibrium defined by eq 8, which is lower than the observed concentration of 10 mM. The difference in concentration threshold for zigzag structure formation corresponds to a difference in formation energy of ∼20 kJ/mol, which is within standard DFT uncertainties.
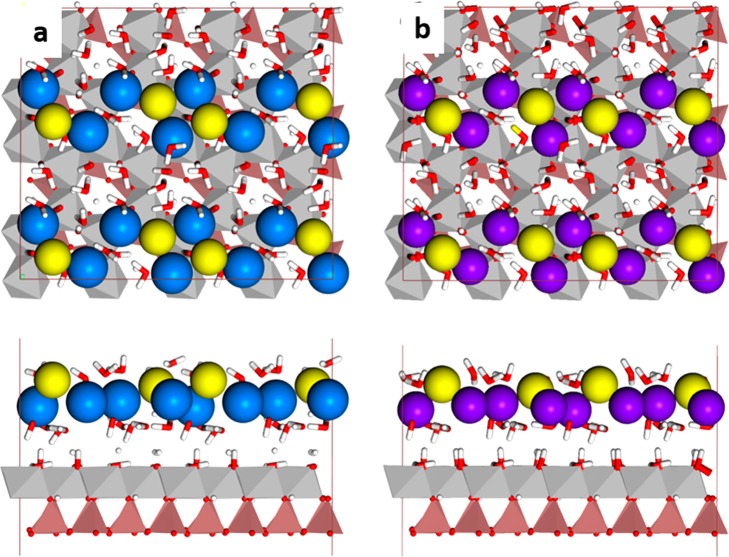
The DFT calculations suggest that all the cations are located at virtually the same height above the kaolinite surface, which is in agreement with the experiments (Figure 4c). The OH– ion that is located down the plane of Ca2+ ions, bridging two Ca2+ ions, is responsible for the positive surface charge via partial protonation. We have previously predicted the pK value for the water to OH– deprotonation for the similar structure on the gibbsite surface, where it was found to be ∼5 for the Mg structure and ∼10 for the Ca structure.49 These values are significantly lower than for the hydration of the free cations in the solution, and partial OH– to water protonation on the surface leads to a weak positive surface charge, consistent with experiments (Figure 3). The OH– can furthermore be exchanged by a Cl– ion if the CaCl2 concentration is increased, as suggested by previous DFT calculations for the gibbsite system.49 The Cl– ion, on the other hand, is larger, and for kaolinite, it adsorbs in quasi-3-fold hollow sites on the cation zigzag structure further away from the surface compared to the plane formed by the cations (Figure 4f). The predicted structure agrees with the single rows observed with the AFM at higher salt concentrations, although DFT predicts a single zigzag row with a very small angle, which is not distinguishable from a single straight row in the AFM experiments. In the case of MgCl2, the Cl– ions form completely straight rows (Figure 5). The vertical position of the Cl– ions is 1–1.5 Å above the Ca2+ plane. The OH– to Cl– ion exchange disables OH– protonation and with it the mechanism for positive surface charge generation. Upon Cl– exchange, the surface structure becomes neutral, which explains the decrease in σ at high salinity. The OH– vs Cl– exchange energies predicted by the DFT calculations are 76 kJ/mol for the Ca structure. This is close to what was observed on the basal plane of synthetic gibbsite nanoparticles, but according to the DFT calculations the OH– to Cl– exchange is less favorable on kaolinite, probably because DFT overestimates the stability of the Ca(OH)2 structure or because the approximations used in DFT calculations are not fully correct. The DFT calculations predict the Cl– structure to form at concentrations > 10 M.
Figure 5.
Structural models produced by DFT calculations: (a) Ca2(OH)3Cl adsorbed on gibbsite, which produces a single zigzag row with a very small angle, and (b) the same surface but with chloride included, i.e., Mg2(OH)3Cl, which produces more straight single rows We have outlined four of the unit cells that we used in the calculations with a white box, which indicates the periodic boundary conditions.
Preliminary DFT calculations on the formation of a similar zigzag structure on the silica facet suggest that the lack of hydrogen bonding to the surface results in a much more compact structure which has a significantly lower formation energy of about −90 (kJ/mol)/Ca(OH)2. This suggests that the formation of a zigzag row on the silica facet would only form for concentrations of about 1–10 M, which is a 5–6 orders of magnitude higher concentration than for the gibbsite facet. Thus, qualitatively the DFT calculations suggest a quite different adsorption behavior for the two basal planes of kaolinite in the presence of CaCl2.
Two significant features of the charging behavior of the kaolinite basal planes can be observed. First, we have demonstrated that the two facets of kaolinite—the silica facet and the gibbsite facet—differ significantly in their surface chemistry characteristics. At pH 6, the silica-like basal plane displays on average a negative surface charge density of −0.05 e/nm2 and the gibbsite facet a weak positive charge density of approximately +0.025 e/nm2, corresponding to one charge per 20–40 surface unit cells. This contradicts the assumption that both facets of kaolinite carry a permanent negative charge due to isomorphous substitution. Second, we conclude from our force measurements that the basal planes of kaolinite do carry charge that varies with pH and salt concentration. The silica facet was found to be negatively charged for pH 4 and above, whereas the alumina facet was found to be positively charged below pH 7 and negatively charged above pH 7. Compared to macroscopic studies that reveal charge values averaged over the total particle surface, i.e., edges and basal planes, our measurements are more specific without the need for assumptions regarding the relative weight of edge vs basal plane sites. Gupta et al. observed a similar pH dependency of the basal planes of kaolinite using colloidal probe AFM spectroscopy.35,38 Our 2D charge mapping also reveals that the surface charge of the particles displays lateral variations that correlate with the presence of topographic defects such as steps. Charge heterogeneity is present even on topographically rather smooth terraces of facets. Therefore, we believe that our extracted average charge values (Figure 2) from specific smooth terraces may be less affected by the contributions from defects (e.g., steps) of lower charge density that are unavoidably included in the wide lateral average of the colloidal probe technique. Regions with defects, depending on their surface chemistry, may dominate the apparent surface charge measured in a colloidal probe AFM measurement and thereby suggest a different surface chemistry of the basal plane than the true intrinsic one. In light of the strong similarity between the gibbsite facet of kaolinite and the sapphire substrate, with an IEP near pH 7, we believe that the doubly coordinated hydroxyl groups (≡Al–OH2OH) on the basal plane, with a pKa value near 5, are responsible for the pH-dependent surface charge of the gibbsite facet. This is in line with the predictions of Bickmore et al. and Jodin et al.72,73 for sapphire surfaces. The protonation/deprotonation of the ≡Si–OH groups on the silica facet, and on the amorphous SiO2 substrate, with a pKa value near 6.9, correlates nicely with our measured surface charge values.
AFM measurements performed in CaCl2 (pH 6) solutions show a clear and unequivocal preferential adsorption of divalent ions on the gibbsite facet of kaolinite. Atomic resolution imaging demonstrates that the Ca2+ and Cl– ions do not adsorb randomly at the gibbsite facet, but form preferentially ordered structures such as zigzag rows or linear rows due to ion–substrate attractive interactions controlled by the water at the interface. DFT calculations show that the ion’s hydration energy has to dominate over ion–substrate electrostatic interactions for this ordering to take place. The position and orientation of hydroxyl groups and the location of the hydrogen bonded water impose the distribution and distance between adjacent bounded Ca2+ ions. The weakly charged gibbsite facet of kaolinite provides an appropriate hydration landscape that allows for the formation of Ca2+ ionic structures stable enough to be observed by AFM imaging. In contrast, highly mobile Na+ cations on the surface and the loose hydration state prevent a structural organization of these ions on the surface.
AFM data and DFT calculations show that divalent Ca2+ ions can adsorb onto the gibbsite facet of a kaolinite particle and not only onto the edges of the particle as was assumed earlier. This should be taken into account when interpreting the surface charge measurements using macroscopic electrokinetic techniques. Moreover, DFT calculations suggest that indeed Ca4(H2O)12(OH)8 and not bare Ca2+ ion adsorb on gibbsite facet, as measured by Bargar et al.62,63,70,71 using GI-XAFS for Pb2+ and Co2+ ions on a hydroxylated sapphire-0001 surface (which, as pointed out above, is very similar to the gibbsite basal plane). These observations also justify the earlier assumption of Yukselen and Kaya44 and Hunter and James,45 that divalent ions like Co2+, Cu2+, Cd2+, Pb2+ and Ca2+ show a strong affinity for the basal planes of kaolinite. Yet, it should be pointed out that the macroscopic measurements of Yukselen and Kaya44 and Hunter and James36 are not able to determine on which basal planes adsorption of cations took place and do not rule out possible aggregation phenomena. This study presents, to the best of our knowledge, the first direct observation, using atomic resolution imaging, of a 3D divalent cation–anion structure at the gibbsite facet of a kaolinite particle.
Conclusion
In conclusion, in the present work, we characterize the charge distribution on the basal planes of kaolinite particles under variable pH and salt concentrations using dynamic force microscopy. The surface charge of the silica facet is always negative and increases in magnitude with increasing pH, while, for the gibbsite facet, the surface charge is positive for 4 < pH < 6 and becomes negative for higher pH (∼9). The surface charge of the gibbsite facet at pH 6 increases with concentration up to 10 mM CaCl2 and starts to decrease upon further increasing the salt concentration to 50 mM. The increase of surface charge is explained in the context of Ca2+ ion adsorption, while chloride ion adsorption at higher CaCl2 concentrations makes the surface charge neutral. Our conclusions are well-supported by the atomic scale imaging as well as the DFT calculations. The results reported here have important implications for the understanding and modeling of the electrical surface properties of kaolinite nanoparticles, which play such a vital role in various industrial applications including enhanced oil recovery.
Experimental Section
Sample Preparation
Kaolinite powder (KGa-1) was kindly provided by T. Hassenkam and S. L. S. Stipp (University of Copenhagen). A suspension of the powder (∼1.5 mg/mL) is prepared using deionized water (Millipore Inc.). A 20–30 μL aliquot of this suspension is drop cast onto sapphire or mica substrates. Kaolinite nanoparticles have two different facets, a negatively charged silica facet and a positively charged gibbsite facet (at neutral pH).48 By adsorbing them on sapphire or mica, we can expose either the gibbsite or silica facet to the fluid. After a residence time of 2 min, the samples are gently dried by blowing air over them and rinsed with copious amounts of deionized water to remove loosely bound clay particles from the substrate. Prior to drop deposition, the sapphire substrates are cleaned with isopropanol, ethanol, and water and by subsequent plasma cleaning (PDC-32G-2, Harrick Plasma) for 20–25 min, while the mica substrates are freshly cleaved. Sodium chloride and calcium chloride (puriss, ACS reagent grade, Sigma-Aldrich) solutions are prepared by dissolving the salt in deionized water. The pH is adjusted by adding appropriate amounts of a HCl or NaOH solution. All experiments are performed in a closed fluid cell that allows for liquid exchange; the electrolyte solutions are injected and removed using a syringe. The temperature of the cell is kept constant at T = 22.7 ± 0.5 °C.
AM-AFM Force Spectroscopy
We use a commercial Asylum Research Cypher ES with blue drive which provides thermal excitation. Rectangular cantilevers (MikroMash NSC36/Cr-Au BS) with a gold backside coating are used for the spectroscopy measurements. To calibrate the instrument for amplitude modulation (AM) force spectroscopy the fast capture mode is used to record the power spectrum of the cantilever from which the cantilever stiffness, kc, quality factor, Q, and resonance frequency, f0, are obtained. Typical values are kc ∼ 0.5 N/m, f0 ∼ 18 kHz, and Q ∼ 2.9. In AM force spectroscopy, amplitude and phase of the cantilever deflection are measured as a function of the tip–substrate distance. From the measured amplitude and phase, the tip–sample interaction force is determined by considering the motion of the tip of the cantilever as that of a simple harmonic oscillator (SHO). This force conversion procedure is described in detail by Liu et al.47 for small amplitude modulation with piezo excitation. Here we use photothermal excitation, for which the slightly modified procedure is given by Klaassen et al.74 It results in an expression for the interaction stiffness:
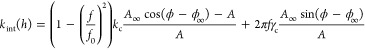 |
1 |
Here A and ϕ are the amplitude and phase measured at a distance h while A∞ and ϕ∞ are determined at h = 150 nm, where the interaction is assumed to be negligibly small. Moreover, f is the driving frequency and f0 the resonance frequency. Integrating kint(h) over h results eventually in the interaction force:
| 2 |
where Π(h) is the disjoining pressure in the liquid under the tip.
Atomic Resolution Imaging
Atomic resolution imaging experiments are also carried out with the Asylum Research Cypher ES. Sharp tips (Arrow UHF-AUD (Nanoworld, Neuchatel, Switzerland); tip radius ∼ 3 nm) are used. To minimize the thermal drift, the system is allowed to thermally equilibrate after fluid injection at room temperature for 20 min before acquiring any data. AM mode is used throughout all the experiments with a free amplitude A0, typically less than 0.5 nm. The ratio of the imaging amplitude set point (A/A0) is kept as high as possible (typically ≥0.9) to minimize the impact of the tip on the surface. A scanning rate of 10–15 Hz is used with a scan resolution of 512 samples per line and 512 lines. So, it takes approximately 40 s to capture one image with 512 scan lines.
DLVO Theory
The disjoining pressure Π between two adjacent surfaces at a distance h is decomposed into contributions from van der Waals interactions, ΠvdW, and electrostatic double layer forces, Πel. The total force on the tip is calculated by integrating Π over the tip surface. Our AFM tips are slightly flattened leading to a local parallel plane geometry (Figure S4). We therefore approximate the total force by F(h) = Atip(Πel + Πvdw), where Atip is the area of the tip. For two parallel interfaces, the van der Waals contribution is written as
| 3 |
where AH is the Hamaker constant. For an atomically flat surface, the electrostatic contribution to the disjoining pressure can be written as
| 4 |
The first term in Πel represents the osmotic repulsion caused by local variations of the ion concentration; the second term represents the direct electrostatic attraction (Maxwell stress). Here, kB is the Boltzmann constant, T the temperature, ci∞ the bulk concentration of the corresponding ion, and εε0 the dielectric permittivity of water. Calculation of the osmotic and electrostatic contribution requires knowledge of the electrostatic potential, ψ(z), in the electrolyte at any position 0 < z < h between the two solid surfaces. This potential is governed by the Poisson–Boltzmann (PB) equation:
| 5 |
where e represents the elementary charge and Zi is the valency of the corresponding ion. To obtain ψ(z) from the PB equation, we need the boundary condition on both substrates. These are determined by surface charge regulation.
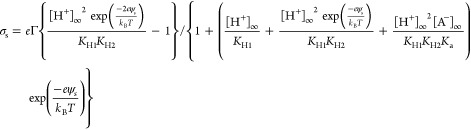
Charge Regulation
Due to surface reactions, the substrates acquire a charge density, σs, that depends on the concentration of the ions near the substrate and so on the local potential, ψs. This dependence is formally written as σs = fs(ψs, c1∞...cn∞, Γ, K1...Km), where Γ is the site density on the substrate and Kj = 10–pkj are the equilibrium constants of the considered surface reactions. Hence, the boundary condition for the PB equation can be formulated as −εε0(n̂∇)s = σs, where n̂ is the normal to the substrate pointing inward the electrolyte. In Tables 1 and 2, we list the surface reactions from which the surface charge–surface potential relations (fs) have been derived for a silica tip, mica and sapphire substrates, and the silica and gibbsite facets of a kaolinite particle. For example, we consider the charging of a silica substrate or a silica facet due to protonation and deprotonation of a surface site SH. This process is described by the chemical reactions:
| 6 |
which have the equilibrium constants KH1 = 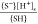 and KH2 =
and KH2 = 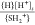 , respectively. The curly brackets denote
a surface density in sites/nm2, and the square brackets
represent a volume density or concentration in mol/L. The deprotonated
sites may be occupied again by counterions from the solutions to form
surface complexes. This is described by a surface reaction:
, respectively. The curly brackets denote
a surface density in sites/nm2, and the square brackets
represent a volume density or concentration in mol/L. The deprotonated
sites may be occupied again by counterions from the solutions to form
surface complexes. This is described by a surface reaction:
| 7 |
with equilibrium constant Kc = 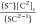 , where Z is the valency
of the cation C. Due to these surface reactions, four surface species
are present on the surface: ∼SH, ∼SH2+, ∼S–, and SCZ–1. Because the total
site density Γ must be conserved, we can write SH + SH2+ + S– + SCz–1 = Γ. Using the
above surface reactions and total site density equations, the densities
of four surface species can be calculated by solving the following
matrix equation:
, where Z is the valency
of the cation C. Due to these surface reactions, four surface species
are present on the surface: ∼SH, ∼SH2+, ∼S–, and SCZ–1. Because the total
site density Γ must be conserved, we can write SH + SH2+ + S– + SCz–1 = Γ. Using the
above surface reactions and total site density equations, the densities
of four surface species can be calculated by solving the following
matrix equation:
 |
8 |
It should be noted that both [H+]s and [Cz]s are
evaluated at the surface and not in bulk. The bulk (indicated
with subscript ∞) and near-surface (subscript s) concentrations
are related via the Boltzmann relation, [H+]s = [H∞]+ exp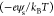 and [Cz]s = [CZ]∞ exp
and [Cz]s = [CZ]∞ exp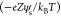 , respectively. The surface charge, σs, can be evaluated from the densities of the surface species.
The final expression for the charge density (σs)
as a function of the surface potential (ψs) has been
shown in Table 1. Following
a similar approach, we also derive the expression for the charge density
on sapphire, mica, and the gibbsite and silica facets of kaolinite,
as noted in Tables 1 and 2.
, respectively. The surface charge, σs, can be evaluated from the densities of the surface species.
The final expression for the charge density (σs)
as a function of the surface potential (ψs) has been
shown in Table 1. Following
a similar approach, we also derive the expression for the charge density
on sapphire, mica, and the gibbsite and silica facets of kaolinite,
as noted in Tables 1 and 2.
Table 1.
| mica/silica/silica facet | ||
|---|---|---|
| reactions | ||
| charge |
|
Table 2.
| sapphire/gibbsite facet | ||
|---|---|---|
| reactions | ||
| charge |
|
Implementation
The calculated force distance curves depend on a number of parameters including the area of the tip Atip, the Hamaker constant AH, the site densities Γ, and the equilibrium constants Kj (or pKj). Beside the pKj values, consistent values for these parameters can be found in literature,48 while the area of the tip is known from SEM imaging; see Figure S4. Therefore, we consider pKH1, pKH2 and pKC or pKA as fit parameters when we compare the experimental data with our calculations. The optimal values for the fit parameters are obtained by maximizing the merit function Q, which is defined as
| 9 |
where Fcal(h) is the calculated force at distance h and Fexp(h) the experimentally obtained value. In most cases good agreement between experimental and calculated forces is obtained. However, the best fitting pairs are not unique; there exists a strong correlation between them. But, as explained by Zhao et al.,75 the resulting surface charge turns out to be insensitive to the considered set of surface reactions, because the double layer contribution of the interaction force, Fexp(h), depends only indirectly via the charge density, σs, on the fit parameters, Kj.
Before we can determine the surface charge density on a substrate, different from silica, we first need to determine the surface charge–potential relation at the silica AFM tip by performing a reference measurement on an equivalent silica substrate. Once the surface charge–potential relation at the AFM tip is known, the surface charge on the other substrate can be determined using the same procedure.
A point of concern in this implementation is the accuracy of the tip area and the zero point determination (h = 0). Assuming a deviation of ±12.5 nm2 in the area of the tip and a deviation ±0.3 nm in the zero point, we recalculate the respective charge values. By considering the standard deviation of all these values, we get an estimate of the accuracy of the calculated charge values for each experimental condition.
Computational Details
Periodic DFT calculations were performed using the program DMol3 with the COSMO-RS implicit solvent,76 the PBE functional, the DNP basis set, and a dispersion correction.77 We used a 1 × 2 unit cell of kaolinite with lattice parameters (0.86840 × 1.01560 nm2) as determined by X-ray diffraction. We constructed the calculation cell to be three molecular layers thick perpendicular to the [001] face and the lowest molecular layer was frozen in bulk positions throughout all calculations. Because inner-shell adsorption was found to be significantly less stable than outer-sphere adsorption for gibbsite,49 we only considered outer-sphere adsorption here. The outer-sphere geometries were created by placing two hydrated divalent cations per primitive cell above the surface and removing three protons from hydration water molecules pointing toward the surface and one proton from a hydration water above the plane of cations. If two hydration waters were judged to be too close to each other, one was removed and the remaining water was left bridging two cations. The structures created this way are charge neutral, which is a good assumption considering that the measured surface charge values are much smaller than a single charge per unit cell.
Formation energy calculations in an aqueous solution of different ion structures on kaolinite (Ca2+, Mg2+, and Cl–) were performed using the reaction panel in COSMOtherm,78 with the DMOL3_PBE_C30_1301 parametrization for the reactions below, where the (aq) state was removed for clarity.
| 10 |
| 11 |
The free energy contributions from the partition functions of translation and rotation for all nonsurface species were included using standard expressions from a DMol3 frequency calculation for the molecules and ions exchanging with the surface (Ca(H2O)62+, Mg(H2O)62+, OH–, H2O, and Cl–), but the effect of vibrations were excluded for two reasons: the computational effort of calculating vibrational frequencies for the large periodic system would be considerably more expensive than the geometry optimization and more importantly, the accuracy of including vibrational entropy and zero point energy for an adsorbed system as complex as this would need careful assessment. The free energy of formation for the zigzag structure (eq 10) was then divided by 4 to get the energy per Ca(OH)2 unit and the free energy for OH– to Cl– exchange (eq 11) was divided by 2 to get the exchange energy per OH–/Cl– ion. Further description of the theoretical details is provided by Siretanu et al.49 and references therein.
Acknowledgments
We thank T. Hassenkam and S. L. S. Stipp (University of Copenhagen) for providing a kaolinite sample for AFM experiments.This work is a part of an Industrial Partnership Program of The Netherlands Organization for Scientific Research (NWO). Financial support was provided through the Exploratory Research (ExploRe) program of BP plc.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b03153.
Effects of pH and CaCl2 solutions, SEM images of AFM tips, and surface potentials (PDF)
Author Present Address
§ Department of Chemical Engineering, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, The Netherlands.
The authors declare no competing financial interest.
Supplementary Material
References
- Harvey C. C.; Murray H. H. Industrial clays in the 21st century: a perspective of exploration, technology and utilization. Appl. Clay Sci. 1997, 11 (5), 285–310. 10.1016/S0169-1317(96)00028-2. [DOI] [Google Scholar]
- Murray H. H. Traditional and new applications for kaolin, smectite, and palygorskite: a general overview. Appl. Clay Sci. 2000, 17 (5), 207–221. 10.1016/S0169-1317(00)00016-8. [DOI] [Google Scholar]
- Sposito G.The chemistry of soils, 2nd ed.; Oxford University Press: New York, 2008. [Google Scholar]
- Mohan K. K.; Vaidya R. N.; Reed M. G.; Fogler H. S. Water sensitivity of sandstones containing swelling and non-swelling clays. Colloids Surf., A 1993, 73, 237–254. 10.1016/0927-7757(93)80019-B. [DOI] [Google Scholar]
- Skrettingland K.; Holt T.; Tweheyo M. T.; Skjevrak I. Snorre Low-Salinity-Water Injection--Coreflooding Experiments and Single-Well Field Pilot. SPE Reservoir Evaluation & Engineering 2011, 14 (02), 182–192. 10.2118/129877-PA. [DOI] [Google Scholar]
- Tang G.-Q.; Morrow N. R. Influence of brine composition and fines migration on crude oil/brine/rock interactions and oil recovery. J. Pet. Sci. Eng. 1999, 24 (2), 99–111. 10.1016/S0920-4105(99)00034-0. [DOI] [Google Scholar]
- Austad T.; RezaeiDoust A.; Puntervold T. In Chemical mechanism of low salinity water flooding in sandstone reservoirs. SPE improved oil recovery symposium; Society of Petroleum Engineers: Richardson, TX, USA, 2010; DOI: 10.2118/129767-MS. [DOI] [Google Scholar]
- Sheng J.Modern chemical enhanced oil recovery: Theory and practice; Gulf: Burlington, MA, USA, 2010. [Google Scholar]
- Bantignies J.-L.; Cartier Dit Moulin C.; Dexpert H. Wettability contrasts in kaolinite and Illite clays: characterization by infrared and X-ray absorption spectroscopies. J. Phys. IV 1997, 7 (C2), C2-867–C2–869. 10.1051/jp4:1997261. [DOI] [Google Scholar]
- Preocanin T.; Abdelmonem A.; Montavon G.; Luetzenkirchen J.. Charging Behavior of Clays and Clay Minerals in Aqueous Electrolyte Solutions — Experimental Methods for Measuring the Charge and Interpreting the Results. In Clays, Clay Minerals and Ceramic Materials Based on Clay Minerals; Morari do Nascimento G., Ed.; Intech: Rijeka, Croatia, 2016; Chapter 3, DOI: 10.5772/62082. [DOI] [Google Scholar]
- Adekola F.; Fédoroff M.; Geckeis H.; Kupcik T.; Lefèvre G.; Lützenkirchen J.; Plaschke M.; Preocanin T.; Rabung T.; Schild D. Characterization of acid–base properties of two gibbsite samples in the context of literature results. J. Colloid Interface Sci. 2011, 354 (1), 306–317. 10.1016/j.jcis.2010.10.014. [DOI] [PubMed] [Google Scholar]
- Liu X.; Lu X.; Sprik M.; Cheng J.; Meijer E. J.; Wang R. Acidity of edge surface sites of montmorillonite and kaolinite. Geochim. Cosmochim. Acta 2013, 117, 180–190. 10.1016/j.gca.2013.04.008. [DOI] [Google Scholar]
- Kosmulski M.Surface charging and points of zero charge; CRC Press: Boca Raton, FL, USA, 2009; Vol. 145. [Google Scholar]
- Kosmulski M. The pH-dependent surface charging and the points of zero charge. J. Colloid Interface Sci. 2002, 253 (1), 77–87. 10.1006/jcis.2002.8490. [DOI] [PubMed] [Google Scholar]
- Schindler P.; Liechti P.; Westall J. Adsorption of copper, cadmium and lead from aqueous solution to the kaolinite/water interface. Netherlands J. Agric. Sci. 1987, 35 (3), 219–230. [Google Scholar]
- Wieland E.; Stumm W. Dissolution kinetics of kaolinite in acidic aqueous solutions at 25 C. Geochim. Cosmochim. Acta 1992, 56 (9), 3339–3355. 10.1016/0016-7037(92)90382-S. [DOI] [Google Scholar]
- Ferris A.; Jepson W. The exchange capacities of kaolinite and the preparation of homoionic clays. J. Colloid Interface Sci. 1975, 51 (2), 245–259. 10.1016/0021-9797(75)90110-1. [DOI] [Google Scholar]
- Smith R.; Narimatsu Y. Electrokinetic behavior of kaolinite in surfactant solutions as measured by both the microelectrophoresis and streaming potential methods. Miner. Eng. 1993, 6 (7), 753–763. 10.1016/0892-6875(93)90006-9. [DOI] [Google Scholar]
- Johnson S. B.; Dixon D. R.; Scales P. J. The electrokinetic and shear yield stress properties of kaolinite in the presence of aluminium ions. Colloids Surf., A 1999, 146 (1), 281–291. 10.1016/S0927-7757(98)00726-2. [DOI] [Google Scholar]
- Pierre A.; Ma K. Sedimentation behaviour of kaolinite and montmorillonite mixed with iron additives, as a function of their zeta potential. J. Mater. Sci. 1997, 32 (11), 2937–2947. 10.1023/A:1018688904094. [DOI] [Google Scholar]
- Hu Y.-h.; Liu X.-w. Chemical composition and surface property of kaolins. Miner. Eng. 2003, 16 (11), 1279–1284. 10.1016/j.mineng.2003.07.006. [DOI] [Google Scholar]
- Gupta V.Surface charge features of kaolinite particles and their interactions. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 2011. [Google Scholar]
- Kosmulski M., The pH dependent surface charging and points of zero charge. VII. Update. Adv. Colloid Interface Sci. 2017. 10.1016/j.cis.2017.10.005 [DOI] [PubMed] [Google Scholar]
- Schroth B. K.; Sposito G.. Surface charge properties of kaolinite; Materials Research Society Symposium Proceedings; Materials Research Society: Pittsburgh, PA, USA, 1997; p 87. [Google Scholar]
- Bolland M. D. A.; Posner A. M.; Quirk J. P. pH-independent and pH-dependent surface charges on kaolinite. Clays Clay Miner. 1980, 28 (5), 412–418. 10.1346/CCMN.1980.0280602. [DOI] [Google Scholar]
- Swartzen-Allen S. L.; Matijevic E. Surface and colloid chemistry of clays. Chem. Rev. 1974, 74 (3), 385–400. 10.1021/cr60289a004. [DOI] [Google Scholar]
- McBRIDE M. B. Origin and position of exchange sites in kaolinite: an ESR study. Clays Clay Miner. 1976, 24, 88–92. 10.1346/CCMN.1976.0240207. [DOI] [Google Scholar]
- Rand B.; Melton I. E. Particle interactions in aqueous kaolinite suspensions: I. Effect of pH and electrolyte upon the mode of particle interaction in homoionic sodium kaolinite suspensions. J. Colloid Interface Sci. 1977, 60 (2), 308–320. 10.1016/0021-9797(77)90290-9. [DOI] [Google Scholar]
- Williams D.; Williams K. Electrophoresis and zeta potential of kaolinite. J. Colloid Interface Sci. 1978, 65 (1), 79–87. 10.1016/0021-9797(78)90260-6. [DOI] [Google Scholar]
- Zhou Z.; Gunter W. D. The nature of the surface charge of kaolinite. Clays Clay Miner. 1992, 40 (3), 365–368. 10.1346/CCMN.1992.0400320. [DOI] [Google Scholar]
- Bolland M. D. A.; Posner A.; Quirk J. Surface charge on kaolinites in aqueous suspension. Aust. J. Soil Res. 1976, 14 (2), 197–216. 10.1071/SR9760197. [DOI] [Google Scholar]
- Van Olphen H.An introduction to clay colloid chemistry: For clay technologists, geologists, and soil scientists; Interscience: New York, 1977. [Google Scholar]
- Tombácz E.; Szekeres M. Surface charge heterogeneity of kaolinite in aqueous suspension in comparison with montmorillonite. Appl. Clay Sci. 2006, 34 (1), 105–124. 10.1016/j.clay.2006.05.009. [DOI] [Google Scholar]
- Schindler P. W.; Stumm W.. The surface chemistry of oxides, hydroxides, and oxide minerals. In Aquatic Surface Chemistry: Chemical Processes at the Particle-Water Interface; Stumm W., Ed.; John Wiley & Sons: New York, 1987; pp 83–110. [Google Scholar]
- Gupta V.; Hampton M. A.; Stokes J. R.; Nguyen A. V.; Miller J. D. Particle interactions in kaolinite suspensions and corresponding aggregate structures. J. Colloid Interface Sci. 2011, 359 (1), 95–103. 10.1016/j.jcis.2011.03.043. [DOI] [PubMed] [Google Scholar]
- Liu J.; Sandaklie-Nikolova L.; Wang X.; Miller J. D. Surface force measurements at kaolinite edge surfaces using atomic force microscopy. J. Colloid Interface Sci. 2014, 420, 35–40. 10.1016/j.jcis.2013.12.053. [DOI] [PubMed] [Google Scholar]
- Yin X.; Miller J. D. Wettability of kaolinite basal planes based on surface force measurements using atomic force microscopy. Miner. Metall. Proc. 2012, 29 (1), 13–19. [Google Scholar]
- Gupta V.; Miller J. D. Surface force measurements at the basal planes of ordered kaolinite particles. J. Colloid Interface Sci. 2010, 344 (2), 362–371. 10.1016/j.jcis.2010.01.012. [DOI] [PubMed] [Google Scholar]
- Sen Gupta S.; Bhattacharyya K. G. Adsorption of heavy metals on kaolinite and montmorillonite: a review. Phys. Chem. Chem. Phys. 2012, 14 (19), 6698–6723. 10.1039/c2cp40093f. [DOI] [PubMed] [Google Scholar]
- Vasconcelos I. F.; Bunker B. A.; Cygan R. T. Molecular dynamics modeling of ion adsorption to the basal surfaces of kaolinite. J. Phys. Chem. C 2007, 111 (18), 6753–6762. 10.1021/jp065687+. [DOI] [Google Scholar]
- Bhattacharyya K. G.; Gupta S. S. Adsorption of a few heavy metals on natural and modified kaolinite and montmorillonite: a review. Adv. Colloid Interface Sci. 2008, 140 (2), 114–131. 10.1016/j.cis.2007.12.008. [DOI] [PubMed] [Google Scholar]
- Coles C. A.; Yong R. N. Aspects of kaolinite characterization and retention of Pb and Cd. Appl. Clay Sci. 2002, 22 (1), 39–45. 10.1016/S0169-1317(02)00110-2. [DOI] [Google Scholar]
- Miranda-Trevino J. C.; Coles C. A. Kaolinite properties, structure and influence of metal retention on pH. Appl. Clay Sci. 2003, 23 (1), 133–139. 10.1016/S0169-1317(03)00095-4. [DOI] [Google Scholar]
- Yukselen Y.; Kaya A. Zeta potential of kaolinite in the presence of alkali, alkaline earth and hydrolyzable metal ions. Water, Air, Soil Pollut. 2003, 145 (1–4), 155–168. 10.1023/A:1023684213383. [DOI] [Google Scholar]
- Hunter R. J.; James M. Charge reversal of kaolinite by hydrolyzable metal ions: an electroacoustic study. Clays Clay Miner. 1992, 40 (6), 644–649. 10.1346/CCMN.1992.0400603. [DOI] [Google Scholar]
- Sutheimer S. H.; Maurice P. A.; Zhou Q. Dissolution of well and poorly crystallized kaolinites: Al speciation and effects of surface characteristics. Am. Mineral. 1999, 84 (4), 620–628. 10.2138/am-1999-0415. [DOI] [Google Scholar]
- Liu F.; Zhao C. L.; Mugele F.; van den Ende D. Amplitude modulation atomic force microscopy, is acoustic driving in liquid quantitatively reliable?. Nanotechnology 2015, 26 (38), 385703. 10.1088/0957-4484/26/38/385703. [DOI] [PubMed] [Google Scholar]
- Kumar N.; Zhao C.; Klaassen A.; van den Ende D.; Mugele F.; Siretanu I. Characterization of the surface charge distribution on kaolinite particles using high resolution atomic force microscopy. Geochim. Cosmochim. Acta 2016, 175, 100–112. 10.1016/j.gca.2015.12.003. [DOI] [Google Scholar]
- Siretanu I.; Ebeling D.; Andersson M. P.; Stipp S. L. S.; Philipse A.; Stuart M. C.; van den Ende D.; Mugele F. Direct observation of ionic structure at solid-liquid interfaces: a deep look into the Stern Layer. Sci. Rep. 2015, 4, 4956. 10.1038/srep04956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velamakanni B. V.; Lange F. F. Effect of interparticle potentials and sedimentation on particle packing density of bimodal particle distributions during pressure filtration. J. Am. Ceram. Soc. 1991, 74 (1), 166–172. 10.1111/j.1151-2916.1991.tb07313.x. [DOI] [Google Scholar]
- Tulpar A.; Henderson D. B.; Mao M.; Caba B.; Davis R. M.; Van Cott K. E.; Ducker W. A. Unnatural proteins for the control of surface forces. Langmuir 2005, 21 (4), 1497–1506. 10.1021/la047896w. [DOI] [PubMed] [Google Scholar]
- Al-Abadleh H. A.; Grassian V. FT-IR study of water adsorption on aluminum oxide surfaces. Langmuir 2003, 19 (2), 341–347. 10.1021/la026208a. [DOI] [Google Scholar]
- Eng P. J.; Trainor T. P.; Brown G. E. Jr; Waychunas G. A.; Newville M.; Sutton S. R.; Rivers M. L. Structure of the hydrated α-Al2O3 (0001) Surface. Science 2000, 288 (5468), 1029–1033. 10.1126/science.288.5468.1029. [DOI] [PubMed] [Google Scholar]
- Hass K. C.; Schneider W. F.; Curioni A.; Andreoni W. The chemistry of water on alumina surfaces: Reaction dynamics from first principles. Science 1998, 282 (5387), 265–268. 10.1126/science.282.5387.265. [DOI] [PubMed] [Google Scholar]
- Hass K.; Schneider W.; Curioni A.; Andreoni W. First-principles molecular dynamics simulations of H2O on α-Al2O3 (0001). J. Phys. Chem. B 2000, 104 (23), 5527–5540. 10.1021/jp000040p. [DOI] [Google Scholar]
- Lodziana Z.; Nørskov J. K.; Stoltze P. The stability of the hydroxylated (0001) surface of alpha-Al2O3. J. Chem. Phys. 2003, 118 (24), 11179–11188. 10.1063/1.1574798. [DOI] [Google Scholar]
- Liu X.; Cheng J.; Sprik M.; Lu X.; Wang R. Understanding surface acidity of gibbsite with first principles molecular dynamics simulations. Geochim. Cosmochim. Acta 2013, 120, 487–495. 10.1016/j.gca.2013.06.043. [DOI] [Google Scholar]
- Franks G. V.; Meagher L. The isoelectric points of sapphire crystals and alpha-alumina powder. Colloids Surf., A 2003, 214 (1), 99–110. 10.1016/S0927-7757(02)00366-7. [DOI] [Google Scholar]
- Franks G. V.; Gan Y. Charging behavior at the alumina–water interface and implications for ceramic processing. J. Am. Ceram. Soc. 2007, 90 (11), 3373–3388. 10.1111/j.1551-2916.2007.02013.x. [DOI] [Google Scholar]
- Kumar N.; Wang L.; Siretanu I.; Duits M.; Mugele F. Salt dependent stability of stearic acid Langmuir–Blodgett films exposed to aqueous electrolytes. Langmuir 2013, 29 (17), 5150–5159. 10.1021/la400615j. [DOI] [PubMed] [Google Scholar]
- Ricci M.; Spijker P.; Voïtchovsky K. Water-induced correlation between single ions imaged at the solid–liquid interface. Nat. Commun. 2014, 5, 4400. 10.1038/ncomms5400. [DOI] [PubMed] [Google Scholar]
- Bargar J. R.; Towle S. N.; Brown G. E.; Parks G. A. XAFS and bond-valence determination of the structures and compositions of surface functional groups and Pb(II) and Co(II) sorption products on single-crystal alpha-Al2O3. J. Colloid Interface Sci. 1997, 185 (2), 473–492. 10.1006/jcis.1996.4574. [DOI] [PubMed] [Google Scholar]
- Bargar J. R.; Brown G. E.; Parks G. A. Surface complexation of Pb(II) at oxide-water interfaces 0.2. XAFS and bond-valence determination of mononuclear Pb(II) sorption products and surface functional groups on iron oxides. Geochim. Cosmochim. Acta 1997, 61 (13), 2639–2652. 10.1016/S0016-7037(97)00125-7. [DOI] [Google Scholar]
- Katz L. E.; Criscenti L. J.; Chen C. C.; Larentzos J. P.; Liljestrand H. M. Temperature effects on alkaline earth metal ions adsorption on gibbsite: Approaches from macroscopic sorption experiments and molecular dynamics simulations. J. Colloid Interface Sci. 2013, 399, 68–76. 10.1016/j.jcis.2012.05.011. [DOI] [PubMed] [Google Scholar]
- Geckeis H.; Lützenkirchen J.; Polly R.; Rabung T.; Schmidt M. Mineral-water interface reactions of actinides. Chem. Rev. 2013, 113 (2), 1016–1062. 10.1021/cr300370h. [DOI] [PubMed] [Google Scholar]
- Perron H.; Domain C.; Roques J.; Drot R.; Simoni E.; Catalette H. Theoretical first step towards an understanding of the uranyl ion sorption on the rutile TiO2(110) face: A DFT periodic and cluster study. Radiochim. Acta 2006, 94 (9–11), 601–607. 10.1524/ract.2006.94.9-11.601. [DOI] [Google Scholar]
- Liu X.; Cheng J.; Sprik M.; Lu X.; Wang R. Surface acidity of 2:1-type dioctahedral clay minerals from first principles molecular dynamics simulations. Geochim. Cosmochim. Acta 2014, 140, 410–417. 10.1016/j.gca.2014.05.044. [DOI] [Google Scholar]
- Bourg I. C.; Sposito G. Molecular dynamics simulations of the electrical double layer on smectite surfaces contacting concentrated mixed electrolyte (NaCl-CaCl2) solutions. J. Colloid Interface Sci. 2011, 360 (2), 701–715. 10.1016/j.jcis.2011.04.063. [DOI] [PubMed] [Google Scholar]
- Porus M.; Labbez C.; Maroni P.; Borkovec M. Adsorption of monovalent and divalent cations on planar water-silica interfaces studied by optical reflectivity and Monte Carlo simulations. J. Chem. Phys. 2011, 135 (6), 064701. 10.1063/1.3622858. [DOI] [PubMed] [Google Scholar]
- Towle S. N.; Bargar J. R.; Brown G. E.; Parks G. A. Sorption of Co (II) on metal oxide surfaces: II. Identification of Co (II)(aq) adsorption sites on the (0001) and (1102) surfaces of α-Al2O3 by grazing-incidence XAFS spectroscopy. J. Colloid Interface Sci. 1999, 217 (2), 312–321. 10.1006/jcis.1999.6351. [DOI] [PubMed] [Google Scholar]
- Bargar J. R.; Fitts J. P.; Brown G. E. Jr; Chambers S. A.; Trainor T. P. In-situ grazing incidence EXAFS study of Pb(II) chemisorption on hematite (0001) and (1–102) surfaces. Langmuir 2004, 20 (5), 1667–1673. 10.1021/la0354133. [DOI] [Google Scholar]
- Bickmore B. R.; Tadanier C. J.; Rosso K. M.; Monn W. D.; Eggett D. L. Bond-valence methods for pK a prediction: Critical reanalysis and a new approach. Geochim. Cosmochim. Acta 2004, 68 (9), 2025–2042. 10.1016/j.gca.2003.11.008. [DOI] [Google Scholar]
- Jodin M.-C.; Gaboriaud F.; Humbert B. Limitations of potentiometric studies to determine the surface charge of gibbsite γ-Al (OH) 3 particles. J. Colloid Interface Sci. 2005, 287 (2), 581–591. 10.1016/j.jcis.2005.02.032. [DOI] [PubMed] [Google Scholar]
- Klaassen A.; Liu F.; Van den Ende D.; Mugele F.; Siretanu I. Impact of surface defects on the surface charge of gibbsite nanoparticles. Nanoscale 2017, 9 (14), 4721–4729. 10.1039/C6NR09491K. [DOI] [PubMed] [Google Scholar]
- Zhao C.; Ebeling D.; Siretanu I.; van den Ende D.; Mugele F. Extracting local surface charges and charge regulation behavior from atomic force microscopy measurements at heterogeneous solid-electrolyte interfaces. Nanoscale 2015, 7 (39), 16298–16311. 10.1039/C5NR05261K. [DOI] [PubMed] [Google Scholar]
- Klamt A.; Schuurmann G. Cosmo - a New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc., Perkin Trans. 2 1993, (5), 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
- Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27 (15), 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Eckert F.; Klamt A.. COSMOtherm, Version C3.0, Release 13.01; COSMOlogic: Leverkusen, Germany, 2013.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.