High-resolution CBV-fMRI allows mapping of laminar activity and connectivity of cortical input and output in human M1

Summary

Layer-dependent fMRI allows measurements of information flow in cortical circuits, as afferent and efferent connections terminate in different cortical layers. However, it is unknown to what level human fMRI is specific and sensitive enough to reveal directional functional activity across layers. To answer this question, we developed acquisition- and analysis-methods for BOLD and cerebral-blood-volume (CBV)-based laminar fMRI, and used these to discriminate four different tasks in the human motor cortex (M1). In agreement with anatomical data from animal studies, we found evidence for somatosensory and premotor input in superficial layers of M1, and for cortico-spinal motor-output in deep layers. Laminar resting-state fMRI showed directional functional connectivity of M1 with somatosensory and premotor areas. Our findings demonstrate that CBV-fMRI can be used to investigate cortical activity in humans with unprecedented detail, allowing investigations of information flow between brain regions and outperforming conventional BOLD results that are often hidden under vascular biases.

eTOC Blurb

Huber et al. demonstrate an MRI method to measure brain activity changes at the spatial resolution of cortical layers in humans. This allows investigations of directional functional connectivity, paving the way for non-invasive studies investigating information flow between brain regions.

Introduction

Neural activity in the human brain evokes local changes in oxygen consumption, blood flow and blood vessel dilation. These hemodynamic changes can be measured with functional magnetic resonance imaging (fMRI). Increasing the spatial resolution allows the measurement of stimulus-driven fMRI and resting-state (rs) fMRI of cortical layers. Based on what is known of cortical function across layers, layer-specific fMRI may allow discrimination of activation that reflects cortical input or output. Layer-specific rs-fMRI may allow assessment of the functional connections that mediate this input and output. Conventional high-resolution blood oxygenation level dependent (BOLD) fMRI is not well suited to resolve layer-specific activity due to its poor spatial specificity (Turner, 2002), unclear noise characteristics, and its non-quantitative and indirect nature (Buxton et al., 2014; Gagnon et al., 2016; Goense and Logothetis, 2006). CBV-based fMRI can provide higher spatial specificity making laminar fMRI more specific and robust (Goense et al., 2012; Huber et al., 2015; Kennerley et al., 2005; Kim et al., 2013; Uludaǧ and Blinder, 2017).

Here, we introduce an fMRI method and analysis pipeline to measure CBV changes with submillimeter resolution. We apply it to discriminate the laminar activity patterns elicited in M1 by four stimuli that differ in their relative contributions of neural activity associated with input and output. Studies in animals have shown that the anatomical connections providing cortico-cortical input to M1 largely terminate in superficial layers (II/III), while cortico-spinal output from M1 originates predominantly in the deep layers (Vb/VI) (Mao et al., 2011; Weiler et al., 2008) (Fig. 1A–B). In this study, we explored whether functional activity in superficial and deep layers can be separated, by modeling them as two signal sources at different cortical depths. We modulated the relative degree of cortical input- or output activity in superficial and deeper layers by using various sensorimotor tasks that rely to different degrees on processing by superficial and deep layers (Fig. 1C). We investigated whether the expected signatures of cortical input and output can be determined from the laminar fMRI profiles. We compared the ability to show layer-dependent activity between CBV-based fMRI and conventional BOLD fMRI. Layer-dependent rs-fMRI was used to show directionality of the laminar functional connectivity patterns.

Fig. 1. Model of the laminar circuitry in M1.

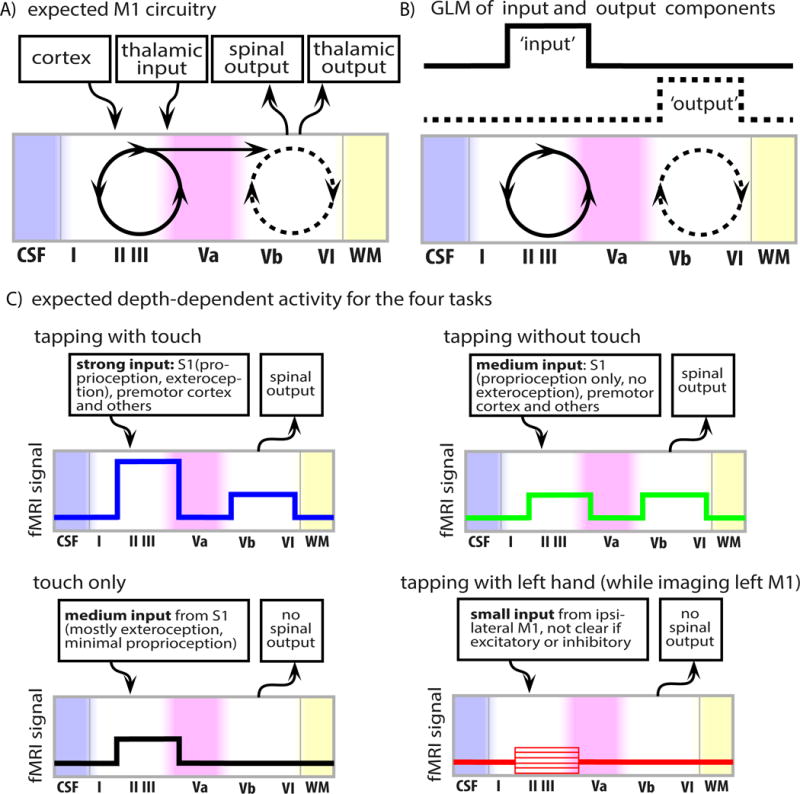
A) The Model of layer-dependent circuitry based on the literature (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008). B) A spatial general linear model (GLM) across laminae is used to separate laminar input- and output-driven functional activity. The GLM consists of two non-overlapping components (boxcar functions) representing input- and output-activity, respectively. C) Expected modulations of cortico-cortical input-activity and cortico-spinal output-activity for the four sensorimotor tasks. Note that for ipsilateral tapping (red in panel C) it is not known whether the input in superficial lamina is predominantly positive or negative.

Results

Task-evoked laminar fMRI

To investigate cortical layer-dependent brain responses reflecting input- and output-driven activity, the motor and sensory activity of the fingers was modulated using four different tasks:

1. Unilateral pinch-like finger-tapping movement, with thumb to forefinger touch. This is expected to evoke strong cortico-spinal output from the primary motor cortex (M1). Furthermore, it is expected to evoke strong cortico-cortical input to M1 from the premotor and somatosensory cortices (Papale and Hooks, 2017; Weiler et al., 2008).

2. The same finger movement as in A, but without contact between the fingers, was used to evoke the similar output-related activation in M1 while we expect a reduced cortico-cortical input to M1 from the somatosensory cortex.

3. Passive touch of stationary fingers with an abrasive cushion was used to provide somatosensory input to M1 without motor output.

4. Unilateral tapping with touch (same task as A), but using the opposite (ipsilateral) hand was employed to evoke inter-hemispheric input.

We simultaneously measured changes in the cerebral blood volume (CBV) and blood oxygenation level dependent (BOLD) response using the SS-SI-VASO method (Huber et al., 2014; Lu et al., 2003) with a 3D-EPI readout (Poser et al., 2010) at 7T. The nominal resolution was 0.75 mm across cortical depths with 1.5 mm thick slices perpendicular to the precentral bank of the central sulcus (Fig. 2A) – i.e. the hand knob. Cortical depths (laminar structures) and cortical distances (columnar structures) in M1 were calculated based on simultaneously acquired anatomical and functional image contrasts (Fig. 2B–C). Task-induced and resting-state fMRI signal changes were analyzed using a coordinate system based on layers and columns that was calculated for each individual subject (Fig. 2B–C and Fig. S5F). We divided the cortex into 20 equi-volume layers. The approximate location of layer Va was assigned based on depth-dependent landmarks visible in the high-resolution anatomical images (Fig. S1).

Fig. 2. Acquisition and analysis methods for measuring laminar fMRI activation patterns in the hand region of M1 induced by right hand finger tapping (with touch) in a single participant.

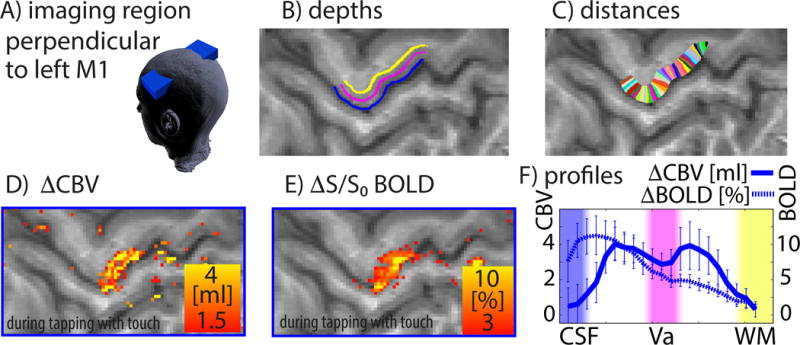
A) The imaging slice is aligned perpendicular to the cortical layers of the hand representation in the left motor cortex, and slices are tilted as indicated by the blue box. B–C) To analyze the high-resolution data, we use a cortical coordinate system of laminar structures and columnar structures. D) The CBV map reveals activity in superficial and deep cortical layers, while the BOLD map in E) shows strongest activity in superficial laminae only. Profiles in F) refer to the columnar structures between the black arrows in C). Error bars refer to standard deviations across 12 consecutive one-minute trials (see also Fig. S1–S3).

Functional MRI signal changes in M1 were found in all 11 participants. Both BOLD- and CBV changes reflect changes in neural activity in M1. In the maps of BOLD signal change, functional activity showed a monotonic decrease across cortical layers (Fig. 2F, dotted trace). CBV changes, however, show two peaks in different laminae (Fig. 2D,F, solid trace): superficial layers II/III with mainly cortico-cortical connections and the deeper layers Vb/VI with afferent cortico-spinal connections. This double peak signature was visible in all participants and was significantly stronger for CBV-responses than for BOLD (see Larkin-F-scores in Fig. S3E and STAR methods section).

Layer-dependent activity was highly reproducible across days (Fig. S2A) and participants (Fig. S3A-B). All participants’ individual results are shown in Fig. S3. Depth-dependent activity modulations across tasks could be detected in individual activation maps (Fig. S2B). Fig. 3A shows the group average responses mapped onto one individual M1 template. The CBV activity in the superficial- and deep cortical laminae differed across tasks. Tapping with touch evoked strongest activity in the superficial input-dominated laminae with a secondary peak in deeper output laminae. Tapping without touch showed a clear reduction of the CBV response in superficial cortical laminae, presumably due to the reduced input from sensory areas. Sensory input alone evoked CBV increases in the superficial M1 input layers only. Tapping with the left (ipsilateral) hand while imaging left M1 evoked negative local CBV changes in superficial input laminae of the thumb-index finger region, which could represent inhibitory transcallosal input (Stefanovic et al., 2004). The BOLD responses showed mostly similar patterns, however, distinctions between layers were less clear.

Fig. 3. Averaged layer-dependent fMRI responses in the motor cortex of all participants in response to four different sensorimotor tasks.

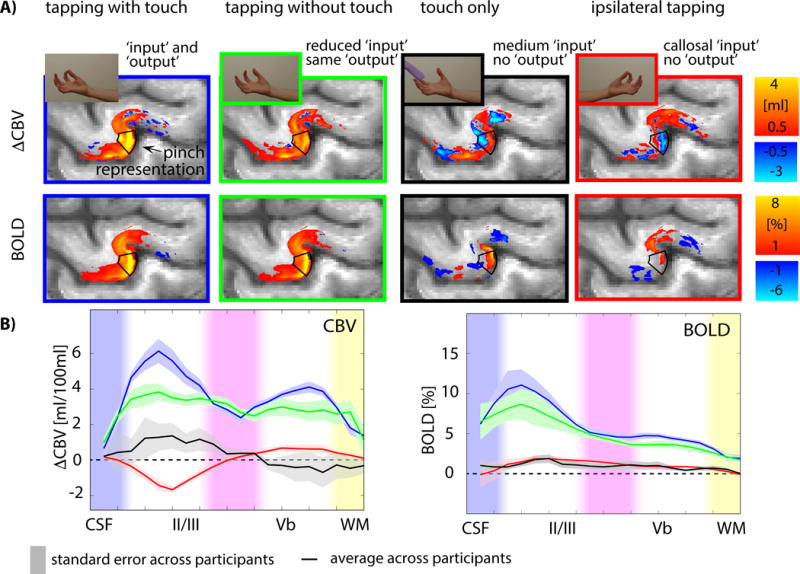
A) The four tasks evoked fMRI signals that varied with cortical depth in the thumb-index finger pinch motor area (indicated by the black box; see also Fig. S5F). B) The average cortical profiles across all participants show different laminar patterns in superficial and deep cortical laminae for the different tasks. Shaded areas refer to the standard error of mean across participants. See also Figs. S2–S4. Individual participant’s responses can be seen in Fig. S3.

The fMRI-based laminar profiles of input and output activity in the area that represents thumb and index-finger motion in M1 (black box in Fig. 3A) were reproducible across participants (Fig. S3).

The input- and output-driven activity in the superficial and deep layers was quantified using the model in Fig. 1B for all profiles, and is shown in Fig. 4 for all tasks and participants. The BOLD signal shows similar features compared to CBV. For both contrasts, the data points of different participants cluster together. However, the clusters overlap less for CBV-fMRI than for BOLD (note the significantly smaller contrast-to-noise-ratio for BOLD compared to CBV-fMRI in Fig. 4C). When applying a leave-one-out classification analysis, the less overlapping VASO data points improve separability leading to a higher classification accuracy compared to BOLD data (Fig. 4D).

Fig. 4. Inter-participant variability of input and output activity for different tasks.

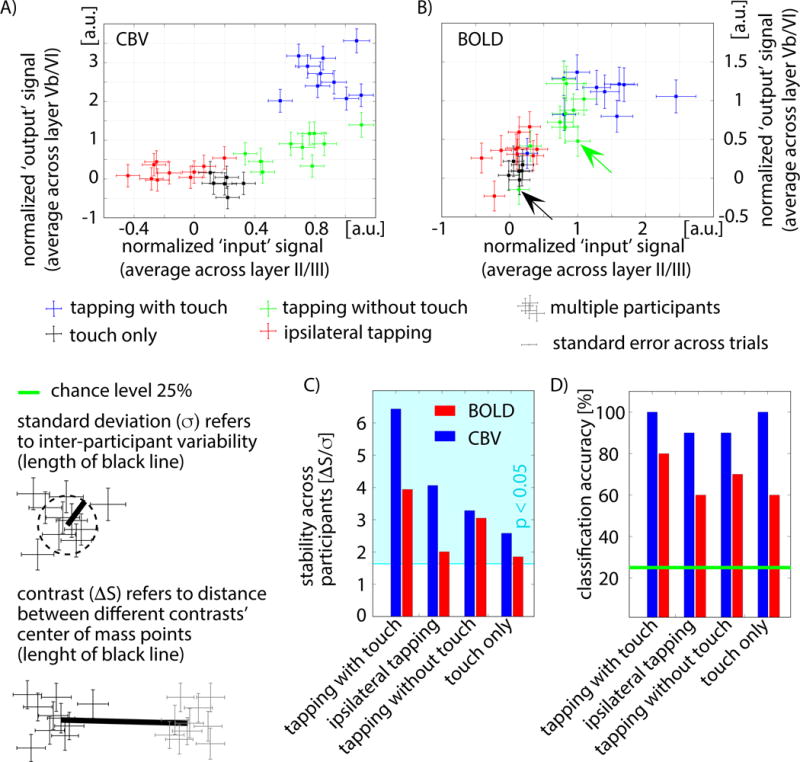
A–B) The participant-specific activity in superficial laminae (x-axis) and deeper laminae (y-axis) represented as scatter plots. Following the model of Fig. 1B, the axes indicate input- and output-driven activity of the different tasks. Each data point refers to one participant’s response to one task (average over trials). It can be seen that different tasks (colors) cluster together. For CBV (panel A), the clusters are more easily distinguishable than for BOLD-fMRI (panel B). The distinguishability between tasks was quantified by means of the contrast-to-noise ratio (ΔS/σ) (panel C), and by means of classification accuracy (panel D). CBV-based fMRI showed higher contrast-to-noise-ratios and a higher classification accuracy of up to 100% across tasks compared to BOLD (bootstrapping: p < 0.05). Conventional BOLD seems to contain similar laminar input-output signatures across tasks as CBV-fMRI (similar distribution of clusters), but with smaller inter-participant separability between tasks.

Laminar resting-state fMRI

Laminar resting-state activity can reveal directional connectivity between brain areas. Similar to task-induced signal changes, resting-state signal changes were largest in superficial and deep cortical laminae (layers II/III and Vb/VI respectively). Within-area characteristics of layer-dependent resting-state time course similarities are shown in the correlation matrices in Fig. 5. Here, resting-state correlation was determined across cortical layers of M1. Values close to the diagonal in upper and deeper layers were higher than off-diagonal values. The off-diagonal correlations suggest that superficial and deep cortical laminae share similarities in their resting-state time courses, while there are also temporal fluctuations that are not simultaneously occurring in superficial and deep layers. In this study, we investigate these similarities and differences of signal fluctuations in superficial and deeper laminae and we compared the signal fluctuations with signal fluctuations in connected brain areas, such as S1, premotor cortex, ipsilateral M1.

Fig. 5. Layer-dependent resting-state features across cortical depths.

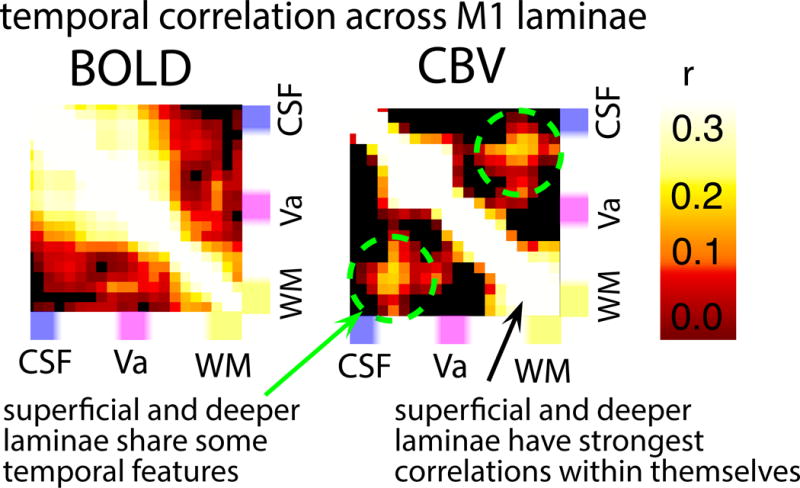
Depiction of single-participant resting-state features, which are the basis of the investigations of functional connectivity later in this paper. Columns and rows of the matrices refer to the same area within M1 of a representative participant. The BOLD fluctuations show strong correlations in superficial layers. The CBV correlation matrix suggests both, strong correlation in superficial layers and strong correlation in deeper layers. Furthermore, there are moderately high correlation values in off-diagonal elements corresponding to moderately synchronized activity between superficial and deep layers (dashed green circles). This suggests that superficial and deeper layers share some features of resting-state fluctuations, while there are still differences and some temporal fluctuation are occurring in individual laminae only.

Figure 6 shows functional maps from a single participant generated using seeds in superficial (blue) and deep (green) layers of M1. The signal fluctuation components that were solely occurring in superficial input laminae were mostly associated with fluctuations in sensory areas, while signal fluctuation components that occurred in deep output laminae, were mostly synchronized with fluctuations in premotor areas and contralateral motor areas. The property that superficial and deep layers showed functional connectivity to different brain areas can be used to infer the directional connectivity of M1. The depicted functional connectivity strength distribution indicates that the fluctuations in premotor areas generate M1 output, while the fluctuations in S1 generates (feedback) input into M1 that is not associated with correspondingly strong output.

Fig 6. CBV-based functional connectivity maps using seeds in different layers of M1.

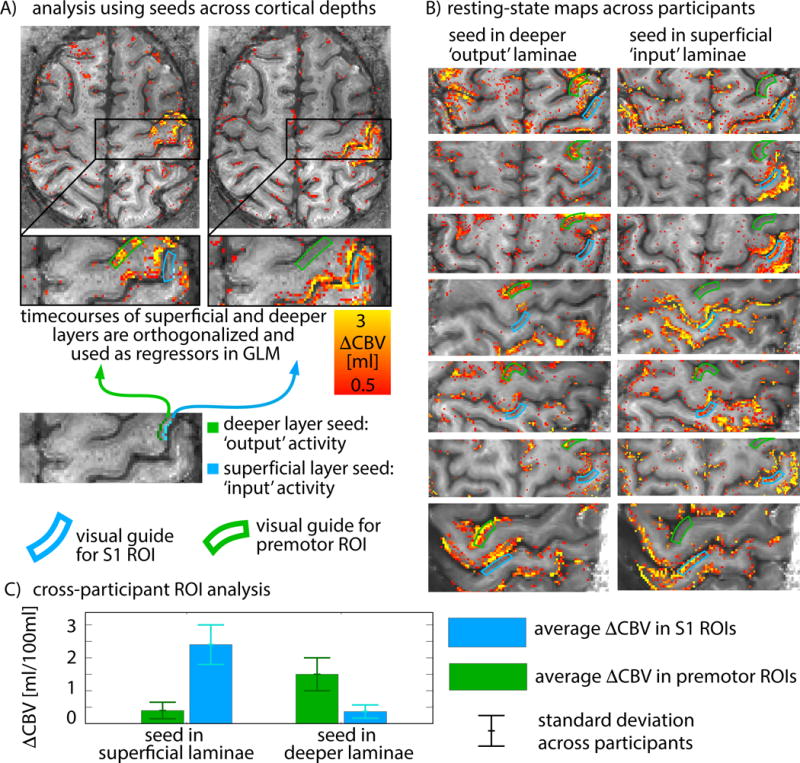
A) Seed regions are taken from the part of the primary motor cortex that shows the strongest tapping-induced activity in superficial and deeper laminae. To account for the fact that superficial and deeper laminae share a lot of similarities (Fig. 5), time courses from seed regions in superficial and deeper laminae are orthogonalized to only represent those components that are unique to the specific laminae. Functional connectivity strengths to the superficial and deeper laminae are investigated in two target ROIs: premotor cortex and primary sensory cortex (green and blue ROIs). B) Functional connectivity maps for seeds in superficial and deeper laminae across participants. In all participants, deeper M1 laminae show strongest functional connectivity with premotor areas, whereas superficial M1 laminae show stronger connectivity with sensory areas. Average functional connectivity strengths are summarized in panel C. Functional connectivity in S1 is significantly stronger (p < 0.01) for seeds in superficial laminae compared to seeds in deeper laminae. Whereas functional connectivity in premotor cortex is significantly stronger (p < 0.01) for seeds in deeper laminae compared to seeds in superficial laminae. These results suggest that output components of M1 are associated with activity in premotor areas. S1, however, is more associated with input to M1 and does not trigger corresponding output.

Fig. 7 depicts how depth-dependent profiles of functional connectivity in M1 differ for seed regions located in primary sensory cortex, premotor cortex and ipsilateral primary motor cortex. Resting-state fluctuations in S1 were predominantly associated with input to M1 (connectivity to superficial layers), while resting-state fluctuations in premotor and ipsilateral motor areas were associated with relatively stronger output activity (connectivity to deep layers). The depth-dependent profiles of functional connectivity with S1, premotor and ipsilateral M1 were significantly different from connectivity with randomly chosen seed regions (Fig. 7C).

Fig. 7. Resting-state laminar functional connectivity for seed regions in cortical areas across the brain.

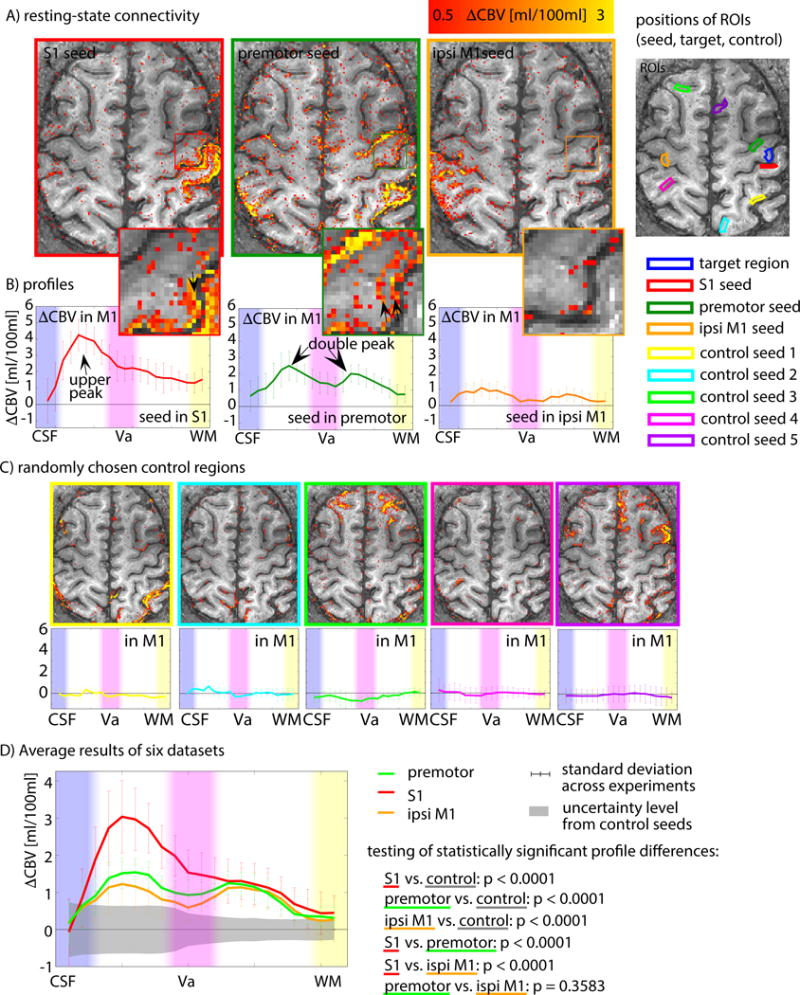
A–B) Cortical depth-dependent functional connectivity of M1 with seed regions of premotor cortex, primary sensory cortex, and ipsilateral primary motor cortex for a representative participant. S1 shows strongest functional-connectivity strengths in superficial laminae of M1, whereas seed regions of premotor cortex and ipsilateral primary motor cortex show increased functional connectivity not only in superficial laminae, but also a relatively stronger secondary peak in deeper laminae. C) To investigate whether the shape of the resting-state profiles is dominated by depth-dependent signal variance or vascular density, they are compared to random control regions outside the sensorimotor system. Locations and functional connectivity with 5 selected random seed regions are depicted. D) Average cortical connectivity profiles in M1 for different seed regions from six datasets. The gray area refers to the confidence interval, where 95% of control ROI connectivity values fall into. The depth-dependent functional connectivity with seed regions of S1, premotor cortex and ipsilateral M1 are significantly different from random control regions (p<0.0001). The data shown here suggest that S1 sends input to M1 without triggering corresponding activity in output laminae. The connections between M1 and premotor cortex produce relatively stronger output activity as well.

Discussion

Using blood-volume-sensitive fMRI task and resting-state fMRI in the human sensorimotor system, we measured directional information processing in the brain. Input to the motor cortex evoked activity in superficial laminae, while motor output yielded activity in deep laminae. This functional connectivity pattern is expected from anatomical tracer studies in animals (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008) and is used here as a support that the proposed method can indeed infer directionality information from laminar fMRI.

Comparing task-based CBV and BOLD fMRI, we showed that the CBV signal can mitigate disadvantages of the BOLD signal. CBV-fMRI can capture depth-dependent activity with higher localization specificity across cortical depth (Fig. 2–3 and Fig. S3). The improved laminar specificity of CBV-fMRI compared to conventional BOLD provides two important practical benefits. Firstly, CBV-fMRI can distinguish between superficial and deeper laminae with higher accuracy than BOLD. This means that input-driven and output-driven activity can be better separated as two separate peaks (Fig. 2D, F) across all participants (Fig. S3A–C) in a statistically significant manner (Fig. S3E). This can elucidate interpretations about the micro-circuitry of the different laminae. Secondly, CBV-fMRI can distinguish between different tasks – conditions that engage the laminar circuitries differentially – with higher accuracy than BOLD. This means that CBV-fMRI can better distinguish the engaged input-output characteristics for the four sensorimotor tasks used in this study. The higher distinguishability is seen in both the significantly higher contrast-to-noise ratio and the higher task classification accuracy across participants (Fig. 4C–D).

The higher localization specificity of CBV-fMRI compared to BOLD-based fMRI is expected from previous animal studies (Goense et al., 2012; Harel et al., 2006; Huber et al., 2014; Kennerley et al., 2005; Kim et al., 2013; Zhao et al., 2006). It is associated with the higher sensitivity of CBV-fMRI to small vessel in close proximity to the layer-specific synaptic activity. Gradient-echo BOLD, however, is predominantly sensitive to draining veins located on the cortical surface (Gagnon et al., 2016; Koopmans et al., 2010; Menon et al., 1995; Polimeni et al., 2010a; Turner, 2002). The draining of the venous blood to the cortical surface makes the laminar origin of the GE-BOLD signal more ambiguous.

The reason for the higher distinguishability of laminar profiles across tasks in CBV-fMRI compared to BOLD (discussed above) can be associated with the fact that BOLD has additional sources of variability in its depth-dependent profiles compared to CBV-fMRI. Due to the non-linear interaction of CBF, CBV and CMRO_2, the BOLD signal is difficult to quantify and difficult to interpret as a measure of brain activity (Buxton et al., 2014). As such, inter-participant variations in venous baseline oxygenation directly scale the BOLD responses without appearing to influence the CBV-responses (Lu et al., 2008). This BOLD confound can affect comparisons of superficial and deep laminae because of their differences in vascularization densities (Uludaǧ and Blinder, 2017). Furthermore, large pial veins that drain distant brain areas (e.g., Fig. S1) could also contaminate the BOLD signal in superficial M1 laminae without affecting the CBV-fMRI signal.

Previous fMRI work in humans suggests that cortical depth-dependent fMRI can address questions about feed-forward vs. feedback-driven activity in auditory and visual cortex using the BOLD signal (Fracasso et al., 2016; Kok et al., 2016; De Martino et al., 2015; Muckli et al., 2015; Olman et al., 2012; Polimeni et al., 2010b). Because of the limitations of BOLD fMRI discussed above, it is difficult to make neuroscientific interpretations based on raw signal changes in individual laminae, so researchers have increasingly turned to higher order analysis methods. Instead of interpreting the raw fMRI signal directly, they use computational approaches to account for vascular biases and reveal more information about the underlying brain mechanisms using relative signal responses (as opposed to absolute signal responses). Neuroscientific interpretations of depth-dependent fMRI have been made based on data processing outcomes such as modulations in the population receptive field properties (Fracasso et al., 2016) or modulations of the population tuning curve widths (De Martino et al., 2015). Other successful approaches of higher order analysis beyond comparing raw activity across cortical depth profiles have been shown as modulations in task classification accuracy (Muckli et al., 2015) to reveal the directional information flow between brain areas.

Using CBV-fMRI in place of BOLD does not preclude the use of such computational approaches. The methodology shown in this study provides high-quality data with minimal contaminations from vascular biases and with Nyquist-level sampling across input and output laminae. This can improve the quality and accuracy of the computational analysis outcomes and allow computational models to reveal finer-scale features and higher-order brain mechanisms.

Aside from CBV-fMRI, there are alternative approaches to obtain a higher localization specificity with BOLD-based fMRI methods: (A) the dependence of the BOLD contrast mechanism on CBV, CBF, and CMRO₂ is well understood and can therefore be used to predict vascular biases in laminar BOLD-fMRI (Gagnon et al., 2013; Heinzle et al., 2016; Markuerkiaga et al., 2016). Theoretically, a model inversion could therefore be used to remove potential vascular biases from experimentally measured cortical profiles (see Fig. S5I and Tab. S1). (B) Partial voluming of signal from neighboring laminae in the same fMRI voxel can limit the depth-specificity of high-resolution fMRI. This effect of partial voluming can be quantified and modeled in a so-called spatial GLM (Kok et al., 2016). Thus, spatial unmixing (GLM-inversion) can be used to improve the depth-specificity of conventional BOLD-fMRI (Fig. S5J and Tab. S1). (C) Spin-echo BOLD acquisition methods are less affected by layer-unspecific large draining veins (Goense and Logothetis, 2006), especially at high field strengths. Spin-echo methods are limited, however, by a smaller sensitivity compared to GE-BOLD – similar to CBV. Furthermore, depending on the specific variant and readout scheme of the spin-echo methodology, it can still contain considerable signal from unspecific veins (see Fig. S4 and (Goense and Logothetis, 2006; Kemper et al., 2015, 2017)). For the specific application of laminar motor cortex imaging at 7T in this study, we found that CBV-fMRI has a better sensitivity-specificity compromise than most spin-echo variants (Fig. S4).

Note the straightforward applicability of the MRI method used here. The high-resolution data of the proposed CBV method provided an unprecedented non-invasive glimpse into the laminar circuits of the human brain. And it does so using widely available MRI scanners and experimental parameters. The MRI sequence is easy to implement and only requires one additional inversion pulse compared to BOLD sequences. Our method used only 12 min of scanning to provide all required functional and anatomical data to allow the identification of increased activity in different cortical layers in a single participant (Figs. 2, S2–S3). Anatomical and functional images are obtained simultaneously, eliminating the need for image registration. This simplifies the data analyses substantially and avoids blurring and errors arising from image registration (Kashyap et al., 2017; Renvall et al., 2016). All data were acquired using hardware that is available on most 7T scanners, without the need for specialized head-gradient coils or high-density RF arrays that have been used in multiple previous depth-dependent fMRI studies.

Despite the advantages of layer-dependent CBV-fMRI and its straightforward applicability, it has some limitations that should be considered when applying this method to neuroscientific studies. The foremost limitation is that the reduced time-course stability of VASO results in a correspondingly higher detection threshold and reduced sensitivity of approximately 50% compared to that of BOLD (Huber et al., 2016a). Hence, single-participant single-slice CBV data are often noisier than GE-BOLD data (Fig. S3), especially for tasks with weak brain activity changes (e.g. Fig. S2B). The higher sensitivity in GE-BOLD compared to VASO comes mostly from additional BOLD signal amplification in the large draining veins. Thus, the additional sensitivity in BOLD is sometimes driven by a widespread signal that is not specific to cortical laminae. This means that in cases where laminar specificity is not necessary (e.g., to find the approximate location of ROIs in the range of several mm), the lower detection threshold of BOLD fMRI will show clear advantages over VASO. The second important disadvantage of VASO is its relatively restrictive MRI sequence parameter space (Huber et al., 2017a). Due to the necessary application of a spin-inversion pulse in VASO, it has a reduced temporal acquisition efficiency of 30–50% compared to that of GE-BOLD. This limits its repetition time (TR) to approximately 1.5–3 s. For TRs in this range, the large number of slices required for whole-brain acquisitions can only be achieved with correspondingly high parallel imaging acceleration factors (Huber et al., 2016a). Since this is not recommended for ultra-high resolution fMRI (Huber et al., 2017a), the imaging coverage of layer-dependent CBV-fMRI is limited to about 30–50% of that of GE-BOLD.

In addition to the known input-output connections of M1, we also described additional layer-dependent connectivity patterns that where unexpected and indicate unexpected findings. We described inter-hemispheric laminar connections between left and right motor cortices. Left-hand finger tapping (while imaging the left M1) evokes negative fMRI activity that is confined to the superficial input layers. This negative signal change in input laminae could refer to inter-hemispheric inhibition (Stefanovic et al., 2004). Note also that the deeper output layers of the left motor cortex during left hand tapping show positive activity. This offers supporting evidence that the cortico-spinal pathways do not all cross the midline between the left and right body sides along their path from cortex to fingers (Donchin et al., 2002), suggesting that left M1 is partially engaged for left hand movements.

Detecting layer-dependent input-output connectivity in the human brain is of great value to multiple neuroscientific research areas. The investigation of neural circuitry in the motor system is particularly valuable to track the layer-dependent innervation changes in Parkinson’s disease, nerve damage induced plasticity (Yu et al., 2014) and hand aphasia (Hallett, 2014). Other processes, like perception or attention, may also leave a layer-dependent signature in the fMRI profiles, as they do in the neural signals (Mehta et al., 2000; Stoner et al., 2014).

In conclusion, our results imply that neural activity in the cortical layers and directional functional connectivity are reflected in non-invasive, CBV-weighted fMRI data. The additional level of detail made available by this method allows not only the investigation of cortical micro-circuitry in vivo in health and disease (Stoner et al., 2014; Yu et al., 2014), but it will help bridge the gap between macroscopic (conventional fMRI) and microscopic (extracellular recordings) measures of brain function.

STAR METHOD

KEY RESOURCE TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Bacterial and Virus Strains
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
Experimental Models: Organisms/Strains
healthy human volunteers	this paper	ClinicalTrials.gov identifier: NCT00001360
Post mortem MRI data	(Stüber et al., 2014)	Fig. S1; https://doi.org/10.1016/j.neuroimage.2014.02.026
Oligonucleotides
Recombinant DNA
Software and Algorithms
SIEMENS VB17A- UHF image reconstruction	SIEMENS Healthineers	IcePAT WIP 571
FSL Software Library v5.0	FMRIB, Oxford	https://fsl.fmrib.ox.ac.uk/fsl/fslwiki
Analysis of Functional NeuroImages (AFNI) AFNI_2011_12_21_2014 and AFNI_17.2.05	NIMH	https://afni.nimh.nih.gov/
Statistical Parametric Mapping v12	Wellcome Trust Centre for Neuroimaging, UCL	http://www.fil.ion.ucl.ac.uk/spm/
Stability weighted RF-coil combination (STARC)	this paper	https://github.com/djangraw/STARC-OptimalCoilCombo
Other

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Laurentius Huber (Laurentius.Huber@nih.gov).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Human participants

Eleven healthy right-handed volunteers (age 23–43 years) participated after granting informed consent under an NIH Combined Neuroscience Institutional Review Board-approved protocol (93-M-0170, ClinicalTrials.gov identifier: NCT00001360) in accordance with the Belmont Report and US Federal Regulations that protect human subjects. The number of eleven participants was chosen based on previous comparable studies (Huber et al., 2015; Muckli et al., 2015). Six participants were males and five participants were non-pregnant females. No analysis on the influence of sex or gender was conducted in this study. Influence on sex and gender are not part of the research questions to be addressed in our IRB protocol (93-M-0170). The research was conducted as part of the NIMH Intramural Research Program (#ZIA-MH002783).

Circuitry model of M1

The connectome of the primary motor cortex is well studied in animal models (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008). A simplified circuitry model of the neurons across cortical depths and their connections to other brain areas is illustrated in Fig. 1A (following Fig. 8 in (Mao et al., 2011) and Fig. 4 in (Weiler et al., 2008)). Connections of M1 from other cortical brain areas are located in superficial cortical laminae (see afferent arrows in Fig. 1A). There is an internal feedback loop within superficial cortical layers, involving II/III and Va (solid loop in Fig. 1A). Internal connections between superficial and deeper cortical layers are unidirectional and go from superficial towards deeper layers (not the other way around). Deeper layers Vb and VI are involved in an additional internal loop (dashed loop in Fig. 1A) and eventually send output to subcortical brain areas and the spinal cord (efferent arrows in Fig. 1A). To a first-order approximation, it can be summarized, that cortico-cortical input activity is dominated from superficial cortical layers, while cortico-spinal output is dominated from the deeper cortical layers (Fig. 1B).

METHOD DETAILS

Experimental setup

Slice-selective slab-inversion (SS-SI) VASO (Huber et al., 2014) was implemented on a MAGNETOM 7T scanner (Siemens Healthineers, Erlangen, Germany) using the vendor-provided IDEA environment (VB17A-UHF). For RF transmission and reception, a single-channel-transmit/ 32-channel receive head coil (Nova Medical, Wilmington, MA, USA) was used. The scanner was equipped with a SC72 body gradient coil (maximum effective gradient strength used here: 49 mT/m; maximum slew rate used: 199 T/m/s). 3^rd order B₀-shimming was done with 3 iterations. The shim volume was covering most of the left anterior part of the brain to achieve optimal B₀-homogeneity in the left motor cortex with residually homogeneous B₀-field distribution down to the Circle of Willis for spin inversion.

Stimulation paradigm and session setup

No participant was in the scanner for longer than 120 min per session. Imaging slice position and slice angle was adjusted individually for every participant to be perpendicular to the forefinger region of M1. This was done based on 1–4 short EPI test runs with 5 measurements (approx. 22 s per test scan) and their online depiction in the vendor-provided 3D-viewer. Each session consisted of 5 functional experiments (runs) of 12 min duration each, corresponding to 480 time frames per scan. Different task conditions were utilized across the 12 min runs. 1.) Resting-state, 2.) tapping of right hand with touch (color = blue in the manuscript), 3.) tapping of right hand without touch (color = green in the manuscript), 4.) being touched with an abrasive cushion without finger movement (color = black in the manuscript), 5.) tapping of the left hand with touch (color = red in the manuscript). Task scans consisted of one-minute blocks (30 s rest and 30 s activity) repeated 12 times. During the motor tasks, participants were asked to mimic a video of a tapping hand shown on a screen inside the bore. The tapping movement consisted of a 2 Hz pinch-like tapping of thumb and forefinger. To minimize sensory activity from touching of neighboring fingers, the tapping task did not involve the middle, ring or pinky fingers. Three participants were invited for multiple sessions to investigate the reproducibility of the results across sessions. All eleven participants underwent the tapping task with touch. Nine participants underwent all four tasks. In six participants, the M1 gyrification pattern allowed imaging of ipsilateral and contralateral responses in the same ROI. Six additional participants were re-invited to participate in additional 24 min resting-state experiments with a whole-slice FOV.

Nonfunctional MR sequence methods

If time permitted, slab-selective isotropic 0.35 mm resolution anatomical data were collected covering the left primary motor cortex with MP2RAGE and Multi-Echo FLASH. Those anatomical data were not used in the pipeline for generating cortical profiles. They are used to compare and validate the approximate position of the cyto-architectonically defined cortical layers of individual participants to the 20 reconstructed cortical depths, in which the data are processed (Fig. S1).

VASO contrast generation methods

The timing of the acquisitions was: TI1/TI2/TR=1100/2600/3000 ms. The blood-nulling time is calculated based on the assumed value of blood T₁=2100 ms (Huber et al., 2016a). The adiabatic VASO inversion pulse is based on the TR-FOCI pulse. The pulse duration was 10 ms and the bandwidth was 6.3 kHz. In order to minimize the risk of inflow of fresh non-inverted blood into the imaging region during the blood nulling time, the inversion-efficiency of the TR-FOCI pulse was adjusted by the implementation of a phase skip of 30°.

Signal readout methods

The 3D-VASO sequence was based on a previous 3D-EPI implementation (Poser et al., 2010). The optimal sequence parameters were tested and found in previous studies (Huber et al., 2016a). No slab-oversampling was applied in the second phase-encoding direction. 3D slice aliasing was minimized using a sharp slab-excitation profile with a bandwidth-time-product of 25. The inversion-recovery nature of VASO results in the acquisition of 3D-EPI segments in a non-steady state. Hence, in order to minimize any T₁-related blurring along the slice direction, individual excitation pulse flip angles were varied along the train of k_z-planes to ensure similar GM signal for every shot. In every 3D-EPI shot, one whole plane of k-space was acquired. The last excitation pulse of every readout was chosen to be nominally 90°. To keep a near-constant GM signal across k-space planes, the flip angles of the preceding planes were adjusted to be respectively smaller. The nominal flip angles adjusted in the sequence code were: 21.0°, 22.9°, 25.0°, 26.8°, 28.4°, 30.5°, 33.3°, 37.3°, 43.7°, 57.4°, 72.5°, 90.0°. The T₁-relaxation between consecutive excitation pulses was estimated assuming a tissue T_1-value of 1800 ms at 7 T. The acquisition of the GRAPPA calibration data followed the FLASH approach. This minimizes segmentation artifacts and results in superior conditioning of the subsequent GRAPPA reconstruction and correspondingly increased tSNR. The same GRAPPA kernels were applied for all volumes of a time series independent of their different contrast. The vendor’s GRAPPA reconstruction algorithms (Siemens software identifier: IcePAT WIP 571) were applied using a 3×4 (read direction × phase direction) kernel. Partial Fourier reconstruction was done with the projection onto convex sets (POCS) algorithm (Haacke et al., 1991) with 8 iterations. No Maxwell-correction was applied to minimize the number of data resampling steps. Finally, the complex coil images were combined as described below.

The acquisition of six additional 24 min scans mentioned above were slightly different than the acquisition protocols with the smaller FOV. The 24 min whole-slice data were acquired with 0.79 mm isotropic resolution, no partial Fourier imaging, and GRAPPA 3. Other parameters were the same.

Coil combination methods

We applied a specialized coil combination scheme called STAbility-weighted RF-coil Combination STARC (Huber et al., 2017b) that is optimized for high resolution fMRI, where EPI-artifacts can be a limiting factor. In contrast to more common coil combination approaches such as Sum-of-Squares (SOS), STARC does not combine coil signal based on signal magnitude strengths. Instead, coil-specific data are combined based on their voxel-wise signal stability strengths. Figs. S5H depicts how the STARC approach improved the overall temporal stability of the fMRI signal in this study. This results in high tSNR values especially in areas of strong artifacts. Consequently, the statistical activity values during a finger tapping experiments are improved and the time courses are stabilized (Fig. S5H).

Contrast separation procedure

The coil-combined data consist of interleaved BOLD and VASO contrasts. These time series are corrected for rigid volume motion and are separated by contrast with effectively half the temporal resolution of TR = 3 s. The VASO contrast is corrected for BOLD contaminations by dynamic division (Huber et al., 2014).

Retrospective motion correction

Head motion can be a limiting factor in high-resolution fMRI. Hence, we tried to take special care to minimize head motion by placing two inflatable air cushions (Pearltec) in the empty space laterally between the participants’ head and the casing of the receive RF coil. Following previous high-resolution studies, datasets with volume displacement larger than the voxel size were discarded. Three participants exceeded this threshold in individual runs. In one case, the participant reported to have coughed and the run was repeated in the same session. In the other two cases, the participants were invited to participate in an additional scan session.

Motion parameters are dominated by the phase-encoding direction. In order to minimize the influence of non-rigid motion and time dependent distortions, motion estimation was conducted with the SPM12 (Functional Imaging Laboratory, University College London, UK) option of spatial weighting. Here, motion estimation was optimized on the motor cortex having the highest weights in the center of the FOV, decreasing towards the distortion-susceptible periphery of the FOV. In order to minimize resampling induced signal blurring, a 4^th order spline was used for motion estimation and resampling. Different motion parameters and their effect on the final result are shown in Fig. S5E.

Physiological noise correction

During all experiments, cardiac and respiratory traces were acquired with a Biopac system Inc (Goleta, CA, USA). BOLD and VASO time series were corrected for physiological noise (Hall et al., 2017) with RETROICOR as implemented in AFNI.

Anatomical reference methods

Conventionally, high-resolution anatomical images are acquired in an additional run during the imaging exam to identify tissue classes of GM, WM and CSF and the corresponding cortical depth within GM. These usually consists of a T₁-preparation followed by a 3D-FLASH readout. However, the application of these anatomical data to the analysis of fMRI study requires EPI-distortion correction and coregistration. The correspondingly required resampling step of the data has been shown to be prone to errors and can additionally result in lowering the resolution up to a factor of 2 (Renvall et al., 2014). Hence, for the most accurate definition of cortical depths, it has been suggested to acquire the anatomical reference data with the identical readout as the functional data (Kashyap et al., 2017; Renvall et al., 2016; van der Zwaag and Marques, 2016). Here we pushed this approach one step further and used the functional data directly as an anatomical reference (Huber et al., 2016b). Using functional data as an anatomical reference renders distortion corrections and spatial registration to other anatomical reference data unnecessary. This avoids registration errors and additional data resampling and hence, it helps to maintain the spatial specificity throughout the evaluation analysis (Fig. S5A).

Segmentation methods

EPI T₁-maps, EPI inverse T₁-weighted images and EPI-phase maps were used to distinguish borderlines of CSF/GM and GM/WM. Since conventional segmentation software packages are inadequately established and validated for application to EPI data with a restricted field of view, a semi-automated segmentation approach with manual intervention is used here. First, lines of high spatial frequency were generated with the ‘3dedge3’-command in AFNI. In a second step, those border-lines were manually corrected and combined with a WACOM (Saitama, Japan) drawing board. T₁-weighted images are most indicative for the CSF/GM border. However, since M1 is highly myelinated (Stüber et al., 2014), the GM/WM borderline can be ill-defined. Since M1 is also very rich in iron (Duyn et al., 2007), the EPI-phase maps could be used for a clearer WM/GM borderline detection. Those borderlines were aligned across different runs (Fig. S5B).

Layering methods

The borderlines of CSF/GM and GM/WM were used as the basis to define cortical depths (a.k.a. laminae). The equi-volume layering approach (Waehnert et al., 2014) was implemented in C++ for its application to EPI data with a restricted FOV. In order to avoid singularities at the edges in angular voxel space, the cortical depths were defined on a finer grid than the original EPI resolution. 20 equi-volume lines were calculated across the cortical depth (Fig. S5C). Please, note that with a nominal 0.75 mm resolution and an approximate cortical thickness of 4 mm in M1 (Fischl and Dale, 2000), the effective resolution allows to detect only 5.5–7.5 independent data points. Hence, the defined 20 cortical depths do not represent the MRI effective resolution.

Smoothing within cortical depths

For the depiction of low tSNR data on a single-participant, single-run, single-slice basis without being dominated by noise, a cortical depth-specific smoothing was implemented. Since this evaluation step is not widely established and only partly investigated yet (Blazejewska et al., 2016; Polimeni et al., 2015), the most relevant signal maps shown in this article are depicted with and without layer-smoothing. Cortical profiles and across-participant averaging of 2D-grids (see below) were evaluated from the unsmoothed data. Signal maps with and without depth-specific smoothing are shown in Fig. S2.

Spatial alignment across participants

The dominant finger movement representation is located in the hand ‘knob’ (also described as ‘knuckle’, ‘omega’, ‘epsilon’, ‘lengthened italic S’, ‘genua’, ‘bayonet-shape’, ‘middle genu’) on the precentral gyrus. Even though, the hand ‘knob’ folding pattern is highly variable across participants (Caulo et al., 2007), it is easily identifiable based on unique landmarks of the gyrification (Yousry et al., 1997). The location of the functional representation of thumb and forefinger pinch-grip-motion is located on the lateral side of the ‘knob’ between the border of BA4a/BA4p (Terumitsu et al., 2006) and the folding location of the lateral end of the hand ‘knob’. The functional depth-dependent signal was compared across participants in a 2D-coordinate system spanned across cortical depths between those landmarks. Fig. S5F depicts the M1 2D-coordinate systems for multiple participants. The location of the lateral border of the hand ‘knob’ was defined as the location with the shortest curvature radius (red arrow in Fig. S5F). Within these cortical coordinate systems, the fMRI responses could be averaged across participants for all tasks in BOLD and VASO.

Positioning laminae with respect to layers

For interpretation of the obtained functional profiles according to known input-output characteristics of different cortical layers I-VI, the approximate location of functional activity with respect to the underlying cytoarchitectonically-defined layers is helpful. The most critical locations are the position of the superficial boundary of layer I and the bottom boundary of layer VI. Here and in most depth-dependent fMRI studies, these segmentation boundaries were obtained from ‘low resolution’ anatomical datasets of 0.75–1 mm voxel sizes. Since the resulting boundaries were defined with an accuracy of 0.75–1 mm, the location of cortical layers could not be assigned with a higher accuracy. In order to confirm the approximate borderlines and the different layers within, we follow the approach outlined earlier (Turner, 2013). Firstly, we identified the MR-sensitive features, landmarks and layer-signatures in ultra-high resolution multi-modal post mortem data. And secondly, we used those features as markers of the cyto- and myeloarchictectonic landmarks in the in-vivo data. For this purpose, we investigated cortical depth-dependent M1 profiles of phosphorus (Fig. S1A) and iron (Fig. S1B), with particle induced X-ray emission (PIXE), T₁, and T₂* maps with MRI (Fig. S1C–D), and SMI 311 stained histology (s). These data were acquired in previous studies (Stüber et al., 2014). In M1, the T₂* relevant iron concentration increases with cortical depth until it reaches a plateau in layer Va (Fig S1). The plateau can be subdivided into two small bumps (Va and Vb, red arrows in Fig S1). Note also that the low concentration of myelin in layer I–III results in very long T₁-values in superficial layers. This is also the case without partial voluming of CSF (Fig. S1C) and must be accounted for, when defining the CSF-GM borderlines in-vivo. The above-mentioned plateau landmarks nearby the center of the cortical depth are also visible in the 0.35 mm isotropic multi-echo FLASH and MP2RAGE data acquired in the participants of this study (red arrows in Fig. S1H). Based on the landmark highlighted in Fig. S1M, the two functional peaks of the VASO data can be assigned to layers II/III and layer Vb, respectively (Fig. S1K).

It is notable that any vascular fMRI contrast depends on the local coupling between neural activity changes and energy demand. Most of the fMRI-relevant energy demand refers to post-synaptic input-driven LFP changes (Logothetis et al., 2001). It is known since the advent of the neuron doctrine, however, that the neuronal cell bodies can be located at a different cortical depths compared to most of their dendrites (Cajal, 1906). Hence, the specificity of cortical depth-depended fMRI relates to the layer specificity of dendrites and cannot necessarily be interpreted with the layer-dependent distribution of the somata.

Comparison with SE-BOLD contrast

To investigate the specificity improvement of CBV-fMRI with alternative promising contrast mechanisms based on spin-echo imaging, four participants were re-invited to participate in 18 experiments. Since different SE-sequences are expected to have different contributions of intra-vascular signal from macro vessels, outer-k-space T₂*-contributions (Goense and Logothetis, 2006) and desired microvascular response, four different SE-BOLD variants were implemented: Additional to VASO (Fig. S4A) and GE-BOLD (Fig. S4B), conventional SE-BOLD (Fig. S4C) was acquired with a C2P sequence from (https://www.cmrr.umn.edu/multiband) (TE = 50 ms) (Auerbach et al., 2013). Additionally, T_1ρ-prep (Rane et al., 2014) was implemented with a spin-locking pulse on resonance, where T_1ρ ≈ T2 (Hua et al., 2014). We included a custom-designed adiabatic spin-locking pulse that is optimized for 7T (Huber et al., 2017c). The magnetization is kept in the transverse plane (on-resonance) for TE = 50 ms (Fig. S4D). An alternative T₂-prep (Fig. S4E) contrast was generated by re-implementing the Phillips sequence from (Hua et al., 2014) into the SIEMENS environment (prep TE = 50 ms). In order to minimize unwanted unspecific intravascular T₂-BOLD signal within large pial veins, we included small diffusion weighting crusher gradients (Boxermann et al., 1995) (Fig. S4F). Other imaging parameters were identical as described above.

QUANTIFICATION AND STATISTICAL ANALYSIS

Quantification of depth-dependent activity

In this study, the CBV activity is defined as the difference of the mean signal during the task vs. the mean signal during rest. To minimize the influence of the transition periods between task and rest periods, the first 9 seconds of activity and rest cycles are disregarded, respectively. We refrain from using inferential statistical significance scores for the quantification of depth-dependent activity changes because they can be hard to interpret in light of the aspects described below.

1. The hemodynamic response functions are different across cortical depths (see Fig. S6A for a representative participant). Hence, depending on the HRF used in the statistical GLM, the model fit might favor some layers over others, introducing biases.

2. The signal quality and stability are heterogeneous across cortical depths (see Fig. S6B for a representative participant). This means that the cortical profiles of absolute signal change, relative signal change and stability-dependent statistical significance scores are not only modulated by the effect size, but also undesirably biased by the depth-dependent baseline noise distribution (compare green and blue profiles in Fig. S6D).

3. The baseline blood volume distribution varies across the cortical depth (Duvernoy et al., 1981). This suggests that the cortical profiles of CBV change are expected to look different if analyzed quantitatively in ml volume change per 100 ml of parenchyma volume as opposed to evaluations in semi-quantitative units of % (compare red and blue profiles in Fig. S6D).

To validate the reproducibility and robustness of the fMRI signal change measure used here with respect to noise, the cortical profiles of the three datasets are compared in Fig. S6E. The red profiles refer to a conventionally acquired dataset in this study (as described above) with an initial excitation flip angle of 21°. The blue profiles refer to the same dataset with the only difference that random Gaussian noise was added to increase the variance by 22%. The green profiles refer to a successively acquired dataset with identical scan and task parameters, with the sole difference, that the initial excitation flip angle was adjusted to be 17°, with correspondingly smaller tSNR. It can be seen that the quantitative profiles of CBV change in units of ml are virtually identical across the different noise levels, while the statistical z-scores show different profiles. This difference could potentially be coming from the different interaction of physiological and thermal noise across cortical depths.

Please note however, that refraining from using inferential statistical significance scores as a measure of depth-dependent brain activity does not prevent us from applying statistical significance tests across tasks, participants and ROIs. In this study, all interpretations and statistical significance tests are based on depth-dependent quantitative signal changes. Statistical tests are not based on depth-dependent significance scores of model fits.

Statistical testing of double peak feature

To validate the statistical certainty of the double-peak response, we employed a Larkin-F-test (Larkin, 1979). Larkin-F-tests should not be confused with conventional F-test generating inferential significance scores. A Larkin test generates Larkin-F-scores based on the likelihood that a distribution is unimodal (consisting of one distribution) or bimodal (consisting of two sub-distributions). The statistical significance of the Larkin-F-scores is estimated by means of p-values referring to the probability that such a Larkin-F-score can be explained by noise only. Here, the noise refers to intertrial variability. Note that in the layer-profiles here, neighboring data-points are not independent from each other. The signal and noise correlation between neighboring voxels is quantified with FSL SMOOTHEST (Nichols, 2008). Hence here, only a Larkin-F-score larger than 12.1 exceeds the significance threshold of p < 0.05 (not a Larkin-F-score of 4, as for independent data points). Since the Larkin-F-scores are not normal distributed, bootstrapping (1000 times resampling) hypothesis testing was applied with to test whether the Larkin-F-scores are statistically higher in CBV-fMRI compared to BOLD-fMRI.

Quantification of directional activity

Based on the known laminar distribution of the circuitry in M1 depicted in Fig. 1A, the depth-dependent profiles of brain activity were characterized by two parameters; input-activity in superficial laminae and output-activity in deeper laminae Fig. 1B. The signal from superficial laminae was averaged and used as input-signal for further analysis (x-axis in Fig. 4). The signal in deeper laminae was averaged and used as output-signal for further analysis (y-axis in Fig. 4). This procedure refers to a straightforward depth-dependent spatial GLM of two boxcars (Fig. 1B). The input-signal and output-signal of every participant was calculated for every task. To account for participant-specific variations in baseline-physiology (e.g. venous baseline oxygenation), these values were normalized by the participant-specific average response of all tasks. Participant-normalized values were used as coordinates in scatter plots shown in Fig. 4.

Statistical testing of task distinguishability

We investigated the distinguishability of different tasks statistically in two ways; firstly, by means of their contrast-to-noise ratio defined as the difference compared to their inter-participant variability (Fig. 4C) and secondly, by means of a classification accuracy (Fig. 4D).

Contrast-to-noise-ratio

The calculation of the contrast-to-noise ratio (ΔS/σ) is indicated in the figure key of Fig. 4: The contrast (ΔS) is defined as the Euclidian distance of the center of mass points of contrasts in the input-output scatter plot described above. The noise term σ is defined as the inter-participant variability of a certain task. Contrast-to-noise-ratio values in Fig. 4C refer to averages of ΔS/σ for one task compared to all the other tasks.

Decodability

To investigate the decodability, a leave-one-out procedure was applied. First, one participant was selected and excluded from the dataset. The center of mass location of all four tasks was calculated from the data of the remaining participants. The data points of the selected participant were then classified based on the Euclidean distance to the center of mass of the remaining data points. For instance, since the green data point in Fig. 4 (green arrow) is closest to the center of mass of all the other green data points, it would be correctly classified as ‘tapping without touch’. However, another green data point in Fig. 4 (black arrow) is closer to the center of mass of the black data points. Hence, the data point at the black arrow would be falsely classified as ‘touch only’. This procedure was done for all participants. The percentage of correctly classified data points is depicted in Fig. 4D.

Statistical comparisons of CBV and GE-BOLD

The performance of CBV-fMRI compared to GE-BOLD results was tested in three different ways. A) The bimodality (quantified by Larkin-F-scores, Fig. S3E) was statistically investigated in a bootstrapping resampling test across all participants between BOLD and VASO. B) The task distinguishability across participants was investigated by means of contrast-to-noise-ratios in a paired t-test between BOLD and VASO (Fig. 4C). C) The task distinguishability across participants was investigated by means of correct classification accuracy in a paired t-test between BOLD and VASO (Fig. 4D).

Quantification of functional connectivity

Quantification of connectivity strength

We started the quantification of connectivity strength by obtaining the signal fluctuations from a seed region. This time course was then used as a normalized regressor and fitted to the time course of signal fluctuations in the target region across cortical depths. The voxel-wise and depth-dependent fits (β-values) were then used as a measure of connectivity in physical units of ml/100ml across cortical depths.

We refrained from the application of the more commonly-used Pearson correlation as a measure for functional connectivity, because of its inherent sensitivity to the signal variance, which undesirably suppresses the noisier superficial cortical laminae. In superficial laminae, the temporal fluctuations are larger compared to deeper layers. This is partly due to the higher relative thermal noise contribution in superficial laminae as seen in SNR profiles in S6F. Here, SNR is estimated as a sum divided by the difference of average even- and odd-numbered time points of fMRI time series as proposed in (Glover and Lai, 1998). Because correlation-based values of functional connectivity are inversely biased from the temporal signal variance, they are not reproducible across different noise levels and they are biased towards higher values in deeper laminae (Fig. S6F). Regression-based quantitative values of functional connectivity, however, are reproducible across different noise levels and are not inversely biased by depth-dependent temporal signal variance (Fig. S6F).

Analysis of seeds across brain laminae

To find areas that predominantly trigger M1 output-activity and areas that predominantly trigger M1 input-activity only, a resting-state analysis was conducted based on the seed regions of superficial lamina in M1 compared to the seed regions in deeper laminae in M1. To account for the fact that superficial and deeper laminae share a lot of similarities (off-diagonal elements in Fig. 4), the seed time courses are orthogonalized (option in FSL Feat) to only represent those features that are unique to the specific laminae. Functional connectivity to the superficial and deeper laminae are investigated in two target ROIs, premotor cortex and primary sensory cortex (indicated in green and blue in Fig. 6). Statistical significance testing was done in a paired t-test using the signal change of the two ROIs with respect to the variability of this signal change across participants.

Analysis of seeds across brain areas

Seed ROI locations of premotor cortex, primary sensory cortex and ipsilateral motor cortex were chosen based on the location of induced activity changes in scans during tapping tasks. The control seed regions were chosen as follows: First, a single GM voxel was randomly chosen out of a GM mask, with the inclusion criteria to be located outside the three central sulci (pre-central sulcus, central sulcus and post-central sulcus). The ‘column’ of that voxel was inflated until it reached the size of the average ROIs of premotor, S1, and ipsilateral M1 seeds. For statistical analysis, 100 random control seed regions (partly overlapping) were used to estimate the noise floor (gray area in Fig. 7D) across cortical depth. Five exemplary seed regions are depicted in Fig 7C. Statistical testing to determine whether laminar resting-state profiles were significantly different from each other was done across participants (Fig. 7D).

DATA AND SOFTWARE AVALIABILITY

The data presented here are available upon request. Downloading access requires a signed data sharing agreement as part of the intramural IRB protocol and is conducted via NIH Acronis Access. All custom written software and evaluation scripts can be accessed via a NeuroDebian virtualbox upon request. The authors are happy to share the 3D-VASO MR sequence upon request under SIEMENS C2P agreement. The coil combination STARC software is available on Github: https://github.com/djangraw/STARC-OptimalCoilCombo.

Highlights.

• A CBV-fMRI method is developed for sampling brain activity across cortical layers

• We can separately measure input and output activity of primary motor cortex

• CBV-fMRI can measure laminar activity with higher accuracy than BOLD-fMRI

• Laminar resting-state fMRI can reveal directional connectivity between brain areas