Summary
The efficiency of doubly robust estimators of the average causal effect (ACE) of a treatment can be improved by including in the treatment and outcome models only those covariates which are related to both treatment and outcome (i.e., confounders) or related only to the outcome. However, it is often challenging to identify such covariates among the large number that may be measured in a given study. In this paper, we propose GLiDeR (Group Lasso and Doubly Robust Estimation), a novel variable selection technique for identifying confounders and predictors of outcome using an adaptive group lasso approach that simultaneously performs coefficient selection, regularization, and estimation across the treatment and outcome models. The selected variables and corresponding coefficient estimates are used in a standard doubly robust ACE estimator. We provide asymptotic results showing that, for a broad class of data generating mechanisms, GLiDeR yields a consistent estimator of the ACE when either the outcome or treatment model is correctly specified. A comprehensive simulation study shows that GLiDeR is more efficient than doubly robust methods using standard variable selection techniques and has substantial computational advantages over a recently proposed doubly robust Bayesian model averaging method. We illustrate our method by estimating the causal treatment effect of bilateral versus single-lung transplant on forced expiratory volume in one year after transplant using an observational registry.
Keywords: Average treatment effect, Causal inference, Group lasso, Variable selection
1. Introduction
Estimating the causal effect of a binary intervention or action (referred to as a “treatment”) on a continuous outcome is often an investigator’s primary goal. Randomized trials are ideal for estimating causal effects because randomization eliminates selection bias in treatment assignment. However, randomized trials are not always ethically or practically possible, and observational data must be used to estimate the causal effect of treatment. When using observational data to estimate the casual effect of treatment, many methods require either modeling the mean outcome conditional on the predictors and the treatment (e.g., regression modeling), or specifying a treatment allocation model (e.g., inverse probability weighting (IPW) and propensity score matching), or both (e.g., doubly robust methods) (Lunceford and Davidian, 2004). Methods that rely on only one such model require that the model be specified correctly and adjust for at least all confounders – variables associated with both treatment and outcome – for consistent estimation of the causal treatment effect. Doubly robust methods, however, fit both an outcome and a treatment model and require only one of them be specified correctly with all confounders for consistent treatment effect estimation.
One approach is to include all available covariates in the specified model(s) to avoid biased estimation. However, including many variables unrelated to outcome and treatment could inflate the variance of the effect estimator. Hence, when there are a large number of possible confounders, some type of variable selection is desirable to achieve unbiased, efficient estimation. VanderWeele and Shpitser (2011) propose a confounder selection criterion that controls for any covariate that is either a cause of treatment or outcome. Though efficiency may improve by including covariates related only to outcome, as shown by Brookhart et al. (2006) for IPW estimators and de Luna, Waernbaum, and Richardson (2011) for non-parametric estimators of the average causal effect (ACE), including all causes of treatment or outcome can still be sub-optimal as these studies also suggest efficiency may decrease when controlling for variables that are related to the treatment but not the outcome. Variable selection methods (e.g., backward variable selection, lasso) based only on the outcome (treatment, respectively) model are popular in practice, but because these methods ignore the relationship between treatment (outcome) and covariates, these methods tend to under-select confounding variables weakly related to the outcome (treatment) but strongly associated with the treatment (outcome). Vansteelandt, Bekaert, and Claeskens (2012) argue that omitting such variables in estimators of the ACE not only introduces bias but also underestimates the uncertainty of the ACE and propose a method based on a focused information criterion which aims at minimizing the mean squared error of the treatment effect estimator.
There has been work to adapt traditional variable selection techniques, which focus on covariates with the greatest predictive ability of treatment or outcome, to jointly select covariates related to treatment and outcome. van der Laan and Gruber (2010) propose a doubly robust semi-parametric method that solves an efficient influence curve equation that is a function of the outcome and treatment models by utilizing numerous data adaptive machine learning algorithms to select variables in a stepwise fashion for the propensity score. Ertefaie, Asgharian, and Stephens (2015) proposed a two-step variable selection method which selects variables using a penalized likelihood in the first step and then separately estimates the causal treatment effect in the second step using a doubly robust regression estimator. A limitation of this method, however, is that it may not select an important confounder if its association with the outcome and treatment have opposite signs; this can occur when the value of the coefficient in the outcome and treatment likelihoods are similar in magnitude. Wang, Parmigiani, and Dominici (2012) propose Bayesian adjustment for confounding (BAC), a method linking the models for treatment and outcome with a dependence parameter. Cefalu et al. (2016) take a similar approach to BAC by developing a two-stage Bayesian model averaged (BMA) doubly robust method that introduces a prior dependence between a covariates’ inclusion in the propensity score and the outcome model that is designed to identify the set of potential confounders based on their association with both treatment and outcome by forcing variables included in the propensity score to be a subset of those included in the outcome model. Despite improved efficiency over standard methods, these approaches must estimate a posterior distribution on some model class, which is typically done using measures (e.g., BIC) that cannot handle situations when the number of covariates is larger than the sample size. Even when the number of predictors is less than the sample size, these methods can be computationally intensive when the number of predictors is large as they must explore all possible treatment and outcome model spaces; with even a modest number of covariates, say 20, over 2 million (221) models must be considered. Moreover, since treatment effect estimates are weighted linear combinations across many models, there is no feature selection and interpretation of covariate effects is difficult.
In this paper, we propose GLiDeR (Group Lasso and Doubly Robust Estimation), a treatment effect estimator which uses a modified adaptive group lasso approach (Yuan and Lin, 2006) to perform simultaneous coefficient regularization and estimation for the treatment and outcome models. Our method is more efficient than standard (doubly robust) backward selection methods and is competitive with the two-stage BMA estimator proposed by Cefalu et al. (2016). However, unlike the two-stage BMA estimator, our proposed method is computationally feasible with a very large number of covariates including cases where the number of covariates is larger than the sample size.
We set up the problem and introduce the group lasso in Section 2. In Section 3, we formulate GLiDeR and summarize the estimation technique. Section 4 provides theoretical justification and asymptotic results for GLiDeR. In Section 5 we present simulation scenarios demonstrating the finite-sample behavior of GLiDeR, and Section 6 provides an application to an observational registry of lung transplant recipients. We conclude in Section 7.
2. Preliminaries
2.1 Doubly robust estimation of treatment effects
The causal effect of binary treatment A on continuous outcome Y is of interest. Letting Y (a) denote the possibly counterfactual outcome for a randomly selected person if assigned treatment A = a, the ACE is Δ ≔ E[Y (1) − Y (0)]. When A is randomized, the vector of potential outcomes {Y (0), Y (1)} is independent of A. Given data (Yi, Ai) on independent subjects i = 1,…,n, is a consistent estimator of Δ.
In an observational study, {Y (0), Y (1)} may depend on A and Δ̂ran may then be inconsistent for Δ. However, it may be reasonable to assume that treatment assignment is ignorable and has positive probability (positivity) given observed covariates, i.e., that there exist covariates X = {X1,…, Xm} such that A ⊥ Y (a)|X and P (A = a|X) > 0, for a = {0, 1}, in which case Δ is consistent. We can then postulate a regression model μ (A, X; α) for E(Y|A, X). If μ(A, X; α0) = E(Y|A, X) for some α0 (i.e., the outcome model is correctly specified), then given a consistent estimator α̂ of α0, the estimator is consistent for Δ (Lunceford and Davidian, 2004). If μ(A, X; α) ≠ E(Y|A, X), then Δ̂reg may be inconsistent for Δ.
Let π(X; γ) be a postulated regression model for the conditional probability of treatment, P (A = 1|X). If π(X; γ0) = P (A = 1|X) for some γ0 (i.e., the treatment model is correctly specified), then a consistent estimator of Δ is the inverse probability weighted (IPW) estimator, , where γ̂ is any consistent estimator of γ0 (Lunceford and Davidian, 2004). If π(X; γ) ≠ P (A = 1|X), then Δ̂IPW may be an inconsistent estimator for Δ.
To address the problem of model misspecification, various authors have proposed doubly robust estimators, which require specification of both an outcome and propensity score model but require only one of them to be correctly specified to yield a consistent estimator for Δ (Lunceford and Davidian, 2004). One such doubly robust estimator is
| (1) |
The preceding has assumed that the observed covariates X are exactly those required to achieve ignorability, i.e., X is precisely the set of confounders of the treatment-outcome relationship. However, in practice, we may have access to a large set of covariates V ⊃ X which are candidates for inclusion in the outcome and treatment models. While the estimators mentioned remain consistent if covariates from V \ X are added to the propensity and outcome models (in addition to X), in Section 4.1, we show that including covariates related only to the outcome can decrease the variance – while adding covariates associated with only the treatment can increase the variance – of the doubly robust estimator. In Section 3, we introduce GLiDeR, a procedure for performing simultaneous variable selection in treatment and outcome models that targets confounders and predictors of only outcome.
2.2 The Group Lasso
Our approach to simultaneous variable selection in the outcome and treatment models uses a modified version of the group lasso (Yuan and Lin, 2006) – a regularization method that acts like the lasso on grouped covariates by forcing all coefficients of each group of variables to be either all zero or all nonzero. We briefly introduce the group lasso technique for a general regression model before describing our particular modification of it in the next section.
Let M be the q × 1 vector of covariates corresponding to a regression model for some response variable R, and let ξ be the vector of associated regression coefficients. In the group lasso, we assume that M is partitioned into K groups {M1,…, MK}; the corresponding blocks of ξ are denoted by ξ(1),…, ξ(K). For a general loss function Φ(R, M; ξ), the group lasso estimator of ξ is , where λ > 0 is the penalty parameter and wk ≥ 0 is the penalty weight for group k. A common choice for each group weight wk is , where ck is the cardinality of group k (i.e., the number of elements in Mk). If we do not want to penalize a specific group, for example an intercept, we let the corresponding wk equal 0. There is no closed form solution to ξ̂GL(λ), but several algorithms exist, including the groupwise majorization descent (GMD) algorithm proposed by Yang and Zou (2015), for finding solutions to this convex optimization problem.
3. GLiDeR
3.1 Notation
Let Vi = {V1i,…, Vpi} denote subject i’s vector of measured covariates, with p possibly large in relation to the sample size n; for the remainder of the paper, we suppress i in our notation except where necessary. We assume as in Section 2.1 ignorability and positivity of treatment assignment given V. Let outcome and propensity models for E(Y|A, V) and P (A = 1|V) be defined by f [μ(A,V; α)] = α1V1+…+αpVp+αp+1+αp+2A, and g[π(V; γ)] = γ1V1 +…γpVp + γp+1, and let Φout(Y, A, V; α) and Φtrt(A, V; γ) denote the outcome and treatment loss functions used to fit these models. In many doubly robust treatment effect estimation problems, f is taken to be the identity function and g is the logit function, so that the outcome and treatment models represent linear and logistic regression. In this case, Φout is the squared error loss and Φtrt is proportional to the binomial negative log-likelihood.
Anticipating the group lasso approach in the next section, we will let β = (α, γ) and define p + 3 groups of this vector: β1 = (α1, γ1),…, βp = (αp, γp), βp+1 = αp+1, β p+2 = γp+1, and βp+3 = αp+2. Note that, for k = 1,…, p, βk is a group of coefficients corresponding to the covariate Vk in the outcome and treatment model, respectively. Our setup differs from the typical one for group lasso, as our groupings correspond to the same covariate appearing in two different regression models, as opposed to sets of related but distinct covariates within the same regression model. Covariate transformations may be included by adding the necessary elements to V and grouping the coefficients of the transformed covariates with those of the untransformed versions. In this manuscript, we do not consider interactions between covariates; while including interactions poses no technical challenges, it is not clear to which group the corresponding columns in the design matrix for the interaction should belong.
3.2 Simultaneous variable selection for the treatment and outcome models
To perform simultaneous variable selection between the treatment and outcome models, we propose to solve a group lasso-like problem with the following characteristics:
- The loss function is taken to be the sum of the loss functions for the treatment and outcome models,
(2) - We use the penalty term
so each summand corresponds to the coefficients associated with a single covariate; λ > 0 is the penalty parameter and Wk is a weight term with Wk = 0 for k > p, that is we do not penalize the intercepts in the treatment and outcome models and the main effect of treatment in the outcome model. We discuss the choice of Wk in Section 3.3. Unlike the usual group lasso setup, where related covariates in the same model are jointly penalized, GLiDeR groups together the coefficients corresponding to the same covariate across the treatment and outcome models. This strategy forces covariates to enter and leave the models simultaneously.
Our simultaneous variable selection procedure therefore consists of solving
| (3) |
where Ystd = Y/sd(Y) is used instead of Y in Equation (3) so the scale of Φout(Y, V; α) (and Φsum(Y, A, V; β), by definition) does not depend on the measurement unit of continuous Y ; and, therefore, estimation of β is not affected by the scale of Y. We also assume the covariates used in (3) are standardized so that the penalty is invariant to scale. Given a solution β̂(λ) of (3), we can plug β̂(λ) = {α̂ (λ), γ̂ (λ)} into μ{A, V; α̂(λ)} and π{V; γ̂ (λ)} to obtain an estimate of Δ at each λ, denoted Δ̂DR(λ), using Equation (1). As with the usual (group) lasso, the degree of variable selection is controlled by λ. We discuss choosing λ in Section 3.4.
3.3 Choosing Wk
Because our goal is to minimize the mean squared error of the treatment effect estimator and, therefore, encourage selection of covariates which are associated with the outcome (which includes confounders) and discourage selection of covariates which are related only to the treatment or unrelated to both outcome and treatment, we propose to set , where the numerator corresponds to the cardinality of group k (the default group penalty weight under the general group lasso formulation) and υk ≠ 0 is an estimate of the regression coefficient in the outcome model for covariate k from a “full” model. When p ≤ n, one can set υk to be the ordinary least squares estimate for covariate k as obtained when fitting the full outcome model. In cases where p > n, one choice is the least squares coefficient estimate of covariate k with the ridge penalty. With transformations in the outcome or treatment model, Wk can be defined by setting the numerator equal to the square root of the total number of predictors in the outcome and treatment models that correspond to covariate k, and υk equal to the l2 norm of the corresponding estimated coefficients. When the weights vary based on the strength of the association between the covariate and outcome, we refer to GLiDeR as “adaptive.” Ertefaie et al. (2015) also propose an adaptive weight so that the magnitude of the penalty on each coefficient is proportional to its contribution to the outcome model but is different than the adaptive weight proposed here as it depends on the least squares (or ridge) estimates of the coefficients in both the outcome and treatment models. Like the general group lasso, if we do not want to penalize a specific group, which is often the case for intercepts or the main effect of treatment in the outcome model, we set the corresponding group weights Wk to zero. This proposed group weight strongly penalizes covariates that are not associated with the outcome (i.e., when |υk| is small) even if they are strongly associated with the treatment. Hence, the adaptive approach used in GLiDeR is aimed to select covariates associated with only the outcome or confounders that are related to both treatment and outcome (i.e., covariates related to the treatment should be selected only if they are also associated with the outcome).
3.4 Choosing λ
Equation (3) defines the solution β̂(λ) as a function of λ. We propose to choose λ by applying cross-validation to the outcome model, since doing so further encourages the (desirable) selection of predictors associated with the outcome. Generalized cross-validation (GCV) or k-fold cross-validation (kCV) is typically used to select the tuning parameter λ in lasso-like problems. Since we consider both outcome and treatment model loss functions in Equation (3) but wish to apply GCV to only the outcome model, the usual GCV statistic requires a modification (kCV is straightforward). For the general group lasso, the GCV statistic at a particular value λ is , where RSS is the residual sum of squares and , where ξ̂aGLj and ξ̃aGLj are the adaptive group lasso and least squares estimators of the jth group of coefficients, respectively, for groups j = 1,…, K with group sizes dj. For GLiDeR, since we want a model selection procedure for the outcome model only, we take the residual sum of squares from the outcome model to use in the numerator and use only the parts of β̂(λ) corresponding to coefficients from the outcome model (denoted (α̂ (λ)) in the denominator, yielding the following modified GCV statistic (noting we have p “groups” of size 2 and 2 terms – the intercept αp+1 and treatment main effect αp+2 – in the outcome model that are unpenalized in separate groups of size 1):
| (4) |
Then is the “optimal” λ. GCV is computationally advantageous since it only needs to be computed from the data once (as opposed to kCV, which needs to be computed an additional k times), and also demonstrates slightly better performance than kCV in the simulation scenarios considered in Section 5 (see Web Table 4 for results comparing GCV and kCV). We thus recommend using the GCV statistic in Equation (4) to select λ. Our final estimate of Δ is then Δ̂DR(λ*) in Equation (1).
3.5 Implementation
To summarize, we now list the steps involved in implementing the GLiDeR procedure.
Step 1 - Define covariate groups: Group outcome and treatment model predictors (assumed to be standardized) as described in Section 3.1. For each group k, compute group weights Wk as described in Section 3.3. For groups k that represent intercepts in either model or the treatment main-effect term in the outcome model, let the corresponding group weight Wk be zero. Scale Y by its marginal standard deviation, as discussed in Section 3.2.
Step 2 - Apply the modified group lasso. Define a sequence of λ values λ1,…, λL, such that λ1 > λ2 > ⋯ > λL ≥ 0 with initial value λ1 defined to be the smallest value λ such that all predictors have zero coefficients, except the terms with group weights (Wk) equal to zero. For l = 1,…, L, apply the GMD algorithm described in Yang and Zou (2015). Web Appendix A gives details of adapting this algorithm for this application.
Step 3 - Select the final model and estimate the doubly robust treatment effect. Use Equation (4) to compute GCV (λl) for l = 1,…, L and let . Plug β̂(λ*) = (α̂, γ̂) into μ(A, V; α̂) and π(V; γ̂) and obtain an estimate of Δ using Equation (1).
4. Asymptotic results
4.1 Efficient variable sets for doubly robust estimators
We begin by showing that including covariates related only to the treatment may increase – while including those related only to the outcome may decrease – the asymptotic variance of the doubly robust estimator, thereby justifying the covariate sets GLiDeR seeks to identify.
We consider doubly robust estimators in the class of (1) and focus attention on estimating μ1 = E{Y (1)}; ideas are similar for estimating E {Y (0) } and, therefore, the ACE, Δ = E {Y(1) − Y(0)}. A doubly robust estimator for μ1 in the class of (1) is
| (5) |
Let α* and γ* be the values of α and γ so that and . If the models are correctly specified, then α* and γ* are the “true” values of the parameters, and if incorrectly specified, then these are the “least false” parameters. To investigate the effect of including certain types of covariates in Δ̂DR,μ1, we will consider the case that γ = γ* and α = α* are known, so that π(V; γ*) and μ(A,V; α*) are known functions of V. When one or both models are correctly specified, we can then show the asymptotic variance of is , which follows from the iterated conditional variance formula. Now consider a new covariate, Z1, and assume that and , where and are the true/least false regression coefficients for Z1 in the treatment and outcome models, respectively. That is, Z1 is conditionally (given V) related to treatment, but conditionally unrelated to the outcome. Then the asymptotic variance of with V and Z1 is
Assuming the propensity score follows a logistic regression model, we can find . Then since ,
If Z1 is independent of V and Y (1), then . If Z1 is centered at zero and normally distributed, we know that , where σ2 is the variance of Z1. Then as Z1 is associated with treatment, and we have so that ΣDR(V, Z1) > ΣDR(V), and ΣDR(V, Z1) gets larger as increases. The same derivation holds for covariate (i.e., is independent of V and ) when Z1 and V are multivariate normal and dependent.
If we instead consider an irrelevant covariate, Z2, which follows the same assumptions as Z1 except that it is conditionally unrelated to the propensity score so that , then a similar argument can be made to show that ΣDR(V, Z2) = ΣDR(V). Lastly, consider covariate Z3, which is assumed to be conditionally related to outcome but conditionally unrelated to treatment. Then the asymptotic variance of with V and Z3 is
which follows assuming (the truth). When the outcome model is correctly specified,
which implies ΣDR(V, Z3) < ΣDR(V) when the regression error does not depend on covariates (i.e., homoscedastic); when the outcome model is misspecified, ΣDR(V, Z3) < ΣDR(V) under homoscedasticity if prediction of Y (1) via μ(1, V, Z3; α*, ) is improved over μ(1, V; α*).
In practice, α and γ are not known and must be estimated. M-estimation techniques can be used to derive the asymptotic variance of the doubly robust estimator when α and γ are estimated, but such derivations do not provide any obvious expressions that reveal the effect on the asymptotic variance of the doubly robust estimator after adding Z1, Z2, or Z3 when one of the models is misspecified; when both models are correctly specified, the asymptotic variance is the same regardless of whether α and γ are known or estimated.
4.2 Targeted covariate sets and double robustness of GLiDeR
We now show GLiDeR can asymptotically recover the set of confounders and covariates related only to outcome, while excluding irrelevant variables and covariates related only to treatment. Specifically, GLiDeR selects a covariate Vj provided . The key theorem is described here; the proof, which uses concentration inequalities from Blazère, Loubes, and Gamboa (2014), appears in Web Appendix B.
Assume no transformations or interactions between covariates (i.e., all groups are of size 2) so that as in Section 3.3. Assume further that there are no confounders such that if the outcome model is misspecified (i.e., the covariate has no linear association with the outcome, which rules out symmetric quadratic or periodic relationships). Then the group weight (Wk) tends to infinity for any covariate that is unrelated to the outcome, which allows covariates that are irrelevant or related only to treatment to be asymptotically excluded from GLiDeR. We can then prove the following theorem:
Theorem 1: Assume the number of covariates p and sample size n are such that . Also assume the Group Stabil condition is satisfied with c0 = 3 and . Let . Then, for sufficiently large λn and with high probability, we have
where 0 < k < 1 and cn > 0 are defined in Web Appendix B. β* = (α*, γ*)T denotes the true/least false coefficient parameters of the outcome and treatment models. The Group Stabil condition – a lower bound on the eigenvalues of the covariance matrix – and cn are discussed in greater detail in Web Appendix B.
The implication of Theorem 1 is that if ζ* = O(1), i.e., the number of groups containing non-zero coefficients does not increase with n, then for suitable λn (described in Web Appendix B) with high probability, so that and for all g such that provided the rate of increase in the number of covariates is o(en). Consequently, under the assumptions given above and in Theorem 1, GLiDeR asymptotically recovers all covariates associated with the outcome, which includes the confounders, even when the outcome model is misspecified, and combined with the estimator in (1), yields a consistent estimator of Δ when either the outcome or treatment model is correctly specified. However, we note that GLiDeR is not doubly robust in the fullest sense since the assumptions of Theorem 1 (and above) rule out some particular data generating mechanisms.
5. Simulations
5.1 Design
We investigate the finite sample behavior of GLiDeR relative to four alternative variable selection approaches to fit models used in treatment effect estimators: (1) the “saturated” method which uses all covariates in fitting the outcome and treatment models to compute Δ̂DR; (2) backward selection on the outcome model (p-stay < 0.05) to select the covariates which are used in fitting the outcome and treatment model to compute Δ̂DR, (3) two-stage model averaged double robust (MADR) estimator proposed by Cefalu et al. (2016), and (4) adaptive lasso to select covariates and estimate the treatment effect using only the outcome model (10-fold cross-validation to select tuning parameter). Note that the first three methods use Equation (1) while the adaptive lasso does not consider a model for the treatment. Numerous simulation scenarios are considered to evaluate the effects of varying levels of confounding, model misspecification, covariate structure, number of irrelevant variables (i.e., covariates unrelated to outcome and treatment), and sample size. For each scenario, we generate potential confounders V = {V1,…, Vp} marginally as N(μυ, ), treatment A as Bernoulli[expit{f (V)}] for some function f (·), where , and outcome Y as N{A + g(V), } for some function g(·).
To vary levels of confounding and model misspecification, we consider the same nine distinct combinations of f (V) and g(V) as in Cefalu et al. (2016) (we refer to these as Scenarios 1–9) with both independent and correlated covariates, and one from Ertefaie et al. (2015) (referred to as Scenario 10) with only independent covariates, which are described in Table 1. For Scenarios 5–9 (which were used in a previous version of Cefalu et al. (2016)) f(V) or g(V) (but not both) is a polynomial function of the covariates, while all methods assume f(V) and g(V) to be linear functions of the covariates, so that the outcome or treatment model (but not both) is misspecified in these scenarios. We also varied the total number of covariates available for Scenarios 1–9 by considering p = 5, 10, and 25 (we do not consider MADR for p = 25 as this would require fitting over 6 million models for each dataset) with a sample size of n = 500, and we varied the sample size by considering n = 250 and n = 500 with 10 covariates. For Scenario 10 we consider p = 100, p = 500, and p = 1000 with a sample size of n = 500 and only consider GLiDeR and the adaptive lasso, and compare them to the saturated method with a ridge penalty for both models due to the large number of covariates. Bootstrap 95% percentile confidence intervals of the treatment effect estimate using GLiDeR are calculated for Scenarios 1–9 and Scenario 10 with p = 100 using 1,000 bootstrap samples. All results represent averages over 1,000 Monte Carlo datasets.
Table 1.
Scenarios considered. Treatment A is generated as Bernoulli[expit{f (V)}], and outcome Y is generated as N (A + g (V), ) where σ2 = 1 for Scenarios 1–9 and for Scenario 10.
| Scenario | f (V) (Treatment) | g (V) (Outcome) | |
|---|---|---|---|
| 1 | 0.4V1 + 0.3V2 + 0.2V3 + 0.1V4 | 0 | |
| 2 | 0.5V1 + 0.5V2 + 0.5V3 + 0.1V4 | 0.5V1 + V3 + 0.5V4 | |
| 3 | 0.1V1 + 0.1V2 + V3 + V4 + V5 | 2V1 + 2V2 | |
| 4 | 0.5V1 + 0.4V2 + 0.3V3 + 0.2V4 + 0.1V5 | 0.5V1 + V2 + 1.5V3 + 2V4 + 2.5V5 | |
| 5 | 0.5V1 + 0.5V2 + 0.1V3 |
|
|
| 6 | V1 + V2 + V5 |
|
|
| 7 | 0.2V1 + 0.2V2 + 0.2V5 |
|
|
| 8 |
|
0.5V1 + 0.5V2 + 0.1V3 | |
| 9 | (X1 + X2 + 0.5X3)2 | 0.5V1 + 0.5V3 + 0.5V4 | |
| 10 | 0.2V1 − 2V2 + V5 − V6 + V7 − V8 | 2V1 + 0.2V2 + 5V3 + 5V4 |
5.2 Results
Table 2 shows the ratio of mean squared error (MSEs) of the average causal treatment effect of GLiDeR, backward selection, MADR, and adaptive lasso (denominator) relative to the saturated variable selection method (numerator) and Monte Carlo (MC) bias and standard deviation for a sample size of 500 and 10 covariates (Scenarios 1–9). Additional results for different sample sizes and number of covariates are given in Web Appendix C. Note that a larger value for the MSE ratio indicates better performance, with a MSE ratio greater than one demonstrating improved treatment effect estimation over the saturated method.
Table 2.
Ratio of MSE (saturated model MSE / alternative method MSE) and Monte Carlo (MC) bias and standard errors for each scenario with sample size n = 500 over 1,000 MC datasets. Scenarios 1–9 have 10 covariates and Scenario 10 has varying covariate set sizes (p). In the simulations with correlated covariates, ρ(Vi, Vj) = 0.6 for i ≠ j ≤ 5 and ρ(Vi, Vj) = 0 for i ≠ j > 5.
| GLiDeR | Backward selection | MADR | Adaptive lasso | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | MSE Ratio |
MC Bias |
MC SD |
MSE Ratio |
MC Bias |
MC SD |
MSE Ratio |
MC Bias |
MC SD |
MSE Ratio |
MC Bias |
MC SD |
| Independent covariates | ||||||||||||
|
| ||||||||||||
| 1 | 1.10 | 0.00 | 0.09 | 1.02 | 0.00 | 0.09 | 1.11 | 0.00 | 0.09 | 1.12 | 0.00 | 0.09 |
| 2 | 1.09 | 0.00 | 0.09 | 1.02 | 0.00 | 0.10 | 1.12 | 0.00 | 0.09 | 1.13 | 0.00 | 0.09 |
| 3 | 2.91 | 0.00 | 0.09 | 1.04 | 0.00 | 0.15 | 3.06 | 0.00 | 0.09 | 3.20 | 0.00 | 0.09 |
| 4 | 1.01 | 0.00 | 0.10 | 1.01 | 0.00 | 0.10 | 1.02 | 0.00 | 0.10 | 0.79 | 0.05 | 0.10 |
| 5 | 1.67 | −0.04 | 0.63 | 1.05 | −0.04 | 0.80 | 1.65 | −0.03 | 0.64 | 1.64 | −0.04 | 0.64 |
| 6 | 18.35 | 0.00 | 0.31 | 0.95 | −0.03 | 1.36 | 18.53 | 0.00 | 0.31 | 16.30 | 0.00 | 0.33 |
| 7 | 1.14 | −0.05 | 0.84 | 1.04 | −0.06 | 0.88 | 1.12 | −0.05 | 0.85 | 1.16 | −0.05 | 0.83 |
| 8 | 1.26 | 0.01 | 0.12 | 1.04 | 0.01 | 0.13 | 1.25 | 0.02 | 0.12 | 1.35 | 0.01 | 0.11 |
| 9 | 1.05 | 0.00 | 0.11 | 1.04 | 0.00 | 0.11 | 1.06 | 0.00 | 0.11 | 1.06 | 0.00 | 0.11 |
|
| ||||||||||||
| Correlated covariates | ||||||||||||
|
| ||||||||||||
| 1 | 1.16 | 0.00 | 0.09 | 1.01 | 0.00 | 0.10 | 1.20 | 0.00 | 0.09 | 1.20 | 0.00 | 0.09 |
| 2 | 1.09 | 0.00 | 0.10 | 1.02 | 0.00 | 0.10 | 1.09 | 0.00 | 0.10 | 1.14 | 0.02 | 0.10 |
| 3 | 5.55 | 0.00 | 0.13 | 0.94 | −0.02 | 0.32 | 5.29 | −0.01 | 0.14 | 7.49 | 0.02 | 0.11 |
| 4 | 1.05 | 0.01 | 0.11 | 1.04 | 0.01 | 0.11 | 1.08 | 0.01 | 0.11 | 0.25 | 0.20 | 0.11 |
| 5 | 3.30 | 0.39 | 1.99 | 1.02 | 0.05 | 3.64 | 2.68 | 0.45 | 2.20 | 2.14 | 0.99 | 2.15 |
| 6 | 305.39 | −0.02 | 0.92 | 1.61 | −0.10 | 12.69 | 74.41 | 0.02 | 1.86 | 199.97 | 0.05 | 1.14 |
| 7 | 1.27 | 0.06 | 0.86 | 1.09 | 0.05 | 0.93 | 1.15 | 0.07 | 0.91 | 1.96 | 0.05 | 0.69 |
| 8 | 1.28 | 0.01 | 0.15 | 1.12 | 0.01 | 0.16 | 1.29 | 0.02 | 0.15 | 1.29 | 0.02 | 0.15 |
| 9 | 1.05 | 0.00 | 0.11 | 1.06 | 0.00 | 0.11 | 1.06 | 0.00 | 0.11 | 1.06 | 0.00 | 0.11 |
|
| ||||||||||||
| Scenario 10 | ||||||||||||
|
| ||||||||||||
| p = 100 | 1.60 | 0.00 | 0.26 | * | * | * | * | * | * | 0.51 | −0.42 | 0.20 |
| p = 500 | 13.65 | −0.06 | 0.32 | * | * | * | * | * | * | 6.22 | −0.42 | 0.20 |
| p = 1000 | 13.76 | −0.14 | 0.29 | * | * | * | * | * | * | 7.43 | −0.39 | 0.20 |
Bold indicates significant difference (5% significance level) between MSEs (testing equality) from the saturated method (full model) vs. the alternative method using the paired t-test.
Apart from a few exceptions, all MSE ratios are greater than one as including all covariates available (saturated method) generally led to treatment effect estimates with higher MC variance. Additionally, backward selection shows a smaller MSE ratio than MADR and GLiDeR in all scenarios except one (Scenario 9 with correlated covariates, where the three ratios are similar) as using backward selection on the outcome model to select covariates for treatment effect estimation was generally more variable than performing variable selection across both the outcome and treatment models (GLiDeR, MADR).
Comparing GLiDeR and MADR, when both models were specified correctly (Scenarios 1–4) or when only the treatment models were misspecified (Scenarios 8 and 9), GLiDeR and MADR performed similarly. However, in all scenarios where the outcome models were misspecified (Scenarios 5–7) with correlated covariates, GLiDeR displayed a less variable treatment effect estimator and significantly greater MSE ratio than MADR; the methods performed similarly in these scenarios with independent data.
The adaptive lasso approach considered here uses only the outcome model for estimation of the treatment effect and is, therefore, more efficient than doubly robust methods when the outcome model is correctly specified. This approach outperformed all methods with a correctly specified outcome model, except Scenarios 4 and 10 with p = 100, where it displayed much greater MC bias and performed significantly worse (MSE ratio < 1) than all methods. In these two scenarios, there is a confounder weakly associated with the outcome but strongly related to treatment (V1 in Scenario 4 and V2 in Scenario 10). The adaptive lasso tends to omit these variables as it considers only the associations in the outcome model and ignores the relationships between treatment and covariates. Excluding these important confounders in Scenarios 4 and 10 introduces a large bias and consequently larger MSE compared to the other methods. GLiDeR, however, selects this important confounder in nearly all datasets in these scenarios (see Web Table 5 for percentage of datasets each covariate is selected by GLiDeR) and accordingly has much smaller bias than adaptive lasso using only the outcome model. In Scenario 10 when the number of irrelevant covariates is increased (p = 500 and p = 1000; n = 500), the bias of GLiDeR also increases as it becomes more challenging to select X2, but the bias is much smaller than that of adaptive lasso and, even with a larger variance, GLiDeR has an MSE ratio approximately twice that of the adaptive lasso. Even with the large bias of the adaptive lasso, it is more efficient than using all covariates with ridge penalty with p = 500 and p = 1000.
GLiDeR achieved coverage rates very close to the nominal 95% in all scenarios that were considered for confidence interval coverage (see Web Table 6).
5.3 Computation time
GLiDeR is dramatically faster than MADR, making it feasible to apply in problems where p is much larger. With p = 10 covariates and sample size n = 500, GLiDeR required 3 seconds while MADR required 10. However, the computation time of GLiDeR scales linearly with the number of covariates p, while the computation time of MADR scales exponentially as 2p. For instance, MADR would take over 1, 000 hours with 30 covariates (ignoring the time for storage and other necessary calculations), while GLiDeR solves the same size problem in less than 20 seconds; in Scenario 10 with sample size n = 500 and p = 100, p = 500, and p = 1000, GLiDeR took approximately 20 seconds, 3.5 minutes, and 11 minutes, respectively, to compute the ACE per dataset over a sequence of 100 λ. All computations were performed using a pure R implementation, rather than a faster language like C.
6. Application
Bilateral lung transplant (BLT) is generally associated with lower short-term survival, but higher quality of life compared to single-lung transplant (SLT) for individuals with lung disease (Aziz et al., 2010). Consequently, the effect of BLT (vs. SLT) on physiologic measures associated with quality of life, such as forced expiratory volume in one second (FEV1), is important for patients who must decide between the two treatment options. Data on lung transplant recipients from May 2005 – September 2011 were obtained from the United Network for Organ Sharing national registry. In this analyses, we focus on patients aged 60 or older with obstructive lung disease (e.g., COPD). The dataset consists of 937 patients (52.7% receiving BLT) and 31 potential confounders, which are summarized in Web Table 7. Missing covariate data were imputed using Multivariate Imputation by Chained Equations (MICE) (Van Buuren and Groothuis-Oudshoorn, 2011). The outcome is FEV1% one year after transplant, where FEV1% is defined as the percentage of the predicted value of FEV1 given the person’s age, height, gender, and race. Patients who died were given an FEV1 of 0, the worst possible score. We assume linear and logistic regression models for the outcome and treatment (BLT vs. SLT), respectively. With 31 covariates, we would have to fit 232 (over 4 billion) models to estimate the treatment effect using model averaged methods, making GLiDeR an appealing option.
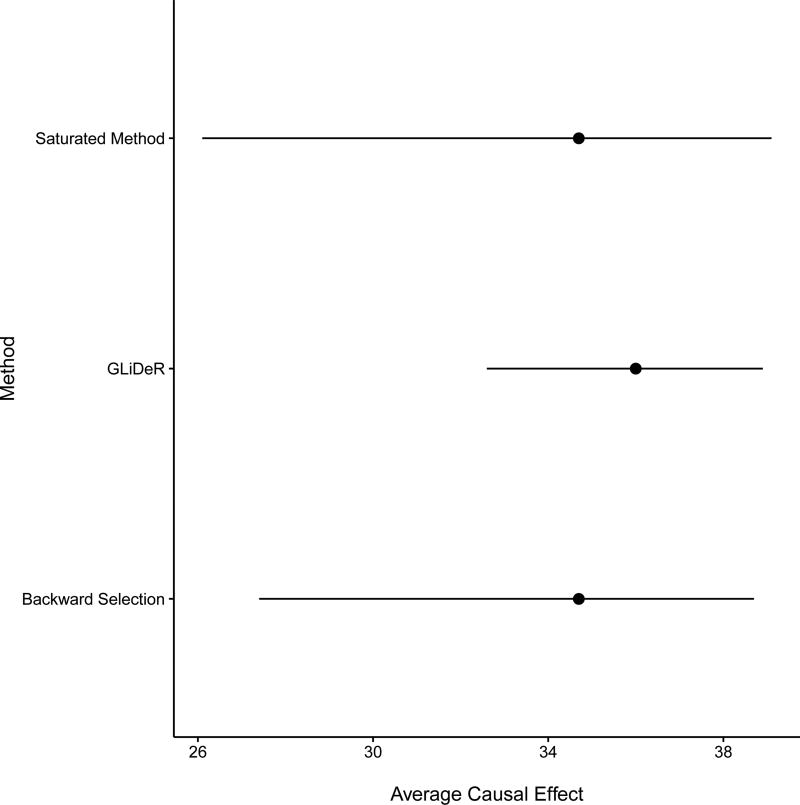
We estimated coefficient values for a sequence of 100 λ values ranging from 0 to the smallest value of λ such that all coefficients are zero. We then selected the optimal λ (denoted λ*) using GCV on the outcome model as described in Section 3.4. For all methods, 1,000 bootstrap samples were used to estimate standard errors and obtain 95% percentile-based confidence intervals (CIs) of the treatment effect estimates. Figure 1 shows the estimated coefficients from the outcome and treatment model for a subset of λ values that were considered. Table 3 displays the selected covariates and estimated coefficients by GLiDeR and backward selection; nine covariates were selected by GLiDeR and six covariates were chosen by backward selection for final estimation of the treatment effect. Figure 2 displays a forest plot comparing point estimates and 95% CIs of the ACE of BLT (vs. SLT) on FEV1% one year after transplant for GLiDeR, backward selection, and the saturated method.
Figure 1.
Coefficient estimates for the outcome (top) and treatment (bottom) models. A white box indicates a coefficient is equal to zero, while a darker box indicates a coefficient is larger in magnitude. Variables are ordered by the magnitude of their outcome model coefficients at λ = 0 (unpenalized model) from largest to smallest.
Table 3.
Variables selected and estimated coefficients (for standardized variables and outcome) by GLiDeR and backward selection.
| GLiDeR | Backward selection | |||
|---|---|---|---|---|
| Covariate | Outcome Coef | Treatment Coef | Outcome Coef | Treatment Coef |
| Ischemic time | −0.075 | −1.018 | −0.060 | −1.154 |
| Age of recipient | 0.097 | 0.171 | 0.114 | 0.270 |
| PO2 | 0.032 | −0.014 | 0.060 | −0.079 |
| Oxygen amount required | −0.052 | −0.088 | −0.060 | −0.261 |
| 6 minute walk distance | 0.019 | −0.004 | 0.061 | −0.044 |
| Height of recipient | −0.058 | 0.008 | * | * |
| Height of donor | −0.015 | 0.005 | * | |
| Local or regional (vs. national) allocation | 0.034 | 0.096 | * | * |
| Center volume | 0.010 | −0.013 | * | * |
| Sex of recipient | * | * | 0.092 | −0.034 |
Covariate was not chosen by method
Figure 2.
Forest plot of point estimates and corresponding Bootstrap percentile 95% confidence intervals of the ACE of BLT (vs. SLT) on FEV1% one year after transplant for GLiDeR, backward selection, and the saturated method.
Using backward selection on the outcome model as described in Section 5.1, the ACE is estimated to be 34.7 with a standard error of 3.4, both equivalent (to one decimal place) to the estimates obtained using all covariates, but with a slightly smaller 95% CI: (27.4, 38.7) with backward selection compared to (26.1, 39.1) using all covariates. The standard errors and CI length using these methods are much larger than those achieved with GLiDeR, where the estimated coefficients at λ* are used in the standard doubly robust estimator in Equation (1) and the ACE of BLT (vs. SLT) is estimated to be 36.0 (FEV1% after one year) with a corresponding standard error of 1.6 and 95% CI of (32.6, 38.9).
These results are consistent with simulations, where GLiDeR generally shows greater efficiency over these methods as the number of covariates is increased (see Web Tables 1 and 3). Even though the differences in estimated treatment effects between GLiDeR and other approaches appear small, the difference in sample means of FEV1% among the treated (BLT) and untreated (SLT) is 33.9, meaning the gap between the effect estimate from GLiDeR and other methods which incorporate covariates is larger than that between those other methods and the sample mean difference. In settings where incorporating covariates makes a bigger difference to the treatment effect estimate, GLiDeR may offer a substantial gain in efficiency.
7. Discussion
Doubly robust estimation of the average causal treatment effect requires working models for both the outcome and treatment given possible confounders. When the number of possible confounders is large it is natural to consider some form of variable selection for the outcome and treatment models. GLiDeR uses an adaptive group lasso approach to perform coefficient regularization and estimation across both treatment and outcome models simultaneously, unlike traditional methods that consider only one model and are thus more likely to exclude important confounders with weak associations in the model under consideration. GLiDeR has desirable theoretical properties, and in simulation experiments outperforms doubly robust approaches which do not incorporate variable selection. It achieves similar efficiency with existing techniques which perform variable selection across both outcome and treatment models, but has substantial computational advantages over these approaches and allows for situations with p > n. Simulations suggest the largest gains in efficiency are achieved when the outcome is misspecified, a frequent occurrence in practice.
GLiDeR targets inference for the average causal treatment effect, Δ. Even though GLiDeR displays good performance in the simulation scenarios considered in this paper, we caution that, like other model selection procedures, its finite sample performance at certain local alternatives can potentially be quite poor, reminiscent of Hodges’ estimator (Leeb and Pötscher, 2008). While the validity of bootstrap intervals was not explored in this paper, percentile bootstrap confidence intervals for Δ had good coverage; how to adapt promising recent developments in post-selection inference to our setting is an area of future research.
Supplementary Material
Acknowledgments
Support for this research was provided by National Cancer Institute grant R01CA214825 and National Institute on Drug Abuse grant R03-DA041870.
Footnotes
Web Appendices referenced in Sections 3.4, 3.5, 4.2, 5.2, and 6 and R code to implement the method are available with this paper at the Biometrics website on Wiley Online Library.
References
- Aziz F, Penupolu S, Xu X, He J. Lung transplant in end-staged chronic obstructive pulmonary disease (COPD) patients: a concise review. Journal of Thoracic Disease. 2010;2:111–116. [PMC free article] [PubMed] [Google Scholar]
- Blazère M, Loubes JM, Gamboa F. Oracle inequalities for a group lasso procedure applied to generalized linear models in high dimension. IEEE Transactions on Information Theory. 2014;60:2303–2318. [Google Scholar]
- Brookhart MA, Schneeweiss S, Rothman KJ, Glynn RJ, Avorn J, Stürmer T. Variable selection for propensity score models. American Journal of Epidemiology. 2006;163:1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cefalu M, Dominici F, Arvold ND, Parmigiani G. Model averaged double robust estimation. Biometrics. 2016 doi: 10.1111/biom.12622. ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Luna X, Waernbaum I, Richardson TS. Covariate selection for the nonparametric estimation of an average treatment effect. Biometrika. 2011;98:861–875. [Google Scholar]
- Ertefaie A, Asgharian M, Stephens DA. Variable selection in causal inference using a simultaneous variable selection method. arXiv preprint arXiv: 1511.08501 2015 [Google Scholar]
- Leeb H, Pötscher BM. Sparse estimators and the oracle property, or the return of Hodges’ estimator. Journal of Econometrics. 2008;142:201–211. [Google Scholar]
- Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine. 2004;23:2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- Van Buuren S, Groothuis-Oudshoorn K. MICE: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software. 2011;45:1–67. [Google Scholar]
- van der Laan MJ, Gruber S. Collaborative double robust targeted maximum likelihood estimation. The International Journal of Biostatistics. 2010;6 doi: 10.2202/1557-4679.1181. Article 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Shpitser I. A new criterion for confounder selection. Biometrics. 2011;67:1406–1413. doi: 10.1111/j.1541-0420.2011.01619.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Bekaert M, Claeskens G. On model selection and model misspecification in causal inference. Statistical Methods in Medical Research. 2012;21:7–30. doi: 10.1177/0962280210387717. [DOI] [PubMed] [Google Scholar]
- Wang C, Parmigiani G, Dominici F. Bayesian effect estimation accounting for adjustment uncertainty. Biometrics. 2012;68:661–671. doi: 10.1111/j.1541-0420.2011.01731.x. [DOI] [PubMed] [Google Scholar]
- Yang Y, Zou H. A fast unified algorithm for solving group-lasso penalized learning problems. Statistical Computing. 2015;25:1129–1141. [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Methodological) 2006;68:49–67. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.