Model Selection and Inference for Censored Lifetime Medical Expenditures

Summary

Identifying factors associated with increased medical cost is important for many micro- and macro-institutions, including the national economy and public health, insurers and the insured. However, assembling comprehensive national databases that include both the cost and individual-level predictors can prove challenging. Alternatively, one can use data from smaller studies with the understanding that conclusions drawn from such analyses may be limited to the participant population. At the same time, smaller clinical studies have limited follow-up and lifetime medical cost may not be fully observed for all study participants. In this context, we develop new model selection methods and inference procedures for secondary analyses of clinical trial data when lifetime medical cost is subject to induced dependent censoring. Our model selection methods extend a theory of penalized estimating function to a calibration regression estimator tailored for this data type. Next, we develop a novel inference procedure for the unpenalized regression estimator using perturbation and resampling theory. Then, we extend this resampling plan to accommodate regularized coefficient estimation of censored lifetime medical cost and develop post-selection inference procedures for the final model. Our methods are motivated by data from Southwest Oncolocy Group Protocol 9509, a clinical trial of patients with advanced nonsmall cell lung cancer, and our models of lifetime medical cost are specific to this population. But the methods presented in this article are built on rather general techniques and could be applied to larger databases as those data become available.

1. Introduction

Many institutions, including governments, hospitals, and private businesses, have great interest in factors associated with increased medical costs. For example, countries with state-run medical insurance programs aim to provide state-of-the-art medicine to their citizens while moderating the financial burden on the economy. In our motivating study, the Southwest Oncology Group (SWOG) clinical trial 9509, Huang (2002) showed that while patients following either one of two competing treatment regimens for nonsmall cell lung cancer had similar survival, one treatment led to significantly lower medical costs compared to the other treatment. In this paper, we seek to identify systematically other predictors associated with differential medical costs in SWOG 9509, estimate their association and draw valid statistical inference on the final estimates. The analysis is complicated because clinical studies have limited follow-up and lifetime medical costs is not fully observed for all study participants.

Suppose Y is lifetime medical cost measured at the end of life, say at time T, and z = (z₁, …, z_d)^T is a d-vector of independent regressors. We assume the natural logarithm of lifetime medical cost is linearly related to the independent variables though the regression model,

$$logY=\sum _{j=1}^d{z}_j{\beta }_j+{\epsilon }_Y,$$ (1)

where β = (β₁,…, β_d)^T are unknown coefficients and the error ε_Y comes from an unknown distribution. The primary scientific interest lies in the coefficient vector β but estimation is challenging because lifetime cost Y is observed only for uncensored observations, i.e. T ≤ C, where C be a censoring random variable. It is well-known that naïve estimators of β, e.g. least squares estimation on uncensored medical costs, work only under restrictive assumptions on the data-generating mechanism and are not, in general, consistent for β (e.g. Lin et al., 1997; Huang and Louis, 1998; Huang, 2002; Jain and Strawderman, 2002). Thus, the statistical objective is to estimate β consistently under reasonably general conditions with the observed data (δY, X, δ, z), where X = min(T, C) and δ = I(T ≤ C).

A principal challenge in estimating β in the presence of censoring is the potential non-identifiability of the conditional distribution [Y|z] when δ = 1 (e.g. Zhao and Tsiatis, 1997; Huang and Louis, 1998). Two estimation strategies that accommodate both the identifiability of [Y|z] and the induced censoring include inverse weighting (Zhao and Tsiatis, 1997; Lin, 2000; Bang and Tsiatis, 2000; Jain and Strawderman, 2002; Tsiatis, 2006) and bivariate modeling of time and cost together (Huang, 2002). Due to space limitations, a detailed review of these strategies is not given here and we refer the interested reader elsewhere in the literature (Huang, 2009). Briefly, the inverse weighting strategy overcomes identifiability concerns by redefining the outcome as time-restricted cost such that the new outcome is identified by definition and overcomes censoring by weighting the uncensored observations in an uncensored least-squares estimator, for example, by the inverse probability of censoring via P(C > t|z), t ≥ 0. Alternatively, Huang (2002) suggested modeling cost and time together, for example, by parameterizing the conditional distribution [(Y,T)|z] as [T|z] and [Y|(T,z)]. Compared with inverse weighting, Huang's (2002) technique models cost outcome Y rather than time-restricted medical cost and estimates nuisance parameters through the conditional distribution [T|z] rather than [C|z]. Nevertheless, both estimation strategies regard cost-scale inference as the primary analytic goal and other aspects of the statistical model as secondary.

Our estimator is based on an extension and application of a theory of penalized estimating function applied to Huang's (2002) calibration regression estimator. If 𝕊_β(β) is a consistent estimating function for β, then Johnson et al. (2008) defined the penalized estimating function

$${\mathbb{S}}_{\beta ,\lambda }(\mathit{\beta })={\mathbb{S}}_{\beta }(\mathit{\beta })-n{\mathbf{q}}_{\lambda }(|\mathit{\beta }|)sgn(\mathit{\beta }),$$ (2)

where sgn(β) = (sign(β_j), j = 1, …, d), q_λ(|β|)sgn(β) is the element-wise product and q_λ(|β|) is a penalty function satisfying conditions that we state in Section 2. A root to the estimating function 𝕊_β,λ(β) is both sparse and satisfies an oracle property (Fan and Li, 2001; Zou, 2006; Johnson et al., 2008). In our medical cost application, there are secondary parameters that must be estimated and, naturally, one might expect that different estimation strategies at this level will have consequences on the cost-scale estimator. We investigate the operating characteristics of two different approaches in this paper.

Variable selection procedures for censored medical cost are given in Section 2. This includes a method that estimates secondary parameters via unregularized estimation and another method that attempts to select variables and estimate parameters in [Y|(T, z)] and [T|z] simultaneously; the former method is our preferred approach and was detailed in an unpublished technical report (Johnson et al., 2012) while the latter method is new and given for comparison purposes. New inference procedures for the unregularized and regularized calibration estimators are given in Section 3. For the regularized case, we adapt the post-selection inference procedures by Minnier et al. (2011) to calibration estimator for lifetime medical cost. We re-analyze the medical cost data from SWOG 9509 in Section 4 and report on our simulation studies in Section 5.

2. Variable Selection for Lifetime Medical Cost

2.1 Regularization in Cost-scale Only

Using a theory of counting processes (Andersen et al., 1993; Kalbfleisch and Prentice, 2002), the weighted log-rank estimating function for inference in the accelerated lifetime model (Tsiatis, 1990; Wei et al., 1990; Ying, 1993), and results for marked processes (Huang and Louis, 1998), Huang (2002) proposed the coefficient estimator for (β, ϑ) in the bivariate regression model

$$\begin{array}{cc}logY=\sum _{j=1}^d{z}_j{\beta }_j+{\epsilon }_Y,& logT=\sum _{j=1}^d{z}_j{\vartheta }_j+{\epsilon }_T,\end{array}$$ (3)

as a root to the system of equations, o_p(n^1/2) = 𝕊(θ) ≡ {𝕊_β(θ), 𝕊_ϑ(θ)},

$${\mathbb{S}}_{\beta }(\mathit{\theta })=\sum _{i=1}^n{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })\{{\mathbf{z}}_i-\overline{\mathbf{z}}(u,\mathit{\vartheta })\}\psi (log{Y}_i-{\mathbf{z}}_i^T\mathit{\beta }){\mathit{\text{dN}}}_i(u,\mathit{\vartheta }),$$ (4)

$${\mathbb{S}}_{\vartheta }(\mathit{\theta })=\sum _{i=1}^n{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })\{{\mathbf{z}}_i-\overline{\mathbf{z}}(u,\mathit{\vartheta })\}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta }),$$ (5)

where (δ_iY_i, X_i, δ_i, z_i) is the observed data for the i-th individual, γ(t, ϑ) is a non-negative weight function, ψ(·) is a strictly monotone function, $R_i(u,\mathit{\vartheta })=I(log{X}_i-{\mathbf{z}}_i^{\mathrm{T}}\mathit{\vartheta }\ge u)$ is the at-risk process, $N_i(u,\mathit{\vartheta })=I(log{X}_i-{\mathbf{z}}_i^{\mathrm{T}}\mathit{\vartheta }\le u,{\delta }_i=1)$ is the counting process, and z̄(u, ϑ) = Σ_jz_jR_j(u, ϑ)/Σ_jR_j(u, ϑ). The statistic 𝕊_ϑ(θ) is the weighted log-rank estimating function (Tsiatis, 1990; Wei et al., 1990) and does not depend on the cost-scale coefficients β. For arbitrary weight function γ(u, ϑ), the estimating function 𝕊_ϑ(θ) is known to be non-monotone, contain multiple roots, some of which may be inconsistent (Fygenson and Ritov, 1994). Under conditions (A)–(E) in Huang (2002), the joint coefficient estimator ${\widehat{\mathit{\theta }}}_0={({\widehat{\mathit{\beta }}}_0^{\mathrm{T}},{\widehat{\mathit{\vartheta }}}_0^{\mathrm{T}})}^{\mathrm{T}}$ is consistent and asymptotically normal with mean θ₀ and covariance n⁻¹{Γ⁻¹Ω(Γ⁻¹)^T}, where Γ = ∇{lim_n n⁻¹𝕊(θ₀)}, n^−1/2𝕊(θ₀) →_d N(0, Ω), and $\mathbb{S}(\mathit{\theta })={\{{\mathbb{S}}_{\beta }^{\mathrm{T}}(\mathit{\theta }),{\mathbb{S}}_{\vartheta }^{\mathrm{T}}(\mathit{\theta })\}}^{\mathrm{T}}$. The asymptotic covariance is not directly estimable because the asymptotic slope matrix Γ depends on the hazard functions of the errors (ε_Y, ε_T) in (3). This point makes statistical inference for θ̂₀, and hence β̂₀, challenging.

The calibration estimator β̂₀ consistently estimates the mark-scale regression coefficients β in (3) but does not perform variable selection. To simultaneously select and estimate cost-scale coefficients, we propose the system of estimating functions,

$${\mathbb{S}}_{\lambda }(\mathit{\theta })=\{{\mathbb{S}}_{\beta ,\lambda }^{\mathrm{T}}(\mathit{\theta }),{\mathbb{S}}_{\vartheta }^{\mathrm{T}}(\mathit{\theta })\},$$ (6)

where 𝕊_β,λ(θ) = 𝕊_β(θ) − nq_λ(|β|)sgn(β) is the penalized estimating function, analogous to (2), and q_λ(|β|) = (q_λ,1(|β₁|), …, q_λ,d(|β_d|))^T satisfies the following two conditions: for fixed β > 0,

• A1. lim_n→∞ n^1/2q_λ(|β|) = 0 and lim_n→∞(∂/∂β)q_λ(|β|) = 0;

• A2. For any K > 0, lim_n→∞n^1/2 inf_{|β|<Kn^−1/2} q_λ(|β|) → ∞.

Conditions A1–A2 are sufficient to define a cost-scale coefficient estimator, say β̂_λ, that achieves an oracle property. In words, the oracle property implies the coefficient estimator is consistent and asymptotically normal, and sets the coefficient estimate exactly to zero for unimportant variables with probability tending to one. The asymptotic properties of β̂_λ are given in Web Appendix A. Note, the system of equations 𝕊_λ(θ) regularizes the cost-scale estimating function but not the time-scale estimating function; we revisit this point in Section 2.2.

The role of ψ(·) in (4) is to moderate the influence of extremely large observations on the mark-scale. But setting ψ(y) = y leads to a computationally efficient estimator and an exact solution to the system of penalized estimating functions. In the sequel, the identity weight function ψ(·) is assumed throughout. Then, one can show that the penalized estimating function 𝕊_β,λ(β, ϑ₀) in 𝕊_λ(θ) is the quasi-gradient of the objective function,

$${\mathbb{Q}}_{\beta ,\lambda }(\mathit{\beta },{\mathit{\vartheta }}_0)=\frac{1}{2}{\{\mathbf{V}({\mathit{\vartheta }}_0)-\mathbf{A}({\mathit{\vartheta }}_0)\mathit{\beta }\}}^{\mathrm{T}}\{\mathbf{V}({\mathit{\vartheta }}_0)-\mathbf{A}({\mathit{\vartheta }}_0)\mathit{\beta }\}+n\sum _{j=1}^d{p}_{\lambda ,j}({\beta }_j),$$ (7)

with (∂/∂β_j)p_λ,j(β_j) = q_λ,j(|β_j|)sign(β_j), V(ϑ) = {A^T(ϑ)}⁻¹w(ϑ), A(ϑ) is the Choleski decomposition of M(ϑ), and $\mathbf{w}(\mathit{\vartheta })={\sum }_{i=1}^n{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })Y_i\{{\mathbf{z}}_i-\overline{\mathbf{z}}(u,\mathit{\vartheta })\}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta })$, and $\mathbf{M}(\mathit{\vartheta })={\sum }_{i=1}^n{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })\{{\mathbf{z}}_i-\overline{\mathbf{z}}(u,\mathit{\vartheta })\}{\mathbf{z}}_i^{\mathrm{T}}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta })$. The expression ℚ_β,λ(β, ϑ₀) is a surrogate loss function depending on the unknown time-scale coefficient ϑ₀. Thus, β̂_λ minimizes ℚ_β,λ(β, ϑ̂₀).

2.2 Simultaneous Regularization on Cost- and Time-scale Coefficients

An alternative approach to model selection for censored medical cost data would be to perform estimation and variable selection over cost- and time-scale coefficients simultaneously. First, there may be a scientific reason to regard both time- and cost-scale coefficients as primary parts of the statistical model. Second, one might hope to achieve a better cost-scale coefficient estimator by removing unimportant time-scale regressors or otherwise regularizing the time-scale parameters. We show one method of joint regularization using effectively the same techniques as in Section 2.1. By replacing β with θ in (6), we define the penalized estimating function

$${\stackrel{\sim }{\mathbb{S}}}_{\lambda }(\mathit{\theta })=\mathbb{S}(\mathit{\theta })-n{\mathbf{q}}_{\lambda }(|\mathit{\theta }|)sgn(\mathit{\theta }),$$ (8)

where q_λ(·) is defined through Conditions A1–A2. Under regularity conditions in Huang (2002, Appendix), Theorem 1 in Johnson et al. (2008) says that a root to 𝕊̃_λ(θ) possesses an oracle property. Hence, both approaches via (6) and (8) result in sparse coefficient estimates on the cost-scale but only (8) results in sparse estimates on the time-scale.

Unfortunately, solving 𝕊̃_λ(θ) using ordinary methods, e.g. local quadratic approximation, is difficult because Γ is not directly estimable. Wang and Leng (2007) proposed an indirect, but asymptotically equivalent, method to finding roots of penalized estimating functions. It is easy to show that under standard conditions on parametric families of distributions, a local approximation to the likelihood is the quadratic function (θ − θ₀)^Tℐ_n(θ − θ₀), where ℐ_n is the information matrix evaluated at θ₀. Under technical regularity assumptions on estimating functions 𝕊(θ), including the asymptotic linearity of 𝕊(θ), Wang and Leng (2007) showed this idea extends to general M- and Z-estimators by replacing ℐ_n with the inverse sandwich matrix. Thus, a penalized local quadratic loss function for our problem is

$${\stackrel{\sim }{\mathbb{Q}}}_{\lambda }(\mathit{\theta })={(\mathit{\theta }-{\mathit{\theta }}_0)}^{\mathrm{T}}{\mathbf{\sum }}^{-1}(\mathit{\theta }-{\mathit{\theta }}_0)+\sum _{j=1}^d{p}_{\lambda ,j}({\theta }_j),$$ (9)

where Σ = Γ⁻¹Ω(Γ⁻¹)^T and p_λ,j were defined in (7). In practice, Σ is unknown and must be estimated; see Section 3.

2.3 Algorithmic and Practical Notes

In the sequel, we consider two weight functions, the Gehan weight function, $\gamma (u,\mathit{\vartheta })=n^{-1}{\sum }_{i=1}^n{R}_i(u,\mathit{\vartheta })$ and the log-rank weight function, γ(u, ϑ) = 1. To compute the Gehan estimate of the time-scale coefficient ϑ, we use the linear programming technique by Jin et al. (2003) to compute the Gehan estimates. Then, we compute the log-rank estimate through their iteratively reweighted Gehan estimate using 5 iterations. The unregularized mark-scale estimate is the solution to a linear system (Huang, 2002). To compute the regularized mark-scale estimates for general penalty function, Johnson et al. (2012) investigated several algorithms for non-concave penalized least squares. Due to space limitations, we refer interested readers to our technical report for details. The results in Sections 4-5 use a multi-stage local linear approximation algorithm.

The regularization parameter λ is determined by minimizing data-dependent information criteria. We define the quadratic function $D(\mathit{\theta })=n^{-1}{\mathbb{S}}^{\mathrm{T}}(\mathit{\theta }){\mathbf{\Omega }}_n^{-1}({\widehat{\mathit{\theta }}}_0)\mathbb{S}(\mathit{\theta })$, where Ω_n(θ₀) is a consistent estimator of the asymptotic covariance matrix Ω(θ₀),

$${\mathbf{\Omega }}_n(\mathit{\theta })=\frac{1}{n}\sum _{i=1}^n{\int }_{-\infty }^{\infty }{\left\{\begin{array}{c}\gamma (u,\mathit{\vartheta })\psi (log{Y}_i-{\mathbf{z}}_i^{\mathrm{T}}\mathit{\beta })\\ \gamma (u,\mathit{\vartheta })\end{array}\right\}}^{\otimes 2}\otimes {\{{\mathbf{z}}_i-\overline{\mathbf{z}}(u,\mathit{\vartheta })\}}^{\otimes 2}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta }),$$

v^⊗2 = vv^T for the vector v and A ⊗ B is the kronecker product of matrices A and B. Following similar arguments to Wei et al. (1990), one can show that D(θ̂_λ) converges to a χ² random variable as n → ∞ with degrees of freedom equal to the number of zero coefficients in θ̂_λ. Thus, our bic-type criterion is bic(λ) = D(θ̂_λ)+log(n)d̂(λ), where d̂(λ) is the cardinality of θ̂_λ, and an aic-type criterion is aic(λ) = D(θ_λ) + 2d̂(λ).

3. Inference Procedures

Similar to Minnier et al. (2011), our resampling procedure is based on perturbation theory. Let (ζ₁, …, ζ_n) be independent and identically distributed random variables, completely independent of the observed data, such that E(ζ₁) = var(ζ₁) = 1. Without loss of generality, let β̂* and ϑ̂* be resampled estimates for β and ϑ, respectively. Suppose that β̂ has influence curve ic_i(β, ϑ) such that E{ic_i(β₀, ϑ₀)} = 0 and

$$\widehat{\mathit{\beta }}-{\mathit{\beta }}_0=n^{-1}\sum _{i=1}^n{\text{IC}}_i({\mathit{\beta }}_0,{\mathit{\vartheta }}_0)+o(n^{-1/2}+\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert +\Vert \widehat{\mathit{\vartheta }}-{\mathit{\vartheta }}_0\Vert ).$$ (10)

If we can show that

$${\widehat{\mathit{\beta }}}^{\ast }-\widehat{\mathit{\beta }}=n^{-1}\sum _{i=1}^n({\zeta }_i-1){\text{IC}}_i({\mathit{\beta }}_0,{\mathit{\vartheta }}_0)+o(n^{-1/2}+\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert +\Vert {\widehat{\mathit{\beta }}}^{\ast }-{\mathit{\beta }}_0\Vert +\Vert \widehat{\mathit{\vartheta }}-{\mathit{\vartheta }}_0\Vert +\Vert {\widehat{\mathit{\vartheta }}}^{\ast }-{\mathit{\vartheta }}_0\Vert ),$$ (11)

then we conclude that, conditional on the observed data, n^1/2(β̂^* − β̂) has the same asymptotic distribution as n^1/2(β̂ − β). Regardless of the tools one employs, the basic goal is to establish (10)–(11); see also, Kosorok (2008, Theorem 10.4). This point guides our investigation below.

3.1 Statistical Inference for β̂

In our resampling scheme, we consider the effect of estimating first the nuisance parameters that are used to calibrate and define the estimating function of interest 𝕊_β(θ₀). Here, we proceed along the lines of Jin et al. (2006), who proposed a two-stage least-squares-type coefficient estimator in the accelerated lifetime model.

Let ℱ_obs = σ{(δ_iY_i, X_i, δ_i, z_i), i = 1,…, n}, $e_i(\mathit{\vartheta })=log{X}_i-{\mathbf{z}}_i^{\mathrm{T}}\mathit{\vartheta }$, and define the perturbed Gehan estimator for the time-scale parameters,

$${\widehat{\mathit{\vartheta }}}^{\ast }=\underset{\mathit{\vartheta }\in {\Re }^d}{arg\; min}\sum _{i=1}^n\sum _{j=1}^n{\zeta }_i{\zeta }_j{\delta }_i\{e_j(\mathit{\vartheta })-e_i(\mathit{\vartheta })\}I\{e_i(\mathit{\vartheta })-e_j(\mathit{\vartheta })\le 0\}.$$ (12)

Subsequently, define the perturbed mark-scale Gehan-type coefficient estimate β̂^* as the solution to the system of equations, $0={\mathbb{S}}_{\beta }^{\ast }(\mathit{\beta },{\widehat{\mathit{\vartheta }}}^{\ast })$, with ${\gamma }^{\ast }(t,\mathit{\vartheta })=n^{-1}{\sum }_{i=1}^n{\zeta }_i{R}_i(t,\mathit{\vartheta })$. Recall, when ψ(y) = y, the estimator β̂^* is exactly a solution to a perturbed linear system, i.e.

$${\widehat{\mathit{\beta }}}^{\ast }={[\sum _{i=1}^n{\int }_{-\infty }^{\infty }{\zeta }_i{\gamma }^{\ast }(u,{\widehat{\mathit{\vartheta }}}^{\ast })\{{\mathbf{z}}_i-{\overline{\mathbf{z}}}^{\ast }(u,{\widehat{\mathit{\vartheta }}}^{\ast })\}{\mathbf{z}}_i^{\mathrm{T}}{\mathit{\text{dN}}}_i(u,{\widehat{\mathit{\vartheta }}}^{\ast })]}^{-1}\sum _{i=1}^n{\int }_{-\infty }^{\infty }{\zeta }_i{\gamma }^{\ast }(u,{\widehat{\mathit{\vartheta }}}^{\ast })\{{\mathbf{z}}_i-{\overline{\mathbf{z}}}^{\ast }(u,{\widehat{\mathit{\vartheta }}}^{\ast })\}{Y}_i{\mathit{\text{dN}}}_i(u,{\widehat{\mathit{\vartheta }}}^{\ast }),$$

${\overline{\mathbf{z}}}^{\ast }(u,\mathit{\vartheta })={\sum }_{j=1}^n{\zeta }_j{\mathbf{z}}_j{R}_j(u,\mathit{\vartheta })/{\sum }_{j=1}^n{\zeta }_j{R}_j(u,\mathit{\vartheta })$ and γ^*(u, ϑ) was defined earlier. Using arguments similar to Jin et al. (2006), one can show that conditional on ℱ_obs, n^1/2(β̂^* − β̂₀) has the same asymptotic distribution as n^1/2(β̂₀ − β₀). Then, a confidence interval is constructed by repeatedly generating (ζ₁, …, ζ_n) and solving for β̂^* a large number of times, then using the percentiles from the empirical distribution of resampled estimates. Analogously, if ( ${\widehat{\mathit{\theta }}}_1^{\ast },\dots ,{\widehat{\mathit{\theta }}}_B^{\ast }$) are the perturbed coefficient vectors obtained from perturbing the data B times, then $B^{-1}{\sum }_{b=1}^B{({\widehat{\mathit{\theta }}}_b^{\ast }-{\widehat{\mathit{\theta }}}_0)}^{\otimes 2}$ is an estimator for Σ/n. Small sample studies to evaluate the resampling procedures for variance estimation are given in Web Appendix B.

3.2 Statistical Inference for β̂_λ

Similarly, let ${\widehat{\mathit{\beta }}}_{\lambda }^{\ast }$ be a root to the perturbed penalized estimating function ${\mathbb{S}}_{\beta ,\lambda }^{\ast }(\mathit{\beta },{\widehat{\mathit{\vartheta }}}^{\ast })$, where ϑ̂^* is the perturbed time-scale coefficient estimate, e.g. see (12) for Gehan weight, and

$${\mathbb{S}}_{\beta ,\lambda }^{\ast }(\mathit{\beta },\mathit{\vartheta })={\mathbb{S}}_{\beta }^{\ast }(\mathit{\beta },\mathit{\vartheta })-n{\mathbf{q}}_{\lambda }(|\mathit{\beta }|)sgn(\mathit{\beta }).$$

However, when ψ(y) = y, ${\mathbb{S}}_{\beta ,\lambda }^{\ast }(\mathit{\beta },{\mathit{\vartheta }}_0)$ is the quasi-gradient of

$${\mathbb{Q}}_{\beta ,\lambda }^{\ast }(\mathit{\beta },{\mathit{\vartheta }}_0)\frac{1}{2}{\{{\mathbf{V}}^{\ast }({\mathit{\vartheta }}_0)-{\mathbf{A}}^{\ast }({\mathit{\vartheta }}_0)\mathit{\beta }\}}^{\mathrm{T}}\{{\mathbf{V}}^{\ast }({\mathit{\vartheta }}_0)-{\mathbf{A}}^{\ast }({\mathit{\vartheta }}_0)\mathit{\beta }\}+n\sum _{j=1}^d{p}_{\lambda ,j}({\beta }_j),$$

V^*(ϑ) = {A^*T(ϑ)}⁻¹w^*(ϑ), A^*(ϑ) is the Choleski decomposition of M^*(ϑ), and

$$\begin{array}{c}{\mathbf{w}}^{\ast }(\mathit{\vartheta })=\sum _{i=1}^n{\zeta }_i{Y}_i{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })\{{\mathbf{z}}_i-{\overline{\mathbf{z}}}^{\ast }(u,\mathit{\vartheta })\}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta }),\\ {\mathbf{M}}^{\ast }(\mathit{\vartheta })=\sum _{i=1}^n{\zeta }_i{\int }_{-\infty }^{\infty }\gamma (u,\mathit{\vartheta })\{{\mathbf{z}}_i-{\overline{\mathbf{z}}}^{\ast }(u,\mathit{\vartheta })\}{\mathbf{z}}_i^{\mathrm{T}}{\mathit{\text{dN}}}_i(u,\mathit{\vartheta }).\end{array}$$

Therefore, ${\widehat{\mathit{\beta }}}_{\beta ,\lambda }^{\ast }={arg\; min}_{\mathit{\beta }\in {\Re }^d}{\mathbb{Q}}_{\beta ,\lambda }^{\ast }(\mathit{\beta },{\widehat{\mathit{\vartheta }}}^{\ast })$. Let 𝒜 = {j|β_0j ≠ 0}, β_𝒜 = {β_0j|j ∈ 𝒜}, β̂_𝒜 = {β̂_λ,j|j ∈ 𝒜}, and ${\widehat{\mathit{\beta }}}_{\mathcal{A}}^{\ast }=\{{\widehat{\beta }}_{\lambda ,j}^{\ast }|j\in \mathcal{A}\}$. By adapting the arguments of Minnier et al. (2011) to the substitution estimator here, under the conditions given in Web Appendix A, one can show that conditional on ℱ_obs, $n^{1/2}({\widehat{\mathit{\beta }}}_{\mathcal{A}}^{\ast }-{\widehat{\mathit{\beta }}}_{\mathcal{A}})$ has the same asymptotic distribution as n^1/2(β̂_𝒜 − β_𝒜). Furthermore, ${lim}_{n}P({\widehat{\beta }}_{\lambda ,j}^{\ast }\ne 0,\text{for}j\in {\mathcal{A}}^c|{\mathcal{F}}_{\mathit{\text{obs}}})=0$. As stated in Remark 3 of Johnson et al. (2008) as well as Zou and Li (2008), conditions A1-A2 apply to many penalty functions including bridge penalty (Frank and Friedman, 1993), hard thresholding (Antoniadis, 1997), scad (Fan and Li, 2001), adaptive lasso (Zou, 2006), and logarithmic penalty (Zou and Li, 2008; Johnson et al., 2008). Thus, at a minimum, the distributional result for n^1/2(β̂_ℱ − β_𝒜) applies to these regularized coefficient estimators.

To improve the finite sample perform of the variance estimators and for comparison purposes, we consider resampling plans similar to those described in Minnier et al. (2011). We consider four different types of confidence intervals based on resamples of the regularized estimates, three of which were considered in Minnier et al. (2011). Let B be the user-defined total number of resamples and define π̂_0j = #{β̂_λ,j = 0}/B, the empirical estimate that β_j = 0 based on the bootstrap resamples for j = 1, …, d. For asymptotically normal confidence intervals, ${\text{CI}}_j^{\mathrm{N}}$, we considered the centered intervals: β̂_λ,j ± z_1−α/2σ̂_j, ${\widehat{\sigma }}_j^2$ is the bootstrap estimate of the sampling variance, ${\widehat{\sigma }}_j^2=B^{-1}{\sum }_{l=1}^B{({\widehat{\beta }}_{\lambda ,j,l}^{\ast }-{\widehat{\beta }}_{\lambda ,j})}^2$. To be consistent with the procedures in Minnier et al. (2011), we set ${\text{CI}}_j^{\mathrm{N}}=\{0\}$ if π̂_0j ≥ p̂_high, p̂_high is an upper threshold such that p̂_high → (1 − α). The percentile interval ${\text{CI}}_j^{\mathrm{P}}$ defines upper and lower endpoints through the (1 − α/2)-sample quantiles of the bootstrap resamples.

In addition to normal and percentile method, we also implemented two versions of highest density intervals (Minnier et al., 2011). Write the conditional density of ${\widehat{\beta }}_j^{\ast }|{\mathcal{F}}_{\mathit{\text{obs}}}$ as the mixture density ${\widehat{\pi }}_{0j}I(b=0)+(1-{\widehat{\pi }}_{0j})p_j^{\ast }(b)$, where $p_j^{\ast }(b)$ is the probability density function of ${\widehat{\beta }}_j^{\ast }$ provided that it is non-zero. Then, the confidence interval is defined piecewise as follows:

$${\text{CI}}_j^{\mathrm{M}}=\{\begin{array}{cc}\{0\}& (\mathrm{a}).\text{Strong evidence}{\beta }_j=0\\ \{b|p_j^{\ast }(b)\ge {\kappa }_1\}\cup \{0\}& (\mathrm{b}).\text{Weak evidence}{\beta }_j=0\\ \{b|p_j^{\ast }(b)\ge {\kappa }_2\}\cup \{0\}& (\mathrm{c}).\text{Weak evidence}{\beta }_j\ne 0\\ \{b|p_j^{\ast }(b)\ge {\kappa }_3\}& (\mathrm{d}).\text{Strong evidence}{\beta }_j\ne 0\end{array}$$ (13)

where $\mathcal{R}(\kappa )=\int I\{p_j^{\ast }(b)\ge \kappa \}{p}_j^{\ast }(b)\mathit{\text{db}}$, ℛ(κ₁) = (1 − α − π̂_0j)/(1 − π̂_0j), ℛ(κ₂) = (1 − α) + α(π̂_0j + p̂_low), ℛ(κ₃) = (1 − α), p̂_low → 0 and p̂_high → (1 − α). The rules proposed by Minnier et al. (2011) for determining strong and weak evidence depended on the proportion π̂_0j and the thresholds, p̂_high and p̂_low: (a) π̂_0j ≥ p̂_high, (b) p̂_low ≤ π̂_0j < p̂_high, (c) α ≤ π̂_0j < max(α, p̂_low), and (d) π̂_0j < α. The four cases in ${\text{CI}}_j^{\mathrm{M}}$ are initially based on the mixture distribution of ${\widehat{\beta }}_j^{\ast }|{\mathcal{F}}_{\mathit{\text{obs}}}$, but Minnier et al. (2011) inflate or deflate the region of each case to improve finite sample performance of the interval estimator. For example, when the evidence is strong for β_j = 0 or β_j ≠ 0, one ignores the mass in the continuous $p_j^{\ast }(b)$ or the atom at zero, respectively. The interval estimator is inflated when there is weak evidence of a non-zero effect in case (c). The exception is when p̂_low ≤ π̂_0j < p̂_high in case (b) where the interval estimator follows directly from the definition of a highest density region for a mixture distribution.

This leads to a second definition of highest density region that reflects the mixture density ${\widehat{\pi }}_{0j}I(b=0)+(1-{\widehat{\pi }}_{0j})p_j^{\ast }(b)$ as is, without artificially manipulating the region for weak effects. Note that case (b) in (13) follows directly from the definition of bivariate mixture for a level-α region while cases (a) and (d) are ∊-approximations to the mixture density since π̂_0j is very close to one or zero, respectively. So, case (c) in (13) for weak effects is the only one that deviates substantially from the mixture density. By combining cases (b)–(c) of ${\text{CI}}_j^{\mathrm{M}}$, we take a more agnostic approach to interval estimation for any effect that lacks strong evidence as an important or unimportant variable. The simple HDR confidence interval is given by

$${\text{CI}}_j^{\mathrm{S}}=\{\begin{array}{cc}\{0\}& (\mathrm{a}).\text{Strong evidence}{\beta }_j=0\\ \{b|p_j^{\ast }(b)\ge {\kappa }_1\}\cup \{0\}& (\mathrm{b}).\text{Indeterminate}\\ \{b|p_j^{\ast }(b)\ge {\kappa }_3\}& (\mathrm{c}).\text{Strong evidence}{\beta }_j\ne 0\end{array}$$ (14)

where case (b) is in effect if α ≤ π̂_0j < p̂_high. Since the confidence interval ${\text{CI}}_j^{\mathrm{S}}$ in (14) is defined identically for cases (a), (b), and (d) from ${\text{CI}}_j^{\mathrm{M}}$ in (13), then we can evaluate directly the effect of artificially inflating the region of weak effects in case (c) of ${\text{CI}}_j^{\mathrm{M}}$.

4. Analysis of Medical Expenditures in SWOG 9509

The randomized Southwest Oncology Group (SWOG) 9509 trial was designed to investigate Paclitaxel plus Carboplatin versus Vinorelbine plus Cisplatin therapies in untreated patients with advanced nonsmall cell lung cancer. The primary study endpoint was survival time (Kelly et al., 2001) and subsequent secondary analyses considered lifetime medical costs (Huang and Lovato, 2002; Huang, 2002). For each of 408 eligible study participants, the lifetime medical cost endpoint was computed from resource utilization metrics, including medications, medical procedures, different treatments on- and off-protocol, and days spent in the outpatient or inpatient clinic. The cost incurred for each type of resource used was computed using national databases and were standardized to 1998 US dollars (Huang, 2002). Resource utilization was measured at 3, 6, 12, 18, and 24 month clinic visits. Both time and cost are modeled on the natural logarithmic scale.

Our analysis merges the cost data from Huang (2002) with another data set of demographic and clinical variables. In all, we considered 18 baseline variables as main effects in the bivariate accelerated failure time model (3). The regressors are treatment arm (tx, 1=Paclitaxel plus Carboplatin, else 0), gender (sex), progression status (prog.stat.), performance status (ps), clinical stage (stage), IIIB by pleural effusion, weight (kg), height (cm), creatinine (creat), albumin (g/dl), calcium (mg/dl), serum lactate dehydrogenase (ldh, U/l), alkaline phosphatase (alkptase), bilirubin (mg/dl), white blood cell count (wbc, cells/microliter), platelet count (platelet, cells/microliter), hemoglobin level (hgb, g/dl), and age (years). Serum lactate dehydrogenase (ldh), alkaline phosphatase (alkptase), and bilirubin are all derived binary random variables, with one indicating that the patient's measurement exceeded the upper limit of normal (ULN). After missing data was removed, we were left with a final sample size of n = 343. Gehan weight function γ(u, ϑ) was used throughout.

Table 1 presents coefficient and standard error estimates for the full model using all 18 covariates. We immediately see that in addition to treatment, there are a number of covariates that are important for one of time or cost but not both. Progression status, performance status, albumin, calcium, bilirubin, and white blood cell count are important for both time and cost. Height, serum lactate dehydrogenase, alkaline phosphatase, and hemoglobin are important for time but not cost while treatment is important for cost but not time. Sex and age are weak predictors for cost and time, respectively, but are not statistically significant at the nominal level. In subsequent analyses using penalized estimating functions, we standardized each of 18 baseline variables to have mean zero and unit variance. This explains why, in Table 1, we present coefficient and standard error estimates for both standardized and non-standardized covariates.

Table 1.

Mark- and time-scale coefficient and standard error estimates from full model fit to 18 covariates from SWOG 9509. All regularized estimation procedures standardize predictors to have mean zero and unit variance. All table entries are multiplied by 100.

Name	Standardized X		Unstandardized X
	Time	Cost	Time	Cost
1. tx	-2.28 (6.09)	16.98 (4.91)	-4.56 (12.16)	33.68 (9.85)
2. sex	3.79 (8.98)	14.73 (9.21)	8.21 (19.47)	31.94 (20.14)
3. prog.stat	45.93 (11.24)	35.13 (5.15)	157.69 (38.57)	123.55 (18.52)
4. ps	-23.01 (5.58)	-9.67 (5.00)	-47.73 (11.57)	-20.38 (10.45)
5. stage	-11.16 (10.82)	7.81 (9.54)	-34.72 (33.68)	25.63 (29.85)
6. pleural	-3.39 (11.49)	2.59 (9.66)	-13.80 (46.84)	10.54 (39.74)
7. weight	4.67 (6.76)	5.18 (5.88)	0.28 (0.41)	0.33 (0.36)
8. height	-17.42 (8.60)	-10.72 (8.12)	-1.70 (0.84)	-1.06 (0.80)
9. creat	6.30 (13.62)	4.37 (8.50)	13.12 (28.34)	9.14 (17.36)
10. albumin	17.53 (6.89)	12.71 (4.94)	22.15 (8.70)	16.06 (6.28)
11. calcium	-15.02 (6.32)	-9.84 (5.37)	-17.54 (7.37)	-11.26 (6.22)
12. ldh	-21.62 (5.54)	-3.74 (4.86)	-44.44 (11.39)	-6.13 (10.06)
13. alkptase	-12.95 (5.71)	-3.96 (5.43)	-28.14 (12.40)	-7.57 (11.89)
14. bilirubin	8.93 (3.76)	8.17 (4.57)	63.05 (26.58)	51.25 (33.10)
15. wbc	-20.60 (6.80)	-14.47 (5.15)	<0.01 (<0.01)	<0.01 (<0.01)
16. platelet	2.88 (6.07)	-2.71 (5.41)	<0.01 (<0.01)	<0.01 (<0.01)
17. hgb	15.26 (5.98)	6.36 (5.57)	8.41 (3.30)	3.43 (3.06)
18. age	-9.48 (5.97)	-1.32 (5.17)	-1.02 (0.64)	-0.10 (0.57)

The results of our model selection procedures using the bic-type criterion are presented in Table 2. Of the 18 variables, we found that when we regularize the cost-scale estimating function only, 6-7 variables are associated with medical cost, including treatment, sex, progression status, performance score, albumin, white blood cell count, and hemoglobin level. Hemoglobin level is a weak effect and adaptive lasso sets the coefficient estimate exactly to zero. We also performed variable selection using the joint regularization approach and found that the best fit model included 13 or 10 cost-scale predictors for lasso or adaptive lasso, respectively. Hence, the models found via joint regularization are approximately 40-50% more complex in the cost-scale than models found via cost-scale regularization only. This point is further explored in Section 5 through simulation studies.

Table 2.

Estimate penalized regression coefficients for lifetime medical cost in SWOG 9509. Tables columns are coefficient estimates (Est.) and proportion of resampled estimates set to zero (π̂_0j).

Name	Regularized estimation
	in cost-only				in cost & time
	lasso		alasso		lasso	alasso
	Est.	π̂0j	Est.	π̂0j	Est.	Est.
1. tx	8.76	0.10	11.56	0.86	14.09	14.59
2. sex	1.39	0.59	4.93	0.94	5.02	6.50
3. prog.stat.	25.76	0	31.78	0	31.19	34.07
4. ps	-5.67	0.26	-4.72	0.98	-6.80	-6.78
5. stage	0	0.92	0	1	3.77	2.92
6. pleural	0	0.85	0	1	0	0
7. weight	0	0.67	0	1	2.39	0.13
8. height	0	0.97	0	1	0	0
9. creat	0	0.97	0	1	0	0
10. albumin	2.41	0.34	4.10	0.98	8.60	8.85
11. calcium	0	0.89	0	1	-4.17	-6.16
12. ldh	0	0.94	0	1	-0.42	0
13. alkptase	0	0.93	0	1	0	0
14. bilirubin	0	0.83	0	1	1.99	0
15. wbc	-7.31	0.15	-11.56	0.94	-8.76	-12.03
16. platelet	0	0.66	0	1	-6.28	0
17. hgb	4.20	0.34	0	0.98	5.39	5.19
18. age	0	0.93	0	1	0	0

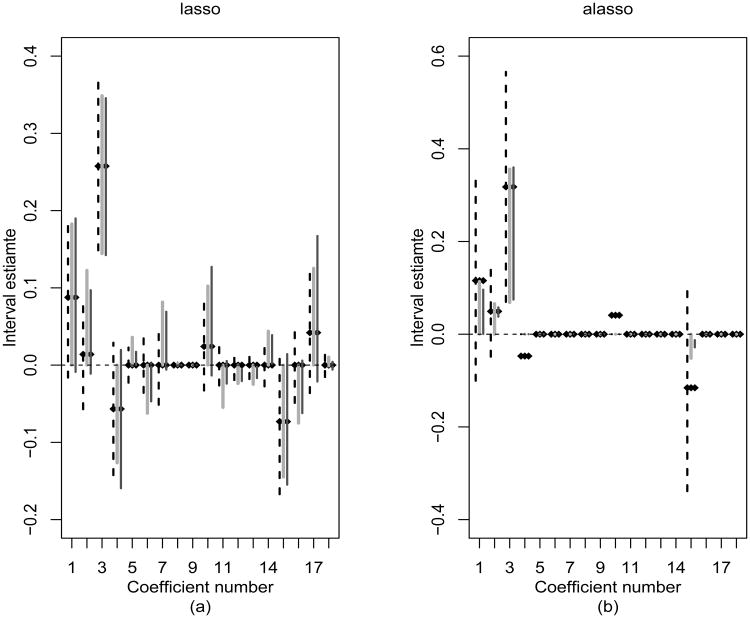
The results of the inference procedures are displayed in the columns of π̂_0js in Table 2 and in Figure 1. Progression status was the only predictor among the 18 in our data set that was a very strong predictor of lifetime medical cost. Of 1000 resampled data sets, neither the adaptive lasso nor lasso set the coefficient estimate for progression status to zero for any resampled data set. On the other hand, treatment, sex, performance score, albumin, white blood cell count, and hemoglobin level were weak effects. For each coefficient, Figure 1 displays the 95% confidence intervals using normal (dashed), percentile (light gray), and highest density methods (black). Progression status is the only strong effect and therefore the only HDR interval that does not contain the singleton {0}. Note that for weak effects, the normal confidence intervals cross zero whereas the percentile method and HDR intervals do not. Adaptive lasso coefficient estimates for sex, performance score, albumin, white blood cell count, and hemoglobin level are extremely close to zero and the confidence intervals, or lack thereof, reflect this fact. Finally, because there was only modest differences between two versions of HDR confidence interval, only HDR(M) from Section 3 was presented in Figure 1.

Figure 1.

95% confidence intervals for the penalized cost-scale regression coefficient estimates. Each coefficient estimate has three interval estimates based on methods from Section 3: normal (dashed), percentile (light gray), and HDR (dark gray). Coefficient numbers across the x-axis are annotated in Tables 1–2.

5. Simulation Studies

5.1 Comparison of Point Estimators

In the first numerical example, we compare variable selection procedures that regularize in the cost-scale only versus simultaneous regularization of time- and cost-scale parameters altogether. As part of this numerical study, we also evaluate the sensitivity of β̂_λ to the choice of calibration vector ϑ. The results here can be used to assess the potential loss in efficiency and predictive ability of β̂_λ when using the time-scale coefficient estimate derived from the full model.

We start by simulating d = 8 predictors as standard normal random variables z = (z⁽¹⁾, …, z⁽⁸⁾) such that corr(z^(j), z^(k)) = 0.5^|k−j|, for j, k = 1, …, 8. Then, we simulated bivariate normal errors, where var(ε_Y) = var(ε_T) = σ² and corr(ε_Y, ε_T) = 0.5 and subsequently defined (Y,T) according the joint model in (3). The non-zero time-scale coefficients are ϑ₁ = ϑ₅ = ϑ₈ = 1, the non-zero cost-scale coefficients are β₁ = 3, β₂ = 3/2, and β₅ = 1 while all other time- and cost-scale coefficients are zero. Note, just as in the SWOG data example, some predictors are important for time only, some are important for cost only, while other predictors affect both cost and time. The censoring random variable C was uniformly distributed Un(0, 6) and the observed data defined accordingly. The data generating process was repeated independently for n observations.

We evaluate the procedures using three summary statistics: median model error, false positive and false negative rates. The cost-scale model error is defined ME = (β̂_λ − β₀)^TE(zz^T)(β̂_λ − β₀), the false negative rate is the average number of non-zero coefficients incorrectly set to zero, and the false positive rate is average number of coefficients whose true value is zero but estimate is non-zero. We refer to Huang's (2002) coefficient estimators as unregularized estimators and the oracles use regressors from the true subset of non-zero regression coefficients in time- and then cost-scale. In addition to computing the estimators described in Section 2, we also compute two similar but hypothetical estimators. The two hypothetical estimators are computed in exactly the same way as β̂_λ except that they calibrate with the true time-scale coefficient ϑ₀ or oracle estimator ϑ_𝒜. Adaptive lasso penalty is used for all regularized estimators and tuning via bic-type criterion. To gauge the success of the combined estimator θ̃_λ in selecting important time-scale variables, we computed the regularized coefficient estimator in the accelerated lifetime model (Johnson, 2009). Table 3 presents simulation results over 100 Monte Carlo datasets.

Table 3.

Simulation results comparing model selection procedures. Table entries include the median model error (ME), false positive (FP) rate, and false negative (FN) rate. Cost-scale coefficient estimation is a function of the calibration coefficient vector.

n	σ	Regression & Variable Selection Procedures	Calibration Coefficients	Time-scale Estimates			Cost-scale Estimates
				ME	FP	FN	ME	FP	FN
60	3	Unregularized	ϑ̂0	1.65	1.00	0	2.39	1.00	0
		Oracles	ϑ̂𝒜	0.48	0	0	0.64	0	0
		Time-scale only	ϑ̂λ	1.47	0.17	0.34	-	-	-
		Cost- & time-scale	ϑ̃λ	1.33	0.31	0.22	1.80	0.38	0.04
		Cost-scale only	ϑ0	0	0	0	1.68	0.39	0.04
			ϑ̂𝒜	0.48	0	0	1.65	0.38	0.05
			ϑ̂0	1.65	1.00	0	1.70	0.37	0.04
60	1	Unregularized	ϑ̂0	0.19	1.00	0	0.22	1.00	0
		Oracles	ϑ̂𝒜	0.06	0	0	0.06	0	0
		Time-scale only	ϑ̂λ	0.10	0.14	0	-	-	-
		Cost- & time-scale	ϑ̃λ	0.10	0.19	0	0.21	0.23	0
		Cost-scale only	ϑ0	0	0	0	0.14	0.09	0
			ϑ̂𝒜	0.06	0	0	0.12	0.11	0
			ϑ̂0	0.19	1.00	0	0.10	0.10	0
90	1	Unregularized	ϑ̂0	0.09	1.00	0	0.15	1.00	0
		Oracles	ϑ̂𝒜	0.03	0	0	0.05	0.00	0
		Time-scale only	ϑ̂λ	0.04	0.07	0	-	-	-
		Cost- & time-scale	ϑ̃λ	0.06	0.14	0	0.14	0.19	0
		Cost-scale only	ϑ0	0	0	0	0.07	0.03	0
			ϑ̂𝒜	0.03	0	0	0.07	0.04	0
			ϑ̂0	0.09	1.00	0	0.06	0.04	0

The first observation is that calibrating 𝕊_β,λ(θ) in (6) with the full model coefficient estimator ϑ̂₀ is an effective variable selection strategy if evaluated with cost-scale metrics. If we calibrated with the true value ϑ̂₀ or oracle estimator ϑ̂_𝒜, the cost-scale model error, false positive and negative rates are so similar that they are within error of the Monte Carlo study. Even for n = 90 with modest censoring, the estimator β̂_λ possesses operating characteristics close to the oracle β̂_𝒜. Our second observation is that joint regularization reduces model error and false positive rate in both time- and cost-scale. But, to accomplish this task, the joint variable selection procedure balances good performance across both scales and, hence, the cost-scale performance of β̃_λ is somewhat less than that of β̂_λ in Table 3. For example, the median model error of β̃_λ is about twice that of β̂_λ at n = 90 and σ = 1. At the same time, ϑ̃_λ reduces model complexity and model error in the time-scale which is obviously not the case with the unregularized time-scale coefficient estimator ϑ̂₀.

5.2 Comparison of Interval Estimators

To examine the operating characteristics of different interval estimators, we conducted numerous simulation studies in the context of our application. We simulated data according to the bivariate accelerated failure time model in (3), with standard normal regressors that followed a first-order Markov model corr(z^(j), z^(k)) = (0.5)^|j−k| and errors that followed a bivariate normal distribution with mean zero, unit variance and covariance cov(ε_Y, ε_T) = 0.5. The time-scale regression coefficients were all equal to one whereas the mark-scale model is chosen to have varying levels of complexity (Tibshirani and Knight, 1999). For each of four different designs, the true regression coefficients are clustered in two groups as described in the following two steps.

1. Set the initial coefficients to β_7+k,h = β_14+k,h =(h − k)², |k| < h, h = 1,…, 4;

2. Scale the initial coefficient values to yield a theoretical R² = 0.75, where we define $R^2=\{{\mathit{\beta }}^{\mathrm{T}}E({\mathbf{z}}_1{\mathbf{z}}_1^{\mathrm{T}})\mathit{\beta }\}/\{{\mathit{\beta }}^{\mathrm{T}}E({\mathbf{z}}_1{\mathbf{z}}_1^{\mathrm{T}})\mathit{\beta }+E({\epsilon }_Y^2)\}$.

Censoring times were independently generated from Un(0, 6) distribution. For all scenarios, observed data are generated for a random sample of size n = 75. The simulation scenarios are designed after numerical studies proposed by earlier authors (Tibshirani and Knight, 1999; Wu et al., 2007; Johnson, 2008), however, none of these earlier works focused on interval estimation and none considered induced censoring.

In the current simulation studies, we considered the four interval estimators discussed earlier in Section 3 for several penalty functions discussed in the literature. These penalty functions include bridge (Frank and Friedman, 1993), lasso (Tibshirani, 1996), hard thresholding (Antoniadis, 1997), scad (Fan and Li, 2001), adaptive lasso (Zou, 2006), and logarithmic penalty (Zou and Li, 2008; Johnson et al., 2008). Due to space limitations, part of the simulation results are given in Table 4 while most results have been moved to Supplementary Material. As in Minnier et al. (2011), we used the hdrcde package in R to implement the highest density regions. Here, we used an Epanechnikov kernel for density estimation with Silverman's rule-of-thumb bandwidth. Otherwise, default settings of the hdr() function were used. Although Minnier et al. (2011) proposed thresholds for adaptive lasso based on the Gaussian linear model with orthonormal design, it is not clear the same definitions should apply uniformly across the class of penalty functions considered here. For this reason, we adopted static cutoffs of p̂_high ≡ p_high = 0.95 and p̂_low = 0.49, the upper bound in the definition proposed by Minnier et al. (2011, p. 1374). Note, that our static definition of p̂_low does not satisfy p̂_low → 0 and so the interval α ≤ π̂_0j < max(α, p̂_low) that defines weak evidence of β_j ≠ 0 in ${\text{CI}}_j^{\mathrm{M}}$ may be too liberal. However, our definition of the simple interval estimator ${\text{CI}}_j^{\mathrm{S}}$ effectively sets p̂_low = α = 0.05 and allows for an indirect investigation into the effects of our proposed static rule for p̂_low in ${\text{CI}}_j^{\mathrm{M}}$.

Table 4.

Simulation results for interval estimators. All table entries are multiplied by 100.

β̂λ	Model	Subset	Feature	Normal	Percentile	HDR(M)	HDR(S)
alasso	1	𝒜c	Coverage	98.1	99.4	98.2	98.2
			Length	65.0	57.1	67.3	54.5
		𝒜	Coverage	94.5	93.0	96.5	92.5
			Length	84.2	76.8	75.4	72.6
	2	𝒜c	Coverage	97.5	99.2	98.1	98.1
			Length	64.7	57.3	67.9	54.7
		𝒜	Coverage	96.2	90.8	92.2	88.8
			Length	77.7	67.2	75.8	62.8
	3	𝒜c	Coverage	97.7	99.1	98.0	98.0
			Length	64.1	57.6	68.5	55.0
		𝒜	Coverage	94.0	89.3	89.2	85.7
			Length	73.8	64.4	75.1	60.3
	4	𝒜c	Coverage	98.1	98.9	98.3	98.3
			Length	63.7	56.8	67.1	53.9
		𝒜	Coverage	94.1	87.8	90.0	84.1
			Length	72.4	63.0	74.6	59.4
lasso	1	𝒜c	Coverage	97.7	98.1	96.9	96.9
			Length	61.4	54.3	76.8	53.5
		𝒜	Coverage	89.5	90.5	89.5	88.0
			Length	82.1	71.8	71.2	70.0
	2	𝒜c	Coverage	97.5	98.1	96.6	96.6
			Length	59.7	53.7	75.2	52.8
		𝒜	Coverage	95.7	90.2	94.2	90.2
			Length	69.3	61.3	74.7	59.5
	3	𝒜c	Coverage	97.5	98.5	96.5	96.5
			Length	59.2	53.6	75.1	52.7
		𝒜	Coverage	94.4	90.1	94.9	89.8
			Length	65.8	58.8	74.9	57.1
	4	𝒜c	Coverage	96.9	98.6	96.9	96.9
			Length	58.7	52.9	74.6	52.1
		𝒜	Coverage	95.0	89.1	94.3	89.9
			Length	64.3	57.5	75.0	55.9

In Table 4, we present the empirical coverage probabilities (ECP) and interval lengths of 95% confidence intervals averaged over coefficients belonging to the active and inactive sets. Due to the construction of the simulation scenarios, the cardinality of the active set ranges from 2 to 14 in Models 1 and 4, respectively, and the cardinality of the inactive set is defined as the difference from d = 21. Results for all methods are based on 1000 resamples for each of 100 Monte Carlo data sets. The average length of the confidence intervals in the inactive set was longest for HDR(M) and shortest for HDR(S). In the active set, the normal-type interval estimator had the ECP close to the nominal coverage across all four models, the ECP of HDR(M) was similar to the percentile method, and HDR(S) had the worst coverage among the four intervals estimators considered. Compared to the percentile method with similar coverage, the HDR(M) intervals were longer in Models 2–4 and shorter in Model 1. In general, we found that the simple interval estimator HDR(S) had shorter intervals than HDR(M) but also substantially worse coverage probabilities. These observations led us to conclude that inflating the confidence region for weak effects as proposed by Minnier et al. (2011) results in measurable improvement over a literal interpretation of the mixture distribution of ${\widehat{\beta }}_j^{\ast }|{\mathcal{F}}_{\mathit{\text{obs}}}$ to guide the HDR interval estimator as in ${\text{CI}}_j^{\mathrm{S}}$. Finally, although the resampling methods are only a heuristic for the lasso, we found that, on the active set, the normal and HDR(M) confidence intervals cover the true value close to the nominal level for Models 2–4, on average, while the percentile method under covers by about 5 percentage points.

6. Discussion

In this paper, we proposed model selection and inference methods for censored lifetime medical cost by applying a theory of penalized estimating function to Huang's (2002) calibration estimator. We regarded β and ϑ as the primary and secondary parts, respectively, of a statistical model (Boos and Stefanski, 2013, 1.2) and, as such, estimated ϑ as simply as possible that led to an estimator β̂_λ with the desired asymptotic properties. At the request of two anonymous reviewers, we also investigated joint regularized estimation of time- and cost-scale parameters together using penalized estimating functions via least-squares approximation (LSA). In theory, both β̂_λ and β̃_λ will possess the oracle property but our simulation studies suggest that β̂_λ is superior to β̃_λ in finite samples if evaluated with cost-scale metrics as in Table 3. But if we consider the combined model error and complexity across both cost- and time-scales, then joint regularization is better. A third alternative to what was presented in Section 2 is to consider a richer class of methods that has separate regularizations on the cost- and time-scale. Tuning such a procedure could be accomplished using D(θ) defined in Section 2.3 and information criteria defined analogously. But, in this case, the optimal regularization parameters would be computed by minimizing the information criteria over a 2-dimensional surface of regularization parameters rather than over a line, as we proposed via LSA. Thus, although the point estimate from two separate regularizations in time and cost may not be expensive to compute, tuning such a procedure would be significantly more complex computationally than our joint regularization method and post-selection inference would consequently be more laborious as well.

Finally, we investigated post-selection inference procedures by Minnier et al. (2011) applied to our regularized calibration estimator. Although the penalized calibration regression estimator does not, strictly speaking, belong to the class of estimators considered in Minnier et al. (2011), the post-selection inference technique operates exactly the same way after the resampling plan is justified. For adaptive lasso, scad, and similar penalty functions, we found that confidence intervals based on the normal approximation performed surprisingly well. Confidence intervals based on percentiles and HDR performed well when the signal-to-noise ratio was high and not as well when the signal-to-noise ratio was low. Based on the construction of our simulation studies, this conclusion can be read another way. When the signal is composed of many weak predictors as opposed to a few strong predictors, the coverage probability of percentile and HDR confidence intervals on the active set decreases below the nominal level. As stated in Minnier et al. (2011), limitations of HDR can partly be attributed to difficulty in accurately identifying the active set 𝒜 in finite samples. At the same time, we found that HDR performed well in finite samples when there are small number of strong predictors. The real difficulty arises when there are many weak effects, and this may be a deficiency of the coefficient estimator rather than HDR itself (Pötscher and Schneider, 2009, 2010).