Conformational dynamics of the TTD–PHD histone reader module of the UHRF1 epigenetic regulator reveals multiple histone-binding states, allosteric regulation, and druggability

Abstract

UHRF1 is a key mediator of inheritance of epigenetic DNA methylation patterns during cell division and is a putative target for cancer therapy. Recent studies indicate that interdomain interactions critically influence UHRF1's chromatin-binding properties, including allosteric regulation of its histone binding. Here, using an integrative approach that combines small angle X-ray scattering, NMR spectroscopy, and molecular dynamics simulations, we characterized the dynamics of the tandem tudor domain–plant homeodomain (TTD–PHD) histone reader module, including its 20-residue interdomain linker. We found that the apo TTD–PHD module in solution comprises a dynamic ensemble of conformers, approximately half of which are compact conformations, with the linker lying in the TTD peptide–binding groove. These compact conformations are amenable to cooperative, high-affinity histone binding. In the remaining conformations, the linker position was in flux, and the reader adopted both extended and compact states. Using a small-molecule fragment screening approach, we identified a compound, 4-benzylpiperidine-1-carboximidamide, that binds to the TTD groove, competes with linker binding, and promotes open TTD–PHD conformations that are less efficient at H3K9me3 binding. Our work reveals a mechanism by which the dynamic TTD–PHD module can be allosterically targeted with small molecules to modulate its histone reader function for therapeutic or experimental purposes.

Introduction

Epigenetic memory of cell identity requires the faithful propagation of DNA methylation patterns through cell division and is dependent on the function of UHRF1 (ubiquitin-like containing RING and PHD fingers 1). UHRF1 is a pentadomain protein that is targeted to hemimethylated DNA and repressive histone H3K9me3 modification states, where it recruits DNMT1 for the methylation of cytosine residues on daughter strands during DNA replication (for recent reviews of UHRF1, see Refs. 1–3). Dysregulation of DNA methylation is a hallmark of many cancers, and UHRF1 has been suggested as a target for anti-cancer therapy (2, 4). It is overexpressed in multiple cancer lines (5, 6) and thought to play a critical role in the down-regulation of tumor suppressor proteins (2). Importantly, the ability of UHRF1 to maintain DNA methylation patterns is dependent on its H3K9me3-binding function.

Hemimethylated DNA is recognized by the SRA domain (SET and RING-associated), whereas H3K9me3 marked chromatin is recognized by the plant homeodomain (PHD)³ and tandem tudor domain (TTD), which are connected by a 20-residue linker to form the TTD–PHD histone reader module (see Fig. 1A). The PHD in isolation recognizes the unmodified N terminus of H3 (7, 8), whereas the TTD binds to the H3K9me3 mark (9). The crystal structure of H3-bound TTD–PHD (10, 11) shows that the two domains can bind to their target sites cooperatively. This coordinate binding requires the linker to be bound to a peptide-binding groove formed at the interface of the TTD_N/TTD_C subdomains; disruption of linker-groove contacts prevents high-affinity binding of TTD–PHD to H3K9me3. One putative mechanism to disrupt multivalent binding is by phosphorylation of the linker at Ser²⁹⁸ by PKA or PIM1 (10, 12, 13). It is unclear to what degree cooperative histone interaction occurs in the context of full-length UHRF1. Some studies indicate that the module may adopt histone-binding states that are solely PHD– or TTD–mediated (14, 15).

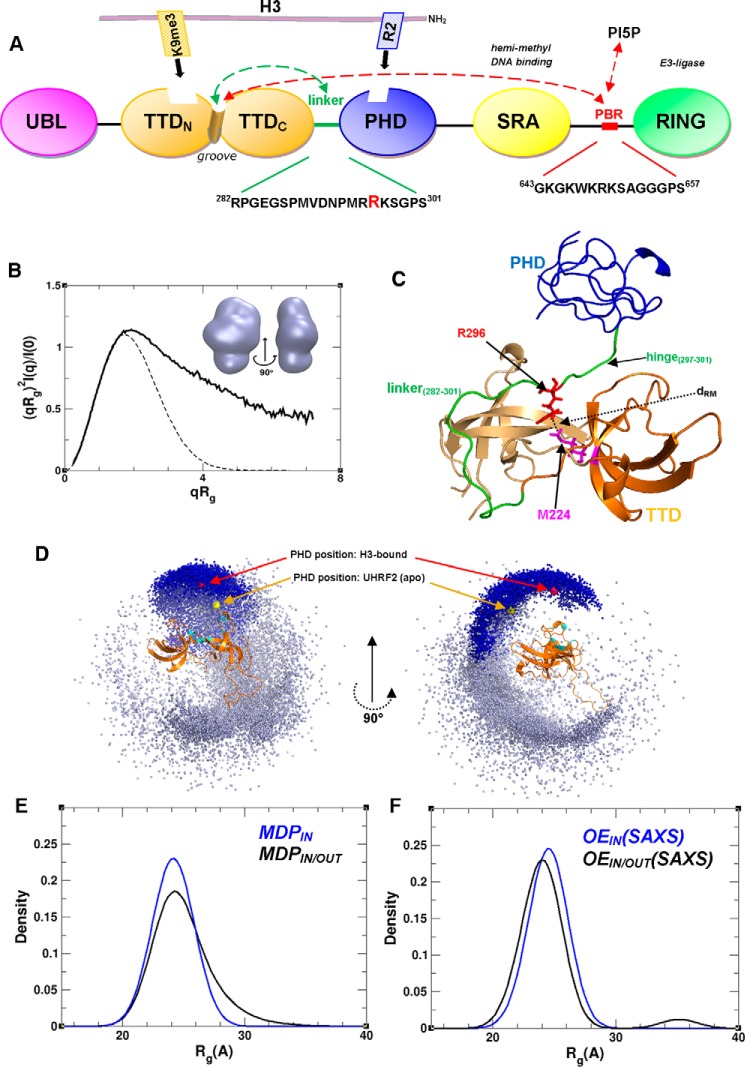
Figure 1.

A, UHRF1 domain arrangement showing the basic function of each domain. The 20-residue TTD–PHD interdomain linker sequence is displayed (with the critical Arg²⁹⁶ in red), as well as that of the PBR, which has been implicated in allosteric regulation of histone binding through its reversible interaction with the TTD groove or PI5P (14). B, comparison of the experimental dimensionless Kratky plot for TTD–PHD (solid line) with the theoretical plot for a globular protein (dashed line). Inset, ab initio SAXS-predicted molecular envelope of the module is shown from two points of view. C, ribbon representation of TTD–PHD based on its structure in the H3-bound state (PDB code 3ASK) (10). The Cα atoms of Arg²⁹⁶ and Met²²⁴ are used as reference positions for the linker and groove, respectively, to assess their relative positioning (d_RM) in various TTD–PHD conformers. D, the position of PHD centers of mass (calculated as the average position of the atoms in the PHD, weighted according to their mass) in TTD–PHD structures from MDP_IN (dark blue spheres) and MDP_IN/OUT (dark and light blue spheres) superimposed with the TTD (as a ribbon diagram). TTD residues that bind to the H3 peptide are displayed in cyan. The red sphere shows the PHD center of mass in the H3-bound UHRF1 TTD–PHD (PDB code 3ASK) (10). The yellow sphere shows the PHD center of mass in apo TTD–PHD of UHRF2 (crystal structure, PDB code 4TVR). E, R_g distribution in MDP_IN/OUT and MDP_IN. F, R_g distribution in OE_IN/OUT(SAXS) and OE_IN(SAXS).

Histone and DNA binding by UHRF1 is regulated by long-range interdomain and linker-domain interactions within the full-length protein (14–17). Gelato et al. (14) showed that a polybasic region (PBR-UHRF1_643–657) in the linker between the SRA and RING (really interesting and new gene) domains regulates the transition between PHD- and TTD–mediated histone reader states, through its reversible binding to the TTD groove or the phospholipid PI5P (see Fig. 1A). The PHD has also been reported to interact with the SRA domain in a UHRF1 state where histone binding is restricted (15, 16). These studies suggest that disruption of interdomain interactions could be a mechanism to pharmacologically target UHRF1. A detailed structural and dynamic picture of how these putative large-scale intramolecular rearrangements give rise to altered UHRF1-binding states remains elusive.

In this report we describe an integrated biophysical approach to characterize the scope of interdomain motion exhibited by the TTD–PHD histone reader module and its recognition of H3K9me3. In its apo form, we find that the unit is highly dynamic, populated with both extended and compact states. Using a fragment-based drug discovery approach, we identified a compound, 4-benzylpiperidine-1-carboximidamide (BPC) that binds to the open conformation, thereby preventing efficient recognition of H3K9me3.

Results

The UHRF1 TTD–PHD reader is highly dynamic in solution

To assess the conformational heterogeneity of the TTD–PHD histone reader module, we used small angle X-ray scattering (SAXS) in solution. The SAXS-derived ab initio molecular envelope is extended in shape with dimensions of ∼87 × 47 × 23 Å (Fig. 1B). The dimensionless Kratky plot is bell-shaped, with a maximum at a position that is shifted to higher coordinate values than expected for a globular protein and with poor convergence at high q values; this indicates the presence of flexibility/disorder. Furthermore, the average R_g value (24.5 Å) (Table 1) is more than 25% larger than the theoretical value expected for a globular protein of the same mass.

Table 1.

SAXS parameters for UHRF1 TTD–PHD with and without the presence of BPC

SAXS parameters	TTD–PHDa	TTD–PHD/BPCb
I(0)c	0.057	0.021
Rg (Å)d	24.5	27.1
Rg (Å) reale	24.9	27.2
Dmax (Å)f	83	94
Vcg	274.3	284.4
Mwh	25.5 (27.9)	24.2 (28.1)
NSD (SAXS envelope)i	0.75 ± 0.07	0.79 ± 0.02

^a UHRF1_126–366.

^b UHRF1_126–366 with BPC (4 mm, containing 4% DMSO).

^c Intensity at q = 0.

^d Based on Guinier fit.

^e From GNOM (36).

^f Maximum distance between atoms from GNOM.

^g Volume of correlation (37).

^h M_w estimated from SAXS using V_c (37). The M_w expected from the sequence is shown in parentheses.

ⁱ NSD, normalized spatial discrepancy. The values are the average and standard deviation from 15 runs of DAMMIF (38).

In the published crystal structure of H3K9me3-bound TTD–PHD, the relative orientation of the two domains is fixed and stabilized by independent TTD and PHD interactions with the histone peptide and through the binding of the linker within the TTD groove (10), for which Arg²⁹⁶ is a key residue (Fig. 1C). Our SAXS analysis indicates that there is no specific orientation of the two domains relative to one another in the apo state. The level of interdomain motion within the reader module depends on conformational flexibility mediated by the linker and can be principally defined by two distinct types of mobility. In the first case, the Arg²⁹⁶-containing linker is bound within the TTD groove, and the mobility of the two domains is mediated largely by a 5-residue flexible “hinge” region (UHRF1_297–301) (Fig. 1C). In the second case, the entire linker (UHRF1_282–301) is flexible and exists in both TTD-bound and unbound states. The degree to which these two types of mobility are reflected in the dynamic behavior of the TTD–PHD unit was explored.

We employed an ensemble fitting approach in which molecular dynamics combined with rigid-body modeling was used to generate an initial set of conformations that approximate the conformational space available to the TTD–PHD reader. Then using the SES method (18), SAXS and NMR relaxation data were used to identify the dominant conformational states within the structural pool. We generated two initial sets of TTD–PHD conformations. The first set (molecular dynamics pool-IN (MDP_IN)) contains 6,000 TTD–PHD conformations generated with the linker bound to the TTD groove. The second set (MDP_IN/OUT) contains the entire MDP_IN pool and an additional 10,000 conformations with the linker displaced from the groove (Fig. 1D). SAXS data fitting was used to generate two optimal ensembles: OE_IN(SAXS) and OE_IN/OUT(SAXS), from their respective starting structural pools. Both ensembles fit the SAXS data equally well (χ_saxs = 0.21). The R_g distribution of OE_IN(SAXS) has a broad peak centered at R_g = 24.5 Å, similar to its initial starting pool (MDP_IN), whereas the OE_IN/OUT(SAXS) displays a bimodal R_g distribution, with major (R_g = 24.0 Å) and minor (R_g = 35 Å) peaks corresponding to compact and extended reader conformations (Fig. 1, E and F). The SAXS-fitted OEs largely reproduce the conformational space of their starting pools, but in comparison to each other, do not overlap, as would be expected if the TTD–PHD unit possessed restricted flexibility (supplemental Fig. S1). Our fitting of the SAXS data suggests that OE_IN/OUT(SAXS) reflects the dynamic range of TTD–PHD in solution more accurately than OE_IN(SAXS) and provides evidence for TTD–PHD states where the groove is exposed.

NMR relaxation data reflect partially coupled TTD–PHD interdomain motion

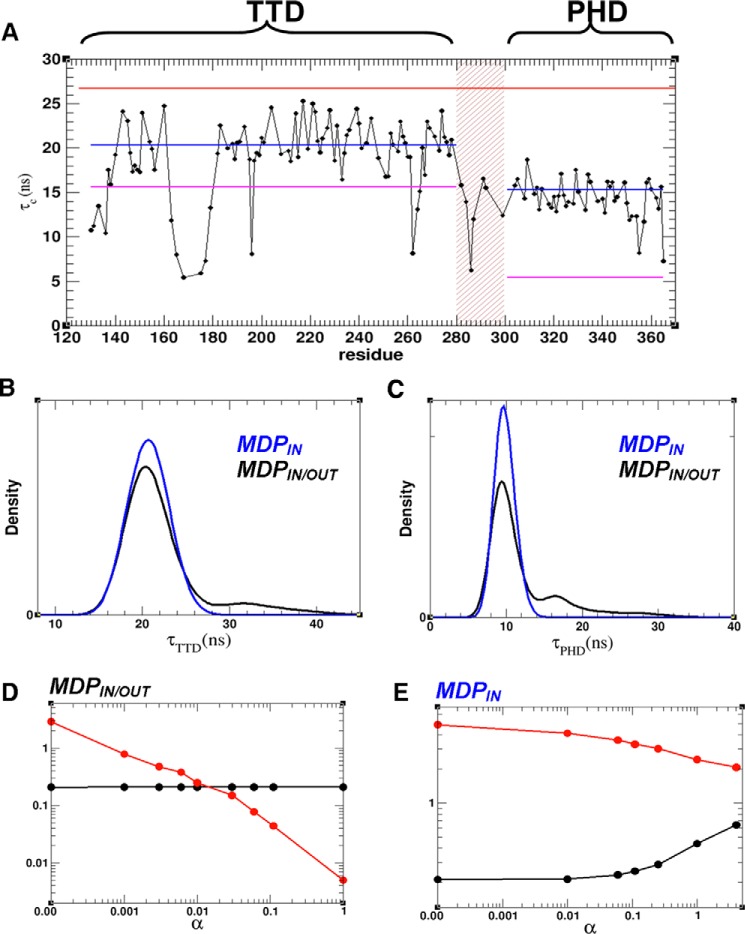
TROSY-based ¹H/¹⁵N/¹³C triple-resonance backbone spectra were acquired to assign backbone TTD–PHD resonances (in a ∼80% deuterated sample). We could assign 203 amide resonances, of which 134 were located in the TTD, 11 in the linker and 58 in the PHD (supplemental Fig. S2). The assignments were used as the basis for residue-specific ¹⁵N relaxation and ¹H-¹⁵N heteronuclear NOE measurements (supplemental Fig. S2 and supplemental Table S2). NOE values averaged across the ordered parts of the two domains are approximately the same (0.73 ± 0.06), with reduced values in loops (e.g. residues 163–180) and in the linker, indicating higher flexibility for these regions. The two domains exhibit different T₁ and T₂ values, and this is most evident comparing their local correlation time (τ_c) determined for each residue (from T₁/T₂ ratios) (Fig. 2A and supplemental Table S2). The results of fitting NMR relaxation data to a standard diffusion model using the program MODELFREE (19) are shown in Table 2. The data fit better when the TTD and PHD are considered individually rather than as a single unit with the two domains rigidly attached (see reduced χ² in Table 2), which indicates the presence of interdomain flexibility. The best fit for both domains was obtained with an axial symmetric diffusion model where τ_m = 20.32 ± 0.65 ns for the TTD, and τ_m = 15.36 ± 0.81 ns for the PHD (Table 2 and Fig. 2A). The domains are tumbling with different rates; however, the rotational correlation times values predicted by HYDRONMR (20) indicate that the domain motion is coupled (supplemental Table S3 and Fig. 2A).

Figure 2.

Interdomain flexibility of the TTD–PHD module from NMR relaxation and SAXS data. A, local correlation time (τ_c) determined for each residue from experimental T₁/T₂ ratios (black spheres). The apparent global correlation times of the two domains derived by fitting to a standard diffusion model for each domain separately (blue horizontal line). The theoretical τ_c values predicted by HYDRONMR (20) for full-length TTD–PHD (red horizontal line) and for individual domains separately (magenta horizontal line). B and C, distribution of HYCUD-predicted (22) global τ_c values in MDP_IN/OUT and MDP_IN for the TTD (B) and PHD (C). D and E, goodness of fit of MDP_IN/OUT (D) and MDP_IN (E) to SAXS (χ_saxs, black circles) and NMR (χ_relax, red circles) data shown as a function of the weighting factor α. Ensemble fitting to both SAXS and NMR data were performed simultaneously by minimizing residual χ² = χ_saxs² + α · χ_relax² at different values of α.

Table 2.

Rotational diffusion parameters of the TTD and PHD within UHRF1 TTD–PHD

The diffusion parameters were determined by fitting the known crystal structure (PDB code 3ASK) to ¹⁵N-relaxation data (acquired at 800 MHz) using Modelfree4.15 (19). Fitting was performed for the full-length construct and each domain individually.

	TTD	PHD	TTD–PHDa
τm (ns)b	20.32 ± 0.65	15.36 ± 0.81	15.65 ± 0.07
Anisotropyc	1.17 ± 0.05	1.41 ± 0.06	1.37 ± 0.04
Reduced (c2)d	4.4	3.9	23.1

^a UHRF1_126–366.

^b Overall rotational correlation time, τ_m = 1/2(D_par + 2D_per), where D_par and D_per are parallel and perpendicular principal values of the axially symmetric rotational diffusion tensor, respectively.

^c Degree of anisotropy of diffusion tensor, D_par/D_2per.

^d Goodness of fit.

The HYCUD approach was recently developed to predict rotational correlation times of globular domains within flexible modular systems (21, 22). We used our two MD-generated pools of TTD–PHD structures (MDP_IN and MDP_IN/OUT) to carry out HYCUD-based predictions of the effective rotational correlation times of the TTD (τ_TTD) and PHD (τ_PHD). Using MDP_IN, both τ_PHD and τ_TTD-predicted distributions are bell-shaped curves with peaks positioned at ∼ 10 and 21 ns, respectively (Fig. 2, B and C), whereas the distributions derived from predictions using MDP_IN/OUT are right-skewed with the major peaks extending up to ∼35 and ∼45 ns for τ_PHD and τ_TTD, respectively. The predicted average τ_c values for the TTD from both MDP_IN/OUT and MDP_IN pools are in good agreement with the experimental value, but those for the PHD are smaller and in better agreement with the value predicted from MDP_IN/OUT (Tables 2 and 3 and supplemental Table S3).

Table 3.

Global structural parameters and goodness of fit to the experimental data for different ensembles of TTD–PHD

Data used	OEIN/OUTa		MDPIN/OUTb	MDPINb
	SAXS + NMR	SAXS
χsaxsc	0.21	0.21	0.93	0.52
<τTTD> (ns)d	20.9 ± 2.0	21.1 ± 1.7	22.0 ± 4.7	20.6 ± 1.9
<τPHD> (ns)d	15.0 ± 8.1	9.9 ± 1.3	11.9 ± 4.9	9.7 ± 1.0
Rg (Å)e	24.1 ± 2.6	24.3 ± 2.4	24.8 ± 2.0	24.0 ± 0.9
Dmax (Å)e	83.3 ± 8.4	85.6 ± 6.8	85.4 ± 7.9	85.8 ± 6.4
Pboundf (%)	51	57	40	100

^a OEs selected from MDP_IN/OUT using the SES method (18).

^b MDP_IN/OUT and MDP_IN with uniform weights.

^c Goodness of fit for fitting to SAXS data.

^d Average and standard deviation values of the correlation time; τ_c for each member of the ensemble was predicted using the HYCUD method (21, 22).

^e Average and standard deviation.

^f Percentage of structures with the linker bound to the TTD groove.

Ensemble fitting using both SAXS and NMR data indicates that the TTD–PHD module adopts compact and extended conformations

Using the HYCUD method, the correlation time (τ_c) of a domain is calculated as a simple average from predicted τ_c values for all members of an initial structural ensemble, each with equal weighting. As we demonstrated above, the HYCUD-predicted τ_PHD and τ_TTD values do not agree with experimentally determined values. We therefore modified the HYCUD-based prediction algorithm by introducing non-uniform weights for conformers in the ensemble and then used the SES method to optimize and combine SAXS and NMR relaxation data to estimate appropriate weights. For this purpose, the discrepancy between the predicted and experimental data is measured χ² = χ_saxs² + α · χ_relax², where χ_saxs and χ_relax measure the goodness of fit to SAXS and relaxation data, respectively (Equation 1), and the parameter α regulates the contribution of the relaxation data (see “Experimental procedures” for details). The results of SES fitting of the initial MDP_IN/OUT and MDP_IN pools at different values of the parameter α are shown in Fig. 2. In the case of MDP_IN/OUT, increasing the value of α from 0 to 1 gradually results in progressive improvement of relaxation data fitting, whereas SAXS data fitting remains the same. At α = ∼0.01, an OE is generated from fitting MDP_IN/OUT to the SAXS and NMR data equally well (Fig. 2D). In contrast, we failed to find any value of α, such that MDP_IN can be fitted satisfactorily to both SAXS and NMR data (Fig. 2E).

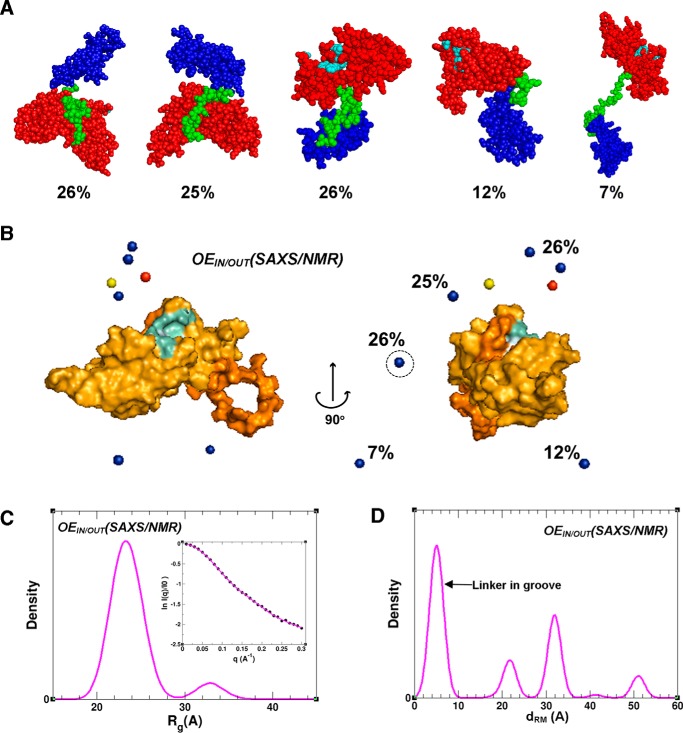
We performed recovery of solution ensembles of the TTD–PHD by fitting MDP_IN/OUT to SAXS and NMR data (α = 0.06). The optimal ensemble, OE_IN/OUT(SAXS/NMR), fits the SAXS data well (χ_saxs = 0.21), and likewise, the predicted τ_PHD (∼15.0 ns) and τ_TTD (∼20.9 ns) are in good agreement with experimental values (Tables 2 and 3). The five most populated states comprising 96% of this ensemble are shown in Fig. 3A. The structures can be divided into two groups based on the positioning of the linker. In the first group, which we call the “bound” state, the linker occupies the TTD groove. These conformers cluster around either the observed H3K9me3-bound TTD–PHD crystal structure, or interestingly, the domain arrangement seen in apo TTD–PHD of UHRF2 (Fig. 3B and supplemental Fig. S3). All conformers in the bound state are compact (Fig. 3, C and D), with an R_g of ∼22–24 Å, which corresponds to the major R_g distribution peak. In the second group, that we call the “open” state, the TTD groove is solvent-exposed. In this state, there are both compact and extended conformers that correspond to the major R_g distribution peak (∼24 Å) and to the minor peak centered at ∼33 Å (Fig. 3C). The relative population of bound states in OE_IN/OUT(SAXS/NMR) is 51% (Table 3).

Figure 3.

Dynamic ensemble of the TTD–PHD reader in solution derived from SAXS and NMR data. A, the most populated (based on weighted %) conformers from OE_IN/OUT(SAXS/NMR). The TTD, PHD, and linker are colored in red, blue, and green, respectively. TTD residues that form the aromatic cage are displayed in cyan. B, the position of PHD centers of mass in the most populated conformers from OE_IN/OUT(SAXS/NMR) (blue spheres) superimposed with the TTD (as a surface representation). Residues that bind to the H3 peptide are displayed in cyan. The red sphere shows the PHD center of mass in H3-bound UHRF1 TTD–PHD (PDB code 3ASK) (10), and the yellow sphere shows the PHD center of mass in apo TTD–PHD of UHRF2 (PDB code 4TVR). The average populations (%) are displayed. (See also supplemental Fig. S3 for comparison.) C, R_g distribution in OE_IN/OUT(SAXS/NMR). The inset shows the experimental SAXS profile plotted with the theoretical profile averaged over the ensemble. D, the distribution of Cα-Cα distance between residues Arg²⁹⁶ and Met²²⁴ (i.e. d_RM; refer to Fig. 1C diagram) in OE_IN/OUT(SAXS/NMR).

Allosteric modulation of the TTD–PHD module with small molecules

There is strong evidence that the 15-residue PBR (UHRF1_643–657) between the SRA and RING domains is involved in the allosteric regulation of TTD–PHD histone binding. This occurs through competitive displacement of the linker from the TTD groove (Fig. 1A). In full-length UHRF1, this results in the failure of UHRF1 to recognize H3K9me3 caused by a transition from TTD–mediated to PHD–mediated histone binding (14). We performed a screen of fragment-sized small molecules to identify compounds that could, in a manner analogous to the PBR, bind to the TTD groove, block linker–groove interactions, and promote open TTD–PHD conformations.

We designed a fragment library containing 2,040 compounds that was initially screened against isolated TTD (UHRF1_121–286) using a fluorescence polarization (FP) assay that tracked the displacement of a N-terminally tagged H3K9me3 peptide (H3K9me3_(1–25)). From this screen, eight putative TTD-binding hits were identified. Analysis of amide peak movement in the (¹H-¹⁵N) HSQC spectra of the TTD in the presence of the fragments indicates that the binding of two, BPC and a tricyclic imine, occurs in the groove. Because of limited commercial availability of the tricyclic amine, we focused only on BPC. The binding of this compound occurs close to (or within) the Arg²⁹⁶-binding pocket; we observe significant perturbation of Trp²³⁸ and Phe²⁷⁸ resonances that form part of the pocket, and in Gly²³⁶, which is directly adjacent to it (Fig. 4A and supplemental Fig. S5). We also see chemical shift changes in non-surface exposed residues that are close to or are in contact with the groove. A similar amide peak perturbation pattern is observed when the TTD is titrated with a 15-residue peptide corresponding to the PBR, resulting from its binding in the groove (supplemental Fig. S5). Further characterization of BPC binding to isolated TTD was performed using ITC and DSF, with an estimated K_D of 50 μm (supplemental Fig. S5) and a calculated ligand efficiency of 0.38 (which is defined as the binding energy per heavy atom).

Figure 4.

BPC and PBR peptide binding promote open TTD–PHD conformations. A, BPC (with its chemical structure displayed) binds close to the Arg²⁹⁶-binding pocket. Asp¹⁴², Glu¹⁵³, Ala²⁰⁸, Met²²⁴, Trp²³⁸, and Phe²⁷⁸ combine to form the pocket in the TTD groove. Residues showing significant chemical shift perturbations upon BPC binding are colored orange, and those that are not assigned in this construct are in cyan. Met²²⁴ (blue), at the base of the pocket, is not significantly shifted. B, (¹H-¹⁵N) TROSY overlays show that titration of TTD–PHD with either BPC or PBR peptide (at ∼250 μm protein/750 μm ligand) show substantial broadening and/or movement of linker resonances (boxed). Some TTD residues (brackets) at the interface of the groove (e.g. Gly²³⁶) are shifted or broadened as well. PHD resonances remain largely unaffected by binding (ovals). For clarity, only well resolved resonances are labeled. C, normalized pair distance distribution function P(r) calculated from SAXS data for TTD–PHD bound to BPC (4 mm, 4% DMSO) and for apo TTD–PHD. D, comparison of the R_g distribution in OE_IN/OUT(SAXS) and OE_BPC(SAXS) derived from SAXS data for apo and BPC-bound TTD–PHD, respectively. E, distribution of d_RM (refer to Fig. 1C diagram) in the OE_IN/OUT(SAXS) and OE_BPC(SAXS). F, ITC curves show a cooperative profile for TTD–PHD binding to H3K9me3_(1–15). G and H, the presence of BPC (at 1.5 mm, 4% DMSO, ∼ 30:1 fragment:protein) (G) or PBR peptide (at 1.5 mm, ∼30:1 peptide:protein) (H) reduces the TTD–PHD binding affinity for the histone peptide. This is consistent with a putative shift from a cooperative to a PHD–mediated binding mode.

We used NMR and SAXS analysis to assess whether BPC could promote open conformations of TTD–PHD, in a manner comparable with that of the UHRF1 PBR. In (¹H-¹⁵N) TROSY spectra of the reader titrated with BPC, significant conformational broadening and/or movement of amide peaks can be observed in residues spanning the entire length of the linker. Exchange broadening is clearly observed for Arg²⁸², Gly²⁸⁴, Asp²⁹¹, Asn²⁹², Met²⁹⁴, and Ser³⁰¹ amide resonances at 1:3 protein/BPC ratios, with perturbations also seen with Gly²⁸⁶ and Gly²⁹⁹ (Fig. 4 and supplemental Fig. S6). TTD residues that form part of or are close to the Arg²⁹⁶-binding pocket (e.g. the ²³⁶GFW²³⁸ triad and Ala²⁰⁸) also exhibit exchange broadening and/or chemical shift changes, consistent with compound binding close to this site (supplemental Fig. S6). PHD resonances are, by comparison, unaffected by the presence of BPC, and in a separate titration, we confirmed there was no interaction between the fragment and this domain (supplemental Fig. S8). A strikingly similar peak broadening/perturbation pattern is observed in spectra of TTD–PHD when it is titrated with the 15-residue PBR peptide (Fig. 4B and supplemental Fig. S6).

SAXS profiles of TTD–PHD collected in the presence of BPC demonstrate an increase in the overall dimensions resulting from BPC binding (Tables 1, supplemental Table S1, and Fig. 4C). The R_g-based Kratky plot is shifted to higher coordinate values with respect to its position for apo TTD–PHD (supplemental Fig. S4). Also, the pair-distance distribution function exhibits a broad extended tail with a shallow secondary shoulder observed at ∼50 Å (Fig. 4C), indicating extended reader conformations. We performed SES fitting of SAXS data collected for TTD–PHD in the presence of BPC using MDP_IN/OUT. The optimal ensemble, OE_BPC(SAXS), fits the data reasonably well in the q range of 0 < q < 0.2. The R_g distribution is bimodal with the major peak at ∼25 Å and a minor peak at ∼34 Å (Fig. 4D). In comparison with the R_g distribution of the optimal ensemble generated for apo TTD–PHD (i.e. OE_IN/OUT(SAXS)), the position of the major peak is shifted by 1 Å, and the minor peak has a larger height, indicating that there is a higher percentage of extended conformations. Interestingly, the distance that specifies the relative position of the linker with respect to the TTD groove (d_RM) shows that the 6,000 starting structures in the pool in which the linker is bound to the groove make zero contribution to OE_BPC(SAXS) (Fig. 4E). Taken together, these data indicate that BPC binds in the TTD groove and disrupts the interaction with the linker, shifting the ensemble equilibrium toward less compact structures. These less-compact, “linker-out” conformers should be unable to bind to H3K9me3 peptides in a cooperative manner (as in PDB code 3ASK (10, 23)) and, in addition, be unable to bind via the isolated TTD because groove-H3K9me3 contacts found to be essential for this binding mode, as reported by Nady et al. (9), are blocked.

To evaluate the effect of BPC on histone binding by the reader module, we compared the binding affinity of TTD–PHD with H3K9me3 peptide in the presence of both BPC and PBR peptide (Fig. 4). Apo TTD–PHD was found to exhibit cooperative H3K9me3_(1–15) binding (K_D = 1.2 μm, n = 1.0) resulting from dual TTD-/PHD–mediated interaction, consistent with previous studies (10) (Fig. 4F and supplemental Fig. S9). The increased K_D (∼5-fold) for H3K9me3 in the presence of BPC (Fig. 4G) or PBR peptide (Fig. 4H) is fully consistent with a transition from a cooperative (i.e. PHD– and TTD–dependent) binding mode to one mediated by the PHD only.

Discussion

Large-scale intramolecular rearrangements play a critical role in UHRF1 function, consistent with a dynamic framework in which its conformational equilibria are shifted in response to the chromatin state and aggregate presence of other proteins and cellular factors with modulating influences (14–16). One noted example of this conformational modulation is that induced by the lipid PI5P, which regulates the transition between TTD- and PHD–mediated histone-binding states through its reversible interaction with the PBR element (UHRF1_643–657) (14) (Fig. 1A). Structural insight into large-scale UHRF1 intramolecular rearrangements has been obscure.

Our study shows that the UHRF1 TTD–PHD histone reader is highly dynamic in its apo state, with clear evidence of open and extended conformations (Fig. 5). We have applied a novel integrated approach where both SAXS and NMR relaxation data are used to determine OEs from starting pools of conformers derived from MD simulations and rigid-body modeling. Our results indicate that TTD–PHD structures in which the linker is bound to the TTD groove are not favored over those where it is unbound. Linker positioning has been shown to be a critical determinant of histone-binding behavior, because cooperative, high-affinity interaction necessitates that it occupy the groove (10). Interestingly, even when the linker is positioned in the groove, there is evidence of additional flexibility mediated by the hinge region (UHRF1_297–301). The linker-bound structures (Fig. 5A) in our OE are clustered around two configurations: in the first, the domain orientation is similar to that seen in the cooperative binding mode (PDB code 3ASK), whereas in the second, the domain orientation is similar to that seen in the crystal structure of apo UHRF2 TTD–PHD (PDB code 4TVR). Open conformers where the linker is out of the groove (Fig. 5B) reveal a vulnerability of the TTD to allosteric regulation by competitive binding of entities such as the PBR or drug-like small molecules (Fig. 5D).

Figure 5.

Apo and H3-binding states of the TTD–PHD histone reader. The apo TTD–PHD OE is consistent with conformers in which the linker is positioned both in (A) and out (B) of the TTD groove. When the linker is in the groove, the relative positions of the domains have two favorable orientations: the first is very similar to the H3-bound state described by Arita et al. (10) where histone binding is cooperatively mediated by the PHD and TTD (C); the second resembles the orientation adopted by apo TTD–PHD in its paralog UHRF2. Both extended and compact conformers are populated when the linker is out of the groove (B) and provide a clear mechanism for histone-binding states mediated independently by the PHD and/or TTD (C). Gelato et al. (14) described the formation of a PBR-bound state where the linker is forced out of the groove as a mechanism for allosteric regulation of histone binding; BPC can similarly promote open reader states (D).

UHRF1 is a potential therapeutic target, because it is essential for the maintenance of DNA methylation patterns and highly expressed in most cancers (2, 4). To date, only one UHRF1 inhibitor has been identified, a uracil derivative that interferes with the SRA domain (24). Because H3K9me3 binding is a requirement for UHRF1 function (25) and can be disrupted by the PBR through its association with the TTD (14), we hypothesized that allosteric disruption of the cooperative (23), high-affinity binding mode of the TTD–PHD module may be an attractive strategy for small molecule antagonists of UHRF1 function. An important aspect of intramolecular interactions is the high effective concentration of interacting regions within a single macromolecule. Such effects may pose a challenge for the development of drug-like small molecules that can efficiently compete with these interactions. Here, using an FP H3-peptide displacement assay with the isolated TTD, we identified the small fragment BPC as a linker-competitive binder to the TTD groove, with a K_D close to 50 μm (supplemental Figs. S5 and S8). Saturating concentrations of this highly soluble compound can induce open conformers of the TTD–PHD module and reduce its affinity for H3K9me3 peptides (Fig. 4 and supplemental Figs. S5 and S6). BPC should prove useful as a tool for in vitro investigations that seek to relate open TTD–PHD conformations with specific UHRF1-binding modes. The small size and high ligand efficiency of the compound suggest that it can be further optimized for potency. An attractive approach could be to link compounds such as BPC that bind in the TTD groove, with those designed for interaction with the aromatic cage, which recognizes the trimethyl lysine of H3K9me3. Recent successes in identifying small molecule antagonists of methyl lysine reader domains bodes well for this approach (26–28).

Experimental procedures

Protein expression and purification

UHRF1_126–366 corresponding to the TTD–PHD module and UHRF1_121–286 corresponding to the TTD were expressed and purified as described previously (9). TTD–PHD was purified with and without an N-terminal His tag, and in cases where the tag was removed, this was by overnight incubation with TEV protease at 4 °C (9). For isotopically labeled proteins used for NMR spectroscopy (¹⁵N-labeled, ¹⁵N/¹³C-labeled, or ¹⁵N/¹³C/²H-labeled), cells were grown in M9 minimal medium supplemented with [¹⁵N]ammonium chloride (1 g/liter), [¹³C]glucose (2 g/liter) when required, and 80% D₂O when required.

NMR spectroscopy

NMR samples were buffered in 20 mm sodium phosphate (pH 7.5), 150 mm NaCl, 5 mm DTT, 5 mm β-mercaptoethanol, 2 mm TCEP, and 10 μm ZnSO₄. The protein concentration was between 200 and 300 μm for all samples. The data were collected at 25 °C on Bruker spectrometers equipped with cryoprobes and operating at 500, 600, or 800 MHz. The assignment of backbone TTD–PHD resonances was accomplished using the ABACUS method (29) for which standard backbone and ¹⁵N-edited NOESY spectra were collected using ¹⁵N/¹³C/²H- or ¹⁵N/¹³C-labeled protein. All 3D experiments were acquired using non-uniform sampling and processed using the software MDDGUI (30) or qMDD (31). ¹⁵N-Labeled TTD–PHD was used to acquire ¹⁵N T₁ and T₂ relaxation and ¹H-¹⁵N heteronuclear NOE measurements (32) collected using standard Bruker pulse schemes in an interleaved manner. For T₁ measurements, the variable delay was set to 0.1, 0.4, 0.8, 1.5, 2.0, 2.5, 3.5, and 5 s. For T₂ measurements, the variable delay was set to 16, 32, 48, 64, 80, 96, 128, and 144 ms. The D1 was 3 s for all experiments. Reported values were the average from two measurements. All spectra were processed using NMRPipe (33) and analyzed with SPARKY (34).

SAXS data collection and analysis

All SAXS samples were buffered in 20 mm Tris (pH 7.5), 150 mm NaCl, 5 mm DTT, 5 mm β-mercaptoethanol, 2 mm TCEP and 10 μm ZnCl₂, and data were collected at concentrations ranging from ∼1 to 5 mg/ml. Measurements were carried out at Beamline 12-ID-B of the Advanced Photon Source, Argonne National Laboratory. The energy of the X-ray beam was 14 Kev (wavelength λ = 0.8856 Å), and two setups (small- and wide-angle X-ray scattering) were used simultaneously in which the sample to 2M detector distance was adjusted to achieve scattering q values of 0.006 < q < 2.6 Å⁻¹, where q = (4π/λ)sinθ, and 2θ is the scattering angle. To reduce radiation damage and obtain good statistics, thirty 2D images were recorded for each buffer or sample solution using a flow cell, with an accumulated exposure time of 0.4–2.0 s. No radiation damage was observed as confirmed by the absence of systematic signal changes in sequentially collected X-ray scattering images. The scattering profile of the protein was calculated by subtracting the background buffer contribution from the sample buffer profile using the program PRIMUS (ATSAS package, EMBL) (35). Concentration series measurements for a sample were carried out to remove the scattering contribution caused by interparticle interactions and to extrapolate the data to infinite dilution. Guinier analysis and the experimental radius of gyration (R_g) estimation from the data of infinite dilution were performed using PRIMUS. The pair distance distribution function, P(r), and the maximum dimension of the protein, D_max, in real space were calculated with the indirect Fourier transform using the program GNOM (36). To avoid underestimation of the molecular dimension and consequent distortion in low resolution structural reconstruction, the parameter D_max, the upper end of distance r, was chosen such that the resulting PDDF has a short, near zero-value tail at large r. The R_g from P(r) analysis was also reported. The molecular weights were estimated using V_c (37) in the q range of 0 < q < 0.3 Å⁻¹. Fifteen ab initio shape reconstructions (molecular envelopes) were generated using DAMMIF (38) and averaged with DAMAVER (39). The structural models were superimposed and overlaid with the averaged envelope using SUPCOMP (40). The theoretical scattering intensity of a structural model was calculated and fitted to the experimental scattering intensity using CRYSOL (41).

Structural characterization of TTD–PHD using SAXS and NMR data

We used an ensemble approach for the structural characterization of the TTD–PHD in solution by utilizing the SES protocol (18). The strategy on which the SES method is based consists of two main steps: 1) generate the initial ensemble of conformations to approximate the conformational space available for a system in solution and 2) find the optimal population weight for each member of the initial ensemble that minimizes the discrepancy between the ensemble-predicted and the observed experimental data. The goodness of the ensemble fit is measured as χ². We used the following expression for χ²,

$${\chi }^2={\chi }_{\text{saxs}}^2+\alpha \hspace{0.17em}\text{·}\hspace{0.17em}{\chi }_{\text{relax}}^2$$ (Eq. 1)

where

$${\chi }_{\text{saxs}}^2={{\displaystyle \sum _{i=1}^{N_{\text{q}}}\left[\frac{{\displaystyle \sum _{k=1}^{{\text{N}}_{\text{ens}}}{I}_{\text{calc}}^{\text{k}}\left(q_{\text{i}}\right)\text{·}{w}_{\text{k}}-I_{\exp }\left(q_{\text{i}}\right)}}{{\sigma }_{\text{saxs}}\left(q_{\text{i}}\right)}\right]}}^2$$ (Eq. 2)

$${\chi }_{\text{relax}}^2={\left({\displaystyle \sum _{k=1}^{N_{\text{ens}}}{\tau }_{\text{TTD}}^{\text{k}}\text{·}{w}_{\text{k}}-{\tau }_{\text{TTD}}^{\text{exp}}}\right)}^2/{\sigma }_{TTD}^2+{\left({\displaystyle \sum _{k=1}^{N_{\text{ens}}}{\tau }_{\text{PHD}}^{\text{k}}\text{·}{w}_{\text{k}}-{\tau }_{\text{PHD}}^{\text{exp}}}\right)}^2/{\sigma }_{PHD}^2$$ (Eq. 3)

where I_exp(q) is the experimental SAXS scattering intensity, N_q is the number of experimental points, σ_saxs(q) is the experimental error, I_calc^k is the scattering intensity predicted for the kth conformation, τ_TTD^exp and τ_PHD^exp are the experimental rotational correlation times for the TTD and PHD, respectively, σ_TTD and σ_PHD are the experimental errors, τ_TTD^k and τ_PHD^k are correlation times predicted for the kth conformation, N_ens is the number of conformations in the initial ensemble, w_k is the population weight associated with the kth conformation in the ensemble, and α is the weighting factor for the NMR relaxation data. In the case α = 0, only SAXS data is used to optimize weights w_k. Equation 1 can be represented in the matrix form,

$${\chi }^2\left(w,\alpha \right)={\Vert \mathrm{C}\left(\alpha \right)·w-\mathrm{B}\Vert }_2^2$$ (Eq. 4)

where matrix C is of size (N_q + 2, N_ens) and consists of predicted SAXS and NMR relaxation data for all members of the initial ensemble, matrix B consists of corresponding experimental values, ||·|| is the vector l₂-norm, and w is the vector of weights. To construct the C matrix, the 30-point SAXS profiles in the range 0 < q < 0.3 Å⁻¹ were predicted using CRYSOL, and two overall rotational correlation times, one for the TTD and one for the PHD, were predicted using HYCUD (21, 22). The ill-posed problem of finding vector of weights, w, that minimizes χ²(w, α) under the condition w_k ≥ 0 is solved using the SES approach (18). We used the SES module of the ARMOR package to generate a number of sparse solutions for different ensemble sizes with multiorthogonal matching pursuit algorithm. The ARMOR output was analyzed to select the optimal ensemble size using the l-curve (18), and the vector of the optimal weights, w, was calculated by averaging over top near optimal solutions with similar value of χ².

RBP_IN/OUT and RBP_IN ensemble generation

Rigid-body pools were generated using RANCH (42). In these simulations, ordered parts of the TTD–PHD were assumed to be rigid, whereas disordered parts were represented by random chains. RBP_IN/OUT was generated by assuming that the His tag (in constructs containing it), the flexible TDD_N loop (UHRF1_163–180), and the entire linker (UHRF1_282–301) are disordered. RBP_IN was generated assuming that the His tag (for constructs containing it), the flexible TDD_N loop (UHRF1_163–180), and the five-residue hinge region of the linker (UHRF1_297–301) are disordered. Both pools consist of 30,000 TTD–PHD conformations.

MDP_IN/OUT and MDP_IN generation

The initial pools of TTD–PHD conformations were obtained in two steps. In the first step, we performed all-atom MD simulations of TTD–PHD. Eight replica MD trajectories, each ∼150 ns long, were generated at 300 K. Four of these replicas were started from different conformations with the TTD groove occupied by the linker, whereas the other four replicas were started from conformations with the linker displaced from the groove. No bound-to-unbound or unbound-to-bound transitions of the linker were observed along the MD trajectories. Over the course of the simulations, the two domains retained their overall structure, with no ordered-to-disordered transitions, as indicated by the low root mean square deviation for TTD and PHD backbone atoms (∼3.5 and 3.3 Å, respectively) in MD-generated conformers. This is in agreement with NMR data (supplemental Fig. S7). Each 10-ps frame was saved during MD simulations, which resulted in 65,200 conformations of the TTD–PHD with the linker positioned in the groove and 55,460 conformations with the linker out of the groove. In the second step, we performed k-means clustering of the generated conformations using metrics that specify the relative position of the TTD and PHD, yielding 6,000 and 8,000 clusters of conformers with the linker in and out of the groove, respectively. To improve on relatively poor sampling of the conformers with the linker out of the groove in MD simulations, we also added 2,000 additional clusters, produced initially by rigid-body modeling, of open/extended TTD–PHD conformers. The representative structures of these clusters were used to construct MDP_IN/OUT and MDP_IN.

All-atom molecular dynamics simulations

A modified Generalized Born implicit solvent model (43) was exploited in the MD simulations to accelerate sampling of the conformational space for each of the systems. All simulations used an integration step of 2 fs with fixed bonds between hydrogen atoms and heavy atoms. The temperature was controlled by carrying out Langevin dynamics with the damping coefficient set to 2 or 5 ps⁻¹. The cut-off for non-bonded Lennard-Jones and electrostatic interactions was set to 18 Å. The ionic strength was set to 0.15 m. All simulations were performed using NAMD 2.9 code (44) with the AMBER Parm99SB parameter set (45). A zinc AMBER Force Field (46) was used for PHD residues that coordinate three zinc ions.

FP, ITC, and DSF measurements

For FP assays, the TTD (UHRF1_121–286) was buffered in 20 mm Tris (pH 8.5), 50 mm NaCl, 3% DMSO, and 0.01% TX100. N-terminal FITC-labeled H3K9me3_(1–25) peptide was synthesized and purified by Tufts University Core Services (Boston, MA). Titrations and compound binding assays were performed in a 10-μl volume at a constant labeled peptide concentration of 0.04 μm. For compound screening and titrations, a non-saturating fixed protein concentration of 8 μm TTD was used. FP assays were performed in 384-well Axygen plates using a Synergy 4 microplate reader (BioTek). An excitation wavelength of 485 nm and an emission wavelength of 528 nm were used.

For ITC measurements of TTD–PHD (UHRF1_126–366) interaction with H3K9me3, samples were dialyzed into a buffer containing 10 mm HEPES (pH 7.5), 150 mm NaCl, 1 mm TCEP, and 30 μm ZnCl₂. H3K9me3_(1–15) peptide, in the same buffer, was brought to a concentration of 0.50 mm. A preliminary peptide injection of 0.06 μl was followed by subsequent 2-μl injections into the sample cell containing 167 μl of 50 μm TTD–PHD. Where indicated, 1.5 mm BPC or 1.5 mm PBR peptide was included in the injection syringe and sample cell. The reported K_D and n values are based on the average from two measurements. For ITC measurements of TTD (UHRF1_121–286) interaction with BPC, the protein was buffered in 20 mm Tris (pH 7.4), 50 mm NaCl, and 5% DMSO. BPC was brought to a concentration of 2.5 mm and injected into the sample cell containing 40 μm protein. The data were acquired on a Nano ITC from TA Instruments at 25 °C and fitted with an independent-binding site model using NanoAnalyze software (v3.7.0).

DSF measurements were performed with a Light Cycler 480 II instrument from Roche Applied Science. TTD (UHRF1_121–286) was buffered at 0.1 mg/ml in 0.1 m HEPES (pH 7.5), 0.15 m NaCl, and 5× Sypro Orange. Sypro Orange was purchased from Invitrogen as a 5,000× stock solution, and it was diluted 1:1,000 to yield a 5× working concentration. Experiments were run in the absence and presence of 3 mm BPC. DSF was carried out by increasing the temperature from 20 to 95 °C at a heating rate of 4 °C/min, and data points were collected at 1 °C intervals. The temperature scan curves were fitted to a Boltzmann sigmoid function, and the T_m values were obtained from the midpoint of the transition as described previously (47).

Author contributions

R. S .H. acquired and analyzed NMR data. A. L. interpreted NMR relaxation data, analyzed SAXS data, and performed structural modeling. L. F. acquired and processed SAXS data under the supervision of Y.-X. W. A. I. performed the initial fragment screen with UHRF1-TTD under the supervision of P. J. B. G. S. characterized the interaction of BPC with UHRF1-TTD. D. I. performed the ITC experiments. S. D., L. K., and M. S. O. designed constructs and prepared samples for SAXS, NMR analysis, and binding studies. R. S. H., A. L., and C. H. A. wrote the manuscript. C. H. A. supervised the project.