An Alternative to Post-Hoc Model Modification in Confirmatory Factor Analysis: The Bayesian Lasso

Abstract

As a commonly used tool for operationalizing measurement models, confirmatory factor analysis (CFA) requires strong assumptions that can lead to a poor fit of the model to real data. The post-hoc modification model approach attempts to improve CFA fit through the use of modification indexes for identifying significant correlated residual error terms. We analyzed a 28-item emotion measure collected for n = 175 participants. The post-hoc modification approach indicated that 90 item-pair errors were significantly correlated, which demonstrated the challenge in using a modification index, as the error terms must be individually modified as a sequence. Additionally, the post-hoc modification approach cannot guarantee a positive definite covariance matrix for the error terms. We propose a method that enables the entire inverse residual covariance matrix to be modeled as a sparse positive definite matrix that contains only a few off-diagonal elements bounded away from zero. This method circumvents the problem of having to handle correlated residual terms sequentially. By assigning a Lasso prior to the inverse covariance matrix, this Bayesian method achieves model parsimony as well as an identifiable model. Both simulated and real data sets were analyzed to evaluate the validity, robustness, and practical usefulness of the proposed procedure.

Confirmatory factor analysis (CFA) is a commonly used technique for studying theory-driven hypotheses regarding observed and unobserved variables. CFA has been extensively applied to research areas in psychology and the social sciences including personality assessment (Briggs & Cheek, 1986; Marsh & Hocevar, 1985), organizational studies (Stone-Romero, Weaver, & Glenar, 1995), and quality of life research (Hays, Anderson, & Revicki, 1993). Using CFA, the number of factors is assumed to be known a priori and is thus treated as a fixed number in the estimation procedure. Unlike exploratory factor analysis (EFA), CFA requires the observed variables to have zero loadings on all factors except the appropriate ones, which are a priori specified in the model. The increasing use of CFA is partly due to its relative ease to set up, its robustness to mild deviations from the underlying assumptions (e.g., Curran, West & Finch, 1996; Flora & Curran, 2004; Hu, Bentler, & Kano, 1992), and its important role in structural equation modeling (SEM; see Brown, 2006, p. xi; Thompson, 2004, p. 110), which has undergone rapid growth as a tool for studying causal relationships (Hershberger, 2003). For a recent review of CFA, see DiStefano and Hess (2005).

Researchers using CFA for various purposes often encounter a dilemma. Although in many ways theory-based CFA is more compelling than its counterpart of more exploratory work, sometimes the theory being tested simply does not fit the data well. Using the Big Five Personality data, Muthén and Asparouhov (2012) demonstrated that even in well-established theory, CFA may not fit well and possible correlated residuals may exist among items. When such a scenario occurs, it is tempting for researchers to revert to EFA, compare the results derived from the two different approaches, and make changes for a separate round of CFA exercise. For example, items that were found to cross-load on more than one factor in EFA are considered for deletion in the subsequent analysis. Recent work in Bayesian factor analysis proposed using different priors such as ridge regression prior or spike and slab prior - to shrink cross-loadings in EFA toward zero (Muthén and Asparouhov, 2012; Lu, Chow, & Loken, 2016). Another possibility is to use modification indexes (MIs) for identifying components in the model that could be tweaked for the purpose of improving overall goodness-of-fit. Typically, a constrained parameter is modified to become a free parameter and if the corresponding MI suggests that the improvement of model fit is significant, the model with the freed parameter will be used. This approach, sometimes known as post-hoc model modification (PMM, Kaplan, 1990; Sörbom, 1989), has been popularized by software programs such as LISREL (Jöreskog & Sörbom, 1984) and Mplus (Muthén & Muthén, 1998–2013), both of which allow users to examine MIs and make changes to a number of parameters. Although critics of the method views MI as either a form of data snooping or a devious departure from the theory-driven paradigm (Steiger, 1990), there are several advantages to the modification approach from a practical point of view. First, CFA is a restrictive tool because hypotheses are rarely available that allow the specification of a simple factor pattern that agrees with real data. Second, the standard for acceptance for CFA models, such as criterion of percentage of variance accounted for, is higher than the standard of acceptance for EFA models (Bentler & Bonett, 1980). Such a high standard cannot always be achieved in practice. Lastly, when used appropriately, the PMM approach may pinpoint pockets of misspecification in the model, which could lead to modification and a more robust model (MacCallum, 1995; Sörbom, 1989).

One problem in using the PMM methodology is that the related statistical hypothesis testing can only be sequentially applied to nested models. Suppose model A containing a fixed parameter ψ₁ = 0 is nested within model B, which contains the freed parameter of ψ₁. A chi-squared statistic of one degree of freedom is used to evaluate whether the improvement due to the change of freeing the ψ₁ parameter is statistically significant. If another parameter ψ₂ needs to be tested, it must be tested after the testing of parameter ψ₁. Although the sequential testing procedure in PMM using MI can be used to modify a CFA model, the post-hoc procedure cannot simultaneously identify locations where modifications are needed. In other words, PMM may lead to a suboptimal solution. MacCallum (1986) examined specification searches and found methods such as MI tend to produce incorrect results. A second problem with PMM is that the procedure may not be practical when the number of items is large. For an CFA on 30 items, even when a small percentage, say 5%, of covariances deviate from the diagonal matrix assumption, there would be 22 flagged covariances. This is complicated by the possibility of false discovery; how PMM would control for spurious significant findings is far from clear. Additionally, there is no guarantee that the modified covariance matrix is positive definite, a critical requirement for the model based on the estimated parameters to form a proper joint density. We will return to these issues in more depth in the Discussion section.

In this paper we adopt the view that CFA is a modeling effort in which (1) the researcher has a theory-based factor structure in mind for the measures in the traditional CFA sense, and (2) the residual covariance structure in the error terms across all variables is not necessarily diagonal, but only a few of the off-diagonal elements are bounded away from zero. In particular, these covariance terms are treated as nuisance parameters — deviations from the theory-driven factor model that need to be accounted for but otherwise of little substantive interest. In other words, we do not adjust a CFA model post hoc but rather start with a comprehensive CFA model that allows for correlated residual errors between measures after accounting for the latent factors. Using a full correlated-error model has its own problems that the covariance matrix for the error terms can be quite large. Using the aforementioned example of CFA for 30 measures, the 30 × 30 covariance matrix contains 435 distinct off-diagonal entries. We propose the use of a highly sparse representation of the covariance matrix. The technical implementation of such an idea is through the Bayesian Lasso (Least Absolute Shrinkage and Selection Operator) approach, in which the entire residual covariance matrix for all observed measures are modeled as a sparse structure that contains only a few covariance entries bounded away from zero.

Consider a researcher who uses SEM for a substantive analysis that requires CFA on a 20-item response data set. Suppose that although the 3-factor model is an interpretable model and consistent with the theory, the 4-factor model offers better fit in terms of goodness-of-fit indexes such as CFI and RMSEA. Additionally, further examining the 3-factor model result reveals that 5%, or a 10-residual correlation, still lingers in the covariance matrix. Suppose the researcher prefers the 3-factor solution but has concerns using the diagonal 3-factor structure because the CFA result could be biased, and perhaps more important, that the bias could percolate to the other SEM components. In such a scenario, what can the researcher do? She can dismiss the error covariances and defend the solution using theory, or she can use PMM whose limitations we have discussed. An alternative is to use the Bayesian Lasso. The greatest practical benefits that we see for the Bayesian Lasso in this situation include (1) the ability to retain a more parsimonious factor structure that could be more consistent with the theory by treating off-diagonal errors as a nuisance factor, and (2) the use of a defensible statistical method for handling the limited and yet non-negligible number of error covariances. In contrast to PMM, the Lasso approach avoids the form of p-value hacking inherent in PMM. In other words, truly zero covariance that shows up as significant due to sampling error is likely to be shrunken to near zero, and truly non-zero covariance will likely be detected and adjusted for in the CFA analysis. As a result, the researcher can specify a theory-based confirmatory factor-structure and adjust the model using a data-driven process instead of tediously modifying one parameter at a time.

The third practical benefit of the Bayesian Lasso method is that it can prevent or at least reduce the propagation of bias in CFA to SEM estimates. In a study using simulated data that we provide later, we demonstrate this effect using a simple SEM example. In addition to the above-mentioned practical benefits, the Bayesian Lasso also enjoys many technical benefits, compared with other methods including PMM. First, it is a formal statistical model that maintains the positive definiteness property of the covariance matrix. Second, unlike a CFA model with a fully specified error covariance under a frequentist framework, the Bayesian Lasso model is identifiable. Third, as we shall see, the Bayesian Lasso can easily incorporate an additional step of imputation in handling missing values. This could be very useful for data sets that contain partially missing values — e.g., when participants miss a response on some items but not all. Fourth, the Bayesian Lasso model generally fits the data better. By limiting the denseness of the covariance in terms of deviation from a diagonal form, the Bayesian Lasso is able to achieve an optimal tradeoff between overall fit and model complexity. Finally, the Bayesian Lasso can be used as a diagnostic tool for affirming or refuting theory-based factor configurations. As we shall see from the simulation experiments, specific patterns in the residual covariance matrix often signal certain forms of misspecification. An excessive amount of covariance error terms would suggest that the CFA is not fitting well and that the researcher should investigate –this is an advantage that a global goodness-of-fit index would not offer.

The Bayesian Lasso factor model proposed in this paper can be viewed as a specific implementation of Bayesian structural equation modeling (SEM) as discussed in Muthén and Asparouhov (2012). The authors argued that in many SEM applications, unnecessary restrictions to models are applied to represent hypotheses derived from substantive theories. As hypotheses are reflected in parameters fixed at zero, they proposed to replace parameters of exact zeros with approximate zeros via a Bayesian analysis using small variance priors. For the Bayesian Lasso factor model, limiting the numbers of nonzero (or not-so-close-to-zero) parameters is especially important as we focus on the residual covariance matrix and the number of parameters that grow quickly with the dimension of the problem. Without the Lasso component, a Bayesian approach for handling residual covariance would be to free the covariance parameters and assign prior distributions to the covariance entries. However, such a generic Bayesian approach would not necessarily lead to a sparse solution. As previously pointed out, Muthén and Asparouhov (2012) demonstrated the use of a ridge-regression prior for exploring the presence of cross-loadings in CFA as an example of the Bayesian SEM approach. The Bayesian Lasso in this paper is a special implementation of the Bayesian SEM for CFA covariance structures, not for cross-loading. The current approach is also analogous to some local dependent models in item response theory (IRT; e.g., Ip et al., 2004). Similar to local dependent item response models, the Bayesian Lasso approach treats the set of nonzero entries in the error covariance matrix as a means of achieving a better goodness-of-fit, but is otherwise only of peripheral interest.

The remainder of the paper is organized as follows: First, we provide an overview of the Bayesian and Lasso approaches. We then describe the CFA model with Bayesian covariance Lasso prior and outline the estimation procedure. Next we describe several simulation studies for evaluating the proposed procedure. An analysis of a real data set collected from a study on emotion is then presented. Finally, we provide a discussion.

The Bayesian Covariance Lasso Prior CFA Model

Bayesian Analysis

The Bayesian approach is well recognized in the statistics and psychology literature as an attractive way of analyzing a wide variety of models (see for example, Congdon, 2005, 2007, 2014, and the references therein). The most attractive features of the Bayesian approach in statistical modeling and data analysis are as follows (Gelman et al., 2004; Congdon, 2007). First, it allows the use of genuine prior information in addition to the information available in observed data to produce results. Second, sampling-based Bayesian methods rely less on large-sample asymptotic theory, thereby producing reliable results even with relatively small sample sizes. Third, it provides better statistics for goodness-of-fit and model comparison as well as other useful statistics; for example, point estimates and interval estimates on parameters and probability values on hypotheses. Lastly, compared with maximum likelihood (ML)-based methods, the Bayesian approach is conceptually simple and can be implemented in complex models that are more difficult to fit using classical methods.

A typical Bayesian analysis can be outlined in the following steps:

1. Define a model M with unknown parameter θ;

2. Assign prior distribution of θ under model M, p(θ|M), which reflects the prior information from some sources, such as the knowledge of experts, analyses of similar data or past data, and so on.

3. Construct the likelihood function p(y|θ, M) based on the observed data y and the model M defined in Step 1;

4. Determine the posterior distribution of θ by incorporating the sample information in p(y|θ, M) and prior information in p(θ|M) through p(θ|y, M) ∝ p(y|θ, M) × p(θ|M), where p(θ|y, M) is the posterior of θ;

5. Calculate the quantities of interest for θ (for example, point estimates and interval estimates) based on the posterior distribution of θ in Step 4.

Lasso Model

Regularization is a general approach that requires additional model information for improving a solution that is inherently unstable or too complex for meaningful interpretation. In frequentist framework, the Lasso approach implements regularization by adding a penalty term to the usual likelihood so that the model would move toward a solution that contains fewer parameters. In general, frequentist Lasso tends to produce some coefficients that are exactly zero, which not only helps to increase predictive accuracy, but also enjoys desirable properties including improved interpretability and numerical stability. Suppose the set of parameters in a model is denoted by θ and θ_j denotes individual parameters, j = 1, ⋯, p. Specifically a Lasso approach uses the following objective function:

$$PL(\mathit{\theta })=log(p(\mathbf{y}\mid \mathit{\theta },M))+\lambda \sum _{j=1}^p\mid {\theta }_j\mid =LL(\mathit{\theta })+\lambda \sum _{j=1}^p\mid {\theta }_j\mid ,$$ (1)

where PL(θ) and LL(θ) are respectively the penalized and the usual log-likelihoods based on model M, and λ ≥ 0 is a tuning parameter that determines the amounts of shrinkage (Tibshirani, 1996). A larger λ value tends to increase the penalty for more complex models that have more parameters. Because each tuning parameter value corresponds to a fitted model, selecting λ can be viewed as a model selection problem. Tibshirani (1996) proposed the quadratic programming algorithm to find the Lasso solutions and described methods such as cross-validation to select the tuning parameter λ in Eq. 1.

In Bayesian framework, the key quantity is the posterior distribution p(θ|y, M) ∝ p(y|θ, M) × p(θ|M), where p(θ|M) is the prior distribution. Compared to a frequentist approach in which inference is based on the likelihood term p(y|θ, M), the Bayesian posterior contains the additional term for the prior p(θ|M). This is an important observation as it is the connection to a regularization approach such as Lasso. The log posterior in a Bayesian approach takes the general form

$$log(p(\mathbf{y}\mid \mathit{\theta },M))+log(p(\mathit{\theta }\mid M))=LL(\mathit{\theta })+\text{LPrior}(\mathit{\theta }),$$

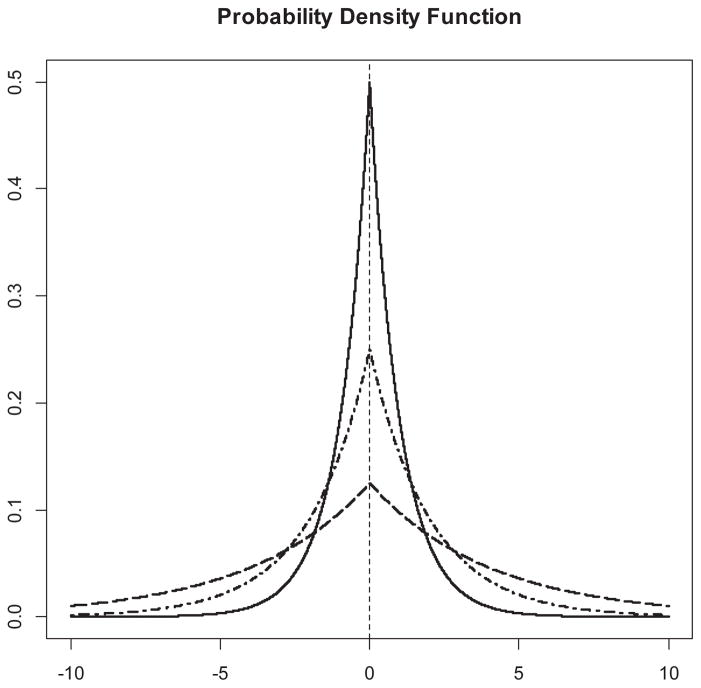
where LPrior(θ) represents the log prior (possibly multivariate). Thus, if the appropriate form of prior distribution is chosen, the log prior distribution in Bayesian analysis tends to play the role of the penalty function in Lasso. For example, Tibshirani (1996) suggested that Lasso estimates can be interpreted under the Bayesian framework when the θ_j’s are assigned independent and identical double-exponential priors, $\frac{\lambda }{2}exp(-\lambda \mid {\theta }_j\mid )$. The probability density functions of double exponential with some different values of λ were presented in Fig. 1. Like the normal distribution with zero mean, this distribution is unimodal and symmetrical. However, it has a sharper peak than the normal distribution. The plots revealed that the larger the value of λ, the more the probability density function concentrated around zero.

Figure 1.

Probability density function of double exponential with three different values of λ: 1.0 (solid), 0.5 (dot-dash) and 0.25 (long-dash).

Algorithms for implementing Lasso include Efron et al. (2004), Friedman et al. (2007, 2010), and Wu and Lange (2008). However, none of these algorithms provide a valid measure of standard error, which can be problematic for the frequentist Lasso (Kyung et al., 2010). Park and Casella (2008) proposed Gibbs sampling for the Lasso with the double-exponential priors in the hierarchical model, which was the first explicit treatment of a Bayesian Lasso regression; see also Hans (2009). Compared with the frequentist Lasso, the Bayesian Lasso provides a valid measure of standard error (Kyung et al., 2010). Moreover, the sampling-based Bayesian framework also provides a flexible way of estimating the shrinkage parameter λ along with other parameters simultaneously, which lessens the heavily computational burden in selecting the optimal values of λ via a commonly used cross-validation procedure.

In recent years, a tremendous amount of work has been done to apply Lasso and L₁-like penalties to the traditional models (Tibshirani, 2011). One example is the graphical Lasso (Yuan & Lin, 2007; Friedman et al., 2007) for fitting a sparse Gaussian graph that applied the L₁-penalty — i.e., the sum of |θ_j |, to the inverse covariance matrix for graph-edge selection. The modeling of the inverse covariance matrix (or the precision matrix), instead of the covariance matrix, was an innovation proposed by Dempster (1972). For a joint multivariate normal distribution, zero entry of the precision matrix at the (i, j) position corresponds to conditional independence of the corresponding variables i and j given all other variables. Compared with zero entry of the covariance matrix at the (i, j) position which only implies non-correlation between variables i and j, the conditional independence assumption is both stronger and more interpretable (Edwards, 2000). Indeed, a sparse inverse covariance matrix implies a sparse graphical model or path diagram of which conditional independence relationships between variables can be directly read off. The graphical Lasso is also known as covariance Lasso (Khondker et al., 2013). Because our proposed model was inspired by the Bayesian approach for covariance Lasso in Khondker et al. (2013) and Wang (2012) hereafter we refer the proposed model as Bayesian covariance Lasso CFA.

Bayesian Covariance Lasso for Confirmatory Factor Analysis

Suppose y₁, y₂, ⋯, y_n are independent random observations and each y_i = (y_i1, y_i2, ⋯, y_ip)^T satisfies the following factor analysis model:

$${\mathbf{y}}_i=\mathit{\mu }+\mathbf{\Lambda }{\mathit{\omega }}_i+{\mathit{\epsilon }}_i,i=1,2,\cdots ,n,$$ (2)

where μ is p × 1 vector of intercepts, and Λ is a p × q factor-loading matrix that reflects the relation of observed variables in y_i with the q × 1 latent factors in ω_i. Moreover, it is assumed that ω_i follows N[0, Φ], and ε_i is a p×1 random vector of measurement errors, or residuals, which is independent of ω_i and follows N[0, Ψ]. Following a standard modeling approach for CFA, the number of latent factors and the structure of Λ are specified a priori. In contrast to the common diagonality assumption about Ψ in factor analysis, in our model, the variance-covariance matrix Ψ is not necessarily diagonal.

The proposed Bayesian covariance Lasso for CFA assigns prior distributions for the inverse of the covariance matrix instead of directly for the covariance matrix. Let Σ = Ψ⁻¹ = (σ_ij)_p×p. Together with a positive definiteness constraint on the covariance matrix, independent exponential priors and the double exponential priors are respectively assigned for the diagonal and the off-diagonal elements of Σ (Wang, 2012). The double exponential density has the form $\frac{\lambda }{2}exp(-\lambda \mid {\sigma }_{ij}\mid )$, i < j, whereas the exponential density function has the form $\frac{\lambda }{2}exp(-\frac{\lambda }{2}{\sigma }_{ii})$. For a full Bayesian Lasso approach, instead of using cross-validation methods, an appropriate hyperprior is assigned to λ. Specifically, λ ~ Gamma(α_λ0, β_λ0), where α_λ0 and β_λ0 are hyperparameters whose values are preassigned. This Bayesian method of modeling λ has been applied in the context of Bayesian Lasso regression models (Hans, 2009; Park & Casella, 2008). The common choices for these hyperparameters are α_λ0 = 1 and β_λ0 to be small.

For the structural parameters involved in μ, Λ, and Φ, the following conjugate prior distributions are assigned (Lee, 2007). For k = 1, ⋯, p,

$$\mathit{\mu }~N({\mathit{\mu }}_0,{\mathbf{H}}_{\mu 0}),{\mathbf{\Lambda }}_k~N({\mathbf{\Lambda }}_{0k},{\mathbf{H}}_{0k}),{\mathbf{\Phi }}^{-1}~\text{Wishart}({\mathbf{R}}_0,{\rho }_0),$$ (3)

where ${\mathbf{\Lambda }}_k^T$ is the kth row of Λ; μ₀, Λ_0k, ρ₀, and positive definite matrices H_μ0, H_0k, and R₀ are hyperparameters whose values are assumed to be given to represent the available prior knowledge that may be obtained from the subjective knowledge of field experts and/or analysis of past or closely related data.

Gibbs Sampler and Positive Definiteness of Covariance Matrix

The Gibbs sampler (Geman & Geman, 1984), which is a form of Markov chain Monte Carlo (MCMC; Gilks, Richardson, & Spiegelhalter, 1996), combined with the idea of data augmentation (Tanner & Wong, 1987), iteratively simulates observations from the full conditional distributions such that eventually the posterior distribution of the parameters of interest and latent quantities can be empirically represented by a collection of simulated values. For example, in a simple model of two parameters θ₁, θ₂, the Gibbs sampler would iteratively draw values from the full conditional distributions p(θ₁|θ₂, y) and p(θ₂|θ₁, y), where y represents the data. If the full conditional distributions are standard distributions, simulating observations from them is rather straightforward and fast. For nonstandard conditional distributions, the Metropolis-Hastings (MH) algorithm can be used (see Hastings, 1970; Metropolis et al., 1953 for more details). Suppose the parameters of interest from the kth iteration in the Gibbs sampler is denoted by ${\mathit{\theta }}^{(k)}=({\theta }_1^{(k)},{\theta }_2^{(k)},\cdots ,{\theta }_m^{(k)})$. It has been shown that under mild regularity conditions, the joint distribution of ( ${\theta }_1^{(k)},{\theta }_2^{(k)},\cdots ,{\theta }_m^{(k)}$) converges to the desired posterior distribution [θ|y, M], after a sufficiently large number of iterations (called a burn-in phase), say K. After discarding the observations obtained at the burn-in phase (or say, after convergence), statistical inference of θ can be carried out on the basis of the simulated samples {θ^(K+j) : j = 1, 2, ⋯, J}. For example, Bayesian point estimates and standard error estimates of θ can be produced by using the corresponding posterior means and their posterior covariance matrix of the simulated samples.

The specification of the Bayesian covariance Lasso CFA model allows a block Gibbs sampling scheme to be implemented for statistical inference. An outline of the implementation of the block Gibbs sampler is given in Appendix 1. The block Gibbs sampler offers a convenient way to handle missing values. Under the Missing-At-Random (MAR) assumption (Little & Rubin, 1987), missing values were imputed. In other words, the conditional distributions of a missing variable uses data from other variables to inform the imputation. The block Gibbs sampler eventually provides an estimate of Σ that can be inverted to obtain Ψ = Σ⁻¹. Detailed model specification and full conditional distributions are described within the R codes provided in the online Supplementary Materials Section 1 on the journal website.

Under the proposed block Gibbs sampler, it can be proved that covariance matrix estimate is positive definite. The mathematical proof of positive definiteness of Σ is included in Appendix 2. The positive definiteness of Σ implies that Ψ is also positive definite. The result is an important technical innovation because the positive definiteness of the covariance matrix is a necessary condition for a valid CFA solution.

Convergence Monitoring, Goodness-of-Fit, Uncertainty Estimates, and Identifiability Checking

The convergence of the MCMC algorithm is monitored by the estimated potential scale reduction (EPSR) value (Gelman, 1996) of each individual parameter of interest. The EPSR value can be calculated from several parallel sequences of simulated observations generated independently via different starting values. For more details of computation of the EPSR value, please refer to Gelman (1996). The whole simulation procedure is said to be converged if all the EPSR values are less than 1.2. Once the algorithm is judged to converge, a large number of draws can then be sampled from the joint posterior distribution to produce Bayesian point estimates and standard errors estimates of the unknown parameters and latent variables. The EPSR value can be obtained by using an R package called coda (Plummer et al., 2006).

The goodness-of-fit of the posited model was tested via the posterior predictive (PP) p-value (Gelman, Meng, & Stern, 1996; Scheines e al., 1999) as introduced in Lee (2007) for SEMs and related models. As discussed in Muthén and Asparouhov (2012), the PP p-value is akin to a model fit index. Here we used the PP p-value as a complementary statistic for assessing the goodness-of-fit of a single model, given that the Bayesian Lasso was already used as a model selection tool. The implementation of the PP procedure in Mplus can be found in Asparouhov and Muthén (2010) and a brief overview can be found in Muthén and Asparouhov (2012). A model is considered plausible if the PP p-value estimate is not far from 0.5.

Analogous to the measure of confidence interval in a frequentist’s approach, the Bayesian approach uses the concept of Highest Posterior Density (HPD) intervals to characterize the uncertainty associated with an estimated parameter. The 100(1 − α)% HPD interval (Box & Tiao, 1992; Chen & Shao, 1999) for an unknown parameter θ is defined as

$$H(\delta )=\{\theta :p(\theta \mid \mathbf{y},M)\ge \delta \},$$

where δ is the largest constant such that ∫_H(δ) p(θ|y, M)dθ = 1 − α. The HPD interval can also be obtained by using the R package coda, which was used for the analysis in this paper.

A key issue using a full covariance matrix for errors in CFA is model identifiability, for example, the model is not identified if the parameters are redundant. Under a frequentist framework, freeing all the residual covariance parameters violates the counting rule (Kaplan, 2009) — i.e., the number of free parameters is less than or equal to p(p + 3)/2, where p is the dimension of y_i — that generally leads to an unidentified model. Using the data setting in the simulation study 1 as an example, when p = 10, the number of free parameters is 76, which is greater than 10×(10+3)/2 = 65, meaning that the model is unidentified. In a practical implementation such as using Mplus, when all residual co-variances are specified to be freely estimated under the ML framework, an error message appears, stating that the degree of freedom for this model is negative and that the model is not identified will be returned. Under the Bayesian framework, model identification can be achieved by the provision of prior information in restricting the range of individual elements in the covariance matrix. The Bayesian Lasso method does not, however, exactly assign zero values to off-diagonal elements in the covariance matrix; it shrinks the more weakly related parameters close to zero faster (Park & Casella, 2008), and as a result, avoids the nonidentification problem. Kaufman and Press (1973) proved that the Bayesian CFA model with an inverse-Wishart prior for the full Ψ matrix is identified. For the proposed CFA model with a covariance Lasso prior, identifiability can be empirically evaluated by examining the convergence of an MCMC sequence of the parameters. One common way to do this is to generate parallel MCMC sequences with different starting values and check that the sequences mix well via trace plots. An alternative is to check EPSR values (<1.2). Both methods were used to check identifiability in our subsequent data analysis.

Empirical Studies

Study 1: Parameter Recovery When the Model is Correctly Specified

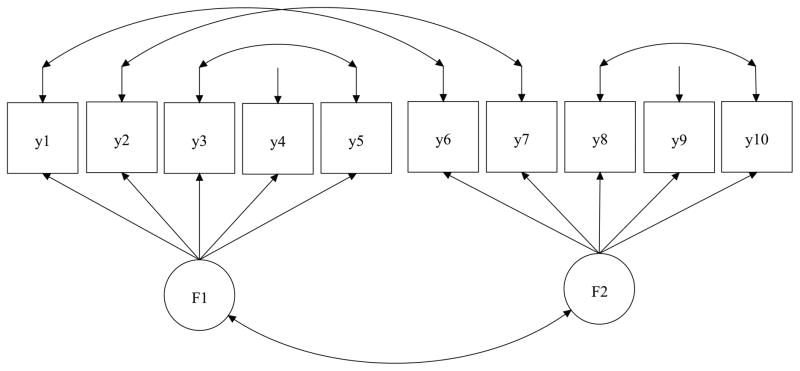
The main purpose of this section is to evaluate the parameter recovery of the proposed CFA model with a Bayesian covariance Lasso prior when the model is correctly specified. A data set was simulated based on the model specified in Eq. 2 with the number of observed variables set at p = 10 and the number of factors set at q = 2. It was assumed that Eq. 2 contained the following structure:

$${\mathbf{\Lambda }}^T=\left(\begin{array}{cccccccccc}1.0& {\lambda }_{21}& {\lambda }_{31}& {\lambda }_{41}& {\lambda }_{51}& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 1.0& {\lambda }_{72}& {\lambda }_{82}& {\lambda }_{92}& {\lambda }_{10,2}\end{array}\right),\mathbf{\Phi }=\left(\begin{array}{cc}{\varphi }_{11}& {\varphi }_{12}\\ {\varphi }_{21}& {\varphi }_{22}\end{array}\right),$$

where the 1’s and 0’s are fixed for identification purpose, and

$$\mathbf{\Psi }=\left(\begin{array}{cccccccccc}{\psi }_{11}& 0.0& 0.0& 0.0& 0.0& {\psi }_{16}& 0.0& 0.0& 0.0& 0.0\\ 0.0& {\psi }_{22}& 0.0& 0.0& 0.0& 0.0& {\psi }_{27}& 0.0& 0.0& 0.0\\ 0.0& 0.0& {\psi }_{33}& 0.0& {\psi }_{35}& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& {\psi }_{44}& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& {\psi }_{53}& 0.0& {\psi }_{55}& 0.0& 0.0& 0.0& 0.0& 0.0\\ {\psi }_{61}& 0.0& 0.0& 0.0& 0.0& {\psi }_{66}& 0.0& 0.0& 0.0& 0.0\\ 0.0& {\psi }_{72}& 0.0& 0.0& 0.0& 0.0& {\psi }_{77}& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& {\psi }_{88}& 0.0& {\psi }_{8,10}\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& {\psi }_{99}& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& {\psi }_{10,8}& 0.0& {\psi }_{10,10}\end{array}\right).$$

All elements in Ψ were considered free and accordingly estimated. The model structure was presented in Fig. 2(a). The true values of the structural parameters were set as follows: μ = (μ₁, μ₂, ⋯, μ₁₀)^T = (0.5, 0.5, ⋯, 0.5)^T, λ₂₁ = λ₇₂ = λ₈₂ = 0.8, λ₃₁ = λ₄₁ = λ₉₂ = 0.5, λ₅₁ = λ_10,2 = 0.3, ϕ₁₁ = ϕ₂₂ = 1.0, ϕ₂₁ = 0.3, and ψ_kk = 0.36, for k = 1, 2, 6, 7, 8; ψ_kk = 0.50, for k = 3, 4, 5, 9, 10; ψ₁₆ = ψ₆₁ = ψ₂₇ = ψ₇₂ = ψ₃₅ = ψ₅₃ = ψ_8,10 = ψ_10,8 = 0.3. Two levels of sample sizes were used, N = 200 and N = 500, and for each sample size 100 replications were generated.

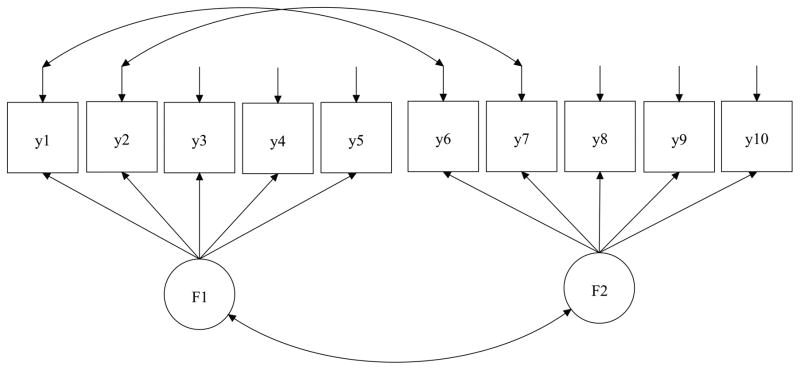
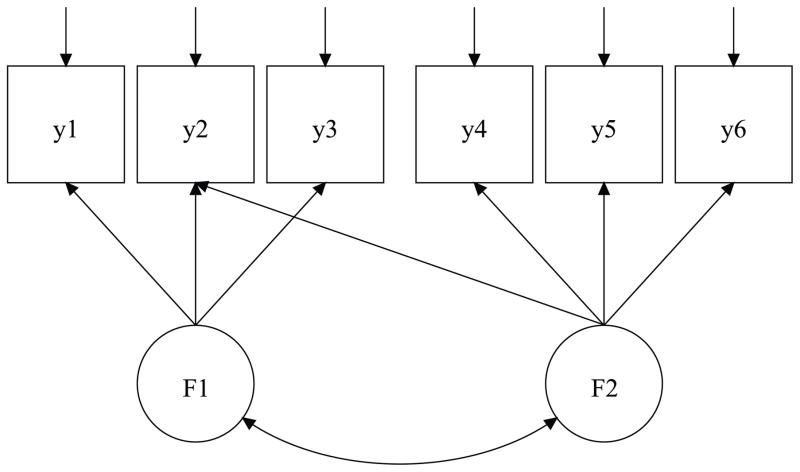
Figure 2.

Model Structure in Simulation Studies 1–3.

Additionally, a sensitivity analysis regarding inputs in the prior distributions was conducted by perturbing the prior input as follows:

Perturbed Input I: The elements in μ₀ and Λ_0k were taken as 0.0, and H_μ0 and H_0k were taken as diagonal matrices with all diagonal elements equal to 4.0 in appropriate order. ρ₀ = 6, R₀ = 6I₂, where I₂ is an identity matrix, α_λ0 = 1, and β_λ0 = 0.01.

Perturbed Input II: The elements in μ₀ and Λ_0k were taken as true values, and H_μ0 and H_0k were taken as identity matrices in appropriate order. ρ₀ = 3, R₀ = 6I₂, where I₂ is an identity matrix, α_λ0 = 1, and β_λ0 = 0.005.

Several test runs were initially conducted to determine the approximate number of MCMC iterations that would be required for achieving convergence. It was observed that the algorithm converged in less than 5,000 iterations, as indicated by the EPSR values being less than 1.2. In the actual run, we used the more conservative number of iterations of 10,000 for the burn-in. For each replication, we used 10,000 draws subsequent to the burn-in period for deriving required statistics. Based on 100 replications, the bias of the estimates (BIAS), the mean of the standard error estimates (SE), and the root mean squares (RMS) error between the estimates and the true values were computed. Table 1 summarizes the results of the simulation study with N = 200. Both BIAS and RMS values were quite small, indicating that the Bayesian estimates of the unknown parameters are generally accurate. Additionally, it can be seen that for the given level of sample size, the Bayesian estimates perform well under different prior inputs, suggesting that the analysis results are not sensitive to how prior inputs are specified. The result for N = 500 is similar to that for N = 200. Briefly, for most unknown parameters, the BIAS, SE and RMS reduced when sample size was increased to N = 500. To save space, we do not present the full result for N = 500.

Table 1.

Summary Statistics for Bayesian Estimates Under Perturbation Input I and II Priors (N=200, Covariance Lasso Prior)

		Perturbed Input I			Perturbed Input II
Par	True	BIAS	SE	RMS	BIAS	SE	RMS
μ1	0.5	−0.008	0.083	0.086	−0.017	0.083	0.086
μ2	0.5	−0.011	0.071	0.074	−0.019	0.071	0.074
μ3	0.5	−0.006	0.062	0.054	−0.011	0.062	0.054
μ4	0.5	0.001	0.062	0.074	−0.004	0.062	0.073
μ5	0.5	−0.004	0.055	0.054	−0.008	0.055	0.054
μ6	0.5	−0.011	0.083	0.082	−0.021	0.081	0.083
μ7	0.5	−0.014	0.071	0.068	−0.022	0.071	0.069
μ8	0.5	0.001	0.072	0.068	−0.008	0.071	0.068
μ9	0.5	0.002	0.062	0.063	−0.003	0.062	0.063
μ10	0.5	0.003	0.055	0.058	0.001	0.055	0.058
λ21	0.8	0.006	0.045	0.034	0.007	0.045	0.034
λ31	0.5	0.059	0.135	0.094	0.063	0.136	0.094
λ41	0.5	−0.003	0.094	0.067	−0.001	0.095	0.065
λ51	0.3	0.063	0.124	0.095	0.067	0.125	0.098
λ72	0.8	0.010	0.043	0.031	0.010	0.042	0.031
λ82	0.8	0.036	0.124	0.093	0.039	0.123	0.095
λ92	0.5	−0.006	0.084	0.053	0.005	0.084	0.054
λ10,2	0.3	0.082	0.127	0.118	0.084	0.127	0.120
ψ11	0.36	0.035	0.143	0.101	0.039	0.145	0.102
ψ22	0.36	0.017	0.103	0.072	0.018	0.103	0.073
ψ33	0.50	−0.028	0.106	0.062	−0.030	0.107	0.062
ψ44	0.50	0.011	0.082	0.056	0.010	0.082	0.056
ψ55	0.50	−0.031	0.079	0.062	−0.033	0.080	0.063
ψ66	0.36	0.016	0.132	0.098	0.018	0.132	0.096
ψ77	0.36	0.008	0.095	0.064	0.008	0.095	0.062
ψ88	0.36	−0.016	0.134	0.060	−0.019	0.113	0.061
ψ99	0.50	0.018	0.076	0.058	0.017	0.076	0.057
ψ10,10	0.50	−0.042	0.083	0.074	−0.044	0.084	0.075
ψ16	0.3	−0.051	0.102	0.096	−0.049	0.102	0.095
ψ27	0.3	−0.034	0.075	0.065	−0.034	0.075	0.064
ψ35	0.3	−0.045	0.085	0.065	−0.047	0.086	0.066
ψ8,10	0.3	−0.065	0.100	0.086	−0.067	0.101	0.087
ϕ11	1.0	0.002	0.168	0.106	−0.001	0.170	0.107
ϕ21	0.3	0.039	0.115	0.091	0.038	0.114	0.092
ϕ22	1.0	0.009	0.164	0.120	0.007	0.163	0.119

We also compared the performance of the Bayesian CFA that used the proposed Lasso prior to a standard Wishart prior distribution using the same simulated data sets. The simulation experiment, which is not fully reported here due to space limitations, suggests that the proposed Lasso prior distribution performs better than the Wishart prior in terms of bias and RMS. For example, in N = 200 and 500, compared with the Wishart prior, the L₁ loss for the Bayesian Lasso method was respectively reduced by 67% and 75%. The better performance of the Lasso prior may be due to (1) the priors were applied to correctly specified models and the Lasso prior expects the covariance structure to be sparse, which is indeed the case, and (2) the flexibility of the Lasso prior as compared to the Wishart prior, which tends to concentrate probability mass at the expected value.

Study 2: The Power of Detecting Significant Residual Covariances and the Potential Problem of Capitalization on Chance

Simulation Study 2 evaluates the performance of the proposed model in detecting genuine nonzero residual covariances and investigates the extent of capitalization on the chance the proposed model may suffer from as pointed out by MacCallum (1986) and thus both power and Type I error rates will be examined. A data set was simulated based on the model structure specified with the number of observed variables set at p = 10 and the number of factors set at q = 2. Two residual correlations ψ₁₆ and ψ₂₇ were set to non-zero values. The set-up is visualized in Fig. 2(b). Two levels of factor loadings (0.5, 0.8), two levels of factor correlation (0.3, 0.7), and three levels of residual correlation (0.0, 0.3 and 0.7) were specified, resulting in a total of 2 × 2 × 3 = 12 different conditions. A sample size of 250 was used for all the conditions and 100 replications were generated for each condition. For each condition, power for detecting individual nonzero residual correlation ψ₁₆ and ψ₂₇ as well as the average Type I error rate over zero residual correlations was calculated based on the 100 replications. The results are summarized in the top half of Table 2. It can be seen that in general the power of detecting ψ₁₆ and ψ₂₇ is satisfactory except for ψ₂₇ under conditions 5 and 7, of which residual correlations are at the lower level of 0.3. By comparing these results to the patterns of other conditions of which residual correlation is low, we suspected that lower power is due to the larger ratio between factor loading (0.8) and residual correlation (0.3). In order to test this hypothesis, four additional settings (13–18) were considered for different levels of factor loading (0.3, 0.5, 0.8) and one level of residual correlation (0.2). The results are reported in the bottom half of Table 2. It seems plausible that a low ratio of residual correlation and factor loading would result in low power.

Table 2.

Power of Detecting the Significant Residual Covariances and the Average of Type I Error Rates of Falsely Detecting the Nonsignificant Residual Covariances

	Loading	Factor Corr.	Residual Corr.	Power1	Power2	Ave.Type I
1.	0.5	0.3	0.3	0.99	0.90	1.76%
2.	0.5	0.3	0.7	1.00	1.00	3.27%
3.	0.5	0.7	0.3	1.00	0.91	2.08%
4.	0.5	0.7	0.7	1.00	1.00	7.88%
5.	0.8	0.3	0.3	0.74	0.47	1.00%
6.	0.8	0.3	0.7	1.00	1.00	1.29%
7.	0.8	0.7	0.3	0.76	0.56	0.00%
8.	0.8	0.7	0.7	1.00	1.00	1.00%
9.	0.5	0.3	0.0	-	-	1.53%
10.	0.5	0.7	0.0	-	-	2.12%
11.	0.8	0.3	0.0	-	-	1.00%
12.	0.8	0.7	0.0	-	-	1.00%
13.	0.3	0.3	0.2	0.86	0.78	1.91%
14.	0.3	0.7	0.2	0.95	0.91	5.19%
15.	0.5	0.3	0.2	0.77	0.49	1.73%
16.	0.5	0.7	0.2	0.87	0.52	1.78%
17.	0.8	0.3	0.2	0.22	0.15	1.00%
18.	0.8	0.7	0.2	0.21	0.19	1.00%
19.	0.3	0.3	0.7	1.00	1.00	3.12%
20.	0.3	0.7	0.7	1.00	1.00	7.75%

Note:

Power1: The power of detecting the significance of ψ₁₆.

Power2: The power of detecting the significance of ψ₂₇.

Ave.Type I: The average of Type I error rates for falsely detecting the nonsignificant residual covariances.

For Type I error rates — i.e., capitalization on chance when residual correlation is actually zero — the results in Table 2 reveal that the Bayesian covariance Lasso CFA procedure can maintain detection of spurious nonzeros at approximately the nominal rate of 5%. When both the correlation between the factors and the residual correlation are high (conditions 4 and 20), the Type I error rate tends to elevate slightly above the nominal rate.

Study 3: Diagnostic Tool for Misspecification with Cross-loading

Because the CFA is a strong model that places strict assumptions on the pattern of factor loading, it is prone to misspecification. For example, an item may cross-load on more than one factor. The performance of the Bayesian Lasso under such a situation would be of interest because residual correlations may manifest and sound an alarm. Thus, a study of the performance of the Bayesian covariance Lasso under a misspecified model is important for an understanding of the relationship between the various model components as well as potential use as a diagnostic tool.

We conducted a simulation experiments for two scenarios of misspecification with cross-loading. A data set was simulated based on the model specified in Eq. 2 with the number of observed variables set at p = 6 and the number of factors set at q = 2. It was assumed that Λ contained the following overlapping structure:

$${\mathbf{\Lambda }}^T=\left(\begin{array}{cccccc}1.0& 0.8& 0.8& 0.0& 0.0& 0.0\\ 0.0& {\lambda }_{22}& 0.0& 1.0& 0.8& 0.8\end{array}\right),$$

where the 1’s and 0’s are fixed for identification purpose, and Ψ is assumed to be a diagonal matrix. Item 2 is cross-loaded on both factors 1 and 2 with respective loadings of 0.8 and λ₂₂. The model structure is visualized in Fig. 2(c). Four settings were considered: {λ₂₂ = 0.3, N = 250}, {λ₂₂ = 0.3, N = 500}, {λ₂₂ = 0.8, N = 250}, and {λ₂₂ = 0.8, N = 500}. For each setting, 100 replications were generated. The data set was analyzed under the proposed CFA model with the Bayesian covariance Lasso prior and the following non-overlapping factor structure of Λ:

$${\mathbf{\Lambda }}^T=\left(\begin{array}{cccccc}1.0& {\lambda }_{21}& {\lambda }_{31}& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 1.0& {\lambda }_{52}& {\lambda }_{62}\end{array}\right).$$ (4)

Due to space limitations, we only report the full results for the high cross-loading cases of which λ₂₂ = 0.8 with N=500, and highlight findings for N=250, as well as for the low cross-loading cases of which λ₂₂ = 0.3. Table 3 reports the patterns of significant residual covariances detected in the 100 replications. The most frequently detected significant residual covariances were {ψ₄₂, ψ₅₂, ψ₆₂} (across factor 1 and 2), and {ψ₅₄, ψ₆₄, ψ₆₅} (within factor 2). It can be seen that when the cross-loading for item 2 is substantial (λ₂₂ = 0.8) and the sample size is N=500 (250), the total numbers of significant residual covariances for ψ₄₂, ψ₅₂, ψ₆₂, ψ₅₄, ψ₆₄, and ψ₆₅ are then respectively 97 (94), 99 (91), 99 (93), 99 (96), 98 (96), and 99 (97), all out of 100. (See Table 3.) The patterns reveal that when the Bayesian Lasso model was misspecified by treating λ₂₂ as zero, significant residual covariances are present between item 2 and the items that are loaded on factor 2 as well as the residual covariances amongst items that are on factor 2. Interestingly, the cross-loading (in this case item 2) appears to induce correlations to all of the item pairs within the factor to which the item belongs. When the cross-loading for item 2 is small (λ₂₂ = 0.3), the pattern of significant residual covariance is not as obvious. For example, the total number of significant residual covariances for the above parameters for N = 250 are 4, 4, 7, 5, 5, and 3, and for N = 500, 18, 17, 17, 21, 24, and 15. The Bayesian Lasso procedure is not powered to detect small residuals at these sample sizes. In summary, we observe that for both low and high cross-loading, when the sample size becomes larger, the trend of significant residual covariances becomes more apparent. When an item that belongs to a primary factor is cross-loaded on a different factor, it tends to “infect” all of the items within its primary factor. We conducted a separate experiment to examine more complex cross-loading. The patterns of residual covariances were consistent with what we observed but became more complex when the cross-loading patterns varied. The full results of the additional simulation experiments are not reported here.

Table 3.

Patterns of Significant Residual Covariances and the Total Number of Specific Patterns During 100 Replications (λ₂₂ = 0.8, N = 500).

	Pattern															Total1
	ψ21	ψ31	ψ32	ψ41	ψ42	ψ43	ψ51	ψ52	ψ53	ψ54	ψ61	ψ62	ψ63	ψ64	ψ65
	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	0	0	0	0	1	0	0	1	0	1	0	1	0	0	1	1
	0	0	0	0	0	0	0	1	0	1	0	1	0	1	1	2
	0	0	0	0	1	0	0	1	0	1	0	1	0	1	1	72
	0	0	0	0	1	0	1	1	0	1	0	1	0	1	1	1
	1	0	0	0	1	0	1	1	0	1	0	1	0	1	1	1
	0	0	0	0	1	0	0	1	0	1	1	1	0	1	1	2
	1	0	0	0	1	0	1	1	0	1	1	1	0	1	1	2
	1	0	0	1	1	0	1	1	0	1	1	1	0	1	1	3
	1	0	0	1	1	0	1	1	1	1	1	1	0	1	1	1
	1	0	0	0	1	0	1	1	0	1	0	1	1	1	1	1
	0	0	0	0	1	0	0	1	1	1	0	1	1	1	1	1
	0	0	1	0	1	1	0	1	1	1	0	1	1	1	1	1
	1	0	1	1	1	0	0	1	0	1	1	1	1	1	1	1
	1	0	0	1	1	0	1	1	0	1	1	1	1	1	1	1
	1	0	0	1	1	0	1	1	1	1	1	1	1	1	1	1
	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1
	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	7
Total2	19	0	10	14	97	9	19	99	12	99	19	99	14	98	99

Note: Each row corresponds to a pattern where “1” represents significance detected by 95% HPD.

Total1: The total number of specific pattern during 100 replications.

Total2: The total number of the significance of ψ during 100 replications.

Study 4: Analysis of Emotion with Bayesian Covariance Lasso CFA

The Bayesian covariance Lasso CFA, was applied to a data set collected from a study on emotions and diet in women (Lu, Huet, & Dubé, 2011). Data were collected from a sample of n = 186 Caucasian adult non-obese women in a large North American city. Participants, who were recruited through a local advertisement, all signed an informed consent form before engaging in the study. Each participant received a small incentive for participating. The study protocol was approved by the human subjects ethics committee of McGill University, Canada. Twenty-eight items were selected to cover the entire spectrum of positive and negative affects. The selected items were adapted from the Consumption Emotions Set (CES) (Richins, 1997), which includes 47 emotion descriptors (items) representing the broader range of emotions consumers most frequently experience in consumption situations. To keep the questionnaire concise, Lu, Huet, and Dubé (2011) selected 28 emotion items that were found most relevant to food consumption from the literature on eating behaviors (Canetti, Bachar, & Berry, 2002) and excluded those less eating-relevant emotion items. Participants were asked to indicate the degree to which they experienced each of the emotions at the present moment by placing a mark on a 15-cm visual analogue scale with 0 cm indicating “don’t feel the emotion at all” and 15 cm indicating “feel it intensely.” The scales were then transformed into numerical scales ranging from 0 to 150 mm with 1-mm gradations. Each participant reported her emotional states every 2 hour, 6 times per day over 10 observation days. In the current study, the response data from the third time point of observation were used to demonstrate the proposed method.

For the data used in the current study, out of 186 participants, n = 11 of cases were deemed to have high proportions (60% or more) of missing values were not included in the analysis, resulting in a sample size of n = 175. Six participants had 3.6% and one participant had 25% of missing values in their responses. The missing values were assumed to be MAR and the Gibbs sampler scheme imputed values for the missing data in our implementation (see Section on Gibbs sampler). All raw data were treated as continuous and standardized.

To conduct the proposed Bayesian covariance Lasso CFA, we first needed to determine the factor structure of the items. Arguably, the CES contains the most extensive list of emotion descriptors of emotions. However, the number of identified emotion factors (hereafter called emotions) in either valence — positive emotion (PE) or negative emotion (NE) — are substantial in the CES. Table 4 contains the list of identified emotions and emotion descriptors from CES. Although prior work on eating-related emotion has identified four to six emotions, only a few used a two-factor model of positive and negative emotional valence (e.g., Han & Back, 2008). Macht (1999) reported that four emotions — joy, anger, fear, sadness — could change the characteristics of eating. In a study of eating in everyday life, Macht & Simons (2000) found 6 emotions that covered different emotional states relaxation, joy, anger, sadness, and tension. In the original analytic work in Lu, Huet, and Dubé (2011), a total of 28 items (emotion descriptors) and 5 emotions were represented by the following descriptors and identified in a CFA happy, peaceful, angry, ashamed, and worried. A comparison of the 5 identified factors to the CES emotions is provided in Table 4.

Table 4.

Identified Emotion Factors and Emotion Descriptors.

Emotions in the Consumption Emotions Set	Emotions in Lu et al.’s paper	Emotions in 6-factor model
Positive emotions:
Joy: Happy; Joyful; Pleased Love: Loving; Sentimental; Warmhearted Optimism: Optimistic; Encouraged; Hopeful Contentment: Contented; Fulfilled Peacefulness: Calm; Peaceful; Romantic love: Sexy; Romantic; Passionate Excitement: Excited; Thrilled; Enthusiastic Surprise: Surprised; Amazed; Astonished	Happy/Joyful: Happy; Joyful; Elated; Amused; Loving; Sentimental; Warm-hearted; Optimistic; Encouraged; Hopeful; Fulfilled; Accomplished Peaceful: Calm; Peaceful; Serene; Contented	Joyful: Joyful; Elated; Amused; Loving; Sentimental; Warm-hearted; Optimistic; Encouraged; Hopeful; Contented: Contented; Fulfilled; Accomplished Peaceful: Calm; Peaceful; Serene
Negative emotions:
Sadness: Depressed; Sad; Miserable Anger: Frustrated; Angry; Irritated Worry: Nervous; Worried; Tense Shame: Embarrassed; Ashamed; Humiliated Envy: Envious; Jealous Discontent: Unfulfilled; Discontented Loneliness: Lonely; Homesick Fear: Scared; Afraid; Panicky Others: Guilty; Proud; Eager; Relieved	Angry: Depressed; Sad; Miserable; Frustrated; Angry; Annoyed Worried: Nervous; Worried; Tense Ashamed: Embarrassed; Ashamed; Guilty	Angry: Depressed; Sad; Miserable; Angry; Happy Worried: Frustrated; Annoyed; Nervous; Worried; Tense Ashamed: Embarrassed; Ashamed; Guilty

Partly because the focus of Lu, Huet, and Dubé (2011) was to test how location (home vs. away-from-home) moderated the relationship between emotion and food choice, some low-arousal positive emotions such as peaceful and calm that were often experienced at home were included while other positive emotions not directly related to this context such as surprised and amazed were not included. On the other hand, negative emotions such as guilty and ashamed have been known to be associated with overeating and junk food consumption. The ashamed factor in the 5-factor solution (Table 4) reflects this salient feature of the study. While the original CFA in Lu, Huet, and Dubé (2011) appears to have some limitations (e.g., the use of an averaged data set), as pointed out by a reviewer, we followed the 5-factor model for our illustration of the Bayesian covariance Lasso CFA after examining the emotion structure and seeing its agreement with the CES. In the next section we provide alternative factor analyses of the same data set and compare the results to the 5-factor CFA.

In summary, the Bayesian covariance Lasso CFA that we considered is defined in Eq. 2 with p = 28, q = 5. The PE factors were labeled Happy/Joyful (ξ₁; 12 items), Peaceful (ξ₂; 4 items), and the NE factors were labeled Angry/Depressed (ξ₃; 6 items), Ashamed (ξ₄; 3 items), and Worried/Tense (ξ₅; 3 items). A non-overlapping factor structure of Λ with fixed zero entries at the appropriate positions and the covariance matrix among the factors Φ can be expressed as follows:

$$\mathbf{\Lambda }=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ {\lambda }_{21}& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ {\lambda }_{12,1}& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& {\lambda }_{14,2}& 0& 0& 0\\ 0& {\lambda }_{15,2}& 0& 0& 0\\ 0& {\lambda }_{16,2}& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& {\lambda }_{18,3}& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& {\lambda }_{22,3}& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& {\lambda }_{24,4}& 0\\ 0& 0& 0& {\lambda }_{25,4}& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 0& 0& {\lambda }_{27,5}\\ 0& 0& 0& 0& {\lambda }_{28,5}\end{array}\right),\mathbf{\Phi }=\left(\begin{array}{ccccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}& {\varphi }_{14}& {\varphi }_{15}\\ {\varphi }_{21}& {\varphi }_{22}& {\varphi }_{23}& {\varphi }_{24}& {\varphi }_{25}\\ {\varphi }_{31}& {\varphi }_{32}& {\varphi }_{33}& {\varphi }_{34}& {\varphi }_{35}\\ {\varphi }_{41}& {\varphi }_{42}& {\varphi }_{43}& {\varphi }_{44}& {\varphi }_{45}\\ {\varphi }_{51}& {\varphi }_{52}& {\varphi }_{53}& {\varphi }_{54}& {\varphi }_{55}\end{array}\right).$$

Following common practice in CFA, each factor contained a loading value of one for one of the measurement variables for the identification of the scale of the latent factor.

The following hyperparameter values were used in the analysis: μ₀ and Λ_0k fixed at vector 0, H_μ0, H_0k fixed at four times the identity matrices with appropriate dimensions, and ρ₀ = 12, R₀ = 6I, α_λ0 = 1, and β_λ0 = 0.01.

To assess the convergence behavior of the Gibbs sampler in the analysis, the EPSR values of the parameter sequences using different starting values were calculated, which suggested that the Gibbs sampler converged in fewer than 3,000 iterations. In our actual implementation, the Bayesian analysis results were obtained using 20,000 simulated draws from the posterior distributions subsequent to a burn-in period of 5,000 iterations. The program is written in R (R Core Team, 2013). Conducting the real data analysis using a PC with Intel Core i7-2600@3.40 GHz CUP and 8G RAM took about 45 minutes. Sample codes for fitting the Bayesian covariance Lasso CFA to the emotion data are included in Supplementary Materials Section 2 on the journal website.

For the proposed Bayesian Lasso model, the PP p-value was 0.517, providing evidence that the model fitted reasonably well to the sample data. The Bayesian estimates of the unknown parameters in Λ, Φ, the diagonal elements in Ψ, and their corresponding 95% Highest Posterior Density (HPD) intervals are presented in Table 5. It can be seen that all factor loading estimates are statistically significant and substantial in magnitude, which suggest strong associations between the latent factors and their corresponding indicators. As expected, from the estimates of ϕ_ij ’s, the PE factors are positively correlated, the NE factors are positively correlated, and the PE factors and NE factors are negatively correlated.

Table 5.

Bayesian Estimates (Est) of the Unknown Parameters in Λ, Φ, the Diagonal Elements in Ψ, and Their Corresponding 95% HPD Intervals in Real Data

Item	Est of λ	HPD of λ	Est of ψkk	HPD of ψkk
1.Joyful	1.000*	-	0.497	(0.349, 0.641)
2.Happy	0.780	(0.583, 0.963)	0.670	(0.487, 0.859)
3.Elated	0.840	(0.623, 1.055)	0.648	(0.497, 0.819)
4.Amused	0.735	(0.523, 0.942)	0.728	(0.547, 0.907)
5.Optimistic	1.067	(0.848, 1.303)	0.423	(0.289, 0.561)
6.Hopeful	1.056	(0.822, 1.309)	0.436	(0.304, 0.582)
7.Encouraged	1.038	(0.803, 1.270)	0.457	(0.324, 0.594)
8.Fulfilled	0.972	(0.758, 1.186)	0.518	(0.371, 0.678)
9.Accomplished	0.967	(0.755, 1.190)	0.526	(0.384, 0.681)
10.Warm-hearted	1.102	(0.876, 1.337)	0.410	(0.289, 0.548)
11.Loving	1.020	(0.792, 1.255)	0.490	(0.356, 0.638)
12.Sentimental	0.758	(0.540, 0.995)	0.722	(0.554, 0.908)
13.Serene	1.000*	-	0.338	(0.227, 0.469)
14.Calm	0.925	(0.756, 1.101)	0.441	(0.307, 0.590)
15.Peaceful	0.998	(0.844, 1.168)	0.336	(0.211, 0.473)
16.Contented	0.774	(0.579, 0.989)	0.610	(0.433, 0.797)
17.Frustrated	1.000*	-	0.338	(0.210, 0.465)
18.Annoyed	0.984	(0.830, 1.131)	0.373	(0.240, 0.511)
19.Angry	0.718	(0.533, 0.917)	0.631	(0.471, 0.810)
20.Miserable	0.635	(0.424, 0.877)	0.684	(0.491, 0.886)
21.Sad	0.573	(0.374, 0.779)	0.734	(0.540, 0.935)
22.Depressed	0.763	(0.566, 0.975)	0.583	(0.405, 0.764)
23.Ashamed	1.000*	-	0.462	(0.270, 0.659)
24.Guilty	0.840	(0.551, 1.135)	0.595	(0.384, 0.818)
25.Embarrassed	0.694	(0.413, 0.973)	0.707	(0.492, 0.940)
26.Nervous	1.000*	-	0.277	(0.188, 0.374)
27.Tense	1.001	(0.860, 1.137)	0.241	(0.157, 0.339)
28.Worried	0.951	(0.818, 1.082)	0.302	(0.202, 0.407)

Par	Est	HPD
ϕ11	0.547	(0.367, 0.742)
ϕ22	0.688	(0.478, 0.897)
ϕ33	0.719	(0.522, 0.933)
ϕ44	0.610	(0.388, 0.851)
ϕ55	0.782	(0.585, 1.013)
ϕ21	0.403	(0.265, 0.538)
ϕ31	−0.143	(−0.252, −0.036)
ϕ32	−0.264	(−0.398, −0.136)
ϕ41	−0.068	(−0.173, 0.042)
ϕ42	−0.145	(−0.275, −0.017)
ϕ43	0.330	(0.193, 0.470)
ϕ51	−0.135	(−0.252, −0.022)
ϕ52	−0.250	(−0.382, −0.118)
ϕ53	0.622	(0.459, 0.796)
ϕ54	0.379	(0.232, 0.536)

Note: The items with asterisks are fixed to identify the scale of the latent factor. PE-general: items 1–12; PE-peacefulness: items 13–16; NE-general: items 17–22; NE-shame: items 23–25; NE-worry: items 26–28.

Altogether, 29, or 7.6% significant residual covariance estimates ψ_ij (i < j) resulted out of 378 (= C(28, 2)) in Ψ. Table 6 reports the 95% HPD intervals of significant residual covariances between pairs of observed variables. The results show that after conditioning on the PE and/or NE factors, dependence between measurements—some within the same factor and some between factors — remains. The strongest covariances are observed for the within-factor item pair Miserable/Sad (0.30), and Angry/Miserable (0.25) (for NE), and Fulfilled/Accomplished (0.20), and Joyful/Happy (0.16) (for PE). Some cross-factor negative correlations, for example Happy/Sad (−0.27), and Happy/Depressed (−0.2), are also noted.

Table 6.

The Significant Residual Covariance Estimates (Est) and Their Corresponding 95% HPD Intervals in Real Data

Residual Covariance	Est	HPD
Joyful with Happy	0.157	(0.030, 0.296)
Happy with Amused	0.140	(0.004, 0.270)
Happy with Sentimental	−0.123	(−0.234, −0.008)
Happy with Contented	0.130	(0.006, 0.260)
Happy with Miserable	−0.162	(−0.280, −0.043)
Happy with Sad	−0.266	(−0.401, −0.132)
Happy with Depressed	−0.200	(−0.323, −0.073)
Elated with Amused	0.160	(0.038, 0.298)
Optimistic with Hopeful	0.121	(0.009, 0.232)
Optimistic with Guilty	−0.111	(−0.217, −0.015)
Hopeful with Encouraged	0.112	(0.010, 0.226)
Fulfilled with Accomplished	0.198	(0.078, 0.330)
Fulfilled with Contented	0.163	(0.048, 0.284)
Fulfilled with Sad	−0.108	(−0.222, −0.002)
Accomplished with Loving	−0.093	(−0.186, −0.009)
Accomplished with Contented	0.128	(0.020, 0.241)
Loving with Frustrated	0.086	(0.001, 0.169)
Sentimental with Sad	0.176	(0.050, 0.298)
Contented with Sad	−0.159	(−0.287, −0.045)
Annoyed with Depressed	−0.098	(−0.193, −0.009)
Angry with Miserable	0.245	(0.087, 0.392)
Angry with Sad	0.139	(0.008, 0.284)
Angry with Embarrassed	0.222	(0.093, 0.359)
Miserable with Sad	0.304	(0.140, 0.476)
Miserable with Depressed	0.180	(0.034, 0.337)
Miserable with Embarrassed	0.224	(0.090, 0.365)
Sad with Depressed	0.226	(0.070, 0.383)
Sad with Worried	0.112	(0.007, 0.237)
Guilty with Embarrassed	0.227	(0.047, 0.409)

Comparison with Other Factor Analytic Models

To gain a deeper understanding of the behavior of the Bayesian covariance Lasso model, the following CFA models were used in the comparison: the 5-factor CFA model with the Bayesian covariance Lasso prior (M₁), the 5-factor CFA model with diagonal Ψ (M₂), and a CFA model with diagonal Ψ (M₃), whose number of factors would be determined by an EFA. For the model (M₃), the EFA (with oblique rotation), based on factors with eigenvalues > 1, revealed a 6-factor structure (Table 4). The 6-factor structure agreed reasonably well with the emotions identified in the CES. Two observations were made. First, compared to the 5-factor model, Fulfilled and Accomplished from the factor Happy/Joyful, together with Contented from the factor Peaceful, were separated out as a distinct factor. Second, the item Happy, to our surprise, was loaded in the Angry factor with high negative loading. Referring to Table 6, most of the significant residual covariances found in M₁ were among these items. In other words, if one is willing to let the data select the number of factors (via EFA), additional factors that group observed measurements with high error covariance would be revealed. The total explained variance of the 6-factor structure was 70.40%, compared with 66.49% in the 5-factor structure (M₂). Hereafter, M₃ refers to the 6-factor CFA model with diagonal Ψ.

We applied multiple criteria to ascertain the quality of the three comparison models. First we examined traditional goodness-of-fit indexes. Several model fit indices, which are commonly reported in SEM software such as Mplus (Muthén and Muthén, 1998–2013), are presented in Table 7. The results indicate that neither 5-factor diagonal model M₂ nor the 6-factor diagonal M₃ fit the data very well, although the 6-factor model is slightly better than the 5-factor model. Model M₁, which contains 29 significant residual covariances as identified by the Bayesian covariance Lasso, fitted the data better in terms of all of the conventional fit indices (Table 7). For example, the RMSEA of M₃ is only approximately half of that of either the 5- and 6-factor diagonal models, and the CFI of M₃ is higher than the cutoff of 0.9 while the other two models were below.

Table 7.

Goodness-of-fit Statistics of Different Models Fitted to the Emotion Data by Mplus

	AIC	BIC	RMSEA	CFI	TLI	SRMR
5-factor with diagonal Ψ	11504.630	11802.120	0.103	0.797	0.775	0.074
6-factor with diagonal Ψ	11440.847	11754.161	0.098	0.819	0.796	0.090
5-factor with 29 residual covariances	10907.638	11292.615	0.054	0.925	0.909	0.065

Note: AIC: Akaike Information Criterion; BIC: Bayesian Information Criterion; RMSEA: Root Mean Square Error of Approximation; CFI: Comparative Fit Index; TLI: Tucker Lewis Index; SRMR: Standardized Root Mean Square Residual.

For both TLI and CFI, 0.9 represents adequate fit and 0.95 good fit. RMSEA < 0.05 indicates good fit, between 0.05 and 0.08 acceptable fit. SRMR < 0.08 considered adequate. For AIC and BIC, smaller value indicates better fit.

We further examined the impact of relaxing the diagonality requirement of the covariance on model goodness-of-fit in terms of differences in observed and expected (fitted) correlations between pairs of measurements. Various similar diagnostics have been proposed for latent class models; see for example, Garrett and Zeger (2000), and Reboussin, Ip, and Wolfson (2008). Unlike a latent class analysis that focuses on binary indicators, the CFA model contains continuous indicators. We defined an analogous version of Reboussin, Ip, and Wolfson’s (2008) log-odds-ratio check as follows:

$$z_{ij}=\frac{r_{ij}^{\mathit{obs}}-r_{ij}^{\mathit{est}}}{{\sigma }_{ij}^{\mathit{est}}},$$ (5)

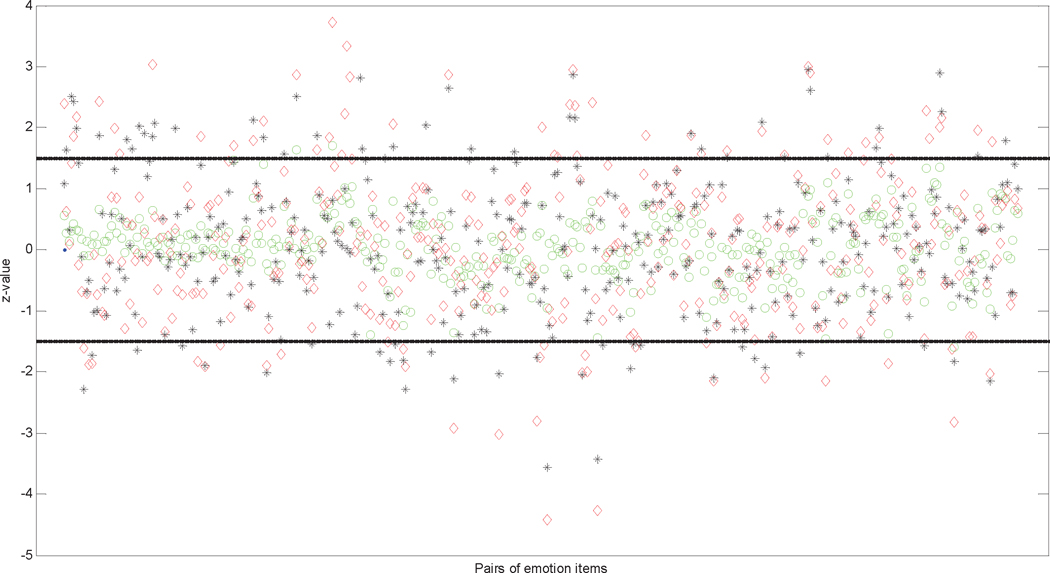
where $r_{ij}^{\mathit{obs}}$ is the correlation coefficient between item i and item j calculated from the observed data, and $r_{ij}^{\mathit{est}}$ and ${\sigma }_{ij}^{\mathit{est}}$ are, respectively, the Bayesian estimates of the correlation coefficient between item i and item j and the corresponding standard error estimates calculated from the simulated samples of the parameters. The idea behind the use of the z-value is that if the model is correctly specified, the observed and expected correlations between pairs of measurements in a covariance structure analysis should be close. In other words, a z-value plot can be used as a visual tool for assessing what might have gone wrong at the item-pair level. As suggested by Reboussin, Ip, and Wolfson (2008), the relative magnitude of the z-values were examined and threshold levels of ±1.5 were used for determining a significant deviation. A model that produces many large z-values would suggest that the model could be misspecified.

For these three comparison models, Fig. 3 displays the z-values for different pairs of emotion items among the 28 emotion items. Under model M₂, there is strong evidence that dependence exists between many pairs of items. Increasing the number of factors to 6 (M₃) apparently reduces the number of large z-values. Additionally, the proposed model M₁ results in smaller z-values and no z-value exceeds the threshold of 1.5 in either direction. In other words, M₁ (5-factors with residual correlation) fits the data well and the fit is comparable, if not superior to, M₃ (6 factors with no residual correlation).

Figure 3.

z-values for the 5-factor CFA model with a covariance Lasso prior (o), the 5-factor CFA model with diagonal Ψ (◇), and the 6-factor CFA model with diagonal Ψ (*) fitted to the emotion data. The z-value is calculated for each pair of the 28 emotion items.

A conundrum that a researcher using factor analytic method often faces is that, while more factors can help to achieve a better fit, some factors may not be of substantive interest. As a highly restrictive model, the CFA requires that the number of factors and to which factor an item belongs are predetermined, and that no correlation between item pairs is allowed given the factor structure. As demonstrated by the emotion example of 28 items, result from data analysis may not perfectly agree well with a theory-guided factor structure. While increasing the number of factors (from 5 to 6 in the emotion example) could improve goodness-of-fit, the interpretation of the model becomes less clear as one of the factor contains both PE (Happy) and NE (Angry) emotions. The previous analysis and comparison are not meant to be support one theory over another; the purpose is to demonstrate that the relaxation of the diagonal assumption of the covariance matrix by replacing the covariance with a sparse structure can be used as an approximation to the theory. The solution keeps the factor structure intact and moves the solution empirically closer to real data. The empirical example also shows how the Bayesian covariance Lasso CFA can be used as a diagnostic tool. First, if a large number of significant residual covariance terms are present relative to the size of the matrix, or large individual covariances exist, it would then suggest that the entire CFA approach needs to be revised, or that additional steps need to be taken, such as removing items. Although we are not aware of any existing guideline for how large is “large,” without controlling for multiple comparisons, we would surmise that > 10% of significant covariances or absolute values of correlation > 0.5 should raise serious concern. Further studies are needed to provide guidelines for determining when an CFA needs to be refuted. The emotion example here shows weak-to-moderate residual covariances between some item pairs that signifies a certain level of item redundancy within the same factor. However the covariances do not appear to suggest a high level of clustering within and across factors. We suspect that a residual dependence between some item pairs arises partly because participants were unable to clearly distinguish certain descriptors of emotions that only have subtle differences in meaning — e.g., Miserable and Sad, and Optimistic and Hopeful.

Study 5: Bias Reduction in Structural Equation Models

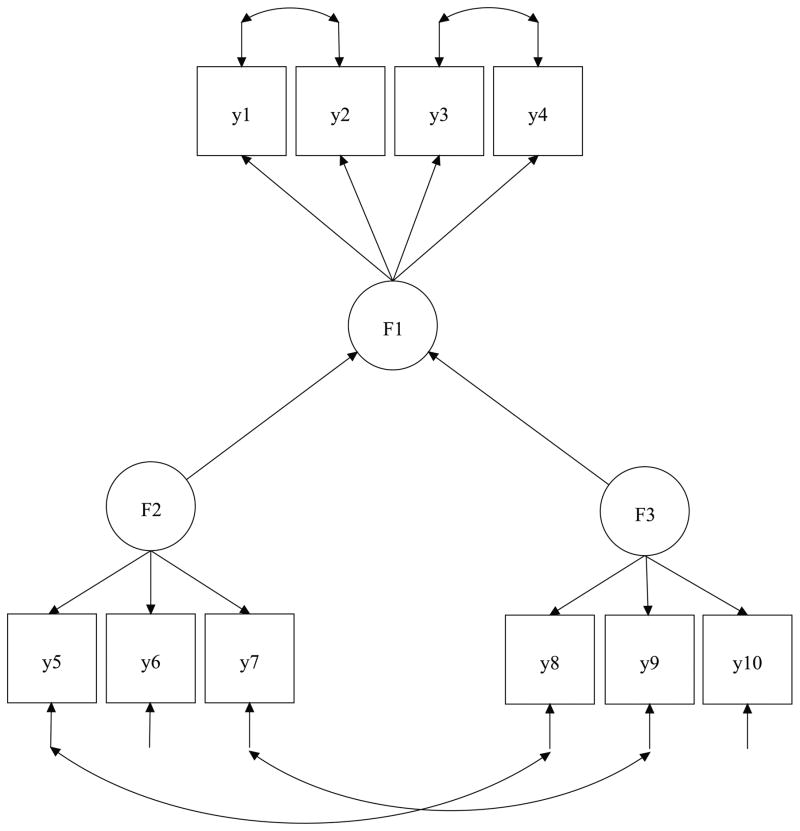
To illustrate the bias propagation problem for SEM and how the Bayesian covariance Lasso method can reduce bias in SEM parameter estimates, we simulated response data using a simple SEM example. The path diagram of the model is presented in Fig. 4. The SEM involves 10 observed variables that are related with 3 latent factors ω_i = (η_i, ξ_i1, ξ_i2), where η_i is endogenous factor, and ξ_i1 and ξ_i2 are exogenous factors that follow a bivariate normal distribution with mean zero and variance-covariance Φ. The specification of Λ and Φ, and the values of their parameters are given by:

$${\mathbf{\Lambda }}^T=\left(\begin{array}{cccccccccc}1.0& 0.8& 0.5& 0.3& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 1.0& 0.5& 0.8& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 1.0& 0.8& 0.5\end{array}\right),\mathbf{\Phi }=\left(\begin{array}{cc}1.0& 0.3\\ 0.3& 1.0\end{array}\right),$$

where the 1’s and 0’s in Λ are fixed for identification purpose. μ = (μ₁, μ₂, ⋯, μ₁₀)^T = (0.5, 0.5, ⋯, 0.5)^T and

Figure 4.

Model Structure in Simulation Study 5.

$$\mathbf{\Psi }=\left(\begin{array}{cccccccccc}0.36& 0.30& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.30& 0.36& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.36& 0.30& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.30& 0.36& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.36& 0.0& 0.0& 0.30& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.36& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.36& 0.0& 0.30& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.30& 0.0& 0.0& 0.36& 0.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.30& 0.0& 0.36& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.0& 0.36\end{array}\right).$$

All elements in Ψ were considered free parameters and estimated accordingly. The structural component of the generative model is given by the regression equation:

$${\eta }_i={\gamma }_1{\xi }_{i1}+{\gamma }_2{\xi }_{i2}+{\delta }_i,$$

where γ₁ = 0.6, γ₂ = −0.6, and δ_i follows a normal distribution with mean 0 and variance 0.36. Two levels of sample sizes were used, N = 200 and N = 500, and for each sample size 100 replications were generated. The generated data was analyzed by two models: SEM with the proposed Lasso prior to Ψ and SEM with the diagonal Ψ. Based on the 100 replications, bias, SE, and RMS values were computed. Table 8 shows the results for the parameters of interest γ₁ and γ₂.

Table 8.

Summary Statistics for Bayesian Estimates under SEM with the proposed Lasso prior to Ψ and SEM with the diagonal Ψ.

			N=200			N=500
	Par	True	BIAS	SE	RMS	BIAS	SE	RMS
SEM with Lasso prior to Ψ	γ1	0.6	0.033	0.085	0.087	0.028	0.065	0.063
	γ2	−0.6	−0.030	0.086	0.079	−0.035	0.066	0.068
SEM with diagonal Ψ	γ1	0.6	0.149	0.089	0.173	0.122	0.056	0.136
	γ2	−0.6	−0.144	0.090	0.167	−0.133	0.056	0.143

Compared to results using diagonal covariance, the Bayesian Lasso method applied to Ψ results in smaller values in BIAS and RMS in the SEM regression parameters, suggesting that the Bayesian estimates of the γ’s are more accurate than those estimated by SEM with the diagonal Ψ. The simulation result here is not meant to fully capture the patterns of bias in SEM due to a violation of the diagonal error covariance assumption, but rather to illustrate the potential effects of the propagation of biases to other parts of the SEM and the reduction in propagation bias when the residual covariance is properly modeled.

Discussion

Whether using EFA or CFA, the goal of factor analysis is to explain the covariances between multiple observed variables by means of a small and known number of underlying latent variables, or factors (Bollen, 1989). From a purist point of view, the ideal factor structure for CFA would be one in which each measurement is loaded on only one factor, and the factors completely explain away the covariation in the measurements — i.e., the factors are independent and no correlated residual errors exist in the measurements. This kind of “ideal” CFA may not exist in reality, and if it does, a price has to be paid in terms of sacrifice of validity. The items written for attaining an ideal factor structure would likely be highly restrictive and lead to a construct that is too narrow to meaningfully function in practice —a phenomenon referred to by Ip (2010) as the validity-versus-dimensionality dilemma (the number of factors signifies the dimension of the model).

The dilemma can be examined by going back to a fundamental question: how do factor analytic models capture covariation amongst measured variables? In the current factor analysis literature, there is, in fact, more than one mechanism that can be utilized to explain measurement covariation. Three mechanisms have been identified: (C₁) latent factors, (C₂) correlation between factors, and (C₃) correlated residual error terms. For the ease of discussion, we call these covariation mechanisms. The mechanism C₂ is routinely implemented in CFA, and its presence actually implies that observed variables that belong to different factors are conditionally correlated given the factors. See also Fabrigar et al. (1999) for a discussion of oblique versus orthogonal factors. Thus a purist would not have included C₂ in the CFA. In this sense, there is nothing magical about C₃, although its inclusion in the CFA often creates more controversy than its counterpart C₂. From a purist view, C₁ is the only signal and the other mechanisms should not happen — the noise component should be entirely captured by the variance of the error component. A more realistic view is that C₁ is a signal as per the researcher’s specification (based on theory), but noise does appear in various forms, including C₂ and C₃.

Modification Index and Implementation

Examining the MI procedure in Mplus as an example can illuminate how the covariation mechanisms, especially the way in which C₃ is handled in practice. Under the maximum likelihood framework, Mplus first fits a CFA with diagonal residual covariance matrix Ψ to the data and identifies a set of candidates for modification by applying a threshold to the MIs of all estimated pairwise residual covariances. In the analysis of the emotion data, Mplus produced 90 residual covariances of which the MI values were greater than the prescribed threshold value of 3.84. The number of residual covariances identified by PMM is substantially higher than that identified by the Bayesian Lasso procedure. If the PMM approach is to be fully implemented, one would begin with the largest MI of the 90 residual covariances, add the corresponding covariance term to the CFA, rerun the model, and examine the chi-squared test statistic. Rerunning the model is necessary because changing in a single parameter in a model could affect other parts of the solution (MacCallum, Roznowski, & Necowitz, 1992). The procedure thus has to be repeated many times, leading to a long series of modifications to the initial CFA model. While it is generally suggested that modifications should be used sparingly (MacCallum, 1995), no standard or guideline exists for choosing the number of modifications — only that the number probably should not be as high as 90 as our real data example suggested. Adding to the complexity of finding a rule for stopping model modification is the fact that adding off-diagonal entries to a positive definite covariance matrix may make it non-positive definite, a technical and highly challenging issue (Pourahmadi, 2011) in covariance estimation that cannot be satisfactorily solved by directly manipulating individual off-diagonal elements. Adding to the list of procedure woes is the incremental test statistic for MI, which is not exactly distributed as χ² with one degree of freedom when the statistic is based on a post-hoc model modification (Bentler, 2007). It is possible that the deviation is not substantial. However, it is not at all clear when the chi-squared distribution is a good approximation. As pointed out by Lu, Chow and Loken (2016), no sampling distribution is currently available for the purpose of quantifying the uncertainties associated with MIs, and model complexity is not explicitly accounted for in the use of MIs.

Post-Hoc Modification versus the Bayesian Lasso

The practical implementation of PMM described above makes it clear that researchers can, or are at least tempted to, selectively report incremental MI statistics that support their desired model. Researchers, of course, can be encouraged to provide justification of added parameters based on theory (MacCallum, 1995). However, as asked by Steiger (1990) in a rhetorical question regarding the PMM approach: “What percentage of researchers would ever find themselves unable to think up a theoretical justification for freeing a parameter?” If one assumes that the answer is near zero, as Steiger did, it means that different researchers could report different CFA models of different fit indices even when they apply the same method to the same data, which is an unflattering situation that is not beneficial to the scientific enterprise of psychology (Jackson, Gillapsy, & Purc-Stephenson, 2009).

The residual covariance matrix reveals important information about the quality of the CFA. Unfortunately, the matrix is often underreported in the literature. From our own experience with secondary data analysis, we suspect many studies using CFA contained substantial numbers of residual covariances that were either not carefully examined and ignored, or not reported. Unlike other goodness-of-fit indexes, the failure to report on residual covariance is often overlooked in the review process of CFA studies. McDonald & Ho (2002) encouraged SEM researchers to publish a correlation matrix and discrepancies as well as goodness of fit indexes “so that readers can exercise independent and critical judgment.” We believe that the same can be said about residual covariance.

From the covariation mechanism perspective, PMM represents a half-hearted effort that attempts to “fix” the lack of fit problem using a questionable covariance matrix modification technique, a questionable test statistic, and questionable tactics to achieve model parsimony. There are often “rules” and cautionary remarks about making minor tweaks using MIs, which are more or less reflections of the ad-hoc nature of the procedure and the ambiguity regarding what is considered a minor adjustment and sufficiently good fit. Indeed, the issue of false discovery of spurious residual covariance in PMM is technically challenging, partly because of the iterative nature of PMM. It was suggested that the temptation of tweaking more MIs of even better fit should be resisted because (a) overuse of modifications violates the purpose of CFA of precise theoretical propositions and the goal of parsimony, and (b) MIs are likely to include model improvement suggestions that are specific to the sample being examined (Bowen, 2014; Bowen & Guo, 2011). These are good points, but these concerns are precisely the reason modern statistics exist. Specifically, modern statistical techniques which appropriately penalizes overfitting to the sample data, have been extensively developed to address such problems. The Bayesian covariance Lasso CFA offers such a solution that has many practical and technical benefits and should be considered to be included into a quantitative psychologist’s toolbox.

Appendix

1. Gibbs sampler for Bayesian Covariance Lasso CFA

The Gibbs sampler used for the Bayesian covariance Lasso CFA model is better described as a block Gibbs sampler because a group of parameters can be simultaneously simulated from a multivariate conditional distribution. Let Y = (y₁, ⋯, y_n) be the observed data and Ω = (ω₁,…,ω_n) be the matrices of latent factors. The details of the block Gibbs sampler which is implemented by iteratively simulating observations from the full conditional distributions are provided as follows:

1. Generate Ω from p(Ω|Y,μ,Λ,Φ, Ψ);

2. Generate Λ from p(Λ|Y,Ω,μ,Φ, Ψ);

3. Generate Φ from p(Φ|Y,Ω,μ,Λ, Ψ);

4. Generate μ from p(μ|Y,Ω,Φ,Λ, Ψ);

5. Generate Σ from p(Σ|Y,Ω,μ,Λ,Φ, τ, λ) and compute Ψ = Σ⁻¹.

Except for p(Σ|Y,Ω,μ,Λ,Φ, τ, λ), the other conditional distributions are standard densities including the normal and inverse-Wishart distributions. Simulating observations from these standard distributions is generally straightforward and efficient. The details for both the standard and non-standard conditional distributions are given in Supplementary Materials Section 1 on the journal website. 39

2. Proof of Positive Definiteness of the Inverse Covariance Matrix Σ

Theorem

Suppose we start with a positive definite current value of Σ and sample from the Gibbs procedure described in Appendix 1. It is guaranteed that the positive definite constraint on Σ is maintained at all subsequent iterations.

Proof

Following the iterative block Gibbs sampler described in Appendix 1 and the specific conditional distributions in the Supplementary Materials Section 1 on the journal website, assume that at iteration t the value of Σ^(t) is positive definite. Therefore all of the leading principal minors of Σ^(t) are positive and so are all its diagonal elements.

Define

$$\mathbf{\sum }=\left(\begin{array}{cc}{\mathbf{\sum }}_{-kk}& {\mathit{\sigma }}_k\\ {\mathit{\sigma }}_k^T& {\sigma }_{kk}\end{array}\right).$$ (A1)

where σ_kk is the kth diagonal element of Σ, σ_k = (σ_k1, ⋯, σ_k,k−1, σ_k,k+1, ⋯, σ_kp)^T is the vector of all off-diagonal elements of the kth column, and Σ−_kk is the (p − 1) × (p − 1) matrix resulting from deleting the kth row and kth column from Σ. After updating the kth column ${({\mathit{\sigma }}_k^T,{\sigma }_{kk})}^T$, we only need to prove that ${\sigma }_{kk}^{(t+1)}$ is positive and |Σ^(t+1)| is positive.

Because ${\mathbf{\sum }}_{-kk}^{(t)}$ is positive definite, its inverse ${({\mathbf{\sum }}_{-kk}^{(t)})}^{-1}$ is also positive definite, so there exists a unique lower triangular matrix L with real and strictly positive diagonal elements, such that ${({\mathbf{\sum }}_{-kk}^{(t)})}^{-1}=\mathbf{L}{\mathbf{L}}^T$. For γ simulated from the prior distribution Gamma(α_λ0, β_λ0), the element ${\sigma }_{kk}^{(t+1)}=\gamma +{({\mathit{\sigma }}_k^{(t+1)})}^T{({\mathbf{\sum }}_{-kk}^{(t)})}^{-1}{\mathit{\sigma }}_k^{(t+1)}=\gamma +{({\mathit{\sigma }}_k^{(t+1)})}^T(\mathbf{L}{\mathbf{L}}^T){\mathit{\sigma }}_k^{(t+1)}=\gamma +{({\mathbf{L}}^T{\mathit{\sigma }}_k^{(t+1)})}^T({\mathbf{L}}^T{\mathit{\sigma }}_k^{(t+1)})>0$ since ${({\mathbf{L}}^T{\mathit{\sigma }}_k^{(t+1)})}^T({\mathbf{L}}^T{\mathit{\sigma }}_k^{(t+1)})\ge 0$.

To complete the proof, observe that $\mid {\mathbf{\sum }}_{-kk}^{(t)}\mid >0$ and γ > 0, $\mid {\mathbf{\sum }}^{(t+1)}\mid =\mid {\mathbf{\sum }}_{-kk}^{(t)}\mid \times \mid {\sigma }_{kk}^{(t+1)}-{({\mathit{\sigma }}_k^{(t+1)})}^T{({\mathbf{\sum }}_{-kk}^{(t)})}^{-1}{\mathit{\sigma }}_k^{(t+1)}\mid =\gamma \mid {\mathbf{\sum }}_{-kk}^{(k)}\mid >0$.