Precisely and Accurately Inferring Single-Molecule Rate Constants

Abstract

The kinetics of biomolecular systems can be quantified by calculating the stochastic rate constants that govern the biomolecular state versus time trajectories (i.e., state trajectories) of individual biomolecules. To do so, the experimental signal versus time trajectories (i.e., signal trajectories) obtained from observing individual biomolecules are often idealized to generate state trajectories by methods such as thresholding or hidden Markov modeling. Here, we discuss approaches for idealizing signal trajectories and calculating stochastic rate constants from the resulting state trajectories. Importantly, we provide an analysis of how the finite length of signal trajectories restrict the precision of these approaches, and demonstrate how Bayesian inference-based versions of these approaches allow rigorous determination of this precision. Similarly, we provide an analysis of how the finite lengths and limited time resolutions of signal trajectories restrict the accuracy of these approaches, and describe methods that, by accounting for the effects of the finite length and limited time resolution of signal trajectories, substantially improve this accuracy. Collectively, therefore, the methods we consider here enable a rigorous assessment of the precision, and a significant enhancement of the accuracy, with which stochastic rate constants can be calculated from single-molecule signal trajectories.

Introduction

In single-molecule, kinetic studies of biomolecular systems, experimental data consisting of a signal originating from an individual biomolecule is collected as a function of time.¹ This signal is, or can be converted into, a proxy for the underlying biomolecular state of the system. For instance, the intramolecular fluorescence resonance energy transfer (FRET) efficiency (E_FRET) that is measured between two fluorophore-labeled structural elements of an individual biomolecule in a single-molecule FRET (smFRET) experiment depends on the distance between the two structural elements and can therefore be converted into a proxy for the conformational state of the biomolecule.² Similarly, the distance that is measured between two optically trapped microbeads that are tethered to each other by an individual biomolecule in a single-molecule force spectroscopy experiment is a proxy for the conformational state of the biomolecule.^3,4 Investigating the kinetics of biomolecular systems using such single-molecule approaches eliminates the ensemble averaging that is inherent to bulk approaches. Thus, these approaches can reveal transient and/or rare kinetic events that are typically obscured by ensemble averaging, but that can often be critically important for elucidating biological mechanisms. In order to take full advantage of the unique and powerful mechanistic information provided by single-molecule experiments, however, the observed signals must be sensitive enough to unambiguously resolve the biomolecular states that are sampled during the experiment.

To obtain relevant kinetic information about a biomolecular system from such single-molecule experiments, the inherently noisy, experimental signal versus time trajectories (i.e., signal trajectories) obtained from observing individual biomolecules are typically transformed, or idealized, into biomolecular state versus time trajectories (i.e., state trajectories). This idealization process is not trivial, as limitations in signal- and temporal-resolution can easily obscure the relevant biomolecular states. Under the most favorable conditions, a researcher can sometimes manually select the signal data point where the biomolecule transitions to a new state. Unfortunately, this process is subjective and time consuming, and often the data is not sufficiently resolved to use this approach. A second method involves manually setting a signal threshold that, once crossed by the experimental signal, indicates a transition to a new state but this approach is still subjective and difficult to implement when more than two biomolecular states are present. A third, more rigorous and widely adopted method uses hidden Markov models (HMMs) to transform the inherently noisy signal trajectories into state trajectories by estimating the underlying, ‘hidden’ state responsible for producing the signal during each measurement period in a signal trajectory.^5,6 An advantage of using HMMs for this transformation is that they can manage many states simultaneously, and that methods have been developed to select the correct number of states present in the trajectory.^7-10 Regardless of the method that is used to idealize a signal trajectory into the corresponding state trajectory, the state trajectories can then be used to calculate stochastic rate constants and obtain kinetic information about the observed biomolecular system.

Herein, we begin by comparing the deterministic rate constants that are obtained from ensemble kinetic studies with the stochastic rate constants that are obtained from single-molecule kinetic studies as a means for introducing the conceptual framework that is typically used to analyze and interpret single-molecule kinetic data. We then clarify the basis of several approaches for calculating stochastic rate constants from single-molecule state trajectories. We go on to describe how the finite lengths of signal trajectories restrict the precision of these approaches, and demonstrate how Bayesian inference-based versions of these approaches provide a natural method to account for the precision of the calculated stochastic rate constants. We then end by addressing how the finite lengths and limited time resolutions of signal trajectories restrict the accuracy of these approaches, and describing methods to correct for the effects of the finite length and limited time resolution of the signal trajectories in order to increase the accuracy of these approaches. The methods we examine here for assessing the precision and improving the accuracy of the approaches that are currently used to calculate stochastic rate constants from single-molecule data greatly improve the analysis and interpretation of single-molecule kinetic experiments.

Single-Molecules and Stochastic Rate Constants

In bulk kinetic experiments, the large number of molecules present in an ensemble yields well-defined, ensemble-averaged approaches to equilibrium that mask the individual behaviors of the underlying molecules.¹¹ Thus, these approaches to equilibrium are traditionally described as time-dependent changes in the concentrations of reactants, reaction intermediates, and/or products that are modeled using phenomenological, differential rate equations.¹² Notably, bulk reaction kinetics and the rate equations that are used to model them are: (i) continuous in that individual molecules are not observed to undergo reactions, but rather the reaction is observed and described in terms of changes in concentrations, and (ii) deterministic in that an initial set of concentrations determines the subsequent values of the concentrations. By fitting changes in the concentrations of reactants, reaction intermediates, and/or products as they approach their equilibrium concentrations to these deterministic rate equations, one can obtain the deterministic rate constants that characterize the kinetics of the bulk system.¹³

In contrast with bulk reaction kinetics, however, single-molecule reaction kinetics are: (i) discrete in that individual molecules are observed to undergo reactions, and (ii) stochastic in that, even at equilibrium, reactions occur at random times that are often, but not always, independent of previous conditions. These differences between bulk and single-molecule reaction kinetics make it inappropriate to use the deterministic rate equations used to describe bulk reaction kinetics to account for the stochastic reactions that are observed at the single-molecule level.¹¹ Therefore, in order to describe single-molecule reaction kinetics, stochastic approaches like the chemical master equation and the stochastic simulation algorithm were developed to model the time evolution of discrete reactions in which the behavior of individual molecules could be observed.^12,14-18 These stochastic methods aim to quantify the kinetics of the molecular system by modeling the occurrence of individual reactions with probability distributions that are governed by stochastic rate constants, as opposed to modeling changes in concentrations with differential equations that are governed by deterministic rate constants. In order to quantify the kinetics of biomolecular systems observed in signal trajectories recorded using single-molecule biophysical techniques, therefore, we must adopt such a stochastic approach.

Consider the reaction coordinate of a biological process, such as protein folding or ligand binding. Due to the multiplicity of interactions present in biomolecular systems, the forward and reverse reactions along this reaction coordinate can often be considered as separate, elementary reactions that occur randomly and independently of the history of the system (i.e., in what states the biomolecule has been in and for how long).^19,20 Such stochastic reactions are called Markovian when the probability of a reaction occurring (i.e., a transition between states) depends only upon the current state of system; when these probabilities are time-dependent, or, rather, depend upon the previous state(s) of the system, the reaction is called non-Markovian. As a result of the constant transition probability of Markovian reactions, the lengths of time that a biomolecule spends in a particular state before a transition occurs, called the dwell times, t, are distributed according to an exponential distribution of the form

$$p(t_i\mid k_i)=k_i{e}^{-k_i{t}_i},$$ (1)

where p(t_i∣k_i) is the probability distribution function (PDF) of a dwell time in the i^th state lasting length t_i given the stochastic rate constant k_i, where k_i = Σ_j≠i k_ij Here, k_i is the net stochastic rate constant out of the i^th state, and k_ij are the stochastic rate constants governing the individual Markovian reactions out of the i^th state. For instance, if there are multiple, parallel, Markovian reactions out of the i^th state, the net stochastic rate constant that describes the length of time spent in the i^th state, k_i, will be the sum of the individual stochastic rate constants governing each of the parallel reactions, k_ij. Effectively, the dwell times in the i^th state, t_i, even if they are sorted into only those that transition to the j^th state, will be distributed according to this net stochastic rate constant, k_i. It follows then that, regardless of the final state, the average dwell time spent in the i^th state, < t_i >, is the reciprocal of this net stochastic rate constant, k_i. Finally, while it is not possible to distinguish among the collection of stochastic rate constants, k_ij, that describe the individual Markovian reactions exiting the i^th state by analyzing the observed dwell times spent in the i^th state, t_i, the number of times that an individual molecule enters a particular j^th state will depend upon the stochastic rate constant k_ij and can therefore be used to quantify k_ij.

Interestingly, the ergodic hypothesis asserts that the dwell time PDF for an individual molecule observed for a very long amount of time is equivalent to the dwell time PDF comprised of many identical, individual molecules, each observed for very short periods of time.¹² Thus, because many experimental factors, such as the photobleaching of fluorophores, limit the length of time that an individual biomolecule can be continuously observed, the latter approach of observing many individual biomolecules for very short periods of time is often taken. Regardless of which approach is taken, Onsager’s regression hypothesis^18,21 asserts that this ‘microscopic’ dwell time PDF of an individual molecule is equivalent to the ‘macroscopic’ relaxation to equilibrium of an ensemble of molecules described by traditional chemical kinetics. Therefore, when monitoring the reaction of one biomolecule, or of multiple, identical, individual biomolecules, the observed single-molecule reaction kinetics are equivalent to those that would be measured in bulk, if it were possible to observe them despite the ensemble averaging — this is especially significant for situations were the biomolecular population or event of interest is too rarely sampled to observe using a bulk, ensemble-averaged signal.

Before describing how to quantify the single-molecule stochastic rate constants k_i and k_ij described above, we must note the several complications that have already arisen. First, the exponential dwell time PDF described above assumes that time is continuous, but single-molecule signal trajectories are comprised of a sequence of discrete measurements that are spaced by, at minimum, the acquisition period of the measurement during which the signal was time averaged to acquire a single data point. Errors can therefore be introduced into these stochastic rate constant calculations if the discretized state trajectories misrepresent the temporal behavior of the molecule(s) as it samples state-space (i.e., the finite set of states available to it). Secondly, these stochastic rate constant calculations require several assumptions about the observed single-molecule data, including that a sufficient number of events were observed to accurately represent the ensemble average, that there are no subpopulations present in the sample, and that the system is at equilibrium and will not change over time, resulting in non-Markovian behavior. These assumptions are inherently difficult to confirm due to the small amounts of information present in a state trajectory from an individual molecule.

Calculating Stochastic Rate Constants from Signal Trajectories

Approaches to Calculating Stochastic Rate Constants

As mentioned above, stochastic rate constants govern the Markovian nature with which a single molecule samples state-space during a reaction. The dwell time, t, in a particular state is governed by the sum of all of the stochastic rate constants exiting that state, while the number of transitions between particular states depends upon the particular stochastic rate constant describing that reaction. Below, we discuss how stochastic rate constants for Markovian reactions can be quantified by considering the distribution of dwell times, or the probability of transitioning between particular states. Before describing these methods, however, we will briefly discuss how the properties of state trajectories that facilitate stochastic rate constant calculations can be quantified such that they can be easily incorporated into the various stochastic rate constant calculation methods.

The state trajectories described above are each composed of a series of sequential, discretized data points, where each data point indicates the state occupied, during a measurement period of length τ, by the single molecule corresponding to the signal trajectory being analyzed; it is worth noting that this state was inferred from a time-averaged signal collected during the measurement period τ. From these sequential data points that comprise a state trajectory, we can obtain a dwell time list, n_ij, where each entry is the number of contiguous measurement periods, τ’s, that the single-molecule is observed to spend in a state, i, before transitioning to a second state, j. This is a discretized list of the dwell times in state i, t_i, that transition to state j, and it has the form: n_ij = [5, 13, 12, 7, …]. Additionally, we can construct a counting matrix, M, for each state trajectory where the matrix elements, M_ij, represent the number of times that the state trajectory began in state i at measurement n (i.e., at time t = 0) and ended in state j at measurement n+1 (i.e., at time t = τ). M is related to n_ij such that the off-diagonal elements of M, M_ij, are the number of entries in the corresponding n_ij, and the on-diagonal elements of M, M_ij, are

$${\mathit{M}}_{\mathit{ii}}=\sum _{j\ne i}\left(\left(\sum {\mathit{n}}_{\mathit{ij}}\right)-{\mathit{M}}_{\mathit{ij}}\right),$$ (1)

where Σn_ij is the sum of the entries in n_ij. M may be row normalized, such that each element in a row (i.e., with the same i) is divided by the sum of that row to yield the transition matrix, P. The off-diagonal elements of the transition matrix P, P_ij, give the frequency that an individual molecule in state i has transitioned to state j at the next measurement period. Below, we detail several methods to explain how the stochastic rate constants that characterize kinetic processes may be obtained from the calculated dwell time list, n_ij, counting matrix, M, or transition matrix, P.

Dwell Time Distribution Analysis

One method to calculate stochastic rate constants from a state trajectory is by analyzing the distribution of observed dwell times. A state trajectory can be thought of as a sequence of discrete measurements that report on whether a transition has occurred between two measurements. These ‘transition trials’ are reminiscent of a series of repeated Bernoulli trials from probability theory,²² which are events where the outcome is either a success with probability p, or a failure with probability 1 − p. In this analogy, a successful Bernoulli trial would be when the single molecule transitions from state i at measurement period n to state j at measurement period n+1, whereas a failed Bernoulli trial would be when, instead, the single molecule remains in state i at measurement period n+1.

The number of repeated, failed trials before a success (i.e., a transition) occurs is distributed according to the geometric distribution probability mass function (PMF),²²

$$P(n\mid p)=p{(1-p)}^n,$$ (2)

where n is the number of failed trials and p is the probability of a success. Therefore, the PMF of the number of measurement periods until a transition occurs in a Markovian state trajectory can be modeled using the geometric distribution. From the geometric distribution, we expect that the mean number of successive measurement periods in state i, 〈n_i〉, until a transition out of state i occurs is,

$$\langle n_i\rangle =\frac{1-P_i}{P_i},$$ (3)

where, P_i the probability of a successful transition out of state i to any other state, j. Given a particular state trajectory in a Markovian system, an estimate of the mean number of measurement periods before a transition out of state i occurs, 〈n_i〉, would then allow the probability of a successful transition out of state i to be calculated by solving this equation. The maximum-likelihood estimate of 〈n_i〉 is the total number of measurement periods observed to be in state i divided by the total number of transitions out of state i,

$$\langle n_i\rangle =\frac{{\sum }_j(\sum n_{\mathit{ij}})}{{\sum }_{j\ne i}{M}_{\mathit{ij}}},$$ (4)

where Σn_ij is the sum of all entries in n_ij and the M_ij are the total number of observed transitions from state i to state j. Solving this equation yields the probability of a successful transition,

$$P_i=\frac{{\sum }_{j\ne i}{M}_{\mathit{ij}}}{{\sum }_{j\ne i}{M}_{\mathit{ij}}+{\sum }_j\left(\sum n_{\mathit{ij}}\right)}.$$ (5)

As mentioned in the previous section, the dwell times that a single molecule will spend in a particular state before transitioning to a different state, t’s, in a Markovian system are distributed according an exponential distribution. Therefore, for such a Markovian system, the probability that a transition out of state i occurs within a measurement period, τ, in a signal trajectory is the integral of the exponential distribution PDF from t = 0 to t = τ the measurement period, which is

$$P_i={\int }_0^{\tau }{k}_{\mathit{ij}}·e^{-k_i·t}·\mathit{dt}=(1-e^{-k_i·\tau }).$$ (6)

This equation implies that a stochastic rate constant can be calculated as

$$k_i=\frac{-\ln (1-P_i)}{\tau },$$ (7)

if the transition probability, P_i, can be quantified as described above. Notably, the stochastic rate constant obtained by considering the dwell times in a particular state will be a sum of multiple stochastic rate constants, except in cases when there is only one state to transition to (e.g., two-state systems). Analyzing only the dwell times that a single molecule spends in state i before transitioning to a particular state j still yields the same sum of the stochastic rate constants, and not the associated k_ij. The major advantage of analyzing the distribution of dwell times, however, is that deviations from Markovian behavior can be observed as non-geometric behavior and then this non-Markovian behavior can be analyzed.

Interestingly, a careful consideration of these equations reveals a limitation in the application of this dwell time distribution analysis method, which is the fact that the geometric distribution requires the state trajectories to have discrete dwell times that last {0, 1,2,…} measurement periods, τ, before a transition occurs. Unfortunately, in a state trajectory, dwell times, t, of zero measurement periods, τ, are never included in the dwell time lists, n_ij, because a dwell time must be at least one measurement period, τ, long for it to be associated with a particular state. The result is an undercounting of M due to the exclusion of all zero measurement period-long dwell times (n = 0, or, equivalently, t < τ), and a subsequent miscalculation of P_i. This undercounting is exacerbated by the fact that, from the geometric distribution, the highest probability dwell times are the zero measurement period-long dwell times (n = 0). As a result, stochastic rate constants calculated using the dwell time distribution analysis method are misestimates, and, more specifically, underestimates of the true stochastic rate constant. Nonetheless, this underestimate can easily be accounted for by conditioning the geometric distribution PMF such that only dwell times that are greater than zero measurement periods, τ, in length are considered (n > 0, or, equivalently, t > τ.

Here, we will condition the geometric distribution PMF so that it only considers n > 0, and denote these discrete dwell time lengths with n^★ ∈ {1,2,…} to maintain clarity. From the law of conditional probability, we note that

$$\begin{array}{c}P\left(n^{★}\mid p,n>0\right)=\frac{P(n\mid p,n=0\cap n>0)}{P(n\mid p,n=0)},\\ P\left(n^{★}\mid p\right)=\frac{p{\left(1-p\right)}^{n^{★}}}{1-(1-{\left(1-p\right)}^{0+1})},\\ P\left(n^{★}\mid p\right)=p{\left(1-p\right)}^{n^{★}-1}=\frac{1}{1-p}·P(n\mid p).\end{array}$$ (8)

Therefore, the geometric distribution PMF conditioned upon all dwell times being greater than zero measurement periods in length is equivalent to the regular geometric distribution PMF divided by 1 − p. Because P(n^★∣p) is proportional to P(n∣p) in a manner that does not depend upon n, the expectation values of P(n*∣p) (e.g., the mean) are also proportional to those of P(n∣p) in the same manner due. Therefore,

$$\langle n^{★}\rangle =\frac{1}{1-p}\langle n\rangle .$$ (9)

We can then follow the same derivation of P_i above in Eqn. (6), but substitute this expression for 〈n^★〉 in place of 〈n〉. This yields,

$$\begin{array}{lll}\langle n_i^{★}\rangle & =& \frac{{\sum }_j\sum n_{\mathit{ij}}}{{\sum }_{j\ne i}{M}_{\mathit{ij}}}=\frac{1}{1-P_i}·\frac{1-P_i}{P_i},\mathrm{and\; therefore}\\ & & P_i=\frac{{\sum }_{j\ne i}{M}_{\mathit{ij}}}{{\sum }_j\sum n_{\mathit{ij}}}.\end{array}$$ (10)

Interestingly, this is the identical result for the transition probability P_ij that is obtained with the transition probability expansion analysis described in the following section.

For further insight into this expression, consider that, from the Poisson distribution, the expected value for the number of transitions out of state i is 〈M_i〉 = k_i · T_i, where T_i is the total time spent in state i. Then, from Eqn. (10) we find that

$$P_i=\frac{{\sum }_{j\ne i}{M}_{\mathit{ij}}}{{\sum }_j\sum n_{\mathit{ij}}}\approx \frac{T_i{\sum }_j{k}_{\mathit{ij}}}{T_i/\tau }={\sum }_j{k}_{\mathit{ij}}\tau =k_i\tau .$$ (11)

Note that the expression for the P_i that is calculated here is different then in Eqn. (6). From the Taylor series

$$e^x=1+\frac{x^1}{1!}+\frac{x^2}{2!}+\cdots ,$$ (12)

we see that Eqn. (11) is the Taylor series expansion of the transition probability given by Eqn. (6), but truncated after the first-order term. Notably, since this expression in Eqn. (11) is conditioned upon only the observation of dwell times, t’s, that are greater than zero measurement periods, τ’s, in length, this conditioned, dwell time distribution analysis is insensitive to the types of missed dwells in state i that are less than one measurement period, τ, long. As we will show further below, however, it is sensitive to other types of missed events.

Finally, it is worth noting that stochastic rate constants for a particular reaction pathway out of state i, k_ij, can be calculated from k_i by equating the splitting probability, $p_{\mathit{ij}}^{\mathrm{split}}$, and the observed branching ratios as

$$\begin{array}{c}{p}_{\mathit{ij}}^{\mathrm{split}}=\frac{k_{\mathit{ij}}}{{\sum }_j{k}_{\mathit{ij}}},\\ \frac{M_{\mathit{ij}}}{{\sum }_{j\ne i}{M}_{\mathit{ij}}}\approx \frac{k_{\mathit{ij}}}{k_i},\mathrm{and\; therefore}\hfill \\ k_{\mathit{ij}}=\frac{M_{\mathit{ij}}}{{\sum }_{j\ne i}{M}_{\mathit{ij}}}·k_i.\hfill \end{array}$$ (13)

Since we will not discuss this approach in the section on Bayesian inference further below, we note here that the calculation of the k_ij described above can be recast with a Bayesian inference approach by utilizing a Dirichlet distribution as the conjugate prior and a multinomial distribution as the likelihood function (vide infra). Regardless, while this dwell time distribution analysis approach to calculating individual stochastic rate constants is quite effective, and it has the benefit of allowing the dwell times to be checked for non-Markovian behavior that would render the calculated stochastic rate constants much less meaningful, a more straightforward method to calculate the stochastic rate constants for each parallel reaction pathway of an individual molecule is to analyze the transition probabilities for each pathway.

Transition Probability Expansion Analysis

Another method for calculating stochastic rate constants is to consider the observed frequency with which a single molecule transitions from one state to another. For the discrete state trajectories considered here, this is equivalent to determining whether the single molecule in state i during a measurement period, n, is in state j during the subsequent measurement period, n+1. Since this data consists of multiple Bernoulli trials of whether or not the transition has occurred, the probability of a particular transition can be modeled with the binomial distribution. The binomial distribution is appropriate for modeling the number of successful trials (i.e., transitions from state i to state j, M_ij) from a certain number of performed trials (i.e., the number of times the single molecule was in state i in the state trajectory, Σn_ij) that can each succeed with a fixed probability (i.e., P_ij) as,

$$P(m\mid n,p)=\left(\begin{array}{c}n\\ m\end{array}\right)p^m{\left(1-p\right)}^{n-m},$$ (14)

where m is the number of successful trials, n is the total number of trials, and p is the probability of a successful trial. From the mean of the binomial distribution, 〈m〉 = np, we will take frequentist approach to statistics and substitute

$$M_{\mathit{ij}}\approx \left({\sum }_{j\ne i}(\sum n_{\mathit{ij}})\right)P_{\mathit{ij}}=\left({\sum }_j{M}_{\mathit{ij}}\right)P_{\mathit{ij}}.$$ (15)

Here, we have equated P_ij with the observed frequency of the transitions from state i to state j. However, in an experiment, only a finite number of transitions from state i to state j are observed; as such, the equality will only be approximate. Regardless, according to the central-limit theorem, as the number of measurements increase, M_ij should approach the mean value dictated by the binomial distribution; thus, barring a small number of measurements (e.g., less than ~100 measurements), we might reasonably estimate that

$$P_{\mathit{ij}}=\frac{M_{\mathit{ij}}}{{\sum }_j{M}_{\mathit{ij}}},$$ (16)

and from this expression, estimate k_ij using Eqn. (7).

Now, we will consider the accuracy of calculating a stochastic rate constant in this manner. Interestingly, given a particular amount of time spent in state i in a state trajectory, T_i, the Poisson distribution indicates that

$$\langle M_{\mathit{ij}}\rangle =k_{\mathit{ij}}·T_i\approx k_{\mathit{ij}}·\left({\sum }_j{M}_{\mathit{ij}}\tau \right),$$ (17)

where the substitution for T_i is generally accurate, excepting the types of missed events which we will discuss further below. With this in mind, by substituting Eqn. (17) into Eqn. (16), we find that

$$P_{\mathit{ij}}=\frac{k_{\mathit{ij}}·{\sum }_j{M}_{\mathit{ij}}·\tau }{{\sum }_j{M}_{\mathit{ij}}}=k_{\mathit{ij}}·\tau .$$ (18)

Therefore, rather than being corrected to a Taylor series expansion of the transition probability truncated at the first order term, as was the case in the dwell time distribution analysis approach described in the previous section, this method of calculating transition probabilities is inherently a Taylor series expansion of the transition probability truncated at the first order term. Regardless, the transition probability expansion analysis approach described here and the dwell time distribution analysis approach described above are therefore equivalent methods of calculating stochastic rate constants, which are accurate only when k_ijτ is small (i.e., much less than one) and the higher-order terms of the Taylor series expansion are therefore negligible.

When k_ijτ is large (i.e., approaching and greater than 1), however, the probability of experimentally recording measurements where more than one state is occupied during a measurement period becomes substantially high. Neither the process of idealizing a signal trajectory into a state trajectory nor performing the first-order expansion of the Taylor series is well justified in such a situation. Regardless, before discussing the precision associated with calculating stochastic rate constants from individual molecules, we would like to note here that the transition probability expansion analysis approach described in this section has the added benefit of being insensitive to missed dwells, as will be discussed further below. Finally, as will also be discussed further below, this type of analysis approach is analogous to using the transition matrix from an HMM for P_ij.

Methods for Calculating Stochastic Rate Constants

Manual Idealization of Signal Trajectories

In order to calculate stochastic rate constants using either the dwell time distribution- or transition probability expansion analysis methods described above, a signal trajectory must first be idealized into a state trajectory. This state trajectory can then be quantified as described above to obtain the parameters necessary to calculate stochastic rate constants. One approach to idealizing a signal trajectory is to identify the states that are sampled by the signal trajectory, as well as the measurement periods during which transitions between the states take place, by visual inspection (e.g., as in Refs. 23-25). Even in cases where the experimental signals corresponding to the various states are well separated and the signal trajectory has an excellent signal-to-noise ratio, however, it is still difficult and time consuming to locate the exact measurement period during which a transition occurs. In cases where the signals are insufficiently separated and/or the signal trajectory has a poor signal-to-noise ratio, therefore, this method can become quite subjective, such that different researchers, who will generally have slightly different criteria for what constitutes a state or a transition, can produce different state trajectories from the same signal trajectory, and thus different stochastic rate constants.

A more robust approach is to systematically employ a user-defined signal threshold such that transitions from one state to another state can be pinpointed by identifying the measurement periods in a signal trajectory during which the signal crosses the threshold (e.g., as in Refs. 26-29). Typically, thresholds are defined by generating a histogram of all of the signal values that are sampled throughout the entire signal trajectory, and subsequently identifying signal boundaries (i.e., thresholds) for each state that minimize overlap of the signal values corresponding to neighboring states. When more than two states are present, different thresholds can be used to define each state so as to allow for more flexibility when dealing with multiple states, however, it can be difficult to unambiguously specify these thresholds. Unless the signals corresponding to the various states are well separated and the signal-to-noise ratio of the signal trajectory is exceptional, there is often significant overlap between the signal values corresponding to neighboring states. As a result, natural fluctuations in the signal due to noise can result in spurious transitions that cross the threshold. This will result in the misidentification of transitions in the state trajectory, which can propagate into a misestimation of the stochastic rate constants. One approach to guard against the effects of these spurious transitions, as well as to dispel concern about the subjectivity of a user-defined signal threshold, is to repeat the process of idealizing the signal trajectory and calculating the stochastic rate constants using several, slightly different values for the user-defined signal thresholds (e.g., favoring one state, favoring the other state, exactly between, etc.), and demonstrating the robustness of the calculated stochastic rate constants to the choice of threshold (e.g., as in Refs. 28,29).

Hidden Markov Models

HMMs are a popular method to analyze signal versus time trajectories obtained from biophysics experiments^7,10,30-33— detailed descriptions can be found elsewhere.^19,34 Briefly, in an HMM, the time-averaged signal recorded during each measurement period, τ, in a signal trajectory is assumed to be representative of some ‘hidden’ state (i.e., the state trajectory). The underlying, hidden state trajectory, which is not directly observed, is then assumed to behave as a Markovian process that is governed according to transition probabilities. As discussed above, the transition probabilities of a single molecule in a Markovian system are related to stochastic rate constants governing the biomolecular system. With an HMM, the probability that a signal originates from a particular hidden state is calculated while considering the hidden state of the previous time period in order to explicitly account for the transition probability. Notably, in an HMM, the values of the signal that are observed when a single molecule is in a particular hidden state are typically assumed to be distributed according to a normal distribution PDF (i.e., the observed signals will be a Gaussian mixture model). Using this approach, one ‘estimates’ an HMM that describes the signal in terms of a discrete number of states, and that provides, as parameters, the signal emission probabilities of each state as well as the transition probabilities as a transition probability matrix, P, from each state.

With the optimal estimate of the HMM describing a signal trajectory, two different methods can be used to calculate stochastic rate constants. In the first method, the idealized, state trajectory can be obtained from the HMM and then quantified as described for use with the dwell time distribution, or transition probability expansion analysis approaches. This idealized, state trajectory is obtained by applying the Viterbi algorithm to the HMM in order to generate the Viterbi path.³⁵ The Viterbi path, which gives the idealized state trajectory directly, is the most likely sequence of hidden states that not only would yield the observed signal values given the optimal signal emission probabilities, but that would most likely have arisen from the optimal transition probabilities. As such, it is important to note that, by using an HMM to idealize a signal trajectory, the resulting idealized state trajectory, and emission- and transition probabilities have been forced to be as Markovian as possible. Therefore, if there is any non-Markovian behavior present in the biomolecular system under investigation, it will be masked and made to appear Markovian. To avoid this shortcoming of HMMs, the idealized state trajectory can be generated using a different approach, such as thresholding.

The second method for calculating stochastic rate constants from the optimal HMM estimate involves directly using the transition probabilities obtained from the HMM. While, on its surface, this method seems to bypass the use of idealized, state trajectories, the process of estimating the optimal HMM that describes the data inherently involves estimating the hidden states that generated the signal trajectory, and therefore involves the use of idealized, state trajectories. From an HMM, individual stochastic rate constants can be calculated using Eqn. (7) and the transition probability matrix, which is analogous to that calculated from an idealized, state trajectory. This approach is equivalent to transition probability expansion analysis. As with calculating stochastic rate constants from the Viterbi path, it must be noted that this second HMM method also enforces Markovian behavior.

Finally, we note that in the smFRET literature alone, there are several software packages available for HMM-based analysis of E_FRET trajectories. Of these packages, there are two types of approaches to estimating the optimal HMM that describes the data: maximum-likelihood approaches (e.g., QuB,³⁶ HaMMy,³³ and SMART³⁷) and Bayesian approaches (e.g., vbFRET^7,8 and ebFRET^9,10). There are many benefits to using Bayesian HMMs over maximum-likelihood HMMs. First, unlike Bayesian HMMs, maximum-likelihood HMMs are fundamentally ill-posed mathematical problems — essentially, individual states can ‘collapse’ onto single data points, which yields a singularity with infinite likeliness that is not at a reasonable HMM estimate. Second, as we will discuss in the next section, Bayesian approaches naturally incorporate the precision with which a certain amount of data can determine the parameters of the HMM by learning the probability distribution of the transition probabilities instead of finding one set of transition probabilities. In addition to providing the precision, this allows one to combine the results from multiple, individual molecules, and simultaneously learn consensus, stochastic rate constants from an ensemble of single molecules. Third, while maximum-likelihood approaches can result in HMMs that are significantly over-fit and that consequently overestimate the number of hidden states present in a signal trajectory, Bayesian approaches are inherently able to select the correct number of hidden states present in a signal trajectory. For example, with maximum-likelihood HMMs, a better HMM estimate of the signal trajectory is obtained simply by adding additional hidden states; in the extreme case, there would be one hidden state for each data point. Although the HMM in this extreme case would fit the data perfectly, it would not be very meaningful, nor would it be a useful model for predicting the future behavior of the system. While the use of heuristic approaches such as the Bayesian- and Akaike Information Criteria (BIC and AIC, respectively) have been proposed to help select the correct number of states in maximum-likelihood HMMs, these are approximations to true Bayesian approaches that are valid only under certain conditions and that, in practice, we find do not work well for the HMM-based analysis of smFRET data. Additionally, Bayesian HMMs have been shown to be more accurate than maximum-likelihood HMMs for the analysis of signal trajectories where the dwell-times, t’s, in the hidden states are transient relative to the measurement period, τ.⁷ Finally, there is effectively no added computational cost between the maximum-likelihood- and Bayesian- approaches to HMMs, as both implement the same algorithms to calculate the probabilities associated with the HMM (e.g., the forward-backward algorithm), so speed is not a concern. Given the benefits of the Bayesian approach over the maximum-likelihood approach for HMMs, we recommend using Bayesian HMMs when analyzing signal trajectories from single-molecule biophysical experiments.

Precision of Calculated Rate Constants

Using Bayesian Inference to Quantify Precision

The finite length of a signal trajectory ensures that only a finite number of randomly distributed dwell times and transitions will be observed during the duration of the signal trajectory. The fact that only a finite number of dwell times and transitions are observed in a signal trajectory limits the precision with which a stochastic rate constant can be calculated from that signal trajectory. With the observation of more dwell times and transitions, this precision will increase, and eventually the value of the calculated stochastic rate constant will converge to the value of the ‘true’ stochastic rate constant. Here, we demonstrate how to rigorously quantify this precision, and therefore the amount of information contained in a single signal trajectory, through the use of Bayesian inference.

One simplistic attempt to account for variability in the number of dwell times and transitions that are observed is to report the statistical uncertainty in the calculated stochastic rate constant in the context of ‘bootstrapping’ of the data.³⁸ Bootstrapping is an attempt to simulate the data of future experiments from a set of observed data. From the analysis of bootstrapped, ‘future’ data, any variation in subsequently calculated properties can attributed to the uncertainty present in the original dataset. For example, when calculating stochastic rate constants from a state trajectory as described above, the bootstrapping process would involve creating a resampled data set, $n_{\mathit{ij}}^{\prime }$, by randomly sampling from n_ij with replacement such that, after each sample is drawn, the sampled data point is placed back into the population before the next sample is drawn. The new, bootstrapped transition probability, $P_{\mathit{ij}}^{\prime }$, can then be calculated from $n_{\mathit{ij}}^{\prime }$, and this yields new, bootstrapped stochastic rate constants, $k_{\mathit{ij}}^{\prime }$. The bootstrapping process is then repeated several times, and the reported stochastic rate constant k_ij is given as the mean of the set of bootstrapped $k_{\mathit{ij}}^{\prime }$, with the uncertainty of the reported k_ij given as the standard deviation of the set of bootstrapped $k_{\mathit{ij}}^{\prime }$. It is important to note, however, that bootstrapping inherently assumes that the collected data accurately represents the characteristics of an infinitely large amount of data. Consequently, bootstrapping artificially inflates the dataset in a way that perpetuates any misrepresentations of the infinitely large amount of data that are present in the actual dataset. The smaller the collected dataset is, the more likely it is to misrepresent this infinitely large amount of data. In practice, bootstrapping single-molecule results, where there are often only several hundreds of individual molecules in a dataset, perpetuates these misrepresentations and leads to inaccurate rate constants, all the while not providing a reasonable estimate of the statistical error present in the calculation.

Consider the following, extreme, hypothetical calculation where only one transition with a one measurement period-long dwell time (i.e., n_ij = [1]) has been observed in one signal trajectory. Using the conditioned dwell time distribution- or transition probability expansion analysis approaches, we find that, in this case, P_ij is equal to 1.0, and that all of the bootstrapped $P_{\mathit{ij}}^{\prime }$ are also equal to 1.0. Thus, in this case, there is no uncertainty in the calculation of the transition probability, or, consequently, in the stochastic rate constant, and this stochastic rate constant is infinitely large. Nonetheless, we know intuitively that the stochastic rate constant is probably not infinity, and that there must be some uncertainty in this calculation, even though it employs only one measurement. The uncertainty lies in the fact that the one transition we have observed simply cannot be representative of the stochastic rate constant governing an entire ensemble or even an individual molecule. Likewise, we should suspect that P_ij is probably a poor estimate of the true transition probability. It is easy to imagine that after recording a few more measurements from that hypothetical single molecule, we might calculate a different value of P_ij, and that the extra data would give us a better sense of the uncertainty in P_ij. This extreme example illustrates how the analyses of the stochastic rate constant calculations described above are insufficient by themselves, even when supplemented by bootstrapping. Fortunately, in contrast to these intrinsic shortcomings, Bayesian inference provides a statistically rigorous manner with which to encode our intuition that the number of observations should change our knowledge about P_ij, and systematically address the uncertainty in the calculation of stochastic rate constants.

Bayesian inference is a statistical method grounded in the Bayesian approach to probability (see Ref. 39 for a pedagogical introduction). In Bayesian inference approaches, the parameters of a model that has been developed to describe experimentally observed data are treated as probability distributions that reflect the consistency of the particular parameter values with the data. These probability distributions can then be updated if new data is acquired so as to be consistent with the new, as well as any previous, data. This approach is analogous to the way that a scientific hypothesis is tested and then updated with each new laboratory experiment.³⁹ In the context of quantifying a state trajectory, Bayesian inference allows us to formulate a hypothesis about the underlying stochastic rate constants of a system (i.e., the probability of certain stochastic rate constants producing the observed state trajectory), and then to update that hypothesis as each transition, or lack thereof, is observed in the state trajectory. In this way, we can use Bayesian inference to describe the probability distribution of a stochastic rate constant as each measurement period in a signal trajectory is analyzed.

The foundation of Bayesian inference is Bayes’ rule, which can be written mathematically as

$$P(\mathrm{\Theta }\mid D)\propto P(D\mid \mathrm{\Theta })·P(\mathrm{\Theta }),$$ (19)

where Θ represents the parameters of the model, and D represents the data values. The first, second, and third terms are referred to as the ‘posterior’, the ‘likelihood’, and the ‘prior’, respectively. Bayes’ rule can be expressed verbally as: the probability of the model’s parameter values after observing the data is proportional to the product of (i) the probability of observing the data given those particular parameter values, and (ii) the initial probability of those parameters. More succinctly, the posterior probability is proportional to the product of the likelihood and the prior probability.

With a model for experimental data (i.e., expressions for the likelihood and the prior probability distribution), we can calculate the posterior probability distribution, and learn about the distribution of parameter values that are consistent with the experimental data. Unfortunately, for some models, these calculations can be analytically and numerically difficult, making their practical use relatively intractable. However, there are certain conditions that significantly simplify these calculations. Specifically, certain pairs of likelihood functions and prior distributions are complementary in that they yield posterior distributions that are of the same algebraic form as the prior distribution. In such a case, the prior is called the conjugate prior for that particular likelihood function. The benefit of using a conjugate prior with its corresponding likelihood function is that simple updating rules can be applied to the parameters of the conjugate prior probability distribution to yield the resulting posterior probability distribution. These calculations typically amount to the addition of certain experimental values. As such, the use of conjugate priors and likelihood functions circumvents the computationally expensive need to calculate the posterior probability distribution for every possible point in the entire probability space.

Below we describe how to employ Bayesian inference using conjugate priors and likelihood functions in both the dwell time distribution- and the transition probability expansion analysis approaches described above for calculating stochastic rate constants from state trajectories in a manner that is extremely tractable, and easy to employ.

Bayesian Dwell Time Distribution Analysis

To perform Bayesian inference upon the exponentially distributed dwell times that a single molecule will spend in a particular state in a state trajectory, we must first identify the likelihood function and its conjugate prior probability distribution that will serve as a model of the observed data. As described above, the number of consecutive, discrete measurement periods, n, that such a single molecule will spend in a particular state is distributed according to the geometric distribution PMF. Therefore, in this model, the geometric distribution PMF is the likelihood function for observing some number of sequential measurements in state i before transitioning to state j, and this depends only upon one parameter: the transition probability out of state i, P_i. Mathematically, the geometric distribution PMF is constructed such that the conjugate prior for this likelihood function is the beta distribution PDF,

$$p\left(P\mid \alpha ,\beta \right)=P^{\alpha -1}{(1-P)}^{\beta -1}/B(\alpha ,\beta ),$$ (20)

where B(x, y) is the beta function of x and y.

The beta distribution PDF is often used to describe the probability of a probability, P (in this case, of a successful transition out of state i, P_i), because, much like a probability, the PDF is defined continuously between 0 and 1.³⁴ Additionally, the beta distribution PDF is a function of only two parameters, α and β, which have intuitive interpretations relating to probabilities. Notably, when α = β = 1, the beta distribution is flat, as all values of P have equal probabilities. In this case, the beta distribution mathematically expresses a lack of knowledge about P in a similar manner as the equal, a priori probability assumption of statistical mechanics.¹² Along these lines, larger values of α and/or β yield more defined and peaked distributions, which expresses the increased knowledge about P. As we will discuss below, the process of performing Bayesian inference amounts to modifying the initial values of α and β in a data-dependent manner to yield a posterior, beta distribution PDF with updated values of α and β. In this sense, Bayesian inference mathematically encodes a method to express the incremented knowledge that originates from new information.

By using the geometric distribution PMF as a likelihood function, and the beta distribution PDF as its conjugate prior, we can now calculate the posterior probability distribution of the transition probability, P_i, from a state trajectory. We begin by assuming that all transition probabilities are initially equally probable. Therefore, the prior probability distribution is a beta distribution PDF with α = β = 1. The posterior probability distribution will be another beta distribution PDF where α and β are interpreted as α₀ plus the number of successful transitions, and β₀ plus the number of unsuccessful transitions, respectively, where the subscript 0 refers to the prior probability distribution. Thus, for the transitions out of state i in a state trajectory, the posterior probability distribution is a beta distribution with $\alpha =1+{\sum }_{j\ne i}{M}_{\mathit{ij}}$, and $\beta =1+{\sum }_j(\sum n_{\mathit{ij}})$. Therefore, since the mean of the beta distribution is α/(α+β), the mean transition probability out of state i after having observed the state trajectory is

$$\langle P_i\rangle =\frac{1+{\sum }_{j\ne i}{M}_{\mathit{ij}}}{1+{\sum }_{j\ne i}{M}_{\mathit{ij}}+1+{\sum }_j(\sum n_{\mathit{ij}})}.$$ (21)

This mean value of the transition probability converges to the maximum likelihood estimate of P_i given in the previous section when α ≫ 1 and β ≫ 1. Note that the maximum likelihood estimate of P_i is equivalent to the mode of the beta distribution PDF, which is (α − 1)/(α + β − 2).

The benefit of this Bayesian inference approach is that the posterior probability distribution of P_i not only provides a mean value, but also speaks to the uncertainty inherent in P_i due to limited number of dwell times observed in state i. This uncertainty can be expressed in the form of a credible interval. A credible interval, which is similar to the frequentist idea of a confidence interval, is the range in which a certain percentage of the probability density of the PDF resides; typically one uses a 95% credible interval as this is similar to ±2σ for a normal distribution, but this choice is arbitrary. The upper- and lower boundaries of the credible interval can be found through the inverse of the cumulative distribution function of the beta distribution. Many standard computational programs come with a function to do this, which is sometimes called the ‘inverse function of the regularized incomplete beta function’, I_x(α, β), where α and β are the posterior probability distribution parameters and x is the fraction of the boundary (e.g., 0.025 for 2.5%). For instance, in Matlab this function is called betaincinv.

Finally, let us consider the application of this Bayesian approach to observed data from a state trajectory where the length of a dwell time must be at least one measurement period in length (n ≥ 1) in order to be associated with a particular state, as discussed earlier. Previously, we conditioned the geometric distribution PMF to only consider dwell times of at least one measurement period in length to address this problem. Now we must adapt our Bayesian inference approach to allow for this conditioning. Due to the linearity of this conditioning, and since the total likelihood function is the product of the likelihood function from each individual data point, the conditioned posterior probability distribution contains an extra term of ${\left(\frac{1}{1-P}\right)}^{\left({\sum }_{j\ne i}{M}_{\mathit{ij}}\right)}$. This is equivalent to setting ${\beta }^{\prime }=\beta -{\sum }_{j\ne i}{M}_{\mathit{ij}}$, where β′ is the parameter used in the beta distribution for the posterior probability distribution, and β is the parameter calculated above. Using α and β′ as the parameters for a beta distribution PDF, the posterior probability distribution of the transition probability, P_i, can be accurately and precisely quantified as a function of each successive, observed dwell time, even though dwell times of zero length are missed in the state trajectory (Fig. 1). With a sufficient number of measurements, this approach yields the same mean transition probability as the maximum likelihood estimate of the transition probability expansion analysis, thereby rendering this approach insensitive to some types of missed events that we will discuss further below.

Figure 1. Maximum Likelihood versus Bayesian Approaches to Calculating Transition Probabilities.

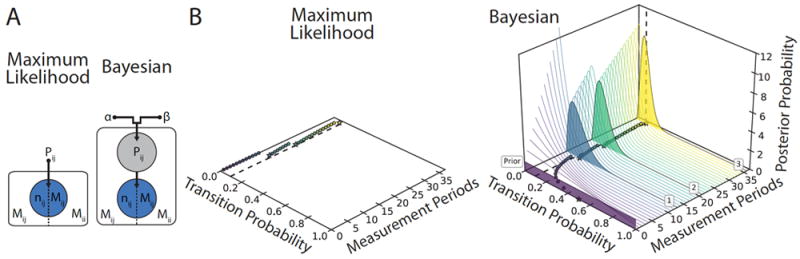
(A) Graphical models of maximum likelihood (ML) (left), and Bayesian (right) based methods for calculating the transition probability from state i to state j, P_ij. Each model is divided in half to give the dwell time distribution analysis (left) or the transition probability expansion analysis (right). Blue circles represent the observed variables, grey circles represent hidden variables, and black dots represent fixed parameters. The Bayesian model expands upon the ML model by using a probability distribution to describe P_ij. (B) The calculations of P_ij from three dwell times using ML (left)- and Bayesian (right)-based approaches are plotted as a function of increasing measurement periods (i.e., observations in a state trajectory). The true transition probability is shown with a dashed line. Both the ML value and the mean of the posterior probability distribution value of P_ij calculated with dwell-time distribution analysis (stars) and transition probability expansion analysis (circles) are shown. Additionally, for the Bayesian approach, the posterior probability distributions are plotted for dwell time distribution analysis (filled curves) and for transition probability expansion analysis (thin curves). The prior probability distribution, and the numbers of the dwell times are denoted in boxes. Notably, the Bayesian-based approach yields non-zero transition probabilities, and also provides the uncertainty in P_ij in the form of a probability distribution.

To be concrete, we will use this Bayesian dwell time distribution analysis approach to analyze the extreme, hypothetical case of the single observed transition introduced in the previous section. The posterior probability distribution would be a beta distribution with α = (1 + 1) = 2, and β′ = (1 + 1 − 1) = 2. This yields 〈P_i〉 = 0.66, with a lower-bound of P_i = 0.16, and an upper-bound of P_i = 0.99 for the 95% credible interval. Notably, the mean value of the transition probability calculated using the Bayesian dwell time distribution analysis approach is not infinitely large, as was the estimate of P_i using the maximum-likelihood approach as described earlier, and, by noting that the credible interval is consistent with a wide range of transition probabilities, this method inherently accounts for the large uncertainty in the transition probability that we intuitively expect (Fig. 1).

The transition probabilities calculated with this approach can also be transformed into the stochastic rate constants with Eqn. (7). Therefore, this Bayesian inference-based method also provides an intuitive, explicit expression for how the uncertainty in the stochastic rate constants, k_i, diminishes with additional observations. One interesting case is that when no measurements have been made, the posterior distribution of the rate constants is equivalent to the prior distribution; all rate constants from 0 to ∞ are therefore equally probable. Thus, this analysis method is a very objective approach to analyzing transition probabilities from discrete state trajectories, and it is one that intrinsically encodes a statistically rigorous approach to the precision of such calculations.

Bayesian Transition Probability Expansion Analysis

We can also extend the transition probability expansion analysis approach to account for the precision of these calculations in a statistically robust manner with the application of Bayesian inference. Since the probability of undergoing a transition from state i to state j during a measurement period, n, was modeled with the binomial distribution, the binomial distribution will be the likelihood function used to perform Bayesian inference. The binomial distribution depends upon a single parameter: the probability of a success, P, which, in this case, is the transition probability P_ij. Mathematically, the conjugate prior to the binomial distribution is also the beta distribution, which is consistent with the interpretation of the beta distribution as describing the probability of a probability. Without any foreknowledge of the transition probability or, equivalently, the stochastic rate constant, we will use a flat, uninformative prior of α₀ = β₀ = 1. From this prior probability distribution, the resulting posterior probability distribution for P_ij is a beta distribution with α = 1 + M_ij, and $\beta =1+\left({\sum }_j{M}_{\mathit{ij}}\right)-M_{\mathit{ij}}$. Interestingly, while this posterior probability distribution can be quantified for each observed transition trial, it is equivalent to the posterior probability distribution calculated using Bayesian dwell time distribution analysis once all of the transition trials that comprise a particular dwell time have been analyzed (Fig. 1). For the extreme example of a state trajectory with one transition from a one measurement period-long dwell time (n_ij = [1]) the posterior probability distribution would then be α = (1 + 1 = 2), and β = (1 + 1 − 1) = 1. The mean and the credible interval for the beta distribution can then be calculated as described above, as can the stochastic rate constants related to these transition probabilities.

Interestingly, a more encompassing, Bayesian approach to inferring transition probabilities is obtained by considering all of the parallel reaction pathways out of state i at once. In this case, the multivariate generalization of the binomial distribution, which is called the multinomial distribution, is more appropriate for the likelihood function, as it models the probability of a Bernoulli trial where there are different types of successes — although only one type of success is chosen at a time. The conjugate prior to the multinomial distribution is the Dirichlet distribution,

$$p(\mathit{x}\mid \mathit{\alpha })=\frac{1}{\mathit{B}(\mathit{\alpha })}{\prod }_{i=1}^K{x}_i^{{\alpha }_i-1},$$ (22)

where bold characters denote a vector and B(x) is the multinomial beta function of x. Unsurprisingly, the Dirichlet distribution is the multivariate generalization of the beta distribution; in fact, in the case of only one type of success (i.e., in one dimension) they are equivalent. Analogously, we will use a flat, uninformative prior of α_ij = 1, such that each j^th element of α is unity. As a result, the posterior probability distribution is α_ij= 1 + M_ij. In order to analyze the transition probability of an individual reaction pathway out of state i from this posterior probability distribution of the transition probabilities for all the possible transitions, we can marginalize the posterior Dirichlet distribution. The result is that the posterior probability distribution for one of the reaction pathways is a beta distribution with α = α_ij = 1 + M_ij, and $\beta ={\beta }_{\mathit{ij}}=\left({\sum }_j{\alpha }_{\mathit{ij}}\right)-{\alpha }_{\mathit{ij}}=\left({\sum }_{j}1\right)+\left({\sum }_j{M}_{\mathit{ij}}\right)-\left(1+M_{\mathit{ij}}\right)$. This is equivalent to the binomial result for a two-state system given at the start of this section. Regardless, the most notable aspect of this treatment is that the mean posterior probability distribution is equivalent to the transition probability matrix that is calculated using an HMM. Notably, the Bayesian-based HMMs go even further, and utilize Dirichlet distributions such as this one to describe the posterior probability distributions of the transition probabilities.^7-10 As such, both this Bayesian transition probability expansion analysis approach and the Bayesian-based HMMs are able to describe the precision associated with the transition probabilities calculated from a finite number of transitions by calculating a credible interval from the marginalized distribution as described above.

Importantly, unlike maximum-likelihood methods, the Bayesian inference-based approach to transition probability expansion analysis enables the statistically robust analysis of trajectories where there are not only zero transitions to a particular state, but also when there are no transitions at all during a state trajectory. In these cases, the on-diagonal elements of M, M_ii, will reflect the measurements from the state trajectory that were assigned to state i, even though the final state was unclear. In doing so, the prior probability distribution accounts for the numerical instability that would otherwise yield infinitely precise estimates of stochastic rate constants that are zero when using the maximum-likelihood approach.

Accuracy of Calculated Stochastic Rate Constants

Characterizing Missed Events

While discretized, idealized state trajectories can be used to analyze the single-molecule reactions, many factors complicate the quantification of these state trajectories, and limit the amount of information that can be extracted from them. For instance, if the underlying single-molecule reaction is faster than the time resolution (i.e., the integration time of each measurement) of the experimental technique used to record the signal trajectories from which the state trajectories originate, then there is a risk that excursions to states with dwell times, t, that are significantly shorter than the measurement period, τ, will be missed. The consequence of this type of situation is that the idealized, discretized state trajectory will contain missing transitions, misclassified transitions, and missed dwells such that it is no longer a reasonable representation of the underlying single-molecule reaction. As a rule of thumb, the effects of missed events in a state trajectory begin to become pronounced when, for a stochastic rate constant, k, the condition kτ > 0.1 is true (i.e., k is greater than about 1/10^th of the acquisition rate). This is because, for a Markovian reaction, the exponential distribution dictates that when kτ = 0.1 about 10% of the dwell times will be shorter than the measurement period, τ. This percentage increases as the stochastic rate constant increases, leading to a substantial number of missed events. In the sections that follow, we discuss how missing such events when transforming signal trajectories into state trajectories complicates the process of analyzing single-molecule kinetic data using state trajectories (Fig. 2), and then discuss how one might correct for these effects in order to ensure the accuracy of analyzing single-molecule kinetic data using state trajectories.

Figure 2. Types of Missed Events.

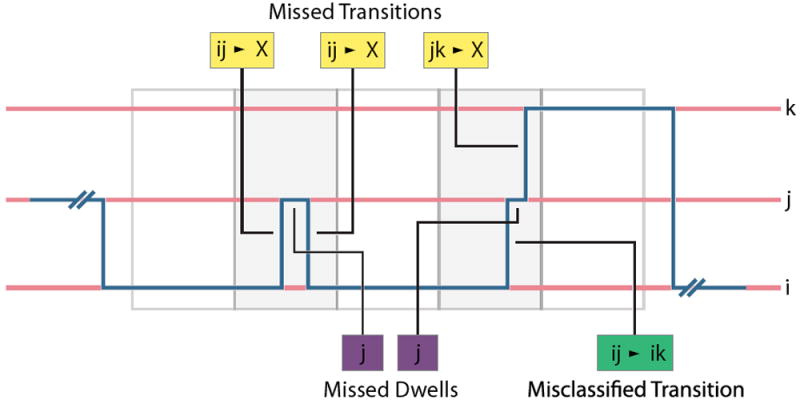
An example of a single molecule’s path through state-space is shown in blue, and it transitions between three states (i, j, and k) shown in red. Measurement periods over which the experimental signal is time averaged are shown as alternating white and grey boxes. Missed transitions are shown in yellow, misclassified transitions are shown in green, and missed dwells are shown purple.

Finite Length of Signal Trajectories

Many factors limit the length of the signal trajectories that can be collected from individual biomolecules using single-molecule kinetic techniques. Superficially, the patience of the experimenter and the practical data storage limitations of computers restrict this length. Practically, the stability of the biomolecular system can limit the length of an experiment; for instance, many enzymes become inactive after a certain time spent at room temperature under in vitro conditions, or, depending on the acid-base properties of the reactants and products of the reaction being investigated, the buffering capacity of a buffer might saturate. More commonly, however, is the fact that the signal corresponding to an individual molecule can simply be lost, for instance, by photobleaching of a fluorophore, or by dissociation of a tether, and such an event terminates the signal trajectory. Regardless of the cause, signal trajectories are finite in length and do not extend infinitely. Thus, considering the ergodic hypothesis, the data from a single molecule will consequently not contain enough information to completely characterize a system. In an extreme case, one can imagine a state trajectory where no transitions occur before signal loss. Such a situation places a clear limitation on the precision with which the dynamics of the single-molecule system can be quantified. This consideration applies to all state trajectories generated during the analysis of single-molecule kinetic data, because all of these trajectories will have a finite length.

Missed Transitions

Consider a single molecule that dwells in a particular state, i, for some length of time, t. Eventually, the single molecule will transition to a new state, j. If the dwell time, t, in j is shorter than the measurement period, τ, there is a chance that the single molecule might transition back to i during the measurement period (Fig. 2, yellow boxes). This is more likely to occur with increasingly fast rate constants for the transition from j to i. In such a case, neither the initial transition from i to j, nor the subsequent transition from j to i would be registered in the state trajectory. Instead, the single molecule would appear to have remained in i throughout this measurement period, n, – not having transitioned to the new state; this event is called a missed transition, and they affect the n_ij, and thus M. The direct consequence of the missed transition is that the number of transitions from i to j, M_ij, would be underestimated, ultimately resulting in an underestimation of k_ij. Additionally, as a result of the missed transition, the initial dwell time in i would be overestimated, because it would be the combined length of the initial dwell time and the following dwell time in i, consequently resulting in an overestimation of M_ii, and, ultimately, an underestimation of k_ij. Similarly, in this example, the transition back from j to i is also missed, resulting in an underestimation of M_ij, and therefore an underestimation of k_ji.

Misclassified Transitions

A related occurrence is that of misclassified transitions, rather than of missed transitions. In this case, a single molecule beginning in state i could transition to state j, where it dwells for a period of time, t, that is less then the measurement period, τ. Instead of transitioning back from j to i, as in the example above, however, the single molecule could transition to a third, distinct state, k. In this case, the initial dwell time in i can approximately be correctly measured from the state trajectory, but the transition from i to j will be misclassified as a transition from i to k, and the transition from j to k will be entirely missed (Fig. 2, green box. As a result of this misclassification, M_ij will be underestimated, while M_jk will be overestimated. These misestimations result in an underestimation of k_ij, and an over-estimation of k_jk. Moreover, in cases where j is an obligatory intermediate in the transition from i to k, such misclassified transitions could lead to an incorrect kinetic model in which the fact that j is an obligatory intermediate is not deduced, and, instead, direct transitions from i to k are erroneously concluded to occur.

Missed Dwells

In the example of the missed transition from state i to state j given in above, we described a dwell time, t, in state j that was shorter than the measurement period, τ. This transient dwell time, which resulted in the missed transition, is called a missed dwell because it is so short that the time spent in j was not registered in the state trajectory (Fig. 2, purple boxes). While the missed dwell is closely related to the missed transitions (it is causal), it and its effects are conceptually distinct from a missed transition. The missed dwell in j yields an underestimation of M_jj, and, consequently, an overestimation of k_jx, where x stands for any state accessible from j. However, it also can provide drastic overestimates of the entries in n_ix, which, as we show below, can seemingly distort otherwise normal Markovian behavior.

Correcting Rate Constants for the Finite Length of Signal Trajectories

Biomolecular systems may undergo very long-lived dwell times, t, relative to the finite length of a signal trajectory. For example, in an smFRET experiment, signal loss due to fluorophore photobleaching can occur before a transition occurs. In such a case, the entire state trajectory is typically discarded, and is not included in any subsequent dwell time distribution analysis. This is because the arbitrary experimental end time of the signal trajectory truncates the last and only dwell time, and it is therefore unclear to which n_ij such a dwell time belongs. As a result, such long-lived dwell times are typically unclassified, and systematically excluded from further analyses, which can result in a misestimated counting matrix, M, but, also, it reduces the amount of data in M to a point where any subsequent calculation of a stochastic rate constant will be extremely imprecise.

Fortunately, there is a straightforward correction that can be employed to correct for this loss of the excluded data, which relies on a control experiment. By including the unclassified dwell times in the i^th state into M_ii, the counting matrix is augmented to account for the effect of not having observed a transition during the finite length of the signal trajectory. This is true if the finite length of the trajectory is due to stochastic causes (e.g., photobleaching, or dissociation of a tether) or deterministic causes (e.g., prematurely terminated data collection).⁴⁰ Notably, the uncertainty in the transition probabilities quantified by the Bayesian inference approaches introduced in the previous sections accounts for the unobserved transitions. One complicating factor, however, is that any resulting stochastic rate constant calculated from this counting matrix will be the sum of the parallel reaction pathways of both the reaction under consideration, as well as the stochastic causes of signal termination. Mathematically, this can be expressed as

$$K_{\mathit{ij}}^{\mathrm{obs}}=K_{\mathit{ij}}+K_{\mathit{st}},$$ (23)

where $k_{\mathit{ij}}^{\mathrm{obs}}$ is the observed stochastic rate constant from states i to j calculated from the augmented counting matrix, and k_st is the stochastic rate constant governing the stochastic termination of the signal trajectory. Fortunately, k_st can be measured using a control experiment performed at the single-molecule level or at the ensemble level (e.g., by measuring the rate of photobleaching or of dissociation of a tether. Therefore, the true stochastic rate constant in the absence of these signal-terminating processes, k_ij, can be calculated using Eqn. (23). Finally, we note that this correction can easily be extended to address additional considerations, such as inactive subpopulations, as it simply entails modifying the on-diagonal elements of the counting matrix, M, to account for otherwise ignored contributions.

Correcting Stochastic Rate Constants for Missed Dwells and Transitions

One well-characterized method to correct for the effects of missed dwells and missed transitions upon the calculation of stochastic rate constants is through the augmentation of the kinetic mechanism with ‘virtual states’.⁴¹ This method originated in the field of single-molecule conductance measurements on ion channels, where researchers such as Colquhoun and Hawkes pioneered the use of HMMs to analyze the stochastic kinetics of individual ion channel opening and closing events.¹⁹ The general approach of this method to correct stochastic rate constants is to consider the expected number of missed dwells in a particular state. These expected, missed dwells are then classified into virtual states, which then account for any missed dwells without artificially contaminating the dwells that were actually observed. While this method was developed in Ref. 41, and reviewed several times since,^19,42 we briefly explore it here for completeness.

Assume that there is some ‘cutoff time’, τ_c, for which a dwell time shorter than τ_c would become a missed dwell in a state trajectory. Interestingly, τ_c is related to the distinction in signal between two states in a signal trajectory, more than to a particular dwell time. For instance, if one is assigning states in a state trajectory based upon the crossing of a threshold, then τ_c is the amount of time in a state that yields a time-averaged signal that crosses that threshold. Along these lines, τ_c is also related to the noise and other particulars of the recording equipment used in the experiment. Unfortunately, it remains an open question as to how to exactly determine τ_c.^41,42 For example, consider the asynchronicity of the stochastic transitions between states relative to the start of a measurement period in a signal trajectory. For an arbitrary dwell time of length t = τ, the measurement period length, a single molecule will, at least, occupy the state for one half of a measurement period, and, at most, for all of a measurement period; the exact amount depends upon the exact times when the transition occurred, and when the measurement began. Regardless, given an evenly spaced threshold, both of these observed dwell times of length τ would time average the signal past the threshold — either during the measurement period, n, where the transition occurred, or during the neighboring one, n+ 1. However, given several dwell times of the exact same length τ/2 < t < τ, only some of these dwell times would pass the threshold and be detected; the success of these detections would depend only upon the stochastic time of the transition relative to the beginning and end time of the measurement period. Therefore, any static value of τ_c stochastically excludes only some, but not all, of the dwell times of these lengths. Regardless, τ_c should hypothetically be between 0, and τ.

To perform the stochastic rate constant correction, consider a single-molecule experiment on a reversible, two-state system, 1 ⇌ 2, with forward and reverse stochastic rate constants of k₁₂ and k₂₁, and where measurements are made with a measurement time period, τ. For instance, this reaction could be a conformational change, ligand binding event, or folding process between states 1 and 2 of a biomolecular system. In this case, the forward reaction occurs from state i = 1 only to state j = 2, while the reverse reaction occurs from state i = 2 only to state j = 1. For a particular observed dwell time in state 1, the following dwell time in state 2 can either be a missed dwell, or an observed dwell if it is of length t < τ_c, or t > τ_c, respectively. Since each missed dwell can induce a missed transition in a state versus time trajectory, this criterion also allows us to split the true number of transitions in a state trajectory into those that are observed transitions, and those that are missed transitions. Furthermore, by considering the mean of the Poisson distribution, an equivalent statement can be made for the stochastic rate constants; therefore, the true stochastic rate constants can be partitioned as

$$k_{\mathrm{true}}=k_{\mathrm{observed}}+k_{\mathrm{missed}}.$$ (24)

From Eqn. (24), we can calculate a corrected stochastic rate constant, k_corrected, in place of k_true, by utilizing a virtual state to account for the contribution for k_missed. Since we know the dwell times assigned to the virtual state are those that were missed, this expression can be written as

$$k_{\mathrm{corrected}}=k_{\mathrm{observed}}+f_{\mathrm{missed}}·k_{\mathrm{corrected}},$$ (25)

where f_missed is the fraction of the total transitions that are missed transitions. Because a missed dwell in the subsequent state causes a missed transition in the state of interest, for a Markovian system f_missed in state 1 is the fraction of dwell times in state 2 that are less than τ_c, which is f_missed = 1 − e^{−k₂₁τ_c}. An equivalent expression can be written for the f_missed in state 2. Therefore, by substituting this expression into Eqn. (25), we find

$$\begin{array}{llll}{k}_{12,\mathrm{corrected}}& =& k_{12,\mathrm{observed}}·e^{k_{21,\mathit{corrected}}{\tau }_c},& \mathrm{and}\\ k_{21,\mathrm{corrected}}& =& k_{21,\mathrm{observed}}·e^{k_{12,\mathit{corrected}}{\tau }_c}.& \end{array}$$ (26)

This resultant set of coupled equations is non-linear, so the solution to the corrected stochastic rate constants can be calculated numerically by minimizing the sum of squares of these equations.⁴² Without the correction, the observed stochastic rate constants for a two-state system begin to become inaccurate when the stochastic rate constants become faster then one-tenth of the acquisition rate, τ⁻¹. This correction increases the region over which stochastic rate constants can be accurately calculated, such that the corrected stochastic rate constants are now ~90% accurate when they approach the acquisition rate; the inaccuracy is partially due to an unclear choice of τ_c, and also that the correction assumes a well quantified k_observed, which may not be the case, especially given any misclassified transitions. Additionally, there are sets of true stochastic rate constants that do not provide a solution to these equations, and those that do unfortunately have two solutions—one with faster stochastic rate constants and one with slower stochastic rate constants—so, it can be challenging to pick the proper solution.⁴¹

Seemingly Non-Markovian Behavior Induced by Missed Dwells

While we have described how to partially account for missed dwells and missed transitions when calculating stochastic rate constants from state trajectories, the assumptions used to both calculate the observed stochastic rate constants and to correct the observed stochastic rate constants rely on the system being Markovian. Experimentally, many single-molecule systems seem to exhibit non-Markovian behavior,^43,44 and this is typically assessed, if at all, by checking to see whether the discrete dwell times observed in a particular state are distributed according to the geometric distribution PMF (Markovian) or not (Non-Markovian). Again, all of the methods described above that directly address stochastic rate constants assume Markovian behavior, and should not be applied in the case of non-Markovian behavior. Additionally, it is worth noting that model selection for HMMs depends upon this assumption as well.^7-10 With these limitations in mind, here we demonstrate that one particularly detrimental consequence of missed dwells in an otherwise Markovian state trajectory is the introduction of seemingly non-Markovian behavior.

To demonstrate the introduction of seemingly non-Markovian behavior into a Markovian system during the analysis of state trajectories, consider a single-molecule kinetic experiment that is performed on a reversible, two-state, Markovian system, 1 ⇌ 2, with forward and reverse rate constants k₁₂ and k₂₁, respectively. As before, in this case the forward reaction occurs from state i = 1 only to state j = 2, while the reverse reaction occurs from state i = 2 only to state j = 1. If even one of these stochastic rate constants is relatively fast compared to the acquisition rate, there will be many missed dwells for that state. To be concrete, one such system might be where k₁₂ = 0.5 sec^-1, k₂₁ = 10.0 sec^-1, and τ = 0.1 sec; here k₂₁ is equal to the acquisition rate while k₁₂ is 20 times slower, and we therefore expect that there will be many missed dwells in state 2. The subsequent missed events can be readily observed in a signal trajectory (Fig. 3).

Figure 3. Seemingly Non-Markovian Behavior from a Markovian, Two-state System.

(Left) Plot of the first 60 sec of a signal trajectory from a simulated two-state, Markovian system. A state trajectory for this system was simulated for 2.5×10⁶ sec, and then the corresponding signal with signal means of 0 and 1 for states 1 and 2, respectively, was time averaged for each measurement period to create a signal trajectory. A negligible amount of Gaussian noise was added for visibility. The red line denotes the threshold used to idealize the data back into a state trajectory for analysis. Many dwells in the upper state are so transient that they result in missed dwells and missed transitions. (Right) Histograms of the observed dwell times for state 1 (top), and state 2 (bottom). The red curves are geometric distribution PMFs conditioned upon dwell times greater than 1 measurement period, which were calculated using the exact stochastic rate constants that were used for the simulation. Deviations are the apparent non-Markovian behavior. Contributions from observed dwell times comprised of compounded dwell times are shown as dashed curves.

After idealizing this signal trajectory into a state trajectory, perhaps by using a threshold, the observed length of each dwell time is used to calculate the stochastic rate constants. While the observed length of a dwell time in the state trajectory depends upon the true length of the dwell time in question, it also depends upon the true lengths of previous and subsequent dwell times. This is evident by considering the effect that a missed dwell has upon the state trajectory. Consider a dwell time in state 1 that is longer than the measurement period, τ, which is followed by a dwell time in state 2 that is shorter than the measurement period, τ (Fig. 2). Since this short dwell time in the transiently occupied state 2 will be missed, the previous and subsequent dwell times in state 1 are compounded together to create an overly long, observed dwell time in the state trajectory. These compounded dwell times can be composites of two, three, four, or higher integer-numbers of dwells in state 1; where the exact number is one more than the number of missed events in state 2. This dwell time compounding phenomenon also occurs for the dwell times in state 2, when the subsequent dwell time in state 1 is too short; nonetheless, in this example, there are rarely any missed dwells in state 1 because K₁₂ is so slow.

Observed dwell times that are actually several compounded dwell times introduce seemingly non-Markovian behavior into the state trajectory. This is apparent when inspecting the distribution of the lengths of the observed dwells in the state trajectory (Fig. 3, left). If the system is Markovian, these discrete dwell times should be distributed according to the geometric distribution PMF as described above. However, it is clear that the geometric distribution PMF does not adequately describe the distribution of these observed dwell times in this example, especially for the dwell times in state 1 (Fig. 3, right). Despite the Markovian behavior used to simulate this two-state system, the fast stochastic rate constant k₂₁ yields a dwell time distribution with behavior that is seemingly non-Markovian. As such, it is important to recognize that, in this particular situation, analysis methods that assume Markovian behavior would be deemed inappropriate for analyzing this data. Beyond the problem of attempting to correct for missed events, in order to accurately calculate stochastic rate constants from single-molecule kinetic data recorded on systems governed by such fast stochastic rate constants, a new approach must be developed that would effectively enable ‘temporal super-resolution’ of the data collected from any single-molecule kinetic technique. Recently, we have developed a Bayesian-inference based method to do this that we call Bayesian Inference for the Analysis of Subtemporal Resolution Data (BIASD) (manuscript in preparation).

Conclusions

While we highlighted several well-established methods for calculating stochastic rate constants from state trajectories, the reporting of the precision associated with the resultant stochastic rate constants has often been underappreciated. Here, we have shown that a common Bayesian inference-based framework is able to provide the uncertainty associated with the analysis of every data point in a statistically robust manner; thus, not only does it provide an intuitive method to integrate concerns about precision into stochastic rate constant calculations, but it helps to maximize the efficiency of the experiment by enabling the analysis of the entirety of the data. In addition, we categorized the types of missed events that often appear after idealizing signal trajectories into state trajectories, and discussed the consequences of these missed events as well as some of the methods that can be implemented to account for them and improve the accuracy of stochastic rate constant calculations. Perhaps in the future, more detailed, statistical descriptions of the underlying molecular dynamics present in the signal trajectories, such as that offered by BIASD, will be developed to further overcome these limitations.