Longitudinally and inter-site consistent multi-atlas based parcellation of brain anatomy using harmonized atlases

Abstract

As longitudinal and multi-site studies become increasingly frequent in neuroimaging, maintaining longitudinal and inter-scanner consistency of brain parcellation has become a major challenge due to variation in scanner models and/or image acquisition protocols across scanners and sites. We present a new automated segmentation method specifically designed to achieve a consistent parcellation of anatomical brain structures in such heterogeneous datasets. Our method combines a site-specific atlas creation strategy with a state-of-the-art multi-atlas anatomical label fusion framework. Site-specific atlases are computed such that they preserve image intensity characteristics of each site’s scanner and acquisition protocol, while atlas pairs share anatomical labels in a way consistent with inter-scanner acquisition variations. This harmonization of atlases improves inter-study and longitudinal consistency of segmentations in the subsequent consensus labeling step. We tested this approach on a large sample of older adults from the Baltimore Longitudinal Study of Aging (BLSA) who had longitudinal scans acquired using two scanners that vary with respect to vendor and image acquisition protocol. We compared the proposed method to standard multi-atlas segmentation for both cross-sectional and longitudinal analyses. The harmonization significantly reduced scanner-related differences in the age trends of ROI volumes, improved longitudinal consistency of segmentations, and resulted in higher across-scanner intra-class correlations, particularly in the white matter.

1. Introduction

The rapid growth of investigations incorporating neuroimaging data in recent years has brought new opportunities for studying brain structure and function (Van Horn and Toga, 2014). Particularly, longitudinal and multi-site magnetic resonance imaging (MRI) are becoming standard elements of neuroimaging studies, as they allow investigation of subtle progressive changes in brain structure over time and for large samples. An increasing number of longitudinal MRI studies are currently underway (Hedman et al., 2012; Mills and Tamnes, 2014), collecting image data over long time periods, sometimes going up to many decades. In addition, opportunities to pool data across studies provides large sample sizes enabling to address questions regarding interactive effects of various predictors, which is not possible within a single sample. However, a major challenge in longitudinal, as well as in multi-site, studies is the variability in scanners and image acquisition protocols. Thus, the development of image analysis techniques and analytical methods that are robust to such potential imaging variations is crucial to our ability to derive clinically useful imaging measurements, i.e. accurate and reliable measurements with high sensitivity to detect brain changes over time and across subject groups.

Automated identification and delineation of anatomical structures on MRI images is a fundamental task in neuroimaging. In recent years there has been a notable improvement in segmentation accuracy and reproducibility using multi-atlas segmentation (MAS) methods, which combine deformable registration and label fusion for transferring atlas labels of anatomical regions of interest (ROIs) to the target image space (Iglesias and Sabuncu, 2014). The consensus labeling increases the segmentation accuracy, as multiple warped atlases provide complementary information about the anatomy, and they correct each other’s errors. Moreover, subject-specific regional selection or weighting of different atlases provides a way for locally matching the atlas dictionaries to the individual anatomy. MAS is now considered the state-of-the-art technique for segmenting the brain into anatomical structures, and has been applied in various studies for assessing regional changes in brain volume, for deriving imaging biomarkers in a range of neurological conditions, and for elucidating processes like brain development or aging (Heckemann et al., 2011; Oishi et al., 2013; Habes et al., 2016). However, most analyses, as well as validations for diverse MAS methods, have been limited to relatively homogeneous datasets without significant scanner or image acquisition variability. Like all segmentation methods, MAS is sensitive to image contrast variations, which may result in systematic over- and under-segmentation of brain tissues in a way that is inconsistent across scanners and imaging protocols.

The influence of scanner differences on MR image contrast and their effect on tissue segmentation has been previously reported (Clark et al., 2006). Han et al. (2006) evaluated the precision of an automated cortical thickness measurement within- and across-scanner platforms and field strengths, and found that the thickness measurements across field strengths (specifically between 1.5T and 3T scans) were slightly biased, suggesting that this measurement bias must be taken into account in the design of multi-site or longitudinal studies. Jovicich et al. (2009) assessed the impact of various image acquisition variables on the volumes of anatomical structures computed through atlas based segmentation, and similarly concluded that combining data across platforms and across field-strengths introduces a bias that should be considered in the design of multi-site studies. A comprehensive analysis in Kruggel et al. (2010) investigated the influence of scanner hardware and imaging protocol on the variability of morphometric measures using 1073 multi-site MRI examinations of 843 subjects. In agreement with previous findings, this study showed that using different acquisition conditions in the same subject, the variance of volumetric measures was up to 10 times greater, which is mainly explained by scanner-dependent differences in the tissue contrast between GM and WM.

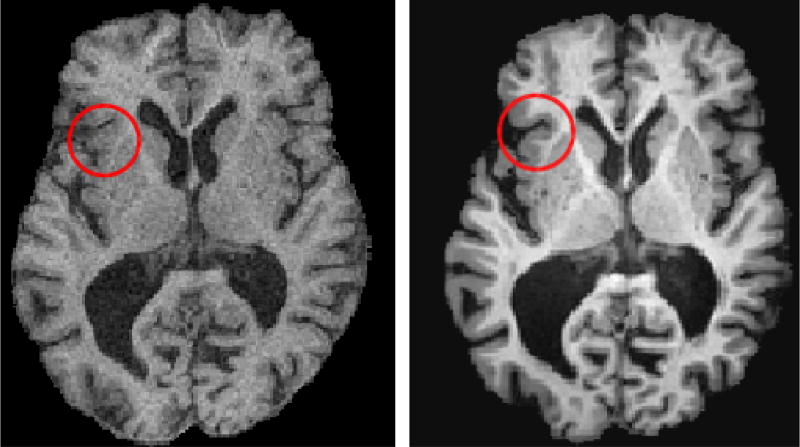
In this paper, we address this important challenge, and we present a new MAS framework that is specifically designed to achieve a consistent parcellation of anatomical brain structures in longitudinal MRI datasets with inter-scanner and/or imaging protocol differences. A typical example that motivates our work is shown in Figure 1. This example highlights tissue contrast differences between two consecutive scans of the same subject acquired using a 1.5T SPGR protocol in a GE scanner and using a 3T MPRAGE protocol in a Philips scanner. The proposed method is founded on a relatively recent multi-atlas segmentation method that utilizes a rich ensemble of warped atlases (Doshi et al., 2016). We extend the common MAS framework, however, by introducing a site-specific atlas creation strategy, by which a different set of atlases is computed for each different MRI site³. These atlases are subsequently used for segmenting all images from the same site. The site-specific atlases share the same ROI labels, imposing the consistency of segmentations, while each atlas set preserves the image intensity characteristics of the specific site. We should note that, after the atlas creation, which is performed only once for a dataset, the segmentation is performed individually for each image using the standard MAS framework. In this regard, our method is considerably different from 4D image registration and segmentation methods (Xue et al., 2006; Fan et al., 2007; Roy et al., 2013; Csapo et al., 2013) for which a model is calculated using all time series of a subject, thus requiring recalculation of the model for each new scan. Our method is also different from Han and Fischl (2007), one of the few methods that addressed the same problem within the atlas-based segmentation framework, as in their work an atlas renormalization procedure was applied for each new target image, and adjustment of the intensity model was performed individually for each ROI.

Figure 1.

An example that illustrates differences in tissue contrast between GM/WM and GM/CSF in two consecutive scans of the same BLSA participant acquired in scanners with different field strengths, protocols and manufacturers (left 1.5T GE SPGR, right 3T Philips MPRAGE). The SPGR image was linearly aligned to the MPRAGE image space.

The development of our segmentation method, which is available in our image processing portal as a web-accessible application⁴, was motivated by data and the scientific objectives of the neuroimaging substudy of the Baltimore Longitudinal Study of Aging (BLSA) (Resnick et al., 2000, 2003), which has collected a variety of longitudinal datasets since 1994 to investigate age related changes in brain structure as early markers of cognitive decline and Alzheimer’s disease. BLSA has acquired longitudinal MRI images of aging adults (2 to 15 time points) using either 1.5T SPGR or 3T MPRAGE protocols that also varied with respect to scanner vendor (GE and Philips respectively). We hypothesized that the proposed method would improve the longitudinal consistency of the segmentations of anatomical regions, suggesting that it could be a useful tool for the harmonization of brain volume measurements in longitudinal studies.

2. Materials and Methods

2.1. MRI Dataset Description

The BLSA study is a prospective longitudinal study of aging and early markers of Alzheimer’s Disease. The neuroimaging component of BLSA has followed individuals since 1994 with annual or semi-annual imaging and clinical evaluations (Resnick et al., 2000, 2003). At the time of our analysis the BLSA data sample included 2036 scans from 721 subjects, for the most part acquired using two different scanners and acquisition protocols. Specifically, from February 1994 through July 1999, MR scanning was performed on two similarly configured GE Signa 1.5 Tesla scanners, to acquire a high-resolution volumetric “spoiled grass”(SPGR) series. A third GE 1.5 T Signa scanner with a slightly different configuration was used between 1999 and 2005. From 2009 on, all scans were acquired on a single Philips 3T scanner using a 3D “magnetization prepared rapid gradient echo” (MPRAGE) sequence.

In our validation experiments, we used two samples derived from the complete BLSA dataset. Sample-A was obtained by using the first 1.5T SPGR and first 3T MPRAGE scan of each participant, and was used for assessing cross-sectional age trends of calculated ROI volumes for the two scanner types. Sample-B was used for evaluating longitudinal consistency of MRI volumes and was obtained by including all scans from participants for whom both 1.5T SPGR and 3T MPRAGE scans were acquired. The sample characteristics of these two datasets are presented in table 1.

Table 1.

Demographic characteristics of the BLSA samples used in validation experiments.

Sample-A: Cross-sectional
	Total	1.5T GE SPGR (1999–2005)	3T Philips MPRAGE (2008 onwards)
Number of subjects	650	154	496
Number of females	338	63	275
Age		70.2 (7.9)	71.4 (8.1)
		56.0–85.9	55.0–86.0
Race (White,Black,Other)	453 (69.7%)	139 (90.3%)	314 (63.3%)
	168 (25.9%)	15 (9.7%)	153 (30.9%)
	29 (4.5%)	0 (0%)	29 (5.9%)
Education	16.8 (2.5)	16.5 (2.7)	16.9 (2.4)
	8.0–21.0	8.0–21.0	8.0–21.0
Sample-B: Longitudinal
	Total	1.5T GE SPGR (1999-2005)	3T Philips MPRAGE (2008 onwards)
Number of subjects	63	63	63
Number of females	30	30	30
Race (White,Black)	51 (81.0%)
	12 (19.0%)
Education	17.0 (2.3)
	12.0–21.0
Number of scans	671	519	152
Number of scans per subject	11.3 (3.2)	8.2 (2.4)	2.4 (1.2)
	2–17	1–11	1–5
Follow up time (years)	17.7 (1.9)	8.6 (2.7)	3.2 (2.0)
	13.2–20.6	0–11.7	0–6.2
Age at first MPRAGE scan			80.6 (6.2)
			69.1–95.1
Age at last SPGR scan		74.7 (7.4)
		56.2–91.1
Interval (yrs) between last SPGR and first MPRAGE	5.9 (3.2)
	2.1–17.3

2.2. Multi-atlas segmentation of ROIs

Atlas-guided segmentation of anatomical regions involves deforming (warping) an atlas image into the target space to establish spatial correspondences between the two images, and then transferring the atlas ROI labels to the target image. In the multi-atlas setting, labels from multiple warped atlases are fused together to determine the final labels. We apply a new consensus labeling framework (Doshi et al., 2016) for ROI segmentation, called MUSE⁵, which was the top-ranking method in an extensive challenge (Doshi et al., 2013). This method uses a broad ensemble of warps that reflects variations due to the choice of the atlas, as well as the registration method and deformation parameters.

In the ensemble construction, we use two extensively validated registration algorithms, “Deformable Registration via Attribute Matching and Mutual-Saliency Weighting” (DRAMMS, v1.4.1) (Ou et al., 2011) and Advanced Normalization Tools (ANTS, v1,9.x with symmetric normalization transformation and with the probability mapping as the similarity metric) (Avants et al., 2008), as well as an ensemble of 35 atlases. For both methods, the main parameter that regulates the smoothness of the deformation field is sampled at two operational points (DRAMMS: regularization weights of 0.1 and 0.2, ANTS: gradstep of 0.25 and 0.5), combining both a smooth and a more aggressive registration, trading the deformation smoothness with higher matching between the warped atlas and the target images.

The reference atlas dataset consists of 35 3T MPRAGE brain MRI scans from 30 subjects scanned as part of the OASIS project and their corresponding ROI labels, which were provided as publicly available data in the 2012 MICCAI Challenge on Multi-Atlas Labeling⁶. ROI labels on atlas images were created semi-automatically using the brainCOLOR labeling protocol⁷.

2.3. Site-specific atlas generation

The ROI segmentation via multi-atlas label fusion is preceded by an atlas creation procedure that essentially aims to create a collection of mutually-consistent site-specific atlases from the image dataset. The first step of this process is the selection of a representative subset of subjects (k=32 in our experiments) whose scans will be used to create scanner-specific atlases. In atlas harmonization, a major challenge is to establish the correspondences between images from distinct sites, as the differences between images are both due to inter-subject variations in anatomy and due to scanner and protocol related image contrast differences. In our atlas construction procedure, we take advantage of the existence (in a longitudinal study) of multiple images from the same person in order to minimize inter-subject anatomy differences. Let I = {I_s,t ∈ {SITE₁, SITE₂} | s = 1, …, n ; t = 1, …, t_s} denote a set of longitudinal images acquired using two different scanners and with a variable number of time points for each subject, where I_s,t : Ω ⊂ R³ → R represents the 3D image acquired from subject s at time point t. Let τ(I_s,t) be the scan date of image I_s,t, such that ∀_{(Is,t∈{SITE1}, Is,t′∈{SITE2})} τ(I_s,t′) > τ(I_s,t). Also, let SITE₂ be selected as the “reference site”, for instance because SITE₂ scanners are more recent and have better tissue contrast. We determine k subjects with the shortest inter-scan date difference between consecutive scans from different sites:

$$s^{\ast }=\underset{s=\{(s_i,t_i)|i=1,\dots ,k\}\in S}{\text{arg min}}\sum _{i=1}^k\tau (I_{s_i,t_i+1})-\tau (I_{s_i,t_i})$$ (1)

where S is the set of indexes for all scans from SITE₁ for which the consecutive scan is from SITE₂.

The selection procedure aims to maximize correspondences between selected image pairs. However, the registration process may not be straightforward, since intervals may be present between scan times, thereby posing a challenge emanating from brain changes occurring during these intervals. To overcome this challenge, we propose next a robust registration strategy. We construct the image sets $T=\{(T_{{\mathit{\text{SITE}}}_1}^n,T_{{\mathit{\text{SITE}}}_2}^n)|n=1,\dots ,k\}$, where $T_{{\mathit{\text{SITE}}}_1}^n=\{I_{(s_n,t_n)},I_{(s_n,t_n-1)},\dots ,I(s_n,t_n-p)\}\in \{{\mathit{\text{SITE}}}_1\}\},T_{{\mathit{\text{SITE}}}_2}^n=\{I_{s_n,t_n+1}\}\in \{{\mathit{\text{SITE}}}_2\}$ and (s_n,t_n) ∈ s*. Note that for the reference site (SITE₂) a single scan is directly designated as the atlas image for each selected subject. For creating the SITE₁ atlases, in the other hand, multiple (i.e. p + 1) SITE₁ scans are selected for each subject, which are deformably registered to the corresponding SITE₂ scan using multiple transformations, and fused into a single atlas image:

$$A_{{\mathit{\text{SITE}}}_1}^n=\underset{i\in \{0,\dots ,p\},\theta \in \mathrm{\Theta }}{\cup }{\mathrm{\Phi }}_{\theta }(T_{{\mathit{\text{SITE}}}_1}^{n_i},T_{{\mathit{\text{SITE}}}_2}^n)$$ (2)

where ${\mathrm{\Phi }}_{I_t}^{\theta }(I_s)$ is a deformable transformation that maps every voxel of a source image I_s to a target image I_t space, Θ is the parameter vector that combines important parameters for variations of the deformation, specifically the deformation algorithm and the amount of regularization, and ∪ is the data fusion operator. For data fusion, we used here the voxelwise average of all warped images. We used two different deformable registration algorithms, specifically DRAMMS and ANTS, and two smoothness parameters (DRAMMS: regularization weights of 0.1 and 0.2, ANTS: gradstep of 0.25 and 0.5), similar to Doshi et al. (2016), and p was set to 1, resulting in 8 different warped images in total in the creation of each SITE₁ atlas. It’s important to note that the use of multiple warps, as well as multiple SITE₁ images in the atlas image creation procedure was motivated by the objective of obtaining a robust registration to SITE₂ image space.

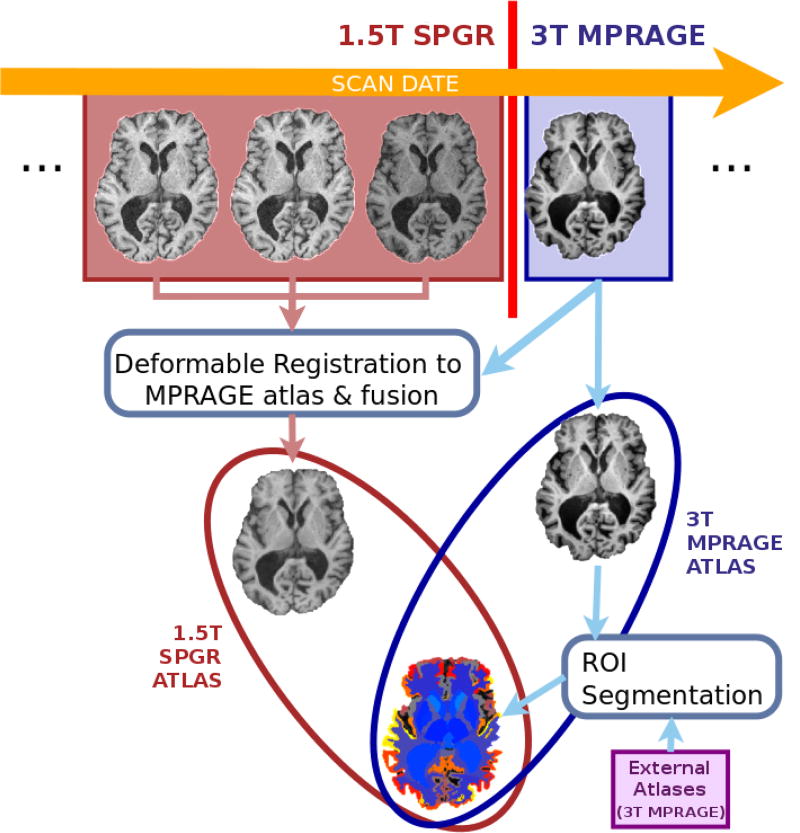
ROI label images for A_SITE2 are calculated through MUSE using external atlases as described in section 2.2. For A_SITE1, the ROI label images are not computed, but the ROI labels that were calculated for A_SITE2 are used as reference segmentations, with the aim of harmonizing the ROI definitions for the two different sites. An outline of the creation of a site-specific atlas pair is shown in figure 2. The same procedure is applied on all selected scans in S* for creating a site-specific atlas set with k pairs of mutually-consistent atlases, which are subsequently used for parcellation of all scans in the dataset using MUSE.

Figure 2.

Illustration of the the site-specific atlas creation procedure. The figure shows the creation of “one pair of atlases” for a longitudinal dataset with a change in scan protocol from 1.5T SPGR to 3T MPRAGE. The MPRAGE ROI label image is computed by applying the standard multi-atlas segmentation using external atlases. SPGR-atlas image is generated by deformably warping multiple SPGR images to MPRAGE image space and data fusion. The two atlas images in the same image space share the same ROI label definitions, while preserving the site-specific intensity characteristics of the original scan.

3. Results

From the complete BLSA sample we selected k = 32 subjects for the site-specific atlas creation. The average age of the selected subjects at the time of the first MPRAGE scan was 81.6 ± 6.9 (69.0 – 95.0) years. The average time between the last SPGR and the first MPRAGE scan was 4.2 ± 0.4 (2.7 – 4.9) years. The procedure described in section 2.3 was applied to create site-specific BLSA atlas datasets with 32 pairs of (SPGR and MPRAGE) atlas images and their ROI label images.

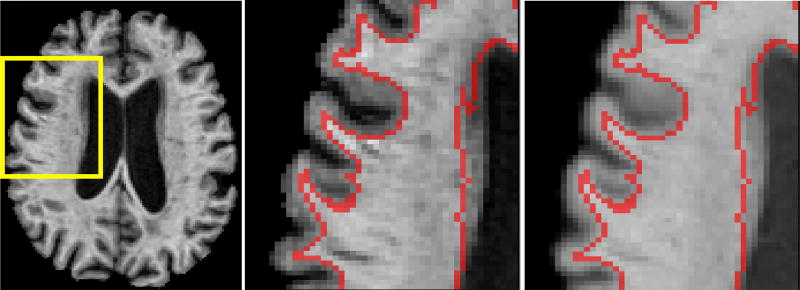
Figure 3 presents an example of the final SPGR and MPRAGE atlases. As shown in the figure, the two atlas images have different image contrasts, reflecting the differences in the intensity profiles of the original scans. Also, the SPGR-atlas image is smoother than the MPRAGE-atlas image, as it was constructed through the combination of multiple warps. Importantly, the MPRAGE-atlas image, which was used to determine ROI labels for both atlases, has higher image contrast, and thus can guide the segmentation of difficult-to-segment low-contrast areas on SPGR scans, while also enforcing consistency.

Figure 3.

Example of SPGR and MPRAGE atlases and the ROI labels. Left: The MPRAGE image; Middle: The ROI labels overlaid on the MPRAGE-atlas image (only the WM/GM boundary is shown); Right: The ROI labels overlaid on the SPGR-atlas image that was generated using the atlas creation procedure.

Each T1-weighted scan in the complete BLSA dataset, including scans used for constructing the site-specific atlases, has been segmented into ROIs by applying MUSE using the site-specific atlases. A direct quantitative evaluation of the segmentation accuracy is not possible, as there are no ground-truth ROI labels available for the BLSA scans. Hence, we performed a comparative analysis of the cross-sectional and longitudinal age trends of ROI volumes obtained from the two scanner types. We compared the “harmonized” ROI volumes, i.e. those extracted by applying MUSE with harmonized site-specific atlases, against the “unharmonized” ROI volumes that were obtained using standard MUSE with external atlases. We included in this analysis the values for 23 large ROIs that correspond to a lobar-level parcellation of the brain.

3.1. Cross-sectional age effects

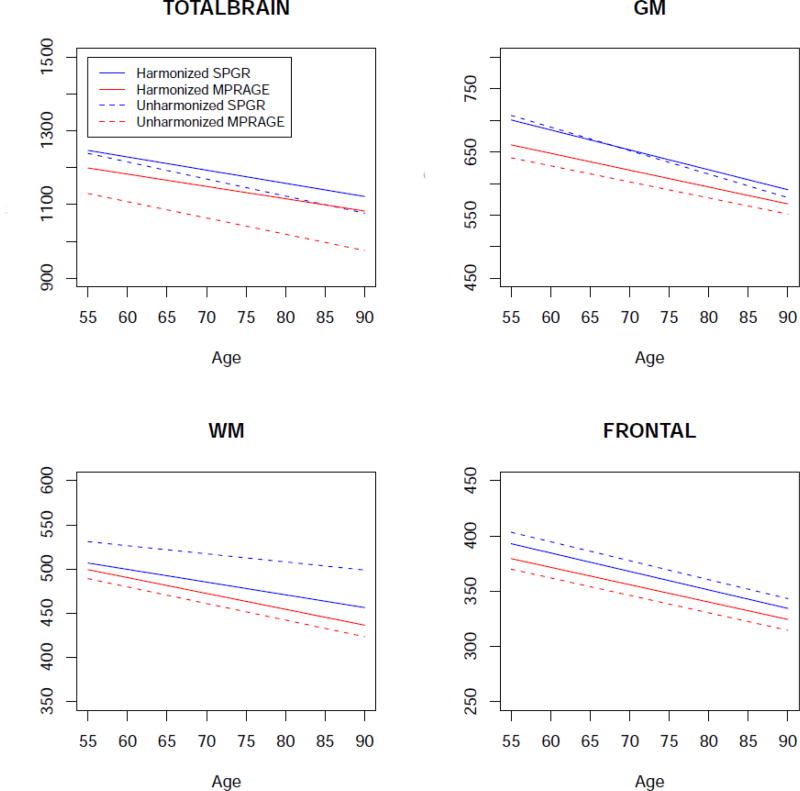
We first investigated cross-sectional relationships with age for the SPGR and MPRAGE scans, using the baseline SPGR and MPRAGE scans (Sample-A). In the cross-sectional analyses our main assumption was that regardless of the scanner type, subjects in similar age and disease conditions should have similar brain volumes. Figure 4 shows plots of sex-adjusted cross-sectional associations between age and volumes of total brain, WM, GM, and the frontal lobe (GM and WM together). As shown in the figure, SPGR and MPRAGE results were more similar for harmonized than unharmonized data.

Figure 4.

Cross-sectional age trends for total brain, GM, WM and the frontal lobe (GM and WM together) for the two scanner types, and for harmonized and unharmonized values. The values in y axis are in cm³.

We used ordinary least squares regression to model cross-sectional relationships between age and ROI volumes for the SPGR and MPRAGE data. The model we used in the linear regression was:

$$Y_i={\beta }_0+{\beta }_1\times {\mathit{\text{SEX}}}_i+{\beta }_2\times {\mathit{\text{AGE}}}_i+{\beta }_3\times {\mathit{\text{MPRAGE}}}_i+{\beta }_4\times {\mathit{\text{SEX}}}_i\times {\mathit{\text{AGE}}}_i+{\beta }_5\times {\mathit{\text{AGE}}}_i\times {\mathit{\text{MPRAGE}}}_i+{\epsilon }_i$$ (3)

In this model, age was centered at 55, sex was coded as −0.5 for female and 0.5 for male, and the MPRAGE variable was used as a binary variable that coded the scanner type, i.e. with value 1 for MPRAGE scans and 0 for SPGR scans. This kind of coding implies that the intercept value is the average volume between males and females at age 55 for SPGR, and β₂ with age is the average age effect across males and females for SPGR data. β₃ is the difference in intercept values between MPRAGE and SPGR, and was used to evaluate the amount of shift between the scanners. β₅ is the difference between MPRAGE and SPGR in the slopes of the age trends and was used to evaluate differences between scanners in age associations.

The percentage difference in intercept and the difference in slope between SPGR and MPRAGE for unharmonized and harmonized samples for the 24 ROIs are presented in Tables 2 and 3. At the intercept, harmonized data showed smaller differences between SPGR and MPRAGE compared with unharmonized data for 22 of 24 regions. For 5 of 24 regions unharmonized data showed significant differences between SPGR and MPRAGE in the slope of age trends. In contrast, only 1 of the 24 regions based on harmonized data showed significant differences between SPGR and MPRAGE in age associations.

Table 2.

Percentage difference in intercept between SPGR and MPRAGE in the cross-sectional sample

	Unharmonized		Harmonized
ROI	% difference in intercept	p-value	% difference in intercept	p-value
TOTALBRAIN	−8.8	<0.0001	−3.83	0.014
GM	−9.49	<0.0001	−5.62	<0.0001
WM	−7.88	<0.0001	−1.48	0.38
FRONTAL	−8.28	<0.0001	−3.44	0.04
LIMBIC	−6.87	<0.0001	−0.36	0.85
OCCIPITAL	−11.44	<0.0001	−4.71	0.012
PARIETAL	−11.51	<0.0001	−5.63	0.0006
TEMPORAL	−8.27	<0.0001	−4.13	0.013
DEEP WM GM	−0.6	0.69	0.42	0.78
CEREBELLUM	−9.64	<0.0001	−4.58	0.0065
VENTRICLE	−1.35	0.95	−4.01	0.85
BASAL GANGLIA	−0.61	0.76	0.08	0.97
CORPUS CALLOSUM	−4.41	0.076	−4.05	0.1
FRONTAL GM	−8.16	<0.0001	−4.86	0.0049
LIMBIC GM	−6.87	<0.0001	−0.36	0.85
OCCIPITAL GM	−11.54	<0.0001	−6.51	0.0006
PARIETAL GM	−12.02	<0.0001	−7.29	<0.0001
TEMPORAL GM	−10.08	<0.0001	−6.92	<0.0001
DEEP GM	−3.93	0.011	−3.01	0.05
FRONTAL WM	−8.4	<0.0001	−1.95	0.29
OCCIPITAL WM	−11.27	<0.0001	−1.46	0.5
PARIETAL WM	−11	<0.0001	−3.91	0.029
TEMPORAL WM	−6.44	0.0003	−1.21	0.51
DEEP WM	6.99	0.0003	8.49	<0.0001

Table 3.

Difference in slope of the age trends between SPGR and MPRAGE in the cross-sectional sample

	Unharmonized		Harmonized
ROI	difference in slope	p-value	difference in slope	p-value
TOTALBRAIN	0.22	0.83	0.24	0.83
GM	1.18	0.048	0.48	0.41
WM	−0.96	0.055	−0.35	0.47
FRONTAL	0.14	0.72	0.10	0.79
LIMBIC	0.07	0.086	0.04	0.29
OCCIPITAL	−0.19	0.17	−0.21	0.14
PARIETAL	0.13	0.50	0.08	0.68
TEMPORAL	0.02	0.93	0.08	0.72
DEEP WM GM	0.03	0.56	0.03	0.56
CEREBELLUM	−0.01	0.94	−0.03	0.84
VENTRICLE	0.07	0.74	0.09	0.68
BASAL GANGLIA	0.01	0.76	0.01	0.52
CORPUS CALLOSUM	0.04	0.046	0.04	0.051
FRONTAL GM	0.53	0.008	0.24	0.22
LIMBIC GM	0.07	0.086	0.04	0.29
OCCIPITAL GM	0.05	0.57	−0.08	0.38
PARIETAL GM	0.25	0.015	0.11	0.29
TEMPORAL GM	0.19	0.10	0.10	0.36
DEEP GM	0.02	0.16	0.02	0.14
FRONTAL WM	−0.40	0.059	−0.14	0.49
OCCIPITAL WM	−0.24	<.0001	−0.13	0.026
PARIETAL WM	−0.12	0.23	−0.03	0.77
TEMPORAL WM	−0.17	0.15	−0.03	0.82
DEEP WM	0.00	0.85	−0.01	0.26

3.2. Longitudinal analyses

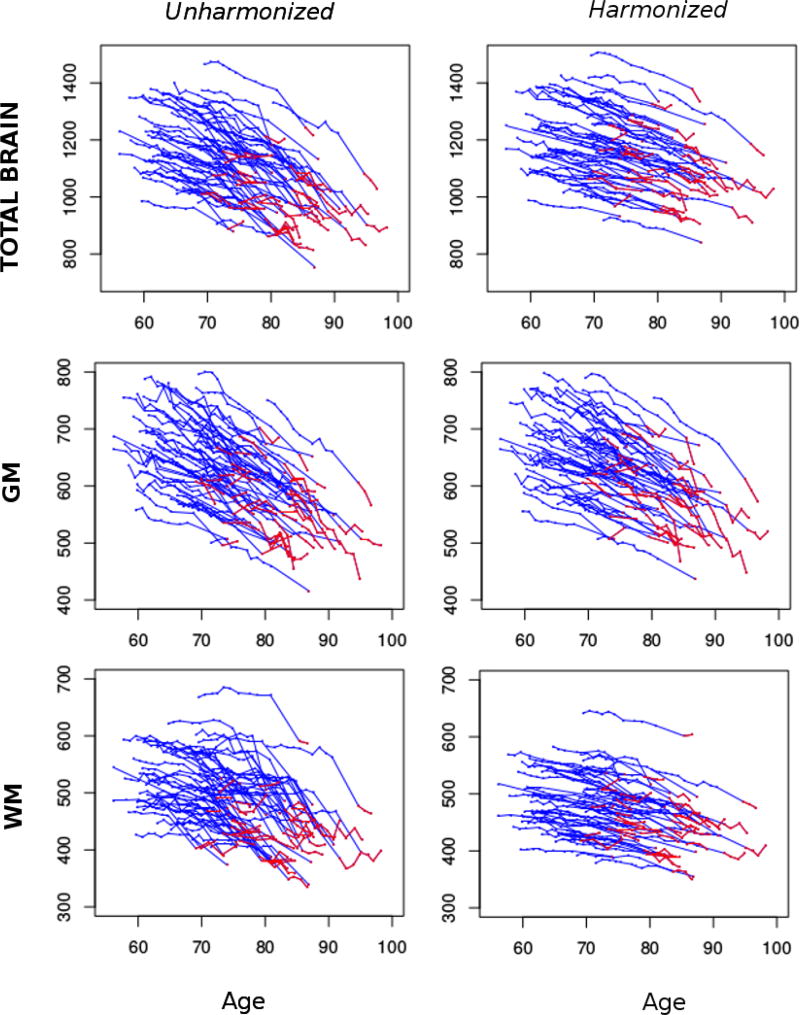
For the longitudinal analyses, we used all time points from participants that had both SPGR and MPRAGE scans (Sample-B). The unharmonized and harmonized datasets were based on exactly the same subjects and time points. Longitudinal age trajectories of major ROIs for unharmonized and harmonized datasets are shown in figure 5.

Figure 5.

Longitudinal age trajectories for total brain, GM and WM using standard multiatlas segmentation (left) and using the proposed harmonization method (right). SPGR scans are shown with blue color and MPRAGE scans are shown with red color.

3.2.1. Intra-class correlations

We used intra-class correlations (ICC) to assess the within-subject consistency of ROIs derived from SPGR and MPRAGE scans. A separate linear mixed effect model was fit with each ROI as a dependent variable. The intercept was used both as the fixed effect and the random effect to partition the variance into between-subject and within-subject variance. We calculated the intra-class correlation (ICC) for each ROI independently using:

$$\mathit{\text{ICC}}=\frac{{\sigma }^2(b)}{{\sigma }^2(b)+{\sigma }^2(w)}$$ (4)

where σ²(b) is the between-subject variance and σ²(w) is the within-subject variance. The ICC was calculated for SPGR scans only and across SPGR and MPRAGE scans. The summary statistics of ICC values over the 24 regions for harmonized and unharmonized datasets are shown in table 4. Consistent with the results of the cross-sectional analysis, the harmonization greatly improved the longitudinal consistency of the data with significantly increased ICC values across SPGR and MPRAGE scans. In 22 of 24 regions ICC values were higher in harmonized than unharmonized datasets, and ICC values were unchanged in other 2 regions. On average, the ICC increased from 0.75 to 0.85. The effect was particularly significant in the white matter (WM) regions, with ICC increasing from 0.69 to 0.91 for total WM, and from 0.56 to 0.88 for occipital WM.

Table 4.

Intra-class correlations (ICC) of the volumes of 24 ROIs for the longitudinal sample

	Unharmonized		Harmonized
	SPGR	SPGR and MPRAGE	SPGR	SPGR and MPRAGE
Mean	0.95	0.75	0.95	0.85
Max	0.99	0.95	0.99	0.96
3rd Qu	0.97	0.81	0.98	0.89
Median	0.96	0.73	0.96	0.87
1st Qu	0.92	0.70	0.94	0.80
Min	0.89	0.56	0.89	0.72

3.2.2. Longitudinal difference in intercept from SPGR to MPRAGE

To investigate the effect of the scanner change on the longitudinal trajectories of MRI volumes, i.e. to estimate the difference in the levels of MRI volumes after the scanner change, we used linear mixed effect models with each ROI volume as a dependent variable. The predictors included intercept, scanner (SPGR/MPRAGE), interval and scanner × interval. The interval variable was anchored at the beginning of the MPRAGE (interval = 0), so that follow-ups for SPGR scans are negative and followups for MPRAGE scans are positive. Please note that in this analysis we did not evaluate the differences in the slopes of MRI volumes, because the average number of time points for the MPRAGE scans was low (n=2.4 ± 1.2). The model was estimated for all 24 regions, and we report the percentage difference in intercept values in table 5. The results were in agreement with the cross-sectional analysis, showing a consistent reduction in the intercept shift from SPGR to MPRAGE, with the most significant effect in the WM.

Table 5.

Percentage difference in intercept between SPGR and MPRAGE for the longitudinal sample

	Unharmonized		Harmonized
ROI	% difference in intercept	p-value	% difference in intercept	p-value
TOTALBRAIN	−8.18	<.0001	−2.29	<.0001
GM	−2.99	<.0001	−2.02	<.0001
WM	−14.23	<.0001	−3.71	<.0001
FRONTAL	−8.34	<.0001	−2.69	<.0001
LIMBIC	−1.43	0.0049	3.63	<.0001
OCCIPITAL	−15.8	<.0001	−8.63	<.0001
PARIETAL	−10.9	<.0001	−4.99	<.0001
TEMPORAL	−7.17	<.0001	−1.81	<.0001
DEEP WM GM	4.2	<.0001	5.26	<.0001
CEREBELLUM	−6.65	<.0001	−1.67	<.0001
VENTRICLE	5.34	0.0019	5.71	0.0008
BASAL GANGLIA	4.17	<.0001	6.63	<.0001
CORPUS CALLOSUM	3.81	<.0001	3.34	<.0001
DEEP GM	1.62	<.0001	3.2	<.0001
FRONTAL GM	0.85	0.0587	−0.21	0.62
LIMBIC GM	−1.43	0.0049	3.63	<.0001
OCCIPITAL GM	−9.07	<.0001	−8.53	<.0001
PARIETAL GM	−3.71	<.0001	−3.45	<.0001
TEMPORAL GM	−4.13	<.0001	−2.86	<.0001
FRONTAL WM	−16.2	<.0001	−5.08	<.0001
OCCIPITAL WM	−25.29	<.0001	−8.81	<.0001
PARIETAL WM	−17.13	<.0001	−6.45	<.0001
TEMPORAL WM	−9.87	<.0001	−0.81	0.0035
DEEP WM	9.92	<.0001	7.14	<.0001

4. Discussion

In this paper we addressed a major challenge of volumetric brain analyses in longitudinal MRI studies. In many longitudinal studies changes in scanners and imaging protocols between time points are unavoidable due to the duration of the study and rapid changes in scanner hardware and software technology. In addition to the importance of harmonization in longitudinal studies, harmonization of MRI images is also a critical task for multi-site analyses, where multiple MRI datasets are pooled and analyzed together (Van Horn and Toga, 2014). Common approaches for addressing this challenge are to analyze volumetric measurements from different studies independently, or to “correct” them by including the scanner type or site as a covariate in the final statistical analysis. In the former case the data are not used to their full potential, while in the latter case the correction may capture spatially specific patterns of scanner related variations in the data only at a level limited by the resolution of the ROI definitions. To over-come these obstacles, we proposed a new method to harmonize MRI scans with inter-scanner differences, and we showed that the proposed approach achieved consistent segmentations of anatomical structures. We believe that our method will be a valuable analysis tool for long-duration longitudinal studies and multi-site studies, as well as for facilitating post-hoc efforts to combine data across multiple studies.

One way to harmonize images would be to apply a transformation on each target image to make them consistent with the intensity profile of a common reference model, for example applying histogram matching techniques, either globally, or using more advanced local alignment techniques. In Roy et al. (2010) an atlas based image synthesis technique using patch-based matching was applied for generating a synthetic high-resolution MPRAGE image from its low-resolution SPGR acquisition. However, these approaches change the input images, and hence should be viewed as complementary to our approach, which does not modify the image data itself but rather creates mutually-consistent inter-scanner atlases. The fact that a multitude of such atlases are used in the final labeling might add robustness, relative to an approach that is based on a single image harmonization of each subject’s scan.

Another advantage of our method is that the site-specific atlas creation is done only once for every scanner type. Consequently, processing of new images does not necessitate any further computation, as long as there are no further changes in the scanner and image acquisition approaches.

Our method was motivated by the needs of our longitudinal neuroimaging program and leverages the existence of multiple scans from the same subject in the construction of scanner-specific atlases. Thus, a direct application of the method in multi-site data analyses, i.e. for pooling MRI images from different datasets and analyzing them together, may not be possible. However, to overcome this limitation a small set of subjects may be scanned in multiple sites/scanners to be used for atlas creation. Importantly, our results indicate that this multi-site scanning of the same person procedure does not need to be completed in a very short time period, since our registration process can account for brain changes between consecutive scans, as it did herein with a scanning interval of more than 4 years, on average. Alternatively, the method can also be extended by relaxing this dependency and selecting as atlases subjects with the highest image similarity, after matching them, for example based on age and sex. Such an extension is beyond the scope of this work and will be investigated in future work.

The robustness of our approach in generating longitudinally consistent segmentations is highlighted in the statistical analyses we performed. Significant differences between the two scanner types were observed in cross-sectional and longitudinal age trends of unharmonized ROI volumes, both in the slope of age-related brain volume changes and in the intercept values. Harmonization reduced the observed differences to a great extent and additional statistical adjustment for scanner will further reduce scanner-associated variation.

Some limitations of our work should be noted. Our method significantly alleviates the scanner change problem, but does not totally eliminate it. A scanner term still needs to be included as a covariate in statistical analyses. Second, the final ROI segmentations are performed using scanner and protocol specific atlases, for which the ROI labels were obtained through multi-atlas segmentation using external reference atlases. Any errors in the computation of the reference atlases will be propagated into subsequent segmentations. To address this issue, we performed a visual quality verification on the ROI labels of study-specific atlases. Furthermore, the multi-atlas framework is generally very robust in correcting errors in individual atlases and in local areas. Third, the harmonization was limited to the use of computed harmonized atlases within a general MAS framework, and thus did not benefit from further processing of input images, such as intensity harmonization of each individual input image, or more sophisticated 4D processing that would involve all time series from a subject. While these alternative techniques might have helped in harmonization, more complex models would bring the risk of over-fitting, as well as the need for costly re-processing with addition of new data.