An MR-based Model for Cardio-Respiratory Motion Compensation of Overlays in X-Ray Fluoroscopy

Abstract

In X-ray fluoroscopy, static overlays are used to visualize soft tissue. We propose a system for cardiac and respiratory motion compensation of these overlays. It consists of a 3-D motion model created from real-time MR imaging. Multiple sagittal slices are acquired and retrospectively stacked to consistent 3-D volumes. Slice stacking considers cardiac information derived from the ECG and respiratory information extracted from the images. Additionally, temporal smoothness of the stacking is enhanced. Motion is estimated from the MR volumes using deformable 3-D/3-D registration. The motion model itself is a linear direct correspondence model using the same surrogate signals as slice stacking. In X-ray fluoroscopy, only the surrogate signals need to be extracted to apply the motion model and animate the overlay in real time.

For evaluation, points are manually annotated in oblique MR slices and in contrast-enhanced X-ray images. The 2-D Euclidean distance of these points is reduced from 3.85 mm to 2.75 mm in MR and from 3.0 mm to 1.8 mm in X-ray compared to the static baseline. Furthermore, the motion-compensated overlays are shown qualitatively as images and videos.

I. Introduction

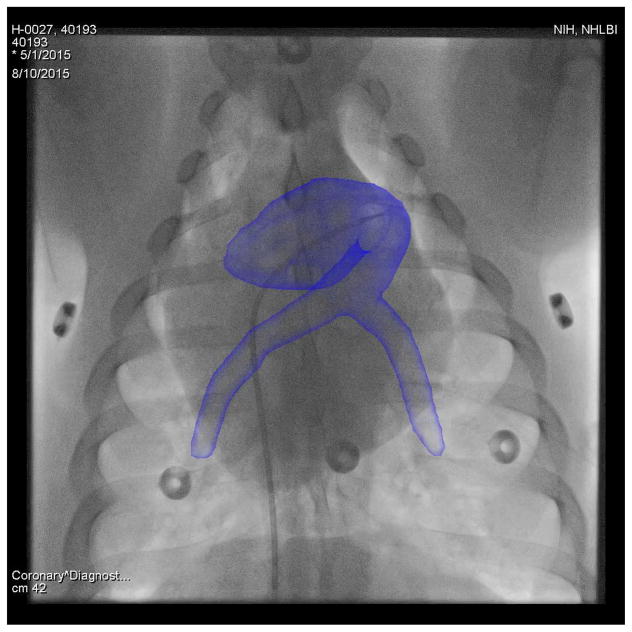
X-ray fluoroscopy is an important modality for guidance of minimally-invasive interventions. It has good spatial and temporal resolution and clearly visualizes interventional devices and bones. However, the contrast of soft tissue is low and 3-D information is lost due to the transparent projection to 2-D. To remedy these drawbacks, fusion of the X-ray images with previously acquired overlays has been proposed [1]–[3], which is also known as augmented fluoroscopy. The overlays are rendered semi-transparently directly on top of the X-ray images, see Fig. 1. These roadmap overlays are generated from 3-D modalities such as magnetic resonance imaging (MR), computed tomography (CT), or rotational C-arm CT. X-ray fused with MR imaging (XFM) is particularly interesting, because MR offers complementary features. It has good soft tissue contrast, provides functional and anatomical information in 3-D, and does not use ionizing radiation. The goal of XFM is to reduce procedure times, X-ray dose, and amount of injected contrast agent [4], [5].

Fig. 1.

Augmented fluoroscopy using an MR-based overlay onto an X-ray image of a pig. Best viewed in color.

The early approaches for augmented fluoroscopy [1]–[3] and current commercial systems feature static overlays. The roadmap image is registered to the X-ray coordinate system once and then automatically follows the changes of the C-arm and table position. If the patient moves, the registration is invalidated and the overlay is positioned incorrectly relative to the live images and the patient. For infrequent rigid motion of the patient relative to the table, a manual or automatic re-registration can be performed [6]. However, respiratory and cardiac motion are non-rigid and inevitable in thoracic and abdominal interventions. Thus, static overlays are not in correspondence with the fluoroscopic images most of the time, as visualized in the supplementary material. Without correction of the motion between overlay and fluoroscopic image, the accuracy of the overlay might not be sufficient for some procedures. For example, pulmonary vein isolation requires an accuracy of 5 mm [7], while other sources use 2 mm as a threshold for cardiac applications [8].

A. Motion Compensation in X-Ray Fluoroscopy

Cardiac and respiratory motion compensation for overlays in X-ray fluoroscopy is an active research topic. There are two fundamental approaches. In the first approach, motion compensation is based solely on the X-ray images. Brost et al. compensated cardiac and respiratory motion of the left atrium based on catheter tracking in 3-D [8]. For abdominal interventions, Ross et al. tracked the in-plane motion of the diaphragm and used it to compensate overlays of the liver vasculature [9]. Schneider et al. built a rigid 3-D motion model for coronary arteries from biplane angiograms [10] based on principal component analysis (PCA) and compensated motion using constrained registration. In contrast, Shechter et al. built a deformable 3-D motion model from the angiograms and used cardiac phase and diaphragm tracking as surrogate signals [11].

In the second fundamental approach, a pre-procedural motion model is built and used for motion compensation during the intervention. King et al. presented a 3-D affine model for respiratory motion correction [12]. The model was built from 2-D sagittal MR slices. The diaphragm position was used as the respiratory surrogate signal and the influence of cardiac motion was removed by cardiac gating. Faranesh et al. used real-time MR imaging on three planes to create a 3-D affine motion model [13]. 2-D in-plane motion was computed for each plane and a separate 3-D affine transformation was fitted for each cardiac and respiratory phase. Surrogate signals were derived from electrocardiography (ECG) and diaphragm tracking. De Senneville et al. created a motion model based on PCA for motion compensation in MR [14]. Peressutti et al. presented a Bayesian respiratory motion model for echocardiography [15]. The affine motion model was based on low resolution dynamic 3-D MR images. More information on different types of motion models can be found in [16].

There are some limitations in the methods proposed in the literature. A parametric motion model, e. g., rigid or affine, is commonly used [8], [10], [12], [13], [15]. This is an approximation of the real motion that is only sufficient for some cases, e. g., the motion of small regions of interest. Another limitation is the use of the diaphragm as a respiratory surrogate [12], [13]. Especially in X-ray, it cannot be ensured that the diaphragm is visible, for example because of a small field of view or the chosen C-arm angulation. Some methods are restricted to respiratory motion compensation only, which reduces accuracy or necessitates cardiac gating [12], [15].

B. MR Motion Models

There are three different types of imaging sequences to acquire motion-resolved data from MR. The simplest approach is to acquire MR images as fast as possible. 2-D slices can be acquired with frame rates of above 10 Hz using parallel imaging and fast protocols, e. g., balanced steady-state free precession (bSSFP). Unfortunately, 3-D imaging is not yet fast enough to capture cardiac motion directly. The frame rate for 3-D imaging can be up to 2 – 4 Hz [15], [17]. In addition, there is a trade-off between resolution and acquisition speed.

An alternative approach is binning or gating. A surrogate signal of the desired motion, e. g., ECG for cardiac motion or a navigator for respiratory motion, is acquired together with the raw MR k-space data. The k-space data is sorted into bins based on the surrogate signal and a separate MR volume is reconstructed for each bin. In respiratory binning, one approach is to use a radial sampling trajectory with self-gating based on the center of k-space [18], [19]. Tokuda et al. acquired additional navigator echoes to sort the k-space samples into respiratory bins in a multi-slice protocol [20]. For cardiac binning, there are acquisition protocols that require a single [21] or multiple breath-holds, but free-breathing CINE imaging has also been proposed [22]. Binning enables the creation of 4-D MR with multiple phases or bins, high resolution, and a large field of view. However, it only yields an average motion cycle. Furthermore, dependencies between cardiac and respiratory motion cannot be captured unless a 5-D MR with two binning dimensions is acquired. Recent developments using compressed sensing reconstruction might make this feasible [23].

The third alternative to create 4-D MR images is slice-stacking [17], [24]–[30]. A stack of parallel slices is acquired with real-time MR imaging and retrospectively sorted into volumes. Sorting is often performed using a surrogate signal, for details see Section I-C. The main difference to binning is that complete 2-D slices are acquired and reconstructed at high spatial and temporal resolution before reordering. In consequence, differences in the motion patterns over time can be measured. So far, this approach has only been used to handle respiratory motion at a fixed or averaged cardiac state or for a field of view that excludes the heart.

C. MR Respiratory Signals

In 4-D MR imaging, many different sources of respiratory signals have been proposed, including external devices [28], [30], the center of k-space [18], [19], [23], [26], the body area [25], [27], body boundary [26], navigator signals [20], and navigator slices [29]. Recently, dimensionality reduction has become popular in MR [17], [31], [32] and other applications [32], [33]. It has the advantage of being purely data-driven, so there are no geometric or frequency assumptions and no manual interaction is necessary. In addition, specific MR acquisition protocols or pre-reconstruction information like k-space data is not required. Furthermore, for our application, a corresponding respiratory signal during the fluoroscopy-guided intervention must be derivable.

D. Contribution

In this paper, we propose a cardiac and respiratory motion model of the whole heart for motion compensation in XFM. The idea is to use MR imaging to create a motion model in addition to the overlays. To this end, 3-D MR volumes that resolve cardiac and respiratory motion are required. A new slice stacking method is developed to create the 3-D+t MR images from a stack of 2-D+t MR slices. The novelty is that cardiac as well as respiratory motion is resolved using our slice stacking method. Furthermore, temporal regularity of the 3-D+t MR volumes is enhanced in an energy minimization formulation. The cardiac information is based on ECG data acquired with skin electrodes. The respiratory information is extracted directly from the MR images using dimensionality reduction, which means a navigator slice does not need to be acquired. For the respiratory signal extraction, we propose a new method that automatically detects and aligns the corresponding respiratory signals from the MR slices.

A subject-specific, fully deformable motion model is generated from 3-D+t MR. This is achieved by deformable registration of all 3-D volumes to an automatically determined reference volume. To enable interventional use of the motion model, a fast, linear, direct correspondence between surrogate signals and motion is learned.

II. Methods

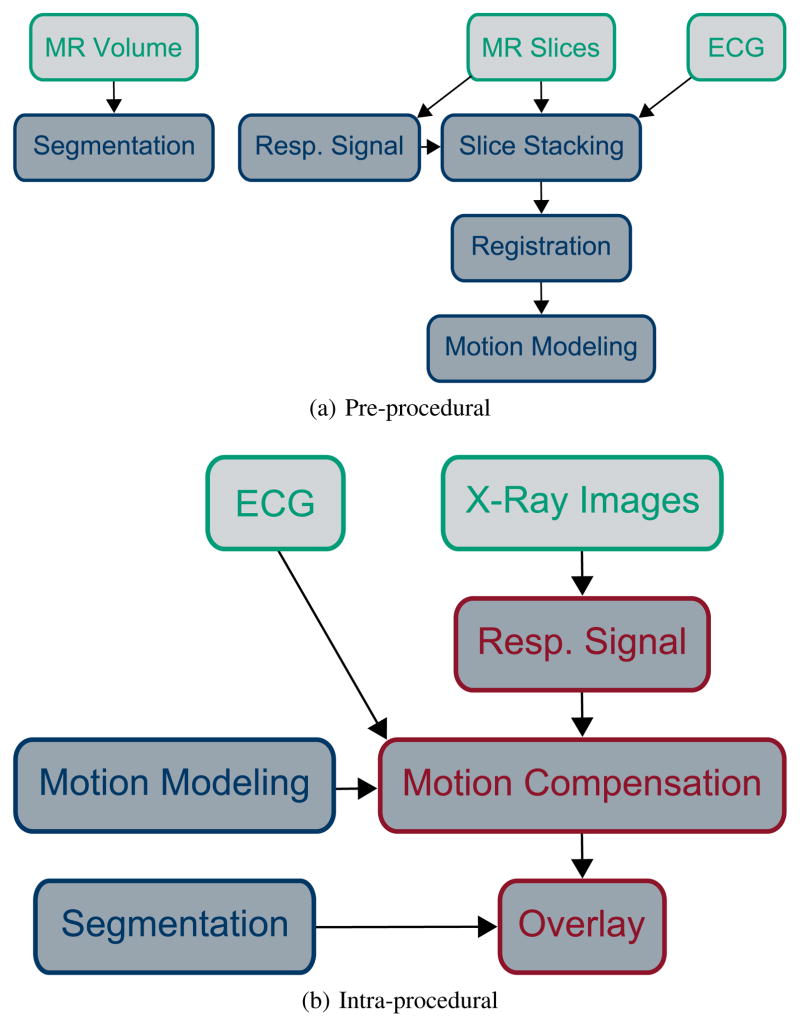
An overview of the pre-procedural steps of the proposed method is given in Fig. 2a. The MR slices are stacked into volumes of consistent cardio-respiratory state (Section II-B). These volumes are registered to a reference phase (Section II-E1) to estimate the 3-D motion. A regression model is built to relate the 3-D motion and the surrogate signal (Section II-E2). A separate MR volume is acquired for segmenting the overlay. The intra-procedural steps for motion compensation in fluoroscopy are given in Fig. 2b. The motion model is driven by a surrogate signal based on X-ray images and ECG (Section II-F). The motion is used to animate the segmentation as an overlay on the X-ray image in real time.

Fig. 2.

Illustration of MR-based motion compensation for augmented fluoroscopy. Input data is colored in green, pre-procedural processing steps in blue, real-time processing steps in red. Two MR acquisitions are necessary, a 3-D volume for segmenting the structures of interest and dynamic MR slices for motion modeling. ECG is required in MR and X-ray to inform about the cardiac phase. X-ray images are displayed to the physician and used to extract the respiratory signal during the intervention. Best viewed in color.

A. Materials

All experiments were performed at the National Heart, Lung, and Blood Institute of the National Institutes of Health in Bethesda, MD, USA. MR-only experiments were performed on volunteers and combined MR and X-ray experiments were performed on pigs. Six healthy Yorkshire swine were anesthetized with ketamine (25mg/kg), midazolam (15mg/kg), and glycopyrrolate (0.01mg/kg), and maintained on isoflurane (2–3%) with mechanical or manual ventilation. Femoral vascular access was obtained with ultrasound guidance. The experiments were approved by the institutional review board (for humans) or institutional animal care and use committee (for animals) and performed according to contemporary NIH guidelines. The MR images were acquired on a 1.5 T scanner (Aera, Siemens Healthcare, Erlangen, Germany). The ECG was measured using vectorcardiogram computed from the standard four-electrode set delivered with the MR scanner. The X-ray images were acquired on a floor-mounted, bi-plane, flat-panel X-ray C-arm system (Artis, Siemens Healthcare, Forchheim, Germany). The transfer between the MR scanner and the X-ray system was performed on a table moving on rails (MIYABI, Siemens Healthcare, Forchheim, Germany).

B. Motion-Resolved MR Volume Generation

For slice stacking, sagittal slices p^(t)[n] ∈ ℝ^D_p are acquired at N adjacent slice positions and T images per slice. Sagittal slices are used because respiratory motion then is mostly in-plane, which leads to less space-dependent phase shift [27]. N ∈ {17, …, 20} is chosen such that the slices cover the region of interest. The slices with a slice thickness of 6–8 mm and a pixel spacing of 1.75 – 2.25 mm are acquired with a bSSFP sequence. BSSFP offers high frame rates, good contrast between blood and heart muscle, and is robust to motion and flow [34]. A flip angle of 50° and an echo time of 1.1 ms is used. With an acceleration factor of 2, a frame rate around 10 Hz is realized. Imaging is performed for 20 s per slice, such that T ∈ {174, …, 190}. The slices are acquired sequentially, i. e., slice 1 for 20 s, then slice 2 for 20 s, etc. The first 5 images of each slice are discarded to avoid the transient magnetization.

For segmentation of the overlay, a static whole-heart 3-D MRI is acquired with respiratory self-navigation [35]. It features a 3-D radial bSSFP sequence with a flip angle of 50° – 115° and a reconstructed size of 160³ – 192³ voxels with 1.15 – 1.38 mm isotropic voxel size.

C. Slice Stacking using a Markov Random Field

As described in Section I-C, most methods for slice stacking directly match the images from different slices based on a description of their motion state. As we want to resolve cardiac and respiratory motion in the MR volumes, we describe the motion state of each slice using a surrogate signal s^(t)[n] ∈ ℝ^S containing cardiac and respiratory components, see Section II-D. In addition, we extend this with the idea of temporal smoothness, which assumes that the relative sequence of motion states is similar in all slices, i. e., if the image t₁ of slice n is assigned to image t₂ in the reference slice, then it is likely that the image t₁ + 1 of slice n corresponds to t₂ + 1. However, this assumption is only valid if the slices are acquired sequentially.

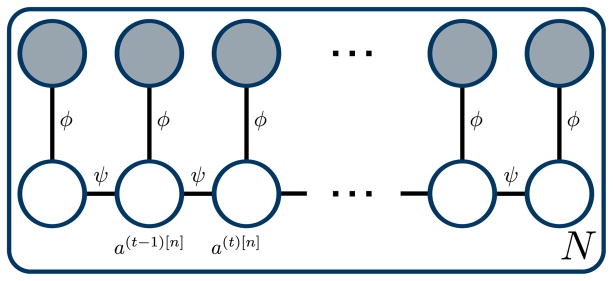
Our approach is formulated as a second-order Markov random field (MRF). The random variable A^(t)[n] represents the image number in slice n that is assigned to image t in the reference slice, where t ∈ {1, …, T } and n ∈ {2, …, N}. Without loss of generality, n = 1 denotes the reference slice. Each A^(t)[n] is assigned a discrete label a ∈ {1, …, T }. As a common MRF notation, A^(t)[n] = a is abbreviated as a^(t)[n].

The MRF energy is defined as

$$\sum _{n=2}^N\left[\sum _{t=1}^T{\varphi }^{(t)[n]}\left(a^{(t)[n]}\right)+\mu \sum _{t=2}^T\psi \left(a^{(t-1)[n]},a^{(t)[n]}\right)\right],$$ (1)

where ϕ^(t)[n] is an unary inter-slice similarity term and ψ a binary smoothness term. The corresponding graphical model is illustrated in Fig. 3.

Fig. 3.

Graphical model for slice stacking. Random variables are displayed as circles. Observed variables are shaded.

The unary inter-slice similarity term is a weighted squared Euclidean distance of the surrogate signals

$${\varphi }^{(t)[n]}(a)={\Vert \mathit{w}\odot \left({\mathit{s}}^{(t)[1]}-{\mathit{s}}^{(a)[n]}\right)\Vert }_2^2,$$ (2)

where ⊙ denotes the element-wise product. Each dimension of the surrogate signal can be weighted differently using w ∈ ℝ^S.

The temporal smoothness term is an absolute distance function truncated with the threshold η ∈ ℝ

$$\psi (a,b)=min(\eta ,\mid a-b+1\mid ).$$ (3)

There is no penalty if temporal neighboring frames in the reference slice are assigned to temporal neighbors in the target slice. The penalty for skipped frames increases linearly until the maximum penalty η is reached. Discontinuities in the assignment of more than η frames receive a constant penalty, such temporal distant frames can be assigned to each other if the surrogate signals match well.

The optimal assignment a^* is given by the minimum of Eq. (1), which corresponds to maximum-a-posteriori (MAP) inference in the MRF. The energy decomposes into independent optimization problems for each slice, as indicated by the plate notation in Fig. 3. Thus, belief propagation converges to the global optimum. If the temporal smoothness Eq. (3) was omitted, the minimum of Eq. (1) would be identical to directly matching the surrogate signals. Using a^*, T 3-D MR volumes q^(t) ∈ ℝ^D_q, D_q = ND_p are generated as

$${\mathit{q}}^{(t)}={\left({\mathit{p}}^{(t){[1]}^{\top }},{\mathit{p}}^{(a^{\ast (t)[2]}),{[2]}^{\top }},\dots ,{\mathit{p}}^{(a^{\ast (t)[N]}),{[N]}^{\top }}\right)}^{\top }.$$ (4)

The surrogate signal of the volume is by definition identical to the surrogate signal of the reference slice s = s^[1].

D. Surrogate Signals

The surrogate s^(t)[n] ∈ ℝ^S is generated independently for each slice. It consists of a respiratory dimension ${\mathit{s}}_1^{(t)[n]}={\mathit{r}}^{(t)[n]}$ and two cardiac dimensions ${\mathit{s}}_2^{(t)[n]}={\mathit{c}}_1^{(t)[n]},{\mathit{s}}_3^{(t)[n]}={\mathit{c}}_2^{(t)[n]}$, i. e., S = 3. To weight the surrogate components, we use w = (1, 0.5, 0.5)^⊤, ensuring that overall the respiratory and cardiac components are equally weighted. The generation of c^(t)[n] and r^(t)[n] is described in the following two sections.

1) Cardiac Surrogate Signal

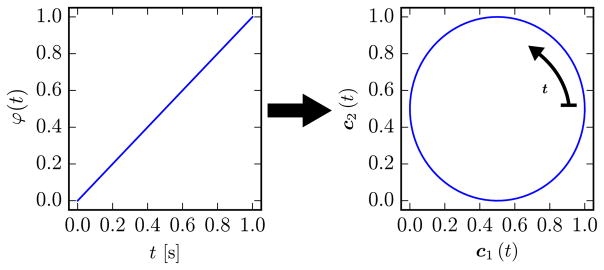
The cardiac surrogate signal c^(t)[n] is based on the ECG signal for each slice n. ECG is available in MR scanners for patient monitoring and cardiac-triggering. The ECG signal itself is not an adequate surrogate signal, since it has similar values for most of the cardiac cycle, which are not directly related to the motion magnitude of the heart. However, prominent features such as the R-peaks are informative and are usually used as triggers. The time since the last R-peak is retrospectively converted to a linearly increasing cardiac phase φ^(t)[n] ∈ [0, 1). To reflect the continuity of cardiac motion between end-diastole (φ = 1) and start-systole (φ = 0), the cardiac phase is embedded into a 2-D circle as

$${\mathit{c}}_1^{(t)[n]}=cos\left(2\pi {\phi }^{(t)[n]}\right)$$ (5)

$${\mathit{c}}_2^{(t)[n]}=sin\left(2\pi {\phi }^{(t)[n]}\right).$$ (6)

This circular embedding is visualized in Fig. 4.

Fig. 4.

The linear cardiac phase is embedded in a 2-D circle to enforce a consistent position of end-diastole and start-systole.

2) Respiratory Surrogate Signal

The respiratory surrogate signal r^(t)[n] is derived from the respective MR image p^(t)[n]. For reasons that will be detailed later, PCA is used instead of nonlinear manifold learning for dimensionality reduction. PCA is the orthogonal linear transformation that maximizes the variance of the projected embeddings. PCA is computed independently for each slice n as the eigendecomposition C^[n]E^[n] = E^[n]Λ^[n] of the MR slice covariance matrix C^[n], where E^[n] is the eigenvector matrix and Λ^[n] the diagonal eigenvalue matrix, which is ordered by decreasing eigenvalues ${\mathbf{\Lambda }}_{0,0}^{[n]}>\dots >{\mathbf{\Lambda }}_{K,K}^{[n]}$. We compute up to K eigenvectors, as only the largest eigenvalues are of interest in our application. The low-dimensional embedding, from which the surrogate signal is derived, is computed as

$${\stackrel{\sim }{\mathit{r}}}_k^{(t)[n]}={\left({\mathit{E}}^{{[n]}^{\top }}\right)}_k{\mathit{p}}^{(t)[n]},$$ (7)

where the subscript k selects the k-th row of a vector or matrix.

Dimensionality reduction methods suffer from an ambiguity of sign and ordering [36]. In our case, this means it is unknown which PCA component k contains respiratory motion and whether high or low signal values correspond to exhalation. These ambiguities could be avoided if the slices were embedded jointly [24]. However, the manifolds in our application are not similar enough, because two independent motion patterns occur in the images, and cardiac motion is only visible in a subset of the slices. Joint embedding is evaluated as an alternative method in the experiments (Section III).

To remove the ordering ambiguity, prior information about the frequency of breathing is used to find the respiratory component. The K possible 1-D signals are the dimensions k of the low-dimensional embedding ${\stackrel{\sim }{\mathit{r}}}_k^{(t)[n]}$. The respiratory surrogate ${\mathit{r}}^{(t)[n]}={\stackrel{\sim }{\mathit{r}}}_{\kappa [n]}^{(t)[n]}$ is chosen as

$${\kappa }^{[n]}=\underset{k}{\text{argmin}}\left\{k\mid {\mathrm{f}}_{min}\le \underset{f}{\text{argmax}}\left|\mathcal{F}\left\{{\stackrel{\sim }{\mathit{r}}}_k^{[n]}\right\}\right|\le {\mathrm{f}}_{max}\right\},$$ (8)

where |ℱ| is the magnitude of the Fourier transform and f_min = 0 Hz, f_max = 1.5 Hz. Intuitively, the highest-variance dimension k of the PCA with the peak frequency inside the specified frequency range for breathing is selected. As the eigenvalues are sorted by decreasing magnitude, the selection can be performed using the argmin over indices. A similar strategy was employed in [14] for separating physiological motion and noise. Additionally, we suppress noise in the signal by forward-backward filtering with a third-order Butterworth filter with the same passband as above.

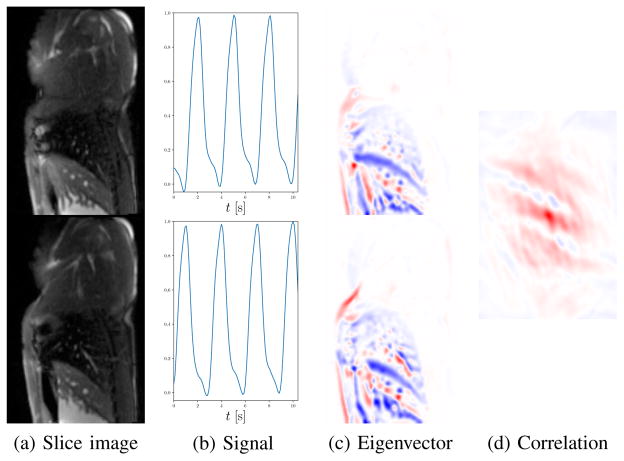
To remove the sign ambiguity, we make use of the respiratory eigenvectors ${\mathit{E}}_{\ast ,{\kappa }^{[n]}}^{[n]}$. The notation *, κ^[n] selects the κ^[n]-th column of the matrix E^[n]. The alignment procedure is visualized in Fig. 5. For each slice, the respiratory eigenvector indicates which pixels gets brighter/darker relative to the mean during breathing. This behavior should be similar for all slices up to differences due to anatomy. The agreement of the eigenvector signs is determined using the normalized cross-correlation (NCC) between the eigenvector images. Similar to template matching and convolution, spatial shifts are scanned and NCC is computed for each shift. For the shift with the maximum absolute value of NCC, the sign of the NCC indicates whether or not the eigenvectors are aligned. As the appearance of distant MR slices changes considerably, we sequentially align the sign of neighboring slices ${\mathit{E}}_{\ast ,{\kappa }^{[n]}}^{[n]}$ and ${\mathit{E}}_{\ast ,{\kappa }^{[n+1]}}^{[n+1]}$. This idea to use the eigenvectors for alignment is the reason we prefer PCA over manifold learning. PCA eigenvectors give spatial information, whereas the eigenvectors occurring in manifold learning give the coordinates of the low-dimensional embeddings. To align eigenvectors resulting from manifold learning, additional prior information would be required [36].

Fig. 5.

Respiratory signal alignment for neighboring MR slices. PCA embedding of the slice images (a) results in a respiratory signal for each slice (b). The signals themselves have no inherent temporal correspondence and are not sufficient to determine the sign ambiguity. The PCA eigenvectors (c) indicate how the intensity of the images changes with respiration. The maximum NCC (d) between the eigenvectors is positive if the respiratory signals are aligned, and negative if the signs are flipped. In (c) and (d), negative values are blue, 0 is white, and positive values are red. In this example, the correlation is positive, which means there is no sign flip between the respiratory signals in (b). Best viewed in color.

The respiratory signal of each slice is normalized along the whole sequence to [0, 1] approximately, using the following method that is robust to outliers. The minimum and maximum peaks of the respiratory signal are detected, and the medians of the respective extrema are used for linear normalization. With this approach, the respiratory signal can be out of the range [0, 1] for deep inhales or exhales. However, the influence of single deep inhalations or exhalations on the signal range is restricted, which is important since the slices are acquired sequentially and can have different respiratory patterns. In addition, the same normalization of the respiratory signal must be achieved under X-ray for applying the motion model.

There is a remaining global sign ambiguity, i. e., whether a respiratory signal of 0 corresponds to exhale or inhale. The procedure described above only aligns the sign of the respiratory signals relative to each other. To define the global sign, we exploit the general property of human respiration that more time is spent in exhalation than in inhalation [37]. As this property is more stable over long time scales, the sign of the respiratory signals is defined such that the temporal median of the respiratory signal of all slices is smaller than 0.5.

E. Motion Model

This section describes how the patient-specific, cardiac and respiratory motion model is built from the previously generated MR volumes by using registration and regression.

1) Registration

All T 3-D MR volumes q^(t) are registered to a reference volume q⁽¹⁾ to estimate the motion m^(t) ∈ ℝ^3D_q. The reference volume is selected automatically according to the cardio-respiratory state of the static MR volume for segmentation, usually end-diastole and end-expiration.

Pair-wise, deformable 3-D/3-D registration is performed in a variational framework based on the evaluation work of Werner et al. [38]. A NCC data term is combined with diffusion regularization and diffeomorphic transformations. It is optimized in a multi-resolution strategy using gradient descent. The parameters for registration are the number of resolutions N_level, the regularization weight γ, the step length τ and the number of iterations N_iter of the optimizer.

2) Regression Model

In a direct correspondence motion model, f: s ↦ f (s) = m directly maps a surrogate signal s to a motion field m. A linear function is used

$$f(\mathit{s})=\mathit{M}\mathit{s}+\overline{\mathit{m}},$$ (9)

because it is fast to evaluate in the application phase of the motion model. Moreover, training is possible from relatively few samples. In the literature, linear regression is a common approach for respiratory motion modeling from low-dimensional surrogates [16]. It has been shown to be as accurate as more complex regression methods for this application [39]. The parameters M ∈ ℝ^3D_q×S, m̄ ∈ ℝ^3D_q are trained from T samples consisting of surrogate signals s^(t) as inputs and motions m^(t) as targets. The training method is ridge regression with the regularization weight λ.

In principle, the input motions allow to capture inter-cycle and intra-cycle variation [16]. However, the surrogate signals restrict the flexibility. The circular embedding of the cardiac phase in Eq. (6) prevents inter-cycle variation, i. e., the estimated cardiac motion follows the same path in each cycle, albeit at different speeds depending on the RR interval. Intra-cycle variation, i. e., different cardiac motion during systole and diastole, is possible. The respiratory surrogate r^(t)[n] is a 1-D amplitude signal, which means it does not distinguish between inhalation and exhalation. However, varying breathing depth and breathing frequency can be captured. This would not be possible with a phase-based respiratory surrogate.

F. Motion Compensation in X-Ray

Our prototype transparently renders 3-D mesh overlays given in the C-arm coordinate system onto X-ray images. Originally, the meshes and the motion model are given in MR coordinates. Both coordinate systems are registered manually based on multi-modal skin markers, which have been shown to yield accurate registration [7], [40].

To compensate the motion of the overlay during the fluoroscopy-guided intervention, the main tasks are to determine the surrogate signals, to apply the motion model, and to transform the mesh vertices. As in MR, the cardiac surrogate signal comes from the simultaneously acquired ECG. The difference is that the cardiac phase is calculated based on extrapolated RR intervals, as future triggers as in MR postprocessing are not available. The respiratory signal is extracted from the X-ray images using kernel PCA on multi-resolution patches [33], which ensures robustness to disturbances occurring in interventional X-ray, such as contrast agent injection or automatic exposure control. This method contains a training phase of 45 images for each C-arm position, during which the same amplitude normalization is applied as for the MR respiratory signal. The output of the motion model is computed by applying Eq. (9). The mesh vertices are transformed in MR coordinates after linearly interpolating the corresponding position in the motion field.

G. Implementation

The general pipeline was implemented in Python based on its scientific libraries (NumPy, SciPy, scikit-learn). However, the MRF energy function and its optimization (OpenGM [41]) and the registration (ITK [42]) are implemented in C++. The motion model application and the mesh rendering are implemented on the GPU using OpenGL and Glumpy.

III. Experiments

The following setup is used in the experiments. Due to the lack of data and accurate ground truth, all the hyperparameters were tuned manually such that visually good results were seen in the algorithm steps. For slice stacking, the weight is μ = 0.001 and the truncation is η = 32, see Section II-C. K = 3 components are used in the PCAs for respiratory signal extraction from MR. The parameters for registration are set to N_level = 4, γ = 0.02, τ = 10.0, and N_iter = 1000. The motion model uses the regularization weight λ = 0.1. In X-ray, the respiratory signal estimation uses the settings from [33] and is applied to the whole sequence.

A. MR Statistics

To give an intuition of the real-time MR slice images that are acquired for motion modeling, we qualitatively show some statistics of the MR images. The magnitude of the motion is visualized using temporal minimum and maximum intensity projections of a slice in an exemplary dataset.

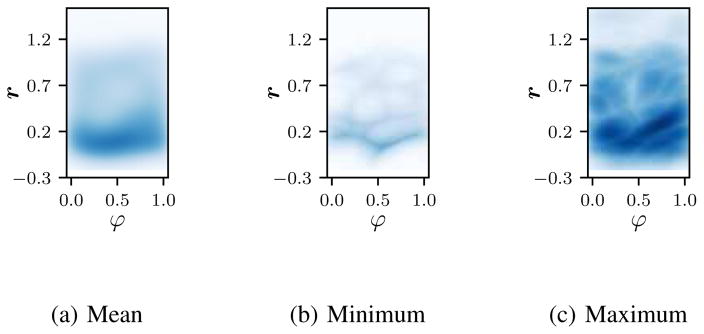
Another interesting statistic is the coverage of the cardio-respiratory plane. The cardio-respiratory plane is a 2-D plane spanned by the cardiac phase φ and the respiratory signal r. A high coverage means that many images are acquired in that cardio-respiratory state. Since cardiac phase and respiratory signal are continuous quantities, we estimate their probability density function using kernel density estimation (KDE). We use KDE with a Gaussian kernel with a standard deviation of 0.1. The evaluation is based on a single free-breathing volunteer dataset with 20 slices and 169 frames per slice. An independent KDE is performed for each slice, and we show the point-wise mean, minimum, and maximum density.

B. MR Slice Motion

To compare slice stacking with binning for 4-D MR volume generation and motion compensation, 4-D respiratory binned MR, 4-D cardiac binned MR, and real-time sagittal slices were acquired for two volunteers and one pig. The volunteers were free breathing, while the pig was on a ventilator.

For respiratory binning, 5 breathing phases are acquired with a T1-weighted, self-gated, radial stack-of-stars sequence [19]. The reconstructed volume of size 192 × 192 × (28 – 40) has a resolution of (1.35–2.08)×(1.35–2.08)×(3–4) mm. For cardiac binning, 30 cardiac phases are acquired with a bSSFP CINE sequence during free breathing, retrospectively cardiac binned and compensated for respiratory motion [22]. The 4-D volume is created by stacking 2-D slices, where each slice is acquired for 8 s, independently reconstructed, and sorted according to the ECG trigger times. The reconstructed volume of size (160 – 192) × (120 – 128) × (17 – 20) has a resolution of (1.75 – 2.34) × (1.75 – 2.34) × (6 – 8) mm. As an alternative to the proposed slice stacking method, we implemented and compare to the self-alignment of manifold (SAM) technique proposed by Baumgartner et al. [24]. The parameters of this method were chosen similar to the ones proposed in the original publication with additional fine-tuning: σ₁ = 0.15, σ₂ = 0.15, μ₂ = 0.01, k = 30, and d = 4. For respiratory binning, cardiac binning, and for both slice stacking methods, a motion model as in Section II-E is created. These motion models are evaluated regarding their ability to compensate the observable patient motion in MR.

For this evaluation, additional real-time slices were acquired in non-sagittal orientations, e. g., short axis view, and four chamber view. Key points were tracked using template matching with manual correction. In total, 34 key point trajectories from 14 sequences are evaluated. The motion models are applied on the evaluation slices to estimate the motion of the key points. A difference is that the respiratory surrogate is created from tracking structures moving with respiratory motion, e. g., the top of the diaphragm or the chest, instead of the method described in Section II-D2 to avoid a bias towards our method.

The estimated position of the key point is compared to the ground truth position for each point in time. As the ground truth position can only be annotated in 2-D in the slice, the estimated 3-D position is projected into the evaluation slice and compared using the 2-D in-plane Euclidean distance. As a baseline, a static overlay is used. This corresponds to keeping the position of the key point fixed in the reference phase for all images.

C. X-Ray Key Points

To apply the complete motion compensation workflow, a reference 3-D MR for annotation and registration, real-time MR slices for motion modeling, and X-ray images for evaluation are acquired for 5 pig datasets. There are 2–3 biplane X-ray acquisitions with contrast agent injection into the left ventricle (LV) and the left and right pulmonary artery (PA). Images of size 1024 × 1024 pixels with a pixel size of 0.15 – 0.31 mm are acquired. The frame rate is 15 Hz and the length of the image sequences used for evaluation is 151 to 301 frames.

Besides our complete proposed method, we train models that only compensate one of the motions to show the relative influence of respiratory and cardiac motion. This is achieved by restricting the input of the motion model learning (Section II-E2) to only a respiratory surrogate or only a cardiac surrogate. Consequently, the cardiac motion states are averaged in the respiratory motion model and vice versa. As a baseline, we use non-motion-compensated overlays, i. e., fixed at the reference phase without any motion. Additional comparison is done with SAM slice stacking with the same parametrization as in Section III-B.

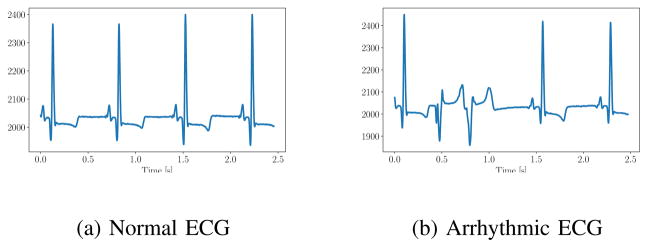
We measure the 2-D error of key points in contrast-enhanced images. Key points for respiratory motion include branching points of the PAs. For cardiac motion, points on the heart shadow are used. Initially, we tried to inject contrast agent into the LV and use key points on the LV. However, the injection in the LV frequently caused premature ventricular contraction. Due to this arrhythmia, which is evident in the ECG (Fig. 6), the heart moves abnormally. This type of motion is not observed in the 4-D MR and cannot be compensated with our model. This limitation is further discussed in Section V.

Fig. 6.

ECG of a pig during normal fluoroscopic imaging (a) and during contrast agent injection in the left ventricle (b) causing arrhythmia.

The trajectories of key points are annotated manually in X-ray sequences. Different key points are annotated in each plane of the biplane sequence, depending on visibility. The key points are also marked in the reference 3-D MR, which would usually be used for segmentation of the overlay. To accurately mark the 3-D point corresponding to the 2-D key points, the 2-D point of an image close to the reference phase is backprojected to 3-D using the projection geometry of the X-ray image. A 3-D point close to the backprojection line and to the anatomy of interest is chosen. In total, 35 point trajectories are evaluated on 20 X-ray sequences, between one and four trajectories per sequence. The error of the key points is measured on the detector plane using the 2-D Euclidean distance.

D. Comparison of Manual and Automatic Ventilation

The proposed method relies on reproducible motion patterns for MR slice stacking and for motion compensation. With a ventilation machine, the respiratory motion is regular in amplitude and frequency. To test the variability during MR scanning, the volunteer datasets were acquired free breathing and the animal datasets were acquired while the pigs were on a ventilation machine. A similar MR key point evaluation as in Section III-B is performed using 24 trajectories from free-breathing volunteer scans and 42 trajectories from ventilated pig scans. To evaluate the robustness of the whole motion compensation pipeline w. r. t. variable breathing patterns, X-ray sequences were acquired with manual and with automatic ventilation. During manual ventilation, varying breathing depths and frequencies were simulated. The same X-ray key point evaluation as in Section III-C is performed. From the 20 X-ray sequences, 12 were recorded during automatic ventilation and 8 during manual ventilation.

E. Comparison of Regression Methods for MR Motion Model

In this experiment, the regression used in the MR motion model is investigated more thoroughly. We propose to use linear regression, which is compared to kernel ridge regression (KRR) and to principal component regression (PCR) here [43]. In KRR, a Gaussian radial basis function kernel with a bandwidth of 0.5 is used. The PCA in PCR is computed with 10 components. The regression methods are evaluated on the training data with the coefficient of determination R², which measures how much of the variance in the training data is captured. Furthermore, we evaluate the X-ray key point error from Section III-C for all three motion models to demonstrate their influence on the whole pipeline.

F. X-Ray Overlay

The error at key points is a quantitative but sparse measure. The general impression of the quality of the motion compensation is defined by how well the whole overlay matches the fluoroscopic images. This can also be seen using contrast agent injection. To generate the overlay, we segment the PAs and the LV manually in the reference 3-D MR. The same 5 datasets as in the previous experiment are used. For the LV, the same arrhythmia problem occurs.

Quantitative results for this use case are challenging and inaccurate. In X-ray, the contrast agent flows in and out of the structures, so they are only partially visible most of the time. Error measures are dominated by these structural differences due to contrast filling and not by the misalignment due to motion. Furthermore, the annotation of the contrast agent is very difficult due to the high number of frames and the varying and low contrast. Therefore, we show qualitative results only.

G. Runtime

Since the proposed method is targeted for interventional use, the runtime is important. In particular, respiratory signal extraction, motion model application, and overlay rendering in X-ray are crucial. These steps are performed during the intervention and must run in real time. Slice stacking, 3-D/3-D registration, and motion model training are less time-critical, since they are performed pre-procedurally. The runtime of all processing steps is measured for 5 datasets. This experiment is executed on a consumer notebook with an Intel Core i7-3720QM CPU with 8 GB of RAM and a NVIDIA Quadro K2000M.

IV. Results

A. MR Statistics

In Fig. 7, the temporal minimum and maximum intensity projections of a sagittal slice through the LV are shown. The size of the blood pool in the LV is much smaller in the minimum intensity projection image. A part of this is also due to respiratory motion of the heart. This can be seen at the most inferior level of the heart, which moves by 7mm between Fig. 7a and Fig. 7b. In addition, the magnitude of the respiratory motion of the diaphragm can be seen nicely. For the top of the diaphragm, the visible motion in these images corresponds to 17.5mm in the vertical direction.

Fig. 7.

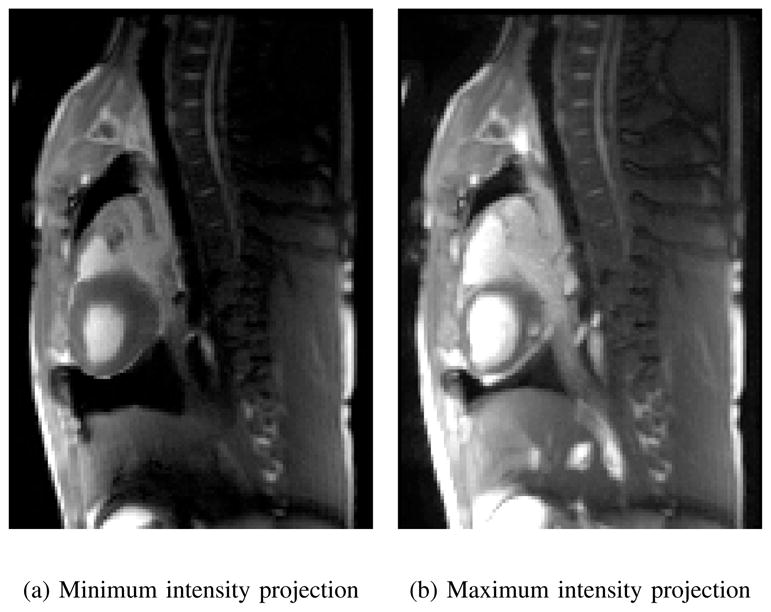
The pixel-wise minimum (a) and maximum (b) intensity of a slice acquired for slice stacking indicates the extent of cardio-respiratory motion.

The cardio-respiratory plane of one dataset is provided in Fig. 8. The mean plane (Fig. 8a) shows that more time is spent in end exhale than in other respiratory states, illustrating the property that is used as a heuristic for the global respiratory signal sign, cf. Section II-D2. The cardiac phases are distributed equally. This is due to the way the cardiac phase is computed as the relative time between two R-peaks and due to the trigger-independent acquisition of the MR images. In the minimum image, it can be seen additionally that full inhale and very deep exhalations did not occur in all slices.

Fig. 8.

Coverage of cardio-respiratory plane for the real-time slices for an exemplary dataset. The mean (a), point-wise minimum (b) and point-wise maximum (c) density over all the slices is shown. Best viewed in color.

B. MR Slice Motion

For the static baseline, the key points move by 3.85 ± 2.61 mm from the reference. All models reduce the motion compared to the baseline. Cardiac binning has an error of 3.80 ± 2.62 mm and respiratory binning an error of 2.92 ± 2.24 mm. The combination of both brings the error down to 2.82 ± 2.3 mm. Slice stacking using SAM leads to an error of 3.09 ± 2.4 mm. With 2.76 ± 2.3 mm, our proposed slice stacking has the lowest error. The difference to the baseline is significant for the proposed method and for respiratory binning. However, possibly due to the small sample size, the difference between respiratory binning and the proposed slice stacking is not significant. Statistical testing was performed with the Wilcoxon signed rank test and p < 0.01.

C. X-Ray Key Points

The numerical results are summarized in Table I. The experiment is separated into trajectories dominated by cardiac motion (left), respiratory motion (middle), and all trajectories (right). For all trajectories, the error of the static overlay is 3.01 ± 1.46 mm. This is reduced to 2.66 ± 1.1 mm using the cardiac model. The respiratory and the joint model have similar errors in the range of 1.8 mm. This amounts to a reduction by 40%. For comparison, the SAM-based model leads to an error of 2.17 mm. Note that the results are biased towards static overlays, because the errors are averaged over time and most of the time is spent in the reference phase. The difference between all methods and the static overlay is significant for all models. Joint and respiratory model are significantly better than the cardiac model, but not significantly different from each other. Statistical testing was performed with the Wilcoxon signed rank test and p < 0.01.

TABLE I.

Results of X-ray motion compensation on porcine data (mean Euclidean distance in mm ± standard deviation)

	Cardiac Traj.	Respiratory Traj.	All Traj.
Joint	2.20 ± 0.89	1.63 ± 0.94	1.79 ± 0.96
Respiratory	2.25 ± 0.86	1.62 ± 0.95	1.79 ± 0.97
Cardiac	2.32 ± 0.99	2.80 ± 1.11	2.66 ± 1.10
SAM	2.90 ± 1.30	1.89 ± 1.05	2.17 ± 1.21
None	2.66 ± 1.12	3.15 ± 1.55	3.01 ± 1.46

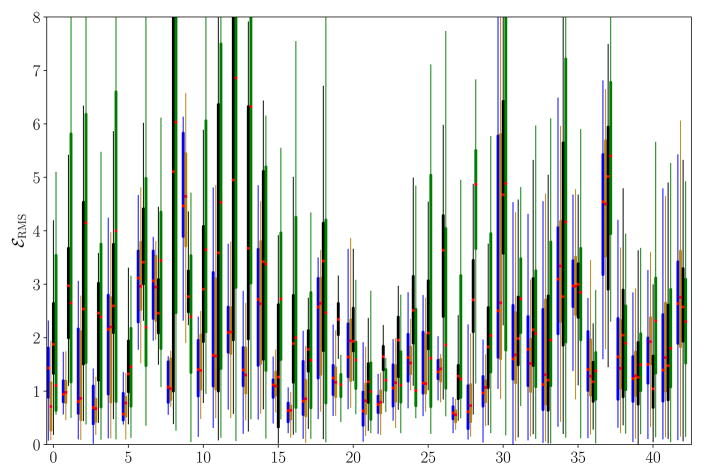
In Fig. 9, the residual motion per trajectory is shown as boxplots for the different versions of the proposed motion model, i. e., joint cardio-respiratory (left), respiratory only (middle left), cardiac only (middle right), and the static baseline (right). In most sequences, the residual motion is reduced by all motion models. Respiratory motion is incorrectly estimated in trajectories 7 and 9, where the breathing depth is varying and the motion is overestimated. The cardiac motion model more often performs worse than the static baseline, particularly in trajectories 19, 22, 23, 24, 26, and 34, often due to a phase offset between true and estimated motion.

Fig. 9.

Boxplots of the root mean square error per keypoint trajectory for the cardio-respiratory (left), respiratory (middle left), and cardiac motion model (middle right) and for the static baseline (right). Trajectories 0–30 are dominated by respiratory motion, while the others are mostly influenced by cardiac motion. Best viewed in color.

D. Comparison of Manual and Automatic Ventilation

In the MR key point experiment, the motion for the free-breathing human subjects without motion compensation is 4.76 ± 2.63 mm. Using our motion compensation method, the error is reduced to 3.51 ± 2.48 mm. For the pig datasets, the motion without compensation is only 1.86 ± 0.92 mm, which can be reduced to 1.11 ± 0.48 mm with the proposed method. In the X-ray key point experiment, the manual ventilation motion without compensation is 3.76 ± 1.66 mm, which is lowered to 2.38 ± 1.06 mm with motion compensation. For automatic ventilation, the initial motion magnitude of 2.57 ± 1.12 mm is reduced to 1.44 ± 0.70 mm after motion compensation.

E. Comparison of Regression Methods for MR Motion Model

The coefficient of determination R² on the training data is 0.66 for linear regression and 0.64 for PCR. For KRR, R² is 0.7, showing its increased modeling power. To analyze the distribution of the motion types, the R² is also evaluated for linear regression only with the respiratory surrogate, where it is 0.62, and only with the cardiac surrogates, where it is 0.04. In the X-ray key point experiments, linear regression has a residual error of 1.79±0.96 mm and PCR of 1.78±0.96. KRR has a slightly higher error of 1.82 ± 0.94 mm. The differences between PCR and linear regression are marginal. If the number of PCA components is increased to 10 in PCR, both methods yield identical results. The higher R² of KRR together with the slightly higher key point error indicates an overfitting on the training data.

F. X-Ray Overlay

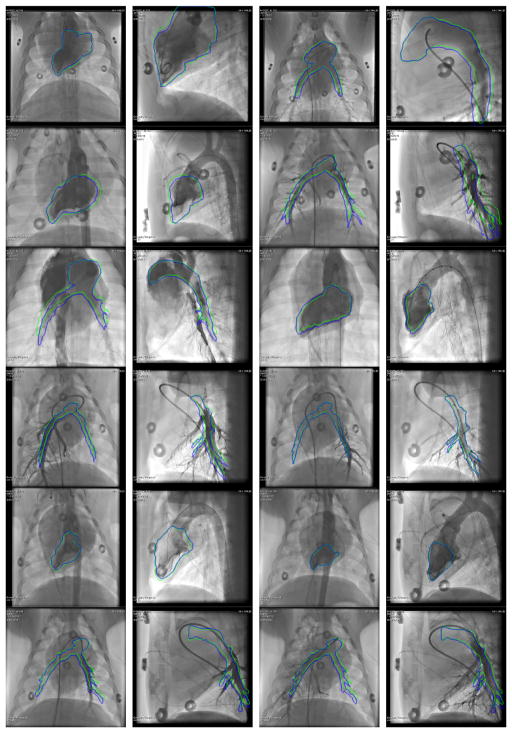
In Fig. 10, the static mesh and the mesh with motion compensation are overlaid jointly onto an X-ray image. Only the outlines of the meshes are shown to avoid occlusions. All 24 sequences with contrast agent injection are included. For the angiograms of the left ventricle, both overlays often do not match the lumen, e. g., rows 2 and 5 in columns 1 and 2. This is in part due to premature ventricular contraction and in part due to model errors. The motion-compensated overlay is still closer to the true lumen than the non-compensated. For the angiograms of the pulmonary arteries, the motion-compensated overlay fits the contrast agent nicely in the anterior-posterior (AP) acquisitions, e. g., row 1, 2, and 6 in column 3. In the lateral acquisitions, the correspondence of contrast agent and overlay is harder to assess due to occlusions of the left and the right pulmonary artery. Note that two consecutive images in Fig. 10 are consecutive AP and lateral acquisitions of the same scene, e. g., row 1 columns 1 and 2.

Fig. 10.

Outline of the static (green) and the motion-compensated overlay (blue) for all sequences with contrast agent injection. From each sequence, an image with good contrast filling and as much motion as possible relative to the reference phase is displayed. Best viewed in color. In the supplementary material, a video of each sequence with and without motion compensation is available.

In addition to the images here, all results are also shown as videos in the supplementary material. In these videos, the static and motion-compensated mesh are overlaid separately onto the corresponding X-ray sequence and visualized side-by-side using mesh rendering. The videos demonstrate the performance of motion compensation for different cases, for example respiratory motion of the pulmonary arteries and cardiac motion of the left ventricle during normal rhythms and during arrhythmias caused by contrast agent injection.

G. Runtime

First, the runtimes of the pre-procedural steps to create the motion model are reported. Slice stacking using the proposed method is performed in 40.1 ± 3.6 s. The registration of the 3-D MR volumes requires 2.6 ± 1.3 hours per dataset. As there are 176 to 185 volumes in a dataset, this means that a single 3-D/3-D registration is processed in 52.8±26.1 seconds. Another 1.3 ± 0.1 s are needed to learn the regression model.

The overall runtime of the intra-procedural processing is 10.7 ± 5.8 ms per image. This includes the computation of the surrogate signals on the CPU, the transfer of image and surrogate data to the GPU, and the application of the motion model and the rendering of the overlay on the GPU. With 7.8 ± 2.3 ms per image, the majority of the runtime is spent for extracting the respiratory signal from the image. The processing time is well below the shortest sampling intervals usually used in fluoroscopy, which is 66.7 ms, i. e., the method is real-time-capable. In a clinical product, an additional delay of the display of the X-ray image by 11 ms might not be tolerable. In this case, an additional surrogate signal or motion prediction step would be required [44].

V. Discussion

The MR slice motion experiments show that slice stacking is competitive with binning approaches for motion modeling. The proposed method to stack slices based on cardiac and respiratory surrogate signals is relatively simple. Additionally, some other properties of the MR sequence for slice stacking are advantageous for our application. Firstly, only one scan is necessary instead of two, reducing the scan and setup complexity. Secondly, this scan resolves cardiac and respiratory motion, such that derived motion models can capture the dependency between them. Thirdly, slice stacking gives multiple cardiac and respiratory cycles, instead of one binned average. Last but not least, a multi-slice, real-time MR sequence is available on modern scanners from all major vendors. In this work, we used the bSSFP sequence, but the method is not limited to this sequence. Depending on the application, other fast MRI sequences could be used [28], [45]. This simplifies reproduction and distribution of our method.

In our experiment to evaluate the full motion compensation workflow based on X-ray images (Section IV-C), the joint motion model gives the lowest errors. The apparent 2-D motion was reduced by 40% on average for both motion types. In relation to previously published results, this is state of the art. The following reported percentages are based on different datasets and measures, thus, the values are not directly comparable. King et al. achieved a reduction of respiratory motion between 23% and 79%, but cardiac motion was excluded by gating [12]. Shechter et al. reduced cardio-respiratory motion of the coronaries by 48 – 63% [11]. The reduction achieved by Faranesh et al. was between 8% and 52% for aorta and right coronary artery [13]. The motion model based on SAM slice stacking [24] leads to comparable results for the respiratory trajectories, but fails for cardiac trajectories. This is an indicator that SAM focuses mostly on the dominant motion type, i. e., respiratory motion, and largely ignores cardiac motion.

The comparison of our motion compensation method on free-breathing/manually ventilated subjects and automatically ventilated subjects from Section IV-D confirms the expectations. The motion magnitude is lower for automatic ventilation, as indicated by the lower mean error without motion compensation. Additionally, in both the MR experiments and the X-ray experiments, the percentage of the motion that can be compensated is higher in the datasets with automatic ventilation. This means that also the variability of the motion is lower with automatic ventilation. However, the results for manual ventilation are encouraging as well. The relative performance of the motion compensation is only worse by 7–12 percentage points.

Regarding the different types of motions, the motion in cardiac trajectories is generally not compensated as well as the motion in respiratory trajectories. Cardiac motion is spatially less smooth and therefore harder to estimate using registration. To investigate the influence of the registration on those results, we computed the motion fields with additional regularization weights γ. This is the main influence on the smoothness of the motion fields in the registration. For the X-ray key point experiments of Section III-C, the cardiac trajectories without motion compensation have an error of 2.66 ± 1.12, which was reduced to 2.20 ± 0.89 with the standard setting of γ = 0.02. For a larger regularization of γ = 0.05, the error is 2.23 ± 0.85, and for a smaller regularization of γ = 0.005, the error is reduced to 2.15 ± 0.94. However, for the respiratory trajectories, the trend is reversed, i. e., slightly smaller errors for larger γ and higher errors for smaller γ. Thus, even though optimized registration parameters can improve cardiac motion compensation results, it is not the main reason why respiratory motion is captured better than cardiac motion. A more important reason seems to be the relationship of the surrogate signal with the cardiac motion, as indicated by the low R² score for the cardiac model in Section III-E. However, it has to be considered that one reason for the low score is the fact that cardiac motion has a smaller magnitude than respiratory motion and only covers a small part of the field of view. Another issue is the less accurate annotations in the X-ray image for cardiac trajectories, since the heart shadow lacks prominent key points. All in all, the quantitative results for cardiac motion compensation in Section III-B and Section III-C are not satisfactory. Further work is required to better compensate and better evaluate the cardiac component of the motion model. Nevertheless, the motion-compensated overlays presented in the supplementary material and Section III-F subjectively fit the cardiac motion well and improve the perception of the motion.

Of course, our method for motion compensation is not perfect and there are residual errors. All steps in the proposed pipeline can introduce some inaccuracies, e. g., misregistrations in the 4-D MR or insufficient capacity of the motion model. These are the interesting errors for this study. However, there are other sources of error that are not directly related to motion compensation but still influence the results. First of all, the manual annotation of 2-D point trajectories in X-ray is error-prone because of transparency effects such as foreshortening, overlapping structures, and varying contrast levels. Second, other steps in the workflow can adversely affect the evaluated measures. For example, the rigid registration of the coordinate systems of X-ray and MR based on skin markers cannot account for non-rigid movements of the subject during transfer. We use the rail-based table to minimize this issue. Third, the behavior and appearance of the anatomical target region can change during the intervention. The stiffness of devices such as guidewires or needles distorts the anatomy and changes its mechanics. The physician might also interact with and alter the anatomy, for example ablation or biopsy. For Section IV-F, there is the additional issue of segmentation. Due to noise, low resolution, and partial volume effects in MR, the manual segmentation of PAs and LV does not exactly correspond to the contrasted lumen in X-ray.

Another limitation of the presented approach is the compensation of abnormal motions. Abnormal motions can occur in respiration, e. g., coughing, or in the heart, e. g., arrhythmias. The majority of motions observed during MR imaging are normal. Furthermore, the surrogate signals are low-dimensional representations of the motion state. Thus, the motion learned by the linear model is dominated by the normal motions. This is good, because most motions during the intervention are normal as well. The model can adapt to changing rates or amplitudes of the motion. However, more complex motion patterns cannot be learned due to these limiting factors. For use in a clinical setting, the ability to deal with abnormal motions still has to be improved or the cases of failure have to be highlighted to the clinicians. Currently, the proposed method is not equipped to detect false overlays. This would be an interesting direction for future work.

An important alternative to patient-specific motion models, as proposed here, would be a population-based statistical motion model. A statistical model would enable a reduction in MR scan time and computation time and could increase the robustness of the method. However, it is more difficult to deal with abnormalities. The major limitation would occur for abnormal anatomies, for example in the case of structural heart disease, where it is challenging to fit a population-based model. However, the need for guidance is particularly high, since the anatomy and the motions are different for each patient.

For clinicians, the compensation of cardiac and respiratory motion in image fusion is important, depending on the application [1]. The fact that the overlays are static in current systems is a problem in the transcatheter treatment of structural heart disease [46]. In all cardiac interventions, target structures such as pulmonary veins, valves, and coronaries, are affected by both types of motion. Correction of cardiac motion matters most for precise targeting. Respiratory motion affects the whole heart and can be described well with parametric models [12], such that compensation is feasible and generally advantageous. For interventions in other areas of the thorax and abdomen, only respiratory motion occurs and should be compensated.

Considering runtime, only the transfer time between MR and X-ray is available for creating the motion model. In the hybrid OR setup with a C-arm and an MR scanner in the same room, there are only around 10 minutes between the acquisition of the MR images and the start of the interventional procedure. With the current solution, we do not yet meet that goal. The computationally most intensive task is registration. (T – 1) 3-D/3-D registrations have to be performed to create the motion model. To reduce this time, better hardware to compute the (T – 1) registrations in parallel, a more efficient GPU-based implementation, or a simplified registration method, e. g., non-diffeomorphic transformations, is required. Alternatively, the number of time steps could be reduced, which leads to a trade-off between accuracy and runtime. The runtime of the application phase during the intervention already fulfills real-time constraints. This is achieved with a CPU and GPU implementation of respiratory signal extraction and motion model application.

VI. Conclusion

We have presented a new method for motion compensation of overlays in augmented fluoroscopy. The method uses real-time MR imaging to create a 3-D model of cardiac and respiratory motion. This motion model is driven by surrogate signals. The cardiac surrogate signal is based on ECG and respiratory surrogate signal is extracted from the MR images. The model can be applied in the fluoroscopy-guided intervention because ECG is also available and a corresponding respiratory signal can be extracted from the X-ray images. To the best of our knowledge, it is the first method to compensate cardiac and respiratory motion in a fully deformable manner. In the experiments, we showed that cardiac and respiratory motion are reduced substantially. The motion model can be applied during the intervention in real time. However, the runtime of model generation is not yet clinically acceptable.

The approach for respiratory signal extraction still has some drawbacks. The respiratory signal extraction must be retrained for each C-arm position [33], leading to short time without motion compensation for each position. Additionally, it is assumed that the respiratory signals for MR and X-ray are equivalent to each other, because they are extracted from the images in a similar manner. However, the signals depend on the breathing patterns during the training phase. Ideally, a mapping between the different signals would be trained, but this is infeasible because there is no concurrent X-ray and MR imaging. One solution to these problems with image-based respiratory signal extraction would be an external respiratory sensor that is attached during MR and X-ray. However, this has other issues such as drift and synchronization. A fusion of image-based and sensor-based respiratory signals is a promising direction for research.

In the future, we want to apply the method to human patient data. The datasets used here come from pig experiments, which have different motion characteristics. Furthermore, all pigs were anesthetized and on a ventilation machine during MR scanning. Consequently, the motion variability is small. To test how the model handles variability, we used manual ventilation during X-ray imaging in some pigs, but this was just a first step in that direction.

Furthermore, the proposed workflow should be evaluated in a clinical prototype. Pediatric cardiology is a suitable clinical specialty for initial testing. Many patients are anesthetized, leading to reproducible motions, and have structural heart disease, where the abnormal anatomy increases the need for advanced guidance systems. However, the method is very general and can be applied to all kinds of fluoroscopy-guided thoracic and abdominal interventions. Further work is needed to evaluate the value of animated overlays to the physicians in terms of reducing fluoroscopy time, contrast dose, and improving overall procedure success rates.