Local Fitness Landscapes Predict Yeast Evolutionary Dynamics in Directionally Changing Environments

Abstract

The fitness landscape is a concept that is widely used for understanding and predicting evolutionary adaptation. The topography of the fitness landscape depends critically on the environment, with potentially far-reaching consequences for evolution under changing conditions. However, few studies have assessed directly how empirical fitness landscapes change across conditions, or validated the predicted consequences of such change. We previously evolved replicate yeast populations in the presence of either gradually increasing, or constant high, concentrations of the heavy metals cadmium (Cd), nickel (Ni), and zinc (Zn), and analyzed their phenotypic and genomic changes. Here, we reconstructed the local fitness landscapes underlying adaptation to each metal by deleting all repeatedly mutated genes both by themselves and in combination. Fitness assays revealed that the height, and/or shape, of each local fitness landscape changed considerably across metal concentrations, with distinct qualitative differences between unconditionally (Cd) and conditionally toxic metals (Ni and Zn). This change in topography had particularly crucial consequences in the case of Ni, where a substantial part of the individual mutational fitness effects changed in sign across concentrations. Based on the Ni landscape analyses, we made several predictions about which mutations had been selected when during the evolution experiment. Deep sequencing of population samples from different time points generally confirmed these predictions, demonstrating the power of landscape reconstruction analyses for understanding and ultimately predicting evolutionary dynamics, even under complex scenarios of environmental change.

AN important concept to aid our understanding of adaptive evolution is the fitness landscape (Wright 1932; Orr 2005). A fitness landscape is a multi-dimensional genotype-fitness map consisting of a single orthogonal axis for each locus at which variation exists, plus an additional axis for fitness. The added value of the fitness landscape for understanding adaptation lies primarily in its explicit incorporation of epistasis, where mutations combine to affect fitness in a way unexpected from their individual effects. Mutational effects may change in magnitude or sign depending on the genetic background in which they occur (i.e., magnitude or sign epistasis), and this can have crucial consequences for evolution. A change in sign will render some evolutionary pathways inaccessible, and several such interactions can together act to separate peaks of higher fitness, thus potentially constraining evolution to a limited subset of genotype space (Weinreich et al. 2005; Poelwijk et al. 2007).

The prevalence and overall nature of epistasis play a key role not only in understanding and predicting adaptation, but also in theories on the evolution of sex, speciation, robustness, and evolvability (Kondrashov 1988; Whitlock et al. 1995; Kondrashov and Kondrashov 2001; de Visser and Krug 2014). As such, a significant body of work has been dedicated to characterizing the topography of the fitness landscape for several empirical examples (Kogenaru et al. 2009; de Visser and Krug 2014). These studies generally combine a limited number of mutations in all possible ways and then determine (a proxy of) fitness for each individual genotype, and have found ample evidence for epistatic interactions and landscape ruggedness, particularly within enzymes and when individual mutational effects are large (Schenk et al. 2013; de Visser and Krug 2014). Some authors have gone even further and used the acquired topographical information to make predictions about the course and outcome of evolution (Weinreich et al. 2006; Lozovsky et al. 2009; Szendro et al. 2013), and, in the case of the antibiotic resistance enzyme TEM β-lactamase, these predictions were partly confirmed using an in vitro evolutionary approach (Salverda et al. 2011).

While empirical fitness landscape reconstructions appear promising for predicting evolution under constant conditions, they have one important shortcoming. The pathways that are predicted to be followed, as well as their eventual outcomes, generally involve the selection of multiple mutations, which can take hundreds of generations. However, in nature, environments are seldom constant for such extended periods of time. Traditionally, ecology and evolution were thought to occur on different time scales, and selection was thought to maximize fitness in the mean environment (Carroll et al. 2007). However, it is increasingly recognized that there is in fact considerable overlap between these time scales, so that changes in ecological conditions may matter for evolution, particularly in rapidly evolving microbes (Bohannan and Lenski 2000; Bell 2013). This implies that, if we are to fully understand evolution in more realistic settings, we need to take into account how selection pressures change, and, thus, how the fitness landscape changes in response to changes in the environment (Mustonen and Lassig 2009).

Several previous studies have assessed how the topography of the fitness landscape changes across environments by characterizing empirical fitness landscapes in the presence of different selection pressures, and at different intensities of the same selection pressure. These analyses have shown that the shape of the fitness landscape can change dramatically, even when environmental differences are limited (Hayden and Wagner 2012; de Vos et al. 2013; Flynn et al. 2013; Mira et al. 2015), and indicate potentially far-reaching consequences of different regimes of environmental change for evolution. First, different concentrations of the same chemical may select for different genotypes (Ogbunugafor et al. 2016). Second, fluctuating conditions can open up new pathways to higher fitness that are inaccessible in constant environments (de Vos et al. 2015). By contrast, no predictions from landscape reconstructions exist about the effect of different rates of directional environmental change on evolutionary dynamics, despite the fact that such environmental change is common in nature, with pollution and climate change as prominent examples. Furthermore, no study to date has yet directly evaluated how useful fitness landscape reconstructions are for predicting evolution in changing environments by exposing organisms to the involved scenarios of change and determining the temporal phenotypic and genotypic consequences.

We previously evolved replicate populations of Saccharomyces cerevisiae for 500 generations in the presence of either gradually increasing or constant high concentrations of the heavy metals cadmium (Cd), nickel (Ni), and zinc (Zn; Gorter et al. 2016). While Cd is toxic already at comparatively low concentrations, Ni and Zn are toxic at high concentrations only. This difference in the nature of the selection pressure likely had crucial consequences for evolution under different rates of directional environmental change. That is, for all metals, we found that fitness increase under gradual change was delayed, and that populations exposed to both rates of change eventually reached the same fitness. However, the mutational dynamics underlying this observation were different for the unconditionally toxic metal Cd vs. the conditionally toxic metals Ni and Zn. Specifically, whole-genome sequencing of evolved clones revealed that nine genes acquired SNPs and small indels in multiple lines from the same treatment (Gorter et al. 2017; Table 1), suggesting that mutations in these genes were important for adaptation. Importantly, for Cd, the same multi-hit genes (SMF1 and FET4) were mutated under both gradual and abrupt change, while for Ni and Zn, different multi-hit genes were mutated under gradual and abrupt change (VIP1 vs. BUL1, VTC4 and WHI2 for Ni, and PMA1 vs. UBP6 and UBP3 for Zn). This suggests that genotype-by-environment (G × E) interactions across different concentrations of the same metal were important within the context of our experiments, and, moreover, that the nature of this concentration G × E was different for the unconditionally toxic metal Cd vs. the conditionally toxic metals Ni and Zn.

Table 1. Coding mutations in multi-hit genes per evolved clone.

Line		SMF1	FET4	VIP1	BUL1	VTC4	WHI2	UBP6	UBP3
Increasing Cd	1	X
	2	Xa	Xa
	3	Xb
	4	X
	5	Xa
	6	Xa	Xa
High Cd	1	X	Xa
	2	X	Xa
	3	X	Xa,c
	4	X	Xa
	5	Xa	Xa
	6	X	Xa
Increasing Ni	1			Xa
	2
	3			X
	4
	5
	6
High Ni	1				Xa
	2				Xa
	3					X	Xa
	4					X	Xa
	5
	6					X	Xa
Increasing Zn	1
	2
	3
	4
	5
	6
High Zn	1							Xa	X
	2							Xa	X
	3							X
	4
	5							X
	6

Adjusted from Gorter et al. (2017). Note that most evolution lines contained several additional mutations apart from the ones listed here, including diploidization (see Table S1 in File S1). However, each of these mutations occurred in unique genomic regions, so that we have no direct evidence that they were adaptive. Additionally, the large majority of the mutations listed here was homozygous, suggesting that diploidization was a secondary adaptation, and that the mutations listed here were among the first to fix and drive adaptation. Mutations in PMA1 (in two replicate lines from the increasing Zn treatment) were exclusively heterozygous, and thus likely occurred after the strains containing them had diploidized, which implies that they were secondary adaptations. Because PMA1 is an essential gene (i.e., its homozygous deletion mutants are lethal), we did not include this gene in our analyses, which were performed on haploid strains.

^aStop codon or frameshift mutation.

^bHeterozygous.

^cDouble heterozygous.

In addition to these general observations, we noted that several mutations always occurred in particular combinations in our evolved clones (Table 1). In response to the Cd treatments, mutations in FET4 never occurred without those in SMF1. Similarly, in response to the constant high Zn treatment, mutations in UBP3 were found only in combination with mutations in UBP6. This suggests that, in both cases, the selection of one mutation was contingent upon the presence of the other, indicating epistasis (G × G). In response to the constant high Ni treatment, mutations in VTC4 and WHI2 were found in combination multiple times. Mutations in WHI2 have previously been reported to decrease Ni tolerance in isolation (Arita et al. 2009), raising the possibility that they were selected specifically in the background of mutations in VTC4, again suggesting contingency and epistasis. Finally, in response to high Ni, we either found mutations in VTC4 and WHI2 in combination, or in BUL1 in isolation. This also suggests epistasis, although, in this case, mutations appear to have prevented rather than enabled each other’s selection.

The above findings may be explained within a G × E framework that we envisioned previously, which relies on the distinction between magnitude G × E and reranking G × E (Gorter et al. 2016). This framework makes predictions about evolutionary dynamics and outcomes in changing environments based on the nature of the selection pressure, and can, in principle, be applied to any selection pressure or scenario of environmental change. Within the context of our experiments, magnitude G × E refers to the case where the same genotypes are selected at different metal concentrations, but selection is stronger at higher concentrations. For the fitness landscape, this implies that it can have any shape, i.e., epistatic interactions (G × G) of various nature are possible. Additionally, the overall height of the landscape will increase with metal concentration (G × E) as fitness differences between genotypes become larger. However, individual mutational steps do not change in sign across environments, and, as such, the overall shape of the landscape will be comparable across concentrations (that is, magnitude epistasis will remain magnitude epistasis, sign epistasis will remain sign epistasis). While this does not preclude a significant G × G × E interaction per se (identical ranking can be associated with varying individual fitness differences), it does imply that the variance associated with such interaction is likely limited. By contrast, within the context of our experiments, reranking G × E refers to the case where different genotypes are selected at different concentrations. In this case, individual mutational steps will commonly change in sign across environments, and, as such, the overall shape of the landscape will change considerably across concentrations (i.e., magnitude epistasis can change into sign epistasis and vice versa). This implies a significant G × G × E interaction by definition. Because under reranking G × E mutations are beneficial at some concentrations but not others, evolution will be directed along different pathways depending on the dynamic of environmental change.

Our previous findings (Gorter et al. 2016, 2017) are consistent with the predictions from our G × E framework, but do not provide direct evidence for it. Specifically, for Cd, we found mutations in the same genes in response to both gradual and abrupt change, and this suggests magnitude G × E. Conversely, for Ni and Zn, we found mutations in different genes in response to gradual and abrupt change, and this suggests reranking G × E. We also repeatedly found mutations in specific combinations, suggesting that epistasis was important within the context of adaptation to all three metals. Taken together, these observations provide strong circumstantial evidence for the validity of our G × E framework. However, a direct test would require determining the height and shape of each fitness landscape under the relevant conditions. Specifically, for Cd, we should find that the height, but not the shape, of the landscape changes across concentrations, and that similar evolutionary pathways are followed under different regimes of environmental change. Conversely, for Ni and Zn we should find that the shape, and possibly the height, of the landscape changes across concentrations, and that different evolutionary pathways are followed under different regimes of environmental change.

Here, we set out to test these predictions using two complementary approaches. First, we generated fitness landscapes for each metal by constructing mutants with all possible combinations of the parallel mutations that we found in our evolved clones. Because most of these mutations likely confer a reduction or loss of function [i.e., they introduced frame shifts or stop codons, or were predicted to be deleterious based on changes in sequence similarity to a set of homologous protein sequences (PROVEAN score < −2.5 (Choi et al. 2012; Gorter et al. 2017))], we used deletion mutants to approximate their effects. We then measured the fitness of each mutant at different metal concentrations, which allowed us to test our hypotheses about how the height and/or shape of each landscape changes with concentration, and make predictions about the likely consequences that this had for evolutionary dynamics and outcomes. Second, for the more extensive Ni landscape, we tested these predictions using deep sequencing of population samples isolated from our evolution experiment at different time points. Our results confirm that the height, and/or shape, of the fitness landscape change considerably across metal concentrations, depending on the metal used. Moreover, the landscape reconstructions correctly predicted which mutations were selected at what time in our evolving populations. Taken together, this demonstrates the power of our approach and theoretical G × E framework for understanding and predicting evolution.

Materials and Methods

Strains

We used a set of haploid strains from the S. cerevisiae deletion collection (Giaever et al. 2002; Giaever and Nislow 2014) as the basis for our reconstruction mutants. In these strains, single ORFs are replaced with a KanMX cassette, which confers geneticin (G418) resistance (Goldstein and McCusker 1999). The strains used as the basis for the deletion collection are essentially isogenic with the ancestral strains from our evolution experiment (Gorter et al. 2016). That is, they are based on the closely related haploid BY4730, BY4739, BY4741, and BY4742 strains, which differ only in mating type and the presence of the HIS auxotrophic marker, while our ancestral strains were derived from the diploid BY4743 strain [=BY4741/BY4742 (Brachmann et al. 1998; Wloch-Salamon et al. 2008)].

All single mutants in our study, as well as the “ancestral” strain (i.e., the ΔHO::KanMX mutant) are MATa strains from the deletion collection. Conversely, double, triple, and quadruple mutants were generated via gene replacement followed by multiple rounds of mating, sporulation, and selection. Specifically, we amplified the HphMX cassette, which confers hygromycin resistance, and shares its promoter and terminator sequences with the KanMX cassette, from strain W26 (MATa/his3/leu2/LYS/ura3/MET/ΔHO::HphMX) using primers Repl-F (CAGACGCGTTGAATTGTCCC) and Repl-R (CTGGGCAGATGATGTCGAGG). The resulting PCR product was transformed into a set of MATα strains to replace the KanR gene with the HphR gene, and these strains were then crossed to MATa strains containing a different deletion to yield double heterozygous diploids. Sporulation followed by tetrad dissection and replica plating onto geneticin and hygromycin was used to isolate haploid double deletion mutants. Finally, we performed mating assays with tester strains W23 (MATα/his3/leu2/lys/ura3/MET/ΔHO::NatMX) and W24 (MATa/his3/leu2/lys/ura3/MET/ΔHO::NatMX) to determine the mating type of each mutant.

This entire procedure (i.e., mating, sporulation, and selection) was repeated to generate triple and quadruple mutants. However, in this case, a resistance phenotype is insufficient to ascertain strain genotype. We thus performed colony PCR on candidate strains using the deletion collection confirmation primers, in combination with a primer internal to the HphR gene (Hph-3′: TCGTCCATCACAGTTTGCCA), to identify the desired mutants. To generate the competitor strain for the fitness assays, we replaced the KanR gene in the ΔHO::KanMX mutant with the NatR gene (amplified from W24 using the same approach as for HphR/W26), which confers nourseothricin resistance.

An overview of all reconstruction strains can be found in Table 2.

Table 2. Overview of all reconstruction mutants.

Strain	Genotype	Phenotype	Details (Source or Parental Strain Pair)
Ancestor	MATa ΔHO::KanMX	genR	From deletion collection
Δsmf1	MATa Δsmf1::KanMX	genR	From deletion collection
Δfet4	MATa Δfet4::KanMX	genR	From deletion collection
Δsmf1Δfet4	MATa Δsmf1::KanMX Δfet4::HphMX	genR hphR	MATa Δsmf1::KanMX × MATα Δfet4::HphMX
Δvip1	MATa Δvip1::KanMX	genR	From deletion collection
Δbul1	MATa Δbul1::KanMX	genR	From deletion collection
Δvtc4	MATa Δvtc4::KanMX	genR	From deletion collection
Δwhi2	MATa Δwhi2::KanMX	genR	From deletion collection
Δvip1 Δbul1	MATa Δvip1::KanMX Δbul1::HphMX	genR hphR	MATa Δvip1::KanMX × MATα Δbul1::HphMX
Δvip1 Δvtc4	MATa Δvip1::KanMX Δvtc4::HphMX	genR hphR	MATa Δvip1::KanMX × MATα Δvtc4::HphMX
Δvip1 Δwhi2	MATa Δvip1::KanMX Δwhi2::HphMX	genR hphR	MATa Δvip1::KanMX × MATα Δwhi2::HphMX
Δbul1 Δvtc4	MATa Δbul1::KanMX Δvtc4::HphMX	genR hphR	MATa Δbul1::KanMX × MATα Δvtc4::HphMX
Δbul1 Δwhi2	MATa Δbul1::KanMX Δwhi2::HphMX	genR hphR	MATa Δbul1::KanMX × MATα Δwhi2::HphMX
Δvtc4 Δwhi2	MATa Δvtc4::KanMX Δwhi2::HphMX	genR hphR	MATa Δvtc4::KanMX × MATα Δwhi2::HphMX
Δvip1 Δbul1 Δvtc4	MATa Δvip1::KanMX Δbul1::HphMX Δvtc4::KanMX	genR hphR	MATa Δvip1::KanMX Δbul1::HphMX × MATα Δvtc4::KanMX
Δvip1 Δbul1 Δwhi2	MATa Δvip1::KanMX Δbul1::HphMX Δwhi2::KanMX	genR hphR	MATa Δvip1::KanMX Δbul1::HphMX × MATα Δwhi2::KanMX
Δvip1 Δvtc4 Δwhi2	MATa Δvip1::KanMX Δvtc4::HphMX Δwhi2::KanMX	genR hphR	MATa Δvip1::KanMX Δvtc4::HphMX × MATα Δwhi2::KanMX
Δbul1 Δvtc4 Δwhi2	MATa Δbul1::KanMX Δvtc4::HphMX Δwhi2::KanMX	genR hphR	MATa Δbul1::KanMX Δvtc4::HphMX × MATα Δwhi2::KanMX
Δvip1 Δbul1 Δvtc4 Δwhi2	MATa Δvip1::KanMX Δbul1::HphMX Δvtc4::KanMX Δwhi2::HphMX	genR hphR	MATa Δvip1::KanMX Δbul1::HphMX × MATα Δvtc4::KanMX Δwhi2::HphMX
Δubp3	MATa Δubp3::KanMX	genR	From deletion collection
Δubp6	MATa Δubp6::KanMX	genR	From deletion collection
Δubp3 Δubp6	MATa Δubp3::KanMX Δubp6::HphMX	genR hphR	MATa Δubp3::KanMX × MATα Δubp6::HphMX
Competitor	MATa ΔHO::NatMX	natR	MATa ΔHO::NatMX

Assays

To determine the relative fitness of the reconstruction mutants, we performed competition assays in triplicate as described previously (Lenski et al. 1991; Gorter et al. 2016). Briefly, strains were pregrown from frozen in 0.5× YPD medium, and then cultured together with the competitor strain in the presence of different concentrations of the appropriate metal (0, 1, 2, and 3 μM CdCl₂; 0, 83, 167, and 250 μM NiCl₂; 0, 117, 233, and 350 μM ZnCl₂) for 24 hr. Plating on geneticin and nourseothricin before and after competition was used to determine the relative number of doublings, or relative fitness, of each strain.

Similar assays were also used to confirm the absence of any genetic background effects on fitness within the context of our experiments. In this case, we determined fitness of the ΔHO::KanMX and ΔHO::NatMX reconstruction mutants relative to the ancestral strains from our evolution experiment, W24 (MATa/his3/leu2/lys/ura3/MET/ΔHO::NatMX) and W20 (MATa/his3/leu2/LYS/ura3/met/ΔHO::KanMX), respectively, in the presence of all concentrations of all metals in triplicate. These assays revealed no effect of genetic background on fitness (F_1,35 = 0.28, P = 0.60), in any of the assay environments (effect of metal, concentration, and metal × concentration: P > 0.30 in all cases).

When performing the above assays, we observed that the effective metal concentrations had changed compared with the assays performed for our original study (Gorter et al. 2016). That is, the same concentrations of Ni and Zn reduced overall yield more strongly in our current assays, while Cd had a smaller reductive effect. This difference in reductive effect may be due to subtle differences in the composition of our—undefined—media, which can have large consequences (Joho et al. 1988; O’Keefe et al. 2006; Corbacho et al. 2011). Nonetheless, we were unable to remedy this problem experimentally, and thus chose to correct our measurements for this effect. To do so, we cultured a pair of pregrown control strains (W20 and W24 mixed in equal volumes) in the presence of different metal concentrations for 24 hr. Based on the reduction in yield observed during the fitness assays, concentrations were chosen such that they were likely to include most of the relevant dose-response curve for each metal (Cd: 0, 1, 2, 3, 4, 5, and 6 μM; Ni: 0, 28, 56, 83, 167, 250 μM; Zn: 0, 15, 29, 58, 117, 233, and 350 μM). Both prior to, and after, 24 hr of growth, we determined the number of colonies for each replicate to establish the relative reduction in yield. This reduction was then scaled to the change in yield of a control sample grown in the absence of metals to express yield in the presence of metals as a percentage of yield in their absence. All assays were performed in duplicate. An equivalent number of observations was taken from the data generated for our original paper (Gorter et al. 2016), and analyzed in the same way.

Data analysis

Fitness correction:

To determine the effect of metal concentration on yield under the original and the present conditions, we fitted a linear model to the yield data for all metals separately under both conditions, forcing the intercept through 100 (= percentage yield at 0 μM metal). The slopes of these dose-response regression lines were then used to calculate the conversion relationship between metal reductive effect in the original and the present assays (Supplemental Material, File S2 and Table S3 in File S2). This analysis confirmed that Cd had a lower (∼50%) reductive effect in the current assays, while Ni and Zn had a stronger reductive effect (∼200 and ∼120%, respectively). Specifically, 3 μM Cd, 250 μM Ni, and 350 μM Zn in the original assays (= final high concentrations) are equivalent to 6.7 μM Cd, 130 μM Ni, and 293 μM Zn in the current assays, respectively.

To translate our measured fitness values to the original conditions, we fitted a quadratic regression of log-transformed fitness on metal concentration for each mutant separately, and used the previously determined metal conversion relationships to predict fitness of each mutant under the original assay conditions. We then added the residuals from the model to the predicted fitness values to obtain the converted “raw” data points that we used for further analysis. Log transformation was employed to correct for increasing variance, while the quadratic terms allowed for the modeling of the nonlinear effects of metal concentration on fitness that we observed for a substantial part of all mutants. The regressions for the single mutants were also used to predict their fitness across the complete range of metal concentrations used in the experiment. See File S2 for details.

Statistical analyses:

We used general linear models to evaluate the G × G × E interactions within each reconstructed fitness landscape. First, we fitted models with log-transformed fitness as the response variable, and mutant genotype (four or 16 levels for Cd/ Zn and Ni, respectively), metal concentration (four or three levels for Cd/Zn and Ni, respectively), and the interaction between these effects as categorical explanatory variables. We used these models to assess the significance of each individual mutational step at each metal concentration. Next, we reformulated the models to test our hypotheses about G × G × E. That is, we replaced mutant genotype with separate factors for each mutation, and fitted models with all individual mutations (two levels each), metal concentration (as above), and the interactions between these effects (that is, up to three-way interactions for Cd/Zn, and up to five-way interactions for Ni) to the data. In each case, we used sequential backward elimination to find the minimal adequate model and report statistics from deletion tests. In these analyses, log transformation of fitness was used not only to correct for increasing variance, but also because it enables direct testing of a multiplicative null model of epistasis.

To investigate whether loss-of-function mutants of VTC4 had a different fate than amino acid change mutants of this gene, we fitted linear regressions of frequency on time for each mutant separately. We then tested whether these slopes were positive/negative more often for either type of mutant using Fisher’s exact test.

All statistical analyses were performed in R 3.0.2 (R Core Team 2013).

Sequencing

To investigate evolutionary dynamics in our previously performed long-term laboratory evolution experiment [75 transfers/500 generations; for details see Gorter et al. (2016)], we revived frozen whole population samples isolated at different transfer time points (T = 25, T = 50, and T = 75) from all lines evolved in the presence of either gradually increasing or constant high concentrations of NiCl₂ (lines NI1–6: 16.7–250 μM, and lines NH1–6: 250 μM). Genomic DNA was isolated according to standard procedures, and the VIP1, BUL1, VTC4, and WHI2 genes were amplified using an optimized PCR protocol with the Phusion High-Fidelity DNA polymerase (NEB) and the deletion collection confirmation primers located upstream and downstream of each gene. As a control, three separate PCRs were performed for each gene on genomic DNA isolated from the ancestral strain W20. For each replicate population, as well as the three control reactions, cleaned up PCR products from all genes were mixed in equimolar ratios. Libraries were prepared from these mixtures using the Nextera XT DNA library preparation kit (Illumina), and these were then sequenced by Illumina MiSeq with 2 × 300 bp paired-end reads, by the Cologne Centre for Genomics.

Sequencing reads were analyzed using the CLC Genomics Workbench 8.5.1. Reads were trimmed to remove adapter sequences and low quality regions (Q < 30) and mapped to the reference sequence of each of the four genes (VIP1, BUL1, VTC4, and WHI2) using standard parameter settings. Average coverage per gene across populations was high, ranging from 6622x for BUL1 to 8294x for VTC4. We used the low frequency variant detector to call SNPs and small indels that were present in >1% of the reads and annotated the variants using the S. cerevisiae CDS track. We tried to further reduce the threshold for variant calling, but this yielded variants in the control reactions. Such variants are likely due to PCR and/or sequencing errors, or, alternatively, may represent very low frequency variants maintained by drift or mutation-selection balance under standard culture conditions, and are therefore not relevant to our selection regimes.

Data availability

Sequencing reads have been deposited at NCBI under BioProject PRJNA418223. Strains are available on request.

Results

We previously evolved replicate populations of S. cerevisiae for 500 generations in the presence of either gradually increasing or constant high concentrations of the heavy metals Cd, Ni, or Zn (Gorter et al. 2016), and found that adaptation to these selection regimes occurred repeatedly through specific combinations of mutations that reduced or abolished the function of a limited number of genes (Table 1; Gorter et al. 2017). To explain these observations, and gain more insight into evolutionary dynamics in directionally changing environments in general, we here reconstructed the underlying local fitness landscape for each metal by deleting all repeatedly mutated genes per metal, both by themselves and in combination. This yielded landscapes of four (Cd and Zn: two genes → 2² combinations) or 16 (Ni: four genes → 2⁴ combinations) different genotypes.

To assess how the effect of each mutation depended on the genetic background, as well as the environment, we then determined the fitness of each mutant relative to a differently marked control strain in the presence of different concentrations of the selective metal. Specifically, we assayed each mutant in the presence of the final, or constant high, metal concentration used in the selection experiment, as well as two intermediate concentrations (33 and 67% of the final concentration), and in the absence of additional metals. However, when performing these assays, we observed that the effective metal concentrations had changed compared with the assays performed for our original study (Gorter et al. 2016). Since we were unable to remedy this problem experimentally, we chose to correct our measurements for this effect (see Materials and Methods and File S2). Additionally, in the case of Ni, the increased effective metal concentration introduced a very large measurement error at the highest assay concentration (in 80% of all competitions the less fit competitor formed fewer than five colonies). We therefore excluded all data from this condition from our analyses, and instead used the data collected at lower Ni concentrations to calculate fitness under the original conditions in the presence of the final, high Ni concentration, and at 50% of this concentration.

Cadmium

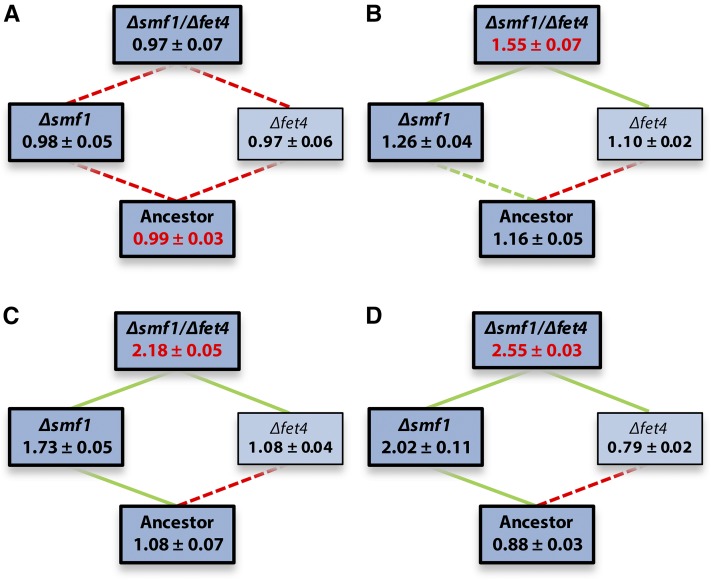
We used the corrected fitness landscapes to test several of our hypotheses about the effect of the rate of directional environmental change on evolution. For Cd, we anticipated that the height of the fitness landscape would increase with metal concentration, but that its shape would remain roughly constant across concentrations, because the same mutations are beneficial at different metal concentrations, but selection is stronger at high concentrations. This should result in the same pathways being followed under gradual and abrupt change. In support of this prediction, we found that the total variance in fitness (∼ height of the fitness landscape) increased significantly with Cd concentration (Figure 1; Levene’s test for equality of variances: F_3,12 = 12.31, P = 0.0006). This was largely due to the increased fitness of Δsmf1 strains at higher metal concentrations (i.e., G × E: Δsmf1 × Cd concentration: F_3,38 = 89.12, P < 0.0001). As anticipated, the Δfet4 mutation was beneficial only in the background of Δsmf1 (i.e., G × G: Δsmf1 × Δfet4: F_1,38 = 20.60, P < 0.0001). However, we found no evidence that the shape of the fitness landscape changed across concentrations: the G × G × E interaction was nonsignificant (Δsmf1 × Δfet4 × Cd concentration: F_1,32 = 2.86, P = 0.052), and, moreover, the fitness ranking of all four genotypes was the same at all metal concentrations.

Figure 1.

Predicted fitness ± SEM of reconstruction mutants in the presence of 0 (A), 1 (B), 2 (C), or 3 (D) µM CdCl₂. Edge color reflects how the addition of each mutation (i.e., from bottom to top) affects fitness (green, increase; red, decrease; significance was assessed using a linear model fitted to all Cd data). Solid lines represent significant changes, dotted lines nonsignificant ones. After sequential Bonferroni correction, all comparisons remain significant. Bold, darker boxes correspond with (combinations of) mutations found in clones isolated from the evolution experiment. Red fitness values represent global optima.

As a result, none of the individual mutational steps changed in sign across Cd concentrations, and the Δsmf1Δfet4 double mutant consistently represented the global fitness optimum in the presence of Cd (Figure 1). This optimum is accessible via a single pathway only, leading to the straightforward prediction that evolution under both Cd regimes will lead to the initial selection of a loss-of-function mutation in SMF1, followed by selection of a loss-of-function mutation in FET4. Because fitness differences are larger at high Cd concentrations, this process should be faster following abrupt change. Indeed, we previously found that all six populations exposed to constant high Cd concentrations contained mutations in both SMF1 and FET4 (Table 1). Conversely, only two of the populations exposed to increasing Cd concentrations contained this combination of mutations, while the other four populations from this treatment contained a mutation in SMF1 in isolation. This may indicate that these populations had not yet acquired a mutation in FET4 due to delayed adaptation.

Zinc

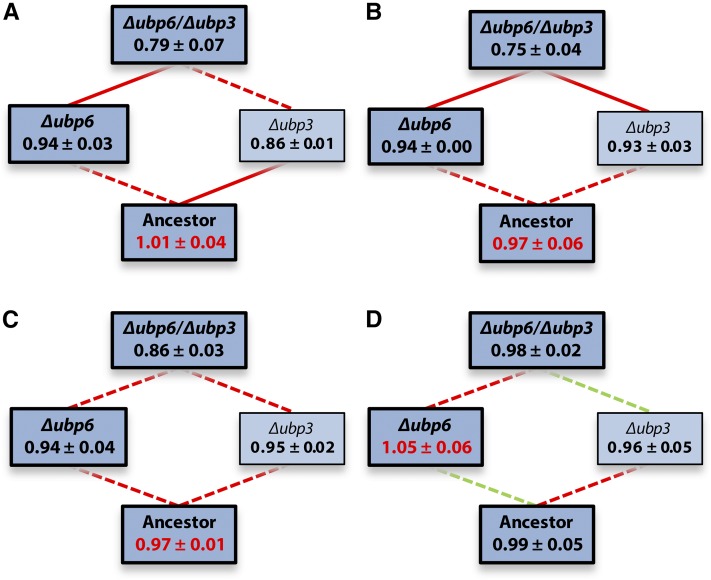
For Zn, we predicted that the shape of the fitness landscape would change across concentrations, because different mutations are beneficial at different metal concentrations, and that this would have consequences for the evolutionary pathways followed under different regimes of environmental change. In contrast to Cd, the total variance in fitness was similar at different Zn concentrations (Figure 2; Levene’s test for equality of variances: F_3,12 = 0.83, P = 0.50), suggesting that the overall height of the fitness landscape was comparable across concentrations. In contrast to our expectations, the shape of the landscape did not change significantly with concentration (i.e., G × G × E: Δubp6 ×Δubp3 × Zn concentration: F_3,32 = 0.77, P = 0.52). Moreover, neither the G × E interactions nor the G × G interaction were significant (P > 0.10 in all cases), and, instead, the minimal model predicted that both the Δubp6 and the Δubp3 mutation confer a fitness decrease, while the highest Zn concentration consistently increases mutant fitness (P < 0.02 in all cases).

Figure 2.

Predicted fitness ± SEM of reconstruction mutants in the presence of or 0 (A), 117 (B), 233 (C), or 350 (D) µM ZnCl₂. Edge color reflects how the addition of each mutation (i.e., from bottom to top) affects fitness (green, increase; red decrease; significance was assessed using a linear model fitted to all Zn data). Solid lines represent significant changes, dotted lines nonsignificant ones. After sequential Bonferroni correction, only the comparisons at 117 μM remain significant. Bold, darker boxes correspond with (combinations of) mutations found in clones isolated from the long-term evolution experiment. Red fitness values represent global optima.

Nonetheless, between 233 and 350 μM Zn, all four genotypes changed in rank, and 50% of the mutational steps changed in sign. Accordingly, the global optimum changed from the ancestral genotype to the Δubp6 single mutant. Taken together, these observations suggest that at least part of the explanation for the lack of significant G × G × E may be, that for the Zn landscape fitness differences are small relative to measurement error. Δubp6 increased fitness marginally at the high concentration at which mutations in this gene were selected during the evolution experiment. By contrast, for Δubp3, there was no indication that it increased fitness in any environment, either by itself or in combination with Δubp6. In fact, a previous study reported that this mutation decreases Zn tolerance (Dziedzic and Caplan 2011), making it hard to explain why we found mutations in UBP3 in response to our high Zn selection regime. One possibility is that the amino acid changes in our evolution lines altered rather than abolished UBP3 function (neither of the two observed mutations in this gene is a stop codon or frame-shift mutation), in which case the deletion mutant phenotype does not accurately reflect their effect.

Nickel

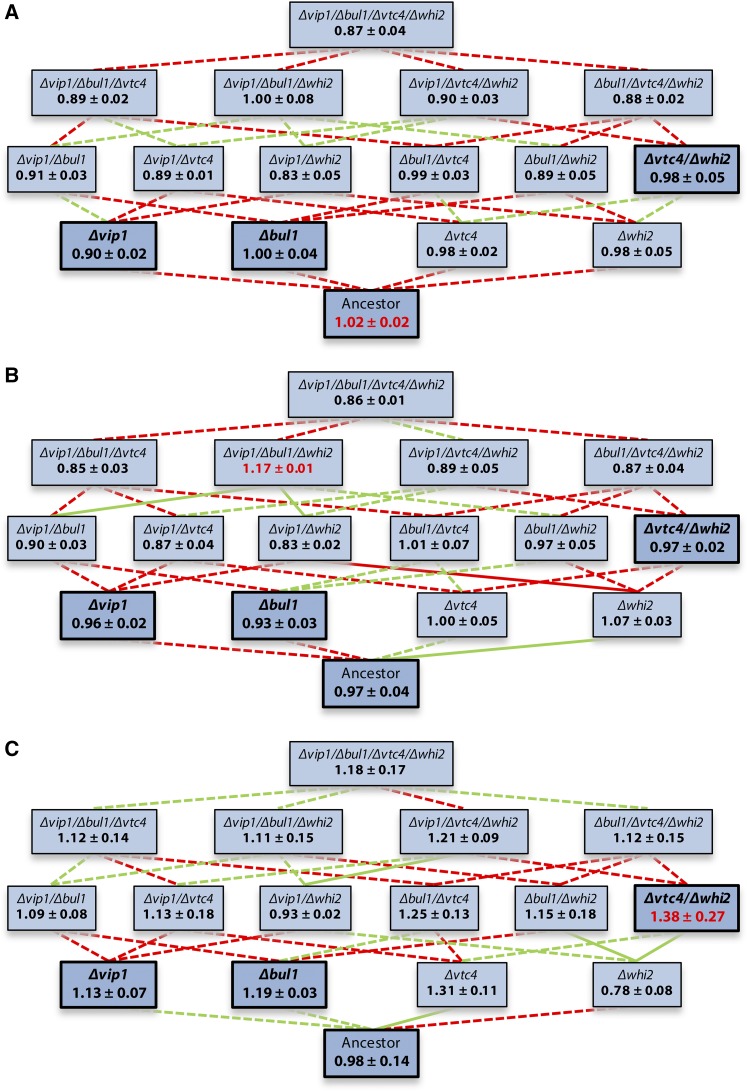
For Ni, as for Zn, we predicted a change in the shape of the fitness landscape as a function of concentration, with distinct consequences for the evolutionary pathways followed under different rates of change. Because it is composed of four rather than two genes, the results for the Ni landscape were considerably more complex (Figure 3). However, the same general statistics that we used to characterize differences between landscapes for Cd and Zn can also be obtained for the Ni. First, the height of the Ni landscape increased with concentration, but this was not significant (Levene’s test for equality of variances: F_2,45 = 1.84, P = 0.17). Second, the shape of the landscape changed across concentrations, as shown by a significant G × G × G × E interaction (Δvip1x Δbul1 × Δvtc4 × Ni concentration: F_2,108 = 3.74, P = 0.027). In addition to this interaction, the minimal model for this landscape contained two G × G ×G interactions involving Δwhi2: Δbul1x Δvtc4 × Δwhi2 (F_1,108 = 7.75, P = 0.006), and Δvip1x Δbul1 × Δwhi2 (F_1,108 = 4.74, P = 0.032). These patterns seem complex, but can be explained for a large part by the deletions of VIP1, VTC4, and BUL1, each of which significantly increased fitness at 250 μM Ni only. However, one of these mutations conferred a similar fitness increase as two or three of them (effect of number of mutations: F_2,36 = 0.51, P = 0.61), indicating diminishing returns epistasis. Additional effects that were present at all concentrations included a decreased fitness of the Δbul1Δvtc4Δwhi2 mutant and an increased fitness of the Δvip1Δbul1Δwhi2 and Δvtc4Δwhi2 mutants, compared with expectations based on the fitness of single and double mutants. However, for the latter two mutants, this appears to be due almost entirely to their fitness effects at one specific concentration: 125 μM in the case of Δvip1Δbul1Δwhi2, and 250 μM in the case of Δvtc4Δwhi2.

Figure 3.

Predicted fitness ± SEM of reconstruction mutants in the presence of 0 (A), 125 (B) or 250 (C) µM NiCl₂. Edge color reflects how the addition of each mutation (i.e., from bottom to top) affects fitness (green, increase; red, decrease; significance was assessed using a linear model fitted to all Ni data). Solid lines represent significant changes, dotted lines nonsignificant ones. After sequential Bonferroni correction, only the changes from Δwhi2 to Δvtc4Δwhi2 and Δbul1Δwhi2 at 250 µM remain significant. Bold, darker boxes correspond with (combinations of) mutations found in clones isolated from the long-term evolution experiment. Red fitness values represent global optima.

Between the two Ni environments (i.e., 125 μM vs. 250 μM Ni), the majority of all 16 genotypes changed in rank, and, crucially, 47% of the individual mutational steps changed in sign. This cannot be explained by the increased dimensionality of the landscape: when considering the sub landscapes composed of two mutations each (ancestor, both single mutants, and double mutant), the majority of all genotypes still changed in rank. Moreover, 63% of the mutational steps changed in sign, on average, and, for the Δvtc4Δwhi2 combination that we found in our evolution experiment, this percentage was even higher (75%). Consistently, both complete landscapes had a different global optimum, which was accessible from the ancestor in the case of 250 μM only. Taken together, these results suggest that evolutionary dynamics will be very different under different regimes of environmental change for Ni. Specifically, at intermediate Ni concentrations, only mutations in WHI2 should be selected (and possibly mutations in VTC4 followed by mutations in BUL1, although these mutations confer only marginal fitness increases). Conversely, at high Ni concentrations mutations in VIP1, BUL1, and VTC4 should be selected, while mutations in WHI2 should be selected against. In this environment, the Δvtc4Δwhi2 mutant represents the global fitness optimum, suggesting that at high Ni concentrations selection of mutations in WHI2 is contingent upon the presence of mutations in VTC4.

These predictions are in good agreement with our sequencing results for clones from the constant high Ni treatment: we repeatedly found mutations in either BUL1 in isolation, or in VTC4 and WHI2 in combination (Table 1). The fact that we did not find any mutations in VIP1 may, in this case, be explained by the smaller fitness benefit of Δvip1 relative to Δbul1 and Δvtc4. However, why, in response to increasing Ni concentrations, mutations in VIP1 rather than BUL1, VTC4, and WHI2 were found (Table 1), is not immediately clear. Mutations in WHI2 may have increased in frequency, and subsequently been lost again, because they are beneficial at intermediate Ni concentrations only. Conversely, Δvip1 confers a benefit at 250 μM only, but there its benefit is smaller than that of Δbul1 and Δvtc4.

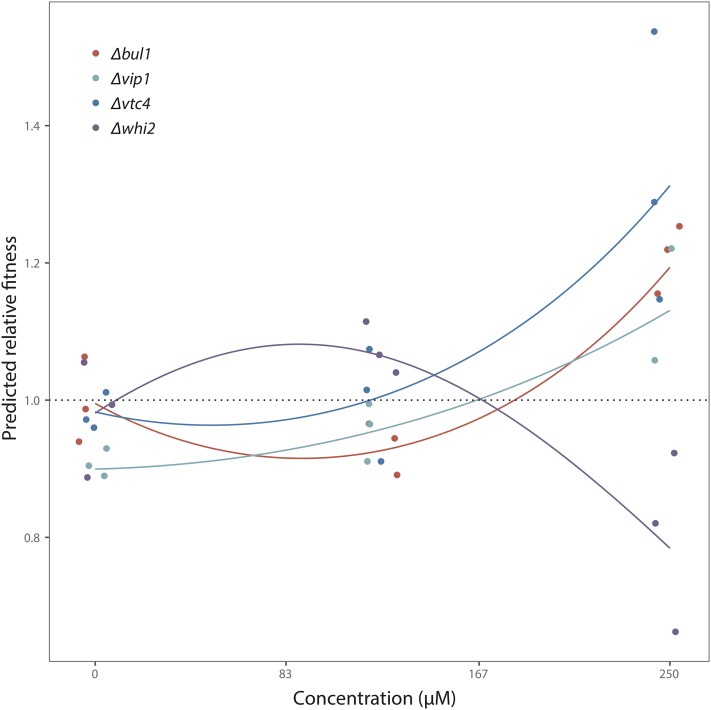
A possible explanation for finding mutations in VIP1 under increasing Ni is that mutations in this gene start to increase fitness at lower Ni concentrations than mutations in VTC4 or BUL1. To assess this possibility, we plotted the predicted fitness as a function of (original) metal concentration for all four single mutants (Figure 4). This revealed considerable uncertainty in the fitness estimates for each of our mutants. Nonetheless, it also provided support for our hypothesis that Δvip1 becomes beneficial at a lower concentration (166 µM) than Δbul1 (182 µM). This suggests that mutations in VIP1 were selected starting from transfer T = 45, while mutations in BUL1 were selected from transfer T = 50, and conferred a higher fitness than VIP1 from T = 60 onwards. By contrast, mutations in VTC4 are predicted to both become beneficial at an earlier time point, and confer a larger benefit than both other mutants over the entire concentration range up to 250 µM. The mutations in VTC4 in our evolved clones were never stop-codon or frame-shift mutations (Table S2 in File S1, NH3 and NH4), raising the possibility that these mutations confer a smaller benefit than loss-of-function mutations in the same gene, which may explain why we found mutations in VIP1 rather than VTC4 in response to increasing Ni concentrations. However, if that were the case, it is unclear why we did not find loss-of-function mutations in our evolution experiment instead. One possibility is that Δvtc4 has antagonistic pleiotropic effects that do not play out over the course of our fitness assays. For example, it was recently reported that Δvtc4 causes genomic instability (Bru et al. 2016), which may have detrimental effects in the long term.

Figure 4.

Predicted relative fitness of single-gene deletion mutants as a function of Ni concentration. Predictions are based on quadratic regressions of log-transformed fitness on metal concentration for each mutant separately. Colored dots represent transformed replicate fitness measurements for each mutant, and are jittered for increased visibility.

Sequencing

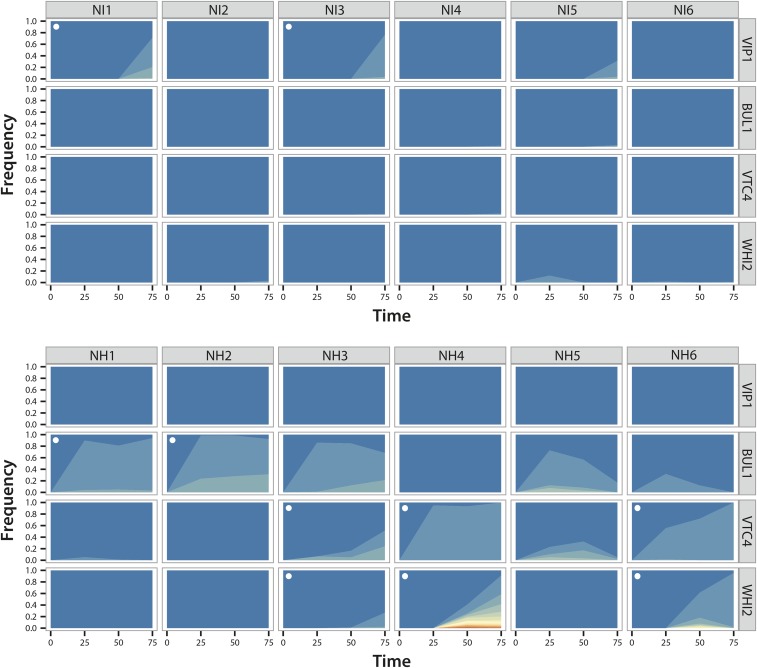
The aim of our landscape reconstructions was to increase our understanding of how the height and shape of the fitness landscape change in response to different rates of directional environmental change, and how this, in turn, may have affected the evolutionary trajectories in our evolution experiment. Our reconstructions were able to explain a substantial part of our whole-genome sequencing results (Table 1), but also generated new predictions about the underlying adaptive dynamics. These predictions were relatively straightforward for Cd, with the same mutations predicted to be selected more slowly under increasing vs. constant high concentrations, but more subtle for Ni, with different mutations predicted to be selected at different times under increasing vs. constant high concentrations of this metal. To test these predictions, we amplified VIP1, BUL1, VTC4, and WHI2 from population samples isolated at different time points (T = 25, T = 50, and T = 75) for all evolution lines exposed to Ni. Deep sequencing of the resulting PCR product was then used to determine the relative frequency of different alleles at these four loci over time. This analysis revealed extensive clonal interference within and between loci, and confirmed that evolutionary dynamics under gradually increasing and constant high Ni concentrations were fundamentally different (Figure 5 and Table S2 in File S1).

Figure 5.

Evolutionary dynamics of replicate yeast populations exposed to increasing (NI) or constant high (NH) concentrations of Ni at the repeatedly mutated loci VIP1, BUL1, VTC4, and WHI2. Colors depict different alleles and their frequency over time (in transfers). Blue shading represents the wild type allele. White dots indicate the presence of a mutation in the corresponding gene in the sequenced clone from that population. In all cases, the mutations that we previously identified in the sequenced clones were also present in the corresponding population samples from T = 75 at appreciable frequencies

Specifically, under gradually increasing Ni concentrations, mutations in VIP1 were selected repeatedly, but, as predicted by our landscape analyses, this happened only during the final stage of the experiment. At T = 50, no mutation in VIP1 had yet reached the detection threshold of 1% (although one of the mutations that we found at T = 75 was present at 0.13%), but, at T = 75, half of the populations contained such mutations at frequencies ranging from 43 to 77%. In line with our finding that Δwhi2 confers a fitness advantage at low Ni concentrations, we found a loss-of-function mutation in this gene in isolation at T = 25 in one line (at a frequency of 12% (NI5)). At T = 50, this mutation was no longer detectable, consistent with such mutations being detrimental at higher Ni concentrations. Furthermore, mutations in BUL1, VTC4, and WHI2 were present at T = 75 at very low frequencies (<3%) in two replicate lines each, in the same and different populations than the VIP1 mutations (Table S2 in File S1). This confirms that BUL1 and VTC4 mutations are also under selection at this final time point, and suggests that this has been so for a shorter time than for VIP1. Mutations in WHI2 were present in the two populations that had no mutations in any of the other genes. Because these lines contain other mutations that are known to increase Ni tolerance [loss-of-function of BSD2 (NI2) and VPS38 (NI6) (Arita et al. 2009)], it is possible that WHI2 mutations were selected specifically in their background, analogous to their selection in the background of VTC4 mutations.

In contrast to the gradually increasing treatment and consistent with their absence in the sequenced clones from T = 75, we never found mutations in VIP1 in the populations exposed to constant high Ni concentrations. Conversely, mutations in BUL1 and/or VTC4 were present in all populations from the first sequenced time point (T = 25, although at low frequency in some populations), and, in four populations (NH1, NH3, NH5, and NH6; Figure 5 and Table S2 in File S1), multiple alleles of these two genes showed clonal interference. This competition generally persisted for many transfers, with comparatively small increases in the relative frequency of VTC4 alleles, suggesting that they have a small selective advantage relative to BUL1 alleles. Interestingly, all loss-of-function mutants of VTC4 decreased in frequency over time, while amino acid change mutants increased in frequency with a single exception (Fisher’s exact test: P = 0.048). This supports our previous hypotheses that these two classes of mutations are fundamentally different, and that Δvtc4 has detrimental effects in the long term. In population NH5, both BUL1 and VTC4 mutants eventually decreased in frequency, implying that they were outcompeted by another, more beneficial, mutant (this is also the population that contained the single VTC4 amino acid change mutant that decreased in frequency). A likely candidate gene for this is VTC1, which contained a loss-of-function mutation in the evolved clone from this line. Our landscape reconstructions predicted (nearly reciprocal) sign epistasis between Δvtc4 and Δbul1 at 250 µM Ni, which may explain why we never found mutations in both genes in the same clone. However, in population NH3, the joint frequency of such mutations at T = 75 is 1.2, which clearly exceeds 1. Because Δvtc4 marginally increases fitness in the Δbul1 background, this suggests that mutations in VTC4 were selected in a BUL1 mutant background in at least some cases.

One of the main predictions from our landscape analyses was that WHI2 mutations would only be selected in the background of VTC4 mutations at high Ni concentrations. The deep sequencing results support this: mutations in WHI2 never occurred before VTC4 mutations rose to appreciable frequencies, and, after their addition, VTC4 mutants increased in frequency relative to BUL1 mutants when they were in competition (populations NH3 and NH6). Remarkably, in population NH4, we simultaneously found up to 14 different alleles of WHI2. Although no WHI2 allele had yet reached the threshold of 1% at T = 25 for this population, five WHI2 alleles found at T = 50 were present at this time at lower frequencies, suggesting that they were selected from a very early stage.

Discussion

The fitness landscape is a concept that is increasingly used for understanding and predicting evolutionary adaptation (Wright 1932; Orr 2005; de Visser and Krug 2014). The topography of the fitness landscape depends critically on the environment, which has potentially far-reaching consequences for evolution under changing conditions (Taute et al. 2014). However, few studies have assessed directly how empirical fitness landscapes change across conditions, or validated the predicted consequences of such change. We previously evolved replicate yeast populations in the presence of either gradually increasing or constant high concentrations of the heavy metals Cd, Ni, and Zn, and analyzed their phenotypic (Gorter et al. 2016) and genomic changes (Gorter et al. 2017). Here, we reconstructed the local fitness landscapes underlying adaptation to each metal by deleting all repeatedly mutated genes, individually and in combination. Fitness assays revealed that the height and/or shape of each local fitness landscape changed considerably across metal concentrations, with distinct qualitative differences between unconditionally and conditionally toxic metals. This change in topography had particularly crucial consequences in the case of Ni, where a substantial part of the individual mutational fitness effects changed in sign across concentrations. Based on the Ni landscape analyses, we made several predictions about which mutations had been selected when during our evolution experiment. Deep sequencing of population samples from different time points generally confirmed these predictions, demonstrating the power of landscape reconstruction analyses for understanding and predicting evolutionary dynamics, even under complex scenarios of environmental change.

Change in landscape topography across concentrations depends on the selective metal

Our results are consistent with our hypotheses as outlined in the Introduction. Based on a previously developed G × E framework (Gorter et al. 2016), we predicted that for Cd—which is toxic already at comparatively low concentrations—the height of the fitness landscape would increase with metal concentration, but that its overall shape would not change. The rationale behind this is that the same evolutionary solution, reducing the internal Cd concentration to a minimum, should be favored at all external metal concentrations, but more strongly so at high concentrations. Indeed, our results show that, while the mutations in the Cd landscape interact epistatically (that is, the benefit of Δfet4 was contingent upon the presence of Δsmf1), the nature of this interaction does not change across concentrations, so that the same adaptive trajectory is accessible under both gradual and abrupt change. However, fitness differences between genotypes were larger at high concentrations, implying that selection should be faster following abrupt change. These findings are in good agreement with our previous phenotypic and genomic analyses, and suggest that, for Cd, the exact scenario of environmental change (e.g., gradual, sudden, or fluctuating) may affect the timing of selection, but will have limited effect on the outcome of evolution at the genetic level.

By contrast, for Zn and Ni—toxic at high concentrations only—we predicted that the shape of the fitness landscape would change substantially across metal concentrations. The reason for this is that, in this case, different evolutionary solutions should be favored at different external metal concentrations. For Zn, we found limited evidence for this hypothesis. That is, fitness ranking of genotypes changed across Zn concentrations, but the G × G × E interaction was not significant, possibly because fitness differences were small relative to measurement error. Alternatively, it is possible that the fitness correction that we used was imprecise. However, qualitative results (i.e., no significant G × G × E interaction, Δubp3 detrimental at all concentrations) were the same for analyses based on the uncorrected fitness measurements (data not shown), suggesting that our conclusions are not qualitatively affected by the way we corrected fitness.

For Ni, we found strong evidence that the shape of the fitness landscape changed across concentrations. That is, in the Ni landscape, mutations interacted epistatically (G × G), and these interactions changed significantly across concentrations (G × G × E). At the final high Ni concentration (250 μM), selection of Δwhi2 was contingent upon the presence of Δvtc4, while Δvip1, Δbul1, and Δvtc4 mutually excluded each other. However, between 125 and 250 μM Ni, almost half of the individual mutational effects changed in sign, which had important consequences for the predicted evolutionary dynamics. Extension of this analysis to other concentrations suggests pervasive changes in the fitness ranking of genotypes, implying that, in the case of Ni, evolutionary dynamics and outcomes depend strongly on the exact scenario of environmental change. For example, if we had chosen to perform our experiments at 80% of the current concentration (200 µM NiCl₂), we might have found mutations in VIP1, rather than BUL1 or VTC4. Similarly, our deep sequencing results showed that mutations in both BUL1 and VTC4 were present at low frequencies at the final time point of several of the increasing Ni populations. This allows one to speculate that, under continued exposure to constant high Ni concentrations, it will be only a matter of time before mutations in VIP1 are outcompeted by these, now fitter, mutants. In our current study, we considered only a limited number of loci, based on the presence of mutations in multiple populations. However, it seems plausible that similar patterns exist for other loci as well, so that, under gradually increasing Ni concentrations, several mutations were selected but subsequently lost again as the concentration increased.

Landscape analyses correctly predict evolutionary dynamics despite uncertainties

We used deep sequencing of population samples from different time points to test the predictions from our landscape reconstructions about evolutionary dynamics in response to gradually increasing and constant high Ni concentrations. For practical reasons, these predictions were based on several simplifying assumptions. First, we used gene knock-out constructs to approximate the effect of each mutation. Second, we used an arguably crude measure based on relative yield to correct our fitness estimates for uncontrolled changes in effective metal concentrations in the competition assays. Finally, we did not differentiate between significant and nonsignificant fitness differences between genotypes when making predictions. For the Cd landscape, fitness ranking of all genotypes, and, thus, accessibility of mutational pathways, was the same at all Cd concentrations, and our predictions would have been similar if we had made different assumptions (e.g., if we had assumed a linear relationship between concentration and fitness, also see File S2). Conversely, for the Ni landscape, fitness ranking, and, thus, accessibility of mutational pathways, changed considerably across concentrations, and our predictions would have been fundamentally different if we had made different assumptions. Nonetheless, the deep sequencing results for the populations evolved in the presence of Ni fit our predictions remarkably well. Most notably, the reconstruction analyses correctly predicted the global timing of selection of mutations in VIP1 and WHI2 in response to gradually increasing Ni concentrations, as well as the interference between mutations in BUL1 and VTC4, and the order of selection of mutations in VTC4 and WHI2, at constant high Ni concentrations. This shows the validity of our approach: based on analyses of constructed fitness landscapes we could, to some extent, predict which mutations were selected at what time, even under complex scenarios of environmental change.

Of course, our predictions were based on information about the mutations that happened, and hence were predictions in retrospect (de Visser and Krug 2014). Moreover, since we assessed fitness for a limited number of mutations and environments only, and measurement error in our assays was substantial, these predictions were qualitative rather than quantitative. Yet, for evolutionary forecasting in the true sense, detailed quantitative predictions with confidence intervals are essential, because such predictions can generate testable hypotheses about the relative prevalence of alternative mutational pathways (Weinreich et al. 2006; Lozovsky et al. 2009; Szendro et al. 2013) under different scenarios of change. Such predictions would require an increased number of replicate fitness measurements and assay environments, in combination with population genetic models that explicitly link fitness effects to fixation probabilities. While this is clearly beyond the scope of the current study, our work shows that landscape reconstructions can yield partial predictions based on knowledge of key mutations, which is a small, but essential step toward a priori predictions.

Extensive clonal interference within and between loci

Our deep sequencing results revealed extensive clonal interference within and between loci. Clonal interference between mutations at different loci is commonly observed in microbial evolution experiments (Barrick and Lenski 2013; Lang et al. 2013), and several studies have reported clonal interference between alleles of the same locus (Lee and Marx 2013; Hong and Gresham 2014; Maharjan et al. 2015). The repeated occurrence of mutations in the same genes is often used as an indication for the selective advantage of such mutations (Elena and Lenski 2003). However, the simultaneous presence of up to 14 alleles of the same gene—WHI2—within a single population (NH4; Figure 5) is remarkable, and quite puzzling at first sight. If these mutations are so beneficial, why did we not observe one of them going to fixation before the others occurred? One possibility is that the WHI2 locus is a mutational hotspot, for example, because of a larger target size for loss-of-function mutations, or because it is more highly expressed, which may induce mutagenesis (Kim et al. 2007; Jinks-Robertson and Bhagwat 2014). However, WHI2 is the shortest of all genes that we studied, and does not have a disproportionate number of codons that are one mutation removed from a stop codon. Similarly, there is no clear reason why it should be overexpressed under our experimental conditions. Another potential explanation for our observations lies in the fact that, at high Ni concentrations, mutations in WHI2 are only beneficial in the background of mutations in VTC4, which themselves provide a large benefit. When the frequency of VTC4 mutants in the population is low, few WHI2 mutations will occur in genotypes also carrying VTC4 mutations, but, when they do, they will rise to appreciable frequencies relatively quickly. By contrast, when the frequency of VTC4 mutants in the population is high, many double mutants will occur, but their selective advantage relative to the rest of the population will be small, so that they will need many transfers to rise in frequency. The combination of these effects may have led to the apparently simultaneous invasion of multiple double mutants as VTC4 was spreading through the population, followed by a period with only limited further increase in frequency once VTC4 came to dominate the population.

Epistatic interactions may indicate functional relationships

Our fitness landscape analyses revealed substantial epistasis. These interactions are not only interesting for their evolutionary consequences, they also provide valuable information about the functional relationship between the involved genes (Segre et al. 2005; Collins et al. 2007; Costanzo et al. 2010). Specifically, synergistic epistasis, where the combined effect of mutations is more extreme than expected from their individual effects, may indicate that mutations affect parallel pathways (Segre et al. 2005; de Visser et al. 2011). We observed two cases of positive synergistic epistasis: the Δsmf1Δfet4 and Δvtc4Δwhi2 double mutants both have a higher fitness (in the presence of Cd and Ni, respectively) than expected from the single mutant fitnesses. Indeed, Smf1p and Fet4p function in parallel, because they are two of the main importers through which Cd can enter the cell, with a more central role for Smf1p (Wysocki and Tamas 2010). For the VTC4WHI2 pair it is harder to explain the epistatic effects that we found. Vtc4p is part of the vacuolar transporter chaperone complex that is involved in the sorting of V-type ATPases, which drive Ni transport to the vacuole via the generation of a proton gradient (Nishimura et al. 1998; Muller et al. 2003; Luo et al. 2016). Conversely, Whi2p is required for full activation of the general stress response (Kaida et al. 2002), a seemingly unrelated function. One way in which these two genes may interact is that mutations in VTC4 first act to reduce the toxic effects of Ni exposure. Then, mutations in WHI2 can be selected because they restore the unstressed physiological state of the cell—such adaptations are frequently among the first to be selected in laboratory evolution experiments (Philippe et al. 2007; Harrison et al. 2015; Rodriguez-Verdugo et al. 2016).

For the Δubp6Δubp3 double mutant, we also expected to find synergistic epistasis, but we found no evidence for this. In fact, a previous study reported antagonistic epistasis—where the combined effect of mutations is less extreme than expected from their individual effects, which may indicate that mutations affect the same molecular pathway—between these mutations, although this was based on their individually deleterious effect in the absence of metal (Collins et al. 2007). Consistent with such antagonistic epistasis, Ubp6p and Ubp3p both act to deubiquitinate proteins targeted for degradation, with a more central, downstream role for the proteasome-associated Ubp6p (Finley et al. 2012; Isasa et al. 2015). Taken together, this information reinforces our conclusion that the UBP3 deletion mutant probably does not accurately reflect the effect of the missense mutations that we found in this gene.

A final prominent case of epistasis in our study was the antagonistic (diminishing returns) epistasis between Δvip1, Δbul1, and Δvtc4. Interestingly, Δvtc4 was previously found to interact synergistically with both Δvip1 and Δbul1 to decrease fitness in the absence of metal beyond what was expected from their individual deleterious effects (Costanzo et al. 2010), suggesting that these genes function in related, but not identical, pathways. One way to explain this discrepancy with our results is that these three mutants interact synergistically with respect to both Ni tolerance and growth. However, at the Ni concentrations used in our evolution experiment, one mutation is sufficient for increasing Ni tolerance, so that the combined effect on growth causes the observed antagonism with respect to fitness. In line with this, at the highest Ni concentration that we used for our assays (but that we left out of our further analyses for reasons outlined in the Results) we found that the triple mutant represented the global optimum in the Ni landscape.

Our results are potentially broadly relevant

While we generated landscapes for the evolution of tolerance to just three metals, our results are potentially relevant for a much broader range of selection pressures and regimes of environmental change. Specifically, some selection pressures may resemble Cd in that they select for the same evolutionary “solutions” at all intensities (magnitude G × E/change in height of the fitness landscape), while others may resemble Ni and Zn in that they select for different “solutions” at different intensities (reranking G × E/change in shape of the fitness landscape). Potential examples of the first category include antibiotics and radiation (which are always “bad”), whereas potential examples of the second category include temperature and nutrient levels (which are “good” or “bad” depending on the intensity of the selection pressure). Nevertheless, factors other than the nature of the selection pressure may also affect the relative importance of magnitude and reranking G × E under different scenarios of change. For example, if the genetic architecture of a trait under selection is such that it directly trades off with growth, different mutations will be selected under different rates of change even for “simple” selection pressures like antibiotics. Such trade-offs are likely particularly pronounced under natural conditions, implying that magnitude G × E may have a more limited role to play under these circumstances.

We have shown that knowing whether magnitude or reranking G × E is more important within the context of a given selection pressure can help to predict the evolutionary consequences of different rates of directional environmental change. However, similar predictions can be made about, for example, fluctuating conditions (or any regime of environmental change for that matter): in the case of magnitude G × E, such a regime should have only limited consequences for evolutionary outcomes. Conversely, in the case of reranking G × E, the frequency of fluctuations will be very important, because this will determine whether mutations can be reverted before they go to fixation. This type of information is important not only for understanding evolution under changing conditions in nature, but for instance potentially also for the design of antibiotic cycling therapies or the selection of improved crops. Taken together, our results imply that already limited knowledge of the nature of a given selection pressure can help to predict the evolutionary consequences of different scenarios of environmental change.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300519/-/DC1.