Evidence for Selection-by-Environment but Not Genotype-by-Environment Interactions for Fitness-Related Traits in a Wild Mammal Population

To understand how organisms may adapt to environmental changes, it is necessary to determine how environmental conditions influence evolution in wild...

Abstract

How do environmental conditions influence selection and genetic variation in wild populations? There is widespread evidence for selection-by-environment interactions (S*E), but we reviewed studies of natural populations estimating the extent of genotype-by-environment interactions (G*E) in response to natural variation in environmental conditions and found that evidence for G*E appears to be rare within single populations in the wild. Studies estimating the simultaneous impact of environmental variation on both selection and genetic variation are especially scarce. Here, we used 24 years of data collected from a wild Soay sheep population to quantify how an important environmental variable, population density, impacts upon (1) selection through annual contribution to fitness and (2) expression of genetic variation, in six morphological and life history traits: body weight, hind leg length, parasite burden, horn length, horn growth, and testicular circumference. Our results supported the existence of S*E: selection was stronger in years of higher population density for all traits apart from horn growth, with directional selection being stronger under more adverse conditions. Quantitative genetic models revealed significant additive genetic variance for body weight, leg length, parasite burden, horn length, and testes size, but not for horn growth or our measure of annual fitness. However, random regression models found variation between individuals in their responses to the environment in only three traits, and did not support the presence of G*E for any trait. Our analyses of St Kilda Soay sheep data thus concurs with our cross-study review that, while natural environmental variation within a population can profoundly alter the strength of selection on phenotypic traits, there is less evidence for its effect on the expression of genetic variance in the wild.

THE evolutionary dynamics of a phenotypic trait are dependent upon the strength of associations between the trait and fitness (selection), and the expression of additive genetic variation in the trait (Lynch and Walsh 1998). Manipulation of the environment or natural variation in environmental conditions is associated with varying strength of selection (Siepielski et al. 2013; Wood and Brodie 2016). There is also evidence that patterns of genetic variance can change across varying environmental conditions in laboratory and wild animal populations (Hoffmann and Merilä 1999; Charmantier and Garant 2005; Wood and Brodie 2015; Rowiński and Rogell 2017), termed genotype-by-environment interactions (G*E). However, it is less clear how ubiquitous or strong G*E are in natural populations and how patterns of genetic (co)variance between multiple traits may vary with the environment (Gienapp and Brommer 2014). Further, very few studies have estimated the simultaneous effect of environmental variation on selection and genetic variation in a population (Wood and Brodie 2016). It is therefore useful to estimate how patterns of selection and genetic (co)variance change across environmental conditions in wild populations to determine how such populations may respond to environmental change.

There is abundant evidence to suggest that the strength of natural selection on a trait, commonly measured as the strength of the phenotypic association between a trait and fitness, varies with environmental conditions (selection-by-environment interactions, which we will term S*E). In many studies, the strength of selection increases with environmental harshness, such as high population density (PD), low resource availability, or an unfavorable climate (Price et al. 1984; Milner et al. 1999a; Garant et al. 2007; Pelletier et al. 2007a; Visser et al. 2015). Much rarer than changes in the strength of selection are changes in its direction (Siepielski et al. 2013), although such fluctuating selection has been observed: for example, Soay sheep (Ovis aries) horn growth is positively associated with fitness under favorable conditions, but negatively under poor conditions (Robinson et al. 2008), and selection on forehead patch size in collared flycatchers (Ficedula albicollis) has changed from positive to negative with increasing temperatures over the past 34 years (Evans and Gustafsson 2017). Environmental conditions may also alter the shape of trade-offs between fitness components: for example, under harsher conditions the production of fewer, larger offspring may be favored over more, smaller offspring (Verhulst 1998; Wilson et al. 2009). Finally, the strength of selection may in fact weaken in the very harshest environments, due to a loss of variance in fitness, and thus, we may ultimately expect to see the strongest selection in intermediate environmental conditions under which the variance in fitness and “opportunity for selection” is the greatest (Arnold and Wade 1984).

There is also evidence that expression of genetic (co)variance can vary across environmental conditions, and there are a number of hypotheses as to why this may be the case [reviewed elsewhere, see for example Hoffmann and Merilä (1999) and Rowiński and Rogell (2017)]. The findings of empirical studies of G*E, meanwhile, vary across contexts. In experimental studies of plants, evidence for G*E is abundant (Des Marais et al. 2013): plants of different genotypes or from different populations show marked variation in their phenotypic responses to a range of environmental variables such as irrigation, temperature, light, stress, and density (Westerman and Lawrence 1970; Stivers et al. 1971; Westerman 1971; Khan et al. 1976; Schlichting 1986; Mazer and Schick 1991; Pigliucci et al. 1995a,b; Shaw et al. 1995). Laboratory studies of animals also frequently indicate G*E in response to experimental manipulation of environmental conditions (Vieira et al. 2000; Valdar et al. 2006; Ingleby et al. 2010). However, findings in natural populations of animals have been inconsistent to date. Two reviews have concluded that the heritability of traits tends to increase under more favorable conditions (Merilä and Sheldon 2001; Charmantier and Garant 2005), potentially reflecting decreases in residual variation in improved conditions as well as, or instead of, increased expression of genetic variation. Several studies have investigated G*E as a method of estimating the heritability of phenotypic plasticity (or individual-by-environment interactions, I*E) for laying date in passerine birds, with some finding evidence in support of G*E (Nussey et al. 2005) and others finding no evidence (Brommer et al. 2005, 2008). Indeed, a more recent analysis of G*E for laying date and clutch size found no evidence for G*E in laying date in either of two populations, but did find evidence of G*E for clutch size in one population (Husby et al. 2010). More recent studies have also used G-matrix comparison of suites of traits to show that patterns of genetic (co)variance remain relatively unchanged in starkly contrasting environmental conditions in great tits, Parus major (Garant et al. 2008), blue tits Cyanistes caeruleus (Delahaie et al. 2017), and humans (Bolund et al. 2015), despite profound changes in phenotypic means between environments. Finally, a study of a collared flycatcher population showed that the structure of a G-matrix of morphological traits varied considerably over a 25-year period, although the changes were not predictable, directional, or related to changes in phenotypic means across time (Björklund et al. 2013). Systematic evidence for changes in genetic variance across environmental conditions is therefore not apparent in more recent studies in wild animal populations (Table 1 and Supplemental Material, Table S1 in File S3; see Discussion for further consideration of the studies reviewed).

Table 1. A summary of studies, in chronological order, testing for G*E across natural (as opposed to experimentally-manipulated) environmental variation in wild animal populations, where G*E could be changes in either additive genetic variance and/or heritability.

Study	Species	Environmental variable/predictor	Number of traits studied	Number of traits showing G*E
Gebhardt-Henrich and van Noordwijk (1991)	Great tit (Parus major)a	Mean juvenile size	2	1
Larsson (1993)	Barnacle goose (Branta leucopsis)a	Mean juvenile size	3	(3)
Larsson et al. (1997)	Common gull (Larus canus)a	Mean juvenile size	1	(1)
Qvarnstrom (1999)	Collared flycatcher (Ficedula albicollis)a	Mean juvenile size	1	0
Reale et al. (1999)	Bighorn sheep (Ovis canadensis)b	Season	3	(3)
Coltman et al. (2001)	Soay sheep (Ovis aries)b	Season	2	1
Garant et al. (2003)	Atlantic salmon (Salmo salar)c	Food abundance	1	(1)
McAdam and Boutin (2003)	Red squirrel (Tamiasciurus hudsonicus)b	Food abundance	1	0
Ernande et al. (2003)	Pacific oyster (Crassostrea gigas)d	Food abundance	3	(3)
Garant et al. (2004)	Collared flycatcher (Ficedula albicollis)a	NAO	4	2
Brommer et al. (2005)	Collared flycatcher (Ficedula albicollis)a	Spring temperature	1	0
Garant et al. (2005)	Great tit (Parus major)a	Population density	1	1
Nussey et al. (2005)	Great tit (Parus major)a	Spring temperature	1	1
Wilson et al. (2006)	Soay sheep (Ovis aries)b	Mean juvenile survival	1	1
Pelletier et al. (2007b)	Bighorn sheep (Ovis canadensis)b	Time period	4	1
Brommer et al. (2008)	Common gull (Larus canus)a	Spring temperature	1	0
Garant et al. (2008)	Great tit (Parus major)a	Spring temperature	3	0
Robinson et al. (2009)	Soay sheep (Ovis aries)b	Mean juvenile survival	3	2
Husby et al. (2010)	Great tit (Parus major)a	Spring temperature	2	1
McGaugh et al. (2010)	Painted turtle (Chrysemys picta)e	Heating degree days	2	0
DiBattista et al. (2011)	Lemon shark (Negaprion brevirostris)c	Time period	2	0
Husby et al. (2011)	Great tit (Parus major)a	Spring temperature	1	1
Björklund et al. (2013)	Collared flycatcher (Ficedula albicollis)a	Time period	4	4
Bolund et al. (2015)	Human (Homo sapiens)b	Time period	4	0
Delahaie et al. (2017)	Blue tit (Cyanistes caeruleus)a	Population	7	0
Bolund and Lummaa (2017)	Human (Homo sapiens)b	Time period	4	4

See Table S1 in File S3 for full information, including the traits, the time period studied, and the direction of any observed changes. Where the environmental predictor is given as “mean juvenile size/survival,” the measure of environmental quality is the mean size or survival rate of that year’s cohort; in years where juveniles are larger or survive better, environmental quality is assumed to be higher. Where numbers in the final column are given in parentheses, it indicates that the authors interpreted a change in genetic variance or heritability, but that no formal statistical test was performed. G*E, genotype-by-environment interactions; NAO, North Atlantic Oscillation.

^aBird species.

^bMammal species.

^cFish species.

^dBivalve species.

^eReptile species.

Quantifying changes in genetic (co)variance and selection across environmental conditions is important since such change can constrain or facilitate evolution, though studies investigating changes in the expression of genetic variance and the strength of selection across environmental gradients simultaneously are rare (Wood and Brodie 2016). Birth weight in Soay sheep was shown to be under positive selection and show substantial (maternal) genetic variance (Wilson et al. 2005), but a negative correlation between genetic variance expressed and the strength of selection across environmental conditions appeared to constrain evolution of this trait (Wilson et al. 2006). In years of poor environmental conditions there was low genetic variance for birth weight, but strong selection for higher birth weight, while in favorable years there was higher genetic variance but weak selection, constraining the expected response to selection (Wilson et al. 2006). In contrast, a study of a great tit population showed that additive genetic variance for laying date increased in warmer years and that selection for earlier laying date was also stronger in warm years (Husby et al. 2011). These results lead to the prediction that an evolutionary response to selection should be strong in warm years but weak in cooler years, facilitating the evolution of earlier laying dates. A recent simulation study and literature review showed that simultaneous S*E and G*E should have the potential either to drive or to constrain evolutionary change, dependent on how exactly the two covary, but also confirmed that empirical studies rarely quantify both (Wood and Brodie 2016). Thus, concurrent studies of S*E and G*E are important if we are to predict how natural populations may respond to environmental change (Kruuk et al. 2008; Wood and Brodie 2016).

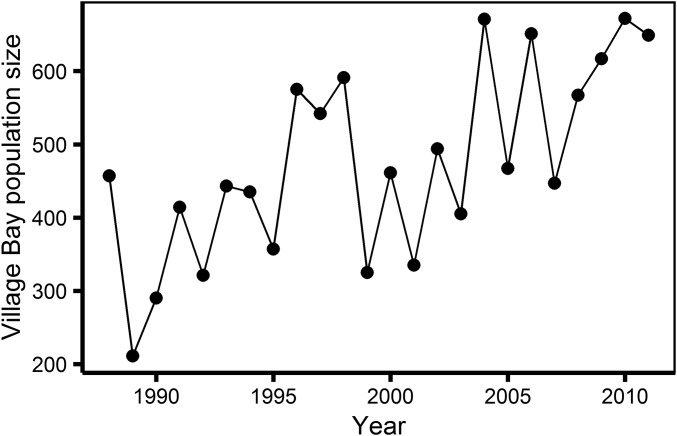
In this study, we estimated the extent of both S*E and G*E in a wild population experiencing extreme variation in ecological conditions. The unmanaged Soay sheep population of St Kilda is characterized by severe fluctuations in population size (Figure 1), due largely to variation in mortality rates arising from the effects of population density on food availability (Clutton-Brock et al. 1991) and also to subsequent effects on numerous aspects of performance, including body weight and growth (Clutton-Brock et al. 1992), parasite burden (Hayward et al. 2009), and reproductive performance (Pemberton et al. 1999; Clutton-Brock et al. 2004a; Hayward et al. 2013). We aimed to determine the extent to which this extreme variation in environmental conditions influenced variation in selection and genetic (co)variance in six morphological and life history traits, all putatively linked to fitness, plus a measure of annual contribution to fitness. Previous work in this population has provided evidence for substantial additive genetic variance for a variety of life history, morphometric, and physiological traits (Milner et al. 2000; Coltman et al. 2001; Wilson et al. 2005, 2006; Robinson et al. 2009; Bérénos et al. 2014, 2015; Hayward et al. 2014), and has also found evidence that patterns of genetic (co)variance for several traits may change across environmental conditions (Wilson et al. 2006; Robinson et al. 2009). Here, we used interannual variation in population density as a measure of environmental quality. Our data set comprised large numbers of repeated measures of individual phenotypes in years of different population densities, with which we were effectively able to model individual “reaction norms” in response to density. Our results reveal evidence for S*E but not G*E.

Figure 1.

Estimated number of sheep inhabiting Village Bay on the island of Hirta, St Kilda, during the Augusts of 1988–2011.

Materials and Methods

Study population and data collection

Soay sheep are descended from the domesticated sheep present in northwest Europe in the Bronze Age, and are thought to have been taken to the St Kilda archipelago (57°49′N, 08°34′W, 65 km northwest of the Outer Hebrides, Scotland) several thousand years ago (Clutton-Brock et al. 2004b). A population has lived on the island of Soay [99 hectares (ha)] since their arrival in St Kilda, but there is evidence that they interbred with the now-extinct Scottish Dunface sheep breed in the mid-19th century (Feulner et al. 2013). The largest island in the St Kilda archipelago, Hirta (638 ha), was home to a human population until 1930, when the people were evacuated along with their modern domesticated livestock. In 1932, 107 Soay sheep were moved from Soay to Hirta, from which Hirta’s current unmanaged population grew. The sheep population living in the Village Bay (c. 170 ha) area of Hirta has been the subject of an intensive individual-based study since 1985 (Clutton-Brock et al. 2004b). Females give birth in spring (March–April) and over 95% of lambs born in Village Bay are captured within a week of birth, weighed, blood and tissue sampled for genetic analysis, and tagged for future identification. In August, ∼50% of sheep in Village Bay are captured over a 2-week period and a series of measurements are taken, including body weight, hind leg length, horn length and growth increment, testicular circumference, ectoparasite counts, and fecal samples. During the rut in October and November, males compete for access to estrous females and any untagged males are captured, tagged, and genotyped. The majority of mortality occurs during the winter from starvation exacerbated by intestinal parasite infection (Gulland 1992). Frequent censuses and searches of the study area from February onward ensure that the carcasses of most casualties are found and death dates assigned. Ten censuses are conducted in each of the lambing, August, and rut periods of the year. We estimated PD in any year as the number of individuals of all ages recorded alive in Village Bay during the August censuses (Figure 1): this is therefore the density experienced by the sheep between lambing (April) and the start of winter. PD was used as our measure of environmental variation because it varies considerably between years, and influences fitness (Clutton-Brock et al. 1991, 1992; Milner et al. 1999b) and selection (Milner et al. 1999a). We used phenotypic measurements taken in August toward the end of the plant growth period (April–August). Conception occurs during the November rut and mortality occurs in the subsequent winter. Increased PD is associated with stronger selection on coat and horn phenotype in the Soay sheep (Moorcroft et al. 1996; Clutton-Brock et al. 1997), and with stronger negative associations between genomic inbreeding coefficients and body size, survival, and breeding success, indicating inbreeding depression-by-environment interactions (Pemberton et al. 2017).

Pedigree construction

A full description of genotyping and pedigree construction in the study population has been provided previously (Bérénos et al. 2014). Briefly, individuals were genotyped at 37,037 single-nucleotide polymorphisms (SNPs), located throughout the genome, using the Ovine SNP50 BeadChip (Illumina). The pedigree was constructed primarily using molecular assignment of maternities and paternities, which were inferred simultaneously using 315 unlinked SNPs with high minor allele frequency in the R package MasterBayes (Hadfield et al. 2006). All assignments were made with 100% confidence. Since not all sheep have SNP genotypes, particularly those alive prior to 1990, further assignments were made using observational data (maternities) or microsatellites (paternities). Specifically, further maternities were assigned to females observed to be closely associated with a lamb after birth, while further paternities were assigned based on genotyping at 14–18 microsatellite markers (Morrissey et al. 2012) if confidence of assignment was > 95% (Bérénos et al. 2014). The final pedigree (Bérénos et al. 2014) consisted of 6740 individuals, with 5981 maternal links, 4593 paternal links, and a maximum of 10 generations.

Phenotypic traits

We analyzed data on six phenotypic traits, measured during the Augusts of the years 1988–2011, and a seventh, annual contribution to fitness, which was measured across the subsequent winter. Not all measurements were taken in the early years of the study, although an estimate of annual fitness was associated with each phenotypic measurement. All individuals measured were of known age and the identity of their mothers was known. The traits used were as follows:

Body weight:

This was measured to the nearest 0.1 kg at capture in August. A total of 5093 measurements were available for 2597 individuals.

Hind leg length:

This was measured in millimeters from the tubercalcis of the fibular tarsal bone to the distal end of the metatarsus (Milner et al. 1999a). We only considered data up to age three for this trait, since beyond this it is stable (Hayward et al. 2015) and, unlike the other traits that are to a certain extent condition-dependent, leg length cannot decline as age advances. In total, 3741 measurements were available for 2531 individuals aged 0–3 years.

Strongyle fecal egg count (FEC):

We counted the number of strongyle nematode eggs per gram of feces collected in August using a modified version of the McMaster egg-counting technique (Craig et al. 2006). Egg counts were grouped into bins of 100 eggs and counts of > 2000 were collapsed into the highest bin (2% of samples). This is a combined count for five strongyle species, the eggs of which are indistinguishable by eye (Gulland and Fox 1992). A total of 4464 counts were collected from 2308 individuals.

Horn length and horn growth:

We measured horn length (in millimeters) from the base of the horn and along the outer curvature to the tip, while horn growth increment in a given year was measured from the base of the skull and along the outer curvature to the first growth increment (Johnston et al. 2013). We only used data collected from males with the large, curved, “normal” horn phenotype (Clutton-Brock et al. 2004b), and did not use data from females. In total, 1189 measurements of horn length from 742 males and 809 measurements of horn growth from 483 males were collected.

Testicular circumference:

We measured testicular circumference (in millimeters) at the widest point of the scrotum as a proxy for testes mass (Preston et al. 2012). A total of 1378 measurements were taken from 974 males.

Annual fitness:

We calculated annual contributions to an individual’s lifetime fitness (“annual fitness” from herein) in a given year as an individual’s genetic contribution to the following year’s population (Brommer et al. 2007). For an individual with phenotypic traits measured in August of year t, their annual fitness for t was calculated based on their survival to the following spring and on the number of offspring (determined from assignments made by the population pedigree) born in that spring to a female or sired by a male. Annual fitness w of individual i measured in year t was thus calculated as $w_{i,t}= p_{i,t}+ \left(1/2r_{i,t}\right)$, where p is the survival of an individual to May 15th of the following year and r is the number of lambs born to that individual in the following spring.

Statistical workflow

Selection: associations between phenotypic traits and annual fitness:

We first investigated the patterns of selection on the phenotypic traits described above, and the extent to which selection varied with PD. We tested for associations between our six phenotypic traits and annual fitness using linear mixed-effects models (LMMs) using maximum likelihood in the package “lme4” (Bates et al. 2015) in R ver. 3.2.1. Our main aims were to determine whether each trait’s association with annual fitness was: (1) linear or curvilinear, (2) sex-specific, or (3) dependent upon PD. The response variable in all models W_it was annual fitness (+1), which was natural log-transformed prior to analysis. For each trait, we therefore started with a base model (model 1.0):

$$W_{it}\mathrm{\sim }\mu +\left(Ag{e}_{it}\ast Se{x}_i\right)+in{d}_i+y{r}_t+m_m+b{y}_k+e_{it}$$ (model 1.0),

where annual fitness W_it of individual i is measured in year t, dependent on fixed effects of the overall mean $\mu ,$ individual age Age_it (a categorical variable ranging from 0 to 11 in females and 0 to 7 in males), sex Sex_i, and the interaction between age and sex. ind_i, yr_t, m_m, and by_k are random effects accounting for variation associated with repeated measures taken from the same individuals, in the same years, with the same mothers, and from the same birth years respectively, and e_it is the residual effect for each observation. In models of horn length and horn growth, we added an individual’s genotype at the SNP10 locus as an additional fixed categorical variable with three levels (CC, CT, and TT) due to its association with variation in horn length (Johnston et al. 2011) and annual fitness (Johnston et al. 2013). For each trait of interest in turn, we then sequentially added terms in more complex models: a continuous linear fixed effect of PD b*PD_t, where b is the regression coefficient of PD in the August of the year of measurement t (model 1.1); model 1.1 plus a linear effect of the trait of interest (model 1.2), to test for linear selection on the trait; model 1.2 plus a quadratic effect of the trait (model 1.3), to test for nonlinear selection on the trait; depending on whether the quadratic term was significant, model 1.2 or 1.3 plus an interaction between the linear trait term and sex (model 1.4); and, finally, model 1.2 or 1.3 plus an interaction between the linear trait term and PD (model 1.5), to test for S*E. The interaction between the trait and sex was never significant, and so we did not enter the trait-by-sex and trait-by-density interactions into the same model. Our final model (1.5) was therefore typically:

$$W_{it}\mathrm{\sim }\mu +\left(Ag{e}_{it}\ast Se{x}_i\right)+trai{t}_{it}\ast P{D}_t+in{d}_i+y{r}_t+m_m+b{y}_k+e_{it}$$,

where trait_it is the trait of interest (e.g., body weight) and PDt is the PD in year t. We tested the statistical significance of these terms by comparing model 1.2 with model 1.1; model 1.3 with model 1.2; model 1.4 with model 1.2 or 1.3; and model 1.5 with model 1.2 or 1.3; we used likelihood ratio tests (LRTs) where the χ²-distributed test statistic is calculated as −2 * (LogLik_model1 – LogLik_model2), with the P-value calculated based on one degree of freedom.

Animal models: the additive genetic basis of phenotypic trait variance:

We next estimated the contribution of additive genetic effects to phenotypic variance in our six traits of interest, plus annual fitness, using quantitative genetic animal models using the software ASReml 3.0 (Gilmour et al. 2009). These are an extension of LMMs, which use information from the population pedigree to estimate the contribution of relatedness to phenotypic variance in a given trait (Henderson 1950) and are commonly used in ecological studies (Kruuk 2004; Charmantier et al. 2014). We fitted separate models (model 2.1) for each of the six phenotypic traits and annual fitness:

$$Trai{t}_{it}\mathrm{\sim }\mu +\left(Ag{e}_{it}\ast Se{x}_i+bP{D}_t\right)+{\mathit{\alpha }}_{\mathit{i}}+p{e}_i+y{r}_t+m_m+b{y}_k+e_{it}$$ (model 2.1),

where the trait of individual i is measured in year t, dependent on fixed effects of individual age, sex, their interaction, and PD as above, and with the random effects as above but with the individual random effect now separated into the additive genetic effect α_i and the “permanent environment” effect pe_i, which accounts for variation between individuals not due to additive genetic effects, including nonadditive genetic effects, behavior, and habitat quality (Kruuk and Hadfield 2007). The heritability of each trait was calculated by dividing the additive genetic variance by the phenotypic variance, which is the sum of the variance components having accounted for the fixed effects. The significance of each variance component was assessed by LRTs comparing the full model with a model omitting the variance component of interest, with the P-value calculated based upon 1 d.f.

Univariate random regression models (RRMs): I*E and G*E:

We next aimed to determine changes in genetic variance across increasing PD by running a series of RRMs in ASReml. PD was standardized to a range of −1 to +1. Each phenotypic trait and annual fitness was fitted as the response variable in turn in the following series of univariate models. To account for possible changes in residual variance with increasing PD, we fitted models with a heterogeneous residual structure. Thus, we assigned each record in our data sets to a quartile of PD and allowed the residual variance to vary across quartiles (i.e., fitting four rather than one residual variance components), though the residual covariance between density quartiles was zero.

Table 2 sets out the range of different models fitted, and the question to which each pertains. Our initial model (model 3.1) was an LMM with the trait of interest as the response variable, fixed effects of age, sex, their interaction and PD, and random effects of individual identity (ID), year, maternal identity, and birth year (Table 2). We then (model 3.2) added an I*E term to the random effects compartment of an RRM to test for variance between individuals in their response to PD, i.e., testing for variation in the slope of individual reaction norms (Table 2). In model 3.2, the (co)variance of the ID component is modeled as a 2 × 2 unstructured variance–covariance matrix, where the two diagonal elements are the between-individual variance for the intercept of the trait and the between-individual variance for the slope of the trait on density, respectively, while the off-diagonal term is the covariance between individuals’ intercept and slope effects. Next, we extended model 3.1 to separate the individual variance component into additive genetic and permanent environment effects (Table 2, model 3.3). Note that model 3.3 is the same as model 2.1, with the addition of heterogeneous residual structure. Next, we extended model 3.3 by adding an I*E term (Table 2, model 3.4). Finally, we extended model 3.4 by splitting the variation between individuals in their response to density into additive genetic and permanent environment (i.e., everything other than the additive genetic) components (Table 2, model 3.5). Each model was tested against the immediately preceding one using an LRT with two degrees of freedom, with the exception of model 3.3, which was tested against model 3.1.

Table 2. Structure of RRMs used to test for I*E and G*E for Soay sheep traits.

Model	Question	Structure	Description
3.1	NA	Traitit ∼ μ + (Ageit*Sexi + bPDt) + indi + yrt + mm + byi + eit	LMM with heterogeneous residual structure
3.2	Is there I*E?	Traitit ∼ μ + (Ageit*Sexi + bPDt) + indi + indi*PDit + yrt + mm + byi + eit	Random regression model with heterogeneous residual structure
3.3	Is there VA for the trait?	Traitit ∼ μ + (Ageit*Sexi + bPDt) + αi + pei + yrt + mm + byi + eit	Animal model with heterogeneous residual structure
3.4	Is there I*E and VA?	Traitit ∼ μ + (Ageit*Sexi + bPDt) + αi + pei + indi*PDit + yrt + mm + byi + eit	Random regression animal model with individual-by-density
3.5	Is there G*E?	Traitit ∼ μ + (Ageit*Sexi + bPDt) + αi + pei + αi*PDit + pei*PDit + yrt + mm + byi + eit	As 3.4, with additive G*E

All model terms are described previously for models 1.1 or 2.1 except for: in models 3.1–3.5, e_it is the residual variance in the trait estimated in each of the four quartiles of population density; in model 3.2 and model 3.4, ind_i*PD_it is the random regression of a first-order polynomial of the individual effect in the trait ind_i as a function of PD; and in model 3.5, α_i*PD_it is the random regression term for the additive genetic effect and pe_i*PD_it is the random regression term for the permanent environment effect. Note that model 3.3 is the same as model 2.1, except that model 3.3 has a heterogeneous residual structure, with the residual variance varying across four quartiles of population density. NA, not applicable; PD, population density; I*E, individual-by-environment interactions; V_A, additive genetic variance; G*E, genotype-by-environment interactions.

Multivariate models: changes in patterns of trait (co)variance:

Since our morphometric traits are very likely to be correlated, and since selection does not act upon phenotypic traits in isolation, we aimed to construct multivariate models to test for changes in patterns of individual and additive genetic (co)variance across PD. We only included traits for which we found evidence for significant I*E or G*E. The multivariate analyses that we attempted are briefly described in File S1. However, in general, we found multivariate models highly troublesome to implement, even where we fitted only I*E rather than the more demanding G*E, because they consistently failed to converge; this is likely to reflect the limitations of the size and structure of the data set, and the large number of parameters to be estimated, to fit a model of such complexity.

Data availability

The data used in all analyses are available via the Dryad data repository.

Results

Selection: associations between phenotypic traits and annual fitness

Our selection analyses indicated three major results (Table 3). First, there was evidence for linear selection on all traits, and for nonlinear selection on some. Second, individuals had, on average, lower annual fitness at higher PD. Since both of these results largely confirm previous observations in this population, these results are described in more detail in File S1. Our third and most important result was that the strength of the associations with annual fitness were stronger at higher PD for the majority of traits. There was evidence for density-specific selection (trait*PD interactions or S*E) for five out of the six phenotypic traits: body weight, hind leg length, strongyle FEC, horn length, and testicular circumference (Table 3, models 1.5). For each of these traits, the strength of the association between the trait and fitness, and hence the strength of directional selection, was stronger at higher density, as evidenced by the tighter grouping of contours at higher density in figures of body weight (Figure 2A), hind leg length (Figure 2B), strongyle FEC (Figure 2C), horn length (Figure 2D), and testicular circumference (Figure 2F). However, there was no evidence for density-specific selection for horn growth, with the positive association between horn growth and annual fitness (Figure 2E) not interacting with PD (Table 3). There was no evidence for sex-specific associations between any of the traits measured in both sexes and annual fitness (Table 3), and there was no qualitative change in results when genotype at the SNP10 locus was excluded from models of horn length and horn growth.

Table 3. Selection on phenotypic traits.

Trait	Model	Structure	Estimate	SE	Vs.	χ21	P value
Body weight	1.0	Age*Sex
	1.1	1.0 + PD	−0.0683	0.0225	1.0	8.41	0.004
	1.2	1.1 + Trait	0.0337	0.0018	1.1	356.72	< 0.001
	1.3	1.2 + Trait2	0.0001	0.0001	1.2	0.59	0.443
	1.4	1.2 + Trait*Sex (M)	−0.0059	0.0033	1.2	3.26	0.071
	1.5	1.2 + Trait*PD	0.0038	0.0006	1.2	34.54	< 0.001
Hind leg length	1.0	Age*Sex
	1.1	1.0 + PD	−0.0631	0.0263	1.0	5.49	0.019
	1.2	1.1 + Trait	0.7476	0.0577	1.1	163.50	< 0.001
	1.3	1.2 + Trait2	−0.5528	0.2179	1.2	6.35	0.012
	1.4	1.3 + Trait*Sex (M)	−0.1024	0.1110	1.2	1.18	0.278
	1.5	1.3 + Trait*PD	0.1337	0.0369	1.2	12.71	< 0.001
Strongyle FEC	1.0	Age*Sex
	1.1	1.0 + PD	−0.0700	0.0224	1.0	8.82	0.003
	1.2	1.1 + Trait	−0.0112	0.0012	1.1	79.26	< 0.001
	1.3	1.2 + Trait2	0.0000	0.0000	1.2	0.01	0.903
	1.4	1.2 + Trait*Sex (M)	0.0030	0.0024	1.2	1.61	0.204
	1.5	1.2 + Trait*PD	−0.0026	0.0009	1.2	7.78	0.005
Horn length	1.0	Age
	1.1	1.0 + PD	−0.1179	0.0454	1.0	6.58	0.010
	1.2	1.1 + Trait	0.1697	0.0287	1.1	34.07	< 0.001
	1.3	1.2 + Trait2	0.0288	0.0077	1.2	13.81	< 0.001
	1.4	1.3 + Trait*Sex (M)	NA	NA	NA	NA	NA
	1.5	1.3 + Trait*PD	0.0217	0.0091	1.3	5.65	0.017
Horn growth	1.0	Age
	1.1	1.0 + PD	−0.1071	0.0488	1.0	4.91	0.027
	1.2	1.1 + Trait	0.1300	0.0496	1.1	6.59	0.010
	1.3	1.2 + Trait2	−0.0263	0.0565	1.2	0.22	0.639
	1.4	1.2 + Trait*Sex (M)	NA	NA	NA	NA	NA
	1.5	1.2 + Trait*PD	0.0309	0.0296	1.2	1.06	0.302
Testicular circumference	1.0	Age
	1.1	1.0 + PD	−0.0685	0.0479	1.0	2.17	0.104
	1.2	1.1 + Trait	0.2199	0.0334	1.1	42.62	< 0.001
	1.3	1.2 + Trait2	0.1162	0.0393	1.2	8.75	0.003
	1.4	1.2 + Trait*Sex (M)	NA	NA	NA	NA	NA
	1.5	1.3 + Trait*PD	0.0518	0.0195	1.3	7.06	0.008

Linear mixed-effects models (LMMs) were used to test for associations between annual fitness and six phenotypic traits, and the interaction between this association and population density (PD). The estimate and SE are given for the model parameter denoted under “Structure”; “Vs.” indicates which model the given model was tested against using a likelihood ratio test; the χ²₁ statistic and P-value were calculated from the likelihood ratio test comparison of the two models. For the size of the data sets and number of individuals measured in each data set, see the Materials and Methods. The models highlighted in bold italics are depicted in Figure 2. M, male; FEC, fecal egg count; NA, not applicable.

Figure 2.

Contour plots of selection, showing positive associations between the six phenotypic traits and annual fitness, with trait–fitness associations generally strongest at higher population density. (A–D and F) Each point on plots represents a single individual measured at a given combination of the trait (x-axis) and population density (y-axis). Round points are females and crosses are males. Contours show predicted annual fitness at different combinations of the trait and density (with darker shading indicating higher fitness values). (E) Plot shows selection on horn growth, which did not vary with population density, so we simply show the relationship between horn growth and annual fitness. Each point shows an individual male’s fitness at a measurement of horn growth. The solid line shows the predicted change in annual fitness with increasing horn growth; the broken lines show the prediction ± 1 SE.

Parameter estimates for all terms included in the final models for each trait (for body weight, hind leg length, strongyle FEC, horn length, and testicular circumference, model 1.5 in Table 3; for horn growth, model 1.2 in Table 3) are provided in Table S2 in File S3.

Animal models: the additive genetic basis of phenotypic trait variance

Five traits had a significant additive genetic basis (Table S3 in File S3), with heritability estimates h² (± SE) as follows: body weight, h² = 0.14 ± 0.03; hind leg length, h² = 0.21 ± 0.04; strongyle FEC, h² = 0.03 ± 0.01; horn length, h² = 0.15 ± 0.06; and testicular circumference, h² = 0.19 ± 0.07. Meanwhile, two traits showed nonsignificant additive genetic effect variance: horn growth, h² = 0.09 ± 0.09 and annual fitness, h² = 0.01 ± 0.01. Considering the other random effects in the models, between-year variation accounted for a low proportion of phenotypic variation in hind leg length and horn growth (both 0.01 ± 0.01), but accounted for 8–18% of phenotypic variation in the other traits. Birth year accounted for < 10% of phenotypic variation in all traits, but was statistically significant in all cases. Maternal effects accounted for < 1% of the variance in strongyle FEC, but up to 10% in the other traits (Table S3 in File S3).

Univariate RRMs: I*E and G*E

We tested for I*E and G*E using univariate RRMs; a summary of results is shown in Table 4. We found that PD was negatively associated with body weight and annual fitness, and positively associated with strongyle FEC, but found no association between PD and any other traits (File S1). We found statistical support for I*E for three traits, but did not find any support for G*E in any trait, as detailed below.

Table 4. RRMs were used to test for I*E and G*E for each of our six traits, plus annual fitness.

Trait	Model	Variance components	χ2	d.f.	P value
Body weight	3.1	ID
	3.2	ID + ID*PD	3.16	2	0.206
	3.3	VA + VPE	40.36	1	< 0.001
	3.4	VA + VPE + ID*PD	2.92	2	0.232
	3.5	VA + VPE + VPE*PD + VA*PD	5.00	2	0.082
Hind leg length	3.1	ID
	3.2	ID + ID*PD	0.00	2	0.999
	3.3	VA + VPE	49.22	1	< 0.001
	3.4	VA + VPE + ID*PD	0.00	2	0.999
	3.5	VA + VPE + VPE*PD + VA*PD	0.00	2	0.999
Strongyle FEC	3.1	ID
	3.2	ID + ID*PD	0.66	2	0.719
	3.3	VA + VPE	5.50	1	0.019
	3.4	VA + VPE + ID*PD	0.54	2	0.763
	3.5	VA + VPE + VPE*PD + VA*PD	0.86	2	0.651
Horn length	3.1	ID
	3.2	ID + ID*PD	33.68	2	< 0.001
	3.3	VA + VPE	10.80	1	0.005
	3.4	VA + VPE + ID*PD	31.52	2	< 0.001
	3.5	VA + VPE + VPE*PD + VA*PD	5.82	2	0.054
Horn growth	3.1	ID
	3.2	ID + ID*PD	0.00	2	0.999
	3.3	VA + VPE	1.64	1	0.200
	3.4	VA + VPE + ID*PD	0.00	2	0.999
	3.5	VA + VPE + VPE*PD + VA*PD	0.00	2	0.999
Testicular circumference	3.1	ID
	3.2	ID + ID*PD	22.52	2	< 0.001
	3.3	VA + VPE	9.90	1	0.002
	3.4	VA + VPE + ID*PD	19.66	2	< 0.001
	3.5	VA + VPE + VPE*PD + VA*PD	2.80	2	0.247
Annual fitness	3.1	ID
	3.2	ID + ID*PD	6.34	2	0.042
	3.3	VA + VPE	0.74	1	0.390
	3.4	VA + VPE + ID*PD	6.22	2	0.045
	3.5	VA + VPE + VPE*PD + VA*PD	3.12	2	0.210

For each model, the variance components structure of the individual and/or additive genetic variance component is given, where ID, individual identity; V_A, additive genetic variance; V_PE, permanent environment variance; and PD, population density. Other details of model structure are provided in the Materials and Methods. Also shown are the χ² statistics and P-values associated with the likelihood ratio test used to compare the model in question with a model omitting the term in question. FEC, fecal egg count.

There was no support for I*E for body weight, hind leg length, strongyle FEC, or horn growth (Table 4, model 3.2). For each of these traits, the best-supported model was model 3.3, which divides the variance for the individual effect into variances for the additive genetic and permanent environment effects, a model that is identical to model 2.1 but with a heterogeneous error structure. Therefore, for these traits, we found no evidence for either I*E or G*E.

There was support for I*E for both horn length and testicular circumference: for both of these traits, model 3.2 had stronger statistical support than model 3.1, which omitted the ID*PD term (Table 4). For both traits there was also support for separating the individual variance into the additive genetic variance (V_A) and the permanent environment variance (V_PE) (model 3.3). Again for both traits, in models where the variance for the individual intercept was separated into V_A and V_PE, there was support for the V_PE*PD interaction (model 3.4), but not for the V_A*PD interaction (model 3.5). In both traits, the individual intercept–slope covariance was positive, especially so for testicular circumference (Table S4 in File S3), suggesting an increase in between-individual variation in these traits with increasing PD from the point where standardized density was zero. We also tested for interactions between genotype at the SNP10 locus and PD in models of horn length and horn growth, as another test for G*E. The model structure was the same as model 3.3 (Table 4), but with an additional fixed effects interaction between SNP10 genotype and PD. However, the interaction was not significant for either horn length (F = 0.91, DF = 2, P = 0.404) or horn growth (F = 0.60, DF = 2, P = 0.551). Thus, we found evidence for I*E interactions, but not for G*E for horn length and testicular circumference in males.

Finally, there was support for the ID*PD variation in random slopes for annual fitness, since model 3.2 was marginally supported over model 3.1 (Table 4). As expected, there was no support for separating the variance in the individual intercept into V_A and V_PE effects (model 3.3). Finally, in models where variation in the individual intercept was separated into the V_A and V_PE, there was marginal support for the V_PE*PD interaction (model 3.4), and no support for the V_A*PD interaction (model 3.5). Thus, our analyses supported marginal individual-by-density interactions for annual fitness, but not genotype-by-density interactions.

Parameter estimates for the individual, permanent environment and additive genetic variance components for models 3.1–3.5 for each of the seven traits are provided in Table S4 in File S3.

Discussion

Evidence to date suggests that environmental conditions have substantial effects on patterns of selection (S*E) in wild populations (Price et al. 1984; Milner et al. 1999a; Garant et al. 2007; Pelletier et al. 2007a; Visser et al. 2015; Evans and Gustafsson 2017). However, our review of evidence for G*E in the wild indicates less clear evidence for effects of environmental variation on the expression of genetic variance underlying phenotypic traits (Table 1 and Table S1 in File S3). Our analyses of simultaneous S*E and G*E in a wild sheep population also reflected this general pattern. We considered six phenotypic traits that were all under selection: all showed associations with annual fitness, a composite measure of individual survival and reproduction across the subsequent year. For five of the six traits, the association with fitness was stronger at higher PD, leading to the conclusion that the strength of directional selection was stronger under less favorable environmental conditions (Figure 2 and Table 3) and that there was evidence for S*E. Five traits also showed significant levels of additive genetic variance (Table S3 in File S3). Our low heritability estimate for lifetime breeding success is in line with lower estimates for traits closely related to fitness in other wild populations (Teplitsky et al. 2009; Postma 2014). Despite there being some evidence for I*E for several traits, there was no support for G*E in any trait. The lack of I*E and G*E dissuaded us from making a substantial effort to explore multivariate patterns; the multivariate model we attempted experienced difficulty converging (File S1; Tables S5 and S6 in File S3). A recent study used simulations to show that covariance between selection and genetic variation across environmental conditions can have substantial implications for evolutionary dynamics (Wood and Brodie 2016). However, a literature review in the same study showed that the number of studies that simultaneously estimate S*E and G*E in wild populations, and hence are able to estimate the covariance between selection and genetic variation across environments, is currently limited to two (Wilson et al. 2006; Husby et al. 2011). Our ultimate aim was to add useful new estimates for an additional six traits here, plus annual fitness, to the literature, admittedly in the same population as a previous study (Wilson et al. 2006). However, based on no evidence for G*E in any trait (i.e., no evidence for variation in genetic variance across PD), we have to conclude that the covariance between selection and genetic variance across environments would be zero for all traits considered here. Below, we discuss the main findings from our analyses in turn: first, the evidence for changes in selection pressures across worsening environmental conditions in the Soay sheep population, and second, the varied conclusions from our review of estimates of G*E in wild populations and our own study in the Soay sheep, and the role of statistical power in this conclusion.

Selection is generally stronger under less favorable conditions

The major finding of our selection analysis was that, in common with many previous studies of natural populations (Price et al. 1984; Milner et al. 1999a; Garant et al. 2007; Pelletier et al. 2007a; Visser et al. 2015), selection was stronger under less favorable environmental conditions. Specifically, the association between our study traits and annual contribution to fitness was stronger in years of higher PD. The shape of the interactions (Figure 2) are informative as to the relative strength of the effects of density and trait variation on fitness. For example, the relatively vertical contours in Figure 2A suggest that changes in body weight are a stronger predictor of fitness than are changes in density, despite significant S*E, which suggests that the association between body weight and fitness is stronger at higher density. Conversely, the more horizontal contours on Figure 2C suggest that a change in density is a more important determinant of fitness than change in FEC, despite significant S*E. Several previous studies of the Soay sheep population have shown that each of the traits we analyzed was under selection and that, for some traits, selection strengthened in years of more adverse conditions (see File S1 for further discussion of our results in the context of previous work on the Soay sheep). Our results are also in broad agreement with a recent study of inbreeding in the Soay sheep, which found that the negative relationships between genomic inbreeding coefficient and traits including size, reproductive success, and survival, were also stronger in years of higher PD (Pemberton et al. 2017). Taken together, our results suggest that differences in performance between individuals are exacerbated when both competition for food and parasite transmission pressure are likely to be at their highest.

We found that sexual selection on male Soay sheep, evidenced by a positive association between testicular circumference and annual fitness, was stronger in years of high PD. A possible explanation is that in years of high PD the male:female ratio is high (∼1:1), while in years of low density, usually indicative of a previous winter of high male-biased mortality, it is very low (1:4) (Clutton-Brock et al. 2004a). Thus, in years of low density, more males are likely to gain access to females and hence more males should sire offspring, while in high-density years, only the most vigorous males can succeed (Pemberton et al. 2004). All of these results demonstrate that environmental variation can have profound and unpredictable effects on patterns of natural and sexual selection, making long-term studies of wild populations essential for studying how selection pressures are influenced by a changing environment (Cockburn et al. 2008). The importance of intimate knowledge of the study system is particularly apparent in studies of changes in sexual selection across environmental gradients. For example, in superb fairy wrens (Malurus cyaneus), sexual selection on males is stronger in years of heavy summer rainfall, which constitute favorable conditions, since such conditions enable a great proportion of males to molt into their nuptial plumage, increasing the intensity of intrasexual competition and hence the strength of selection (Cockburn et al. 2008). Meanwhile, the strength of sexual selection is weakened in sand gobies (Pomatoschistus minutus; Järvenpää and Lindström 2004) and three-spined sticklebacks (Gasterosteus aculeatus; Candolin et al. 2007) experiencing eutrophication, since in turbid waters females are unable to assess male sexual coloration, and thus mating success is less dependent upon male traits and hence selection is stronger under favorable conditions.

The absence of evidence for G*E: comparisons with previous studies

The second principal finding of our study was the absence of evidence for significant G*E for any trait; indeed, I*E were also rare (Table 4). Two previous studies have reported evidence for significant G*E in the Soay sheep, estimating increased (maternal) genetic variance for offspring birth weight (Wilson et al. 2006), and increased (additive) genetic variance for lamb body weight and strongyle FEC (Robinson et al. 2009) under more favorable environmental conditions (measured as the proportion of lambs that survived their neonatal period). Several differences between our work and these two previous studies are immediately apparent, all of which could be responsible for discrepancies in our results. First, the two previous examples involve measures on lamb traits only; second, we used a larger data set and an improved pedigree; and third, we used a different environmental measure. An important point is therefore that any estimate of G*E is specific to the focal trait and chosen environmental axis. We also note an issue with the previous analyses that has become apparent with more recent exploration of such model structures: neither study fitted a term to account for potential interactions between (maternal) permanent-environment effects and the environmental measure. With repeated measures (either of mothers or of individuals), failure to also model maternal environment effects or permanent environment effects as a function of the environmental covariate can inflate estimates of G*E (e.g., R. Vega Trejo, M. Head, M. Jennions, and L. Kruuk, unpublished results), in the same way as failing to fit maternal effects or permanent environment effects can inflate estimates of additive genetic variance (Kruuk and Hadfield 2007). The likely impact on models of these data remains to be explored.

Our review of published studies only indicated weak support for G*E in wild populations experiencing natural environmental heterogeneity. Of the 93 estimates of changes in additive genetic variance or heritability with environmental conditions included in Table S1 in File S3, 51 (55%) showed no significant change with environmental conditions; 16 (17%) showed positive or negative changes which were not statistically tested; and only 26 (28%) showed significant positive (16), negative (6), or inconsistent (4) changes. It is also perhaps salient to note that more recent estimates in Table 1 and Table S1 in File S3 have both been better able to provide statistical tests of comparisons between or across environments, and that conclusions of absence of G*E have become more common in recent times (Table 1 and Table S1 in File S3 are ordered by publication year). Some early studies indicating evidence for G*E used statistical methods that have since been superseded, such as performing animal models on best linear unbiased predictors of individual reaction norms extracted from models allowing individual variation in the trait–environment relationship (e.g., Nussey et al. 2005). In addition, a study of great tits supported the presence of G*E for clutch size, despite the environmental measure in question (spring temperature) being more closely associated with laying date, for which there was no evidence of G*E (Husby et al. 2010). In a later study, G*E for laying date in great tits was supported, with a model fitting V_PE*E and V_A*E effects supported over a model that fitted only intercepts of V_PE and V_A (Husby et al. 2011). However, by comparing these two models, Husby et al. (2011) could not definitely determine whether the improvement in model fit was due to V_PE*E or V_A*E. Similarly, these models cannot determine whether the change in additive genetic variance across the environmental gradient is significant. Therefore, it seems that our review concurs with the observation that, in interesting contrast to the abundant evidence of S*E (Wood and Brodie 2016), compelling evidence for G*E in wild populations is still rare (Gienapp and Brommer 2014).

The results obtained from our study, and the overall impression of the studies of G*E in wild animal populations listed in Table S1 in File S3, are clearly at odds with the narrative from studies of G*E in other contexts. As described in the Introduction, experimental studies of animal populations frequently show evidence for G*E (Vieira et al. 2000; Valdar et al. 2006; Ingleby et al. 2010), as do studies of plant populations in the greenhouse (Westerman and Lawrence 1970; Stivers et al. 1971; Westerman 1971; Khan et al. 1976; Mazer and Schick 1991; Pigliucci et al. 1995a,b; Shaw et al. 1995). The same is also true of reciprocal transplant experiments, such as the classic studies of Clausen, Keck, and Hiesey (Clausen et al. 1940, 1947, 1948; Hiesey et al. 1942; Clausen and Hiesey 1958), which have been comprehensively reviewed and summarized (Nunez-Farfan and Schlichting 2001). These studies provided evidence for G*E from reciprocal transplant studies of populations of sticky cinquefoil (Potentilla glandulosa; Rosaceae; now Drymocallis glandulosa) and yarrow (Achillea millefolium; Asteraceae) living at altitudes ranging from 30 to 3050 m (Clausen et al. 1940, 1947, 1948; Hiesey et al. 1942; Clausen and Hiesey 1958). A reason for the success of laboratory studies in detecting G*E may be the nature of the experimental manipulations, which are designed to maximize the opportunity to detect G*E. For example, they may place organisms in conditions that are extremely stressful and/or likely to be outside the natural range. Similarly, the transplant experiments of Clausen, Keck, and Hiesey moved plants across distances of almost 200 miles and 3000 m of altitude into alien biotic and abiotic conditions (Clausen et al. 1940). We also attempted to maximize our ability to detect G*E within our population: while a number of environmental variables could have been considered, we chose PD because of its known associations with fitness (Clutton-Brock et al. 1991, 1992; Milner et al. 1999b) and selection (Moorcroft et al. 1996; Clutton-Brock et al. 1997; Milner et al. 1999a), and most of our traits were known to have considerable additive genetic variance (Table S3 in File S3) and to be influenced by PD (Table S4 in File S3).

Caveats and conclusions

One of the two main results of our study is that we found no evidence in support of significant G*E or I*E, despite using data from a well-monitored wild population that has previously provided evidence for G*E in other traits, and with sample sizes and pedigree structures comparing favorably to previous studies in wild populations using similar statistical techniques (Gienapp and Brommer 2014). Therefore, we investigated whether a lack of statistical power in our data set and pedigree could influence our ability to detect significant G*E in our analysis (File S2). We constructed a simulated data set with the same structure as observed in the true data set and taking body weight as an example trait. We simulated breeding values and permanent environment effects for intercepts and slopes of the trait on density using the “phensim” function in the R package “pedantics” (Morrissey et al. 2007) as well as cohort, year, and maternal and residual effects for each observation. The (co)variances for all of the above were those estimated in the original analyses except for the additive genetic variance in slopes (V_A(slope)) and the covariance between additive genetic intercept and slope (Cov_A(int,slope)). In our simulations, V_A(slope) was varied across 12 values ranging from 0.05 to 2, and for each of these Cov_A(int,slope) was set to −0.3, 0, or +0.3. For each simulated data set, we tested the significance of V_A(slope) and the proportion of simulations in which it was significant. We found that our data enabled us to detect significant (P < 0.05) G*E when V_A(slope) was > 0.5 with ∼80% power (Figure S1); our actual V_A(slope) estimate for body weight was 0.23 ± 0.12 (Table S4 in File S3). We compared the change in the heritability generated by our simulated values with the observed power: our estimated V_A(slope) for body weight (0.23) resulted in a heritability value that would change by an overall magnitude of 0.05 (a change from 0.13 to 0.18), while our data had 80% power to detect G*E associated with a maximum change in heritability of ∼0.08 (Figure S2 and Figure S3; a change from 0.12 to 0.20). Overall, we conclude that our data set had the power to find statistical support for levels of G*E with a relatively small impact on overall phenotypic variance, but that our estimates fell below this.

A caveat of our study is that although we have assessed G*E in six traits (plus annual fitness), we have done so across only a single environmental variable; it is reasonable to conjecture that the results would have been quantitatively different had we used (for example) a climatic variable. However, PD appears to fulfill many desirable characteristics of an environmental variable for detecting G*E: it varies widely, it influences the traits under selection (strongly), and it influences the strength of selection. As a small, isolated population, it is also worth mentioning the potential role of inbreeding in our ability to detect G*E: a recent laboratory study demonstrated that inbred Drosophila demonstrated greater plasticity in wing shape in response to temperature than outbred populations (Schou et al. 2015). Recent work on the Soay sheep show that although close inbreeding is rare, nonzero genomic inbreeding coefficients are common and there is inbreeding depression for size traits (Bérénos et al. 2016) that is intensified under high PD (Pemberton et al. 2017). However, the Drosophila laboratory study showed no effect of inbreeding on plasticity for other traits (Schou et al. 2015), and while it is possible inbreeding influenced I*E or G*E for our traits, a future study of the Soay sheep could test this explicitly. The scarcity of evidence for G*E in previous studies of wild populations and our current study contrasts with the frequent evidence for G*E in laboratory systems (Vieira et al. 2000; Valdar et al. 2006; Ingleby et al. 2010; Des Marais et al. 2013). Studies in wild populations, including our own, have endeavored to rigorously account for other factors that may otherwise inflate estimates of G*E, such as fitting permanent environment effects and modeling with heterogeneous residual variance structures, due to high concerns about such biases arising in uncontrolled environments. On the other hand, experimental studies may maximize the amount of genetic variation available by comparing inbred lines and measuring differences in genetic variation between two extreme or even completely novel environments, potentially increasing the likelihood of detecting G*E. This is not to say that G*E is impossible to detect in wild populations: it will certainly be population-, environment-, and trait-dependent. That said, the paucity of evidence for G*E in the wild, as described in Table 1 and elsewhere (Gienapp and Brommer 2014), suggests that it is, in general, harder to detect G*E outside of experimental studies.

Many previous studies on the Soay sheep have shown that the traits we studied are strongly positively correlated and that, as such, a multivariate framework may seem more appropriate for the analyses that we have conducted. The fact that univariate models found scant evidence for I*E, and none whatsoever for G*E, meant that we did not approach the full model that we would ideally have liked to interrogate for these data: a seven-trait animal RRM. The difficulty we had in persuading even a two-trait (horn length and testicular circumference) RRM to converge illustrates the difficulty that researchers are faced with when conducting multivariate analyses in natural populations: data sets are seldom large, well-structured, or complete enough to conduct the “ideal” analysis, as discussed elsewhere (Kruuk et al. 2008; Clutton-Brock and Sheldon 2010; Charmantier et al. 2014). Thus, while we do not believe our ability to detect G*E in single traits is due to a lack of statistical power, our ability to explore multivariate patterns clearly is.

In this study, we used 24 years of data collected from > 2000 individuals in a pedigreed wild population to show that a strongly fluctuating environmental variable, PD, influenced the strength of selection on, but not the expression of, genetic variance in six morphological and life history traits. The association between five of the six study traits and annual contribution to fitness was stronger in high-density (harsher) years, but there was little evidence for I*E or G*E for any of our traits or annual fitness. Opposing patterns of selection and genetic variation have been suggested to be a mechanisms for maintenance of variation in fitness-related traits in nature (Wood and Brodie 2016), and while there is some empirical support for such conditions being met (Wilson et al. 2006; Husby et al. 2011), our study did not find further evidence for this. While our results do not enable us to make any bold statements about the mechanisms maintaining variation in natural populations, our findings do show that many of our traits have the ability to respond to selection. Our results add to the growing evidence that selection pressures may be heavily shaped by environmental conditions, but that G*E may not have as large, or as detectable, effects in wild populations experiencing naturally-varying environmental fluctuations, compared to experimentally manipulated populations.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300498/-/DC1.