Estimating Realized Heritability in Panmictic Populations

Abstract

Narrow sense heritability $\left(h^2\right)$ is a key concept in quantitative genetics, as it expresses the proportion of the observed phenotypic variation that is transmissible from parents to offspring. $h^2$ determines the resemblance among relatives, and the rate of response to artificial and natural selection. Classical methods for estimating $h^2$ use random samples of individuals with known relatedness, as well as response to artificial selection, when it is called realized heritability. Here, we present a method for estimating realized $h^2$ based on a simple assessment of a random-mating population with no artificial manipulation of the population structure, and derive SE of the estimates. This method can be applied to arbitrary phenotypic segments of the population (for example, the top-ranking p parents and offspring), rather than random samples. It can thus be applied to nonpedigreed random mating populations, where relatedness is determined from molecular markers in the p selected parents and offspring, thus substantially saving on genotyping costs. Further, we assessed the method by stochastic simulations, and, as expected from the mathematical derivation, it provides unbiased estimates of $h^2.$ We compared our approach to the regression and maximum-likelihood approaches utilizing Galton’s dataset on human heights, and all three methods provided identical results.

NARROW sense heritability $\left(h^2\right)$ is a key concept in quantitative genetics. $h^2$ is technically defined as the ratio of additive genetic variance (the variance of breeding values) to the total phenotypic variance $\left(h^2={\sigma }_a^2/{\sigma }_p^2\right),$ and represents the fraction of the phenotypic variation of a quantitative trait that is transmissible from one generation to the next. $h^2$ determines the degree of resemblance between relatives, and the rate of response to artificial and natural selection; therefore, estimating $h^2$ is often the first step in applied plant and animal breeding programs as well as evolutionary genetics studies. $h^2$ is also the upper limit for the accuracy of predicting phenotypes from molecular marker data (genomic prediction), and, hence, is required knowledge for common diseases in humans in the context of precision medicine (Yang et al. 2010).

Because $h^2$ determines the degree of resemblance among relatives, classical methods for estimating $h^2$ use the observed phenotypic correlation among closely related individuals, and their average coefficient of relationship, to estimate $h^2.$ One such classical method is regression of offspring phenotypic values on midparent phenotypic values (offspring-parent regression), for which the regression coefficient, b, provides an unbiased estimate of $h^2.$ Other classical methods involve ANOVA of full and half-sibling families, and analysis of relatives with different degrees of relatedness using maximum-likelihood-based approaches. These methods require designed experiments in which pedigrees are constructed by mating specific males and females, or natural matings for which at least one parent is known are utilized. These designs can maximize the precision of the $h^2$ estimates given sample size constraints by manipulating both the numbers of families and family sizes.

However, these designs are not always applicable. For example, pedigrees are not usually known in natural populations. In this case, $h^2$ can be estimated using molecular markers to reconstruct pedigrees (Lynch and Walsh 1998; Aykanat et al. 2014). However, this is followed by variance component analysis based on the reconstructed pedigree, as is done for designed experiments, and, hence, also requires genotyping a large random sample of the population. More recently, “genomic heritability” has been estimated in populations of individuals that have been genotyped for large numbers of molecular markers using whole genome marker regressions (Yang et al. 2010). Genomic heritability is the fraction of the genetic variance that can be explained by regression on the markers, and will only be equivalent to the true $h^2$ when all causal variants are genotyped, such as with sequence data; or when the true causal variants are in perfect linkage disequilibrium with the markers (de los Campos et al. 2015). A major disadvantage of all marker-based methods for estimating $h^2$ is the expense of genotyping, so methods that can reduce this cost are desirable.

Here, we propose a method to estimate $h^2$ from natural populations that is related to the concept of realized $h^2.$ Traditionally, realized $h^2$ is estimated by comparing the response to selection $\left(R\right)$ to the selection differential $\left(S\right).$ The estimate of $h^2,$ $R/S,$ requires specific matings. We show here that the realized $h^2$ concept can be generalized to a randomly mating natural population in which phenotypic values of a quantitative trait have been scored for the parental and offspring generations. The $h^2$ is estimated from the proportion of offspring from a defined range of phenotypes (for example, the top p offspring) that were produced by the p parents from the same defined phenotypic range. Thus, one only needs to determine relatedness of the selected subset of p parents and p offspring from the same truncated fraction of the phenotypic distribution, saving substantially on genotyping costs. Of course, one needs to assume neutrality of the DNA markers (such as highly polymorphic SSRs) to estimate pedigree within the truncated subsets. Assuming this approach, we derive the $h^2$ estimate and its associated SE.

Methods

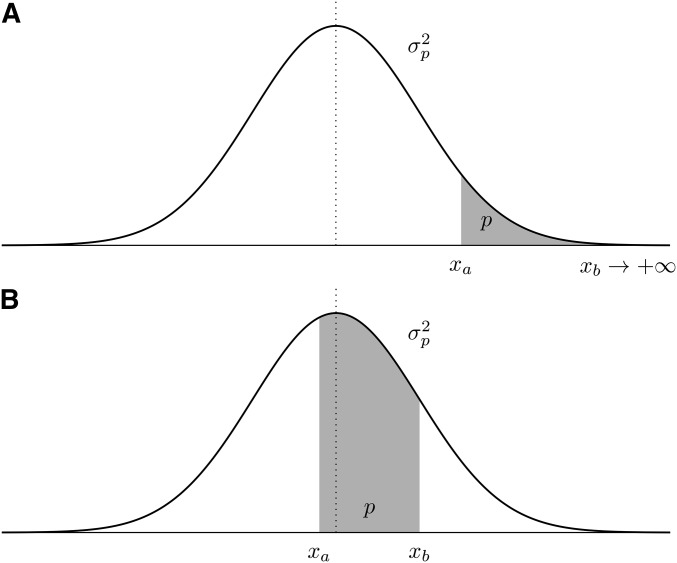
We assume a population in Hardy-Weinberg equilibrium, where the offspring ($F_1$) are derived from the parental population (P) by random union of gametes, and there is no selection. We assume the phenotype of an individual for a quantitative trait (X) is the sum of an independent additive genetic value (a) and environmental deviation (e), and that a and e are normally distributed in the population. It follows that the phenotypic variance of X corresponds to ${\sigma }_p^2={\sigma }_a^2+{\sigma }_e^2,$ and thus $X\sim N\left(\mu ;{\sigma }_p^2\right).$ We now rank the individuals in the P and $F_1$ populations by their respective phenotypic values. From this ranking, we can determine the top-ranking proportion p of the $F_1$ population, as well as r, the percentage of cases when one or both parents of the top-ranking offspring individuals belong to the corresponding truncated p fraction of the P population (Figure 1a). It should be emphasized that the parents in P mate randomly, producing the $F_1$ offspring, and, therefore, this scenario differs from conventional truncation selection as the top p proportion of the parental population were not “selected” and constrained to mate among themselves. Rather, both top-ranking parents and offspring are only “inspected” to calculate r. We postulate that $h^2$ may be calculated based on the three parameters: p, r, and ${\sigma }_p^2.$

Figure 1.

Normal distribution of a quantitative trait (identical in the P and $F_1$ populations). The truncation proportion p (gray area) is delimited by the left ($x_a$) and right ($x_b$) truncation points, respectively. Two scenarios are depicted: (A) one-sided truncation, and (B) two-sided truncation.

It follows that the case for truncation selection (Figure 1a) can be generalized to the case of a two-sided truncation with $X\in \left(x_a,x_b\right)$ (Figure 1b).

This approach differs from classical methods to estimate $h^2$ in that it does not rely on the degree of resemblance among relatives or variance component decomposition. This method resembles a realized $h^2$ estimate, but it differs from classical realized $h^2$ because it is applicable to panmictic populations, and does not require experimentally controlled crosses among selected parents. This strategy was motivated by a mathematical analysis of the effect of phenotypic preselection on reducing contamination rate in seed orchards of forest trees (Lstibůrek et al. 2012). This approach is similar to methodology developed to estimate $h^2$ for binomial (threshold) traits (Crittenden 1961; Falconer 1965), but here we are concerned with normally distributed quantitative traits.

Mathematical derivation

We begin with the derivation of the more general two-sided truncation scenario. Let $X\sim N\left(\mu ;{\sigma }_p^2\right)$ and $X\in \left(x_a;x_b\right),$ then we follow the transformation properties of the normal distribution $X\sim N\left(0;1\right)$ and $X\in \left(\alpha ;\beta \right),$ where

$$\begin{array}{c}\alpha =\frac{x_a-\mu }{{\sigma }_p};\\ \beta =\frac{x_b-\mu }{{\sigma }_p}.\end{array}$$ (1)

For given $x_a$ and $x_b,$ one may calculate the area p of the truncated distribution (Figure 1) as

$$p=\Phi \left(\beta \right)-\Phi \left(\alpha \right),$$ (2)

where $\Phi \left(\alpha \right)$ and $\Phi \left(\beta \right)$ are the cumulative distribution functions (cdf) of the normal distribution $N\left(0;1\right).$ The corresponding truncated distribution is then (Johnson et al. 1994)

$$\begin{array}{c}\text{E}\left[X_P\right]=\mu +i{\sigma }_p;\\ \mathrm{Var}\left[X_P\right]=\left(1-k\right){\sigma }_p^2.\end{array}$$ (3)

The selection intensity (i) is then defined as

$$i=-\frac{\phi \left(\beta \right)-\phi \left(\alpha \right)}{\Phi \left(\beta \right)-\Phi \left(\alpha \right)},$$ (4)

where $\phi \left(\alpha \right)$ and $\phi \left(\beta \right)$ are the probability density functions of the standardized normal distribution, and the coefficient k is

$$k=\frac{\beta \phi \left(\beta \right)-\alpha \phi \left(\alpha \right)}{\Phi \left(\beta \right)-\Phi \left(\alpha \right)}+{\left(\frac{\phi \left(\beta \right)-\phi \left(\alpha \right)}{\Phi \left(\beta \right)-\Phi \left(\alpha \right)}\right)}^2.$$ (5)

We can trace the likelihood that one or both parents of a given offspring originate from the truncated subset p. The number of parents satisfying this origin is binomially distributed as $Y_1\sim Bi\left(1;p\right)$ when tracking one side of the parentage, and $Y_2\sim Bi\left(2;p\right)$ when tracking both sides of the parentage. In these cases, the respective likelihoods that one parent or both parents, respectively, originate from p are enumerated in Table 1.

Table 1. Likelihoods and coefficients.

	$P\left(Y\right)$	B
$Y_1=1$	p	0.5
$Y_2=2$	$p^2$	1

$Y_1$ and $Y_2$ are the number of parents originating from the truncated subset p when tracing one or two sites of the parentage, respectively. $P\left(Y\right)$ is the corresponding likelihood, and B is the coefficient introduced in Equation 6.

Then, for one of the two above scenarios, the expected value and variance of the offspring in $F_1$ are

$$\begin{array}{c}\text{E}\left[X_{F_1}\right]=\mu +Bi{h}^2{\sigma }_p;\\ \mathrm{Var}\left[X_{F_1}\right]=\left(1-0.5Bk{h}^4\right){\sigma }_p^2.\end{array}$$ (6)

where the coefficient B is provided in Table 1.

Let $p*$ be the proportion of the above offspring (Equation 6) belonging to the interval $\left(\alpha ;\beta \right)$ of $F_1.$ In our remaining analyses, we utilize the central limit theorem, i.e., the normal approximation of the above distribution. Utilizing the same transformation properties of the normal distribution (Equation 1), the area $p*$ is given by

$$p*=\Phi \left(\frac{\beta -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}}\right)-\Phi \left(\frac{\alpha -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}}\right).$$ (7)

Let N be the size of the $F_1$ population. Then, $N_{F_1}$ is the number of $F_1$ individuals in the interval $\left(x_a;x_b\right).$ $N_{P\left(Y\right)}$ is the subset of $N_{F_1}$ where the parent(s) originate from the interval $\left(x_a;x_b\right)$ in P, according to Y. Next, we introduce a variable r, the relative frequency of offspring in the truncated proportion in $F_1$ with parent(s) originating from the truncated proportion of P, according to Y, where

$$r=\frac{N_{P\left(Y\right)}}{N_{F_1}}.$$ (8)

Next, we utilize the earlier binomial expansion, and

$$r=\frac{N_{P\left(Y\right)}}{N_{F_1}}=\frac{Np*P\left(Y\right)}{Np}=\frac{p*P\left(Y\right)}{p}.$$ (9)

With the knowledge of p and r, we can ascertain the unknown $p*,$ thus

$$\frac{pr}{P\left(Y\right)}=\Phi \left(\frac{\beta -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}}\right)-\Phi \left(\frac{\alpha -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}}\right).$$ (10)

Therefore, $h^2$ is the implicit function of r, p, and ${\sigma }_p^2.$ (Additional variables in the equation are all functions of these three input parameters.) The above formulation is general, and could be used with mathematical solver software to calculate an estimate of $h^2.$ Computer code to solve for $h^2$ using Equation 10 written in R language (R Core Team 2013) is provided in a public repository (Lstibůrek 2017). Next, we derive analytical solutions (i.e., deterministic equations) to estimate $h^2$ for two specific cases.

Case 1: centered two-sided truncation:

Provided both $x_a$ and $x_b$ are symmetrically allocated around the mean of P and $F_1,$ $h^2$ is calculated as (see Supplemental Material, File S1 for derivation)

$$h^2=\frac{\sqrt{2}}{\left|Q\right|}{\left(\frac{Q^2-{\alpha }^2}{Bk}\right)}^{\frac{1}{2}},$$ (11)

where $Q={\Phi }^{-1}\left(0.5-pr/2P\left(Y\right)\right).$

Case 2: right-sided truncation:

When $x_b\to +\mathrm{\infty }$ (Figure 1), one may calculate $h^2$ as (see File S1 for derivation)

$$h^2=\frac{2\alpha Bi\pm {\left[4{\alpha }^2{B}^2{i}^2-2\left(2B^2{i}^2+B{Q}^{\prime 2}k\right)\left({\alpha }^2-Q^{\prime 2}\right)\right]}^{\frac{1}{2}}}{\left(2B^2{i}^2+B{Q}^{\prime 2}k\right)},$$ (12)

where $Q^{\prime }={\Phi }^{-1}\left(1-pr/P\left(Y\right)\right).$ There are two solutions of the above equation, and verification using Equation S1.7 provides the unique one.

Variance of the ${\mathit{h}}^{\mathit{2}}$ estimate:

The SE associated with the general $h^2$ estimate (Equation 10) is (see File S1 for derivation)

$$SE\left\{h^2\right\}=\frac{{\left(1-0.5h^{4}kB\right)}^{\frac{3}{2}}}{\left|\phi \left(b\right)\left(-iB+0.5h^2\beta kB\right)-\phi \left(a\right)\left(-iB+0.5h^2\alpha kB\right)\right|}\times \frac{p}{P\left(Y\right)}\sqrt{r\left(1-r\right)}\frac{1}{\sqrt{n}},$$ (13)

where n is the number of progeny in p, $h^2\ne 0$ under symmetric two-sided truncation, and a and b are

$$\begin{array}{c}a=\frac{\alpha -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}},\\ b=\frac{\beta -Bi{h}^2}{\sqrt{1-0.5Bk{h}^4}}.\end{array}$$ (14)

The SE of the $h^2$ estimate for the scenario of right-sided truncation (Equation 12) is

$$SE\left\{h^2\right\}=\frac{{\left(1-0.5h^{4}kB\right)}^{\frac{3}{2}}}{\left|-\phi \left(a\right)\left(-iB+0.5h^2\alpha kB\right)\right|}\frac{p}{P\left(Y\right)}\sqrt{r\left(1-r\right)}\frac{1}{\sqrt{n}}.$$ (15)

Equations 13 and 15 are both products of two components, where the first (leftmost) is associated with the type and intensity of truncation, and the second (rightmost) depicts the variance of r, including the sample size n.

Utilizing the mathematical derivation outlined above, we claim that estimates of $h^2$ and the corresponding SE are asymptotically unbiased.

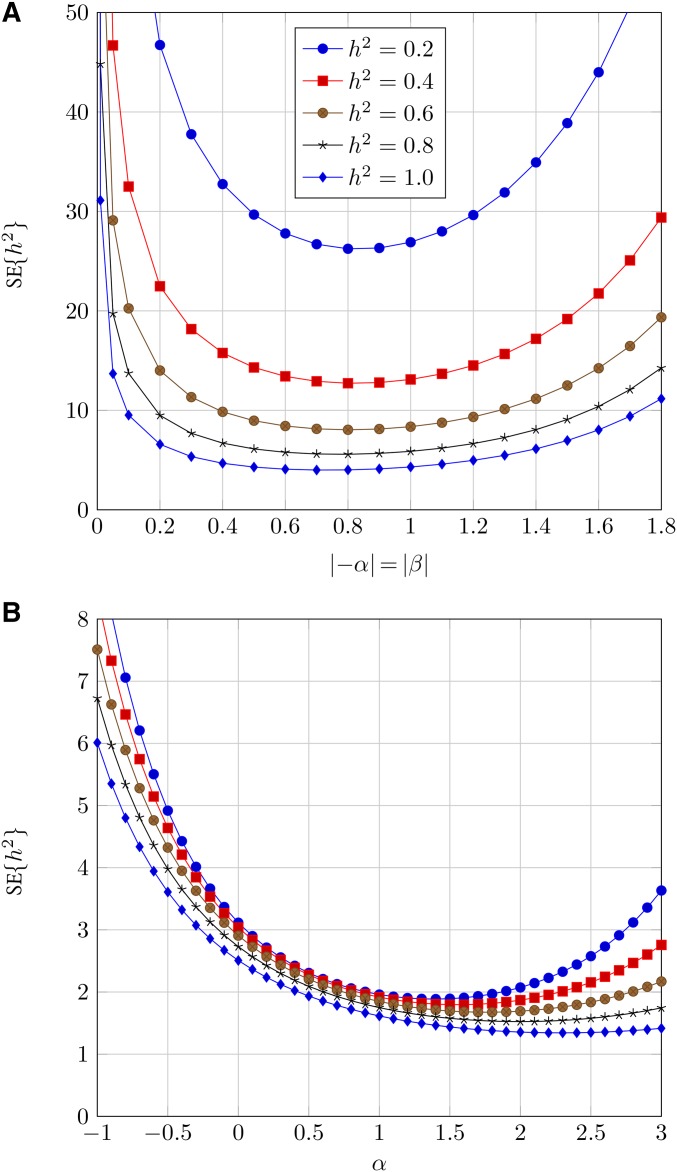
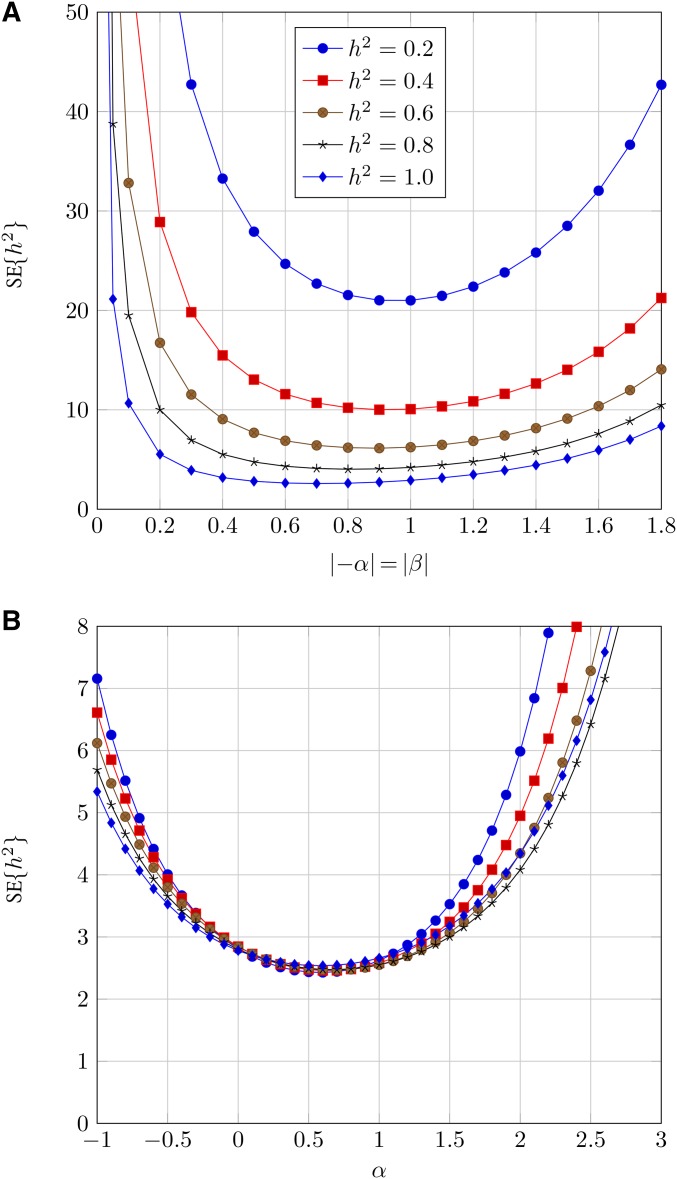
The SE are provided for the two likelihoods ($Y_1=1$ and $Y_2=2$) and one- or two-sided truncations in Figure 2 and Figure 3. The SE is comparable to existing methods, i.e., regression analysis; thus, the number of samples providing reliable estimate of $h^2$ is in the magnitude of “hundreds.”

Figure 2.

SE of the $h^2$ estimate (SE$\left\{h^2\right\}$) for $\left(Y_1=1\right)$ (tracking one side of the parentage): (A) centered two-sided truncation, (B) right-sided truncation. To calculate actual SE$\left\{h^2\right\},$ values on the y-axis should be multiplied by factor $1/\sqrt{n},$ i.e., scaled by the experimental sample size.

Figure 3.

SE of the $h^2$ estimate (SE$\left\{h^2\right\}$) for $\left(Y_2=2\right)$ (tracking both sides of the parentage): (A) centered two-sided truncation, (B) right-sided truncation. To calculate actual SE$\left\{h^2\right\},$ values on the y-axis should be multiplied by factor $1/\sqrt{n},$ i.e., scaled by the experimental sample size.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Computer simulation

As noted above, our formal theoretical derivations using normal distributions are not strictly true with truncation. Therefore, we verified our analytical approach by stochastic simulation, where $h^2$ was estimated for a hypothetical panmictic population as follows. Additive polygenetic effects of 10,000 unrelated and noninbred parental individuals were sampled from the normal distribution $N\left(0;{\sigma }_a^2\right),$ assuming the infinitesimal genetic model. The environmental deviation was drawn from $N\left(0;{\sigma }_e^2\right).$ Subsequently, 10,000 individual offspring were generated. Parents were randomly mated and polygenic additive genetic values in offspring were drawn from $N\left(\overline{a};0.5{\sigma }_a^2\right),$ where $\overline{a}$ is the respective midparental additive genetic value. The environmental deviation was assigned as for the parental population.

Next, 1000 offspring with trait’ values $X\in \left(x_a;x_b\right)$ were inspected, and r was calculated for each of the likelihood scenarios $\left(Y_1=1;Y_2=2\right)$ by evaluating the trait value of parents. $h^2$ was then estimated by solving Equation 10. Simulations were repeated for 100 independent stochastic iterations, and means and variances were calculated across all runs, and compared to the true parameter ${\sigma }_a^2/{\sigma }_p^2.$ Computer code to perform the simulation written in R language is provided in a public repository (Lstibůrek 2017).

The simulations showed that the normal approximation of the assumed $F_1$ distribution (Equation 6) is justified, since the expected value of $h^2$ estimates were nearly identical to the true parameters across 100 independent stochastic simulations for all assumed scenarios ($h^2$ from 0 to 1), $\alpha =$ 0, 0.5, and 1, and $\beta =+\mathrm{\infty }$ across the two likelihoods (Table 2).

Table 2. Results of computer simulations.

		$Y_1=1$			$Y_2=2$
	$h^2$	$\widehat{r}\pm$ SD	${\widehat{h}}^2\pm$ SD	P value	$\widehat{r}\pm$ SD	${\widehat{h}}^2\pm$ SD	P value
$\alpha =0.0$	0.0	$0.501\pm 0.018$	$0.003\pm 0.113$	0.762	$0.249\pm 0.015$	$-0.005\pm 0.095$	0.577
	0.2	$0.530\pm 0.017$	$0.190\pm 0.104$	0.329	$0.284\pm 0.016$	$0.215\pm 0.098$	0.139
	0.4	$0.566\pm 0.016$	$0.413\pm 0.099$	0.185	$0.316\pm 0.015$	$0.409\pm 0.094$	0.323
	0.6	$0.596\pm 0.018$	$0.592\pm 0.105$	0.463	$0.349\pm 0.017$	$0.608\pm 0.102$	0.461
	0.8	$0.631\pm 0.020$	$0.795\pm 0.113$	0.661	$0.381\pm 0.020$	$0.796\pm 0.115$	0.739
	1.0	$0.666\pm 0.018$	$0.985\pm 0.097$	0.117	$0.420\pm 0.016$	$1.017\pm 0.093$	0.067
$\alpha =0.5$	0.0	$0.307\pm 0.019$	$-0.009\pm 0.093$	0.316	$0.095\pm 0.012$	$-0.005\pm 0.099$	0.595
	0.2	$0.350\pm 0.020$	$0.203\pm 0.096$	0.775	$0.121\pm 0.011$	$0.203\pm 0.082$	0.753
	0.4	$0.393\pm 0.020$	$0.405\pm 0.092$	0.596	$0.149\pm 0.013$	$0.399\pm 0.091$	0.946
	0.6	$0.436\pm 0.020$	$0.601\pm 0.090$	0.907	$0.178\pm 0.016$	$0.597\pm 0.105$	0.793
	0.8	$0.481\pm 0.019$	$0.797\pm 0.081$	0.741	$0.211\pm 0.016$	$0.805\pm 0.098$	0.631
	1.0	$0.529\pm 0.017$	$0.992\pm 0.066$	0.250	$0.244\pm 0.016$	$1.005\pm 0.098$	0.612
$\alpha =1.0$	0.0	$0.161\pm 0.016$	$0.009\pm 0.088$	0.317	$0.025\pm 0.007$	$-0.006\pm 0.118$	0.624
	0.2	$0.197\pm 0.017$	$0.198\pm 0.082$	0.835	$0.039\pm 0.008$	$0.202\pm 0.111$	0.876
	0.4	$0.238\pm 0.018$	$0.390\pm 0.084$	0.213	$0.053\pm 0.009$	$0.380\pm 0.100$	0.052
	0.6	$0.287\pm 0.017$	$0.599\pm 0.070$	0.894	$0.074\pm 0.011$	$0.597\pm 0.107$	0.792
	0.8	$0.339\pm 0.022$	$0.800\pm 0.083$	0.953	$0.096\pm 0.011$	$0.806\pm 0.094$	0.545
	1.0	$0.395\pm 0.021$	$0.997\pm 0.071$	0.630	$0.119\pm 0.014$	$1.001\pm 0.117$	0.957

$Y_1$ and $Y_2$ are the number of parents originating from the truncated subset p when tracing one or two sites of the parentage, respectively. α denotes the left truncation, $h^2$ is the input narrow-sense heritability (simulation parameter), $\widehat{r}$ and ${\widehat{h}}^2$ are the corresponding estimates of r and $h^2$ in a given scenario, reported with respective SD (calculated across independent stochastic iterations), and P-value is the respective level of significance in comparing $h^2$ and ${\widehat{h}}^2.$

Demonstration using human height

We used Galton’s well-known dataset of human heights (Galton 1886). The dataset includes 205 families with adult heights of 934 children, in family sizes range from 1 to 15 children. The dataset is publicly available as R package (Friendly et al. 2017), and we used it for our demonstration. Hanley (2004) analyzed this original dataset, and he was particularly addressing the issue of Galton’s original adjustment for the gender, i.e., all heights of women were multiplied by 1.08. First, we reproduced Hanley’s calculations, and received identical estimates of the regression coefficient b (Table 1 in Hanley 2004). Then, we considered Galton’s original adjustment, where $\widehat{b}$ = 0.71 (regression of the heights of children on midparent values), which provides the direct estimate of $h^2.$ We used restricted maximum-likelihood approach to verify these findings using the animal genetic model in ASReml (Gilmour et al. 2009), where the random pedigree effect was the single factor in the model.

As expected, we received identical estimate of $h^2=0.71$ and SE of 0.04 (identical to the SE of b in our regression analysis). Then, we followed our approach and analyzed offspring in the right site of the distribution (truncation >0.5 of the standardized normal distribution), i.e., approximately one-third of Galton’s dataset. We assumed tracking one side of the parentage, as it leads to the lower SE (compare Figure 2b and Figure 3b). All children values (adjusted dataset by Galton) were sorted. Then we started assessing the tallest child and compared, whether the mother’s height was above the same truncation. We recorded all positive values (as 1s); the sum for one parentage across all truncated children (278) was 122 and for the second parentage 137. We averaged these values and divided the result by 278 and obtained the value of $\widehat{r}=\mathrm{0.47.}$ Then, assuming Equation 10, we estimated $h^2$ to be 0.73 with SE 0.07 (the error is actually <0.07 since we averaged two $\widehat{r}$ values).

Discussion

The main methodological message of this study is that it is possible to estimate $h^2$ within a panmictic population without a planned experiment, and without performing a complete pedigree reconstruction across the entire phenotypic distribution of parental and offspring populations in order to implement traditional variance component estimation. Our approach provides a way to estimate $h^2$ by genotyping only a small proportion of the parental and offspring populations (e.g., the right-hand tail of the distributions), and estimating the proportion of that subset of offspring that arose from that subset of parents. It is thus an estimate of realized $h^2,$ derived from quantifying the relatedness among exact phenotypic subsets of parental and offspring populations.

Much formal quantitative genetics theory follows a simple biological principle: the additive genetic value of an offspring is the midparent additive genetic value plus the Mendelian sampling term. The phenotype is further determined by adding an error term, where each offspring is allocated a random environmental variate from the corresponding normal distribution. This reasoning is the key to understanding the approach presented here: parents are sampled from the population P independently and randomly (with replacement) and they form the corresponding normal distribution $F_1.$ Thus, all parental combinations occur with the same probability, i.e., random mating. Variation in family sizes is therefore an integral part of the model and the model is thus experimentally tailored to truly panmictic populations.

The classical methods for estimating $h^2$ using offspring–parent or offspring–midparent regression, and ANOVA-based approaches promote experimental efficiency by artificially manipulating the family structure with respect to the actual family numbers and sizes, so that the SE are minimized. Similarly, we can assess the experimental parameters α, β, and progeny sample size n that minimize SE$\left\{h^2\right\}$ determined by our method. An extension of the classical methods is to use restricted maximum likelihood approach (Patterson and Thompson 1971) for variance decomposition, both in synthetic and wild populations, provided variance-covariance of phenotypic records is specified by use of a relationship matrix (i.e., complete pedigree linking respective records to the base population), and assumptions of the infinitesimal model hold (Sorensen and Kennedy 1984).

The approach outlined here is different, as it allows $h^2$ to be estimated based on the truncated, rather than a random, subset, thus pedigree relationship is needed only within the truncated subsets of the distribution. Regression based on a truncated subset produces a biased $h^2$ estimate because the entire population sample (and particularly extreme values) are needed to estimate the slope of the regression line. It is possible to modify the regression procedure where most of the effort is applied to families of parents with phenotypes at both ends of the distribution, which would yield a precise estimate (Hill 1990). The increase in efficiency is because parents with phenotypes near the mean provide little information on the slope of the regression. However, we show here that $h^2$ can be estimated based on either phenotypes near the mean, or from phenotypic observations in only one extreme of the distribution. These arbitrary truncations applied to the normal distribution are different from the traditional approaches and could offer experimental scenarios that have not yet been considered in genetic studies. Our approach is based on determining the means and variances of P and $F_1$ populations and the relative frequency of offspring in the truncated proportion in $F_1$ with parent(s) originating from the truncated proportion of P. Provided the panmictic assumptions hold, our approach is therefore experimentally very simple and general.

First, it is clear that the precision of $h^2$ estimate will be much higher for one-sided truncation than for centered two-sided truncation. Comparing Figure 2 and Figure 3, we see that the SE$\left\{h^2\right\}$ from centered two-sided truncation are on the order of 5–10$\times$ those from one-sided truncation. In fact, close inspection of Equations 13 and 15 reveals that the minimum SE$\left\{h^2\right\}$ is obtained from the one-side truncation scenario. Next, we can assess the optimum α, the standardized truncation point. For $Y_1=1$ (tracking only one side of the parentage), the optimum α will generally be between 1 and 2 SD (Figure 2b). For $Y_2=2$ (tracking both sides of the parentage), the optimum α is between 0 and 1 SD across a range of $h^2$ (Figure 3b).

We now consider how this method could be implemented in practice. The first step is to calculate phenotypic means and variances in both the P and $F_1$ populations. The second step is to genotype a random sample of individuals in the right-truncated tail of the $F_1$ (say $n=500$ in the phenotypic range from $\alpha =1.5$ SD above the mean up to $\beta =+\mathrm{\infty }$) as well as parents belonging to the equivalent phenotypic range in the P population. The pedigree can then be inferred from these genotype data. The coefficient r can then be calculated by evaluating if $Y_1=1,$ i.e., tracking one side of the parentage. We can then use Equation 12 to calculate $h^2.$ If the true $h^2=0.6,$ then the SE$\left\{h^2\right\}=1.694\times 1/\sqrt{500}=0.076$ (Equation 15 and Figure 2b). If α is 2 SD above the mean, the corresponding SE$\left\{h^2\right\}=1.691\times 1/\sqrt{500}=0.076,$ i.e., identical, but the amount of genotyping effort in the parental population is greatly reduced. Note that traditional regression on one parent provides SE$\left\{h^2\right\}=2/\sqrt{500}=0.089$, and that on midparent values gives SE$\left\{h^2\right\}=\sqrt{\left(2/500\right)}=0.063$ (Falconer and Mackay 1996).

We will now explain how (in theory) Galton could have utilized our approach to collect the dataset. First, he would need estimates of the mean and variance of the trait in a population (we assume that records would be available without much investment). Then, he could choose to measure 278 children >0.5 SD above the average and check in the same manner parental values. With unknown parentage, pedigree assembly could be reduced from 934 to 278 children, reducing significantly the cost of sample collection, DNA extraction, and genotyping. Reduced sample size could also be possible with regression analysis, assuming a random sample (of say 278 children) across the entire range of the distribution with higher SE. However, the main methodological message of the current study is that we can estimate $h^2$ based on the tail of the distribution. Regression in such a case would result in a biased estimate (e.g., the same truncated dataset would produce $\widehat{b}\text{estimate}={\widehat{h}}^2\text{estimate}=0.31$).

We could speculate that our approach is less sensitive to the presence of outliers as all individuals above the truncation contribute equally to r. In regression analysis, outliers are most influential in either extreme of the distribution with respect to the slope of the regression line. In the ASReml analysis (Gilmour et al. 2009) that we performed on the same dataset, three possible outliers were suggested. When we removed these from the analysis, $h^2$ changed to 0.72 (SE was identical).

In summary, we propose an alternative formulation of $h^2.$ Under the assumptions of Hardy-Weinberg equilibrium, the $h^2$ of a quantitative trait in a given population is directly related to the likelihood of a phenotypic subset of parents passing their respective alleles onto the corresponding phenotypic subset of offspring. Future work is needed to compare the efficiency of this method to other existing methods; to estimate nonadditive genetic effects; to assess robustness with respect to the genetic architecture of the trait; and to assess the sensitivity of the approach to assumptions of Hardy-Weinberg equilibrium.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300508/-/DC1.