Dynamics of translation can determine the spatial organization of membrane-bound proteins and their mRNA

Significance

Unlike their eukaryotic counterparts, bacterial cells are composed of a single compartment. This allows many rapidly diffusing macromolecules, such as proteins and mRNAs, to be evenly distributed in the cell. Important exceptions are proteins embedded in the cell membrane, which transport material and information across the membrane. Often these proteins attach to the membrane before their translation is complete, anchoring their mRNAs to the vicinity of the membrane. This coupling between translation and localization suggests that the dynamics of translation may shape the spatial organization. In this paper, we use a canonical model of nonequilibrium statistical physics to characterize this connection and show how tunable kinetic properties allow the cell to regulate the spatial organization of both mRNAs and proteins.

Abstract

Unlike most macromolecules that are homogeneously distributed in the bacterial cell, mRNAs that encode inner-membrane proteins can be concentrated near the inner membrane. Cotranslational insertion of the nascent peptide into the membrane brings the translating ribosome and the mRNA close to the membrane. This suggests that kinetic properties of translation can determine the spatial organization of these mRNAs and proteins, which can be modulated through posttranscriptional regulation. Here we use a simple stochastic model of translation to characterize the effect of mRNA properties on the dynamics and statistics of its spatial distribution. We show that a combination of the rate of translation initiation, the availability of secretory apparatuses, and the composition of the coding region determines the abundance of mRNAs near the membrane, as well as their residence time. We propose that the spatiotemporal dynamics of mRNAs can give rise to protein clusters on the membrane and determine their size distribution.

Recent imaging techniques reveal the subcelllular locations of macromolecules in bacteria (1, 2). In contrast with the prevailing view of the bacterial cell as a spatially homogeneous reactor, these studies reveal an unexpected degree of subcellular organization. In particular, some mRNAs have been shown to exhibit distinct localization patterns (3, 4). Large-scale assays demonstrate that mRNAs that code for inner-membrane binding proteins are highly enriched near the membrane (5). This is believed to be the result of cotranslational insertion, whereby a nascent peptide is inserted into the membrane as soon as a membrane-targeting signal or domain has been translated, bringing the translating ribosome and the entire polysome to the vicinity of the membrane (6, 7). Mechanisms of cotranslational insertion are under intense research due to their importance and universality (8, 9). Membrane association of mRNAs has also been suggested to affect the organization of the bacterial chromosome through “transertion,” the mechanism by which cotranslational insertion and transcription occur simultaneously (7, 10, 11).

In bacteria, messenger RNAs are translated in the cytoplasm by diffusible ribosomes. Ribosomes bind the mRNA at a dedicated ribosomal binding site (RBS) at the upstream (5’) end and translate the coding region until they reach a stop codon, where they release the newly synthesized protein and the mRNA. This suggests that translation can be localized near the membrane as long as one of the translating ribosomes is attached to a membrane-bound nascent protein. The rate of translation initiation varies widely among different genes and is influenced by physiological and environmental cues. Elongation rate is less sensitive, but rare codons may stall the elongating ribosome and slow down translation.

Here we use a simple model, based on the totally asymmetric exclusion process (TASEP) (12, 13), to investigate how the dynamics of translation determines the spatial pattern of membrane-bound proteins and their mRNAs. We find that within the range of parameters typical to model bacteria, the spatial organization of mRNAs can range from a homogeneous distribution to a strong bias toward the membrane. We show how these patterns are determined by the organization of the coding sequence, the presence of slow codons, the rate of translation initiation, and the availability of auxiliary proteins required for membrane targeting (referred to as the secretory machinery). By calculating the distribution of the number of proteins placed together in the membrane, we suggest implications of mRNA localization on the organization of proteins on the membrane. We thus propose a mechanism for the formation of protein clusters in the membrane and investigate its implications on the regulation of their size distribution.

Model

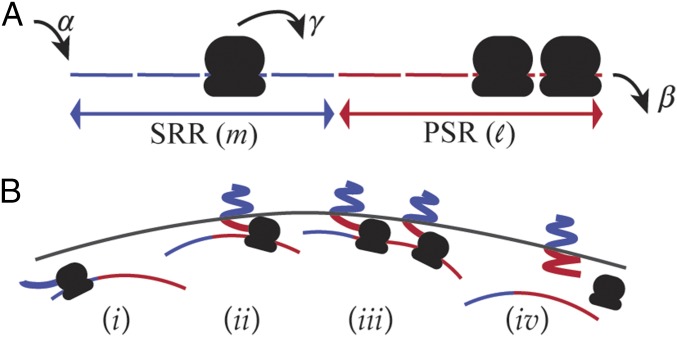
We model an mRNA molecule as a one-dimensional lattice with $L$ sites and open boundaries (Fig. 1A). Each site can be occupied by at most one ribosome. A ribosome enters the first site of the lattice at a rate $\alpha$ if that site is empty. Once in the lattice, they move unidirectionally, hopping from one lattice site to the next at a rate $\gamma$ when it is empty. Ribosomes at the very last site exit the lattice at a rate $\beta$. This model, known as the TASEP, is a canonical model of nonequilibrium statistical mechanics and has been used—among many other things—to study aspects of translation (14–17).

Fig. 1.

Model for membrane targeting by cotranslational insertion. (A) Schematic view of the TASEP with open boundaries. The signal recognition region (SRR) comprises the first $m$ sites, and the postsignaling region (PSR) the last $\mathrm{\ell }$. (B) Localization of an mRNA to the membrane vicinity ($i$). An mRNA is freely diffusing in the cell as long as no translating ribosome has completed translating the SRR ($ii$). A translating ribosome in the PSR is attached to a membrane-bound nascent protein and brings the mRNA to the membrane vicinity ($iii$). The mRNA remains anchored to the membrane as long as there are ribosomes in the PSR ($iv$). When the last of these ribosomes completes translation and detaches from the mRNA, the mRNA diffuses away from the membrane.

In the cell, the translation initiation rate $\alpha$ depends on the concentration of free ribosomes, which varies with the growth rate and stress level of the bacteria. The initiation rate of individual mRNAs depends on the affinity of ribosomes to their RBS, as well as their folding structure, which may interfere with ribosome binding (18). In addition, the rate of translation initiation can be dynamically controlled by the cell for posttranscriptional regulation [e.g., through small regulatory RNAs (19)]. Thus, the rate $\alpha$ can vary significantly across growth and stress conditions and from gene to gene. Our focus is therefore on studying the effect of $\alpha$ on mRNA localization and its implications.

In contrast, the elongation rate $\gamma$ is less sensitive to growth conditions and cannot be readily controlled in individual genes (10, 20), and we mostly ignore such variation. However, some mRNAs harbor individual or adjacent codons that locally slow down elongation through mechanisms that include competition for scarce tRNAs or unfavorable mRNA structure (21). While such “slow codons” are rare, their impact can be substantial. We explore this possibility toward the end of the paper.

Ribosomes translate the mRNA one codon at a time, while their footprint extends to about 10 codons. Previous models have taken this into account by extending the length of the exclusion interaction (14). This generalization yields results that are qualitatively similar to the simple TASEP. To maintain the simplicity of the model and to make use of known exact results, we use here the simple TASEP and understand that a site in this model corresponds to about 10 codons. This means that $\gamma \simeq 1-2$/s, and typical values for $\alpha /\gamma$ can be found in a range between 0.01 and 0.2 (20, 22, 23). For convenience, we assume that $\beta$ is equal to $\gamma$, as they are typically not significantly different (20, 24, 25).

To describe a configuration of the model we define for each site $i=1\dots L$ the occupancy variable ${\tau }_i$, which takes the value $1$ if site $i$ is occupied by a ribosome and 0 if it is not. The average occupancy $⟨{\tau }_i⟩$ is known exactly (12, 13) and is reproduced in Supporting Information.

Much of the interest in the TASEP stems from the fact that on an infinite lattice this model exhibits nonequilibrium phase transitions. With $\beta =\gamma$, it exhibits two phases: a low-density phase ($\alpha /\gamma <1/2$) and a maximal-current phase ($\alpha /\gamma \ge 1/2$). In the low-density phase, the correlations between ribosomes are short-ranged, and as a result, the flux, namely the rate of protein production, is smoothly increasing with $\alpha$. In contrast, the maximal current phase is characterized by long-range correlations, and the flux is independent of $\alpha$. Some of the distinct behaviors that characterize the different phases of the TASEP can still be found in finite lattices, like the ones we study here to represent the coding regions of mRNAs. However, except for highly translated mRNAs such as those encoding ribosomal proteins, we expect the translation of most mRNAs in bacteria to fall in the low-density phase (20, 22–25).

To model cotranslational insertion to the membrane, we divide a lattice of length $L$ into two regions (Fig. 1A). The first $m$ sites comprise the SRR, whose complete translation yields a nascent protein that is targeted to the membrane. This region may be coding for a signal that is recognized by a signal-recognition particle (SRP), which targets proteins to the inner membrane, or it may include the code for a membrane binding domain, whose presence is required for membrane insertion. Thus, the length of the SRR can range from 30 bases coding for the targeting signal to a few kilobases coding several domains, corresponding to $m$ between 5 and ∼100. The following $\mathrm{\ell }$ sites make up the PSR. This region can be extremely small if translation of the entire protein is required for a folded structure that is targeted to the membrane or as large as the entire protein if all that is required is a short signal at its N terminus. In this model, a ribosome in the PSR is physically attached to a peptide that can be targeted to the membrane, in which case it carries with it the entire polysome to the membrane vicinity (Fig. 1B).

The data we present below mostly considers PSRs of sizes 10 to 30 sites, corresponding to domains of 100 to 300 amino acids. In part, this choice is motivated by two membrane-bound proteins of Escherichia coli, the Glucose PTS transporter PtsG and the Shikimate transporter ShiA, whose translation is regulated by small regulatory RNAs (respectively, SgrS and RyhB) (26–28). The bulk of our results consider the case where translocation to the membrane and the targeting process are not rate limiting (20, 29). In this case, mRNAs are found near the membrane whenever there is a ribosome in the PSR. The case where a required apparatus is rate limiting is discussed toward the end of the paper. All Monte-Carlo simulations reported below were done on a lattice of size $L=100$, using a random sequential update scheme. To ensure convergence to steady state, we discard the first 20% of the Monte-Carlo sweeps.

Results

Our aim in this paper is to show how different properties of the mRNA—including the initiation rate $\alpha$, the size of the PSR, the presence of slow codons, and the availability of secretory machinery—affect the spatiotemporal organization of mRNAs. In turn, we use these results to investigate the implications on the formation and size distribution of protein clusters in the membrane.

Distribution of Residence Times Near the Membrane.

Our first task is to obtain the distribution $\mathrm{\Phi }(t)$ of the residence time $t$ spent by an mRNA near the membrane. We start by making the simple assumption that an mRNA is anchored to the membrane whenever there are ribosomes in the PSR. $\mathrm{\Phi }(t)$ is therefore the distribution of times from an entry of a ribosome to an empty PSR to a complete evacuation of PSR.

At very small $\alpha$, when the density of ribosomes on the mRNA is very low, a ribosome that enters the empty PSR leaves it at the other end before any other ribosome enters (case $ii$ of Fig. 1B). In this case, $\mathrm{\Phi }(t)$ is given approximately by a Gamma distribution. At higher values of $\alpha$ it becomes likely that when a ribosome finishes translating the mRNA, there are other ribosomes in the PSR behind it (case $iii$ of Fig. 1B). This case is addressed in Supporting Information, using the known steady-state gap distribution between particles in the TASEP (30). This analysis allow us to obtain the Laplace transform of the residence time distribution:

$$\stackrel{\sim }{\mathrm{\Phi }}(s)=\frac{(1-{\mathrm{{\rm Y}}}_{\text{PSR}}){\gamma }^{\mathrm{\ell }}{(\gamma +s)}^{-\mathrm{\ell }}}{1-{\mathrm{{\rm Y}}}_{\text{PSR}}{\gamma }^{g+1}{(\gamma +s)}^{-(g+1)}},$$ [1]

where ${\mathrm{{\rm Y}}}_{\text{PSR}}$ is the probability that when a ribosome finishes translation, the PSR behind it is empty (Fig. S1). To obtain $\mathrm{\Phi }(t)$, we compute the inverse Laplace transform of $\stackrel{\sim }{\mathrm{\Phi }}(s)$ numerically. We confirmed the validity of this analysis by comparing with results of Monte-Carlo simulations (Fig. S2A).

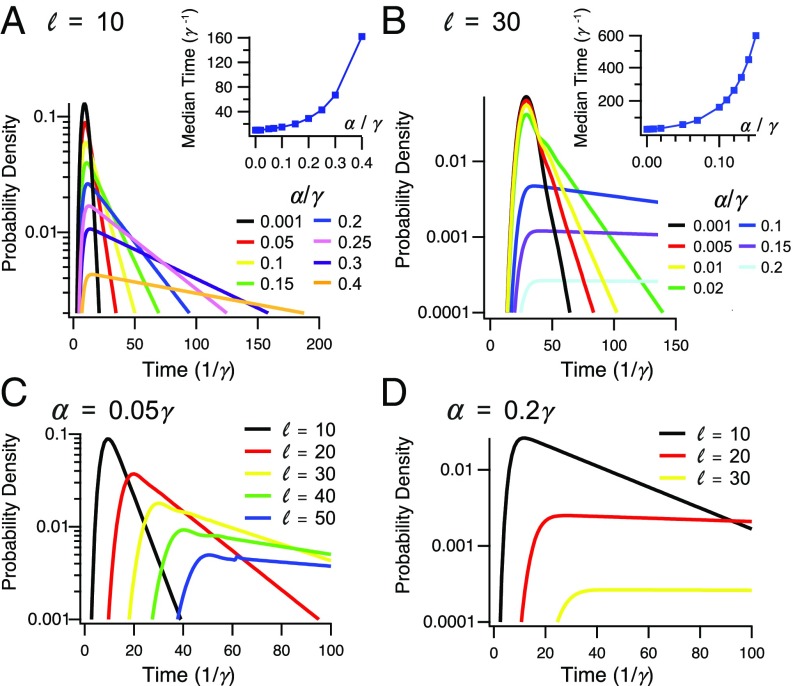
The residence time distribution $\mathrm{\Phi }(t)$ and its median are depicted in Fig. 2 for different translation initiation rates $\alpha$ (Fig. 2 A and B) and for several lengths $\mathrm{\ell }$ of the PSR (Fig. 2 C and D). As expected, for small values of $\alpha$ the distribution is well-approximated by a Gamma distribution that is dominated by the time it takes a ribosome to walk through the PSR (on average $\mathrm{\ell }/\gamma$). For a very short PSR, the median residence time near the membrane exceeds the typical lifetime of a bacterial mRNA (a few minutes) when $\alpha$ take values at the higher end of the typical range. With a larger PSR, this is also true for more moderate values of $\alpha$. However, our results suggest a very broad distribution of residence times near the membrane, suggesting frequent events in which an mRNA leaves the membrane after a short stay, even under the condition where the mean residence time is very long.

Fig. 2.

Distribution of residence times near the membrane. (A) The effect of translation initiation rate $\alpha$ on the probability density for a PSR of size $\mathrm{\ell }=10$. (Inset) Mean residence time increases with the ratio $\alpha /\gamma$ between translation initiation and elongation. (B) Same, for a PSR of size $\mathrm{\ell }=30$. (C) The effect of length $\mathrm{\ell }$ of the PSR on the probability density for $\alpha =0.05\gamma$. (D) Same, for $\alpha =0.2\gamma$.

Distribution of Residence Times Away from the Membrane.

We now consider the probability distribution for the residence time away from the membrane, which we denote by $\mathrm{\Theta }(t)$. Periods spent away from the membrane correspond to time intervals in which no ribosome on the mRNA is attached to a nascent peptide that is targeted to the membrane; namely, no ribosome resides in the PSR. In Supporting Information we obtain an exact expression for $\mathrm{\Theta }(t)$ in terms of the particle gap distribution, which is known exactly for the TASEP. This expression can be evaluated more easily using a mean-field approximation of this distribution, and we verified the validity of this approximation using Monte-Carlo simulations (Fig. S2B).

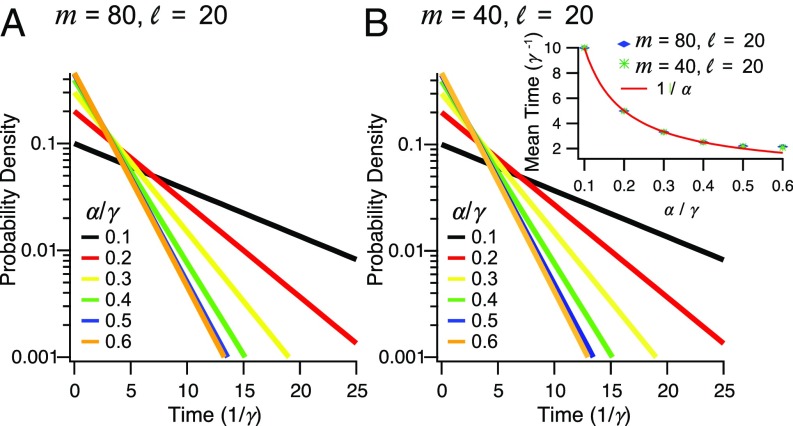
Fig. 3 shows the distributions of residence time away from the membrane for different lengths of the SRR and for different values of $\alpha$. The length of the SRR has only a minor effect on this distribution. When the SRR is long, it is likely that at the time when the PSR is emptied one or more ribosomes are present in the SRR. The distribution $\mathrm{\Theta }(t)$ is then dominated in these cases by the waiting time for the arrival of the most forward ribosome to the PSR and is given approximately by $\alpha e^{-\alpha t}$. When the SRR is short, however, it is possible that the departing ribosome leaves the mRNA completely unbound. We note that the length of the PSR itself is not expected to have any significant effect on these results (Fig. S3), due to the absence of long-range correlations at low $\alpha$.

Fig. 3.

Distribution of residence times away from the membrane. (A) The effect of translation initiation rate $\alpha$ on the probability density for an SRR of size $m=80$ and a PSR of size $\mathrm{\ell }=20$. (B) Same, for a SRR of size $m=40$ and a PSR of size $\mathrm{\ell }=20$. (Inset) Mean residence time decreases with the ratio $\alpha /\gamma$ between translation initiation and elongation. The line $1/\alpha$ is shown for comparison.

The waiting time distribution saturates at $\alpha \simeq 0.5$. This is the effect of the maximal current phase, which makes the flux of ribosomes rather insensitive to the precise value of $\alpha$. Irrespective of the details of the waiting time distribution, the mean time spent away from the membrane is given by $1/\alpha$ for $\alpha \lesssim 0.5$, where it saturates at approximately $2/\gamma$ (Fig. 3B, Inset).

Subcellular mRNA Organization.

In previous sections we calculated the residence time of an mRNA near and away from the membrane. We now explore the implications of cotranslational membrane insertion on the subcellular organization of both mRNAs and the proteins they encode.

When an mRNA is not kept near the membrane by a ribosome that synthesizes an already-bound nascent protein, it is free to diffuse in the cytoplasm. Once one of the translating ribosomes clears the SRR, this free diffusion can bring the nascent peptide to the membrane, where it will be inserted. Diffusion of polysomes in the bacterial cell is very fast (31), such that an mRNA in the middle of a cell is expected to reach the membrane in 0.5 to 4 s. Compared with the translation rate of $\sim 15$ codons per second, we take transport to the membrane to be instantaneous and simply describe mRNA localization in terms of one of two states: cytoplasmic and membrane-localized (20, 29). We assume that different events in which an mRNA becomes localized occur at independent positions on the membrane.

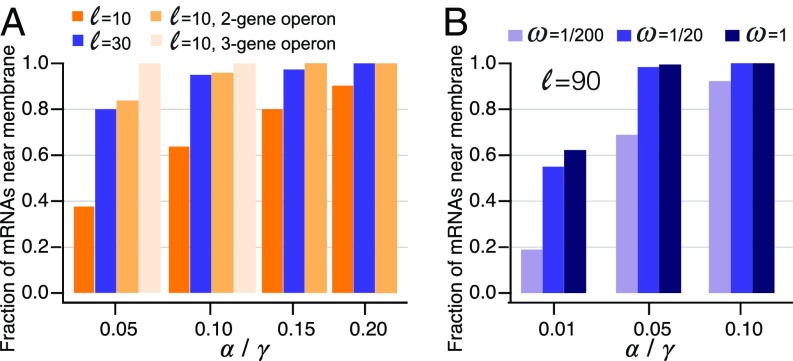
In Fig. 4A we show the steady-state ratio between the probabilities of the two states. With short- and medium-length PSRs, a population of mRNAs can be significantly represented both near the membrane and in the free-diffusion state, as long as its translational activity is not very high. Importantly, in these cases, the subcellular localization of these mRNAs can be modulated significantly by posttranscriptional regulation of translation initiation. This can be done, for example, by small regulatory RNAs, as in the case of shiA, whose translation is activated by the small RNA RyhB (28).

Fig. 4.

Enrichment of mRNAs near the inner membrane. (A) Fraction of mRNAs in the membrane-localized state at steady state increases with the translation rate, the length of the PSR, and the number of genes in the operon. Error bars are smaller than ${10}^{-3}$ and are not plotted. (B) With limited secretory system, even transcripts with long PSRs can be found away from the membrane.

The situation is different if a protein presents a membrane-targeted domain early in its coding sequence. This, for example, is the case for proteins whose N terminus sequence is recognized by the SRP. Unless the translation of such an mRNA is extremely inefficient, our model predicts that such mRNAs spend their entire lifetime in the vicinity of the membrane. This is also true for mRNAs that have shorter PSR but are translated with high efficiency. However, as discussed below, these conclusions are revised if the secretory machinery (such as the SRP) is scarce or rate-limiting.

Many RNA nucleases are found on or near the membrane, possibly accelerating mRNA turnover there (5). In this case, transcripts that are more biased toward the membrane have a shorter lifetime and are expected to produce fewer proteins (Fig. S4). Notably, if degradation occurs through a multistep process (e.g., through recruitment of small RNAs), this modulation depends on the structure of the residence time distribution $\mathrm{\Phi }(t)$ and not only on its mean.

Possible Implication for Protein Clustering on the Membrane.

A possible by-product of mRNA localization concerns the organization of proteins in the membrane. Superresolution microscopy revealed that many membrane proteins show nontrivial organization, such as a tendency to form clusters of different sizes (32, 33). We asked what contribution the localization dynamics of mRNAs may have on the clustering structure of the membrane proteins they encode. To address this question, we postulated that proteins translated from a single mRNA during a single stay near the membrane form a single cluster. Mechanisms that keep these proteins together can include protein–protein interactions, which come into play cotranslationally and prevent fully translated proteins from diffusing away, as well as translocation into lipid rafts (34). The size of this cluster is therefore the number of proteins produced during a single stay of the mRNA near the membrane.

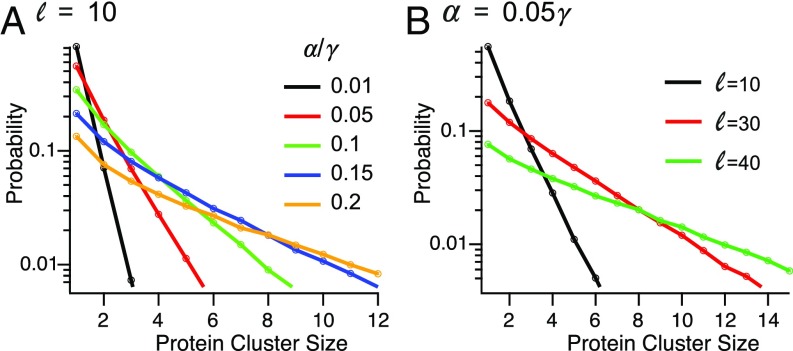
We approximated the frequency of a cluster of size $c$ by multiplying the proportion of clusters of size $c$ with ${(1-d)}^{c-1}$, which represents the probability of an mRNA surviving the production of $c$ proteins. We took $d$, the probability that the mRNA is degraded during the production of a protein, to be $1/11$, giving a mean lifetime of 10 proteins for an mRNA (35). The average number of proteins per cluster increases about 10-fold over the relevant range of $\alpha$ (Fig. 5A). Therefore, changes in translation initiation rate, due, for example, to posttranscriptional regulation, can affect the granularity of the organization of proteins in the membrane. As before, mRNAs with longer PSRs show a broader distribution of residence time near the membrane. As a result, the cluster size distribution for such proteins is broader, and the mean cluster size is larger (Fig. 5B).

Fig. 5.

The effect of mRNA localization on protein clustering in the membrane. (A) The effect of $\alpha$ on the probability distribution for the number of proteins produced during a single stay of an mRNA near the membrane, for a PSR of size $\mathrm{\ell }=10$. (B) The effect of $\mathrm{\ell }$ on the probability distribution for the number of proteins produced during a single stay of an mRNA near the membrane, for $\alpha =0.05\gamma$.

In many cases, several membrane-bound proteins are encoded together on a polycistronic mRNA. In our model, we assume that such an mRNA molecule is anchored to the membrane as long as there is a ribosome in the PSR of any of the coding regions. This, of course, increases the fraction of transcripts near the membrane considerably (Fig. 4A) as well as the typical cluster size. As an important consequence, these clusters are heterogeneous, composed of the different components encoded by the mRNA.

The Effect of Slow Codons on Membrane Organization.

Translational elongation occurs at an approximately even rate along the coding sequence. However, specific codons or codon sequences in some mRNAs can be translated at a significantly reduced rate (36, 37), earning them the name slow codons. Mechanisms behind this slowdown include sequences of codons associated with scarce tRNAs and sequences that lead to unfavorable mRNA structures (21). In some cases, the effect of slow codons is amplified under extreme conditions, such as stress or limited growth (38). Synonymous mutations in these codons have no effect on the translated proteins, yet it is now well established that these mutations are neither random nor neutral (39, 40).

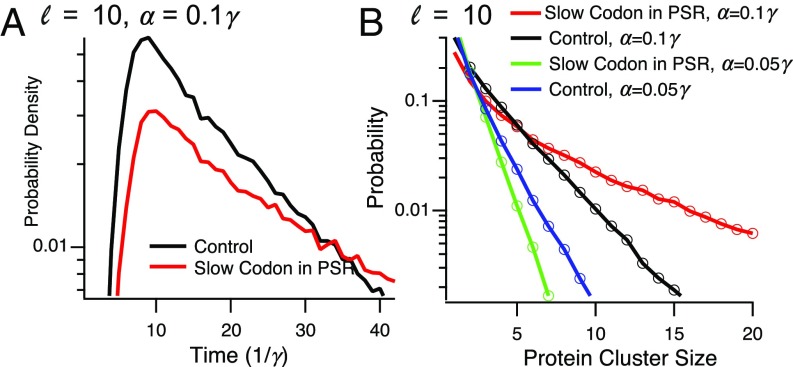
In E. coli, effects of slow codons on the elongation rate have been reported in the range of 2–5-fold (41). To model the effect of a slow codon on mRNA localization, we let the hopping rate from a “defect” site (corresponding to a few codons) be $\gamma /5$. A defect site can reside either in the SRR, in the PSR, or both. In Fig. 6A, we show the effect of slow codons on the distribution of residence time near the membrane. A slow codon in the PSR, but not in the SRR, can have a significant effect on this distribution, making the mRNA effectively trapped near the membrane. This is because the defect site causes a ribosome “traffic jam,” making it more unlikely that the PSR would become free of ribosomes. Since the position or length of this traffic jam is not important for mRNA localization, the position of the slow codon has no effect on this distribution. As expected, these results carry to the approximate number of proteins produced during a single stay near the membrane (called above the cluster size), as shown in Fig. 6B.

Fig. 6.

Effect of a slow codon on mRNA localization. (A) The effect of a slow codon on the distribution of residence times near the membrane, for $\alpha =0.1\gamma$ and $m=90,\mathrm{\ell }=10$. (B) The effect of a slow codon on the distribution of the number of proteins synthesized at a single location. Parameters are as in A, with the case $\alpha =0.05\gamma$ included.

Limited Secretory Machinery Skews the Distribution of Protein Clusters.

Cotranslational insertion requires components of the secretory machinery. While these components are highly abundant in the cell (9), it is estimated that at times they can be engaged by about half the proteome, suggesting that under some conditions their availability may be rate limiting for membrane targeting. To consider such cases, we assume that once the SSR is translated, insertion of the peptide to the membrane occurs with a finite rate $\omega$. The parameter $\omega$ reflects the availability of the secretory machinery and can depend on cellular conditions but is otherwise independent of the other parameters of the model. For example, under conditions in which 1% to 10% of the $\sim$200 copies of the SRP are available to engage new peptides (9), one may expect $\omega /\gamma$ in the range $1/30$ to $1/3$.

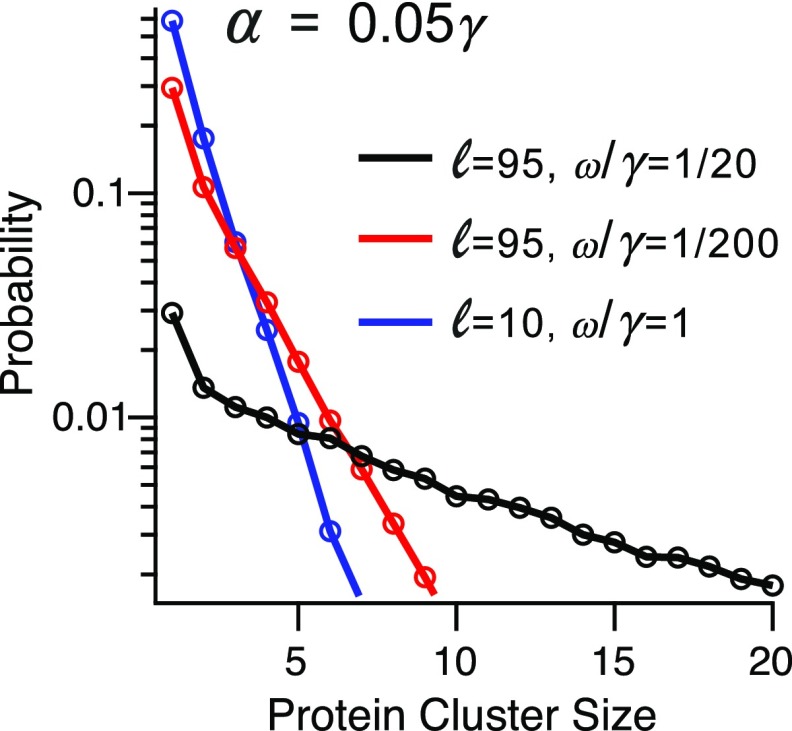
Our results above correspond to the case $\omega \gg \gamma$, where the protein becomes anchored as soon as the targeting domain is translated. Simulations of our model at the complimentary case $\omega \le \gamma$ (Fig. 4B) demonstrate that in this case mRNAs with short PSR spend most of their time away from the membrane, while mRNAs with long PSR are no longer titrated continuously to the membrane. Thus, with limited secretory machinery even the localization of mRNAs that code for long proteins carrying a N terminus signal can be modulated. In cases where mRNA localization induces protein clusters, the engagement rate $\omega$ affects the size distribution of these clusters (Fig. 7). In particular, with small $\omega$, the cluster size can be highly limited even when the PSR is very long.

Fig. 7.

The effect of having different levels of secretory machinery for $\alpha =0.05\gamma$, $L=100$, and PSR sizes of $\mathrm{\ell }=10$ and $\mathrm{\ell }=95$. It is seen that the distribution of protein cluster size can vary greatly depending on the availability of secretory machinery.

Conclusions and Discussion

Recent large-scale superresolution microscopy experiments confirmed that mRNAs of membrane–protein coding genes are enriched in the vicinity of the membrane (5) and that some membrane proteins tend to cluster on the membrane (32, 33). In this work, we study a model for the effect of translation dynamics on the subcellular organization of membrane proteins and their mRNAs. We show that this internal organization has a strong impact on the enrichment of transcripts near the membrane. When the PSR is short, the mRNA distribution is highly dependent on the rate of translation initiation and can range from an (almost) homogeneous distribution at low initiation rates to a highly skewed distribution toward the membrane at high rates. Transcripts with long PSRs, on the other hand, are effectively trapped near the membrane even when the translation rate is not particularly high and the associated secretory machinery (if any) is nonlimiting. This is also the case for polycistronic mRNAs that code for multiple membrane binding proteins. Having limited secretory machinery, on the other hand, may recover variability in membrane enrichment of such transcripts.

The rate of translation initiation of specific genes can be controlled posttranscriptionally in response to environmental and physiological cues by small regulatory RNAs (19), riboswitches (42), and more. Our results indicate that in some cases a by-product of this regulation can be a shift in the spatial distribution of the target mRNAs.

Together with recent experimental results, our model suggests that the bias of mRNAs toward the membrane can be graded and dynamically controlled. It is therefore important to ask whether this spatial organization may have an intended function and whether it has implications on other cellular functions. It has been suggested that enrichment of an mRNA species near the membrane may increase its degradation rate, due to the membrane localization of key ribonucleases (5). Since ribosomes are known to be biased away from the nucleoid, mRNAs that reside near the membrane may be more efficiently translated (43). The combination of these two phenomena may imply that membrane-enriched mRNAs are more susceptible to sRNA regulation (27, 44). In addition, localization of mRNAs to the vicinity of the membrane by the first translated protein guarantees that subsequent proteins are already synthesized near the membrane. This prevents translational stalling that is caused by synthesizing hydrophobic domains in the aqueous environment inside the cell (10).

Here we propose that in addition, mRNA localization to the membrane may impact the spatial organization of proteins in the membrane. Recent imaging data suggest that many protein families tend to form clusters on the membrane (45, 46). Clustering is believed to play important roles, for example, in the sensitivity of extracellular receptors (47). The prevalent models for the formation and dynamics of these clusters rely on slow diffusion in the heterogeneous membrane and the thermodynamics of interactions between proteins in the cluster (48). However, how proteins of the same species find each other in the crowded membrane is not well understood.

Our model suggests a mechanism for nucleation of such clusters as well as an opportunity for the cell to control their initial sizes. In this mechanism, cluster formation is facilitated by a burst of proteins translated from a single mRNA anchored to the membrane. Such a cluster can be heterogeneous if the mRNA is polycistronic and encodes multiple membrane binding proteins, such as different components of a transporter or receptor. These proteins can stay together through interactions that occur cotranslationally or by embedding in a lipid raft that limits diffusion (34). Interestingly, in some cases, operons that encode inner-membrane proteins also encode outer-membrane proteins that are not inserted cotranslationally (such as fecA of E. coli, which encodes an outer-membrane porin and shares a transcript with genes that encode the ferric dicitrate ABC transporter). In this case, our model would suggest that long residence times of such polycistronic mRNAs near the membrane can facilitate translocation of these proteins to the outer membrane.

Together, our analysis predicts several possible effects of the translation initiation rate $\alpha$ and the structure of the mRNA on the spatial distribution of mRNAs and membrane-bound proteins as well as on localization-dependent lifetime of the mRNA. These predictions can be tested experimentally by measuring the effects of perturbations to the initiation rate or the structure of polycistronic mRNAs using smFISH and superresolution microscopy. Perturbation to the initiation rate can be done by introducing mutations to the RBS or by controlling the abundance of a small regulatory RNAs (see Supporting Information for details).

Previously it has been proposed that coupling between insertion, translation, and transcription (known as transertion) may facilitate formation of membrane domains (49). In this model, it is assumed that the locus on the chromosome where these proteins are encoded is fixed in space and is held close to the membrane through a chain of DNA–RNA polymerase–mRNA–ribosome–proteins–membrane. This model, however, does not consider what happens to proteins that are translated after the transcription of the mRNA is complete. Our model suggests that these mRNAs may remain anchored to the membrane and synthesize a burst of proteins at the same location.

Transertion is also presumed to have an impact on the structure of the chromosome itself (7, 10, 11). Our model, which suggests that some mRNAs can reside continuously near the membrane, supports the idea that mRNAs may stably anchor the chromosome to the membrane. Thus, the residence time distribution we calculate here can be used for future modeling of chromosome dynamics in vivo.

Additionally, we show that rare slow codons in the PSR can dramatically increase the time spent near the membrane. In some cases, the slowdown of translation in such codons is only significant under starvation. This raises the possibility that some mRNAs that harbor these codons can be more skewed toward the membrane during starvation, potentially resulting in faster degradation or in modulation of protein clusters. Interestingly, bioinformatics and experimental investigations have previously shown that PSRs of membrane–protein coding mRNAs are enriched for slow codons (50, 51).