Joint Modeling of Survival Time and Longitudinal Outcomes with Flexible Random Effects

Abstract

Joint models with shared Gaussian random effects have been conventionally used in analysis of longitudinal outcome and survival endpoint in biomedical or public health research. However, misspecifying the normality assumption of random effects can lead to serious bias in parameter estimation and future prediction. In this paper, we study joint models of general longitudinal outcomes and survival endpoint but allow the underlying distribution of shared random effect to be completely unknown. For inference, we propose to use a mixture of Gaussian distributions as an approximation to this unknown distribution and adopt an Expectation-Maximization (EM) algorithm for computation. Either AIC and BIC criteria are adopted for selecting the number of mixtures. We demonstrate the proposed method via a number of simulation studies. We illustrate our approach with the data from the Carolina Head and Neck Cancer Study (CHANCE).

1 Introduction

In biomedical or public health research, it is common that both longitudinal outcomes over time and survival endpoint are collected for the same subject along with the subject’s characteristics or risk factors. Investigators are interested in finding important variables which can predict both longitudinal outcomes and survival time. For this purpose, simultaneous modeling is needed since the two different types of outcomes are correlated within the same subject. Dr. Jack Kalbeisch has done important and influential work in the area of joint modeling of longitudinal data and survival time.

Among the existing approaches for the joint analysis of longitudinal data and survival time, modeling survival time conditional on longitudinal data or vice versa was more widely considered, compared to simultaneous modeling. Estimating the distribution of survival time given longitudinal data was studied by numerous authors, for example, Tsiatis, De Gruttola, and Wulfsohn (1995), Wulfsohn and Tsiatis (1997), Henderson, Diggle and Dobson (2000), Tsiatis and Davidian (2001), Xu and Zeger (2001a,b), Song, Davidian and Tsiatis (2002), Larsen (2004), Tseng, Hsieh and Wang (2005), Hsieh, Tseng and Wang (2006), Song and Wang (2007), Ye, Lin and Taylor (2008), Huang, Stefanski and Davidian (2009) and Chakraborty and Das (2010) among others. The trend of longitudinal outcomes conditional on survival time was studied by Wu and Carroll (1988), Hogan and Laird (1997), Wang, Wang and Wang (2000), Albert and Follmann (2000, 2007), Liu, Wolfe and Kalbeisch (2007), and Ding and Wang (2008) among others. On the other hand, simultaneous models of longitudinal outcome and survival time were proposed by Xu and Zeger (2001b) and Zeng and Cai (2005a, 2005b) and further studied by Elashfoff, Li and Ni (2007, 2008), Liu, Ma and O’Quigley (2008), Rizopoulos, Verbeke and Molenberghs (2008), Rizopoulos, Verbeke, Lesaffre and Vanrenterghem (2008), Choi, Cai, Zeng, and Olshan (2015), and Choi, Cai, and Zeng (2017). Wang and Taylor (2001), Brown and Ibrahim (2003), Dunson and Herring (2005), Chen, Ghosh, Raghunathan, and Sargent (2009), Hu, Li and Li (2009), Ghosh, Ghosh and Tiwari (2011), Huang, Li, Elashfoff and Pan (2011) and Baghfalaki, Ganjali and Verbeke (2016) studied simultaneous modeling from the Bayesian perspective.

In most of existing methods, random effects are incorporated to accommodate latent dependence between survival time and longitudinal data. Furthermore, random effects are conventionally assumed to be normally distributed and this assumption plays a vital role in parameter estimation and inference. However, the latter is not testable using observed data and moreover, it is well documented that misspecifying normality assumption can lead to serious bias in estimation (Neuhaus, Hauck, and Kalbeisch, 1992; Kleinman and Ibrahim, 1998; Heagerty and Kurland, 2001; Agresti, Caffo, and Ohman-Strickland, 2004). This concern was also noted in joint models (Wulfsohn and Tsiatis, 1997; Wang, Wang and Wang, 2000) and the assumption was relaxed by Song, Davidian and Tsiatis (2002) in a proportional hazard model depending on longitudinal process requiring only that random effects have density belonging to a class of smooth densities studied by Gallant and Nychka (1987) who suggested a seminonparametric (SNP) density estimator. In a similar setting of joint models for a time-to-event endpoint, Tsiatis and Davidian (2001) proposed conditional score estimators (CSEs) that require no assumption on the distribution of the random effects. Li, Zhang, and Davidian (2004) also considered CSEs in joint models for a simple endpoint of a generalized linear model with covariates that are subject-specific random effects in a linear mixed effect model for measurements. The issue of robustness of joint models to the distributional assumption on random effects was further discussed by some authors. Hsieh, Tseng and Wang (2006) suggested that the maximum likelihood estimators (MLEs) in joint models with a primary time-to-event endpoint and a longitudinal covariate process are robust to the violation of the random effect model assumption when there is rich enough information available from the longitudinal data (i.e. the longitudinal data should not be too sparse or carry too large measurement errors). Rizopoulos, Verbeke, and Molenberghs (2008) concluded that the effect of misspecifying the random effects distribution in joint models of survival and longitudinal processes becomes minimal (converging to zero) as the number of repeated longitudinal measurements per individual increases. Huang, Stefanski and Davidian (2009) presented diagnostic tools that can reveal adverse effects of random effect model misspecification in joint models of a primary endpoint and a longitudinal process by improving the remeasurement method for structural measurement error models (Huang, Stefanski and Davidian, 2006) which was derived from the simulation-extrapolation (SIMEX) method developed by Cook and Stefanski (1994) and Stefanski and Cook (1995). As an effort to resolve the issue, instead of using Gaussian random effects and errors, Dirichlet process (DP) priors were assumed to model the distribution of individual random effects and error distribution in a fully Bayesian approach by Ghosh, Ghosh and Tiwari (2011) who considered a multiple-changepoint model for longitudinal process and a proportional hazards model for dropout time.

Alternatively, some studies considered latent class memberships to be shared between longitudinal marker trajectory and risk of event under the structure of assuming a heterogeneous population of subjects who can be divided into latent homogenous subgroups and modeling an individual’s probability of belonging to a latent class via a multinomial logistic regression. The joint latent class model for a longitudinal biomarker and an event-time outcome subject to censoring was proposed by Lin, Turnbull, McCulloch and Slate (2002) who generalized the latent class models of Muthén and Shedden (1999) and Lin, McCulloch, Turnbull, Slate and Clark (2000) for a longitudinal biomarker and a binary outcome in the setting of complete follow-up. Garre, Zwinderman, Geskus and Sijpkens (2008) used a Bayesian approach to fit a joint latent class changepoint model for survival prediction with longitudinal biomarker readings. Recently, Proust-Lima, Séne, Taylor and Jacqmin-Gadda (2014) studied the joint latent class models in details in comparison with the joint shared random effects models. On the other hand, to allow the heterogeneous population in joint shared random effects models of continuous longitudinal measurements and event time data, Rizopoulos, Verbeke and Molenberghs (2008) and Huang, Li and Elashoff (2010) proposed parameterizations of normal random effects and most recently Baghfalaki, Ganjali and Verbeke (2016) considered a finite mixture of normal distributions as the distribution for random effects. Heterogeneity of the shared random effects was also assessed in Baghfalaki, Ganjali and Verbeke (2016) by adopting the graphical method of Verbeke and Molenberghs (2013) which presented the gradient function as an exploratory diagnostic tool for the assumed distribution of random effects in mixed models.

In this paper, we seek to alleviate the problems due to violation of normality of random effects when considering simultaneous models in the joint analysis of general longitudinal outcomes (continuous or categorical) and survival time, by assuming the underlying distribution of random effects is completely unknown. For estimating model parameters, we propose to use a mixture of Gaussian distributions as an approximation for the unknown random effect distribution. Using a finite mixture of parametric distributions to approximate an unknown distribution has been mostly studied in other context, including linear mixed effect models (Verbeke and Lesaffre, 1996; Verbeke and Molenberghs, 2000; Xu and Hedeker, 2001; Zhang and Davidian, 2001; Lemenuel-Diot, Mallet, Laveille, and Bruno, 2005; Cheon, Albert, and Zhang, 2012) and generalized linear mixed effect models (Komárek and Verbeke, 2002; Verbeke and Lesaffre, 1996; Fieuws, Spiessens, Draney, 2004; Caffo, Ming-Wen and Rohde, 2007; Cagnone and Viroli, 2012). Also, finite normal mixture models were studied by many authors and in particular the work by Dr. Kalbeisch and his colleagues includes Lesperance and Kalbeisch (1992), Neuhaus, Hauck and Kalbeisch (1992) and Chen and Kalbeisch (1996, 2005). In the joint modeling framework, Baghfalaki, Ganjali and Verbeke (2016) used a finite mixture of normal distributions for the shared random effects in survival time and continuous longitudinal data processes and developed a Bayesian procedure for estimation and inference. Therefore, this is the first time we extend this method to joint models of general longitudinal data – incorporating both continuous and categorical types – and survival time. With the approximation, an expectation-maximization (EM) algorithm can be used for parameter estimation in the joint models. We also adopt the Akaike’s information criterion (AIC) (Akaike, 1973) and the Bayesian information criterion (BIC) (Schwarz, 1978) in this paper for selecting the number of mixtures.

The outline of this paper is as follows. In Section 2, we present a simultaneous modeling for longitudinal outcomes and survival time with random effects from an unknown distribution, and describe the inference procedure. Asymptotic properties of the proposed estimators are investigated in Section 3, and numerical results from simulation studies are given in Section 4. Our proposed method is illustrated with the data from the Carolina Head and Neck Cancer Study (CHANCE) in Section 5. In Section 6, we discuss some further consideration.

2 Models and Inference Procedure

2.1 Model Formulation and Notation

We use Y(t) to denote the value of a longitudinal marker process at time t. Suppose Y(t) is from a distribution belonging to exponential family in order to incorporate both continuous and categorical measurements. Let T denote survival time, and suppose that the survival time T is possibly right censored. Suppose a set of n subjects are followed over an interval [0, τ], where τ is the study end time. Denote ${\mathit{b}}_i^{\ast }$, i = 1, …, n, as a vector of subject-specific random effects of dimension d_b and ${\mathit{b}}_i^{\ast }$ ’s are mutually independent. Different from the traditional joint models, we assume the underlying distribution of ${\mathit{b}}_i^{\ast }$ is completely unknown and denote its density as $f({\mathit{b}}_i^{\ast })$.

Given the random effects ${\mathit{b}}_i^{\ast }$, the observed covariates, and the observed outcome history till time t, we assume that the longitudinal outcome Y_i(t) at time t for subject i follows a distribution from the exponential family with density,

$$\text{exp }\{\frac{y_i{\eta }_i(t)-B({\eta }_i(t))}{A(D_i(t;\varphi ))}+C(y_i,D_i(t;\varphi ))\}$$ (1)

with ${\mu }_i(t)=\mathrm{E}(Y_i(t)|{\mathit{b}}_i^{\ast })=B\prime ({\eta }_i(t))$ and ${\upsilon }_i(t)=\text{Var}(Y_i(t)|{\mathit{b}}_i^{\ast })=B″({\eta }_i(t))A(D_i(t;\varphi ))$, satisfying

$${\eta }_i(t)=g({\mu }_i(t))={\mathit{X}}_i(t)\mathit{\beta }+{\stackrel{\sim }{\mathit{X}}}_i(t){\mathit{b}}_i^{\ast }$$

and υ_i(t) = υ(μ_i(t))A(D_i(t; ϕ)), where g(·) and υ(·) are known link and variance functions respectively, X_i(t) and X̃_i(t) are the row vectors of the observed covariates for subject i and may include external time-dependent covariates, and β is a column vector of coefficients for X_i(t). X_i(t) does not include intercept and it does not contain any covariates in X̃_i(t) because the intercept and any potential common covariates for fixed effects are combined with the corresponding random effects in X̃_i(t) so that mean of random effects does not have any restriction. The random effect ${\mathit{b}}_i^{\ast }$ is allowed to differ for different individuals.

Given the random effects ${\mathit{b}}_i^{\ast }$, the observed covariates, and the observed survival history before time t, the conditional hazard rate function for the survival time T_i of subject i is assumed to follow a Stratified multiplicative hazards model,

$${\lambda }_s(t)\text{ exp}\{{\stackrel{\sim }{\mathit{Z}}}_i(t)(\mathit{\psi }◦{\mathit{b}}_i^{\ast })+{\mathit{Z}}_i(t)\mathit{\gamma }\},$$ (2)

where, for any vectors a₁ and a₂ of the same dimension, a₁◦a₂ denotes the component-wise product; Z_i(t) and Z̃_i(t) are the row vectors of the observed covariates and may share some components; ψ is a vector of parameters of the coefficients for random effects; γ is a column vector of coefficients for Z_i(t); and λ_s(t) is the s-th stratum baseline hazard rate function so that the baseline hazard rate is allowed to vary across levels of the stratification variable. Note that Z_i(t) and Z̃_i(t) do not include dummy variables for strata since baseline hazard rate is stratum-specific. For notation, we use common fixed effects and random effects across strata in both hazard and longitudinal models. However, the model is flexible and allows for possibly different covariate effects for different strata, which can be accommodated by including interaction terms of the covariates with the indicator variables for the stratification variable. Subjects in different strata are assumed to be independent. In addition, X̃_i(t) and Z̃_i(t) have the same dimensions as ${\mathit{b}}_i^{\ast }$ ’s.

Under models (1) and (2), the two outcomes Y(t) and T are independent conditional on the covariates and the random effects. The parameter ψ in model (2) characterizes the dependence between the longitudinal outcomes and the survival time due to latent random effect: When the m-th component of ψ is 0 (i.e. ψ_m = 0), it implies that the dependence between the survival time and longitudinal responses is not due to the corresponding latent variable ${\mathit{b}}_{\mathit{\text{im}}}^{\ast }$; ψ_m ≠ 0 implies that such dependence may be due to the corresponding latent variable ${\mathit{b}}_{\mathit{\text{im}}}^{\ast }$.

Let n_i be the number of observed longitudinal measurements for subject i, and assume that the distributions of n_i and the observation times for longitudinal measurements are independent of the parameters of interest conditional on ${\mathit{b}}_i^{\ast }$ in this joint model. We also assume n_i is bounded, which is a reasonable assumption in many biomedical studies. The observed data from n subjects are (n_i, Y_ij, X_ij, X̃_ij), j=1, …, n_i, i=1, …, n, and (V_i, Δ_i, S_i, {(Z_i(t), Z̃_i(t)) : t≤V_i}), i=1, …, n, where for subject i, (Y_ij, X_ij, X̃_ij) is the j-th observation of (Y_i(t), X_i(t), X̃_i(t)), C_i is the right-censoring time and assumed to be independent of T_i, Y_i(t), and random effects conditional on all covariates, V_i = min(T_i, C_i), S_i denotes the stratum, and Δ_i = I(T_i ≤ C_i). For all n subjects, we write $\mathit{Y}={({\mathit{Y}}_1^T,\dots ,{\mathit{Y}}_n^T)}^T$, Y_i = (Y_i1, …, Y_ini)^T, V = (V₁, …, V_n)^T, and ${\mathit{b}}^{\ast }={({\mathit{b}}_1^{\ast T},\dots ,{\mathit{b}}_n^{\ast T})}^T$. Then, the likelihood function of the complete data (Y, V, b*) has the form,

$$\begin{gathered} L_c(\mathit{Y},\mathit{V},{\mathit{b}}^{\ast })=\prod _{i=1}^{n}f({\mathit{Y}}_i|{\mathit{b}}_i^{\ast })(\prod _{s=1}^S{[f(V_i|{\mathit{b}}_i^{\ast })]}^{I(S_i=s)})f({\mathit{b}}_i^{\ast }) \\ =\prod _{i=1}^n\text{ exp }\{\sum _{j=1}^{n_i}[\frac{Y_{\mathit{\text{ij}}}({\mathit{X}}_{\mathit{\text{ij}}}\mathit{\beta }+{\stackrel{\sim }{\mathit{X}}}_{\mathit{\text{ij}}}{\mathit{b}}_i^{\ast })-B(\mathit{\beta };{\mathit{b}}_i^{\ast })}{A(D_i(t_j;\varphi ))}+C(Y_{\mathit{\text{ij}}};D_i(t_j;\varphi ))]\} \\ \times (\prod _{s=1}^S{\left[{\lambda }_s{(V_i)}^{{\Delta }_i}\text{ exp }\right\{{\Delta }_i[{\stackrel{\sim }{\mathit{Z}}}_i(V_i)(\mathit{\psi }◦{\mathit{b}}_i^{\ast })+{\mathit{Z}}_i(V_i)\mathit{\gamma }] \\ -{\int }_0^{V_i}\text{ exp }\{{\stackrel{\sim }{\mathit{Z}}}_i(u)(\mathit{\psi }◦{\mathit{b}}_i^{\ast })+{\mathit{Z}}_i(u)\mathit{\gamma }\}d{\Lambda }_s(u)\left\}\right]}^{I(S_i=s)}) \\ \times f({\mathit{b}}_i^{\ast }), \end{gathered}$$ (3)

and the full likelihood function of the observed data (Y, V) is expressed as

$$L_f(\mathit{Y},\mathit{V})={\int }_{{\mathit{b}}^{\ast }}{L}_c(\mathit{Y},\mathit{V},{\mathit{b}}^{\ast })d{\mathit{b}}^{\ast }.$$ (4)

2.2 Inference Procedure

Since the distribution of the random effects is completely unknown, it is necessary to estimate this distribution nonparametrically. However, since there are no observations associated with such latent random effects, a fully nonparametric estimation can be numerically unstable. Instead, we propose to estimate this unknown distribution via an approximation by a series of parametric distributions. Particulary, we choose to use a finite mixture of normal distributions to approximate this unknown distribution where the number of mixtures will be chosen based on data.

For the subject-specific random effects ${\mathit{b}}_i^{\ast }$ in Section 2.1, we approximate the distribution of ${\mathit{b}}_i^{\ast }$ with a mixture of a finite number of d_b-dimensional multivariate normal distributions. That is, the distribution of ${\mathit{b}}_i^{\ast }$ is approximated by ${\sum }_{k=1}^K{w}_k𝒩({\mathit{\mu }}_k,{\mathit{\sum }}_b)$, where K is the number of mixture components. We denote the probability of belonging to component k by w_k, such that ${\sum }_{k=1}^K{w}_k=1$. μ_k is the mean of the k-th component and it is assumed that each component has the same covariance matrix Σ_b. This constraint is needed to avoid infinite likelihoods (Böhning, 1999). We write w = (w₁, …, w_K−1)^T, the vector of K − 1 component probabilities, and $\mathit{\mu }={({\mathit{\mu }}_1^T,\dots ,{\mathit{\mu }}_K^T)}^T$, the vector of all component means which are ordered from the largest to the smallest (μ₁ > μ₂ > ⋯ > μ_K) for identifiability of component labels. We introduce b_i and α_i = k, (k = 1, …, K), as the i-th subject’s random effects following the mixture distribution and the k-th component of the mixture from which b_i is sampled, respectively. The distribution of α_i is then described by P(α_i = k) = w_k and, given α_i = k, b_ik ~ 𝒩(μ_k, Σ_b). Thus, ${\mathit{b}}_i={\sum }_{k=1}^{K}I({\alpha }_i=k){\mathit{b}}_{\mathit{\text{ik}}}$, where I(α_i = k) is the indicator of belonging to component k. For n subjects, $\mathit{b}={({\mathit{b}}_1^T,\dots ,{\mathit{b}}_n^T)}^T$ and α = (α₁, …, α_n)^T.

Now we estimate and make inferences on the parameters θ = (β^T, ϕ^T, Vech(Σ_b)^T, μ^T, w^T, ψ^T, γ^T)^T, where Vech(·) operator creates a column vector from a matrix by stacking the diagonal and upper-triangle elements of the matrix, and the baseline cumulative hazard functions with S strata, Λ(t) = (Λ₁(t), …, Λ_S(t))^T, where ${\Lambda }_s(t)={\int }_0^t{\lambda }_s(u)\mathit{\text{du}}$, s = 1, … S. The parameters β and ϕ are from the longitudinal model, ψ and γ are from the hazard model, and μ, w, and Σ_b are associated with the random effects. The likelihood function (3) of the complete data (Y, V, b, α) and the full likelihood function (4) of the observed data (Y, V) for (θ, Λ) have the following forms respectively,

$$\begin{gathered} L_c(\mathit{\theta },\mathit{\Lambda };\mathit{Y},\mathit{V},\mathit{b},\mathit{\alpha }) \\ =\prod _{i=1}^n\prod _{k=1}^K{\left[\text{exp }\right\{\sum _{j=1}^{n_i}[\frac{Y_{\mathit{\text{ij}}}({\mathit{X}}_{\mathit{\text{ij}}}\mathit{\beta }+{\stackrel{\sim }{\mathit{X}}}_{\mathit{\text{ij}}}{\mathit{b}}_{\mathit{\text{ik}}})-B(\mathit{\beta };{\mathit{b}}_{\mathit{\text{ik}}})}{A(D_i(t_j;\varphi ))}+C(Y_{\mathit{\text{ij}}};D_i(t_j;\varphi ))]\}\times (\prod _{s=1}^S{\left[{\lambda }_s{(V_i)}^{{\Delta }_i}\text{ exp }\right\{{\Delta }_i[{\stackrel{\sim }{\mathit{Z}}}_i(V_i)(\mathit{\psi }◦{\mathit{b}}_{\mathit{\text{ik}}})+{\mathit{Z}}_i(V_i)\mathit{\gamma }]-{\int }_0^{V_i}\text{ exp }\{{\stackrel{\sim }{\mathit{Z}}}_i(u)(\mathit{\psi }◦{\mathit{b}}_{\mathit{\text{ik}}})+{\mathit{Z}}_i(u)\mathit{\gamma }\}d{\Lambda }_s(u)\left\}\right]}^{I(S_i=s)})\times {(2\pi )}^{-d_b/2}{|{\mathit{\sum }}_b|}^{-1/2}\text{ exp }\{-\frac{1}{2}{({\mathit{b}}_{\mathit{\text{ik}}}-{\mathit{\mu }}_k)}^T{\mathit{\sum }}_b^{-1}({\mathit{b}}_{\mathit{\text{ik}}}-{\mathit{\mu }}_k)\}\times w_k]}^{I({\alpha }_i=k)} \end{gathered}$$

and

$$L_f(\mathit{\theta },\mathit{\Lambda };\mathit{Y},\mathit{V})=\sum _{\mathit{\alpha }}{\int }_{\mathit{b}}{L}_c(\mathit{\theta },\mathit{\Lambda };\mathit{Y},\mathit{V},\mathit{b},\mathit{\alpha })d\mathit{b}.$$

The proposed estimation method is to calculate the maximum likelihood estimates for (θ, Λ(t)) over a set of θ and Λ(t). We let each Λ_s(t) of Λ(t), s = 1, …, S, be a non-decreasing and right-continuous step function with jumps only at the observed failure times belonging to stratum s.

EM-algorithm is used for calculating the maximum likelihood estimates. In the EM-algorithm, b_i and α_i are considered as missing data for i = 1, …, n. Therefore, the M-step solves the conditional score equations from complete data given observations, where the conditional expectation can be evaluated in E-step. The procedure involves iterating between the following two steps until convergence is achieved: at the m-th iteration,

• (1) E-step Calculate the conditional expectations of some known functions of b_i and α_i, needed in the next M-step, for subject i with S_i = s given observations and the current estimate $({\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)})$. The conditional expectation is calculated using the Gauss-Hermite Quadrature numerical approximation, denoted as $E[q({\mathit{b}}_i,{\alpha }_i)|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]$ for a known function q(b_i, α_i).

• (2) M-step After differentiating the conditional expectation of complete data log-likelihood function given observations and the current estimate (θ^(m), Λ^(m)), the updated estimator (θ^(m+1), Λ^(m+1)) can be obtained as follows: (β^(m+1), ϕ^(m+1)) solves the conditional expectation of complete data log-likelihood score equation using one-step Newton-Raphson iteration; For the covariance matrix of random effects,

  $${\mathit{\sum }}_b^{(m+1)}=\frac{1}{n}\sum _{i=1}^n\sum _{s=1}^S\sum _{k=1}^K\mathrm{E}[I({\alpha }_i=k)({\mathit{b}}_{\mathit{\text{ik}}}-{\mathit{\mu }}_k){({\mathit{b}}_{\mathit{\text{ik}}}-{\mathit{\mu }}_k)}^T|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_i=s);$$

  For the k-th mixture component (k = 1, …, K),

  $${\mu }_k^{(m+1)}=\frac{{\sum }_{i=1}^n{\sum }_{s=1}^S\mathrm{E}[I({\alpha }_i=k){\mathit{b}}_{\mathit{\text{ik}}}|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_i=s)}{{\sum }_{i=1}^n{\sum }_{s=1}^S\mathrm{E}[I({\alpha }_i=k)|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_i=s)}$$

  and

  $$w_k^{(m+1)}=\frac{1}{n}{\sum }_{i=1}^n{\sum }_{s=1}^S\mathrm{E}[I({\alpha }_i=k)|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_i=s);$$

  (ψ^(m+1), γ^(m+1)) solves the partial likelihood score equation from the full data using one-step Newton-Raphson iteration,

  $$\sum _{i=1}^n\sum _{s=1}^S{\Delta }_i\left\{\right(\begin{array}{c}\hfill E[({\stackrel{\sim }{\mathit{Z}}}_i^T(V_i)◦{\mathit{b}}_i)|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]\hfill \\ \hfill {\mathit{Z}}_i\hfill \end{array})-\frac{{\sum }_{l:V_l\ge V_i}\left(\begin{array}{c}\hfill E[({\stackrel{\sim }{\mathit{Z}}}_l^T(V_i)◦{\mathit{b}}_l)\text{ exp}\{{\stackrel{\sim }{\mathit{Z}}}_l(V_i)(\mathit{\psi }◦{\mathit{b}}_l)+{\mathit{Z}}_l(V_i)\mathit{\gamma }\}|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]\hfill \\ \hfill E[{\mathit{Z}}_l(V_i)\text{ exp}\{{\stackrel{\sim }{\mathit{Z}}}_l(V_i)(\mathit{\psi }◦{\mathit{b}}_l)+{\mathit{Z}}_l(V_i)\gamma \}|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]\hfill \end{array}\right)I(S_l=s)}{{\sum }_{l:V_l\ge V_i}E[\text{exp}\{{\stackrel{\sim }{\mathit{Z}}}_l(V_i)(\mathit{\psi }◦{\mathit{b}}_l)+{\mathit{Z}}_l(V_i)\mathit{\gamma }\}|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_l=s)}\}I(S_i=s)=\mathbf{0};$$

  ${\Lambda }_s^{(m+1)}$ is obtained as an empirical function with jumps only at the observed failure time,

  $${\Lambda }_s^{(m+1)}(t)=\sum _{i:V_i\le t}\frac{{\Delta }_{i}I(S_i=s)}{{\sum }_{l:V_l\ge V_i}\mathrm{E}[\text{exp }\{{\stackrel{\sim }{\mathit{Z}}}_l(V_i)({\mathit{\psi }}^{(m+1)}◦{\mathit{b}}_l)+{\mathit{Z}}_l(V_i){\mathit{\gamma }}^{(m+1)}\}|{\mathit{\theta }}^{(m)},{\Lambda }_s^{(m)}]I(S_l=s)}.$$

  The expressions of the conditional expectation and the conditional score equations calculated in the E- and M-steps for continuous longitudinal outcomes following a normal distribution and for binary longitudinal outcomes with survival time are given in Supplementary Materials (Web Appendix A).

The observed information matrix via Louis (1982) formula is adopted to obtain the variance estimate for (θ̂, Λ̂(t)). The variance of $\sqrt{n}$ θ̂ is asymptotically equal to the corresponding sub-matrix of the inverse of the calculated observed information matrix.

3 Asymptotic Properties

In this section, we provide asymptotic properties of the proposed estimator (θ̂, Λ̂(t)) with θ̂ = (β̂^T, ϕ̂^T, Vech(Σ̂_b)^T, μ^T, w^T, ψ̂^T, γ̂^T)^T and Λ̂(t) = (Λ̂₁(t), …, Λ̂_S(t))^T, when assuming that random effects b_i follow a finite mixture of normal distributions. We need the following conditions.

• (A1)The true parameter ${\mathit{\theta }}_0={({\mathit{\beta }}_0^T,{\mathit{\varphi }}_0^T,\text{Vech}{({\mathit{\sum }}_{b0})}^T,{\mathit{\mu }}^T,{\mathit{w}}^T,{\mathit{\psi }}_0^T,{\mathit{\gamma }}_0^T)}^T$ belongs to a known compact set Θ which lies in the interior of the domain for θ.
• (A2)The distribution of random effects b_i is a mixture of a finite number of d_b-dimensional multivariate normal distributions with means $\mathit{\mu }={({\mathit{\mu }}_1^T,\dots ,{\mathit{\mu }}_K^T)}^T$ and a common covariance matrix Σ_b. i.e. ${\mathit{b}}_i~{\sum }_{k=1}^K{w}_k𝒩({\mathit{\mu }}_k,{\mathit{\sum }}_b)$, where K is the number of mixture components.
• (A3)The true baseline hazard rate function λ₀(t) = (λ₁₀(t), …, λ_S0(t)) is continuous and positive in [0, τ], where τ is the time of study end.
• (A4)For the censoring time C, P(C ≥ τ|Z, Z̃, X, X̃) = P(C = τ|Z, Z̃, X, X̃) > 0.
• (A5)For the number of observed longitudinal measurements per subject n_N, P(n_N > d_b|X, X̃) > 0 with probability one, and P(n_N ≤ n₀) = 1 for some integer n₀.
• (A6)Both X^TX and X̃^TX̃ are full rank with positive probability. Moreover, if there exist constant vectors c₁ and c₂ such that, with positive probability, for any t, Z(t)c₁ = α₀(t) and Z̃(t)◦c₂ = 0 for a deterministic function α₀(t), then c₁ = 0, c₂ = 0, and α₀(t) = 0.

Assumption (A4) means that, by the end of the study, some proportion of the subjects will still be alive and censored at the study end time τ, and thus the maximum right censoring time is equal to τ. Assumption (A5) implies that some proportion of the subjects have at least d_b longitudinal observations, and there exists an integer n₀ such that all subjects have a finite number of longitudinal observations which are not larger than n₀. Consistency and asymptotic distribution of the proposed estimator are summarized in the following two theorems.

Theorem 1

Under the assumptions (A1)~(A6), as n → ∞, the maximum likelihood estimator (θ̂, Λ̂(t)) is consistent under the product norm of the Euclidean distance and the supremum norm on [0, τ]. That is, ‖θ̂ − θ₀‖ + sup_t∈[0,τ] ‖ Λ̂(t) − Λ₀(t)‖ → 0, a.s., where $\Vert \hat{\mathit{\Lambda }}(t)-{\mathit{\Lambda }}_0(t)\Vert ={\sum }_{s=1}^S|{\hat{\Lambda }}_s(t)-{\Lambda }_{s0}(t)|$.

Theorem 2

Under the assumptions (A1)~(A6), as, n → ∞, $\sqrt{n}{({(\hat{\mathit{\theta }}-{\mathit{\theta }}_0)}^T,{(\hat{\mathit{\Lambda }}(t)-{\mathit{\Lambda }}_0(t))}^T)}^T$ weakly converges to a Gaussian random element in R^d_θ × ℓ^∞[0, τ] × ⋯ × ℓ^∞[0, τ], and the estimator θ̂ is asymptotically efficient, where d_θ is the dimension of θ and ℓ^∞[0, τ] is the normed space containing all the bounded functions in [0, τ].

The proofs of Theorems 1 and 2 follow similar steps as in Choi et al. (2013) and Zeng and Cai (2005b). However, since the distribution for random effects in our method is a finite mixture of normal distributions, some regularity conditions such as parameter identifiability and invertibility of information operators need treatment specific to our models. The latter are non-trivially different from Choi et al. (2013) and Zeng and Cai (2005b). The technical proofs are provided in the Supplementary Materials (Web Appendix B).

4 Simulation Studies

In this section, we present the results from our simulation studies. First, to assess finite sample properties of the proposed maximum likelihood estimators, two sets of simulations with different generalized linear mixed models for the longitudinal outcomes are performed. Continuous and binary data are considered for longitudinal process in the simulations in Sections 4.1 and 4.2, respectively. Then, we conduct simulation studies for examining the robustness of the assumed mixture distribution in Section 4.3. Selection procedures for the number of mixtures by AIC and BIC criteria are assessed through simulation studies in Section 4.4.

4.1 Continuous Longitudinal Outcomes and Survival Time

In this section, we assume Y_ij follow a Gaussian distribution given a subject-specific random intercept. Specifically we have

$$Y_{\mathit{\text{ij}}}={\mathit{X}}_{\mathit{\text{ij}}}\mathit{\beta }+b_i+{\epsilon }_{\mathit{\text{ij}}}={\beta }_1{X}_{1i}+{\beta }_2{X}_{2i}+{\beta }_3{X}_{3\mathit{\text{ij}}}+b_i+{\epsilon }_{\mathit{\text{ij}}},$$

for j = 1, …, n_i, where ${\epsilon }_{\mathit{\text{ij}}}~𝒩(0,{\sigma }_y^2)$, and

$$h(t|b_i)=\lambda (t)\text{ exp}\{\psi b_i+{\mathit{Z}}_i(t)\mathit{\gamma }\}=\lambda (t)\text{exp}\{\psi b_i+{\gamma }_1{Z}_{1i}+{\gamma }_2{Z}_{2i}\},$$

where $b_i~{\sum }_{k=1}^K{w}_k𝒩({\mu }_k,{\sigma }_b^2)$, K is the number of mixture components, and K = 2 and K = 3 are simulated. X_1i ≡ Z_1i are generated from a Bernoulli distribution with success probability being 0.5, and X_2i ≡ Z_2i are simulated from the uniform distribution between 0 and 1. They are included in both hazard and longitudinal models. There is one additional covariate denoted as X_3ij, the time at measurement, which is a time-dependent variable included in the longitudinal model. We suppose the longitudinal data are observed for every 0.1 unit of time, and thus X_3ij has the value of every 0.1 unit ranging over 0 through 2.4. The average number of longitudinal observations (n_i) per subject is 7–8 with the range of 1 to 24. To generate the survival time, we first generate u_i from uniform (0,1) distribution. For a given hazard function λ, the survival time is then generated by t_i = −log(u_i) × exp{−(ψb_i+γ₁Z_1i+γ₂Z_2i)}/λ. Censoring time is generated from the uniform distribution between 0.4 and 2.4 so that the censoring proportion is around 25~35%. The observed survival time is obtained by the minimum of the generated survival and censoring times. For summarizing the performance of the estimated baseline cumulative hazards over simulations, we consider three time points: 0.9, 1.4, and 1.9, which correspond to the quartiles of the true survival distribution.

We consider ψ = −0.1 indicating negative dependency between longitudinal process and survival time model. The parameters in the longitudinal and hazard models are chosen as β₁ = 1, β₂ = −0.5, β₃ = −0.2, ${\sigma }_y^2=0.5$, ψ = −0.1, γ₁ = −0.1, γ₂ = 0.1, and λ(t) = 1. The parameters in the mixture distribution for random effects are μ₁ = −1.5, μ₂ = 1.5, and w₁ = 0.4 for K = 2 and μ₁ = −3, μ₂ = 0, μ₃ = 3, w₁ = 0.4, and w₂ = 0.3 for K = 3. The weight of the last mixture component (w₂ and w₃ for K = 2 and K = 3 respectively) is determined from the restriction ${\sum }_{k=1}^K{w}_k=1$. The variance of random effects ${\sigma }_b^2$ is chosen as 0.3. Different sample sizes (n=400, 800) are simulated with 1000 replications. The results of the maximum likelihood estimates for $\mathit{\theta }={({\mathit{\beta }}^T,{\sigma }_y^2,{\mathit{\mu }}^T,{\mathit{w}}^T,{\sigma }_b^2,\psi ,{\mathit{\gamma }}^T)}^T$ and the baseline cumulative hazards at the three time points and their respective standard error estimates are reported in Table 1. The simulation study is conducted using R. In Table 1, “True” gives the true values of parameters; the averages of the maximum likelihood estimates from the EM algorithm are in “Est.”; the sample standard deviations from 1000 simulations are reported in “SSD”; “ESE” is the average of 1000 standard error estimates based on the observed information matrix; “CP” is the coverage proportion of 95% confidence intervals based on the estimated standard error “ESE”. Satterthwaite (1946) method is used for the coverage probabilities of ${\sigma }_y^2$ and ${\sigma }_b^2$.

Table 1.

Summary of simulation results of maximum likelihood estimation using mixtures of Gaussian distributions for random effects in the joint modeling of continuous longitudinal outcomes and survival time.

			n=400				n=800
Mixture	Par.	True	Est.	SSD	ESE	CP	Est.	SSD	ESE	CP
2	β 1	1.0	.983	.066	.068	.958	.985	.047	.048	.947
	β 2	− .5	− .529	.107	.119	.969	− .540	.079	.084	.947
	β 3	− .2	− .203	.033	.033	.955	− .203	.024	.024	.952
	${\sigma }_y^2$	.5	.500	.014	.014	.954	.500	.010	.010	.948
	μ 1	−1.5	−1.478	.081	.088	.962	−1.469	.060	.062	.938
	μ 2	1.5	1.524	.075	.082	.966	1.530	.055	.058	.940
	w 1	.4	.400	.025	.033	.991	.401	.018	.023	.981
	${\sigma }_b^2$	.3	.296	.029	.029	.955	.298	.020	.020	.958
	ψ	− .1	− .102	.040	.039	.950	− .100	.028	.028	.946
	γ 1	− .1	− .101	.123	.121	.945	− .105	.085	.085	.952
	γ 2	.1	.102	.209	.210	.954	.096	.144	.147	.950
	Λ(.9)	.9	.911	.130	.128	.950	.909	.087	.090	.955
	Λ(1.4)	1.4	1.421	.206	.202	.942	1.415	.139	.141	.952
	Λ(1.9)	1.9	1.939	.304	.295	.953	1.924	.205	.205	.950
3	β 1	1.0	.983	.070	.071	.947	.984	.049	.050	.956
	β 2	− .5	− .543	.116	.123	.952	− .543	.085	.087	.922
	β 3	− .2	− .203	.034	.034	.949	− .204	.024	.024	.960
	${\sigma }_y^2$	.5	.500	.014	.014	.957	.500	.010	.010	.950
	μ 1	−3.0	−2.970	.084	.090	.954	−2.968	.064	.063	.909
	μ 2	.0	.028	.093	.097	.954	.032	.069	.068	.933
	μ 3	3.0	3.030	.089	.094	.954	3.034	.063	.066	.925
	w 1	.4	.400	.025	.033	.992	.400	.018	.023	.983
	w 2	.3	.299	.024	.029	.980	.300	.017	.020	.977
	${\sigma }_b^2$	.3	.295	.029	.029	.956	.298	.021	.021	.946
	ψ	− .1	− .101	.024	.024	.956	− .101	.017	.017	.941
	γ 1	− .1	− .091	.112	.119	.963	− .096	.085	.084	.950
	γ 2	.1	.088	.215	.207	.946	.114	.146	.146	.944
	Λ(.9)	.9	.913	.125	.127	.948	.897	.088	.088	.951
	Λ(1.4)	1.4	1.417	.202	.200	.949	1.402	.141	.140	.949
	Λ(1.9)	1.9	1.928	.297	.292	.946	1.908	.206	.204	.948

From Table 1, we can see that even for the smaller sample size (n=400), the bias of the estimates from EM algorithm is negligible for most cases. The estimated standard errors calculated from the observed information matrix are close to the sample standard deviations from the 1000 estimates, and the 95% confidence interval coverage rates are close to 0.95 except for weights of the mixture components. The coverage rates of weights are improved for larger sample size in both 2 and 3 mixtures. The estimates for the parameters in the longitudinal and hazards models (β, ${\sigma }_y^2$, ψ, γ and Λ(t)) perform well for different mixtures.

4.2 Binary Longitudinal Outcomes and Survival Time

In this section, we assume that Y_ij is a binary outcome following

$$P(Y_{\mathit{\text{ij}}}=y_{\mathit{\text{ij}}}|b_i)=\text{exp }\{y_{\mathit{\text{ij}}}{\eta }_{\mathit{\text{ij}}}-\text{log}(1+\text{exp}\{{\eta }_{\mathit{\text{ij}}}\})\},y_{\mathit{\text{ij}}}=0,1,$$

with η_ij = X_ijβ+b_i = β₁X_1i+β₂X_2i+β₃X_3ij+b_i for j = 1, …, n_i, and we consider the same hazards model and simulation setting as those used in Section 4.1 except the followings. The parameters in the mixture distribution for random effects are μ₁ = −3, μ₂ = 3, and w₁ = 0.4 for K = 2 and μ₁ = −6, μ₂ = 0, μ₃ = 6, w₁ = 0.4, and w₂ = 0.3 for K = 3. The binary longitudinal data are generated for every 0.1 and 0.05 units of time for the mixture of 2 and 3 normal distributions, respectively, and X_3ij, the time at measurement, has the values of every 0.1 and 0.05 units corresponding to the mixture distributions ranging over 0 through 2.4. Thus, the average numbers of longitudinal observations (n_i) are 7–8 with the range of 1 to 24 and 15–16 with the range of 1 to 48 for the mixture of 2 and 3 distributions, respectively.

The results of the maximum likelihood estimates for $\mathit{\theta }={({\mathit{\beta }}^T,{\mathit{\mu }}^T,{\mathit{w}}^T,{\sigma }_b^2,\psi ,{\mathit{\gamma }}^T)}^T$ and baseline cumulative hazards at the given three time points and their respective standard error estimates are reported in Table 2. Similar to the results for the continuous longitudinal outcomes, Table 2 shows that overall the estimates perform well even for the smaller sample size n = 400 with small biases. The parameters of interest in longitudinal and hazards models have the estimated standard errors which are close to the sample standard deviations. Meanwhile, the estimated standard errors of the parameters of mixture components which are means of random effects and weights appear to be overestimated being larger than their sample standard deviations, which leads to the wide confidence interval.

Table 2.

Summary of simulation results of maximum likelihood estimation using mixtures of Gaussian distributions for random effects in the joint modeling of binary longitudinal outcomes and survival time.

			n=400				n=800
Mixture	Par.	True	Est.	SSD	ESE	CP	Est.	SSD	ESE	CP
2	β 1	1.0	1.029	.193	.201	.960	1.015	.143	.141	.942
	β 2	− .5	− .508	.292	.323	.966	− .495	.205	.227	.965
	β 3	− .2	− .200	.166	.180	.966	− .203	.116	.127	.968
	μ 1	−3.0	−3.046	.241	.275	.968	−3.034	.164	.193	.970
	μ 2	3.0	3.016	.211	.253	.976	3.011	.142	.177	.984
	w 1	.4	.401	.025	.033	.993	.400	.017	.023	.991
	${\sigma }_b^2$	.3	.329	.133	.195	.940	.332	.092	.136	.956
	ψ	− .1	− .099	.021	.021	.949	− .099	.015	.015	.955
	γ 1	− .1	− .103	.121	.122	.959	− .098	.087	.086	.947
	γ 2	.1	.091	.210	.211	.944	.104	.142	.149	.958
	Λ(.9)	.9	.910	.131	.130	.955	.900	.088	.091	.956
	Λ(1.4)	1.4	1.421	.209	.206	.934	1.402	.142	.143	.956
	Λ(1.9)	1.9	1.932	.310	.299	.941	1.899	.205	.207	.948
3	β 1	1.0	.988	.167	.171	.953	.993	.123	.121	.947
	β 2	− .5	− .519	.268	.287	.960	− .516	.189	.203	.967
	β 3	− .2	− .208	.126	.128	.957	− .206	.091	.091	.951
	μ 1	−6.0	−5.844	.353	.483	.967	−5.872	.260	.342	.963
	μ 2	.0	.023	.172	.194	.970	.018	.127	.138	.966
	μ 3	6.0	6.024	.397	.504	.984	6.006	.303	.349	.971
	w 1	.4	.402	.025	.035	.995	.402	.018	.024	.989
	w 2	.3	.298	.025	.034	.986	.298	.017	.024	.985
	${\sigma }_b^2$	.3	.277	.095	.100	.977	.289	.070	.072	.966
	ψ	− .1	− .102	.014	.015	.955	− .101	.011	.010	.946
	γ 1	− .1	− .103	.121	.120	.955	− .107	.085	.084	.948
	γ 2	.1	.104	.201	.208	.961	.099	.147	.146	.949
	Λ(.9)	.9	.909	.128	.130	.950	.911	.094	.092	.930
	Λ(1.4)	1.4	1.421	.202	.207	.960	1.420	.147	.146	.946
	Λ(1.9)	1.9	1.926	.297	.302	.958	1.929	.220	.213	.946

4.3 Sensitivity for Model-Misspecification

In this section, we conduct simulation studies to examine the sensitivity of the assumed mixture distribution. We consider continuous longitudinal outcomes and survival time with the same setting used in Section 4.1 except for the true distribution of random effects. Random effects are generated from a mixture of a t-distribution with 10 degrees of freedom and non-centrality of −1 and a Gamma distribution with shape and scale parameters of 7 and 1/8 respectively. We assume equal probability for the two distributions. We fit 5 sets of simultaneous models assuming different mixtures for random effects which are 1 normal distribution without mixture and the mixtures of 2, 3, 4 and 5 normal distributions, and we compare the results for the parameters of interest in longitudinal and hazards models and the estimated density plots of random effects. Table 3 shows the results of longitudinal and hazards models from assuming the 5 different models for random effects. As the number of mixtures increases, the changes in bias and coverage rate are more pronounced in the longitudinal model than in the hazards model; it is clear that bias gets smaller and coverage rates become closer to the 95% nominal level in the longitudinal model while biases are similarly small and coverage rates are close to the nominal level over all assumed distributions. From the table, we also find that bigger number of mixtures produces estimates that are closer to the true values in the longitudinal model while estimates in hazards model are less sensitive to the number of distributions in mixture. In other words, when the true distribution of random effects is not a Gaussian distribution, the use of mixture is effective in longitudinal model while the inference on hazards model is reasonable regardless of mixture.

Table 3.

Summary of simulation results of sensitivity for model-misspecification

		1 Normal distribution				Mixture of 2 Normal distributions
Par.	TRUE	Est.	SSD	ESE	CP	Est.	SSD	ESE	CP
Longitudinal model
β 1	1.0	.947	.085	.095	.931	.965	.074	.074	.928
β 2	− .5	− .591	.122	.164	.975	− .582	.118	.128	.933
β 3	− .2	− .203	.024	.025	.964	− .202	.024	.025	.961
${\sigma }_y^2$	.5	.501	.010	.010	.948	.501	.010	.010	.948
Hazards model
ψ	− .1	− .102	.034	.033	.942	− .101	.034	.033	.943
γ 1	− .1	− .093	.083	.085	.949	− .095	.083	.084	.953
γ 2	.1	.107	.144	.147	.949	.105	.144	.147	.949
Λ(.9)	.9	.906	.089	.089	.943	.907	.089	.089	.944
Λ(1.4)	1.4	1.408	.139	.140	.945	1.409	.139	.140	.945
Λ(1.9)	1.9	1.911	.202	.203	.956	1.911	.202	.203	.956
		Mixture of 3 Normal distributions				Mixture of 4 Normal distributions
Par.	TRUE	Est.	SSD	ESE	CP	Est.	SSD	ESE	CP
Longitudinal model
β 1	1.0	.977	.061	.060	.935	.978	.061	.060	.934
β 2	− .5	− .557	.101	.105	.930	− .555	.101	.104	.928
β 3	− .2	− .202	.024	.024	.961	− .202	.024	.024	.959
${\sigma }_y^2$	.5	.501	.010	.010	.950	.501	.010	.010	.952
Hazards model
ψ	− .1	− .101	.034	.033	.941	− .101	.034	.033	.940
γ 1	− .1	− .096	.083	.084	.954	− .096	.083	.084	.951
γ 2	.1	.103	.143	.146	.951	.102	.143	.146	.951
Λ(.9)	.9	.906	.089	.089	.945	.907	.089	.089	.943
Λ(1.4)	1.4	1.408	.139	.140	.947	1.409	.139	.140	.946
Λ(1.9)	1.9	1.910	.200	.203	.958	1.911	.202	.203	.956
		Mixture of 5 Normal distributions
Par.	TRUE	Est.	SSD	ESE	CP
Longitudinal model
β 1	1.0	.985	.055	.054	.943
β 2	− .5	− .536	.092	.095	.928
β 3	− .2	− .202	.024	.024	.955
${\sigma }_y^2$	.5	.500	.010	.010	.946
Hazards model
ψ	− .1	− .102	.034	.033	.945
γ 1	− .1	− .098	.085	.084	.948
γ 2	.1	.108	.144	.146	.952
Λ(.9)	.9	.904	.090	.089	.944
Λ(1.4)	1.4	1.403	.137	.139	.947
Λ(1.9)	1.9	1.905	.200	.202	.954

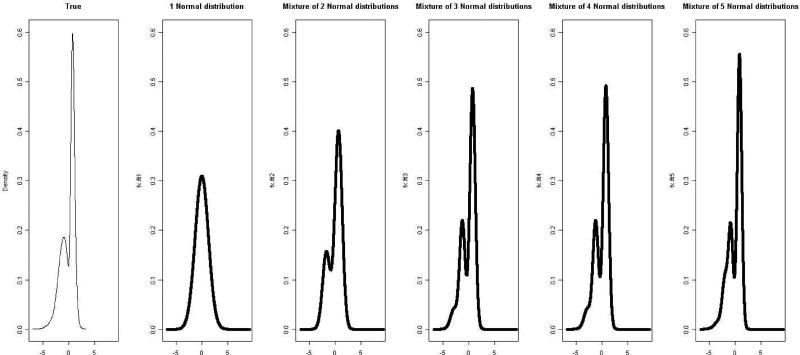
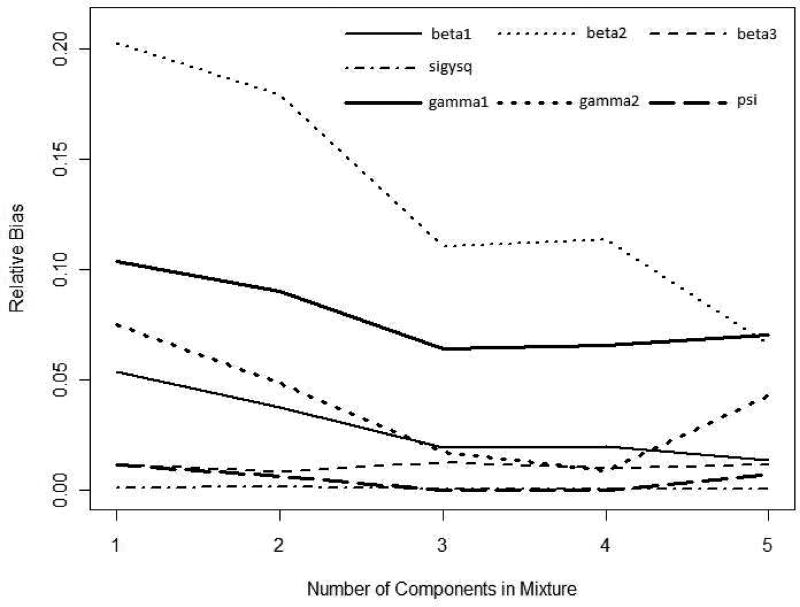
Figure 1 shows the true and estimated density plots of random effects. From these density plots, all the mixture models of 2, 3, 4 and 5 normal distributions produces similar shapes to the true distribution while one normal distribution does not. The mixture of 5 normal distribution appears to be close to the true density. Figure 2 shows the relative bias plot of the parameters in longitudinal and hazard models which are denoted with thin and thick lines respectively. The relative biases are calculated from the median absolute biases divided by their absolute true values. Figure 2 confirms what we observe in Table 3.

Fig. 1.

Density plots from simulation results of sensitivity for model-misspecification

Fig. 2.

Relative bias plot of parameters in longitudinal and hazard models (thin and thick lines respectively) from simulation results of sensitivity for model-misspecification

For further investigation of the sensitivity to model-misspecification, we conducted additional simulations under another true mixture distribution of random effects – the mixture of non-central t₂₀(−2) and Gamma(7, 1/8) – which is more deviated from normal distribution, with heavier tailed and more left-shifted t-distribution in mixture. We fit the same 5 sets of simultaneous models assuming different mixtures for random effects which are 1 normal distribution with no mixture and the mixtures of 2, 3, 4 and 5 normal distributions. Their results, density plots and relative bias plots are provided in the Supplementary Materials (Table 1 and Figures 1 and 2 of Web Appendix D.1). Although the results show slightly bigger biases and inconsistent coverage rates when compared to those for the original true mixture, overall trends appear to be similar. The overall conclusion appears to be similar.

4.4 Selection of the Number of Mixture Distributions

We adopt AIC and BIC for selection of the number of normal distribution in mixture and assess these selection procedures through simulation studies in this section. AIC gives a penalty to a model with more parameters and BIC gives a penalty to a model with more parameters and larger sample size. Given a data set, competing models are ranked according to their AIC (or BIC), with the one having the lowest AIC (or BIC) being the best. Chen and Kalbeisch (1996), who proposed a method for consistent estimation for the mixing distribution and the number of mixture components, mentioned that different penalty methods will provide similar results in many instances and also the application results by their method were consistent to those by AIC and BIC. Thus, the use of AIC and BIC will be a reasonable choice.

Continuous longitudinal outcomes and survival time are considered with the same setting used in Section 4.1. Random effects are generated from a mixture of 3 normal distributions. We fit 5 sets of simultaneous models with different mixtures for random effects which are 1 normal distribution without mixture and the mixtures of 2, 3, 4 and 5 normal distributions. AIC and BIC values are calculated for all 5 fitted mixture models in each data set and we report frequencies of mixture models selected as best by AIC and BIC among 1000 data sets. Sample sizes of 200 and 800 are considered.

The result shows that for the sample size of 200 both AIC and BIC mostly select the true distribution of a mixture of 3 normal distributions as best – 969 and 990 out of 1000 simulated data sets, respectively. For the large sample size of 800, the mixture of 3 normal distributions is selected by both AIC and BIC for all 1000 simulated data sets. This demonstrates that the number of mixture distributions is properly selected by AIC and BIC even for small sample sizes.

5 Analysis of the CHANCE Study

The Carolina Head and Neck Cancer Study (CHANCE) is a population based epidemiologic study conducted at 60 hospitals in 46 counties in North Carolina from 2002 through 2006 (Divaris et al. 2010). Patients were diagnosed with head and neck cancer (oral, pharynx, and larynx cancer) from 2002–2006. Their survival status was collected up to 2007 and their Quality of Life (QoL) was evaluated over time for three years after diagnosis. QoL information was collected through questionnaires. Based on summary scores of the five domains of self-perceived quality of life including Physical Well-Being (PWB), Social/Family Well-Being (SWB), Emotional Well-Being (EWB), Functional Well-Being (FWB) and Head and Neck Cancer Specific symptoms (HNCS), patient’s QoL information was classified into satisfaction or dissatisfaction with life. Survival time is defined as the time to death from diagnosis. Demographic and life style characteristics, medical histories and clinical factors are also collected. Ending in December 2007, information on QoL has been obtained from 554 head and neck cancer patients in the analysis. Based on the death information through 2007 available from the National Death Index (NDI), 85 of 554 patients died and the censoring rate is 85%. All censoring was due to the termination of study and thus the noninformative censoring assumption is appropriate for this study. The number of observations per patient ranges 1 to 3 with average of 1.93. It is of interest to elucidate the variables which are associated with both QoL satisfaction and survival time for patients with head and neck cancer. In particular, we are interested in the comparison between African-Americans and Whites since it is known that African-Americans have a higher incidence of head and neck cancer and worse survival than Whites. The longitudinal QoL satisfaction outcomes and survival time are correlated within a patient, and this dependency should be taken into account in the analysis.

We apply our proposed method to Head and Neck Cancer Specific symptoms (HNCS) among QoL domains with survival time. Longitudinal HNCS QoL outcomes are binary measurements with 1 (“satisfied”) and 0 (“dissatisfied”). We are interested in investigating which factors are related to QoL satisfaction and the risk of death. In the full models for both longitudinal QoL and survival time, we consider race (African-Americans, Whites), the number of 12 oz. beers consumed per week (None, <1, 1–4, 5–14, 15–29, ≥ 30), household income (0–10K, 20–30K, 40–50K, ≤ 60K), surgery (Yes/No), radiation therapy (Yes/No), chemotherapy (Yes/No), primary tumor site (Oral & Pharyngeal, Laryngeal) and tumor stage (I, II, III, IV) as categorical, and age at diagnosis (range: 24–80), the number of persons supported by household income (range: 1–5), body mass index (BMI) (range: 15.66–56.28) and the total number of medical conditions reported (range: 0–6) as continuous. Additionally, 2 interactions with race, i.e. race × the total number of medical conditions reported and race × tumor site, are included in both models since we are particularly interested in the difference of QoL and survival between African American and White. Time at survey measurement is included as a time-dependent covariate for the longitudinal QoL outcome. A random intercept for the dependence between the QoL satisfaction and the risk of death is included in both models and assumed to follow an unknown distribution.

For the full model, we first considered 5 different distributions for random effects which are 1 normal distribution without mixture and the mixtures of 2, 3, 4 and 5 normal distributions, and both AIC and BIC selected a mixture of 3 normal distributions with their lowest values as best. Then, we conducted backward variable selection based on the Likelihood Ratio Test (LRT) from the full model using a mixture of 3 normal distributions for approximating the random effect. Table 4 gives the results from the final models after removing non-significant covariates by LRT. From the “Simultaneous” columns, we see the number of 12 oz. beers consumed per week, household income and tumor stage are significantly associated with both patients’ HNCS QoL satisfaction and hazard of death. Using 30 or more of 12 oz. beers consumed per week as the reference group, all categories of the smaller amount are in general associated with higher odds of being satisfied while the categories of ‘none’ and ‘5 to 14’ of 12 oz. beers consumed per week are associated with lower risk of death. Higher household income is generally associated with higher odds of being satisfied and lower risk of death. Both patients’ HNCS QoL satisfaction and risk of death are significantly different for patients in different tumor stages. On the other hand, race (African-American), radiation therapy, the number of persons supported by household income, and BMI are selected only in the HNCS QoL longitudinal model while the number of medical conditions reported is significant only in the hazard model. The results indicate that African-Americans, patients not treated with radiation therapy, patients in the family with the smaller number of persons supported by household income, or patients with higher BMI are associated with higher odds of being satisfied, but the risk of death is not affected by these factors. On the other hand, higher number of reported medical conditions is associated with higher risk of death, but it is not associated with HNCS QoL satisfaction. Furthermore, time at survey measurement is statistically significant in the HNCS QoL longitudinal model implying that patients have higher odds to be satisfied over time. The parameter ψ for the dependence between longitudinal HNCS QoL and survival time is negative and is statistically significant with p-value as 0.008. This means the longitudinal HNCS QoL and survival time are correlated and some latent factors which increase HNCS QoL satisfaction also decrease the risk of death. Although not provided in Table 4, we have additional parameters of the mixture distribution for random effects in the simultaneous modeling. The obtained estimates of three means of random effects are −3.146, 0.376 and 1.730 with their estimated mixing probabilities of 0.147, 0.105 and 0.748, respectively, and the common variance estimate of random effects is 0.637. In particular, the mixing probabilities are significant at significance level 0.05, which strengthens the mixture of 3 normal distributions with the estimated 3 means of random effects.

Table 4.

Results from final models of simultaneous and separate analyses for the Quality of Life and survival time for the CHANCE study

		Simultaneous			Separate†
Parameter		Est.	ESE	P-value	Est.	ESE	P-value
HNCS QoL longitudinal model
Intercept	β 0				1.190	.390	.002
Race (ref= White): African American	β 1	.900	.399	.024	.511	.256	.047
# of 12 oz. beers consumed per week (ref=30 or more)
– None	β 2	.858	.428	.045	.622	.300	.038
– less than 1	β 3	1.119	.600	.062	.735	.396	.064
– 1 to 4	β 4	1.588	.563	.005	1.268	.326	<.001
– 5 to 14	β 5	1.450	.428	.001	1.018	.279	<.001
– 15 to 29	β 6	1.007	.531	.058	.547	.327	.095
Household income (ref= level1: 0–10K)
– level2: 20–30K	β 7	− .337	.358	.346	− .328	.258	.204
– level3: 40–50K	β 8	.633	.440	.151	.250	.282	.376
– level4: ≥ 60K	β 9	1.960	.509	<.001	1.045	.286	<.001
Radiation therapy (ref= No) : Yes	β 10	−1.668	.608	.006	−1.048	.280	<.001
Tumor stage (ref= I)
– II	β 11	− .683	.554	.218	− .352	.330	.286
– III	β 12	−2.012	.534	<.001	−1.198	.314	<.001
– IV	β 13	−1.826	.507	<.001	−1.057	.277	<.001
# of persons supported by household income	β 14	− .388	.140	.006
BMI	β 15	.061	.026	.021
Time at survey measurement (years)	β 16	.354	.093	<.001	.254	.067	<.001
Hazards model
Random effect coefficient	ψ	− .206	.078	.008
# of 12 oz. beers consumed per week (ref=30 or more)
– None	γ 1	− .705	.347	.042
– less than 1	γ 2	− .156	.393	.692
– 1 to 4	γ 3	− .712	.385	.064
– 5 to 14	γ 4	− .991	.348	.004
– 15 to 29	γ 5	− .579	.370	.117
Household income (ref= level1: 0–10K)
– level2: 20–30K	γ 6	− .206	.274	.453	− .219	.263	.406
– level3: 40–50K	γ 7	− .884	.341	.010	− .928	.331	.005
– level4: ≥ 60K	γ 8	−1.401	.374	<.001	−1.393	.358	<.001
Tumor stage (ref= I)
– II	γ 9	− .255	.443	.564	− .295	.435	.498
– III	γ 10	.168	.403	.677	.136	.389	.727
– IV	γ 11	.950	.306	.002	.914	.295	.002
Total # of medical conditions reported	γ 12	.207	.095	.030	.205	.091	.025

P-value for testing ${\sigma }_b^2$ being zero is based on a mixture of 0 and χ² distribution with 1 degree of freedom with equal mixing probabilities.

^†Standard packages assuming one normal component for random effects were used for separate model fit.

For the purpose of comparison, we also conducted separate analyses for longitudinal HNCS QoL and survival time whose results are given in the last three columns of Table 4. Comparing the results from the simultaneous and separate analyses in Table 4, we can see our simultaneous analysis identifies two additional factors (the number of persons supported by household income and BMI) in the HNCS QoL longitudinal model and one additional factor (the number of 12 oz. beers consumed per week) in the hazard model.

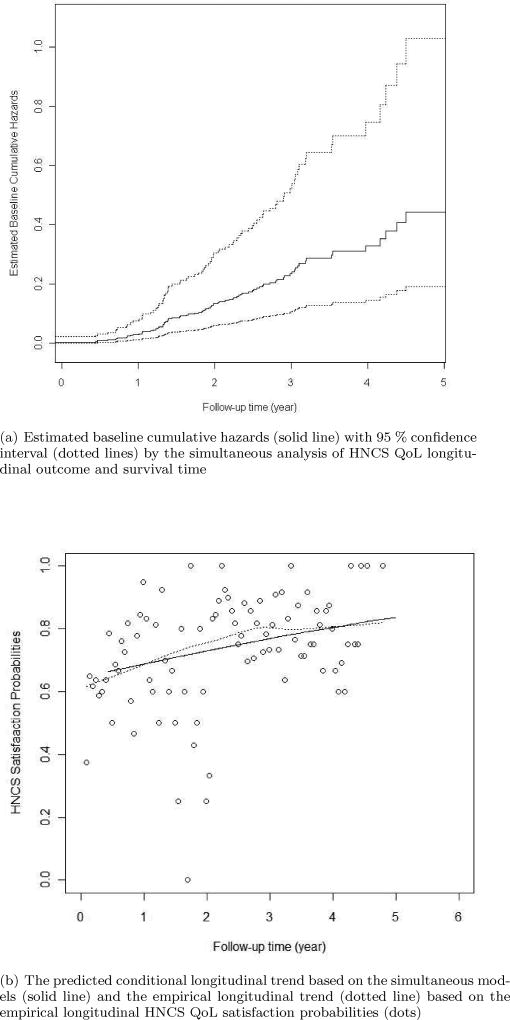
Figure 3(a) shows the estimated baseline cumulative hazard rates over follow-up time with 95% confidence interval. The estimated baseline cumulative hazard rates look at at the very early time within a year, but soon appear to be linearly increasing. Figure 3(b) shows the predicted conditional longitudinal trend of HNCS QoL satisfaction probabilities based on the simultaneous models (solid line) and the empirical longitudinal trend of HNCS QoL satisfaction probabilities (dotted line) based on the empirical longitudinal HNCS QoL satisfaction probabilities (dots). The predicted conditional probability of HNCS QoL satisfaction is calculated as the conditional expectation of the conditional probability of HNCS QoL satisfaction given the subject is alive at time t. That is, E_b,α [P(Y(t) = 1|T > t) | θ̂, Λ̂] using model notations in Section 2. The empirical probability of HNCS QoL satisfaction is calculated for every 0.05 unit of time at survey measurements. From Figure 3(b), the longitudinal trend of HNCS QoL satisfaction probabilities appears to be increasing over time and the empirical probabilities also gradually increase over time.

Fig. 3.

Plots of the CHANCE study analysis

We also applied the rest four unselected distributions for random effects – one normal distribution without mixture and the mixtures of 2, 4 and 5 normal distributions – to the final simultaneous models derived under the mixture of 3 normal distributions and compared their results (provided in the Supplementary Materials – Tables 2–5, respectively, of the Web Appendix D.2) to those in Table 4. Most of the covariates in the final models yielded same conclusions under different distributions assumed for random effects except one covariate. The detail is given in Paragraph 1 of the Web Appendix D.2. On the other hand, overall, the estimates for same variables are similar under all mixtures but slightly different from those under one normal distribution.

In addition, we conducted simulations under the settings similar to the CHANCE data with the high censoring rate = 85% and the low average number of longitudinal observations per patient (n_i) = 1.93, and we compared the results to the simulation studies presented in Section 4.2. The results given in the Supplementary Materials (Table 6 of Web Appendix D.2) are for the mixture of 2 distributions, sample size (n) of 400, and ${\sigma }_b^2=0.5$ from 1000 data sets. Due to very sparse events, about 17% of the simulated datasets did not converge or encountered problems with variance estimation. Thus, the table only reports the convergent cases and the results show that the bias is reasonably small and that the coverage probabilities are reasonable, although conservative for the coefficients in the longitudinal model. The numerical issues on convergence and variance estimation occurred more for the larger number of mixture components but were recovered for the increased n and n_i and the decreased censoring rate, ${\sigma }_b^2$ and number of predictors included in the joint models.

6 Concluding Remarks

We have relaxed normality assumption of random effects in the simultaneous modeling of longitudinal outcomes and survival time. Assuming the underlying distribution of random effects to be unknown, we used a mixture of Gaussian distributions as an approximation for the random effect distribution. We developed a maximum likelihood estimation method for the proposed simultaneous models and presented asymptotic properties of the proposed estimators. The proposed estimation procedure using EM algorithm has been assessed via simulation studies for both continuous and binary longitudinal data with survival time. The proposed estimates performed well in finite samples. The variance estimates based on the observed information matrix approximate the true variance well in finite samples. Simulation studies indicated that, when the true distribution of random effects is not normal, mixture distributions yield less biased estimates than no mixture and all the estimated density plots of random effects based on mixture distributions appear to have similar shapes to the true distribution. Furthermore, simulation studies also showed that the number of mixture distributions is properly selected by AIC and BIC. The proposed method was applied to data from the CHANCE study.

Consideration of general distributions other than normal distribution in joint modelling is novel. Our method demonstrates the better fit of the real data using 3 mixture distributions, as compared to existing approaches which rely on one single normal random effect.

Alternatively, one may consider the seminonparameteric (SNP) method which is another way to approximate non-normal distributions. However, using mixture normal distributions has a better computational advantage. As described in Section 2, we can treat random effects as a mixture of multiple independent normal variables so the EM algorithm can be easily coined to facilitate computation. In contrast, SNP density does not have this property so the computation has to directly maximize the likelihood function, which is highly nonlinear, over a large number of parameters. Developing the SNP method can be a worthwhile effort for future work.

One generalization of the proposed model is to allow both random intercept and random slope. In this case, we can consider a bivariate mixture normal distribution to approximate their joint distribution. However, the computation will be much more intense due to the higher dimensional numerical integration in the E-step and the increased number of the mixing components. Alleviating the computational intensity of the method for high dimensional random effects will be an interesting topic of investigation of further study.

When estimating variances by the Louis method (1982) as employed in this paper, the information matrix may not be positive definite. This could be due to relatively sparse events because of high censoring or large number of covariates in the model. When there is a problem in estimating the variance, one alternative approach is to use bootstrap method, although bootstrap method is computationally intensive.

7 Supplementary Materials

EM algorithm referenced in Sections 2.2 and technical proofs for Theorem 1 and Theorem 2 referenced in Section 3 are provided in Electronic Supplementary Materials.