Correlations in Scattered X-Ray Laser Pulses Reveal Nanoscale Structural Features of Viruses

Abstract

We use extremely bright and ultrashort pulses from an x-ray free-electron laser (XFEL) to measure correlations in x rays scattered from individual bioparticles. This allows us to go beyond the traditional crystallography and single-particle imaging approaches for structure investigations. We employ angular correlations to recover the three-dimensional (3D) structure of nanoscale viruses from x-ray diffraction data measured at the Linac Coherent Light Source. Correlations provide us with a comprehensive structural fingerprint of a 3D virus, which we use both for model-based and ab initio structure recovery. The analyses reveal a clear indication that the structure of the viruses deviates from the expected perfect icosahedral symmetry. Our results anticipate exciting opportunities for XFEL studies of the structure and dynamics of nanoscale objects by means of angular correlations.

Graphical Abstract

Since the original idea to image individual biomolecules with intense ultrashort x-ray pulses was proposed [1,2], its practical implementation for materials research and structural biology applications has become one of most attractive challenges at x-ray free-electron lasers (XFELs) [3–5]. It was predicted that diffraction patterns from single particles could be measured in “diffraction before destruction” experiments before the sample is destroyed by intense radiation [2,6–9], and, hence, their damage-free structure could be discerned. Substantial technological achievements have now made it possible to perform such measurements [10–13]. Together with recent algorithmic developments for data recognition and classification [14–17], orientation determination [18–23], and phase retrieval [24–26], these achievements have allowed for the advancement of the single-particle coherent x-ray diffraction imaging [12,27] technique at XFELs from 2D applications for rather large samples [28,29] towards 3D imaging of nanoscale objects [11–13]. However, the image resolution of reconstructed biological samples demonstrated so far has been limited; thus, further theoretical and experimental efforts are needed to establish single-particle imaging (SPI) techniques at XFELs [30].

Alternative methods for structural characterization of bioparticles at XFELs are of great interest [31]. Serial femtosecond crystallography (SFX) at XFELs offers outstanding possibilities for structure determination of samples that can be crystallized [32,33]. In contrast, the fluctuation x-ray scattering (FXS) technique [34,35] aims to recover the structure of a single particle from a translationally and rotationally disordered ensemble of many reproducible particles by using pulse lengths below the particles’ rotational diffusion times [34–40]. This technique is based on the analysis of angular cross-correlation functions (CCFs) from intensity fluctuations measured from a finite number of particles in the beam, yielding an information content far beyond what can be obtained using traditional small- and wide-angle scattering techniques. FXS is expected to be especially advantageous for weakly scattering objects that cannot be crystallized, and can potentially close the gap between SPI and SFX techniques, especially in the time-resolved domain [41,42].

Recently, it has been demonstrated that the FXS approach can be used to reconstruct the structure of an individual object from a 2D disordered ensemble of reproducible objects [43–45]. Unfortunately, an effective algebraic formalism of the CCFs developed for the 2D case [43] cannot be directly applied when particles can have arbitrary positions and orientations in 3D space. Therefore, additional assumptions or symmetry constraints are typically required to determine the 3D structure of a particle [38,46–50]. A substantial theoretical advance in this direction has been recently achieved by demonstrating that single-particle electron density can be reconstructed from comparably limited FXS information by means of a multitiered iterative phasing (MTIP) algorithm [40]. MTIP is an extension of standard iterative phasing methods that concurrently recovers the real-space 3D structure and its reciprocal-space intensity directly from the FXS data, without applying symmetry constraints. In this Letter, we employed angular cross-correlations for model-based analysis as well as ab initio structure recovery using MTIP, for SPI data of aerosolized viruses measured at the Linac Coherent Light Source (LCLS).

We applied the FXS approach to single-particle scattering data, which can be considered the limiting case of a dilute solution with one particle in the x-ray beam [46–48]. The key idea to employ the CCFs for structure recovery is based on the fact that orientationally averaged CCFs preserve higher-order information about a 3D object as compared to conventional small-angle x-ray scattering (SAXS) [51,52]. Here we applied the two-point CCF C_ij(q₁, q₂, Δ)=〈I_i(q₁, φ)I_j(q₂, φ+Δ)〉_φ [34,40,47,53–56], where q_k(k = 1; 2) is the magnitude of the scattering vector, Δ and φ are the angular coordinates, 〈…〉_φ defines the angular average, and the subscripts i and j indicate that intensities I_i(q_k, φ) are correlated between the ith and jth diffraction patterns. For structural analysis, we used the difference spectrum [56],

$${\stackrel{\sim }{C}}^n(q_1,q_2)={\langle C_{ii}^n(q_1,q_2)\rangle }_i-{\langle C_{ij}^n(q_1,q_2)\rangle }_{i\ne j},$$

where $C_{ii}^n(q_1,q_2)$ and $C_{ij}^n(q_1,q_2)$ are the Fourier components (FCs) of the CCFs C_ii(q₁, q₂, Δ) and C_ij(q₁, q₂, Δ), respectively, and 〈…〉_i and 〈…〉_i≠j denote statistical averages over diffraction patterns (see Supplemental Material [57]). The difference FCs C̃ⁿ(q₁, q₂) help to mitigate various systematic issues and improve the FXS data quality as compared to ${\langle C_{ii}^n(q_1,q_2)\rangle }_i$ alone [38,56,64].

The experiment was carried out at the Atomic Molecular Optics (AMO) beam line [65] of LCLS [4]. The aerodynamic lens stack system [10] with a gas dynamic virtual nozzle [66] was employed to introduce single virus particles of ~70 nm size into the focused XFEL beam of photon energy E = 1.6 keV. The data used in the presented analysis were measured by a pair of pnCCD detectors with a resolution of 11.6 nm at the detector edge. A detailed description of the experimental setup and sample preparation can be found in Ref. [67]. A large scattering data set containing about 3 × 10⁶ diffraction patterns was filtered to select only high-intensity single hits with more than 4500 ADUs/pixel on average. These patterns were further classified according to the scattering particle size to minimize polydispersity effects (see Refs. [57,67] for preprocessing details). The resulting data sets with polydispersity PD = 3 nm used in the following analysis contained 332 diffraction patterns from rice dwarf virus (RDV) particles, with size variation from 69 to 72 nm, and 566 patterns from PR772 bacteriophage particles, with size variation from 67.5 to 70.5 nm.

Experimental SAXS profiles, 〈I_i(q, φ)〉_φ,i, determined for RDV and PR772, together with their representative diffraction patterns, are shown in Figs. 1(a) and 1(b), respectively. The amplitudes of the ensemble-averaged FCs C̃ⁿ(q, q) ≡ C̃ⁿ(q) determined for the case q₁ = q₂ = q are shown in Figs. 1(c) and 1(d) for RDVand PR772, respectively. It can be readily shown that ${\langle I_i(q,\phi )\rangle }_{\phi ,i}={\langle I_i^0(q)\rangle }_i$ and ${\stackrel{\sim }{C}}^n(q)={\langle {\mid I_i^n(q)\mid }^2\rangle }_i$, where $I_i^n(q)$ are the angular FCs of scattered intensity [57]. Therefore, a combination of 〈I_i(q, φ)〉_φ,i and C̃ⁿ(q) represents a generalized SAXS data set, where the C̃ⁿ(q) for n ≠ 0 can be considered as “higher-order SAXS” terms. Because of the small-angle scattering geometry of our experiment and the limited particle sizes, only six FCs of even orders n = 2, 4, 6, 8, 10, and 12 make significant contribution to the Fourier spectrum of the CCFs [Figs. 1(c) and 1(d)], which clearly stand out from the background level formed by the degenerate FCs of odd orders n. Noticeable features in the spectra of RDV and PR772 suggest that two viruses have distinguishable features. However, the one-dimensional (1D) plots of C̃ⁿ(q) contain only a small fraction of information accessible by the two-point CCF. Clearly, one can determine the FCs C̃ⁿ(q₁, q₂) also at different q₁ and q₂, for instance, as shown in Figs. 1(e) and 1(f). The full set of FCs C̃ⁿ(q₁, q₂) consist of N_q such plots, where N_q is the sampling in the q direction.

FIG. 1.

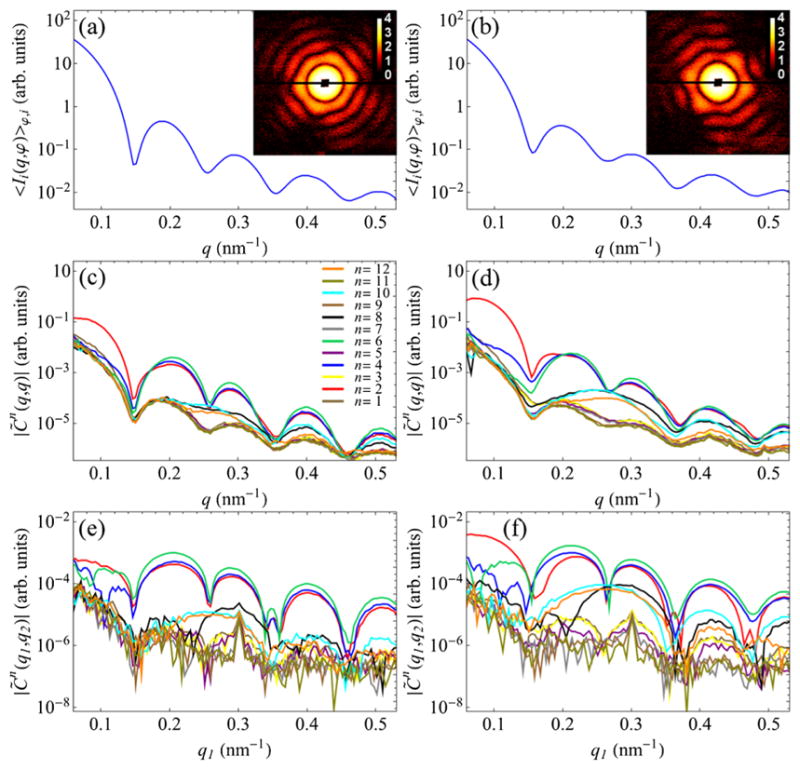
(a),(b) Experimental SAXS profiles 〈I_i(q, φ)〉_φ,i (log scale) determined for (a) RDV and (b) PR772 viruses. The insets in (a) and (b) display randomly chosen high-intensity single-particle diffraction patterns for corresponding particles. (c)–(f) Amplitudes of the FCs C̃ⁿ(q₁, q₂) for n = 1, …, 12 determined for (c),(e) RDV and (d,f) PR772 viruses at (c,d) q₁ = q₂ = q and (e,f) at fixed q₂ = 0.3 nm⁻¹ as a function of q₁.

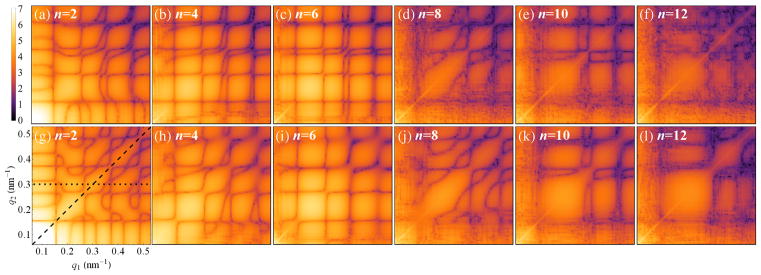
The entire correlation data set can be conveniently visualized in the form of 2D maps of C̃ⁿ(q₁, q₂) for each FC of order n separately, as shown in Fig. 2. Importantly, these correlation maps comprise a fingerprint of the whole 3D structure of each virus and clearly indicate the differences between RDV and PR772, which are obvious even at the moderate resolution of the present experiment. We used these maps for comparison with simulated structures as well as for ab initio reconstruction of the virus structures.

FIG. 2.

Experimental 2D correlation maps (log scale, arb. units) of the amplitudes of the FCs |C̃ⁿ(q₁, q₂)| for n = 2, 4, 6, 8, 10 and 12, determined for (a)–(f) RDV and (g)–(l) PR772 viruses. The legend and axes on the bottom-left map are the same for all 2D maps of the amplitudes |C̃ⁿ(q₁, q₂)| in this Letter. The dashed line (q₁ = q₂ = q) in (g) indicates a section through all 2D maps for n ≤ 12, which produce the plots in Figs. 1(c) and 1(d), while the dotted line corresponds to the plots in Figs. 1(e) and 1(f) for RDVand PR772, respectively.

Both RDV and PR772 are expected to possess an icosahedral-shaped capsid; therefore, it is interesting to compare the determined correlation maps (Fig. 2) with the results of simulations for icosahedral particles. The 2D maps for the FC of order n = 2 simulated for the RDV capsid atomic structure [68] [Protein Data Bank (PDB) entry 1UF2], as well as for several bead-model structures, are presented in Fig. 3. We focused our model-based comparison on the lowest even-order harmonic n = 2 (see Ref. [57] for extended data), which typically can be associated with simple structural distortions like extension or compression, or anisotropic distribution of electron density in the particle. The first striking observation is that the simulated data for an icosahedral RDV capsid structure [Fig. 3(a)], determined to 3.5 Å resolution by x-ray crystallography [68], look substantially different from our experimental result for RDV [Fig. 2(a)]. A general q-dependent misfit of the two maps can be explained by the fact that we observe scattering from a filled, instead of an empty, RDV capsid in our experiment. However, even a bead model of a solid icosahedral particle of 71 nm in size that gives the best fit to the experimental SAXS profile for RDV does not reproduce the respective experimental CCF data [compare Figs. 3(b) and 2(a)], which are more sensitive to structural features of the underlying scattering object. For instance, notice the difference between the results for a bead model of a solid particle [Fig. 3(b)] and a hollow icosahedral particle of the same size with a spherical void of a diameter d = 30 nm [Fig. 3(c)].

FIG. 3.

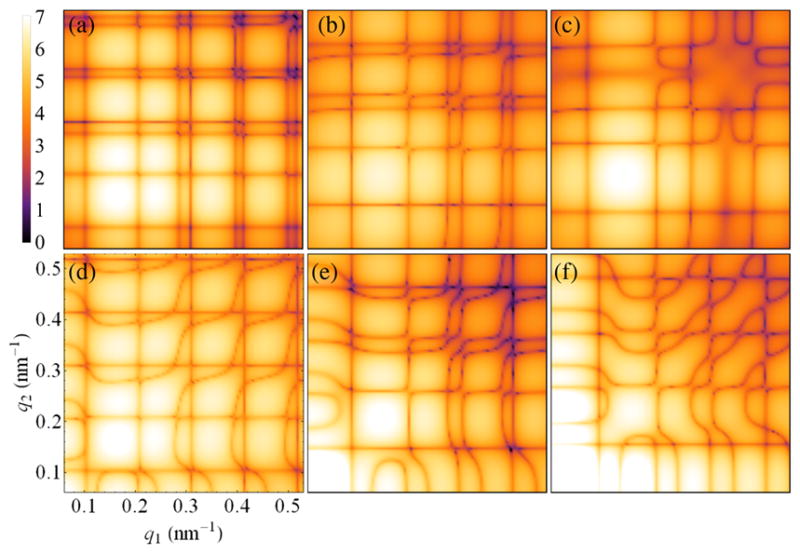
Simulated 2D correlation maps (log scale, arb. units) of the amplitudes of the FCs |C̃ⁿ⁼²(q₁, q₂)| for n = 2 determined for (a) the atomistic structure of the empty RDV capsid, and bead models of the (b) solid icosahedral particle, (c) hollow icosahedral particle with a spherical void, (d) empty RDV capsid model compressed by 3% along the fivefold symmetry axis, (e),(f) solid icosahedral particle compressed by (e) 3% and (f) 7% (see text). Notice prominent similarity of the simulated and experimental maps shown in Figs. 3(e) and 2(a), as well as Figs. 3(f) and 2(g).

We found that the similarity between the experimental and simulated correlation data increases if one applies a small distortion to the model capsid structure. The correlation map simulated for the empty RDV capsid compressed by about 3% (relative to the original size) along one of the fivefold symmetry axes [Fig. 3(d)] reveals characteristic features observed in the experimental map for RDV [Fig. 2(a)]. By applying a similar type of distortion (3% compression) to a solid icosahedral particle [Fig. 3(e)], we were able to reproduce the experimental result for RDV [Fig. 2(a)] very closely. A larger distortion (7% compression) applied to a solid icosahedral particle leads to the correlation map in Fig. 3(f), which closely resembles the experimental result for PR772 [Fig. 2(g)]. Note that the suggested compressions of the icosahedron give the virus particle an oblate character, which is supported by a generalized Guinier analyses [57,69]. Clearly, correlation maps provide a detailed fingerprint of the whole 3D structure of a single object. In this case, we revealed structural features in RDV that correspond to only 3% (or about 2 nm) of its overall size, which is much smaller than the experimental resolution (about 12 nm at the detector edge).

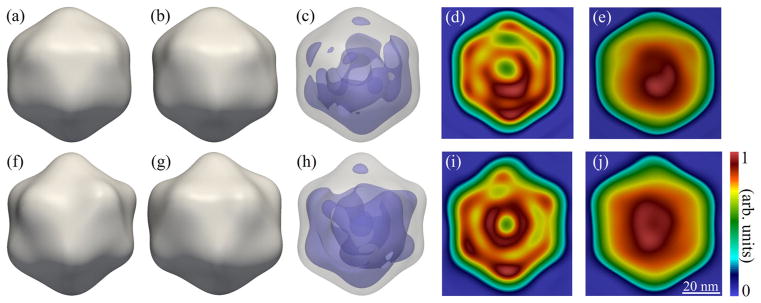
As compared to a 1D SAXS profile, correlation maps provide N_qn_tot (where n_tot is the total number of significant FCs of the CCF) times more measurements, which, in the present case, gives about 2 orders of magnitude increase in information content compared to SAXS. As in SAXS analysis, these data can be incorporated into a real-space model fitting procedure to recover the 3D structures [49]. Here we go beyond the uniform-density approximation employed in such models and perform ab initio reconstructions of the virus structures using the MTIP algorithm [40]. MTIP does not require solving the orientation-determination problem as is needed in conventional SPI techniques. Here we did not impose any symmetry constraints or model assumptions, apart from a finite support, during structure recovery [57]. The recovered structures for RDV and PR772 (Fig. 4) show a mostly icosahedral capsid with minor distortions, consistent with the model analysis described above, as well as an anisotropic distribution of density inside the particles [70]. Note that, even though the internal distribution of material is unlikely to be perfectly reproducible, the internal density of the reconstructions is statistically relevant and can be viewed as an average over the internal heterogeneity. Resolution estimates were calculated using both a phase retrieval transfer function (PRTF) [71,72] and Fourier shell correlations (FSC) [73–75] with the respective established cutoffs of 1/e and 0.5. We obtained resolutions of 17.7 nm for RDV and 16.9 nm for PR772 using the PRTF, and 13.5 nm for RDV and 12.6 nm for PR772 using the FSC [57].

FIG. 4.

Reconstructed images of RDV (top row) and PR772 (bottom row). Two different views (corresponding to a 72 degree rotation about the top axis) of the reconstructed RDV (a),(b) and PR772 (f),(g) particles, as well as density plots showing nonuniformities in the internal distribution of material inside the viruses (c),(h), 2D slices through the center of the reconstructed densities (d),(i), and 2D projections of the reconstructed densities (e),(j). The isosurfaces for the capsid and internal material were calculated at 45% and 84% of the maximum density for RDV, and at 47% and 78% for PR772, respectively. The viewing directions for the 2D slices and projections in (d),(e),(i), and (j) are given by the normal to the page for the structures shown in (a),(b),(f), and (g), respectively.

Observed deviations of the particle structures from ideal icosahedral could have several origins. For one, there may be natural asymmetries in the RDVand PR772 structures, which is particularly relevant for the distribution of genetic material inside the viruses. Such information could be difficult to reveal in conventional crystallography, where information is averaged over all symmetry-equivalent orientations of the virus structure in a crystal, or in single-particle imaging techniques that enforce symmetry constraints. Another possibility is that particle distortions could potentially be induced during sample preparation or injection. For instance, particles might be covered with organic debris contained in the buffer, which stick to the virus particle while the solution droplet evaporates during sample injection (see model results in Ref. [57]). While our ab initio reconstructions of virus structures support the idea that intrinsic structural features are incompatible with exact icosahedral symmetry, further systematic analysis is required to provide unambiguous interpretation of our observations. Irrespective of their origin, the observed structural features are statistically relevant, since the orientationally averaged correlation maps contain a fingerprint of the whole 3D structure, and are unhindered by polydispersity [57].

In this work, we outlined an efficient route for structural analysis of nanoscale objects at XFELs by means of angular cross-correlations, bridging the gap between conventional imaging and crystallography methods. We applied our approach to the scattering data from single aerosolized RDV and PR772 particles measured at LCLS and revealed nanoscale features of viruses, with deviations from icosahedral symmetry. We showed that CCFs preserve a substantial amount of structural information, which, in the present study, enabled observation of structural features of viruses at the nanometer scale. Overall, FXS generalizes the concept of small-angle scattering, yielding an increase in information content by several orders of magnitude. Moreover, appropriately constructed correlation maps comprise a fingerprint of the whole 3D structure of a scattering object and represent a valuable statistical tool for structural analysis. These 2D correlation maps can be especially useful to follow fast dynamical changes in the structure, for instance, as a response to external stimulus [41,42], which is a key component of structural studies at XFELs.

We demonstrated that angular cross-correlations represent an exceptional source of data for model-based comparison and ab initio structure recovery. Since these cross-correlations self-consistently characterize the whole 3D structure of an object, the problem of orientation determination typically encountered in conventional SPI algorithms can be omitted, which significantly improves the process of structure recovery. Analysis of polydispersity effects suggests that our approach can also be applied in the case of scattering from a system of multiple particles with some degree of poly-dispersity. This offers a fascinating opportunity to explore the full potential of the multiple-particle FXS technique to increase the resolution of the recovered structures and/or reduce radiation damage of biological species, going beyond the limits of conventional single-particle schemes.