Improved Free-Energy Landscape Quantification Illustrated with a Computationally Designed Protein-Ligand Interaction

Abstract

Quantifying the energy landscape underlying protein-ligand interactions leads to an enhanced understanding of molecular recognition. A powerful yet accessible single-molecule technique is atomic force microscopy (AFM)-based force spectroscopy, which generally yields the zero-force dissociation rate constant (k_off) and the distance to the transition state (Δx^‡). Here, we introduce an enhanced AFM assay and apply it to probe the computationally designed protein DIG10.3 binding to its target target ligand, digoxigenin. Enhanced data quality enabled an analysis that yielded the height of the transition state (ΔG^‡ = 6.3 ± 0.2 kcal mol⁻¹) and the shape of the energy barrier at the transition state (linear-cubic) in addition to the traditional parameters [k_off (= 4 ± 0.1 × 10⁻⁴ s⁻¹) and Δx^‡ (= 8.3 ± 0.1 Å)]. We expect this automated and relatively rapid assay to provide a more complete energy landscape description of protein-ligand interactions and, more broadly, the diverse systems studied by AFM-based force spectroscopy.

COMMUNICATION

Force-induced unbinding quantifies the free-energy landscape: Applying force to a protein-ligand interaction speeds up the kinetics of dissociation. Applying advanced models to the relationship between the dissociation rate and applied force reveals new insights into the energy landscape of dissociation.

Molecular recognition between proteins and ligands is fundamental to biology. Correct recognition of antigens by antibodies, substrates by enzymes, and ligands by receptors is essential to most biological processes. In addition, the ability to custom-design proteins with precise and selective molecular recognition for a target molecule would enable the development of biosensors for a wide array of biological and medical applications.

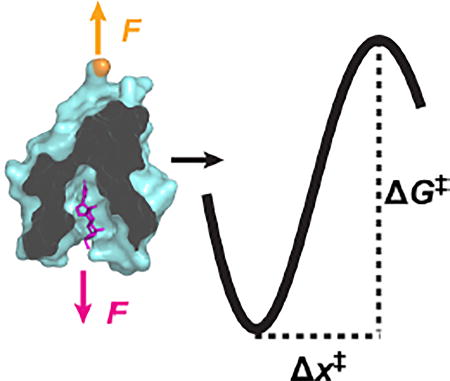
Characterizing the strength of natural and computationally designed protein-ligand interactions is usually done in bulk assays, yielding measurements of K_D. For instance, DIG10.3, which binds the steroid digoxigenin (Dig), is the first computationally designed protein to achieve a picomolar level dissociation constant (K_D) to its target ligand.^[1] Indeed, DIG10.3 exhibits an affinity that rivals that of anti-Dig antibodies.^[2] Molecular details of the bound state are provided by structural studies (e.g., x-ray crystallography) and have confirmed the computationally predicted binding mode.^[1] However, experimental determination of the process of dissociation remains elusive. Hence, understanding of protein-ligand interactions would benefit from an expanded description of the free-energy landscape that governs dissociation, including the height (ΔG^‡) and distance (Δx^‡) to the transition state along with the shape of the free-energy barrier at the transition state.

Single-molecule force spectroscopy (SMFS) is a powerful technique to characterize protein-ligand interactions.^[3–7] In such assays, a force applied across the protein-ligand interaction promotes detachment. The resulting data, often taken with an atomic force microscope (AFM) over a range of stretching velocities and thereby loading rates (∂F/∂t),^[7] yields insight into the energy landscape underlying the protein-ligand interaction projected onto the stretching axis.^[8]

Standard analysis uses the Bell-Evans model, which predicts a linear relationship between the most probable rupture force and log (∂F/∂t) and thereby yields the dissociation rate constant at zero applied force (k_off) and Δx^‡.^[9] The Bell-Evans model also predicts the dissociation rate constant k increases exponentially with F, given by k(F) = k_off exp(FΔx^‡/k_BT), where k_BT is the thermal energy. Recently, a Bell-Evans analysis was used to characterize Dig bound to anti-Dig (anti-Dig•Dig) via acoustical force spectroscopy.^[10] The resulting data, similar to prior AFM studies of anti-Dig•Dig,^[11] showed two linear regimes, one for low and one for high loading rates. Such data are often interpreted as two distinct energy barriers along the stretching axis (though rebinding when using short linkages at low loading rates complicates interpretation^[12]).

A more advanced analysis developed by Dudko and colleagues^[13] yields important additional information: ΔG^‡ and the shape of the free-energy landscape at the transition state. In this model, the application of F not only alters the height of the barrier but moves the transition state towards the bound state. As a result, k(F) initially increases exponentially with F like the Bell-Evans model but deviates from this dependency at higher F. While this more sophisticated model has been used to analyze macromolecular folding studies on custom-built optical-traps,^[14] it has not yet been applied to the AFM-based molecular-recognition studies since its application requires higher-quality data than has been achieved using standard commercially available AFMs.^[15] Yet, in part, it’s the accessibility and ease-of-use of commercial AFMs that make such AFM-based studies so popular.^[7]

Here, we used SMFS to characterize the DIG10.3-Dig interaction, denoted as DIG10.3•Dig. Specifically, we developed an optical-trapping assay to initially assess the suitability of DIG10.3•Dig for SMFS studies and an AFM-based assay to quantify this interaction. The data quality in the AFM-based studies was improved by integrating low-drift cantilevers,^[16] site-specific coupling,^[17] and corrected pulling geometries.^[18] These improvements resulted in the rapid acquisition of hundreds of constant-force traces on a commercial AFM. The resulting data directly revealed a non-exponential dependency of k(F), in quantitative agreement with the predictions of the Dudko model.^[13] Using this analysis, we determined ΔG^‡ and the shape of the free-energy barrier at the transition state (linear-cubic) in addition to the traditional parameters (k_off and Δx^‡). Thus, this work extends AFM-based SMFS to rapidly determine ΔG^‡ in molecular-recognition studies, in particular, and AFM-based force spectroscopy studies, in general.

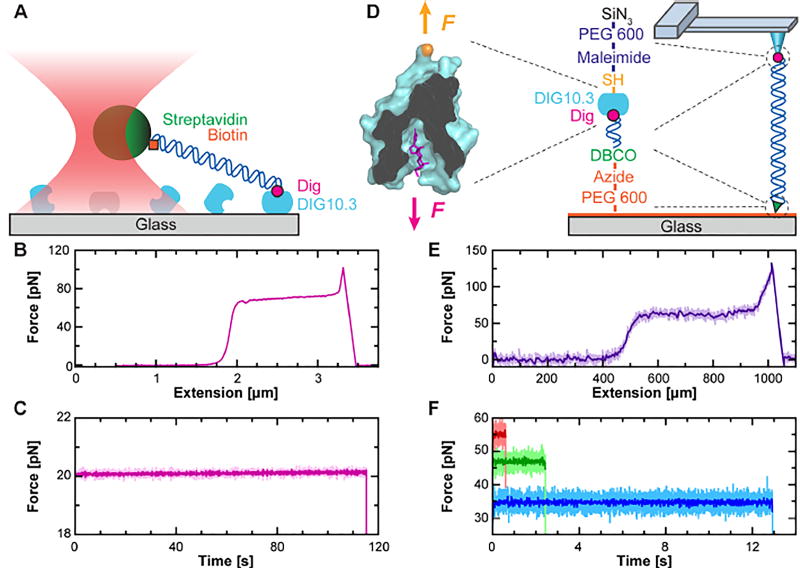
As a first step, we adapted a previously used surface-coupled optical-trapping assay^[19] by simply replacing anti-dig with DIG10.3 (Figure 1A). In this assay, the DIG10.3 was passively adsorbed onto KOH-cleaned coverslips. We then stretched a 2-µm-long DNA molecule labeled at its 5'-ends with Dig and biotin via a streptavidin-coated microsphere held in an optical trap. A resulting force-extension curve acquired by moving the sample surface at constant velocity (2 µm s⁻¹) showed the canonical DNA overstretching transition^[20,21] at 65 pN (Figure 1B). With this simple assay, we also performed optical-trapping experiments at constant F. Individual traces showed DIG10.3•Dig often withstood 20 pN for more than 100 s (Figure 1C). Hence, the DIG10.3•Dig interaction was sufficiently robust for application in many existing low-to-moderate force SMFS assays, including those used to characterize DNA-based molecular motors^[22] and nucleic-acid structures.^[23,24]

Figure 1.

Single-molecule force spectroscopy (SMFS) studies using DIG10.3•Dig. A) Schematic of DIG10.3•Dig being used in an optical-trapping-based SMFS assay. B) Force-extension curve shows DNA being stretched with an optical trap undergoing the overstretching transition at 65 pN. Data smoothed to 500 Hz. C) A force-vs-time trace shows the lifetime of DIG10.3•Dig stretched under constant force by an optical trap. Data smoothed to 40 Hz (light pink) and 10 Hz (dark pink). D) Cartoon of the coupling scheme for AFM-based assay showing force applied to the ligand and a N-terminal cysteine variant of DIG10.3. DIG10.3 was covalently coupled to a maleimide-functionalized, PEG-coated AFM tip via a maleimide-thiol bond. Dig-labeled DNA was covalently coupled to an azide-functionalized, PEG-coated coverslip using dibenzocyclooctyl (DBCO), a copper-free click chemistry reagent. Abbreviations: SiN3, silicon nitride. E) Force-extension curve taken using an AFM also shows the DNA’s overstretching transition. Data smoothed to 50 kHz (light purple) and 50 Hz (dark purple). F) Force-vs-time traces using an AFM show the lifetime of DIG10.3•Dig stretched at constant force. Data smoothed to 1 kHz (light colors) and 50 Hz (dark colors).

To rapidly quantify the 1D free-energy landscape of DIG10.3•Dig, we developed an AFM-based assay where all of the linkages were covalent, except DIG10.3•Dig (Figure 1D). Hence, any rupture could be attributed to the dissociation of DIG10.3•Dig, rather than failure of another linkage (e.g., the biotin-streptavidin coupling or the non-specific adsorption of DIG10.3 to the coverslip). Moreover, we automated data acquisition, a capability not present in our custom optical trap.^[25]

Assembly of this assay started with a PCR-amplified, 635-nm-long DNA to introduce distinct 5' labels, Dig and dibenzocyclooctyl (DBCO), a copper-free click chemistry reagent. We then covalently coupled this DNA via the DBCO to an azide-functionalized coverslip.^[17] The surface density of the DNA was purposely kept low to promote attachment to a single DNA molecule. In parallel, we covalently coupled a variant of DIG10.3 with an N-terminal cysteine to maleimide-functionalized cantilevers. Non-specific adhesion was minimized by using a PEG-coating on both the cantilever and the coverslip.

To improve the overall quality of the AFM data, a number of important technical improvements were integrated. First, we improved force stability by chemically etching the metal coating off of the cantilever, achieving sub-pN force stability over 100 s.^[16] Next, we improved the accuracy of the assay by positioning the DNA’s anchor point to the coverslip directly below the AFM tip, assuring a vertical stretching geometry.^[18] This alignment is particularly important when using stiff linkers like DNA (persistence length = 50 nm) where large lateral offsets (~180 nm) between the tip and the DNA anchor point on the coverslip have been observed for short (650-nm) DNA.^[18] Finally, we improved force precision by performing all of the measurements with a single cantilever, similar to prior work on the unfolding of proteins.^[26]

We initiated this improved assay by lowering a DIG10.3-coated AFM tip towards a coverslip sparsely coated with Dig-labeled DNA and then pressing the tip gently (100 pN) into the coverslip for 2 s. This force was relatively low compared to the ~1,000 pN generally used to promote non-specific attachment.^[27] We next retracted the tip from the surface at constant velocity (1 µm s⁻¹) while using a real-time triggering scheme that stopped the retraction when F > 20 pN at an extension x > 150 nm. This scheme selected for a connection consistent with stretching DNA (rather than surface adhesion). We then performed an automated centering routine to position the DNA anchor point directly under the tip.^[18] Next, we either stretched the DNA at a constant velocity (Figure 1E) or held the DNA and thereby the DIG10.3•Dig complex under constant F (Figure 1F). Upon rupture, the cantilever was lowered back to the surface and often reattached to the same individual DNA molecule, improving throughput as outlined in Figure S1.

To precisely characterize DIG10.3•Dig energetics, we needed to verify that a single DNA was stretched via DIG10.3•Dig. First, we only analyzed force-extension curves that showed a single rupture that returned to F = 0 pN, consistent with a single molecule attached to the AFM tip. Next, we demonstrated the vast majority of linkages to the tip were via DIG10.3•Dig by blocking digoxigenin-labeled DNA with the anti-Dig antibody, which dramatically reduced tip attachment (Figure S2). Finally, as discussed above, the only non-covalent linkage in the assay was DIG10.3•Dig, so ruptures could be attributed to the dissociation of that interaction (though dissociation arising from force-induced unfolding of DIG10.3 remains a possibility as in all SMFS protein-ligand assays).

Constant-force measurements provided a more direct comparison to theoretical predictions, although such measurements are more technically challenging to implement. In particular, both the Bell-Evans^[9] and the Dudko^[13] models have clear predictions for k(F). Constant-velocity measurements lead to more complicated predictions of the distribution of rupture forces.^[13,28] As discussed above, we met the key requirement of constant force by using cantilevers that featured sub-pN stability over 100 s.^[16] In contrast, the same cantilever with its gold-coating drifts ~50 pN over 100 s, even 2 h after immersion in liquid.^[16]

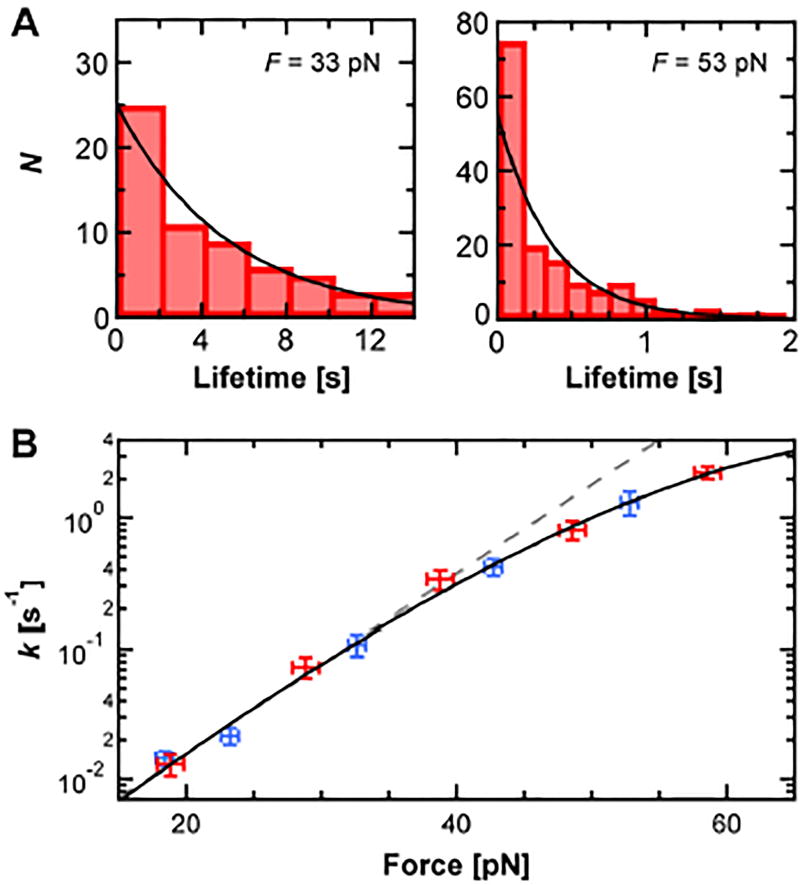
Using an automated data-acquisition process, we recorded Dig10.3•Dig lifetimes over a range of F. Histograms of the resulting lifetimes (N ≈ 50–250 per F) were analyzed to deduce a dissociation rate constant k(F) at each F from a fit to a single exponential (Figure 2A). Larger F led to shorter lifetimes and thus a higher dissociation rate constant (Figure 2B). Below 40 pN, k(F) scaled exponentially with F and therefore increased linearly on a log-linear plot (Figure 2B, dashed line). Yet, at higher F, k(F) deviated from this linearity. To verify that this curvature was reproducible, we took two independent sets of data over two sequential days using the same individual cantilever for improved precision (Figure 2B, red and blue). The resulting data showed quantitative agreement, providing assurance that this curvature was reproducible.

Figure 2.

Quantifying DIG10.3•Dig under force. A) Histograms of DIG10.3•Dig lifetime at two different forces (33 and 53 pN, N = 65 and 159 respectively) were analyzed by fitting to an exponential (black line). B) The dissociation rate constant k as a function of F shows curvature on a log-linear plot. Two data sets taken on consecutive days are shown (red and blue). The resulting data was fit to the Dudko model (Eq. 1, black line). Error bars represent the standard error of k (N ≈ 50–250 per point; N_total = 1,081) and standard deviation of F. Gray dashed line represents a Bell-Evans fit to the data below 40 pN.

To see if the observed non-exponential scaling of k(F) was consistent with the Dudko analysis,^[13] we fit the data using

$$k(F)=k_{\text{off}}{(1-\frac{\mathit{\text{vF}}\mathrm{\Delta }{x}^{‡}}{\mathrm{\Delta }{G}^{‡}})}^{\frac{1}{v}-1}\text{exp}\left(\frac{\mathrm{\Delta }{G}^{‡}}{k_{\mathrm{B}}T}\right[1-{(1-\frac{vF\mathrm{\Delta }{x}^{‡}}{\mathrm{\Delta }{G}^{‡}})}^{\frac{1}{v}}\left]\right)$$ (1)

The fit showed excellent agreement between our data and this model (Figure 2B, black line). The resulting parameters were k_off = 4.1 ± 0.4 × 10⁻⁴ s⁻¹, Δx^‡ = 8.3 ± 0.1 Å, ΔG^‡ = 6.3 ± 0.2 kcal mol⁻¹ and v = 0.67 ± 0.02. Uncertainties correspond to the standard errors for fitting parameters. This value of v quantitatively agrees with the value of 2/3 predicted by Dudko and colleagues^[13] for a linear cubic potential at the transition state (whereas a cusp potential would correspond to v = 0.5 and the simpler Bell-Evans model corresponds to v = 1).

How do SMFS measurements of DIG10.3•Dig compare to those of anti-Dig•Dig? As the DIG10.3•Dig data were taken at constant force, we compared our results to the lower-loading rate barrier in the recent anti-Dig•Dig experiments.^[10] In particular, k_off for DIG10.3•Dig is 6-fold higher than anti-Dig•Dig, despite a lower K_D, implying a faster k_on since K_D = k_off/k_on. Interestingly, Δx^‡ for DIG10.3•Dig was about half of that for anti-Dig•Dig (Δx^‡ = 15.4 ± 0.7 Å). As a result, whereas DIG10.3•Dig has a higher intrinsic k_off, the lifetime of DIG10.3•Dig at F > 10 pN is predicted to be longer than for anti-Dig•Dig (Figure S3). This result arises from the difference in force sensitivity due to a smaller Δx^‡. On a practical note, the overall similarity in interaction lifetime over the 5–20 pN range suggests that DIG10.3, which was expressed in E. Coli, can easily substitute for anti-Dig in a wide range of current SMFS assays.

The determination of ΔG^‡ demonstrated here in a commercial AFM opens the door to a more complete and accessible determination of free-energy landscape parameters of diverse protein-ligand systems. However, we note that resolving the curvature visualized in Figure 2B—essential to constraining ΔG^‡ and v within the Dudko model—required advances in both the quality and quantity of data. Quality was improved by using cantilevers that featured sub-pN stability,^[16] which was essential since k(F) scales exponentially with F at low F. Moreover, a sufficient quantity of high-quality data was equally critical. Initial studies with ~20 lifetimes at each F did not show the curvature seen in Figure. 2B. Only when we acquired ~50–250 lifetimes at each F was the curvature well defined and reproducible. Finally, while using DNA may seem inconvenient, the distinct advantage of a long spacer over the much shorter PEG linkers commonly used in many SMFS studies of molecular recognition is that the extended DNA rapidly recoils upon rupture, preventing rebinding artifacts that can alter interpretation.^[12]

In summary, we developed an enhanced constant-force AFM-based assay to provide an expanded description of the free-energy landscape underlying protein-ligand interactions. We demonstrated it by characterizing a computationally designed protein-ligand interaction and applying a more sophisticated analysis to yield ΔG^‡ and the shape of the energy barrier at the transition state in addition to the traditional parameters (k_off and Δx^‡). By doing so in an automated and relatively rapid manner (~2 days), we anticipate this assay will provide a more complete energy landscape description of diverse natural protein-ligand interactions as well as experimental feedback to further optimize computationally designed interactions. In turn, enhanced computationally designed protein-ligand interactions offer promising capabilities in diagnostics and therapeutics. Finally, our improved AFM-based assay is not limited to protein-ligand interactions but can be immediately adopted to studies of protein-protein interactions^[29] and proteins unfolding under constant force.^[30]