Inverted Encoding Models of Human Population Response Conflate Noise and Neural Tuning Width

Abstract

Channel-encoding models offer the ability to bridge different scales of neuronal measurement by interpreting population responses, typically measured with BOLD imaging in humans, as linear sums of groups of neurons (channels) tuned for visual stimulus properties. Inverting these models to form predicted channel responses from population measurements in humans seemingly offers the potential to infer neuronal tuning properties. Here, we test the ability to make inferences about neural tuning width from inverted encoding models. We examined contrast invariance of orientation selectivity in human V1 (both sexes) and found that inverting the encoding model resulted in channel response functions that became broader with lower contrast, thus apparently violating contrast invariance. Simulations showed that this broadening could be explained by contrast-invariant single-unit tuning with the measured decrease in response amplitude at lower contrast. The decrease in response lowers the signal-to-noise ratio of population responses that results in poorer population representation of orientation. Simulations further showed that increasing signal to noise makes channel response functions less sensitive to underlying neural tuning width, and in the limit of zero noise will reconstruct the channel function assumed by the model regardless of the bandwidth of single units. We conclude that our data are consistent with contrast-invariant orientation tuning in human V1. More generally, our results demonstrate that population selectivity measures obtained by encoding models can deviate substantially from the behavior of single units because they conflate neural tuning width and noise and are therefore better used to estimate the uncertainty of decoded stimulus properties.

SIGNIFICANCE STATEMENT It is widely recognized that perceptual experience arises from large populations of neurons, rather than a few single units. Yet, much theory and experiment have examined links between single units and perception. Encoding models offer a way to bridge this gap by explicitly interpreting population activity as the aggregate response of many single neurons with known tuning properties. Here we use this approach to examine contrast-invariant orientation tuning of human V1. We show with experiment and modeling that due to lower signal to noise, contrast-invariant orientation tuning of single units manifests in population response functions that broaden at lower contrast, rather than remain contrast-invariant. These results highlight the need for explicit quantitative modeling when making a reverse inference from population response profiles to single-unit responses.

Introduction

Bridging knowledge derived from measurements at different spatial and temporal scales is a significant challenge for understanding the link between neural activity and behavior. Although much work has focused on linking single-unit measurements to behavior, there is increasing recognition of the importance of population-scale representations (Benucci et al., 2009; Graf et al., 2011; Churchland et al., 2012; Mante et al., 2013; Fusi et al., 2016). In human neuroscience, these bridging challenges are even more severe as many of the core building blocks of knowledge learned from invasive animal experiments are difficult to verify and replicate in humans. It is therefore often unknown whether basic phenomena from the single-unit literature are applicable to humans, let alone how these phenomena will manifest at the larger scale of population activity that is typically interrogated by noninvasive measurement of the human brain.

Recently, an encoding model approach has proven useful in the analysis of large-scale population activity measured by functional imaging (Naselaris et al., 2011; Serences and Saproo, 2012) and offers the promise of bridging knowledge from different species and scales of measurements. Encoding models are built on fundamental results in visual physiology, by encoding complex stimuli in lower dimensional representations, such as receptive field or channel models. The assumption is that, if these neural representations are operative in human cortex, then large-scale measurements of activity represent the aggregated responses of these basic neural operations. For example, a channel-encoding model (Brouwer and Heeger, 2009, 2013) has been used to examine continuous stimulus dimensions, such as color or orientation, where it is reasonable to expect that there are large groups of neurons, or channels with known selectivity, and that voxel responses can be modeled as linear combinations of such channels. These channel-encoding models have been used to examine responses for orientation, color, direction, and speed of motion and somatosensory response to better understand apparent motion (Chong et al., 2016), cross-orientation suppression (Brouwer and Heeger, 2011), normalization (Brouwer et al., 2015), speeded decision making (Ho et al., 2012), attention (Scolari et al., 2012; Garcia et al., 2013; Saproo and Serences, 2014; Ester et al., 2016), working memory (Ester et al., 2013, 2015), perceptual learning (Byers and Serences, 2014; Chen et al., 2015), biases in motion perception (Vintch and Gardner, 2014), and exercise (Bullock et al., 2017) using both functional imaging and EEG (Garcia et al., 2013; Bullock et al., 2017) measurements. Inverting these models to form predictions of channel response from cortical measurements produces tuned response profiles. The interpretations of these tuned response profiles are encouraging for the effort of bridging across measurements as they have shown results in concordance with expectations from electrophysiological measurement of phenomena, such as decision-making reliance on off-target populations (Purushothaman and Bradley, 2005; Scolari et al., 2012) and feature-similarity gain (Treue and Maunsell, 1996; Saproo and Serences, 2014) and response gain (McAdams and Maunsell, 1999; Garcia et al., 2013) modulation effects of attention.

Here we test the ability of the channel-encoding model approach to bridge single-unit and population-scale measurement by asking whether the well-known property of contrast-invariant orientation tuning is manifest in predicted channel responses from human primary visual cortex. We reasoned that examining whether orientation tuning bandwidth of human cortical population responses change with contrast would provide a good test case for the use of encoding models to bridge measurements because there is a clear prediction of invariance from single-unit measurements (Sclar and Freeman, 1982). However, contrary to the electrophysiology literature, we found that an encoding model produced channel response functions that increased in bandwidth as contrast was lowered. Computational modeling revealed that these effects can be explained by the reduced signal-to-noise ratio (SNR) of cortical responses at lower contrast. These results emphasize that bridging different levels of measurement through these analyses requires explicit quantitative statements of how properties of single units are expected to manifest in population activity.

Materials and Methods

Subjects.

Six healthy volunteers (ages 33–42, two female) from the RIKEN Brain Science Institute community participated in the experiment; all had normal or corrected-to-normal vision and were experienced subjects in functional imaging experiments. The study protocol was approved by the RIKEN Functional MRI Safety and Ethics Committee, and all subjects gave written consent to experimental procedures in advance of participating in the experiment.

Stimuli.

Stimuli were generated using MGL, a set of MATLAB (The MathWorks) routines for implementing psychophysical experiments (http://gru.stanford.edu/mgl). Stimuli were back projected onto a screen using an LCD projector (Silent Vision 6011; Avotec) at a resolution of 800 × 600 and a refresh rate of 60 Hz. Subjects viewed the screen via an angled mirror attached to the head coil. The projector was gamma corrected to achieve a linear luminance output.

Visual stimuli were sinusoidal gratings (spatial frequency: 0.7 cpd) in a circular aperture (10°), located to the left or the right of a central fixation cross (1°) at an eccentricity of 8°. The gratings were either low (20%) or high (80%) contrast, and could be in 1 of 8 evenly spaced orientations from 0° to 180° (see Fig. 1).

Figure 1.

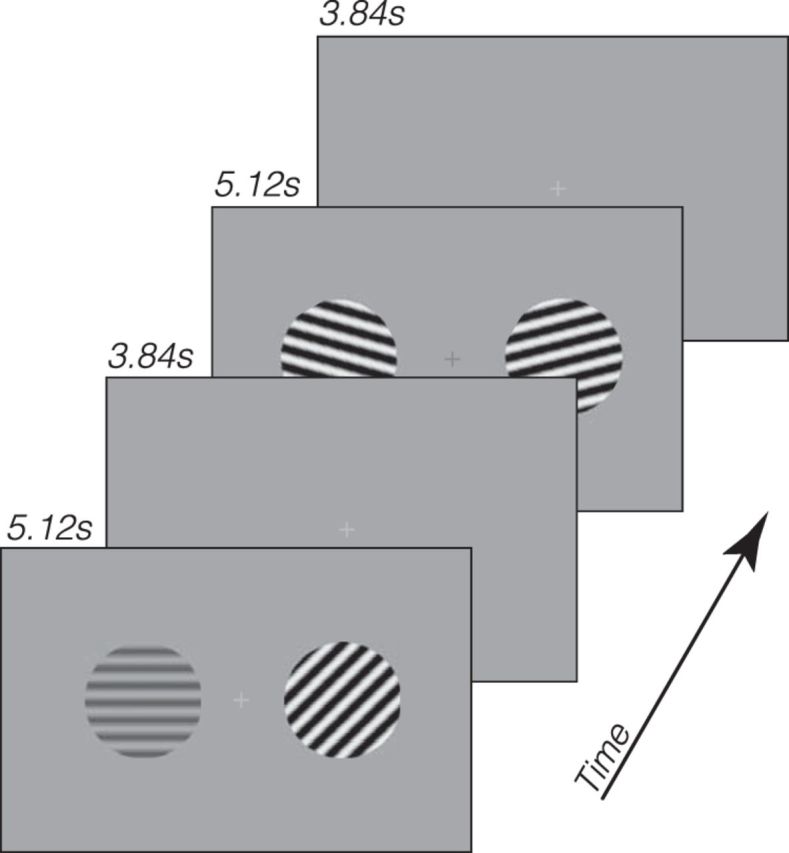
Schematics of the experiment. Low- and high-contrast gratings of eight possible orientations were presented, with contrast and orientation independently randomized for each visual field. A luminance change-detection task was performed at the fixation to control subjects' fixation and state of attention.

Task and procedures.

On each trial, two gratings were presented for 5.12 s, followed by a 3.84 s intertrial interval. During the grating presentation, the phases of both gratings were updated every 0.2 s. The phase of each grating was randomly chosen from 1 of 16 uniformly distributed phases from 0 to 2π, and the starting time of the phase update of each grating was randomly determined such that the phase updates of the two gratings were asynchronous. The phase updates were implemented to reduce retinal adaptation and afterimages. The contrast and orientation of each grating were randomly chosen on each trial such that each combination of contrast (two levels) and orientation (eight levels) was presented three times in each run (48 trials in total). Although the intertrial interval was short, which could result in nonlinear summation of responses from the previous trial (Boynton et al., 1996), the trial randomization procedure served to minimize previous trial effects as, on average, they would come from a random trial type. In addition, a fixation period of 5.12 s preceded each run, making each run 435.2 s in the scanner. Subjects completed 9 runs in the scanner (432 trials in total), which yielded 27 trials per orientation/contrast combination.

While the gratings were presented in the periphery, subjects performed a luminance discrimination task at fixation. On each trial in this task, the fixation cross dimmed for 0.4 s twice, separated by a 0.8 s interval, and subjects had to indicate in which interval the cross appeared darker. The magnitude of dimming was held constant for one interval while the magnitude of dimming in the other interval was controlled by a one-up two-down staircase. Subjects pressed one of two keys (1 or 2) to indicate their response. The fixation task was performed continuously throughout a run and was asynchronous with the display of the grating stimuli. This task was used to control subjects' attention and ensure a steady behavioral state and eye fixation. The independently randomized contrast and orientations of the two gratings on either side also served as an internal check of the fixation quality, as any systematic bias of eye position for one stimulus would not be systematic for the other.

MRI methods.

Imaging was performed with a Varian Unity Inova 4T whole-body MRI system (now Agilent Technologies) located at the RIKEN Brain Science Institute (Saitama, Japan). A volume RF coil (transmit) and a four-channel receive array (Nova Medical) were used to acquire both functional and anatomical images.

Each subject first participated in a separate scanning session to obtain their retinotopic maps (see below for more details), using standard procedures. During this session, a high-resolution 3D anatomical T1-weighted volume (MPRAGE; TR, 13 ms; TI, 500 ms; TE, 7 ms; flip angle, 11°; voxel size, 1 × 1 × 1 mm; matrix, 256 × 256 × 180) was obtained, which served as the reference volume to align all functional images. The reference volume was segmented to generate cortical surfaces using Freesurfer (Dale et al., 1999). Subsequently, the anatomy volumes taken at the beginning of each session were registered to the reference volume so that the cortical regions in the functional scans were aligned with the retinotopy. All analyses were performed in the original (nontransformed) coordinates before being mapped to the cortical surface and specific visual regions.

During the main experiment, functional images were collected using a T2*-weighted EPI sequence (TR, 1.28 s; TE, 25 ms; flip angle, 45°; sensitivity encoding with acceleration factor of 2). We collected 29 slices at an angle approximately perpendicular to the calcarine sulcus, with resolution of 3 × 3 × 3 mm (FOV, 19.2 × 19.2 cm; matrix size, 64 × 64). The first four volumes in each run were discarded to allow T1 magnetization to reach steady state. In addition, a T1-weighted (MPRAGE; TR, 11 ms; TI, 500 ms; TE, 6 ms; flip angle, 11°; voxel size, 3 × 3 × 3 mm; matrix, 64 × 64 × 64) anatomical image was acquired to be used for coregistration with the high-resolution reference volume collected in the retinotopic session.

Various measures were taken to reduce artifacts in functional images. During scanning, respiration was recorded with a pressure sensor, and heartbeat was recorded with a pulse oximeter. These signals were used to attenuate physiological signals in the imaging time series using retrospective estimation and correction in k space (Hu et al., 1995).

Retinotopic mapping procedure.

In this separate scanning session, we mapped each subject's occipital visual areas using well-established phase-encoding methods (Sereno et al., 1995; DeYoe et al., 1996; Engel et al., 1997), so only a brief description is provided here. We presented rotating wedges and expanding/contracting rings over multiple runs and averaged runs of the same type. Then a Fourier analysis was applied to the averaged time course to derive the polar angle map and eccentricity map from the wedge and ring data, respectively. Borders between visual areas were defined as phase reversals in the polar angle map of the visual field. The map was visualized on computationally flattened representations of the cortical surface generated by FreeSurfer. For each subject, we could readily define many visual areas, including V1, V2, V3, and hV4. However, we will mainly focus on V1 in this study.

BOLD data analysis.

Data were processed and analyzed using mrTools (http://gru.stanford.edu/mrTools) and other custom code in MATLAB. Preprocessing of functional data included head movement correction, linear detrend, and temporal high-pass filtering at 0.01 Hz. The functional images were then aligned to high-resolution anatomical images for each participant, using an automated robust image registration algorithm (Nestares and Heeger, 2000). Functional data were converted to percentage signal change by dividing the time course of each voxel by its mean signal over a run, and data from the 9 scanning runs were concatenated for subsequent analysis.

Voxel selection.

We used an event-related (finite impulse response or deconvolution) analysis to select voxels in V1 that responded to the stimulus presentation. Each voxel's time series was fitted with a GLM with regressors for 16 conditions (2 contrasts × 8 orientations) that modeled the BOLD response in a 25 s window after trial onset. The design matrix was pseudo-inversed and multiplied by the time series to obtain an estimate of the hemodynamic response for each stimulus condition. Because the stimulus was independently randomized in the left and right visual field, we fitted two event-related models for each subject: one based on the stimulus in the left visual field and one based on the stimulus in the right visual field.

For each voxel, we also computed a goodness-of-fit measure (r² value), which is the amount of variance in the BOLD time series explained by the event-related model (Gardner et al., 2005). In other words, the r² value indicates the degree to which a voxel's time course is modulated by the task events; hence, we can use it to select voxels in V1 that were active during the experiment. We selected voxels whose r² values were >0.05, which yielded ∼100 voxels in each V1 in each hemisphere. Subsequent analysis focused on imaging data in this subset of V1 voxels. Our results did not vary substantially with the voxel selection criterion. For example, when we varied the r² cutoff to select a larger number of V1 voxels (∼150), the tuning widths of the channel response function were 30.6 and 49.9 degrees for the high- and low-contrast stimulus, respectively. For a smaller number of V1 voxels (∼65), the tuning widths values were 22.7 and 38.7 degrees, respectively.

Channel-encoding model.

We used a channel-encoding model (also referred to as an “encoding model” for brevity below), proposed by Brouwer and Heeger (2009) to characterize the orientation tuning of V1 voxels. Conceptually, the model assumes each voxel's response is some linear combination of a set of channels, each channel having the same bandwidth, but with a different preferred stimulus value. We refer to the tuning functions that specify the channels as “model basis functions,” which together span the range of all stimulus values. The intuition is that each voxel's response is due to populations of neurons that are tuned to different stimulus values and the analysis proceeds by trying to determine which combination of these neural populations (channels) are most responsible for a voxel's response. For every stimulus presentation, the ideal response of each channel is calculated based on the stimulus value and model basis functions. The weights of each channel that best fit each voxel's response in the least-squares sense are determined using linear regression from a training dataset. Once these weights are fit, the model can be inverted on a left-out test dataset to reconstruct channel responses from observed voxel responses. The average channel responses relative to the actual presented stimulus is called a channel response function.

To use as training and test data for the channel-encoding model, we obtained single-trial BOLD responses for each V1 voxel with the following procedure. For each V1 hemisphere, we first averaged the event-related BOLD response (see Voxel selection) across all voxels and conditions, which served as an estimate of the hemodynamic impulse response function in each V1 hemisphere. We then constructed a delta function for each individual trial (with the delta corresponding to the time at which the trial began), and convolved it with the estimated hemodynamic impulse response function, to produce a design matrix coding for each individual trial in each condition. The design matrix was then pseudo-inversed and multiplied by the time series to obtain an estimate of the response amplitude for each individual trial in each voxel. We call the set of response amplitudes across all voxels in a V1 hemisphere a response “instance.”

We fit the encoding model to the instances with a fivefold cross-validation scheme, in which four-fifths of the trials were randomly selected to be the training data and the remaining one-fifth of trials constituted the test data. This analysis was performed on instances for the high-contrast and low-contrast trials separately (216 trials per contrast). Our encoding model consisted of 8 evenly spaced channels (i.e., model basis functions) from 0° to 180°, with each channel a half-wave rectified sinusoid raised to the power of 7. These basis functions were chosen to approximate single-neuron's orientation tuning function in V1. In the following exposition, we adopted the notation from Brouwer and Heeger (2009). The training instances can be expressed as a m × n matrix B₁, where m is the number of voxels and n is number of trials in the training data. We then constructed hypothetical channel outputs given the stimulus orientation on each trial of the training dataset, which yielded a k × n matrix C₁, where k is the number of channels (i.e., k = 8). Each column in the C₁ matrix represented a set of ideal response to the stimulus orientation on that trial from the eight channels. A weight matrix W (m × k) relates the observed data B and the hypothetical responses as follows:

Each row of W represents the relative contribution of the eight channels to that voxel's response. The least-square estimate of W was obtained with the following equation (T indicates the transpose of the matrix):

The test instances can be expressed as a m × p matrix B_2, where p is the number of trials in the test data. The estimated channel response to each test stimulus (Ĉ₂) can then be estimated using the weights W as follows:

Ĉ₂ is a k × p matrix, with each column representing each channel's response to the stimulus on that test trial. The columns of Ĉ₂ were circularly shifted such that the channel aligned to the test stimulus on that trial was centered in the orientation space. The shifted columns were then averaged to obtain a mean channel response. This procedure was repeated in each fold of the cross-validation, and the mean channel responses from each fold were further averaged to obtain what we will refer to as a “channel response function.” For each V1 hemisphere in each participant, we obtained channel response functions for both the contralateral and ipsilateral stimulus, separately for the high-contrast and low-contrast conditions.

In addition to the channel response function, we also calculated a goodness-of-fit measure of the encoding model. In each cross-validation fold, after we obtained estimates of the channel weights Ŵ, we also constructed another set of hypothetical channel outputs given the actual stimulus orientation in the test data, C₂ (this is a matrix similar to C₁ but for the test trials, and differs from Ĉ₂, which is the estimated channel responses based on the voxel responses). The predicted voxel response can be obtained via the following:

To the extent that the encoding model provides a good fit to the data, the predicted response B_2pred (m × p) should be similar to the observed response, B₂. We can thus calculate the amount of variance explained by the model as follows:

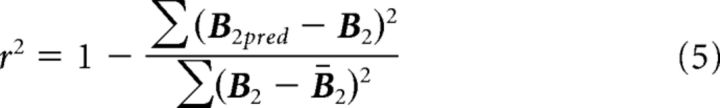B₂ is the mean voxel responses across voxels and trials, and the summation was performed across voxels and trials (i.e., all values in the m × p matrix). We calculated r² from each fold of the cross validation and averaged them across the folds to obtain a single measure of the goodness of fit, for each contrast. This r² is different from the r² that represents the goodness of fit of the event-related model (see Voxel selection). In the remainder of this report, we will focus on this r² value that indexes the goodness of fit of the channel-encoding model.

Quantifying the channel response function.

We fitted a circular bell-shaped function (von Mises) to the channel response function as follows:

Where κ is the concentration parameter that controls the width of the function, μ is the mean, x is the orientation, A is the amplitude parameter, and y₀ is the baseline. Thus, there were four free parameters of the fit: baseline (y₀), amplitude (A), mean (μ), and concentration (κ). Because orientation is on [0, π], whereas the von Mises function spans the interval [0, 2π], orientation values were multiplied by 2 during the fit, after which the fitting results were scaled back to [0, π]. Fitting was performed using a nonlinear least square method, as implemented in MATLAB. To ease the interpretation of the results, we report the half-width at half-maximum instead of the concentration parameter κ because the latter is inversely related to the variance.

Linking neuronal tuning to channel response: a computational model.

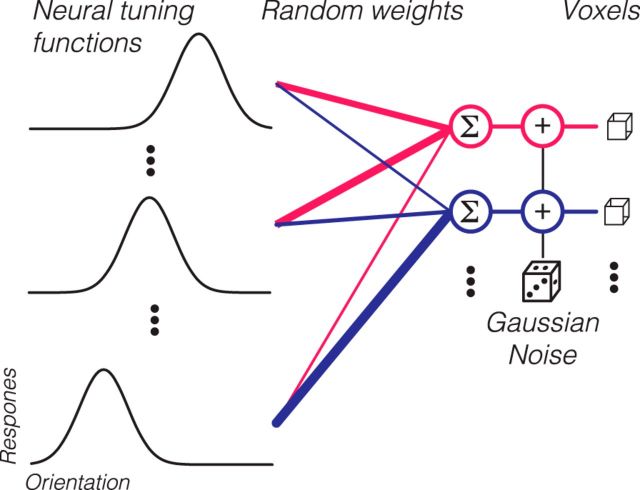
We implemented a computational model that links neuronal tuning to channel response functions, using the assumptions underlying the channel-encoding model. Given that the channel response function is a highly derived statistic, this modeling effort was used to clarify how various assumptions of neural tuning and signal to noise would manifest in channel response functions. Specifically, we used this model to fit our observed data and simulate other scenarios to test the validity of the encoding model. The schematic of the model is outlined in Figure 3. The model contains 100 V1 voxels, comparable with the actual number of voxels used in our data analysis (see above). Each voxel is assumed to contain neurons tuned to all orientations, whose tuning functions are described by von Mises functions (see above). The preferred orientations (μ) are evenly distributed across all possible orientations in 1° increments (left column, “Neural tuning functions”), forming 180 classes of neurons. The width of the neural tuning function is specified by the concentration parameter, κ, which is the same for all neurons but can be manipulated across different simulations. The area under the orientation tuning function for neurons was normalized to 1 so that the average firing rate for each neuron would not vary with tuning width. For each voxel, a weight vector, w, was generated by randomly sampling 180 numbers from [0, 1]. This weight vector specifies how much each class of neurons contributes to the voxel's response. For an input stimulus with an orientation, θ, the response of each neuron is calculated according to its tuning function (see Eq. 6). For each voxel, the responses of individual neurons are multiplied by the weight vector, w, and then summed to arrive at a predicted response (middle column, “Random weights”). To calculate the final voxel response, Gaussian noise, N(0, σ), is then added to this response to simulate physiological and thermal noise in BOLD measurements. Thus, each voxel's response is determined by neuronal tuning width (κ), weight vector (w), and noise (σ). w is randomly generated for each voxel in each simulation, whereas κ and σ are parameters that we examined systematically in several simulations (see Results).

Figure 3.

Schematic of the model linking neuronal response to channel response. Each voxel (right column) received randomly weighted responses from orientation-tuned neurons (left column). After weighting and summing, random Gaussian noise was added to obtain simulated voxel responses.

We simulated experiments with the same basic setup as our empirical study: 8 possible orientations, with each orientation shown 27 times (trials). For each trial, we obtained a vector of voxel responses (instances), calculated as above. Then all the trial instances were subjected to the same analysis as the real data described above (i.e., cross-validation in which four-fifths of data were used to obtain the channel weights and one-fifth of the data was used to obtain channel response functions). We used the same exact code to analyze the synthetic and real data.

Computation of the posterior distributions.

We computed the probability of different stimulus values given the test data (i.e., the posterior distribution) using a technique from van Bergen et al. (2015). The method begins with finding the weights of the channel-encoding model as above. After removing the signal due to the encoding model, a noise model is fit to the residual response. The noise model assumes that each individual voxel's variability is Gaussian with one component that is independent among voxels and another that is shared across all voxels. Each of the channels is modeled to have independent, identically distributed Gaussian noise. This leads to a covariance matrix for the noise as follows:

Where Ω is the noise model's covariance matrix, I is the identity matrix, ♦ denotes element-wise multiplication, τ is a vector containing each voxel's independent standard deviation, ρ is a scalar between 0 and 1, which controls the amount of shared variability among voxels, σ is the SD of each channel, and Ŵ is the estimated weight matrix from Equation 2. This noise model with parameters, τ, ρ, and σ is fit via maximum likelihood estimation to the residual and can be used to compute the probability of generating any particular response given a stimulus value. Inversion of this equation using Bayes' rule and a flat prior allows one to compute the probability of any stimulus value given a response, the posterior distribution (for a derivation and detailed explanation, see van Bergen et al., 2015). All analysis followed the same fivefold cross-validation scheme used for the encoding model by which four-fifths of the data were used to fit the model weights and noise model parameters and the one-fifth left-out data were used to compute the posterior distribution using Bayes' rule. Results are shown averaged across all five left-out folds.

Results

We measured BOLD responses from retinotopically defined V1 to oriented sinusoidal gratings (Fig. 1) and used the resulting data to train and test a channel-encoding model. We first report average (univariate) activity across voxels. Although responses averaged across subjects and voxels in V1 did not show any apparent selectivity for orientation (Fig. 2A), they were, as expected (Boynton et al., 2012), greater for higher-contrast compared with low-contrast contralateral stimuli (compare red vs yellow). Consistent with the laterality of V1, responses did not vary with contrast of the ipsilateral stimulus (black). The presence of a strong contrast response for the contralateral stimuli, but a complete absence of such a response for ipsilateral stimuli, also suggests that subjects maintained stable central fixation.

Figure 2.

A, Group-averaged mean BOLD response across V1 for each orientation, separately for the contralateral and ipsilateral high- and low-contrast stimuli. B, Group-averaged channel response functions from V1 to a high-contrast grating. Contra, Response calculated for the contralateral stimulus; Ipsi, response calculated for the ipsilateral stimulus. C, Same as B, except for low-contrast grating. D, Group-averaged channel response functions to the low- and high-contrast grating in the contralateral visual field (symbols, same as the contralateral response in B, C). Solid lines indicate best-fitting von Mises functions to each contrast level. Error bars indicate SEM across participants.

Despite this lack of orientation selectivity, channel response functions obtained from the encoding model and averaged across subjects displayed peaked responses at the true orientation of the contralateral stimulus for both high-contrast (Fig. 2B, red) and low-contrast (Fig. 2C, yellow) stimuli. We computed r², a measure of goodness of fit, which showed that the channel-encoding model accounted for 31% and 13% (high- and low-contrast contralateral stimuli, respectively) amount of the variability of the data. The ability to recover these peaked functions of orientation is consistent with previous studies using classification approaches (Kamitani and Tong, 2005) and is presumably due to biases in response to orientation, which differ for individual voxels but are eliminated when responses are averaged across voxels. As expected from the lateralization of V1, these channel response functions are flat when constructed for the ipsilateral stimulus (black), thus serving as an internal control on the validity of the encoding model approach.

However, contrary to the expectations of contrast invariance, channel response functions were broader for low-contrast compared with high-contrast contralateral stimuli (Fig. 2D, compare yellow with red). Fitting a bell-shaped function (von Mises) to the subject-averaged channel response functions revealed that the tuning width went from 25.6 to 42.0 degrees (half-width at half-height) as contrast was lowered. Amplitude was also decreased for the low-contrast stimuli from 0.27 to 0.23, where 1 would be the ideal height of the channel response function if voxel responses contained noise-free information about stimulus orientation. This pattern of results was also evident in individual subject's channel response functions. Nine of 12 hemispheres showed a decrease in tuning width as contrast was decreased (p = 0.013, t₍₁₁₎ = −2.60, one-tailed paired t test). Ten of 12 hemispheres had lower amplitude for the low-contrast condition (p = 0.042, t₍₁₁₎ = 1.90, one-tailed paired t test). We also examined extrastriate areas V2, V3, and hV4 and found similar results. In V2, tuning width went from 21.3 to 75.5 degrees and amplitude went from 0.25 to 0.19 as contrast was lowered. In V3, tuning width went from 17.8 to 88.6 degrees and amplitude went from 0.23 to 0.18 as contrast was lowered. Finally, in hV4, tuning width for high-contrast stimuli was 14.2 degrees and channel response function was essentially flat for low-contrast stimuli. Below, we focus on results from V1, which is best informed by neurophysiological results (Sclar and Freeman, 1982; Skottun et al., 1987; Carandini et al., 1997).

Although the lack of contrast-invariant channel response functions might imply broader neuronal tuning at low contrast in human visual cortex, we instead considered whether it might be due to the weaker stimulus-driven signal at lower contrast. As noted above, BOLD responses had lower amplitude with lower contrast (Fig. 2A). Given that many sources of noise in BOLD are non-neural (e.g., hemodynamic variability and head motion) and thus not expected to vary with signal strength, these lower-amplitude responses result in lower SNR of the measurements made with lower contrast. Indeed, the amount of variance accounted for by the encoding model, r², was significantly lower for low-contrast compared with high-contrast stimuli for 12 of 12 hemispheres (p < 0.001, t₍₁₁₎ = 5.58, one-tailed paired t test). In the extreme case, channel response functions built on responses without any signal, as for the ipsilateral stimulus, are flat. Thus, we reasoned that the lower SNR measurements at low contrast could also result in flatter (i.e., broader) channel response functions.

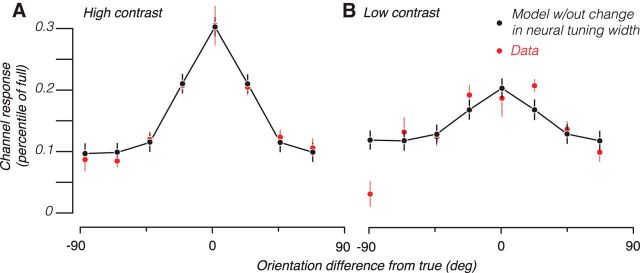
To test whether reduced SNR at low contrast, rather than changes in neural tuning, could account for the increased channel response bandwidth at low contrast, we built simulations (Fig. 3; see Materials and Methods). Briefly, each simulated voxel received randomly weighted responses from simulated orientation-tuned neurons. Different voxels had different weightings of the neuronal responses, thus resulting in weak, but different, orientation selectivity across voxels. We added random Gaussian noise to these voxel responses and trained and tested the encoding model using the same procedures as we did for the actual BOLD data. We varied the SD of the added noise (σ) to produce channel response functions that best fit the empirical data (in the least-squares sense) from the high-contrast trials (Fig. 4A). We then noted that, in the empirical data, there was a 42.2% decrease in neural response from high to low contrast across voxels (Fig. 2A). We therefore decreased neural response by this amount for all the simulated neurons and found that the resulting channel response function to be a reasonable fit for the low-contrast data (Fig. 4B). Importantly, this good correspondence between model predictions and data was achieved without fitting any parameter because the only thing we changed in the simulation was to decrease the magnitude of response across all neurons according to the value found from the empirical data. This suggests that reductions in response magnitude, and therefore SNR, are sufficient to produce changes in channel response width commensurate with what we observed.

Figure 4.

Model predictions of empirical channel response functions. A, Empirical channel response function for contralateral high-contrast stimuli (red symbols, same data as in Fig. 2B) were fit by the computational model, with the best-fitting channel response shown in black symbols and lines. B, Empirical channel response function for contralateral low-contrast stimuli (red symbols, same data as in Fig. 2C) and the channel response from the same model used in A (black symbols and lines), except that the neuronal response amplitude was reduced. Error bars indicate SE across subjects and hemispheres.

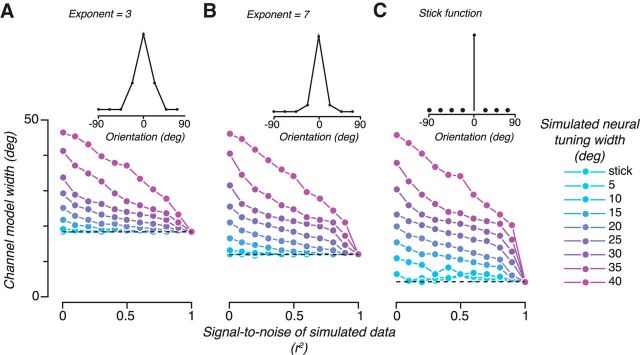
Although tuning width is not expected to change with contrast, what if we had tested a property for which we expect a neural tuning width change? Do channel response functions track changes in neural tuning width? We simulated neural tuning functions from 5 to 40 degrees half-width at half-height as well as a “stick function,” which responds only to a single orientation maximally and does not respond to any other orientation and computed channel response functions under different amounts of noise (Fig. 5A, cyan to magenta curves represent different neural tuning widths). We found that the resulting channel response functions did indeed track the neural tuning widths, but as the goodness-of-fit r² increased (achieved by varying the SD of the added noise; Fig. 5B, abscissa), the difference in channel response widths was diminished (Fig. 5B, larger splay of curves on the left vs right side). Thus, channel response functions can reflect underlying neural tuning widths; but perhaps counterintuitively, the better the goodness of fit of the encoding model, the less difference the neural tuning width makes.

Figure 5.

Model simulations of how channel response function varies with neural tuning, SNR, and model basis function. Each panel uses a different model basis function (shown in the top graph) to derive channel responses from synthetic data generated with different combinations of signal to noise (r², x-axis) and neural tuning width (colored lines). The width of the channel response function is plotted on the y-axis. Horizontal dashed lines indicate the width of the model basis function. A has a half-wave rectified sinusoid with exponent of 3, B has a half-wave rectified sinusoid with exponent of 7 and C has a stick function; shown in the top graph.

To understand why better goodness of fit implies worse model discriminability of underlying neural tuning functions, it is important to note that the absolute width of channel response functions is, in the limit of no noise, determined by the basis functions used in the encoding model and not by the neural tuning widths themselves. We simulated two variations of the encoding model in which we varied the model basis function widths. We increased the basis function width by decreasing the exponent on the sinusoidal basis to 3 (Fig. 5A) and decreased the basis function width by using stick filters (Fig. 5C). For all the simulations, as the goodness of fit increases, the recovered channel response functions approach the width of the model basis function (dashed line) rather than the neuronal response width (for both the channel response functions and the model basis functions, we use the fitted half-width at half-height as our measure of tuning width; therefore, the stick functions do not have infinitely narrow tuning). Given that the encoding model is essentially a linear regression model, this is not an unexpected outcome. Linear weights are being determined to best map the voxel responses unto ideal channel responses. As long as the voxel responses are determined by stimulus orientation, then the regression model will be able to recreate exactly any model basis functions that can be formed as linear combinations of the represented orientations.

The above analysis suggests that, although absolute neural tuning width may not be readily determined from the channel response function width, changes in tuning width might be meaningful if SNR does not change between conditions. That is, reading vertically for one level of goodness of fit in Figure 5A–C, the channel response function width changes systematically as a function of neural tuning width. Might we be able to determine that neural tuning width has changed if we observe data in which we have matched goodness of fit of the encoding model? Although this does not occur for changes in contrast, this could be the case for potential modulation of tuning width by cognitive factors, such as attention and learning.

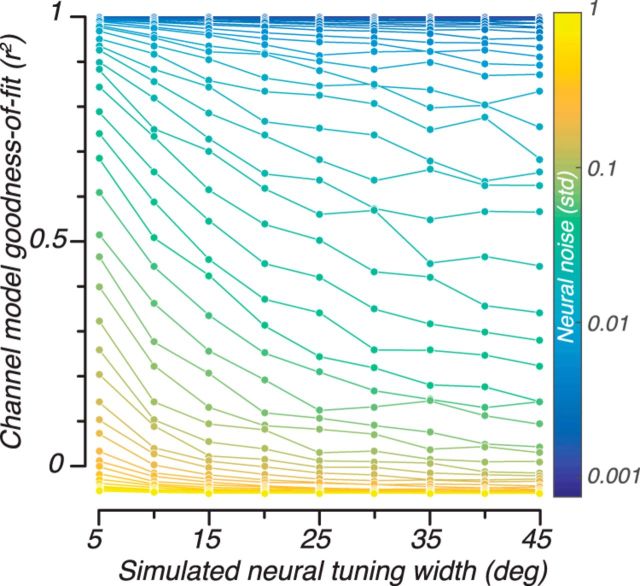
However, changes in neural tuning width also result in changes in the model's goodness of fit, thus complicating the possibility of interpreting changes in channel response width. We simulated different neural tuning widths from 5 to 45 degrees half-width at half-height (Fig. 6, abscissa) for different amounts of additive noise (SD ranging on a logarithmic scale from 0.001 to 1, blue to yellow curves). As can be appreciated by the downward slopes of the curves in Figure 6, as the neural tuning widths get larger, the fit of the encoding model gets worse (lower r², ordinate). The reason for this worsened fit is because as neural tuning width gets wider, there is less information about orientation available to fit the model. In the extreme, a flat neural tuning function would result in no orientation-specific response and the encoding model would fail to fit the data completely. Each curve in the simulation is what one might expect to measure if neural tuning width is the only variable that changes in the experiment and noise is due mostly to external factors that do not change with conditions. That is, if one expects only an increase in neural tuning width, the resulting channel response functions would be expected to have both wider tuning and lower r². This pattern of results would make it difficult, if not impossible, to determine whether the changes in tuning were due to decreased SNR, decreased neural tuning width, or some combination of both.

Figure 6.

Model simulations of how goodness of fit of the encoding model (r²) varies with neural tuning width and noise level in the synthetic data. Different colors represent different amounts of Gaussian noise added to the simulated neural response.

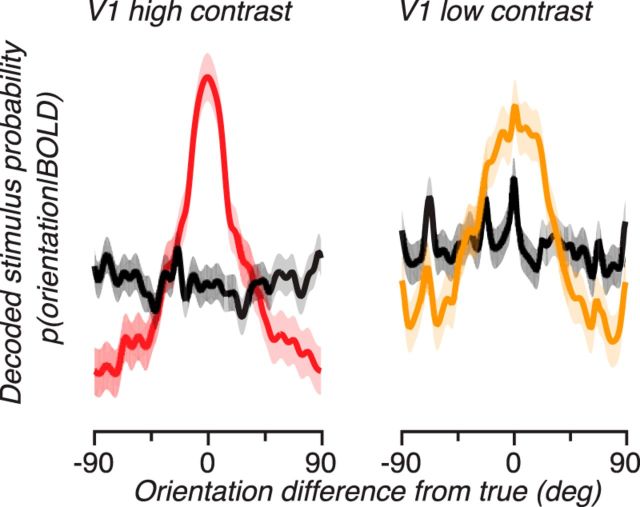
These empirical and simulation results suggest caution in interpreting changes in channel response functions because they could be due to either or both changes in neural tuning width and changes in signal strength. What better ways are there for interpreting these functions? A recent report (van Bergen et al., 2015) proposes to transform these channel response functions into posterior distributions that show the probability of different stimulus values given the measured response. We applied the same analysis to our channel response functions, by estimating the distribution of noise in the voxels and channels to determine the probability of measuring responses given any oriented stimulus and then applying Bayes' rule with a flat prior to obtain the probability of various stimuli given the responses we measured in a left-out validation dataset (see Materials and Methods; Fig. 7). This resulted in posterior distributions that were peaked around the actual orientation for the contralateral stimulus (red and yellow curves) but flat for the ipsilateral stimulus (black curves), thus replicating the results on channel responses. This transformation of the results into posterior distributions allows for a more straightforward interpretation of the encoding model approach, encouraging interpretation in terms of the certainty by which a given neural response tells us what the stimulus was, rather than what it implies about underlying neural tuning functions.

Figure 7.

Posterior distributions from the Bayesian analysis. These functions represent the probability that a given stimulus (measured by the offset from the true orientation, x-axis) caused the observed BOLD response. Red represents posterior distributions for high-contrast contralateral stimuli. Yellow represents posterior distributions for low-contrast contralateral stimuli. Black represents posterior distributions for ipsilateral stimuli. Shaded region represents the SE over subjects and hemispheres.

Discussion

Using an encoding model approach, we built channel response functions for orientation and found that, unlike contrast-invariant single units, they were broader at lower contrast. Simulations showed that this effect could be fully explained by the measured decrease in overall neural response between high and low contrast, which results in lower SNR. As signal to noise is increased, channel response functions become narrower, until, in the limit of no noise, they approximate the shape of the model basis function (and not the underlying neural tuning function). While changes in underlying neural selectivity in our model could be reflected in channel response functions, our results demonstrate that changes in channel response functions do not necessarily reflect changes in underlying neural selectivity.

Orientation selectivity of single-unit responses has been shown to be invariant to image contrast (Sclar and Freeman, 1982; Skottun et al., 1987; Carandini et al., 1997), suggestive of a general neural computational mechanism (Carandini and Heeger, 2011) by which visual perception can remain relatively unaffected by differences in visibility of stimuli. Despite this central theoretic importance, obtaining noninvasive measurement of selectivity bandwidth from human cortex has been technically difficult because orientation selectivity is organized into cortical columns (Hubel and Wiesel, 1962, 1968; Blasdel and Salama, 1986; Bonhoeffer and Grinvald, 1991), much smaller than the typical spatial resolution of BOLD (Ogawa et al., 1990, 1992) measurements. While direct measurements of such columnar structures in humans have been achieved (Cheng et al., 2001; Sun et al., 2007; Yacoub et al., 2007, 2008), multivariate analysis using pattern classification approach to decode orientation and motion direction (Haynes and Rees, 2005; Kamitani and Tong, 2005, 2006) from distributed activity patterns has become a more common approach (Norman et al., 2006). However, this classification approach generally produces a categorical outcome, for example, which of two orientations was more likely to have resulted in the measured response pattern and thus is not typically used for probing selectivity bandwidth of neural representations. The encoding model approach allows one to reconstruct a response profile for a stimulus that has a tuning bandwidth that can be inspected across different contrasts.

Although we found an increase in the bandwidth of channel response functions for lower-contrast stimuli from human V1, this increase could be fully accounted for by the measured reduction of response amplitude due to contrast, thus reconciling our data with contrast-invariant orientation tuning. We recognize that contrast invariance at the population level as measured with BOLD is not guaranteed, even if single-unit spiking responses display contrast invariance. Systematic relationships between contrast sensitivity and selectivity for orientation could result in population responses changing selectivity with contrast. For example, if the least orientation-selective neurons saturate their responses at lower contrast than the most selective neurons, then population response would become more selective as contrast increases because population response would be dominated by the most selective neurons. However, no such systematic relationship has been observed and population spiking responses appear contrast-invariant in cats (Busse et al., 2009), consistent with our results. Furthermore, BOLD measurements may be better correlated with local field potentials than spiking activity (Logothetis et al., 2001), which could also result in deviations of BOLD population measures of contrast invariance and spiking activity of neurons. If BOLD measures are sensitive to subthreshold, synaptic activity that can contribute to local field potentials, broadening of channel response functions that we observed could be reflective of subthreshold activity, if such activity is not contrast-invariant. However, intracellular measurements of membrane potentials show that selectivity does not broaden at lower contrast. Indeed, selectivity is slightly increased at low contrast (Finn et al., 2007), consistent with our interpretation that channel response function broadening at low contrast is due to reduction in signal to noise.

Given our results, bridging effects of attention on single units with effects uncovered using encoding models of functional imaging measurements (Sprague et al., 2015) may be similarly complicated as bridging contrast invariance effects. Single-unit studies have suggested that neurons change gain, not selectivity bandwidth (McAdams and Maunsell, 1999; David et al., 2008) with spatial attention, a key finding that has shaped our understanding of neural mechanisms of attention (Carrasco, 2011; Ling et al., 2015). In human population measurements, improved orientation encoding has been found when orientation (but not contrast) is task relevant (Jehee et al., 2011; Ling et al., 2015). Although it would be of interest to know whether these population effects of attention reflect differences in neural tuning bandwidth, selective attention, similar to image contrast, also modulates response amplitudes (Brefczynski and DeYoe, 1999; Gandhi et al., 1999; Kastner et al., 1999; Kastner and Ungerleider, 2000; Reynolds and Chelazzi, 2004) and thus is expected to improve SNR for population measures. Similarly to contrast effects, attention should be expected to bias channel response functions toward a narrower tuning, even if neural tuning bandwidth does not change.

A similar disconnect between single-unit and population measures impacts even simpler measures of cortical response that do not require multivariate approaches. Contrast sensitivity can be directly imaged because single units monotonically increase response with contrast (Albrecht and Hamilton, 1982; Sclar et al., 1990; Busse et al., 2009), resulting in a population response that also monotonically increases (Tootell et al., 1998; Boynton et al., 1999; Logothetis et al., 2001; Avidan and Behrmann, 2002; Olman et al., 2004; Gardner et al., 2005). Spatial attention has generally been shown to shift contrast response vertically upward when measured with functional imaging (Buracas and Boynton, 2007; Li et al., 2008; Murray, 2008; Pestilli et al., 2011; Hara and Gardner, 2014), which appears to be different from the variety of effects from contrast-gain to response-gain reported for single units (Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002; Williford and Maunsell, 2006; Lee and Maunsell, 2010; Pooresmaeili et al., 2010; Sani et al., 2017). Consideration of normalization and the size of the attention field relative to stimulus-driven responses can give rise to effects that can account for single-unit responses and EEG measures (Reynolds and Heeger, 2009; Itthipuripat et al., 2014). But predictions of this normalization model of attention may differ for single units and population measures as different neurons in a population can be exposed to different balance of attention field and stimulus drive, giving rise to additive shifts when considered as a population (Hara et al., 2014). Relatedly, response gain changes may also manifest as additive shifts when directly examining voxel feature selectivity (Saproo and Serences, 2010).

While neural tuning width can be reflected in channel response functions, neural tuning width and signal-to-noise changes are intertwined, making it hard to disentangle their effects. For example, one might examine conditions in which signal to noise is matched and then hope to attribute changes in channel response function bandwidth solely to changes in neural tuning bandwidth. However, our simulations show signal-to-noise measures, such as the variance accounted for by the encoding model (r²), covary with neural tuning width. As neural tuning width broadens, there is less modulation of voxel response with orientation; thus, the encoding model shows a decrease in r². Therefore, even pure changes in neural tuning width would result in conditions with lower r², making it hard to attribute changes in channel response functions solely to changes in neural tuning width.

The results of our simulation are agnostic to the source of selectivity for orientation in voxels. One possible source of orientation information are the irregularities of columnar organization, which could give rise to small, idiosyncratic biases in voxels (Boynton, 2005; Swisher et al., 2010). However, large-scale biases for cardinal (Furmanski and Engel, 2000; Sun et al., 2013) and radial (Sasaki et al., 2006) orientations have been reported, and these biases have been shown to be an important source of information to drive classification (Freeman et al., 2011, 2013; Beckett et al., 2012; Wang et al., 2014; Larsson et al., 2017; but see Alink et al., 2013; Pratte et al., 2016). Large-scale biases may result from vascular (Gardner, 2010; Kriegeskorte et al., 2010; Shmuel et al., 2010) or stimulus aperture (Carlson, 2014) related effects. Our simulations do not require, or exclude, any topographic arrangement of biases. Regardless of the source of orientation bias, channel response function widths would be expected to broaden as signal to noise decreases.

More generally, our results suggest a “reverse-inference” problem (Aguirre, 2003; Poldrack, 2006) when interpreting outputs from inverted encoding models. Forward encoding from hypothetical neural responses to population activity is a powerful tool, but reversing this process to infer about neural responses is problematic when there is not a one-to-one mapping between single-unit and population measures. Consequently, this reverse-inference problem is not restricted to channel-encoding models but will occur for other encoding model approaches, such as population receptive fields (Dumoulin and Wandell, 2008) or Gabor wavelet pyramids (Kay et al., 2008), if one were to invert these models to infer properties of the underlying neural responses. For contrast and orientation, both increases in response amplitude and neural selectivity can result in narrower bandwidth of the channel response functions, so reverse inference requires taking both into account. Regardless of which neural change has occurred, read-out of these responses, be they in the brain or from external measurement, will have less certainty about what stimulus has caused those responses. Techniques that represent the output of encoding models as posterior distributions (van Bergen et al., 2015) offer a straightforward interpretation of the uncertainty in determining stimulus properties from cortical responses.