Impaired hippocampal place cell dynamics in a mouse model of the 22q11.2 deletion

Abstract

Hippocampal place cells represent the cellular substrate of episodic memory. Place cell ensembles reorganize to support learning but must also maintain stable representations to facilitate memory recall. Despite extensive research, the learning-related role of place cell dynamics in health and disease remains elusive. Using chronic two-photon Ca²⁺ imaging in hippocampal area CA1 of wild-type and Df(16)A^+/− mice, an animal model of 22q11.2 deletion syndrome, one of the most common genetic risk factors for cognitive dysfunction and schizophrenia, we found that goal-oriented learning in wild-type mice was supported by stable spatial maps and robust remapping of place fields toward the goal location. Df(16)A^+/− mice showed a significant learning deficit accompanied by reduced spatial map stability and the absence of goal-directed place cell reorganization. These results expand our understanding of the hippocampal ensemble dynamics supporting cognitive flexibility and demonstrate their importance in a model of 22q11.2-associated cognitive dysfunction.

Episodic memory, the encoding of personal experience organized in space and time, is a fundamental aspect of cognition¹. Episodic memory dysfunctions are highly debilitating symptoms of various neurological, cognitive and psychiatric disorders, including schizophrenia (SCZ)². Cognitive deficits in general appear to be the strongest predictor of SCZ patients’ functional outcomes³; however, neural circuit dynamics supporting episodic memory and the manner in which they fail in SCZ remains poorly understood. To this end, we studied a well characterized animal model of cognitive dysfunction and SCZ, the Df(16)A^+/− mouse model of the 22q11.2 deletion syndrome (22q11.2DS)⁴.

The well documented role of the hippocampus in episodic and spatial memory^1,5–7, combined with morphological and functional alterations of the hippocampus in SCZ patients^8,9, collectively points to a central role of this brain area in the pathophysiology of cognitive memory deficits in SCZ¹⁰. In particular, physiological and morphological alterations have been reported specifically in area CA1—the hippocampal output node—in SCZ patients¹¹, suggesting a potentially primary role for this area in disease pathophysiology.

Principal cells throughout the hippocampus are selectively active in specific locations within an environment (place cells)¹². Place cells collectively form cognitive maps representing spatial components of episodic memories^6,13, the long-term stability of which is a widely posited prerequisite for reliable learning^14–18. Place cell map stability is affected by attentional and task demands, and place cell maps also incorporate goal-related information during learning^15,19–25. In particular, reorganizing place cell maps to enrich goal locations was found to predict memory performance²⁶. Therefore, monitoring place cell ensemble dynamics during goal-directed learning may provide a tractable entry point for understanding how episodic memory deficits arise from genetic mutations associated with SCZ.

Two-photon Ca²⁺ imaging in awake mice during head-fixed behaviors allows for the chronic recording of physiological activity from individual place cells, as well as their ensemble activity as a whole. By tracking the activity of place cell populations in Df(16)A^+/− mice and wild-type (WT) littermates through each phase of a goal-oriented learning task, we identified specific aspects of place cell map stability that evolved with learning, as well as alterations in the stability and plasticity of these cognitive maps in the mutant mice. Our findings highlight reduced stability and impaired goal-directed reorganization of hippocampal place cells as fundamental components of 22q11.2-deletion-linked cognitive dysfunction.

RESULTS

Df(16)A^+/− mice are impaired in a head-fixed goal-oriented learning task upon changes in both context and reward location

To facilitate chronic recording from hippocampal CA1 place cells during learning, we designed a head-fixed variation of goal-oriented learning (GOL; Fig. 1a,b and Online Methods) tasks that have been previously used in freely moving rodents²⁶, allowing for chronic two-photon functional Ca²⁺ imaging. Our task consisted of three sessions per day, with 3 days (d) for each of three conditions (27 total sessions per mouse). In Condition I, mice learned a single fixed reward location, then remembered that location while the environmental context and local cues were altered (Online Methods) in Condition II, and the reward was moved in Condition III.

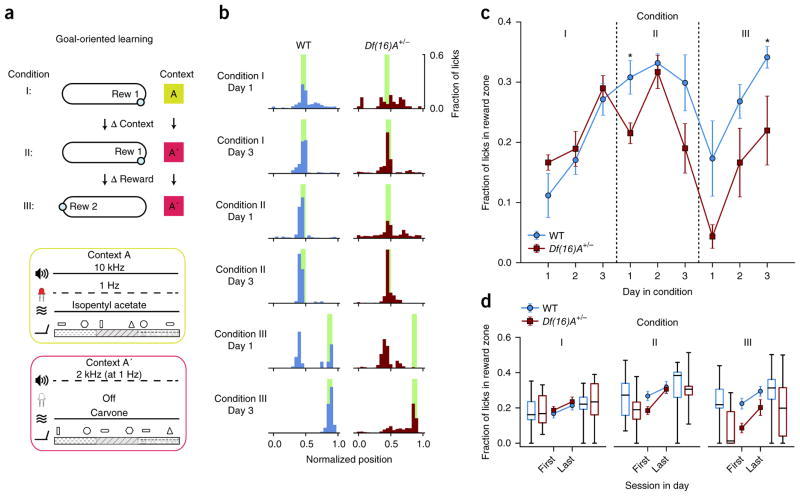
Figure 1.

Differences in learning performance between Df(16)A^+/− and WT mice in GOL task. (a) The three conditions of the GOL task. Mice spend 3 d in each condition. Contexts A and A′ are composed of different auditory, visual, olfactory and tactile cues (Online Methods), varied between Condition I and Condition II. The location of the hidden reward (blue circles, Rew 1 and Rew 2) is switched between Condition II and Condition III. Water-deprived mice trained to run on a linear treadmill were introduced to a novel environmental context (Context A) consisting of a feature-rich fabric belt and specific background with nonspatial odor, tones and blinking light patterns (Context A) on the first day of the experiment. Operant water rewards were available at a single unmarked location on the belt (Rew 1 in Conditions I and II; Rew 2 in Condition III); if the mouse licked in the correct location they received a water reward, but no water was administered if they did not lick in the reward location or if they licked outside the reward location (Condition I, 3 d and 3 sessions per d). The time of each lick as well as the position of the mouse on the treadmill were recorded both to determine when to deliver water rewards and to provide a readout of learning. To test the ability of mice to adjust to changes in the task conditions, mice were exposed to an altered context (Context A′: same sequence of belt materials, shuffled local cues, different nonspatial odor, tone and light; Online Methods), while maintaining the same reward location relative to the belt fabric sequence (Condition II, 3 d and 3 sessions per d). During the last part of the task, the location of the hidden reward was changed while maintaining the familiar context from Condition II (Condition III, 3 d and 3 sessions per d). (b) Example histograms of lick counts by position for a WT mouse (blue) and a Df(16)A^+/− mouse (red) on the first and last days of each condition. Green bars, reward locations. As the mice learned the reward location they switched from exploratory licking along the entire belt to focused licking only at the reward location, suppressing licking at other locations. Hence licking became increasingly specific for the reward location. (c) Learning performance of WT and Df(16)A^+/− mice based on fraction of licks in the reward zone (n = 6 mice per genotype, main effects described in Results section, post hoc tests with Benjamini-Hochberg correction, Condition I, two-way mixed-design RM ANOVA, main effect of day: F_2,20 = 28.235, P < 0.0001; Condition II, two-way mixed-design RM ANOVA, main effect of genotype: F_1,10 = 6.297, P = 0.031; main effect of day: F_2,20 = 4.076, P = 0.033; Day 1: P = 0.015 ; Condition III, two-way mixed-design RM ANOVA, main effects of day: F_2,20 = 15.762, P < 0.0001; main effect of genotype: F_1,10 = 7.768, P = 0.019; day × genotype interaction P = 0.932: n.s.; Day 3: P = 0.022). Error bars represent s.e.m. (d) Learning performance for WT and Df(16)A^+/− mice on the first and last session of each day by Condition. Across all conditions, both genotypes performed better at the end of the day. During Condition I, WT and Df(16)A^+/− mice performed similarly throughout the day (main effects described in Results section), while in Condition II, Df(16)A^+/− mice were more impaired at the start of the day (post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of session: F_1,10 = 40.506, P < 0.0001; genotype × session interaction: F_1,10 = 6.404, P = 0.030; main effect of genotype, P = 0.213: n.s.), and in Condition III they additionally never reached WT levels (post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of genotype: F_1,10 = 6.433, P = 0.030; main effect of session: F_1,10 = 53.237, P < 0.0001; genotype × session interaction P = 0.085: n.s.). Center line in box plot is the median, the top and bottom of the box denote the 1st and 3rd quartile of the data, respectively, and the whiskers mark the full range of the data. *P < 0.05.

Our overall analysis of behavior during the GOL task revealed general differences among genotypes, which developed in a condition-dependent manner (linear mixed-effects model, fixed effects for genotype and condition, day nested under condition as covariate, mouse as random effect; significant effect of: genotype: F_1,83.049 = 5.675, P = 0.019; genotype × Condition interaction: F_2,82.988 = 5.450, P = 0.006; Condition: F_2,82.988 = 23.554, P < 0.0001). Specifically, the initial analysis revealed significant differences for Conditions II (P = 0.028) and III (P = 0.0008) among the two genotypes (for formulas, see Online Methods). We found that both Df(16)A^+/− mice and WT littermates had a similar ability to learn the initial location of the hidden reward, as assessed by the suppression of unrewarded licks outside of the reward zone and an increase in the fraction of licks within the reward zone (post hoc tests for Condition I with Benjamini-Hochberg correction: two-way mixed-design repeated-measures (RM) ANOVA, main effect of day: F_2,20 = 28.235, P < 0.0001; genotype × day interaction, P = 0.608 and main effect of genotype, P = 0.319: nonsignificant (n.s.); Fig. 1b,c and Supplementary Fig. 1). During this initial learning period, both WT and Df(16)A^+/− mice explored the task at similar levels (Supplementary Fig. 2).

A change in the environmental context (Condition II) had no detectable effect on WT animals, as their learning of the reward location in the new context continued to improve until their performance plateaued. However, in the Df(16)A^+/− mice, task performance dropped on the first day and was overall worse than WT mice during Condition II (post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of genotype: F_1,10 = 6.297, P = 0.031; main effect of day: F_2,20 = 4.076, P = 0.033; day 1: P = 0.015; day × genotype interaction: P = 0.239, n.s.; Fig. 1b,c). Although not significant, the drop in performance and increase in variability on the third day of Condition II for WT and Df(16)A^+/− mice might have arisen from differences in attention or motivation. By this point mice had been training in the task for 6 consecutive days and were performing relatively well, so the task had become familiar and it is possible that they were less water-deprived and thus overall less motivated.

Finally, changing the reward location while maintaining a familiar context (Condition III) challenged Df(16)A^+/− mice to a greater degree than WT animals, as they were significantly impaired in acquiring the new reward location (post hoc tests with Benjamini-Hochberg correction, Condition III, two-way mixed-design RM ANOVA, main effects of day: F_2,20 = 15.762, P < 0.0001; main effect of genotype: F_1,10 = 7.768, P = 0.019; day × genotype interaction: P = 0.932, n.s.; day 3: P = 0.022; Fig. 1b,c). Thus, although Df(16)A^+/− mice were initially able to perform a spatially guided reward task, learning deficits were revealed by manipulation of task parameters, specifically the environmental context or the reward location. Assessment of learning by anticipatory licking, although a much less sensitive behavioral readout, revealed the same pattern of learning performance and differences among the two genotypes (Supplementary Fig. 3).

We noticed during the task that Df(16)A^+/− mice appeared to be relatively more impaired at the start of each day, so to identify differences in the overnight consolidation of the task memory, we compared task performance at the beginning and the end of the day during each condition (Fig. 1d). Overall, there was a strong effect of the first versus last session of the day and a significant genotype–condition interaction, as previously detected (linear mixed-effects model, fixed effects for condition, session and genotype, session as covariate, random effect for mouse; genotype effect: F_1,90.473 = 7.638, P = 0.007; session effect: F_1,159.244 = 22.612, P < 0.0001; genotype × condition interaction: F_2,90.347 = 3.732, P = 0.028). During Condition I, in which we observed no learning deficit in the Df(16)A^+/− mice, both WT and Df(16)A^+/− mice performed at comparable levels throughout the day, and both performed better at the end of the day than at the beginning (Condition I, post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of session: F_1,10 = 6.901, P = 0.025; main effect of genotype, P = 0.437 and genotype × session interaction, P = 0.975, n.s.). During Condition II, in which we observed an overall decrease in task performance in the Df(16)A^+/− mice, we found that the Df(16)A^+/− animals performed more poorly on the first session of each day, before reaching WT performance levels by the end of the day (Condition II, post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of session: F_1,10 = 40.506, P < 0.0001; F_1,10 = 6.404, genotype × session interaction: P = 0.030; main effect of genotype: P = 0.213, n.s.). Finally, during Condition III, in which we observed the most robust learning deficit in the Df(16)A^+/− mice, we found that Df(16)A^+/− mice performed significantly worse throughout the entire day (Condition III, post hoc tests with Benjamini-Hochberg correction: two-way mixed-design RM ANOVA, main effect of genotype: F_1,10 = 6.433, P = 0.030; main effect of session: F_1,10 = 53.237, P < 0.0001, genotype × session interaction: P = 0.085, n.s.). Collectively, these results indicate that deficits in overnight consolidation likely contributed to the differences we observed between genotypes.

Differences in place cell properties at the neuronal population levels in the Df(16)A^+/− mice

We used two-photon Ca²⁺ imaging of large neuronal populations in the CA1 pyramidal layer during the GOL task to assess the basic coding properties of place cells (Fig. 2a,b). Spatially tuned Ca²⁺ transients (Fig. 2c) were detected in both WT and Df(16)A^+/− mice, but we found that the fraction of identified neurons that exhibited place cell properties was about 25% smaller in Df(16)A^+/− mice compared to WT mice across all sessions (place cell fraction: averaged by mouse, independent samples t test, t = 1.620, P = 0.140; linear mixed-effects model with mouse as random factor F_1,10.917 = 3.086, P = 0.107; Fig. 2d). This effect was not driven by a silent fraction of cells in the Df(16)A^+/− mice or by differences in our sampling of the pyramidal cells between the genotypes, as the available place cell population was similar cumulatively over all imaging sessions (lifetime place coding: P = 0.244; Supplementary Fig. 4a), but individual cells were identified as place cells in fewer sessions (fraction of sessions a place cell: P < 0.0001; Supplementary Fig. 4b). Furthermore, the spatial tuning of individual place cells in Df(16)A^+/− mice was less diffuse, as indicated by differences in the number of place fields per place cell (place fields per place cell: WT, 1.180 ± 0.004, n = 12,571, place cells × sessions; Df(16)A^+/−, 1.110 ± 0.004, n = 7,683, place cells × sessions; linear mixed-effects model with number of place fields and genotype as fixed factors and mouse ID as random factor: number of place fields × genotype interaction: F_3,38.000 = 5.054, P = 0.005; genotype effect for: single place field; P = 0.0037, two fields per place cell; P = 0.010, three fields per place cell; P = 0.755, see formula in Online Methods; Fig. 2e), slightly narrower place fields (place field width: linear mixed-effects model with mouse as random factor: F_1,11.164 = 4.371, P = 0.060; Fig. 2f and Supplementary Fig. 4e), less variability in Ca²⁺ transient firing locations (circular variance; inset averaged by mouse, Welch’s t test, t = 2.327, P = 0.0491; linear mixed-effects model with mouse as random factor: F_1,11.006 = 5.695, P = 0.036; Fig. 2g) and less out-of-field firing (transient specificity: P < 0.0001; Supplementary Fig. 4d).

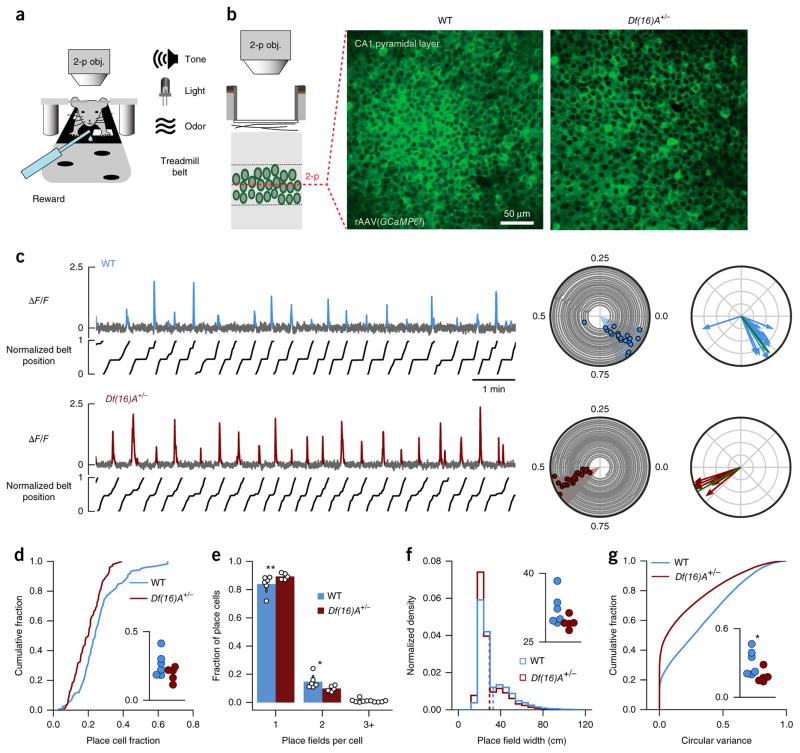
Figure 2.

Altered place cell properties in Df(16)A^+/− mice. (a) Schematic of head-fixed behavioral setup. Two-photon objective, 2-p obj. (b) Mice were injected with AAV1/2(Synapsin-GCaMP6f) (rAAV(GCaPM6f)) in dorsal hippocampal area CA1 to express the genetically encoded Ca²⁺ indicator GCaMP6f in neurons located in the CA1 pyramidal layer. Mice were then implanted with a head-post and imaging window to provide long-term optical access to the CA1 pyramidal layer. Left: schematic of two-photon Ca²⁺ imaging in the CA1 pyramidal layer. Right: representative two-photon fields of view across the pyramidal layer showing cross-sections of GCaMP6f-expressing cell bodies from a WT mouse (middle) and a mouse Df(16)A^+/− (right). We chronically imaged 179–621 regions of interest (ROIs; Online Methods) corresponding to cell bodies in each field of view. (c) Left: GCaMP6f Ca²⁺ fluorescence (ΔF/F) traces from two example spatially tuned CA1 place cells in WT and Df(16)A^+/− mice during 10-min sessions. Significant Ca²⁺ transients are highlighted in blue or red, and treadmill position is shown below the traces. Middle: polar trajectory plots showing significant running-related transients for the same example cells. Animals’ position (angle) over time (radius), gray; onset times of significant running-related calcium transients, colored circles. Shaded slices denote place fields. Right: transient vector plots showing the position (angle) and occupancy-normalized weight of each running-related transient (radius), as used to calculate occupancy-normalized transient rate histograms and transient circular variance. Green lines, transient resultant vector (magnitude = 1 – circular variance). (d–g) Compared to WT, Df(16)A^+/− mice had (d) a smaller fraction of cells per experiment with significant spatial information (place cell fraction: WT: 0.2553 ± 0.0109, n = 124 sessions; Df(16)A^+/−: 0.1924 ± 0.0079, n = 98 sessions; P < 0.0001; inset: averaged by mouse, independent samples t test, t = 1.620, P = 0.140; linear mixed-effects model with mouse as random factor: F_1,10.917 = 3.086, P = 0.107), (e) fewer multipeaked place cells (place fields per place cell; WT: 1.180 ± 0.004, n = 12,571 PC × sessions; Df(16)A^+/−: 1.110 ± 0.004, n = 7,683 PC × sessions; linear mixed-effects model with number of place fields and genotype as fixed factors and mouse as random factor: number of place fields × genotype interaction: F_3,38.000 = 5.054, P = 0.005 ; genotype effect for single place field, P = 0.0037; for two fields per PC, P = 0.010; for three fields per PC, P = 0.755), (f) narrower place fields (place field width; WT: 32.531 ± 0.135, n = 12,571 PC × sessions; Df(16)A^+/−: 29.532 ± 0.144, n = 7,683 PC × sessions; linear mixed-effects model with mouse as random factor: F_1,11.164 = 4.371, P = 0.060; dashed vertical lines indicate means) and (g) lower circular variance (WT: 0.310 ± 0.0013, n = 43,068 cells × sessions; Df(16)A^+/−: 0.189 ± 0.0014, n = 27,397 cells × sessions, linear mixed-effects model with mouse as random factor: F_1,11.006 = 5.695, P = 0.036; inset: averaged by mouse, Welch’s t test, t = 2.327, P = 0.0491). *P < 0.05, **P < 0.01.

Spatial map is less stable in Df(16)A^+/− compared to WT mice

To examine the evolution of spatial maps throughout the GOL task, we repeatedly imaged the same populations of individually identified neurons throughout the 27 sessions of the GOL task (cells per mouse, mean ± s.d.; WT: 463 ± 37, n = 6 mice; Df(16)A^+/−: 479 ± 84, n = 5 mice) and looked at two aspects of stability: place cell population stability (recurrence probability: probability of a cell being identified as a place cell in paired sessions) and individual pyramidal cell firing stability (centroid shift: distance between centroid of firing in paired sessions). Combining all conditions and sessions, we found that individual place cells recurred from day to day significantly above chance levels in WT and Df(16)A^+/− mice (recurrence probability: WT versus shuffle: P = <0.0001; Df(16)A^+/− versus shuffle: P < 0.0001; Fig. 3a), but a significantly smaller fraction of place cells re-occurred from day to day in Df(16)A^+/− than WT mice (WT versus Df(16)A^+/−: independent samples t test, t = 5.72, P < 0.0001; aggregated by mouse, independent samples t test, t = 2.611 P = 0.028; Fig. 3a). This decreased overlap in place cell population in the Df(16)A^+/− mice was primarily driven by decreased stability overnight, as this difference was not observed within a day from session to session (linear mixed-effects model with genotype and elapsed time as fixed effects and mouse as random effect; genotype × elapsed time interaction: F_1,145.754 = 5.858, P = 0.017; post hoc analysis, WT versus Df(16)A^+/−, session-to-session: F_1,10.659 = 0.664, P = 0.433; day-to-day: F_1,10.086 = 20.534, P = 0.001, significant after Benjamini-Hochberg correction; Fig. 3b), again suggesting a disruption in overnight consolidation, as seen with the Df(16)A^+/− behavioral performance (Fig. 1d).

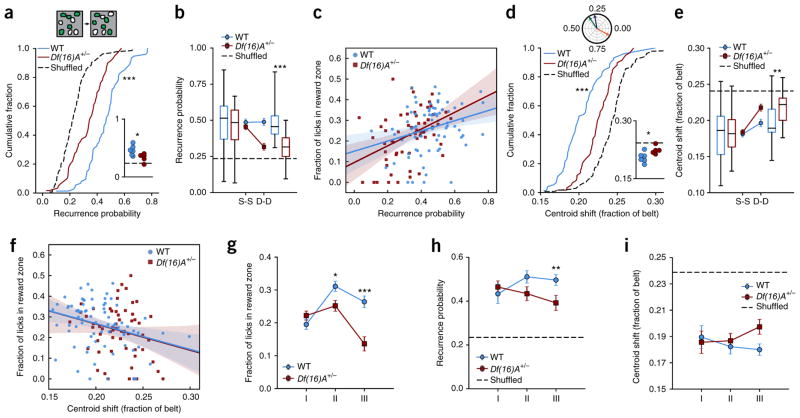
Figure 3.

Disrupted stability of place cell population in Df(16)A^+/− compared to WT mice. (a) Top: example of place cell recurrence. In a given field of view, a subset of all cells has significant spatial tuning each day (place cells, green). The overlap in this population is the recurrence probability (40% in this example). Bottom: distribution of recurrence fractions from day to day for WT and Df(16)A^+/− mice for all sessions (dotted line is cell-identity shuffle distribution: WT: 0.456 ± 0.015, n = 74 sessions, Df(16)A^+/−: 0.327 ± 0.017, n = 59 sessions, shuffle: 0.229 ± 0.009, n = 133 sessions; WT vs. shuffle: Welch’s t test, t = 12.64, P < 0.0001; Df(16)A^+/− vs. shuffle: Welch’s t test, t = 5.124, P < 0.0001; WT vs. Df(16)A^+/−: independent samples t test, t = 5.72, P < 0.0001) and aggregated by mouse (inset; horizontal dotted line is cell-identity shuffle: WT vs. Df(16)A^+/−: independent samples t test, t = 2.611, P = 0.028). (b) Mean fraction of cells that reoccur as place cells from session to session (S-S) or day to day (D-D) for WT and Df(16)A^+/− mice (dotted line is mean place cell fraction; linear mixed-effects model with genotype and elapsed time as fixed effects and mouse ID as random effect; genotype × elapsed time interaction: F_1,145.754 = 5.858, P = 0.017; post hoc analysis, WT vs. Df(16)A^+/−, S-S: F_1,10.659 = 0.664, P = 0.433; D-D: F_1,10.086 = 20.534, P = 0.001, significant after Benjamini-Hochberg correction). (c) Correlation of place cell recurrence with performance throughout the task. Solid lines, linear regression fit; shaded regions, 95% confidence intervals calculated from bootstrap resampling (Pearson’s correlation coefficient, WT: 0.288, P = 0.013; Df(16)A^+/−: 0.416, P = 0.001; WT correlation vs. Df(16)A^+/− correlation, Fisher z-transformation of correlations, general linear model (GLM), univariate ANOVA: genotype × z recurrence probability interaction: F_1,132 = 0.599, P = 0.440; alternatively: linear mixed effects model with genotype as fixed effect, recurrence probability as covariate and mouse ID as random effect: genotype × recurrence probability interaction: F_1,129 = 1.083, P = 0.300; recurrence effect: F_1,129.000 = 18.197, P < 0.0001). (d) Top: preferred spatial tuning is represented as vectors where the angle is the position on the treadmill of maximal activity. Across three sessions (green, blue and orange lines), spatial preference is generally stable (green to blue sessions), though salient events or changes to the environment can induce remapping (blue to orange sessions). The centroid shift is the angle between these vectors, represented as the fraction of the belt. Bottom: distribution of mean centroid shift from day to day per session (dotted line is cell-identity shuffled distribution: WT: 0.204 ± 0.003, n = 74 sessions, Df(16)A^+/−: 0.224 ± 0.003, n = 59 sessions, shuffle: 0.242 ± 0.002, n = 133; WT vs. shuffle: independent sample t test, t = −9.42, P < 0.0001; Df(16)A^+/− vs. shuffle: independent samples t test, t = −4.25, P < 0.0001; WT vs. Df(16)A^+/−: independent samples t test, t = −4.71, P < 0.0001) and aggregated by mouse (inset; horizontal dashed line is cell-identity shuffle; independent samples t test, t = 2.58, P = 0.0295). (e) Mean centroid shift from S-S or D-D for WT and Df(16)A^+/− mice (dotted line is mean centroid shift, linear mixed-effects model with genotype and elapsed time as fixed effects and mouse ID as random effect, genotype × elapsed time interaction: F_{1, 38,078.993} = 15.042, P < 0.0001; post hoc analysis, WT vs. Df(16)A^+/−, S-S: F_1,11.137 = 0.303, P = 0.593; D-D, F_1,10.577 = 8.724, P = 0.014, significant after Benjamini-Hochberg correction). (f) Correlation of mean day-today stability with performance throughout the task. Solid line and shaded regions as in d (Pearson’s correlation coefficient, WT: −0.306, P = 0.008; Df(16)A^+/−: −0.218, P = 0.097; WT correlation vs. Df(16)A^+/− correlation, Fisher z transformation of correlations, GLM, univariate ANOVA: genotype × R stability–probability interaction: F_1,132 = 0.268, P = 0.605; linear mixed effects model with genotype as fixed effect, centroid shift as covariate and mouse ID as random effect: genotype × centroid shift: F_1,133.000 = 0.001, P = 0.982; centroid shift: F_1,133.000 = 8.804, P = 0.004). In b and e, center line in box plot is the median, the top and bottom of the box denote the 1st and 3rd quartile of the data, respectively, and the whiskers mark the full range of the data. (g–i) Task performance and population stability by genotype follow similar trajectories across conditions. Error bars represent s.e.m. of total number of sessions by mouse. Bonferroni-corrected post hoc tests comparing genotype per condition. (g) Fraction of licks in the reward zone by condition (two-way ANOVA, main effect of genotype P < 0.0001, main effect of condition P < 0.0001, genotype × condition interaction: P < 0.0001; post hoc comparisons: Condition II, P = 0.011; Condition III, P < 0.001). (h) Recurrence probability by condition (linear mixed-effects model with condition and genotype as fixed effects and mouse as random effect, genotype effect: F_1,11.084 = 7.293, P = 0.021, genotype × condition interaction: P = 0.083; post hoc comparisons: Condition III, P = 0.004). (i) Mean centroid shift by condition (linear mixed-effects model as before, genotype effect: F_1,10.107 = 6.771, P = 0.026). *P < 0.05, **P < 0.01, ***P < 0.001.

We next looked at the shift in firing locations in both WT and Df(16)A^+/− mice to assess the similarity of spatial tuning from day to day. We found that while preferred firing locations of all cells were more stable than chance in both genotypes (centroid shift: WT versus shuffle: independent sample t test, t = −9.42, P < 0.0001; Df(16)A^+/− versus shuffle: independent samples t test, t = −4.25, P < 0.0001; Fig. 3d; place field correlation: WT versus shuffle: P < 0.0001; Df(16)A^+/− versus shuffle: P < 0.0001; Supplementary Fig. 5a), the spatial tuning in Df(16)A^+/− mice was significantly less stable from day to day compared to WT mice (centroid shift: WT versus Df(16)A^+/−: independent samples t test, t = −4.71, P < 0.0001) and aggregated by mouse (independent samples t test, t = 2.58, P = 0.0295; Fig. 3d; place field correlation: WT versus Df(16)A^+/−: P < 0.0001; Supplementary Fig. 5a). Also, just as the active place cell population overlap was similar within day between WT and Df(16)A^+/− mice, spatial tuning was also not different between WT and Df(16)A^+/− mice from session to session within the same day (centroid shift: linear mixed-effects model with genotype and elapsed time as fixed effects and mouse as random effect, genotype × elapsed time interaction: F_{1, 38,078.993} = 15.042, P < 0.0001; post hoc analysis, WT versus Df(16)A^+/−, session-to-session: F_1,11.137 = 0.303, P = 0.593; day-to-day, F_1,10.577 = 8.724, P = 0.014, significant after Benjamini-Hochberg correction; Fig. 3e; place field correlation: genotype × elapsed time interaction: P = 0.0051; post hoc analysis, WT versus Df(16)A^+/−, session-to-session: P = 0.613; day-to-day, P < 0.0001; Supplementary Fig. 5b). Taken together, spatial maps were less stable in Df(16)A^+/− compared to WT mice from day to day (but not from session to session), as seen by lower recurrence of place cells and a larger shift in spatial tuning centroids, reflecting disrupted spatial maps in the mutant mice.

Task performance correlates with spatial map stability

If the stability of place fields over time provides the basis for spatial and episodic learning^15–18, we would expect that the relative stability of place cell maps would reflect task performance. Indeed, on a per-session basis the overlap in the identity of place cells from day to day correlated with learning performance across all conditions of the GOL task for both groups (recurrence probability versus fraction of licks in reward zone: Pearson’s correlation coefficient, WT: 0.288, P = 0.013; Df(16)A^+/−: 0.416, P = 0.001; WT correlation versus Df(16)A^+/− correlation, Fisher z transformation of correlations, general linear model, univariate ANOVA: genotype × z-recurrence probability interaction: F_1,132 = 0.599, P = 0.440; alternatively: linear mixed effects model with genotype as fixed effect, recurrence probability as covariate and mouse as random effect: genotype × recurrence probability interaction: F_1,129 = 1.083, P = 0.300; recurrence effect: F_1,129.000 = 18.197, P < 0.0001; Fig. 3c). This finding suggests that this coding strategy is implemented by both WT and Df(16)A^+/− mice, though the overall decreased population stability in the Df(16)A^+/− mice contributes to the impaired task performance—the Df(16)A^+/− mice are shifted lower on the recurrence–performance curve. In a similar manner to recurrence probability, place cell firing location stability also correlated with task performance for the WT mice and trended similarly in the Df(16)A^+/− mice (centroid shift versus fraction of licks in reward zone: Pearson’s correlation coefficient, WT: −0.306, P = 0.008; Df(16)A^+/−: −0.218, P = 0.097; WT correlation versus Df(16)A^+/− correlation, Fisher z-transformation of correlations, general linear model, univariate ANOVA: genotype × z stability interaction: F_1,132 = 0.268, P = 0.605; linear mixed effects model with genotype as fixed effect, centroid shift as covariate and mouse as random effect: genotype × centroid shift: F_1,133.000 = 0.001, P = 0.982; centroid shift F_1,133.000 = 8.804, P = 0.004; Fig. 3f; place field correlation; Spearman’s correlation coefficient, WT: 0.335, P = 0.004; Pearson’s correlation coefficient, Df(16)A^+/−: 0.224, P = 0.088; Supplementary Fig. 5c).

In addition, as suggested by the overall correlation of task performance with stability, the trajectory of these metrics across conditions mirrors the trajectory of the behavioral deficit in the task. Namely, just as we did not see a difference in behavior during Condition I (Figs. 1c and 3g), stability was also similar between WT and Df(16)A^+/− mice during Condition I, but while the WT place cell population continued to stabilize in Condition II and III, the Df(16)A^+/− population stability dropped off as the task demands change (recurrence probability: linear mixed-effects model with condition and genotype as fixed effects and mouse as random effect, genotype effect: F_1,11.084 = 7.293, P = 0.021; condition × genotype interaction, ns; Fig. 3h; centroid shift: linear mixed-effects model as before, genotype effect: F_1,10.107 = 6.771, P = 0.026; Fig. 3i). Thus, the learning strategy employed by both genotypes did involve the formation and maintenance of stable hippocampal spatial maps, but the stability of these maps was impaired in Df(16)A^+/− mice, particularly from day to day and when the task demands changed, as reflected in their decreased performance on the GOL task.

Goal-oriented learning requires dorsal hippocampal area CA1 and relies on allocentric navigation

To confirm the necessity of the hippocampus to our GOL task, we pharmacologically silenced bilateral dorsal hippocampus area CA1 using the GABA_A-receptor agonist muscimol during initial learning of a fixed reward location (Online Methods). Mice in which the hippocampus was silenced during initial learning of the reward location performed significantly worse than mice with an active hippocampus (Mann-Whitney U test, Days 1–3, muscimol to saline versus saline to muscimol: U = 126.5, P < 0.0001; Supplementary Fig. 7) and mice that successfully learned the task with an active hippocampus showed a significant drop in task performance following dorsal hippocampus inactivation (saline to muscimol, Mann-Whitney U test, Days 1–3 versus Day 4: U = 111, P = 0.0235), now performing similar to the initially silenced training group (Day 4, independent samples t test, saline to muscimol versus muscimol to saline: t = 0.633, P = 0.535).

Local cues and fabric segments of the treadmill belt are aimed to primarily provide an allocentric reference frame for spatial maps during the GOL task, but mice could in principle also use egocentric, path-integration strategies^5,21,27 to find the reward location. To elucidate the relative contribution of allocentric navigation and path integration in the learning task, we imaged WT mice in the absence of local cues on the treadmill belt, where we found that place cells were practically absent (place cell fraction, cue-rich versus cue-free: independent samples t test, t = 3.006, P = 0.004; Supplementary Fig. 8a,b), and the tuning of all cells was significantly more diffuse (circular variance, cue-rich versus cue-free: Mann-Whitney U test, U = 499,131, P < 0.0001; Supplementary Fig. 8c). Furthermore, in the case of path integration, we would expect that during the transition from Condition I to II, when fabric sequence is the only belt feature remaining constant, place cells near the fabric transitions would be more stable than place cells farther from the fabric transitions, as errors in path integration would accumulate with distance^21,27. Instead, we found no difference in stability that could have been due to the distance from the initial preferred tuning to the nearest fabric transition (two-way ANOVA, main effect of binned distance: F_2,24 = 0.024, P = 0.977; Supplementary Fig. 8d). These results together suggest that egocentric navigation alone would be insufficient to maintain place cell firing, and thus mice primarily employ allocentric navigational strategies for learning in the GOL task.

Disrupted sharp wave-ripple activity in Df(16)A^+/− mice

Decreased task performance following long delays (i.e., overnight), coupled with the decreased recurrence and similarity of neuronal ensemble activity from day to day, suggests a consolidation deficit in the Df(16)A^+/− mice. Reactivation and consolidation of memories of previous experiences are thought to occur during sharp wave-ripples (SWRs), large-amplitude and high-frequency events detected in the local field potential during quiet wakefulness and sleep²⁸. To assess SWR activity in WT and Df(16)A^+/− mice, in a separate cohort of mice we implanted electrodes in hippocampal area CA1 to record the local field potential and detect SWRs (Supplementary Fig. 9ab , and Online Methods). During periods of immobility, we found that Df(16)A^+/− mice had significantly more SWRs (Wilcoxon rank-sum test, h = 3,777.5, P < 0.001; Supplementary Fig. 9c,f), though the SWRs were irregular, as reflected by a higher mean ripple-band power (Wilcoxon rank-sum test, h = 98,423, P < 0.001; Supplementary Fig. 9d,g) and a higher peak frequency in the ripple-band (Wilcoxon rank-sum test, h = 94,798, P < 0.001; Supplementary Fig. 9e,h). This dysregulation of hippocampal excitability during periods of rest in Df(16)A^+/− mice provides a possible mechanism behind their failure to efficiently retain a memory of the reward location.

Change in context induces disrupted place cell stability in Df(16)A^+/− mice

In addition to deficits following the overnight period, Df(16)A^+/− mice showed significantly impaired performance after a change in context during Condition II in the GOL task (Condition II, Day 1; Fig. 1b,c), which comprised a change in both the nonspatial (tone, light and odor) and proximal spatial cues (shuffled local cues on belt, constant fabric sequence). When we compared the day-to-day stability of place fields in WT and Df(16)A^+/− mice across this transition (Condition I–Day 3 to Condition II–Day 1), we found that place fields in WT mice were significantly more stable than in Df(16)A^+/− mice (WT: 0.195 ± 0.008, n = 6; Df(16)A^+/−: 0.227 ± 0.002, n = 5; independent samples t test: t = −3.626, P = 0.0055; Fig. 4a). Since this change of local cues from Condition I to Condition II dissociated position relative to the sequence of fabrics and position relative to the cues, we looked at coding of space relative to these two distinct reference frames in the WT and Df(16)A^+/− mice. We looked at all the place cells that were active near a cue on the last day of Condition I and asked whether on the first day in Condition II it fired closer to that same cue (‘cue-preferring’) or to the position relative to the fabric sequence where the cue was previously (‘position-preferring’; Online Methods). We found a significantly different distribution of cue-preferring and position-referring cells between WT and Df(16)A^+/− mice (Pearson chi-square test: χ² = 85.7776, P < 0.0001; Fig. 4b), with notably fewer position-preferring cells in the Df(16)A^+/− mice and a significantly lower ratio of cue- to position-preferring cells per mouse (independent samples t test: t = −3.172, P = 0.0131; Fig. 4c). Thus, changes to the nonspatial context and the shuffling of local cues induced remapping and disrupted the stability of spatial maps in Df(16)A^+/− mice significantly more than in WT mice, and in particular, fewer cells remained anchored to the task-relevant belt reference space.

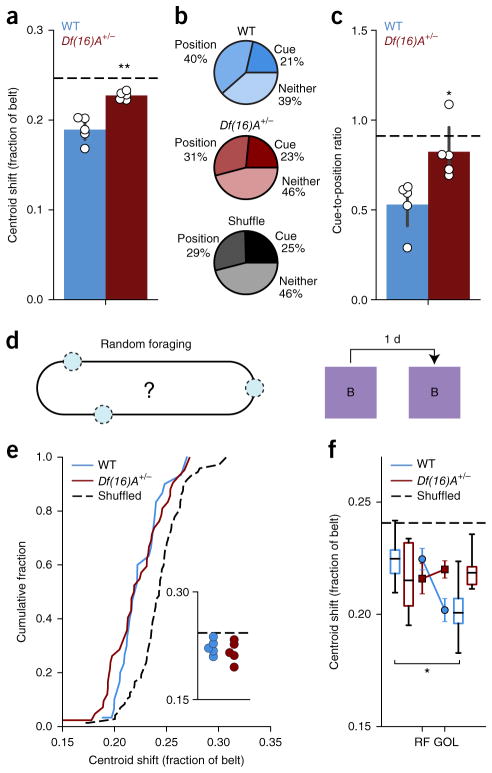
Figure 4.

Lack of context change and task-dependent stability of spatial maps in Df(16)A^+/− mice. (a) Mean centroid shift from the last day of Condition I to the first day of Condition II (WT: 0.195 ± 0.008, n = 6; Df(16)A^+/−: 0.227 ±0.002, n = 5; independent samples t test: t = −3.626, P = 0.0055). Horizontal dashed line represents shuffled data. Error bars represent s.e.m. for mice. (b) Fraction of all cells classified as place-preferring (position), cue-preferring (cue) or neither (pooled across mice) for WT, Df(16)A^+/− and shuffled data (Pearson chi-square test: ±² = 85.7776, P < 0.0001). (c) Ratio of the number of cue-preferring to place-preferring cells per mouse for WT mice, Df(16)A^+/− mice (independent samples t test: t = −3.172, P = 0.0131) and shuffled data (horizontal dashed line). Error bars represent s.e.m. for mice. (d) Schematic of RF task. Rewards (blue circles) are presented randomly throughout the belt in the same context (Context B): same belt fabric sequence but different auditory, visual, olfactory and tactile cues. (e) Distribution of mean centroid shift per session from day to day during RF task (dotted line is cell-identity shuffled distribution; WT: 0.222 ± 0.004, n = 30 session pairs; Df(16)A^+/−: 0.220 ± 0.004, n = 42 session pairs; shuffle: 0.244 ± 0.002, n = 72; WT vs. shuffle: independent sample t test: t = −5.05, P < 0.0001; Df(16)A^+/− vs. shuffle: Welch’s t test, t = −5.12, P < 0.0001; WT vs. Df(16)A^+/−: independent samples t test: t = 0.451, P = 0.653) and aggregated by mouse (inset; horizontal dashed line is cell-identity shuffle; WT vs. Df(16)A^+/−: independent samples t test: t = 0.799, P = 0.448). (f) Comparison of mean centroid shift per mouse in the RF and GOL tasks (GOL data replotted from Fig. 3e; linear mixed-effects model, genotype × task interaction: F_1,19.471 = 4.316, P = 0.051; effect of task: F_1,19.471 = 4.924, P = 0.039; post hoc analysis: WT, GOL vs. RF: F_1,11.285 = 10.472, P = 0.008, significant after B Benjamini-Hochberg correction; Df(16)A^+/−, GOL vs. RF: F_1,8.562 = 0.006, P = 0.940). In box plots, center line represents the median, the top and bottom of the box denote the 1st and 3rd quartile of the data, respectively, and the whiskers mark the full range of the data. *P < 0.05, **P < 0.01

Task-dependent stabilization of place cell populations is impaired in Df(16)A^+/− mice

To better understand the conditions in which place cell stability is affected in the Df(16)A^+/− mice, we used a separate random foraging (RF; Fig. 4d and Online Methods) task that did not require spatial learning. From day to day, preferred firing locations were more stable than expected by chance in both WT and Df(16)A^+/− mice (WT: 0.222 ± 0.004, n = 30 session pairs; Df(16)A^+/−: 0.220 ± 0.004, n = 42 session pairs; shuffle: 0.244 ± 0.002, n = 72; WT versus shuffle: P < 0.0001; Df(16)A^+/− versus shuffle: P < 0.0001), but in contrast to during the GOL task, they were not significantly different from each other (WT versus Df(16)A^+/−: independent samples t test: t = 0.451, P = 0.653; and aggregated by mouse: independent samples t test: t = 0.799, P = 0.448; Fig. 4e). More specifically, the WT spatial tuning was significantly stabilized in the GOL task while the Df(16)A^+/− spatial tuning was not (linear mixed-effects model, genotype × task interaction: F_1,19.471 = 4.316, P = 0.051, effect of task: F_1,19.471 = 4.924, P = 0.039, post hoc analysis WT, GOL versus RF: F_1,11.285 = 10.472, P = 0.008, significant after Benjamini-Hochberg correction; Df(16)A^+/−, GOL versus RF: F_1,8.562 = 0.006, P = 0.940; Fig. 4f). This finding suggests that the presence of a salient reward location selectively stabilizes hippocampal spatial maps in WT mice, a phenomenon absent from Df(16)A^+/− mice.

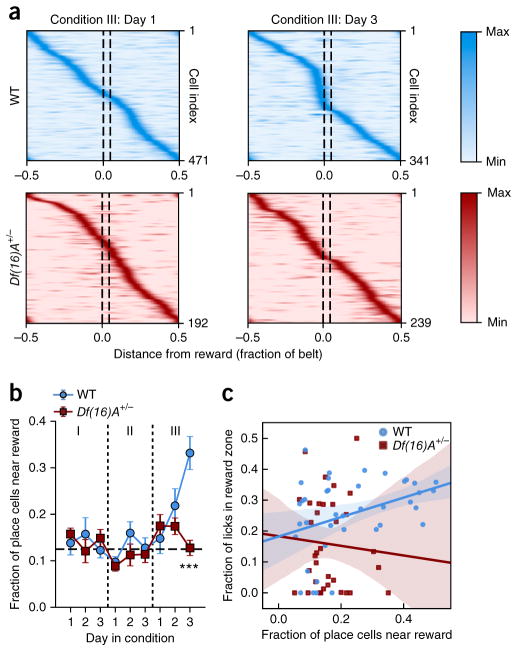
Enrichment of goal location by place cells in WT but not Df(16)A^+/− mice

Place maps incorporate goal-related information^{19,20,22–24,26}, particularly as an over-representation of goal locations by place cells²³, which has been shown to correlate with learning performance²⁶. While we did not observe place cell enrichment during initial goal learning in a novel context (Condition I) or the subsequent change of context (Condition II), upon learning the new reward location in an already familiar context (Condition III), we found robust and organized remapping of place cells toward the new reward location in WT mice, though this goal-directed reorganization was strikingly absent in Df(16)A^+/− mice (linear mixed-effects model, condition and genotype as fixed effects and day nested under condition as covariate, with mouse as random factor: genotype × condition × interaction: F_2,174.406 = 4.257, P = 0.016; genotype × day (nested under condition) interaction: F_3,112.789 = 3.257, P = 0.024; post hoc analysis with Benjamini-Hochberg correction for multiple comparisons, Conditions I and II: no significant effect of genotype; Condition III genotype effect: F_1,71.243 = 8.776, P = 0.004; genotype × day interaction: F_1,64.041 = 12.307, P = 0.001; Day 3: P < 0.0001; Fig. 5a,b). Additionally, we found that the magnitude of place cell enrichment at the goal location correlated with learning performance in WT mice (Pearson correlation, z = 0.362, P = 0.023; Fig. 5c) but not in Df(16)A^+/− mice (Pearson correlation, z = −0.068, P = 0.791; Fig. 5c). Alternatively, use of a linear mixed-effects model with genotype as factor and fraction of place cells near the reward location as covariate in fixed effects and mouse as random factor showed no overall effect of the covariate on the fraction of licks in the reward zone (F_1,72.829 = 0.229, P = 0.634; genotype × fraction of place cells near the reward location interaction, P = 0.143, n.s). However, post hoc analysis revealed a significant effect of the number of place cells near the reward location on the mouse performance for WT mice (linear mixed-effects model with fraction of place cells near the reward location as covariate in fixed effects and mouse ID as random factor, significant effect of the covariate: F_1,31.460 = 11.436, P = 0.002, significant after Benjamini-Hochberg correction). Thus, place cell enrichment supports learning of new reward locations in a familiar context in WT animals, while in Df(16)A^+/− mice, the lack of place cell enrichment is associated with significantly worse performance during this phase of the GOL task.

Figure 5.

Place field enrichment of goal location. (a) Tuning profiles for all place cells in WT and Df(16)A^+/− mice on the first and last days of Condition III. Each row is an individual place cell. The intensity corresponds to the normalized transient rate in each spatial bin along the x axis. Goal location is between dotted lines. WT mice show more place cells near the reward by Day 3, an enrichment lacking in Df(16)A^+/− mice. (b) Fraction of place cells near the goal location (within 1/16 of the belt length) across all days of the experiment. Horizontal dotted line is uniformly distributed fraction (linear mixed-effects model, condition and genotype as fixed effects and day nested under condition as covariate, with mouse ID as random factor: genotype × condition × interaction: F_2,174.406 = 4.257, P = 0.016; genotype × day (nested under condition) interaction: F_3,112.789 = 3.257, P = 0.024; post hoc analysis with Benjamini-Hochberg correction for multiple comparisons, Conditions I and II: no significant effect of genotype; Condition III, genotype effect: F_1,71.243 = 8.776, P = 0.004; genotype × day interaction: F_1,64.041 = 12.307, P = 0.001; Day 3: t = 4.669, P < 0.0001). Error bars are s.e.m. of place cell number. (c) Place cell goal-zone enrichment is correlated with task performance during Condition III in WT but not Df(16)A^+/− mice (WT: Pearson correlation: 0.362, P = 0.023; fraction of licks in the reward zone: F_1,31.460 = 11.436, P = 0.002, significant after Benjamini-Hochberg correction; Df(16)A^+/−: Pearson correlation: −0.068, P = 0.791). Linear regression and confidence intervals as in Figure 3c. ***P < 0.001.

Modeling of place cell dynamics suggests that place field shift is the primary factor leading to reward enrichment

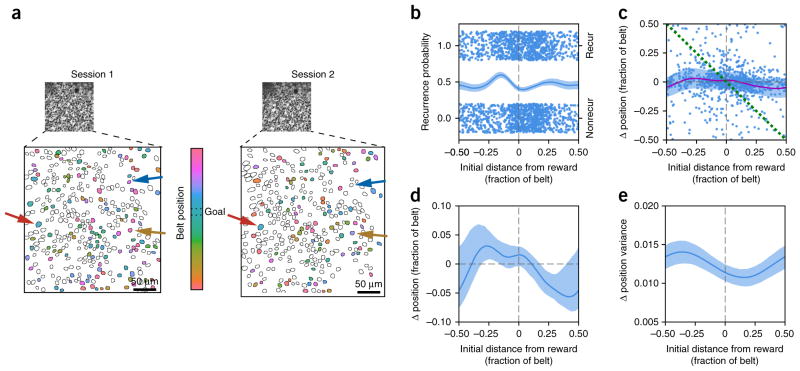
Several aspects of place cell population dynamics may explain the enrichment of firing fields at the goal location in the familiar context. For example, place cells within the reward zone may be more likely to recur; existing place fields may shift toward the reward²⁹; or place fields at the reward location may be selectively stabilized (Supplementary Fig. 10). To distinguish between these possibilities, we calculated the mean position-dependent recurrence probability and centroid shift (Fig. 6). We found a slight increase in the recurrence probability of place cells that were active immediately preceding the reward (Fig. 6b), and, on average, place fields drifted toward a location on the belt just after the reward zone, such that fields preceding it tended to shift forward and fields following it tended to shift backwards (Fig. 6c,d). In addition, place fields just after the reward location shifted more consistently, as evidenced by a relatively lower place field shift variance (Fig. 6c,e). We next modeled day-to-day shifts in the population of spatially active cells and their preferred spatial tuning based on these parameters (Fig. 7a, Supplementary Fig. 11 and Online Methods).

Figure 6.

Session-to-session place field shift dynamics. (a) Example fields of view from two consecutive sessions. Background is time-averaged GCaMP6f movie. Place cells are colored corresponding to their spatial tuning within each session. The color bar shows the mapping of place field location on the belt. The reward zone for these sessions was between the dotted lines. Place fields are generally stable (red arrow), but some shift their place field (yellow arrow), while others stop being spatially active (blue arrow). (b) Recurrence probability as a function of original distance from the reward. For all pairs of consecutive sessions during Condition III, each place cell during the first session is plotted with the centroid of its place field along the x axis and whether or not it was also a place cell in the second session on the y axis (top cluster is place cell in second session; bottom cluster is not a place cell; random y-axis jitter within each cluster for visualization). Cyclic logistic regression fit with 95% confidence interval from cross-validation plotted on left axis. (c) Session-to-session place field shift as a function of original distance from the reward. For all pairs of consecutive sessions during Condition III, each place cell during the first session is plotted with the centroid of its place field along the x axis and the change in centroid position in the second session along the y axis. Data is fit as a continuous series of von Mises distributions for each position, with the offset (solid purple line) and variance (shaded band, 1/κ, where κ is the concentration parameter) shown. Green dotted line denotes cells that move directly to the reward position in the second session. While it is possible that a subset of the goal-enriching cells are reward cells that directly follow the reward, the larger effect is the gradual drift of the entire place cell population toward the reward, not the active recruitment of reward cells directly remapping to the reward location (for example, lack of cells clustered around green dotted line). (d) Same offset curve (solid line, shaded region is 90% confidence interval calculated from refitting bootstrap resampled data) as in c. Positive values to the left of the zero-crossing and negative values to the right correspond to drift toward the reward position. (e) Same variance fit as in c, plotted independently. Shaded region represents 90% confidence interval calculated from refitting bootstrap resampled data. Place field shift is most consistent (minimum variance) at a position that corresponds to the most stable place field location from d, just after the goal location.

Figure 7.

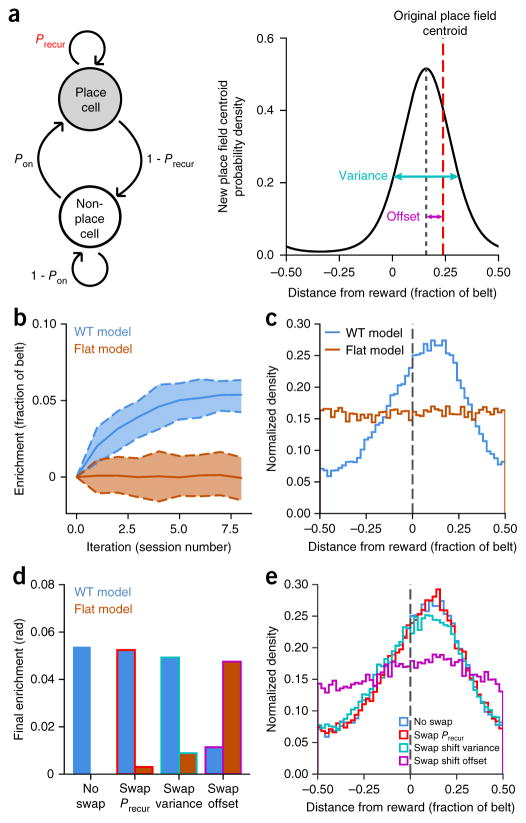
Place field drift toward reward drives enrichment in the place field dynamics model. (a) Schematic of place cell recurrence (left) and stability (right) model including the four parameters that were fit from our data: non-place cell to place cell transition probability (P_on), place cell recurrence probability by position (P_recur), session-to-session place field shift variance and session-to-session place field shift offset. (b) Mean population enrichment by simulated iteration (solid lines) for WT and flat parameter sets (dashed lines: 90% confidence intervals from 100 simulations). WT parameters reproduce the enrichment observed during Condition III. (c) Final distribution of place fields after eight iterations for WT and flat-model parameters. Vertical dashed line denotes reward location. (d) Mean population enrichment after eight iterations with true-fit parameters and then with swapping each set of position-dependent parameters individually between WT and the flat model: recurrence probability (P_recur), place field shift variance and place field shift offset. (e) Final WT place field distributions after eight iterations with the same parameter swaps as in d. Mean place field shift (offset) toward the reward is revealed as the main factor underlying enrichment in GOL.

Simulating the same number of session transitions as in our experimental scheme, our model shows gradual enrichment of the goal location similar to the observed enrichment we saw in the WT mice during Condition III (Fig. 7b,c). In contrast, when we run the model with data taken from Condition I or II, we do not see enrichment of the reward location, as expected (Fig. 7b,c and Supplementary Fig. 12). We next swapped parameters one by one between our WT model and flat model (flattened parameter fits; see “Modeling goal-directed remapping” section in Online Methods) and reran the simulation to see the effect of each parameter individually on the final goal enrichment. The only parameter with a significant effect on the final place field enrichment is the place field shift offset (Fig. 7d,e and Supplementary Fig. 13). We conclude that place field enrichment of goal locations is driven by an active recruitment of place fields shifting coherently toward the reward location: place fields before the reward shift forward, and place fields after the reward shift backwards.

Absence of enrichment in the Df(16)A^+/− mice is through lack of place field shift toward reward

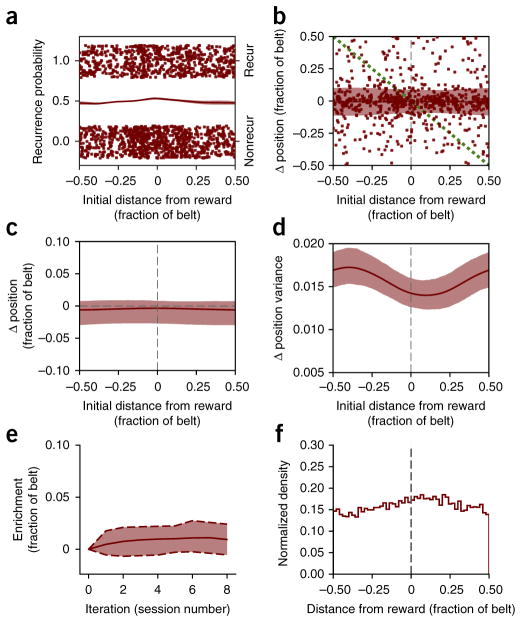
While we saw robust place field enrichment of the reward location in WT mice following a change in the reward location, population enrichment was completely absent in Df(16)A^+/− mice. We calculated the position-dependent recurrence probability and centroid shift (as in Fig. 6) during Condition III with the Df(16)A^+/− data and saw no dependence on position for any of these properties (Fig. 8a–d). Consistent with previous studies³⁰, across the entire belt, on average, place fields shifted slightly backwards (Fig. 8c), and when we simulate session-to-session place field shifts with our model we do not see any enrichment of the goal location (Fig. 8e,f). So, while WT place fields shift toward the reward location, leading to an over-representation of this location, this effect is disrupted in Df(16)A^+/− mice.

Figure 8.

Df(16)A^+/− mice place fields do not drift toward goal and the model produces no enrichment. (a) Place cell recurrence by distance from reward, as in Figure 6b. (b) Session-to-session place field shift as a function of original distance from the reward, as in Figure 6c. (c,d) Place field shift and variance fits from b, as in Figure 7c,d (shaded region is 90% confidence interval calculated from refitting bootstrap resampled data). (e) Unlike the WT model, the enrichment model with Df(16)A^+/− parameters shows no enrichment (see Fig. 7b). (f) Final distribution of place fields after eight iterations for Df(16)A^+/− parameters.

DISCUSSION

Our study provides a comparative characterization of learning-related neural population dynamics in hippocampal area CA1 in WT mice and mutant mice carrying a SCZ-predisposing genetic lesion. We found that mice carrying the 22q11.2 deletion, one of the strongest genetic risk factors for cognitive dysfunction and SCZ, exhibit compromised stability and plasticity of hippocampal place cell maps during spatially guided reward learning. By tracking place cell dynamics over different phases of a multiday learning task, our study extends previous findings^14–18 by showing a positive correlation between place cell map stability and learning performance in both WT and Df(16)A^+/− mice. Indeed, task performances and spatial map stabilities for each genotype followed a similar trajectory as task demands changed; task performance and stability were most similar during Condition I, Df(16)A^+/− mice were slightly impaired in Condition II and the largest difference was observed in Condition III (Supplementary Fig. 4). These findings suggest that the neural coding strategy employed during all phases of a spatial reward learning task relies on the formation and maintenance of stable hippocampal representations. Our results also show task-dependent stabilization of spatial maps in WT mice, an effect possibly mediated by the attentional demands of GOL^15,24,25,31. In contrast, place field stability between GOL and RF tasks was indistinguishable in Df(16)A^+/− mice, indicative of a failure to conditionally stabilize spatial maps. However, Df(16)A^+/− mice were comparable to WT littermates in their ability to initially learn a reward location, as well as in baseline place cell stability, which suggests that the Df(16)A^+/− learning deficit was related to the stabilization and rearrangement of spatial maps in response to changing task demands (Condition I; Fig. 1c,d and Supplementary Fig. 4).

Our results also suggest that the memory deficit throughout the GOL task may result from impaired consolidation processes. Df(16)A^+/− mice were capable of solving this task, but they were significantly impaired at the beginning of each day (Fig. 1d), and their spatial maps were less stable overnight than those of the WT mice (Fig. 3b,e). In that respect, the altered SWR activity we observed in the Df(16)A^+/− mice may underlie the decreased stability of spatial maps. Although we did not directly assess SWR-related place cell reactivation²⁸, the increased rate and power of SWRs we observe in the Df(16)A^+/− mice (Supplementary Fig. 9), similarly to the effect seen in other SCZ mouse models^32,33, could reflect either a failure to selectively reactivate task-related representations or a compensatory mechanism, as aberrant SWRs are not efficiently consolidating task memories.

As an alternative explanation, it is possible that compromised forgetting mechanisms drive the behavioral deficits of the Df(16)A^+/− mice. Place cell remapping has been proposed as a population-based coding mechanism that supports storage of similar memories with minimal interference^34–36. Therefore, compromised forgetting mechanisms in terms of in place cell remapping toward the reward location in the Df(16)A^+/− mice might reflect enhanced interference in forming new memories or recalling earlier memories. Another possibility is that an inability to suppress licking due to impaired impulsivity control could also contribute to the lagging performance in the Df(16)A^+/− mice.

While the effect of time cannot be completely excluded over the course of our multiday learning model, our results are more consistent with an interpretation in which distinct hippocampal coding strategies are employed as learning demands change in our task. Specifically, learning of a reward location in a novel environment is primarily supported by the stability of spatial maps, while learning of a change in reward location in an otherwise familiar environment is additionally dependent on the plasticity of these maps, as place cells shift toward the new reward location in WT mice (Figs. 5–8). Prior studies of goal-directed learning were mostly performed in familiar environments^{19,20,22–24,26}, and our results here are in line with previous observations showing that prominent changes in place cell firing in response to a goal were elicited when the pattern of the reinforcement was changed in the same environment^19,20,24,25, following several trials in the same maze²⁶, translocation of a reward location^19,24 or during the probe trial in an annular water maze²³. Previous literature has also demonstrated that CA1 place fields undergo experience-dependent stabilization during the transition from a novel to familiar context^37–39, including experience-dependent changes in place fields shift and directionality^30,40. Therefore, one potential explanation for the lack of reward-related enrichment during Conditions I and II is that goal-directed place cell dynamics were obscured by conflicting demands related to the formation of a stable contextual representations. Additional changes within a stabilized (or well-encoded) context, such as the incorporation of reward-related information, could occur through goal-directed reorganization of place fields, resulting in over-representation of place fields near the reward in WT mice.

We find that WT place fields before the reward tended to shift forward, while place fields after the reward shifted backwards during learning of a new reward location in a familiar environment (Fig. 6c,d). This finding is consistent with the prior observation of gradual shifts place fields toward goal locations²⁹. Df(16)A^+/− mice failed to employ a goal-location enrichment-coding strategy and were significantly delayed in learning the new reward location. The fact that the Df(16)A^+/− mice still improved their behavioral performance despite their lack of goal-related remapping implies that Df(16)A^+/− mice rely on other alternative, albeit less-efficient, strategies to find the reward location. Although we find that self-motion-generated information alone is not sufficient for the maintenance of stable firing fields, local cues and fabric segments of the belt could, in principle, also serve as anchors to reduce error accumulation in path integration^21,27. Df(16)A^+/− mice did not track position as accurately as WT mice when local cues were shuffled (Condition II, Day 1; Figs. 1c and 4a), indicating that Df(16)A^+/− mice overly rely on local cues (but not the fabric segments; Supplementary Fig. 6d) and potentially egocentric navigational strategies. Nonetheless, this topic deserves further exploration.

The observed decrease in the fraction of spatially tuned cells and altered firing field properties at the neuronal population level, although only partially corroborated in the level of mouse population, could be an additional contributor to the disruption in the processing of spatial information in the Df(16)A^+/− mice. The tendency toward unimodal and narrower place fields we observed in the Df(16)A^+/− mice may be sufficient to support accurate spatial coding by combining independent location estimates from individual cells under basal conditions. In contrast, during modification of task contingencies⁴¹, place cells with multiple fields and high rate of spatial information could increasingly contribute to population coding in WT but not in Df(16)A^+/− mice.

Bidirectional interactions between the hippocampus and the pre-frontal cortex play a critical role in normal memory processing⁴². In this respect, we note that learning deficits were revealed in the mutant mice by manipulations of the environmental context and the reward location, conditions requiring cognitive flexibility, and that the decreased fraction of cells tracking the place reference frame following a shuffling of the local cues during the GOL task (Fig. 4b,c) suggests a misattribution of salience to irrelevant cues. These behavioral and neuronal abnormalities together point to impaired interactions between the prefrontal cortex and the hippocampus, a feature of both SCZ patients and animal models of SCZ^43,44.

Disrupted spatial map stability and plastic reorganization in the Df(16)A^+/− mice could result from deficits in local circuit dynamics, long-range communication or neuromodulation, all of which would presumably be attributable to the deficiency of one or more genes in the 22q11.2 locus^4,43,45. While the precise mechanisms remain to be determined, our findings indicate that impaired stability and the inability of hippocampal place fields to reorganize in response to salient information together represent important neuronal correlates of memory deficits in Df(16)A^+/− mice. Given that the memory deficit revealed by the GOL task is reminiscent of episodic memory deficits and learning impairments in 22q11.2-deletion carriers^46,47, impaired hippocampal ensemble dynamics may be a central component of cognitive memory dysfunctions emerging from the 22q11.2DS and SCZ in general⁴⁸. In SCZ patients with and without the 22q11.2 deletion, cognitive dysfunction is a key manifestation of SCZ, is highly correlated with functional outcome and is a robust indicator of the risk of developing a psychotic illness^49,50. Investigations of 22q11.2DS as a genetic model could thus aid in elucidating neurobiological mechanisms underlying the development of cognitive dysfunction under the assumption that the diversity of dysfunction that occurs at the molecular, cellular and synaptic levels could be functionally convergent at the level of altered neuronal ensembles⁴⁵.

ONLINE METHODS

All experiments were conducted in accordance with the US National Institutes of Health guidelines and with the approval of the Columbia University Institutional Animal Care and Use Committee.

No statistical methods were used to predetermine sample sizes but our sample sizes are similar to those reported in previous publications^51–53.

Mice and viruses

For all experiments we used adult (8–12 weeks) male and female Df(16)A^+/− and wild-type (WT) littermates that had been backcrossed into C57BL/6J background for over ten generations. Hemizygous Df(16)A^+/− mice carry a 1.3-Mb deficiency on chromosome 16, in a region syntenic to the human 22q11.2 region and encompassing 27 genes, from Dgcr2 to Hira^51,54. Mice were housed in the Columbia University vivarium (1–5 mice per cage) and were maintained on a 12-h light/dark cycle. Experiments were performed during the second half of the light portion of the cycle. GCaMP6f expression in neurons located in the hippocampal CA1 pyramidal layer was induced with a recombinant adeno-associated virus (rAAV) expressing GCaMP6f⁵⁵ under a Synapsin promoter (rAAV1/2(Synapsin-GCaMP6f)). Viral delivery to dorsal CA1 was performed by stereotactically injecting 50 nL (10-nL pulses) of rAAV at three dorsoventral locations using a Nanoject syringe (−2.3 mm AP; −1.5 mm ML; −0.9, −1.05 and −1.2mm DV relative to bregma). Optimal levels of viral expression of GCaMP6f occur 3–4 weeks postinjection. A subset of Df(16)A^+/− mice were crossed with mice expressing Cre-recombinase under interneuron promoters (Som, Pvalb, VIP)⁵² to identify interneurons located in the CA1 pyramidal layer to exclude them from further analysis. However, none of these crosses completely label the interneuron population in the pyramidal layer (data not shown), and therefore putative interneurons were identified and excluded from image analysis based on morphological criteria (see the “Data processing for Ca²⁺ imaging” section, below). In total, 6 WT mice (5 males and 1 female) and 6 Df(16)A^+/− mice (4 males and 2 females) were used for behavioral analysis. One of the male Df(16)A^+/− mice was excluded from the imaging analysis due to poor quality of the imaging window. Experimenters were blind to mouse genotype throughout the experiment and initial data preprocessing steps. Littermate mutant and wild-type mice from at least five different litters were used and randomly assigned to each experiment (GOL and RF). For the hippocampus inactivation experiment, wild-type C57Bl6j mice were used and were randomly assigned to the two experimental groups.

Imaging window implant

Mice were surgically implanted with an imaging window over the left dorsal hippocampus, along with a steel head-post for head-fixation during the experiments as described previously^52,53. Imaging cannulas were constructed by gluing (Norland optical adhesive) a 3-mm glass coverslip (64-0720, Warner) to a cylindrical steel cannula (3.0-mm diameter, 1.5-mm height). The surgical protocol was performed as described previously^52,56. Analgesia was continued for 3 d postoperatively.

Behavioral training

After recovery from surgery but before the beginning of the behavioral experiments, mice were water deprived (>85% predeprivation weight) and habituated to handling and to the experimental setup including imaging equipment (shutter sounds, laser, objective). Next, water-deprived mice were head-fixed and trained to operantly lick to receive water rewards (water delivered in response to tongue contact with a capacitive sensor) at random hidden locations while running on a single-fabric, cue-free treadmill for 10 d (one 15-min trial/d). Mice initially received 40 randomly placed rewards per lap, and the reward frequency was decreased until the mice ran reliably for 3 randomly placed rewards per lap at a rate of at least 1 lap per min. Upon entering the reward zone, a drop of water was delivered in response to every other lick from the mouse. Water delivery stopped either when the mouse traveled 10 cm past the beginning of the reward zone or 3 s had elapsed. Randomization of reward zones during training encouraged mice to continuously run and lick simultaneously.

Goal-oriented learning

For GOL, the reward location was fixed to a 20-cm reward zone within the ~2-m long treadmill belt (180–200 cm) during context presentation as described below (see “Contexts” section). Under this set up, each mouse was trained to learn the initial reward position for 3 × 10-min trials/d, separated by ~1 h for three consecutive days (Days 1–3, Context A, Condition I, 9 sessions total). We then changed the treadmill belt and nonspatial context, and mice were given 3 × 10-min trials/d for three consecutive days (Days 4–6, Context A′, Condition II) under this changed context. In Condition III, the reward zone was moved to a new location, while the other features of the belt and context were kept the same as in Condition II. Mice were given 3 × 10-min trials/d for three consecutive days to learn the new reward position (Days 7–9, Context A′, Condition III). As a point of clarity, we use the term ‘context’ to refer to the entire environment and set of features present during the experiment, including the fabric belts, local cues, nonspatial odor, tone and light, as well as the head-fix apparatus and the microscope itself, but, notably, not the uncued reward location. We always use ‘position’ in reference to the sequence of three distinct belt fabrics, which were always in the same order throughout all conditions of the experiment.

Random foraging

For RF, water-deprived mice were trained to run for water rewards that were randomly administered nonoperantly throughout cue-rich belts. When the experiment started, mice received, on average, 3 water rewards per lap, but positions of the rewards from lap to lap remained random. This task involved no learning of a particular reward position, as the reward schedule was changed such that water was presented to the mice probabilistically as they ran, independent of both position on the belt and whether or not they licked. Mice ran 2 sessions per d, either in the same context or in paired contexts as described below (see “Contexts”).

Behavioral readout

We used the location and quantity of licks to measure performance on the goal-directed task. As a measure of learning, we computed the fraction of licks in the goal window, where the goal window was spatiotemporally defined as the time when the animal was eligible for rewards (within both the 20-cm spatial zone and the 3-s temporal window).

Comparison of GOL task to freely moving goal-directed learning task in Dupret et al

The GOL task used in this study was motivated by the cheeseboard maze task used by Dupret and colleagues²⁶. The hidden reward cheeseboard maze used by Dupret et al. requires rats to learn the location of hidden food rewards over successive trials. In their primary task, these locations were uncued, and following learning, rats would travel directly to each baited location to retrieve the food reward. To facilitate chronic two-photon functional imaging from hippocampal CA1 place cells throughout learning, we designed this head-fixed paradigm for mice on a linear treadmill instead of a freely moving maze. Our head-fixed goal-oriented learning task required mice to learn the unmarked (‘hidden’) location (a single location instead of three as in Dupret et al.²⁶) of water rewards (instead of food) over successive laps (instead of discrete trials). Mice searched for these rewards by sampling the lick port, which only dispensed water in the correct location, while traversing a circular treadmill. In Dupret et al.²⁶, rats moved around the cheeseboard maze and sampled each well to find the baited reward locations. Both tasks use measures of behavioral efficiency to determine the degree of learning; Dupret et al.²⁶ looked at the length of the path taken by the rats to collect all of the rewards, and in our task we (in effect) looked for the suppression of wasted/unrewarded licks. In essence, both of these tasks require animals to remember a location in space where a reward had previously been received and effectively return to that reward location to receive another reward. Both of these tasks depend on normal activity in hippocampal area CA1 to complete this task (Supplementary Fig. 5).

Stimulus presentation

Visual, auditory and olfactory stimuli were presented and all behavior signals digitized as described previously^52,53,56. To track the linear position of the treadmill, we established three registration anchors at known positions along the belts and interpolated between them using a quadrature-encoded movement signal tied to the rotation of the treadmill wheels. Registration anchors were marked by radio-frequency identification (RFID) buttons (16 mm, 125 kHz; SparkFun Electronics) at evenly spaced positions along the belt and were detected when they passed over a fixed RFID reader (ID-12LA, SparkFun). The rotational quadrature signal was produced by marking treadmill wheels with offset tick marks, and this signal was encoded by a pair of photodiodes (SEN-0024, SparkFun) aligned to the wheels (<0.5 cm resolution).

Contexts

Distinct multisensory contexts were created using the system described in our previous work⁵². This included presentation of a constant odor (carvone or isopentyl acetate), blinking red LED (100-ms duration at 1 Hz or off) and either a pure tone (10 kHz) or continuous beeps (2 kHz, 100-ms duration at 1 Hz). All spatial information was presented to the mice via the treadmill belts. The 2-m long imaging belts used in these experiments were constructed by stitching together 3 fabrics and then adhering six local tactile cues. Paired contexts (A–A′) consisted of two belts with an identical sequence of three fabrics and the same local cues, but the order of the cues was randomized between the two belts. Preservation of the fabric order allowed for comparison of spatial representations between contexts. In addition, each belt was paired with a unique multisensory context, such that when a mouse experienced context A′ after A, the belt was the same fabric sequences as in A but paired with a new local cue order and with a change in the background odor, light and tone. The composition of the first context (A) was randomized between mice.

Hippocampal inactivation

To selectively silence dorsal hippocampus during the GOL task, we infused the GABA_A-agonist muscimol (Sigma) through chronically implanted cannulae. Guide cannulae (24-gauge stainless steel) were implanted in wild-type C57BL/6J mice bilaterally over dorsal area CA1 (anteroposterior, −1.7 mm; mediolateral, ±1.5 mm; dorsoventral, −1.0 mm) and plugged with dummy cannulae (31-gauge stainless steel wire) matching the inner dimension of the guide cannula. The injection cannulae (31-gauge stainless steel) extended 0.5 mm past the end of the guide cannulae, targeting CA1. Surgical procedures were similar to those for imaging window implantation, except that a modified head post was used to accommodate the bilateral guide cannulae. Following implantation, mice were given 3 d to recover before head-fixation habituation, followed by 2 weeks of GOL task training (see the “Behavior training” section above.).

To test for effects of dorsal hippocampus silencing on GOL, we used a modified GOL task model that consisted of a single condition (all days used the same belt, context and reward location). On the first day, mice were randomly divided into two groups (saline, n = 4 and muscimol, n = 3). The saline group was infused with 0.9% saline (0.15 μL at 0.25 μL/min) for the first 3 d (3 sessions per d, 30 min between sessions) and then switched to muscimol (0.15 μL of 1 μg/μL at 0.25 μL/min) on the fourth day as a reversal trial. The muscimol group received the opposite drug schedule: muscimol on the first 3 d and saline on the fourth day. To allow for drug diffusion, injection cannulae were left in place for 2 min following infusion. Mice were briefly head-restrained on a separate training treadmill during drug infusion. Infusions were performed sequentially (one hemisphere at a time) with a 5-μL Hamilton syringe and microinfusion pump (World Precision Instruments). Following infusions, the dummy cannulae were replaced and mice returned to the homecage for 30 min before behavior training/testing.

In vivo two-photon imaging

All imaging was conducted using a two-photon 8-kHz resonant scanner (Bruker). We acquired 300-μm × 300-μm images (512 × 512 pixels) at 7–30 Hz using a 920-nm laser (50–100 mW, Coherent) through the approximate midline of the CA1 pyramidal cell body layer. To align the CA1 pyramidal layer with the horizontal two-photon imaging plane, we adjusted the angle of the mouse’s head using two goniometers (±10° range, Edmund Optics). All images were acquired with a Nikon 40× NIR water-immersion objective (0.8 NA, 3.5 mm WD) in distilled water. Green (GCaMP6f) fluorescence was detected with a GaAsP PMT (Hamamatsu Model 7422P-40). A custom dual stage preamp was used for optimal signal amplification before digitization (Bruker).

Data processing for Ca²⁺imaging

All imaging data were analyzed using the SIMA software package written in Python (https://github.com/losonczylab/sima)⁵. Motion-artifact correction was achieved by implementing a plane-wise version of the 2D hidden Markov model^56–58. Segmentation was performed on each field of view (FOV) by manually drawing polygons around GCaMP6f-labeled somata for the first imaged session of each FOV. Polygons were drawn along the inner edge of the cytosolic border to minimize neuropil contamination. Putative interneurons in the pyramidal layers, predominantly GABAergic basket cells^59–61, were identified and excluded from further analysis based on their multipolar and morphologically larger soma diameter compared to CA1 pyramidal cells^62–64 and on their higher baseline and nuclear fluorescence, consistent with their higher baseline tonic firing rate in vivo^61,65–67. Regions of interest were imported to the SIMA project’s ROI Buddy graphical user interface⁵⁸ and were transformed to the other imaging sessions of the same FOV using a piecewise-affine transformation. This tool also allowed for registration of the regions of interest (ROIs) across experiments, allowing us to track identified cells across imaging sessions.

GCaMP6f fluorescence time-series were extracted from the ROIs using SIMA as previously described⁵⁸. We computed the relative fluorescence changes (ΔF/F) as previously described⁶⁸, with a uniform smoothing window t₁ = 3 s and baseline size t₂ = 60 s.

To identify significant calcium events, we modified a method first implemented by Dombeck et al. in 2007⁶⁹ and since used by both our lab^52,53,70 and others^57,71. The general idea is that for a ΔF/F calcium trace, positive and negative deflections from 0 should occur with equal probability for any noise associated with the photon counting/image acquisition and also for uncorrectable motion along the dorsoventral axis (z axis) of the mouse. This assumption allows us to empirically calculate the false-positive rate for each putative event and thus identify a duration and amplitude threshold above which an event has a fixed (5%) maximum false-positive rate, the level at which there are 20 times more positive events than negative events. To implement this approach, we identified putative events by finding consecutive imaging frames that started 2 s.d. above or below the mean, ended when the signal fell down to 0.5 s.d. above/below the mean and lasted for at least 250 ms. These events were classified by their duration and amplitude (in sigma, s.d.) and binned into 0.5-sigma amplitude and 250-ms duration bins. For each bin, we then calculated the associated false-positive rate as the ratio of negative to positive events. We only included positive events from amplitude–duration bins with a false-positive rate less than or equal to 0.05.

Data analysis

Selection of spatially tuned cells

When evaluating the spatial tuning of pyramidal cells, we restricted our analysis to running-related epochs, defined as consecutive frames of forward locomotion (an imaging frame in which at least one forward pair of beam breaks occurred) at least 1 s in duration and with a minimum peak speed of 5 cm/sec. Consecutive epochs separated by < 0.5 s were merged. Running-related transients were defined as those that were initiated during a running-related epoch.

To identify cells with significant spatial tuning, we calculated the spatial information relative to an empirically calculated shuffle distribution. For each cell we first computed the spatial information⁷² content as

$$I_N=\sum _{i=1}^N{\lambda }_{i}ln\frac{{\lambda }_i}{\lambda }{p}_i$$

where λ_i and p_i are the transient rate and fraction of time spent in the ith bin, λ is the overall firing rate, and N is the number of bins. We computed I_N for multiple values of N = {2,4,5,10,20,25,50,100}. We then created 1,000 random reassignments of the transient onset times within the running-related epochs and recomputed the values of $I_N^s$, where s is the index of the shuffle. To roughly correct for biases in the calculation of mutual information, we then subtracted the mean of this null distribution from all estimates to obtain values

$${\widehat{I}}_N=I_N-\frac{1}{1000}\sum _{s=1}^{1000}{I}_N^s.$$

Finally, we computed a single estimate of the information content for the true transient onset times, $\widehat{I}=\underset{N}{\mathit{max}}{\widehat{I}}_N$, and for the shuffles, ${\widehat{I}}_s=\underset{N}{\mathit{max}}{I}_N^s$. The spatial tuning P value was taken as the fraction of values of s for which Î exceeded Î_s. Cells falling in the top 5% of their respective shuffle distributions were classified as place cells on the basis of their spatial information content.

For all cells, rate maps were formed by dividing the number of transients initiated in each spatial bin by the occupancy of that bin. We calculated rate maps with 100 position bins and smoothed with a Gaussian kernel (σ = 3 bins). To define place fields for cells that were identified as containing significant spatial information, we fit each local maximum in the rate map with a Gaussian, merged overlapping putative fields and then discarded any with an area less than 50% of the largest.

Place cell properties

For each cell, we calculated a spatial tuning vector as

$$\sum _j\frac{e^{i{\theta }_j}}{o\left({\theta }_j\right)},$$

where θ_j is the position of the mouse at the onset time of the jth running transient, and o(θ_j) is the fraction of running frames acquired at position θ_j. The circular variance is defined as 1 minus the magnitude of this mean resultant vector (smaller values convey sharper tuning specificity). Transient sensitivity is defined for a place cell as the fraction of laps in which a significant Ca²⁺ transient occurred in a place field. Transient specificity is defined as the fraction of significant Ca²⁺ transients that occurred within a place field. Single-cell sparsity is defined as described previously⁷³ as

$$s=\frac{{\left(\frac{1}{n}{\sum }_i{r}_i\right)}^2}{\frac{1}{n}{\sum }_i\left(r_i^2\right)}$$

where r_i is the transient rate in in spatial bin i of n total bins. Lifetime place coding is the fraction of all cells that were ever previously identified as a place cell by the nth session they were imaged.

Remapping analysis

Recurrence probability was defined for a given pair of experiments as the fraction of place cells in the first experiment that were also identified as a place cell in the second experiment. The centroid shift for each cell was defined as the distance between the spatial tuning vectors calculated for a pair of experiments. As noted above (see “Goal-oriented learning” section), the actual treadmill belts used for the experiments ranged from 180 to 200 cm, so we normalized the values to the length of the belt to directly compare centroid shift values. These values range on the interval [−0.5, 0.5), and the units have been labeled ‘fraction of belt’. In Figures 3 and 4 we plot the absolute value of this shift. A cell was required to have fired at least one transient in both experiments for inclusion. In our analysis of cell firing location following the shifting of local cues, we define a ‘cueness’ metric for all cells that fired within ±5% (belt units) of the cue before cue shift as

$$c=\frac{d_p}{d_p+d_c}$$

where d_p is the distance from the activity centroid after cue shift to the position of the preferred cue on the fabric sequence before the cue shift, so a d_p value of 0 means that cell maintained its firing at the location where the cue had been. We defined d_c similarly, as the distance from activity centroid after cue shift to the new position of the cue after the cue shift, so that a d_c value of 0 means that a cell’s activity followed the movement of the cue exactly (and a value of 0.5 means it is now at the opposite side of the belt). So the cueness metric, c, has a value of 1 for a cell that followed the cue and a value of 0 for a cell that stayed at the original cue position. All cells with cueness >0.67 were classified as ‘cue-preferring’ and all cells with cueness < 0.33 were classified as ‘place-preferring’. Cueness shuffle distributions were calculated by randomizing the cell identities before and after the cue shift. The fraction of place fields near the reward was defined as the fraction of place cells with a spatial tuning vector within 1/16 of a belt length of the reward zone.

Shuffle distributions

For recurrence probability shuffle distributions, we selected every pair of experiments and calculated the fraction of place cells in the first experiment that were still place cells in the second experiment (recurrence probability), as well as the fraction of all cells in the second experiment that were identified as place cells (recurrence probability chance level). We pooled this chance-level calculation across all pairs of experiments in both genotypes to create the shuffle CDF and inset bar. Centroid shift and place/cue-preferring shuffle distributions were calculated by randomly choosing 10,000 pairs of activity centroids (taken from correctly paired experiments but ignoring cell identity) and calculating the difference in centroid position or the distance to the cue/position.

Recurrence and stability by position

Recurrence and stability as a function of position were calculated from all data during Condition III, the only condition during which we detected remapping toward the reward location. For every session, we first identified the significantly spatially tuned cells, and then for these place cells we calculated the activity centroid position relative to the reward location (positions after the reward are positive; those before the reward are negative). To get a continuous estimate of recurrence as a function of position, we used nonparametric logistic regression to fit a cyclic cubic spline to whether a place cell recurred (1) or not (0) for all place cell pairs of sessions. Overfitting was controlled for by leave-one-out cross-validation, which determined an appropriate smoothness penalty on the spline. Confidence intervals were calculated by generating 1,000 new datasets of the same size as the original, by resampling with replacement. Splines were fit to each new dataset, and the confidence interval was defined as the 5th and 95th percentiles of the fit values^74,75.

Session-to-session place field shift by position was modeled as a continuous series of von Mises distributions, defined as

$$\mathit{VMS}=f\left(x\mid \mu ,\kappa \right)=\frac{e^{\kappa cosx-\mu }}{2\pi I_0(\kappa )},$$

where x is the distance from the reward, I₀ is the modified Bessel function of order 0, μis the offset (mean of the distribution) and κ is the concentration (1/κ is analogous to variance). Both the offset and concentration parameters are assumed to change smoothly across the belt. We first fit the mean shift (offset) of place fields as a function of their initial position as a cyclic cubic spline, minimizing mean squared error between the predicted and actual second session shift. Using this fit as the offset for the von Mises distributions, we fit the concentration factor again as a cyclic cubic spline, minimizing the negative log-likelihood of the actual data. Similarly, overfitting was controlled by leave-one-out cross-validation to determine the penalty on the second derivative of the splines. Confidence intervals were calculated by resampling the original dataset as described above.

LFP acquisition and SWR analysis

Wideband signals were acquired at 25 kHz using a digital acquisition system (Intan Technologies, Los Angeles) from n = 2 WT and 2 Df(16)A^+/− mice. For each mouse, LFP signals from a four-channel silicon probe (NeuroNexus, Ann Arbor) centered around the stratum pyrami-dale layer of CA1 were recorded for 20 min while the mouse was head-fixed on a cue-free treadmill belt, with randomly distributed water rewards. LFP signals were subsequently derived by bandpass filtering wideband signals between 0.1 and 625 Hz and downsampling to 1,250 Hz. For each animal, a pyramidal-layer recording site was chosen based on the amplitude of LFP ripple-events and on its location dorsal to the sites showing prominent negative sharp-waves, which are visible in the stratum radiatum. LFP signals originating in the pyramidal layer during epochs that did not show evidence of muscle-related electrical artifacts and in which the animal was immobile (velocity < 3 cm/s) were included in the analysis. Gabor wavelet spectrograms were computed between 1 and 250 Hz; power within each frequency band was subsequently z-scored within each session. To detect sharp-wave/ripple events, the pyramidal layer LFPs were bandpass filtered at the ripple-band frequency (125 to 250 Hz), rectified, smoothed with a 25-ms STD Gaussian kernel and z-scored. For the main analysis, ripples were detected as ‘trigger’ peaks at least 6 s.d. above the mean, with the ripple ‘edges’ set at 2 s.d. above the mean. The trigger thresholds also varied between 2 and 9 s.d. above the mean. Across all conditions, candidate ripple events occurring within 30 ms of each other were concatenated, and only ripples lasting at least 30 ms were included. Ripple incidence rates were calculated by binning immobility epochs into non-overlapping 30-s bins and calculating the ripple incidence within these bins.

Modeling goal-directed remapping

All parameters in our model of session-to-session recurrence and remapping were fit from our WT and Df(16)A^+/− place cell data, separately for each condition. To determine how the reward affected stability of place cells, we used WT mouse data from sessions during Condition III, the sessions in which we saw robust remapping toward the reward location, to calculate the session-to-session place cell recurrence probability as well as the mean and variance of the place field centroid shift, as a function of the original place field’s distance from the reward location (Fig. 6 and see the “Recurrence and stability by position” section). For the flat model, recurrence, shift offset and shift variance were all set to the mean across all positions from the WT fits.

Our model assumes that every cell has a preferred spatial tuning each day and that the tuning is either latent (non-place cell) or expressed as significant spatial activity (place cell). This assumption is supported by the observation that even when a cell is not identified as a place cell, it retains a ‘memory’ of the last time it was spatially active, firing more closely to the old place field than expected by chance. Specifically, for all place cells from pairs of experiments separated by one session, the mean place field centroid shift variance between those two sessions was independent of the spatial information in the middle session (Supplementary Fig. 11). At each iteration (similar to one elapsed session) of the model (Fig. 7a) a fixed fraction of non-place cells become spatially active, which we denote as P_on (WT: 24.83%; Df(16)A^+/−: 20.58%). Place cells remain spatially active as place cells with a position-dependent recurrence probability, which we denote as P_recur(x_i). Finally, all cells shift their place field location, with the new position being drawn from a von Mises distribution with position-dependent offset μ(x_i) and concentration κ(x_i) as described previously: P(x_{i +1}|x_i) = VMS(x_i + μ(x_i), κ(x_i))

For all simulations, we ran eight iterations, similar to the eight transitions between the nine sessions within each condition of our experiment. We calculated the mean enrichment as the mean absolute centroid distance to the reward across all place cells minus the expected mean distance from the reward (0.25).

For all model simulations, initial spatial tuning and place cell identity were chosen pseudorandomly; initial place cell identities and masks were randomized until the mean distance to the reward was less than 0.00001 but then held constant across 100 simulations of eight iterations each. For enrichment by iteration curves (Figs. 7b and 8e and Supplementary Figs. 10a,b and 11), the mean and 90% confidence intervals are calculated from the 100 simulations. Final distribution histograms (Figs. 7c,e and 8f and Supplementary Figs. 10c,d and 11) are aggregated across all simulations.

To compare the influence of each set of parameters to the final enrichment, we reran the simulation with each of the parameters swapped between WT and flat-model fits (Fig. 7d,e and Supplementary Fig. 13). For example, the WT enrichment for swap P_recur is the simulation run with all WT-fit parameters, except with P_recur kept the same for all positions and equal to the mean, effectively removing the dependence on the distance to reward by flattening out the fits.

Statistics

Behavioral results were analyzed with a linear mixed-effect model or mixed-design repeated-measures two-way ANOVA. Differences in conditions were revealed by use of single linear combinations of parameters with the following formulae

$$\begin{gathered} \text{Var}\left(\beta 1+\beta 2\right)=\text{Var}\left(\beta 1\right)+\text{Var}\left(\beta 2\right)+2\text{Cov}\left(\beta 1-\beta 2\right); \\ Z=\frac{\beta 1+\beta 2}{\mathit{SDvar}\left(\beta 1+\beta 2\right)} \end{gathered}$$

Z was then transformed to P value. All data was tested for equal variance (Levene’s test) and for normal distribution (Kolmogorov-Smirnov normality test). Means were compared by two-sample unpaired t tests, unless the variances were significantly different or the data was not normally distributed, in which cases we used Welch’s t test or Mann-Whitney U test, respectively. Wilcoxon rank-sum tests were used to compare genotypes in SWR data. Chi-squared tests, Cox regression or two-way mixed-effects ANOVA were used for all other individual parameter comparisons. The Benjamini-Hochberg procedure was used for multiple comparisons post hoc analyses with FDR = 0.1. Linear regression analyses with Pearson’s correlation coefficient were calculated for correlations of behavioral performance and place cell stability and enrichment (Figs. 3 and 5). Comparisons of significant correlations between groups were made with GLM after z-score transformation with z-transformed variables on the x axis as covariates. Cox regression was used to compare lifetime place coding between genotypes (Supplementary Fig. 4a). All analyses were performed with SPSS software. Unless otherwise noted, values are plotted as mean ± s.e.m. A life Sciences Reporting Summary is available online.

Plotting

For all box and whisker plots (Figs. 1d, 3b,e and 4f, and Supplementary Fig. 5b), the center line is the median, the top and bottom of the box denote the 1st and 3rd quartile of the data, respectively, and the whiskers mark the full range of the data.

Data availability and code availability

The datasets generated and analyzed during the current study are available in the Dryad Digital Repository at https://dx.doi.org/10.5061/dryad.rq560. Data analysis and simulation code are available on GitHub at https://github.com/losonczylab/Zaremba_NatNeurosci_2017.