Force Field Parametrization of Metal Ions from Statistical Learning Techniques

Abstract

A novel statistical procedure has been developed to optimize the parameters of nonbonded force fields of metal ions in soft matter. The criterion for the optimization is the minimization of the deviations from ab initio forces and energies calculated for model systems. The method exploits the combination of the linear ridge regression and the cross-validation techniques with the differential evolution algorithm. Wide freedom in the choice of the functional form of the force fields is allowed since both linear and nonlinear parameters can be optimized. In order to maximize the information content of the data employed in the fitting procedure, the composition of the training set is entrusted to a combinatorial optimization algorithm which maximizes the dissimilarity of the included instances. The methodology has been validated using the force field parametrization of five metal ions (Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺, and Na⁺) in water as test cases.

1. Introduction

A proper sampling of the phase space of large systems (up to a million of atoms) is currently achievable by employing classical Molecular Mechanics (MM) computer methods such as Molecular Dynamics (MD) and Monte Carlo (MC) simulations.¹ These techniques are commonly based on molecular force fields (FF), whose simple energy functions enable the predictions of structural and thermodynamic properties at a computational cost which is significantly lower if compared to quantum mechanics (QM) and hybrid QM/MM computations. The accuracy of FF-based methods strictly depends on the quality of the corresponding parameters, which are optimized in order to reproduce experimental and/or QM data. The selection of the appropriate FF for a particular chemical investigation is crucial since this choice strictly affects the reliability of the obtained results. Several FFs are nowadays available, each one specifically trained on a chemical domain of interest. Such domains can be large (as in the case of the Universal Force Field²) or limited to particular classes such as biological systems and small organic compounds as in the case of the FFs developed in the field of biomolecular simulations.³⁻⁷ In some cases, users may need to modify the entire FF or reparametrize only some terms such as the potential of flexible dihedrals, which largely affect molecular conformations. This issue is particularly important when spectroscopic calculations have to be performed, as in these cases specificity is preferred over transferability. Different software tools were recently distributed with the aim of developing intramolecular FF using QM energies, gradients, and Hessian matrix, computed on optimized structures, as reference data.⁸⁻¹¹ Among them, the ForceBalance method¹² deserves a special mention, since it provides a scheme to avoid overfitting based on a regularization procedure. Other efforts are generally directed to the refinement or the computation ex novo of atomic charges,^13,14 often resorting to the inclusion of virtual sites (VS) to mimic somehow polarizability effects.^7,15 In this scenario, the classical modeling of metal ions is still maybe regarded as a stand-alone issue. Ions parameters for biomolecular FFs have been historically developed in water solution, as done by Stote and Karplus¹⁶ and, more recently, Jensen and Jorgensen,¹⁷ and subsequently transferred within metalloprotein catalitic site.¹⁸ Major challenges are related to the proper treatment of non-negligible QM effects, which are hard to include within classical descriptions.¹⁹ In this context, the limits of the simple electrostatic plus Lennard-Jones (LJ) model emerge, and a transition to more flexible, multiparameters potential (e.g., by means of polarization) becomes necessary.²⁰⁻²² Therefore, the availability of techniques capable of optimizing FFs of any functional form can be crucial.

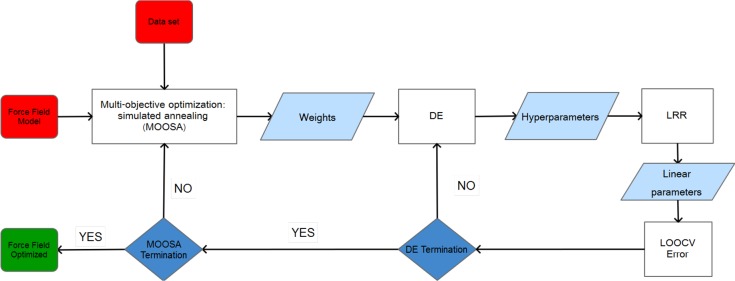
The purpose of this work is the presentation of a general procedure to generate nonbonded FFs of metal ions without altering the functional form and the parameters of the FF of the other atoms of the system, so that they could be easily integrated into consolidated MM packages. To achieve this goal a novel fitting procedure, called linear ridge regression differential evolution (LRR-DE), is proposed. It exploits a combination of machine learning techniques, that in recent years are increasingly finding applications in computational chemistry.²³⁻²⁶ More specifically, the LRR-DE procedure is inspired by the work of Suykens et al.,²⁷ in which the hyperparameters of the least-squares support vector machine (LSSVM) classifier²⁸ are optimized minimizing the leave-one-out cross-validation error by means of the coupled simulated annealing (CSA) algorithm.²⁹ In order to adapt such an approach to the parametrization of analytical forms, in this procedure LSSVM is replaced by the linear ridge regression technique and CSA by differential evolution,^30,31 a metaheuristic optimization algorithm which is effective in the exploration of high dimensionality search spaces. Therefore, LRR-DE uses linear ridge regression to optimize the linear parameters of a tunable model and differential evolution to optimize the nonlinear parameters, minimizing the leave-one-out cross-validation (LOOCV) error. In the most general form of the methodology ab initio forces and energies of sampled configurations are used as reference output, leading to a multiobjective optimization problem. Some of the features which characterize the proposed method, such as a regularized multiobjective cost function, aimed to prevent overfitting, and the ability to optimize either linear and nonlinear parameters, are already implemented in the ForceBalance tool. However, significant novelties can be outlined. The combination of algebraic techniques and metaheuristics employed in LRR-DE, using the LOOCV error as criterion to optimize the nonlinear parameters, enforces the protection from the overfitting and increases the efficiency in finding the global minimum in the parameters space. Moreover, the weights which tune the contribution of the single objective functions are predetermined in ForceBalance. In contrast, the proposed protocol introduces the optimization of the weights so as to obtain the most balanced compromise solution. A further innovative element introduced in this work is the sampling procedure, based on the combinatorial optimization of the training set in order to maximize the dissimilarity of the instances and thus the coverage of the conformational space. This technique, which ensures the maximization over the interpolative domain, is complementary or alternative to iterative sampling approaches proposed by other authors.^12,32 A high level flowchart of the algorithm is shown in Figure 1. The paper is organized as follows. In section 2 the LRR-DE procedure is illustrated, while the sampling methodology is presented in Section 3. Section 4 presents the validation of the methodology, using the parametrization of the FFs of five metal ions (Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺ and Na⁺) in water as test cases.

Figure 1.

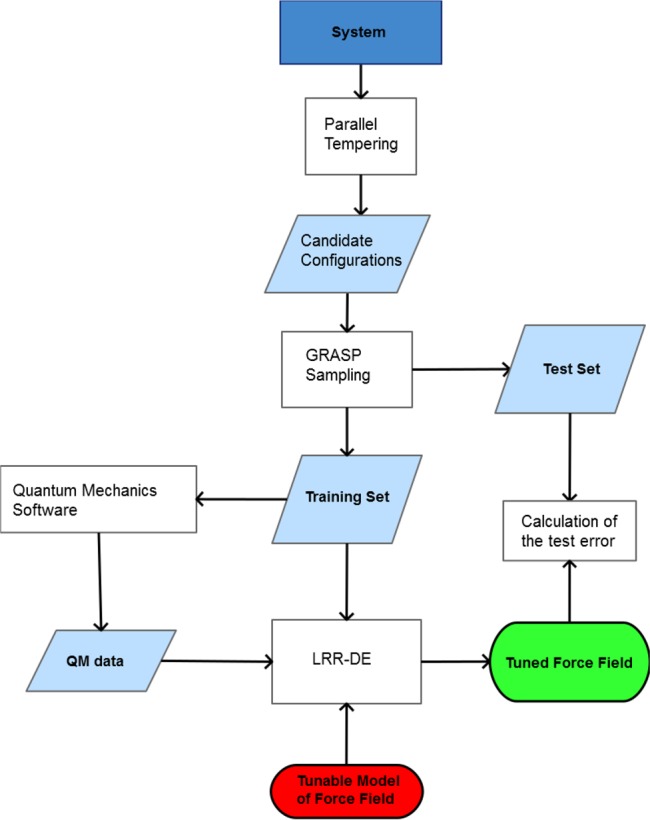
High level flowchart of the proposed algorithm.

2. Method

2.1. Current Status of Parametrization Procedures of Nonbonded Metal Ions Force Fields

The generation of metal ions FFs has been extensively discussed by Li and Merz in a recent review.³³ Methods for parametrizing nonbonded FFs of metal ions are based primarily on the reproduction of experimental thermodynamic and structural quantities. In the pioneering work of Aqvist,³⁴ the parametrization of 12-6 Lennard-Jones potentials of a set of ions was performed using the hydration free energies as a reference and the FEP method³⁵ to calculate the MM estimates. Babu and Lim³⁶ used the same method exploiting the relative HFEs with respect to the Cd²⁺ value to generate the FFs of 24 divalent metal ions. Joung and Cheatham³⁷ parametrized 12-6 Lennard-Jones potentials of monovalent ions employing as reference HFE, crystal lattice energies, and crystal lattice constants. Li, Merz, and co-workers³⁸⁻⁴⁰ developed the parameters of over 50 metal ions reproducing HFE, ion-oxygen distances (IOD), and coordination numbers (CN). In general, the methods that employ experimental references suffer from two difficulties: (i) The availability of data is usually limited to a reduced number of solvents, sometimes only to water. (ii) The exploration of the parameter space, usually performed through a grid search, requires a molecular dynamics or Monte Carlo simulation for each trial solution, making the process inefficient and applicable only to simple functional forms. Both problems can be solved using QM data as target values in the fitting. However, only a very small number of methods based on QM references has been developed. The more significant ones are the works of Floris et al.⁴¹ and Wu at al.²² The method proposed by Floris et al. optimizes the ion–water potential reproducing ab initio energies calculated for [M(H₂O)n]^q+, where the number of the explicit water molecules (n) is one or two, and the rest of the solvent is described by the Polarizable Continuum Model (PCM).⁴³ Therefore, the performances of the method are dependent on the quality of the solvent description. Moreover, the application of PCM precludes the possibility of parametrizing the FFs in heterogeneous environments. These limitations have been overcome in the recent application of the force-matching method by Wu et al. to parametrize the short–long effective functions (SLEF) model in protein environment. In the Wu et al. methodology a squared deviations cost function defined with respect to a sample of QM/MM references is minimized using a local optimizer. The procedure here presented maintains the desirable properties of the Wu et al. approach and introduces further advances in order to generate a transferable nonbonded pairwise force field to model metal ions interactions in metalloproteins. In fact, the multiobjective optimization allows a tight control on the performances of the model. The application of a regularized cost function and the tuning of the hyperparameters through the leave-one-out cross-validation protect from overfitting. The combination of algebraic and metaheuristic optimization ensures the efficient detection of the global minimum of the cost function in the parameter space.

2.2. The Linear Ridge Regression Differential Evolution Procedure

Given a data set {x_l, y_l}, where x_l is the l-th input vector, and y_l is the corresponding output value, an interpolative general model can be built as a linear combination of the functions φ(x, θ), called predictors or descriptors in the language of statistical learning

1

where {C} and {θ} are the linear and nonlinear parameters of the model, respectively. In the linear ridge regression technique,⁴⁴⁻⁴⁸ the optimal linear parameters are obtained minimizing the regularized cost function

2

where M is the size of the data set, and λ is the regularization parameter. The introduction of the regularization term prevents the overfitting penalizing high values of the linear parameters. In order to evaluate properly the regularization term, all the descriptors are scaled with respect to the relative standard deviations

3

The minimization of the cost function (eq 2), in the scaled form, can be performed analytically solving the system of linear equations

4

and the solutions are given by the normal equation

5

where H is the M × N_functions matrix of the scaled descriptors, I is the N_functions × N_functions identity matrix, and y is the vector of the output.

The evaluation of eq 5 can be performed if the values of λ and {θ} parameters have been previously established; therefore, they are considered as hyperparameters. In order to obtain the optimal values of the hyperparameters, the criterion here employed is the minimization of the cross-validation error.

2.2.1. Cross-Validation

Cross-validation (CV)⁴⁸ is a resampling method applied in statistical learning for the model assessment and model selection. In order to estimate the accuracy of a regression model on observations not included in the training set, a test set of instances should be available. However, this is usually not the case. CV overcomes this obstacle executing multiple fittings of subsets of the training set and evaluating the errors on the remaining data. In the k-fold CV, the data set is randomly split into k equally sized subsets. Each of these subsets is used in turn as a test set, while the remaining k – 1 are used for the training. Therefore, k models are built, and each one provides a validation error averaging the deviations of the predictions with respect to the data point of the corresponding test set. The cross-validation error is computed as the mean of the k validation errors. An illustrative scheme of the cross-validation technique is shown in Figure 2.

Figure 2.

Cross-validation scheme. Reprinted from ref (23). Copyright 2013 American Chemical Society.

When k is equal to the number of the instances of the data set, the case is called leave-one-out cross-validation (LOOCV). LOOCV provides an approximated unbiased prediction of the expected test error, because the training sets of the subsets are almost identical to the general training set. In statistical learning, the minimization of the LOOCV error is a standard criterion to optimize the hyperparameters of the model. The LOOCV error is computed as

6

y_est^(−l)(x_i, λ,{θ}) is the prediction for the l-th instance, using the model trained with all the data except the l-th instance. Eq 6 represents the mean squared error (MSE); the mean absolute error (MAE) can be equally used, nevertheless the MSE is more sensitive to the outliers; therefore, it is a better choice to reduce the occurrence of large errors of the model. Calculating this estimate can be computationally demanding because it requires repeating the resolution of eq 5M times. However, for the linear ridge regression method the following relationship holds⁴⁹

7

where y_est(x_l, λ,{θ}) is the prediction of the model trained with the complete data set for the l-th instance, and h_l is the leverage defined as

8

Formula 7 reduces of a factor M the computational cost of the estimate of LOOCV_error, nevertheless an efficient method is necessary to sample the hyperparameters space: each evaluation of LOOCV_error in fact involves the calculation of the elements of the H matrix (unless {θ} = ) and the solution of the normal eq 5.

2.2.2. Optimization of the Hyperparameters by Means of Differential Evolution

The minimization of LOOCV_error (eq 7) with respect to the hyperparameters λ and {θ} is a nonconvex optimization; therefore, a metaheuristic algorithm is necessary to search for the global minimum of the objective function. To accomplish this task, the procedure here presented exploits the evolutionary algorithm known as differential evolution (DE), in the basic version DE/rand/1/bin. DE has been proved to be very competitive in benchmarks tests⁵⁰ and in real world applications⁵¹ compared to other global optimization algorithms. Moreover it offers the great advantage of providing stable performances varying the parameters on which it depends. This technique has been already applied to the optimization of hyperparameters for a support vector machine classifier⁵² providing better results than grid search and particle swarm optimization algorithms. Recently, DE has been identified as a convenient global optimizer also in computational chemistry.^53,54

DE is a population-based derivative-free algorithm that consists of three main steps: mutation, crossover, and selection. After a set {ρ_i} of N trial solution vectors defined in the domain of the objective function is randomly initialized, the three steps of the algorithm proceed iteratively on each vector ρ_i (called target vector) of the population until a tolerance criterion is satisfied. In the mutation step, a donor vector is created through the differential mutation operation

9

where F is a parameter of the algorithm called differential weight, and the indices p, q, and r are chosen randomly with the condition p ≠ q ≠ r ≠ i. This implies that the size of the population must be larger than four units.

In the crossover step, the donor vector exchanges its components with ρ_i. According to the binomial scheme, the crossover is performed following the rule

10

where U(0, 1)_i,j is a random number selected from a uniform distribution in the range [0,1], j_rand ∈ [1,D] (D being the dimension of the vectors) is a random integer, and Cr is a parameter of the algorithm called crossover rate. In all the applications conducted in this work, F and Cr have been set to 0.7 and 0.85, respectively, as result from calibrations on some test cases.

In the selection step, the objective function is evaluated in u_i. If the new vector yields a lower or equal value than ρ_i, it will replace the target vector in the next generation.

When the termination condition is satisfied, the best solution provides the optimal hyperparameters.

2.2.3. Properties of LRR-DE

The LRR-DE procedure is a method capable of reproducing data by optimizing the parameters, both linear and nonlinear, of a model chosen by the user. The application of the regularization and cross-validation protects the optimization from overfitting. The DE algorithm guarantees high efficiency in the search of the optimal hyperparameters. These features make LRR-DE suitable to optimize the parameters of physical models with respect to experimental or ab initio data.

As a simple illustrative example, the LRR-DE method is applied to the fitting of the potential energy curve of the Zn²⁺···H₂O interaction, calculated at the MP2/aug-cc-pVTZ level, as a function of the only variable d, the interatomic distance between the zinc ion and the oxygen atom. A training set of 16 points is employed to build models of increasing complexity. The results are collected in Table 1, and the analytical expressions of the models are shown in Table 2. In Figure 3 the graphical representations of two cases are shown.

Table 1. Mean Squared Errors (MSE), in (kcal/mol)², for Five Models Optimized To Reproduce the MP2/aug-cc-pVTZ Potential Energy Curve of the Zn²⁺···H₂O Interaction^a.

model	linear parameters	nonlinear parameters	MSE (LOOCV)	MSE (test)
12-3	2	0	719.040	768.565
Exp-3	2	1	3.530	3.526
12b-3	2	1	0.525	0.434
12b-3-G	3	3	0.079	0.068
12b-3b-G	3	4	0.001	0.002

^aThe test errors are calculated with respect to 100 points not included in the training set.

Table 2. Analytical Expressions of the Models Tested in the Fitting of the Potential Energy Curve of the Zn²⁺···H₂O Interaction.

model	analytical expression
12-3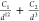
Exp-3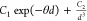
12b-3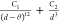
12b-3-G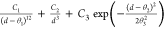
12b-3b-G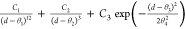

Figure 3.

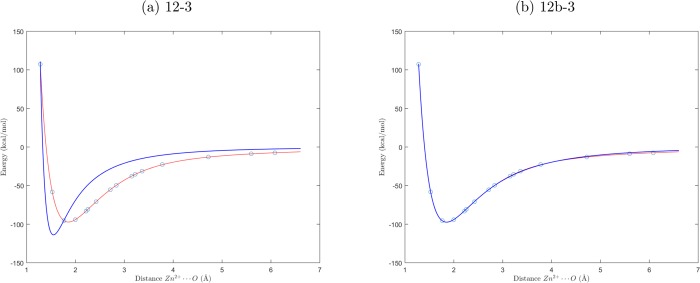
Graphical representation of the potential energy curves of the models 12-3 (blue line, a) and 12b-3 (blue lines, b), compared with the target data (red line), namely the MP2/aug-cc-pVTZ energies (red lines) for the Zn²⁺···H₂O interaction. The blue circles are the points included in the training set.

The simplest considered model, 12-3, includes a repulsive d^–12 term analogous to that of the Lennard-Jones potential and an attractive d^–3 term to account for the charge-dipole interaction. The performance of this model is poor, as can be seen by observing Figure 3(a). The reduction of the error is drastic if the d^–12 term is substituted by an exponential repulsion. Even better results can be obtained employing a buffered d^–12 term to describe the repulsion. Both the exponential and buffered d^–12 terms have a nonlinear parameter. Further terms, even without an immediate physical interpretation, can be added to the models to reduce the errors. For instance, in the 12b-3-G and 12b-3b-G models a Gaussian function is included, resulting in a significant performance improvement. This simple univariate example highlights the crucial role of the descriptor selection in the outcome of the fitting. In general, the choice of the functional form of the model can be made evaluating the performances in the reproduction of the quantities of reference in relation to the particular operational needs. It is worth noting that LRR-DE does not use constraints in the optimization of the linear coefficients. Therefore, the sign of each term, which indicates if it describes a repulsion or an attraction, emerges spontaneously from the optimization, and it is not imposed by the user. However, the j-th linear parameter can be fixed to a constant value, K, performing the fitting of the other parameters with respect to the output subtracted of the contribution of the j-th descriptor (y_l – Kφ_j(x_l)). This possibility has been exploited in the validation tests to generate force fields with the electrostatic component defined by the formal charge of the ions. Tighter control can be exerted on the nonlinear parameters by defining the lower and upper limits of the search domain.

2.3. Single-Objective Application of the LRR-DE Procedure: The Force-Matching Approach

The application of the LRR-DE procedure to the generation of force fields of metal ions can be performed using as target output one or more types of reference quantities, calculated with ab initio methods or obtained by the experiments. In this section the single-objective case is illustrated, in which only one type of reference data is used, namely the ab initio forces on the metal ion. This approach recalls the force-matching method^32,55,56 with the important differences that here the cost function is regularized and the hyperparamaters are tuned to minimize the cross-validation error.

Assuming that the potential of the metal ion is the result of the sum of pairwise potentials with respect to all the other atoms

11

where R_l is the l-th configuration of the system, if V_M–i is expressed as a linear combination of functions v

12

the k-th component of the molecular mechanics model of force exerted on the metal (F_M,k^MM(R_l)) as a result of interactions with all other atoms is given by

13

14

where D_ij is a characteristic parameter of the i-th atom, assuming that the combination rule for the j-th function is multiplicative.

The model of the force field corresponds to eq 1 if the following identity is set

15

then the LRR-DE procedure can be applied if the target output is set equal to the ab initio forces, F_M,k^QM, and the scaled values of the descriptors are assigned to the elements of the H matrix, according to eq 3.

2.4. Generalization to the Multiobjective Fitting

The multiobjective optimization of the parameters exploits simultaneously different types of reference output, for example the ab initio forces on the metal ion, the forces on the nearest neighbor atoms from the metal ion, the contribution to the total energy due to the force field to optimize, different levels of the theory for the calculations, and systems of different composition. The simplest way to approach a multiobjective optimization problem is the reduction to a single-objective one building a weighted cost function. In this case eq 2 becomes

16

where w_b is the scaled weight of the b-th set of targets, of size M_b, calculated as

17

In eq 17, w_b^′ are the effective weights, subject to constraints w_b ∈ [0, 1] and ∑_b^N_bw_b = 1. The definition of their values is the topic of the subsection 2.4.1.

The minimization of the weighted cost function with respect to the linear parameters is given by a normal equation that includes the weights

18

being W is the diagonal matrix containing the w_b values. In this case M = ∑_b^N_bM_b. Eqs 7 and 8 must be modified as follows to take into account the weights

19

20

In order to be used as reference data in the LRR-DE procedure, a quantity has to be expressed as a linear combination of the v functions or of their derivatives. In the case of the forces on other atoms, this condition is satisfied by setting

21

and the unscaled elements of the H matrix

22

where F_A,k^QM is the ab initio k-component of the force on the atom A for the l-th configuration, and f_Ai,k is the k-component of the force on the atom A due to the i-th atom calculated with the force field kept constant in the fitting process.

The ab initio references for the contribution of the force field of the metal ion to the total energy of the system can be calculated as the difference

23

where E_env^QM(R_l) is the energy of the R_l configuration without the metal ion, and E_M is the energy of the isolated metal ion. The unscaled elements of the H matrix in this case are

24

The global H matrix, in the multiobjective fitting, is then the result of the concatenation of two or more matrices, each one relating to a specific quantity of reference.

2.4.1. Optimization of the Weights in the Multiobjective Fitting

In multiobjective optimization, the utopia point,⁵⁷OF°, is defined as the vector of the single objective functions in which each component, OF_b^°, corresponds to the global minimum in its relative space with respect to the variables to be optimized. In practice the utopia point is generally unattainable, and two common approaches are adopted to address the problem: (i) identify the set of Pareto solutions,⁵⁸ leaving to the decision maker the choice on which to use, and (ii) locate a compromise solution⁵⁹ minimizing the distance from the utopia point. Both alternatives involve some degree of arbitrariness. Here, as a criterion for obtaining the optimal weights, the second approach is adopted, using the Chebyshev metrics in a normalized space⁶⁰ as a method for calculating the distance from the utopia point:

25

The application of the Chebyshev distance involves the use of the minimax criterion:

26

It implies that the maximum component of the vector OF^norm(C, θ; w) is minimized with respect to the weights. This choice aims at achieving the most balanced compromise solution. The result of the minimization depends on the choice of the OF_b^max, that corresponds to the worst acceptable value for the b-th objective function. The optimization of eq 26 is performed using the simulated annealing algorithm.⁶¹ The proposed variations for the weights are executed by applying an adaptive heuristics that reduces the number of the function evaluations and exploits the monotone relationship between w_b and OF_b.

Figure 4 shows a summary scheme of the LRR-DE procedure. Three levels of optimization are performed in nested cycles: at the lowest one the fast algebraic solution of eq 18, at the intermediate level the metaheuristic tuning of the hyperparameters, and at the highest level the optimization of the weights of the multiobjective cost function.

Figure 4.

Flowchart of the LRR-DE procedure.

3. GRASP Sampling

In order to build the training set for the fitting, a set of representative configurations of the environment of the metal must be selected. The sampling must be performed carefully to obtain a general and balanced model maintaining the size of the training set such as the computational cost of the technique is affordable.

Assuming to have a criterion for deciding if a set of configurations is better than another, the selection of the best training set would be a NP-hard problem of combinatorial optimization. Therefore, the sampling issue can be separated in three distinct problems: (i) generate the candidate configurations to be included in the training set, (ii) propose a model to determine the fitness of a training set, and (iii) identify an approximated procedure to solve the combinatorial problem of maximization of the fitness. In Appendix A, a solution to each of these problems is proposed. In particular, the application of the greedy randomized adaptive search procedure⁶² (GRASP) is exploited for the third step. For this reason, the whole procedure is called GRASP sampling.

4. Validation

The algorithm has been validated by applying it to the parametrization of the force fields of five metal ions in water: Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺, and Na⁺. The TIP3P model⁶³ has been used to describe the water molecules.

Particular attention has been addressed in the case of the zinc ion, which has been used as reference for the calibration of the method. QM/MM calculations on large spherical clusters and pure QM calculations on clusters of lower size have been initially considered as references. Although the first type of calculation reproduces more closely the actual situation in which common FFs are used, it involves two disadvantages: (i) a bias is introduced by the MM part of the calculation, and (ii) the number of atoms involved is very large, increasing the computational cost of the fitting. Therefore, in this work, pure QM calculations on small clusters have been chosen as references, verifying that the size of the model systems was sufficiently large through a systematic study with a variable number of water molecules (see the next section). As a level of theory, the B3LYP functional in combination with the cc-pVDZ basis set has been selected.

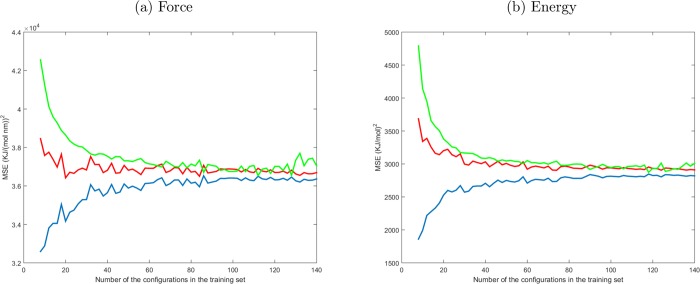
A large basin of candidate configurations has been generated using parallel tempering, and a set of 160 elements has been extracted through the GRASP sampling procedure. The appropriate size of the training set (N_train) has been identified by performing a statistical convergence test, applying the LRR-DE method to the fitting of the forces and the energies for the cluster [Zn(H₂O)₁₂₈]²⁺ case. Starting from a training set of 8 elements and incrementing the size progressively, the three linear parameters of the 12-6-1 FF have been optimized with respect to the QM references. For each size of the training set, 256 independent training sets have been generated selecting randomly N_train configurations, without repetition, from the total of 160 available and using the remaining 160 – N_train configurations as a test set. The averages of the resulting mean squared errors are shown in Figure 5. The graphs confirm that the LOOCV error (red lines) constitutes a better estimate of the test error (green lines) with respect to the training set errors (blue line). In fact, the LOOCV errors and test errors converge to the same value when the size of the training set is greater than 60. The values of the test errors decrease rapidly when the training set size is small and converge to a constant value when N_train is greater than 100 instances. Therefore, in all the following fittings training sets of 120 elements have been employed, so as to provide sufficient generality to the obtained models.

Figure 5.

Mean of 256 tests of the MSE for the training set (blue line), leave-one-out cross-validation (red line), and test set (green line), increasing progressively the size of the training set. The model 12-6-1 has been used to perform the fitting. In each test the elements of the training set are selected randomly from the 160 configurations, and the remaining are used as a test set.

4.1. Systematic Comparative Study of Binary Potentials

In order to calibrate the methodology, the optimization of the parameters of 12 binary pairwise models (see Table 3) has been performed using as reference systems the [Zn(H₂O)_n]²⁺ clusters with n equal to 6, 16, 32, 64, and 128 water molecules. The models consist of a repulsive term, activated only for the zinc–oxygen interaction, and the Coulomb potential. The clusters are built extracting the n closest water molecules to the zinc ion for each of the 160 sampled configurations (see Figure 6). The results have been compared to Li et al.³⁸ (Li, hereafter) and Hartree–Fock (HF) estimates. In standard conditions of temperature and pressure, the coordination number of the zinc ion in bulk water is six,⁶⁴ and the mean number of molecules included in the first and second spheres of coordination is about 30 (see Figure S1 in the Supporting Information). Therefore, the smallest cluster considered corresponds to the extraction of the first sphere of coordination, the [Zn(H₂O)₁₆]²⁺ cluster is representative of the first shell of coordination and part of the second one, and the larger clusters include all the molecules of the first two coordination spheres and beyond. For the largest clusters, [Zn(H₂O)₁₂₈]²⁺, the average distance of the furthest oxygen is 9.6 Å. The parametrization of the force fields has been executed in single-objective mode with the forces on the zinc ion as output references for each cluster, in two-objective mode, contemplating simultaneously forces on the zinc ion and energies of the same cluster, and in four-objective mode, considering all the possible couplings of forces and energies for two types of clusters. In all cases, the resulting force fields have been tested on the QM forces on zinc ion, the energies (y_l in eq 23) and the forces on the nearest oxygen and hydrogen atoms for all the clusters, so as to evaluate their capacity in predicting quantities unused in the fitting. The complete results of this study are reported in the Supporting Information. As a significant case, the 12b-1 FF data are shown in Tables 4, 5, 6, and 7, and analyzed below.

Table 3. Analytical Expressions of the Two-Terms Models Tested in the Systematic Comparative Study.

model	analytical expression	no. of nonlinear parameters
14-1		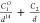0
12-1		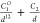0
10-1		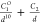0
8-1		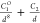0
6-1		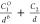0
14b-1		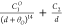1
12b-1		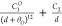1
10b-1		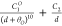1
8b-1		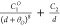1
6b-1		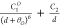1
Exp-1		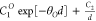1
Exp2-1		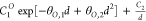2

Figure 6.

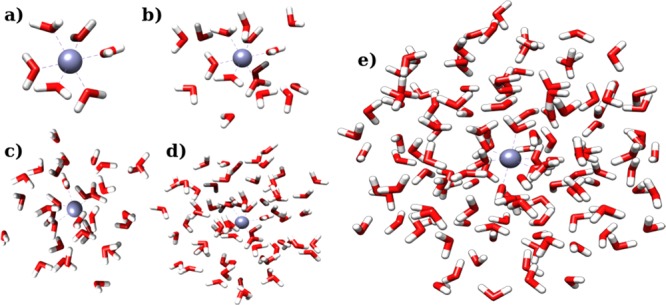
Representative structures of the extracted clusters containing 6 (a), 16 (b), 32 (c), 64 (d), and 128 (e) water molecules.

Table 4. Mean Absolute Errors (kJ/mol for the Energies, E, and kJ/(mol nm) for the Forces, F) in the Prediction of the Quantities Indicated in the First Column, Using as Training Set the Data Indicated in the First Row and the 12b-1 Model^a.

	training set
test set	F(Zn, 6H2O)	F(Zn, 16H2O)	F(Zn, 32H2O)	F(Zn, 64H2O)	F(Zn, 128H2O)	Li et al.	HF
E(6H2O)	761.97	530.02	551.62	559.56	576.14	116.71	153.47
E(16H2O)	949.67	650.46	691.86	703.52	726.39	68.36	146.89
E(32H2O)	998.71	669.10	719.59	732.93	758.65	74.38	136.58
E(64H2O)	1060.05	702.01	761.09	776.03	804.42	69.96	129.74
E(128H2O)	1083.49	706.46	771.29	787.29	817.46	77.10	113.38
F(Zn, 6H2O)	92.95	117.31	113.81	111.44	111.08	627.34	65.13
F(Zn, 16H2O)	191.20	175.86	177.88	178.36	179.11	604.13	71.97
F(Zn, 32H2O)	168.91	160.55	159.70	159.41	159.70	603.82	74.96
F(Zn, 64H2O)	167.94	162.12	161.04	160.58	160.79	605.57	73.59
F(Zn, 128H2O)	165.53	160.95	159.46	158.92	158.96	604.22	73.81
F(6O, 6H2O)	312.62	284.89	269.23	261.93	252.14	1650.26	767.28
F(6O, 16H2O)	302.87	357.11	338.21	329.26	316.50	1727.30	808.86
F(6O, 32H2O)	286.98	370.51	349.89	340.15	325.87	1752.40	807.00
F(6O, 64H2O)	285.65	363.77	343.25	333.63	319.68	1745.70	808.01
F(6O, 128H2O)	285.94	362.59	342.19	332.58	318.42	1744.27	808.02
F(12H, 6H2O)	259.02	301.66	285.63	282.95	278.63	356.05	527.17
F(12H, 16H2O)	298.62	347.19	329.60	326.57	403.66	403.66	617.26
F(12H, 32H2O)	293.34	348.17	329.14	325.80	408.32	408.32	630.00
F(12H, 64H2O)	296.21	349.11	330.48	327.21	407.67	407.67	629.47
F(12H, 128H2O)	296.36	349.04	330.52	327.29	322.08	407.36	629.30
optimized charge	1.529	1.787	1.709	1.694	1.670

^aThe values of the errors for the same data set used in the training process are marked in bold. F(6O, nH₂O) are the forces on the six oxygen atoms closest to the zinc ion for the cluster with n water molecules. F(12H, nH₂O) are the forces on the 12 hydrogen atoms closest to the zinc ion for the cluster with n water molecules.

Table 5. Mean Absolute Errors (kJ/mol for the Energies, E, and kJ/(mol nm) for the Forces, F) in the Prediction of the Quantities Indicated in the First Column, Using as Training Set the Data Indicated in the First Row and the 12b-1 Model^a.

	training set
test set	2-o(6H2O)	2-o(16H2O)	2-o(32H2O)	2-o(64H2O)	2-o(128H2O)	Li et al.	HF
E(6H2O)	23.39	32.42	55.39	72.37	96.84	116.71	153.47
E(16H2O)	49.05	40.46	53.40	67.63	92.18	68.36	146.89
E(32H2O)	88.38	55.27	41.09	45.45	60.94	74.38	136.58
E(64H2O)	120.15	76.97	44.57	42.50	50.37	69.96	129.74
E(128H2O)	159.29	108.18	61.61	49.05	43.38	77.10	113.38
F(Zn, 6H2O)	191.19	185.30	179.20	176.33	173.07	627.34	65.13
F(Zn, 16H2O)	211.04	206.28	202.59	200.78	198.25	604.13	71.97
F(Zn, 32H2O)	209.46	201.74	196.89	195.42	192.96	603.82	74.96
F(Zn, 64H2O)	205.33	198.76	194.40	192.81	190.19	605.57	73.59
F(Zn, 128H2O)	203.45	198.02	193.99	192.08	189.89	604.22	73.81
F(6O, 6H2O)	980.81	963.04	921.68	891.74	855.18	1650.26	767.28
F(6O, 16H2O)	1060.42	1042.81	1001.63	971.78	935.36	1727.30	808.86
F(6O, 32H2O)	1084.55	1066.84	1025.49	995.56	959.06	1752.40	807.00
F(6O, 64H2O)	1077.10	1059.38	1018.04	988.11	951.59	1745.70	808.01
F(6O, 128H2O)	1075.69	1058.00	1016.69	986.76	950.18	1744.27	808.02
F(12H, 6H2O)	480.17	462.79	447.00	443.84	439.29	356.05	527.17
F(12H, 16H2O)	527.06	509.90	494.26	491.13	486.62	403.66	617.26
F(12H, 32H2O)	535.97	518.37	502.29	499.07	494.43	408.32	630.00
F(12H, 64H2O)	533.35	515.96	500.16	497.00	492.44	407.67	629.47
F(12H, 128H2O)	532.67	515.32	499.51	496.35	491.78	407.36	629.30
optimized charge	2.385	2.335	2.288	2.279	2.266

^aThe values of the errors for the same data set used in the training process are marked in bold. The notation 2-o(nH₂O) indicates that a two-objective optimization has been performed, using as references the energies and the forces for the cluster with n water molecules. F(6O, nH₂O) are the forces on the six oxygen atoms closest to the zinc ion for the cluster with n water molecules. F(12H, nH₂O) are the forces on the 12 hydrogen atoms closest to the zinc ion for the cluster with n water molecules.

Table 6. Mean Absolute Errors (kJ/mol for the Energies, E, and kJ/(mol nm) for the Forces, F) in the Prediction of the Quantities Indicated in the First Column, Using as Training Set the Data Indicated in the First Row and the 12b-1 Model^a.

	training set
test set	4-o(6H2O/16H2O)	4-o(6H2O/32H2O)	4-o(6H2O/64H2O)	4-o(6H2O/128H2O)	4-o(16H2O/32H2O)	Li et al.	HF
E(6H2O)	25.61	28.53	29.24	30.89	35.95	116.71	153.47
E(16H2O)	41.35	44.18	46.61	52.51	44.60	68.36	146.89
E(32H2O)	58.82	42.31	41.40	43.98	42.66	74.38	136.58
E(64H2O)	78.20	47.29	44.14	44.39	50.92	69.96	129.74
E(128H2O)	107.01	61.87	53.79	45.98	71.39	77.10	113.38
F(Zn, 6H2O)	185.57	186.28	188.44	192.61	181.84	627.34	65.13
F(Zn, 16H2O)	208.47	210.93	212.95	216.36	205.24	604.13	71.97
F(Zn, 32H2O)	203.07	203.76	205.45	208.34	198.47	603.82	74.96
F(Zn, 64H2O)	199.92	200.09	202.17	205.84	196.22	605.57	73.59
F(Zn, 128H2O)	199.22	200.70	202.97	206.32	196.13	604.22	73.81
F(6O, 6H2O)	993.07	1006.81	1012.74	1023.06	967.19	1650.26	767.28
F(6O, 16H2O)	1072.67	1086.38	1092.28	1102.56	1046.95	1727.30	808.86
F(6O, 32H2O)	1096.83	1110.57	1116.51	1126.82	1070.99	1752.40	807.00
F(6O, 64H2O)	1089.38	1103.12	1109.05	1119.37	1063.54	1745.70	808.01
F(6O, 128H2O)	1087.95	1101.68	1107.61	1117.93	1062.14	1744.27	808.02
F(12H, 6H2O)	450.33	420.78	412.58	400.61	439.72	356.05	527.17
F(12H, 16H2O)	497.57	468.27	460.14	448.28	487.05	403.66	617.26
F(12H, 32H2O)	505.69	475.54	467.16	454.89	494.87	408.32	630.00
F(12H, 64H2O)	503.49	473.78	465.48	453.39	492.87	407.67	629.47
F(12H, 128H2O)	502.86	473.12	464.85	452.82	492.22	407.36	629.30
optimized charge	2.298	2.210	2.185	2.148	2.267

^aThe values of the errors for the same data set used in the training process are marked in bold. The notation 4-o(nH₂O/mH₂O) indicates that a four-objective optimization has been performed, using the energies and the forces for the clusters with n and m water molecules. F(6O, nH₂O) are the forces on the six oxygen atoms closest to the zinc ion for the cluster with n water molecules. F(12H, nH₂O) are the forces on the 12 hydrogen atoms closest to the zinc ion for the cluster with n water molecules.

Table 7. Mean Absolute Errors (kJ/mol for the Energies, E, and kJ/(mol nm) for the Forces, F) in the Prediction of the Quantities Indicated in the First Column, Using as Training Set the Data Indicated in the First Row and the 12b-1 Model^a.

	training set
test set	4-o(16H2O/64H2O)	4-o(16H2O/128H2O)	4-o(32H2O/64H2O)	4-o(32H2O/128H2O)	4-o(64H2O/128H2O)	Li et al.	HF
E(6H2O)	33.15	32.69	56.33	51.59	75.72	116.71	153.47
E(16H2O)	46.97	51.79	58.16	63.37	75.96	68.36	146.89
E(32H2O)	41.29	42.82	42.31	46.23	51.19	74.38	136.58
E(64H2O)	44.95	43.36	42.59	43.80	45.09	69.96	129.74
E(128H2O)	57.99	47.83	53.13	45.43	44.09	77.10	113.38
F(Zn, 6H2O)	183.09	187.52	177.81	178.21	174.69	627.34	65.13
F(Zn, 16H2O)	207.22	210.86	202.25	203.36	200.09	604.13	71.97
F(Zn, 32H2O)	199.97	202.71	195.81	195.77	193.75	603.82	74.96
F(Zn, 64H2O)	197.27	200.33	193.65	193.69	191.55	605.57	73.59
F(Zn, 128H2O)	197.39	200.87	193.18	193.63	191.03	604.22	73.81
F(6O, 6H2O)	987.41	1007.83	922.47	942.65	890.63	1650.26	767.28
F(6O, 16H2O)	1067.08	1087.40	1002.41	1022.52	970.67	1727.30	808.86
F(6O, 32H2O)	1091.20	1111.59	1026.27	1046.45	994.44	1752.40	807.00
F(6O, 64H2O)	1083.75	1104.14	1018.82	1039.01	986.99	1745.70	808.01
F(6O, 128H2O)	1082.31	1102.69	1017.48	1037.63	985.64	1744.27	808.02
F(12H, 6H2O)	424.58	409.41	438.89	422.85	435.14	356.05	527.17
F(12H, 16H2O)	472.03	457.00	486.22	470.31	482.50	403.66	617.26
F(12H, 32H2O)	479.41	463.91	494.02	477.65	490.20	408.32	630.00
F(12H, 64H2O)	477.62	462.27	492.03	475.87	488.27	407.67	629.47
F(12H, 128H2O)	476.95	461.66	491.38	475.21	487.61	407.36	629.30
optimized charge	2.221	2.175	2.264	2.216	2.253

^aThe values of the errors for the same data set used in the training process are marked in bold. The notation 4-o(nH₂O/mH₂O) indicates that a four-objective optimization has been performed, using the energies and the forces for the clusters with n and m water molecules. F(6O, nH₂O) are the forces on the six oxygen atoms closest to the zinc ion for the cluster with n water molecules. F(12H, nH₂O) are the forces on the 12 hydrogen atoms closest to the zinc ion for the cluster with n water molecules.

Table 4 reports the MAEs obtained training the 12b-1 force field with the single-objective fitting. The LRR-DE procedure is a method capable of reproducing data of the fitted quantities for the considered model, achieving errors about four times lower than the standard Li force field. It can be better appreciated by observing Figure 7, where the comparison between the QM forces and those predicted by the model for a test set of 40 instances not included in the training set is shown. As consequence of Newton’s third law, also the errors of the forces on the oxygen atoms are drastically reduced with respect to the Li estimates. In addition, from the data it emerges that the forces in clusters of different size than the one used in the training can be reproduced with good accuracy. On the other hand, the force fields trained on the forces produce high errors in the prediction of the energies, indicating that these models are not sufficiently general. In order to overcome this drawback, the transition to a multiobjective fitting is necessary. Table 5 reports the results for the two-objective fittings, considering simultaneously the forces and the energies for a given cluster. The inclusion of the energies in the output references achieves a remarkable reduction of the MAEs for this quantity at the price of a moderate yet acceptable increase in error on the forces. Even more general force fields can be generated if the fitting is performed on data of clusters of two different sizes (Tables 6 and 7). In fact, the MAEs resulting from the four-objective fitting are considerably lower than the errors produced by Li for both the forces and the energies. From the tables it can be noticed that the deviations of the HF forces from the B3LYP references are lower than those provided by model 12b-1, which however reproduces the energies more accurately. Therefore, as a general recipe for the production of the force fields tested in the molecular dynamics applications four-objective fittings have been exploited, employing as system references the clusters [M(H₂O)₃₂]ⁿ⁺ and [M(H₂O)₁₂₈]ⁿ⁺ (4-o(32H₂O/128H₂O) hereafter). The multiobjective fittings produce larger errors in the prediction of the forces on oxygen atoms with respect to the single-objective ones. However, they remain considerably lower if compared with Li. For this reason the forces on the coordinating atoms have not been included as output references in the systematic study.

Figure 7.

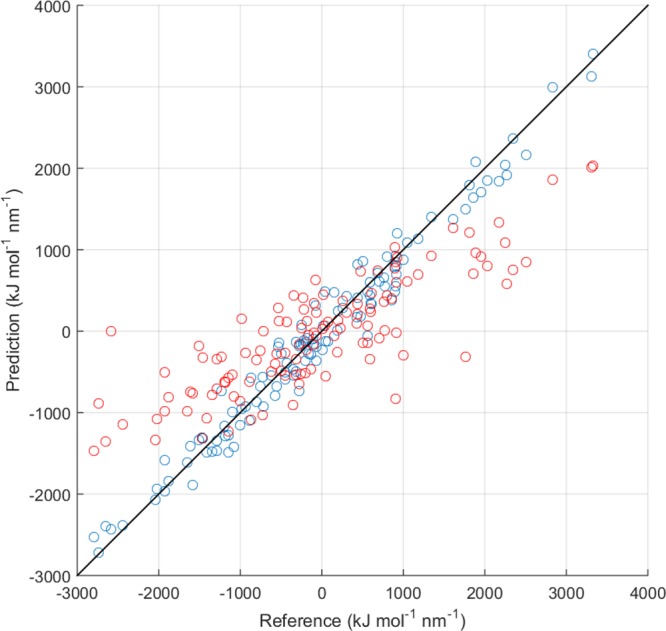
Graphical comparison of the prediction of 12b-1 model (blue points) and Li (red points) predictions of the forces on the zinc ion in the [Zn(H₂O)₁₂₈]²⁺ cluster with respect to the B3LYP/cc-pVDZ reference for a test set of 40 configurations.

Table 8 shows the comparison of the performances of the 12 potentials considered in the systematic study for the 4-o(32H₂O/128H₂O) fitting. Except for the case 6-1, that produces larger errors, all the potentials provide comparable results in the reproduction of the energies. Conversely, the errors for the forces are more dependent on the repulsive part of the potential employed. More specifically, the use of a repulsive term dependent on a nonlinear parameter guarantees better performances. Notable is the modest result of the 12-1 model, that exploits the repulsive term of the Lennard-Jones potential; only the r^–14 term produces a worse agreement with the QM forces.

Table 8. Mean Absolute Errors (kJ/mol for the Energies, E, and kJ/(mol nm) for the Forces, F) in the Prediction of the Quantities Indicated in the First Column, for the Model Indicated in the First Row Trained Using the Four-Objective Fitting 4-o(32H₂O/128H₂O).

test set	14-1	12-1	10-1	8-1	6-1	14b-1	12b-1	10b-1	8b-1	6b-1	Exp-1	Exp2-1
E(6H2O)	62.93	47.92	31.47	46.79	150.95	49.85	51.59	53.88	57.08	61.65	38.96	34.45
E(16H2O)	48.96	47.97	49.55	61.90	105.31	62.61	63.37	64.39	65.81	67.84	57.77	55.63
E(32H2O)	47.78	46.17	45.04	46.24	57.78	46.00	46.23	46.56	47.03	47.80	44.67	44.12
E(64H2O)	50.95	49.08	46.69	44.29	43.61	43.77	43.80	43.85	43.94	44.12	43.61	43.59
E(128H2O)	50.35	48.36	46.45	45.72	53.72	45.28	45.43	45.63	45.95	46.51	44.52	44.26
F(Zn, 6H2O)	327.64	274.35	223.32	185.69	198.66	177.43	178.21	179.42	181.62	186.26	174.29	174.07
F(Zn, 16H2O)	327.38	282.93	241.33	208.37	212.90	203.20	203.36	203.76	204.68	206.98	203.66	204.60
F(Zn, 32H2O)	321.05	274.73	231.99	200.83	206.63	195.50	195.77	196.27	197.44	199.95	196.09	197.21
F(Zn, 64H2O)	322.22	275.33	231.20	198.14	202.86	193.49	193.69	194.08	194.84	197.11	194.02	195.35
F(Zn, 128H2O)	321.93	274.64	230.37	198.69	201.52	193.50	193.63	193.96	194.89	197.42	194.27	195.60
F(6O, 6H2O)	1326.13	1231.41	1117.21	984.41	876.50	938.52	942.65	948.91	959.33	979.15	920.07	916.11
F(6O, 16H2O)	1404.42	1309.95	1196.19	1064.08	956.60	1018.41	1022.52	1028.76	1039.13	1058.86	1000.02	996.08
F(6O, 32H2O)	1429.27	1334.73	1220.76	1088.18	980.36	1042.32	1046.45	1052.71	1063.12	1082.94	1023.88	1019.93
F(6O, 64H2O)	1422.20	1327.51	1213.41	1080.74	972.86	1034.88	1039.01	1045.27	1055.68	1075.50	1016.42	1012.47
F(6O, 128H2O)	1420.76	1326.11	1211.99	1079.30	971.52	1033.51	1037.63	1043.89	1054.28	1074.06	1015.08	1011.13
F(12H, 6H2O)	351.11	362.23	381.43	419.41	512.29	421.22	422.85	425.12	428.55	434.59	411.19	406.56
F(12H, 16H2O)	398.68	409.88	429.15	466.91	558.59	468.70	470.31	472.56	475.96	481.95	458.77	454.18
F(12H, 32H2O)	403.08	414.87	435.00	474.14	568.32	475.99	477.65	479.96	483.47	489.63	465.74	461.00
F(12H, 64H2O)	402.56	414.09	433.86	472.39	565.41	474.23	475.87	478.17	481.63	487.71	464.08	459.40
F(12H, 128H2O)	402.28	413.73	433.40	471.74	564.75	473.57	475.21	477.50	480.97	487.05	463.45	458.80

The proposal of a novel functional form for the force fields of the metal ions goes beyond the scope of this work; however, the systematic comparative study provides the following useful indications in this regard: (i) the optimal charge to reproduce the forces on the metal ion is lower than the formal charge (Table 4), (ii) in the single-objective fitting, the optimal charge for the smallest cluster is lower with respect to the clusters of larger size (Table 4), (iii) the introduction of the energies in the references has the effect to increase the value of the optimal charge over the formal charge (Tables 5, 6, and 7), and (iv) the use of a repulsive term including a nonlinear parameter is necessary to achieve good performances in the reproduction of the forces (Table 8). Tables 4, 5, 6, and 7 are all related to the data of the model 12b-1; however, the behavior described in the points (i), (ii), and (iii) is common to all the tested potentials (Supporting Information). From a physical point of view, these results can be justified by the effects of the charge transfer from the ion to the coordinating water molecules and of the nonpoint-like structure of the ion. Both effects are expected to vanish at large distances, where a Coulomb potential generated by the formal point charge describes adequately the ion interactions. Therefore, a generic three-terms force field for metal ions that implements the indications emerged from the systematic comparative study has the form

27

where V_rep(θ) is the repulsive part of the potential, q_F is the formal charge of the ion, f(r)_dump is a dumping function which goes to zero beyond the first coordination shell of the ion, and g(r)_flex is a function that provides the necessary flexibility to meet simultaneously the points (i), (ii), and (iii). An explicit form for the potential of eq 27 is

28

The third term of this FF, here labeled as 12b-1_F-E1Gr, recalls the physical meaning pursued by the model proposed by Wu et al.²² to describe zinc charge interactions in metalloenzymes catalytic sites. In this context, the employment of such functional form has only illustrative purposes to highlight the potentiality of the LRR-DE method in the optimization of models of general functional forms. Therefore, the 12b-1_F-E1Gr FF has been tested and compared to the 12-6-1 (Lennard-Jones combined with Coulomb potential, optimizing the charge value) and 12-6-1_F (Lennard-Jones combined with Coulomb potential, with the charge of the ion set equal to the formal charge) FFs only in terms of structural properties.

4.2. Parameters Optimization and Molecular Dynamics Simulations

The 12-6-1, 12-6-1_F, and 12b-1–1EGr force fields have been trained using the 4-o(32H₂O/128H₂O) fitting for the cases of the Zn²⁺ ion in water and tested in MD simulations. Properties derivable from MD have been also compared with Babu and Lim parameters,³⁶ as well as the already cited Li: performances of these two sets of parameters have been re-evaluated in this paper by applying the same computational protocol reported in the corresponding original work (see Figure 8). Uniform values have been assigned to the weights of the objective functions, and they have been optimized according to the procedure explained in subsection 2.4.1 only if unsatisfactory errors for a QM reference have been observed. Table 9 reports the mean absolute errors of the three-terms models with respect to QM references of the zinc-water clusters. The larger flexibility of the 12b-1_F-E1Gr force field allows for reducing the errors, in particular in the reproduction of the forces. The accuracy of the 12-6-1 forces is significantly higher than the 12-6-1_F ones. This behavior is a consequence of the fact that the LRR-DE optimization provides a negative parameter for the r^–6 term when the charge is a free parameter. Thus, the r^–6 term contributes in describing the repulsion, and as a consequence, the QM forces are reproduced with the 6-1 quality (Table 8). Both 12-6-1_F and 12-6-1 FFs overcome the performance provided by Li. The same trend is observed in the results of the MD simulations. In fact, the radial distribution function (g(r)) between zinc ion and water oxygen obtained with the 12-6-1_F model presents a slightly better agreement with the EXAFS data⁶⁵ than the Li prediction (see Figure 10). A more consistent improvement is achieved with the 12-6-1 and 12b-1_F-E1Gr potentials, as can be appreciated in Figure 10. Broadly speaking, the ion-oxygen distance is well reproduced by the employed models, and their performances are better than polarizable models,^66,67 which predict lower values when compared to the experimental ones. As the flexibility of the FF is improved, the height of the peak diminishes while its width increases, thus becoming comparable with results provided by ab initio investigations,^67,68 as well as with the experimental EXAFS data. Moreover, it is worth noticing that the g(r) peak obtained with the 12-6-1 model (where only three parameters - i.e., Lennard-Jones parameters and the electrostatic charge - are optimized) is in line with the one predicted by even more flexible models, such as the one proposed by Chillemi et al.,⁶⁵ where 9 parameters are optimized. As regarding the hydration free energy (HFE), the prediction provided by the 12-6-1 model is considerably more accurate than the estimates of 12-6-1_F and Li. In particular, the deviation between the experimental reference and the 12-6-1 estimate is lower than 5 kJ/mol, while for 12-6-1_F and Li is larger than 100 kJ/mol. Taking into account the parameters generated by Babu for the zinc ion, the LRR-DE 12-6-1_F model offers a slightly worse reproduction (of 0.01 Å) of the IOD value. However, an opposite behavior is observed in the reproduction of HFE, where the performance of Babu FF is poor, with a deviation from the experimental value of roughly 175 kJ/mol.

Figure 8.

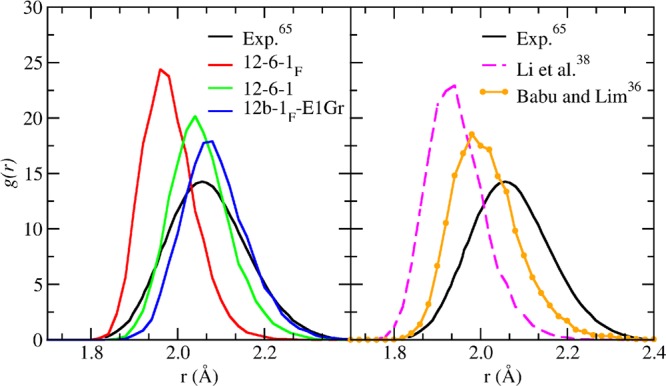
Radial distribution functions between zinc ion and water oxygens, using the 12-6-1_F, 12-6-1, 12b-1_F-E1Gr (left panel) and Li³⁸ and Babu³⁶ models (right). In both panels, the comparison with the experimental profile⁶⁵ is provided.

Table 9. Mean Absolute Errors (kJ/mol for the Energies and kJ/(mol nm) for the Forces) in the Prediction of the Quantities Indicated in the First Column, for the Model Indicated in the First Row.

test set	12-6-1F	12-6-1	12b-1F-E1Gr	12b-1	Li et al.	HF
E(6H2O)	49.12	77.48	70.75	51.59	116.71	153.47
E(16H2O)	49.36	74.34	59.45	63.37	68.36	146.89
E(32H2O)	47.73	49.84	41.48	46.23	74.38	136.58
E(64H2O)	51.42	44.35	43.33	43.80	69.96	129.74
E(128H2O)	49.38	47.92	43.81	45.43	77.10	113.38
F(Zn, 6H2O)	280.69	194.72	141.48	178.21	627.34	65.13
F(Zn, 16H2O)	287.11	210.88	184.37	203.36	604.13	71.97
F(Zn, 32H2O)	279.35	204.67	180.99	195.77	603.82	74.96
F(Zn, 64H2O)	280.30	201.49	180.38	193.69	605.57	73.59
F(Zn, 128H2O)	279.54	201.66	179.97	193.63	604.22	73.81
F(6O, 6H2O)	1242.78	1003.25	611.03	942.68	1650.26	767.28
F(6O, 16H2O)	1321.28	1082.85	692.46	1022.52	1727.30	808.86
F(6O, 32H2O)	1346.07	1107.02	714.92	1046.45	1752.40	807.00
F(6O, 64H2O)	1338.86	1099.57	707.54	1039.01	1745.70	808.01
F(6O, 128H2O)	1337.46	1098.12	706.39	1037.63	1744.27	808.02
F(12H, 6H2O)	356.05	451.17	356.05	422.85	356.05	527.17
F(12H, 16H2O)	403.66	498.40	403.66	470.31	403.66	617.26
F(12H, 32H2O)	408.32	506.54	408.32	477.65	408.32	630.00
F(12H, 64H2O)	407.67	504.33	407.67	475.87	407.67	629.47
F(12H, 128H2O)	407.36	503.70	407.36	475.20	407.36	629.30

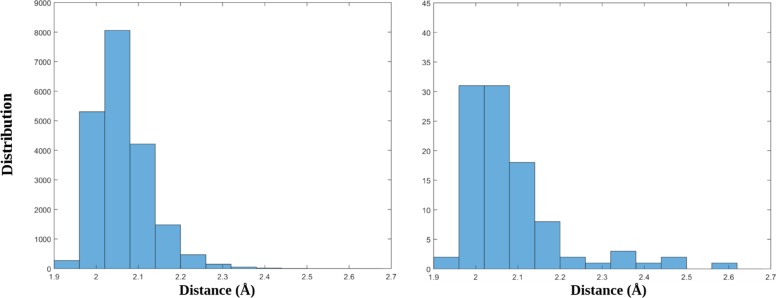
Figure 10.

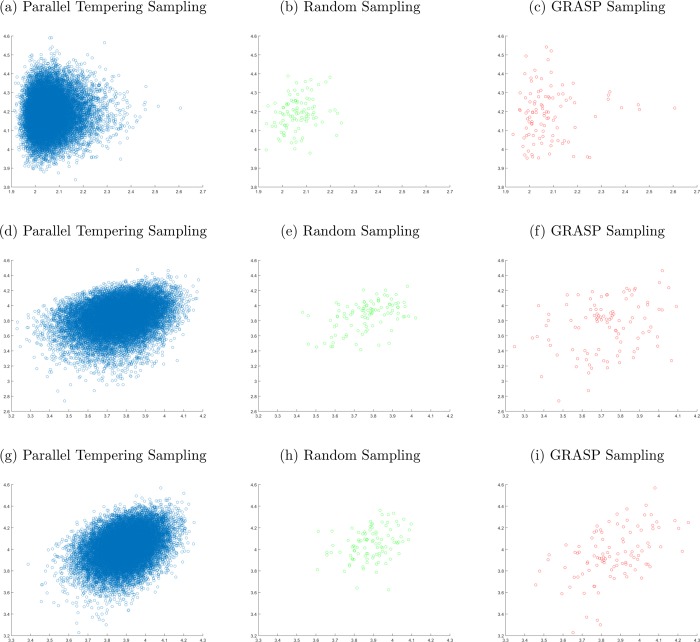
Radial distribution of the sixth closest atom of oxygen to the zinc ion in the parallel tempering sample (a) for the Zn²⁺/H₂O system and in a subset of the first one obtained by the combinatorial optimization of a selection of the first one that maximizes eq 31 (b). For the parallel tempering sample the elements are 20000; in the subset they are 100.

The whole protocol already used for zinc ion has been extended to the optimization of the FF models for Ni²⁺, Mg²⁺, Ca²⁺, and Na⁺ ions in bulk water. In the cases of Ca²⁺ and Na⁺, forces on coordinating oxygens have been included in the training, thus performing a six-objective fitting. Such measure turned out to be necessary, since errors on these quantities were larger than expected. Table 10 collects the estimates of the position of the first peak of the radial distribution function, the HFE, and the coordination number of the ion for the five considered systems.

Table 10. Simulated IOD Peak (Å), Free Energy of Hydration (HFE, kJ/mol) and Coordination Number (CN) Values Using the Developed Parameters for the Considered Force Fields^a.

		IOD	MAE(IOD)	HFE	MAE(HFE)	CN
Zn2+	Li et al.	1.93	0.16	–1849.33	105.85	6
	Babu and Lim	1.98	0.11	–1779.53	175.65	6
	12-6-1F	1.97	0.12	–1801.39	153.79	6
	12-6-1	2.04	0.05	–1960.62	5.44	6
	12b-1F-E1Gr	2.07	0.02			6
	Exp.	2.09 ± 0.006		–1955.18		6
Ni2+	Li et al.	1.92	0.14	–1874.01	105.86	6
	Babu and Lim	1.98	0.08	–1800.74	179.13	6
	12-6-1F	1.97	0.09	–2022.78	42.91	6
	12-6-1	2.01	0.05	–2082.59	102.72	6
	12b-1F-E1Gr	2.03	0.03			6
	Exp.	2.06 ± 0.01		–1979.87		6
*Mg2+	Li et al.	2.03	0.06	–1724.23	105.85	6
	Babu and Lim	2.08	0.01	–1651.10	178.98	6
	12-6-1F	2.01	0.08	–1759.79	70.29	6
	12-6-1	2.03	0.06	–1871.92	41.84	6
	12b-1F-E1Gr	2.06	0.03			6
	Exp.	2.09 ± 0.004		–1830.08		6
*Ca2+	Li et al.	2.49	0.03	–1399.97	105.01	8
	Babu and Lim	2.61	0.15	–1328.19	166.79	8.3
	12-6-1F	2.46	0.00	–1431.76	73.22	8
	12-6-1	2.53	0.07	–1551.43	46.45	8
	12b-1F-E1Gr	2.50	0.04			8
	Exp.	2.46		–1504.98		8
Na+	Joung and Cheatham	2.34	0.01	–374.89	10.05	5.87
	12-6-1F	2.34	0.01	–389.53	24.69	5.91
	12-6-1	2.34	0.01	–389.95	25.11	5.95
	12b-1F-E1Gr	2.35	0.00			5.72
	Exp.	2.35 ± 0.06		–364.84		5–6

^aResults are compared with the ones of Li et al., Babu and Lim, Joung and Cheatham, and experimental data. The mean absolute errors are with respect to the experimental references.

The optimized 12-6-1_F on nickel divalent cation overcomes the performances of Li and Babu in terms of HFE estimation. Compared to the 12-6-1_F force field, Babu offers a better agreement with the experimental IOD value (of 0.01 Å). As regarding the 12-6-1 model, the experimental HFE is exceeded by 102.72 kJ/mol; however, the prediction of the ion-oxygen distance (IOD) is improved 0.9 Å with respect to the Li²¹ data. The experimental IOD is reproduced even better by the 12b-1_F-E1Gr model, and the experimental ion–water oxygen radial distribution function⁶⁵ is reproduced with quite good accuracy (see Figure S2 in the Supporting Information).

For the magnesium ion, the peak of the g(r) provided by the MD simulation with the 12-6-1_F model has a deviation larger than 0.02 Å from the experimental data with respect to the Li prediction. The g(r) is correctly reproduced by Babu parameters. On the other hand, 12-6-1_F gives a reduction of the error of about 35 and 108 kJ/mol in the HFE estimate with respect to the Li and Babu force fields, respectively. As for the zinc case, also for the magnesium ion, the 12-6-1 model produces a large improvement in the HFE prediction. Among all the considered FFs, the 12b-1_F-E1Gr model provides the best agreement with the experimental data for the g(r) peak position. The 12-6-1 and 12b-1_F-E1Gr FFs give estimates in good agreement with the state-of-art pairwise potentials⁶⁹ and polarizable models.⁶⁷ Moreover, a satisfactory comparability with AIMD and QM/MM simulations, which predict ion-oxygen distance values between 2.08 and 2.13 Å,⁶⁷ is observed.

The 12-6-1_F model for the calcium ion trained with the LRR-DE procedure offers better performances than Li and Babu in the prediction of the peak position as well as in the HFE estimation. Again, the 12-6-1 force field produces a further increase in accuracy for the HFE, at the expense of a slightly worse result in the g(r) peak position. Also the performance of the 12b-1_F-E1Gr model is less satisfactory than in the previous cases. However, such measures are in line with those coming from a recent AIMD simulation which provides a metal-ion distance in the first coordination shell of 2.51 ± 0.07.⁷⁰

In the case of the sodium ion, LRR-DE performances are compared to the ones offered by Joung and Cheatham parameters.³⁷ The LRR-DE models give an excellent agreement with the experimental data in the prediction of the peak position of the radial distribution function. QM/MM simulations conducted on the hydrated ion present a certain variability in the computed metal–oxygen distance, ranging from 2.33 to 2.42.⁷¹⁻⁷³ The HFE calculated with the 12-6-1 and 12-6-1_F models produce a decrease of accuracy of 15 kJ/mol with respect to the Cheatham estimate. However, it is worth noting that sodium Lennard-Jones parameters were specifically optimized by Joung and Cheatham in order to reproduce the HFE value.³⁷

All the computed g(r) profiles for Ni²⁺, Mg²⁺, Ca²⁺, and Na⁺ are reported in the Supporting Information (Figure S2). The second hydration shell (i.e., the second peak in the IOD profile) is highlighted in Figure S3. No notable difference can be appreciated in the peak position for the FFs tested. However, on average, the height of the peak predicted by Babu appears to be lower. In all cases the coordination numbers of the ions are consistent with those experimentally observed. Properties computed with Babu and Li parameters coincide with previous investigations.³⁸

All the experimental quantities explored in this investigation are reproduced with good accuracy by all the tested LRR-DE optimized models even if not directly considered during the parameter fitting procedure. Therefore, the discussed optimization method has been proved to be general, since the considered structural and thermodynamic properties are reproduced with comparable accuracy with respect to standard FFs, directly optimized in order to reproduce such quantities. Since the presented method is designed to refine only the FF of the metal ion, the optimized parameters are specific for the description of the surrounding environment, and the general performances are affected by the implicit approximations included in this model. The obtained FFs have not been tested in environments not considered in the training, and the quality of the performances are not guaranteed in such cases. Transferable FFs can be generated using this methodology, if an appropriate sampling which considers interactions with a wide range of atom types is executed.

4.3. Computational Details

Classical simulations were performed either under periodic boundary conditions (PBC), using GROMACS 4.6.5,⁷⁴ or under spherical nonperiodic boundary conditions (NPBC), using a locally modified version of the Gaussian code.⁷⁵ PBC were used for parallel tempering runs and for simulations using the 12-6-1_F and 12-6-1 force fields, while NPBC were employed for testing the 12b-1_F-E1Gr force field; the latter choice was made to avoid any PBC-induced spurious effect due to a nonzero system charge⁷⁶⁻⁸² and hence assess with more precision the outcome of the 12b-1_F-E1Gr model.

Under PBC, the systems were composed of one metal ion, surrounded by 2178 water molecules, leading to a cubic box of size 40 Å. The rigid TIP3P model⁶³ has been used to describe the water molecules. Fastest degrees of freedom were constrained with the LINCS algorithm.⁸³ In the sampling step, the metal ions have been modeled using parameters designed by Åqvist³⁴ (Mg²⁺, Na⁺), Merz⁸⁴ (Zn²⁺), and Li³⁸ (Ni²⁺, Ca²⁺). Each system was minimized using the steepest descent algorithm implemented in GROMACS using a convergence threshold on the root-mean-square forces of 1 kJ·mol^–1·cm^–1. Systems were slowly heated from 0 to 298 K in NVT ensemble for 1 ns and then equilibrated in NPT conditions for 1 ns to reach uniform density. The final structure for each system was considered as the starting point for the parallel tempering simulations. A number of 25 replicas were employed, covering a temperature range of 100 K, from 298 to 398 K. Temperature distribution of single replicas in the chosen range was established so as to attempt an exchange rate of 0.25.⁸⁵ Each replica was equilibrated in the NPT ensemble for 500 ps, using the stochastic velocity rescale algorithm.⁸⁶ The time step was set equal to 2 fs. Production runs were conducted in the NVT ensemble for 5 ns, for a total simulation time of (5 ns × 25 replicas) 125 ns. Electrostatic interactions were described through the PME method, whereas van der Waals interactions were considered applying a cutoff of 10 Å. Instead, no PME was employed in the simulations of Babu and Lim parameters: following their original simulation protocol,³⁶ a large cutoff value of 2 Å was applied to compute nonbonded interactions. The FFs generated with the LRR-DE procedure were tested by initially equilibrating the systems in the NPT ensemble for 500 ps. After that, production run time was set to 5 ns in the NVT ensemble. Cutoff values of 19 Å for both LJ and real-space PME were used.

Under NPBC, the systems were composed of a spherical water box with a radius of 20 Å, including 1111 H₂O molecules and a metal ion at the center of the box; systems were embedded in a PCM⁸⁷ spherical cavity of 21.8 Å. Ions were positioned at the center of the cavity and kept frozen during the simulations. As for PBC, systems were slowly heated from 0 to 298.15 K in a NVT ensemble using four discrete steps and the stochastic velocity rescale algorithm. The time step was increased from 0.25 to 2.0 fs, and the thermostat coupling constant was set to 1 ps; in production runs, configurations were saved every 500 steps. Solvent density across the spherical box was controlled by means of the GLOB method⁸⁸ as implemented in a locally modified version of Gaussian.⁸⁹

Radial distribution functions were computed either using standard tools available in GROMACS (PBC) software or using an in-house written code (NPBC) on the last 1.5 ns of simulation. Free energy of hydration values was computed using the Bennett acceptance ratio (BAR)⁹⁰ implemented in GROMACS. A number of 21 windows were used. Corresponding λ values were chosen ranging from 0 to 1, in steps of 0.05. Each window was run for 500 ps. The first 100 ps was considered to equilibrate the systems and therefore not included in the final HFE computation. All the QM calculations were performed using the Gaussian 09 package⁹¹ at the B3LYP/cc-pVDZ level. Singlet spin-state has been considered for all the ions except Ni²⁺, for which the triplet has been found to be more stable than the singlet spin state in the QM model systems. All the parameters optimized with LRR-DE are provided in the Supporting Information (Tables S1–S3).

5. Conclusions

A novel statistical procedure (called LRR-DE) has been developed to optimize the parameters of a model so as to reproduce the general behavior of a system, given a representative data set. The fundamental feature of the method is the combination of the linear ridge regression and cross-validation techniques with the metaheuristic algorithm differential evolution. This machinery allows for optimizing both linear and nonlinear parameters of a model of generic functional form. The application of the regularization and the cross-validation avoids the problem of overfitting, if the training set is chosen properly. This aim is achieved applying the GRASP sampling, a combinatorial technique capable of maximizing the dissimilarity of the elements of the data set. A methodology based on LRR-DE has been derived to parametrize the nonbonded force fields of metal ions, using ab initio quantities as references. From the calibration phase, performed on the case of the zinc ion in water, a general protocol for the fitting has been identified. This involves the use of both the forces and the energies computed on clusters of different sizes as references. The application of the multiobjective optimization is optionally activated, and further reference data can be considered if unsatisfactory errors for a certain type of data have been obtained. The validation of the methodology has been performed exploiting the cases of five ions in water, for which several quantitative results of comparison, both experimental and computational, are available. The performances of the force fields trained with LRR-DE have proved to be of comparable or better quality with respect to standard FFs, as the summary Table 11 attests. The possibility of the LRR-DE procedure to use as reference QM forces and energies of different systems simultaneously offers great margins of applicability to the method. In particular, the method is suitable for the optimization of FF of metal ions in a heterogeneous environment, such as in the case of protein cofactors, for which experimental thermodynamic data are usually unavailable. The procedure can be applied to generate transferable FFs, if an appropriate sampling which considers interactions with a wide range of atom types is executed. Moreover, the capacity of the method to tune generic models makes it the ideal tool for optimizing FF with more sophisticated functional forms than those commonly used in molecular dynamics programs.

Table 11. Mean Absolute Deviations from the Experimental References for the Position of the First IOD Peak (MAE(IOD Peak)) and the Hydration Free Energy (MAE(HFE)) for the Considered Divalent Ions^a.

force field	MAE(IOD peak)	MAE(HFE)
Li et al.	0.10	105.64
Babu and Lim	0.09	177.64
12-6-1F	0.07	85.05
12-6-1	0.06	49.11
12b-1F-E1Gr	0.03

^aMAE(IOD peak) is expressed in Å, and MAE(HFE) is expressed in kJ/mol.

Appendix

A. GRASP Sampling

A.1. Generation of the Candidate Configurations

In this work, the generations of the candidate configurations have been performed with the parallel tempering⁹²⁻⁹⁴ technique using a pre-existing FF. It is suitable for this purpose, because it explores a large portion of the free-energy landscape of a molecular system. The configurations are drawn for each replica at regular intervals of extension comparable to the time scale of the significant events of the system considered and proceeds up to obtain a sufficiently large pool of candidates (tens of thousands). Alternative approaches aimed to the generation of the candidate configurations can be considered, such as the extraction from a MD trajectory or a metadynamics sampling, as well as from pre-existent databases. Moreover, procedures which iteratively improve the FF through subsequent sampling and fitting steps can be used in order to correctly reproduce the physics of the investigated system, as proposed by previous works.^12,32

A.2. The Metal-Centric Dissimilarity Score

Since the aim of the present work is the optimization of the FF of a specific atom, the evaluation of the fitness of a possible training set should be focused on the environment of that atom. More specifically, the configurations included in the training set should maximize the representativeness of the situations in proximity of the metal ion. In order to achieve this goal, a dissimilarity score of a set of configurations focused on the neighborhood of the metal is proposed.

As descriptor of the l-th configuration, the vector d_l is used, whose elements are the Euclidean distances between the metal and all other atoms. Each i-th component of the vector d_l is transformed applying a Gaussian kernel as follows

29

where the parameter σ is a measure of the distance from the metal which identifies the most significant region to sample.

The Euclidean distance between the l-th and j-th configurations in the k-space is

30

δ_lj is invariant with respect to the translations or rotations of the system, moreover it satisfies the coincidence axiom (δ_lj = 0 if and only if l ≡ j) and the symmetry condition (δ_lj = δ_jl). As consequence of the transformation of eq 29, k_li – k_ji is amplified with respect to d_li – d_ji where the derivative of the Gaussian function is larger. This occurs in correspondence to d = σ as shown in Figure 9. For d → 0 and d ≫ σ, conversely the differences in the k-space vanish; therefore, in those zones the information is compressed.

Figure 9.

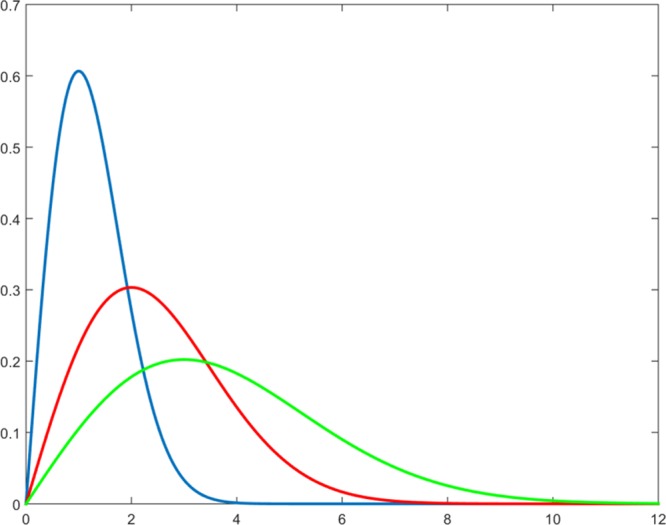
Absolute value of the derivatives of the Gaussian function for three values of the parameter: σ = 1 (blue line), σ = 2 (red line), σ = 3 (green line).

The metal-centric dissimilarity score of the set {k}, constituted by N_TS configurations selected among N_PT candidates, is defined as the mean value of the N_loc distances from the N_loc nearest configurations weighed for an exponential factor, 2^N_loc–j:

31

In this formula, the j-th configuration is the j-th nearest one to the l-th configuration. The exponential weight has two roles: (i) it assigns more importance to the nearest configuration in the score, and (ii) it makes the score near independent from the N_loc value. The dissimilarity score is related to the inverse of the local density of the points in the k-space. If the configurations are selected in order to maximize the score, for a given value of N_TS, a stratified sampling of the environment of the metal is obtained. That is, the distributions of the distances between the metal ion and the atoms included in the spherical shell centered in d = σ are flatter than the distributions generated by the parallel tempering simulations. This aspect can be appreciated by observing the histograms in Figure 10. The stratification of the sampling obtained by the combinatorial optimization that maximizes eq 31 is even more evident considering the distribution of the configurations in two dimensions. Figure 11 compares three combinations of coordinates describing the configurations in the d-space, namely the parallel tempering set, a random set extracted by the first one, and the GRASP sampling.

Figure 11.

Distribution of 20000 configurations obtained by parallel tempering (PT) sampling for the Zn²⁺/H₂O system in two-dimensional projections (a), (d), (g) and 100 instances selected from the first set by random sampling (b), (e), (h) and combinatorial optimization of the dissimilarity score (c), (f), (i), respectively. The configurations are described by the distances of atom types from the zinc ion. The couple coordinates in the rows are dO6-dO12, dO7-dH13, and dO8-H14, respectively. The nomenclature dXn means the distance between the n-th nearest X atom to the zinc ion.

The maximization of the coverage offered by a stratified sampling increases the probability of performing the fitting in interpolation regime instead of extrapolation regime.

A.2.1. The Dimensionality Reduction and Permutational Symmetry

The number of the atoms of the system of interest is generally in the order of thousands, nevertheless the dimensionality of the k vector can be reduced without loss of information because only a few components have a value different from zero. This measure assures that the calculation of the dissimilarity score is affordable in the combinatorial optimization step.

To ensure the permutational invariance of the dissimilarity score, a further arrangement of the k vector is necessary, namely all the equivalent atoms are placed in ordered positions with respect to the distance from the metal ion. In this context, two atoms of the same element are considered equivalent if they can exchange their positions through a move compatible with the dynamics of the system generating indistinguishable configurations.

A.3. The Combinatorial Optimization of the Training Set

The maximization of the dissimilarity score (eq 31) with respect to the candidate configurations is performed exploiting an adapted form of the greedy randomized adaptive search procedure⁶² (GRASP). GRASP is a combinatorial optimization method consisting of two main phases repeated iteratively: construction and local search. In the first one a greedy randomized adaptive strategy is employed to build a feasible solution that is refined by a subsequent local search. The operation is repeated saving the best solution found.

The construction phase starts selecting randomly one configuration from the candidate set. In order to extract the second configuration, the Euclidean distances from the first one are calculated for all the remaining candidates, and a configuration is selected randomly from the subset of the instances further than the 99-th percentile. In an analogous way the following N_loc – 2 configurations are chosen. From this point on the construction phase proceeds iteratively by cumulative addition of a new element that maximizes the dissimilarity score. The new element is selected from a list of ordered candidates, {s_i}, composed evaluating the dissimilarity score of the set {{S_i–1} + s_i}, where {S_i–1} is the partial solution composed by i – 1 elements. The selection of the subsequent element is performed according to an exponential probability distribution that attributes the maximum value to the first element of the ordered list.

In the local search phase, the solution is modified one element at a time, and the trial solution is accepted if the dissimilarity score increases. This operation is performed using three different strategies: random substitution, proposal of new elements sorted by distance from the centroids of the partial solution, and local refinement.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00779.

• Details of the optimized FFs (PDF)

• Complete data related to the systematic comparative study of binary potentials (XLSX)

Author Contributions

^¶ F.F. and G.D.F. contributed equally to this work.

The authors declare no competing financial interest.