Abstract
Stratified medicine seeks to identify biomarkers or parsimonious gene signatures distinguishing patients that will benefit most from a targeted treatment. We evaluated 12 approaches in high‐dimensional Cox models in randomized clinical trials: penalization of the biomarker main effects and biomarker‐by‐treatment interactions (full‐lasso, three kinds of adaptive lasso, ridge+lasso and group‐lasso); dimensionality reduction of the main effect matrix via linear combinations (PCA+lasso (where PCA is principal components analysis) or PLS+lasso (where PLS is partial least squares)); penalization of modified covariates or of the arm‐specific biomarker effects (two‐I model); gradient boosting; and univariate approach with control of multiple testing. We compared these methods via simulations, evaluating their selection abilities in null and alternative scenarios. We varied the number of biomarkers, of nonnull main effects and true biomarker‐by‐treatment interactions. We also proposed a novel measure evaluating the interaction strength of the developed gene signatures. In the null scenarios, the group‐lasso, two‐I model, and gradient boosting performed poorly in the presence of nonnull main effects, and performed well in alternative scenarios with also high interaction strength. The adaptive lasso with grouped weights was too conservative. The modified covariates, PCA+lasso, PLS+lasso, and ridge+lasso performed moderately. The full‐lasso and adaptive lassos performed well, with the exception of the full‐lasso in the presence of only nonnull main effects. The univariate approach performed poorly in alternative scenarios. We also illustrate the methods using gene expression data from 614 breast cancer patients treated with adjuvant chemotherapy.
Keywords: Biomarker‐by‐treatment interactions, High‐dimensional, Precision medicine, Stratified medicine, Survival, Variable selection
1. Introduction
In randomized controlled trials (RCT), the treatment benefit is often measured as an average across the study population but, in the era of stratified medicine, an increasing interest is devoted to identify patients more likely to benefit from the treatment. Unaccounted biomarker‐by‐treatment interactions can dramatically lower the statistical power (Betensky et al., 2002), which may be one of the reasons why RCTs have often failed to show a benefit of the drug in oncology (Buyse and Michiels, 2013). Hence, it is important to identify in RCTs (prospectively or retrospectively) these biomarker‐by‐treatment interactions, also called treatment‐effect modifiers or predictive biomarkers (Michiels et al., 2007; Royston and Sauerbrei, 2008; Buyse et al., 2013). An example is the phase III IPASS trial that showed an overall benefit on progression‐free survival (PFS) of gefitinib as compared to carboplatin plus paclitaxel in advanced nonsmall cell lung cancer patients (Mok et al., 2009), with a high benefit in patients with epidermal growth factor receptor (EGFR) mutation and a harm in patients without it. Another treatment‐effect modifier is the Kirsten rat sarcoma (KRAS) mutation for the effect on PFS of anti‐EGFR monoclonal antibodies in advanced colorectal cancer (Amado et al., 2008). Recently, also gene signatures (i.e., combination of multiple treatment‐effect modifiers) have been proposed: for example, an 8‐gene and a 14‐gene signature for trastuzumab in early breast cancer (Pogue‐Geile et al., 2013; Perez et al., 2015) and a 84‐gene signature for MAGE‐A3 immunotherapy in melanoma and nonsmall cell lung cancer (Ulloa‐Montoya et al., 2013).
From a statistical viewpoint, Rothwell (2005) put forward that the only reliable approach for assessing the predictiveness of biomarkers is to test their interaction with the treatment. Thus, the general framework for identifying treatment‐effect modifiers is a model with the main effects of both the treatment and the biomarkers, and the biomarker‐by‐treatment interactions. However, with genomic biomarkers, high dimensionality (much more biomarkers p than sample size n) often makes the model nonidentifiable. We propose several methods to select a sparse set of treatment‐effect modifiers among a large number of candidates in an RCT in the framework of Cox regression models (Cox, 1972). In Section 2, we describe 12 possible approaches. In Section 3, we evaluate via simulations their selection performance and we consider a novel measure to evaluate the biomarker‐by‐treatment interaction strength of the developed gene signatures. In Section 4, we present an analysis of publicly available gene expression data in breast cancer. In Section 5, we discuss the findings.
2. Methods
2.1. Penalties on the full biomarker‐by‐treatment interaction model
In a proportional hazards regression model, the full biomarker‐by‐treatment interaction model is
| (1) |
with, , and the regression coefficients for the treatment T (+0.5 the experimental and −0.5 the control arm), the standardized biomarkers , i = 1, …, p, and their interactions , respectively. Of note, the second sum in (1) is the component estimating the biomarker‐dependent treatment effect. Semiparametric estimates (Cox, 1972) of the regression parameters are obtained by maximizing the partial log‐likelihood . However, in a high‐dimensional setting (2p + 1), the model is nonidentifiable. To overcome this issue, penalized regression maximizes the penalized log‐likelihood , by adding a penalty such as the ridge (Hoerl and Kennard, 1970) or the lasso (Tibshirani, 1996, 1997). In all cases that we consider here, penalization is applied to ( whereas α remains unpenalized.
The first penalization considered uses the lasso penalty for both the’s and the’s to perform variable selection and hence, identify treatment‐effect modifiers:
The main effects and the interactions are equally penalized (same shrinkage parameter). We call this approach full‐lasso throughout the paper. This approach lacks the hierarchy constraint: the main effect of a biomarker can be discarded ( irrespective of whether the associated interaction is. Although this can affect the interpretability of and the calibration of the model (Bien et al., 2013), this is of minor importance in the context of selection.
Despite the simplicity of this method, main effects and interactions can have very different sizes. It seems more appropriate to penalize them unequally: using differently weighted penalties for the ’s and the ’s, the approach is similar to the adaptive lasso (alasso), which penalizes large coefficients less than smaller ones to stress differences between them (Zou, 2006; Zhang and Lu, 2007). In this spirit, we estimate weights in a preliminary model including the treatment and all the biomarker main effects and interactions with the treatment, with a ridge penalty on the’s and the’s
to control their magnitude. In a second stage, two strategies to estimate the weights are considered: one with biomarker‐specific (alasso (Sw)) and one with grouped (alasso (Gw)) weights. The alasso (Sw) strategy estimates weights as the inverse of the absolute ridge coefficients:
The alasso (Gw) strategy estimates a common weight for all’s and one for all’s as their average:
In order to force the hierarchy constraint, we considered a further approach (ridge+lasso) with a ridge penalty on the main effects, which are then all kept in the model while controlling for overfitting:
Because optimization of both λ and is computationally demanding and weakens generalizability, we favor precise optimization of λ with rough selection of. In the context of the elastic net, Zou and Hastie (2005) estimated λ for a grid of given and chose the best (). In our case, we first estimate the’s in a model without interactions and then fixed them via an offset in the final model (1). Sensitivity analyses showed no relevant difference between the two strategies (data not shown).
To the aim of forcing the hierarchy constraint while performing selection on both the ’s and the, we also consider a group‐lasso approach (Yuan and Lin, 2006), which selects prespecified groups of variables. In our context, p groups are defined:
2.2. The modified covariates approach
Rather than the full interaction model (1), Tian et al. (2014) proposed a model with no main effects and modified covariates, defined as the product of each and the treatment T (= ±0.5):
| (2) |
This corresponds to model (1) with only the interaction part and no main effects. The lasso penalty is used to perform variable selection in model (2).
2.3. Dimension reduction of the biomarker main effects
A compromise between including only interactions and all the main effects is achieved by reducing the space dimension of the main effects through a principal components analysis (PCA, Hastie et al., 2001). However, the principal components are computed independently of the outcome. To overcome this drawback, partial least squares (PLS, Martens and Naes, 1989) regression computes the linear combinations that are the most associated to survival. These orthogonal transformations allow reducing the number of parameters in the model:
| (3) |
with the first linear combinations of the biomarkers. We apply a lasso penalty to the interactions for identifying treatment‐effect modifiers and remains unpenalized.
2.4. The gradient boosting
Boosting techniques exploit the repeated fitting of a weak estimator to iteratively obtain a model maximizing the partial log‐likelihood. In a high‐dimensional setting, the process starts from the null model and one coefficient is updated at each step. This iterative process stops when the model achieves a balance between bias and variance. In this study, we focus on gradient boosting (Friedman, 2001; Bühlmann and Yu, 2003) which consists in a componentwise L2‐boosting: the possible updates are computed on each predictor, and the best is retained after penalization to update the model. The treatment effect is estimated preliminarily and then fixed as an offset. The gradient boosting does not impose the hierarchy constraint.
2.5. Univariate approach with FDR control
A straightforward approach consists in testing the interaction of the treatment with each biomarker through a Wald test in a model incorporating the treatment, the biomarker and their interaction (Michiels et al., 2011). In order to perform variable selection, we adjust the interaction p‐values using the Benjamini and Hochberg procedure (1995) and keep biomarkers with adjusted p‐value < 0.05.
2.6. Arm‐specific prognostic effects
The last two approaches considered estimate the arm‐specific prognostic effects of biomarkers and then compare them to identify treatment‐effect modifiers. The so‐called two‐interaction model (two‐I model) replaces in model (1) the main effects by a second interaction term for the control arm:
| (4) |
and representing the prognostic effect of the i‐th biomarker in the experimental () and control () arm, respectively. A lasso penalty is applied to both the’s and the’s. A biomarker i is considered as treatment‐effect modifier only if one of the two effects, is kept in the model and the other is not.
Alternatively, we incorporate the estimates of the two‐interaction model (4) in the full interaction model (1) as weights of an adaptive lasso penalty. Let and be the estimates of model (4) under a ridge penalty; model (1) is now penalized as follows:
These arm‐specific prognostic weights (Aspw) yield smaller weights for interactions with larger difference between the two arm‐specific prognostic effects. In addition, the higher such difference, the lower the weight of the associated main effect, which favors (even though not forces) the hierarchy constraint.
2.7. Implementation
The methods outlined so far were implemented in R v3.1.2 with packages: glmnet (Friedman et al., 2010; Friedman et al., 2016) for lasso and ridge penalties, grplasso (Meier, 2015) for group‐lasso penalty, corpcor (Schäfer et al., 2015) for principal components, plsRcox (Bertrand et al., 2014) for PLS, and mboost (Hothorn et al., 2016) for gradient boosting. Of note, the grplasso R‐package can only be used for generalized linear models, thus, we implemented a Poisson model over two‐month intervals, corresponding to a piecewise constant hazard model which approximates rather well the Breslow estimator in the Cox model (Pawitan, 2005). We use fivefold cross‐validation (CV, Verweij and van Houwelingen, 1993, 1994) to estimate the shrinkage parameters λ and λ2, the number of principal components K, and the number of iterations for the gradient boosting (with shrinkage factor (ν) fixed to 0.1). As CV for the PLS gave extremely poor results (data not shown), we decided to keep only the first component. The R code is provided in the supplementary material.
3. Simulation study
We performed simulations to compare methods in terms of selection of the treatment‐effect modifiers in high‐dimensional Cox models. We also evaluated the interaction strength of the selected biomarkers.
3.1. Data generation
We generated p = 500 or 1000 unit‐variance ( Gaussian biomarkers with autoregressive correlation () within 25‐ or 50‐biomarker blocks, respectively. A total of n = 500 patients per data set were randomly assigned (1:1) to the experimental or control arm. We generated exponential survival times by fixing for each treatment arm:, the baseline (i.e., ) median survival time; m 1, the median survival time for a one‐unit increase of an active biomarker; and the associated log‐hazard ratio . We generated independent censoring from a distribution, reflecting a trial with three‐year accrual and two‐year follow‐up.
3.2. Simulation scenarios
Table 1 shows the null (i.e., no treatment‐effect modifier) and alternative scenarios (i.e., at least one treatment‐effect modifier) considered in the simulations. In the complete null scenario, , whatever the treatment. In the second null scenario, there was a strong treatment effect and in the third, 10 (for p = 500) or 20 (for p = 1000) biomarkers were strongly prognostic. In alternative scenarios 4 and 5, no biomarker had an effect in the control arm, while one and 10 or 20 treatment‐effect modifiers doubled the median survival time in the treatment arm (HR+ = 0.5). In scenario 6, we combined prognostic biomarkers (HR+ = HR– = 0.5) and treatment‐effect modifiers (HR– = 1, HR+ = 0.5). Simulations were performed with p = 500 (scenarios 1a–6a) and p = 1000 (scenarios 1b–6b). The censoring rate was 10–37%. We also considered a setting tuned on the application of Section 4 (scenario 1c–6c): higher censoring (60–80%) and lower biomarker effects (randomly drawn from for main effects and for interactions). The biomarkers were randomly allocated to correlation blocks, independently of their effects. As sensitivity analyses, we considered Weibull times with shape 0.5 and 2 (Supporting Information Fig. S1), and we forced correlation between predictive, and between predictive and prognostic biomarkers (Supporting Information Fig. S2). For each data set, another one with the same parameters was generated for external validation to evaluate the interaction strength of the developed signatures.
Table 1.
Design of the simulation study
| Two hundred fifty repetitions per scenario | Median survival time (years) | Hazard ratio | Average censoring probability | |||||
|---|---|---|---|---|---|---|---|---|
| X = 0 | h(X = 1)/h(X = 0) | |||||||
| T– | T+ | T– | T+ | T– | T+ | |||
| p = 500 biomarkers | (1a) | Complete null | 1.0 | 1.0 | 1.0 | 1.0 | 0.10 | 0.11 |
| (2a) | Treatment effect only | 1.0 | 2.0 | 1.0 | 1.0 | 0.10 | 0.31 | |
| (3a) | 10 prognostic markers | 1.0 | 1.0 | 0.5 | 0.5 | 0.30 | 0.30 | |
| (4a) | One treatment modifier | 1.0 | 1.0 | 1.0 | 0.5 | 0.10 | 0.15 | |
| (5a) | 10 treatment modifiers | 1.0 | 1.0 | 1.0 | 0.5 | 0.10 | 0.29 | |
| (6a) | 10 treatment modifiers + | 1.0 | 1.0 | 1.0 | 0.5 | 0.30 | 0.35 | |
| 10 prognostic markers | 0.5 | 0.5 | ||||||
| p = 1000 biomarkers | (1b) | Complete null | 1.0 | 1.0 | 1.0 | 1.0 | 0.11 | 0.10 |
| (2b) | Treatment effect only | 1.0 | 2.0 | 1.0 | 1.0 | 0.11 | 0.31 | |
| (3b) | 20 prognostic markers | 1.0 | 1.0 | 0.5 | 0.5 | 0.35 | 0.35 | |
| (4b) | One treatment modifier | 1.0 | 1.0 | 1.0 | 0.5 | 0.11 | 0.15 | |
| (5b) | 20 treatment modifiers | 1.0 | 1.0 | 1.0 | 0.5 | 0.11 | 0.35 | |
| (6b) | 20 treatment modifiers + | 1.0 | 1.0 | 1.0 | 0.5 | 0.35 | 0.39 | |
| 20 prognostic markers | 0.5 | 0.5 | ||||||
| p = 500 biomarkers | (1c) | Complete null | 1.0 | 1.0 | 1.0 | 1.0 | 0.65 | 0.66 |
| (2c) | Treatment effect only | 1.0 | 2.0 | 1.0 | 1.0 | 0.65 | 0.81 | |
| (3c) | 10 prognostic markers | 1.0 | 1.0 | exp () | exp () | 0.60 | 0.61 | |
| (4c) | One treatment modifier | 1.0 | 1.0 | 1.0 | exp () | 0.66 | 0.64 | |
| (5c) | 10 treatment modifiers | 1.0 | 1.0 | 1.0 | exp () | 0.66 | 0.59 | |
| (6c) | 10 treatment modifiers + | 1.0 | 1.0 | 1.0 | exp () | 0.61 | 0.58 | |
| 10 prognostic markers | exp () | exp () | ||||||
: control arm, : experimental arm, X: biomarker, randomly drawn from U(−0.5, −0.1), randomly drawn from U(−0.7, −0.1).
3.3. Evaluation criteria
The primary objective of this study was to compare methods to correctly identify the true treatment‐effect modifiers. The secondary objective was to evaluate how well the selected biomarkers predict a differential treatment effect for future patients.
We considered two criteria for selection of true positive (TP) treatment‐effect modifiers: the false discovery rate FDR = FP/(TP + FP), that is, the rate of false positive (FP) biomarkers among those selected (Genovese and Wasserman, 2002), and the false negative rate FNR = FN/(TP + FN), that is, the rate of false negatives (FNs) among the true treatment‐effect modifiers (Pawitan et al., 2013). In scenarios including main effects, we reported the number of prognostic FPs. We also computed the area under the precision‐recall curve (AUPRC, Davis and Goadrich, 2006), translating the ability of discarding inactive biomarkers more likely than active ones independently of the tuning parameters. The AUPRC, based on FDR and FNR, is more pertinent than the area under the ROC curve when there are many more inactive than active biomarkers.
Selection methods can also serve as a global test of the presence of any interaction signal in the biomarker set (Michiels et al., 2011; Michiels and Rotolo, 2015); the empirical rejection probability is the type‐I error rate in null scenarios (corresponding to the FDR as any selected biomarker is a FP), and is the power in the alternative scenarios.
The biomarker‐treatment score for patients in the validation set (V) is the cross product between the coefficients of the interactions retained in the training set (tr) and their biomarkers:
The lower the score, the higher the treatment benefit. We propose a gene signature interaction strength criterion similar to Schemper (1988) and Michiels et al. (2011), measuring the concordance between and the survival time in each treatment arm. We estimated such within‐arm concordance via the C‐statistic of Uno, one of the least biased estimators in the presence of censoring (Uno et al., 2011). Then, we computed the difference of the two C‐statistics (ΔC‐statistics): the larger the difference, the higher the interaction strength. We computed the ΔC‐statistics both in the training and validation sets.
3.4. Results
Tables 2 and 3 and Figs. 1 and 2 summarize the results of simulations. The methods can be grouped into four main groups according to their performances.
Table 2.
Proportion of models selecting at least one biomarker‐by‐treatment interaction for all the methods among 250 replications
| Univariate | Modified covariates | PCA+lasso | PLS+lasso | Ridge+lasso | Group‐lasso | Two‐I model | Full‐lasso | Alasso (sw) | Alasso (gw) | Alasso (aspw) | Gradient boosting | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Null scenarios | Scenario 1a | 0.07 | 0.39 | 0.38 | 0.36 | 0.39 | 0.48 | 0.41 | 0.01 | 0.14 | 0.00 | 0.42 | 0.68 |
| Scenario 2a | 0.06 | 0.35 | 0.43 | 0.38 | 0.39 | 0.56 | 0.44 | 0.01 | 0.12 | 0.00 | 0.37 | 0.66 | |
| Scenario 3a | 0.06 | 0.37 | 0.24 | 0.41 | 0.47 | 1.00 | 1.00 | 0.88 | 0.20 | 0.00 | 0.32 | 1.00 | |
| Scenario 1b | 0.06 | 0.38 | 0.35 | 0.32 | 0.38 | 0.52 | 0.40 | 0.01 | 0.12 | 0.00 | 0.36 | 0.68 | |
| Scenario 2b | 0.04 | 0.41 | 0.43 | 0.43 | 0.38 | 0.52 | 0.38 | 0.02 | 0.16 | 0.00 | 0.38 | 0.69 | |
| Scenario 3b | 0.08 | 0.45 | 0.27 | 0.42 | 0.58 | 1.00 | 1.00 | 0.98 | 0.32 | 0.00 | 0.55 | 1.00 | |
| Scenario 1c | 0.05 | 0.56 | 0.57 | 0.50 | 0.56 | 0.56 | 0.40 | 0.03 | 0.25 | 0.00 | 0.51 | 0.73 | |
| Scenario 2c | 0.04 | 0.55 | 0.56 | 0.61 | 0.56 | 0.46 | 0.37 | 0.00 | 0.13 | 0.00 | 0.44 | 0.65 | |
| Scenario 3c | 0.06 | 0.53 | 0.49 | 0.58 | 0.60 | 1.00 | 1.00 | 0.51 | 0.63 | 0.00 | 0.73 | 1.00 | |
| Alternative scenarios | Scenario 4a | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.15 | 1.00 | 1.00 |
| Scenario 5a | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.66 | 1.00 | 1.00 | |
| Scenario 6a | 0.59 | 0.90 | 0.80 | 0.94 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 0.55 | 1.00 | 1.00 | |
| Scenario 4b | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 0.19 | 1.00 | 1.00 | |
| Scenario 5b | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 0.78 | 1.00 | 1.00 | |
| Scenario 6b | 0.43 | 0.78 | 0.64 | 0.90 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 0.28 | 1.00 | 1.00 | |
| Scenario 4c | 0.27 | 0.66 | 0.70 | 0.65 | 0.68 | 0.72 | 0.76 | 0.20 | 0.48 | 0.00 | 0.65 | 0.76 | |
| Scenario 5c | 0.74 | 0.94 | 0.93 | 0.89 | 0.98 | 0.99 | 1.00 | 0.73 | 0.96 | 0.10 | 0.97 | 0.99 | |
| Scenario 6c | 0.51 | 0.86 | 0.83 | 0.82 | 0.91 | 1.00 | 1.00 | 0.97 | 0.99 | 0.14 | 0.99 | 1.00 |
Null scenarios: type‐I error or FDR. Alternative scenarios: power.
Table 3.
Selection performance of the methods in alternative scenarios
| Univariate | Modified covariates | PCA+lasso | PLS+lasso | Ridge+lasso | Group‐lasso | Two‐I model | Full‐lasso | Alasso (sw) | Alasso (gw) | Alasso (aspw) | Gradient boosting | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 4a | Selected biomarkers | 4 | 14 | 13 | 14 | 14 | 24 | 18 | 2 | 2 | 0 | 3 | 7 |
| TP / FP(pFP) | 1 / 3(0) | 1 / 13(0) | 1 / 12(0) | 1 / 13(0) | 1 / 13(0) | 1 / 23(0) | 1 / 18(0) | 1 / 1(0) | 1 / 1(0) | 0 / 0(0) | 1 / 2(0) | 1 / 6(0) | |
| AUPRC | 1.00 | 0.98 | 0.98 | 0.95 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | ||
| Scenario 5a | Selected biomarkers | 14 | 43 | 42 | 49 | 49 | 100 | 78 | 20 | 20 | 3 | 18 | 37 |
| TP / FP (pFP) | 6 / 8(0) | 9 / 34(0) | 9 / 33(0) | 9 / 40(0) | 9 / 40(0) | 10 / 90(0) | 9 / 69(0) | 9 / 11(0) | 9 / 11(0) | 2 / 1(0) | 9 / 9(0) | 10 / 27(0) | |
| AUPRC | 0.53 | 0.63 | 0.61 | 0.64 | 0.68 | 0.71 | 0.78 | 0.78 | 0.78 | 0.81 | 0.68 | ||
| Scenario 6a | Selected biomarkers | 2 | 25 | 15 | 29 | 37 | 109 | 99 | 23 | 14 | 1 | 13 | 38 |
| TP / FP (pFP) | 1 / 1(0) | 4 / 21(1) | 4 / 11(0) | 6 / 23(1) | 7 / 30(1) | 10 / 99(10) | 9 / 90(0) | 9 / 14(0) | 8 / 7(0) | 1 / 0(0) | 8 / 5(0) | 10 / 29(1) | |
| AUPRC | 0.27 | 0.25 | 0.37 | 0.38 | 0.43 | 0.21 | 0.75 | 0.69 | 0.71 | 0.71 | 0.62 | ||
| Scenario 4b | Selected biomarkers | 4 | 13 | 13 | 14 | 14 | 25 | 18 | 2 | 2 | 0 | 2 | 7 |
| TP / FP (pFP) | 1 / 3(0) | 1 / 12(0) | 1 / 12(0) | 1 / 13(0) | 1 / 13(0) | 1 / 24(0) | 1 / 17(0) | 1 / 1(0) | 1 / 1(0) | 0 / 0(0) | 1 / 1(0) | 1 / 6(0) | |
| AUPRC | 1.00 | 0.99 | 0.98 | 0.94 | 0.98 | 1.00 | 0.98 | 0.99 | 0.98 | 0.99 | 0.99 | ||
| Scenario 5b | Selected biomarkers | 19 | 55 | 50 | 64 | 62 | 127 | 101 | 26 | 31 | 6 | 26 | 46 |
| TP / FP (pFP) | 8 / 11(0) | 14 / 41(0) | 14 / 36(0) | 16 / 48(0) | 16 / 46(0) | 20 / 107(0) | 18 / 83(0) | 13 / 13(0) | 15 / 16(0) | 4 / 2(0) | 15 / 12(0) | 16 / 31(0) | |
| AUPRC | 0.42 | 0.45 | 0.45 | 0.49 | 0.51 | 0.53 | 0.63 | 0.63 | 0.62 | 0.65 | 0.51 | ||
| Scenario 6b | Selected biomarkers | 1 | 20 | 12 | 30 | 39 | 124 | 110 | 28 | 14 | 1 | 13 | 35 |
| TP / FP (pFP) | 1 / 1(0) | 4 / 16(1) | 4 / 8(0) | 7 / 22(1) | 9 / 30(1) | 19 / 106(20) | 17 / 93(1) | 13 / 15(1) | 8 / 6(0) | 0 / 0(0) | 8 / 6(0) | 13 / 22(1) | |
| AUPRC | 0.19 | 0.16 | 0.26 | 0.27 | 0.28 | 0.17 | 0.54 | 0.48 | 0.47 | 0.48 | 0.35 | ||
| Scenario 4c | Selected biomarkers | 1 | 8 | 8 | 6 | 8 | 12 | 14 | 0 | 1 | 0 | 2 | 4 |
| TP / FP (pFP) | 0 / 0(0) | 0 / 8(0) | 0 / 8(0) | 0 / 6(0) | 0 / 7(0) | 1 / 12(0) | 1 / 13(0) | 0 / 0(0) | 0 / 1(0) | 0 / 0(0) | 0 / 2(0) | 0 / 4(0) | |
| AUPRC | 0.36 | 0.34 | 0.34 | 0.25 | 0.34 | 0.44 | 0.33 | 0.35 | 0.25 | 0.37 | 0.40 | ||
| Scenario 5c | Selected biomarkers | 3 | 28 | 27 | 23 | 32 | 51 | 51 | 4 | 9 | 0 | 8 | 21 |
| TP / FP (pFP) | 1 / 1(0) | 5 / 23(0) | 5 / 22(0) | 4 / 19(0) | 5 / 27(0) | 7 / 44(0) | 7 / 44(0) | 2 / 2(0) | 4 / 6(0) | 0 / 0(0) | 3 / 5(0) | 5 / 16(0) | |
| AUPRC | 0.27 | 0.29 | 0.32 | 0.27 | 0.33 | 0.44 | 0.33 | 0.35 | 0.27 | 0.35 | 0.35 | ||
| Scenario 6c | Selected biomarkers | 2 | 22 | 17 | 19 | 27 | 73 | 75 | 6 | 8 | 0 | 7 | 27 |
| TP / FP (pFP) | 1 / 1(0) | 3 / 19(0) | 3 / 14(0) | 3 / 16(0) | 4 / 22(1) | 7 / 66(8) | 7 / 68(3) | 3 / 4(0) | 3 / 5(0) | 0 / 0(0) | 3 / 4(0) | 5 / 22(0) | |
| AUPRC | 0.21 | 0.22 | 0.26 | 0.24 | 0.29 | 0.19 | 0.32 | 0.33 | 0.26 | 0.34 | 0.31 |
TP: true positive, FP: false positive, pFP: prognostic false positive, AUPRC: area under the precision‐recall curve.
Figure 1.
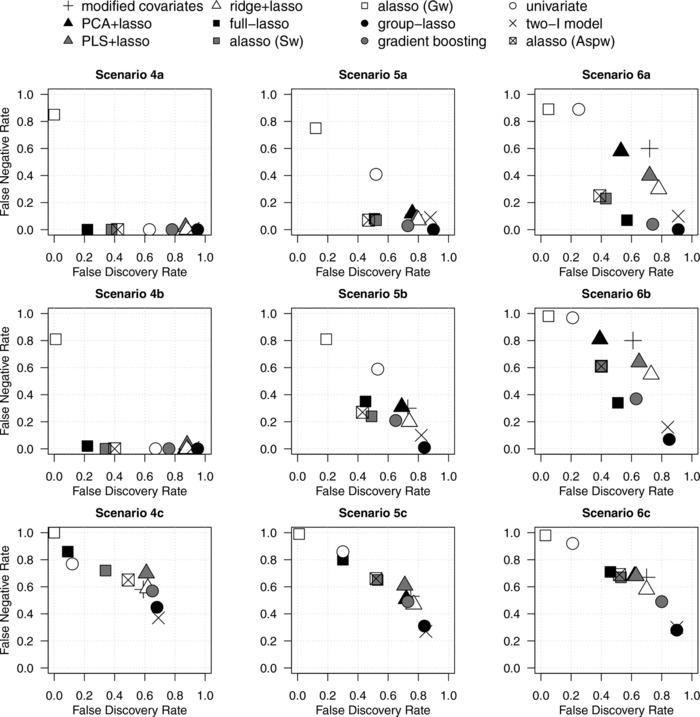
False Negative Rate (FNR) against the False Discovery Rate (FDR) in alternative scenarios. Average quantities across 250 replications.
Figure 2.
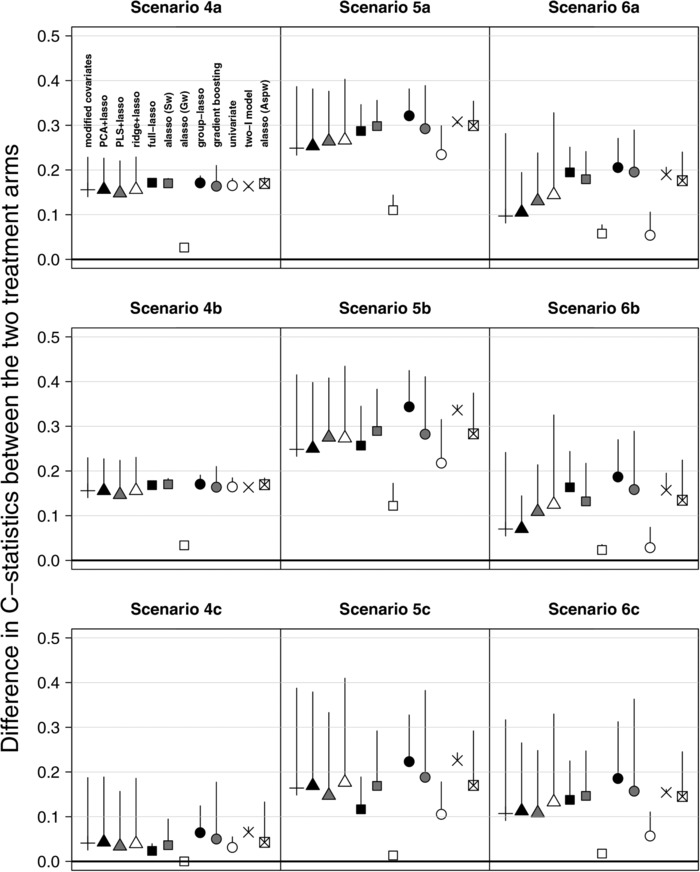
Difference in arm‐specific C‐statistics (ΔC‐statistics) in alternative scenarios in the training and validation set. Vertical lines represent the reduction in ΔC‐statistic from the training set to the validation set. Average quantities across 250 replications.
The univariate approach controlled well the type‐I error in null scenarios (Table 2), but was very conservative in alternative scenarios, especially in presence of main effects (Table 3). This is illustrated by low FDR and large FNR (Fig. 1), and by very low power (e.g., 0.59 and 0.43 in scenarios 6a and 6b, Table 2). Low FDR and large FNR are not due to the adjusted p threshold chosen for discarding biomarkers, as shown by the AUPRC, which is often ≤0.5 (Table 3). Consequently, the interaction strength is low (Fig. 2).
The second group contains methods not performing selection of the main effects: the modified covariates, dimension reduction approaches (PCA+lasso and PLS+lasso), and ridge+lasso. In the null scenarios, their type‐I error was moderate (0.24‒0.58) to high (0.49‒0.61) with low and high censoring, respectively (Table 2). In alternative scenarios (Fig. 1, Table 3) with no main effects (scenarios 4–5), these methods identified most of the treatment‐effect modifiers (small FNR), but together with many FPs (large FDR); they predicted fairly well the individual treatment benefit (Fig. 2). However, in presence of main effects (scenario 6), these methods were more conservative and missed most of treatment‐effect modifiers, implying low power (Table 2) and low interaction strength (Fig. 2); these figures were lower for p = 1000 than for p = 500. In general, the PLS+lasso and ridge+lasso, which account for the outcome in dimension reduction of the main effect matrix, performed slightly better than the PCA+lasso and modified covariates. This was less evident with smaller biomarker effects (scenario 6c). In addition, the poor results of the modified covariates were amplified when treatment‐effect modifiers were also correlated with prognostic biomarkers (Supporting Information Fig. S2) while the PCA+lasso and the PLS+lasso were not impacted by such correlation. The AUPRC of these four methods was often ≤0.5. Of note, in the alternative scenarios, their interaction strength ΔC‐statistics were highly impacted by overfitting (Fig. 2), especially for the modified covariates and the ridge+lasso.
In the third group, the group‐lasso and the two‐I model identified properly the treatment‐effect modifiers in general, but often together with several prognostic biomarkers, notably in null scenarios. In null scenarios without prognostic biomarkers (1–2a and 1–2b), the two‐I model and the group‐lasso had type‐I error of 0.38–0.44 and 0.48–0.56, respectively, which increased to 1 in presence of main effects (scenario 3, Table 2). On the other hand, these methods identified almost all the treatment‐effect modifiers in alternative scenarios (Table 3), but with a lot (often >100) of FPs, notably for p = 1000. This led to very high FDR (Fig. 1) and power (Table 2). Despite the high number of FPs, the group‐lasso had fairly large AUPRC (Table 3). However, in the scenario 6, it selected all the prognostic biomarkers (i.e., FPp), thus yielding high FDR and low AUPRC. Both the two‐I model and the group‐lasso had quite high ΔC‐statistics (Fig. 2).
In the fourth group, we found methods that do not impose the hierarchy constraint: the full‐lasso and the three kinds of adaptive lasso (with either specific (Sw), grouped (Gw), or arm‐specific prognostic (Aspw) weights). In the null scenarios 1 and 2, the adaptive lasso (Sw or Gw) and the full‐lasso selected no biomarkers in most of cases, resulting in a low type‐I error (Table 2). However, the latter was highly affected by the prognostic biomarkers (scenarios 3a and 3b, type‐I error: 0.88–0.98). The adaptive lasso (Aspw) had a moderately high type‐I error in scenarios 1–2a and 1–2b (0.36–0.42), and large in presence of only prognostic biomarkers (0.55, p = 1000). In the alternative scenarios, the full‐lasso and two adaptive lassos (Sw and Aspw) identified most of the treatment‐effect modifiers, with slightly worse results for p = 1000 than for p = 500. With p = 500, they well identified the treatment‐effect modifiers with few FPs and performed the best in terms of FNR, FDR (Table 3, Fig. 1) and interaction strength (Fig. 2). However, with p = 1000, the adaptive lasso (Sw and Aspw) performed much worse in presence of main effects (scenario 6b) by selecting much less biomarkers (on average: 14 and 13 biomarkers, respectively, and FNR = 0.61, Table 3); this poor results were amplified when treatment‐effect modifiers were also correlated with prognostic biomarkers (Supporting Information Fig. S2). The adaptive lasso (Gw) selected the null model in most of cases (leading to a FDR ≈ 0, FNR ≈ 1, low power and interaction strength; Table 2, Figs. 1 and 2). However, in terms of AUPRC, it performed as well as the full‐lasso and the two other versions of adaptive lasso (Table 3). This means that the selected tuning parameter is too high and that the method could perform better by selecting a lower parameter. With higher censoring and lower effects sizes (scenarios 4–6c), the four methods performed similarly to the other methods, by selecting fewer biomarkers (Table 3) and with low AUPRC (Table 3). Although not forced, the hierarchy constraint is maintained for more than 50% of the interactions in alternative scenarios.
The gradient boosting did not behave like any of the abovementioned groups of methods. In null scenarios, similarly to the group‐lasso, it had high type‐I error (0.66–1) even with low censoring (scenarios 1–3a and 1–3b; Table 2). However, in alternative scenarios, it performed as well as the methods not imposing the hierarchy constraint: good selection of the treatment‐effect modifiers, with few FPs (Table 3). In addition, it was not that conservative with p = 1000. The gradient boosting had quite good interaction strength, but was highly impacted by overfitting in some scenarios (Fig. 2).
In the sensitivity analysis generating data from Weibull distribution, the variation of the hazards over time (decreasing or increasing) did not affect the relative performances of any method (Supporting Information Fig. S1).
4. Application
We applied the methods compared so far to publicly available data from the Gene Expression Omnibus database (http://www.ncbi.nlm.nih.gov/geo, last accessed on June 1, 2016) to identify treatment‐effect modifiers in 614 breast cancer patients (Desmedt et al., 2011; Hatzis et al., 2011) receiving anthracycline‐based adjuvant chemotherapy with (n = 507) or without (n = 107) taxane. The three‐year distant‐relapse free survival was 78% (95% CI: 74–82%) and 79% (95% CI: 71–87%), respectively. We preprocessed the expression data of 22,277 genes (Affymetrix array) via frozen robust multiarray (McCall et al., 2010) and cross‐platform normalization (Shabalin et al., 2008). We removed genes with interquartile range ≤1. We standardized the remaining p = 1689 genes.
Patients were randomly assigned to a training set (315 patients) and a validation set (299 patients). The results (Table 4) show a large spread in the number of selected biomarkers between methods: 0–39. The modified covariates, PCA+lasso, PLS+lasso, and ridge+lasso were highly concordant, with 14 biomarkers selected by at least three methods. Most of those selected by the two‐I model (10/34) and group lasso (3/4) were not selected by the other methods. All the biomarkers selected by the univariate approach were also selected by the gradient boosting. The alasso (Aspw) identified two genes and the alasso (Sw) identified only the IFIH1 gene, common to almost all the other methods except for the group‐lasso and the univariate approaches. Importantly, the IFIH1 gene expression is already known for being associated with recurrence in nonresponders to taxane‐based chemotherapy in early breast cancer (Magbanua et al., 2015) and is included in two patents to predict the benefit of taxanes (Gehrmann and Von Törne, 2009; Wang et al., 2014). Functional studies also suggested that the IFIH1 expression is associated with resistance to taxanes in prostate cancer (Marín‐Aguilera et al., 2011). This single gene had a moderate interaction strength (ΔC‐statistics = 0.06). By selecting more biomarkers, the other methods slightly improved interaction strength (Table 4). Interestingly, the gradient boosting and the alasso (Aspw) had the highest ΔC‐statistics (0.18 and 0.14, respectively).
Table 4.
Selected treatment‐effect modifiers and interaction strength of the developed signature in the breast cancer application
| Number of selected biomarkers | ΔC‐statistics | |
|---|---|---|
| Univariate | 4 | 0.10 |
| Modified covariates | 21 | 0.09 |
| PCA+lasso | 13 | 0.12 |
| PLS+lasso | 20 | 0.01 |
| Ridge+lasso | 39 | 0.04 |
| Group‐lasso | 4 | 0.06 |
| Two‐I model | 34 | 0.12 |
| Full‐lasso | 0 | 0 |
| Alasso (Sw) | 1 | 0.06 |
| Alasso (Gw) | 0 | 0 |
| Alasso (Aspw) | 2 | 0.14 |
| Gradient boosting | 8 | 0.18 |
5. Discussion
Parsimonious gene signatures aim at selecting patients more likely to benefit from a treatment (Buyse and Michiels, 2013; Hingorani et al., 2013). Although this needs identifying the treatment‐effect modifiers (Michiels et al., 2011), no clear guidance has been established yet on how to do in high‐dimensional spaces. Biomarker selection can have multiple aims, at least two of which of particular interest: selecting markers which have a biologic role and selecting patients likely to benefit from the therapy. In this paper, we focused on sparse selection and compared 12 methods to find treatment‐effect modifiers while limiting the FP selection. Indeed, for practical use of the biomarker score, determining a few biomarkers with high accuracy (e.g., ELISA) is usually preferred compared to less‐accurate technologies (e.g., mass spectroscopy). Obviously, the chosen methods undersample all the possible approaches. We also proposed a novel metric about interaction strength prediction because this is tightly related to correct biomarker selection.
Based on the results of the simulation study, different groups of methods were identified. First, the straightforward way for identifying interactions via univariate models should be avoided when biomarkers are correlated, even with FDR control. If a method starting from the null model would be considered, the gradient boosting is an option, but it does not control at all the type‐I error in null scenarios. Methods that do not perform selection of the main effects are quite well powered, except in presence of prognostic biomarkers as compared to methods performing selection on the main effects. Of note, keeping all the main effects could be a practical drawback, as sparse prognostic signatures can be assessed easily and reliably on different platforms (e.g., by RT‐PCR). Dimension reduction of the main effect matrix independently of the outcome (PCA) has negative impact in presence of strong main effects. Conversely, methods performing variable selection on the main effects perform globally well, irrespective of whether the hierarchy constraint is forced. As an exception, the group‐lasso is highly impacted by the presence of main effects due to the groups that can not separate the main effect and the interaction of each biomarker. To overcome this drawback, testing strategies could be considered to evaluate remaining interactions (Lockhart et al., 2014). In any case, further arbitrary choices would be required. Another further development could consist in an adaptive group‐lasso with weights based on the interaction only. The model estimating the arm‐specific prognostic effects identified rather well the treatment‐effect modifiers in the simulations study. Nevertheless, to allow for treatment modifiers that have prognostic effects in each of the treatment arms, a contrast test would be needed between the two prognostic effects, which is not straightforward in a penalized model. Finally, we would like to stress: (i) the importance of external data for investigating the interaction strength, as most of the methods are impacted by overfitting, notably the modified covariates and the two‐step methods; (ii) and that the identification of interactions is difficult and requires a lot of events, whatever the method.
For all but one methods, the list of interactions retained is defined by a tuning parameter estimated via the Verweij and van Houwelingen (1993, 1994) CV criterion. However, note that this technique is sometimes suboptimal, finding too conservative tuning parameters for the adaptive lasso (Gw) and too lenient ones for the group‐lasso. For this latter case, we previously reviewed and compared empirical extensions of the lasso penalty to reduce the FPs in high‐dimensional Cox regression models (Ternès et al., 2016).
In the application to the gene expression data set in breast cancer, the methods behaved quite differently in terms of number of selected biomarkers and of interaction strength. This application can only be viewed as an illustration, as no gold standard is available to infer which biomarker truly modifies the treatment effect and the expression data were not collected in the context of a randomized clinical trial. However, the gene selected by most of the methods was already suggested to predict resistance to taxane‐based chemotherapy in the literature. Adjusting the models on clinical factors was beyond the aim of the present study but is another interesting point. Such factors could be considered as prognostic factors not subjected to competitive selection, or they could be used as candidates for treatment‐covariate interactions, just like the biomarkers. Yet, no consensus has been reached on how to deal with clinical factors in this context. For a fair comparison, we estimated the effect of the clinical factors (nodal status and tumor grade) and fixed them as an offset for all the methods. The R code used to download the clinical and gene expression data and to apply the 12 methods is available as supplementary material.
Conflict of interest
The authors have declared no conflict of interest.
Supporting information
Figure S1: False negative rate against the false discovery rate in alternative scenarios for time‐decreasing
(1st row) and time‐increasing (2nd row) hazards. Average quantities across 250 replications.
Figure S2: False negative rate against the false discovery rate in alternative scenarios for several
correlation structures between active markers. Average quantities across 250 replications.
Supporting FigureS1
Supporting Information
Acknowledgment
Nils Ternès acknowledges financial support by Foundation Philanthropia Lombard‐Odier (PhD scholarship).
References
- Amado, R. G. , Wolf, M. , Peeters, M. , van Cutsem, E. , Siena, S. , Freeman, D. J. , Juan, T. , Sikorski, R. , Suggs, S. , Radinsky, R. , Patterson, S. D. and Chang, D. D. (2008). Wild‐type KRAS is required for panitumumab efficacy in patients with metastatic colorectal cancer. Journal of Clinical Oncology 26, 1626–1634. [DOI] [PubMed] [Google Scholar]
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false dicovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B 57, 289–300. [Google Scholar]
- Bertrand, F. , Maumy‐Bertrand, M. and Meyer, N. (2014). plsRcox: Partial least squares regression for Cox models and related techniques. R‐package version 1.7.2.
- Betensky, R. A. , Louis, D. N. and Cairncross, J. G. (2002). Influence of unrecognized molecular heterogeneity on randomized clinical trials. Journal of Clinical Oncology 20, 2495–2499. [DOI] [PubMed] [Google Scholar]
- Bien, J. , Taylor, J. and Tibshirani, R. (2013). A lasso for hierarchical interactions. The Annals of Statistics 41, 1111–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bühlmann, P. and Yu, B. (2003). Boosting with L2 loss: regression and classification. Journal of the American Statistical Association 98, 324–339. [Google Scholar]
- Buyse, M. and Michiels, S. (2013). Omics‐based clinical trial designs. Current Opinion in Oncology 25, 289–295. [DOI] [PubMed] [Google Scholar]
- Buyse, M. , Michiels, S. , Sargent, D. J. , Grothey, A. , Matheson, A. and de Gramont, A. (2011). Integrating biomarkers in clinical trials. Expert Review of Molecular Diagnostics 11, 171–182. [DOI] [PubMed] [Google Scholar]
- Cox, D. R. (1972). Regression models and life‐tables (with discussion). Journal of the Royal Statistical Society: Series B 34, 187–220. [Google Scholar]
- Davis, J. and Goadrich, M. (2006). The relationship between Precision‐Recall and ROC curves. Proceedings of the 23rd International Conference on Machine Learning. ACM, Pittsburgh PA, 233–240.
- Desmedt, C. , Di Leo, A. , de Azambuja, E. , Larsimont, D. , Haibe‐Kains, B. , Selleslags, J. , Delaloge, S. , Duhem, C. , Kains, J.‐P. , Carly, B. , Maerevoet, M. , Vindevoghel, A. , Rouas, G. , Lallemand, F. , Durbecq, V. , Cardoso, F. , Salgado, R. , Rovere, R. , Bontempi, G. , Michiels, S. , Buyse, M. , Nogaret, J.‐M. , Qi, Y. , Symmans, F. , Pusztai, L. , D'Hondt, V. , Piccart‐Gebhart, M. and Sotiriou, C. (2011). Multifactorial approach to predicting resistance to anthracyclines. Journal of Clinical Oncology 29, 1578–1586. [DOI] [PubMed] [Google Scholar]
- Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Annals of Statistics 29, 1189–1232. [Google Scholar]
- Friedman, J. , Hastie, T. and Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Friedman, J. , Hastie, T. , Simon, N. and Tibshirani, R. (2016). glmnet: Lasso and elastic‐net regularized generalized linear models. R package version 2.0‐5.
- Gehrmann, M. and Von Törne, C. (2009). Prediction of breast cancer response to taxane‐based chemotherapy. U.S. Patent Application 12/307,590.
- Genovese, C. and Wasserman, L. (2002). Operating characteristics and extensions of the false discovery rate procedure. Journal of the Royal Statistical Society: Series B 64, 499–517. [Google Scholar]
- Hastie, T. , Friedman, J. , and Tibshirani, R. (2001). Model Assessment and Selection. Springer, New York, NY. [Google Scholar]
- Hatzis, C. , Pusztai, L. , Valero, V. , Booser, D. J. , Esserman, L. , Lluch, A. , Vidaurre, T. , Holmes, F. , Souchon, E. , Wang, H. , Martin, M. , Cotrina, J. , Gomez, H. , Hubbard, R. , Chacón, J. I. , Ferrer‐Lozano, J. , Dyer, R. , Buxton, M. , Gong, Y. , Wu, Y. , Ibrahim, N. , Andreopoulou, E. , Ueno, N. T. , Hunt, K. , Yang, W. , Nazario, A. , DeMichiele, A. , O'Shaughnessy, J. , Hortobagyi, G. N. and Symmans, W. F. (2011). A genomic predictor of response and survival following taxane‐anthracycline chemotherapy for invasive breast cancer. Journal of the American Medical Association 305, 1873–1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hingorani, A. D. , van der Windt, D. A. , Riley, R. D. , Abrams, K. , Moons, K. G. M. , Steyerberg, E. W. , Schroter, S. , Sauerbrei, W. , Altman, D. G. and Hemingway, H. (2013). Prognosis research strategy (PROGRESS) 4: stratified medicine research. British Medical Journal 346, e5793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoerl, A. E. and Kennard, R. W. (1970). Ridge regression: biased estimation for nonorthogonal problems. Technometrics 42, 80–86. [Google Scholar]
- Hothorn, T. , Bülhmann, P. , Kneib, T. , Schmid, M. , Hofner, B. , Sobotka, F. and Scheipl, F. (2016). mboost: Model‐based boosting. R package version 2.6‐0.
- Lockhart, R. , Taylor, J. , Tibshirani, R. J. and Tibshirani, R. (2014). A significance test for the lasso. The Annals of Statistics 42, 413–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magbanua, M. J. M. , Wolf, D. M. , Yau, C. , Davis, S. E. , Crothers, J. , Au, A. , Haqq, C. M. , Livasy, C. , Rugo, H. S. , I‐SPY 1 TRIAL Investigators , Esserman, L. , Park, J. W. and van ’t Veer, L. J. (2015). Serial expression analysis of breast tumors during neoadjuvant chemotherapy reveals changes in cell cycle and immune pathways associated with recurrence and response. Breast Cancer Research 17, 73, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marín‐Aguilera, M. , Codony‐Servat, J. , Kalko, S. G. , Fernández, P. L. , Bermudo, R. , Buxo, E. , Ribal, M. J. , Gascón, P. and Mellado, B. (2011). Identification of docetaxel resistance genes in castration‐resistant prostate cancer. Molecular Cancer Therapeutics 11, 329–339. [DOI] [PubMed] [Google Scholar]
- Martens, H. and Naes, T. (1989). Assessment, validation and choice of calibration method In: Multivariate Calibration. (eds. Martens H. and Naes T.) Wiley, Chichester, pp. 237–266. [Google Scholar]
- McCall, M. N. , Bolstad, B. M. and Irizarry, R. A. (2010). Frozen robust multiarray analysis (fRMA). Biostatistics 11, 242–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier, L. (2015). grplasso: Fitting user specified models with Group Lasso penalty. R package version 0.4‐5.
- Michiels, S. , Koscielny, S. and Hill, C. (2007). Interpretation of microarray data in cancer. British Journal of Cancer 96, 1155–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michiels, S. , Potthoff, R. F. and George, S. L. (2011). Multiple testing of treatment‐effect‐modifying biomarkers in a randomized clinical trial with a survival endpoint. Statistics in Medicine 30, 1502–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michiels, S. and Rotolo, F. (2015). Evaluation of clinical utility and validation of gene signatures in clinical trials In: Matsui S., Buyse M. and Simon R. (Eds.), Design and Analysis of Clinical Trials for Predictive Medicine. CRC Press, New York, NY, pp. 187–206. [Google Scholar]
- Mok, T. S. , Wu, Y. , Thongprasert, S. , Yang, C. , Saijo, N. , Sunpaweravong, P. , Han, B. , Margono, B. , Ichinose, Y. , Nishiwaki, Y. , Ohe, Y. , Yang, J.‐J. , Chewaskulyong, B. , Jiang, H. , Duffield, E. L. , Watkins C. L., Armour, A. A. and Fukuoka, M. (2009). Gefitinib or Carboplatin‐Paclitaxel in pulmonary adenocarcinoma. New England Journal of Medicine 361, 947–957. [DOI] [PubMed] [Google Scholar]
- Pawitan, Y. (2013). In All Likelihood: Statistical Modelling and Inference Using Likelihood. OUP Oxford, Oxford, UK. [Google Scholar]
- Pawitan, Y. , Michiels, S. , Koscielny, S. , Gusnanto, A. and Ploner, A. (2005). False discovery rate, sensitivity and sample size for microarray studies. Bioinformatics 21, 3017–3024. [DOI] [PubMed] [Google Scholar]
- Perez, E. A. , Thompson, E. A. , Ballman, K. V. , Anderson, S. K. , Asmann, Y. W. , Kalari, K. R. , Eckel‐Passow, J. E. , Dueck, A. C. , Tenner, K. S. , Jen J., Fan, J.‐B. , Geiger, X. J. , McCullough, A. E. , Chen, B. , Jenkin, R. B. , Sledge, G. W. , Winer, E. P. , Gralow, J. R. and Reinholz, M. M. (2015). Genomic analysis reveals that immune function genes are strongly linked to clinical outcome in the North Central Cancer Treatment Group N9831 adjuvant trastuzumab trial. Journal of Clinical Oncology 33, 701–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pogue‐Geile, K. L. , Kim, C. , Jeong, J.‐H. , Tanaka, N. , Bandos, H. , Gavin, P. G. , Fumagalli, D. , Goldstein, L. C. , Sneige, N. , Burandt, E. , Taniyama, Y. , Bohn, O. L. , Lee, A. , Kim, S.‐I. , Reilly, M. L. , Remillard, M. Y. , Blackmon, N. L. , Kim S.‐R., Horne, Z. D. , Rastogi, P. , Fehrenbacher, L. , Romond, E. H. , Swain, S. M. , Mamounas, E. P. , Lawrence Wickerham, D. , Geyer Jr, C. E. , Costantino, J. P. , Wolmark, N. and Paik, S. (2013). Predicting degree of benefit from adjuvant trastuzumab in NSABP trial B‐31. Journal of the National Cancer Institute 105, 1782–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothwell, P. M. (2005). Treating individuals 2: subgroup analysis in randomised controlled trials: importance, indications, and interpretation. Lancet 365, 176–186. [DOI] [PubMed] [Google Scholar]
- Royston, P. and Sauerbrei, W. (2008). Interactions between treatment and continuous covariates: a step toward individualizing therapy. Journal of Clinical Oncology 26, 1397–1399. [DOI] [PubMed] [Google Scholar]
- Schäfer, J. , Opgen‐rhein, R. , Zuber, V. , Ahdesmäki, M. , Duarte Silva, A. P. and Strimmer, K. (2015). corpcor: Efficient estimation of covariance and (partial) correlation. R‐package version 1.6.8.
- Schemper, M. (1988). Non‐parametric analysis of treatment–covariate interaction in the presence of censoring. Statistics in Medicine 7, 1257–1266. [DOI] [PubMed] [Google Scholar]
- Shabalin, A. A. , Tjelmeland, H. , Fan, C. , Perou, C. M. and Nobel, A. B. (2008). Merging two gene‐expression studies via cross‐platform normalization. Bioinformatics 24, 1154–1160. [DOI] [PubMed] [Google Scholar]
- Ternès, N. , Rotolo, F. and Michiels, S (2016). Empirical extensions of the lasso penalty to reduce the false discovery rate in high‐dimensional Cox regression models. Statistics in Medicine 35, 2561–2573. [DOI] [PubMed] [Google Scholar]
- Tian, L. , Alizadeh, A. A. , Gentles, A. J. and Tibshirani, R. (2014). A simple method for estimating interactions between a treatment and a large number of covariates. Journal of the American Statistical Association 109, 1517–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B 58, 267–288. [Google Scholar]
- Tibshirani, R. (1997). The lasso method for variable selection in the Cox model. Statistics in Medicine 16, 385–395. [DOI] [PubMed] [Google Scholar]
- Ulloa‐Montoya, F. , Louahed, J. , Dizier, B. , Gruselle, O. , Spiessens, B. , Lehmann, F. F. , Suciu, S. , Kruit, W. H. J. , Eggermont, A. M. M. , Vansteenkiste, J. and Brichard, V. G. (2013). Predictive gene signature in MAGE‐A3 antigen‐specific cancer immunotherapy. Journal of Clinical Oncology 31, 2388–2395. [DOI] [PubMed] [Google Scholar]
- Uno, H. , Cai, T. , Pencina, M. J. , D'Agostino, R. B. and Wei, L. J. (2011). On the C‐statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine 30, 1105–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verweij, P. J. M. and van Houwelingen, H. C. (1993). Cross‐validation in survival analysis. Statistics in Medicine 12, 2305–2314. [DOI] [PubMed] [Google Scholar]
- Verweij, P. J. M. and van Houwelingen, H. C. (1994). Penalized likelihood in Cox regression. Statistics in Medicine 13, 2427–2436. [DOI] [PubMed] [Google Scholar]
- Wang, E. , Li, J. , O'Connor‐McCourt, M. and Purisima, E. (2014). Paclitaxel response markers for cancer. U.S. Patent Application 14/361,153.
- Yuan, M. and Lin, Y. (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B 68, 49–67. [Google Scholar]
- Zhang, H. H. and Lu, W. (2007). Adaptive lasso for Cox's proportional hazards model. Biometrika 94, 691–703. [Google Scholar]
- Zou, H. (2006). The adaptive lasso and its oracle properties. Journal of the American Statistical Association 101, 1418–1429. [Google Scholar]
- Zou, H. and Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: False negative rate against the false discovery rate in alternative scenarios for time‐decreasing
(1st row) and time‐increasing (2nd row) hazards. Average quantities across 250 replications.
Figure S2: False negative rate against the false discovery rate in alternative scenarios for several
correlation structures between active markers. Average quantities across 250 replications.
Supporting FigureS1
Supporting Information


