A Large Panel of Drosophila simulans Reveals an Abundance of Common Variants

Abstract

The rapidly expanding availability of large NGS data sets provides an opportunity to investigate population genetics at an unprecedented scale. Drosophila simulans is the sister species of the model organism Drosophila melanogaster, and is often presumed to share similar demographic history. However, previous population genetic and ecological work suggests very different signatures of selection and demography. Here, we sequence a new panel of 170 inbred genotypes of a North American population of D. simulans, a valuable complement to the DGRP and other D. melanogaster panels. We find some unexpected signatures of demography, in the form of excess intermediate frequency polymorphisms. Simulations suggest that this is possibly due to a recent population contraction and selection. We examine the outliers in the D. simulans genome determined by a haplotype test to attempt to parse the contribution of demography and selection to the patterns observed in this population. Untangling the relative contribution of demography and selection to genomic patterns of variation is challenging, however, it is clear that although D. melanogaster was thought to share demographic history with D. simulans different forces are at work in shaping genomic variation in this population of D. simulans.

Introduction

The recent influx of high throughput sequencing has enabled an entirely new scale of examination of the effects of demography and selection on patterns of genomic variation. Where before these analyses were often based on a handful of loci sampled from a limited number of individuals, data sets are becoming available that provide genome-wide information from potentially hundreds of individuals (Grenier et al. 2015; Lack et al. 2015, 2016). To these experiments, we can apply the population genetic models that were developed in the era of limited sequencing, including an examination of standing variation, linkage disequilibrium, and selection.

Drosophila melanogaster has been the model species for population genetic research since the advent of the field, providing evidence for pervasive adaptation at the molecular level (Aguade et al. 1989; Begun and Aquadro 1992; Fay et al. 2002; Smith and Eyre-Walker 2002; Bierne and Eyre-Walker 2004; Andolfatto 2005; Shapiro et al. 2007; Eyre-Walker and Keightley 2009; Sella et al. 2009; Schneider et al. 2011; Kousathanas and Keightley 2013; Garud et al. 2015). Drosophila simulans, the closest relative of D. melanogaster, is of particular interest to population genetics because both D. melanogaster and D. simulans are presumed to have a similar demographic history, yet population genetic and ecological work suggests very different signatures of selection and demography. They are both thought to have originated in or around Africa (D. melanogaster, southern-central Africa, D. simulans, Madagascar) followed by an out-of-Africa expansion ∼10,000 years ago, with a subsequent colonization of the Americas in the past few hundred years (David and Capy 1988; Lachaise et al. 1988; Baudry et al. 2004; Li and Stephan 2006; Thornton and Andolfatto 2006). D simulans was recorded on the east coast of North America in 1920 (Sturtevant 1920). A large survey of the Pacific coast at the same time did not find evidence of D. simulans (Sturtevant 1920).

Differences in the patterns of divergence in the D. melanogaster and D. simulans lineages have been observed that suggest interesting differences in biology between the two species (Andolfatto 2005; Begun et al. 2007; Haddrill et al. 2008). Drosophila melanogaster shows strong clinal differentiation while D. simulans does not (Weeks et al. 2002; Hoffmann and Weeks 2007; Schmidt and Paaby 2008; Machado et al. 2015; Sedghifar et al. 2016). The species differ in their habitat use and seasonal abundance, with some evidence that D. simulans may come from a more temperate ancestral climate than D. melanogaster (Parsons 1977; McKenzie and McKechnie 1979; David and Van Herrewege 1983; Singh 1989; Milan et al. 2012; Machado et al. 2015; Sedghifar et al. 2016). In general, non-African D. simulans have been found to have higher within population diversity compared with D. melanogaster, and to be less geographically differentiated (Singh 1989; Machado et al. 2015; Sedghifar et al. 2016). In the past, work on American populations of D. melanogaster has suggested a complex demographic history of bottlenecks, admixture, and selection (Glinka et al. 2003; Haddrill et al. 2005; Corbett-Detig and Hartl 2012; Langley et al. 2012; Garud et al. 2015; Lack et al. 2015, 2016; Pool 2015). Past studies on particular loci or gene regions in African, Asian, and American D. simulans have found haplotypes at intermediate frequency, though the authors diverge in their conclusions that this is due to population contraction, admixture, directional selection, or balancing selection (Hasson et al. 1998; Hamblin and Veuille 1999; Rozas et al. 2001; Quesada et al. 2003; Sanchez-Gracia and Rozas 2007). Begun et al. (2007) detected an excess of high-frequency polymorphisms in D. simulans, suggesting recurrent adaptive evolution.

The importance of different types of selection for adaptation, such as soft versus hard sweeps, and the expectations for their genomic signature is contentious (Hermisson and Pennings 2005; Przeworski et al. 2005; Barrett and Schluter 2008; Macpherson et al. 2008; Karasov et al. 2010; Kelly et al. 2013; Messer and Petrov 2013; Ferrer-Admetlla et al. 2014; Jensen 2014; Garud et al. 2015; Schrider et al. 2015). For example, whether soft sweeps are an important part of adaptation has been debated in the literature for 20 years, including whether or not they can be reliably distinguished from hard sweeps (Hermisson and Pennings 2005, 2017; Przeworski et al. 2005; Pennings and Hermisson 2006a,b, Pritchard et al. 2010; Messer and Petrov 2013; Jensen 2014; Garud et al. 2015; Schrider et al. 2015). It has remained a central question in population genomics, as it addresses fundamental questions about the tempo and mode of adaptation. Disentangling the signatures of different demographic events and selective sweeps is very difficult, as many scenarios will create similar patterns of variation and linkage. Deep sequencing of local populations increases our ability to recognize and differentiate between models of demography and selection, both because measures of haplotype diversity, linkage disequilibrium (LD), and the frequency of polymorphisms will more accurately represent the population value and because it provides more power to detect soft sweeps (Akey et al. 2004; Ross-Ibarra et al. 2008; Ramirez-Soriano and Nielsen 2009; Tennessen et al. 2010, 2012).

We investigate patterns of variation in D. simulans, and look for evidence of demography and selection in shaping this variation. We sequenced a new panel of 170 genotypes of D. simulans collected from a large organic orchard population in Zuma Beach (CA). We summarize patterns of variation in this population using Tajima’s D, π, and LD. We find an abundance of common variants, leading to pervasive positive Tajima’s D. We simulate several demographic and selective scenarios to investigate the potential causes of the patterns of variation in this population. We look for evidence of admixture within the population using two types of tests (PCA and ADMIXTURE). We examine the haplotype structure in the population, to better understand patterns of polymorphism, their frequency, and relationship to LD in the population. The authors intend this panel to be a valuable addition to the Drosophila community, complementing the DGRP (Mackay et al. 2012) and the DSPR (King et al. 2012) by enabling GWAS analyses and comparison between two closely related species.

Materials and Methods

All analysis scripts and documentation to reproduce results are located at: https://github.com/signor-molevol/signor_popgen_2016.

Drosophila Strains

The D. simulans lines were collected in the Zuma organic orchard in Zuma beach, California on the consecutive weekends of February 11th and 18th of 2012 from a single pile of fermenting strawberries. Single-mated females were collected and their offspring identified as being D. simulans. This was followed by 15 generations of full sib mating of their progeny. These strains are available upon request.

Library Preparation

DNA was extracted from 20 whole female flies using the Gentra Puregene kit (Qiagen). Libraries were prepared by RAPiD-Genomics, LLC using standard protocols and sequenced at the USC Genome Center. Prior to sequencing, the samples were pooled according to their molar concentrations for equal representation. Reads were single end 100 bp, sequenced on the illumina Hiseq across 10 lanes per 96 samples. The intended coverage per library was 10×, although ultimately some libraries were over or underrepresented. Raw data have been deposited to the Sequence Read Archive, accession number: SRP075682.

Mapping and SNP Discovery

Libraries were demultiplexed by barcode using standard protocols. Libraries were trimmed and cleaned using SolexaQA (v. 2.2), assembled using BWA mem (v. 0.7.5), and processed with samtools (v. 0.1.19) using default parameters (Cox et al. 2010; Li 2015). The reference genome was D. simulans version 2.01 as described in Hu et al. (2013). PCR duplicates were removed using Picard MarkDuplicates (v. 1.89) and GATK (v. 3.3) was used for indel realignment and SNP calling using default parameters (http://picard.sourceforge.net) (McKenna et al. 2010). SNPs were called using Haplotypecaller to call SNPs jointly and GenotypeGVCFs to call SNPs individually for each genome (McKenna et al. 2010). There were few qualitative differences in the downstream results, and those from Haplotypecaller were used. Files were produced using default filtering (phred score of 30), no additional filtering was applied (McKenna et al. 2010). GATK is slightly biased toward the calling of heterozygous SNPs (0–0.005 minimum and maximum) such that it should be the most unbiased toward low-frequency SNPs among the available SNP calling software (Hwang et al. 2015).

Filtering

SNPs that could not be placed on chromosomes (meaning SNPs belonging to fragmented portions of the D. simulans assembly) were excluded from the analysis, as were nonbiallelic loci, lines with >25% missing data, and loci with >10% missing data. The final data set included 170 genotypes and 5,998,575 loci. Of these SNPs, there were 1.2 million with no missing data. Drosophila simulans does not have segregating inversions (Ashburner and Lemeunier 1976), which is where the majority of heterozygosity is observed in D. melanogaster (Mackay et al. 2012; Grenier et al. 2015; Lack et al. 2015; Palmieri et al. 2015). Thus, while residual heterozygosity was observed it is not biased toward particular regions of the genome in D. simulans (supplementary fig. S1, Supplementary Material online). The residual heterozygosity did not alter our conclusions (see Sensitivity Analysis). In previous analyses, individuals with a genome-wide IBD >20% are removed from data sets of this type (Garud et al. 2015), however, none were observed in this data set according to PLINK pairwise IBD estimation (Purcell et al. 2007).

Summary Statistics

Nucleotide diversity (π), and Tajima’s D can both provide insight into the demographic and selective history of a population. π Tajima’s D and were calculated in 10-kb windows using VCFtools (v0.1.14) (Tajima 1989; Danecek et al. 2011).

Annotating SNPs

Differences in π and Tajima’s D between gene regions that are presumed to be more or less neutral can be help distinguish between demography and selection. The gff files for the D. simulans v2 genome were used to annotate SNPs (exon, intron, 3′-UTR, 5′-UTR) with bedtools intersect (Quinlan and Hall 2010). The vast majority of introns were short, and they were split into groups based on length and presumed differences in selective regime (long introns > 120 bp, introns < 120 bp, bp 8–30 of introns < 65 bp) (Parsch et al. 2010). Annotated features <40 bp were excluded from the analysis, corresponding to <1% of annotated features.

Linkage Disequilibrium

The decay of linkage disequilibrium can help determine the appropriate scale with which to examine haplotype structure in a population, and can also help clarify the selective or demographic forces shaping variation in the population. LD (r²) was calculated within windows of 10 kb using VCFtools (v1.14) geno-r2 and PLINK (v1.07) r2 (Purcell et al. 2007; Chang et al. 2015) with the LD filter set to 0 to report all pairwise comparisons within a window. We excluded 1-mb regions of low recombination at centromeres and telomeres. However, more was excluded if there were significant reductions in diversity for a broader region as seen in figure 1, calculated as extended negative Tajima’s D or values of$\pi$ <½ the chromosomal average (Sedghifar et al. 2016). For this portion of the analysis only, we filtered out SNPs with very low and high frequency (.05 and .95) to avoid inflated estimates of LD from the effects of sampling (Nuzhdin and Turner 2013). Plots of LD were smoothed by averaging LD values binned according to the distance between SNPs, with two different bin sizes to reflect rapid decay of LD. From 0- to 300-bp bins were 20-bp nonoverlapping windows, while from 300- to 10-kb windows were 150 bp (Garud and Petrov 2016). While LD or Tajima’s D alone can suggest certain modes of selection or demography, examining their association may reveal additional information. For example, if low LD is associated with high Tajima’s D, this suggests that balancing selection may be mediating the relationship. The average LD value was compared with the value of Tajima’s D for each window that was an outlier. Regression lines were fit for the data corresponding to positive D and negative D separately.

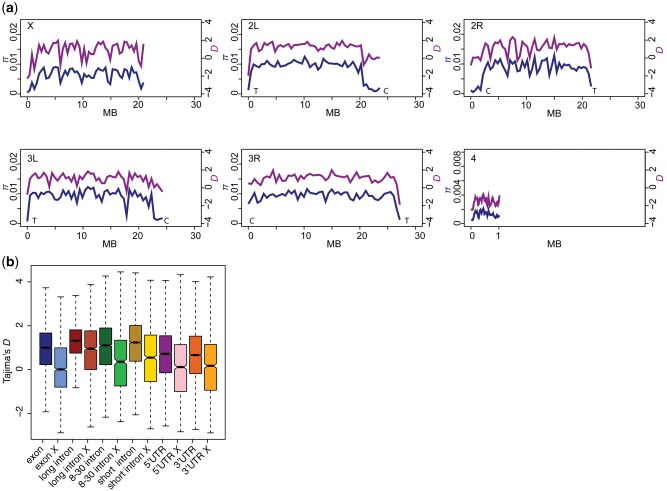
Fig. 1.—

Summary statistics. (a) For each chromosome, Tajima’s D (pink) and$\pi$ (blue) are plotted in 10-kb windows. The genomic coordinates are split into 10-kb windows along the x-axis. Each data point represents a single window. Note that the axis for π (blue) is on the left-hand side while Tajima’s D (pink) is on the right. For clarity, chromosome 4 is on a different y-axis for π, due to its small size. Location of centromeres and telomeres for each chromosome are indicated at the lower edges of each graph. All lines were smoothed using local regression in R. (b) The median and distribution (boxes are first and third quartile) of Tajima’s D for each annotation category. Notches at the median are calculated as described in boxplot.stats in R and correspond roughly to the 95% confidence interval for the medians.

Sensitivity Analysis

It is possible that some patterns in the data could be produced by how it was processed, so we sought to investigate this possibility by evaluating the sensitivity of our analysis to different steps in the data processing. We lowered the phred score threshold from 30 to 20 to examine the effect on the results of Tajima’s D and LD. To examine the effect of SNP calling method, we used both HaplotypeCaller to call SNPS jointly and GVCF to call them individually (McKenna et al. 2010). To investigate the effect of inbreeding on this population’s parameters, 82 of the most inbred lines were reanalyzed (data not shown). The coefficient of inbreeding was calculated using VCFtools (v0.1.14) (Danecek et al. 2011). The quality of variant calls was also compared with the level of heterozygosity for all lines. We examined the effect of masking heterozygous bases and excluding SNPs with missing data. We also used different software to calculate our metrics (data not shown). To evaluate the possibility that the results were due to protocols implemented within VCFtools (Danecek et al. 2011), three windows were run through a custom R script to calculate Tajima’s D (Steige et al. 2015).

Simulations

We wanted to focus on potential demographic and selection scenarios that could produce the patterns of variation seen in our population, namely the positive Tajima’s D. For example, a population bottleneck would produce negative values of Tajima’s D, and thus is not considered here. Populations were simulated using MSMS (Ewing and Hermisson 2010) with a population size of 2×10⁶ (Przeworski et al. 2001) for regions of 10⁵ bp. We sampled 170 individuals to match the depth of our data and assumed a neutral mutation rate of μ = 3×10⁻⁹ (Przeworski et al. 2001) and a recombination rate of ρ = 5×10⁻⁷ cM/bp (Presgraves 2005; Garud et al. 2015). Drosophila simulans is predicted to have a higher recombination rate than D. melanogaster, thus this value should be conservative for purpose of LD based statistics such as H12 (True et al. 1996). We assume ∼10 generations per year (Li et al. 1999; Przeworski et al. 2001; Stephan and Li 2007; Garud et al. 2015).

Demographic Simulations

We simulated demographic models with 1×10³ replicates. We simulated five potential admixture scenarios, as admixture has been suggested as a potential explanation for the haplotype structure seen in some populations of D. simulans (Hamblin and Veuille 1999). No specific admixture regimes have been suggested for D. simulans, thus we simulated potential admixture by isolating the two populations beginning ∼250 years ago and admixing in equal proportions ∼50 years ago. In addition, we simulated a scenario in which the populations were isolated 5,000 and 500,000 years ago. We also simulated a combination of admixture and population contraction, where the populations separate 5,000 years ago followed by a bottleneck to 1% of the original population size for 30 years in one population. The other population is stable until 80 years before the end of the simulation, at which point there is a 30-year bottleneck to 1% of the original population size followed by admixture of each population in equal proportions. Lastly, we simulated a population in which a 200-year bottleneck to 1% of the original population size preceded splitting. Following this, the populations were isolated for 5,000 years, until 80 years before the end of the simulation when there is a 30-year bottleneck in one population followed by admixture in equal proportions.

We also simulated the simplest scenario, a constant population of 2×10⁶ based on predictions for the effective population size of D. simulans (Przeworski et al. 2001). Population contraction has also been proposed as a potential demographic force in D. simulans, thus we simulated several potential population contractions to explore how the timing and length of contraction would affect the nucleotide frequency spectrum (Wall et al. 2002; SchÖfl and Schlötterer 2006). We simulated a population contraction of 1% for 120 years, 100 years before sampling. We simulated two population contractions to 0.1% of the original population size, one for 60 years and the other 120 years, both ending 100 years before sampling. Lastly, we simulated a 0.1% population contraction for 60 years, ending 40 years before sampling. The authors note that in our exploration of parameter space these demographic scenarios more closely mimicked our observed data, for example, longer bottlenecks resulted in excessive loss of variation compared with our population, less severe bottlenecks did not sufficiently elevate Tajima’s D, and more severe bottlenecks (0.01%) created much greater variance in Tajima’s D than seen in our population. However, we are not trying to uncover the exact demographic history of D. simulans, but rather understand the general forces that may have been shaping variation in this population.

Simulations of Selection

A summary of the simulations performed can be seen in supplementary table S2, Supplementary Material online, though only some of these simulations will be considered in full. We simulated a hard sweep and an incomplete sweep without demography, s = 0.1 and conditioning upon ending frequencies of 1 and 0.5, respectively. We simulated a complete soft sweep without demography with s = 0.1 and $\theta =0.3$ where $\theta =4{\mathrm{N}}_e\mu$. We also simulated soft sweeps from standing variation with different starting frequencies, either 5×10⁻⁶ or 1.25×10⁻⁵, and different starting times (either 40 or 70 years ago) (supplementary table S2, Supplementary Material online). For the remainder of the simulations, we included demography, in this case population contractions, as they more closely recapitulated the observed data than the other demographic scenarios we simulated. This included a subset of the aforementioned population contractions—either 120 years ending 100 years ago or 60 years ending 40 years ago. The contractions were either to 1% or 0.1% of the original population size. Selection commenced before, during, or at the completion of the contractions. The selection coefficient was always 0.1, though for simulations of balancing selection this applied to the heterozygote. This value was chosen for s as it more closely recreated the haplotype structure seen in D. simulans than lower values. For all simulations except balancing selection, we assumed codominance, where the homozygous individual carrying two copies of the beneficial allele has twice the fitness of the heterozygous individual. The range of mutations rates for sweeps was between 0 and 0.5, where anything 0.2 and below was primarily hard. The beneficial allele was always placed at the center of the locus. For all MSMS simulations, Tajima’s D was output using the –oTPi flag within the program, and H12 was calculated for each simulated population using scripts from (Crisci et al. 2016).

Admixture

PCA

We wanted to investigate possible admixture in the population, where a PCA with either a long tail or a clear division into separate groups would suggest admixture (Ma and Amos 2012). To ensure that uncorrected LD did not distort, the PCA SNPs were thinned using VCFtools (v1.14) (Danecek et al. 2011) to intervals of 500 bp. The data set was also filtered to contain only autosomes. The PCA analysis was performed using SNPRelate (Zheng et al. 2012) and standard commands.

Admixture

The possibility of admixture can also be evaluated using maximum likelihood estimation of ancestry. The vcf file containing all chromosomes was converted to bed format using bcftools (v1.19) and PLINK (v1.07) (Purcell et al. 2007; Li et al. 2009). Population structure was estimated by using the ADMIXTURE program, a model based estimation of ancestry that uses maximum likelihood (Alexander et al. 2009). The best model was determined by selecting the value of K with the lowest cross-validation error.

H12

To identify selective sweeps across the chromosome arms, we implement a haplotype homozygosity test (H12) (Garud et al. 2015). H12 considers the frequency of the two most frequent haplotypes, where H2 is the haplotype homozygosity for the second most common haplotype only. When a sweep is hard, H2 should be very small, because only one haplotype should be present at a high frequency, that is, H1 will be high. For soft sweeps, H2/H1 will increase as a sweep becomes increasingly soft. For this analysis, heterozygous genotypes were coded as missing data, and sites with missing data were excluded from the analysis. SNPs were analyzed in windows of 400 SNPs with steps of 50 SNPs. We calculated H12 for each of the demographic scenarios described above to determine if our choice of window size was conservative. Haplotypes were grouped only if they matched at every site. We grouped together tracts of elevated H12, choosing the highest value within the tract to represent the peak. We defined the edge coordinates of each peak as the SNPs with the largest and smallest coordinates across the contiguous windows (Garud et al. 2015; Garud and Petrov 2016).

To confirm the expected relationships between the test statistics, we compared H12 and H2/H1 with Tajima’s D. We plotted the top 50 H12 windows for each chromosome arm, and the H2/H1 values for those top H12 windows, against the average Tajima’s D for each window of H12. The edge coordinates of the windows were defined as the largest and smallest coordinates across contiguous windows. Tajima’s D was calculated in windows of 10 kb, thus they were matched to the windows of H12 as the first and last window of Tajima’s D that overlapped the edge coordinate of the H12 window.

Results

Six Million Variants Identified in D. simulans

SNPs were filtered for missing data and a phred score of at least 30, and in the resulting data set the call rate was 96%. We recovered 5,998,575 high-quality biallelic single nucleotide polymorphisms (SNPs), at an average of 5.06 polymorphisms per 100-bp window across the genome. About 15 generations of inbreeding is not expected to remove all variation from individual lines, and selection on deleterious mutations can also strongly counteract inbreeding (Wang et al. 1999). No unexpected relatedness was observed. The vcf files were deposited at https://zenodo.org/communities/genetics-datasets/? page=1&size=20.

π is Consistent with Previous Estimates in D. simulans

In comparison with D. melanogaster estimates from European, African, Asian, and American populations (π = 0.003–0.0084) (Langley et al. 2012; Mackay et al. 2012; Grenier et al. 2015; Lack et al. 2016), the Zuma population of D. simulans exhibits higher π (π_avg =0.009, π_max=0.018), consistent with other estimates in D. simulans ∼0.01 (fig. 1a and table 1) (Begun et al. 2007; Kofler et al. 2015). In European and US populations of D. melanogaster, variation on the X chromosome is strongly depleted, even after correction for its reduced population size (X_4/3) (Langley et al. 2012; Mackay et al. 2012). This varies considerably by population (Grenier et al. 2015), and is most often found in derived non-African populations where complex demographic scenarios are likely responsible (Singh et al. 2007). In D. simulans, variation on the X is less depleted than in D. melanogaster, but D. simulans also exhibits statistically significant depletion of variation on the X (average π for autosomes = 0.00918, average for X = 0.00822 [corrected for reduced N_e]; t-test P < 2.2e-16; Begun et al. 2007). The fourth chromosome in D. melanogaster does not recombine and has very little variation (Wang et al. 2002; Grenier et al. 2015). There is more recombination on the D. simulans fourth chromosome (Wang et al. 2004), and we observe less depletion of variation (π_A = 0.0092, π₄ = 0.0012) compared with D. melanogaster (π_A = 0.005–0.0075, π₄ = 0.0004–0.0015) (Wang et al. 2002; Langley et al. 2012; Mackay et al. 2012) (table 1).

Table 1.

Summary Statistics

Summary Statistics	2L	2R	3L	3R	X	4
SNP density (per 100 bp)	5.010	4.850	5.090	5.460	4.870	3.160
π avg.	0.009	0.009	0.009	0.009	0.008218a	0.001
π median	0.010	0.009	0.010	0.010	0.006	0.001
π min.	0.000	0.000	0.000	0.000	0.000	0.000
π max.	0.018	0.018	0.017	0.018	0.013	0.003
Tajima’s D avg.	1.114	1.104	1.075	1.122	0.650	−1.513
Tajimas D med.	1.262	1.231	1.169	1.179	0.813	−1.529
Tajima’s D min.	−2.565	−2.509	−2.380	−2.656	−2.906	−2.648
Tajima’s D max.	3.394	3.948	4.443	3.229	3.190	−0.075
% significant positive D	8.439	10.143	6.966	5.778	8.297	0.000
% significant negative D	0.763	0.510	0.289	0.258	4.124	33.330
% positive D	86.047	85.178	88.746	94.479	73.381	0.000
% negative D	9.033	9.587	7.007	5.263	26.139	100
% neutral D (D=0)	4.920	5.230	4.250	0.258	0.480	0.000
LD avg.	0.123	0.120	0.113	0.116	0.160
LD median	0.047	0.050	0.042	0.042	0.070

Note.—For each chromosome or chromosome arm, we have summarized the population genetic parameters for the Zuma population of Drosophila simulans. This includes SNP density, π, Tajima’s D, and linkage disequilibrium. For the X chromosome, π is scaled by 4/3 to account for its reduced population size.

^aScaled by 4/3.

Tajima’s D

We find a surprising abundance of intermediate frequency variants (positive Tajima’s D) and relatively fewer regions with an excess of low-frequency variants (negative Tajima’s D) (fig. 1a). Using Tajima’s conservative critical values for n = 175 (−1.765∼2.095) (Tajima 1989), we find that between 5% and 10% of the windows of positive Tajima’s D are significant (table 1). This is an unusual result given previous studies of Drosophila that recovered largely negative values of Tajima’s D (Parsch et al. 2001; Wall et al. 2002; Braverman et al. 2005; Ometto et al. 2005; Nolte and Schlötterer 2008; Fabian et al. 2012; Langley et al. 2012; Mackay et al. 2012; Campo et al. 2013; Hübner et al. 2013).

Tajima’s D Varies between Gene Regions

We calculated Tajima’s D for each gene region (exon, long intron >120, short intron <120, bp 8–30 of introns <65, 5′-UTR, 3′-UTR) split between the X and autosomes to determine if different regions exhibit different patterns of Tajima’s D (fig. 1b). Tajima’s D was calculated in windows using gene regions within 10 kb of one another, for example, all introns within a gene that is <10 kb would be included in a single window. Short introns are thought to be evolving the most neutrally, though they will still be effected by demographic events (Parsch 2003; Parsch et al. 2010). The median and distribution of each category is shown in figure 1b. Long introns on the autosomes have the largest values of Tajima’s D (mean 1.24), and it is larger than either 8- to 30-bp introns <65 bp on the autosomes (P value < 2.2e-16, Mann–Whitney U-test) or exons on the autosomes (P value < 2.2e-16, Mann–Whitney U-test). The variance in the distribution of Tajima’s D is different for long introns compared with 8- to 30-bp introns < 65 bp (0.8 and 1.4, respectively, supplementary fig. S2, Supplementary Material online). The difference is significant between long introns and introns <120 bp on the autosomes, though it is less significant than the other comparisons (P value = 0.0001479 Mann–Whitney U-test). The difference between the X and the autosomes was significant for every category (P value < 2.2e-16, Mann–Whitney U-test). However, no significant differences are observed between autosomal 5′-UTRs and 3′-UTRs (P value = 0.09, Mann–Whitney U-test), between X 5′-UTRs and 3′-UTRs (P = 0.438, Mann–Whitney U-test), or between exons on the X and 5′-UTRs or 3′-UTRs on the X (5′-UTR P = 0.4299, 3′-UTR P = 0.0815, Mann–Whitney U-test).

Comparison with Simulated Populations

The proposed demographic scenarios produce a wide range of Tajima’s D values (fig. 2a and b). The parameters chosen to model pure admixture did not produce a positive Tajima’s D, rather increasing amounts of separation produced increasingly negative Tajima’s D, thought the effect is not large (fig. 2a). Bottlenecks in both admixed populations did not have an appreciable effect on Tajima’s D, whereas a bottleneck in the population prior to splitting, followed by a bottleneck in one lineage, created a very negative Tajima’s D (fig. 2a). This is a small sample of the many possible demographic scenarios incorporating admixture, thus it does not rule it out as a potential cause of the observed patterns. However, these simulations do not provide support for admixture as an underlying cause.

Fig. 2.—

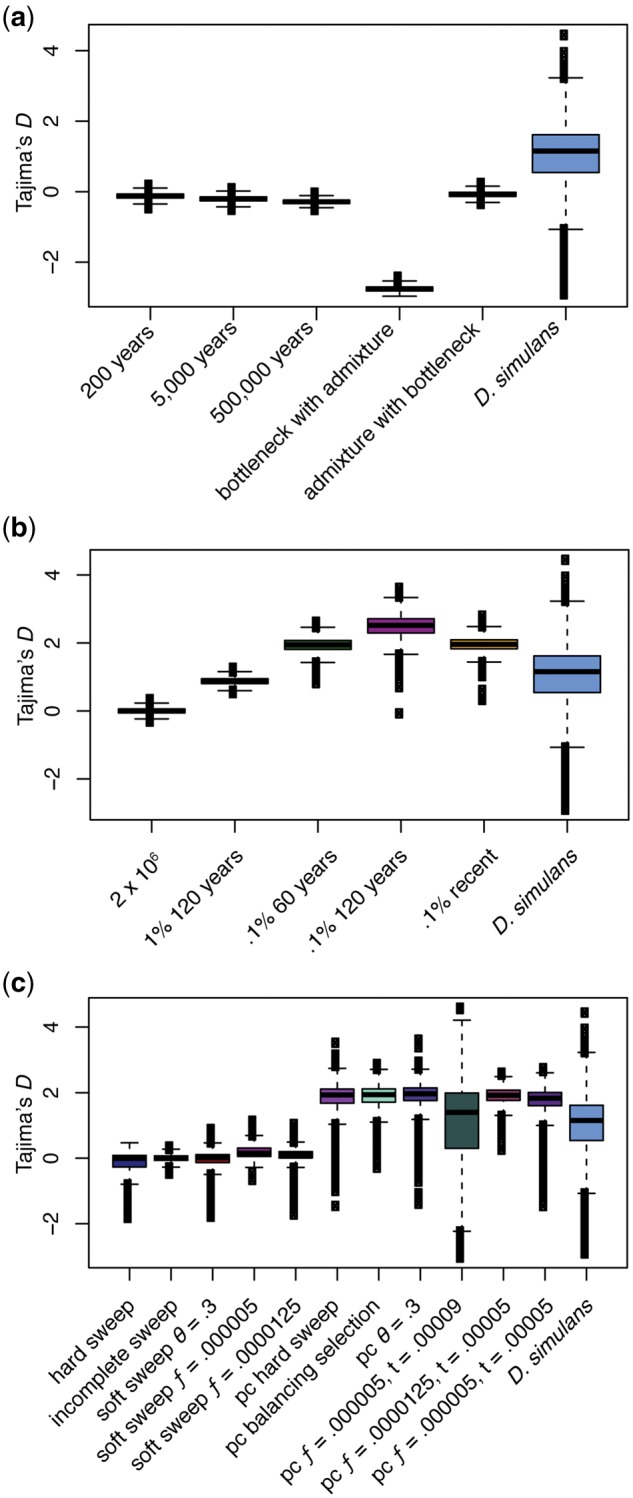
Each simulation was performed for a region 10⁵ bp and Tajima’s D was calculated in windows of 10 kb. Recombination was $\rho =$5×10⁻⁷ and mutation $\mu =$3×10⁻⁹. Here, Tajima’s D in demographic simulations is shown compared with Drosophila simulans. (a) Admixture simulations, including admixture with a bottleneck prior to splitting, and a bottleneck along one lineage prior to admixing (bottleneck with admixture), and admixture with bottlenecks in both populations after isolation (admixture with bottleneck). (b) Constant population size and population contractions of different degrees and durations. A recent bottleneck to 0.1% for 60 years resembles the data as much as slightly older bottlenecks, and is used in concert with the simulations of selection in the following figure. (c) Tajima’s D in different simulations of selection compared with D. simulans. Not all of the simulations listed in supplementary table S2, Supplementary Material online, are included here, only those that most resemble the D. simulans data or illustrate the difference between selection alone and selection with demography. All population contractions were to 0.1% of the population for 60 years, terminating 40 years prior to sampling. For all simulations s = 0.1, ƒ refers to the starting frequency of the selected mutation, and t is its time of introduction with units of 4N_e.

A constant population size maintained an average Tajima’s D of zero as expected (fig. 2b). Population contraction had the largest effect on Tajima’s D out of the simulations performed, with contractions to 0.1% ending either 100 or 40 years prior to sampling producing roughly the same distributions (fig. 2b). Contraction to 0.1% for 120 years elevated Tajima’s D above that observed, whereas a 1% contraction for 120 years did not elevate it sufficiently. Notably, none of the demographic scenarios produce the variance seen in the D. simulans population (e.g., variance of Tajima’s D for a contraction of 1% for 120 years = 0.01, D. simulans = 0.8) (fig. 2b).

Many different demographic and selective scenarios could create the patterns seen in D. simulans. We explored simulations of selection and selection with demography, focusing on scenarios that more closely recapitulated our data (fig. 2c). Selection without demography, both hard, incomplete, and soft sweeps, produced a negative spread of Tajima’s D values but did not produce the elevated Tajima’s D seen in our population (fig. 2c). It is possible that other scenarios not modeled, or scenarios such as balancing selection with competing mutations rather than heterozygote advantage, could produce more elevated values of Tajima’s D. Simulations of selection including demography, in this case a population contraction to 0.1% for 60 years, 40 years prior to sampling, produced elevated Tajima’s D with means and variances more similar to that observed in our population (fig. 2c). Selection from standing genetic variation with a starting frequency of 20 copies, starting during the population contraction, had a mean of 1 much as D. simulans, though a larger variance (t = 0.00009, 1.6 vs. 0.8). Selection on standing variation with either 50 or 20 copies with selection concurrent with the end of the population contraction had larger means (t = 0.00005, 1.7–1.9) and smaller variances (0.08–0.3). A hard sweep had a lower mean (0.5) but a more similar variance to D. simulans (0.6). When demography is incorporated with selection in MSMS the timing of selection must be set, thus it is possible that sweeps that finished more or less recently would present more similar values to D. simulans.

Linkage Disequilibrium

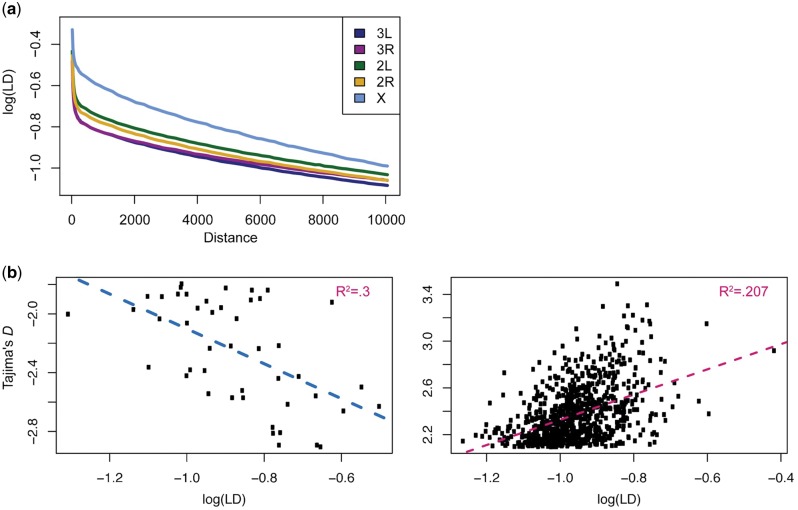
We assessed the scale of LD decay in the D. simulans data set using r² to calculate pair-wise LD at distances from a few base pairs to 10 kb (fig. 3a). LD is shown on a log scale to better illustrate smaller values. We found a rapid decay of LD within 200 bp on all autosomes, much as in D. melanogaster (Garud et al. 2015) (fig. 3a). It should be noted that our estimates of LD are likely somewhat inflated relative to recent estimates from D. melanogaster. We do not have detailed knowledge of recombination rate and potential admixture, both of which have been used to filter D. melanogaster data sets, excluding >50% of the genome in some cases (Garud et al. 2015; Garud and Petrov 2016; Lack et al. 2016). Admixture may increase or decrease LD depending on the scenario, but regions of reduced recombination could not be excluded here other than at centromeres and telomeres. All other filtering that we performed prior to calculating LD was the same as that performed in D. melanogaster. We compared the relationship between LD and positive values of Tajima’s D and found that it is slightly positive (P value < 0. 001; fig. 3b). Between LD and negative values of Tajima’s D, the relationship is negative, meaning that lower values of Tajima’s D have a higher LD (fig. 3b). The purpose of this comparison is to guide the investigation into potential demographic and selective forces shaping the population, for example, if a high Tajima’s D was associated with a low LD then long-term balancing selection would be a natural area to investigate. This is not the pattern we observe, so we will focus on selective scenarios such as short-term balancing selection and hard or soft sweeps.

Fig. 3.—

Linkage disequilibrium. (a) Decay of linkage disequilibrium on the X and autosomes calculated by distance. LD is binned initially in windows of 20 bp until 300 bp and 150 bp thereafter. Shown is the log(LD) of the mean of each of these bins. Regions of low recombination have been filtered out. (b) The relationship between LD and outliers of Tajima’s D with regression lines plotted for negative and positive values of Tajima’s D separately. This is to highlight the possibility for different relationships between LD and Tajima’s D depending upon the selective regime—for example, that lower (higher) values of Tajima’s D may be associated with higher (lower) values of LD. The R² value of for each of these lines is shown in the upper right hand corner of each graph.

Sensitivity Analysis

To confirm that our results were robust, we performed a number of different sensitivity analyses. The GATK pipeline is known to call SNPs more promiscuously than other pipelines, thus biasing in favor of rare variants. To test the effect of increasing the number of rare variants, we lowered the quality threshold to a phred score of 20 (data not shown). In addition, we called SNPs using a different SNP calling protocol, GenotypeGVCFs, which calls SNPs individually for each genotype (data not shown). We also examined the effect of masking heterozygous bases and excluding SNPs with missing data (supplementary text S1 and fig. S3, Supplementary Material online). None of these calculations had a qualitative effect on our results. We also recalculated Tajima’s D using R scripts (courtesy of Benjamin Laenen) to determine if there was a bias arising from with the software (VCFtools). We found no differences in the values of Tajima’s D (data not shown). Lastly, we examined the relationship between heterozygous calls and call quality and found no relationship (supplementary text S1 and fig. S3, Supplementary Material online). These results support the conclusion that Tajima’s D is robust to biases arising from technical issues. Any residual bias should be toward calling more rare SNPs.

To determine if the level of heterozygosity was affecting our results, we recalculated our summary statistics using subsets of individuals with different levels of inbreeding (data not shown). This will also help us to determine if our results are being driven by an unusual subset of individuals within the panel. We reduced our data set to the 82 most inbred genotypes and recalculated all of the summary statistics. Again, our results were unaffected, supporting the conclusion that the observed patterns are not the result of methodological or computational artifacts.

Admixture

Admixture could cause the elevated Tajima’s D in our population. A PCA analysis found no evidence of admixture, as there is no tail to the distribution as would be expected if individuals were sampled from an admixed population (supplementary text S1 and fig. S4, Supplementary Material online) (Ma and Amos 2012). It is possible that every individual is equally admixed and therefore appearing as one population. We also performed an analysis of population structure with the algorithm ADMIXTURE (Alexander et al. 2009). Using the value of K (number of populations) with the lowest cross validation score, we determined that the best model fit in ADMIXTURE for these samples is a single ancestral population (supplementary text S1 and fig. S4, Supplementary Material online). Admixture cannot be ruled out, but these results do not explicitly support admixture as being the reason behind the presence of intermediate frequency haplotypes in this population. It is a given that demography contributes to the patterns observed here, including the genome-wide elevated Tajima’s D, so we will focus instead on outliers determined by simulations of selection and demography.

H12

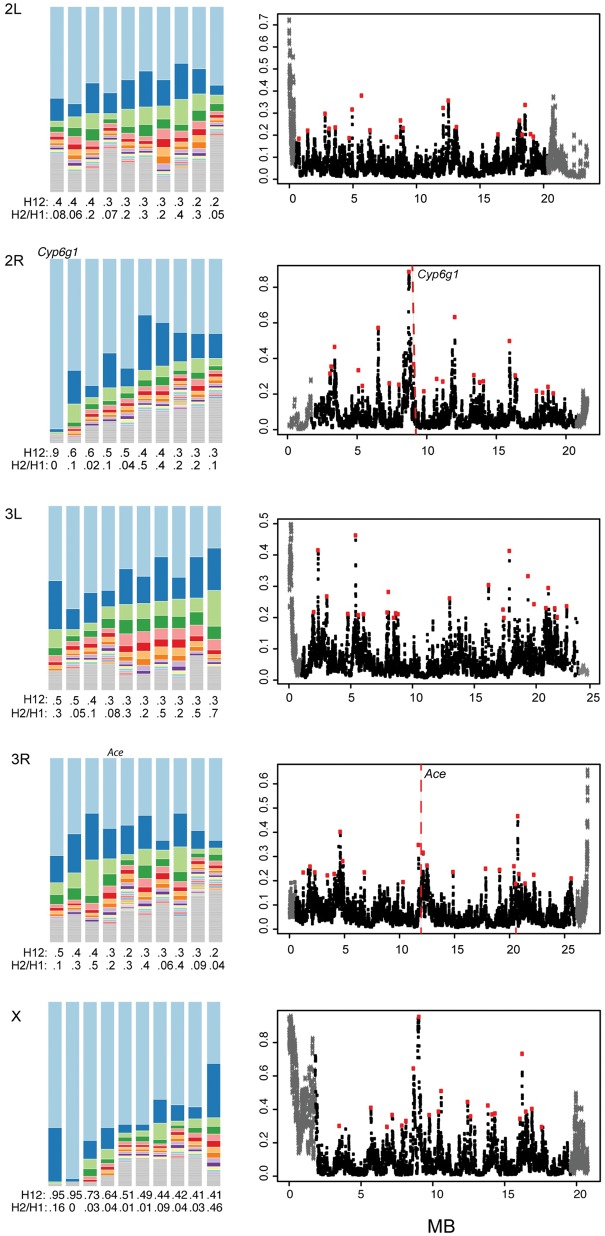
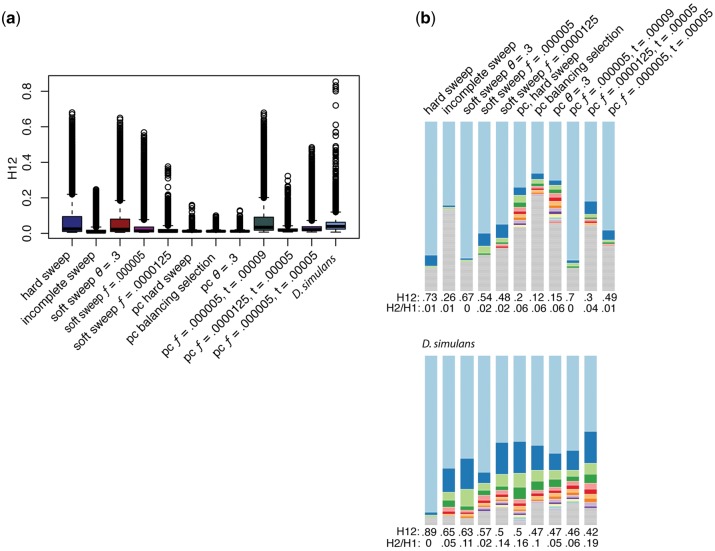
To investigate potential sweeps occurring in this population, we will use a haplotype diversity test (H12) (Garud et al. 2015; Garud and Petrov 2016). In this test, high values of H12 indicate a sweep, but the relative frequency of the second most frequent haplotype is indicated by the corresponding H2/H1 values (Garud et al. 2015). A high value of H12 with a correspondingly high value of H2/H1 indicates a higher frequency of the second haplotype. A high value of H12 and a low value for H2/H1 suggests that a second haplotype does not segregate at an appreciable frequency (Garud et al. 2015). In the D. simulans population, the mean H12 was 0.05, with a median of 0.04 (fig. 4). The highest values of H12 are 0.95, and are found on the X chromosome. The third largest value of H12 is 0.89, and corresponds to the interval containing Cyp6g1. Cyp6g1 has been previously inferred to be involved in selective sweeps in response to insecticides (Schlenke and Begun 2004; Schmidt et al. 2010; Kolaczkowski et al. 2011; Garud et al. 2015; Sedghifar et al. 2016).

Fig. 4.—

Haplotype Diversity. Shown are the results of the H12 scan for each chromosome other than the fourth, due to its overall reduced recombination rate. On the right-hand side are the scans in windows of 400 bases, with window centers separated by 50 SNPs. Gray regions indicate regions of the chromosome arms with reduced recombination that were not included in the final analysis. Red points indicate the top peaks for each chromosome. The dotted red lines indicate two positive controls from Drosophila melanogaster, Cyp6g1, and Ace. On the left-hand side, the haplotype frequency spectra for the top ten intervals from each chromosome are shown. The height of the top shaded region in light blue indicates the proportion of that haplotype in the population. Colors after that indicate the second, third, and so on most frequent haplotypes while regions in gray indicate singletons. Most sweeps, with the exception of Cyp6g1, have second haplotypes sorting at appreciable frequencies.

Comparison with Simulated Populations

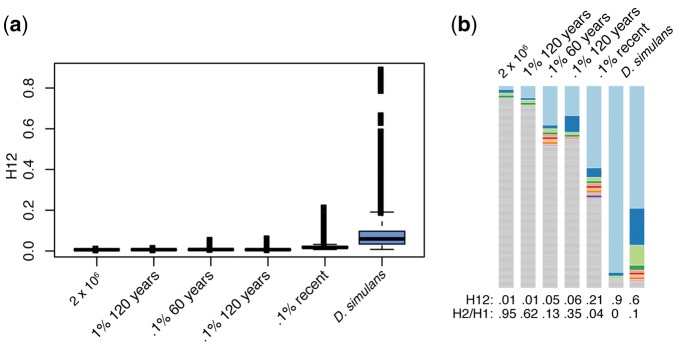
Window size is an important parameter for this test, and is generally based on the extent of LD in a population. We note that while decreasing the window size in the demographic scenarios to 300 SNPs does increase the presence of haplotype structure, it does not do so enough to alter any of our conclusions. In addition, while the results are quantitatively changed by an increase in window size to 500 SNPs in the D. simulans population, they are not qualitatively different (data not shown). Admixture did not produce values of Tajima’s D comparable with that seen in our population, thus we will not discuss it further here. However, the authors note that the scenarios we simulated did not produce appreciable haplotype structure (data not shown). A recent bottleneck to 0.1% did produce appreciable haplotype structure, with a top H12 of 0.21 and an H2/H1 of 0.04 (fig. 5). A recent bottleneck to 0.1% and a bottleneck ending 100 years ago to 0.1% produced similar distributions of Tajima’s D, however, given the increased haplotype structure in the more recent bottleneck, we will focus on this demographic scenario when demography and selection are combined (fig. 5).

Fig. 5.—

Demographic simulations and H12. (a) The spread of H12 values in each of the demographic scenarios that were simulated. Demography does not substantially elevate Tajima’s D though population contraction does have more haplotype structure than the other demographic scenarios. (b) An example of the haplotype structure under each of the demographic scenarios, with the highest H12 value for each scenario shown. Again, the most frequent haplotype is shown in light blue and the second most frequent in dark blue. Gray regions indicate singletons.

Simulations of selection or selection with demography produced a variety of H12 patterns. For genome-wide H12 values selection without demography produced elevation of H12 higher to that seen in D. simulans, despite not producing elevated Tajima’s D (figs. 2 and 6). Soft sweeps from repeated mutation and hard sweeps had means (0.07, 0.08) higher than D. simulans (0.05). However, the median for D. simulans was higher (0.04), than for hard sweeps (0.025) or soft sweeps from repeated mutation (0.023). Population contraction with selection from standing variation occurring during the population contraction also had a higher mean (t = 0.00009, 0.074), whereas other simulations from standing variation with population contraction were lower (t = 0.00005, 0.036, 0.022) (fig. 6). However, for the same three simulations, the most similar median also occurred from selection on standing variation occurring during the population contraction (t = 0.00009, 0.035) versus from standing variation occurring at the end of contraction (t = 0.00005, 0.02, 0.017). The contributions of selection and demography are difficult to parse, and the authors do not claim to do so here. However, overall of the simulations which we performed, a population contraction combined with selection from standing variation where selection commences during the contraction produced the most similar values of both Tajima’s D and H12 (t = 0.00009). None of the simulations produced sweeps as soft as in D. simulans, but the highest values of H2/H1 for the highest H12 were from population contraction with hard sweeps, soft sweeps from repeated mutation, and balancing selection (fig. 6). The timing of selection is important, for example, selection on repeated mutation that occurs after a population contraction generally results in a hard sweep due to lost variation (data not shown, supplementary table S2, Supplementary Material online), and selection on standing variation produces very different patterns depending upon whether it beings during the contraction or concurrent to its end (fig. 6). It is likely that more fully exploring this parameter space would yield additional insight into the patterns of variation seen in D. simulans.

Fig. 6.—

Simulations of selection and H12. (a) The spread of H12 values for each of the simulations of selection. While demography and selection elevated Tajima’s D the most, they do not elevate H12 values the most. This may be due to the timing of selection, which had to be modeled differently for combinations of selection and demography. (b) Patterns of haplotype diversity in the top values of H12 from each simulation and Drosophila simulans. Note that we include the highest values of H12 for D. simulans from the autosomes, as these simulations pertain principally to autosomal variation. These selection scenarios are more similar to that observed in D. simulans than demography, however, the high frequency of the second haplotype in D. simulans was not recapitulated in any simulation.

H12 Outliers

A recent population contraction to 0.1% for 60 years produced the highest H12 of all of the demographic scenarios, with a maximum value of 0.17. The lowest value of the top 50 outliers for D. simulans is 0.24, we will consider these outliers to be less likely to be caused by demographic factors. To focus on outliers, we selected the 50 intervals with the highest H12 values and annotated all genes contained completely within each interval (supplementary table S1, Supplementary Material online). Some selective sweeps confirmed in previous studies overlapped with genes found in our top 50 intervals (Garud et al. 2015). For instance, Cyp6g1 has repeatedly been implicated in sweeps relating to insecticide resistance, and among our sweeps, we find Cyp6g1 within a window with one of the highest H12 scores (Schlenke and Begun 2004; Schmidt et al. 2010; Kolaczkowski et al. 2011; Garud et al. 2015; Sedghifar et al. 2016). Ace has also repeatedly been implicated in sweeps relating to insecticide resistance and it is within the top 50 peaks for chromosome 3R, but not the top 50 overall (fig. 4) (Fournier et al. 1992; Mutero et al. 1994; Menozzi et al. 2004; Sedghifar et al. 2016).

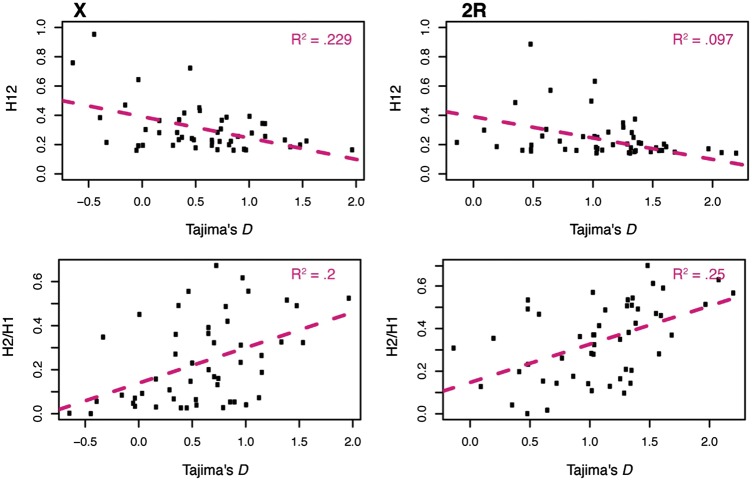
Tajima’s D and H12

We wanted to understand the relationship between H12 and Tajima’s D. They may be correlated under neutrality or selection, but it is also possible they are detecting separate phenomena. For example, are the regions of higher LD that would be detected using H12 the same regions with elevated intermediate frequency variation, or are those regions associated with lower haplotype structure? We plotted the top 50 H12 values from each chromosome arm against the average Tajima’s D within that window. We also plotted the corresponding H2/H1 against Tajima’s D for the same windows. H12 is less able to detect selection the more haplotypes are present (e.g., as might be found in ancient balancing selection), so one might expect a slight negative relationship between values of H12 and Tajima’s D, which is also what we find (P < 0.0001) (fig. 7 and supplementary fig. S5, Supplementary Material online). However, the majority of the Tajima’s D values for the top H12 windows are positive, though neither the positive or negative values are extreme. There is also the expected positive relationship between the H2/H1 values from the top 50 H12 and Tajima’s D. This is the pattern we find on the X chromosome and all of the autosomes other than 3L (P < 0.0003–0.002, 3L P < 0.148) (fig. 7, table 1 and supplementary text S1 and fig. S5, Supplementary Material online). It is unclear why 3L is an exception to this pattern, although it does have more negative values of Tajima’s D than the other autosomes (supplementary text S1 and fig. S6, Supplementary Material online).

Fig. 7.—

H12. (a) Tajima’s D versus H12 and H2/H1. The average Tajima’s D value was calculated for intervals identified as the top 50 H12 scores for each chromosome. Intervals are defined as the smallest and largest edges of each peak, thus adjacent intervals with high H12 scores are considered a single peak. The slight negative relationship between H12 and Tajima’s D is significant for all chromosomes (P < 0.0001), and is expected given the decreasing ability of H12 to detect sweeps as they become softer (supplementary fig. S5, Supplementary Material online). A high value of H2/H1 and H12 indicates a soft selective sweep, so a positive relationship between Tajima’s D and H2/H1 indicates that soft selective sweeps are responsible for the high Tajima’s D values. The relationship is significant at P < 0.0003–0.002 for all chromosomes other than 3L (supplementary fig. S6, Supplementary Material online).

What is most striking about the D. simulans data in comparison with the simulations is the high frequency of the second haplotype. We were not able to reproduce this pattern with any of the demographic or selective scenarios we investigated. Plots of this haplotype structure show that there is a single invariant haplotype at high frequency, followed by a second common haplotype that may or may not be quite diverged. That is the second most common haplotype is generally not a single mutational step away from the most common haplotype, it is often separated by many mutations. Examples of these haplotypes are shown in supplementary figure S7, Supplementary Material online, along with an example of a hard sweep.

Discussion

Demographic Scenarios

Our simulations of demographic scenarios suggest that this population of D. simulans could have undergone a population bottleneck. Other, unexplored, demographic scenarios could likely produce the same patterns, however, it is most consistent with the scenarios we explored. In addition, Tajima’s D between different annotation categories (exons and 3′-UTR) do differ, though all are substantially elevated. Long introns are more positive than all other categories, with a reduced variance, suggesting a different selective regime for this category. However, presumably unconstrained bp 8–30 introns < 65 bp are also positive, suggesting that a demographic scenario such as population contraction is involved (Parsch et al. 2010). Drosophila simulans is thought to have colonized the Americas ∼100 years ago, which would have created a population bottleneck. In addition, there may have been bottlenecks associated with an out-of-Africa migration or the spread of Wolbachia strain wRi (Turelli 1984; Turelli and Hoffmann 1995). Ecologically, there is no reason to expect seasonal cycling of population abundance that could lead to demographic signatures of contraction (Behrman et al. 2015). There is a year-round supply of food, as well as temperature changes that are well within the tolerable range for D. simulans. Furthermore, D. simulans has been collected in various locations in Southern California from January to November (Turelli and Hoffmann 1995; Ballard et al. 2008; San Diego Stock Center). This is not to say that there will be no seasonal selection on traits such as desiccation resistance, but there is likely no seasonal population collapse and expansion or recolonization (Behrman et al. 2015). In addition, D. simulans has a lower F_ST than D. melanogaster when geographical clines are sampled (Machado et al. 2015; Sedghifar et al. 2016). Less clinal variation in D. simulans compared with D. melanogaster could indicate more recent spread, reflecting the possibility of a recent population contraction and expansion in D. simulans (Machado et al. 2015; Sedghifar et al. 2016). It is possible that a different demographic scenario created this elevated Tajima’s D, though of the simulations we performed it resembled the data more than other demographic scenarios.

A relative excess of intermediate frequency alleles is expected during some admixture scenarios (Gillespie and Turelli 1989). However, we did not find evidence of admixture in our PCA or ADMIXTURE analyses and the simulations of admixture that we performed. There are many possible scenarios for admixture, and it is possible that if the two populations were isolated for longer than 500,000 years that it would have produced a more pronounced change in Tajima’s D. In addition, selection in each population prior to admixture may have elevated Tajima’s D, though bottlenecks in the isolated populations did not. The particular scenarios simulated here tended to create more negative Tajima’s D the longer the populations were separated. It is possible that a different combination of admixture and contraction could produce the observed values of Tajima’s D. The evidence here does not support admixture, however, it cannot be ruled out as potentially contributing to the observed patterns in D. simulans.

Selection

Of the parameter space we explored, selection without demography was able to create high-frequency haplotypes and high H12 values, but did not elevate Tajima’s D or create the variance in Tajima’s D seen in our population. Selection alone could be responsible for the patterns observed in D. simulans, though the elevated Tajima’s D across all categories of gene regions (introns and exons) suggests a role for demography. Hard sweeps, balancing selection, and soft sweeps from repeated mutation, combined with a population contraction, all created elevated Tajima’s D and haplotype structure, though H12 was not as high as in D. simulans. Soft sweeps from standing variation produced similar patterns, though a sweep from standing variation that begins during the population contraction rather than at its conclusion increased the variance in Tajima’s D in a way more similar to D. simulans. However, these sweeps tended toward single haplotypes at high frequency compared with D. simulans. The D. simulans H12 outliers are characterized by a high frequency of the second haplotype, which we were unable to recapitulate in any of our simulations. Overall, the timing of both population contractions and selection appear to be important in producing haplotype structure, but likely many different demographic and selective scenarios could create the observed patterns.

Overall H12 values in D. simulans were much higher than that observed in North American D. melanogaster, with a maximum of 0.89 in this panel and 0.24 in D. melanogaster (Garud and Petrov 2016). Of the top ten potential sweeps, there are more haplotypes at high frequency in North American D. melanogaster, with values as high of H2/H1 as 0.54 in D. melanogaster, whereas values of H2/H1 are only as high as 0.3 in D. simulans. However, the top 50 sweeps in D. simulans contain values of H2/H1 as high as 0.7. North American D. melanogaster likely has a different demographic history than D. simulans, which certainly contributes to this difference, or the sweeps in D. melanogaster may be older. Previous work on clines of Australian and North American D. simulans found shared SNPs associated with extreme values of F_ST between populations, which suggested local adaptation from standing variation (Sedghifar et al. 2016).

Conclusion

Understanding the effect of demography and selection on variation in the genome is a difficult goal given the complexity of the potential realities of both factors. In general, sampling has been done sparsely across a species range, and while deep sequencing of a single population of a species is becoming more routine, few experiments exist to date of the depth considered here. Our observations are consistent with previous literature on D. simulans, which found invariant haplotypes at intermediate frequency in both African and non-African populations (Hasson et al. 1998; Hamblin and Veuille 1999; Rozas et al. 2001; Quesada et al. 2003; Sanchez-Gracia and Rozas 2007). In general, our results are suggestive of a contribution of both demography and selection to the patterns of variation observed in D. simulans. It is difficult to determine if this is the type of selection involved as the timing and strength of selection as well as its interaction with demographic factors can create similar patterns in response to different inputs. Of the simulations performed here, that which is most consistent with D. simulans is a soft sweep from standing variation combined with a population contraction.

Our insights into the Zuma D. simulans population’s dynamics reveal a complex population exposed to a myriad of demographic and selective forces. Separating out the effects of demography and selection is one of the major goals of population genetics, and we cannot say definitely what is shaping the genome-wide patterns of diversity we observe in this population. However, the demographic simulations performed here are more suggestive of the conclusion that D. simulans has undergone a recent population bottleneck. In addition, among outlier regions of the genome with invariant haplotypes at high or intermediate frequency, the pattern of variation appears to be more consistent with soft sweeps than with hard sweeps, though this is not conclusive. Furthermore, California D. simulans populations appear to have a very different demographic and selective history than D. melanogaster, the causes of which will be interesting to disentangle in the future.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.