Abstract
Cells rely on focal adhesions (FAs) to carry out a variety of important tasks, including motion, environmental sensing, and adhesion to the extracellular matrix. Although attaining a fundamental characterization of FAs is a compelling goal, their extensive complexity and small size, which can be below the diffraction limit, have hindered a full understanding. In this study we have used single-molecule localization microscopy (SMLM) to investigate integrin β3 and paxillin in rat embryonic fibroblasts growing on two different extracellular matrix-representing substrates (i.e., fibronectin-coated substrates and specifically biofunctionalized nanopatterned substrates). To quantify the substructure of FAs, we developed a clustering method based on expectation maximization of a Gaussian mixture that accounts for localization uncertainty and background. Analysis of our SMLM data indicates that the structures within FAs, characterized as a Gaussian mixture, typically have areas between 0.01 and 1 μm2, contain 10–100 localizations, and can exhibit substantial eccentricity. Our approach based on SMLM opens new avenues for studying structural and functional biology of molecular assemblies that display substantial varieties in size, shape, and density.
Introduction
Focal adhesions (FAs) are cellular macromolecular assemblies consisting of dynamic protein complexes that are localized near the cell membrane. FAs affect nearly all aspects of a cell’s life, including, but not limited to, adhesion, directional migration, cell proliferation, differentiation, survival, and gene expression (1). Despite having been studied for several decades, the inner architecture of FAs is still not completely understood. In part, this is due to the limitations of conventional fluorescence microscopy for FA analysis. FAs are molecularly diverse structures, containing a large number of proteins (2). Therefore, their investigation requires imaging techniques that offer sufficient multiplexing capabilities (3). Moreover, FAs have a size that is typically in the order of a micron or less, and therefore their internal spatio-temporal organization is not fully resolvable with conventional microscopy.
During the last decade, several superresolution microscopy techniques have been employed to image FAs (4, 5, 6, 7, 8, 9). An important insight from these studies was that FAs are not homogeneous spatial structures. Initially, photoactivated localization microscopy (PALM) was used to reveal that FAs can consist of patches of proteins with submicron dimensions (4, 9). Later on, Bayesian localization microscopy and structured illumination microscopy showed that many FAs exhibit discontinuous elongated (or fiberlike) substructures (5, 6). Moreover, single-particle tracking demonstrated that proteins can diffuse within FAs (7, 8), which again suggests that they have an internal spatial organization. However, dedicated tools that allow a systematic quantitative analysis of the FA substructure are still lacking.
For quantitative analysis of the internal spatial organization of FAs, single-molecule localization microscopy (SMLM) can potentially be implemented (10, 11). SMLM data consist of the localizations of individual photoactivatable or photoswitchable fluorescent molecules. Therefore, a variety of methods have been developed to identify and characterize clusters of such localizations (12, 13). These methods are often applied to investigate clusters of receptors in the cell membrane. Such clusters are usually radially symmetric, spatially well separated, and homogeneous in size and density. FA substructures, on the other hand, cannot be characterized similarly. Indeed, adhesions structures can vary from subdiffraction entities composed of a couple of different proteins (e.g., focal complexes or nascent adhesions) to assemblies of many proteins measuring several microns (e.g., FAs) (14). Moreover, FA subunits are densely packed; therefore, they cannot be resolved using a conventional microscope. Finally, FAs usually have an elongated shape, and the same is possibly true for their subcomponents. Therefore, it is not clear if established SMLM clustering methods are suitable for the identification of FA substructures.
In this study we have designed, to the best of our knowledge, a novel approach to investigate the FA substructure. We used expectation maximization of a Gaussian mixture (EMGM) (15) to interpret SMLM data in terms of spatial probability distributions. EMGM allows us to quantify the properties of closely packed localization patterns that exhibit substantial varieties in size, density, and shape, and is therefore well suited for studying the inner architecture of FAs. Importantly, we improved the classical EMGM framework to account for localization uncertainties and the presence of a localization background, both being ubiquitous in SMLM data.
The other goal of this study was to quantify the properties of the subunits of which FAs are composed. For this purpose, we used PALM, an implementation of SMLM that is popular for imaging FAs (4, 9, 16, 17, 18), because it makes use of photoactivatable fluorescent proteins that can be genetically expressed. More in particular, we used PALM to image integrin β3 and paxillin in fixed rat embryonic fibroblasts (REFs), a well-known cell line for FA investigation. Cell experiments were performed using fibronectin-coated substrates and specifically biofunctionalized nanopatterned substrates, on which ordered patterns of nanoscale adhesive spots were provided (19, 20). Such nanopatterned substrates have already been used to indirectly probe the behavior of FAs on the nanoscale (21). In this way, the spatial organization of integrin binding sites is precisely controlled, ensuring that the observed substructures are innate to FAs. Application of our improved version of EMGM on the PALM data allowed us to determine that FAs are composed of structures with areas between 0.01 and 1 μm2, containing 10–100 localizations, and exhibiting substantial eccentricities.
Materials and Methods
Microscope
PALM imaging was carried out on a custom-built microscope (22, 23). A 50-mW 405-nm laser (Cube; Coherent, Santa Clara, CA), a 100-mW 488-nm laser (Sapphire; Coherent), and a 100-mW 561-nm laser (Excelsior; Spectra-Physics, Santa Clara, CA) were used for excitation/activation. The three lasers were focused into the back focal plane of the objective mounted on an inverted optical microscope (IX71; Olympus, Melville, NY). We used a 100× objective (UApo N 100×; Olympus) with a numerical aperture of 1.49 configured for total internal reflection fluorescence (TIRF). A dichroic mirror (493/574 nm BrightLine; Semrock, Rochester, NY) and an emission filter (405/488/568 nm StopLine; Semrock) were used to separate fluorescence and illumination light. The fluorescence light was detected by an electron-multiplying charge-coupled device (EMCCD) camera (iXon DU-897; Andor Technology, South Windsor, CT). An adaptive optics system (Micao 3D-SR; Imagine Optic, Orsay, France) and an optical system (DV2; Photometrics, Tucson, AZ) equipped with a dichroic mirror (T565lpxr, Chroma Technology, Bellows Falls, VT) were placed in front of the EMCCD camera.
Imaging procedure
Cells were imaged in PBS at room temperature. Before imaging, 100 nm gold fiducial markers (C-AU-0.100; Corpuscular, Cold Spring, NY) were added to the sample for lateral drift monitoring. Axial drift correction was ensured by a nanometer positioning stage (Nano-Drive; Mad City Labs, Madison, WI) driven by an optical feedback system (22). Excitation of the mEos2 was done at 488 nm or 561 nm with ∼10 mW power (as measured in the back focal plane of the objective). The mEos2 was activated at 405 nm with ∼2 mW power. The gain of the EMCCD camera was set to 100 and the exposure time to 50 ms. For each experiment, 10,000 camera frames were recorded.
Substrate preparation
Quasi-hexagonal patterns of gold nanoparticles (AuNPs) were prepared on 25-mm-diameter microscope coverslips (No. 1.5 Micro Coverglass; Electron Microscopy Sciences, Hatfield, PA) by means of block-copolymer micelle nanolithography as previously described (19, 20, 24) (Supporting Material). Fibronectin-coated coverslips were prepared by first cleaning with an oxygen plasma and then incubating with PBS containing 50 μg/mL fibronectin (Bovine Plasma Fibronectin; Invitrogen, Carlsbad, CA) for 30 min at 37°C. To remove the excess of fibronectin, the coverslip was washed with PBS before seeding the cells.
Cell culture and fixation
The REF cells (CRL-1213, ATCC) were grown in DMEM supplemented with 10% fetal bovine serum, 1% penicillin-streptomycin, 1% nonessential amino acids, and 1% glutamine, at 37°C with 5% CO2. The cells were transfected by electroporation (Neon Transfection System; Invitrogen), which was performed on ∼106 cells using 1 pulse of 1350 V lasting for 35 ms. The amount of DNA used for the transfection was 4 μg for both the mEos2-paxillin-22 vector and the mEos2-Integrin-β3-N-18 vector. Approximately 2.105 transfected cells were seeded on individual coverslips and grown in cell culture medium without penicillin-streptomycin, at 37°C with 5% CO2. The cells were washed with PBS ∼20 h after transfection (Fig. S1), and then incubated in PBS with 2.5% paraformaldehyde at 37°C for 10 min. After removing the fixative, the cells were again washed with PBS, and the coverslip was placed into a custom-made holder.
PALM data analysis
The recorded images were analyzed by a custom-written algorithm (MATLAB; The MathWorks, Natick, MA) that was adapted from a previously published algorithm (4, 23). First, peaks were identified in each camera frame by filtering and applying an intensity threshold. Only peaks with an intensity at least four times the background were considered to be emitters. Subsequently, each emitter was localized by maximum likelihood estimation of a 2D Gaussian distribution (25). When peaks appeared during several consecutive frames within the same pixel, they were assumed to correspond to the same emitter, and the emitter images in these frames were summed before maximum likelihood estimation. Drift was corrected in each frame by subtracting the average position of the fiducial markers from the positions of the emitters in that frame. The localization uncertainty for each emitter was obtained from the Cramér-Rao lower bound of the maximum likelihood procedure (26). PALM images were generated by plotting a 2D Gaussian centered on each fitted position with a SD equal to the corresponding localization uncertainty. Only positions with a localization uncertainty <40 nm were used.
EMGM procedure
The EMGM procedure (Supporting Material) was implemented in MATLAB (The MathWorks). The initial values of the parameters that describe a mixture consisting of K components were estimated by deleting a component from the previously estimated mixture consisting of K-1 components and adding two new components that were generated from the deleted one (Supporting Material). Additionally, one new Gaussian component was generated from the background component of the previously estimated mixture. This was done three times for each of the original K-1 Gaussian components and the background component, resulting in a total of 3K initializations. In the case of K = 1, the initialization was done randomly three times. The procedure was stopped when the null hypothesis that the previously estimated K-1 component mixture is the correct one was fulfilled (Supporting Material). For this purpose, we simulated the distribution of likelihood increments when comparing the K-1 and K component models under the null hypothesis. This distribution is obtained by simulating 100 datasets assuming the K-1 solution, and applying EMGM on each dataset, for both K-1 and K mixture components. If the real likelihood increment had a p value <0.01 under the null hypothesis, it was assumed that the K-1 component solution is the correct one. Before analysis, the PALM data was split into overlapping 2 × 2 μm areas, and the EMGM analysis was performed on each area separately (Fig. S2). Afterwards, identical mixture components in different EMGM results were combined according to a criterion based on the correlation between their posterior probabilities (Supporting Material).
Results
EMGM
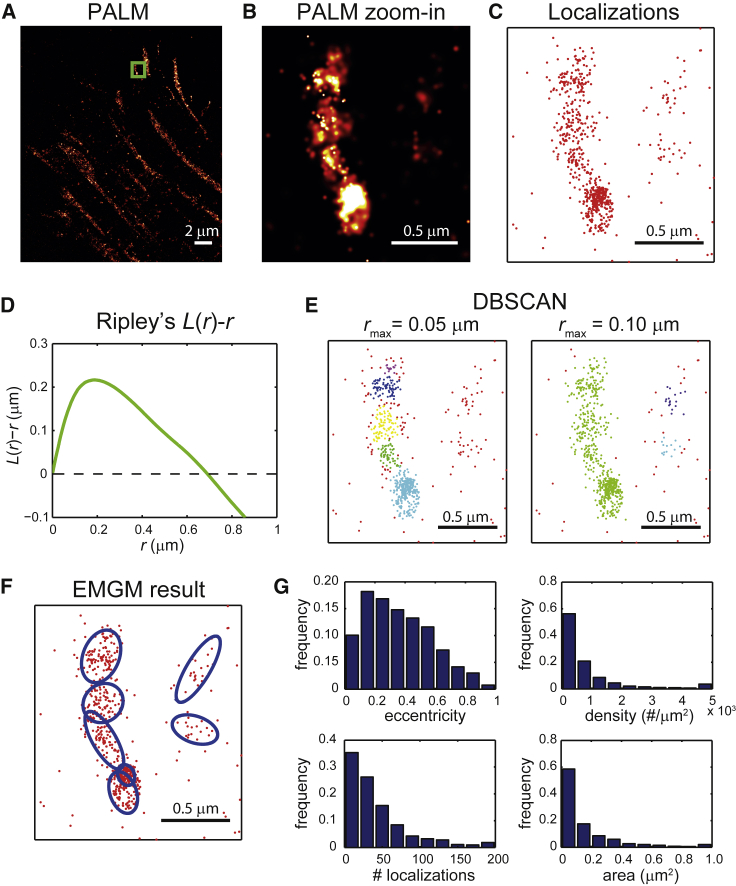
FAs display a substantial variety in size, shape, and density, and their substructure potentially as well. Quantifying the properties of the FA substructure with SMLM clustering methods is therefore challenging. Clusters in SMLM data are often characterized using the pair correlation function (27) or Ripley’s K(r) or L(r) function (28). These functions describe the density around a certain point as a function of the distance r from that point. As an illustration, we used PALM to image integrin β3 in a REF cell (Fig. 1 A). We used Ripley’s L(r)-r function (29) to analyze a subset of the data (Fig. 1, B–D). This function shows a peak ∼0.2 μm, indicating that the degree of clustering is highest on this length scale. However, it is difficult to interpret this result in terms of FA substructure properties, especially considering the heterogeneity in size and shape of the FAs themselves.
Figure 1.
Application of SMLM clustering algorithms to PALM data of FAs. (A) Given here is a PALM image of a fixed REF cell expressing integrin β3 labeled with mEos2. (B) Given here is a zoom-in PALM image corresponding to the green rectangle in (A). (C) Given here is a scatter plot of the mEos2 localizations corresponding to the green rectangle in (A). (D) Given here is Ripley’s L(r)-r as a function of r, obtained from the localizations in (C). (E) Shown here are clusters obtained from the localizations in (C) by DBSCAN. The minimum number of localizations was set to 10, and two values were chosen for the maximum search radius rmax: 0.05 and 0.10 μm. The different colors of the localizations indicate to which cluster they belong; the background localizations are red. (F) Shown here is a result of EMGM analysis of the localizations in (C). The red dots symbolize the localizations, and the blue ellipses the 2σ error ellipses of the components. (G) Histograms show the eccentricity b/a, localization density, number of localizations, and area πab of the 2σ error ellipses of the components obtained by EMGM from the complete PALM data set in (A). The rightmost bins in each histogram (except for the eccentricity histogram) contain all values within that bin and larger.
Such difficulties can be avoided by clustering methods that identify individual clusters based on criteria related to the local density of localizations, such as the nearest neighbor method (30) or density-based spatial clustering of applications with noise (DBSCAN) (31). We applied DBSCAN (32) to the same subset of the PALM data mentioned above (Fig. 1 E). One value for the DBSCAN search radius identified several substructures in the FA, whereas a larger value did not. However, the large search radius identified two clusters that were considered to be background by the small search radius. It is clear that DBSCAN can handle the heterogeneity in size and shape of FAs, but identification of FA substructures largely depends on the values used for parameters that are related to a localization density threshold. Such a threshold is challenging to define, because FA substructures exhibit a variety of localization densities and can be closely packed (Fig. 1, A and B).
The difficulties related to established SMLM clustering methods prompted us to develop an approach based on EMGM (15). The main assumption of EMGM is that FAs can be modeled by a mixture of bivariate Gaussian probability distributions (Supporting Material). After choosing initial values for the parameters of each Gaussian component, the posterior probability that a certain localization was generated from a certain Gaussian component is evaluated (i.e., the expectation step). The Gaussian component parameters are then reestimated using the new posterior probabilities (i.e., the maximization step) and the likelihood of the updated Gaussian mixture is calculated and checked for convergence.
To apply EMGM on SMLM data, we used a “greedy learning” approach (33) to initialize the parameters of the Gaussian components, and a model selection procedure based on hypothesis testing (34) to determine the number of components in the mixture (Supporting Material). However, the specific nature of SMLM data poses some additional challenges for EMGM. One problem is that not all localizations are necessarily part of the structure of interest, but can instead belong to a background. In the case of a simple uniform background, the EMGM algorithm can be readily adjusted (Supporting Material). Moreover, the localizations in SMLM data contain measurement uncertainties (35). This localization uncertainty can be described by a spatial probability distribution that is usually modeled as a Gaussian. EMGM can therefore be adapted by convolving the probability distributions that describe the mixture and the localization uncertainties (Supporting Material).
Evaluation of EMGM on simulations
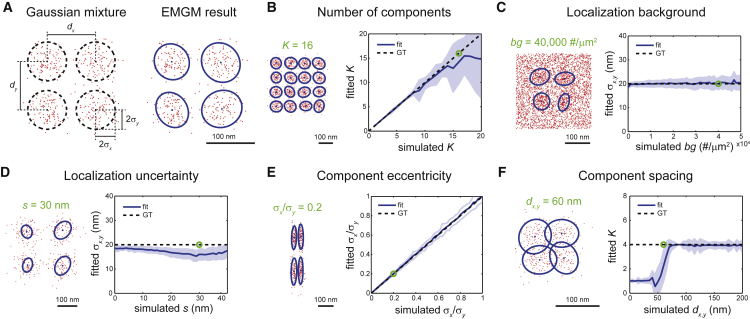
The performance of the EMGM algorithm adapted for SMLM data was evaluated and validated by applying it to simulated data. We simulated mixtures consisting of K closely spaced Gaussian components described by identical spatial probability distributions (i.e., 2D symmetric Gaussians with SD σx = σy = 20 nm) and containing an identical number of positions (i.e., 100) (Fig. 2 A, and Supporting Material). Such components have similar characteristics to nascent adhesions or, more speculatively, to the substructure of larger FAs.
Figure 2.
Evaluation of EMGM using simulated data. (A) On the left is an example of a simulated Gaussian mixture consisting of K = 4 components, each containing 100 localizations, described by a symmetric 2D Gaussian distribution with a SD σx = σy = 20 nm. The Gaussian centers are placed in a square grid with spacing dx,y = 100 nm. On the right is the EMGM result. The red dots symbolize the localizations. The blue dots symbolize the center positions and the blue ellipses symbolize the 2σ error ellipses of the components. (B) On the right, the average number of mixture components correctly identified by EMGM as a function of the simulated K. On the left is an example EMGM result for K = 16. (C) On the right is the average SD σx,y of the mixture components calculated by EMGM as a function of the simulated localization background density bg. On the left is an example EMGM result for bg = 40,000 #/μm2. (D) On the right is the average σx,y calculated by EMGM as a function of the simulated localization uncertainty s. On the left is an example EMGM result for s = 30 nm. (E) On the right is the average eccentricity σx/σy of the mixture components calculated by EMGM as a function of the simulated σx/σy. On the left is an example EMGM result for σx/σy = 0.2. (F) On the right is the average number of mixture components correctly identified by EMGM as a function of the simulated spacing dx,y. On the left is an example EMGM result for dx,y = 60 nm. The simulated Gaussian mixtures in (C–F) consist of K = 4 components, similar to (A). The dashed lines in (B–F) represent the ground truth, and the shaded areas represent the SD (n = 100).
First, we verified the performance of our proposed initialization scheme and model selection procedure. The results show that the simulated mixtures are correctly identified, provided K is <10 (Fig. 2 B; Fig. S3). Interestingly, simulations of random Gaussian mixtures that are closer to the experimental reality confirm this finding (Fig. S4). We used 3K initializations for a mixture with K components (Supporting Material). Increasing the number of initializations does not substantially improve the EMGM performance (Fig. S5).
Next, we simulated the effect of a uniform localization background density bg and a localization uncertainty s. The results indicate that the adapted EMGM correctly predicts σx,y for values of bg up to 25,000 #/μm2 when K = 4 (Fig. 2 C; Fig. S6). For larger values of K, the method performs well for bg values up to 10,000 #/μm2 (Fig. S7). Our EMGM approach also captures the effect of the apparent increase in σx,y due to localization uncertainties for values of s up to 30 nm (Fig. 2 D; Fig. S8). Unlike for the localization background, this limit does not seem to depend on the number of components (Fig. S9). Note that the largest values of s and bg included in these simulations are typically not encountered in good-quality SMLM data.
Because one cannot assume that the substructures of FAs are radially symmetric, the component shape should be accounted for by the EMGM algorithm. We simulated mixture components with decreasing σx and simultaneously increasing σy (Supporting Material). The results (Fig. 2 E) clearly show that the algorithm correctly predicts the changing eccentricity σx/σy. The adapted EMGM should also be able to distinguish closely spaced substructures inside FAs. Toward this end, we simulated Gaussian mixtures with a decreasing spacing dx,y between the component centers (Fig. 2 F, and Supporting Material). The adapted EMGM performs well when dx,y is >70 nm, or more generally when the relative spacing dx,y/σx,y is >4 (Fig. S10). A smaller dx,y (or dx,y/σx,y) results in a significant overlap in the spatial probability distribution of two adjacent components.
It should be noted that the results (Fig. 2) depend on the number of localizations that are contained by the components. The sensitivity of the EMGM algorithm strongly decreases for components containing ∼10 localizations (Fig. S11).
Application of EMGM on experimental data
To demonstrate the application of our EMGM algorithm, we made use of the SMLM data of a REF cell expressing mEos2-labeled integrin β3 (Fig. 1, B and C). Similar to DBSCAN applied with the small search radius (Fig. 1 E), EMGM also finds several FA substructures (Fig. 1 F). Moreover, EMGM identifies two structures on the right as well, as indicated by the DBSCAN result using the large search radius (Fig. 1 E).
We next proceeded to apply the EMGM algorithm on the whole PALM dataset (Fig. 1 A). Because the simulation results (Fig. 2 B) indicate that our algorithm works best for a small number of components, we reduce their number by applying a scanning procedure, consisting of splitting the original field of view into smaller overlapping areas, and by subsequently applying EMGM to each of these areas (Fig. S2). The size of these areas has to be chosen carefully, as clipping of mixture components should be avoided, while ensuring that only a few are included. Afterwards, the results are combined, by merging identical Gaussian components in overlapping regions based on the correlation between their posterior probabilities, while excluding Gaussian components that belong to structures that were clipped during the splitting procedure (Supporting Material).
EMGM characterizes FA substructures in terms of bivariate Gaussian probability distributions. The properties of such a distribution can be translated into more intuitive properties using the error ellipse, i.e., the line that describes a constant probability density. The major axis a and the minor axis b of an ellipse define its area and shape (Fig. S12). We therefore describe the FA substructure shape by the eccentricity b/a (similar to the definition above). To calculate the area, we choose the 2σ error ellipse, corresponding to twice the SD of the Gaussian distribution. This error ellipse defines the area in which there is a probability to find ∼95% of all localizations belonging to the mixture component. We pooled the area and eccentricity values of all identified components in our PALM data set (Fig. 1 G). Most components have an area <0.5 μm2 with a peak ∼0.1 μm2, and many exhibit some degree of eccentricity, with most values <0.8. The EMGM algorithm also returns the posterior probability of each localization belonging to a specific Gaussian distribution, which gives the total number of localizations of each FA substructure (Supporting Material). Making the simplifying assumption that the localizations are uniformly distributed within the 2σ error ellipse, this leads to a characteristic localization density. Most FA substructures have a localization density <2000 #/μm2, and contain <100 localizations (Fig. 1 G).
Integrin and paxillin
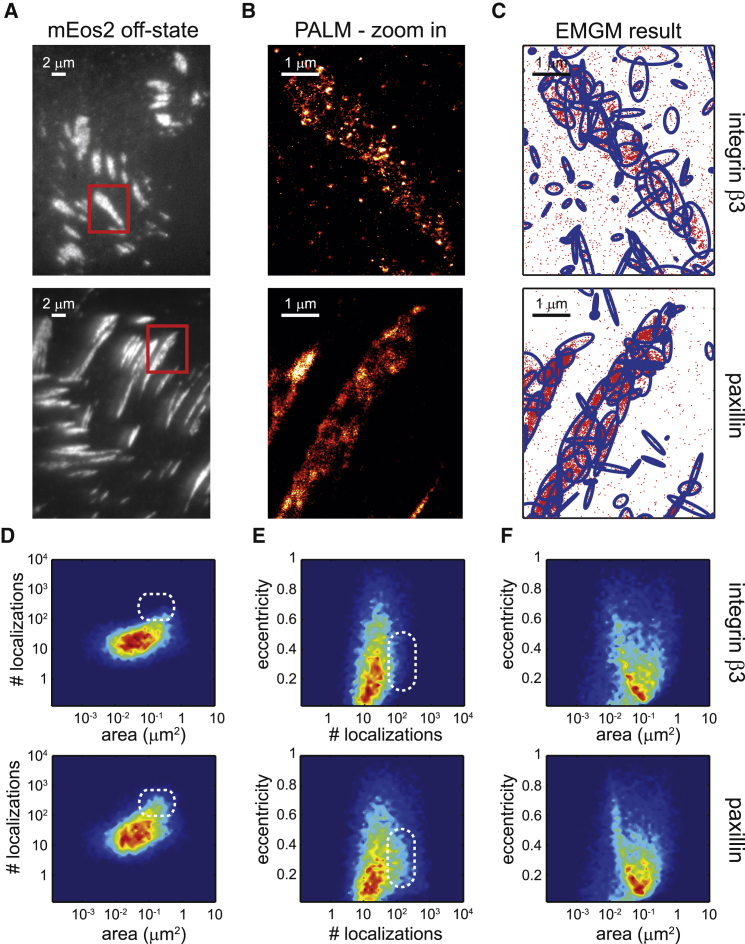
After the evaluation of the adapted EMGM, we applied our method to investigate the substructure of FAs in cells growing on often-used fibronectin-coated substrates. We used PALM to image fixed REF cells (n = 10) expressing paxillin or integrin β3 labeled with mEos2 (Fig. 3, A and B). To identify the FA substructure, we applied the adapted EMGM to each of these PALM datasets (Fig. 3 C). As discussed above, the properties of individual mixture components, defined as bivariate Gaussians, can be described by three parameters: eccentricity, area, and number of localizations. We plotted these quantities as a function of each other, for both paxillin and integrin β3 (Fig. 3, D–F). Most mixture components contain between 10 and 100 localizations, and have an area between 0.01 and 1 μm2 (Fig. 3 D). The components with the lowest number of localizations are mainly located outside the FA structure (Fig. S13). The paxillin case displays a slightly more pronounced tail toward components that contain more localizations (up to 1000 localizations). These components are situated within the FA structure (Fig. S14), explaining the visual difference between paxillin and integrin β3 (Fig. 3 B). When plotting the eccentricity as a function of the number of localizations (Fig. 3 E), it is again apparent that the paxillin FA substructures can contain more localizations than the integrin ones. Furthermore, the mixture components in both cases appear to be eccentric, with most values <0.7. The FA substructures containing fewer localizations appear to be somewhat more eccentric, a tendency that is more apparent in the paxillin case. A similar observation can be made when plotting the eccentricity as a function of the area (Fig. 3 F). The larger the FA substructure, the more eccentric it seems to be. Interestingly, both paxillin and integrin objects seem to have similar areas, with a peak ∼0.1 μm2.
Figure 3.
EMGM analysis of PALM data of integrin β3 or paxillin on fibronectin-coated substrates. (A) Given here are summed TIRF images of the mEos2 off-state of fixed REF cells expressing integrin β3 or paxillin labeled with mEos2, growing on fibronectin-coated substrates. (B) Given here are zoom-in PALM images corresponding to the red rectangles in (A). (C) Shown here is the result of the EMGM analysis of the PALM data shown in (B). The red dots symbolize the localizations, and the blue ellipses symbolize the 2σ error ellipses of the mixture components. (D–F) Given here is the result of the EMGM analysis of PALM data corresponding to different REF cells (n = 10): (D) number of localizations in each mixture component as a function of the area of its 2σ error ellipse, (E) eccentricity of the 2σ error ellipse of each mixture component as a function of its number of localizations, and (F) eccentricity of the 2σ error ellipse of each mixture component as a function of its area. The dashed white rounded rectangles in (D) and (E) are visual guides.
Nanopatterned substrates
The FA substructure properties (Fig. 3) have been obtained from REF cells growing on fibronectin-coated substrates, which do not have well-controlled binding sites (especially considering the presence of extracellular matrix proteins in the cell culture medium). It can therefore not be guaranteed that the observed FA substructure is innate; it might simply be reflecting how the integrin binding sites on the fibronectin-coated substrate are organized on the nanoscale level. Such difficulties in interpretation of the data can be avoided by making use of a substrate where the integrin binding site locations are precisely controlled. We have therefore made use of block-copolymer micelle nanolithography to pattern substrates with a quasi-hexagonal grid of 8-nm-diameter AuNPs (19, 20) (Supporting Material). The AuNPs are functionalized with cyclic arginyl-glycyl-aspartic acid peptides, using a flexible polyethylene glycol spacer. The area between the AuNPs is passivated with a polyethylene glycol layer, ensuring that integrins can only adhere to the peptides immobilized on AuNPs. This enables a more unambiguous interpretation of the observed FA substructure. We chose a 56-nm spacing between the AuNPs, which was shown to result in good cell adhesion (19). Furthermore, we also tested a 119-nm spacing, which poses more challenges for adhering cells (20).
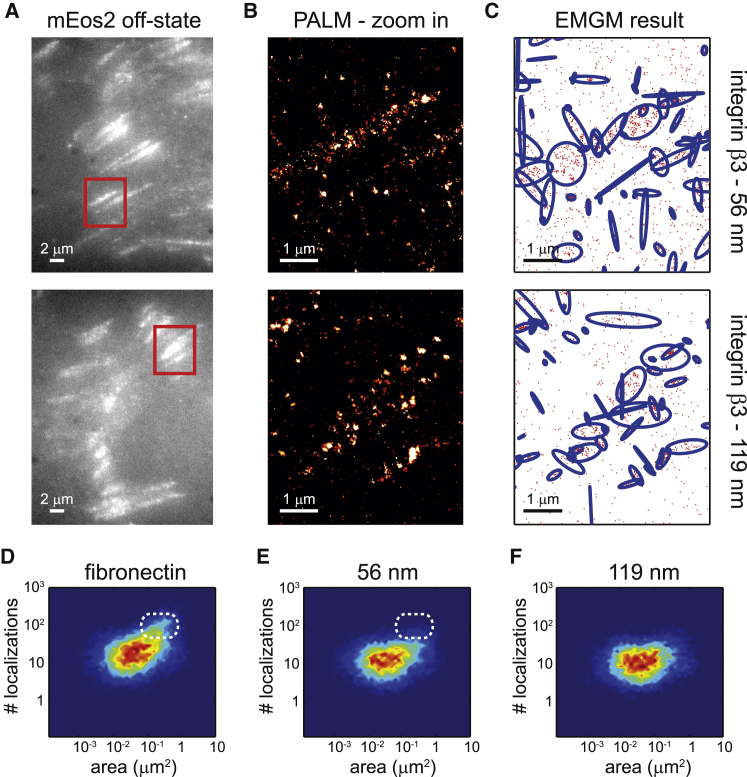
We again imaged fixed REF cells (n = 10) expressing integrin β3 labeled with mEos2 (Fig. 4, A and B). Next, we applied the adapted EMGM to each of the PALM datasets, to investigate the FA substructure (Fig. 4 C). We plotted the number of localizations as a function of the area, for both the 56- and 119-nm AuNP spacings (Fig. 4, E and F). The fibronectin case (Fig. 4 D) was added for comparison. It is clear that the objects on the fibronectin-coated substrate can contain up to 100 localizations, whereas the localization numbers on the 56-nm spacing substrate are generally below that level (Fig. 4, D and E). Interestingly, the FA substructure areas are very similar between both types of substrates, mostly between 0.01 and 1 μm2 (Fig. 4, E and F). The FA substructure observed on the nanopatterned substrates does not appear in contradiction with the results obtained from fibronectin-coated substrates.
Figure 4.
EMGM analysis of PALM data of integrin β3 on nanopatterned substrates. (A) Shown here are summed TIRF images of the mEos2 off-state of fixed REF cells expressing integrin β3 labeled with mEos2, growing on nanopatterned substrates with 56- or 119-nm spacing between the AuNPs. (B) Shown here are zoom-in PALM images corresponding to the red rectangles in (A). (C) Given here is the result of the EMGM analysis of the PALM data shown in (B). The red dots symbolize the localizations, and the blue ellipses symbolize the 2σ error ellipses of the mixture components. (D–F) Given here is the result of the EMGM analysis of PALM data corresponding to different REF cells (n = 10). The number of localizations in each mixture component is shown as a function of the area of its 2σ error ellipse, for (D) fibronectin-coated substrates (Fig. 3D), (E) nanopatterned substrates with 56-nm spacing, and (F) nanopatterned substrates with 119-nm spacing. The dashed white rounded rectangles in (D) and (E) are visual guides.
Isolated and overlapping mixture components
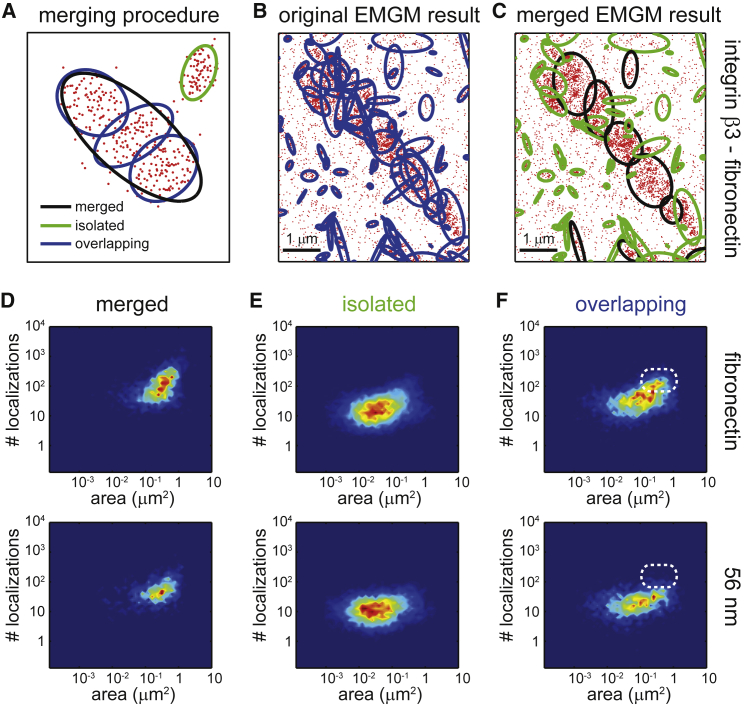
The interpretation of the EMGM results can be complicated (Figs. 3 C and 4 C). Especially inside dense and large structures, which visually appear to be FAs, one can observe several components that overlap, based on their 2σ error ellipses. The isolated mixture components, on the other hand, seem to correspond with smaller structures that could be nascent adhesions or focal complexes. We, therefore, performed a postanalysis step on EMGM results (Fig. 5 A, and Supporting Material). We split the mixture components into two categories: the ones whose 1σ error ellipse overlaps with at least one other 1σ error ellipse, called the “overlapping” components, and the ones whose 1σ error ellipse does not overlap with another one, called the “isolated” components. A new object can be calculated from a set of overlapping components, giving rise to a third category, called the “merged” components (Fig. 5 A, and Supporting Material). Application of this merging procedure on a previously obtained EMGM result (Fig. 3 C) shows that there are indeed several components that overlap (Fig. 5, B and C).
Figure 5.
Merging procedure applied on EMGM results for integrin β3. (A) Given here is an illustration of the concept of merging overlapping mixture components based on overlapping error ellipses. The red dots symbolize the localizations. The black/green/blue ellipses represent the 2σ error ellipses of the merged/isolated/overlapping mixture components. (B) Given here is an EMGM result for PALM data of a fixed REF cell growing on a fibronectin-coated substrate and expressing integrin β3 labeled with mEos2 (Fig. 3C). (C) Shown here is a result of the merging procedure applied on the EMGM result in (B). (D–F) Shown here is a result of the merging procedure applied on EMGM results for integrin β3 (Figs. 3D and 4E). The number of localizations in each mixture component is shown as a function of the area of its 2σ error ellipse, for (D) the merged components, (E) the isolated components, and (F) the overlapping components. The dashed white rounded rectangles in (F) are visual guides.
We applied the merging procedure on the EMGM results of REF cells (n = 10) expressing integrin β3 labeled with mEos2, growing on fibronectin-coated (Fig. 3 D) and 56-nm spacing nanopatterned (Fig. 4 E) substrates. As expected, on both types of substrate, the merged objects tend to have a larger area (up to 1 μm2) and contain more localizations (up to 1000 localizations) than the isolated and overlapping objects (Fig. 5 D–F). The isolated components exhibit a similar behavior on both substrate types (Fig. 5 E). Both cases exhibit FA substructures with an area between 0.01 and 0.1 μm2, containing <100 localizations. The overlapping components are also not showing much difference between both substrate types, although the ones on the fibronectin-coated substrate can contain more localizations (Fig. 5 F). Interestingly, the isolated and overlapping objects on the nanopatterned substrate also behave quite similarly (Fig. 5, E and F). The overlapping FA substructures are therefore not necessarily artifacts found by EMGM in a dense localization environment.
Discussion
We propose, to the best of our knowledge, a new way to explore the properties of unknown structures as observed by SMLM. Using EMGM, we interpret patterns in SMLM data as a mixture of bivariate Gaussians. This approach allows us to describe densely packed structures that can display strong heterogeneities in size, shape, and density, and is therefore well suited for investigation of the substructure of FAs.
However, application of EMGM to SMLM data is not without challenges. The result can be influenced by the choice of the initial values for the mixture component properties, and the number of components needs to be chosen as well. We identified an initialization procedure and a selection criterion for the number of components that gives good results for mixtures consisting of a small number of components (e.g., <10 for our simulated data). To allow analysis of larger numbers of components, we used a scanning procedure that consists of splitting the SMLM data into smaller overlapping areas, and performing EMGM on each area separately. It is important to note that, unlike some SMLM clustering methods, the EMGM approach essentially does not depend on the choice of a free parameter (except for the area size of the scanning procedure).
The properties of SMLM data pose challenges to the classic EMGM algorithm. One complication is the localization uncertainty, which leads to an overestimation of the SD of the Gaussian mixture components. An important contribution of this work is that we improved the EMGM approach to account for this effect. For reasonable localization uncertainties (e.g., <30 nm for our simulated data), we found that the adapted EMGM worked well. We would like to point out that the effect of localization uncertainties is ignored by most existing SMLM clustering methods. Besides localization uncertainty, we also adjusted the EMGM algorithm to account for the presence of a uniform localization background. The method was found to perform excellently for any realistic level of background (e.g., up to 10,000 #/μm2 for our simulated data).
To investigate the inner architecture of FAs, we performed SMLM imaging of FAs in fixed REF cells. We first explored the use of points accumulation in nanoscale topography (36) for imaging integrin β3 (Supporting Material). Our points accumulation in nanoscale topography data suggests that not all integrins are accessible for antibodies (Fig. S15). To avoid antibody labeling problems, we therefore opted for PALM. We imaged integrin β3 and paxillin in fixed REF cells on fibronectin-coated substrates. The EMGM algorithm allowed us to identify integrin β3 objects with a typical area in the range between 0.01 and 1 μm2, and containing between 10 and 100 localizations. Paxillin objects were found to have a similar area, but can contain more localizations, up to 1000. We attribute this difference to a treelike organization of the FAs, rooting from isolated integrin islands, and expanding toward the actin filaments due to cross-linking and multivalent binding of paxillin and other proteins to their recruiting components. The equivalent diameter of the smallest objects was found to be ∼100 nm (using the 2σ error ellipse area, which is 0.01 μm2 for the smaller objects). This indeed justifies the need for superresolution microscopy to investigate the inner structure of FAs. Most objects were found to exhibit a substantial eccentricity, with values down to 0.1. An algorithm that does not assume radial symmetry, such as EMGM, is therefore essential for the analysis of the FA substructure.
A fibronectin coating is often used to ensure good cell adhesion to the substrate. However, it is important to rule out that the observed FA substructure is a mere artifact of the binding sites presented by such fibronectin-coated substrates. We therefore repeated the experiments on substrates that were patterned with a quasi-hexagonal grid of functionalized AuNPs. Our EMGM algorithm identified integrin β3 objects with areas in the same range as on fibronectin-coated substrates, whereas the number of localizations was lower, typically not exceeding 100. The FA substructure observed on the nanopatterned and fibronectin-coated substrates do not contradict each other.
The EMGM results sometimes display strongly overlapping mixture components, which is mathematically perfectly possible, but difficult to interpret. One possibility is that the background within the FAs is more complex than a simple uniform distribution. This could lead to the background partially being characterized by some of the mixture components, whereas the others are actual FA substructures. Note that our scanning procedure already captures background heterogeneities on the scale of the scanned areas. Another possibility is that a bivariate Gaussian is not the most accurate model for the FA subunits. To a certain extent, a postanalysis step can provide more insight. We performed a merging procedure that describes FA substructures either as isolated Gaussian components, or a combination of several overlapping components. We hypothesize that a substantial set of the isolated components (areas between 0.001 and 0.01 μm2, and number of localizations between 10 and 100), correspond to focal complexes or nascent adhesions. The overlapping mixture components, which appear to belong to FAs, have areas and localization numbers in the same range as the isolated components. This suggests that the observed objects are indicative of the real FA substructure. The merged components have a maximal area ∼1 μm2 and contain up to 1000 localizations, which can be interpreted as an upper limit for the FA substructure.
We envisage several ways in which our EMGM approach could be extended or adapted to allow a systematic and detailed study of the inner architecture of FAs. Several FA proteins could be investigated in multicolor mode to assess their spatial relationship. In this context, it could be of interest to develop an extension of EMGM that allows us to investigate the colocalization of the mixture components. It would also be interesting to develop a 3D implementation of EMGM for the investigation of FA substructure in both the lateral and axial direction, as observed for instance by iPALM (18). It seems worthwhile to explore the possibility of incorporating models other than the Gaussian bivariate distribution, and other types of background besides the uniform one. Note that the effect of repetitive localizations on EMGM should be investigated, because photoactivatable fluorescent proteins can be localized more than once due to a phenomenon called “photoblinking” (37). Using transient transfection, a population of endogenous proteins will not be fluorescently labeled, and the labeled proteins might be overexpressed. Techniques such as CRISPR/cas9 can bring solutions to this problem (38).
Conclusions
We have used PALM to investigate FAs in REF cells growing on fibronectin-coated substrates and specifically biofunctionalized nanopatterned substrates, on which ordered patterns of nanoscale adhesive spots were provided. To quantify the FA subunit properties, we developed a method based on EMGM that accounts for localization uncertainty and background. Analysis of our PALM data indicates that integrin β3 and paxillin structures within FAs have areas between 0.01 and 1 μm2, contain 10–100 localizations, and can exhibit substantial eccentricities. We believe that our EMGM-based approach is generic enough for the investigation of various other SMLM imaged nanoscale structures as well, especially for closely packed protein structures, or objects that display strong radial asymmetries and differences in size and density.
Author Contributions
H.D., J.P.S., and A.R. conceived the study. H.D. and D.S. developed the adapted EMGM algorithm. H.D. performed the simulations. H.D., I.P., and L.F. prepared the samples. H.D. performed the PALM experiments. H.D. analyzed the simulated and experimental data. H.D., I.P., J.P.S., and A.R. wrote the manuscript. All authors reviewed and approved the manuscript.
Acknowledgments
The mEos2-paxillin-22 vector and the mEos2-Integrin-β3-N-18 vectors were kindly provided by Dr. Michael Davidson and Dr. Catherine Galbraith.
H.D., J.P.S., and A.R. acknowledge the support of the Max Planck-EPFL Center for Molecular Nanoscience and Technology. Parts of the research leading to these results have received funding from the European Research Council/ERC Grant Agreement no. 294852, SynAd. J.P.S. is the Weston Visiting Professor at the Weizmann Institute of Science and part of the excellence cluster CellNetworks at the University of Heidelberg.
Editor: Catherine Galbraith.
Footnotes
Supporting Materials and Methods, fifteen figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)31076-7.
Supporting Citations
References (39, 40) appear in the Supporting Material.
Supporting Material
References
- 1.Zamir E., Geiger B. Molecular complexity and dynamics of cell-matrix adhesions. J. Cell Sci. 2001;114:3583–3590. doi: 10.1242/jcs.114.20.3583. [DOI] [PubMed] [Google Scholar]
- 2.Zaidel-Bar R., Itzkovitz S., Geiger B. Functional atlas of the integrin adhesome. Nat. Cell Biol. 2007;9:858–867. doi: 10.1038/ncb0807-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Harizanova J., Fermin Y., Zamir E. Highly multiplexed imaging uncovers changes in compositional noise within assembling focal adhesions. PLoS One. 2016;11:e0160591. doi: 10.1371/journal.pone.0160591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Betzig E., Patterson G.H., Hess H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 5.Hu S., Tee Y.H., Hersen P. Structured illumination microscopy reveals focal adhesions are composed of linear subunits. Cytoskeleton (Hoboken) 2015;72:235–245. doi: 10.1002/cm.21223. [DOI] [PubMed] [Google Scholar]
- 6.Morimatsu M., Mekhdjian A.H., Dunn A.R. Visualizing the interior architecture of focal adhesions with high-resolution traction maps. Nano Lett. 2015;15:2220–2228. doi: 10.1021/nl5047335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rossier O., Octeau V., Giannone G. Integrins β1 and β3 exhibit distinct dynamic nanoscale organizations inside focal adhesions. Nat. Cell Biol. 2012;14:1057–1067. doi: 10.1038/ncb2588. [DOI] [PubMed] [Google Scholar]
- 8.Shibata A.C.E., Fujiwara T.K., Kusumi A. Archipelago architecture of the focal adhesion: membrane molecules freely enter and exit from the focal adhesion zone. Cytoskeleton (Hoboken) 2012;69:380–392. doi: 10.1002/cm.21032. [DOI] [PubMed] [Google Scholar]
- 9.Shroff H., Galbraith C.G., Betzig E. Dual-color superresolution imaging of genetically expressed probes within individual adhesion complexes. Proc. Natl. Acad. Sci. USA. 2007;104:20308–20313. doi: 10.1073/pnas.0710517105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Changede R., Xu X., Sheetz M.P. Nascent integrin adhesions form on all matrix rigidities after integrin activation. Dev. Cell. 2015;35:614–621. doi: 10.1016/j.devcel.2015.11.001. [DOI] [PubMed] [Google Scholar]
- 11.Tabarin T., Pageon S.V., Gaus K. Insights into adhesion biology using single-molecule localization microscopy. ChemPhysChem. 2014;15:606–618. doi: 10.1002/cphc.201301041. [DOI] [PubMed] [Google Scholar]
- 12.Deschout H., Shivanandan A., Radenovic A. Progress in quantitative single-molecule localization microscopy. Histochem. Cell Biol. 2014;142:5–17. doi: 10.1007/s00418-014-1217-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nicovich P.R., Owen D.M., Gaus K. Turning single-molecule localization microscopy into a quantitative bioanalytical tool. Nat. Protoc. 2017;12:453–460. doi: 10.1038/nprot.2016.166. [DOI] [PubMed] [Google Scholar]
- 14.Gardel M.L., Schneider I.C., Waterman C.M. Mechanical integration of actin and adhesion dynamics in cell migration. Annu. Rev. Cell Dev. Biol. 2010;26:315–333. doi: 10.1146/annurev.cellbio.011209.122036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bishop C.M. Springer; Berlin, Germany: 2006. Pattern Recognition and Machine Learning. [Google Scholar]
- 16.Shroff H., Galbraith C.G., Betzig E. Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics. Nat. Methods. 2008;5:417–423. doi: 10.1038/nmeth.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fuchs J., Böhme S., Nienhaus G.U. A photoactivatable marker protein for pulse-chase imaging with superresolution. Nat. Methods. 2010;7:627–630. doi: 10.1038/nmeth.1477. [DOI] [PubMed] [Google Scholar]
- 18.Kanchanawong P., Shtengel G., Waterman C.M. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arnold M., Cavalcanti-Adam E.A., Spatz J.P. Activation of integrin function by nanopatterned adhesive interfaces. ChemPhysChem. 2004;5:383–388. doi: 10.1002/cphc.200301014. [DOI] [PubMed] [Google Scholar]
- 20.Platzman I., Muth C.A., Spatz J.P. Surface properties of nanostructured bio-active interfaces: impacts of surface stiffness and topography on cell-surface interactions. Roy. Soc. Chem. Adv. 2013;3:13293–13303. doi: 10.1039/C3RA41579A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Geiger B., Spatz J.P., Bershadsky A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
- 22.Annibale P., Scarselli M., Radenovic A. Identification of the factors affecting co-localization precision for quantitative multicolor localization microscopy. Opt. Nanoscopy. 2012;1:9. [Google Scholar]
- 23.Deschout H., Lukes T., Radenovic A. Complementarity of PALM and SOFI for super-resolution live-cell imaging of focal adhesions. Nat. Commun. 2016;7:13693. doi: 10.1038/ncomms13693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pallarola D., Platzman I., Spatz J.P. Focal adhesion stabilization by enhanced integrin-cRGD binding affinity. BioNanoMaterials. 2017;18 [Google Scholar]
- 25.Mortensen K.I., Churchman L.S., Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ober R.J., Ram S., Ward E.S. Localization accuracy in single-molecule microscopy. Biophys. J. 2004;86:1185–1200. doi: 10.1016/S0006-3495(04)74193-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sengupta P., Jovanovic-Talisman T., Lippincott-Schwartz J. Probing protein heterogeneity in the plasma membrane using PALM and pair correlation analysis. Nat. Methods. 2011;8:969–975. doi: 10.1038/nmeth.1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Owen D.M., Rentero C., Gaus K. PALM imaging and cluster analysis of protein heterogeneity at the cell surface. J. Biophotonics. 2010;3:446–454. doi: 10.1002/jbio.200900089. [DOI] [PubMed] [Google Scholar]
- 29.Kiskowski M.A., Hancock J.F., Kenworthy A.K. On the use of Ripley’s K-function and its derivatives to analyze domain size. Biophys. J. 2009;97:1095–1103. doi: 10.1016/j.bpj.2009.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Baddeley D., Jayasinghe I.D., Soeller C. Optical single-channel resolution imaging of the ryanodine receptor distribution in rat cardiac myocytes. Proc. Natl. Acad. Sci. USA. 2009;106:22275–22280. doi: 10.1073/pnas.0908971106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Endesfelder U., Finan K., Heilemann M. Multiscale spatial organization of RNA polymerase in Escherichia coli. Biophys. J. 2013;105:172–181. doi: 10.1016/j.bpj.2013.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ester, M., H. P. Kriegel, …, X. Xu. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). pp. 226–231. http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.121.9220.
- 33.Verbeek J.J., Vlassis N., Kröse B. Efficient greedy learning of Gaussian mixture models. Neural Comput. 2003;15:469–485. doi: 10.1162/089976603762553004. [DOI] [PubMed] [Google Scholar]
- 34.Punzo, A., R. P. Browne, and P. D. McNicholas. 2014. Hypothesis testing for parsimonious Gaussian mixture models. arXiv 1405.0377.
- 35.Deschout H., Cella Zanacchi F., Braeckmans K. Precisely and accurately localizing single emitters in fluorescence microscopy. Nat. Methods. 2014;11:253–266. doi: 10.1038/nmeth.2843. [DOI] [PubMed] [Google Scholar]
- 36.Sharonov A., Hochstrasser R.M. Wide-field subdiffraction imaging by accumulated binding of diffusing probes. Proc. Natl. Acad. Sci. USA. 2006;103:18911–18916. doi: 10.1073/pnas.0609643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Annibale P., Vanni S., Radenovic A. Identification of clustering artifacts in photoactivated localization microscopy. Nat. Methods. 2011;8:527–528. doi: 10.1038/nmeth.1627. [DOI] [PubMed] [Google Scholar]
- 38.Ratz M., Testa I., Jakobs S. CRISPR/Cas9-mediated endogenous protein tagging for RESOLFT super-resolution microscopy of living human cells. Sci. Rep. 2015;5:9592. doi: 10.1038/srep09592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Busemeyer J.R., Wang Y.M. Model comparisons and model selections based on generalization criterion methodology. J. Math. Psychol. 2000;44:171–189. doi: 10.1006/jmps.1999.1282. [DOI] [PubMed] [Google Scholar]
- 40.Vinga S., Almeida J.S. Rényi continuous entropy of DNA sequences. J. Theor. Biol. 2004;231:377–388. doi: 10.1016/j.jtbi.2004.06.030. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.