Is Aggregate-Dependent Yeast Aging Fortuitous? A Model of Damage Segregation and Aggregate Dynamics

Abstract

During cytokinesis in Saccharomyces cerevisiae, damaged proteins are distributed unequally between the daughter and mother cells. The retention of these proteins is correlated with yeast aging. Even though evidence suggests that aggregates are retained due to an underlying molecular mechanism, the debate on whether an active mechanism is necessary for this asymmetry remains unsolved. In particular, passive diffusion and a bud-specific dilution remain as possible explanations. Here, a computational and mathematical model is provided to test whether passive mechanisms alone are sufficient to account for the aggregate distribution patterns and the aggregate kinetics observed in living cells. To this author’s knowledge, this is the most comprehensive model available on this subject and the only one combining key potentially essential passive-only mechanisms proposed in existing bibliography—namely, the geometrical effect of the dividing yeast cell on the diffusion of protein aggregates, and the possibility of aggregate binding and aggregate formation at different rates. Results suggest that although passive processes alone can reproduce certain averaged observables from experimental bibliography, they are insufficient to vindicate aggregate activity observed in living budding yeast cells. These results are complemented by showing that under basic forms of active quality control, discrepancies between the outputs of the model and experimental bibliography are reduced.

Introduction

Aging in unicellular organisms is strongly associated with asymmetric cellular division (1), asymmetrical distribution of damage (2, 3), or both (4). In asymmetrically dividing organisms as budding yeast Saccharomyces cerevisiae, this process gives rise to an “aging” and an “immortal” lineage. The aging lineage consists of an old mother cell with a decreased survival rate, whereas the immortal one of a new, healthy daughter cell having a longer lifespan and a full replicative potential (5, 6, 7) of 25–30 generations. Studies (4, 8, 9) have observed that the difference in the average lifespan between the two outcomes of yeast cell division is highly connected to the asymmetrical distribution of Hsp-104-associated protein aggregates between them. Indeed, oxidized proteins, such as Hsp-104-associated aggregates affect mortality of yeast cells by deteriorating their fitness and maintenance at late stages of the life cycle (7, 10, 11).

Despite being of vital importance in the understanding of aging, the mechanisms causing the asymmetry in the inheritance of Hsp-104-associated aggregates in budding yeast remain unclear. In particular, whether or not an active quality control (AQC) mechanism is necessary remains indecisive. This debate has transcended to symmetrically dividing organisms that divide damage asymmetrically, where it was recently suggested that neither fission yeast Schizosaccharomyces pombe (3) nor Escherichia coli (12) require active spatial quality control machinery. Indeed, in E. coli, although damage usually concentrates at the old pole cell (13), aggregates seemingly follow Stokes-Einstein diffusion and segregate asymmetrically as a consequence of crowding in nucleoids. Likewise, in S. pombe, where aggregates also undergo diffusion, asymmetric distribution of damage is facilitated by aggregate fusion.

Returning to S. cerevisiae, arguing in favor of the presence of an active quality-control machinery acting throughout budding yeast’s cytokinesis are the experimental studies (4, 9, 14, 15), which suggest a dependence on concentrations of compounds in the cytoplasm and on the actin-cytoskeleton. Mutated yeast cells without SIR2, a gene related to actin nucleation, show a more balanced distribution of damaged proteins among the two compartments after cell division (9, 14), although not showing any differences in the neck’s diameter. Additionally, when the formation of the actin-cytoskeleton is suppressed with Latrunculin-A, which binds to the actin molecules hindering their bonding, the segregation of Hsp104-associated proteins is hampered. Thus, experiments indicate that chemical reactions between the actin and the Hsp-104-associated protein molecules facilitate transport of aggregates away from the progeny. In addition to these studies, (16) suggests that the underlying mechanism causing asymmetric segregation is instead (active) confinement of the Hsp104-associated aggregates to the organellar surfaces (of the nucleus and the vacuole) inside yeast cells. This confinement isolates damaged proteins in inclusions, namely the IPOD and the JUNQ, which are themselves attached to the surfaces of these organelles, thus avoiding their crossing of the neck. Furthermore, attachment to mitochondria has also been claimed to contribute to the asymmetric inheritance of aggregates (17). More recently, (7, 18) discovered the existence of a protein deposit that accumulates misfolded proteins, thus favoring their aggregation. In (18), it was proposed that retention of the deposit inside the mother cell occurs as its precursors bind to the endoplasmic reticulum with the mediation of farnesylated YDJ1, predominantly to the structures close to the nuclear envelope.

The arguments against the necessity of an active quality control machinery to justify asymmetric segregation of damaged proteins were first presented in (19, 20). In (19), aggregate motion was tracked and concluded to be consistent with anomalous diffusion (subdiffusion due to confinement), with no directional bias. According to their observations, the 2D mean square displacement of aggregates behaves according to

$$\langle r^2\left(t\right)\rangle =4D{t}^{\alpha },\alpha <1,$$ (1)

where t denotes time, and D is the (constant) diffusion coefficient. In (19), they use this as an argument against active transport which, they argue, would be consistent with superdiffusion (α > 1) instead. Furthermore, it is suggested that the low concentration of aggregates in the bud is a consequence of the low probability of the aggregates’ trajectory to cross the neck and reach the bud. Hence, aging in yeast cells could be completely stochastic. This result was later complemented by a mathematical model presented in (21) in which aggregate concentration in both compartments (the mother and the bud) was approximated throughout cell division. They assumed a fixed number of aggregates with a fixed size and a fixed diffusion coefficient that was later observed to be potentially inaccurate. Indeed, more recently, (22) used both experiments and a mathematical model based on the work in (3) studying damage distribution in symmetrically dividing fission yeast, to suggest that—although passive as well—the main force behind the asymmetrical distribution of damage was aggregate fusion combined with the bud-specific dilution rate associated with polarized growth during division. Nevertheless, their mathematical model did not consider cross-compartment crossings—based on the experimental evidence from (19, 22)—and focused only on the establishment of asymmetrical distributions as a consequence of volume-based dilution rates affecting aggregate formation. Thus, it either assumed a mechanism of aggregate retention by the mother (and the daughter), or assumed that geometry was enough to account for the low number of crossings.

In this article, a computational and mathematical model is presented that aims to study the sufficiency of passive-only mechanisms. It is believed that this model can contribute substantially to the debate, as it relies on simpler experimental measurements than those required when testing in favor of active transport or aggregate retention in perinuclear or perivacuolar deposits.

To this author’s knowledge, it is the first to include key passive mechanisms and the most comprehensive one available. Furthermore, it relates single-division with lifecycle processes to study the impact of the asymmetrical distribution of damage on aggregate-dependent aging in budding yeast.

In the short-term component of the model, it is the aim here to reproduce single-division inner-cell aggregate kinetics. It is based on experiments that analyze aggregate dynamics at short timescales, as are those studying aggregation and damage distribution for one cell-division cycle after heat or oxidative stress. Moreover, it generalizes both the confined-diffusion-based models in (19, 21) and the aggregate-creation/fusion models introduced in (3, 22).

The long-term component of this model is based on experimental studies observing aggregate-dependent aging and damage accumulation in perturbed or unperturbed wild-type (WT) cells over several generations. It studies consistency between single-cell-division observations and longer timescale data such as expected divisions before senescence or death and damage accumulation/retention over several generations.

It is shown here that whereas passive-only mechanisms—as introduced in the existing literature—can reproduce the experimental data used to defend their sufficiency, notable differences remain between the results from the purely passive model and other experimentally quantified observables. More specifically, the rate of aggregate movement observed between the two compartments (in terms of the average amount of crossings) under the passive-only hypothesis, is nearly an order-of-magnitude higher than it has been measured in the experiments in (19, 22). These differences are improved when introducing a very small (possibly undetectable) degree of aggregate motion bias toward the mother cell, as would be the case under an infrequent active transport (14, 15), or confinement to regions close to organelles (16) or to the cell’s membrane (18). This result points toward the necessity of an active quality-control mechanism, enhanced by passive processes, to justify the kinetics and the degree of asymmetry in the segregation of damaged proteins observed in real-life budding yeast cells.

Materials and Methods

The single-division cycle, passive-only model

To study aggregate kinetics and their distribution during cytokinesis, a short-term component of the passive-only model was constructed. It is schematized in Fig. 1 A together with the key passive mechanisms that are incorporated—namely, that aggregates follow a diffusion process (19) and may bind on collision, grow in size, appear at different rates depending on their compartment, and exhibit different diffusion rates depending on their volume (3, 22).

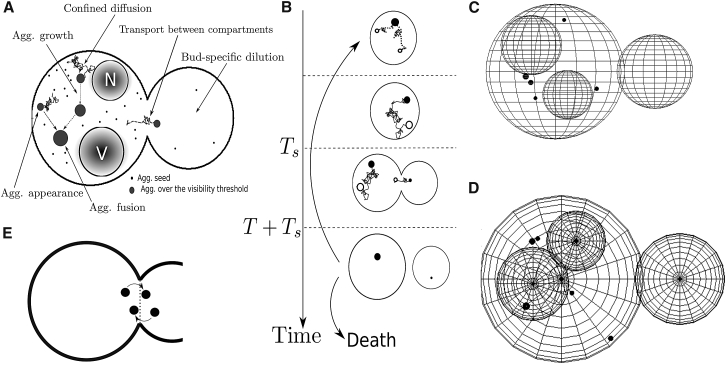
Figure 1.

The passive-only model. (A and B) Schematic representations of the model’s short-term and long-term components. (C and D) Snapshot of the model’s single-division cycle simulation. (E) Example of a crossing of the neck.

In the 3D model, aggregates are either generated at the beginning (a number N) or appear at the mother or bud compartments with the constant rates 1/τ_m and 1/τ_d. They have an initial radius rⁱ_a, which represents the threshold of detection, the minimum aggregate size for which experimental tracking is possible. These aggregates undergo diffusion with a rate D(r_i(t)), where r_i(t) is the radius of aggregate i at time t, inside a domain consisting of two spheres (mother and daughter cells) of radii r_m and r_d(t), respectively, joined by a neck of length l_n. The bud’s radius grows with a constant rate until it reaches its final value r_d(T) at the end of cell division (which happens after a time T). For the results shown in this article, the two organelles of largest size are considered: the vacuole and the nucleus, both static and with radii r_v, r_n, respectively.

Fusion occurs, upon aggregate collision, with a probability p_b. Moreover, aggregates grow (in volume) with a constant rate C_c, which is taken to be 4π/3(rⁱ_a)³/τ_c for consistency with the appearance rate (τ_c is either τ_m or τ_d, depending on the compartment). Continuous aggregate growth relates to the observations in (7), showing that aggregates form and grow progressively, rather than collapsing at advanced ages. In the Supporting Material, equivalent results are presented for a variant of the passive-only model where the rate of growth is proportional to the surface area of the aggregate. I show that under appropriate parameter conversions the conclusions remain the same.

The lifecycle passive-only model

The long-term component of this passive-only model aims to reproduce aggregate-dependent aging dynamics in budding yeast over many generations. For this, I look at damage in cells throughout the entire lifecycle (5), which is composed of several divisions (all following the short-term single-division dynamics introduced above), together with a time between divisions T_s (taken from (23)), in which it is assumed that aggregates simply grow, appear, and bind with the same rates as during cytokinesis. It is assumed that death of cells occurs after N_death divisions, which is deduced from (7, 8). The process follows the scheme presented in Fig. 1 B.

The active quality control variants of the passive-only model

Three extensions of the passive-only model are also presented here, which implement the active quality control mechanisms proposed in the experimental studies in (9, 16, 18). In the first, aggregate motion has a small bias toward the mother’s pole, which represents actin-driven transport. At each time step, with a probability p_s, movement in the x-coordinate in the direction of the bud is reversed, so that aggregates move only in the direction of the mother cell.

In the second, aggregate motion is confined when reaching the periphery of the nucleus or of the vacuole, which can account for organelle-associated confinement. When the center of the aggregate lies at a distance smaller than d_c from the boundary of the organelle, then, every minute, they are to remain confined to their surroundings with a probability p_c.

In the third, aggregates adhere to the cell membrane and remain trapped for a random time, which aims to represent adhesion to the endoplasmic reticulum. More precisely, when aggregates collide against the cell membrane, they attach with a probability p_a and remain stuck every passing minute with probability p_w.

The probability of confinement or attachment is here defined with respect to a minute-based timescale (in contrast to seconds or to the time-step length δt) to facilitate experimental measurements aiming to validate these models.

Model parameter values

The default parameter values that were used to obtain the results in this article were provided by T. Nyström (personal communication), deduced from (3, 22, 23), or carefully calibrated, in the case of AQC, to match experimental results. All parameter values and the references from which they were derived are gathered in Table S1. Bud-specific dilution is taken into account by assuming τ_d to be larger than τ_m by 10-fold.

Numerical simulations

Single-division cycle aggregate dynamics and distribution. The numerical algorithm for the simulation of aggregate dynamics in the short-term, single-division cycle component of the passive-only model is described in the Supporting Material. In Fig. 1, C and D, two perspectives of an instant from a simulation are shown. Throughout the simulations of aggregate kinetics during a single division cycle, statistics are tracked that can be used as a reference for experimental work, i.e., the number of aggregates, the total aggregate volume, the mean square displacement (MSD), and the number of cross-compartment crossings in each direction. For the latter, a crossing is only considered when the entire aggregate (not just its center) passes from one compartment to the other (Fig. 1 E).

Lifecycle damage accumulation and aggregate dynamics. The simulations of the long-term component of the model—aiming to reproduce aggregate-based yeast aging patterns—are detailed in the Supporting Material. After each division cycle is complete, relevant statistics are tracked for comparison with experiments (aggregate volume, aggregate number, probability of inheritance of at least one aggregate and of the largest aggregate—if it exists—by the daughter and the number of crossing events in each direction), as well as the number of aggregates in the mother and their radii to start the next division cycle.

Mathematical analysis and validation of simulations

The work from (24, 25, 26, 27, 28) provides a framework to study transport between two domains analytically. Using their results, aggregate dynamics are estimated throughout the cell-division cycle with a system of ordinary differential equations (ODEs). A similar mathematical model was presented recently in (21). Here, their approach is extended to include fusion and appearance of new aggregates.

The mathematical model designed and used is detailed in the Supporting Material. The system of ODEs in Eq. S2 is numerically integrated by using an explicit method to corroborate the results of the stochastic simulations of aggregate dynamics during the single-division cycle. This is an accurate approximation of the short-term component. It could also provide an upper bound of the mother cell’s aggregation levels for the long-term component over many generations.

Results

In this section, the results obtained from the passive-only model (the short and long-term components) and from its variants are shown, and these offer direct comparison with relevant experimental data gathered from available bibliography. In the case of the single-division cycle (the short-term) component, some of these results are complemented and validated with the approximations calculated from the system of ODEs in Eq. S2 in the Supporting Material.

The passive-only model is shown to be able to reproduce results in agreement with observables from experimental and modeling work defending the sufficiency of passive-only mechanisms. Nevertheless, it is observed that the average number of cross-compartment crossings under the passive-only assumption remains substantially higher than its experimental counterpart. This result is sustained at short and long timescales and under a wide range of the relevant parameters and thus unlikely to be atypical and a consequence of the model’s simplifications.

These differences can be improved when introducing basic, sporadic active-quality-control.

Single-division and passive-only; agreement with averaged observables from experiments supporting passive-only mechanisms and from other experimental and modeling work

Aggregate mean square displacement

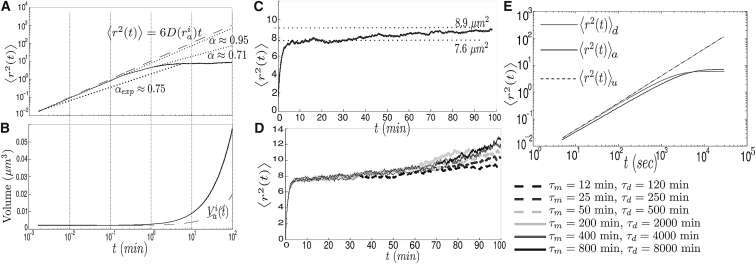
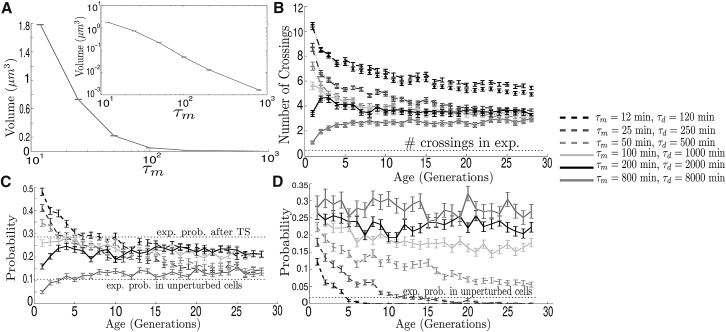
In ((19), see Figure 2), the aggregate MSD exponent α was approximated to be ∼0.75 when tracking aggregate movement after heat-induced aggregation from a 30-min temperature shift (TS) from 30° to 42°C.

Similarly, in the passive-only model, the degree of subdiffusion under high aggregation rates corresponds to α $\simeq$ 0.95 at short timescales and α $\simeq$ 0.71 at intermediate timescales (Fig. 2 A)—although Eq. 1 is no longer valid given the nonconstant aggregate volumes.

Figure 2.

MSD of aggregates in the passive-only model. (A and B) Log-log plot of the MSD of one aggregate (top) and the volume of the same aggregate for which the MSD was computed (bottom). (Dashed lines) Shown here is the unconstrained MSD of an aggregate of radius rⁱ_a (top) and to the volume of one aggregate with initial radius rⁱ_a in the absence of fusion events (bottom). (C) Same as Fig. 2A. (D) Same as Fig. 2C for different rates of appearance and growth of aggregates. (E) Log-log plot of the MSD of a particle in 2D undergoing unconstrained diffusion 〈r²(t)〉_u, diffusion inside an empty cell 〈r²(t)〉_d, or diffusion inside a cell with a vacuole 〈r²(t)〉_a. In all three cases, D = 1 × 10⁻³. In (A) to (C), N = 5, δt = 0.1 s, τ_m = 12 min, and τ_d = 120 min. In (D), N = 1 and δt = 0.25 s; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

Here, a more precise explanation is provided to what is referred to in (19) as “diffusion with a small degree of confinement” by showing the impact of both the geometry and the aggregate fusion and growth, on the MSD.

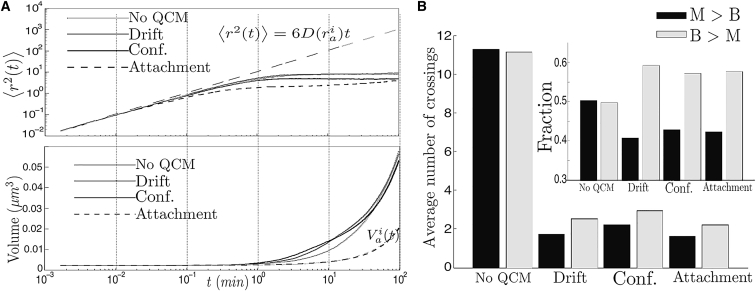
As observed in Fig. 2, A and C, the MSD is slowed at intermediate and long timescales as a consequence of the confined domain. Moreover, it first stabilizes at ∼7.6 μm² before rising to 8.9 μm² once cross-compartment transport is no longer rare. This transition occurs after ∼35 min, which is close to the mean first passage time, 1/κ_m (see the Supporting Material), of an aggregate of radius rⁱ_a (∼32 min).

In Fig. 2, A and B, it is emphasized that not only do barriers have a strong effect on the aggregates’ movement, but on the fusion and growth as well. At intermediate and large timescales, the average volume of the aggregate rises above the constant growth of volume under the absence of fusion. This effect is corroborated in Fig. 2 D, where the MSD is significantly slowed as the rate of aggregation increases. If the rate is low, so that fusion events are rare and growth is reduced, the MSD of initially equally sized aggregates can rise to values at ∼13 μm² after 100 min as a result of a reduction of compartmental retention by the mother. In Fig. S1, the dependence of the MSD is shown on the simulation parameter δt to emphasize that these results are not incidental.

In two dimensions, the effect of barriers and obstacles on the diffusion of particles can be studied analytically (16, 29, 30, 31, 32). This procedure is detailed in the Supporting Material.

Indeed, by representing the cell as a 2D empty disk or as an annulus (when considering only the vacuole), the effect of constraints (the cell membrane and the organelles) can be examined upon the MSD of the aggregates. One observes (Fig. 2 E) that subdiffusion can appear simply as a consequence of constraints, becoming stronger (at short and intermediate timescales) when more barriers are considered.

Asymmetric distribution of aggregate volume and aggregate concentrations during yeast cell division

The passive-only model is shown to be able to reproduce the observations derived from previous modeling approaches in (19, 21, 22). Additionally, in the Supporting Material, possible limitations are mentioned that each of these models can have when on their own.

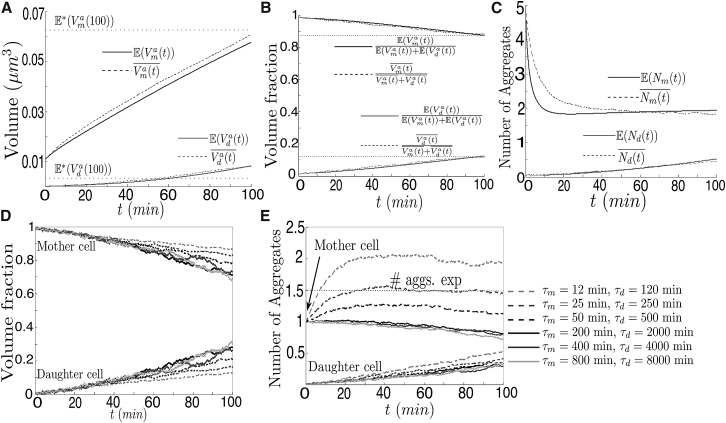
In Fig. 3 A, the time-dependence of aggregate volume is shown for the short-term component of the passive-only model. By comparing the slopes of both curves, it can be inferred that the main drivers behind the asymmetrical distributions are the different rates of growth of existing aggregates and of the appearance of new aggregates in both compartments (bud-specific dilution as proposed in (22)). Because this rate is constant, the function resembles a straight line. If the rate of growth increases in proportion of the surface of the aggregate, the shape of this function rather resembles an exponential (see the Supporting Material). If, as in the model used in (22), no compartmental crossings are assumed, at the end of cell division aggregate volume would be overestimated inside the mother cell by nearly 6% and aggregate volume underestimated inside the daughter by nearly 65%. This is shown by the values of ${\mathbb{E}}^{\text{∗}}\left(V_m^a\left(100\right)\right)$ and ${\mathbb{E}}^{\text{∗}}\left(V_m^a\left(100\right)\right)$ in Fig. 3 B, which denote the aggregate volume in each compartment under no-transport (a closed neck) at the end of the division cycle when numerically integrating the system of ODEs in Eq. S2 in the Supporting Material.

Figure 3.

Aggregate kinetics from the short-term component of the passive-only model. (A–C) Total aggregate volume, fraction of the total aggregate volume, and number of aggregates inside the mother (dark shaded) and the daughter cell (light shaded). (Continuous line) Shown here is the analytical prediction when numerically integrating Eq. S2 in the Supporting Material. (Dotted line) Numerical average from the stochastic simulations of the short-term component of the model. (D and E) Same as (B) and (C) for different rates of appearance and growth of aggregates. (A–C) N = 5, δt = 0.1 s, τ_m = 12 min, and τ_d = 120 min. In (D) and (E), N = 1 and δt = 0.25 s; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

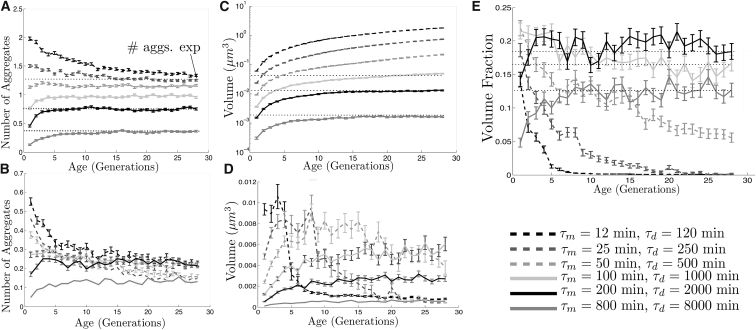
Fig. 3, B and D, shows aggregate volume concentrations in both compartments for different aggregation rates and different N. The initial number of aggregates does not impact strongly the asymmetrical distribution of volume due to the frequency of movement between compartments. On the contrary, aggregation rates (Fig. 3 D) have an important impact on the degree of asymmetry, even though their ratio among compartments is kept constant (τ_d = 10 × τ_m). At high rates (τ_m = 12, τ_m = 12 min), the fraction of volume inside the mother after 100 min is ∼0.88, which is close to the results of the models in ((19), see Figure 7 B) and ((21), see Figure 2). The effect of variations in the diffusion coefficient is weaker under these conditions, because an increase by 10-fold or a reduction by two orders of magnitude varies the fraction of volume in the mother by a maximum of 8% (Fig. S3). At lower rates, resembling those in unperturbed cells, aggregated cross-compartment transport reduces substantially the damage asymmetry by nearly 20% (Fig. 3 D). Under these conditions, diffusion should be slowed to a fair amount (as in (19)) to avoid aggregate escape from the mother, and to maintain a strong asymmetrical distribution of damage.

Number of aggregates during yeast cell division

In Fig. 3 C, the time dependence is shown of the number of aggregates during a single-cell-division cycle. The underestimation of fusion in the stochastic numerical simulations is a consequence of the discretization of time (and the time-step size δt = 0.1 s), given that possible contacts might have been overlooked here. This is highlighted in Fig. S1. The discrepancy disappears at longer timescales where the number of aggregates is smaller, their size is bigger, and their diffusion coefficient decreases. Indeed, at the end of the simulation, both approaches predict that there will be approximately two aggregates in the mother cell and nearly one-half in the daughter.

Fig. 2 A in (18) describes how aggregate deposits in unperturbed WT cells frequently merge. Similarly, Fig. 2 L in (22) shows that fusion events drop aggregate numbers from five to two in the first minutes of cell division after a TS from 30° to 38°C. Moreover, the experimental observations in (3) suggest that not only is aggregate fusion frequent but that it is the main driver of the asymmetrical division of damage in fission yeast. Indeed, aggregate fusion in the passive-only model is very common, as attested by the sharp drop in the number of aggregates from five to two in <10 min. In Fig. 3 C, unlike Figs. 2 L and 3 F in (22), the average number of aggregates in the mother at the end of cell division converges to 2 rather than a value close to 1.5. This is a consequence of the high aggregation rate, because the average time of fusion of “newborn” aggregates with the largest aggregate is larger or equal to the average time of appearance of new aggregates. When having only one initial aggregate (and the same appearance and growth rates), this result is unaltered (Fig. 3 E for τ_m min). At lower rates, resembling those in unperturbed cells, the number of aggregates in the mother can converge to a value close to 1 (consistent with Fig. 2 A in (18), where more than one aggregate in unperturbed cells was rare) or continuously decrease until fusion becomes rare and the number of aggregates in the mother and the daughter depend more strongly on cross-compartment movement between the two domains (Fig. 3 E for τ_m ≥ 25 min).

Single-division and passive-only; disagreement with experimental observables

Average number of cross-compartment crossings during a single-cell-division cycle

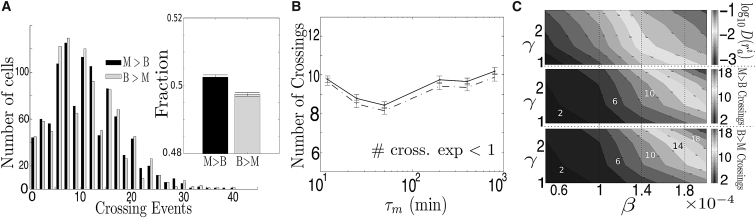
In ((19), see Figure 1), the average number of cross-compartment crossing events per single-cell-division cycle was measured to be close to 0.25 in the case of mother to bud and 0.15 in the case of bud to mother. These measurements were performed after a 30 min TS from 30° to 42°C. Likewise, in (22) (and see Fig. S6), it is shown that only 10–30% cell divisions exhibited bud-to-mother transport after two TS from 30° to 38°C and from 30° to 42°C. In the passive-only model, in a cell with initially five aggregates of small size (as in Fig. 1 in (19)) and with only two aggregates after fusion events in the first 10 min, the average amount of crossings is two orders-of-magnitude higher than reported in ((19), see Figure 4 A). Indeed, the average number of crossings in each direction is 11.16 (B > M) and 11.27 (M > B), and there are runs in which they reach values >30. Moreover, crossing events are so common that there is almost no bias with respect to the direction (Fig. 4 A, inset), showing that most aggregates undergo multiple compartment exchanges during a single-cell-division cycle.

Figure 4.

Differences between the outputs of the passive-only model and experimental observations. (A) Histogram of the total number of cross-compartment crossing events from mother to bud (M > B) and from bud to mother (B > M). (A) (Inset) Fraction of total cross-compartment events in each direction. (B) Average number of crossing events M > B (line) and B > M (dashed line) after a cell division cycle as a function of the parameter τ_m. (C) Logarithm of the diffusion rate of an aggregate with radius rⁱ_a (top), number of crossing events from mother to daughter (middle), and from daughter to mother (bottom) for different values of β and γ after a cell division cycle. In (A), N = 5, δt = 0.1 s, τ_m = 12 min, and τ_d = 120 min. In (B) and (C), N = 1, δt = 0.25 s, and τ_m = 12 min; in (C), τ_d = 120 min; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

It was observed in (22) and Fig. S6 that the number of crossings significantly increased when the TS was raised from 38° to 40°C to hamper polarized growth. In both cases though, the total amount of crossings remained under one event per cell division. Although temperature has a strong effect in this observable—most likely due a decreased mean escape time from the bud as a consequence of its smaller volume and increased diffusion and aggregation—it is unlikely that passive-only responses to variations in temperature can account for the difference between the results of the model and those from experiments. This is demonstrated in Fig. 4, A–C, where the differences remain under strong variations in the initial number of aggregates and in the appearance and growth rates, and also under variations in the diffusion coefficient (although as a default value, the one measured in (22) was used).

Moreover, the difference with experimental results is unaltered under reasonable values of the time-step size (see Fig. S1)—and thus is unlikely to be a consequence of multiple crossings in the event of one cross-compartment displacement.

It is recalled that all aggregates in the simulations have sizes larger than or equal to the threshold of visibility rⁱ_a = 0.08 μm (19, 22), which is a conservative choice known to be larger than the experimental limitations (T. Nyström, personal communication). Hence, the difference between the number of crossings in this work and in experiments is also not a consequence of very small aggregates that would otherwise be undetectable.

Long-term aggregate dynamics: damage accumulation over a lifecycle; comparison with experiments and qualitative dependence on aggregation rates

In Figs. 5 and 6, results are shown of the long-term component of the passive-only model—in which the accumulation of damage is tracked in cells over many divisions—for various appearance and growth rates 1/τ_m and 1/τ_d. Low rates (τ_m = 200 min, τ_m = 800 min) are approximations of aggregation rates in unperturbed cells ((7), see Figure 1 B), whereas high rates (τ_m = 12 min, τ_m = 25 min) are approximations of aggregation rates in heat-exposed or stress-induced cells.

Figure 5.

Long-term dynamics of the model. (A–D) Number of aggregates and total aggregate volume inside the mother cell (top) and inside the daughter cell (bottom) at the end of the cell division. (E) Fraction of total aggregate volume inside the daughter cell at the end of cell division. Error bars correspond to the SE. In all simulations, δt = 0.5 s; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

Figure 6.

Long-term aggregate dynamics. (A) Total aggregate volume inside the mother cell at the end of the 28th division. (Inset) Same as in (A), but in log-log scale. (B–D) Number of crossing events from mother to bud (continuous line) and from bud to mother (dotted line); probability of inheritance of at least one aggregate by the daughter cell at the end of cell division (C); and probability of inheritance of the largest aggregate by the daughter cell, if it exists (D), as a function of the mother’s age (in generations) for different rates of appearance and growth of aggregates. Error bars correspond to the SE. In all simulations, δt = 0.5; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

Aggregate volume, concentration, and numbers throughout the lifecycle

In the long-term component of the passive-only model aggregate volumes, numbers and concentrations depend qualitatively on the parameter τ_m.

It has been discussed in experimental bibliography how oxidative damage gradually accumulates inside cells with passing age (4, 7) and how it generally concentrates into a single aggregate deposit (18, 22). For small values of τ_m (<100 min), aggregate volume inside the mother cell grows with age at an almost constant rate (Fig. 5 B). With respect to the aggregate volume inherited by the daughter, the function rises at short ages to then drop to nearly zero (τ_m = 12 min, 25 min) or to small values (τ_m = 50 min) once a large aggregate with slower diffusion establishes (Fig. 5 A). The aggregate rarely crosses the neck and, due to its size, has a big probability of fusing with smaller aggregates before the latter pass to the bud. This is confirmed in Fig. 5 E where, for small τ_m (and τ_d), the fraction of volume inherited by the daughter drops to values under 0.05 after 28 generations.

For values of τ_m over the threshold of ∼100 min (which is the duration of cell division and which resemble those in unperturbed cells), aggregate volume inside the mother cell converges to a limit value. Furthermore, both the volume and the fraction of volume inherited by the daughter cell rise in the first generations (small aggregates accumulate), to later stabilize after the establishment of intermediate-sized aggregates. It is possible that at longer timescales these curves will decrease again to values close to zero, after large aggregates become predominant, mimicking the behavior of their higher-rate counterparts, which is best displayed by the curve for τ_m = 50 min. However, this appears to be inconsistent with the number of aggregates (shown in Fig. 5, A and B)—which appears to settle in both compartments to an added value ≤1—and with the total aggregate volume (in Fig. 5 C)—which converges to a limit value as well.

It is further confirmed that the transition of gradual accumulation of damage versus stabilization occurs close to τ_m = 100 min by observing in Fig. 6 A that an inflection point of the curve occurs in the neighborhood of this quantity. In the case of growth proportional to the surface area, the transition occurs at ∼τ_m = 250 min—which is reasonable, considering that aggregate growth is exponential.

Probability of inheritance of at least one aggregate by the bud

The probability that a daughter cell inherits at least one aggregate was measured in Fig. 4 G in (9) to be close to 0.3—following a TS from 30° to 42°C—and to be ∼0.10 in WT unperturbed cells ((18), see Figure 3 C).

In Fig. 6 C, it is shown that for values of τ_m < 100 min, the probability drops as the largest aggregate increases in size and its capacity of crossing the neck decreases. Afterward, it stabilizes at values representing the event where small aggregates avoid collision with the largest one inside the mother and either escape to the daughter (if generated in the mother) or remain inside of it (if generated in the daughter).

For values above or equal to the threshold occurring at τ_m $\simeq$ 100 min, the functions rise as a consequence of the accumulative probability of the daughter cell creating an aggregate or of inheritance of the unique aggregate (see Fig. 5 A) to later stabilize at limit values that depend on the ratio of the volumes, the ratio of the appearance rates, and of the time T. In both cases (aggregate and inheritance), most cells (at least 75%) are born aggregate-free and with a probable full replicative lifespan. Moreover, depending on the aggregation rate, the probability of a daughter cell containing at least one aggregate lies within the range 0.14–0.21 for mature mother cells (>10 generations old). The lower bound (τ_m = 800 min) is close to the estimate in (18), whereas the upper bound (τ_m = 12 min) is close to the one in (9) after a TS.

Probability of inheritance of the largest aggregate by the bud

Given a positive number of aggregates, the probability that the largest one is inherited by the daughter was approximated in ((18), see Fig. 3 B) to be ∼0.02 for unperturbed WT cells. It is shown in Fig. 6 D that, once more, there are two different behaviors, depending on the parameter τ_m. In the first (for values smaller than 100 min), the probability drops gradually closer to zero as the largest aggregate increases in size and its capacity for crossing the neck is reduced. In contrast, for values of τ_m over the threshold, and resembling those in unperturbed cells, the probability of the existing aggregate to be in the daughter at the end of the division settles above 0.2. This is substantially higher than the experimental counterpart of 0.02 in (7).

Long-term aggregate dynamics, damage accumulation over a lifecycle; differences with experiments

Average cross-compartment crossings throughout the lifecycle

In Fig. 6 B, the average number of crossing events is shown from the passive-only model as a function of the age of the mother cell. Although with age, due to the formation of larger aggregates, the number of crossing events in both directions decreases, it remains >10-fold higher than in experiments ((19), Figure 1 and (22), Figure S6) and settles at approximately six crossing events, when τ_m = 12 min, and three crossing events, when τ_m is larger. These crossings are almost completely carried out by small aggregates with low mean first passage time. Overall, this either suggests that experimental data in (19) relies on a mechanism of retention or that their threshold of detection was considerably above the one used in these simulations (derived from (22)), which appears unlikely after observing Fig. 1, A–C, in (19), where some aggregates have radii of ∼0.05 μm.

Aggregate kinetics in cells with infrequent active quality control

Aggregate mean square displacement

In Fig. 7 F, it is shown that subdiffusion can also be consistent with an infrequent active mechanism of transport or with an active mechanism of retention, because the effect of the geometry combined with fusion and growth of aggregates remains the strongest force affecting their displacement. That is, α $\simeq$ 0.96 and α $\simeq$ 0.78 at short and intermediate timescales in the case of drift (movement only toward the mother’s pole with probability p_s); α $\simeq$ 0.94 and α $\simeq$ 0.65 in the case or confinement to organellar surfaces; and α $\simeq$ 0.88 and α $\simeq$ 0.6 in the case of attachment to cell membranes. In all four cases, when combining the timescales, the values of α can be considered consistent with the experimental measurements in (19).

Figure 7.

Short-term results from the AQC variants of the passive-only model. (A) Log-log plot for the MSD of an aggregate (top) and the volume of the same aggregate for which the MSD was computed (bottom). (Dashed light lines) Given here is the unconstrained MSD of an aggregate of radius rⁱ_a (top) and of the volume of one aggregate with initial radius rⁱ_a in the absence of fusion events. (B) Average number of crossing events from mother to bud (M > B) and from bud to mother (B > M). (Inset) Proportion of crossing events in both directions. N = 5 and δt = 0.1 s; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

Average number of cross-compartment crossings during a single-division cycle

When introducing active quality control for a single-cell-division cycle, the number of crossings can be significantly reduced by nearly fivefold (Fig. 7 B). Moreover, the proportion of retro and antero movement (Fig. 7 B, inset) becomes more consistent with the experimental estimations in Figure 1 A in (15).

Long-term aggregate dynamics: damage accumulation over a lifecycle; agreement with experiments

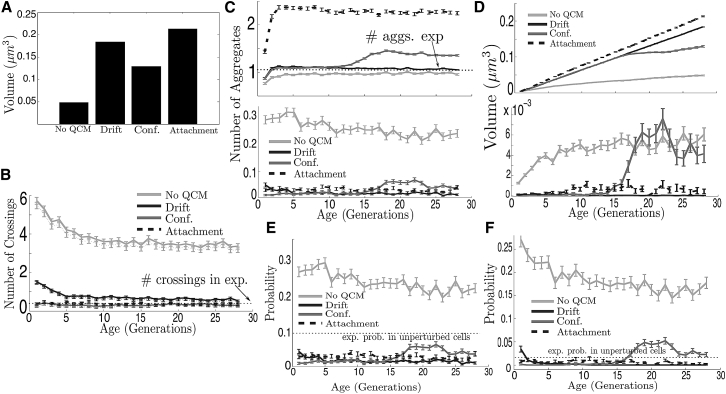
In Fig. 8 A, it is shown that for τ_m = 100 min, all of the three implemented active mechanisms can be very efficient for enhancing the accumulation of damage. After 28 divisions, the total aggregate volume inside the mother is increased by at least threefold and does not stabilize (similarly as in (4)). Although these results indicate that confinement to organellar surfaces is less effective, this is merely a consequence of the overlapping restriction that is forced here on the aggregates and the organelles. After 15 generations, fusion with the largest aggregate becomes restrained if the overlapping condition is imposed with organelles. Thus, smaller aggregates escape more easily and the retention capacity of the mother cell is diminished. However, in the absence of this restriction, and in line with the almost identical volume growth as under drift (Fig. 8 D, top) until the 15th generation, the mother cell under this mechanism should also reach values of total aggregate volume of 0.2 μm³, which is approximately fourfold higher than the volume inside a cell in absence of any form of active quality control. The effect of restrained fusion with the largest aggregate under confinement to organellar surfaces is observed in Fig. 8, C–F.

Figure 8.

Long-term results from the AQC variants of the passive-only model. (A) Total aggregate volume inside the mother cell at the end of the 28th division. (B) Average number of crossing events from mother to bud (continuous line) and from bud to mother (dotted line). (C and D) Total number of aggregates and the total aggregate volume inside the mother cell (top) and inside the daughter cell (bottom). (E) Probability of inheritance of at least one aggregate by the daughter cell at the end of cell division. (F) Probability of inheritance of the largest aggregate, if it exists, by the daughter cell. Error bars correspond to the SE. In all simulations, δt = 0.5, τ_m = 100 min, and τ_d = 1000 min; all other parameters were set to the values in Table S1. Results were averaged over 1024 realizations.

In Fig. 8 C, the number of aggregates is shown in both compartments with and without active mechanisms. Absence of quality control, together with drift and with confinement to organelles, reduces the number of aggregates in the mother cell to similar values close to one aggregate, which is consistent with the experimental quantifications for heat-induced cells in Fig. 2 L (22) and for unperturbed cells in (18) and Figs. 2 and 3. This is also in agreement with the observations in (7, 9). In the case of attachment to cell membranes, as aggregate diffusion is reduced and their collision is thus less frequent, the number of aggregates is significantly higher (it can rise to ∼2.5 times the value in absence of sticky membranes). This suggests that, should this mechanism be present in real-life WT cells, it must be complemented with a machinery supporting aggregate assembly and fusion (17, 18).

Concerning the number of aggregates in the daughter cell, all three mechanisms reduce aggregate inheritance by the daughter cell by fourfold. This is confirmed in Fig. 8 E displaying the probability on inheritance of at least one aggregate by the daughter. Under AQC, the probability is underestimated with respect to experimental measurements. Nevertheless, AQC outperforms passive-only assumptions.

The probability of inheritance of the largest aggregate by the bud remains close to 0.02 in all three variants, which is consistent with the measurements in (18) for WT cells. In the absence of AQC, this probability stabilizes at ∼0.15 under an intermediate rate of appearance and growth close to the threshold value (τ_m = 100 min). As shown in Fig. 6 D for the passive-only model, even with τ_m = 50 min the probability cannot be <0.05 after 28 generations.

In Fig. 8 B, the number of crossing events is shown between compartments under the three forms of active quality control. In all three variants of the original model, the crossing amounts are reduced to values comparable to those measured in (19, 22) and Figs. 1 and S6, which are under one crossing event in each direction per cell division cycle.

Discussion

Single division cycle aggregate dynamics

The results from the single division cycle component of the passive-only model suggest that although the passive-only assumption can reproduce the experimental data used to support it, substantial differences remain between experimental observables and the predictions of the model.

Concerning the MSD of aggregates, the degree of subdiffusion measured in (19) is shown to be consistent with the presence of passive-only mechanisms and can arise as a consequence of the geometrical effect of the dividing yeast cell and of aggregate growth and fusion. However, unless aggregates are subject to a frequent and consistent mechanism of active transport, a degree of subdiffusion as well should be expected under active quality control. This suggests that an MSD consistent with subdiffusion should not be considered a deciding argument when dismissing its presence.

With respect to aggregate kinetics and the asymmetrical accumulation of damage inside yeast cells, it is observed that, although fusion of aggregates and bud-specific dilution can play a major role in its establishment, aggregate cross-compartment transport can have a substantial impact on the level of damage asymmetry. Indeed, similarly to the second law of thermodynamics, an open neck has a balancing effect on the appearance and growth rates of aggregates and decreases the effect of bud-specific dilution on the asymmetrical distribution of damage during cytokinesis. Moreover, rather than the case where aggregates would rarely cross the neck, as observed in (19) and as interpreted in (22), the passive-only assumption is more consistent with an interpretation where aggregate transport is frequent and where the distribution of aggregates is strongly regulated by the relation between compartmental volumes and between aggregation rates. This result suggests that models that do not incorporate either aggregate fusion, growth, or appearance (such as the one in (19, 21)) or cross-compartment transport (such as that in (22)) can potentially underestimate the role of these effects on the asymmetrical distribution of damage in real-life yeast cells.

This result is corroborated by the fact that the average number of cross-compartment crossings in the passive-only model is at least an order-of-magnitude higher than the one observed and quantified in (19, 22). It is suggested that experimental observations in (19, 22) (and see Figs. 1 and S6, respectively) rely on an underlying mechanism of retention.

Long-term aggregate dynamics

The long-term component of the passive-only model, reproducing aggregate accumulation over many generations, shows a qualitative dependence on the rate of appearance and growth of aggregates. Under high rates of aggregation, resembling those after heat or oxidative stress, fusion of aggregates and bud-specific dilution can induce gradual damage accumulation in mother cells and, therefore, aggregate-dependent aging. In contrast, if the rates are low—resembling those in unperturbed cells—rather than becoming saturated with damage, cells without active quality control have aggregate volumes that stabilize by getting rid of damage continuously and at near-constant rates. Hence, although the distribution of damage remains asymmetrical between mother and daughter cells, this behavior would be more consistent with nonaging organisms. Therefore, as observed in (3) for fission yeast, depending on the rate of appearance and growth of aggregates, fusion alone need not be the sole mechanism capable of aggregate-dependent aging in unperturbed WT cells. At low rates, resembling those measured in experiments in (7), other (possibly active) mechanisms of retention and aggregate-compartmentalization are likely required for aggregate-dependent aging to evolve.

This is further confirmed by observing that the average number of cross-compartment crossings measured in the long-term component of the passive-only model remains an order-of-magnitude higher than that measured in (19, 22). This result is sustained under low and high values of the aggregation rates. Thus, results from the passive-only model suggest that although fusion indeed contributes to the asymmetrical distribution of damage, it must be accompanied by a mechanism enhancing gradual damage accumulation and retention, especially in cells that have not been exposed to stress.

When introducing active quality control, in all three of the variants given here, consistency between these results and most of the experimental data used for comparison (MSD, number of crossing events, number of aggregates in cells and probability of inheritance of largest aggregate by the daughter cell) is maintained or improved. The exception is the number of aggregates under attachment to cell walls, which it is suggested must be accompanied by a mechanism enhancing aggregate fusion. Therefore, the presence of AQC in real-life budding yeast cells is at least probable.

Finally, it is highlighted that some experimental observables can accommodate to both passive-only and AQC. Moreover, the averaged regimes of inner cell aggregate kinetics might be similar (the number of aggregates in each compartment and the MSD, for instance) under both assumptions. Nevertheless, a thorough comparison with various experimentally measured quantities is what makes the sufficiency of passive-mechanisms improbable.

Conclusions

This article presents a computational model complemented with a mathematical approximation generalizing the works in (21, 22), aiming to study the sufficiency of passive-only mechanisms behind the asymmetric segregation of damaged proteins (Hsp104-associated aggregates) during cytokinesis and throughout the lifecycle of budding yeast cells. It is analyzed whether aggregate kinetics and the asymmetrical distribution of damage observed in real-life cells are consistent with the absence of active quality control as suggested in (19, 22), or whether it is a consequence of an underlying (possibly active) mechanism that either transports or holds the aggregates inside the mother cell (8, 9, 16, 18), which can then be intensified by the mediation of passive processes.

Results show that although some observables are reproducible under passive-only assumptions, they fail to justify the low amount of cross-compartment movement observed in experiments. Cross-compartment movement was absent in the model in (22) and was not measured in the models in (19, 21), and could be an important argument in favor of active quality control retention mechanisms.

Additionally, it was shown that aggregate fusion and bud-specific dilution can produce gradual damage accumulation with age (as suggested in (22)) only under high rates of aggregate growth and aggregate appearance, which is the case for cells under stress; however, this is unlikely to be the case for unperturbed cells. The rate of aggregate appearance and growth has not been exactly measured, but under low aggregation rates that resemble those approximated in WT unperturbed cells, damage accumulation (and aggregate-dependent aging) occurs in this model solely under the presence of AQC.

Last, three variants of the original passive-only model are introduced in which representations of active quality control that have already been suggested in the existing literature (9, 16, 18) are implemented. Although these results rely on parameters that have no current experimental validation (which is herewith encouraged), simulation results from these alternate AQC versions can improve the above-mentioned differences with available experimental data.

Author Contributions

M.A.-R. designed and performed the research, contributed analytic and numerical tools, analyzed results, and wrote the article.

Editor: Ruth Baker.