Effects of Temperature on the Histotripsy Intrinsic Threshold for Cavitation

Abstract

Histotripsy is an ultrasound ablation method that depends on the initiation of a dense cavitation bubble cloud to fractionate soft tissue. Previous work has demonstrated that a cavitation cloud can be formed by a single acoustic pulse with one high amplitude negative cycle, when the negative pressure amplitude exceeds a threshold intrinsic to the medium. The intrinsic thresholds in soft tissues and tissue phantoms that are water-based are similar to the intrinsic threshold of water over an experimentally verified frequency range of 0.3–3 MHz. Previous work studying the histotripsy intrinsic threshold has been limited to experiments performed at room temperature (~ 20°C). In this study, we investigate the effects of temperature on the histotripsy intrinsic threshold in water, which is essential to accurately predict the intrinsic thresholds expected over the full range of in vivo therapeutic temperatures. Based on previous work studying the histotripsy intrinsic threshold and classical nucleation theory, we hypothesize that the intrinsic threshold will decrease with increasing temperature. To test this hypothesis, the intrinsic threshold in water was investigated both experimentally and theoretically. The probability of generating cavitation bubbles was measured by applying a single pulse with one high amplitude negative cycle at 1 MHz to distilled, degassed water at temperatures ranging from 10°C–90°C. Cavitation was detected and characterized by passive cavitation detection and high-speed photography, from which the probability of cavitation was measured vs. pressure amplitude. The results indicate that the intrinsic threshold (the negative pressure at which the cavitation probability = 0.5) significantly decreases with increasing temperature, showing a nearly linear decreasing trend from 29.8±0.4 MPa at 10°C to 14.9±1.4 MPa at 90°C. Overall, the results of this study support our hypothesis that the intrinsic threshold is highly dependent upon the temperature of the medium, which may allow for better predictions of cavitation generation at body temperature in vivo and at the elevated temperatures commonly seen in high intensity focused ultrasound (HIFU) regimes.

I. INTRODUCTION

Histotripsy is a noninvasive tissue ablation method that controllably fractionates soft tissue through cavitation generated by high pressure (>10 MPa), short duration (<20µs) ultrasound pulses at low duty cycles (<1 %) [1–3]. Histotripsy depends on the initiation and maintenance of a dense cavitation bubble cloud to produce mechanical tissue fractionation [3, 4]. With sufficiently high pressure and dose, histotripsy can completely fractionate soft tissues into an acellular liquid homogenate [5–7]. Histotripsy is currently being studied for many clinical applications where noninvasive tissue removal is desired including benign prostatic hyperplasia [8], kidney stones [9], deep vein thrombosis [10], congenital heart disease [11, 12], and cancer [13, 14].

Dense histotripsy bubble clouds can be generated by two mechanisms, termed shock scattering histotripsy and intrinsic threshold histotripsy. In shock scattering histotripsy, a multicycle histotripsy pulse at high pressure (~3–20 cycles, P– = 10–28 MPa) is used to form a dense bubble cloud through shock scattering from single or sparse initial bubbles expanded during the initial cycles of the pulse [15, 16]. In intrinsic threshold histotripsy, a single pulse with a single dominant negative pressure phase at very high pressure (≤2 cycles, P– = 24–30 MPa) is used to form a dense bubble cloud directly from the negative pressure of the incident wave [17–20]. Using these short pulses, cavitation initiation depends on the amplitude and duration of the applied negative pressure as well as the properties of the media. When the pressure exceeds a distinct threshold intrinsic to the medium, without the contributions from shock scattering, it results in a dense bubble cloud matching the portion of the focal region above the intrinsic threshold [17–20]. In shock scattering histotripsy, the intrinsic threshold for generating a dense bubble cloud is reached by pressure release scattering of very high peak positive shock fronts, resulting in a dense bubble cloud. This shock scattering bubble cloud grows in layers towards the transducer with each reflected shock front that exceeds the intrinsic threshold.

In intrinsic threshold histotripsy, a dense bubble cloud can be predictably and reliably generated when the peak negative pressure, p-, is raised above the intrinsic threshold of a given media. Maxwell et al measured an intrinsic threshold of ~26–30 MPa for soft tissues and tissue phantoms that are water-based using a 1.1 MHz histotripsy transducer, while the threshold for tissue composed primarily of lipids was significantly lower (15.4 MPa for adipose tissue) [18]. The intrinsic threshold measured for water-based soft tissues and tissue phantoms closely matched the intrinsic threshold of water, suggesting that cavitation nucleation occurs in the water inside of these tissues. This hypothesis was further supported by recent work demonstrating that the intrinsic threshold of various water-based soft tissues and tissue phantoms was independent of tissue stiffness and closely matched the intrinsic threshold of water at ultrasound frequencies ranging from 345 kHz to 3 MHz [19].

Previous work has suggested that the histotripsy intrinsic threshold relies upon cavitation nuclei that are intrinsic to the media, and is not dependent upon the gas content of the media and does not require the presence of impurities or stable bubbles inside the media [18, 19]. The term ‘intrinsic’ is used to imply that the nuclei appear to be associated with the properties of the medium itself rather than impurities. This hypothesis is supported by previous studies from several groups using different sample processing methods, which have measured approximately the same threshold for inertial cavitation associated with these nuclei in the range of 24 to 33 MPa in distilled water [18, 19, 21–24]. These negative pressure thresholds are significantly higher than the pressure required to generate cavitation using long duration pulses, high PRF, or constant exposures, as these approaches likely rely on nuclei that are not intrinsic to the media [25–30]. Although such nuclei can also produce cavitation during single-pulse, single-cycle measurements, the short duration and small focal volume of this high pressure pulse makes the cavitation at low pressure amplitudes highly improbable unless nuclei are artificially introduced, since concentration of such impurities is sufficiently dilute [18, 24, 27, 31].

Although previous work studying histotripsy has provided significant insight into the process of generating cavitation using the intrinsic threshold method, these studies have been limited to experiments performed at room temperature (~20°C). Understanding the effects of temperature on the intrinsic threshold is essential to the development of histotripsy therapy approaches using the intrinsic threshold method, including the prediction of the intrinsic threshold at body temperatures in vivo. In addition, understanding the effects of temperature on the intrinsic threshold may provide insight into the effects of temperature on cavitation generation in high intensity focused ultrasound (HIFU) and boiling histotripsy regimes, where the tissue temperature is elevated by long ultrasound pulses for therapeutic purposes.

To test the hypothesis that the intrinsic threshold decreases at higher temperatures, the probability of generating cavitation was measured for 1 MHz pulses applied to distilled, degassed water heated to temperatures ranging from 10°C–90°C. Two numerical models were used to theoretically investigate the effects of temperature on the histotripsy intrinsic threshold and bubble dynamics. First, classical nucleation theory, CNT, was used to simulate the effects of temperature on the cavitation threshold at the focus inside the medium. Next, a single bubble numerical model was used to investigate the effects of temperature on the bubble dynamics of a single nuclei at the focus, with the results of both simulations compared to the experimental results.

II. METHODS

A. Experimental Setup

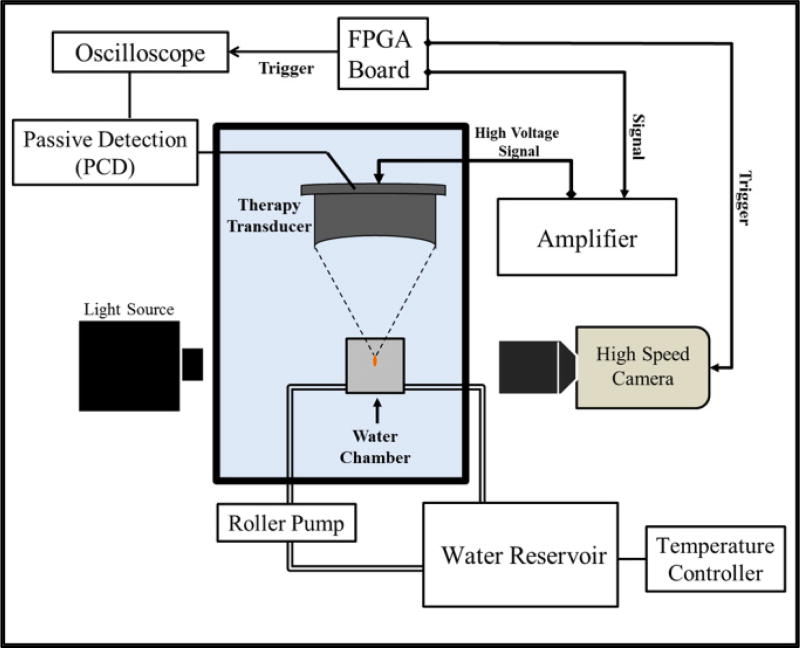
The effects of temperature on the histotripsy intrinsic threshold, p_HIT, were investigated by exposing 1 MHz ultrasound pulses to distilled, degassed water heated to 10°C, 20°C, 40°C, 60°C, 80°C, and 90°C. Table 1 shows the viscosity, surface tension, and speed of sound of water as a function of temperature as measured in the literature [32–34]. Water was degassed to 15% O₂ prior to experiments in order to minimize any stable gas bubbles in the sample. Gas saturation was measured using an O₂ meter (DO200; YSI, Yellow Springs, OH, USA) for each sample prior to testing to ensure consistency throughout all experiments. Water was heated inside a constant temperature water bath, consisting of a slow cooker (Crock-Pot, SCCPVL610-S, Manchester, UK) connected to a sous-vide temperature controller (Dorkfood, DSV, Pensacola, Florida, USA). A roller pump (Masterflex, Cole-Parmer, Vernon Hills, IL, USA) was used to circulate heated water into a cavitation chamber (Fig.1). Water was circulated into the cavitation chamber between experiments at a typical volumetric flow rate between 5–10 mL/s. No water was circulated into the chamber during experiments. The 150-mL cavitation chamber, which has been described in detail in a previous study [18], was used to allow sonication of the sample and simultaneous visualization of the region of interest. The chamber components were made from polytetrafluoroethylene, glass, and 316 stainless steel to operate over a wide temperature range. Two glass windows were inserted into the walls of the chamber to facilitate high-speed photography of the cavitation activity. Acoustic windows in the front and back, made from 12 µm thick, low-density polyethylenemembranes, were added to contain water in the chamber and allow ultrasound propagation into the sample. Fluid inlet and outlet ports were integrated into the top and bottom of the chamber for circulation. The temperature inside the water tank, slow cooker, and cavitation chamber was monitored using three type T hypodermic needle thermocouples (Physitemp Instruments Inc., Clifton, NJ, USA). For experiments, the temperature inside the cavitation chamber was maintained within ±1°C of the reported value, as measured outside the acoustic focus by a thermocouple inserted at the outlet port of chamber.

TABLE I.

VISCOSITY, SURFACE TENSION, AND SOUND SPEED VALUES OF WATER AS A FUNCTION OF TEMPERATURE FROM LITERATURE [32–34].

Temperature (°C)	Viscosity (mPa-s)	Surface Tension (mN-m)	Sound Speed (m/s)
0.1	1.79	75.64	1403
10	1.31	74.23	1447
20	1.00	72.75	1482
30	0.80	71.20	1509
40	0.65	69.60	1529
50	0.55	67.94	1543
60	0.47	66.24	1551
70	0.40	64.47	1555
80	0.35	62.67	1554
90	0.31	60.82	1550
100	0.28	58.91	1543

Figure 1. Experimental Set-up.

Histotripsy pulses were applied to the inside of distilled, degassed water heated to 10°C, 20°C, 40°C, 60°C, 80°C, and 90°C. Heated water was circulated into a 150-mL custom-built cavitation chamber using a roller pump, and the temperature inside the chamber was monitored using a type T hypodermic needle thermocouple. Cavitation was monitored using high speed optical imaging and passive cavitation detection using one of the therapy transducer elements.

B. Ultrasound Pulse Generation

Ultrasound pulses were generated by an 18-element 1 MHz histotripsy transducer. The transducer has an effective 9.8 cm (lateral) × 8 cm (elevational) aperture and a 7 cm focal distance. The focal beam volume (−6 dB) of the transducer was measured to be 6.5 mm (axial) × 1.3 mm (lateral) × 1.5 mm (elevational) using a calibrated fiber-optic probe hydrophone (FOPH) built in-house [35]. To measure the intrinsic threshold in each sample, short pulses (<2 cycles) with a single dominant negative pressure phase were applied to the sample (Fig.2). To generate a short pulse, a custom high-voltage pulser developed in-house was used to drive the transducers. The pulser was connected to a field-programmable gate array (FPGA) development board (Altera DE1 Terasic Technology, Dover, DE, USA) specifically programmed for histotripsy therapy pulsing. This setup allowed the transducers to output short pulses consisting of less than two cycles.

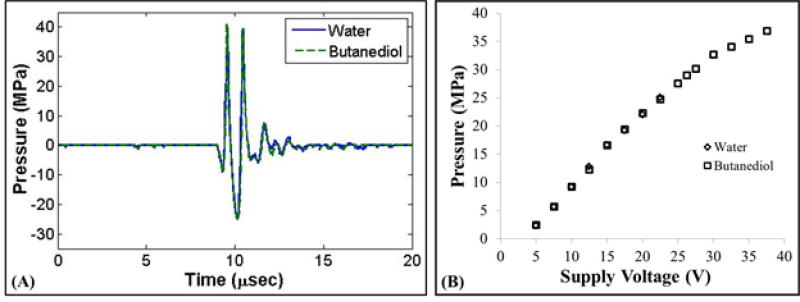
Figure 2. Pressure Calibration.

(A) Example acoustic waveforms produced by the 1 MHz histotripsy transducer measured by the FOPH in water and 1,3 butanediol. (B) Peak negative pressure vs. transducer voltage showed close agreement for the two measurement techniques.

The acoustic output pressure at the focus of the transducer was measured by the FOPH at 20°C in degassed water (15% O₂) for pressures up to a peak negative pressure of ~25 MPa. At higher pressure levels, the acoustic output could not be measured in water due to cavitation at the fiber tip. Therefore, the acoustic pressure was also measured in 1,3 butanediol, which has previously been shown to have a higher threshold for cavitation [18]. This method has been used in a previous study, showing good agreement between the acoustic pressure measurements in water and butanediol [18]. Butanediol has density and sound speed (ρ = 1005 kg/m³, c = 1505 m/s) very similar to water (ρ = 998 kg/m³, c = 1484 m/s), minimizing acoustic reflection at the interface between the two. The fiber probe was positioned in a small container of butanediol, and the probe tip was positioned 5 mm from the water-butanediol interface to ensure the attenuation in butanediol did not alter the measurement significantly. Figure 2 shows a comparison of the acoustic output measured in water at butanediol, with results demonstrating close agreement for the two measurement techniques. Note that, for all experiments, the reported pressure levels were the values measured at 20°C, as the changes in the focal pressure due to differences in water temperature were expected to be small (<5%) based on theoretical calculations using a ray tracing simulation modified from a previous study [36].

For threshold experiments, histotripsy pulses were applied at a pulse repetition frequency (PRF) of 0.5 Hz. The PRF was kept low to minimize the possibility that cavitation from one pulse would change the probability of cavitation on a subsequent pulse. In a previous study [18], it was demonstrated that for PRFs > 1 Hz, cavitation during a pulse increased the likelihood of cavitation on a following pulse, but this effect was not observed for PRFs below 1 Hz, since the residual nuclei from the ultrasound pulse dissolve within ~1 second after the pulse. At each pressure level tested, 100 pulses were applied to the sample for each set of experiments. For 90°C samples, pulses were applied in four subsets of 25 pulses in order to ensure the temperature was maintained within the ±1°C criteria.

C. Cavitation Detection using Optical Imaging

High speed optical imaging was used as a method to detect cavitation (Fig.1). A high-speed, 1 megapixel CCD camera (Phantom V210, Vision Research, Wayne, NJ, USA) was aligned with the transducer focus through the optical window of the chamber. The camera was backlit by a continuous white-light source. The camera was focused using a macro-bellows lens (Tominon 1:4.5, F = 105 mm; Kyocera, Kyoto, Japan), giving the captured images a resolution of approximately 4.8 µm per pixel and a field of view 6.2 mm × 3.8 mm. The camera was triggered to record one image for each applied pulse at a time point approximately corresponding to the maximum bubble expansion, which was determined prior to experiments by changing the delay time on the camera to reconstruct representative radius vs. time curves of the bubbles and identify the time corresponding to maximum bubble expansion. The camera exposure time was 2 µs for all images. After acquisition, shadowgraph images were converted from grayscale to binary by an intensity threshold determined by the background intensity using image processing software (MATLAB; The Mathworks, Natick, MA, USA). Bubbles were indicated as any black regions >5 pixels. By this criterion, the minimum resolvable bubble radius was 12 µm. The number of frames that contained cavitation bubbles was recorded, and the fraction of total frames (out of 100) for which any cavitation was detected was determined as the cavitation probability.

D. Passive Cavitation Detection (PCD)

In addition to high-speed imaging, an acoustic method was also used to identify cavitation in the focal zone, following a previously established method [18, 19, 37]. Since relying upon an image of the bubbles taken at a single time point is a limitation, the PCD method allowed cavitation to be monitored over a much longer time period following the passage of the pulse. For each experiment, one of the transducer’s therapy elements was also used to receive acoustic emission signals for PCD to detect the presence of cavitation in the focal region (Fig.1). The surface area of the element used for PCD was 350 mm². The PCD signal was connected to an oscilloscope (LT372; Lecroy, Chestnut Ridge, NY, USA) with the time window selected to record the backscattering of the therapy pulse from cavitation bubbles [18, 19, 24, 38]. To determine whether cavitation occurred during a pulse, the signal generated by backscattering of the incident pulse from the focus was analyzed following the method used in a previous study [18]. The backscattered pressure amplitude was received by the PCD at the time point corresponding to two times the time of flight for the focal length of the transducer. The integrated frequency power spectrum (S_PCD) of the backscatter signal was used as a measure of whether cavitation occurred, following a previously described method [18]. The largest component of the backscatter was near the center frequency (1 MHz), so the power spectrum of the backscatter signal around this frequency (0.5 to 2.5 MHz) was used as a measure of cavitation presence. This method allowed a quantitative definition of whether a signal was above the threshold for cavitation, based on a comparison with baseline signals measured at low pressure amplitudes where cavitation did not occur [18].

E. Intrinsic Threshold Calculation and Comparison

The probability of observing cavitation, P_cav, followed a sigmoid function, given by

$$P(p_{-})=\frac{1}{2}+\mathit{\text{erf}}\left(\frac{p_{-}-p_{\mathit{\text{HIT}}}}{\sqrt{2{\sigma }^2}}\right)$$ (E1)

where erf is the error function, p_HIT is the negative pressure at which P_cav = 0.5, σ is a variable related to the width of the transition between P_cav = 0 and P_cav = 1, with ±σ giving the difference in pressure from about P_cav = 0.15 to P_cav = 0.85 for the fit. The intrinsic threshold for each sample, p_HIT, is defined as the p- corresponding to P_cav = 0.5 as calculated by the curve fit. Curve fitting for all data sets was performed using an OriginLab curve fitting program (OriginPro 9.1; OriginLab Corporation, Northampton, MA, USA). The fit curves for all samples were analyzed statistically to determine whether the differences in the values of p_HIT were significantly different from each other. The standard errors for p_HIT were estimated by a covariance matrix using the delta method [39]. The curves were compared using a two-sample t-test with statistic $t({\mathit{p}}_{\mathit{\text{int}}1}-{\mathit{p}}_{\mathit{\text{int}}2},\sqrt{{\mathit{\text{SE}}}_1^2+{\mathit{\text{SE}}}_2^2})$ at a 95% confidence interval. Results were considered statistically significant for p<0.05. Note that the standard error does not include the uncertainty in absolute pressure from the hydrophone measurement, only the uncertainty in the fit.

F. Nucleation Theory Simulation

To investigate the effects of temperature on the cavitation threshold predicted for spontaneous nucleation, a theoretical analysis was performed based on classical nucleation theory (CNT) [24, 40–43]. CNT predicts that the cavitation threshold decreases at higher temperatures and the corresponding decrease in the surface energy of the medium [40, 42]. The threshold predicted by CNT, p_CNT, was calculated as

$$p_{\mathit{\text{CNT}}}={\left(\frac{16\pi {\alpha }^3}{3k_{b}T\ast \text{ln}\frac{{\mathrm{\Gamma }}_0{V}_f{\tau }_f}{\text{ln }2}}\right)}^{0.5}$$ (E2)

where α is the surface energy, k_b is the Boltzmann’s constant, T is temperature in Kelvin, Γ₀ is a prefactor, V_f is the focal volume for a given frequency, and τ_f is the time the focal volume is above a given pressure [24, 40, 42–44]. Γ₀ was set to Γ₀ = 10³⁴ and τ _f set to one half of the acoustic period, similar to previous work [24, 42]. V_f was set to 6.64 mm³, as calculated from the −6 dB FWHM beam profiles of the 1 MHz transducer used in this study assuming an ellipsoidal focus. For comparison with experiments, T was varied from 283K to 363K (10°C to 90°C) and the surface energy, α, was set to 27.5% of the macroscopic surface tension of water, as calculated as a function of temperature (Table 1). These values for surface energy were chosen to provide a better match with the experimental results based on previous work suggesting that it is not accurate to use the bulk, macroscopic surface tension values for the surface energy of water [19, 24, 44]. In previous studies, surface energy values between 20%–30% of the macroscopic surface tension of water at 20°C have been used in order to provide a more reasonable agreement with experimentally observed cavitation thresholds [19, 24, 45].

G. Single Bubble Simulation

To provide a theoretical explanation for the bubble behavior observed experimentally, a spherically symmetrical three-dimensional numerical model treating water as a compressible Newtonian fluid with heat transfer was used. In previous studies, a model neglecting heat transfer showed a pressure threshold and bubble behavior matching the histotripsy intrinsic threshold at various frequencies when an initial bubble radius of ~2–3 nm was used [18, 19]. For nuclei of this size, the pressure due to surface tension is the primary factor that determines the cavitation threshold, similar to the Blake threshold [18, 19, 46, 47]. In this study, the effects of temperature on the threshold for generating cavitation and the resulting bubble behavior were first investigated using a 1.94 nm initial bubble, which was chosen to match the experimentally observed cavitation threshold at 20°C. To test the effects of temperature on the cavitation threshold for a 1 MHz histotripsy pulse, simulations exposed a 1.94 nm initial bubble to a single peak negative pressure

$$p_a(t)=\{\begin{array}{cc}{p}_A{\left(\frac{1+\text{cos }[\omega (t-\delta )]}{2}\right)}^n,\hfill & |t-\delta |\le \frac{\pi }{\omega }\hfill \\ 0,\hfill & |t-\delta |>\frac{\pi }{\omega }\hfill \end{array}$$ (E3)

where p_A is the peak negative pressure, ω is the angular frequency of the sound wave, δ is a time delay, and n is a curve-fitting parameter which was set to 3.7 so that the shape of the simulated waveform p- closely matched the shape and duration of the p- from the histotripsy waveform used experimentally. Using this theoretical waveform, previously studies have shown good agreement between simulated and experimentally observed bubble dynamics [19, 20]. For this study, we assume the surrounding medium to have homogeneous properties, and that the bubble contains air and remains spherical. These assumptions allow us to use a numerical model developed in-house for simulating spherical bubble dynamics in general viscoelastic media [48]. To model water in this study, we assume a viscous medium with no elasticity. We consider bubble dynamics governed by the Keller-Miksis equation [49]:

$$(1-\frac{\dot{R}}{c})R\ddot{R}+\frac{3}{2}(1-\frac{\dot{R}}{3c}){\dot{R}}^2=\frac{1}{\rho }(1+\frac{\dot{R}}{c}+\frac{R}{c}\frac{d}{dt})(p_B-p_{\infty }(t)-\frac{2S}{R}-\frac{4\mu \dot{R}}{R})$$ (E4)

which depends on the medium’s sound speed c, density ρ, and surface tension against air S. Here p_∞ (t) is the absolute forcing pressure, r is the radial coordinate, and overdots (˙) denote derivatives with respect to time, t. The absolute forcing pressure, p_∞ (t), is the sum of the atmospheric pressure (p_atm = 101.325 kPa) and the time-dependent forcing pressure, p_a (t). It is commonly assumed that the air within the bubble has a spatially uniform pressure given by the polytropic relationship p_B = p₀ (R₀/R)^3κ where κ = 1.4 is the ratio of specific heats for air, R₀ is the initial bubble radius, and p₀ = p_∞ (0) + 2S/R₀ is the initial bubble pressure. For the purposes of this study, however, we employ a full thermal model that solves the partial differential equations for temperature fields inside and outside of the bubble [50, 51]. The Keller-Miksis equation is coupled to the energy equation inside the bubble (E5) through the internal bubble pressure, p_B:

$${\dot{p}}_B=\frac{3}{R}((\kappa -1)K\frac{\partial T}{\partial r}{|}_R-\kappa p_B\dot{R})$$ (E5)

$$\frac{\kappa -1}{\kappa }\frac{p_B}{T}[\frac{\partial T}{\partial t}+\frac{1}{\kappa p_B}((\kappa -1)K\frac{\partial T}{\partial r}-\frac{r{\dot{p}}_B}{3}\left)\frac{\partial T}{\partial r}\right]-{\dot{p}}_B=\nabla ·(K\nabla T)$$ (E6)

where T is the radially varying temperature of the air inside the bubble, which has ratio of specific heats κ. The thermal conductivity of air inside the bubble is given by K = K_AT + K_B, where K_A and K_B are empirical constants, with $K_A=5.28e^{-5}\frac{W}{m·K^2}$ and $K_B=1.165e^{-2}\frac{W}{m·K}$. Prescribed conditions at the bubble-liquid interface relate the temperature inside the bubble to the temperature of the liquid medium outside of the bubble, T_M: T |_r=R = T_M|_r=R and $K{|}_{r=R}{\frac{\partial T}{\partial r}}_{r=R}=K_M\frac{\partial T_M}{\partial r}{|}_{r=R}$. This medium is assumed to have constant thermal conductivity (K_M), thermal diffusivity (D_M), specific heat (C_p), and density (ρ_∞). The energy equation outside of the bubble

$$\frac{\partial T_M}{\partial t}+\frac{R^2\dot{R}}{r^2}\frac{\partial T_M}{\partial r}=D_M{\nabla }^2{T}_M+\frac{12\mu }{{\rho }_{\infty }{C}_p}{\left(\frac{R^2\dot{R}}{r^3}\right)}^2$$ (E7)

includes a viscous dissipation term: $\frac{12\mu }{{\rho }_{\infty }{C}_p}{\left(\frac{R^2\dot{R}}{r^3}\right)}^2$, where μ is the viscosity of water. Two final boundary conditions complete the system: The temperature of the medium is assumed to approach an ambient temperature, T_∞ as r → ∞ and, due to bubble symmetry, the internal temperature has a gradient of zero at the bubble center. A more detailed discussion of the numerical implementation of this model has been outlined in previous studies [48, 50].

To compare the effects of temperature (10°C to 90°C) on the cavitation threshold, the ambient temperature (T_∞), viscosity (μ), and surface tension (S) of water were varied. The values of viscosity and surface tension as a function of temperature were taken from the literature [32, 33] and are listed in Table 1. The maximum bubble radius was plotted as a function of the peak negative pressure for an initial bubble of 1.94 nm, which was chosen to match the experimental data at 20°C. Additionally, a further simulation was conducted to investigate the range of nuclei corresponding to the experimentally measured thresholds using the values of viscosity and surface tension listed in Table 1.

III. RESULTS

A. Intrinsic Threshold vs. Temperature

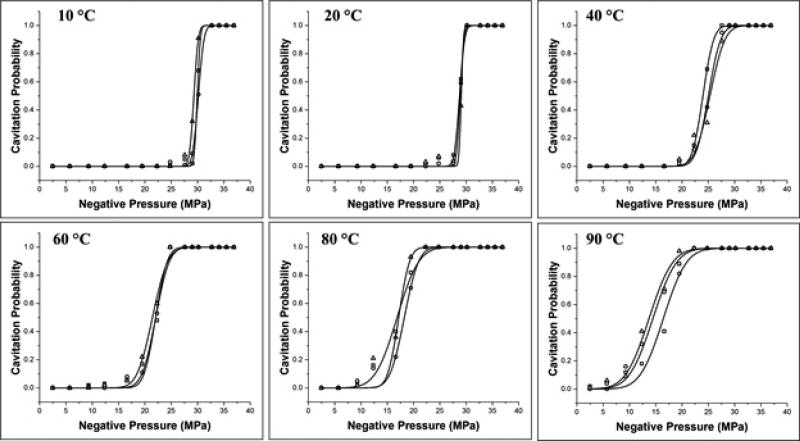
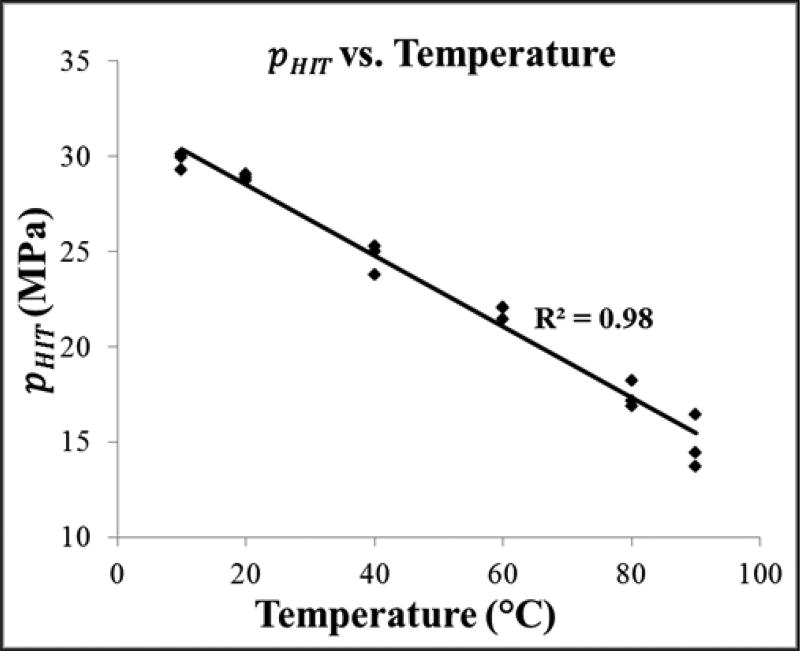
The intrinsic threshold for all samples was compared using the curve fitting method and statistical analysis described above. Comparing the effect of temperature on the histotripsy intrinsic threshold demonstrated a similar function of cavitation probability versus pressure at all temperatures, with p_HIT decreasing as the temperature increased (Fig.3). The p_HIT decreased from 29.8±0.4 MPa at 10°C to 14.9±1.4 MPa at 90°C (Table 2). In general, the standard errors in the estimate of the intrinsic threshold were small compared to the variance between samples at a given temperature. Additionally, results showed a trend of increasing σ_mean with increasing temperature, as has previously been observed in previous studies [24], with σ_mean ranging from 0.7±0.2 MPa at 10°C to 3.5±0.1 MPa at 90°C (Table 2). The effect of temperature on the intinsic threshold was further analyzed by plotting p_HIT as a function of temperature, with linear regression analysis demonstrating that the change in p_HIT with temperature was significant via the Pearson correlation (r = 0.99, R² = 0.98, p<0.05) (Fig.4).

Figure 3. Cavitation threshold curves.

Example probability curves (n = 3) for distilled, degassed water samples heated to 10°C, 20°C, 40°C, 60°C, 80°C, and 90°C. Results show a significant decrease in the intrinsic threshold, p_HIT, with increasing temperature.

TABLE II.

THRESHOLD RESULTS

Temperature (°C)	PHIT(1)	PHIT(2)	PHIT(3)	PHIT (mean)	σ (mean)
10	29.94	30.14	29.30	29.8	0.7
20	28.74	28.87	29.06	28.9	0.6
40	23.79	25.01	25.30	24.7	1.9
60	22.04	22.03	21.43	21.8	2.0
80	16.87	18.24	17.17	17.4	2.4
90	16.43	14.45	13.71	14.9	3.5

Table shows the values for the histotripsy intrinsic, p_HIT, calculated by the fitted curves for each sample, as well as the mean values for p_HIT and σ. All values are pressure im MPa.

Figure 4. Intrinsic threshold comparison.

Scatter plot shows the p_HIT measured for all samples in this work as a function of temperature. Linear regression analysis demonstrated that the change in p_HIT with increasing temperature was significant via the Pearson correlation (r = 0.99, R² = 0.98, p<0.05), with a best fit line of p_HIT = −0.19^*T + 32.24.

B. Optical images of Cavitation Bubble Cloud

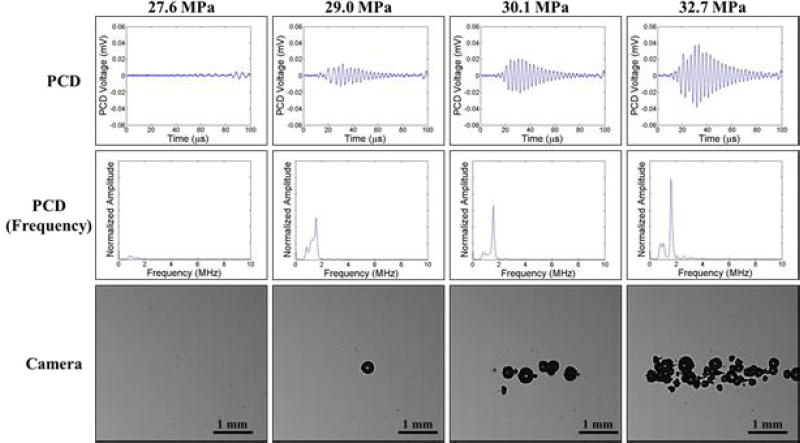
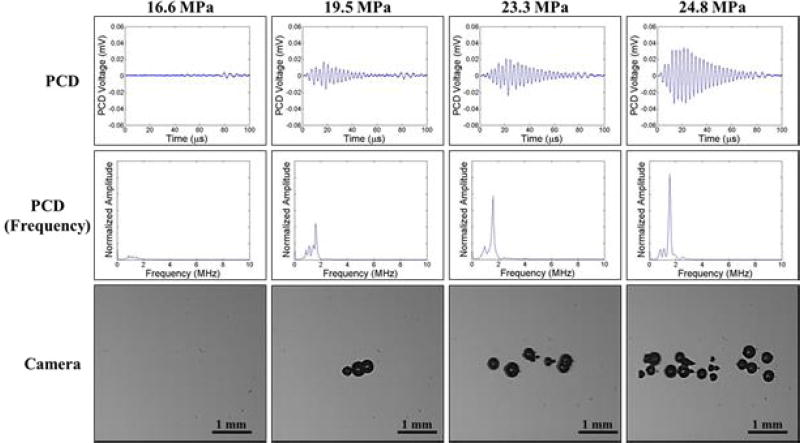
Cavitation bubbles were observed on the high-speed camera when a certain negative pressure was exceeded (Fig.5). As the pressure was further increased above the threshold value at each temperature, the bubbles were visualized in an increasingly larger area with a greater number of bubbles present in the focal region (Fig.5), similar to the behavior of intrinsic threshold bubble clouds observed in previously studies with the bubble cloud matching the portion of the beam profile above the intrinsic threshold [17–20, 37]. Figure 5 shows representative images of bubble clouds generated at all temperatures for selected peak negative pressure values ranging from 16.6–30.1 MPa. Although the bubbles covered a larger area at higher pressure, the diameter of the bubbles that could be individually identified appeared to be consistent between pressure levels at the time point captured by the camera, potentially due to bubble-bubble interactions suppressing the growth of adjacent bubbles or bubble-induced pressure saturation caused by energy loss into each bubble as it forms, as has previously been proposed [20, 52]. When increasing the temperature, the pressure at which cavitation was first observed was reduced (Fig.5). Due to this decrease in threshold, the size of the bubble clouds at a given pressure level increased at higher temperature. However, the appearance of the bubble clouds at all temperatures showed well-defined bubble clouds with similar sized bubbles throughout the cloud with a maximum bubble radius of ~100–200 µm (Fig.5).

Figure 5. Optical Images.

Representative bubble clouds generated at all temperatures for selective peak negative pressures ranging from 16.6 MPa-30.1 MPa.

C. Passive Cavitation Detection (PCD)

In addition to high speed imaging, cavitation was monitored using one of the therapy transducer elements for PCD following a previously established method [18, 19, 37], with results showing close agreement between optical imaging and PCD detection methods. For example, Figure 6 and Figure 7 show example optical images and PCD signals taken for samples heated to 20°C and 80°C, respectively. When cavitation occurred on high-speed images, the PCD signal was a multi-cycle burst of significantly increased amplitude with a center frequency near the therapy transducer frequency. When no cavitation was observed on the camera, the PCD signal amplitude was small. At higher temperatures, the PCD signal arrived at the transducer sooner than at lower temperatures due to the increased speed of sound in the water at 80°C vs. 20°C. However, no noticeable differences in the frequency of the PCD signal were observed at different temperatures.

Figure 6. Cavitation Detection: 20°C.

Images show sample PCD and optical imaging results for pulses applied to distilled, degassed water heated to 20°C. PCD temporal (top) and frequency (middle) signals showed good agreement with high speed optical images of cavitation (bottom).

Figure 7. Cavitation Detection: 80°C.

Images show sample PCD and optical imaging results for pulses applied to distilled, degassed water heated to 80°C. PCD temporal (top) and frequency (middle) signals showed good agreement with high speed optical images of cavitation (bottom).

D. Nucleation Theory Simulation

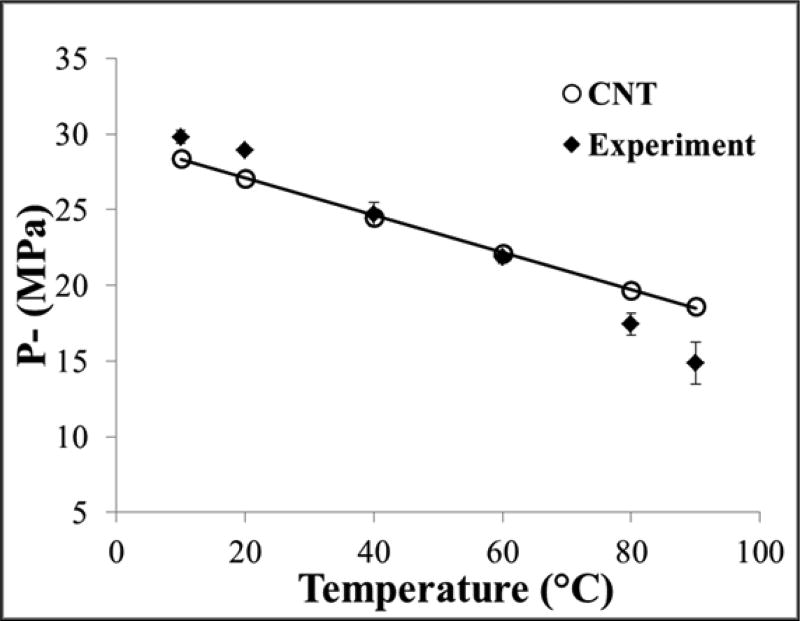
The effects of temperature on the cavitation threshold predicted by classical nucleation theory (CNT) were investigated with a simulation as described in the Methods (E2). CNT results predicted that the cavitation threshold would decrease with increasing temperature and the corresponding decrease in surface energy, with the results ranging from p_CNT = 29.5 MPa at 1°C to p_CNT = 17.5 MPa at 100°C (Fig.8). Comparing the CNT results (p_CNT) with the experimentally measured thresholds (p_HIT) showed similar trends of decreasing threshold with increasing pressure (Fig.8). CNT results demonstrated slightly lower thresholds (compared to experiments) at 10°C and 20°C, close agreement with experiments at 40°C and 60°C, and slightly higher thresholds (compared to experiments) at 80°C and 90°C (Fig.8). The largest difference between p_CNT and p_HIT was 3.7 MPa, which was observed at 90°C.

Figure 8. CNT Simulation.

Classical nucleation theory plot showing the predicted effects of temperature on the cavitation threshold, p_CNT, as well as a comparison with the experimentally measured intrinsic thresholds, p_HIT

E. Stabilized Nuclei Simulation

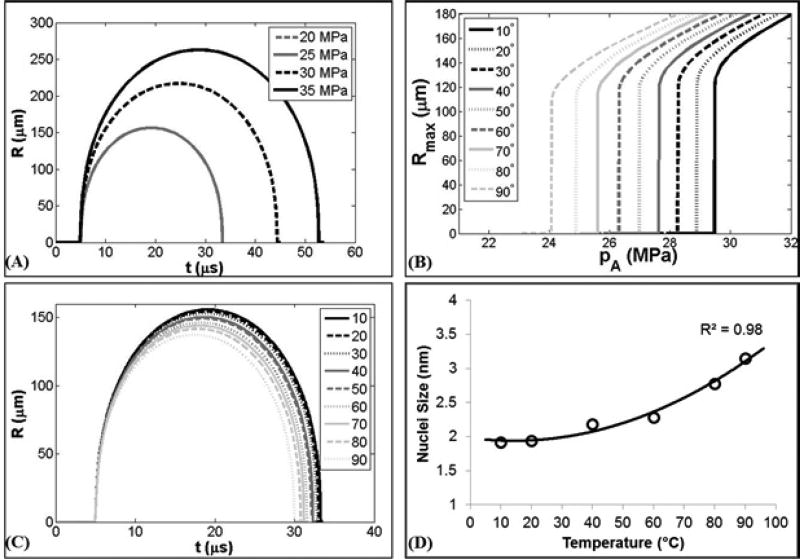
The effects of changing the ambient temperature, as well as the corresponding changes in surface tension and viscosity, on the cavitation threshold and bubble dynamics for a single nuclei were investigated using a single bubble numerical simulation. When the peak negative pressure, p_A, was less than some threshold value, p_SIM, bubble expansion was minimal (R_max < 2 R₀). As p_A was increased above p_SIM, great bubble growth and collapse were observed (R_max > 10⁴ R₀) (Fig.9A). The peak negative pressure corresponding to this transition was defined as the inertial cavitation threshold, p_SIM. Using a 1.94 nm initial bubble, p_SIM was observed to decrease with increasing temperature when using the values for surface tension and viscosity shown in Table 1. For example, Figure 9B shows p_SIM decreased from ~29.5 MPa at 10°C to ~24.1 MPa at 90°C. Although p_SIM significantly decreased with increasing temperature, only small differences in the maximum bubble radius, R_max, were observed at different temperatures (Fig.9C), similar to experimental observations which showed individual cavitation bubbles within the bubble cloud to have a maximum bubble radius between ~100–200 µm at all temperatures (Fig.5). The similar values for R_max for these different conditions is due to the fact that the initial threshold behavior is dominated by surface tension (which significantly decreases with temperature), while the larger expansion behavior and final bubble size are dictated by several competing terms including the applied pressure and viscosity of the fluid. In addition to investigating the changes in the cavitation threshold with changing temperature, the single bubble model was also used to estimate the potential nuclei sizes that would be predicted based on the experimentally observed cavitation thresholds, with the results showing that the experimentally measured thresholds corresponded to initial bubble sizes ranging from 1.92 nm at 10°C to 3.15 nm at 90°C (Fig.9D).

Figure 9. Stabilized Nuclei Simulation.

(A) Example radius vs. time curves for a 1.94 nm initial bubble subjected to a single cycle negative pressure waveform at 20°C. (B) Simulated maximum bubble radius at 10°C–90°C using the values for surface tension and viscosity shown in Table 1 showing a significant decrease in the simulated cavitation threshold, p_SIM, with increasing temperature. (C) Example radius vs. time curves at 10°C–90°C for pressures directly above p_SIM. (D) Initial bubble size at which p_SIM matched p_HIT increased for 10°C–90°C.

IV. DISCUSSION

In this study, the effects of temperature on the histotripsy intrinsic threshold were investigated, with results supporting our hypothesis that increasing temperature decreases the intrinsic cavitation threshold. A nearly linear decrease in the intrinsic threshold was observed as the temperature was increased, ranging from 29.8 MPa at 10°C to 14.9 MPa at 90°C. At higher temperatures, bubble clouds were generated at significantly reduced pressure, but showed no significant changes in the appearance of the bubble clouds (i.e. well-defined bubble clouds matching the region of the focus above the intrinsic threshold). These findings are consistent with our hypothesis that the histotripsy intrinsic threshold decreases at higher temperatures partially due to the decreased surface tension, which has previously been shown to dominate the initial threshold behavior [18, 19], while having only a minor influence on the resulting bubble expansion and collapse behavior [20].

The experimental results were supported by a CNT simulation which showed a significant decrease in the threshold as the temperature was increased from 10°C to 90°C, similar to the trends measured experimentally. Although a slightly larger change in threshold was measured in experiments, the similar trends between CNT and experiments once again demonstrates the ability of a simple CNT calculation to provide a reasonable first-order approximation of the histotripsy intrinsic threshold, as has been shown in previous studies in which CNT closely matched the changes in the intrinsic threshold at different ultrasound frequencies and media [19, 53]. These results demonstrate that CNT can provide a good first-order approximation of the intrinsic threshold if one knows the pulse parameters (i.e. duration and amplitude of the applied negative pressure) and the properties of the media (i.e. temperature and surface energy), with lower frequencies and higher temperatures resulting in a decreased threshold.

In addition to CNT, a single bubble model was used to simulate the effects of temperature on the bubble dynamics of single nuclei, with results showing a distinct threshold response that decreased with temperature. Although the pressure threshold decreased with temperature, only small differences in the maximum bubble radius were observed at the threshold pressure, similar to experimental observations which showed similar sized bubbles generated at different temperatures. This finding makes sense since the initial threshold behavior is dominated by surface tension (which decreases with temperature), while the larger expansion behavior and final bubble size are dictated by several competing terms including the applied pressure and viscosity of the fluid. The single bubble model also showed that the experimentally observed thresholds correlated to an initial bubble size ranging from 1.92 nm at 10°C to 3.15 nm at 90°C. While it is possible that this analysis might shed some light on the critical size of the “intrinsic nuclei” and potential changes in nuclei size with temperature, it remains unclear if the “intrinsic nuclei” are in fact nanometer-sized stable bubbles [23, 54–56] or spontaneous nuclei that form bubbles by energy-density fluctuations described by classical nucleation theory (CNT) [40, 42–44, 57].

The finding that the intrinsic threshold decreases as temperature increases is of significant importance to the development of histotripsy therapy and suggests that the intrinsic threshold in vivo will be predictable based on the local tissue temperature and pulsing parameters. For example, the results of this study calculated that the intrinsic threshold near body temperature using a 1 MHz transducer was ~24.7MPa (40°C). These results also suggest that the intrinsic threshold could be modulated by altering the focal temperature (i.e. using lower amplitude pulses for heating followed by a single large negative pressure cycle), as it is expected that the effects of local temperature elevation on cavitation generation will be similar to the effects of global temperature observed in this study. The benefits of using the intrinsic threshold method include generating well-confined bubble clouds and histotripsy lesions matching the portion of the beam profile above the intrinsic threshold as well as the ability to precisely modulate the bubble dynamics by altering the pulse parameters [17, 19, 20, 58, 59]. In addition to modulating the intrinsic threshold by altering the focal temperature, the results of this study suggest that the intrinsic threshold could be altered using other approaches that change the properties (i.e. surface tension, boiling point) of the media at the focus, as has previously been shown using perfluorocarbon nanodroplets for nanodroplet-mediated histotripsy [31, 37, 60].

In addition to intrinsic threshold histotripsy, the results of this study may also be relevant to generating bubble clouds in the body at elevated temperatures such as in boiling histotripsy. For example, the intrinsic threshold observed at higher temperatures (p_HIT =~15–18 MPa at 80–90°C) is close to the pressure range used for boiling histotripsy (p– =~12–18 MPa) and higher than those used commonly for HIFU thermal ablation (p– =~4–10 MPa) [61–66]. It is possible that the boiling bubble is generated when the temperature at the focus is raised sufficiently high to lower the intrinsic threshold to the level of the incident p–. If this process is responsible for nucleation in boiling histotripsy, then the differences between these two approaches would primarily be differences in the bubble dynamics (i.e. dense bubble cloud vs. single large boiling bubble) and tissue fractionation rather than a difference in nucleation [61–63]. Many of these questions would be answered if precise unequivocal temperature measurements in the media could be made just prior to the “boiling” phenomenon, although these measurements are difficult to obtain (i.e. thermocouples cause cavitation if placed in the field). From this perspective, the nucleation process in boiling histotripsy may be properly described as thermally assisted histotripsy bubble cloud initiation, where elevating temperature serves the purpose of increasing the probability of achieving cavitation nucleation at lower pressure amplitudes. As described above, this form of histotripsy has many useful manifestations.

While the results of this work suggest that the intrinsic threshold in water-based soft tissues will decrease at higher temperatures, changes in the tissue microstructure structure with temperature (i.e. protein denaturing, contraction, hydrolysis) and the corresponding changes in tissue viscoelasticity [64, 67] may impact the cavitation threshold and bubble dynamics in certain tissues. The intrinsic threshold in water-based soft tissues has been shown to be a property of the water inside of the tissue and is therefore independent of tissue stiffness. As a result, thermally induced protein denaturing is not expected to alter the intrinsic threshold (although larger bubble expansion would be expected due to the decreased tissue stiffness), as long as the fluid environment inside of the tissue is not otherwise changed. However, thermally-induced changes in the tissue microstructure may have an indirect impact on the cavitation threshold by altering the fluid environment inside the tissue in cases in which the temperature is raised high enough (i.e. >80–90°C) to cause significant protein contraction [67]. Protein contraction can drive free water out of tissue and cause local tissue dehydration, which would be expected to significantly increase the cavitation threshold. It is therefore possible that the cavitation threshold in certain tissues will decrease up to a certain temperature (due to the decreased intrinsic threshold of water shown in this study) and then increase at higher temperatures (due to local dehydration caused by tissue contraction). Since thermally-induced changes in tissue microstructure are highly dependent upon heating parameters (i.e. temperature, duration) and tissue composition [67], future work will be needed in order to fully characterize the effects of heating on the cavitation threshold in specific tissues of interest.

V. CONCLUSION

In this study, the effects of temperature on the histotripsy intrinsic threshold were investigated by applying 1–2 cycle histotripsy pulses to distilled, degassed water heated between 10°C to 90°C using a 1 MHz histotripsy transducer. Results demonstrated that the histotripsy intrinsic threshold significantly decreased with increasing temperature, showing a nearly linear decrease from 29.8±0.4 MPa at 10°C to 14.9±1.4 MPa at 90°C. The experimental results were supported by a CNT simulation which showed a similar decrease in the threshold as temperature was increased from 10°C to 90°C. A single bubble simulation was also used, with results showing that, although the pressure threshold decreased with temperature, only negligible differences in the maximum bubble radius were observed, similar to experimental observations. Overall, the results of this study indicate that the intrinsic threshold to initiate a histotripsy bubble cloud is highly dependent upon the temperature of the medium, which may allow for a better prediction of cavitation generation at body temperature and at the elevated temperatures commonly achieved in ultrasound thermal therapies.

Biographies

Eli Vlaisavljevich is a postdoctoral fellow in the Department of Biomedical Engineering at the University of Michigan in Ann Arbor, MI. He received a B.S. degree in biomedical engineering from Michigan Technological University in 2010, an M.S. in biomedical engineering from the University of Michigan in 2013, and a Ph.D. in biomedical engineering from the University of Michigan in 2015. Selected honors include a Goldwater Scholarship, a Michigan Tech Provost’s Award for Scholarship, a NSF Graduate Research Fellowship, and a Towner Prize for Outstanding PhD Research. Eli’s research interests include focused ultrasound for noninvasive tissue modulation and ablation, acoustic cavitation, cancer, tissue engineering, and tissue mechanics.

Zhen Xu is a tenured Associate Professor in the Department of Biomedical Engineering at the University of Michigan, Ann Arbor, MI. She received the B.S.E. degree in biomedical engineering from Southeast University, Nanjing, China, in 2001, and her M.S. and Ph.D. degrees from the University of Michigan in 2003 and 2005, respectively, both in biomedical engineering. Her research is focusing on ultrasound therapy, particularly the applications of histotripsy for noninvasive surgeries. She received the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society Outstanding Paper Award in 2006; National Institute of Health (NIH) New Investigator Award at the First National Institute of Biomedical Imaging and Bioengineering (NIBIB) Edward C. Nagy New Investigator Symposium in 2011, and The Federic Lizzi Early Career Award from The International Society of Therapeutic Ultrasound in 2015. She is currently an associate editor for IEEE Transactions on Ultrasound, Ferroelectrics, and Frequency Control (UFFC) and the Women-In-Engineering chair of UFFC.

Adam D. Maxwell is currently an Acting Assistant Professor in the Department of Urology at the University of Washington. He received a B.S. degree in electrical engineering from University of Washington in 2006, an M.S. degree in electrical engineering in 2007, and a Ph.D. in biomedical engineering in 2012, both from University of Michigan. From 2012 to 2014, he was a postdoctoral fellow in the Department of Urology at University of Washington. His research involves development of image-guided ultrasound therapies including focused ultrasound for mechanical tissue ablation (histotripsy) and lithotripsy.

Lauren Mancia is a first year medical student at the University of Michigan, Ann Arbor. In 2012, she graduated summa cum laude with a B.S.E. in engineering physics, and in 2015 she completed an M.S.E. in mechanical engineering, both at the University of Michigan. Her graduate studies were funded by an NSF Graduate Research Fellowship. Lauren’s research interests include numerical modeling of cavitation in tissue and mechanisms for cavitation-induced tissue damage.

Xi Zhang is a Ph.D. candidate in the Department of Biomedical Engineering at the University of Michigan, Ann Arbor. He was born and raised in Shaanxi, China. He received his B.S. degree in electrical engineering with the highest honor from Chongqing University, China, in 2011, and his M.S. degree in electrical engineering from the University of Michigan, Ann Arbor, in 2013. His research interests include non-invasive ultrasound therapy, therapy monitor and feedback, sonothrombolysis, and medical device hardware and software development.

Kuang-Wei Lin was born and raised in Kaohsiung, Taiwan. He received his B.S.E. in electrical engineering from National Taiwan University, Taipei, Taiwan, in 2007, a M.S.E. degree in biomedical engineering from the University of Michigan, Ann Arbor, in 2009, and a Ph.D. in biomedical engineering from the University of Michigan, Ann Arbor, in 2014. His research interests include cavitation-based ultrasound therapies, biomedical imaging, image-guided therapy, and medical imaging systems.

Alexander P. Duryea is currently a Systems Engineer at HistoSonics, Inc. in Ann Arbor, MI. He received the B.S.E. degree in 2009, M.S.E. degree in 2010, and Ph.D. degree in 2015—all in biomedical engineering from the University of Michigan. His dissertation research focused on non-invasive ultrasound therapy, with an emphasis on the application of histotripsy to the treatment of renal calculi. He is continuing work on the development of histotripsy for various indications with HistoSonics, Inc.

Jonathan R. Sukovich is a postdoctoral fellow in the Department of Biomedical Engineering at the University of Michigan. He received a B.S. and Ph.D. degrees in mechanical engineering from Boston University in 2008 and 2013, respectively where he studied laser interactions with water at high pressures and phenomena associated with high energy bubble collapse events. He joined the University of Michigan in the summer of 2013 to study histotripsy for brain applications. His research interests include high energy bubble collapse phenomena, focused ultrasound therapies, and acoustic cavitation.

Timothy L. Hall was born in 1975 in Lansing, Michigan. He is currently an assistant research scientist in the Department of Biomedical Engineering at the University of Michigan. He received the B.S.E. degree in 1998 and M.S.E. degree in 2001, both in electrical engineering, and he received his Ph.D. degree in 2007 in biomedical engineering, all from the University of Michigan. He worked for Teradyne Inc., Boston, MA, from 1998 to 1999 as a circuit design engineer and at the University of Michigan from 2001 to 2004 as a visiting research investigator. His research interests are in high-power pulsed-RF-amplifier electronics, phased-array ultrasound transducers for therapeutics, and sonic cavitation for therapeutic applications.

Eric Johnsen is an assistant professor in the Mechanical Engineering Department at the University of Michigan. His research draws from applied mathematics, numerical analysis, physical modeling and high-performance computing to develop novel techniques for numerical simulations and modeling of flow phenomena. His group uses these tools to uncover the basic physics underlying complex multiscale and multiphysics flows, with an emphasis on multiphase flows (bubbles, droplets), compressible flow (shock and acoustic waves in heterogeneous media), turbulence, plasmas and scientific computing. His work finds applications in biomedical engineering (diagnostic and therapeutic ultrasound), transportation engineering (aeronautical, automotive, naval), energy sciences (inertial fusion, astrophysics). He received his B.S. from the University of California, Santa Barbara, and M.S. and Ph.D. degrees from the California Institute of Technology, all in mechanical engineering; he was then a postdoctoral fellow at the Center for Turbulence research at Stanford. Selected honors include the National Science Foundation CAREER Award and Office of Naval Research Young Investigator Award.

Charles A. Cain was born in Tampa, FL, on March 3, 1943. He received the B.E.E. (highest honors) degree in 1965 from the University of Florida, Gainesville, FL; the M.S.E.E. degree in 1966 from the Massachusetts Institute of Technology, Cambridge, MA; and the Ph.D. degree in electrical engineering in 1972 from the University of Michigan, Ann Arbor, MI. From 1965 through 1968, he was a member of the Technical Staff at Bell Laboratories, Naperville, IL, where he worked in the electronic switching systems development area. From 1972 through 1989, he was in the Department of Electrical and Computer Engineering at the University of Illinois at Urbana–Champaign, where he was a professor of electrical engineering and bioengineering. Since 1989, he has been in the College of Engineering at the University of Michigan, Ann Arbor, as a professor of biomedical engineering and electrical engineering. He was the chair of the Biomedical Engineering Program from 1989 to 1996, the founding chair of the Biomedical Engineering Department from 1996 to 1999, and the Richard A. Auhll Professor of Engineering in 2002. He has been involved in research on the medical applications of ultrasound, particularly high-intensity ultrasound for noninvasive surgery. He was formerly an associate editor of the IEEE Transactions on Biomedical Engineering and the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, and an editorial board member of the International Journal of Hyperthermia and Radiation Research. He is a fellow of IEEE and the American Institute for Medical and Biological Engineering (AIMBE).