Direct Numerical Simulation of Cellular-Scale Blood Flow in 3D Microvascular Networks

Abstract

We present, to our knowledge, the first direct numerical simulation of 3D cellular-scale blood flow in physiologically realistic microvascular networks. The vascular networks are designed following in vivo images and data, and are comprised of bifurcating, merging, and winding vessels. Our model resolves the large deformation and dynamics of each individual red blood cell flowing through the networks with high fidelity, while simultaneously retaining the highly complex geometric details of the vascular architecture. To our knowledge, our simulations predict several novel and unexpected phenomena. We show that heterogeneity in hemodynamic quantities, which is a hallmark of microvascular blood flow, appears both in space and time, and that the temporal heterogeneity is more severe than its spatial counterpart. The cells are observed to frequently jam at vascular bifurcations resulting in reductions in hematocrit and flow rate in the daughter and mother vessels. We find that red blood cell jamming at vascular bifurcations results in several orders-of-magnitude increase in hemodynamic resistance, and thus provides an additional mechanism of increased in vivo blood viscosity as compared to that determined in vitro. A striking result from our simulations is negative pressure-flow correlations observed in several vessels, implying a significant deviation from Poiseuille’s law. Furthermore, negative correlations between vascular resistance and hematocrit are observed in various vessels, also defying a major principle of particulate suspension flow. To our knowledge, these novel findings are absent in blood flow in straight tubes, and they underscore the importance of considering realistic physiological geometry and resolved cellular interactions in modeling microvascular hemodynamics.

Introduction

Microvascular networks in the human body are made of the smallest blood vessels, namely, the capillaries, arterioles, and venules. They are responsible for gas and nutrient transport to tissues, regulation of blood flow in individual organs, and nearly 80% of the work done by the heart. When normal physiological functions of the microcirculation are hindered, major pathological conditions may ensue. For more than a century, beginning with the celebrated work of Jean L. M. Poiseuille, quantitative studies on blood flow in capillary vessels have provided invaluable insights into microvascular hemodynamics (1). Recent advances in experimental techniques, such as intravital microscopy, have made significant progress in this field. In parallel, progress has been made in the theoretical understanding of microvascular blood flow based on mathematical principles of fluid and particulate transport (2).

High-fidelity in silico modeling of blood flow in microvascular networks, however, remains a major challenge. Blood in small vessels behaves as a concentrated suspension primarily composed of red blood cells (RBCs), which are extremely deformable. Analytical solutions are often limited, and computational modeling is needed that can resolve the dynamics and deformation of individual cells while simultaneously extending to a dense suspension (3, 4).

Most cellular-scale modeling studies to date have considered blood flow in simple geometries, such as long, straight tubes of uniform circular cross section, representing an in vitro-like setup. In contrast, the architecture of vascular networks is very complex, and is characterized by bifurcating, merging, and winding vessels (5). Furthermore, the network topology varies from organ to organ: vessels in muscles form arcade-type planar networks, whereas those in the retina and kidney have a treelike topology (6). In a tumor, blood vessels can have trifurcations and short-length shunts, adding further complexity to the geometry (7). In many organs, such as the brain, the average length of a vessel segment between two consecutive bifurcations is as small as a few vessel diameters (8, 9). Such geometrical differences result in significant deviations in hemodynamics between that achieved in a long straight tube versus a vascular network. For example, the hematocrit and velocity profiles over the cross section of a straight tube is naturally symmetric, but most likely asymmetric in vivo (10). Another prominent example is the difference in blood viscosity as determined in vitro and in vivo. In vitro viscosity, which is based on measurements in straight tubes, is found to be less than in vivo viscosity by several factors (11). An additional example is the self-sustained spontaneous oscillations in network flows that are absent in straight, unbranched tubes (12, 13, 14, 15, 16). Evidently, our understanding of blood flow in simple geometry is often inadequate to address the hemodynamics associated with the complex architecture of microvascular networks.

Direct simulation of cellular-scale blood flow in microvascular networks is, however, a daunting task. As such, alternative lower-dimensional approaches exist as a remedy. They generally involve treating each vessel as a 1D straight conduit, and using Poiseuille’s law to specify the pressure-flow relationship (8, 15, 16, 17, 18). Instead of modeling individual cells, the rheological effects of blood are added using empirical correlations for its viscosity, and measures are taken to account for hematocrit partitioning at vascular bifurcations. Although such approaches are able to consider a large number of vessels and have provided insights into the macroscale hemodynamics of vascular networks, they lack the ability to resolve the cellular-scale details that are important in many pathophysiological events, such as sequestration and localized adhesion of platelets, leukocytes, and drug particulates. Furthermore, many geometrical features of the networks that are of physiological importance, such as winding and noncircular vessels, are not considered in the lower-dimensional models. Evidently, the next generation of microvascular blood flow modeling must combine the cellular-scale details along with a realistic representation of in vivo network geometry.

Toward that end, in this article we present a modeling and analysis of blood flow in microvascular networks that resolves with high fidelity both the large deformation and dynamics of each individual blood cell and the highly complex architecture of the vasculature. To our knowledge, several novel and unusual phenomena with potentially significant physiological consequences are predicted. These anomalies are absent in blood flow in simple geometries, and are the direct result of the interaction between the discrete cells and the complex network architecture. This underscores the importance of utilizing realistic physiological geometries in conjunction with cellular-scale microphysics to better understand microvascular hemodynamics.

Materials and Methods

The numerical approach has been described in detail in our recent work (19), and is based on the immersed boundary method (IBM), which provides an accurate and efficient means of modeling the wide variety of complex interfaces present in microvascular network blood flow. The complex vascular walls are modeled using a sharp-interface ghost node IBM, whereas the deformable interfaces of the RBCs are modeled using a continuous forcing IBM. Each of these components is seamlessly integrated into the framework of a coupled finite-volume/spectral flow solver. This approach permits the simulation of actual physiological geometry, without requiring any simplifications or assumptions, while simultaneously resolving the cellular-scale details.

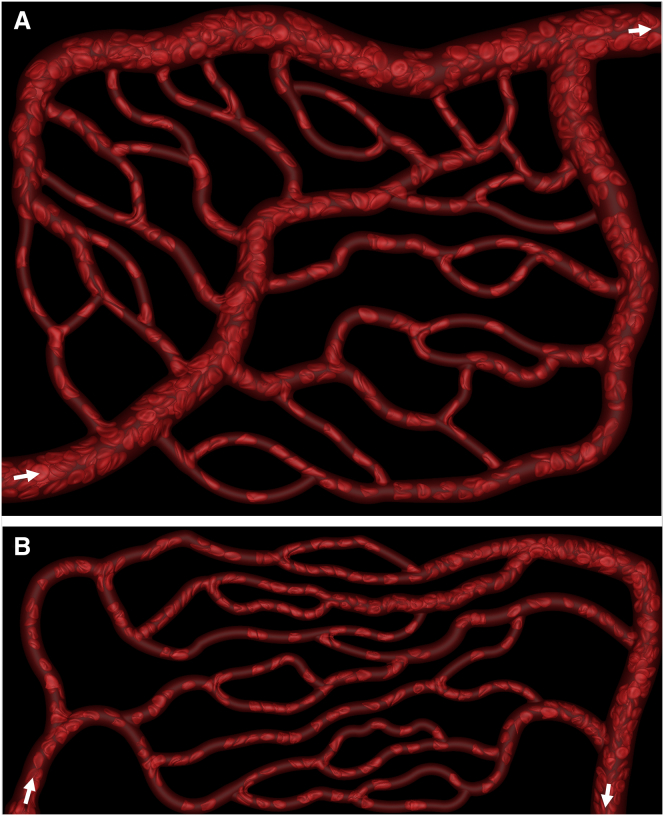
Microvascular networks have been constructed in silico following published in vivo images and data (5, 20, 21, 22, 23). Three different networks are considered, two of which are shown in Fig. 1, and the third in Fig. S3. All of our networks include bifurcating, merging, and winding vessels as observed in vivo. Each network has one main inlet and outlet, and is composed of arterioles, capillaries, and venules. Considering all three networks, there are in total 138 vessels and 45 bifurcations. The vessel diameters range from 6 to 24 μm, and the lengths range from 25 to 165 μm. The average overall path length from inlet to outlet ranges from 500 to 620 μm, and the overall volumes of the regions simulated are ∼1.6 × 10⁶ μm³. The average diameter and length of the capillary vessels are 6 and 68 μm, and the average diameter and length of all vessels are 9 and 65 μm, in agreement with in vivo data (5, 8, 20). In general, the network design utilizes the in vivo data in conjunction with Horton’s law, which describes the relationships between vessel diameters at bifurcations and mergers, capturing the fractal nature of the topology ((20); for details, see the Supporting Material). In each network the hierarchical structure is such that three orders of the Strahler ordering scheme are spanned on both the arterial and venous sides with the smallest capillaries being order zero. At the capillary level, across each of these topologies, the number of upstream bifurcations ranges anywhere from 2 to 12. The vessels are nondeformable with circular areas, but they generally have variable cross sections along their length.

Figure 1.

Snapshots from our direct simulations of blood flow through microvascular networks. Two of the three networks considered are shown. Additional images, animations, and the third network are given in the Supporting Material. Domain sizes are 283 × 222 × 25 μm in (A), and 386 × 165 × 23 μm in (B). Arrows indicate inlets and outlets. To see this figure in color, go online.

The network geometry is first constructed using a standard CAD software, and a triangulated mesh is then generated on the vessel surfaces using GMSH (24). This mesh defines in discrete space the vascular boundaries (see Fig. S4) through which the deformable erythrocytes flow. The total number of RBCs in the three networks considered is ∼1550. The hematocrit is initially maintained in the main feeding artery at ∼30%, and the subsequent cell distribution throughout the networks naturally develops and evolves. Simulations are performed in which flow is driven through the networks with either fixed pressure-boundary conditions or fixed flow-rate conditions. For pressure-boundary conditions, the overall pressure difference between the inlet and outlet is specified in accordance with published in vivo data as (0.3–1.0) Pa/μm ((3–10) × 10⁻³ cm H₂O/μm) (5, 23). For flow-rate boundary conditions, the mean flow rate in the main feeding artery is specified as (2–4.6) × 10⁻¹³ m³/s, also in agreement with in vivo data (5, 23). In total, 12 simulations are performed resulting in ∼550 time-averaged vessel measurements. Considering the number of RBCs passing through each of the networks over the course of the simulations, there are ∼20,000 data points utilized for studying RBC behavior at vascular bifurcations.

Table 1 shows the observed range of average flow rates at the simulation boundaries when the pressure drop is specified, and conversely, the observed range of pressure drops between the simulation boundaries when the flow rate is specified. As seen here, the flow rate specified in the second set of simulations is identical to the average flow rate that is observed in the first set of simulations for the midrange-specified pressure drop. Also, the resulting pressure drop in the second set is similar to those specified in the first set of simulations. Thus, there is no significant difference in terms of average pressure drop or flow rate in the two sets of simulations. Furthermore, any observed trends, phenomena, or conclusions drawn, were the same regardless of the type of boundary conditions specified. The exact time-dependent quantities, however, are different in each case because of the stochastic nature of particulate flow.

Table 1.

Two Different Boundary Condition Types Used in the Simulations

	Specified ΔP'	Resulting Q
	Pa/μm	(m3/s) × 1013
Network A	0.340	3.426
	0.450	4.627
	0.663	7.278
Network B	0.528	2.073
	0.696	2.839
	1.018	4.131
Network C	0.525	1.469
	0.698	2.055
	1.018	3.344
	Specified Q(m>3/s) × 1013	Resulting ΔP'Pa/μm
Network A	4.627	0.429
Network B	2.839	0.712
Network C	2.055	0.777

Specified pressure drop and resulting average flow rate, and specified flow rate and resulting average pressure drop between the simulation boundaries.

The resting shape of the RBCs is taken as the experimentally observed biconcave discocyte with an end-to-end distance of 7.8 μm, surface area 134.1 μm², and volume 94.1 μm³ (5). A continuum description of the cell is used by representing it as a viscous drop made of hemoglobin surrounded by a zero-thickness (i.e., 2D) hyperelastic membrane. The membrane is assumed to possess resistance against shearing, area dilation, and bending. The shearing deformation and area dilation are described following the strain energy function of Skalak et al. (25):

$$W_E=\frac{G_S}{4}\left[\left(I_1^2+2I_1-2I_2\right)+C{I}_2^2\right],$$ (1)

where G_S is the membrane shear elastic modulus, CG_S is the area dilation modulus, I₁ = ε₁² + ε₂² – 2 and I₂ = ε₁² + ε₂² – 1 are the strain invariants of the Green strain tensor, and ε₁ and ε₂ are the principal stretch ratios. The bending resistance is modeled following Helfrich’s formulation for bending energy,

$$W_B=\frac{E_B}{2}\underset{S}{\int }{\left(2\kappa -c_0\right)}^{2}dS,$$ (2)

where E_B is the bending modulus, κ is the mean curvature, c₀ is the spontaneous curvature, and S is the surface area (26). The viscosity of the plasma and hemoglobin is taken to be 0.001 and 0.005 Pa-s, respectively. Because inertia is negligible, the fluid motion is governed by the unsteady Stokes equations and the incompressibility condition

$$\rho \frac{\partial \mathbf{u}}{\partial t}=-\nabla p+\nabla \cdot \mu \left[\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\text{T}}\right]$$ (3)

$$\nabla \cdot \mathbf{u}=0.$$ (4)

The computational domain resembles a box, and is discretized using a rectangular, fixed (Eulerian) mesh of ∼8 × 10⁷ points. The entire network along with the RBCs is immersed in this domain. The no-slip condition is satisfied on the vascular walls using the ghost-node IBM, which enforces a constraint on the Eulerian points immediately exterior to the vascular walls (see Supporting Material for additional details). The details of the method and rigorous validations are provided in our prior work (19). The surface of each cell is discretized using 5120 Delaunay triangles. A finite-element method is used to compute the elastic tension f_E at each vertex of the surface triangles. An expression of bending force density f_B derived from (2) is used. The membrane forces are coupled to the bulk fluid by introducing a source term in the Stokes equation utilizing the 3D Dirac delta function. Details of the computation of f_E and f_B are given in our previous works along with validations for deformable cells (19, 27, 28, 29). Further validations and additional salient details of the methodology are provided in the Supporting Material.

Results

Snapshots of our simulations for two of the networks are shown in Fig. 1. Animations and additional images are given in Figs. S1, S2, and S3, and Movies S1 and S2. As seen here, our virtual microvascular networks are highly complex in geometry and representative of realistic in vivo situations. Cell distributions naturally develop in the networks based on the architecture. Some vessels are observed to be filled with RBCs, whereas others have a reduced number of cells, as is the case in vivo. Extreme deformation and a wide range of RBC shapes are observed as they flow through the networks. In the smallest capillary vessels, cells are observed to assume elongated bullet/parachute and slipper shapes, and flow in a tight-filled, single-file manner. The shapes are never axisymmetric, due to the geometric effects. Two- and multifile motions are observed in larger vessels. In the main feeding and collecting vessels, discoid shapes are often observed. Formation of cell-free regions near vascular walls, and plasma skimming at arterial bifurcations, are observed here. The predicted shapes of individual cells in capillary vessels agree well with experimentally observed shapes, and are compared in Fig. S5.

Comparison with in vivo data

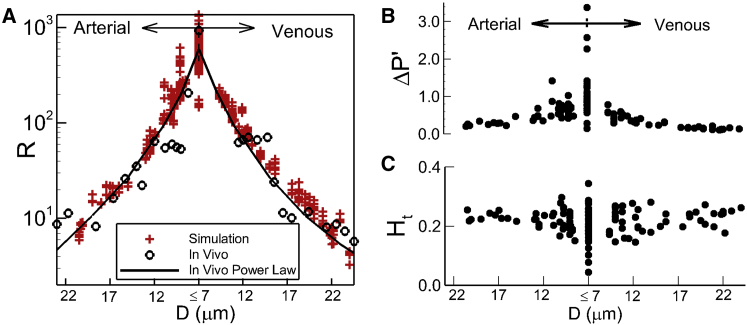
Fig. 2 A provides a quantitative comparison of vascular flow resistance determined from our simulations against in vivo data (23) obtained in the mesentery of a cat. The simulation data reported is from all three networks with each of the considered boundary conditions. Data is time-averaged over ∼0.7 s, during which time the transient patterns in flow properties in each of the network vessels are in a quasi-steady (cyclic) state. Each simulation data point in the figure is the time-averaged data from one vessel, with the corresponding vessel diameter on the abscissa. The time-averaged flow resistance per unit length of a vessel is defined as R = ΔP′/Q, where ΔP′ and Q are the time-averaged pressure drop per unit length and flow rate, respectively, in each vessel. A good agreement between the simulations and the in vivo data is noted. The resistance is maximum at the capillaries and decreases on both the arterial and venous sides with a fourth-order dependence on vessel diameter, as in a Poiseuille’s law relationship. Comparisons of predicted time-averaged pressure drop, wall shear stress, and blood viscosity also agree well with in vivo data, and are shown in Fig. S6.

Figure 2.

(A) Given here is a comparison of predicted time-averaged vascular resistance R per unit length (red symbols (in Pa/(m³/s)/μm × 10⁻¹¹) against in vivo data (black circles) and fourth-order power law (line) fit of in vivo data (23). (B and C) Given here is a time-averaged pressure drop per unit length ΔP′ (in Pa/μm) and hematocrit in different vessels across the networks. To see this figure in color, go online.

Comparisons are made with in vivo data to generally show that predictions from the in silico networks are quantitatively very similar to what has been observed in vivo. It is noted that in physiology the architecture of a network is organ-specific, and thus the simulated networks for this work are more of an average representation of a network structure or hierarchy. As such, the simulation results presented in the subsequent sections are not intended to be representative of what would be found only in the network of a particular organ. Rather, our conclusions and observations represent commonalities associated with general microvascular network topology.

A hallmark of microvascular blood flow is heterogeneity. Prior in vivo studies have reported wide variations of hemodynamic quantities across different vessels within a network (5, 23). Our simulation data reveal a similar heterogeneity. Fig. 2 A shows that the flow resistance can vary by a factor of 4 in vessels of the same diameter within a network. Time-averaged pressure drop per vessel length is presented in Fig. 2 B, which shows nearly an order-of-magnitude variation across capillaries of similar diameters, implying a high-degree of heterogeneity. Fig. 2 C presents the distribution of time-averaged hematocrit. A high degree of heterogeneity is also observed here, where H_t is seen to range from ∼0.04 to 0.35 in the capillaries. This observation also qualitatively agrees with in vivo studies reporting that whereas some capillary vessels are filled with cells, some are almost devoid of cells. Interestingly, we note that the degree of heterogeneity decreases with increasing vessel diameter. This is expected, as it is shown later that the underlying mechanism of heterogeneity is the particulate nature of blood, which has a diminishing effect with increasing vessel diameter. A similar high degree of heterogeneity is also observed in the time-averaged flow rate, wall shear stress, and blood viscosity as predicted by our simulations, and is shown in Figs. S6 and S7.

Temporal heterogeneity

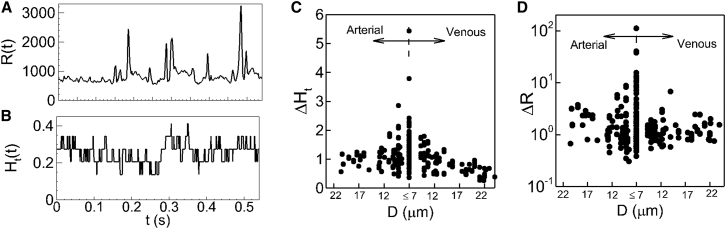
The heterogeneity discussed in prior in vivo studies and shown in Fig. 2 from our simulations represents spatial heterogeneity, i.e., the data for each vessel is averaged over time. In addition to this spatial heterogeneity, our simulations reveal a temporal heterogeneity. That is, hemodynamic quantities show a high degree of variation over time even within one vessel in a network. Variations of flow resistance and hematocrit over time are shown in Fig. 3, A and B, for a specific vessel. As seen here, over time H_t varies from ∼0.13 to 0.41, and $R$ varies from ∼650 to 3200 Pa/(m³/s)/μm × 10⁻¹¹ (500–2400 mm Hg/(mm³/s)/μm) in the specific vessel considered. Similar temporal fluctuations in pressure drop and flow rate are also observed (data given in Fig. S8).

Figure 3.

Temporal heterogeneity. (A and B) Given here is the time history of resistance R(t) (in Pa/(m³/s)/μm × 10⁻¹¹) and hematocrit H_t(t) in one vessel in the network shown in Fig. 1A. (C and D) Shown here are the amplitudes of temporal variations in hematocrit (ΔH_t) and resistance (ΔR) in each vessel.

To quantify the degree of temporal heterogeneity, we measure the amplitude of fluctuation, defined as the difference between the maximum and minimum of flow quantities over the entire simulation time. We then plot the amplitudes scaled by the mean quantities for each vessel in the networks. Fig. 3, C and D, shows distributions of the hematocrit amplitude ΔH_t, and resistance amplitude ΔR. As seen here, the amplitudes exhibit large variations within individual vessels of similar size. ΔH_t varies from ∼0.35 to 5, implying that H_t in a specific vessel at some instances is five times higher than the average value. Distribution of ΔR is even more dispersed as it varies from ∼0.35 to >100, implying that in a specific vessel, flow resistance at certain time instances can be 100-times the average value. Temporal heterogeneity is also observed in pressure drop and flow rate, and is given in Fig. S8. Flow-rate and pressure-drop amplitudes are observed to be as high as 180 and 600%, respectively, of the average values. The magnitude of the time-dependent variable amplitudes is, therefore, significant. Such temporal heterogeneity could be more severe than the spatial heterogeneity when Figs. 2 and 3 are compared. Similar to the spatial heterogeneity, the temporal heterogeneity is maximum in the capillary vessels, and decreases with increasing vessel diameter. The temporal heterogeneity is entirely due to the particulate nature of the blood, which becomes more pronounced in smaller vessels. It would not occur in absence of the cells, and the flow would remain steady.

Note that temporal fluctuations in flow quantities are also present in long, straight vessels, but with significantly smaller amplitudes, often in the range of a few percentage of the mean. In contrast, temporal fluctuations observed in our network simulations exhibit amplitudes that are several factors, and often orders, higher than the mean. As shown later, such temporal fluctuations have severe consequences in pressure-flow and hematocrit-resistance correlations.

RBC jamming at vascular bifurcations

We find that the origin of this significant temporal heterogeneity in the networks is the dynamics of the cell suspension near vascular bifurcations. At all of the vascular bifurcations in the three networks considered, RBCs tend to linger for a while before eventually flowing into the daughter vessels (Fig. 4 A; see Figs. S9 and S10 for additional images; Movies S3 and S4). Although lingering is observed at all bifurcations, it is most pronounced at the capillary bifurcations. During such events, cells near the bifurcations significantly stretch and straddle around both daughter vessels, causing incoming cells to pile up and partly block the entrance to the daughter vessels. Consequently, the flow rates in the daughter vessels are reduced. Lingering is a dominant event observed in our simulations. It can be easily noticed in all of the animations provided in the Supporting Material. Under extreme cases, the lingering is observed to be so severe that it can jam a bifurcation and nearly stop the flow in the affected branches (see Fig. S11; Movies S3 and S4).

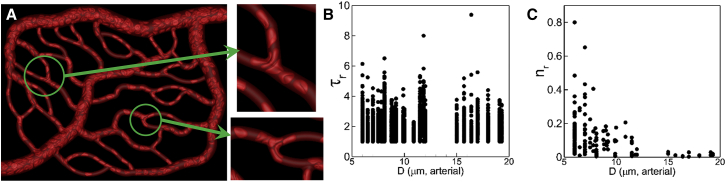
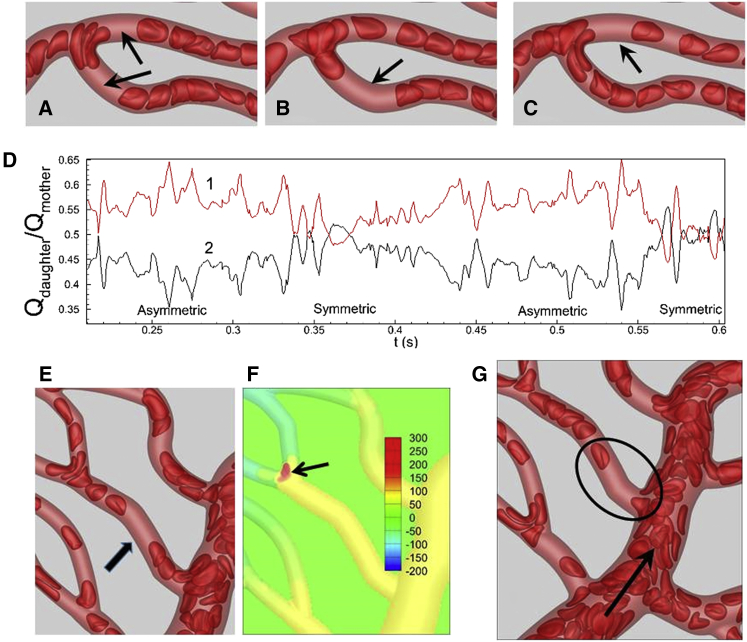
Figure 4.

(A) RBCs are observed to linger (or, jam) at capillary bifurcations. (B and C) Given here is RBC residence time τ_r (dimensionless) and frequency of lingering n_r at bifurcations. To see this figure in color, go online.

To quantify the lingering phenomenon, we compute the dimensionless residence time τ_r = t_r/t₀ of each cell, where t_r is the time spent by an RBC lingering at a bifurcation and t₀ is the time taken by an RBC to pass through the bifurcation without lingering. We also compute the frequency n_r of lingering as the ratio of the number of cells lingering for an extended time to the total number of cells passing through a bifurcation over the entire simulation time. Both quantities are plotted in Fig. 4, B and C, as functions of arterial diameter. As seen here, on average the maximum t_r varies between 4 and 6 over the entire range of diameters considered. This means that at all vascular bifurcations cells can linger 4–6 times longer than the time it would take without lingering. Therefore, the lingering time is significant, and it occurs in all arterial bifurcations. Further, the frequency of lingering is the highest in the capillary vessels and decreases with increasing vessel diameter. Thus, the lingering events are more frequent at the capillary bifurcations.

We find that during a lingering event, the cells at the bifurcation can straddle the daughter vessels either symmetrically or asymmetrically (Fig. 5, A–C; Figs. S9 and S10; Movies S3 and S4). In many bifurcations, we find that the cell lingering occurs in a periodic manner in which the cells straddle more near one daughter vessel at one time, but near the other daughter vessel at other times (Fig. 5, B and C). This is because when cells linger asymmetrically, hematocrit is reduced in the branch that is partially blocked, but is increased in the other branch. As hematocrit builds up, cells start to straddle the second branch, freeing up the first branch which was blocked before. This periodic change in asymmetric lingering favoring one branch or the other requires a continuous influx of cells in the mother vessel. If for any reason hematocrit in the mother vessel is significantly reduced, an asymmetric lingering favoring one daughter vessel can last much longer. Often times we find that as an asymmetric lingering switches from one side to the other, a symmetric lingering can occur in between (Fig. 5). We further find that a symmetric blockage lasts for a longer time, whereas an asymmetric lingering occurs more frequently.

Figure 5.

(A) Shown here is symmetric lingering. (B and C) Shown here is asymmetric lingering in which daughter vessels are blocked periodically. Arrows indicate formation of voids in RBC trains. (D) Shown here is periodic oscillation in flow rates in daughter vessels in (B) and (C) due to switching from symmetric to asymmetric lingering. The flow rates in two daughter vessels are scaled by that in the mother vessel. (E) Given here is void formation (shown by an arrow) in the mother vessel due to cell lingering at a downstream bifurcation. (F) Given here is pressure distribution in arbitrary units showing increased pressure (arrow) at the bifurcation due to cell lingering. (G) Given here is void formation in capillary vessels that emerge from the same side of an arteriole. The arrow indicates flow direction. To see this figure in color, go online.

Cell lingering results in hematocrit reduction upstream and downstream

An immediate consequence of the cell lingering is a reduction of hematocrit in daughter vessels. The hematocrit reduction is manifested by formation of voids in the RBC train, i.e., vessel segments that are devoid of cells (Fig. 5, A–C). For a symmetric lingering, voids are formed in both daughter vessels, whereas for an asymmetric lingering void, formation switches between one branch and the other depending upon which daughter vessel is temporarily blocked. During the periods of time when asymmetric lingering events are predominantly occurring, the flow rates between the two daughter branches tend to be imbalanced. Conversely, when symmetric lingering events are occurring, the flow rates tend to be balanced. Such cycling can be observed in the time-dependent flow rate ratios during symmetric and asymmetric lingering events, as shown for two daughter branches in Fig. 5 D.

Cell lingering at bifurcations not only reduces hematocrit in the daughter vessels, it can also reduce hematocrit in the mother vessel by forming voids. This rather unusual event is shown in Fig. 5 E. Cell lingering at the specific bifurcation considered here increases the local pressure, as shown in Fig. 5 F. Consequently, the pressure difference along the mother vessel decreases. Due to the reduced pressure gradient, RBCs from the main feeding arteriole cannot enter the mother vessel, which leads to the formation of a void.

RBC voids, therefore, are the footprints of cell lingering at bifurcations. The significant temporal heterogeneity as noted earlier is a direct consequence of cell lingering, or alternatively, void formation. In general, voids are present in many vessels throughout the networks (Fig. 1, A and B; Figs. S1–S3, and S9), but are not always the result of cell lingering at bifurcations. Another mechanism of void formation is depicted in Fig. 5 G. This mechanism is observed when two capillary vessels emanate from the same side of a larger arteriole. If cells are drawn in to the first capillary, a cell-free layer is formed along that side of the arteriole. If the distance between the two side branches is not large, the cell-free layer persists, resulting in the formation of a void in the second capillary.

The implications of cell lingering and void formation are significant, and are discussed next in terms of the relationships between different hydrodynamic quantities.

Negative pressure-flow correlation

We first consider the relationship between flow rate (Q)and pressure drop per unit length (ΔP′) in each vessel in our networks. For a long, straight vessel, this relationship is expressed in terms of the well-known Poiseuille’s law as

$$\Delta P^{\mathit{\text{'}}}=R\cdot Q,$$ (5)

Where $R$ is the hydrodynamic resistance per unit length of the vessel. Although valid for long, straight vessels, this relationship is often used in analyzing in vivo data, and also in lower-dimensional modeling of microvascular networks, as noted previously. Poiseuille’s law implies a positive correlation between pressure drop and flow rate, i.e., an increase in pressure drop results in an increase in flow rate, and vice versa.

Do our direct simulations of microvascular networks also yield positive pressure-flow correlations? To investigate this, we compute the pressure drop-flow rate correlation coefficient $C_{\Delta P^{\mathit{\text{'}}}-Q}$ defined as

$$C_{\Delta P^{\mathit{\text{'}}}-Q}=\frac{\langle \left[\Delta P^{\mathit{\text{'}}}\left(t\right)-\langle \Delta P^{\mathit{\text{'}}}\rangle \right]\cdot \left[Q\left(t\right)-\langle Q\rangle \right]\rangle }{\sqrt{\langle {\left[\Delta P^{\mathit{\text{'}}}\left(t\right)-\langle \Delta P^{\mathit{\text{'}}}\rangle \right]}^2\rangle \cdot \langle {\left[Q\left(t\right)-\langle Q\rangle \right]}^2\rangle }},$$ (6)

where ΔP′(t) and Q(t) are the time-series pressure-drop per unit length and flow-rate data in each vessel, and 〈 〉 represents a time-averaged quantity. This correlation coefficient is presented in Fig. 6 A. As seen in the figure, for most vessels $C_{\Delta P^{\mathit{\text{'}}}-Q}$ is positive, confirming the validity of Poiseuille’s law for capturing the general behavior of blood flow in microvessels. However, it can also be noted that for many vessels, the correlation coefficient is very weak. Most strikingly, for several vessels the coefficient is negative. This implies that, for these vessels, an increase in pressure drop is accompanied by a decrease in flow rate, which is in stark contrast to the positive pressure-flow correlation implied by Poiseuille’s law.

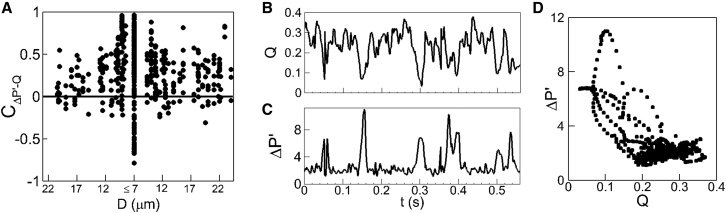
Figure 6.

(A) Shown here is the pressure-drop flow-rate correlation $C_{\Delta P^{\mathit{\text{'}}}-Q}$ obtained in our network simulations. Each data point represents individual vessels. (B and C) Shown here is a time series of flow rate (in m³/s × 10¹³) and pressure drop per unit length (in Pa/μm) in a vessel giving a negative pressure-flow correlation. (D) Given here is a scatter plot of ΔP′(t) versus Q(t) for a specific vessel. See text for an explanation.

The origin of these negative correlations is the RBC lingering phenomenon at vascular bifurcations. Due to cell jamming at a bifurcation, the flow rate into the daughter vessels decreases, while at the same time the pressure at the entrance of the daughter vessel increases, resulting in an increase in pressure drop. A time series of ΔP′(t) and Q(t) for one such vessel is shown in Fig. 6, B and C. It is readily seen here that large increases in ΔP′(t) at ∼0.16, 0.3, and 0.4 s are accompanied by large drops in Q(t). As is evident from the behavior in this vessel, the magnitudes of these temporary increases in ΔP′(t) and reductions in Q(t) can be significant, and in vessels where such events occur frequently, a negative pressure-flow correlation results. As noted in Fig. 6 A, large negative correlations are observed in the smallest diameter capillaries, because it is there that the jamming events are most severe. Large negative correlations are also observed in capillary vessels that directly discharge into venules of much larger diameter.

Further insights into the negative ΔP′ − Q correlation can be obtained by plotting ΔP′ versus Q and analyzing the nature of the data scatter. This is shown in Fig. 6 D for a specific vessel, and data points are obtained at 0.0005 s intervals. The magnitude and frequency of the pressure-drop and flow-rate pulses causing the negative correlation are evident here. The lower-right portion of the figure showing a dense clustering of data points suggests that for most of the simulation, a positive correlation exists. On the other hand, the data points associated with the lingering events causing a negative correlation appear in the middle to upper-left of the figure. Whereas the range over which these data points appear is much greater in magnitude, indicating the severity of the lingering events, the reduced density of the data cluster is indicative of the reduced frequency with which they occur.

Additional data on ΔP′ − Q correlations are given in Fig. S12.

Temporal spikes in vascular resistance

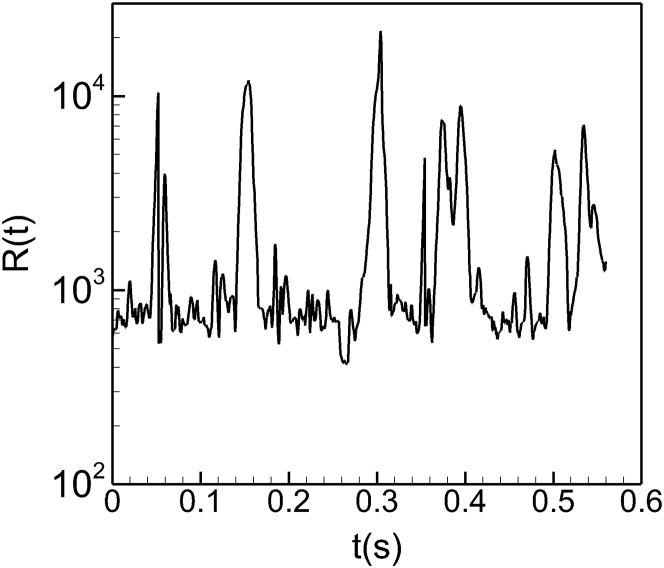
An important consequence of the negative pressure-flow correlation is significant temporal spikes in vascular resistance. Regardless of the correlation behavior, as the flow rate through a vessel decreases the hydrodynamic resistance increases. However, as is clear from Eq. 5, an increase in ΔP′ corresponding to a decrease in Q results in a much more significant increase in resistance than in a vessel with a positive ΔP′ − Q correlation. The time-dependent resistance R(t) of one vessel is shown in Fig. 7, which shows spikes during which the resistance increases by as much as 50 times the average value. Additional data are in Fig. S13. The source of this significant increase in the vascular resistance is the cell lingering at bifurcations. Because of the cell lingering, the flow rate into the daughter vessel decreases whereas the pressure near the entrance to the daughter vessel increases. Consequently, the pressure drop in the daughter vessel increases. This, together with the decrease in flow rate, results in a large increase in resistance.

Figure 7.

Time series of vascular resistance in one vessel showing temporal spikes resulting in a nearly 50-times increase in resistance compared to the mean.

Negative hematocrit-resistance correlation

In microvascular blood flow, and particulate suspension flows in general, the flow resistance increases with increasing hematocrit, or particulate volume fraction. Thus, in general, a positive correlation exists between the vascular resistance and hematocrit. Indeed, empirical relations exist based on in vivo and in vitro data relating these two quantities (11). To see if our simulated networks yield a positive correlation between the time series of vascular resistance R(t) and hematocrit H_t(t), we compute a hematocrit-resistance correlation coefficient $C_{R-H_t}$ defined in a similar manner to Eq. 6. This coefficient is plotted in Fig. 8 A for all vessels in the networks. As can be seen in this figure, on average most vessels yield a positive correlation, implying the usual trend that the vascular resistance increases with increasing hematocrit. However, in several vessels the correlation coefficient is either very small or, interestingly, is negative. This reveals a rather unusual phenomenon: in these vessels, resistance increases with decreasing hematocrit, or vice versa.

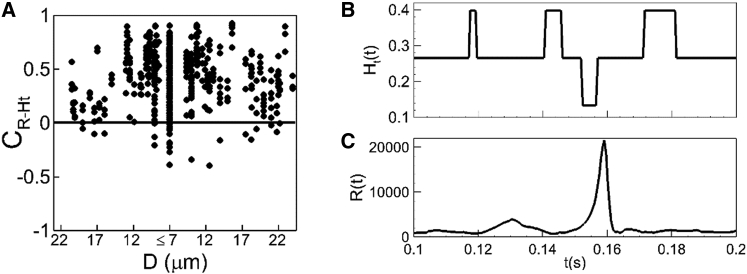
Figure 8.

(A) Given here is the hematocrit-resistance correlation $C_{R-H_t}$. Each data point represents an individual vessel. (B and C) Given here is a time series of hematocrit H_t(t) and resistance R(t) in one vessel showing a negative hematocrit-resistance correlation.

As with the ΔP′ − Q correlation, the origin of the negative R − H_t correlation is the cell lingering at bifurcations. It was noted earlier that the lingering events result in hematocrit and flow-rate reductions in the daughter vessels. At the same time, pressure increases significantly around the bifurcation region, resulting in an increase in the pressure drop in the daughter vessels. Consequently, resistances in these vessels go up despite reductions in hematocrit, resulting in the negative correlation. Fig. 8, B and C, shows one such example for a specific vessel. Here H_t(t) drops from 0.4 to 0.12 at ∼0.15–0.16 s, but R(t) increases by nearly 50 times, resulting in a large negative correlation during this event. At other times, e.g., around 0.12, 0.14, and 0.18 s, H_t(t) increases to 0.4, but R(t) does not show a significant jump, implying that at these times there is also not a strong positive correlation between the two quantities.

Additional data on R – H_t correlation are given in Fig. S14.

An interesting feature of the negative R – H_t correlation is that it takes on a different meaning based on the location of the vessel in the network hierarchy. For capillaries or other vessels on the arterial side (i.e., daughter branches or mother branches), the negative correlation implies an increase in resistance accompanied by a decrease in hematocrit. That is, it occurs as a direct result of the RBC void formation due to lingering, as previously discussed. For vessels on the venous side, however, a negative correlation results from an opposite trend: the resistance decreases with increasing hematocrit. This is observed to occur as an indirect result of the RBC void formation due to lingering. Because of this, the behavior is not dominated by the pulses as with the other negative correlations, but rather is observed over longer periods of time.

This latter behavior is observed in venules that are fed by two merging vessels each with distinctly different RBC patterns. For example, if one feeding vessel has a steady flow of RBCs and the other has a very intermittent flow, then this form of negative correlation occurs. A prominent cause of intermittent flow is the RBC voids generated due to lingering at the bifurcation feeding that vessel. As these voids migrate through the capillary and enter the venule into which it merges, this type of negative correlation results. The hydrodynamic explanation behind this is that in the outlet venule the hematocrit increases with an increase in Q and small change in ΔP′ (i.e., increase in H_t with decrease in R). The first event in the development of this negative correlation is the formation of a void in the vessel feeding the venule. Following this, the void moves through the capillary and into the venule. Thus there is a volume flow-rate contribution to the discharge venule, without a hematocrit contribution. In the downstream vessel this ultimately results in an increase in volume flow rate with little change in ΔP′. Figures are provided in the Supporting Material that further describe this process (Fig. S15).

Discussion

We have presented, to our knowledge, the first 3D simulations studying blood flow in microvascular networks that capture both the cellular-scale microphysics and the highly complex physiological architecture. The number of vessels and bifurcations considered, and the network volumes simulated, as well as the amount of time-averaged data obtained are comparable to the typical volume of data utilized with in vivo analyses. Whereas time-averaged hemodynamic quantities agree quite well with published in vivo data, our simulations also elucidate cellular-scale events at small timescales that are usually not captured in experiments. To our knowledge, several novel and unexpected phenomena are observed from such time-resolved simulations that are the result of the complex interactions between the RBCs and the vascular geometry.

Prior in vivo studies have shown that the distribution of hemodynamic quantities across a microvascular network is heterogeneous; quantities vary across different vessels of similar size (see, e.g., (2, 15, 30)). The heterogeneity referred to in many of these studies is spatial heterogeneity, as quantities are averaged in time. Similar spatial heterogeneity is observed in our simulations. However, a more severe type of heterogeneity is revealed in our simulations when time-dependent data is considered. We show that within the same vessel, hemodynamic quantities can greatly vary over time. Amplitudes of these temporal variations could be several factors and even orders-of-magnitude higher than the average values. This high degree of temporal heterogeneity is absent in blood flow in straight tubes where fluctuations in hemodynamic quantities occur solely due to cell-cell interactions.

In terms of quantifying heterogeneity in microvascular networks, various in vivo works have been performed in which velocities in capillaries were utilized. Considering all of the capillary vessels from each network simulation, the average velocity was ∼0.7 mm/s. This is generally in agreement with the in vivo work of Kleinfeld et al. (31), who measured the average velocities in the neocortical capillaries of a rat to be in the range of 0.5–1.6 mm/s. Similar values have been reported in other in vivo works as well (23, 32, 33). With regard to the time-dependent velocities in all of the capillary vessels from the simulations, these were observed to fluctuate by as much as 2 mm/s, which is also in general agreement with the in vivo work of Tomita et al. (34), who found velocities in capillaries to vary by as much as 1.6 mm/s. Various other in vivo studies on capillary blood flow have been performed (35, 36, 37) in which velocity ranges have been reported to be on the same order as that computed in our simulations.

We show that a major cause of the temporal heterogeneity is the piling-up (i.e., lingering) of RBCs near vessel bifurcations. RBC lingering has been observed in prior in vivo works (e.g., (34, 38)), as well as computational works (39). Often, RBC lingering in our simulations occurs in a cyclical manner resulting in a quasi-periodic variation in hemodynamic quantities that is completely independent of the cardiac cycle. We show that lingering can reduce the hematocrit and flow rate not just in the daughter vessels, but also in the mother vessels. Significant transient events are known to occur when considering the flow of whole blood (40, 41). Periodic oscillations have been predicted in lower-dimensional theoretical modeling of microvascular networks (14, 15, 16), and observed both in vivo (12) and in microfluidic networks (13). Specifically, the experimental studies in (12, 13) considered whole blood, and Forouzan et al. (13) ascribed such oscillations to capillary blockage by leukocytes. In general, inactivated leukocytes are much stiffer than the RBCs and have a much larger transit time through a capillary vessel (42). Thus, oscillations resulting from leukocyte blocking are likely to have a lower frequency than those resulting from RBC lingering. Forouzan et al. (13) also presented power spectra of time-series data, and found different maxima depending on the presence of RBCs only, or RBCs with leukocytes. Our data also show the maxima to occur at the lower end of the frequency spectrum, with the magnitude of the total power fraction on the same order as in (13). However, the range of frequencies in the two studies is significantly different. Our simulations represent 0.7 s of flow, during which ∼1500 samples are taken. The range of frequencies obtained in our simulations is on the order of hundreds of Hz. Thus the fluctuations in flow quantities in the capillaries in our simulations, such as flow rate, directly correspond to individual RBC behavior as each passes through an individual bifurcation. In contrast, in (13), measurements are made over a time interval of 5 min with a sampling frequency of 100 Hz, resulting in a frequency range of <1 Hz. So the fluctuations are more associated with that of either bulk RBC motion, or events that occur over much longer times, such as capillary blockage by white blood cells. Nonetheless, RBC lingering serves as a major cause of microvascular heterogeneity, and is observed throughout our simulations at all bifurcations. Under extreme circumstances it may cause temporary flow stoppage, as also observed in our simulations.

An interesting question concerning the nature of heterogeneity is whether it is a stochastic phenomenon. On the one hand, in a more general sense, heterogeneity can be viewed as deterministic. First, we are able to directly link the RBC lingering events to being the cause of the prominent temporal fluctuations. Second, we are able to link the frequency of these events to vessel size. So in this sense, the degree of heterogeneity is dictated by vessel size, and thus it can be viewed as a deterministic phenomenon. On the other hand, the underlying mechanisms behind each of these time-dependent events that give rise to such heterogeneity, do resemble that of a stochastic phenomenon. The nature of the process that led to the RBCs being in their particular configuration and the deformed states that caused them to pile-up in a manner resulting in this temporary blockage, can be viewed as stochastic in that all of the subsequent RBC interactions leading up to this are too complex to discern a pattern. Thus, heterogeneity can be considered a stochastic phenomenon if one considers the individual events that comprise the averages in quantities.

Vascular resistance is an important quantity that directly controls the amount of blood flow in specific vessels. Blood viscosity measured in vivo was shown to be higher than that measured in vitro using long, straight tubes (11, 30). Accordingly, the in vitro viscosity law would underpredict the network flow resistance. The higher in vivo resistance is attributed in part to the presence of the glycocalyx layer on the surface of endothelial cells lining the blood vessels (43). Our simulations provide another mechanism for increased flow resistance in a network. We show that the cell lingering causes large temporal spikes in vascular resistance. In some instances, magnitudes of these spikes are observed to be orders larger than the mean. This result is in agreement with a prior in vitro study that reported an order-of-magnitude increase in pressure gradient at a bifurcation while flowing deformable disk-shaped particles (44). The lingering mechanism, therefore, can account for the higher in vivo flow resistance.

The cell lingering as observed here may have far-reaching consequences. We show that in several vessels, it results in negative pressure-flow correlations, meaning that an increase in pressure drop is accompanied by a decrease in flow rate, in stark contrast to the positive pressure-flow correlations implied by Poiseuille’s law. In a tube flow, the pressure loss is synonymous with the shear stress and the flow rate is synonymous with the rate of strain. The negative correlation then implies that an increase in stress results in an increase in fluid viscosity. Thus, the blood behavior in these vessels resembles that of a shear-thickening fluid as opposed to a shear-thinning fluid.

An important point to note, however, is that the negative pressure-flow correlation happens only over the periods of time when the lingering events occur. Outside of these lingering events, conditions follow the positive pressure-flow correlation. What this suggests is that in vessels with negative correlation coefficients, the average behavior is dominated by the pulses in flow properties resulting from RBC lingering. If the magnitude of these pulses and/or the frequency with which they occur is significant enough, then negative correlation coefficients result. Although events of this nature are observed in all capillary vessels, the severity of these events varies from vessel to vessel.

The pulses in flow properties caused by the cell lingering would also result in similar time-dependent behavior in the wall shear stress. It is known that both the average and time-dependent variations of the wall shear stress affect the endothelial cell response triggering diverse physiological events. Our findings suggest that in a microvascular network the nature of the time dependence may be dominated by the lingering-induced pulses in the shear stress.

Negative correlations are also found between vascular resistance and hematocrit in several vessels, implying that the flow resistance increases in these vessels whereas hematocrit decreases. This also defies the principle of particulate suspension flow, and is a result of the lingering events that are severe in nature. We observe that the negative resistance-hematocrit correlation serves as a feedback mechanism; cells in the feeding artery can sense the lingering occurring in a downstream bifurcation via the fluid pressure, and be temporarily rerouted avoiding the mother vessel. This autoregulatory function provides a mechanism for efficient distribution of the cells across the network.

Cell lingering is observed to result in the formation of RBC voids in daughter and mother vessels. In prior studies using simple geometry, such as straight tubes, it has been observed that RBCs naturally form clusters and voids purely by cell-cell hydrodynamic interactions (45, 46). In fact, in our simulations voids are also observed to form as a result of cell-cell interactions just as they would in a straight tube. However, when this occurs, a positive resistance-hematocrit correlation is observed. The additional interaction with the vascular geometry is also required for a negative correlation to manifest.

As noted before, these anomalous results cannot occur in flow through straight tubes, and they underscore the importance of considering realistic physiological geometry and cellular interactions in modeling microvascular hemodynamics. These anomalies may become even more severe when whole blood is considered due to both RBC lingering and leukocyte blockage (40). Additionally, diseased RBCs are known to have widely different rheological properties, which can also enhance such events. The magnitude and frequency of such events as observed in our simulations warrants further study into the impact of such events on important physiological phenomena, such as the adaptation mechanisms in the microvasculature at the cellular scale, oxygen and nutrient transport, and efficiency of drug delivery.

For this work, we have utilized RBC membrane properties typical of an average, healthy cell. The effects of the cell properties on the network hemodynamics are not considered here. Specifically, our model does not consider membrane viscosity, which has been a subject of interest in some recent works (47, 48). In our prior works (28, 49) we have shown that the usual value of membrane viscosity does not change the qualitative nature of the RBC deformation; rather, it changes the timescale of transient recovery. Thus, inclusion of membrane viscosity would not alter the occurrence of the phenomena that are observed in our simulations, such as RBC jamming. Of course, in the extreme case of unusually large membrane viscosity, the jamming effect could be very severe.

Conclusions

This work presents, to our knowledge, the first direct simulation of 3D cellular-scale blood flow in physiologically realistic microvascular networks. Prediction of time-averaged hemodynamic quantities agree well with published in vivo data. The RBCs are observed to linger at vascular bifurcations resulting in hematocrit and flow reductions in daughter and mother vessels. The cell lingering results in orders-of-magnitude increase in vascular resistance, and thus provides an additional mechanism for increased blood viscosity in vivo as opposed to in vitro. In several vessels, we find negative pressure-flow correlations in stark contrast to Poiseuille’s law. We also find negative resistance-hematocrit correlations in some vessels, again defying the principle of particulate suspension flows.

Author Contributions

All authors equally contributed in designing and performing research, analyzing data, and writing the article.

Editor: James Grotberg.

Supporting Material

Movie S1. Simulation of RBCs Flowing in the Microvascular Network

See Fig. 1 A in the main text.

Movie S2. Simulation of RBCs Flowing in the Microvascular Network

See Fig. 1 B in the main text.

Movie S3. Closeup Showing Cell Lingering at Bifurcations in the Bottom Part of the Network Shown in Fig. S1

The cell lingering at the top bifurcation causes temporary flow stoppage in the daughter vessels.

Movie S4. Closeup Showing Cell Lingering at Bifurcations in the Top Part of the Network Shown in Fig. S1

The cell lingering on the right causes temporary flow stoppage in the daughter vessels.