Physical Mechanisms Driving Cell Sorting in Hydra

Abstract

Cell sorting, whereby a heterogeneous cell mixture organizes into distinct tissues, is a fundamental patterning process in development. Hydra is a powerful model system for carrying out studies of cell sorting in three dimensions, because of its unique ability to regenerate after complete dissociation into individual cells. The physicists Alfred Gierer and Hans Meinhardt recognized Hydra’s self-organizing properties more than 40 years ago. However, what drives cell sorting during regeneration of Hydra from cell aggregates is still debated. Differential motility and differential adhesion have been proposed as driving mechanisms, but the available experimental data are insufficient to distinguish between these two. Here, we answer this longstanding question by using transgenic Hydra expressing fluorescent proteins and a multiscale experimental and numerical approach. By quantifying the kinematics of single cell and whole aggregate behaviors, we show that no differences in cell motility exist among cell types and that sorting dynamics follow a power law with an exponent of ∼0.5. Additionally, we measure the physical properties of separated tissues and quantify their viscosities and surface tensions. Based on our experimental results and numerical simulations, we conclude that tissue interfacial tensions are sufficient to explain cell sorting in aggregates of Hydra cells. Furthermore, we demonstrate that the aggregate’s geometry during sorting is key to understanding the sorting dynamics and explains the exponent of the power law behavior. Our results answer the long standing question of the physical mechanisms driving cell sorting in Hydra cell aggregates. In addition, they demonstrate how powerful this organism is for biophysical studies of self-organization and pattern formation.

Introduction

How a pattern emerges from an initially near-uniform cell population is a question that has long fascinated biologists and physicists alike, in particular D’Arcy Thompson. In his influential 1917 book On Growth and Form (1), Thompson emphasized the fact that, when one is faced with such a complex phenomenon as the form of a living organism, there can be more than one explanation, depending on the level of understanding one aims to achieve (molecular, cellular, or organismal). Although cellular and molecular processes play key roles in morphogenesis, Thompson insisted on the importance of studying this question from a purely physical perspective.

One of the simplest and best studied examples of pattern formation in which this approach has been fruitful is the spontaneous separation of two randomly mixed cell populations, in a process called cell sorting. Because the dynamics of cell sorting resemble the breaking up of an emulsion of different liquids, physically based mechanisms have long been suggested to explain this process (reviewed in (2)). From a physics perspective, cell populations (tissues) are active, complex fluids. They are active because cell motility is driven by ATP consumption and not by thermal energy. They are complex because they exhibit elastic solid-like behavior on short timescales and viscous liquid-like behavior on long timescales (3). Examples of viscous liquid-type behaviors are rounding of tissue pieces and fusion of tissues upon contact (4). In liquids, both of these processes are driven by surface tension. Accordingly, the Differential Adhesion Hypothesis (DAH) proposed that cell sorting is a direct consequence of differences in tissue surface and interfacial tensions, similar to the breaking up of an emulsion (5). When cells from two tissue types are mixed and able to interact via cell adhesion, they will sort according to their respective tissue surface tensions, whereby the tissue with lower surface tension engulfs the tissue with the higher surface tension (6). Molecularly, tissue surface tensions were originally attributed to differences in adhesion alone (7, 8), but have since been shown to arise from an interplay between cell adhesion and cortical tension (9). Therefore, when we use DAH in this article, we use it to mean this encompassing model, which is basically a fusion of the original DAH and the Differential Interfacial Tension model or any tension-based models of tissue surface tension.

In the theoretical work of Glazier and Graner (10), a Cellular Potts Model (CPM) was created to simulate the behavior of single cells during cell sorting. They demonstrated that differences in interfacial energies were sufficient to drive the spontaneous sorting of two cell populations (11, 12). Since then, this and other models have been refined to include other mechanisms such as coherent motion (13), biochemical dynamics of adhesion molecules (14), or chemotaxis (15). In all cases, differences in tissue surface tensions drive sorting, but the resulting dynamics are modified by these additional mechanisms. However, others have shown that sorting can occur in the absence of differences in tissue surface tension. Such models mostly rely on asymmetries of cell motility to explain sorting, either from intrinsic differences between cell types (16) or from differences in a cell’s immediate surroundings (17). However, there is disagreement on the rules regulating engulfment for a mixture of two cell types with different locomotion properties. Jones et al. (18) found that chick tissues sorted so that the fastest moving tissue ended up on the inside of a mixed cellular aggregate. In contrast, theoretical work showed that when full sorting occurred, faster cells surrounded slower ones and formed streams around them (16).

The freshwater cnidarian Hydra has frequently been used for studies of cell sorting. Hydra is anatomically simple with radial symmetry and two epithelial tissue layers, the ectoderm and the endoderm. Hydra can be dissociated into individual cells that, when reaggregated, can autonomously regenerate whole animals (19). Cell sorting into a sphere-within-a-sphere configuration, with an inner endoderm and outer ectoderm, is the first step in this regeneration process and a necessity for subsequent developmental milestones—the formation of a hollow bilayered sphere, symmetry breaking, and axis formation (19).

Differential surface tension was hypothesized to be key to Hydra cell sorting. Support for this view came from centrifugation experiments, which showed that under similar centripetal forces, endodermal epithelial cells formed larger aggregates than ectodermal epithelial cells, indicating that endoderm has a higher tissue surface tension than ectoderm, in agreement with the DAH (20). How these epithelial cells adhere to each other is currently unknown. One cadherin-like molecule has been reported in dissociated Hydra cells (21), but no functional studies of specific adhesion molecules exist.

Still, direct measurement of adhesion strength of epithelial cell pairs using optical traps (22) found that adhesion between endodermal epithelial cells is stronger than adhesion between ectodermal epithelial cells, in agreement with a DAH-driven sorting process. However, the authors found that heterotypic cell-cell interactions were the weakest of all, in disagreement with the DAH framework, which requires that the heterotypic interaction strength be intermediate between the strongest (endoderm/endoderm) and weakest (ectoderm/ectoderm) interactions. One possible explanation for this discrepancy is time-dependent changes in cell-cell interaction strengths. This idea was confirmed by more recent work which found that cell sorting in Hydra aggregates may have two phases: a short initial phase in which homotypic cell interactions dominate and ectodermal-endodermal interaction does not occur (23), and a second, longer phase, in which ectodermal epithelial cells display a higher affinity for endodermal epithelial cells than for themselves. Because the aggregates investigated in this study were small and nonviable, whether the existence of a short initial phase is relevant for the sorting of large aggregates capable of regenerating into polyps (10³–10⁴ cells) is unknown.

To test whether tissue surface tensions and adhesion differences between ectoderm and endoderm were sufficient to explain sorting or whether other parameters had to be considered, other studies investigated single cell behaviors. For example, Takaku et al. (24), studied the behavior of isolated ectodermal or endodermal epithelial cells when put in contact with a tissue sphere. They found that a single ectodermal epithelial cell in contact with an endodermal aggregate does not migrate into the aggregate, whereas a single endodermal epithelial cell in contact with an ectodermal aggregate does migrate to the interior. They interpreted these findings as indicative of differences in cell motility, although this behavior is also expected from the DAH. Additional experiments were performed that seemed to reveal such differences in motility. For example, they showed that epiboly, the process by which an ectoderm aggregate spontaneously engulfs an endoderm aggregate upon contact, depends on the motility of endodermal but not ectodermal cells (24). Furthermore, they found that in clusters of four cells (two endodermal and two ectodermal), ectodermal homotypic adhesion was more stable than endodermal homotypic adhesion, seemingly in contradiction to the DAH (24). However, as the stability of adhesion depends not only on its strength but also on the activity of the adhering cells, and endodermal cells were observed to be more actively motile, it is possible that endoderm-endoderm adhesions only appeared weaker. Finally, comparisons of experiments and CPM simulations revealed discrepancies in the sorting dynamics: experimental aggregates sorted much faster (19) than the simulated ones (25). This posed questions as to how the observed fast sorting dynamics could be achieved from differences in tissue surface tensions alone without an additional driving force.

In summary, both theoretically and experimentally, the existing data on Hydra cell sorting are insufficient to delineate whether sorting is driven by one of the two proposed classes of models or a combination of both. To definitely determine the driving mechanism, single cell dynamics in physiologically relevant, three-dimensional aggregates, as well as measurements of tissue surface tensions, are needed.

Here, we perform these experiments and resolve this problem by using newly introduced transgenic Hydra (26) and a multiscale approach. We first focus on three-dimensional mixed aggregates, large enough to regenerate into polyps, and present quantitative data on the dynamics of sorting. To determine whether differential surface tensions can drive sorting, we performed rheological measurements of both tissues’ mechanical properties, in particular of their surface tensions. Next, we mapped single cell trajectories within mixed aggregates to address whether the two cell types possess intrinsically different motile properties. Finally, we developed numerical simulations using the three-dimensional CPM based on our experimental conditions, and compared the in silico results to our experimental data. We find that differences in tissue surface tensions are indeed sufficient to reproduce all of our experimental data without any need for differential motility. Moreover, we can explain the observed fast sorting dynamics from the geometry of the aggregate during the process.

Our work answers the long standing question of the physical mechanism by which Hydra cell aggregates sort into tissues. It also demonstrates the unique experimental opportunities this organism provides. It is a system of choice for deepening our understanding of the physical basis of pattern formation and regeneration. In addition, a quantitative comparison of experiments and simulations revealed that the starting geometry of the mixed cell aggregate is a key determinant of the sorting dynamics. To understand cell sorting in other organisms and contexts, it is crucial to revisit existing theoretical works and study, in a systematic way, the role of geometry on cell sorting, especially by trying to mimic real experimental conditions.

Materials and Methods

Hydra care

Mass cultures of the “watermelon” transgenic Hydra vulgaris line (ectoderm GFP/endoderm DsRed2), the inverse watermelon line (ectoderm DsRed2/endoderm GFP), Wnt-GFP (ectoderm DsRed2 expression and GFP under the control of the Wnt3 promoter (27)), and AEP lines were used for experiments. AEP is the strain from which embryos are obtained for making transgenic animals. Animals were kept in Hydra Medium (HM) composed of 1 mM CaCl₂ (Spectrum Chemical, Gardena, CA), 0.1 mM MgCl₂ (Fisher Scientific, Waltham, MA), 0.03 mM KNO₃ (Fisher Scientific), 0.5 mM NaHCO₃ (Fisher Scientific), and 0.08 mM MgSO₄ (Fisher Bioreagents, Pittsburgh, PA), at a pH between 7 and 7.3, at 18°C in a Panasonic incubator. Animals were cleaned daily using standard cleaning procedures from (28). The Hydra were fed two to three times per week with newly hatched Artemia (Brine Shrimp Direct, Ogden, UT). Animals used for experiments were starved for at least 48 h.

Tissue separation

The protocol for separating the ectodermal layer from the endodermal layer is based on (29), with some modifications. Animals were starved for 5–7 days before an experiment. About 10 Hydra were placed in 35 mm petri dishes (CellTreat, Pepperell, MA) and cut, using a sterile scalpel (Surgical Design, Lorton, VA), below the tentacles to remove the head and above the budding zone to remove the peduncle and foot. The resulting body columns were placed for ∼2.5 min in ice-cold HM solution, with the pH adjusted to 2.5 using 2 M HCl, then transferred to Dissociation Medium (DM) composed of 3.6 mM KCl (Research Products International, Mt. Prospect, IL), 6 mM CaCl₂ (Spectrum), 1.2 mM MgSO₄ (Fisher Bioreagents), 6 mM sodium citrate (LabChem, Inc., Zelienople, PA), 6 mM sodium pyruvate (Alfa Aesar, Ward Hill, MA), 6 mM glucose (Sigma, St. Louis, MO), 12.5 mM TES (Sigma), 50 μg/mL rifampicin (Calbiochem, San Diego, CA), at pH 6.9 at room temperature (RT), following (30). The dishes containing the body columns in DM were sealed with tape and swirled to promote separation of tissues. The success rate for separation of the tissue layers was low, with only around 10% of body columns fully separating and around 20% showing partial separation. In this latter case, ectoderm and endoderm pieces would be manually cut free. After separation, samples were further cut with a scalpel to yield pure pieces of either tissue type.

Cell aggregates

Aggregates were prepared essentially according to (19), with some modifications. About 100 Hydra body columns from various lines were prepared by cutting off the head and peduncle/foot and washed three times with DM before a 1 h incubation in DM on ice. The body columns were mechanically dissociated into a single cell suspension with vigorous trituration using a P1000 pipette (Gilson, Middleton, WI). The cells were centrifuged in an Allegra X-15R Centrifuge (Beckman Coulter, Brea, CA) at 4°C, 200 × g, for 5 min and washed twice with ice cold DM. About 1 mL of cell suspension was made from 100 body columns by washing the pellet of single cells through an alcon nylon 40 μm nylon mesh filter (Corning Incorporated, Corning, NY). One hundred microliter aliquots of this cell suspension were placed in separate wells of a 96-well V-shaped plate (Nunc, Roskilde, Denmark) and the plate was centrifuged at 1000 × g for 5 min. Aggregates were cultured in 100% DM for the first 4 h, after which 100 μL of HM was added to each well leading to a 50:50 mix of HM and DM. At 24 h, the aggregates were transferred using Pasteur pipets to a solution of 70:30 DM/HM. Finally, at 48 h, they were transferred to 100% HM for the rest of regeneration. Throughout, aggregates were kept at 18°C. Imaging started 1 h after the aggregates were made by carefully transferring them to 96-well flat-bottom plates (Nunc). The aggregates were imaged every 2 to 5 min using GFP and RFP channels and three-plane z-stack on an Olympus IX81 inverted microscope (Olympus Corporation, Tokyo, Japan), using an ORCA-ER camera (Hamamatsu Photonics, Hamamatsu, Japan) and Slidebook software version 5 (Intelligent Imaging Innovations, Denver, CO).

By visually controlling cell density in the cell mix before centrifugation, we prepared aggregates of different initial sizes, ranging from 10² to 10⁴ cells. Of note, only the largest of these (roughly over 10³ cells) fully regenerate, and we thus focused on these in our experimental analysis.

Analysis of sorting dynamics

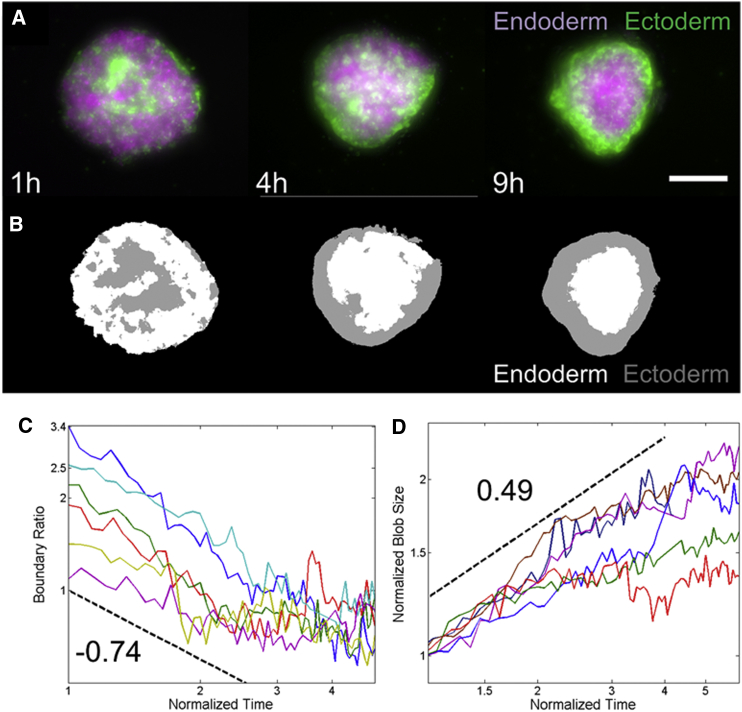
Two-channel z-stack images of aggregates were used for analysis to measure boundary ratio and blob size. The z-stacks were first converted to maximum intensity projection RGB image sequences in ImageJ (http://imagej.nih.gov/ij/; National Institutes of Health, Bethesda, MD). Using a semiautonomous MATLAB (The MathWorks, Natick, MA) script, the red and green channels were normalized to each other based on each channel’s average intensity. The normalized image was then segmented into three regions (background, ectoderm, and endoderm) using the function k-means (Fig. 1 B). We measured the “length” of the boundary between the endoderm and the ectoderm by taking the sum of all the points between the ectoderm and endoderm segments (length of the line separating gray and white clusters in Fig. 1 B). This length is high at initial time points as the frontier between the two domains is rugged and small at longer timescales where the frontier has rounded up and smoothed to a circular shape. The boundary ratio was defined as this length divided by the perimeter of the aggregate. Of note, we find this measurement to be directly proportional to the sorting index used in other works. This index is calculated as the fraction of neighboring cells which are of the opposite cell type, averaged over all cells. On average, each cell will thus have a boundary length equal to the mean sorting index times its contour length. Assuming that all cells have similar sizes, the total boundary length will then be the average boundary length per cell times the number of cells, which is thus also proportional to the sorting index.

Figure 1.

Dynamics of cell sorting. (A) Representative still images of sorting of Hydra watermelon aggregates capable of regeneration. The reduction in radius is a signature of the aggregate rounding up in three dimensions. (B) Automated image analysis of the images in (A) determining the positions of both tissues. The scale bar represents 200 μm. (C) Log-log plot of boundary ratio as a function of normalized time for six representative experiments. The dashed black line shows the behavior of a power law with exponent −0.74. (D) Log-log plot of normalized blob size as a function of normalized time for five representative experiments. The dashed black line shows the behavior of a power law with exponent 0.49. In (C) and (D), the long-term behavior shows saturation of these measurements and therefore deviation from power law behavior. To see this figure in color, go online.

For blob size, we used a segmented image in which one tissue is assigned a value of +1 and the other a value of −1, and the background is set to zero. We then calculated this segmented image’s two-dimensional Fourier transform $S\left(\overrightarrow{k}\right)$. A typical frequency is extracted from this Fourier transform by calculating its weighted average. The typical blob size is then taken to be the invert of that typical spatial frequency and is written:

$$\text{Blob}\text{size}=\frac{{\sum }_{\overrightarrow{k}}{\left|S\left(\overrightarrow{k}\right)\right|}^2}{{\sum }_{\overrightarrow{k}}{\left|S\left(\overrightarrow{k}\right)\right|}^2\left|\overrightarrow{k}\right|}.$$

The blob size and boundary ratios from 17 aggregates were individually linear fitted on a log-log plot to determine the power law exponent. The blob size and boundary exponents were averaged over these 17 measurements and their standard deviations calculated. For plotting purposes, blob sizes and times were normalized by dividing them by their initial values. Of note, this normalization does not alter the exponents that were obtained.

To estimate volumes from two-dimensional imaging, the aggregates were assumed to be ellipsoidal. We fitted an ellipse over the segmented image in ImageJ and used its minor axis length for the width and girth and the major axis as the length of the ellipsoid.

The sorting time, the time it takes for the ectodermal and endodermal cells to be completely separated (no ectodermal cells remain inside the endoderm), was found by having two people individually watch the sorting videos and manually record the time points when the aggregates became sorted. We then averaged and calculated the standard deviation of the manually determined sorting times.

Micropipette aspiration

Tissue pieces were used immediately after they were cut from separated tissue layers. Glass capillaries (model 1B100F-4; World Precision Instruments, Sarasota, FL) were pulled into micro-pipettes using a horizontal laser-based micropipette puller P-2000 (Sutter Instruments, Novato, CA). The resulting micropipettes were manually cut to yield an opening of ∼50 microns (smaller than tissue pieces but larger than a single epithelial cell). Before the experiments, micropipettes were treated with Sigmacote (Sigma) following the manufacturer’s protocol to make them nonadhesive. They were then mounted on a needle holder attached to an M-152 micromanipulator (Narishige, Amityville, NY). The micropipette was connected by hermetically sealed tubing to a plastic syringe used as a water reservoir, and mounted on a stand allowing for manual variation of the syringe’s height. Using the micromanipulator, the micropipette tip was put in contact with the tissue piece before lowering the syringe’s level to apply negative pressure. The aspiration of the tissue piece was imaged every 5–10 s under a MZ16FA stereo microscope (Leica Microsystems, Wetzlar, Germany), using a SPOT RT3 camera (Model 25.1; Diagnostics Instruments, Sterling Heights, MI) controlled by SPOT Basic 5.1 software (Diagnostic Instruments). For surface tension estimates, the radius of the tissue piece was measured from the images in ImageJ as the square root of the projected area divided by π. The radius of the micropipette was also measured using ImageJ. The height difference between the water reservoir and the petri dish containing the tissue piece was slowly manually increased until aspiration began. The height difference was recorded at that time and translated into a critical pressure value according to

$$\Delta P_C=\rho g\Delta h,$$

where $\Delta P_C$ is the critical pressure, $\rho$ is the density of the medium, and $\Delta h$ is the height difference between the water reservoir and the petri dish.

This led to a surface tension estimate per tissue piece. The values presented in the Results are averaged from 13 independent endoderm and 14 independent ectoderm pieces.

For viscosity estimates, the retracted length as a function of time was manually measured in ImageJ and fit in MATLAB as an exponential function of the form $a\left(1-e^{-t/\tau }\right)$. $a$ and $\tau$ were fit parameters with

$$\tau =\frac{3\pi \eta }{E},$$

where $E$ and $\eta$ are the elastic modulus and viscosities, respectively. This led to an estimate of the viscosity for each tissue piece. The values presented in the Results are averaged from 10 independent endoderm and 9 independent ectoderm pieces.

Fusion

The two tissue layers obtained by tissue separation were cut into smaller pieces. Within 5 min postcutting, the two tissue pieces of interest were either put into contact using the hanging drop technique described in (31) or manually brought in contact using hair pins. The fusion process was imaged every minute either on an Olympus IX81 inverted microscope or using an EVOS FL Auto Cell Imaging System (Thermo Fisher Scientific, Waltham, MA).

Rounding up

Pieces from either tissue were manually cut with sterile razor blades into oblong shapes in DM and imaged every minute for 2–3 h under a Leica MZ16FA stereo microscope. Using ImageJ, each piece was fitted to an ellipse at each time point and the aspect ratio was computed as the ratio of the long axis to the short one as a function of time. The dynamics were then fit in MATLAB by an exponential decay function of the form

$$a{e}^{\frac{-t}{\tau }}+b.$$

$a$, $b$, and $\tau$ were fit parameters and the characteristic time $\tau$ was taken to be $\tau =\left(\eta R/\sigma \right)$, with $\eta$ the viscosity of the tissue, $\sigma$ its surface tension, and $R$ the radius of the tissue piece of interest (32). Radii were measured as the geometric mean of the axes of the fitting ellipse at the final time point. Using viscosity estimates from micropipette aspiration experiments, we measured the surface tension of each tissue piece this way and the results presented are averaged over 17 independent endoderm and 15 independent ectoderm pieces.

Single cell dynamics

Aggregates containing 5% of their cells from watermelon animals and 95% from AEP animals were prepared as described above. After 1 h in DM, they were imaged on a Scientifica multiphoton imaging setup (Scientifica, Uckfield, UK) coupled to a MaiTai ultrafast laser (Spectra Physics, Santa Clara, CA) set to 980 nm through a 20× water immersion XLUMP PlanFL objective (Olympus Corporation). Optical slices in both the RFP and GFP channels were acquired at 3 micron-slices and averaged over six acquisitions. This procedure was repeated every 5–10 min over 4–6 h.

Single cells were detected separately for each tissue using the 3d object counter plugin in ImageJ and their center of mass at each time point recorded. These data were analyzed in MATLAB by reconstructing single cell trajectories using open source tracking algorithms (http://www.mathworks.com/matlabcentral/fileexchange/42573-particle-point-analysis?focused=3791012&tab=function). From these tracks, we calculated mean-square displacements, speeds, and autocorrelation functions according to the usual definitions. Directionality was measured as the ratio of the distance traveled between the first and last time points to the total distance traveled in the same interval. Values reported here are averaged over all trajectories for each cell type. The data presented in the Results are from one representative experiment out of eight.

For center of mass corrections, we used mosaic aggregates containing 5% of cells from HyWnt3 promoter::GFP animals allowing us to track ectodermal cells in the RFP channel and 95% from AEP animals. During the 1 h period in DM, aggregates were stained with a Syto12 nuclear dye (Thermo Fisher Scientific) diluted to 1:500 in DM. Aggregates were washed twice in DM before imaging on the two-photon microscope. The analysis was performed as described above. Center of mass was calculated from the mean position of all detected nuclei at each time step and the center of mass position was subtracted from both nuclei and ectodermal cell positions. The corrected positions were then used to calculate mean-square displacements.

Numerical simulations

We used the CompuCell3d (33) software to perform simulations of a CPM. Details on how these simulations are performed can be found in the software’s manual (available at: http://www.compucell3d.org/Manuals). In our case, we used a Hamiltonian H composed of three contributions. The first one modeled cell-cell contacts and was written as follows:

$$H_{\text{adhesion}}=\sum _{i,j\text{neighbors}}J\left(\tau \left(\sigma \left(\overrightarrow{i}\right)\right),\tau \left(\sigma \left(\overrightarrow{j}\right)\right)\right)\left(1-\delta \left(\sigma \left(\overrightarrow{i}\right),\sigma \left(\overrightarrow{j}\right)\right)\right),$$

where the summation applies over all pairs of adjacent pixels $\overrightarrow{i}$ and $\overrightarrow{j}$, $\sigma \left(\overrightarrow{i}\right)$ is the ID number of the cell occupying the pixel $\overrightarrow{i}$, $\tau \left(\sigma \left(\overrightarrow{i}\right)\right)$ is the identity (endoderm, ectoderm, or medium) of that cell, and $\delta \left(x,y\right)$ is the Kronecker function. This formulation means that energy only applies to neighboring pixels that belong to different cells and the energetic cost of that adhesion depends on the identity of both cells involved. For the adhesion energies, we used the parameters in Table 1.

Table 1.

Adhesion Energy Parameters

Tissues	J
Endoderm/medium	300
Ectoderm/medium	200
Endoderm/endoderm	2
Endoderm/ectoderm	75
Ectoderm/ectoderm	100

The relative values of these parameters were chosen to fulfill the following criteria: the adhesion energy between the two tissues has to be intermediate between the two homotypic adhesion energies to account for complete engulfment, and the effective surface tension of the endoderm has to be double that of the ectoderm, in agreement with experiments. The surface tension of one tissue was estimated as

$${\sigma }_{\text{tissue}}=J_{\text{tissue}/\text{medium}}-\frac{J_{\text{tissue}/\text{tissue}}}{2}.$$

The second contribution to the Hamiltonian was the limited compressibility of cells, which means that they resist any deviation from a target volume, leading to the following formulation:

$$H_{\text{volume}}=\sum _{\sigma }{\lambda }_{\text{vol}}{\left(V\left(\sigma \right)-V_t\right)}^2,$$

where the summation applies over all cells, ${\lambda }_{\text{vol}}$ is the inverse compressibility of the cells, $V\left(\sigma \right)$ is the volume of cell $\sigma$, and $V_t$ is the target volume. In our simulations, we used the same compressibility for both cell types with the following parameters: ${\lambda }_{\text{vol}}=20$ and $V_t=64$.

The last contribution represents the cell’s membrane tension. Numerically, this means that there is an energy penalty for the surface of each cell if it deviates from a target value, leading to the following formulation:

$$H_{\text{surface}}=\sum _{\sigma }{\lambda }_{\text{surface}}{\left(S\left(\sigma \right)-S_t\right)}^2$$

where the summation applies over all cells, ${\lambda }_{\text{surface}}$ is the inverse membrane compressibility of the cells, $S\left(\sigma \right)$ is the surface of cell $\sigma$, and $S_t$ is the target surface. In our simulations, we used the same membrane compressibility for both ectodermal and endodermal epithelial cells, with the following parameters: ${\lambda }_{\text{surface}}=5$ and $S_t=96$.

Overall, the Hamiltonian controlling the dynamics was the sum of the three contributions above. The activity of the cells was then represented as a temperature parameter that allows them to overcome local energy barriers to reach the energetically optimal situation. In our simulations, the temperature was set to 1000, with the exception of our simulations of differential motility that kept the same temperature for the endoderm but used 500 for the ectoderm.

Simulations were initialized, in most cases, as rectangular random mixtures of cells (initialized as cubes with four pixel sides) from both cell types. The width and length of the rectangles were kept equal and were varied from 30 to 140 pixels whereas the thickness was kept at 12 pixels, except for the data presented in Fig. S11. For sorting with spherical initial conditions, we initiated the simulation as a random mixture of both cell types in a sphere with a radius of 40 pixels. To simulate fusion, two spheres, in contact, for a single tissue type were initiated with a radius of 22 pixels each.

For analysis, data were saved at intervals ranging from 2 to 30 simulation steps depending on the system size. An image representing the horizontal slice in the middle of the aggregate’s height was recorded and detailed data on the identity of each pixel were saved. The horizontal slices were used to calculate blob sizes and boundary lengths in the same way as described in Analysis of Sorting Dynamics. The saved time series data were used to reconstruct the three-dimensional dynamics of each cell’s center of mass. For cell sorting, we ran triplicates of the simulations at 10 different sizes. For each size, one exponent for blob size and one for boundary length were obtained by linear fitting their dynamics on a log-log plot in MATLAB. The values reported are means of the values obtained for the seven largest aggregate sizes leading to a total of 21 simulations. For single cell dynamics, the data presented come from a single simulation at the largest size studied, but which is representative of all simulations.

Immunohistochemistry

Aggregates from AEP animals were prepared as described above and fixed at different time points in 4% paraformaldehyde in HM for 15 min at RT. They were washed three times for 10 min each in phosphate-buffered saline (PBS), and permeabilized for 5 min in PBS supplemented with 0.5% Triton X-100 (Sigma). A blocking solution was prepared using 1% bovine serum albumin (Fisher Bioreagents), 10% fetal bovine serum (Thermo Fisher Scientific), and 0.1% Triton X-100 in PBS. Aggregates were blocked in this solution for 2 h at RT. The samples were incubated in anti-Hydra laminin, mAb 52 antibody (34), diluted to 1:200 in the blocking solution, overnight at 4°C. Negative controls were performed by omitting the primary antibody and using blocking solution alone. Next, samples were washed six to eight times in PBS at RT over the course of 3–5 h, before incubating overnight in a 1:500 dilution, in blocking solution, of an anti-mouse horseradish peroxidase secondary antibody (Enzo Life Sciences, Farmingdale, NY). The next day, samples were again extensively washed in PBS before a 1 h incubation in PBT (1:2000 Tween [Sigma] and 0.2% bovine serum albumin in PBS). Detection of the horseradish peroxidase secondary antibody was performed in PBT supplemented with 1:10000 H₂O₂ (Avantor, Central Valley, PA) and 1:1000 N-hydroxysuccinimide-fluorescein (Thermo Fisher Scientific) for 30 min. Samples were washed multiple times at RT and incubated overnight at 4°C in PBS. Samples were imaged on an Olympus IX81 inverted microscope. The resulting images were analyzed by measuring the averaged signal intensity in the middle of the aggregate. This value was normalized by the same measurement performed on the negative controls. Results from four different experiments were averaged and their standard deviation calculated.

Centripetal aggregations

Endoderm and ectoderm tissue pieces were dissociated into single cell suspensions in the same manner as used for the preparation of cell aggregates. Cell concentrations were measured using a Brightline hemacytometer (Sigma) and equalized by adding DM to the most concentrated cell suspension. We placed 800 μL of these suspensions in the wells of a 24-well plate (Genesee Scientific, San Diego, CA) on a DS-500E rotary shaker (VWR International, Radnor, PA) for 30 min at 75 Rpm. The resulting aggregates were then imaged under a Leica MZ16FA stereo microscope. Images were analyzed in ImageJ to extract the projected area of each resulting aggregate.

Results

A natural starting point for distinguishing between the most prominent explanations of cell sorting in Hydra, i.e., differential tissue surface tension versus differential motility, is to perform measurements on the dynamics of cell sorting. Then, as the mechanisms driving sorting in these models are either based on tissue rheological properties or single cell motility, we quantitatively assessed these two aspects.

Dynamics of cell sorting in Hydra aggregates

All models of Hydra cell sorting predict that the two initially mixed cell populations spontaneously separate, with ectoderm engulfing endoderm. The dynamics of sorting, however, depend on the model driving forces and their analysis could therefore possibly enable a distinction between the two proposed types of explanation. To test this, we prepared aggregates from transgenic Hydra in which the two epithelial layers express different fluorescent proteins. As expected, the aggregates initially showed a random mixture of both cell types (Fig. 1 A) and were disk-shaped, because cells are aggregated via centrifugation (see Materials and Methods). Over the course of 4–10 h, the two cell populations spontaneously separated and the disk-shaped aggregate rounded up into a solid sphere (Movie S1). The ectodermal cells moved toward the outside of the aggregate whereas the endodermal cells moved toward the center, leading to a sphere-within-a-sphere configuration. Once sorting was complete, the aggregates ejected excess cells as they transitioned into a hollow bilayer epithelial sphere. The bilayer sphere eventually broke symmetry and regenerated into an adult polyp (Fig. S1). Hydra cell aggregates are therefore a true in vivo system, despite their apparent simplicity. Indeed, regeneration from aggregates occurs even in epithelial Hydra that have been reduced to ectoderm and endoderm through removal of the interstitial cell lineage (35). Interstitial stem cells and their progeny thus do not significantly alter cell sorting and the system can be treated as a two-component mixture. The other potentially important player in cell sorting is the extracellular matrix (ECM) (36), which separates the two epithelial tissues in the intact animal. However, using antibody staining we verified that laminin, a major component of Hydra ECM, did not seem to be synthesized at significant levels during the timescale of cell sorting (Fig. S2), in agreement with previous reports (37). Thus, sorting does not appear to depend on the presence of ECM.

To allow for a direct comparison of our experimental results with existing theoretical models and predictions, we focused on measuring quantities that are commonly used in the cell sorting field. One such quantity is the sorting index, which measures the average fraction of neighboring cells that are of the opposite type. In an evenly mixed aggregate, the initial value of the sorting index is 0.5. The index decreases as sorting proceeds and saturates at a value that depends on the system size. The sorting index is difficult to measure experimentally as it requires knowledge of the position, neighbors, and identity of all cells within an aggregate. However, the sorting index is directly proportional to the length of the boundary (see Materials and Methods) between the tissues and therefore follows the same functional form. With the exception of a more complex model taking into account the biochemical dynamics of adhesion proteins (14), this decrease follows a power law for models based on either DAH or differences in motility. The exponents, however, vary depending on the details of the model such as the ratio of cells from both types (38) or the differences in motility built into the model (17).

Using automated image analysis (Fig. 1 B), we measured the length of the boundary between endoderm and ectoderm as a function of time (see Materials and Methods). The boundary length’s decrease seems to follow a power law (Fig. 1 C) with exponent −0.74 ± 0.24 (mean ± SD, n = 17, Fig. S2). This exponent is significantly higher than those reported in various theoretical works, which ranged from −0.025 to −0.33 (13, 16, 17, 38), implying that the observed sorting is faster than previously suggested. We present a more detailed analysis and explanation of this result in the Discussion.

Another quantity used in the cell sorting field is the typical blob (cluster) size of both tissues as a function of time. The definition of the typical blob size varies from one study to the next. Because this measure is also commonly used in the study of phase separation through spinodal decomposition (39), we chose here to use the same definition (see Materials and Methods). This allowed us to directly compare our dynamics to a purely physical situation. This definition also presents the advantage of measuring a single blob size for both tissues instead of having two quantities to characterize the dynamics. The blob size is linked to the total sorting time, as sorting is complete once the typical blob size reaches a value comparable to the system size.

We found that the typical blob size seems to increase as a power law (Fig. 1 D), with an exponent of 0.49 ± 0.24 (mean ± SD, n = 17, Fig. S3). Again, this implies faster sorting than previously reported (11, 13, 38). Of note, scaling rules imply that blob size and boundary ratio should have equal exponents of opposite sign. Our mean values are quite different (0.74 vs. 0.49), but still within experimental uncertainties of each other. The real exponent is likely intermediate between these values. In addition, the analysis of the sorting dynamics and the span of data is limited by the intrinsic timescales of the sorting process. The power law behavior of these quantities can thus be questioned (Fig. S3). However, the precise functional form of these dynamics does not change our observation that sorting is faster than previously published results.

In summary, although studying cell sorting dynamics is instructive, it was insufficient to distinguish between sorting mechanisms. Indeed, different models make predictions on the dynamics of sorting that are quite similar to one another. In particular, although we observe power law behaviors as predicted by most models, our experimentally determined exponents are significantly larger than any previously published values; we therefore cannot draw conclusions on the sorting mechanism from these experiments alone.

However, because the different models for cell sorting also make assumptions and predictions regarding the properties of each tissue separately and/or on the behavior of single cells within aggregates, we performed experiments at these scales to further probe the possible mechanisms explaining cell sorting.

Physical behavior of separated tissues

The DAH is based on the assumption that each tissue behaves like a liquid on long timescales. Sorting is then driven by the effective interfacial and surface tensions of the two tissues. Cells, like liquid molecules, have a lower contact free energy with each other than with the medium. Cellular rearrangements thus tend to minimize the tissue’s contact area with the medium, which is similar to the effect of surface tension in liquids (3, 40).

For full sorting and engulfment to occur, these rheological quantities need to obey the following inequality (6):

$${\sigma }_{\text{endo}}>{\sigma }_{\text{ecto}}+{\gamma }_{\text{endo/ecto}},$$

where $\sigma$ represents the tissue’s surface tensions and ${\gamma }_{\text{endo}/\text{ecto}}$ represents their interfacial tension.

DAH thus predicts that each tissue flows on long timescales and that the effective surface tension of endoderm is higher than that of ectoderm. Because these questions have to be addressed for each tissue separately, this requires their physical separation. To do so, we adapted previously published protocols (29) (see Materials and Methods) to chemically dissolve the ECM, which leads to the physical separation of the tissues.

Using this separation method, we obtained tissue pieces containing only one of the two epithelial cell types, and then observed their long-term behaviors. Tissue pieces rounded up (Movie S2) and fused (Movie S3) on timescales of minutes to a few hours, thus demonstrating liquid behavior. This justifies the use of concepts such as surface tension and viscosity. To determine both of these quantities, we used micro-aspiration experiments (Fig. 2, A–C; Movie S4), in which tissue pieces are aspirated into a micropipette using negative pressure. The pressure needed to initiate aspiration is directly related to the surface tension of the tissue of interest (41) according to

$$\text{Δ}{P}_C=2\sigma \left(\frac{1}{R_p}-\frac{1}{R}\right),$$

where $\Delta P_C$ is the critical pressure required to trigger aspiration, $\sigma$ is the surface tension, $R_p$ is the radius of the micropipette, and $R$ is that of the tissue piece.

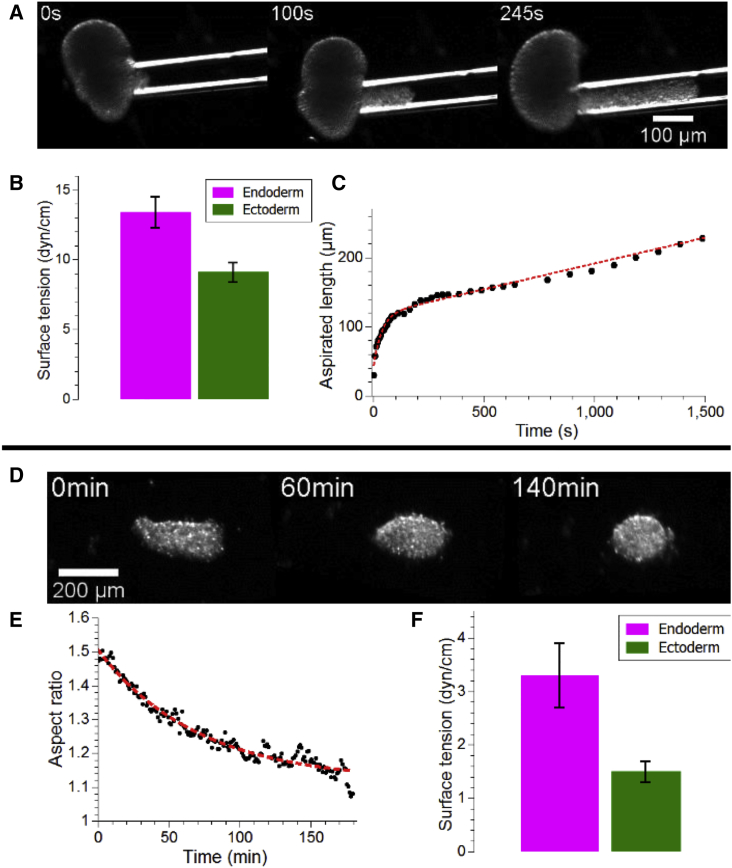
Figure 2.

Rheology of individual tissues. (A) Still sequence of micro-aspiration experiment performed on an endoderm tissue piece. (B) Quantification of surface tensions from micro-aspiration experiments. The bars show mean ± SE; n = 13 and 14 for endoderm and ectoderm, respectively. (C) Sample quantification of aspirated length of an endoderm piece as a function of time showing a short viscoelastic phase used to estimate viscosity, and a long linear phase. The dashed line corresponds to a numerical fit of the data using a short term exponential decay and a long term linear phase as described in the Materials and Methods, in accordance with theoretical models of microaspiration. (D) Still sequence of rounding up experiment on an ectoderm tissue piece. (E) Quantification of aspect ratio as a function of time of the experiment shown in (D), the dashed line represents an exponential fit to the data in black. (F) Quantification of surface tensions from rounding up experiments. The bars show mean ± SE; n = 17 and 15 for endoderm and ectoderm, respectively. To see this figure in color, go online.

We estimated surface tensions this way and found the surface tension of endoderm to be higher than that of ectoderm (Fig. 2 B; Table S1), in agreement with the DAH (13.4 ± 1.1 and 9.1 ± 0.7 dyn/cm, respectively, mean ± SE; n = 13 and 14, respectively). In addition, the first phase of aspiration (Fig. 2 C) is dominated by the visco-elastic response of the tissues, leading to an exponential relaxation. The characteristic time of this relaxation $\tau$ is given by (41)

$$\tau =\frac{3\pi \eta }{E},$$

where $E$ and $\eta$ are the elastic modulus and viscosities, respectively. Using previous measurements of the elastic moduli with parallel plate compression (42), we found the viscosities of endoderm and ectoderm to be 3.7 ± 0.7 10⁴ and 4.8 ± 0.6 10⁴ Pa, respectively (mean ± SE; n = 10 and 9, respectively; Table S1), similar to measurements performed on other cell aggregates including from chicken embryonic cells (3) and mouse sarcoma cells (41, 43).

The viscosity estimates can further be used to independently determine tissue surface tensions from rounding up experiments, because this behavior is driven by surface tension and slowed by viscosity. Similar to what has been reported for other cellular aggregates (32), the dynamics of a Hydra tissue piece rounding up, measured as the decrease of the piece’s aspect ratio over time, was exponential (Fig. 2 E). The characteristic time $\tau$ of this exponential relaxation is given by

$$\tau =A\frac{\eta R}{\sigma },$$

where $R$ is the radius of the tissue piece and $A$ is a numerical prefactor that depends on geometry. This numerical prefactor has been estimated to be on the order of 0.95 in different circumstances (44), but is unknown in our case. Because we are primarily interested in the relative differences between the surface tensions of both tissues, knowledge of this prefactor is not crucial. Using the viscosity measurements obtained by micro-aspiration, we found a higher surface tension for endoderm when compared to ectoderm (3.3 ± 0.6 and 1.5 ± 0.2 dyn/cm, respectively, mean ± SE; n = 17 and 15, respectively) (Fig. 2 F; Table S1). We attribute the difference of these absolute values from the micro-aspiration results to the undetermined prefactor in rounding. The relative differences in surface tensions obtained through both methods are of the same order, although not exactly similar. This difference in relative measurements are likely due to experimental imprecisions and the large variability we observed in the samples.

In principle, fusion experiments could be similarly used to estimate surface tension. However, although endoderm tissue pieces readily fused (Movie S5), ectoderm pieces fused rarely and only if freshly cut surfaces were brought into contact (Movie S5). We attribute these different behaviors to the polarity of ectoderm pieces, which was previously reported (24). Because of polarization, cells in contact with the outside medium may lack adhesion molecules facing out and thus are unable to fuse with a neighboring piece. This lack of boundary cell-cell interaction would have no effect on rounding up and micro-aspiration, and little effect on cell sorting, because polarization would only happen once ectodermal cells reach the aggregate boundary. Thus, although polarization can be neglected in these other experiments, it dominates ectoderm behavior during fusion and complicates estimates of tissue surface tensions from fusion experiments. Furthermore, it has been reported that ectodermal cells form an outer cuticle made of glycoproteins when in contact with the outside medium (45). The purpose of this cuticle in the adult animal is still debated, but it most likely serves as a protecting layer for ectodermal cells. It could also be important in regulating osmotic pressure and/or the composition of the Hydra surface microbiome (45). The cuticle could prevent the adhesion between two different tissue pieces and thus explain the lack of fusion observed in our experiments without having a significant effect on sorting dynamics.

Finally, we repeated a qualitative experiment previously performed by Technau and Holstein (20). We showed that under similar aggregating forces and at similar cell densities, endodermal cells made larger aggregates than ectodermal ones, a signature of their higher cohesiveness (Fig. S4), in agreement with experiments performed at the single cell level (22).

Overall, we demonstrated that both tissues show liquid-like behaviors on long timescales (rounding up, flowing), and that the endoderm has a higher surface tension than the ectoderm. The difference is high enough to explain cell sorting (6). Our estimates of tissue viscosities and surface tensions are in good agreement with previously published values on aggregates of embryonic tissues from chicken (3, 6, 40) or zebrafish (4), which were all on the order of 10⁴–10⁵ Pa for viscosities and 1–30 dyn/cm for surface tensions. Together these results demonstrate that differential surface tension plays an important role during cell sorting in Hydra aggregates.

Single cell dynamics during sorting

Our results show that differences in surface tension can drive cell sorting, but they do not exclude the involvement of other mechanisms such as differences in cell motility. To evaluate whether differential cell motility plays a role in cell sorting in Hydra aggregates, we tracked individual cells during the sorting process. To achieve single cell tracking within the aggregates, we prepared aggregates in which 5% of the cells were transgenic, expressing a fluorescent protein. These aggregates were analyzed using three dimensional two-photon time-lapse imaging. From the resulting videos, we reconstructed single cell trajectories for both tissues, in the first 4–6 h of sorting (Fig. 3 A). We found cell speeds to be on the order of 50 μm/h, constant throughout this time window, and comparable for both cell types (Fig. 3 B). The mean-square displacements (MSDs) of both cell types were weakly super-diffusive (power law with exponent of 1.3–1.4), and again, similar (Fig. 3 C). This indicates that cell motion was mostly random and thus that directed cell motility does not play a role in cell sorting. This is further demonstrated by the fact that cell directionality was also similar for both cell types, despite their differing final positions (inside versus outside) (Fig. 3 D). These results held true for all of the experiments that were analyzed (n = 9). Quantitatively, the MSDs yielded diffusion coefficients on the order of a few hundred microns squared per hour, the same order of magnitude as was reported for two-dimensional Hydra aggregates (46). Finally, we found no differences in speed distributions and velocity autocorrelation functions between ectodermal and endodermal cells (Fig. S5). The velocity autocorrelation functions showed a rapid exponential decrease (on the order of a single experimental time step), which shows that any persistence of single cell motion can be neglected for both tissues, in our experiments.

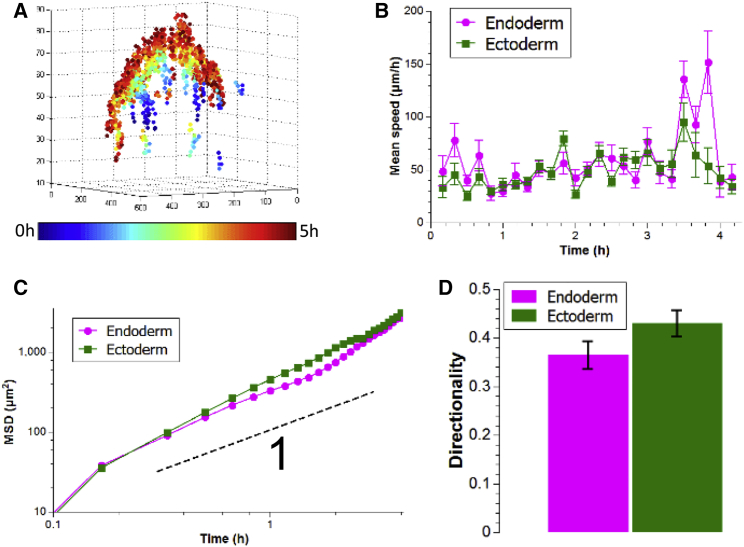
Figure 3.

Single cell dynamics. (A) Reconstructed cell tracks from two-photon imaging color-coded by time. Axes are in microns. (B) Quantification of mean speeds of both cell types from one representative experiment. (C) Log-log plot of MSDs in the same experiment. The black dashed line shows the behavior of a power law with an exponent of one, i.e., purely diffusive motion. This shows that cell motion is slightly super-diffusive. A linear fit yields diffusion constants of 564 ± 63 and 657 ± 23 μm²/h (best fit ± 95% confidence interval) for endoderm and ectoderm, respectively. (D) Quantification of directionality from the same representative experiment. Directionality is averaged over all traceable cells and the bars represent mean ± SD (n = 20 and 17 for endoderm and ectoderm, respectively; p > 0.05). To see this figure in color, go online.

Of note, we observed a general vertical trend in the displacement of the cells, which is explained by the fact that aggregates start in a mostly flat state and round up as they sort. To test if our results were dominated by the global motion of the aggregate, we performed experiments where all nuclei were stained to correct for this global motion and obtained similar results (Fig. S6). This shows that, although important, the global motion of the aggregate does not impact our conclusions. The main difference was that center-of-mass, motion-corrected MSDs were basically linear (Fig. S6), implying that the coherent component of the cell motion is due to rounding up and not cell sorting, again in agreement with experiments performed in two dimensions (47). Finally, these corrected MSDs no longer showed the increasing trend at long times visible in Fig. 3 C. This illustrates that this effect is due to the rounding up of the aggregates and is not a signature of cell sorting.

In summary, our data at the single cell level do not reveal any intrinsic motility differences between the two cell types. This implies that differential motility does not play a role in cell sorting in Hydra aggregates.

DAH-based numerical simulations of cell sorting

Because our experiments showed that differential surface tension governs cell sorting without differential motility playing a significant role, we used numerical simulations to probe the effects of both mechanisms and test their ability to reproduce our experimental data. We applied a CPM to simulate cell sorting using the freely available CompuCell3d software (http://www.compucell3d.org/) (33). The simulations are based on differential adhesive forces between pairs of cells depending on their identities. Individual cells tend to keep their volumes (finite compressibility) and their surface area (finite deformations). To mimic our experiments as closely as possible, simulations were run in three dimensions using various numbers of cells. Initially the aggregates were in a flat configuration with a thickness of three cells and the long sides were varied from 7.5 to 35 cells (Fig. 4 A), leading to a total number of cells ranging from a hundred to several thousand. Although the largest simulated aggregates were smaller than the largest aggregates in the experiments (on the order of 10⁴ cells), they were large enough to model aggregates capable of regeneration. In addition, we tuned the adhesion parameters to obtain a surface tension twice as high for the endoderm as for the ectoderm (see Materials and Methods), the same order of magnitude found in our experimental measurements.

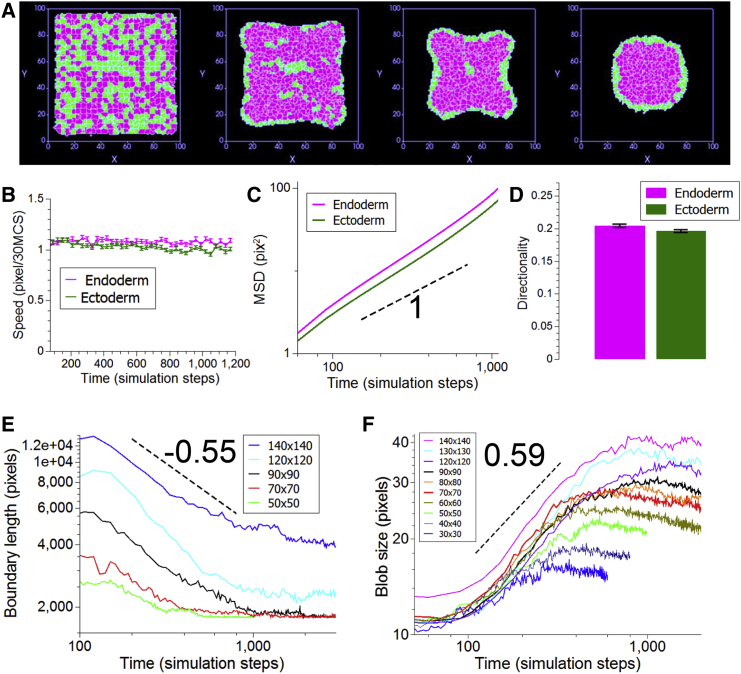
Figure 4.

DAH-based numerical simulations. (A) Still sequence of the middle slice in a simulation. Endodermal cells are shown in magenta (online) and ectodermal cells are shown in green (online). Stills are shown at 0, 300, 800, and 2000 simulation steps. (B) Measurement of speeds over time for a representative simulation at the largest size. (C) Log-log plot of the MSD of the same simulation as in (B). The black dashed line shows the behavior of a power law with an exponent of one or diffusive behavior. A linear fit yields diffusion constants of 0.084 ± 0.004 pixel²/simulation step and 0.07 ± 0.004 pixel²/simulation step (best fit ± 95% confidence interval). (D) Quantification of directionality from the same representative simulation. Directionality is averaged over all cells and the bars represent mean ± SD (n = 1837 for both tissues) (E) Log-log plot of boundary length as a function of time for five different initial sizes. Each plot represents the mean of three independent simulations. The dashed black line shows the behavior of a power law with exponent −0.55. (F) Log-log plot of blob size as a function of time for 10 different initial sizes. Each plot represents the mean of three independent simulations. The dashed black line shows the behavior of a power law with exponent 0.59. For (E) and (F), the sizes are given as number of pixels in the long side of the flat aggregates. To see this figure in color, go online.

As expected, we found that these features were sufficient to drive both cell sorting (Fig. 4 A; Movie S6) and the rounding up of the aggregate observed in experiments (Fig. 1 A).

Regarding single cell dynamics, both cell types showed similar motility behaviors as shown by their respective speeds, MSDs, or directionality (Fig. 4, B–D). We found the MSDs to be slightly super-diffusive (exponent of 1.2–1.3), in agreement with our experimental results (Fig. 3 C). As in our experiments, we found that the velocity autocorrelation functions (Fig. S5) rapidly decay to zero. This shows that in the simulations, as in experiments, persistence of motion does not play a key role in the sorting dynamics.

To quantitatively reconcile length scales between simulations and experiments, we used typical cell sizes (four pixels in simulations and 20 microns in experiments). In simulations, as in experiments, we found that individual cell speeds were constant and similar for both tissues. We thus decided to equalize the speeds, which led to each simulation step being on the order of 10 s. This, in turn, led to sorting times ranging from 1 to 10 h, in agreement with experimental observations (Fig. S7).

For aggregate-scale dynamics in the simulations, we found that both the length of the boundary between the two tissues (Fig. 4 E) and the typical blob size (Fig. 4 F) followed power laws. For larger aggregates, these exponents were independent of size (Fig. S8). The boundary length decreased as the power −0.55 ± 0.11 of time, whereas the blob size increased as the power 0.59 ± 0.03 (mean ± SD, n = 21 simulations at seven different initial sizes). These values are both within the error ranges we obtained in the experiments.

Finally, our model also correctly reproduced the fluid-like behavior of separated tissues as shown by simulations of fusion (Movie S7) and engulfment (Movie S8). Taken together, these results demonstrate that a numerical simulation based solely on DAH, reproducing the geometry of our experiments and with model parameters partly coming from experimental measurements (see Materials and Methods) was sufficient to reproduce the data we obtained at different scales. Therefore, we conclude that DAH is sufficient to explain cell sorting in three-dimensional Hydra aggregates.

It is possible, however, that differential cell motility acts in addition to differential interfacial tensions and speeds up sorting. To test the effect of adding differential motility, we ran simulations including both mechanisms by separately tuning the effective temperatures of both tissues. Clearly, cellular processes are not driven by thermal fluctuations, but temperature here is a measure of the activity of cell extensions and thus models cell activity and motility. In accordance with previously published data suggesting that sorting might be driven by the activity of endodermal epithelial cells only (24), we decreased the effective temperature of ectodermal cells by a factor of two and measured the dynamics. We found that the aggregate-scale dynamics (rounding up, blob size, and boundary length) were indeed accelerated slightly by this change (Fig. S9). However, as expected, this change induced a clear difference in cell speeds between the two tissues, with the endodermal cells being faster than ectodermal ones (Fig. S9). This is in contradiction to our experimental results from single cell tracking experiments (Fig. 3). In addition, models of cell sorting based on differential motility evolve to a final configuration in which islands of slow-moving cells are surrounded by coherent streams of motile ones (16, 48). The final state we obtained during cell sorting does not correspond to an internal stream of endodermal cells and passive ectoderm. Indeed, we find no clear decrease in cell speeds as sorting proceeds (Fig. 3 B). These results, in our opinion, clearly negate any significant role for differences in cell motility in the process of cell sorting in Hydra aggregates.

Discussion

Relevance of the Hydra aggregate model

Hydra‘s self-organizing properties during regeneration from cell aggregates renders it a powerful system for the in vivo study of pattern formation. One could argue, however, that this dissociation-reaggregation of Hydra cells does not occur naturally and thus is not relevant to normal biology. However, the phenomenon yields normal Hydra polyps and thus provides insights into the physical principles that govern cell behavior in an in vivo setting. Moreover, the Hydra aggregate system allows precise analysis of the autonomous properties of cells that contribute to the formation of multicellular structures. This is particularly relevant to our understanding of how multicellularity evolved in animals.

Although this work focused on the physical mechanisms driving cell sorting in Hydra aggregates, future work will need to dissect the underlying molecular machinery that gives rise to the observed surface tension differences.

Importance of geometry

Our quantitative analysis of cell sorting dynamics revealed that sorting in Hydra aggregates is faster than published theoretical predictions. In addition, our results disagree with previous work claiming that full sorting is not observed in Hydra aggregates, that sorting slows down logarithmically, and that sorting could take as long as 100 h (10, 11). The largest aggregates used in our study achieved full sorting in 6–10 h (Fig. 1 A; Fig. S7) before forming a central cavity. Moreover, we only observed partial sorting on shorter timescales and for the largest aggregates studied. Quantitatively, the speed of sorting is reflected by the exponents controlling the dynamics of blob sizes and boundary lengths.

For blob size, our value of 0.49 ± 0.24 is higher than the result reported by Nakajima and Ishihara (38) (1/3) and Belmonte et al. (13) (0.28). Both articles use the DAH model to explain sorting in two dimensions but differ from our experiments in some key aspects. In particular, Nakajima and Ishihara (38) use periodic boundary conditions in two dimensions, making any effect of the outside medium irrelevant, and Belmonte et al. (13) use a modified Vicsek model in two dimensions, in which the ectodermal cells outnumber the endodermal cells three to one.

Similarly, models of sorting driven by differences in cell motility that are either intrinsic (16) or dependent on the cells’ local environment (17) have found slower dynamics than we observed (exponents of −0.22 and −0.17, respectively). Here, too, the underlying models differ from our experiments: Beatrici and Brunnet (16) also used a modified Vicsek model in two dimensions in which both cell types have fixed velocities, one cell type being four times faster than the other one, which is not the case in our experimental data. Of note, the authors of this work only predicted full sorting in the case where faster cells largely outnumbered slower ones, and their final configuration was the opposite of what was shown experimentally in (18). Finally, Strandkvist et al. (17) also used two-dimensional simulations with periodic boundary conditions and tuned the difference in cell motilities to be from 8-fold to 64-fold, two major differences from our experimental setup and observations.

We attribute this difference in dynamics to the specific initial conditions used in our experiments and simulations, i.e., a three-dimensional flat configuration. The equivalent configuration in two dimensions would be a thin line which, to our knowledge, has never been investigated. In addition, it has been shown that dimensionality by itself has a profound effect on the mechanisms of sorting (49). Although sorting in two dimensions was found to rely solely on cytoskeletal fluctuations, hydrodynamic instabilities can also play a role in three dimensions (49).

Because we (Fig. 3 C) and others (46) have established that cell motion is mostly random during Hydra cell sorting, the distance that an ectodermal cell has to travel to get in contact with the outside medium is greatly reduced in a flat geometry. Of note, rounding up of the initially flat aggregates took longer than cell sorting, as observed in experiments (Figs. 1 A and 4 A). This implies that this effect of geometry applied throughout the sorting process. To further probe this, we ran simulations modifying the initial geometry of the aggregates to make them spherical.

This change in geometry induced only partial sorting on timescales in which comparably sized, flat aggregates would fully sort. This result is in agreement with previous results obtained from simulations of DAH in two dimensions from circular initial conditions (10), the direct equivalent of the geometry tested here. Quantitatively, we found that changing the initial geometry decreased the exponent of blob size increase to 0.19 (Fig. S10), a value closer to the theoretical predictions discussed above. Of note, these simulations also showed that the MSDs of both cell types were then diffusive (Fig. S10), further confirming that the coherent component of motion observed both in our experiments and simulations stems from the rounding up of the aggregates.

Finally, to confirm the important role of the initial geometry, we also varied the initial thickness of the square aggregates from three cell sizes to seven and observed the effect of this change on sorting dynamics (Fig. S11). We indeed found that the thicker the initial aggregate, the slower the sorting, further supporting our hypothesis regarding the role of the initial geometry on sorting dynamics.

Distinguishing between models of cell sorting

We have shown through our simulations that differential surface tension is sufficient to recapitulate our experimental data on both the dynamics of sorting and the behavior of single cells. Furthermore, we have incorporated differential motility into the simulations in the form of different temperatures to test whether differences in motility acted in combination with differential surface tension to drive Hydra cell sorting. We incorporated differential motility in the simulation by varying the temperature of the two cell types. Of note, it has been demonstrated experimentally that the motion of retinal cells from chick embryos during sorting was properly captured by the CPM in which temperature models membrane fluctuations (50). Varying temperature separately for both tissues is thus a proper way of modeling intrinsic differences in cell activity and motility. As a result, in these simulations we observed differences in single cell behavior that we did not observe in the experimental data. Therefore, we conclude that differences in motility do not play a dominant role in Hydra cell sorting.

One possibly important process that we could not test with our experimental arrangement is the effect of the local environment on the motility of the cells, i.e., how do cells adjust their motility to the identity of their neighbors? This has been shown to suffice to drive sorting (17) and has been observed experimentally. Rieu et al. (46, 47) quantified the motility of endodermal cells in Hydra cell aggregates of different compositions: pure endoderm, pure ectoderm, and evenly mixed. Overall, their results show that cells move in a mostly random fashion and are most mobile in a purely ectodermal environment. However, differences in motility in response to a cell’s immediate surrounding are expected from the DAH, and intrinsic differences in motility are not required. Indeed, in a purely endodermal cell aggregate, cell adhesions are expected to be stronger and thus cell motion to be more limited. We therefore believe that this aspect does not contradict our results.

In the model proposed by Strandkvist et al. (17), cells react to their environment by changing their persistence time of motion. Persistence can thus also drive cell sorting. We have not studied that aspect here because our experimental data do not reveal any role for persistent motion in cell sorting, but such an effect could be implemented in a CPM (51) and its effect studied.

Conclusions

Our multiscale, interdisciplinary approach has answered a long-standing question regarding the mechanisms driving cell sorting in Hydra regeneration. We found that 1) differences in interfacial tensions between the tissues drive sorting, and 2) there are no intrinsic differences in cell motility between cell types. Our results thus rule out differential motility as a significant contributor to Hydra cell sorting. We confirmed our experimental results using numerical simulations and unexpectedly found that the initial geometry of the system is an important determinant of its sorting dynamics. We propose that this geometrical effect is the reason why our experimental power law exponents disagree with previously published theoretical values. Quite naturally, these previous studies have focused on the most common geometries and boundary conditions (in two dimensions: periodic boundary conditions with no edges or circular geometries), whereas our three-dimensional Hydra aggregates start from a flat configuration and round up as sorting occurs. In light of these results, we suggest that it may be worthwhile revisiting prior theoretical works on cell sorting in other systems and, going forward, simulate new experiments of cell sorting using the same geometrical arrangement that occurs in experiments.

Finally, as the importance of studying physical driving forces in the context of embryonic development is increasingly recognized, our work demonstrates that a similar approach is equally fruitful in studying regeneration, which is an exciting field waiting to be explored in more depth using physical and biomechanical approaches.

Author Contributions

E.-M.S.C. designed research. O.C.-E. and T.T.L. performed experiments. O.C.-E., T.T.L., and W.H.S. analyzed data. O.C.-E. and W.H.S. contributed analytical tools. O.C.-E. performed simulations. R.E.S. consulted on experiments. O.C.-E., R.E.S., and E.-M.S.C. wrote the manuscript.

Editor: Celeste Nelson.

Supporting Material

Movie S1. Time-Lapse Imaging of Sorting of a Watermelon Aggregate

The ectoderm is shown in green and the endoderm in magenta. The change in projected area is a signature of rounding up which occurs on a longer timescale than cell sorting.

Movie S6. Representative Sorting Simulation

A two-dimensional slice in the middle of the aggregate and a three-dimensional view are shown side by side. Axes are in pixels.