Summary
To better understand biophysical mechanisms of mechanosensory processing, we investigated two cell types in the Drosophila brain (A2 and B1 cells) that are postsynaptic to antennal vibration receptors. A2 cells receive excitatory synaptic currents in response to both directions of movement – thus twice per vibration cycle. The membrane acts as a lowpass-filter, so that voltage and spiking mainly track the vibration envelope rather than individual cycles. By contrast, B1 cells are excited by only forward or backward movement, meaning they are sensitive to vibration phase. They receive oscillatory synaptic currents at the stimulus frequency, and they bandpass-filter these inputs to favor specific frequencies. Different cells prefer different frequencies, due to differences in their voltage-gated conductances. Both Na+ and K+ conductances suppress low-frequency synaptic inputs, so cells with larger voltage-gated conductances prefer higher frequencies. These results illustrate how membrane properties and voltage-gated conductances can extract distinct stimulus features into parallel channels.
Introduction
Peripheral cells of the auditory, vestibular, somatosensory, and proprioceptive systems are all specialized to encode time-varying displacements. In vertebrates, these peripheral signals are then relayed to the brain stem or spinal cord, where they are transformed to extract the behaviorally-relevant features of mechanical stimuli. The brainstem and spinal cord are difficult to access for intracellular electrophysiological recording in vivo, particularly in an awake organism. As a result, we have an incomplete picture of the synaptic and cellular mechanisms underlying the first steps of central mechanosensory processing (Abraira and Ginty, 2013; Pickles, 2015; Straka et al., 2016).
Recently, new genetic tools have made it possible to target identified mechanosensory neurons of the Drosophila central nervous system for in vivo intracellular recording (Chang et al., 2016; Clemens et al., 2015; Lehnert et al., 2013; Tootoonian et al., 2012; Tuthill and Wilson, 2016). This approach provides the opportunity to connect neural computations in mechanosensory systems with the cellular mechanisms that implement those computations. Here we use this approach to target neurons in the brain that are postsynaptic to the largest mechanosensory organ in Drosophila, Johnston’s organ.
The function of Johnston’s organ is to encode time-varying deflections of the most distal antennal segment. Flies rely on this organ to evaluate courtship song (Ishikawa et al., 2017; Kamikouchi et al., 2009; Yorozu et al., 2009), to analyze wind cues (Bhandawat et al., 2010; Budick et al., 2007; Duistermars and Frye, 2008; Yorozu et al., 2009), to detect touch (Hampel et al., 2015), and to monitor their own dynamic motor performance and posture (Kamikouchi et al., 2009; Mamiya and Dickinson, 2015; Mamiya et al., 2011). Johnston’s organ is thus conceptually analogous to the vertebrate auditory, somatosensory, proprioceptive, and vestibular sense organs.
Johnston’s organ neurons (JONs) are housed inside the antenna, and their axons project via the antennal nerve to the brain, where they divide into several major branches. Two of these axon branches, A and B, are especially responsive to antennal vibrations, including the vibrations evoked by sound (Kamikouchi et al., 2009; Yorozu et al., 2009). Here we focus on neurons in the brain directly postsynaptic to these vibration-selective JONs – namely, A2 cells and B1 cells. B1 cells are postsynaptic to B-JONs, while A2 cells are postsynaptic to A-JONs and possibly also B-JONs (Figure 1A; Kamikouchi et al., 2009; Lai et al., 2012; Matsuo et al., 2016).
Figure 1. AC/DC responses to mechanical vibrations.
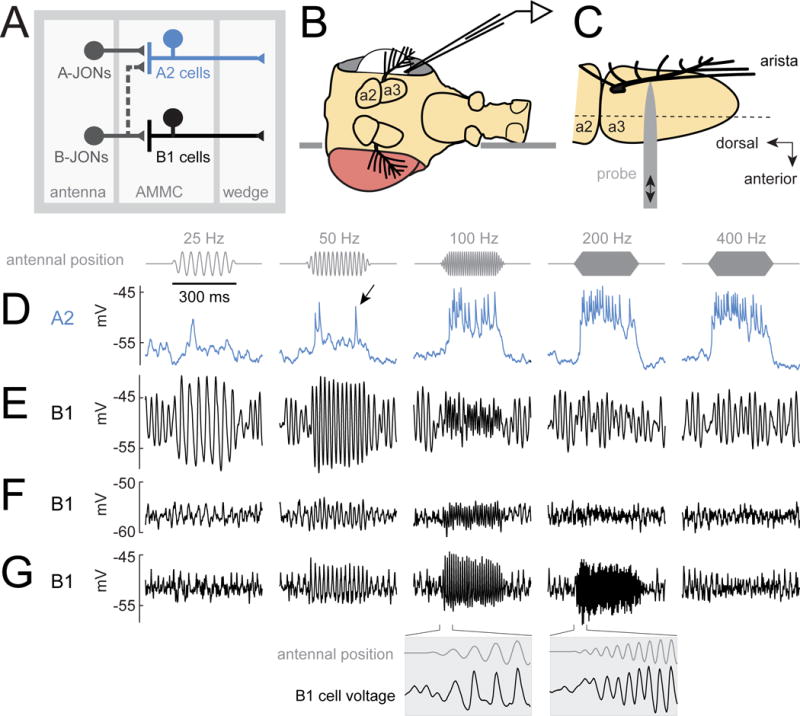
(A) A2 cells receive most of their input from A-type JONs, while B1 cells receive input from B-type JONs. Both A2 and B1 cells project to the wedge, a higher-order processing center for mechanosensory signals.
(B) The fly is inserted into an aperture in a thin platform (horizontal line). The head is rotated 90° relative to the body. One eye is removed, allowing access to the lateral brain. In vivo patch-clamp recordings are performed from the somata of GFP labeled A2 cells and B1 cells in the brain. The dorsal side of the platform is bathed in saline, and the ventral side remains dry.
(C) Antenna viewed from above the prep (i.e., with the lateral side of the antenna facing the viewer, so that the arista points out of the page). A piezoelectric probe is attached to the arista. Linear probe movement causes rotation of the most distal antennal segment (a3). The dashed line indicates the approximate axis of a3 rotation. JONs are housed within the next-most-proximal segment (a2), which does not rotate. JONs encode rotations of a3 relative to a2.
(D) Stimulus-evoked voltage responses in an example A2 cell. Stimuli are sinusoidal oscillations about the resting position of the antenna. The stimulus amplitude is 0.45 μm (mean-to-peak amplitude of the probe’s movement). The antenna’s resting position is zero, and movement toward the head is positive, while movement away from the head is negative. In A2 cells, antennal vibrations elicit depolarizing responses and spikes (arrow, see also Figure S1). Spikes recorded at the soma are small, which is typical of many Drosophila neurons.
(E–G) Same for three example B1 cells. In B1 cells, vibrations elicit sinusoidal modulations of the membrane potential which are phase-locked to the stimulus. Insets below are plotted on a 10× expanded time base. Oscillations prior to stimulus onset are likely due to normal “spontaneous” oscillations in the tension on JONs (Figure S2). See Methods for genotypes used in each figure.
Both A2 and B1 cells are known to respond to sound-evoked antennal vibrations, largely on the basis of calcium imaging data (Lai et al., 2012; Tootoonian et al., 2012; Vaughan et al., 2014). Importantly, silencing B1 cells attenuates behavior evoked by courtship song (Vaughan et al., 2014; Zhou et al., 2015). Moreover, silencing postsynaptic partners of B1 cells also attenuates song-evoked behavior (Zhou et al., 2015). Thus, B1 cells (and potentially also A2 cells) are key elements in the circuits linking auditory stimuli with behavior. However, little is known about the mechanisms that allow B1 and A2 cells to respond selectively to some sounds and not others.
In this study, we used in vivo patch-clamp recordings to investigate what features of antennal vibrations these cells encode, how they transform the synaptic input they receive from JONs, and how these transformations are implemented mechanistically. We show that A2 and B1 cells are co-recruited by many of the same stimuli, but they use qualitatively different coding schemes. Namely, A2 cells use spike rates to encode the overall amount of vibration (the vibration envelope), whereas B1 cells use bidirectional graded potentials to track each vibration cycle. Interestingly, B1 cell membranes behave as intrinsic electrical bandpass filters. Moreover, the mechanism of bandpass filtering in B1 cells is unusual: voltage-gated Na+ and K+ channels work together to suppress low-frequency synaptic inputs, while passive membrane properties selectively suppress high-frequency synaptic inputs. Because B1 cells have diverse cell-intrinsic properties, they filter their synaptic inputs in different ways. Our results show how different features of a mechanical stimulus can be extracted by distinct parallel processing streams in the brain, by virtue of the specialized properties of membranes and ion channels.
Results
AC/DC responses to mechanical vibrations
To perform genetically-targeted whole-cell somatic recordings from A2 cells and B1 cells (Figure 1A), we used selective Gal4 lines to label these cells with GFP (Cachero et al., 2010; Lai et al., 2012; Vaughan et al., 2014). To precisely control the position of the distal antennal segment, we attached a piezoelectric probe to the arista, the rigid branching structure which protrudes from the distal segment (Figures 1B and 1C).
We found that antennal vibrations depolarized A2 cells and elicited spikes (Figure 1D, Figure S1). When the stimulus was a low-amplitude vibration, the time course of the response tracked the vibration envelope, not the cycle-by-cycle modulation of the vibration. At larger vibration amplitudes, we did observe some phase-locking of spikes at certain vibration frequencies (Figure S1), but overall the dynamics of A2 cell responses were most correlated with the vibration envelope. A2 responses increased with vibration frequency (Figure 1D) and vibration amplitude (Figure 2). Thus, A2 cells can be viewed as mainly encoding the overall amount of motion energy in the stimulus – a quantity that grows with both vibration frequency and vibration amplitude.
Figure 2. Diverse vibration frequency tuning.
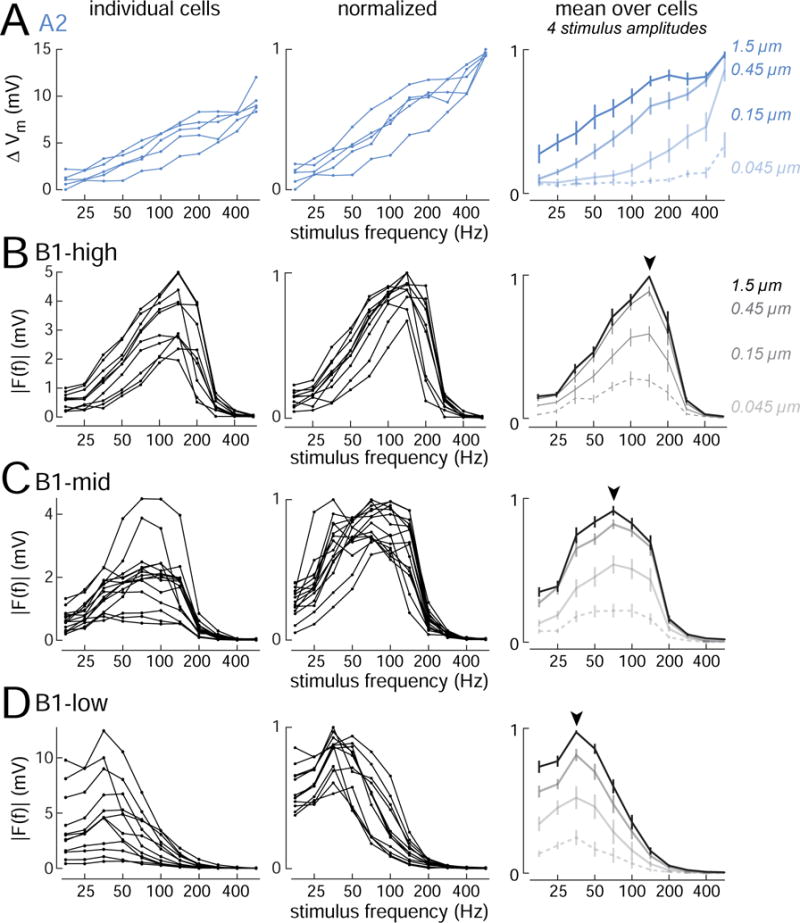
(A) Frequency tuning curves for A2 cells (n=5 cells; stimulus amplitude is 0.45 μm). Response magnitude is calculated as the change in average voltage during the 300 ms stimulus presentation, which is strongly correlated with A2 cell spike rate (Figure S1). Right panel shows cell-averaged responses to four stimulus amplitudes (± SEM across cells). X-axes are logarithmic to emphasize differences in tuning at lower amplitudes.
(B) Same but for B1-high cells (n=10 cells). For all B1 cells, response magnitude is calculated as the amplitude of the Fourier component of the response at the stimulus frequency. Arrowhead indicates modal best frequency.
(C) Same but for B1-mid cells (n=15 cells).
(D) Same but for B1-low cells (n=12 cells). Figure S3 shows the same data sorted by Gal4 line.
The responses of B1 cells differed in several respects from A2 cell responses. B1 cells never spiked in response to mechanical stimuli. B1 cells also showed almost no net voltage change over the duration of a sinusoidal stimulus; in other words, there was no “DC” response. Instead, with each stimulus cycle, their voltage was modulated up and down nearly symmetrically around the cell’s resting voltage (an “AC” response; Figures 1E, 1F, 1G). B1 cells also differed from A2 cells in preferring relatively low frequencies.
In some B1 cells, membrane voltage tended to oscillate even when we did not command a probe movement (Figures 1E, 1F, 1G). These oscillations were largely eliminated when the antennal nerve was cut, and they were present even when the probe was not attached (Figure S2), meaning that they may be driven by the normal small spontaneous vibrations of the antenna (Göpfert et al., 2005).
Diverse vibration frequency preferences in different cell types
To more systematically describe the tuning of A2 and B1 cells, we tested a range of vibration frequencies (17.7 – 565.7 Hz) and stimulus amplitudes (0.045 – 1.5 μm probe displacements). We quantified A2 cell responses as the average change in voltage over the duration of the stimulus, which is correlated with A2 spike rate. We quantified B1 cell responses by taking the magnitude of the voltage Fourier component at the stimulus frequency, because B1 cells respond to vibrations in AC mode rather than DC mode.
We found that all A2 cells shared essentially the same tuning profile: their responses grew monotonically with frequency, up to the highest frequency we tested (Figure 2A). In contrast to the uniformity of A2 cells, B1 cells were relatively diverse (Figures 2B, 2C, 2D). This confirms a previous calcium imaging study indicating that B1 cells are diverse, whereas A2 cells are not (Lai et al., 2012). We found that all B1 cells had bandpass tuning, and all had preferred frequencies < 200 Hz. However, different B1 cells had different preferred frequencies. Thus, we can think of the B1 cell population as an array of bandpass filters having diverse passbands.
We used a k-means algorithm to cluster cells into types based on their frequency tuning curves. Given k=4 clusters, we found that all A2 cells clustered together, and B1 cells clustered into three types. We call these B1 types high, mid, and low (in reference to their preferred vibration frequency; Figures 2B, 2C, 2D). Figure 1 shows individual examples of B1-low (Figure 1E), B1-mid (Figure 1F), and B1-high (Figure 1G).
It should be emphasized that the vibration frequency tuning properties of B1 cells varied along a smooth continuum, and so in this regard, the B1 categories are arbitrary. However, we did find Gal4 lines which respect one category boundary. Specifically, fru-Gal4 labelled only cells having the physiological properties we called “B1-high”, whereas VT27938-Gal4 labelled only cells having the properties we called “B1-mid/low”. We investigated a large panel of Gal4 lines labeling B1 cells, but we did not find a Gal4 line that could distinguish B1-mid from B1-low cells (Figure S3). B1-high cells also had distinctive intrinsic properties (see below), which provides independent support for the B1 categories that arise from the clustering algorithm.
Sensitivity to small stimulus amplitudes was a notable feature of A2 cells and B1 cells. When the stimulus frequency was close to their preferred frequency, both A2 cells and B1 cells responded to even the lowest stimulus amplitude we tested (0.045 μm; Figure 2). This amplitude corresponds to the smallest displacement that evokes a behavioral response (Lehnert et al., 2013).
Direction-sensitivity and opponency in B1 cells
We next investigated how A2 and B1 cells responded to step displacements of the antenna. We tested steps in both directions, positive (toward the head) and negative (away from the head). We found that A2 cells were transiently depolarized by steps in either direction (Figure 3A). This means that A2 cells will be excited by both the positive and negative parts of each vibration cycle. Indeed, A2 cells sometimes fired two bursts of spikes per vibration cycle, under the specific stimulus conditions where A2 spikes show some phase-locking to the stimulus (Figure S1).
Figure 3. Direction-sensitivity and opponency.
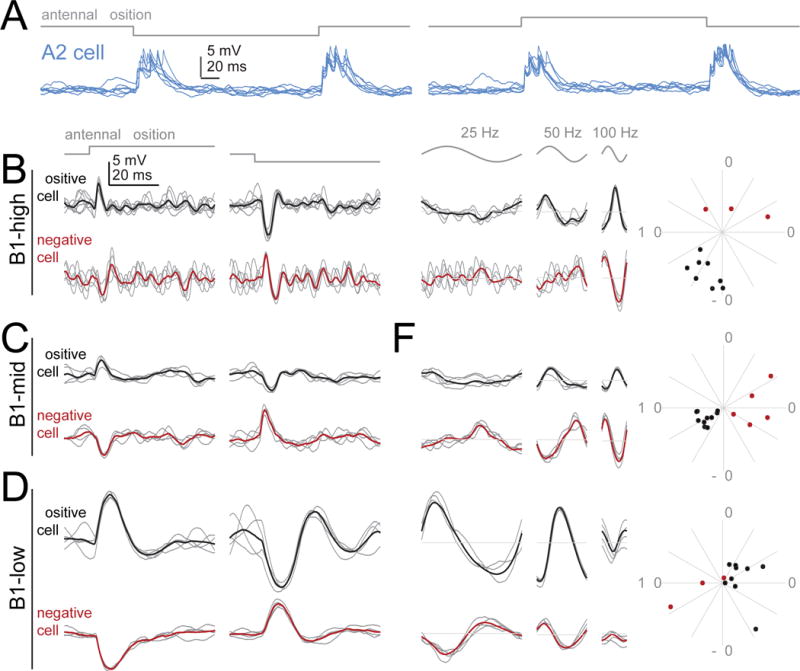
(A) Responses in an example A2 cell to step displacements of the antenna (3 μm away from its resting position). Positive steps push the antenna toward the head; negative steps pull it away. Like all A2 cells, this cell depolarizes transiently in response to both step onset and step offset, for a step in either direction. Responses to 7 stimulus repetitions are overlaid. Voltage scale is the same for all traces in this figure, but note different time scale in (A) versus (B-G).
(B) Responses of two example B1-high cells to step displacements (3 μm). One is depolarized by the positive step, whereas the other is depolarized by the negative step. In both cases, the response begins with a delay of ~2.5 ms from stimulus onset. Gray traces are example trials, black/red traces are the mean of all trials.
(C) Same but for two B1-mid cells.
(D) Same but for two B1-low cells.
(E-G) Responses in the same 6 cells to sinusoidal stimuli (stimulus amplitude is 1.5 μm). The responses of each opponent pair are anticorrelated; this is most obvious at the preferred frequency of each cell type. Radial plots show the phase of the Fourier component at the stimulus frequency (100 Hz for B1-high/-mid, 25 Hz for B1-low). Positive cells (black) were generally about half a cycle out of phase with negative cells (red). For low frequency vibrations, positive cells led the stimulus. As the stimulus frequency increased, the phase lead for positive cells turned into a phase lag. Data are from 11 B1-high cells, 15 B1-mid cells, and 12 B1-low cells.
In contrast to A2 cells, B1 cells were direction-sensitive: inverting the direction of the stimulus inverted the cell’s voltage response (Figures 3B, 3C, 3D). For example, some B1 cells were depolarized by positive steps and hyperpolarized by negative steps. This type of cell would be excited by the positive part of each vibration cycle, and inhibited by the negative parts of each vibration cycle. Other B1 cells were hyperpolarized by positive steps and depolarized by negative steps. We found both “positive cells” and “negative cells” in the B1 -high, -mid, and –low populations (Figure 3). As we would expect, positive cells and negative cells were roughly 180 degrees out of phase when the stimulus was a vibration rather than a step displacement (Figures 3E, 3F, 3G). Thus, the direction preference of a B1 cell (i.e., its preference for positive or negative steps) correlates with the phase of its vibration response.
B1 cell responses were also often biphasic, consisting of depolarization followed by hyperpolarization, or else hyperpolarization followed by depolarization (Figures 3B, 3C, 3D). Notably, the period of this cycle was shortest for B1-high cells, intermediate for B1-mid cells, and longest for B1-low cells. In B1-high cells, for instance, the typical period was just under 10 ms, which matches these cells’ preferences for vibration frequencies just over 100 Hz. By contrast, in B1-low cells, the typical period was approximately 30 ms, which matches these preferences for vibration frequencies around 35 Hz.
Mechanosensory responses depend largely on synaptic input via gap junctions
Next, we asked what sort of synapses provide input to A2 and B1 cells. Johnston’s organ neurons are cholinergic (Ishikawa et al., 2017; Yasuyama and Salvaterra, 1999), so we first tested the effect of pharmacologically blocking nicotinic acetylcholine receptors. This had only a small effect on A2 cell responses (peak responses to step displacements were reduced by 21% on average, n=5 cells, p=0.06, two-sided sign-rank test, data not shown). Blocking nicotinic receptors had a similarly modest effect on the responses of B1 cells (Figures 4A and 4B). When we added the calcium channel antagonist Cd2+ to block synaptic vesicle release in the presence of a nicotinic antagonist, this had no additional effect (200 μM, n=3 cells, data not shown), indicating that all chemical synaptic input to B1 cells requires nicotinic receptors. Together, these observations suggest that the mechanical stimuli drive input to B1 and A2 cells via mixed chemical-electrical synapses rather than purely chemical synapses.
Figure 4. Mechanosensory responses depend largely on synaptic input via gap junctions.
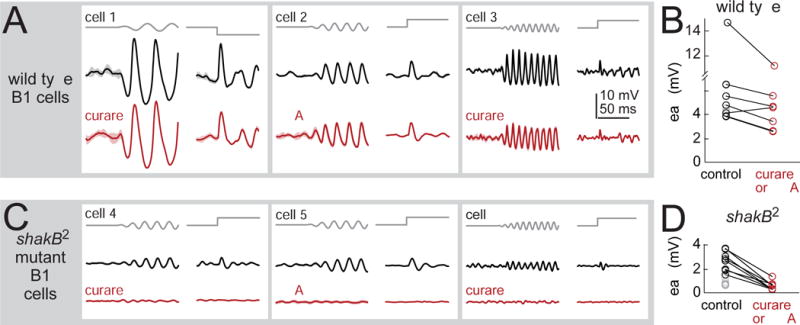
(A) Stimulus-evoked responses of three example B1 cells recorded in wild type flies, before and after blocking nicotinic receptors (with 50 μM curare or 0.5 μM MLA). Vibration frequency was chosen to match the cell’s preferred frequency (25, 50, and 100 Hz) and the direction of the step stimulus was chosen to match the cell’s preferred direction (1.5 μm vibration, 3 μm step). Shaded bands are SEM across trials. Cells were recorded in the GMR45D07-Gal4 line, which labels a mixture of B1 cell types (B1-high, -mid, and -low).
(B) Peak amplitude of B1 responses to the step stimulus. Blocking nicotinic receptors produces a small but significant effect (20 ± 6% reduction, p<0.05, paired two-sided signed-rank test, n=7 cells).
(C) B1 cells in the shakB2 gap junction subunit mutant. Blocking nicotinic receptors essentially abolished stimulus-evoked responses. Sinusoids were 50 or 100 Hz, and all cells were recorded in GMR45D07-Gal4.
(D) Peak amplitude of B1 responses to the step stimulus in shakB mutants. Responses were significantly smaller than wild type (p<10−3, two-sided ranksum test; n=10 wild type cells and n=15 mutant cells). In shakB mutants, nicotinic antagonists reduced responses by 78±4% (p<10−3, paired two-sided signed-rank test; n=8 mutant cells). We corrected p-values for multiple comparisons using a Bonferroni-Holm procedure (3 tests in this figure). Gray symbols are experiments where antagonists were not tested.
JONs express shakB, a gap junction subunit (Pezier et al., 2016), and so we tested the effect of a mutation in the shakB gene (the null allelle shakB2; Baird et al., 1990). In B1 cells, stimulus-evoked responses were significantly reduced in the mutant. Importantly, the residual responses in the mutant were completely abolished by nicotinic antagonists (Figures 4C and 4D). We cannot exclude the idea that the mutant phenotype is due to a developmental artifact. However, because all chemical synaptic input to B1 cells is nicotinic, and because the shakB2 mutation selectively eliminates the non-nicotinic input to B1 cells, it is likely that the mutant phenotype reflects the direct loss of electrical synaptic input to B1 cells. We did not perform recordings from A2 cells in the mutant, but finding that nicotinic antagonists had little effect on A2 cell responses suggests that electrical synapses are the main source of synaptic input to these cells as well.
Synaptic input to these cells may arise from both JONs and other central neurons. In principle, input from JONs might be mediated by gap junctions, while input from central neurons might be mediated by nicotinic receptors, or vice versa. However, it seems likely that JONs form both electrical and chemical synapses onto B1 cells, because the very earliest part of the B1 step response (<10 ms from step onset) was affected by both the shakB mutation and the nicotinic antagonists. This conclusion is also consistent with anatomical data indicating that JONs form both gap junctions and chemical synapses with central neurons (Pezier et al., 2014; Pezier et al., 2016; Sivan-Loukianova and Eberl, 2005).
In summary, our findings show that most of the mechanosensory input to B1 (and possibly A2) cells arrives via electrical synapses. Electrical synapses are notably fast, and so this provides an explanation for why responses to step stimuli can have such a short latency (Figure 3). The ShakB protein can form electrical synapses that are non-rectifying (Phelan et al., 2008), and this may be part of the reason why B1 cells can respond to vibrations with nearly-symmetrical voltage fluctuations above and below their resting potential (Figure 1).
Synaptic currents evoked by mechanical stimuli
In order to better understand the origin of mechanical tuning in A2 and B1 cells, we next asked what synaptic currents these cells receive in response to mechanical vibrations. To voltage clamp these cells, we used a combined genetic-pharmacological approach. First, we knocked down voltage-gated Na+ channels in A2 and B1 cells using transgenic RNAi directed against the DmNaV gene (also known as para). The knockdown construct was expressed under the control of the same Gal4 lines we used to label these cells with GFP. Meanwhile, to block postsynaptic K+ channels, we included both Cs+ and TEA in the patch pipette. Together, these measures almost completely suppressed voltage-gated currents, allowing us to focus on synaptic currents in isolation (Figure S4). (A genetic approach was required to eliminate DmNaV because standard internal pore blockers of voltage-gated Na+ channels are ineffective in Drosophila.)
In A2 cells, step displacements of the antenna in either direction elicited transient inward synaptic currents (Figure 5A). These synaptic currents had a short latency and low jitter, consistent with a monosynaptic connection from JONs (latency 2.37 ±0.09 ms, jitter 0.32±0.18 ms, n=5 cells, mean ± SEM across cells). In A2 cells, vibrations evoked inward currents that grew with vibration frequency; these currents were mainly composed of a DC component, with a small AC component at double the stimulus frequency (Figure 5B). This makes sense if we imagine that both the positive and negative parts of each stimulus cycle elicit inward current; because the current evoked by each half-cycle decays on a time scale slower than the vibration frequency, currents summate across half-cycles to produce a mainly-DC response. We found little AC component in the voltage responses of A2 cells (Figure 1), implying that the membrane acts as a low-pass filter which reduces the small AC component of the cell’s synaptic input.
Figure 5. Synaptic currents evoked by mechanical stimuli.
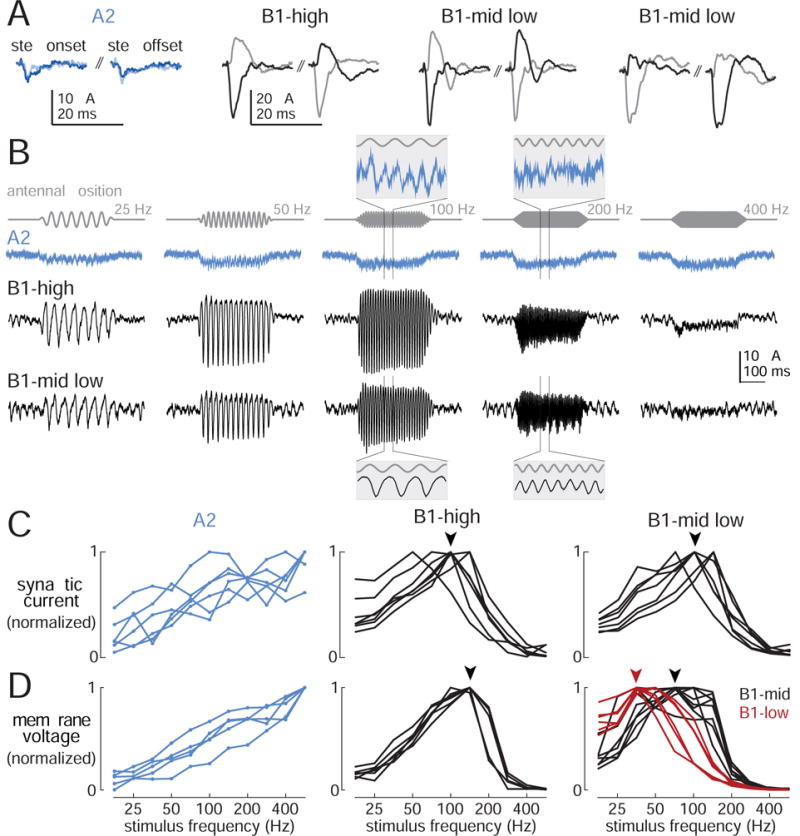
(A)Synaptic currents evoked by step displacements in four example cells (dark: +3 μm step, light: −3 μm step). Step onset occurs at the start of the first trace, step offset at the start of the second trace. The B1-high cell and the first B1-mid/low cell are “positive cells”. The second B1-mid/low cell is a “negative cell”. Scales are identical for all B1 cells.
(B) Synaptic currents evoked by sinusoidal stimuli (0.45 μm). Insets are expanded 10× horizontally and rescaled to arbitrary values in the vertical axis.
(C) Tuning curves showing synaptic current versus frequency, normalized to the maximum for each cell. For A2 cells, the response is measured as the average change in holding current during the stimulus (n=6 cells). For B1 cells, the response is calculated as the magnitude of the Fourier component of the holding current at the stimulus frequency (B1-high: n=7 cells; B1-mid/low: n=7 cells). Stimuli are 0.45 μm in amplitude. Note the similar tuning of synaptic currents in all the B1 cells (comparing currents in fru-Gal4 cells versus VT27938-Gal4 cells, p=0.2, bootstrapped K-S distance). Arrowheads represent modal best frequency for B1-high and B1-mid/low.
(D)Tuning curves for voltage responses recorded in the same cell types (recorded in current-clamp mode with voltage-gated conductances intact). In B1-high cells, voltage tuning is shifted to higher frequencies, as compared to synaptic current tuning (comparing voltage with current in fru-Gal4 cells, p<10−3, bootstrapped K-S distance). By contrast, in B1-mid/low cells, tuning is shifted to lower frequencies (comparing voltage with current in VT27938-Gal4 cells, p<10−4, bootstrapped K-S distance). Stimuli are 0.45 μm. This panel shows a subset of the B1 data in Figure 2 (here, n=5 A2 cells, 7 B1-high, 8 B1-mid, 6 B1-low); these are the data obtained from fru-Gal4 (B1-high) and VT27938-Gal4 (B1-mid/low).
In B1 cells, step displacements evoked responses with short latency and low jitter, again consistent with a monosynaptic connection from JONs (latency 1.96±0.05 ms, jitter 0.21±0.02 ms, n =24 cells). Positive step displacements evoked inward currents in some B1 cells and outward currents in other B1 cells (Figure 5A). Vibrations elicited AC synaptic currents at a frequency equal to the stimulus frequency, with an amplitude that depended on stimulus frequency (Figure 5B).
To compare synaptic currents in different B1 cell types, we relied on the fact that fru-Gal4 selectively labels B1-high cells, whereas VT27938-Gal4 selectively labels B1-mid/low cells (Figure S3). For each of these Gal4 lines, we compared frequency tuning curves computed from synaptic currents (Figure 5C) with frequency tuning curves computed from membrane voltage measured in our current-clamp experiments using the same Gal4 lines (Figure 5D).
This comparison revealed that, in B1-high cells, voltage tuning curves were shifted to significantly higher frequencies, compared to synaptic current tuning curves (Figure 5C and 5D, middle panels). Conversely, in B1-mid/low cells, voltage tuning curves were shifted to significantly lower frequencies, compared to synaptic current tuning curves (Figure 5C and 5D, right panels). Thus, B1-high cells must have intrinsic properties that favor high-frequency synaptic inputs, whereas B1-mid/low cells must have intrinsic properties that favor low-frequency synaptic inputs.
Interestingly, there was no systematic difference between the frequency tuning of synaptic currents in B1-high cells (fru-Gal4 cells) versus B1-mid/low cells (VT27938-Gal4 cells; Figure 5B and Figure S5C). In both cases, synaptic currents were typically largest when vibration frequencies were near 100 Hz. Thus, in response to a vibration, all B1 cell types receive similarly-tuned synaptic input, but they filter that input differently – thereby shifting their voltage tuning curve upward (for B1-high) or downward (for B1-low) in the frequency domain.
Similarly, when we compared synaptic currents evoked by step displacements in B1-high and B1-mid/low cells, we found no systematic difference in the kinetics of these currents (Figure 5A). Recall that step displacements evoke fast voltage responses in B1-high cells and slower voltage responses B1-mid/low cells (Figures 3B, 3C, 3D). This again implies that these cell types receive synaptic input with similar kinetics, but they filter that input differently, thereby generating either fast voltage transients (for B1-high) or slow voltage transients (for B1-mid/low).
A caveat in all our synaptic current recordings is that Na+ channel knockdown is not restricted to the cell that is being recorded. The two Gal4 lines we used (fru and VT27938) drive expression in scattered additional cell types (beyond B1 and A2 cells). In particular, fru-Gal4 drives expression in A-JONs (Stockinger et al., 2005; Yu et al., 2010). However, several lines of evidence indicate that “off-target” Na+ channel knockdown did not substantial alter the tuning of synaptic currents in B1 cells. First, the finding that B1 cell synaptic currents are uniformly tuned to 100 Hz (Figure 5C) was confirmed in a third Gal4 line (VT30609-Gal4, data not shown). Because we made this observation in three Gal4 lines that drive expression in largely nonoverlapping “off-target” cell types, the finding of a uniform result is notable. Moreover, the idea that synaptic currents and voltage responses can have systematically different tuning profiles in the exact same B1 cell is directly supported by experiments where we switched between voltage clamp and current clamp in the same recording (Figure S5). These observations strongly argue that there is a bona fide difference between synaptic current tuning and voltage tuning in B1 cells.
B1 cells rest in depolarization block
Our results indicate that distinct B1 cell types receive similarly-tuned synaptic input, but they filter that input differently, shifting their voltage tuning upward (for B1-high) or downward (for B1-low). Up-shifting is particularly interesting because it implies a role for voltage-gated conductances; it cannot occur in a purely passive membrane. Given that B1 cells never spiked in response to mechanical stimuli, it may seem odd to postulate an important role for voltage-gated conductances in these cells. But B1 cells are far from passive: injecting a large hyperpolarizing current can evoke large spikes. Hyperpolarization-evoked spikes were consistently observed in B1-high cells, but never in B1-mid/low cells (Figure 6A). This suggests that B1-high cells rest in depolarization block, meaning that their resting potential is so depolarized that Na+ channels are largely inactivated and spikes cannot initiate. Depolarization block prevents spiking, but it does not prevent the graded potentials in B1 cells from propagating to their axon terminals (Figure S6; Vaughan et al., 2014). Certain neurons in the fly visual system are known to rest in depolarization block, and like B1 cells, these neurons can generate Na+ spikes after artificial hyperpolarization (Hengstenberg, 1977; Joesch et al., 2008).
Figure 6. B1 cells rest in depolarization block.
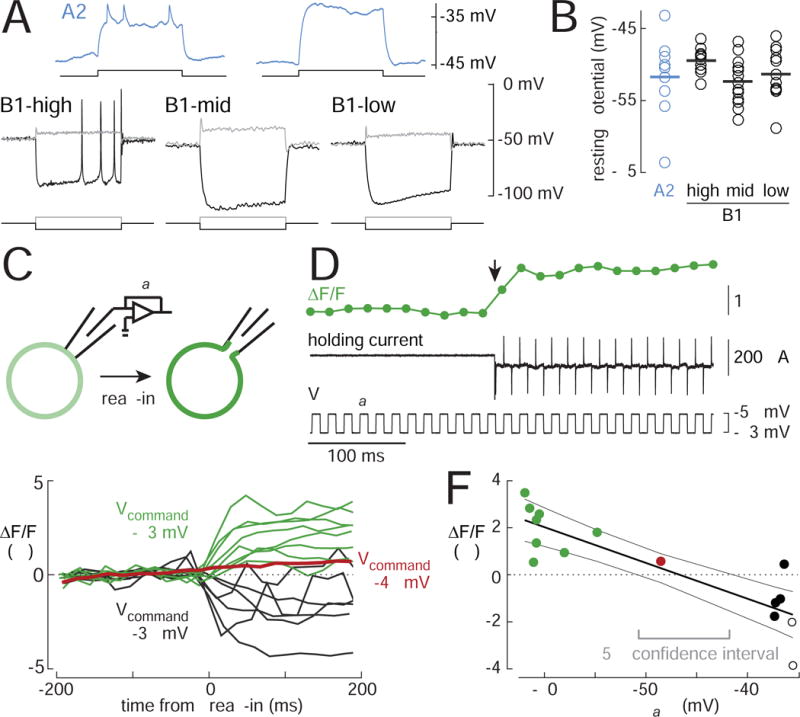
(A) Voltage responses to current injection via the recording electrode. Depolarizing the A2 cell elicits a train of small spikes; these spikes are blocked by TTX (1 μM). By contrast, B1 cells fire only a single small spike at the onset of depolarization. Surprisingly, when B1-high cells are hyperpolarized far below their resting potential, they can fire large spikes. Current steps are 100 ms for A2 cells and 500 ms for B1 cells).
Injected current in these examples was (in pA) +20 (A2), +40/−80 (B1-high), +40/−30 (B1-mid and B1-low).
(B) Resting membrane potential in A2 and B1 cells (n=9, 11, 15, 12 cells). Horizontal lines are means.
(C) Optical measurement of membrane potential. A cell-attached recording is established in voltage-clamp mode, and ArcLight fluorescence in the cell body is imaged before and after “break-in”. ArcLight fluorescence goes up with hyperpolarization and down with depolarization. The change in fluorescence upon break-in should indicate the difference between Vcommand and Vrest.
(D) A typical experiment. Vcommand is stepped rapidly between −63 mV and −58 mV while negative pressure is applied to the patch. Break-in is signaled by the sudden appearance of large current transients. Break-in increases ArcLight fluorescence (arrow).
(E) Overlay of ΔF/F versus time for all experiments. Vcommand was either −63 mV (green), −48 mV (red), or −38 mV (black). Each line represents a different cell (n=15).
(F) ΔF/F (averaged over ~200 ms after break-in) versus Vcommand. Filled circles are B1 cells, empty circles are A2 cells. Black lines indicate linear regression ± 95% confidence intervals (ΔF/F = m· Vcommand +b, m = −0.15% / mV, b = −7.11%). Gray bracket indicates the range of Vrest values within the 95% confidence interval.
Depolarization block is clearly the physiological state of B1 cells, and not an artifact. The resting potential in both A2 and B1 cells (Vrest) was typically around −50 mV (Figure 6B; corrected for electrode junction potential), and we confirmed this measurement using the genetically encoded voltage indicator ArcLight (Cao et al., 2013; Jin et al., 2012). We expressed ArcLight in B1 and A2 cells, and after forming a cell-attached recording, we imaged the fluorescence change in the soma as we ruptured the patch under the pipette tip (Figures 6C, 6D, 6E). Regressing the change in fluorescence against the command voltage yielded Vrest = −47 mV (taken from the x-intercept of the fit, 95% confidence interval is ± 4 mV, Figure 6F). This experiment provides a non-invasive measurement of the resting potential and confirms our measurement from whole-cell recordings (−51 mV, mean of 44 cells, Figure 6B).
Voltage-gated currents at steady-state
Thus far, several observations have indicated that B1 cells have specialized intrinsic properties. To investigate these specializations, we made voltage-clamp recordings to examine the currents that flow when the membrane is stepped to different voltages. We used a K+-based patch pipette solution (rather than a Cs+/TEA-based solution) in order to leave K+ currents intact. We sequentially added TTX to block voltage gated Na+ currents, and then 4-AP plus TEA to block voltage-gated K+ currents (Figure 7A). We interpret the currents that flow in response to voltage steps as “intrinsic currents” because synaptic input was eliminated by cutting the antennal nerve in most experiments; a nicotinic antagonist was also added to the bath.
Figure 7. Voltage-gated currents at steady state.
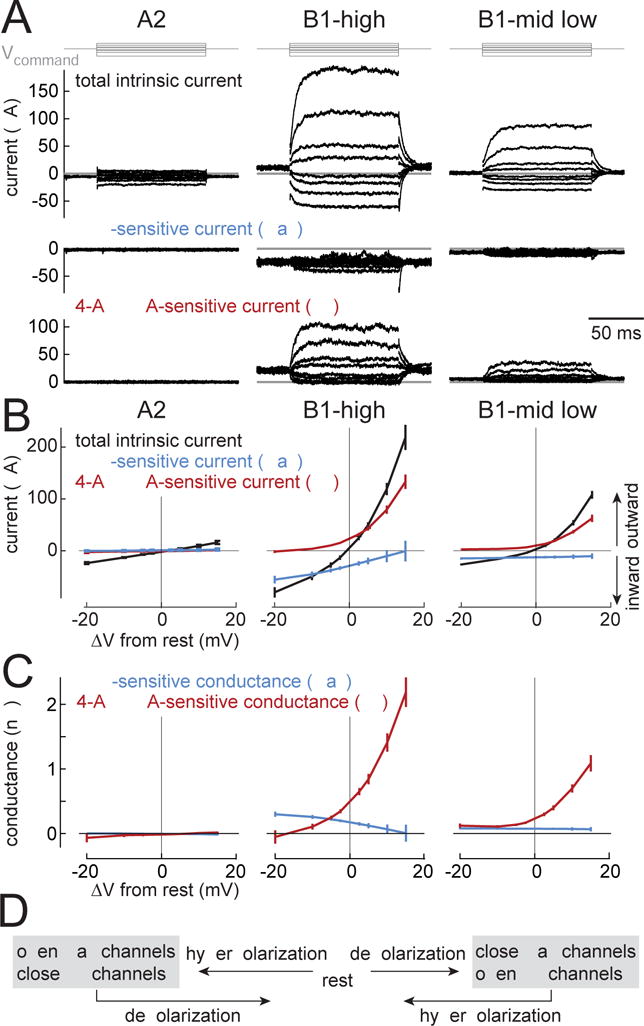
(A) Current responses to voltage steps in an example A2 cell, a B1-high cell, and a B1-mid/low cell. Steps are relative to Vrest (−20, −10, −5, −2.5, 2.5, 5, 10, and 15 mV). Capacitive transients following voltage changes are blanked for clarity. Subtracting the current recorded after adding TTX (1 μM), yields the TTX-sensitive component. Subtracting the current recorded after adding 4-AP (5 mM) and TEA (10 mM) yields the 4-AP/TEA-sensitive component. To isolate intrinsic currents, nicotinic synaptic transmission was blocked (with MLA or curare) and the antennal nerve was cut. In A2 recordings the antennal nerve was left intact in order to identify A2 cells based on their stimulus responses.
(B) Steady-state current versus the voltage change from rest (mean ± SEM across cells). In A2 cells, there is little effect of TTX or 4-AP+TEA (n=5 cells). In B1 cells, by contrast, there are large voltage-gated Na+ currents (TTX-sensitive currents) and large voltage-gated K+ currents (4-AP+TEA-sensitive currents). These voltage-gated currents are systematically larger in B1-high cells versus B1-mid/low cells (n=8 B1-high, n=7 B1-mid/low). Together, TTX, 4-AP, and TEA almost completely block all voltage-gated currents in B1 cells (Figure S4C).
(C) Steady-state conductance versus voltage change from rest (mean ± SEM across cells). Depolarization from rest decreases Na+ conductance and increases K+ conductance, while hyperpolarization has the opposite effect. The small negative conductance values (at −20 mV below Vrest) are artifacts due to a small drift in some recordings during 4-AP/TEA wash-in; the recorded current here is essentially zero; see Methods.
(D) Schematic summary of these data.
We first analyzed the steady-state currents that flow in these cells when we step the voltage to different values above or below Vrest (± 20 mV). When we inspected these steady-state currents, we found several interesting differences between cell types. In A2 cells, the relationship between steady-state current and voltage was linear (Figure 7B). The steady-state membrane conductance (the slope of the I-V relationship) was also relatively small (Figure 7B), and there was no TTX-sensitive conductance or 4-AP/TEA-sensitive conductance. Thus, the only steady-state current we observe in A2 cells is a small passive “leak” current. Of course, A2 cells fire spikes, but the voltage-gated channels in A2 cells seem to be electrotonically distant from the soma.
By contrast, in B1-high cells, the steady-state current had large TTX-sensitive and 4-AP/TEA-sensitive components. The TTX-sensitive component was inward, consistent with a voltage-gated Na+ current (Figure 7B). The 4-AP/TEA-sensitive component was outward, consistent with a voltage-gated K+ current (Figure 7B). Together, these three drugs blocked most voltage-gated currents in all B1 cells (Figure S4).
The voltage-gated currents in B1-high cells had interesting properties near Vrest. Depolarization from rest increased K+ conductance and decreased Na+ conductance (Figure 7C). Both these effects should push the cell back toward Vrest. Conversely, hyperpolarization decreased K+ conductance and increased Na+ conductance (Figure 7C), which again should push the cell back toward Vrest. Thus, in B1-high cells, steady-state voltage-gated K+ and Na+ currents will work together to oppose both depolarization and hyperpolarization. In essence, they will act as “buffers” which dampen the voltage response to any sustained input (Figure 7D).
It is unusual for voltage-gated Na+ currents to oppose depolarization. Normally, these currents amplify rather than suppress depolarization. One reason why the situation is unusual here is that Vrest is relatively depolarized, and so voltage-gated Na+ channels will be partly (but incompletely) inactivated (Olson et al., 2008). Depolarization beyond Vrest should increase the fraction of channels in the inactivated state, yielding a net decrease in the steady-state Na+ current.
We found that B1-mid/low cells were qualitatively similar to B1-high cells, but their voltage-gated conductances were smaller (Figures 7A, 7B, 7C). This means that K+ and Na+ channels will still work as “buffers”, but their effects will be weaker. The weaker active properties of B1-mid/low cells are consistent with our observation that we can evoke spikes in B1-high cells but not B1-mid/low cells (Figure 6A).
Our somatic recordings may provide an incomplete view of conductances outside the soma. However, it seems our access to voltage-gated conductances in B1 cells is better than our access to voltage-gated conductances in A2 cells. B1 spikes are relatively large (Figure 6A), and B1 somatic recordings reveal large voltage-gated currents which are consistent with the occurrence of spikes in B1 cells (Figure 7B, Figure S4).
Frequency-dependence of voltage-gated currents
In the previous section, we focused on steady-state (equilibrium) currents. We next turned to analyzing currents that flow in response to dynamical stimuli (non-equilibrium currents). Our goal was to understand how the intrinsic currents in these cells are changed when the cell’s voltage oscillates, as it does during antennal vibration.
To address this question, we used oscillating voltage commands at different frequencies (Figure 8A). For slow voltage oscillations, the behavior of voltage-gated channels should still be at steady-state (schematized in Figure 7D). However, as oscillation frequency increases, we would expect to see a change in the currents that flow during each cycle. The contribution of voltage-gated channels should decrease, because these channels cannot open and close instantaneously. Conversely, faster oscillations will increase capacitive currents, which are proportional to dV/dt.
Figure 8. Frequency-dependence of voltage-gated currents.
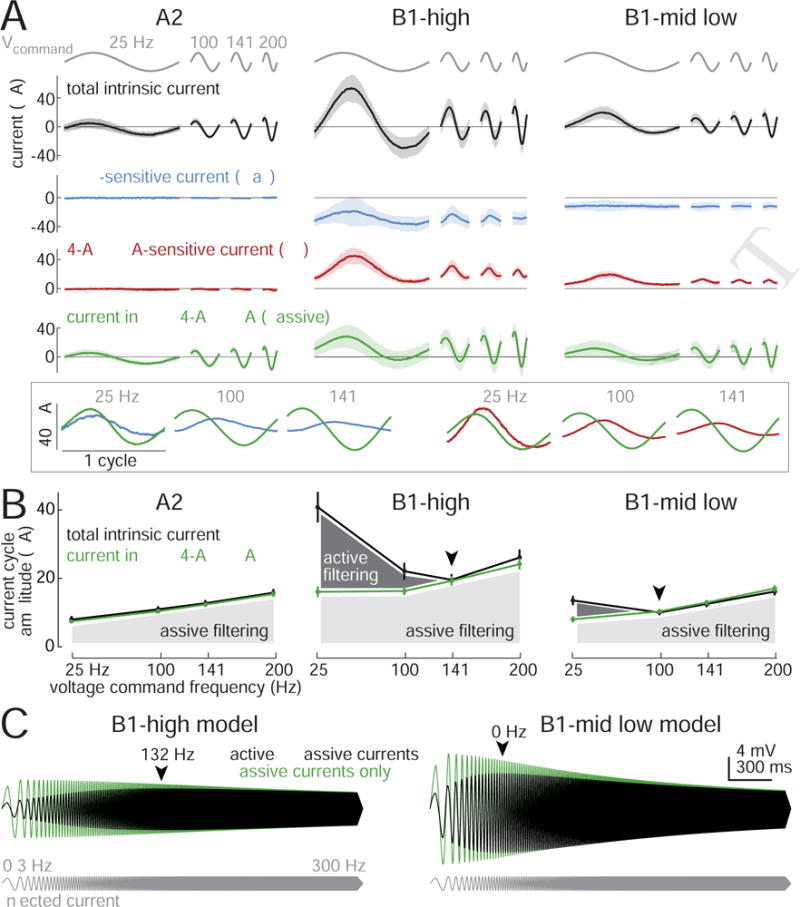
(A) Current evoked by voltage commands oscillating at different frequencies (mean ± SD across cells, n=5 A2 cells, 8 B1-high cells, 7 B1-mid/low cells). Voltage commands were 7.5 mV (peak-to-mean). Inset at bottom shows enlarged versions of mean B1-high currents, color-coded as above. In the inset, currents are centered on the same y-axis and displayed per cycle (not per time) to better illustrate the phase relationships between active and passive currents. The highest frequency (200 Hz) is omitted in the inset because voltage-gated current fluctuations are negligible.
(B) Current amplitude versus voltage command frequency for the same cells. Here current is measured as the magnitude of the Fourier component at the voltage command frequency. In B1 cells, total intrinsic current is a U-shaped function of frequency (arrowheads denote minima of these curves). After adding TTX, 4-AP, and TEA, current in B1 cells grows monotonically with frequency, as in A2 cells, which is what we would expect for a passive RC circuit. The difference between these two curves represents active filtering (dark shading), which diminishes with increasing frequency. Passive filtering (light shading) grows with increasing frequency.
(C) Voltage responses of model B1 cells to sinusoidal current injection. The amplitude of the injected current was held constant, while the frequency of the current was swept up. The model cell responses were spindle-shaped, indicating bandpass tuning (arrowheads denote best frequencies). Removing active currents produced low-pass tuning, just as in real cells (Figure S5). All model parameters were fit to data from Figure 7. Figure S8 contains model details and comparisons with data.
In A2 cells, the current flowing during the voltage oscillations was unaffected by TTX or 4-AP/TEA (Figure 8A). This implies that the current we recorded in A2 cells was simply passive current – i.e., a combination of capacitive current and leak current. The amplitude of the current oscillation grew larger as voltage oscillations became faster, which makes sense because capacitive current grows with dV/dt.
In B1 cells, the amplitude of the current oscillation was large at both low and high frequencies, and was smaller at intermediate frequencies (Figure 8A). Put another way, less injected current was needed to produce intermediate-frequency voltage oscillations. This “U”-shaped relationship between current and frequency (Figure 8B) indicates that B1 cells are intrinsically tuned to favor synaptic input at intermediate frequencies. At the highest frequency, currents were mainly passive (i.e., capacitive and leak currents), since TTX/4-AP/TEA had little effect (Figure 8A). Conversely, at the lowest frequency, currents were mainly active, as indicated by the large effect of TTX/4-AP/TEA.
It is notable that the minimum of this U-shaped function occurred at a higher frequency for B1-high cells than for B1-mid/low cells (Figures 8A and 8B). This difference indicates that the two cell will filter their synaptic inputs differently. This is a satisfying result, because it can explain why B1-high and B1-mid/low cells have different voltage tuning (Figure 2), even though they have similar tuning at the level of synaptic currents (Figure 5).
Importantly, at low frequencies, both the voltage-gated Na+ current and the voltage-gated K+ current were approximately in phase with the voltage command (Figure 8A). This means that that both currents opposed the voltage change. In other words, both Na+ and K+ channels act as “buffers” which tend to suppress slow voltage oscillations –– just the way they tend to suppress steady voltage commands (Figure 7).
As voltage oscillation frequency increased, the amplitude of voltage-gated Na+ and K+ current fluctuations dwindled in B1 cells (Figure 8A). This result implies that voltage-gated channels cannot reach steady-state when the voltage oscillates too quickly, and so their conductance fluctuations are smaller. As a result, voltage-gated currents act as buffers which oppose slow voltage oscillations but not fast voltage oscillations.
In addition, as the oscillation frequency increased, the phase relationship between active and passive currents was shifted. Active currents were approximately in phase with passive currents at low frequencies, but they became almost 90° delayed at higher frequencies (Figure 8A). This means that active and passive currents add constructively at low frequencies but not at higher frequencies. This is yet another reason why we needed to inject a large amount of current to produce the lowest-frequency voltage oscillation, whereas we needed to inject less current as the voltage oscillation approached the cell’s best frequency.
To summarize, we found that voltage-gated currents selectively opposed low-frequency oscillations. Meanwhile, the cell’s capacitive load selectively opposed high-frequency oscillations. Intermediate frequencies were not strongly opposed by either active conductances or passive properties, and so were favored by B1 cells.
To better understand the differences between B1-high and –mid/low cells, we constructed single-compartment leaky integrator models of both B1 cell types. All parameters were fit to data from voltage step experiments (Figure 7); there were no free parameters. For simplicity, the kinetics of voltage-dependent conductances (gNa and gK) were specified by one time constant each (τNa and τK). The differences between the B1-high and B1-mid/low models were as follows: (1) gNa and gK were larger and more strongly voltage-dependent in the B1-high model (taken from Figure 7C data); (2) τK was faster in the B1-high model (Figure S7); (3) the voltage-independent leak conductance was larger in the B1-high model (taken from Figure 7B).
Although we did not fit the models’ parameters with any data from the oscillating voltage experiments (Figure 8A-B), the models nonetheless correctly predicted the bandpass tuning of B1 cells (Figure 8C, Figure S8). Eliminating voltage-dependent conductances transformed the model cells from bandpass filters to low-pass filters (Figure 8C), which matched the behavior of real B1 cells when voltage-gated conductances were blocked (Figures S5 and S8). In summary, these models provide a compact description of how the characteristic passband of B1 cells is specified by the interaction of active and passive filtering properties.
Discussion
In this study, we focused on two different cell types in the Drosophila brain that encode qualitatively different features of mechanical vibrations. A2 and B1 cells differ according to the synaptic currents they receive, and also according to their intrinsic frequency filtering properties. In particular, B1 cells have interesting electrical properties which cast common voltage-gated channels in an unusual role. Here we note some functional implications of these results, and we link these findings with other sensory systems and other excitable cells.
A2 cells as motion energy detectors
Our results imply that A2 cells should be viewed as encoders of motion energy. A2 cells are transiently excited by sustained displacements. They are also excited by both forward and backward displacements. Motion energy is a quantity that is invariant to motion direction, and it grows monotonically with vibration frequency and amplitude, like the responses of A2 cells themselves.
The coding properties of A2 cells are similar to those of mammalian rapidly-adapting (RA) mechanoreceptors (Abraira and Ginty, 2013). Just as A2 cells are transiently excited by both forward and backward antennal movement, RA mechanoreceptors are transiently excited by both forward and backward movement of an object relative to the skin. Thus, when the stimulus is a vibration, these cells are excited twice per cycle (Bolanowski and Zwislocki, 1984).
A2 cells are also similar to certain vertebrate retinal ganglion cells, termed Y/alpha/parasol cells (Masland 2012). When the stimulus is a static visual grating, these retinal ganglion cells are transiently excited irrespective of the spatial phase of the stimulus. Therefore, when the visual stimulus is a dynamic drifting grating or a contrast-reversing grating (a “visual vibration”), these cells are excited twice per cycle (Enroth-Cugell & Robson 1966, Hochstein & Shapley 1976).
What all these cells have in common is sensitivity to stimulus change, regardless of the direction of the change. This means that these cells respond best to rapid fluctuations in the stimulus. In other words, they encode change energy or motion energy.
Direction-sensitivity and opponency in B1 cells
Unlike A2 cells, B1 cells are direction-sensitive. Some B1 cells are depolarized by forward movement and hyperpolarized by backward movement. Meanwhile, other B1 cells have the opposite preference. It is notable that each B1 cell response is simply an inverted version of the response in other B1 cells. Thus, opponent B1 cells encode redundant signals, just with opposite sign conventions.
Because “positive” and “negative” B1 cells have the same short latency to response onset, it seems likely they are both directly postsynaptic to JONs. If so, this would imply that B-JONs exist in both “positive” and “negative” forms. Opponent B-JONs may be located on opposite sides of Johnston’s organ, and so stretched by opposing antennal movements. The possibility of direction-sensitivity among vibration-sensitive JONs has been discussed extensively but never demonstrated (Albert et al., 2007; Göpfert and Robert, 2002; Lehnert et al., 2013; Nadrowski et al., 2008; Pezier and Blagburn, 2013).
Opponent B1 channels could be used to perform a variety of computations. For example, they could be used for eliminating shared transmission noise. Imagine that all B1 cells experience a common random depolarization – due, for example, to network noise. This shared noise is positively-correlated in opponent B1 cells, but the signals carried these opponent B1 cells are negatively-correlated. Downstream neurons could eliminate this shared noise by taking the difference between “positive” cell responses and “negative” cell responses. This is the idea behind a differential amplifier, and there is evidence that the retina uses this noise-reduction strategy as well (Werblin, 2010).
Moreover, opponent B1 channels could be used to compute the azimuthal angle of a sound source. In principle, accurate sound localization would require the brain to compare sound-evoked vibrations at two antennae, taking account of both vibration amplitude and vibration phase. Phase is important because amplitude alone does not provide unambiguous information: for each amplitude ratio, there are four possible sound source angles. Phase cues can reduce this ambiguity. For example, sound coming from the left or right will cause the antennae to move out of phase, whereas sound coming from the front or back will cause the antennae to move in phase (Morley et al., 2012). The brain could use phase information to reduce ambiguity even further – for example, to determine whether the sound source is in front or in back – because Drosophila courtship song pulses have a stereotyped phase profile (Arthur et al., 2013). Thus, a decoder that compared opponent B1 cell responses could determine the azimuthal angle of a singing fly based on both phase and amplitude cues. Meanwhile, because inverting the phase of a vibration does not have a major effect on A2 cell responses, A2 cell responses should be more robust to sound source angle, and so could be used to represent the sound envelope faithfully as a singing male performs his characteristic circling maneuver around a listening female (Hall, 1994).
B1 cells as intrinsic bandpass filters
A notable feature of B1 cells is their bandpass frequency tuning. This stands in contrast to the relatively broad tuning of A2 cells (Lai et al., 2012). Indeed, B1 cells are the only cells in the Drosophila brain which are known to be bandpass-tuned to antennal vibrations. All other cell types seems to be lowpass-tuned (Clemens et al., 2015; Tootoonian et al., 2012).
The frequency selectivity of B1 cells begins with their synaptic inputs, which are bandpass-filtered. This finding suggests that (at least some) B-JONs are also bandpass-filtered. Interestingly, all the B1 cells we recorded from had similarly-tuned synaptic inputs, in spite of the fact that these cells had diversely-tuned voltage responses. We only examined synaptic currents in three genetically-tagged B1 populations (targeted using VT30609, VT27938, and fru), and there may be additional B1 cell types which we did not examine. This caveat aside, it is clear that B1 frequency tuning is not always simply inherited from tuning of B-JONs.
Using oscillating voltage-clamp commands, we found that voltage-gated conductances suppress low-frequency inputs to B1 cells, particularly B1-high cells. Meanwhile, the same conductances have no effect on high-frequency inputs. This is because these conductances open and close at a limited speed, and so cannot track high-frequency voltage fluctuations.
It is well-known that voltage-gated conductances can alter the frequency tuning of an excitable cell. In essence, the kinetics of channel activation and inactivation specify a particular voltage oscillation frequency which is optimal for driving these channels to open and close. AC inputs can be suppressed (or even amplified) depending on how well they match that preferred frequency (Hutcheon and Yarom, 2000). Thus, AC coding allows a cell to bandpass-filter its inputs, depending on the properties of its voltage-gated ion channels.
Vertebrate hair cells are a well-known example of this phenomenon. In hair cells, transduction currents can be bandpass filtered by voltage-gated ion channels. The key players here are voltage-gated Ca2+ channels and Ca2+-dependent K+ channels (Hudspeth and Lewis, 1988). Together, Ca2+ and K+ channels create positive feedback that amplifies voltage oscillations in a particular frequency band. Different hair cell types express different K+ channels, endowing them with different frequency preferences (Fuchs and Evans, 1990; Goodman and Art, 1996).
B1 cells are different from hair cells in the roles that are played by specific ion channels. Whereas hair cells use voltage-gated channels to produce positive feedback, B1 cells use voltage-gated channels to produce purely negative feedback. In other words, instead of amplifying a particular frequency, as hair cells do, B1 cells suppress particular frequencies. This suppression is produced by both voltage-dependent K+ channels and voltage-dependent Na+ channels. K+ and Na+ channels work together to attenuate the small DC component of the synaptic current in B1 cells, leaving mainly the large AC component (Figure S5).
An unusual role for Na+ channels
In many cell types, voltage-gated Na+ channels act as selective amplifiers of rapidly depolarizing synaptic inputs. A rapidly-depolarizing synaptic input opens Na+ channels, leading to even more depolarization. A slowly ramping synaptic input is not as effective at recruiting Na+ channels, due to both Na+ channel inactivation and K+ channel opening. This makes voltage-gated Na+ channels molecular “coincidence detectors” (Azouz and Gray, 2000; Lundstrom et al., 2009; Lundstrom et al., 2008; Ratte et al., 2014; Reyes et al., 1994).
B1-high cells are interesting because they cast Na+ channels in a different role. In B1 cells, Na+ channels do not act as amplifiers of depolarization. Rather, Na+ channels act as “buffers” which antagonize any change in the cell’s voltage. A depolarizing input causes net Na+ closure, not Na+ channel opening. This is because B1 cells rest at a relatively depolarized voltage (−50 mV) where a depolarizing input produces more inactivation than activation. Conversely, a hyperpolarizing input produces net Na+ channel opening. In this manner, Na+ channels buffer voltage against perturbations. Meanwhile, K+ channels also buffer voltage in B1 cells. When the driving frequency of the cell’s synaptic inputs is too fast for Na+ and K+ channels to follow, the synaptic input can escape the effect of the buffer and drive large voltage fluctuations in the cell. Thus, although B1-high cells rest in depolarization block, their Na+ channels are not quiescent – they are actively shaping the cell’s frequency characteristics.
Implications for other systems
Because the voltage-gated conductances in B1 cells are common cellular components, our findings have general implications. In principle, the same components could be used in other central mechanosensory circuits to extract specific temporal features of mechanical stimuli. Indeed, they could be used to extract specific temporal features of any time-varying signal – whether driven by sensory stimulus fluctuations or neural network oscillations. All neurons have some degree of intrinsic frequency selectivity (Hutcheon and Yarom, 2000). Our results extend the range of molecular mechanisms that are known to confer create frequency selectivity on a cell.
More generally, our study illustrates the value of studying biophysics in vivo, with network activity and sense organs intact. These factors specify the real “physiological” range of voltages that the cell experiences. This in turn specifies the voltage regime over which we should study the cell’s voltage-gated conductances. In an awake, embodied brain, this voltage range is likely to be relatively wide, suggesting that voltage-gated channels serve a wider range of computational functions than one might suspect from in vitro studies alone.
Finally, A2 and B1 cells pose interesting questions about neural circuit architecture. B1 cells encode vibrations in a fairly literal manner: their voltage fluctuations look quite like the stimulus itself (or, more properly, a linear transform of the stimulus). On the other hand, A2 cells encode vibration motion energy, a quantity that is invariant to phase, and so a nonlinear transform of the stimulus. As we have pointed out, this is reminiscent of the situation in the vertebrate retina, where linear and nonlinear ganglion cells form parallel coding channels (e.g., X/Y cells). It is also reminiscent of mammalian primary visual cortex, which contains both linear and nonlinear cells (simple and complex cells; Movshon et al., 1978a, b). We do not fully understand the roles of any of these cell types in perception and behavior. The cells we describe here represent an opportunity to understand these sorts of parallel channels both mechanistically and functionally, at the level of biophysics, neural codes, and ultimately the control of behavior.
STAR Methods
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Rachel Wilson (rachel_wilson@hms.harvard.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Flies were raised on cornmeal-agar based medium under a 12-hr dark/12-hr light cycle at 25°C and were used for experiments 1–4 days after eclosion. All experiments involved female flies, except where noted. Transgenic stocks were described previously and were obtained from the Vienna Drosophila Resource Center (VDRC), the Bloomington Drosophila Stock Center (BDSC), or elsewhere, as follows: VT27938-Gal4 in attP2 (VDRC 202860) (Lai et al., 2012), VT30609-Gal4 in attP2 (VDRC 200230) (Lai et al., 2012), GH86-Gal4 (BDSC 36339) (Heimbeck et al., 1999; Lai et al., 2012), VT45599-Gal4 in attP2 (a gift of Ann-Shyn Chiang) (Lai et al., 2012), VT34811-Gal4 in attP2 (VDRC 201267) (Lai et al., 2012), GMR45D07-Gal4 in attP2 (BDSC 49562) (Vaughan et al., 2014), GMR63A03-Gal4 in attP2 (BDSC, then stock 47697, subsequently culled) (Vaughan et al., 2014), fru-Gal4 (constructed by Barry Dickson, a gift of Sarah Certel and Ed Kravitz) (Stockinger et al., 2005), 10XUAS-CD8:GFP in attP40 (BDSC 32186) (Pfeiffer et al., 2010), 20XUAS-CD8:GFP in attP2 (BDRC 32194), 20XUAS-CD8:GFP in attP40 (a gift of Gerry Rubin), UAS-ArcLight in attP2 (BDSC 51056) (Cao et al., 2013), 20XUAS-GCaMP6s in attP40 (BDRC 42746), UAS-dcr2 (BDSC 24646) (Dietzl et al., 2007); UAS-DmNaV-IR (RNAi directed against DmNaV, a.k.a. para, VDRC 6132) and shakB2 (a gift of Robert Wyman) (Baird et al., 1990). General methods for generating the GMR (FlyLight) stocks and VT (Vienna Tile) stocks have been described previously (Jenett et al., 2012; Kvon et al., 2014).
Genotypes for each main figure are listed below. Genotypes for supplemental figures are noted in the corresponding legends.
| Figure 1D (A2): | 20XUAS-CD8:GFP/+;VT30609-Gal4/+ |
| Figure 1E (B1, top): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 1F (B1, center): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 1G (B1, bottom): | 10XUAS-CD8:GFP;fru-Gal4 |
| Figure 2A (A2): | 20XUAS-CD8:GFP/+;VT30609-Gal4/+ |
| Figure 2B (B1-high): | 10XUAS-CD8:GFP;fru-Gal4 (n=8) |
| 20XUAS-CD8:GFP/+;GMR63A03-Gal4/+ (n=1) | |
| 20XUAS-CD8:GFP/+;VT30609-Gal4/+ (n=1) | |
| 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ (male, n=1) | |
| Figure 2C (B1-mid): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ (n=8) |
| GH86-Gal4/+;20XUAS-mCD8:GFP/+ (n=2) | |
| 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ (n=1) | |
| 20XUAS-CD8:GFP/+;VT30609-Gal4 /+ (n=2) | |
| 20XUAS-CD8:GFP/+;VT45599-Gal4/+ (n=2) | |
| Figure 2D (B1-low): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ (n=6) |
| 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ (n=2) | |
| 20XUAS-CD8:GFP/+;VT45599-Gal4/+ (n=1) | |
| 20XUAS-CD8:GFP;GMR45D07-Gal4 (male, n=3) | |
| Figure 3A (A2): | 20XUAS-CD8:GFP/+;VT30609-Gal4/+ |
| Figure 3B,E (B1-high+ example): | 10XUAS-CD8:GFP;fru-Gal4 |
| Figure 3B,E (B1-high− example): | 20XUAS-CD8:GFP/+;VT30609-Gal4/+ |
| Figure 3C,F (B1-mid+ example): | 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ |
| Figure 3C,F (B1-mid− example): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 3D,G (B1-low+ example): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 3D,G (B1-low− example): | 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ |
| Figure 3E-G radial plots: | same experiments as Figure 2B-D, plus one B1-high cell in VT30609 |
| Figure 4A,B (wild type): | 20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ (male, brothers of shakB2 males) |
| Figure 4C,D (shakB2): | shakB2;20XUAS-CD8:GFP/+;GMR45D07-Gal4/+ (male) |
| Figure 5 (A2): | UAS-dcr2/+;20XUAS-CD8:GFP/+;VT30609-Gal4/UAS-DmNaV-IR |
| Figure 5 (B1-high): | UAS-dcr2/+;10XUAS-CD8:GFP/+;fru-Gal4/UAS-DmNaV-IR |
| Figure 5 (B1-mid/low): | UAS-dcr2/+;20XUAS-CD8:GFP/+;VT27938-Gal4/UAS-DmNaV-IR |
| Figure 6A (A2): | 20XUAS-CD8:GFP/+;VT30609-Gal4/+ |
| Figure 6A (B1-high): | 10XUAS-CD8:GFP;fru-Gal4 |
| Figure 6A (B1-mid): | GH86-Gal4/+;20XUAS-mCD8:GFP/+ |
| Figure 6A (B1-low): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 6B: | same experiments as Figure 2A,B |
| Figure 6E,F: | UAS-ArcLight/VT30609-Gal4 (n=12) |
| UAS-ArcLight/GMR45D07-Gal4 (n=3) | |
| Figure 7 (A2): | 20XUAS-mCD8:GFP/+;VT30609-Gal4/+ |
| Figure 7 (B1-high): | 10XUAS-mCD8:GFP/+;fru-Gal4/+ |
| Figure 7 (B1-mid/low): | 20XUAS-CD8:GFP/+;VT27938-Gal4/+ |
| Figure 8: | same experiments as in Figure 7 |
METHOD DETAILS
Dissection and general electrophysiology methods
Each fly was anesthetized by cooling it for <2 min on ice, and then its thorax was inserted into a hole in a piece of titanium foil forming the floor of a recording chamber. The head was turned 90° so that the left side of the head was pointing straight up. The head, thorax, and proboscis were then immobilized with UV-cured epoxy (KemXERT Corp.). Next, a drop of saline was added to the recording chamber. The left eye, photoreceptors, lamina, and optic lobes were removed, exposing the left antennal nerve and the somata of A2 and B1 cells on the left side of the brain. The muscle of the frontal pulsatile organ (muscle 16; Miller, 1994) were severed and the esophagus and gut were removed to reduce brain motion. The perineural sheath was gently torn to expose neural somata on the surface of the brain. In some experiments (indicated in the text), the antennal nerve was severed with forceps near the point where it entered the brain. The recording chamber was then transferred to an BX51F upright compound microscope (Olympus) and visualized with a 40× water immersion objective.
The recording chamber was perfused with saline at a rate of ~2–3 mL/min. The saline solution was composed of (in mM) 103 NaCl, 3 KCl, 5 TES, 8 trehalose, 10 glucose, 26 NaHCO3, 1 NaH2PO4, 4 MgCl2, 1.5 CaCl2. Saline pH was adjusted to 7.2 and osmolarity was adjusted to 270–275 mOsm. Saline was bubbled with 95% O2 / 5% CO2. Stopping the saline perfusion in the recording chamber did not alter the spontaneous voltage oscillations in B1 cells (visible in Figure 1C, especially in the B1-low example cell), meaning that the spontaneous antennal movements that evoked these oscillations are unrelated to the perfusion flow. GFP-labeled neural somata were visualized with epifluorescent illumination, and were cleaned for patch-clamp recording by using a saline-filled large-bore glass pipette under positive pressure to gently displace glia and the somata of surrounding neurons.
Whole-cell patch pipettes were pulled with a P-97 linear puller (Sutter Instruments) from borosilicate glass (OD 1.5 mm, ID 0.89 mm). Pipettes were pressure-polished (Goodman and Lockery, 2000) using a microforge equipped with a 100× inverted objective (ALACPM-2/ALACPM-2SCOPE; ALA Scientific Instruments) to have resistances of ~10–12.5 MΩ. Pressure-polishing allowed us to obtain high seal resistances (> 50 GΩ), and so the seal conductance should make a negligible artifactual contribution to Vrest (<1 mV). For this reason, no hyperpolarizing current was injected into the cell to compensate for the depolarizing seal current. Pipettes were wrapped in Parafilm (Bemis Co.) to reduce capacitance; spikes had smaller amplitude if pipettes were not wrapped. Pipette internal solutions depended on the experimental design (see below).
We used a Multiclamp 700B patch clamp amplifier (Molecular Devices) to control and measure membrane voltage and currents. Bridge resistance was set before a seal was made, and electrode capacitance was compensated after the seal was made. Whole-cell series resistance was <70 MΩ. If the series resistance varied by more than 20%, the recording was omitted from further analysis. Whole-cell capacitance was not compensated.
Recorded voltages and currents were filtered with an 8-pole Bessel filter with a corner frequency of 10 kHz and digitized at 50 kHz via a NiDAQ USB-6343 analog-to-digital converter (ADC) board (National Instruments). Current and voltage output waveforms were generated in MATLAB (MathWorks), using the DAQ toolbox to control the ADC board. Acquisition code is available at https://github.com/tony-azevedo/FlySound.
Drugs were purchased from Sigma were tetraethylammonium chloride (TEA), 4-aminopyridine (4-AP), and methyllycaconitine (MLA). D-tubocurarine chloride (curare) was from Fisher Scientific and tetrodotoxin (TTX) was from Tocris. Curare and MLA completely block or dramatically reduce postsynaptic responses at a variety of other Drosophila central synapses (Gu and O’Dowd, 2006; Mauss et al., 2014; Nagel et al., 2015; Tuthill and Wilson, 2016), and so the modest effects we observe in Figure 4 are unlikely to be due to insufficient concentrations of these drugs. Because these drugs almost completely eliminate responses in shakB2 mutants, it is instead likely that the component of the postsynaptic response which is resistant to curare/MLA is mediated by electrical synapses.
All voltages (Vm measured in current clamp and Vcommand in voltage clamp) were corrected post hoc for an electrode liquid junction potential (Gouwens and Wilson, 2009) of −13 mV. Thus, the typical nominal resting potential in A2 cells and B1 cells was measured as −38 mV, but became −51 after junction potential correction. We applied the same correction to all our recordings, regardless of the exact composition of the pipette internal solution, because all our pipette internal solutions contained 140 mM aspartic acid, and the liquid junction potential arises mainly because of the differential mobility of Cl− (the main anion in the external saline) versus aspartate (the main anion in the internal pipette solution).
Cell-attached recordings
In order to check our conclusion that B1 cells do not normally spike (i.e., they rest in depolarization block), we performed a series of cell-attached recordings from B1 cells. For cell-attached recordings, pipettes (OD 1.5 mm, ID 1.2 mm) had resistances of <2 M Ω. We found that B1 cells never showed spikes in cell-attached recordings, with or without an antennal mechanosensory stimulus (n=17 recordings). As a positive control, we also performed interleaved cell-attached recordings from antennal lobe local neurons, which are known to spike(Wilson et al., 2004). Cell-attached recordings from antennal lobe local neurons were performed from GFP-positive cells in the genotype GH298-Gal4,UAS-CD8:GFP (Stocker et al., 1997). As expected, we found that antennal lobe local neurons always spiked spontaneously in cell-attached mode (n=3 recordings). Antennal lobe local neurons are useful cell type for comparison with B1-high cells, because spikes in B1-high cells (when evoked by hyperpolarization) are even larger than those of antennal lobe local neurons (~80 mV versus ~60 mV), meaning that B1-high spikes should clearly visible in cell-attached mode if they were actually occurring during the recording.
Current clamp recordings
A K+-based pipette solution was used for current clamp recordings (Figures 1, 2, 3, 4, 6A, 6B). This solution was composed of (in mM) 140 KOH, 140 aspartic acid, 10 HEPES, 1 EGTA, 1 KCl, 4 MgATP, 0.5 Na3GTP, 13 biocytin, with pH adjusted using KOH to 7.2 and osmolarity adjusted to 268 mOsm. We found that 5 mM EGTA improved the stability of the access or series resistance over the course of the recordings. The higher concentration of EGTA caused the membrane potential to drift by <±2 mV, but did not otherwise change the currents, and so we combined data from recordings using 1 mM EGTA with recordings using 5 mM EGTA.
Voltage clamp recordings of synaptic currents
A Cs+/TEA-based pipette solution was used for voltage clamp recordings of synaptic currents (Figure 5) in order to minimize the contributions of unclamped voltage-gated K+ currents. This solution contained: (in mM) 140 CsOH, 140 aspartic acid,10 HEPES, 2 EGTA, 1 KCl, 4 MgATP, 0.5 Na3GTP, 5 mM TEA chloride, 13 biocytin. To minimize the contributions of unclamped voltage-gated Na+ currents, we knocked down the DmNaV gene in Gal4-expressing neurons using transgenic RNAi (UAS-DmNaV-IR and UAS-dcr2, see genotypes above). Together, the internal K+ channel antagonists and Na+ channel knockdown eliminated virtually all voltage-gated conductances (Figure S4). Series resistance was compensated by the correction circuitry at 30% and by the prediction circuitry at 84%.
In voltage clamp recordings of synaptic currents, we targeted A2 cells in the VT30609-Gal4 line. This line drives expression in both A2 and B1 cells (Figure S3), but the somata of A2 cells tended to be among the most medial of the GFP-labeled somata, allowing us to bias our patch electrodes towards A2 cells over B1 cells. We confirmed that we correctly targeted A2 cells by visualizing the biocytin fills of these neurons. B1-high cells were identified based on fru-Gal4 expression, whereas B1-mid/low cells were identified based on VT27938-Gal4 expression (Figure S3). It should be emphasized that all of these lines drive expression in cells that do not belong to any of these cell types (i.e., cells that are neither A2 or B1). We could avoid including these “off-target” cells in our recordings by only patching somata with the characteristic location and size of A2/B1 cells. In rare cases where we inadvertently recorded from an “off-target” cell with a nearby soma, we realized this based on the post hoc biocytin fill; none of these cells ever responded to mechanosensory stimuli.
Several observations indicate that voltage clamp was good in these recordings. First, I–V curves were essentially linear (Figure S4A), demonstrating that Na+ channel knockdown and internal Cs+/TEA effectively eliminated voltage-gated conductances. Second, under these conditions, the stimulus-evoked current responses of B1 cells (in voltage clamp) were much faster than the stimulus-evoked voltage responses of B1 cells (in current clamp), which is the hallmark of a well-clamped cell (Figure S5). Third, space clamp artifacts would be expected to attenuate fast oscillations more strongly than they attenuate slow oscillations. However, we confirmed that toggling whole-cell compensation circuitry on the amplifier did not alter the kinetics of step-evoked input currents, again suggesting that voltage clamp was relatively good.
Voltage clamp recordings of voltage-gated currents
To measure voltage-gated currents in Figures 7 and 8, we used the same K+-based pipette solution employed for current clamp recordings (see above). DmNaV was not knocked down in these experiments. Series resistance was compensated by the correction circuitry at 30% and by the prediction circuitry at 84%. Whole-cell capacitance was not compensated; therefore, the currents we recorded represent the combined contributions of leak currents, capacitive currents, and voltage-gated currents.
The resting membrane potential was taken as the command potential at which zero holding current flowed prior to any drug application. After the resting potential was measured, synaptic currents were eliminated by cutting the antennal nerve and blocking nicotinic receptors with 0.5 μM MLA or 50 μM curare. Recordings from A2 cells were an exception: because we do not have a Gal4 line which is specific to A2 cells, we needed to use stimulus-evoked responses to identify these cells within the VT30609-Gal4 line, and so the antennal nerve was left intact, but nicotinic antagonists were still applied after A2 cells were identified.
In each experiment, we first recorded currents that flowed in response to a family of voltage commands. In Figure 7, steps in the command potential away from rest (ΔV from rest) were −40, −20, −10, −5, −2.5, +2.5, +5, +10, +15 mV. Steps of −40 mV from rest are included in Figure S4 but were omitted from Figure 7 because the 4-AP/TEA-sensitive currents that flow at this command potential are a small percentage of the total current; the measured values of the 4AP/TEA-sensitive current at this command potential mainly reflect the small drift in the recording during 4-AP/TEA application. Moreover, a ΔV of −40 mV was also near the assumed K+ reversal potential and thus gave ill-defined values for the conductance. Above +15 mV, input resistance fell dramatically due to increased voltage-gated K+ conductance, increasing the chance of series resistance errors. In Figure 8, the command voltage consisted of oscillations 7.5 mV in amplitude (peak-to-mean).
Next, we applied TTX (1 μM) and re-measured the currents that flowed in response to each voltage command. We then added a cocktail of 4-AP (5 mM) and TEA (10 mM) while keeping TTX in the bath, and we again re-measured the currents. In pilot experiments, we tried several other antagonists of voltage-dependent conductances, including Cd2+, ZD7288, iberiotoxin, and charybdotoxin, but they did not have any effect.
In a few recordings (especially when access resistance was poor), we observed oscillating current responses to large voltage step commands prior to TTX application, indicative of poorly-clamped Na+ currents. We excluded these recordings from our data set.
Given that JONs and B1 cells are electrically coupled (Figure 4), it is worth asking whether voltage-gated channels in JONs might contribute to our measurements of voltage-gated currents in B1 cells. Any contribution from JONs would come from the proximal stumps of severed JON axons, because the experiments in Figures 7 and 8 were performed with the antennal nerve cut. Moreover, a contribution from JONs seems unlikely because specifically knocking down voltage-gated Na+ channels in B1 cells using transgenic RNAi (Figure 5) essentially eliminated voltage-gated Na+ currents in B1 recordings (Figures S4A and S4B). Note that the experiments in Figures S5A and S5B were performed with intact antennal nerves, increasing the likelihood of detecting any JON contribution to voltage-gated Na+ currents. Thus, the Na+ currents we record from B1 somata must arise from Na+ channels in B1 cells themselves, not JONs.
Mechanical stimulation of the antenna
A piezo-controlled linear actuator with 30 μm travel range and a strain gauge (Physik Instrumente) was mounted on a micro-manipulator (Sutter Instruments). A custom-milled attachment coupled the actuator to a tungsten microelectrode which served as a mechanical probe. The tungsten probe was surrounded by epoxy inside a glass pipette for added stability, with the tungsten extending 1 mm past the end of the glass. This probe assembly was screwed into the end of the actuator and oriented 10° below horizontal. The tip of the tungsten probe was coated with anaerobic-curing flange sealant (Loctite 515) and was brought in contact with the arista while the arista was surrounded by saline, after the fly had been mounted in the recording chamber. The arista ipsilateral to the recorded neurons was always the arista targeted for mechanical stimulation (except in calcium imaging experiments, when both aristae were targeted; see below). Because the fly’s head was turned 90º to one side (Figure 1B), the arista (which ordinarily extends laterally from the antenna) was oriented vertically with the distal end pointing up (Figure 1C). The probe was consistently attached to the arista in the same location, at the position at which the large proximal ventral branch of the arista leaves the main trunk (between the third and fourth dorsal branches). The length of the lever arm (the distance between the rotational axis of a3 [dashed line in Figure 1C] and the probe’s contact point) was 165–175 μm. The axial position of the probe was controlled by a high-power amplifier (Physik Instruments), with voltage commands generated in MATLAB and delivered through the DAC board. The output of the actuator’s strain gauge was used to control the position of the actuator through closed-loop feedback. The strain gauge sensor output was sampled at 50 kHz. The closed-loop feedback introduces a delay relative to the amplifier command, and at high oscillation frequencies this delay reduces the amplitude of the probe oscillations. The strain gauge signal was therefore used to correct the voltage command to the amplifier for all stimuli, so that the measured vibration amplitude (at the strain gauge) was constant across vibration frequencies. For a 3 μm step, the rise time was 1.4 ms, and the total time to rise and settle was 1.9 ms.
Several steps were taken to ensure that there was a consistent coupling between the linear action of the actuator and the rotation of the antenna. First, the orientation of the fly’s head was standardized by attaching the proboscis to the bottom of the recording chamber with UV-cured adhesive. Once the recording chamber was mounted under the BX51F microscope, the axis of the chamber corresponding to the anterior-posterior axis of the fly head was rotated so that the probe contacted the arista perpendicular to the axis of antennal rotation. Second, the hydrophobicity of the fly cuticle prevents saline from easily penetrating between articulations of the antennal segments, leading to air bubbles that can restrict rotation of the antenna. To correct this, < 1 μL of 0.2% Triton in PBS was applied to the antenna prior to dissection. A drop of saline (~500 μL) was then applied, typically without forming bubbles, and the solution was exchanged twice to remove any remaining detergent. The detergent was not applied in experiments when the nerve was cut, yet the quality of recordings and the intrinsic physiological properties of A2 and B1 cells were similar, suggesting this protocol did not affect the physiology of central neurons. In addition, bubbles could occasionally be sucked out by mouth pipette, and in these cases the stimulus-evoked responses of central neurons were similar to those in which detergent was used to eliminate bubbles, suggesting the JONs were not affected by the detergent. Third, the flange sealant used to attach the probe to the arista was chosen in part because of its thixotropic properties: the connection between arista and probe tip was strong in the direction of probe movement, but weaker in the shearing direction, such that the probe connection was flexible. The 10° decline in the axis of the probe relative to the vertical orientation of the arista results in a vertical movement of the probe tip of 18% of the horizontal travel, but the flexibility of the joint appeared to minimize vertical motions of the antenna. Fourth, the ability of the antenna to rotate in response to probe movement was checked visually in every experiment. As an early quick check of antennal mobility in every experiment, we found that it was helpful during the dissection to verify that gentle movements of the recording chamber could create visible movements of the antenna, because this allowed us to quickly discard preparations that did not show antennal movement. Finally, rigidity of probe-arista coupling was verified in separate experiments using high-speed video; these measurements showed zero phase lag in the movement of the probe, the arista, and the a3 antennal segment.
Although we took steps to confirm the quality of the coupling between the actuator and the antenna, it is still possible that the antenna was not rotating the same way in every experiment. We could not visually verify every stimulus, because the smallest mechanical stimuli in our test set evoked antennal movements that were too small to see. In particular, there may have been small air bubbles that formed on the posterior side of the antenna during the course of the experiment. This could explain why a few B1 cells had particularly small responses to mechanical stimuli (left column of Figures 2B, 2C, 2D).
It should be emphasized that the antenna ipsilateral to the recorded cell was immersed in saline throughout our experiments. This was necessary in order to access the somata of A2 and B1 cells, which are situated just behind the antenna. Saline has a higher impedance than air, and so saline immersion would change the antenna’s mechanical response to a sound stimulus. This fact is what required us to use a displacement clamp approach (by attaching a piezoelectric probe), in order to overcome the high impedance of the medium surrounding the antenna. Displacement clamp also means that the altered gravitational forces on the antenna (due to rotating the head 90°, Figure 1B) do not affect the antenna’s displacement.
One caveat associated with displacement clamp is that the “resting” position of the antenna may not precisely match the antenna’s natural resting position. We did make every effort to ensure that the antenna was held at its natural resting condition when it was attached to the probe. The attachment of the probe tip to the arista was performed under visual control at high magnification, and the antenna was manipulated into its prior resting position after the attachment was secure. We estimate that we restored the original position of the arista with a precision of 300 nm or better; this amount of offset is comparable to the static offsets created by the normal postural changes of the fly as it walks on inclined surfaces (Kamikouchi et al., 2009). In addition, we performed a set of experiments to verify that the responses of A2 and B1 cells are unaffected by the unavoidable small (≤300 nm) static offsets in the resting position of the antenna which result from the imprecision of visual feedback during probe placement. We found that these offsets had no measurable effect.
Another caveat is that the movement of the a3 antennal segment may not completely specify JON responses. JON responses may be affected by the way that a given antennal movement is brought about. Specifically, in a normal situation, the antenna’s movement is produced by both external forces and the active forces internal to the antenna. These active internal forces amplify small antennal vibrations (Göpfert et al., 2005). Thus, when we use displacement clamp to create a small sinusoidal movement of a3, we may be matching the external (measurable) trajectory of a sound-evoked a3 movement, but we may not be precisely matching the internal forces which are acting on JON dendrites. This means that the vibration-evoked responses we measure in A2 and B1 cells may not precisely match responses to sound-evoked vibrations of the same amplitude. That said, a comparison of A2 and B1 cells is still valid, and this caveat is also probably applicable only to relatively small antennal movements, because large movements are not actively amplified.
Vibration stimuli had frequencies of 17.7, 25, 35.4, 50, 70.7, 100, 141.4, 200, 282.8, 400, and 565.7 Hz. Vibration amplitudes were 0.045, 0.15, 0.45, and 1.5 μm. (Amplitudes for sinusoidal stimuli are always reported as mean-to-peak amplitudes.) We selected these frequencies because they include the range of frequencies where the antenna is most mechanically sensitive. They also cover the range of amplitudes that sound stimuli can evoke (Göpfert et al., 2006; Göpfert and Robert, 2003). Standard step stimuli had 3 μm displacements. For a lever arm length of r = 170 μm (axis of rotation to probe position), a displacement x = 1 μm of the probe tip causes a rotation of ~x/r = 5.9·10−3 radians, or 0.34°, of rotation. For the largest displacements (3 μm), the error due to the small angle approximation is <0.01%, justifying this approximation for all stimuli.
The amplitudes of the vibration stimuli we used were chosen specifically to target the dynamic range of vibration-sensitive JONs. Specifically, intracellular recordings from the giant fiber neuron (GFN, which is electrically coupled to a subset of JONs probably corresponding to A-JONs) showed that the generator current in response to a 100 Hz stimulus reaches half-max at an air particle velocity of 1·10−3 m/s. This stimulus causes a maximal rotation of 1.6·10−3 radians (Lehnert et al., 2013). This air velocity corresponds to a sound intensity value of = 86 dB SVL. Given the placement of the probe in our experiments, this antennal rotation corresponds to a probe movement of 0.26 μm, which corresponds to a value in the middle of the stimulus range. Therefore, our mechanical stimuli are well-positioned to sample the effective dynamic range of vibration-sensitive JONs.
Morphology data collection
During whole-cell recording, cells were filled with biocytin hydrazide (Fisher Scientific and Molecular Probes). After recording, the brain was fixed in 4% para-formaldehyde in phosphate-buffered saline (PBS) for 15 min. The tissue was then washed in PBST (PBS + Triton, 0.2% w/w), placed in blocking solution (PBST + 5% normal goat serum) for 20 min, and then placed for 24 hrs in blocking solution containing a primary antibody for neuropil counterstain (1:50 mouse anti-Bruchpilot, Developmental Studies Hybridoma Bank, nc82-s). After again washing in PBST, the tissue was then placed in blocking solution containing secondary antibodies for 24 hrs (streptavidin AlexaFluor conjugate from Invitrogen, 1:250 goat anti-mouse AlexaFluor conjugate from Invitrogen). The tissue was mounted in Vectashield (Vector Labs) and imaged on a SP8 confocal microscope (Leica Microsystems). Cells were traced in Fiji using the Simple Neurite Tracing plug-in (Longair et al., 2011). In many cases, the neuropil counterstain (anti-Bruchpilot) was omitted and the native autofluorescence of the tissue (along with nonspecific binding of streptavidin and GFP fluorescence) was used as reference.
ArcLight imaging
We used an ORCA-Flash4.0 V2 scientific CMOS digital camera (Hamamatsu) to image wide-field fluorescence of ArcLight expression in B1 or A2 somata in UAS-ArcLight/VT30609-Gal4 flies. A cell-attached recording was formed, and then video acquisition was started at a frame rate of 50 Hz. The patch was then ruptured, and video was acquired continuously until at least 4 s after break-in. Different command potentials were used in different experiments to measure how the change in ArcLight fluorescence depended on the command potential. To estimate the resting potential of the cell, we regressed the change in ArcLight fluorescence (ΔF/F) against the command voltage, and we took the x-intercept of the linear fit as an estimate of Vrest.
Immediately upon break-in, we consistently saw a slow but large run-down in ArcLight fluorescence (τ = ~4s, ~50% decay, data not shown). This decline to steady state was fit with a single exponential over the first 4 s after break-in. We used this exponential fit in each cell to remove the trend from each of the ΔF/F traces in Figure 6E, which slightly increased the estimate of Δ F/F at break-in (by ~0.5%). This run-down in fluorescence does not indicate a change in membrane potential, because we were holding the membrane potential constant at the soma, and the soma should be well-clamped. We do not know the reason for this run-down, but it may be due to the dialysis of some intracellular factor that normally prevents bleaching of the fluorophore.
To determine if ArcLight’s sensitivity conformed to previous reports(Cao et al., 2013; Jin et al., 2012), we measured the relationship between the change in command voltage (ΔVcommand) and the fractional change in ArcLight fluorescence (ΔF/F) after forming a whole-cell recording (after the run-down in ArcLight fluorescence was complete). We found a relatively linear relationship which was consistent with previous reports(Cao et al., 2013; Jin et al., 2012). We considered using this function (relating Δ F/F to Δ Vcommand) as a look-up table to estimate the change in membrane potential from the amplitude of the fluorescence change at break-in. However, within several seconds of break-in, the run-down of ArcLight fluorescence had already obviously altered the relationship between voltage and fluorescence, so that estimates of resting potential based on this function yielded implausible results that were either far above or far below estimates based on other methods (depending on the value of Vcommand).
Calcium imaging
GMR45D07-Gal4 (Vaughan et al., 2014) was crossed with 20XUAS-GCaMP6s (Chen et al., 2013) to drive expression in B1 cells. GCaMP6s fluorescence was visualized with a custom 2-photon microscope (ScanImage). Dendrites and axons of B1 cells were imaged at 64×64 pixel resolution at 16 Hz. The z-level position for imaging axon terminals was ~10 μm proximal to the distal edge of the axon bouton cluster, where the x-y area of the basal fluorescence was largest. Mechanical stimuli were delivered to the ipsilateral antenna as described above. With the head turned 90° so that the fly’s left side pointed up (Figure 1B), the axon terminals on the right side of the brain were too deep to image. Instead, to image activity of axon terminals contralateral to the stimulated antenna, the mechanical probe was moved to the opposite (right) antenna. To do this, the metal floor of the perfusion chamber was bent so that the antenna below the recording chamber was free to move (i.e., the antenna which was surrounded by air rather than saline) and the mechanical probe was placed below the perfusion chamber, visualized with a Firefly USB digital camera (Point Grey) and 40× lenses (InfiniStix), and attached to the antenna with flange sealant.
We never observed GCaMP6s responses in the dendrites of B1 cells on the side contralateral to the stimulated antenna, implying that B1 cells receive input from the ipsilateral antenna alone. Each B1 cell extends axon collaterals to both the ipsi- and contralateral wedge, and those terminals intermingle and are not easily segmented. We assume that the only responsive axon terminals in the wedge are those of the B1 cells that have dendrites ipsilateral to the stimulated antenna. These responsive axon terminals will be intermingled with the terminals of unresponsive (contralateral) B1 axons, and this will diminish the size of the stimulus-evoked fractional change in fluorescence in the region of interest (ΔF/F).
Images were analyzed in MATLAB. Brain motion was reduced with an efficient subpixel registration routine (Guizar-Sicairos et al., 2008). The region of interest (ROI) was defined as the smallest contiguous area that included all pixels in the AMMC having an intensity > +1.6 standard deviations from the mean (over the entire image); ROIs were then extended by 1 pixel in all directions. Occasionally, we detected very large changes in fluorescence (>300%) in a small number of pixels, presumably where a single bouton experienced a large influx of calcium. The time course of fluorescence changes in these small regions was similar to that of the aggregate signal.
Modeling
Modeled voltage dynamics were specified by
| Equation 1 |
where ENa and EK were 162 mV and −51 mV, relative to a resting potential of −47.3 mV (the average holding potential for B1 cells in control conditions in Figure 7). ENa and EK are specified by the ionic concentrations of our internal and external solutions. All other parameters were measured in the experiments shown in Figure 7. The model had no free parameters. The passive leak resistance (R) was 0.52 GΩ for B1 GΩ for B1- mid/low, measured from voltage steps in Figure 7 in the presence of TTX/4-AP/TEA. Capacitance(C) was calculated from the current transients recorded in TTX and 4-AP/TEA, during voltage step onset and offset (blanked in Figure 7); measured values of C were similar for B1-high (~1.7 pF) and B1-mid/low cells (~1.4 pF), and so an intermediate value of 1.6 pF was used for both models. The instantaneous conductances gNa (t) and gK (t) were given by
| Equation 2 |
| Equation 3 |
where and were calculated from spline functions fit to the data in Figure 7c. The time constants τNa and τK were fit to the onset and offset kinetics of the currents recorded at voltage step onset and offset (from the experiments in Figure 7, using steps ≤10 mV). The value of τNa was 10 ms for both B1-high and B1- mid/low. The value of τK was 6 ms for B1-high and 11 ms for B1-mid/low (Figure S7). For simplicity, we chose to use a single time constant for each conductance; this is a reasonable simplification because voltage step onset and offset produced recorded currents with similar kinetics over the relevant voltage range. Over this voltage range, current kinetics were also relatively voltage-independent, which makes it reasonable to use a fixed (voltage-independent) value of τNa τK.
Simulations were run with a time step of 0.1 ms. We began each simulation with a 250-ms window where zero current was injected, to allow voltage and conductances to reach steady state. The voltage settled at 0.4 mV for the B1-high model and 0.03 mV for the B1-mid/low model; this baseline voltage was subtracted from the model output in Figure 8. We then simulated a 2.5-s window where we injected a sinusoidal current with a constant amplitude (10 pA) and a frequency that swept up from 0.3 Hz to 300 Hz (Fig. 8c) or else from 0.3 Hz to 400 Hz (Figure S8D and S8E). Finally, we repeated the current frequency sweep after setting the voltage-dependent conductances gNa and gK to zero, meaning that the only conductance was the passive leak; this model response is shown in Figure 8C (“passive currents only”) overlaid and vertically aligned with the original model response.
In Figure S8D, we calculated the impedance as the ratio of the Hilbert transforms of model output and I(t). In Figure S8E, we examined the sensitivity of fmax to R, C, τNa and τK. We found that fmax depended on all these parameters (except τNa in the B1-mid/low model) and fmax varied smoothly as each parameter was changed; the same was true for f0 and (not shown). Finally, we examined the effect of altering the slope of the conductance-voltage curves that specify gNa(V) and gK(V) by multiplying these curves by a scalar; this had effects that resembled the effects of altering the passive leak conductance, except that changing the leak conductance had no effect on f0, whereas increasing the slope of gNa(V) and gK(V) produced smooth increases in f0 (not shown).
QUANTIFICATION AND STATISTICAL ANALYSIS
Data were analyzed with custom routines written in MATLAB, available at available at https://github.com/tonyazevedo/FlyAnalysis. No statistical methods were used to determine sample sizes in advance, but sample sizes are similar to those reported in other studies in the field.
To quantify the vibration responses of A2 cells, we calculated the trial-averaged mean depolarization during the stimulus window. This metric was well-correlated with spike rates in A2 cells during the stimulus window (Figure S1C). To detect spikes in A2 cells, we applied a high-pass 2-pole Butterworth filter to the voltage waveform, followed by a smoothing operation, and then found peaks above a defined threshold. To quantify the amount of phase-locking in A2 cell spiking responses, we computed the vector strength (VS):
| Equation 4 |
where θi is the phase of each spike relative to the stimulus. A value of 1 indicates all spikes have the same phase, while a value of 0 indicates there is no phase preference. Note that this was computed relative to the phase of the stimulus waveform (the “F1 stimulus”), and not the frequency-doubled version of this waveform (the “F2 stimulus”); when we used the F2 stimulus rather than the F1 stimulus, we obtained roughly similar results, but with less phase-locking at F2. The significance of a vector strength value depends on the number of spikes and the size of the effect. We estimated the probability p of the null hypothesis (no phase-locking) as
| Equation 5 |
where N is the number of spikes. In order to determine which stimuli produced significant phase-locking at the 1.5 μm stimulus amplitude, we computed p for each of the 9 vibration frequencies under consideration (see Figure S1E: 35.4, 50, 70.7, 100, 141.4, 200, 282.8, 400, and 565.7 Hz). For a typical cell, statistically-significant phase-locking was observed for the 200 Hz stimulus and the highest stimulus intensity. For some cells, significant phase-locking was also observed for other frequencies and amplitudes, but this was not reliable across cells (after a Bonferroni-Holm correction for multiple comparisons).
To quantify the vibration responses of B1 cells, calculated the Fourier component of the trial-averaged response at the stimulus frequency (f). The Fourier component at f is a good measure of the response amplitude, because it accounted for 75–95% of the variance (power) in the membrane voltage for all B1 types at values of f near the cell’s best frequency. (At values of f much lower than the cell’s best frequency, the fraction of the power at f began to fall, and the fraction of the power at 2f began to grow.) Our conclusions were unchanged when we used an alternative metric of B1 vibration responses (taking the variance of the voltage instead of quantifying the response as the Fourier component of the voltage at f).
The 42 cells in Figure 2 were assigned to four categories based on the shape of their frequency tuning curves. For each cell, we quantified responses to 11 vibration frequencies for two stimulus amplitudes for which we had data from all cells. We then used a k-means algorithm (k=4) to cluster this set of 42 of vectors (with each vector containing 22 values) using the correlation between vectors as the distance metric. The correlation metric measures similarity in tuning curve shape, but it discards information about absolute response magnitude. The clustering algorithm assigned all the A2 cells to one cluster. These cells had ramping tuning curves, with responses increasing monotonically with frequency. Another cluster (which we called B1-high) contained all the B1 cells that spiked. These cells had bandpass tuning with relatively high preferred frequencies. The remaining two clusters also had bandpass tuning, with intermediate and low preferred frequencies; we called these B1-mid and B1-high. If we used values of k<4, then the spiking B1 cells were divided between two categories; thus, the choice of k=4 clusters was supported by an independent neurophysiological parameter (i.e., the ability of some B1 cells to spike). If we used k=5, the additional small cluster included cells with the noisiest tuning curves that would be classified as either B1-mid or B1-low.
For step displacement stimuli, the latency of synaptic currents was computed by first smoothing each current trace (0.2 ms window), then measuring the maximum rate of increase in inward currents after step onset, and then determining when the tangent line with that maximum rate crossed the response baseline, measured as the mean voltage during the prestimulus period. Finally, a latency for each cell was computed by averaging the latencies measured on individual trials. The jitter for each cell was computed by taking the standard deviation of the latency. We report the mean of these per-cell values (± SEM across cells).
To measure the phase of B1 cell voltage responses (Figures 3E, 3F, and 3G), we took the phase of the Fourier component at the stimulus frequency. For this analysis, we focused on stimulus frequencies which were close to the preferred frequencies for each cell type (100 Hz for B1-high/mid, 25 Hz for B1-low). This analysis showed that “positive” cells lag the stimulus for 100 Hz vibrations (in B1-high and B1-mid cells), whereas “positive” cells lead the stimulus for 25 Hz vibrations (in B1-low cells). Data for this analysis were taken from the cells in Figure 2B-D, plus one B1-high cell recorded in VT30609-Gal4 that was not included in Figure 2B because we did not test the full set of stimulus amplitudes in this cell.
To compare the frequency tuning of synaptic currents with the frequency tuning of stimulus-evoked potentials (Figures 5C and 5D), we first transformed each tuning curve (only the amplitude shown) into a normalized cumulative response curve as a function of log-frequency (n=6–8 curves per data set, see Figure 5 legend). We then measured the Kolmogorov-Smirnov (K-S) distance between all pairwise combinations of current curves and voltage curves. We took the median K-S distance as our test statistic. Next, within a given cell type, we randomly sampled both current and voltage tuning curves (with replacement), drawing 6–8 tuning curves in each sample (so that n values in the mixed data sets were matched to the original data sets), and we measured the median pairwise K-S distance as before. By repeating this random sampling procedure 10,000 times, we constructed a distribution of the test statistic representing the null hypothesis (that synaptic current tuning curves and voltage tuning curves are drawn from the same distribution). For each cell type, we compared the median K-S distance measured between the current data and the voltage data (Ddata) with the distribution of K-S distances measured between resampled mixed data (Drandom). We found that the probability of finding a distance as large as Ddata was <10−3 for B1-high cells (comparing voltage and current in fru-Gal4 cells), and <10−4 for B1-mid/low cells (comparing voltage and current in VT27938-Gal4 cells).
In Figure 7A, capacitive transients at the onset and offset of voltage steps were blanked out. Capacitive currents were then removed using a low-pass IIR filter with a cutoff at 5 kHz, and the resulting filtering artefacts within 220 μs of the voltage steps were then blanked out.
A small number of recordings were discarded prior to any analysis due to drifting access resistance. We excluded one recording from our data set even though the access resistance was stable. This cell was labeled by fru-Gal4 and it was a clear outlier among fru-Gal4 neurons: the transient sodium current was approximately 10% of the mean across fru-Gal4 cells (−41 pA vs. −440 pA, n=23, Figure S4B) and >2 standard deviations from the mean across fru-Gal4 cells included in the study. The excluded neuron also fired spikes that were smaller-amplitude (~40 mV) and wider than other fru-Gal4 neurons, and its tuning was intermediate between B1-high and B1-mid categories.
DATA AND SOFTWARE AVAILABILITY
Data are available from the authors. Acquisition code is available at https://github.com/tony-azevedo/FlySound. Analysis code is available at https://github.com/tony-azevedo/FlyAnalysis.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| mouse anti-Bruchpilot antibody (nc82-supernatant) | Developmental Studies Hybridoma Bank | RRID:AB_2314866 |
| goat anti-mouse AlexaFluor633 (#A21050) | Invitrogen | RRID:AB_2535718 |
| streptavidin AlexaFluor568 (#S11226) | Invitrogen | RRID:AB_2315774 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| TEA chloride | Sigma-Aldrich | T2265 |
| 4-aminopyridine (4-AP) | Sigma-Aldrich | 275875 |
| Methyllycaconitine citrate | Sigma-Aldrich | M168 |
| D-tubocurarine chloride | Fisher Scientific | J60222 |
| tetrodotoxin | Tocris | 1078 |
| Experimental Models: Organisms/Strains | ||
| VT27938-Gal4 in attP2 (#202860) | Vienna Drosophila Resource Center (VDRC) | RRID: FlyBase_FBst0486141 |
| VT30609-Gal4 in attP2 (#200230) | VDRC | RRID:FlyBase_FBst0486499 |
| GH86-Gal4 (#36339) | Bloomington Drosophila Stock Center (BDSC) | RRID:BDSC_36339 |
| VT45599-Gal4 in attP2 | Ann-Shyn Chiang | FlyBase:FBsf0000445463 |
| VT34811-Gal4 in attP2 (#201267) | VDRC | RRID:FlyBase_FBst0486954 |
| GMR45D07-Gal4 in attP2 (#49562) | BDSC | RRID:BDSC_49562 |
| GMR63A03-Gal4 in attP2 (#47697, culled) | BDSC | n/a |
| fru-Gal4 | Sarah Certel / Ed Kravitz | RRID:BDSC_66696 |
| 10XUAS-CD8:GFP in attP40 (#32186) | BDSC | RRID:BDSC_32186 |
| 20XUAS-CD8:GFP in attP2 (#32194) | BDSC | RRID:BDSC_32194 |
| 20XUAS-CD8:GFP in attP2 (#32194) | BDSC | RRID:BDSC_32194 |
| 20XUAS-CD8:GFP in attP40 | Gerry Rubin | n/a |
| UAS-ArcLight in attP2 (#51056) | BDSC | RRID:BDSC_51056 |
| 20XUAS-GCaMP6s in attP40 (#42746) | BDSC | RRID:BDSC_42746 |
| UAS-dcr2 (#24646) | BDSC | RRID:BDSC_24646 |
| UAS-DmNaV-IR (#6132) | VDRC | RRID:FlyBase_FBst0470199 |
| shakB2 | Robert Wyman | FlyBase:FBal0015575 |
Supplementary Material
Figure S1, related to Figure 1: A2 cell spiking responses to vibration stimuli.
Figure S2, related to Figure 1: “Resting” oscillations in B1 cell voltage.
Figure S3, related to Figure 2: Gal4 lines labeling cells of different types.
Figure S4, related to Figure 5: Suppressing voltage-gated conductances.
Figure S5, related to Figure 5: Blocking voltage-gated channels creates low-pass voltage tuning in B1 cells.
Figure S6, related to Figure 6: In vivo calcium imaging in B1 cells.
Figure S7, related to Figure 7: Voltage-gated K+ currents are faster in B1-high cells than in B1-mid/low cells.
Figure S8, related to Figure 8: Frequency selectivity in B1 cells and comparisons with models.
Acknowledgments
We thank Gerald Rubin and Barry Dickson for gifts of fly stocks, and for leading the FlyLight and Vienna Tile projects which generated Gal4 lines critical to this project. We also thank Ann-Shyn Chiang, Sarah Certel, Ed Kravitz, and Robert Wyman for gifts of fly stocks. Stephen Holtz assisted with measurements of piezo-arista coupling. Bruce Bean and members of the Wilson lab provided advice, as well as comments on the manuscript. A.W.A. was supported by NIH fellowship F32 DC013928. R.I.W. is an HHMI Investigator.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author contributions
A.W.A performed the experiments and analyzed the data. A.W.A and R.I.W. designed the experiments, wrote the manuscript, and secured funding.
References
- Abraira VE, Ginty DD. The sensory neurons of touch. Neuron. 2013;79:618–639. doi: 10.1016/j.neuron.2013.07.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert JT, Nadrowski B, Göpfert MC. Mechanical signatures of transducer gating in the Drosophila ear. Curr Biol. 2007;17:1000–1006. doi: 10.1016/j.cub.2007.05.004. [DOI] [PubMed] [Google Scholar]
- Arthur BJ, Sunayama-Morita T, Coen P, Murthy M, Stern DL. Multi-channel acoustic recording and automated analysis of Drosophila courtship songs. BMC Biol. 2013;11:11. doi: 10.1186/1741-7007-11-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci USA. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird DH, Schalet AP, Wyman RJ. The Passover locus in Drosophila melanogaster: complex complementation and different effects on the giant fiber neural pathway. Genetics. 1990;126:1045–1059. doi: 10.1093/genetics/126.4.1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhandawat V, Maimon G, Dickinson MH, Wilson RI. Olfactory modulation of flight in Drosophila is sensitive, selective and rapid. J Exp Biol. 2010;213:3625–3635. doi: 10.1242/jeb.040402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolanowski SJ, Jr, Zwislocki JJ. Intensity and frequency characteristics of pacinian corpuscles. II. Receptor potentials. J Neurophysiol. 1984;51:812–830. doi: 10.1152/jn.1984.51.4.812. [DOI] [PubMed] [Google Scholar]
- Budick SA, Reiser MB, Dickinson MH. The role of visual and mechanosensory cues in structuring forward flight in Drosophila melanogaster. J Exp Biol. 2007;210:4092–4103. doi: 10.1242/jeb.006502. [DOI] [PubMed] [Google Scholar]
- Cachero S, Ostrovsky AD, Yu JY, Dickson BJ, Jefferis GS. Sexual dimorphism in the fly brain. Curr Biol. 2010;20:1589–1601. doi: 10.1016/j.cub.2010.07.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao G, Platisa J, Pieribone VA, Raccuglia D, Kunst M, Nitabach MN. Genetically targeted optical electrophysiology in intact neural circuits. Cell. 2013;154:904–913. doi: 10.1016/j.cell.2013.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang AEB, Vaughan AG, Wilson RI. A mechanosensory circuit that mixes opponent channels to produce selectivity for complex stimulus features. Neuron. 2016;92:888–901. doi: 10.1016/j.neuron.2016.09.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens J, Girardin CC, Coen P, Guan XJ, Dickson BJ, Murthy M. Connecting neural codes with behavior in the auditory system of Drosophila. Neuron. 2015;89:629–644. doi: 10.1016/j.neuron.2015.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietzl G, Chen D, Schnorrer F, Su KC, Barinova Y, Fellner M, Gasser B, Kinsey K, Oppel S, Scheiblauer S, et al. A genome-wide transgenic RNAi library for conditional gene inactivation in Drosophila. Nature. 2007;448:151–156. doi: 10.1038/nature05954. [DOI] [PubMed] [Google Scholar]
- Duistermars BJ, Frye MA. Crossmodal visual input for odor tracking during fly flight. Curr Biol. 2008;18:270–275. doi: 10.1016/j.cub.2008.01.027. [DOI] [PubMed] [Google Scholar]
- Fuchs PA, Evans MG. Potassium currents in hair cells isolated from the cochlea of the chick. J Physiol. 1990;429:529–551. doi: 10.1113/jphysiol.1990.sp018271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman MB, Art JJ. Variations in the ensemble of potassium currents underlying resonance in turtle hair cells. J Physiol. 1996;497(Pt 2):395–412. doi: 10.1113/jphysiol.1996.sp021776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman MB, Lockery SR. Pressure polishing: a method for re-shaping patch pipettes during fire polishing. J Neurosci Methods. 2000;100:13–15. doi: 10.1016/s0165-0270(00)00224-7. [DOI] [PubMed] [Google Scholar]
- Göpfert MC, Robert D. The mechanical basis of Drosophila audition. J Exp Biol. 2002;205:1199–1208. doi: 10.1242/jeb.205.9.1199. [DOI] [PubMed] [Google Scholar]
- Göpfert MC, Robert D. Motion generation by Drosophila mechanosensory neurons. Proc Natl Acad Sci U S A. 2003;100:5514–5519. doi: 10.1073/pnas.0737564100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göpfert MC, Humphris AD, Albert JT, Robert D, Hendrich O. Power gain exhibited by motile mechanosensory neurons in Drosophila ears. Proc Natl Acad Sci U S A. 2005;102:325–330. doi: 10.1073/pnas.0405741102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göpfert MC, Albert JT, Nadrowski B, Kamikouchi A. Specification of auditory sensitivity by Drosophila TRP channels. Nat Neurosci. 2006;9:999–1000. doi: 10.1038/nn1735. [DOI] [PubMed] [Google Scholar]
- Gouwens NW, Wilson RI. Signal propagation in Drosophila central neurons. J Neurosci. 2009;29:6239–6249. doi: 10.1523/JNEUROSCI.0764-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu H, O’Dowd DK. Cholinergic synaptic transmission in adult Drosophila Kenyon cells in situ. J Neurosci. 2006;26:265–272. doi: 10.1523/JNEUROSCI.4109-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guizar-Sicairos M, Thurman ST, Fienup JR. Efficient subpixel image registration algorithms. Opt Lett. 2008;33:156–158. doi: 10.1364/ol.33.000156. [DOI] [PubMed] [Google Scholar]
- Hall JC. The mating of a fly. Science. 1994;264:1702–1714. doi: 10.1126/science.8209251. [DOI] [PubMed] [Google Scholar]
- Hampel S, Franconville R, Simpson JH, Seeds AM. A neural command circuit for grooming movement control. eLife. 2015;4:e08758. doi: 10.7554/eLife.08758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heimbeck G, Bugnon V, Gendre N, Haberlin C, Stocker RF. Smell and taste perception in Drosophila melanogaster larva: toxin expression studies in chemosensory neurons. J Neurosci. 1999;19:6599–6609. doi: 10.1523/JNEUROSCI.19-15-06599.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hengstenberg R. Spike responses of ‘non-spiking’ visual interneurone. Nature. 1977;270:338–340. doi: 10.1038/270338a0. [DOI] [PubMed] [Google Scholar]
- Hudspeth AJ, Lewis RS. A model for electrical resonance and frequency tuning in saccular hair cells of the bull-frog, Rana catesbeiana. J Physiol. 1988;400:275–297. doi: 10.1113/jphysiol.1988.sp017120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 2000;23:216–222. doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- Ishikawa Y, Okamoto N, Nakamura M, Kim H, Kamikouchi A. Anatomic and physiologic heterogeneity of subgroup-A auditory sensory neurons in fruit flies. Front Neural Circuits. 2017;11:46. doi: 10.3389/fncir.2017.00046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenett A, Rubin GM, Ngo TT, Shepherd D, Murphy C, Dionne H, Pfeiffer BD, Cavallaro A, Hall D, Jeter J, et al. A GAL4-driver line resource for Drosophila neurobiology. Cell Rep. 2012;2:991–1001. doi: 10.1016/j.celrep.2012.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin L, Han Z, Platisa J, Wooltorton JR, Cohen LB, Pieribone VA. Single action potentials and subthreshold electrical events imaged in neurons with a fluorescent protein voltage probe. Neuron. 2012;75:779–785. doi: 10.1016/j.neuron.2012.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joesch M, Plett J, Borst A, Reiff DF. Response properties of motion-sensitive visual interneurons in the lobula plate of Drosophila melanogaster. Curr Biol. 2008;18:368–374. doi: 10.1016/j.cub.2008.02.022. [DOI] [PubMed] [Google Scholar]
- Kamikouchi A, Inagaki HK, Effertz T, Hendrich O, Fiala A, Göpfert MC, Ito K. The neural basis of Drosophila gravity-sensing and hearing. Nature. 2009;458:165–171. doi: 10.1038/nature07810. [DOI] [PubMed] [Google Scholar]
- Kvon EZ, Kazmar T, Stampfel G, Yanez-Cuna JO, Pagani M, Schernhuber K, Dickson BJ, Stark A. Genome-scale functional characterization of Drosophila developmental enhancers in vivo. Nature. 2014;512:91–95. doi: 10.1038/nature13395. [DOI] [PubMed] [Google Scholar]
- Lai JS, Lo SJ, Dickson BJ, Chiang AS. Auditory circuit in the Drosophila brain. Proc Natl Acad Sci U S A. 2012;109:2607–2612. doi: 10.1073/pnas.1117307109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehnert BP, Baker AE, Gaudry Q, Chiang AS, Wilson RI. Distinct roles of TRP channels in auditory transduction and amplification in Drosophila. Neuron. 2013;77:115–128. doi: 10.1016/j.neuron.2012.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longair MH, Baker DA, Armstrong JD. Simple Neurite Tracer: open source software for reconstruction, visualization and analysis of neuronal processes. Bioinformatics. 2011;27:2453–2454. doi: 10.1093/bioinformatics/btr390. [DOI] [PubMed] [Google Scholar]
- Lundstrom BN, Hong S, Higgs MH, Fairhall AL. Two computational regimes of a single-compartment neuron separated by a planar boundary in conductance space. Neural Comput. 2008;20:1239–1260. doi: 10.1162/neco.2007.05-07-536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundstrom BN, Famulare M, Sorensen LB, Spain WJ, Fairhall AL. Sensitivity of firing rate to input fluctuations depends on time scale separation between fast and slow variables in single neurons. J Comput Neurosci. 2009;27:277–290. doi: 10.1007/s10827-009-0142-x. [DOI] [PubMed] [Google Scholar]
- Mamiya A, Straw AD, Tomasson E, Dickinson MH. Active and passive antennal movements during visually guided steering in flying Drosophila. J Neurosci. 2011;31:6900–6914. doi: 10.1523/JNEUROSCI.0498-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mamiya A, Dickinson MH. Antennal mechanosensory neurons mediate wing motor reflexes in flying Drosophila. J Neurosci. 2015;35:7977–7991. doi: 10.1523/JNEUROSCI.0034-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuo E, Seki H, Asai T, Morimoto T, Miyakawa H, Ito K, Kamikouchi A. Organization of projection neurons and local neurons of the primary auditory center in the fruit fly Drosophila melanogaster. J Comp Neurol. 2016;524:1099–1164. doi: 10.1002/cne.23955. [DOI] [PubMed] [Google Scholar]
- Mauss AS, Meier M, Serbe E, Borst A. Optogenetic and pharmacologic dissection of feedforward inhibition in Drosophila motion vision. J Neurosci. 2014;34:2254–2263. doi: 10.1523/JNEUROSCI.3938-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller A. The internal anatomy and histology of the imago of Drosophila melanogaster. In: Demerec M, editor. Biology of Drosophila. Cold Spring Harbor Laboratory Press; 1994. pp. 420–534. [Google Scholar]
- Morley EL, Steinmann T, Casas J, Robert D. Directional cues in Drosophila melanogaster audition: structure of acoustic flow and inter-antennal velocity differences. J Exp Biol. 2012;215:2405–2413. doi: 10.1242/jeb.068940. [DOI] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. Spatial summation in the receptive fields of simple cells in the cat’s striate cortex. J Physiol. 1978a;283:53–77. doi: 10.1113/jphysiol.1978.sp012488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. Receptive field organization of complex cells in the cat’s striate cortex. J Physiol. 1978b;283:79–99. doi: 10.1113/jphysiol.1978.sp012489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadrowski B, Albert JT, Göpfert MC. Transducer-based force generation explains active process in Drosophila hearing. Curr Biol. 2008;18:1365–1372. doi: 10.1016/j.cub.2008.07.095. [DOI] [PubMed] [Google Scholar]
- Nagel KI, Hong EJ, Wilson RI. Synaptic and circuit mechanisms promoting broadband transmission of olfactory stimulus dynamics. Nat Neurosci. 2015;18:56–65. doi: 10.1038/nn.3895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson RO, Liu Z, Nomura Y, Song W, Dong K. Molecular and functional characterization of voltage-gated sodium channel variants from Drosophila melanogaster. Insect Biochem Mol Biol. 2008;38:604–610. doi: 10.1016/j.ibmb.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezier A, Blagburn JM. Auditory responses of engrailed and invected-expressing Johnston’s Organ neurons in Drosophila melanogaster. PLoS One. 2013;8:e71419. doi: 10.1371/journal.pone.0071419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezier A, Jezzini SH, Marie B, Blagburn JM. Engrailed alters the specificity of synaptic connections of Drosophila auditory neurons with the giant fiber. J Neurosci. 2014;34:11691–11704. doi: 10.1523/JNEUROSCI.1939-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezier AP, Jezzini SH, Bacon JP, Blagburn JM. Shaking B Mediates Synaptic Coupling between Auditory Sensory Neurons and the Giant Fiber of Drosophila melanogaster. PLoS One. 2016;11:e0152211. doi: 10.1371/journal.pone.0152211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer B, Ngo TTB, Hibbard KL, Murphy C, Jenett A, Truman JW, Rubin GM. Refinement of tools for targeted gene expression in Drosophila. Genetics. 2010;186:735–755. doi: 10.1534/genetics.110.119917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelan P, Goulding LA, Tam JL, Allen MJ, Dawber RJ, Davies JA, Bacon JP. Molecular mechanism of rectification at identified electrical synapses in the Drosophila giant fiber system. Curr Biol. 2008;18:1955–1960. doi: 10.1016/j.cub.2008.10.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickles JO. Auditory pathways: anatomy and physiology. Handb Clin Neurol. 2015;129:3–25. doi: 10.1016/B978-0-444-62630-1.00001-9. [DOI] [PubMed] [Google Scholar]
- Ratte S, Lankarany M, Rho YA, Patterson A, Prescott SA. Subthreshold membrane currents confer distinct tuning properties that enable neurons to encode the integral or derivative of their input. Front Cell Neurosci. 2014;8:452. doi: 10.3389/fncel.2014.00452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes AD, Rubel EW, Spain WJ. Membrane properties underlying the firing of neurons in the avian cochlear nucleus. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivan-Loukianova E, Eberl DF. Synaptic ultrastructure of Drosophila Johnston’s organ axon terminals as revealed by an enhancer trap. J Comp Neurol. 2005;491:46–55. doi: 10.1002/cne.20687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stocker RF, Heimbeck G, Gendre N, de Belle JS. Neuroblast ablation in Drosophila P[GAL4] lines reveals origins of olfactory interneurons. J Neurobiol. 1997;32:443–456. doi: 10.1002/(sici)1097-4695(199705)32:5<443::aid-neu1>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Stockinger P, Kvitsiani D, Rotkopf S, Tirian L, Dickson BJ. Neural circuitry that governs Drosophila male courtship behavior. Cell. 2005;121:795–807. doi: 10.1016/j.cell.2005.04.026. [DOI] [PubMed] [Google Scholar]
- Straka H, Zwergal A, Cullen KE. Vestibular animal models: contributions to understanding physiology and disease. J Neurol. 2016;263(Suppl 1):S10–23. doi: 10.1007/s00415-015-7909-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootoonian S, Coen P, Kawai R, Murthy M. Neural representations of courtship song in the Drosophila brain. J Neurosci. 2012;32:787–798. doi: 10.1523/JNEUROSCI.5104-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuthill JC, Wilson RI. Parallel transformation of tactile signals in central circuits of Drosophila. Cell. 2016;164:1046–1059. doi: 10.1016/j.cell.2016.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan AG, Zhou C, Manoli DS, Baker BS. Neural pathways for the detection and discrimination of conspecific song in D. melanogaster. Curr Biol. 2014;24:1039–1049. doi: 10.1016/j.cub.2014.03.048. [DOI] [PubMed] [Google Scholar]
- Werblin FS. Six different roles for crossover inhibition in the retina: correcting the nonlinearities of synaptic transmission. Vis Neurosci. 2010;27:1–8. doi: 10.1017/S0952523810000076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson RI, Turner GC, Laurent G. Transformation of olfactory representations in the Drosophila antennal lobe. Science. 2004;303:366–370. doi: 10.1126/science.1090782. [DOI] [PubMed] [Google Scholar]
- Yasuyama K, Salvaterra PM. Localization of choline acetyltransferase-expressing neurons in Drosophila nervous system. Microsc Res Tech. 1999;45:65–79. doi: 10.1002/(SICI)1097-0029(19990415)45:2<65::AID-JEMT2>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- Yorozu S, Wong A, Fischer BJ, Dankert H, Kernan MJ, Kamikouchi A, Ito K, Anderson DJ. Distinct sensory representations of wind and near-field sound in the Drosophila brain. Nature. 2009;458:201–205. doi: 10.1038/nature07843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu JY, Kanai MI, Demir E, Jefferis GS, Dickson BJ. Cellular organization of the neural circuit that drives Drosophila courtship behavior. Curr Biol. 2010;20:1602–1614. doi: 10.1016/j.cub.2010.08.025. [DOI] [PubMed] [Google Scholar]
- Zhou C, Franconville R, Vaughan AG, Robinett CC, Jayaraman V, Baker BS. Central neural circuitry mediating courtship song perception in male Drosophila. eLife. 2015;4 doi: 10.7554/eLife.08477. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1, related to Figure 1: A2 cell spiking responses to vibration stimuli.
Figure S2, related to Figure 1: “Resting” oscillations in B1 cell voltage.
Figure S3, related to Figure 2: Gal4 lines labeling cells of different types.
Figure S4, related to Figure 5: Suppressing voltage-gated conductances.
Figure S5, related to Figure 5: Blocking voltage-gated channels creates low-pass voltage tuning in B1 cells.
Figure S6, related to Figure 6: In vivo calcium imaging in B1 cells.
Figure S7, related to Figure 7: Voltage-gated K+ currents are faster in B1-high cells than in B1-mid/low cells.
Figure S8, related to Figure 8: Frequency selectivity in B1 cells and comparisons with models.


