Measuring Precision in Bioassays: Rethinking Assay Validation

Abstract

The m: n : θ_b procedure is often used for validating an assay for precision, where m levels of an analyte are measured with n replicates at each level, and if all m estimates of coefficient of variation (CV) are less than θ_b, then the assay is declared validated for precision. The statistical properties of the procedure are unknown so there is no clear statistical statement of precision upon passing. Further, it is unclear how to modify the procedure for relative potency assays in which the constant standard deviation (SD) model fits much better than the traditional constant CV model. We use simple normal error models to show that under constant CV across the m levels, the probability of passing when the CV is θ_b is about 10% to 20% for some recommended implementations; however, for extreme heterogeniety of CV when the largest CV is θ_b, the passing probability can be greater than 50%. We derive 100q% upper confidence limits on the CV under constant CV models and derive analogous limits for the SD under a constant SD model. Additionally, for a post-validation assay output of y, we derive 68.27% confidence intervals on either the mean or log geometric mean of the assay output using either y ± s (for the constant SD model) or log(y) ± r_G (for the constant CV model), where s and r_G are constants that do not depend on y. We demonstrate the methods on a growth inhibition assay used to measure biologic activity of antibodies against the malaria parasite.

1 Introduction

Before an assay is routinely used in drug development or in scientific studies, consumers of the assay should be reasonably confident that the assay is measuring what they think it is measuring. The tests that are done to study properties of an assay are known as the validation process. Different tests are done on different assays, and some common properties tested are selectivity (how the assay performs in the presence of expected components such as impurities), stability (how the assay performs after the sample has been subjected to different conditions over differing time intervals), accuracy (how close the value of an assay is to its known true value), and precision (how close individual readouts of an assay are when applied to replicates) [1]. An assay that has passed the tests is known as a validated assay. It is good practice to use validated assays in scientific studies, and often regulatory agencies request that assays be validated when used in studies that are reviewed by them.

In practice, once an assay has been validated, the readout from that assay is often treated as if it is measured without error (e.g., with perfect accuracy and perfect precision). Although ignoring error variability is convenient, it may sometimes be useful to have measures of precision for use with assay readouts post-validation to give users an idea of the size of the variability of the readout.

This paper focuses on validation tests for precision in bioassays, focusing on two classes of bioassays, concentration assays and relative potency assays (both defined below).

We begin with the US Food and Drug Administration’s guidance on bioanalytical method validation for what we call “concentration assays”, assays that quantitatively determine concentrations of analytes (e.g., drugs, metabolites, therapeutic proteins) in biological matrices (e.g., blood, plasma, urine, skin) [1]. We measure precision on replicates, which for concentration assays are “multiple aliquots of a single homogeneous volume of biological matrix” ([1], p. 5–6). The guidance recommends an m: n : θ_b procedure for validating an assay for precision: m different sample concentration levels are each measured on n replicates, and if the sample coefficient of variation (CV) for each of the m levels is less than θ_b then the assay passes the precision validation. In this paper we do not differentiate between within-run precision and between-run precision, since both can be statistically evaluated similarly. Some implementations of the m : n : θ_b procedure are 3 : 5 : 15% (for chromatographic methods, p. 5 of [1]), and 3 : 5 : 20% (for ligand binding assays, p. 13 of [1]). Typically, an m:n: θ_b procedure has m between 2 and 6 and n between 3 and 6 (see Table I of [2]).

Although the m : n : θ_b procedure is well defined, to the best of our knowledge its statistical properties have not been studied. This paper fills that need using simple normal error models. We show that if there is homogeneity of CV across the m levels and the true CV is equal to the bound θ_b, then some implementations have overall probability of passing of about 10% (for 3 : 5 : 15% and 3 : 5 : 20% procedures) or 20% (for the 4 : 6 : 20% procedure). We show that if there is extreme heterogeneity of precision between the m levels, the probability of passing the m: n : θ_b procedure can be larger than 50% when the maximum coefficient of variation for one level is θ_b.

For concentration assays, the constant coefficient of variation model is often appropriate. Under that model we measure precision by the CV, which is the standard error of replicates divided by the mean of replicates. A necessarily important property of the CV as a precision parameter for concentration assays is that it is scale invariant, so that changing the units (e.g., from amount of particles per microliter to amount per liter) will not change the precision parameter.

While the constant CV model has been used widely, there could be assays which fit better with a constant SD model. One such assay, and the one that motivated this work, is a growth inhibition assay (GIA) that measures the inhibitory activity of certain antibodies to the growth of malaria parasites in vitro. A constant CV model is a very poor model for the GIA, primarily because the GIA is a relative potency assay, meaning its activity is measured relative to a control sample. The output for a sample x is y(x) = 100(1−a(x)/a(x_control)), where a(x) is some measurement of biological activity in the sample that must be normalized by a similar readout for a control sample, a(x_control). Other relative potency assays have this same structure; for example, standard membrane feeding assays, which measure the inhibition of malaria parasites in mosquitoes [3]. For the GIA, the biological activity measured by a(·) is the amount of growth of malaria parasites in vitro. To see why the constant CV model does not work for the GIA, imagine if the test sample has very little effect on parasite growth, then a(x)/a(x_control) will be close to 1 and the expected value of the readout y(x), say μ(x), will be close to 0. Since the CV is the standard deviation over μ(x), small changes in μ(x) close to zero can have large changes in the CV. Thus, in general the constant CV model is not well suited for relative potency assays. Further, a relative potency assay is not necessarily proportional to the amount of analyte in the sample, since there could be threshold effects where after a certain amount of analyte is in the sample, further increases do not increase the biological activity that is being measured. So there is no need for relative potency assays to be scale invariant, because the scale is determined relative to the control sample. An alternative model that may be appropriate for a relative potency assay is the constant standard deviation (SD) model.

Lio, Lu, and Liao [4] discussed estimating precision under the constant SD model using a random effects model with several levels. Their data example had 80 replicates of a single sample. For biological assays like the GIA, that many replicates per sample is often infeasible.

In order to validate a relative potency assay for precision, a constant SD model may often fit better. Because in this model we cannot use a scale invariant measure of precision such as CV, there is no bound (e.g., CV less than 20%) that will apply to many different assays. The acceptable bound for a constant SD model assay is different for each assay. We suggest that we use the statistical properties of the m: n : θ_b procedure to propose a new nomenclature, so that procedures of this type would be known as m:n: q procedures, where the q is the confidence level for an upper bound of the precision parameter under a model where that precision parameter is constant. The m: n : q nomenclature allows us to more straightforwardly generalize the m:n: θ_b procedure for a constant CV model to a constant SD model. Further, unlike the m: n : θ_b procedure which only results in a binary pass/fail decision, our new procedure results in an upper bound on the precision measure. We can get a binary pass/fail decision from that upper bound, since an assay passes our validation procedure if the upper bound is less than some specified acceptable bound for that assay (although that acceptability bound is not part of the new nomenclature). But we get additional information from the upper bound also. We show that when the precision is constant across all m levels, the upper bound can be interpreted as an upper confidence limit on the precision parameter. Further, we show how to use that upper bound in order to get 68.27% confidence intervals on the expected readout from using the assay on a post-validation sample, x^*. Specifically, for the constant SD model assays the post-validation 68.27% confidence interval for the expected readout is of the form y(x^*) ± s, and for the constant CV models the 68.27% confidence interval for the log geometric mean is of the form log(y(x^*)) ± r_G, where s and r_G are constants that do not depend on y(x^*).

After further delineating the notation (Section 2), we explore the statistical properties of the m: n : θ_b procedure in Section 3. In Section 4, we introduce m: n : q nomenclature, where q represents the confidence level of an upper bound on θ under homogeneity. The m: n : q nomenclature ties the procedure to its statistical properties in an ideal situation, and we give confidence limits for θ under two different constant CV models. In Section 5, we show how to create an m : n : q procedure for the constant SD model. We give an outline of how the m : n : q procedure would be used without the mathematical details in Section 6. In Section 7, we show how to create effective standard deviation intervals, that is, 68.27% confidence intervals for representing the precision of an measurement taken post-validation. In Section 8 we study the statistical properties of our procedure under heterogeneous precision across the m levels. In Section 9 we apply that procedure to some GIA data, and we end with a discussion.

2 Notational Formation of the Problem

Let y(x) be the observed value for the assay for sample x. For example, y(x) would be the measured growth inhibition of sample x in the GIA assay. Let E(Y(x)) = μ(x). In the GIA, μ(x) is the unknown mean growth inhibition from infinite replications of the assay on sample x. For concentration assays, we often work with the geometric mean, μ_G(x) = exp(E [log {Y (x)}]).

Let σ²(x) be the variance. This could represent the between-lab variance, the within-lab variance, or the within-day variance, or some other variance. For applications we must specify which variance we are interested in testing. For this paper, we assume that which variance being tested is clear, and we do not notationally indicate the type of variance. The coefficient of variation will be denoted θ(x) = σ(x)/μ(x). For some models we assume that θ is constant and does not depend on x within the range of interest, and for other models we alternatively assume that σ is constant.

For validation of an assay, we test the assay on m levels. The m sample levels are thought to produce results that cover the range of sufficiently precise measurability of the assay. At each of the m levels, we typically perform n technical replicates. The replicates are at the levels for which the precision needs to be validated. For example, the activity is measured by GIA on a plate, on a particular day, and at a specific lab. If we want to measure the day-to-day precision of the assay at a specific lab, then we repeat the assay on n different days on n aliquots from the same sample in that lab.

3 Statistical Properties of the m:n:θ_b Procedure

3.1 Constant of Coefficient of Variation

Consider the statistical properties of the m:n: θ_b procedure under the constant CV model where θ₁ = ··· = θ_m, and θ_j is the true CV for the jth level. Let θ̂_j be the sample CV estimate. If θ̂_j < θ_b for all j = 1, …, m, then the assay passes the m : n : θ_b validation procedure, otherwise it fails. We consider first the statistical properties of passing the jth level. Let θ̂_j < θ_b be a decision rule for a hypothesis test of H_0j : θ_j ≥ θ_b versus H_1j : θ_j < θ_b. We show in Section S2.1 of the Supplementary materials that for the normal constant CV model if we reject H_0j when θ̂_j < θ_b then this test has significance level α_ℓ (here the ℓ subscript denotes a test on each ℓevel), where ${\alpha }_{\ell }=1-t_{n-1,\sqrt{n}/{\theta }_b}(\sqrt{n}/{\theta }_b)$. The value α_ℓ has the interpretation as the probability of passing one of the m levels, when the true CV for that level is θ_b. As one might suspect the values of α_ℓ are close to 50% because there is about an even chance that θ̂_j < θ_b or θ̂_j ≥ θ_b when the truth is that θ = θ_b. In Table 1 we give the values for α_ℓ for some m:n: θ_b procedures (see [1] and Table I of [2], and note that the 4 : 6 : 20% rule is a validation of precision rule and should not be mistaken for an assay acceptance criteria as in [5]). The α_ℓ values are slightly larger than 50% because of the asymmetry of the distribution of θ̂_j.

Table 1.

Values of α_ℓ = Pr[Pass one level|θ = θ_b] and α_q = Pr[Pass all m levels|θ = θ_b] for an m:n:θ_b procedure under normal constant CV model.

m	n	θb	αℓ	αq	q = 1 − αq
3	5	0.15	0.592	0.207	0.793
3	5	0.20	0.590	0.205	0.795
4	6	0.20	0.580	0.113	0.887

Although significance levels of greater than 50% are not typically acceptable, the overall type I error rate of rejecting ALL m levels is much more reasonable. Under the constant CV model θ = θ_j for all j, and because of independence of the data at different levels, we can test H₀ : θ ≥ θ_b versus H₁ : θ < θ_b by rejecting at the ${\alpha }_q={\alpha }_{\ell }^m$ level when we reject each of the m levels at α_ℓ. So α_q is the total significance level of the m: n : θ_b procedure under the normal constant CV model, where the type I error rate represents the probability of passing the procedure when the true θ = θ_b. Table 1 gives different α_ℓ and α_q levels for some standard m:n:θ_b procedures under the normal constant CV model.

To see how robust these results are to the choice of error distribution we consider the lognormal constant CV model. In this case, we use a different estimator of CV, $\stackrel{\sim }{\theta }=\sqrt{exp(\widehat{\nu })-1}$, where ν̂ is an estimate of the variance of log(Y) (see equation S10). Let θ̃_j be the estimate for the jth sample level, and pass the associated m:n:θ_b procedure if θ̃_j < θ_b for all j = 1, …, m. Then we show in Supplemental Section S3.1 that the probability of passing each level given θ = θ_b is α_ℓ = W_n−1(n − 1), where W_df (x) is the cumulative distribution of a chi-square with df degrees of freedom. When for n = 5 we have α_ℓ = 0.593 (giving $q=1-{\alpha }_{\ell }^3=0.790$) and for n = 6 we have α_ℓ = 0.584 (giving $q=1-{\alpha }_{\ell }^4=0.884$). Comparing to Table 1, we see that these α_ℓ and q = 1 − α_q values from the lognormal constant CV model are very close to those from the normal constant CV model. So the choice between the two constant CV models has little affect on the statistical properties.

3.2 Non-constant CV

Suppose we wanted to show that θ_j < θ_b for j = 1, 2, …, m without assuming constant CV. Under a hypothesis testing framework the hypotheses would be

$$\begin{gathered} H_0:{\theta }_1\ge {\theta }_b\text{or}{\theta }_2\ge {\theta }_b\text{or}\cdots \text{or}{\theta }_m\ge {\theta }_b \\ {H}_1:{\theta }_1<{\theta }_b\text{and}{\theta }_2<{\theta }_b\text{and}\cdots \text{and}{\theta }_m<{\theta }_b. \end{gathered}$$

To reject the null hypotheses, we must reject for all values of θ = [θ₁, θ₂, …, θ_m] in the null. Suppose that θ_j ≪ θ_b for j = 1, …, m − 1 and θ_m = θ_b. Then for standard values of n (e.g., 5 or 6) or larger, Pr[θ̂_j < θ_b] ≈ 1 for j = 1, …, m − 1, and

$$Pr[\text{Pass}\text{the}m:n:{\theta }_b\text{procedure}\mid \theta =[{\theta }_1,\dots ,{\theta }_m]]\approx Pr[{\widehat{\theta }}_m<{\theta }_b\mid {\theta }_m={\theta }_b]={\alpha }_{\ell }.$$

So in the extreme case when one level has CV much much larger than the others and the largest CV is θ_b, the probability of passing the m : n : θ_b procedure is about α_ℓ, which is greater than 50% (see Table 1). As another example, the 3 : 5 : 15% procedure under the normal constant CV model can have up to a 52.3% chance of passing when the largest CV is 16%.

4 Reframing the m : n : θ_b Procedure as Confidence Limits

Using the relationship between hypothesis tests and confidence intervals, we can reframe the m: n : θ_b procedure in terms of confidence limits. Let y_j = [y_j1, …, y_jn] represent the replicates for level j. Using standard normal or lognormal models, we can get a 100(1−α_ℓ)% one-sided confidence interval with an upper bound of θ̄_j ≡ θ̄_j(y_j; 1−α_ℓ). The formulas for θ̄_j are given in the supplement (see equation S4 for the normal model, and equation S11 for the lognormal model). For example, the per-level significance levels given by α_ℓ in Table 1 represent the values such that θ̄_j = θ̂_j in the normal constant CV model. We can get an analogous result for the lognormal constant CV model where we can solve for α_ℓ (e.g., α_ℓ= 0.593 for n = 5) so that θ̃_j = θ̄_j(y_j; 1 − α_ℓ). Thus, when θ̂_j < θ_b for the normal constant CV model (or θ̃_j < θ_b for the lognormal constant CV model), then the m: n : θ_b procedure passes the jth level, which means that the upper 100(1 − α_ℓ)% confidence limit is less than θ_b.

If we assume constant CV (see Section 3.1) so that θ_j = θ for all j, then because of independence of the data at different levels, we can test H₀ : θ ≥ θ₀ versus H₁ : θ < θ₀ by rejecting at the ${\alpha }_q={\alpha }_{\ell }^m$ level when we reject each of the m levels at α_ℓ; in other words, we reject when

$${\overline{\theta }}_{\mathit{max}}\equiv \underset{j=1,2,\dots ,m}{max}{\overline{\theta }}_j({\mathbf{y}}_j;1-{\alpha }_{\ell })<{\theta }_0.$$

Inverting the hypothesis test, we get a 100(1 − α_ℓ)% = 100q% upper confidence limit for θ of θ̄(y, q) ≡ θ̄_max, where y = [y₁, …, y_m]. Then for the appropriate choice of α_ℓ (e.g., such that θ̂_j = θ̄_j), the following two events are equivalent: the data y pass the m: n : θ_b procedure and θ̄(y, q) < θ_b.

In hypothesis testing we often set the significance level at some traditional value (e.g., 0.05), which is associated with some traditional confidence level (e.g., 95%). We propose that we could rename the m: n : θ_b procedures based on the overall confidence level under the constant CV assumption, which we denote as q = 1 − α_q. We propose renaming the m:n:θ_b procedure as a m:n: q procedure. For example, the 3:5:15% procedure in m:n:θ_b nomenclature, would be renamed the 3 : 5 : 79.3% normal constant CV model procedure in m:n: q nomenclature (see the first row of Table 1). The advantage of the new nomenclature is that it is tied to the statistical properties, so that switching from a constant CV model to an analogous procedure for a constant SD models is straightforward.

If there is no need to force equivalence of the m : n : q the procedure to a standard m : n : θ_b procedure, we could use a slightly modified procedure by rounding the overall confidence level, using for example a m: n : q procedure such as a 3 : 5 : 80% procedure or a 4 : 6 : 90% procedure (see Table 1). The associated individual level significance for an m:n: q procedure would be α_ℓ = (1 − q)^1/m.

5 A Validation Procedure for the Constant SD Model

The m : n : q procedure for the constant SD model is formed in an analogous way as for the constant CV model. Let σ_j = σ(x_j) for j = 1, …, m, then if we can assume σ₁ = σ₂ = ··· = σ_m, then we can use an overall 100q% upper confidence limit of

$$\overline{\sigma }(\mathbf{y},q)\equiv \underset{j=1,2,\dots ,m}{max}{\overline{\sigma }}_j({\mathbf{y}}_j,1-{\alpha }_{\ell })$$ (1)

where σ̄_j(y_j, 1−α_ℓ) is the 100(1 − α_ℓ) upper confidence limit for σ_j using standard results for the normal model (see equation S2), and where ${\alpha }_{\ell }={\alpha }_q^{1/m}={(1-q)}^{1/m}$. If σ_b is an acceptability bound on σ, then the m:n: q procedure passes if σ̄(y, q) < σ_b. Although each acceptability bound σ_b is tied to the assay, the level q can be the same between a large class of assays.

6 The Proposed Precision Validation Process

Here is a brief description of our proposed precision validation process, including post-validation measures of precision.

1. Choose either a constant CV or a constant SD model for your assay within the range of application for which you wish to use the assay.

2. Choose a design for the validation procedure. The shorthand notation for the validation design is m:n: q. We measure m levels of some samples, take n replicates on each level, and use the data to calculate an upper bound, which may be interpreted under constant precision across the m levels as a 100q% one-sided upper confidence limit on the precision parameter.

3. Choose a statistical model (e.g., lognormal constant CV or normal constant SD), and calculate the 100q% upper confidence limit for the precision parameter under constant precision, which is the maximum of the m individual confidence limits at level 1−α_ℓ, where α_ℓ = (1 − q)^1/m. Denote this upper bound as either θ̄(q) (for a constant CV model) or σ̄(q) (for a constant SD model).

4. If there is a specified bound (either θ_b or σ_b), then the assay is validated for precision if θ̄(q) < θ_b or σ̄(q) < σ_b. If there is no specified bound, declare the assay validated for precision at θ̄(q) (for the constant CV model) or at σ̄(q) (for the constant SD model) with level q.

5. Calculate a constant, either r or r_G (for constant CV models) or s (for constant SD models) that will be used to create an approximate 68.27% confidence interval on μ(x^*) or μ_G(x^*), and x^* is a post-validation sample assumed to be within the range of applicability of the assay. For the constant SD model, the confidence interval on μ(x^*) is of the form, y(x^*) ± s. If the data are normal with σ₁ = ··· σ_m = σ then y(x^*) ± σ is a 68.27% confidence interval. We call a 68.27% confidence interval of the form c ± d, an “effective standard deviation interval”, and d is the effective SD. For example, for the constant CV model the effective standard deviation interval is a 68.27% confidence interval on either log(μ(x^*)) or log(μ_G(x^*)) and is of the form log(y(x^*)) ± r or log(y(x^*)) ± r_G. The actual coverage of the effective SD intervals will be larger than 68.27% under constant precision, and may be smaller than 68.27% when there is substantial heterogeneity. Details are in Sections 7 and 8.

7 Interpreting Single Sample Results Post-Validation

After an assay has been validated for precision, we want some measure of precision to be used with the assay for any subsequent use. We choose effective standard deviation intervals, although, we could alternatively use 95% confidence intervals on μ(x^*) or on log(μ(x^*)). In the subsections, we study effective standard deviation intevals in the three models when the precision parameters are estimated from an m:n: q procedure.

7.1 The Normal Constant SD Model

First, assume the constant SD model fits, so that σ = σ₁ = σ₂ = ··· = σ_m. Consider an m: n : q validation procedure that gives unbiased variance estimators, ${\widehat{\sigma }}_j^2$ for j = 1, …, m. Let the mean of those estimators be ${\widehat{\sigma }}^2=(1/m){\sum }_{j=1}^m{\widehat{\sigma }}_j^2$. Then by the properties of the normal model and the sum of independent chi square variates,

$$\sum _{j=1}^m\frac{(n-1){\widehat{\sigma }}_j^2}{{\sigma }^2}=\frac{m(n-1){\widehat{\sigma }}^2}{{\sigma }^2}$$

is distributed chi square with m(n − 1) degrees of freedom. So by the independence of σ̂₂ (from the m : n : q procedure) and y(x^*) (from post-validation data), analogously to the usual derivation of the t distribution confidence interval from a normal sample, we get a 100(1 − γ)% confidence interval on μ(x^*) as

$$y(x^{\ast })\pm t_{m(n-1)}^{-1}(1-\gamma /2)\widehat{\sigma },$$ (2)

where $t_{df}^{-1}(q)$ is the qth quantile of the t distribution with df degrees of freedom. When the target nominal level is 68.27, then γ = 1 − 0.6827 = .3173, and we get an effective standard deviation of $s=t_{m(n-1)}^{-1}(0.8413)\widehat{\sigma }$. For example, with a 3 : 5 : q procedure we get s = 1.043 * σ̂ and with a 4:6:q procedure we get s = 1.026 * σ̂.

Another possibility is to use the 100q% upper confidence bound from the m:n: q procedure, σ̄(q), as the effective standard deviation. The advantage of using σ̄(q) as the effective standard deviation is that only one number needs to be reported from the validation process, and it serves as both the precision bound and the effective standard deviation. For typical values of q (e.g., 80% or 90%), using σ̄(q) as the effective standard deviation will give conservative coverge under constant SD and ensure at least 100(1 − γ)% coverage for small to moderate departures from the constant SD assumption (see Section 8).

7.2 The Lognormal or Normal Constant CV Model

First consider the lognormal model and effective standard deviation intervals on log(μ_G) that is statistically analogous to the normal constant SD model. In the lognormal constant CV model, log(Y(x^*)) ~ N(ξ(x^*), ν) and ξ(x^*) = log(μ_G(x^*)) and θ = {exp(ν) − 1}^1/2. Let ν̂ = (1/m)Σν̂_j, where ν̂_j is the unbaised variance estimator of ν_j. Then we can get a 100(1 − γ)% confidence interval on log(μ_G(x^*)) analogously to equation 2 as

$$log(y(x^{\ast }))\pm t_{m(n-1)}^{-1}(1-\gamma /2)\sqrt{\widehat{\nu }}.$$ (3)

The analogous conservative effective SD interval uses

$$r_G=\sqrt{\overline{\nu }(\mathbf{y},q)}=\sqrt{log\{{\overline{\theta }}^2(\mathbf{y},q)+1\}}.$$ (4)

Since μ_G is not defined for the normal constant CV model, we give no confidence intervals for it for that model.

The effective SD intervals for log(μ) under the constant CV models are more complicated. There is no simple form (such as the t distribution confidence intervals of equation 2) for giving confidence interval when using an estimator of θ. Our strategy for creating confidence intervals is three steps. First, we assume that θ is known, and derive the 100(1 − γ)% “log-centered” confidence interval, i.e., a confidence interval of the form log(y)±r(θ, 1 − γ), where r(θ, 1 − γ) is a different function for each model. In the Supplement, we give the form for r(θ, 1 − γ) for the normal constant CV model in equation S8, and for the lognormal constant CV model in equation S12. Second, we propose as an effective SD interval log(y(x^*)) ± r(θ̄, 1 − γ), where θ̄ = θ̄(y, q) is given in Section 4 for the two models. Third, we test the coverage of the confidence interval under the constant CV assumption.

Mathematically, we write the coverage as

$$\mathrm{\Pi }(1-\gamma )=Pr[log\{\mu (x^{\ast })\}\in \{log(Y^{\ast })\pm r(\overline{\theta }(\mathbf{Y},q),1-\gamma )\left\}\right],$$ (5)

where the probability is taken over both the validation data, Y, and the post-validation data, Y^*, which both follow the same model (e.g., lognormal) with the CV parameters θ = [θ₁, …, θ_m] and θ(x^*) = θ^* respectively. Although μ(x) changes between the validation samples, x = x₁, x = x₂, …, x = x_m, and the post-validation sample, x = x^*, Π(1 − γ) does not depend on any μ(x) values except through θ (see Section S4). For this section we assume constant precision so that θ₁ = θ₂ = ··· = θ_m = θ^*, while in Section 8 we study non-constant precision. We use the same Π(1 − γ) expression for both the normal and the lognormal constant CV model. In Table 2 we give the simulated coverages for both models based on 10⁵ simulations with true θ values as θ_b from some m : n : θ_b procedures. We see that the coverages for the nominal 68.27% intervals are conservative and nearly equal for the two constant CV models. The conservativeness allows for some robustness if the constant precision assumption does not hold, as we explicitly discuss in the next section for the interval on μ(x^*) from constant SD model and the interval on log(μ_g(x^*)) from the lognormal constant CV model.

Table 2.

Coverage using the normal constant CV model and lognormal constant CV model for different m:n: q procedures. The value θ is the true CV for the estimation of Π(0.6827) (the coverage of the confidence interval for μ(x^*) using the 100q% upper limit for CV from the procedure). The value Π(0.6827) is estimated by simulation based on 10⁵ replications, and its nominal value is 0.6827.

m:n:q	θ	Normal Constant CV Model	lognormal Constant CV Model
		Π(0.6827)	Π(0.6827)
3:5:80%	0.15	0.770	0.768
3:5:80%	0.20	0.770	0.767
4:6:90%	0.20	0.794	0.785

8 Robustness to the Constant Precision Assumption

Using the maximum of the m 100(1−α_ℓ)% upper limits does not give $q=1-{\alpha }_q=1-{\alpha }_{\ell }^m$ coverage if we cannot assume all θ_j = θ (for the constant CV models) or all σ_j = σ (for constant SD models). This is the same issue as the high probability of passing when max_j=1,…,m θ_j = θ_b under heterogeneity with the m:n:θ_b procedure (see Section 3.2).

We could test the constant precision assumption, but with m:n: q designs like 3:5: q or 4 : 6 : q we have very little power to detect reasonable alternatives. To show this, consider Bartlett’s test of equality of variances [6] under some alternatives. Consider a 4 : 6 : q procedure, and simulate with 10⁴ replications different alternatives. Because Bartlett’s test is invariant to scaling, we report the standard deviations scaled to have the largest of the m values equal to 1. We see in Table 3 that unless the standard deviation ratios are very small (minimum to maximum ratio of 0.5, which corresponds to a variance ratio of 0.25), the power is less than 10%, and even the small ratios only give a power of 35.5%.

Table 3.

Simulated power and simulated coverage using 10, 000 Monte Carlo replications: Simulated power to reject (at the 5 percent level) equal variances (normal constant SD model) or equal coefficient of variations (lognormal constant CV model) using Bartlett’s test. Simulated coverage of max_j σ_j by σ̄(q) (see Section 5) and max_j θ_j by θ̄(q) (see Section 4) and for 4:6:80% and 4:6:90% procedures.

(σ1, σ2, σ3, σ4)	(θ1, θ2, θ3, θ4)	Power(percent)	Coverage 4:6:80%	Coverage 4:6:90%
(1.0, 1.0, 1.0, 1.0)	(1.00, 1.00, 1.00, 1.00)	4.8	80.2	90.1
(1.0, 1.0, 0.9, 0.9)	(1.00, 1.00, 0.85, 0.85)	5.2	72.2	84.7
(1.0, 0.9, 0.8, 0.7)	(1.00, 0.85, 0.72, 0.61)	8.3	55.5	71.6
(1.0, 1.0, 0.5, 0.5)	(1.00, 1.00, 0.41, 0.41)	34.2	55.4	68.7

Consider the lognormal constant CV model, where log(Y) ~ N(ξ, ν). Since $\theta =\sqrt{exp(\nu )-1}$ (see equation S9), testing the null that θ₁ = ··· = θ_m is equivalent to testing the null that ν₁ = ··· = ν_m, and we can use Bartlett’s test on the log tranformed data. Thus, in Table 3 the simulation results for (σ₁, …, σ_m) correspond to (θ₁, …, θ_m) where

$${\theta }_j=\frac{\sqrt{exp({\sigma }_j^2)-1}}{{max}_{i=1}^m\left\{\sqrt{exp({\sigma }_i^2)-1}\right\}}.$$

Consider coverage of the one-sided overall upper confidence limits of θ̄(q) (see Section 4) and σ̄(q) (see Section 5). The derivation requires constant precision over the m levels, but we simulate the actual coverage under different scenarios in Table 3. The simulated coverage is invariant to scale changes, so for example, the results for (σ₁, σ₂, σ₃, σ₄) = (1, 1, 0.9, 0.9) also represent results from (σ₁, σ₂, σ₃, σ₄) = (100, 100, 90, 90). Further, because of the statistical relationship between the two models, the simulated coverages for the normal constant SD model with (σ₁, σ₂, σ₃, σ₄) also represent coverages for the lognormal constant CV model with the θ_j given by equation 6. We find the coverage of σ̄(Y, q) = max_j {σ̄_j(y_j, 1 − α_ℓ)} and θ̄(Y, q) = max_j {θ̄_j(y_j, 1 − α_ℓ)} for the 4 : 6 : q procedure can be much less than the nominal level q if the constant precision assumption fails.

Although we must accept that the 100q% upper limits do not have proper coverage when the constant precision assumption fails, the coverage on the post-validation samples for μ(x^*) or μ_G(x^*) is more robust. Consider first the coverage of the standard deviation intervals for post-validation on the constant SD model. The interval defined by equation 2 gives accurate coverage theoretically when the constant SD holds through all m levels. But when the constant SD assumption fails, we study the coverage on μ(x^*) of using y(x^*) ± s with s = σ̄(y, q) as an effective standard deviation interval and simulating with σ(x^*) = max_j=1,…,m σ(x_j). Table 4 shows that the conservativeness ensures at least nominal coverage even for moderate departures from homogeneity of precision. As with Table 3, the simulation results of Table 4 are invariant to scale changes, so each row represents a class of simulations with the m standard deviations equal to c(σ₁, σ₂, σ₃, σ₄) for any positive constant c. Also, since this is essentially the same statistical problem but on the log scale for the lognormal model (see beginning of Section 7.2), the same simulated coverage applies to log(μ_G) for that model (with the relation between σ and θ values given in equation 6).

Table 4.

Simulated coverage on μ for post-validation interval of the form y ± s, using n=10,000 replications. Ideal coverage is 68.27% and is theoretically acheived when the constant SD assumption holds using $s=t_{m(n-1)}^{-1}(0.8413)\widehat{\sigma }$ (equation 2). We also try s = σ̄(y, 0.80) and s = σ̄(y, 0.90) for 4:6:80% and 4:6:90% procedures.

(σ1, σ2, σ3, σ4)	$s=t_{m(n-1)}^{-1}(0.8413)\widehat{\sigma }$	s= σ̄(y, 0.80)	s = σ̄(y, 0.90)
(1.0, 1.0, 1.0, 1.0)	68.3	75.5	79.4
(1.0, 1.0, 0.9, 0.9)	65.9	73.3	77.3
(1.0, 0.9, 0.8, 0.7)	61.1	69.6	73.6
(1.0, 1.0, 0.5, 0.5)	57.0	69.2	73.2

9 Motivating Application

9.1 The Growth Inhibition Assay

The growth inhibition assay (GIA) is a functional assay that measures how antibodies (immunoglobulin G, IgG) in a blood sample inhibits the growth (and/or invasion) of certain malaria parasites. It is a functional assay in the sense that it is designed to measure the function of a sample, rather than the amount of a specific analyte. The growth inhibition assay is described in detail in [7]. Briefly, the purified IgG from the test sample is mixed with malaria-infected red blood cells (RBCs) in a well of a 96 well plate. A negative control is a well with infected RBCs without test IgG on the same plate. The amount of parasite growth in either of those wells is measured by a biochemical assay specific for parasite lactate dehydrogenase using optical density wavelength of 650 (OD650). Specifically, the GIA from those two wells after adjusting for the OD650 from normal RBCs is

$$\mathit{GIA}=100\left(1-\frac{O{D}_{650}\text{of}\text{infected}\text{RBCs}\text{with}\text{test}\text{IgG}-O{D}_{650}\text{of}\text{normal}\text{RBCs}}{O{D}_{650}\text{of}\text{infected}\text{RBCs}\text{without}\text{any}\text{IgG}-O{D}_{650}\text{of}\text{normal}\text{RBCs}}\right).$$

Following [8] we want to focus our validation process on the intended purposes of the GIA. One main purpose for the assay is to determine whether a given sample has any growth inhibition, and if so, how much. So the general purpose standard deviation interval should be useful in showing the middle 68.27% probable range of any sample. So the effective standard deviation of Y will be a useful statistic.

9.2 Analysis of Replicate Data

For this demonstration, we use GIA replicate measurements on samples, where the GIA is based on two different strains of the Plasmodium falciparum parasite, 3D7 and FVO. Each sample is measured 4 times on 4 different assays. There are 6 samples measured using the 3D7 strain, and in each of the 4 assays each of the 6 samples is measured once. Similarly, there are 7 samples measured using the FVO strain, and in each of 4 different assays each of the 7 samples is measured once. There is statistical dependence due to the samples being all measured on the same assay, so in a proper qualifying procedure each replicate would be measured on a different assay. For the purposes of illustration assume that each replicate is measured on a different assay.

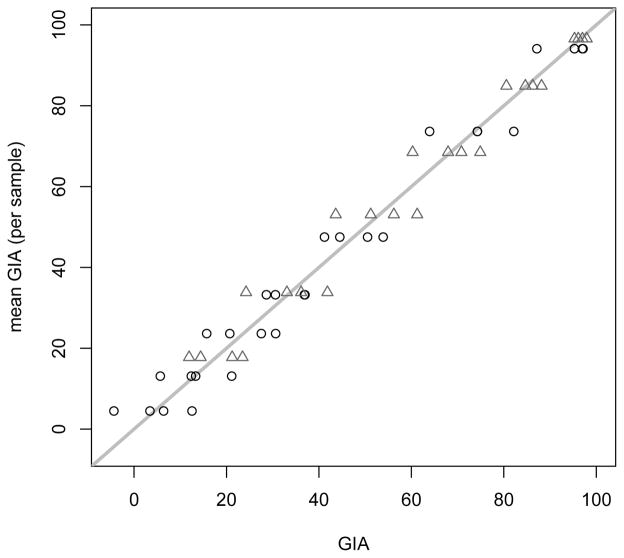
In Figure 1 we plot the mean of the 4 replicates for each sample by its 4 GIA measurements. The constant standard deviation model on the GIA appears reasonable except for very large values of mean GIA (above about 80% the variance looks smaller). Because complete inhibition will give GIA values of 100% with no variation, it is reasonable to expect that very large values of the GIA will have smaller variation. For the puposes of this illustration, assume that the validation procedure was planned only for the data in the range with mean GIA < 80%. For these examples, we use the m: n : 90% procedures, but the m:n:80% ones could have also been used.

Figure 1.

Plot of individual GIA values from each sample by the mean GIA for each sample, for both 3D7 (gray triangles) and FVO (black circles). Line is line of equality.

We start with the 3D7 GIA assays. The range with mean GIA < 80% leaves us with m = 4 levels for testing. We run a 4 : 4 : 90% procedure with a constant normal variance model, so we calculate confidence intervals for σ at the one-sided 1 − (.10)^1/4 = 1 − 0.5623 level. These are given as σ̄_j(0.4377) in Table 5. Although 0.4377 < 0.50, the upper limit σ̄_j(0.4377) is greater than the sample standard deviation because in this case $(n-1)/W_{n-1}^{-1}(0.5623)=1.105>1$ (see equation S2). Although, 0.4377 seems like a strange level for the individual upper limits, it allows us to take the maximum as a 90% confidence limit under constant SD, so that σ̄(.90) = 7.9. We say that between the GIA values of about 18 and 68, the assay passes the 4:4:90 precision validation procedure with a bound of 7.9, and observed GIA values post-validation, y = y(x^*), can be expressed as y ± 7.9. Although the effective standard deviation was calculated without using the values with mean GIA > 80%, since the variance of those values are biologically expected to be less, we can practically extend the range of the precision up to 100%.

Table 5.

4:4:90% procedure on GIA (3D7 strain).

sample	mean(GIA)	sd(GIA)	σ̄j(0.4377)
3D7.2049	17.8	5.48	5.76
3D7.4098	33.8	7.35	7.73
3D7.8196	53.1	7.52	7.90
3D7.16393	68.5	6.18	6.49

Now consider the FVO assays. Again, we consider only the range with mean GIA < 80%. This leaves us with m = 6 levels for testing. We run a 6 : 4 : 90 constant normal SD procedure, so we calculate confidence intervals for σ at the one-sided 1 − (.10)^1/6 = 1 − 0.6813 level under constant SD. These are given as σ̄_j(0.3187) in Table 6. In this case, $(n-1)/W_{n-1}^{-1}(0.6813)=0.853<1$, so that the upper limit of σ is less than its estimate. This choice of confidence level for each sample allows their maximum to be σ̄(0.90) = 6.9. For GIA values between about 5 and 74 the assay passes the 6 : 4 : 90 precision validation procedure with a bound of 6.9, and observed post-validation GIA values, y = y(x^*), can be expressed as y ± 6.9. As for the 3d7, we can practically extend the range of the precision up to 100%.

Table 6.

6:4:90% procedure on GIA (fvo strain).

sample	mean(GIA)	sd(GIA)	σ̄j(0.3187)
FVO.1760	4.5	7.02	6.49
FVO.3520	13.1	6.33	5.84
FVO.7040	23.7	6.72	6.21
FVO.14079	33.3	4.29	3.96
FVO.28158	47.5	5.73	5.30
FVO.56317	73.7	7.47	6.90

The precision bounds of less than 10% (7.9 for 3D7 and 6.9 for FVO) are considered to be acceptable for this type of biological assay, which is used to study the properties of antibodies in preclinical and and clinical vaccine development.

10 Discussion

We have reframed the m: n : θ_b precision validation procedures on constant coefficient of variation models as a series of hypothesis tests over m levels. By reframing the problem this way, we accomplish several goals. First, we highlight the assumptions that are implicit in the usual m:n:θ_b procedure and give some statistical properties of the usual procedure. Specifically, without approximate equality of CV across the m levels, it is possible to have greater than 50% chance of passing the usual m: n : θ_b procedure when the true CV on at least one level is larger than the bound. However, with constant CV, the probability of passing some standard m: n : θ_b procedures when the true CV is equal to the bound θ_b is closer to 10% or 20%. Second, by attaching a statistical model to the procedure, we can show that the maximum of the CV estimates can be interpreted as an upper confidence limit under the constant CV assumption across the m levels. For example, that maximum has confidence level of about 79% for standard 3:5:θ_b procedures and of about 89% for the 4 : 6 : 20% procedure (see Table 1). Third, the reframing of the procedure allowed it to be applied to assays that have constant standard deviation. The new nomenclature is m:n: q where q is the level of the upper limit under constant precision. Assuming that either the standard deviation or the coefficient of variation is fixed and equal for all m levels tested, we have shown how to create a one-sided upper confidence limit on the standard deviation, σ̄(q), or on the CV, θ̄(q), based on the maximum of the upper confidence limits at each level. We showed that after the validation procedure, the subsequent output from a sample can be listed as y ± σ̄(q) (for the constant standard deviation model) or log(y)±r(θ̄(q), 0.6827) or log(y)±r_G(θ̄(q), 0.6827) (for the constant coefficient of variation model), and those intervals have at least 68.27% coverage on μ, log(μ), or log(μ_G) when the m:n: q procedure has values similar to 3 : 5 : 80% or 4 : 6 : 90%. When there are moderate departures from the constant precision assumption the post-validation covearge is still greater than 68.27%, although the coverage for σ̄(q) or θ̄(q) is less than q. Additionally, we only expect the parametric assumptions to hold approximately in practice, so we accept slightly conservative standard deviation intervals to adjust for possible misspecification. Finally, since our procedure is based on upper confidence limits, it will automatically adjust as the replication size (n) changes.

The methods in this paper assume that given a sample x, the n replicates are independent. We also assume that the replicates for different samples are not batched together. Other assay designs not covered here are when a normalizing control is shared between many samples. Further work is needed to deal with designs such as this.

In summary, this paper develops a statistical formalism to address two main shortcomings of current precision validation method. First, we reframe and generalize the standard precision validation method to be applicable not just to a standard constant coefficient of variation model, but also to a constant standard deviation model. Second, we develop precision statistics for routine use with the assay after the validation procedure is completed.

We developed the R package testassay to perform the methods of this paper (see Supplementary Material).