Modeling the depth-sectioning effect in reflection-mode dynamic speckle-field interferometric microscopy

Abstract

Unlike most optical coherence microscopy (OCM) systems, dynamic speckle-field interferometric microscopy (DSIM) achieves depth sectioning through the spatial-coherence gating effect. Under high numerical aperture (NA) speckle-field illumination, our previous experiments have demonstrated less than 1 μm depth resolution in reflection-mode DSIM, while doubling the diffraction limited resolution as under structured illumination. However, there has not been a physical model to rigorously describe the speckle imaging process, in particular explaining the sectioning effect under high illumination and imaging NA settings in DSIM. In this paper, we develop such a model based on the diffraction tomography theory and the speckle statistics. Using this model, we calculate the system response function, which is used to further obtain the depth resolution limit in reflection-mode DSIM. Theoretically calculated depth resolution limit is in an excellent agreement with experiment results. We envision that our physical model will not only help in understanding the imaging process in DSIM, but also enable better designing such systems for depth-resolved measurements in biological cells and tissues.

1. Introduction

Depth selectivity, or the so-called sectioning effect, is important in optical imaging of microscopic objects that have complex 3D features [1–3]. Over the years, many depth-resolved optical microscopy techniques have been proposed including scanning confocal microscopy (SCM) [4,5], structured-illumination microscopy [6,7], two-photon fluorescence microscopy [8,9], light sheet microscopy [10,11], optical coherence tomography (OCT) [12,13], and optical diffraction tomography (ODT) [14,15]. Among these methods, SCM is the most widely implemented microscopy technique. Furthermore, C. J. R. Sheppard and his colleagues have pioneered the development of 3D coherent transfer function (CTF) method to help understand the optical sectioning effect in SCM systems [16,17].

Interferometric microscopy offers extreme sensitivity in measuring sample deformation or absorption along the axial dimension without using fluorescence staining [18–22]. In an interferometric microscopy system, the sectioning effect can be realized via either the spatial- or the temporal-coherence property of light under wide-field imaging mode. OCT, as an interferometric imaging technique, normally uses the temporal-coherence gating effect to achieve depth resolved measurements [13]. Its depth resolution is typically a few microns, which is mainly determined by the bandwidth or the temporal coherence of the light source used. Similarly, the spatial-coherence gating effect has also been utilized in interferometric microscopy to obtain depth-resolved measurements [23]. B. Redding et al. reported a full-field interferometric confocal imaging method, where the spatial coherence was manipulated by using a multimode fiber [24]. The measured spatial resolution however was limited to a few microns. Soon after, Y. Choi et al. demonstrated a reflection-mode dynamic speckle-field quantitative phase microscopy system with ~500 nm lateral resolution and ~1 micron depth resolution [25]. This type of system is promising in studying the nanoscale dynamics of depth-resolved structures such plasma and nucleic membranes in complex eukaryotic cells. If applied to 3D imaging, this reflection phase imaging system can potentially solve the “missing cone” problem during image reconstruction, which otherwise requires priori constraints, such as the non-negativity and piecewise smoothness for convergence [26,27].

Despite of the recent experimental advances in depth-resolved interferometric imaging using dynamic speckle-fields, there has not been a full physical model to describe the sectioning effect in such systems [23]. Most of the previous theoretical analysis of depth resolution was based on small scattering angle approximations or paraxial approximations, including the SCM transfer function calculations [16,17], where the diffraction effects that potentially degrade the image reconstruction quality in high NA imaging are not fully accounted for. Later on, C. J. R. Sheppard’s group has also calculated the 3D CTF for high NA imaging conditions for holographic tomography [28]. Recently, through solving the inverse scattering problem with the diffraction tomography theory, accurate 3D CTF has been obtained for low temporal-coherence interferometric tomography systems, which enabled more precise 3D reconstruction with improved spatial resolution in all dimensions for tissue [29,30] and cellular imaging [31–33]. This highlights the importance of including the diffraction effects in coherent imaging.

In this paper, we have extended the diffraction tomography theory to dynamic speckle-field interferometric microscopy or DSIM. We have successfully developed a model to calculate the axial response function in reflection-mode DSIM systems, which can be used to determine the depth resolution. The theoretically calculated depth resolution agrees well with our previous experimental results [25]. In the following, a full description of the physical model is provided. First of all, we describe a typical reflection-mode DSIM system, including the light scattering process, the interference fields, and the detection measurement function. Then, we solve the scattered field from the inhomogeneous wave equation to calculate the cross-correlation function, which is directly related to the measurement quantity. Finally, we calculate the axial response function of a thin 2D slice to obtain the depth resolution. Our study shows that the depth resolution is proportional to the square of the NA of the illumination and imaging objective. In the discussion section, we also verify that transmission-mode DSIM systems do not have sectioning effects for flat objects.

2. Reflection-mode dynamic speckle-field interferometric microscopy

In this section, we first describe the working principle of a typical reflection-mode DSIM system. Then, we solve the backward scattered field for an arbitrary object to determine the measurement function on the detector plane. This lays the foundation for calculating the axial response function and the depth resolution.

2.1 System configuration and working principle

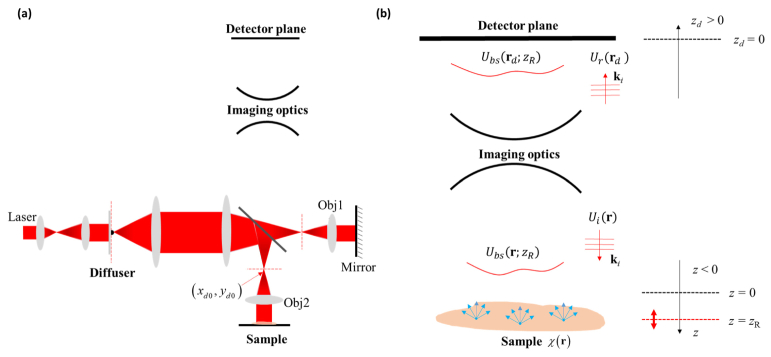
Typically, a Linnik-type interferometer is used in a reflection-mode DSIM system. Figure 1(a) shows the schematic of such a system (more details can be found in [23,25]). The field of interest starts from the diffuser plane, consisting of a disk shape ground glass, which is conjugated to the back focal planes of the reference arm objective (Obj1) as well as that of the imaging arm objective (Obj2). The sample surface, reference mirror, and the detector are also in conjugate planes through imaging optics. When the diffuser rotates at a high-speed (this allows for sufficient averaging of speckles during the camera integration time), the generated dynamic speckle-field forms a smooth distribution in the objective back aperture planes. According to our following theoretical model, it would be ideal for this field distribution to uniformly fill up the back aperture of Obj1 and Obj2 to achieve the optimum illumination with the best sectioning effect. Next, we describe the fields that are involved in the imaging process as described in Fig. 1(b).

Fig. 1.

Illustration of reflection-mode DSIM. (a) The system configuration of a reflection-mode DSIM based on a Linnik-type interferometer; (b) A description of the electromagnetic fields involved in the imaging system.

In our imaging system, the diffuser is in the Fourier plane where the speckle field is generated. Following the theory framework in [23], we assume that the speckle-field, immediately after the diffuser plane, has an angular spectrum distribution, $S\left(k_{xi},k_{yi}\right),$ where $\left(k_{xi},k_{yi}\right)$ is the wavevector. For simplicity, we assume a 1:1 4f relay system between the diffuser plane and the back focal planes (or the back aperture planes) of Obj1 and Obj2. Thus, the speckle angular distribution at the back aperture planes is still $S\left(k_{xi},k_{yi}\right).$ A particular wavevector $\left(k_{xi},k_{yi}\right),$ corresponding to a physical point on the back focal plane of Obj1 at $\left(x_{d0},y_{d0}\right)=\left(f{\lambda }_0{k}_{xi}/2\pi ,f{\lambda }_0{k}_{yi}/2\pi \right)$ where f is the focal length of the objective and ${\lambda }_0$ is the laser wavelength in free space, generates an incident plane wave, $U_i\left(r\right),$in the sample space as shown in Fig. 1(b), given by

$$U_i\left(r\right)=S\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}x+k_{zi}z\right)},$$ (1)

where $\left|k_i\right|=\sqrt{k_{xi}^2+k_{yi}^2+k_{zi}^2}=\overline{n}{\beta }_0=\beta$ from the dispersion relation (due to the fact that the incident field satisfies the homogeneous wave equation), ${\beta }_0={2\pi /\lambda }_0$ is the propagation constant in free space, $\overline{n}$ is the medium refractive index, $\beta$ is the propagation constant in the medium, and $r=\left(x,y,z\right)$ is the position vector. The plane wave illuminates the sample, described by the scattering potential $\chi \left(r\right)=n^2\left(x,y,z\right)-{\overline{n}}^2$ where $n\left(x,y,z\right)$ is the sample refractive index distribution. As a result, a backward scattered field, is generated. To obtain the depth-resolved measurements, the sample needs to be scanned along the axial direction around the focal plane. Assuming the sample focal displacement is $z_R,$ the backward scattered field in the sample and detector space is denoted by $U_{bs}\left(r;z_R\right)$ and respectively, (where$r_d=\left(x_d,y_d,z_d\right)$). On the detector plane, there is also a plane wave component, $U_r\left(r_d\right),$ coming from the reference arm, which has a form similar to that of the incident field,

$$U_r\left(r_d\right)=S\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}{x}_d+k_{yi}{y}_d+k_{yi}{z}_d\right)}.$$ (2)

The backscattered sample and the reference fields interfere at the detector plane, creating an intensity distribution. From the measured intensity, we obtain $2\text{Re}\left\{{\Gamma }_{12}\left(r_d;z_R\right)\right\}=2\text{Re}\left\{U_{bs}\left(r_d;z_R\right)U_r^{*}\left(r_d\right)\right\},$ which is the real part of the cross-correlation function for each $z_R$. In this paper, we are interested in modeling the physical imaging process, thus, we need to fully describe the cross-correlation function, which requires solving the sample scattered field.

2.2 Solving the backward scattered field

The sample scattered field can be described by the inhomogeneous wave equation [14]:

$${\nabla }^2{U}_s\left(r\right)+{\beta }^2{U}_s\left(r\right)=-{\beta }_o^2\chi \left(r\right)U\left(r\right),$$ (3)

where $U\left(r\right)$ is the total driving field which consists of both the incident and the scattered fields, $U\left(r\right)=U_i\left(r\right)+U_s\left(r\right).$ Under the first-order Born approximation, we have $U\left(r\right)\approx U_i\left(r\right)$ that allows us to solve the backward scattered field, denoted as $U_{bs},$ in the z > 0 sample space, for different sample focal displacement as (refer to the Appendix for the derivation)

$$U_{bs}\left(k_{\perp },z;z_R\right)=-\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{-iq\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},-q-k_{zi}\right).$$ (4)

where $k_{\perp }=\left(k_x,k_y\right)$is the Fourier transform variable with respect to $r_{\perp }=\left(x,y\right)$ and $q=\sqrt{{\beta }^2-k_x^2-k_y^2}$is the scattered field axial projection ($k_x$ and $k_y$ have units of m⁻¹). Notice that for simplicity, we will use the same representation for a physical parameter in different spaces by carrying the variables throughout this paper. For example, in Eq. (4) $\chi$ is in the 3D Fourier transform space as evidenced from its variables. The imaging condition ensures that the field at z = 0 (defined at the sample surface) is conjugated with the camera detector plane, z_d = 0. Therefore,

$$U_{bs}\left(k_{d\perp },z_d=0;z_R\right)=-\frac{{\beta }_o^{2}S\left(k_{xi},k_{yi}\right)P\left(k_x,k_y\right)e^{i\left(q+k_{zi}\right)z_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},-q-k_{zi}\right),$$ (5)

where $k_{d\perp }=\left(k_{dx},k_{dy}\right)$ is the Fourier transform variable of the transverse detector coordinate $\left(x_d,y_d\right).$ $\left(x_d,y_d\right)$ and $\left(x,y\right)$ are related through a magnification M, i.e., $\left(x_d,y_d\right)=\left(Mx,My\right)$ and $\left(k_{dx},k_{dy}\right)=\left(k_x/M,k_y/M\right).$ In Eq. (5), the aperture function $P\left(k_x,k_y\right)$ has been introduced, which defines the spatial frequency bandwidth limited by the objective numerical aperture. Next, the scattered field solution will be used to calculate the cross-correlation function to obtain the system response function.

3. System response function

In this section, we will calculate the axial response function in reflection-mode DSIM. First, we calculate the scattered field from a thin step phase object. Then, we calculate the cross-correlating function ${\Gamma }_{12}$ by considering the speckle statistics.

3.1 Thin step object response

A homogeneous thin object, as described in Fig. 2, is used as the sample to calculate the axial response function. The one-dimensional object has an infinite lateral dimensions and an axial width of z_o, thus, its scattering potential can be described with a rectangle function in z as $\chi \left(x,y,z\right)=rect\left(z/z_0\right)$ (the constant part of the scattering potential has been ignored, as it does not contribute to the axial response calculation). The 3D Fourier transform of this scattering potential is

$$\chi \left(k_x,k_y,k_z\right)=\delta \left(k_x\right)\delta \left(k_y\right)\text{sin c}\left(k_z{z}_0\right).$$ (6)

Substituting the above expression into Eq. (5), we obtain the backward scattered field in the sample space as,

$$\begin{array}{c}{U}_{bs}\left(k_x,k_y,z;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_x,k_y\right)e^{-i\sqrt{{\beta }^2-k_x^2-k_y^2}\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2q}\times \\ \delta \left(k_x-k_{xi}\right)\delta \left(k_y-k_{yi}\right)\text{sin c}\left[\left(\sqrt{{\beta }^2-k_x^2-k_y^2}+k_{zi}\right)z_0\right].\end{array}$$ (7)

Next, we take a 2D inverse Fourier transform of Eq. (7) over $\left(k_x,k_y\right)$ . This Fourier transform integral can be directly evaluated by using the delta function property, i.e., $U_{bs}\left(x,y,z;z_R\right)=U_{bs}\left(k_x=k_{xi},k_y=k_{yi},z;z_R\right).$ Hence,

$$\begin{array}{c}{U}_{bs}\left(x,y,z;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{-i\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}}\times \\ \text{sin c}\left[\left(\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}+k_{zi}\right)z_0\right].\end{array}$$ (8)

The dispersion relation of the incident field makes $k_{zi}=\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}.$ Then, Eq. (8) is simplified as,

$$U_{bs}\left(x,y,z;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{-i{k}_{zi}\left(z-2z_R\right)}}{2k_{zi}}\text{sin c}\left(2k_{zi}{z}_0\right).$$ (9)

If $z_0$ is very small, such that $k_{zi}{z}_0\approx 0$ and $\text{sinc}\left(2k_{zi}{z}_0\right)\approx 1$, the scattered field becomes

$$U_{bs}\left(x,y,z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{-i{k}_{zi}z}{e}^{i{k}_{zi}\left(2z_R\right)}}{2k_{zi}}.$$ (10)

At the detector plane, we have

$$U_{bs}\left(x_d,y_d,z_d=0\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{i{k}_{zi}\left(2z_R\right)}}{2k_{zi}}.$$ (11)

Equation (11) is the backward scattering field solution, where the phase term $e^{i{k}_{zi}\left(2z_R\right)}$ signifies the double path of the field in the sample. Interestingly, in transmission-mode operation, the forward scattered field does not have a $z_R$ dependent phase term, indicating that it will not be able to provide the sectioning effect for flat objects (see more details in the discussion part).

Fig. 2.

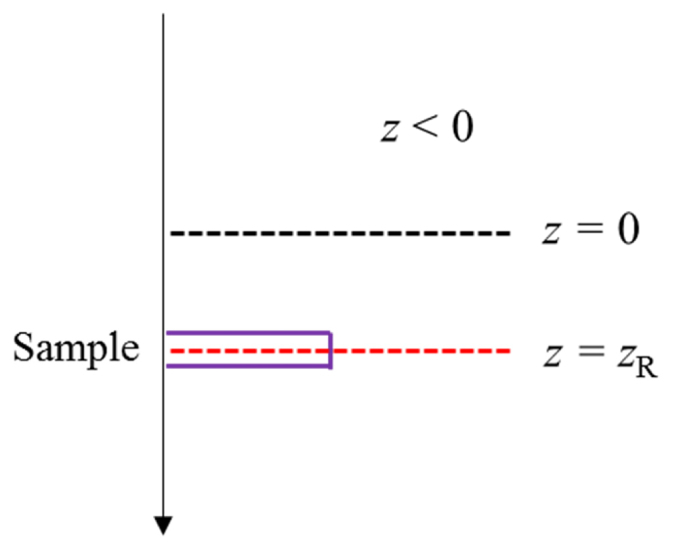
Illustration of a thin step phase object, defined by a rectangle function.

3.2 Speckle-field statistics

Next, we calculate the correlation function while considering the speckle-field statistics. The speckle-field angular spectrum distribution $S\left(k_{xi},k_{yi}\right)$ is a complex function, which can be written as

$$S\left(k_{xi},k_{yi}\right)=\left|S\left(k_{xi},k_{yi}\right)\right|e^{i\phi \left(k_{xi},k_{yi}\right)}=\frac{1}{N^2}A\left(k_{xi},k_{yi}\right)e^{i\phi \left(k_{xi},k_{yi}\right)},$$ (12)

where N² is the number of independent scattering areas. The distributions of $A\left(k_{xi},k_{yi}\right)$ and $\phi \left(k_{xi},k_{yi}\right)$ have the following statistical properties (see Goodman [34]): each of the amplitude and phase elements are statistically independent of each other (i.e., the scattering area elements are unrelated and the strength of a given scattered component bears no relation to its phase); the phase values are uniformly distributed in the primary interval (-π, π). The detector measurement obtains the real part of the cross-correlation function ${\Gamma }_{12}$ between the sample backward scattered field and the reference field, i.e., $2\text{Re}\left({\Gamma }_{12}\right)$, which includes all the speckle wavevector contributions weighted by the distribution function$S\left(k_{xi},k_{yi}\right)$. Therefore, $2\text{Re}\left({\Gamma }_{12}\right)$is a summation of all possible individual correlation pairs $U_{bs}\left(k_{xi},k_{yi}\right)U_r^{*}\left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right),$,

$$2\text{Re}\left({\Gamma }_{12}\right)=2\text{Re}\left(U_{bs}{U}_r^{*}\right)=2\text{Re}\left\{\left[{\displaystyle \sum _{k_{xi},k_{yi}}{U}_{bs}\left(k_{xi},k_{yi}\right)}\right]\left[{\displaystyle \sum _{k_{xi}^{\text{'}},k_{yi}^{\text{'}}}{U}_r^{*}\left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right)}\right]\right\}.$$ (13)

In the above equation, we have changed the notation of $U_{bs}\left(x_d,y_d,z_d=0\right)$ and $U_r\left(x_d,y_d,z_d=0\right)$ to $U_{bs}\left(k_{xi},k_{yi}\right)$ and $U_r\left(k_{xi},k_{yi}\right)$ to make the mathematical operation clearer. With the solution of $U_{bs}$ and $U_r$ given in Eq. (2) and Eq. (11), we can write down the exact form of $2\text{Re}\left({\Gamma }_{12}\right),$ that is

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \sum _{k_{xi},k_{yi}}\left\{{\displaystyle \sum _{k_{xi}^{\text{'}},k_{yi}^{\text{'}}}\frac{1}{k_{zi}}A\left(k_{xi},k_{yi}\right)A\left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right)\text{cos}\left[\left(k_{xi}-k_{xi}^{\text{'}}\right)x+\left(k_{yi}-k_{yi}^{\text{'}}\right)y+k_{zi}\left(2z_R\right)+\Delta \phi \right]}\right\}}.$$ (14)

where $\Delta \phi =\phi \left(k_{xi},k_{yi}\right)-\phi \left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right).$. Using trigonometric identities, we can write $2\text{Re}\left({\Gamma }_{12}\right)$ as

$$\begin{array}{c}2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \sum _{k_{xi},k_{yi}}{\displaystyle \sum _{k_{xi}^{\text{'}},k_{yi}^{\text{'}}}\frac{1}{k_{zi}}A\left(k_{xi},k_{yi}\right)A\left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right)}\text{cos}\left[\left(k_{xi}-k_{xi}^{\text{'}}\right)x+\left(k_{yi}-k_{yi}^{\text{'}}\right)y+2k_{zi}{z}_R\right]\text{cos}\left(\Delta \phi \right)}\\ -{\displaystyle \sum _{k_{xi},k_{yi}}{\displaystyle \sum _{k_{xi}^{\text{'}},k_{yi}^{\text{'}}}\frac{1}{k_{zi}}A\left(k_{xi},k_{yi}\right)A\left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right)}\text{sin}\left[\left(k_{xi}-k_{xi}^{\text{'}}\right)x+\left(k_{yi}-k_{yi}^{\text{'}}\right)y+2k_{zi}{z}_R\right]\text{sin}\left(\Delta \phi \right).}\end{array}$$ (15)

Furthermore, $2\text{Re}\left({\Gamma }_{12}\right)$ can be break into two parts, one is the matched speckle term ($k_{xi}=k_{xi}^{\text{'}},k_{yi}=k_{yi}^{\text{'}}$) whereas the other is the unmatched term ($k_{xi}\ne k_{xi}^{\text{'}}$ or $k_{yi}\ne k_{yi}^{\text{'}}$). Since the probability distribution of $\phi \left(k_{xi},k_{yi}\right)$ and $\phi \left(k_{xi}^{\text{'}},k_{yi}^{\text{'}}\right)$ is uniform, their difference $\Delta \phi$ will also statistically have a uniform distribution in the interval (−2π, 2π). If we take the ensemble average of many speckle patterns, due to rotation of the diffuser that produces uncorrelated speckle patterns, the unmatched correlation terms reduce to zero. Therefore, only the matched terms survive, leaving

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {〈{\displaystyle \sum _{k_{xi},k_{yi}}{A}^2\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)}\frac{\text{cos}\left(2k_{zi}{z}_R\right)}{k_{zi}}〉}_M.$$ (16)

where ${〈〉}_M$ denotes the ensemble average over M distributions. When M is very large, this ensemble average will make a smooth distribution for $A^2\left(k_{xi},k_{yi}\right),$ which is also called the original speckle spectral distribution $T_0\left(k_{xi},k_{yi}\right)$ such that $T_0\left(k_{xi},k_{yi}\right)=A^2\left(k_{xi},k_{yi}\right).$ Note that $T_0\left(k_{xi},k_{yi}\right)$ is also band-limited by the objective aperture function $P\left(k_{xi},k_{yi}\right)$, since the illumination and imaging paths share the same objective lens in the reflection DSIM system. For this reason, we replace the term $A^2\left(k_{xi},k_{yi}\right)$ with $T_0\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)$ in Eq. (16).

3.3 The axial response function

In order to calculate the axial response function, the solution of $2\text{Re}\left({\Gamma }_{12}\right)$ in Eq. (16) is converted into an integral form as below,

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \iint T_0\left(k_{xi},k_{yi}\right)P^2\left(k_{xi},k_{yi}\right)}\frac{\text{cos}\left(2\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}{z}_R\right)}{\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}}d{k}_{xi}d{k}_{yi}.$$ (17)

It is always desired that $T_0\left(k_{xi},k_{yi}\right)$ is uniform within the objective back aperture area for the best depth selectivity. There are many ways to achieve this goal, such as magnifying this distribution with an additional 4f system [25]. For the best sectioning effect, $T_0\left(k_{xi},k_{yi}\right)$ is assumed to be a uniform distribution and $P\left(k_{xi},k_{yi}\right)$ is assumed to be a circular disk function. Thus, $P^2\left(k_{xi},k_{yi}\right)$ will still be a circular disk function that has the same distribution as the radius of the disk is determined by the numerical aperture of the objective. By denoting $k_{xi}=k_r\text{cos}\varphi$ and $k_{yi}=k_r\text{sin}\varphi ,$ the integral in Eq. (17) is converted into the polar coordinates as below,

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \iint P\left(k_r\text{cos}\varphi ,k_r\text{sin}\varphi \right)}\frac{\text{cos}\left(2\sqrt{{\beta }^2-k_r^2}{z}_R\right)}{\sqrt{{\beta }^2-k_r^2}}d{k}_r{d}_{\varphi }.$$ (18)

The range of $k_r$ is limited by the objective numerical aperture through $P\left(k_r\text{cos}\varphi ,k_r\text{sin}\varphi \right)$ to $\left[0,N{A}_{obj}\left(2\pi /{\lambda }_0\right)\right]=\left[0,\left(2\pi \overline{n}/{\lambda }_0\right)\text{sin}\left({\theta }_{\text{max}}\right)\right]=\left[0,\beta \text{sin}\left({\theta }_{\text{max}}\right)\right]$. The integral in $\varphi$ can be dropped out as the function in the integral is circularly symmetric, giving

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \underset{0}{\overset{\beta \text{sin}{\theta }_{\text{max}}}{\int }}\frac{\text{cos}\left(2\sqrt{{\beta }^2-k_r^2}{z}_R\right)}{\sqrt{{\beta }^2-k_r^2}}{k}_r}d{k}_r.$$ (19)

With a variable change, $K=\sqrt{{\beta }^2-k_r^2},$ and $KdK=-k_{r}d{k}_r,$ Eq. (19) becomes

$$2\text{Re}\left({\Gamma }_{12}\right)\propto {\displaystyle \underset{\beta \text{cos}\left({\theta }_{\text{max}}\right)}{\overset{\beta }{\int }}\text{cos}\left(2K{z}_R\right)}dK$$ (20)

The above integral can be easily evaluated to give an analytical solution as

$$2\text{Re}\left({\Gamma }_{12}\right)\propto \beta [\text{sin c}\left(2\beta z_R/\pi \right)-\text{cos}\left({\theta }_{\text{max}}\right)\text{sin c}\left(2\beta \text{cos}\left({\theta }_{\text{max}}\right)z_R/\pi \right)],$$ (21)

where the sinc function is defined as: $\text{sinc}\left(x\right)=\text{sin}\left(\pi x\right)/\pi x.$

The above framework establishes a mathematical model that describes the axial response of the reflection-mode DSIM system: if we know the objective numerical aperture, the illumination wavelength, we can compute $2\text{Re}\left({\Gamma }_{12}\right)$ as a function of $z_R$ to obtain the axial response function in DSIM. Finally, with the axial response function, the depth resolution can also be determined.

4. Depth resolution

In this section, the axial response function model is tested using the specifications from an experimental system, and this model is subsequently used to quantify the sectioning effect in terms of depth resolution. For this study, we use the parameters from our previous experiment [25], which also provides a way to validate our theoretical model. In that reflection-mode DSIM system, the laser wavelength is ${\lambda }_0=0.8$ μm, the sample host medium is water with refractive index $\overline{n}=1.33,$ and two water immersion objectives are used with $N{A}_{obj}=1.$ Inserting these parameters into Eq. (21), we obtain the axial response function as shown in Fig. 3, where the solid black curve is the axial response function, i.e., $2\text{Re}\left({\Gamma }_{12}\right)$ vs. different defocus positions $z_R.$ The dashed red curve is the envelope function, from which the first zero is determined to be around $z_R=0.89$μm, and the half maximum value is found to be around $z_R=0.53$ μm. The depth resolution, $\delta z,$ is defined as the full-width half maximum (FWHM) value which is 1.06 μm, which is in a good agreement with our previous study [25].

Fig. 3.

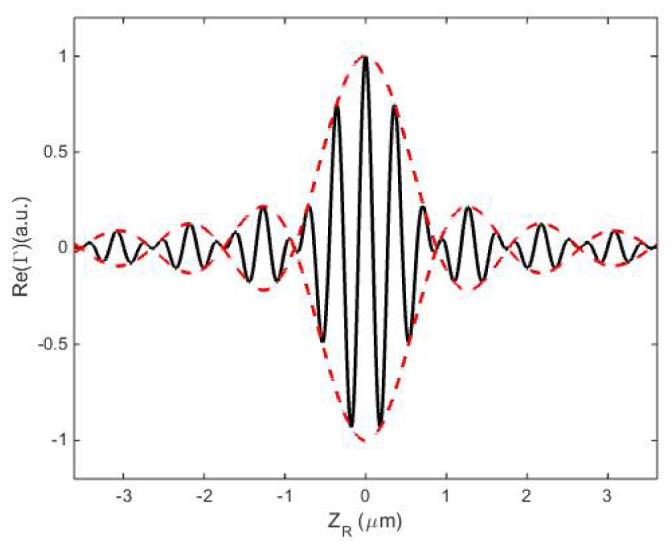
Axial response function with $N{A}_{obj}=1.$ The axial response function is obtained by calculating $2\text{Re}\left({\Gamma }_{12}\right)$ at different defocus position $z_R$.

Next, we study the relationship between the depth resolution and the objective numerical aperture. The depth resolution values are obtained for various $N{A}_{obj}$ ranging from 0.6 to 1.2 with 0.1 intervals. In Fig. 4, the depth resolution $\delta z$ is plotted as a function of $N{A}_{obj}$ in black square markers. Curve fitting shows a $1/N{A}_{obj}^2$trend over the plotted data range; the solid red line is described by $\delta z=1.315/N{A}_{obj}^2-0.262.$ This fitting result is expected as depth resolution normally degrades with $1/N{A}_{obj}^2$ in coherent microscopy. Therefore, in a reflection-mode DSIM system the higher the numerical aperture, the better the depth resolution. According to this calculation, at $N{A}_{obj}=1.2$ a depth resolution as small as 0.65 μm can be achieved. It should be noted that in order to get the best depth resolution, a uniform speckle spectral distribution over the whole back aperture area of the high numerical aperture objective is necessary.

Fig. 4.

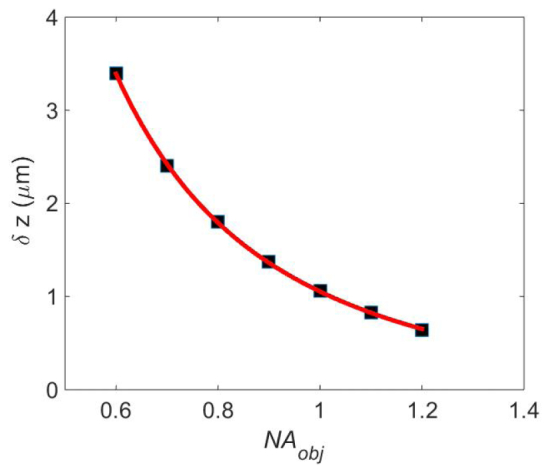
Relationship between depth resolution $\delta z$ (vertical axis) and objective numerical aperture $N{A}_{obj}$ (horizontal axis).

5. Discussion

We have developed a physical model to precisely describe the sectioning effect in a reflection-mode speckle-field illumination interferometric system. The sectioning effect comes from the spatially incoherent illumination. It is also possible to use a broadband source in such a system to further enhance the depth selectivity. However, it is not clear how much depth selectivity can be enhanced with this addition. In principle, this theoretical framework can be extended to incorporate temporal coherence to answer this interesting question. We note that frameworks considering temporal coherence have been reported for transmission case in earlier publications [31,32]. Another important question is whether transmission-mode DSIM can provide sectioning effect. In order to answer this, we calculate the forward scattered field using Eq. (33b) in the Appendix for the same step object described in Section 3. The field is given as

$$\begin{array}{c}{U}_{fs}\left(k_x,k_y,z;z_R\right)=-\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_x,k_y\right)e^{i\sqrt{{\beta }^2-k_x^2-k_y^2}\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2q}\times \hfill \\ \delta \left(k_x-k_{xi}\right)\delta \left(k_y-k_{yi}\right)\text{sinc}\left[\left(\sqrt{{\beta }^2-k_x^2-k_y^2}-k_{zi}\right)z_0\right].\hfill \end{array}$$ (22)

Similarly, we can Fourier transform the field into the spatial domain representation,

$$\begin{array}{c}{U}_{fs}\left(x,y,z;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{i\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}}\times \hfill \\ \text{sinc}\left[\left(\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2}-k_{zi}\right)z_0\right].\hfill \end{array}$$ (23)

The dispersion relation dictates that $k_{zi}=\sqrt{{\beta }^2-k_{xi}^2-k_{yi}^2},$ making

$$\begin{array}{c}{U}_{fs}\left(x,y,z;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{i{k}_{zi}\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2k_{zi}}\text{sinc}\left(0\right)\hfill \\ =\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}{e}^{i{k}_{zi}z}}{2k_{zi}}.\hfill \end{array}$$ (24)

The detector plane $z_d=0$ sees the field at z = 0 plane as

$$U_{fs}\left(x_d,y_d,z_d=0;z_R\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)P\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}y\right)}}{2k_{zi}}.$$ (25)

It turns out that the forward scattered field, as described in Eq. (25), is not a function of $z_R$, thus giving no sectioning effect. Note that the above calculation assumes flat thin objects, with no lateral structures. However, for objects that have lateral features, there will be sectioning as was demonstrated in [36]. The missing axial frequency information in the low transverse region is called the “missing cone” problem in 3D optical imaging. Our following paper will discuss this issue in more details by calculating the 3D CTF in both reflection and transmission-mode DSIM systems.

6. Summary

In conclusion, we have developed a mathematical model to describe the axial response function in reflection-mode dynamic speckle-field interferometric microscopy. This model is based on the diffraction tomography theory and speckle statistics, and provides a spatial correlation function. Using this function, the axial response function is obtained and used to determine the depth resolution. The theoretically calculated depth resolution is in excellent agreement with our experimental results. Using this method, the connection between depth resolution and objective numerical aperture is also studied, which reveals an inverse square law relationship that is also expected. We envision that developed physical model will contribute to the understanding of sectioning effect in spatially incoherent illumination interferometry systems. It can also guide on the design of such systems for better performance in the future.

Appendix: optical diffraction tomography

We start with the inhomogeneous wave equation that describes the scattered field [31,32]:

$${\nabla }^2{U}_s\left(r\right)+{\beta }^2{U}_s\left(r\right)=-{\beta }_o^2\chi \left(r\right)U\left(r\right),$$ (26)

where $U\left(r\right)$ is approximated as $U_i\left(r\right)=S\left(k_{xi},k_{yi}\right)e^{i\left(k_{xi}x+k_{yi}x+k_{zi}z\right)}$. Equation (26) can be solved in the space (or spatial spectrum space) by taking the 3D Fourier transform on both sides, namely

$$\begin{array}{c}\left({\beta }^2-k^2\right)U_s\left(k_x,k_y,k_z\right)=-{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\chi \left(k_x,k_y,k_z\right){ⓥ}_k\delta \left(k_x-k_{xi},k_y-k_{yi},k_z-k_{zi}\right)\hfill \\ =-{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\chi \left(k_x-k_{xi},k_y-k_{yi},k_z-k_{zi}\right),\hfill \end{array}$$ (27)

where $\left(k_x,k_y,k_z\right)$ is the Fourier transform variable of $\left(x,y,z\right)$ and $k^2=k_x^2+k_y^2+k_z^2.$ Assuming the object is centered at $z=z_R,$ i.e., $\chi \left(r_{\perp },z-z_R\right),$ then the above equation can be revised to the following form to incorporate this sample shift:

$$\left({\beta }^2-k^2\right)U_s\left(k_x,k_y,k_z\right)=-{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\chi \left(k_x-k_{xi},k_y-k_{yi},k_z-k_{zi}\right)e^{-i\left(k_z-k_{zi}\right)z_R}.$$ (28)

By re-arranging Eq. (28), the scattered field $U_s\left(k_x,k_y,k_z\right)$ is solved as

$$\begin{array}{c}{U}_s\left(k_x,k_y,k_z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\chi \left(k_x-k_{xi},k_y-k_{yi},k_z-k_{zi}\right)e^{-i\left(k_z-k_{zi}\right)z_R}}{k_z^2-\left({\beta }^2-k_x^2-k_y^2\right)}\hfill \\ =-{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\chi \left(k_x-k_{xi},k_y-k_{yi},k_z-k_{zi}\right)e^{-i\left(k_z-k_{zi}\right)z_R}\frac{1}{2q}\left(\frac{1}{k_z+q}-\frac{1}{k_z-q}\right),\hfill \end{array}$$ (29)

where $q=\sqrt{{\beta }^2-k_x^2-k_y^2}$ (notice that this q is not k_z, because the homogeneous dispersion relation does not apply to the scattered field [35]). The two fractional terms in Eq. (29), 1/(k_z + q) and 1/(k_z - q), correspond to the forward scattered and backward scattered fields, respectively. This can be seen by performing an inverse Fourier transform over Eq. (29) over k_z. The inverse Fourier transform of 1/k_z gives a sign function, sgn(z) (one can also write it as 1-2H(-z) where H(z) is the Heaviside function). We can therefore write

$$\begin{array}{c}{U}_s\left(k_x,k_y,z\right)=-{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)\left[\chi \left(k_x-k_{xi},k_y-k_{yi},z-z_R\right)e^{i{k}_{zi}z}\right]{ⓥ}_z\hfill \\ \frac{1}{2q}\left(sgn\left(z\right)e^{-iqz}-sgn\left(z\right)e^{iqz}\right).\hfill \end{array}$$ (30)

For backward scattering$(z<0)$, we consider the $e^{-iqz}$ term. The backward scattered field, denoted as $U_{bs},$ has the following form

$$U_{bs}\left(k_x,k_y,z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)}{2}\left[\chi \left(k_x-k_{xi},k_y-k_{yi},z-z_R\right)e^{i{k}_{zi}z}\right]{ⓥ}_z\frac{e^{-iqz}}{q}.$$ (31a)

For the forward scattering$(z>0)$, we consider the $e^{iqz}$ term that results in a forward scattered field, denoted as $U_{fs},$ in the form of

$$U_{fs}\left(k_x,k_y,z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)}{2}\left[\chi \left(k_x-k_{xi},k_y-k_{yi},z-z_R\right)e^{i{k}_{zi}z}\right]{ⓥ}_z\frac{e^{iqz}}{q}.$$ (31b)

Next, we write the convolution in z in Eq. (31a) as an integral

$$\begin{array}{c}{U}_{bs}\left(k_x,k_y,z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)}{2q}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left[\chi \left(k_x-k_{xi},k_y-k_{yi},z\text{'}-z_R\right)e^{i{k}_{zi}z\text{'}}\right]}{e}^{-iq\left(z-z\text{'}\right)}dz\text{'}\hfill \\ =\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{-iqz}}{2q}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\chi \left(k_x-k_{xi},k_y-k_{yi},z\text{'}-z_R\right)e^{i\left(q+k_{zi}\right)z\text{'}}}dz\text{'}\hfill \\ =\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{-iqz}}{2q}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\chi \left(k_x-k_{xi},k_y-k_{yi},z-z_R\right)e^{-iWz}}dz.\hfill \end{array}$$ (32)

where $W=-q-k_{zi}.$ The above integral is a Fourier transform over z that turns $\chi$ back to the 3D Fourier transform domain with a phase shift $e^{-iW{z}_R}=e^{i\left(q+k_{zi}\right)},$ which is in addition to the phase term $e^{-iqz},$ giving:

$$\begin{array}{c}{U}_{bs}\left(k_x,k_y,z\right)=-\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{-iqz}{e}^{i\left(q+k_{zi}\right)z_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},-q-k_{zi}\right)\hfill \\ =-\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{-iq\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},-q-k_{zi}\right).\hfill \end{array}$$ (33a)

Following the same derivation, we can write the forward scattered field as:

$$\begin{array}{c}{U}_{fs}\left(k_x,k_y,z\right)=\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{iqz}{e}^{i\left(k_{zi}-q\right)z_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},q-k_{zi}\right)\hfill \\ =\frac{{\beta }_0^{2}S\left(k_{xi},k_{yi}\right)e^{iq\left(z-z_R\right)}{e}^{i{k}_{zi}{z}_R}}{2q}\chi \left(k_x-k_{xi},k_y-k_{yi},q-k_{zi}\right).\hfill \end{array}$$ (33b)

Funding

US National Institute of Health (NIH) grants NIH9P41EB015871-26A1, 1R01HL121386-01A1; the Hamamatsu Corp, and National Research Foundation Singapore through the Singapore MIT Alliance for Research and Technology’s BioSystems and Micromechanics Inter-Disciplinary Research program.